1 Introduction

On August 21, 2017, a MW 3.9 earthquake struck the volcanic island of Ischia (Gulf of Naples, Italy), producing heavy damage and two casualties at Casamicciola (Briseghella et al. 2019), touristic locality famous for thermal baths known to be hit in the XIX century by a series of heavily damaging earthquakes (Cubellis and Luongo 2017; Cubellis et al. 2020), the most devastating of which produced 2300 victims in 1883 (AA.VV. 1998; Carlino et al. 2010). The most recent event is constrained by data acquired by the INGV Italian National Seismic Network, which locate the epicentre below the town of Casamicciola at a depth of ∼1.2 km (D’Auria et al. 2018); strong-motion recordings are also available from the station of Casamicciola (IOCA), the only one in the near-field (the others are on the mainland near Neaples). This station, placed on a class B soil and on a type T1 topographic surface according to the Eurocode 8 classification, exhibited a horizontal peak ground acceleration (PGA) of 0.28 g along the E-W component, 0.19 g in the N-S component and 0.27 g in the vertical component. A comparison between real and code-compliant elastic horizontal response spectra was made by Del Gaudio et al. (2018), who observed that the typical Casamicciola buildings have been subjected to a pseudo-acceleration demand comparable to the one associated to an event with return period of 475 years (10% of exceeding probability in 50 years).

The 2017 earthquake dramatically highlighted the impact that volcano-related seismicity can have on local communities despite the low magnitude of the events. The very shallow hypocentres and the strong attenuation of the ground motion (for Italy, see Lanzano and Luzi 2020) are the main features that, from the macroseismic point of view, determine in volcanic areas high epicentral intensities but relatively small damage areas, in which the intensity varies significantly even over distances of very few kilometres. This condition represents a major issue when dealing with detailed hazard or risk analyses, since in each volcanic zone the attenuation models need to be calibrated specifically. In Italy, the applications to Etna volcano provide a complete case-study, based on original procedures and methodological approaches (Azzaro et al. 2013, 2016, 2017a; D’Amico et al. 2016; Langer et al. 2016; Pessina et al. 2021).

A similar but distinctive situation results for the Neapolitan volcanic district, which presents an extreme variability in the characteristics of the sources and propagation of the seismic energy in the shallow crust (Giudicepietro et al. 2021). As for Ischia, the interest for this peculiar seismotectonic context renewed following the 2017 earthquake, with a number of studies that analyse the most recent seismological and geophysical data in order to constrain better the causative faults of the main historical events (Braun et al. 2018; Calderoni et al. 2019; Trasatti et al. 2019; Cubellis et al. 2020; Nardone et al. 2020; Carlino et al. 2021), and discuss the implications in terms of seismic risk (De Natale et al. 2019; Selva et al. 2019). In this framework, the scarcity of instrumental data recorded at Ischia in the last decades is a matter of fact (D’Auria et al. 2018)—events larger than M 2.5 are totally missing, apart from the 2017 earthquake—and suggests to exploit, as an alternative, the significant intensity dataset available in the historical catalogue.

Evaluating the decay of the macroseismic intensity may therefore be a quick way, although simplified, for obtaining earthquake damage scenarios or assessing seismic hazard at a local scale. The first approaches to the analysis of the intensity attenuation at Ischia were performed by Peruzza (2000) and Azzaro et al. (2006), who found very different attenuation trends compared to the one of the tectonic areas. In particular, the Ischia earthquakes show the highest decay of intensity among the Italian volcanic areas, with a decrease up to 3–4 intensity degrees in just 10 km of distance from the epicentre. However, the macroseismic dataset available at that time for the calibration of the empirical relationships was rather poor, being based on just 1–2 earthquakes, respectively.

Taking advantage of a new macroseismic dataset obtained from the revision of the local earthquake catalogue (Selva et al. 2021), in this paper we tackle the problem of the intensity attenuation at Ischia from both deterministic and probabilistic viewpoints, and propose an application for simulating earthquake scenarios. First, we analyse the decay of the intensity from the source according to an empiric model expressed by a logarithmic regression, then we apply the Bayesian statistics (Rotondi and Zonno 2004) to obtain a probabilistic isotropic attenuation model that better represents the epistemic uncertainty of the macroseismic data. The backward validation of the results is also presented. The probabilistic procedure is finally implemented into a plug-in of QGIS® software to produce seismic scenarios expressed in terms of macroseismic intensity. This application may represent a practical tool not only for preparing emergency plans with an adequate level of accuracy, but also for simulating real-time shake-maps in the framework of the seismic surveillance of this volcanic area.

2 Intensity attenuation in volcanic areas: historical background

In general, the formulation of attenuation laws through empirical models is carried out on large areas, typically at a region or national scale without considering different trends due to particular seismotectonic settings [for Italy, see Gasperini (2001), Albarello and D’Amico (2005), Pasolini et al. (2008a,b) and references herein]. On the other hand, it is widely recognised that the relationships calibrated for tectonic domains cannot be used on volcanoes, characterised by a significantly higher decay responsible for macroseismic effects localised on quite small areas. The use of non-calibrated relationships in volcanic zones produces an excessive overestimation of the intensity expected at a site or, in general, in the spreading of a macroseismic field. This has serious consequences on crucial applications, such as the simulation of earthquake scenarios through ShakeMaps (Michelini et al. 2020) or the quick assessment of damage at an urban scale (Lagomarsino and Giovinazzi 2006; Dolce et al. 2021; and references herein; Pessina et al. 2021).

While the seismic attenuation from instrumental data has been analysed under different perspectives—strong motion (Lanzano and Luzi 2020; Tusa et al. 2020), quality factor Q for P, S and coda waves (Giampiccolo et al. 2021), scattering etc.—the study of the macroseismic intensity attenuation has become, in recent times, essentially hazard-oriented (for Italy, see Albarello and D’Amico 2004; Faccioli and Cauzzi 2006; Gomez-Capera et al. 2020). In a pioneristic study on the regionalisation of the attenuation in Italy, Peruzza (2000) first highlighted the different decay of intensity in some Italian volcanic areas; later, Azzaro et al. (2006) derived specific relationships for all the volcanic districts, finding the highest attenuation trends at Etna and Ischia. Here in particular, ΔI (the difference between the epicentral intensity I0 and the intensities observed at a site IS) reaches 4–5 degrees in 20 km of distance from the epicentre, under the assumption of an isotropic model of attenuation (i.e. point source, symmetric decay). Apart from the uncertainty due to the very few input data, a clear bias in the calculation is introduced by the value (mean) assumed for the hypocentral depth, fixed to 3 km b.s.l according to the determinations available at that time. This value is about twice the one of the 2017 earthquake (D’Auria et al. 2018), that is a not negligible difference for the extremely short distances of Ischia (the island is just 10 km wide in E-W direction).

The probabilistic approach to the analysis of the seismic attenuation in Italy has been developed in order to quantify the intrinsic uncertainty of the decay process (Magri et al. 1994; Rotondi and Zonno 2004; Albarello and D’Amico 2005). In particular, the procedure based on Bayesian statistics proposed by Zonno et al. (2009), was applied to Etna volcano (Azzaro et al. 2013) to estimate the probability distribution of the macroseismic intensity at a site (Iexp) conditioned on I0 and the epicentre-site distance, through a binomial-beta model. Here it was also possible to model the anisotropic effect of the attenuation due to a linear source, made evident from the preferential propagation of intensity (i.e. highest values) along the fault strike and its rapid decrease in the perpendicular direction. Notably in the case of strong earthquakes, the anisotropic model at Etna provides the best results (Rotondi et al. 2016). Unfortunately, the same is not possible for Ischia because of the lack of a direct association earthquake-causative fault based on surface faulting; this information is in part available only for the 2017 event (Nappi et al. 2018, 2021) but the characteristics of intensity distribution on the territory does not allow recognising any anisotropic pattern.

3 Input data

The macroseismic dataset used in this study for the calibration of the attenuation models of Ischia, is taken from Selva et al. (2021), and it is expressed in terms of the Mercalli–Cancani–Sieberg scale (MCS). Through a careful revision of the historical-macroseismic and instrumental seismological data available in the literature, these authors compiled an integrated and homogeneous catalogue of the local seismicity which significantly improves the current version of the Italian parametric earthquake catalogue (hereinafter CPTI15, see Rovida et al. 2022). As for the historical portion of the catalogue, the catalogue by Selva et al. (2021) makes available 16 earthquakes above the damage threshold (I0 > V–VI MCS) (whilst the events in CPTI15 are 12) having a significant number of macroseismic observations referred to the island of Ischia. The epicentral parameters have been calculated following the same procedures adopted in CPTI15 for the volcanic area of Etna (we assume I0 = Imax due to the very shallow depth of the seismic sources) as well as the intensity data, which have been revised and homogenised according to the standard of the Italian macroseismic database (hereinafter DBMI15, see Locati et al. 2022). Note that the 12 degrees MCS scale (Sieberg 1932, see also Musson et al. 2010) is the reference macroseismic scale in the Italian literature about historical seismicity, although other equivalent but more recent scales are also adopted.

For our analysis we use the portion of the catalogue starting from the nineteenth century since for the previous period there are very few and scattered intensity data associated with the most significant earthquakes. In order to limit the uncertainties due to poorly constrained epicentral parameters (epicentre, I0), we consider events having macroseismic fields characterised by a number of intensity data points (Nidp) suitable to model the intensity decay, specifically Nidp ≥ 10 (Table 1). The overall dataset consists of 131 intensity data referred to 4 earthquakes. For the purposes of our analysis, we discard the unconventional macroseismic observations such as “HD, “D”, “F”—generically indicating high damage, damage or felt, respectively—for which the associated uncertainty is significant (Locati et al. 2022), reducing the number of data to 118. Moreover, in the probabilistic model the value of IS expressed with an intensity range (e.g. VII-VIII) is assumed as being of lower degree; such a choice is due to the assumption that ΔI is a discrete variable (see chapt. 4.2).

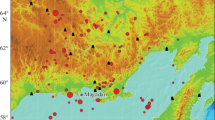
Table 1 Dataset of the earthquakes used in this study, and related parameters (from Selva et al. 2021)
Full size table

Figure 1 shows the locations of the selected earthquakes, which destroyed or severely damaged the northern sector of Ischia. Notably, it is evident the almost uniform distribution on the island of the 54 localities “hosting” 103 intensity data (the other macroseismic observations fall in the far field). Note that the previous analyses by Peruzza (2000) and Azzaro et al. (2006) were based on the very poor macroseismic dataset available at that time in the historical catalogue (namely the 1883 event and the 1881–83 shocks considered, respectively, in the two studies).

Fig. 1
figure 1

Location of the epicentres (red stars) of the 4 earthquakes considered in this study, with the 54 localities (blue dots) represented in the macroseismic observations. a Distribution of the whole intensity dataset as a function of the epicentral distance

Full size image

Finally, Fig. 1a displays the distribution of the intensity dataset as a function of the epicentral distance. It can be observed that most of the macroseismic observations (more than 100 intensity data) are located within 10 km of distance from the source, in practise on the Ischia island whereas only a small part is positioned in the far field (Procida, Pozzuoli and Neaples). This homogeneity on a very short distance allowed a dense sampling of the intensity variation at higher degrees.

4 Attenuation models

The analysis for the computation of the intensity attenuation is performed according to the methodological approaches applied for the volcano-tectonic earthquakes of Etna (Azzaro et al. 2006, 2013). In particular, the attenuation models are estimated both through the classic deterministic approach (empirical relationship), and through a probabilistic procedure that best suits the nature of the macroseismic intensity—which is an ordinal quantity defined on a scale of 12 values—and can also take into account the uncertainty in the decay process.

An element having a significant impact on the computation of the attenuation is the depth from which seismic energy propagates towards a given point on the Earth's surface. Such a factor is of some theoretical importance for the tectonic earthquakes, since the focal depth of the major events (i.e. damaging) may range 8–15 km in Italy. This implies that a part of the seismic shaking is intrinsically attenuated before reaching a site on the surface. On the contrary, in the case of shallow earthquakes occurring in volcanic zones the focal depth is small compared to the epicentre-site distances concerned, that it “virtually” can be considered near-zero.

This is especially true for Ischia, since the instrumental seismicity recorded in the area of Casamicciola Terme—including the zone of the maximum effects of the historical earthquakes—is clustered at a mean depth of about 500 m below sea level (b.s.l.), with the MW 3.9 2017 event located at 1.7 km b.s.l. (D’Auria et al. 2018). Therefore, the analysis of the intensity decay does not take account of the source depth and the epicentral distance can correctly be assumed as the correct parameter to refer to the variation of intensity.

4.1 Deterministic model

The intensity attenuation law has been derived through an empirical model based on a logarithmic regression, according to the methodological approach applied in Azzaro et al. (2006). In Fig. 2, we represent the input dataset of Table 1 plotted as the difference (ΔI) between the epicentral intensity (I0) and the intensity at site (IS) versus the epicentral distance (D). It is evident that data does not show an uniform distribution but are more numerous in the range of distance from 1 to 10 km from the epicentre, see also Fig. 1a. It has to be noted that for short epicentral distances (D < 1 km), ΔI is ca. one degree, so we need to use small bins for short distances and large bins for greater distances. In order to reduce uncertainties and give the same weight at each distance, we considered logarithmic classes of distance defined with bins width of 0.1, and then we calculated the arithmetic average of ∆I for each distance bin (black diamonds in Fig. 2).

Fig. 2
figure 2

Epicentral distances versus ΔI (difference between the epicentral and site intensities) for the earthquakes selected for the analysis (grey circles); black diamonds indicate the arithmetic average of ΔI for distance bin and relative standard deviation σ. The red line represents the attenuation law obtained (dotted when extrapolated for distances outside the upper bound of 20 km)

Full size image

This approach allows obtaining a better resolution at shorter distances (< 10 km), where data are denser. In fact, it can be noted that there are very few observations in the distance range from 10 to 20 km, and the absence of standard deviation (σ) in some average bins indicates that there is one data per bin only. Moreover, note also that considering the strongest earthquake (I0 = XI) occurred at Ischia, for a site located at a distance of 20 km, ΔI is 7 and IS results IV, i.e. a degree which does not produce any damage.

The relation was calculated for different bounds of distance: the best results (lower ε and higher R2) are obtained when data were inverted for distances between 0.4 and 20 km (Table 2). It is noteworthy in Fig. 2 that there is no attenuation for distances shorter than 0.4 km, i.e. we can assume that sites are located inside the earthquake focal volume intersecting the Earth's surface due to the shallowness of the sources.

Table 2 Coefficients of the attenuation relation in the form ΔI = a log10(D) + b, calculated for different distance bounds and statistical parameters of the regression
Full size table

The linear regression between the logarithm of the distance (D) and ΔI is therefore calculated using a dataset of 16 average ΔI representative of 108 macroseismic observations. The calculated relation is:

$$\Delta I = {4}.00{3}\left( { \pm 0.{233}} \right){\text{log}}_{{{1}0}} \left( {\text{D}} \right) + {1}.{713}\left( { \pm 0.{156}} \right)$$
(1)

with a standard error ε = 0.48. In Fig. 2 the new relation (red line) is extended for a further 20 km (dashed red line), maintaining a good performance until a distance D = 40 km.

To test the reliability of the relation, we also calculated the coefficients of the relation [Eq. (1)] using the hypocentral distance DH = (D2 + H2)0.5, for the bound distance 1.6–20 km, and the focal depth of the 2017 earthquake, H = 1.7 km. The root mean square (RMS) of the residuals between observed and calculated intensities is 0.54 and 0.74 for epicentral and hypocentral distances, respectively. The coefficient of determination (R2) between observed and calculated intensities is 0.78 for the epicentral distance, and 0.54 for the hypocentral one. These results confirm the choice of using the epicentral distance for the intensity attenuation at Ischia.

The obtained relationship (Eq. 1) attenuates the seismic energy stronger than the previous ones proposed by Peruzza (2000) and Azzaro et al. (2006), as shown in the comparison in Fig. 3. In particular, Peruzza (2000) used just one event (the 1883 eq) as representative of the seismogenic zone 56 [including at that time both Ischia and Vesuvius, see Meletti et al. (2000)], to estimate the coefficients of the Grandori equation (Grandori et al. 1987, 1988). This relation (green line in Fig. 3) cuts the curve with a flat step of zero-decay for distances smaller than 2 km, to model a somehow circular extended source.

Fig. 3
figure 3

Comparison of the intensity attenuation relationship proposed for Ischia in this work (red line) with the ones existing in the literature; the attenuation trend for the volcano-tectonic Etna earthquakes is also shown (grey dashed line). In contrast, note the extremely different attenuation trend defined for the Italian earthquakes by the Gasperini (2001) bilinear relationship (black dashed-dotted line, representing the decay for events with I0 > VIII and epicentral distance cut off at 30 km)

Full size image

The former relation for Ischia by Azzaro et al. (2006) was calibrated over two events (the 1881 and 1883 eqs) by the same functional form of the relation here proposed, but the attenuation was calculated referring to a focal depth fixed at 3 km b.s.l according to the seismogenic zoning adopted at that time (Meletti et al. 2008). This relation (blue line in Fig. 3) presents a no-attenuation zone for distances smaller than 1 km, but it does not fit the new dataset used in this work at all.

Finally, Fig. 3 also illustrates the difference in the attenuation trend between Ischia and Etna. Although they are both characterised by a very high decay of intensity compared to the tectonic areas, the new relation proposed for Ischia attenuates at a larger extent; for instance, the intensity calculated for a site at a distance of 5 km from the epicentre is two degrees lower than expected at Etna.

4.2 Probabilistic model

A complex phenomenon as the seismic attenuation is affected both by aleatory uncertainty, intrinsic in the phenomenon under investigation, and epistemic uncertainty, due to lack of knowledge or data. The probabilistic model first proposed by Rotondi and Zonno (2004) considers all the sources of uncertainty by assuming \(\Delta I\) as a discrete random variable over the domain \(\left\{ {0,1,...,I_{0} - 1} \right\}\), or in other words, by assuming that the variable \(I_{s} = I_{0} - \Delta I\), at a fixed distance from the epicentre, follows the binomial distribution \(Bin\left( {I_{s } |I_{0 } ,p} \right)\) conditioned on \(I_{0}\) and the parameter \(p \in \left( {0,1} \right)\):

$$Pr\left\{ {I_{s} = i | I_{0} = i_{0} ,p} \right\} = \left(\begin{array}{c}i_0\\ i\end{array}\right)p^{i} \left( {1 - p} \right)^{{i_{0} - i}} \quad i \in \left\{ {0,1,...,i_{0} } \right\}$$
(2)

Then the domain is restricted to be \(\left\{ {1,...,i_{0} } \right\}\) by defining \(Pr\left\{ {I_{s} = 1} \right\} = Pr\left\{ {I_{s} \le 1} \right\}\). Moreover, to consider the spatial distribution of the intensity data points at Ischia, we draw \(L\) (in our case \(L = 40\)) distance bins \(R_{j}\), \(j = 1,2,...,L\), of fixed width around the epicentre of each earthquake and assume that, in all the sites within each \(j\)th distance bin, \(I_{s}\) has the same binomial distribution with parameter \(p_{j}\). Since the ground shaking may differ even among sites located at the same distance, we consider each \(p_{j}\) as a random variable which follows a Beta distribution:

$$Be\left( {p;\alpha ,\beta } \right) = \frac{{\Gamma \left( {\alpha + \beta } \right)}}{\Gamma \left( \alpha \right)\Gamma \left( \beta \right)}\mathop \smallint \limits_{0}^{p} x^{\alpha - 1} \left( {1 - x} \right)^{\beta - 1} dx$$
(3)

where, according to the Bayesian paradigm, values \(\alpha_{j,0}\) and \(\beta_{j,0}\) have to be initially assigned to the \(\alpha\) and \(\beta\) parameters so as to express our prior knowledge on the problem under study; in the following we expose a way to elicit this information from other datasets independent from the one under examination.

Then, through the intensity data of the earthquakes listed in Tab. 1, we update our knowledge on the attenuation process in this volcanic zone; formally, for each fixed \(I_{0}\) value, through Bayes' theorem we update the parameter values in the distance bin \(R_{j}\), \(j = 1,2,...,L\) by:

$$\alpha_{j} = \alpha_{j,0} + \mathop \sum \limits_{n = 1}^{{N_{j} }} i_{s}^{\left( n \right)} \qquad \beta_{j} = \beta_{j,0} + \mathop \sum \limits_{n = 1}^{{N_{j} }} \left( {I_{0} - i_{s}^{\left( n \right)} } \right)$$
(4)

where \(N_{j}\) is the total number of data points \(D_{j}\) inside \(R_{j}\) and \(i_{s}^{\left( n \right)}\) is the intensity felt at the \(n\)-th site. Consequently the estimate of \(p_{j}\) is given by its posterior mean:

$$\hat{p}_{j} = E\left( {p_{j} |D_{j} } \right) = \frac{{\alpha_{j,0} + \mathop \sum \nolimits_{n = 1}^{{N_{j} }} i_{s}^{\left( n \right)} }}{{\alpha_{j,0} + \beta_{j,0} + I_{0} \cdot N_{j} }}$$
(5)

To make the estimate of the \(p\) parameter vary with continuity, we smooth the estimates \(\hat{p}_{j}\), \(j = 1,...,L\) with the method of least squares, using an inverse power function \(g\left( d \right) = \left[ {c_{1} /\left( {c_{1} + d} \right)} \right]^{{c_{2} }}\). In this way it is possible to assign the smoothed binomial probability of \(I_{s}\) at any distance d from the epicentre by:

$$Pr_{smooth} \left\{ {I_{s} = i | I_{0} = i_{0} ,g\left( d \right)} \right\} = \left(\begin{array}{c}i_0\\ i\end{array}\right)g(d)^{i} \left( {1 - g\left( d \right)} \right)^{{i_{0} - i}} \quad i \in \left\{ {0,1,...,I_{0} } \right\}$$
(6)

and to use the mode (intensity with the highest probability, Iexp) of this distribution to forecast the intensity that could be felt at the distance d from the epicentre of a future event of intensity \(I_{0}\).

This approach has already been followed to analyse the intensity attenuation of the Italian seismicity (Rotondi et al. 2008a; Zonno et al. 2009) while the volcanic areas, because of their peculiarity, have been examined separately by using the macroseismic data available at that time (Rotondi et al. 2008b; Zonno et al. 2008). More recently, in Rotondi et al. (2016) the probabilistic model has been applied to a revised macroseismic database for the volcanic area of Mt. Etna. This database was not so large to allow a reliable estimation of the probability distribution of the macroseismic intensity at site. Since in the context of Bayesian statistics the information provided by the data can be integrated with extra information related to the same phenomenon, the larger Italian macroseismic database DBMI11 [the previous release of DBMI15, see Locati et al. (2022)] has been exploited as a learning set for the analysis of the macroseismic attenuation at Etna. In particular, the results on the intensity attenuation of the Italian seismicity has been exploited to express our knowledge on the attenuation process prior to this study, namely, to assign prior values to \(\alpha_{j,0}\) and \(\beta_{j,0}\). We apply the same procedure to the case study of Ischia, which also has a very small macroseismic database. In brief, we consider the huge dataset of the Italian macroseismic database DBMI15 (Locati et al. 2022) that, with 123,956 intensity data related to 3228 earthquakes, constitutes the primary source of information on the spatial distribution of the macroseismic effects of the Italian earthquakes. Following the procedure proposed by Zonno et al. (2009), we build a learning dataset made up of the most significant macroseismic fields excluding the earthquakes in volcanic areas: 441 macroseismic fields which have epicentral intensity \(I_{0} \ge V\) MCS and number of data points \(N_{ip} \ge 40\). To find out if there are classes of fields that appear homogeneous from the viewpoint of attenuation, we first summarise the attenuation of each macroseismic field by computing median, mean and third quartile of the epicentre-site distances related to the same decay \(\Delta I\) class (\(\Delta I = 0,1,...,I_{0} - 1\)) and we collect these statistical summaries in a \(\left[ {n \times \left( {3 \times max I_{0} } \right)} \right] = \left( {441 \times 33} \right)\) matrix, \(n\) being the number of the earthquakes. Then we apply to this matrix a hierarchical agglomerative clustering method (Kaufman and Rousseeuw 1990) implemented in the free software R (R Development Core Team 2008) by the AGNES (AGglomerative NESting hierarchical clustering) routine in order to group the macroseismic fields according to different attenuation trends. On the basis of the silhouette criterion, 4 classes of attenuation trend are identified, from the quickest \(C_{A}\) to the slowest \(C_{D}\).

The same statistical summaries (median, mean and third quartile of the epicentre-site distances) have been here computed for the Ischia dataset (see Table 1) and compared graphically with those of each of the four above mentioned classes; the best agreement is obtained from the class \(C_{B}\) by reducing the width of the distance bins by a factor \(k = 20\). Hence, we exploit this information by assigning to the prior parameters \(\alpha_{j,0}\), \(\beta_{j,0}\) the values obtained for the parameters \(\alpha_{j}\), \(\beta_{j}\) of the posterior distribution of \(p_{j}\) in that class and by modelling the attenuation in Ischia through bins of 0.5 km instead of 10 km as adopted for the Italian territory. In this way we can assign the value of the rescaled inverse power function:

$$g\left( d \right) = \left[ {\frac{{\frac{{c_{1,B} }}{k}}}{{\frac{{c_{1,B} }}{k} + d}}} \right]^{{c_{2,B} }}$$
(7)

of the class \(C_{B}\) at each distance bin \(R_{j}\) to the corresponding \(p_{j,0 }\), and then, deduce the hyperparameters \(\alpha_{j,0}\), \(\beta_{j,0}\) of the prior distribution of \(p_{j}\) from this value by inverting the theoric formulas for \(E\left( {p_{j} } \right)\) and \(var\left( {p_{j} } \right)\) of the Beta distribution according to the procedure indicated in Rotondi et al. (2016). Then, through the earthquakes in Table 1 the \(\alpha_{j,0}\), \(\beta_{j,0}\) parameters have been updated [see Eq. (4)] and the estimates \(\hat{p}_{j}\) of the \(p_{j}\) parameters evaluated at each of the \(L = 40\) bins [see Eq. 5)]; finally these values have been approximated through the inverse power function \(g\left( d \right)\), so as to obtain the parameters \(c_{1}\), \(c_{2}\) reported in Table 3, in order to have the probability distribution of \(I_{s}\) at any distance \(d\) from the epicentre. We notice the lack of earthquakes with epicentral intensity \(I_{0} X\) in the Ischia dataset (Table 1). In this case, according to the Bayesian paradigm, the prior distribution reflects all the available knowledge when no data are available; therefore, the prior distribution is also assumed as a posterior distribution (Table 3).

Table 3 Parameters of the inverse power function \(g\left( d \right)\) which provides the value of the parameter \(p\) of the binomial distribution at any epicentral-site distance \(d\)
Full size table

Figure 4 shows the probability distribution of \(I_{s}\) as a function of the distance from the epicentre for different values of the epicentral intensity \(I_{0}\). We remind that the mode of these distributions (value associated with the maximum probability) is assumed as estimate of \(I_{s}\) at each distance bin.

Fig. 4
figure 4

Probability function of the intensity at a site \(I_{s}\) at different epicentral-site distances (colours correspond to bins of 1 km), conditioned on 4 values of epicentral intensity \(I_{0}\). *indicates the epicentral intensity class lacking macroseismic observations, for which we used the parameters from the prior distribution model

Full size image

4.3 Comparison and validation of results

To judge the predictive power of these methods, we perform a retrospective analysis by comparing the observed macroseismic intensities of the earthquakes in Table 1 with the forecast ones, on the basis of three validation criteria, two probabilistic and one deterministic (see Rotondi and Zonno 2004). In brief, the first is the logarithmic scoring rule based on the logarithm of the likelihood function expressed through the smoothed binomial distribution:

$$score_{bin} = - \frac{1}{N}log\mathop \prod \limits_{n = 1}^{N} \left( {\begin{array}{*{20}c} {I_{0} } \\ {i_{s}^{\left( n \right)} } \\ \end{array} } \right)g(d_{n} )^{{i_{s}^{\left( n \right)} }} (1 - g\left( {d_{n} } \right))^{{\left( {I_{0} - i_{s}^{\left( n \right)} } \right)}}$$
(8)

\(N\) being the number of felt reports and \(d_{n}\) the distance of the \(n\)th site from the epicentre. The second probabilistic criterion is given by the \(p\left( A \right)/P\left( B \right)\) ratio between the probability that the fitted model Prsmooth assigns to the realisation \(A\) and the probability of the predicted value \(B\):

$$odds_{bin} = - \frac{1}{N}log\mathop \prod \limits_{n = 1}^{N} \frac{{Pr_{smooth} \left( {i_{s}^{\left( n \right)} |D} \right)}}{{Pr_{smooth} \left( {i_{smooth}^{\left( n \right)} |D} \right)}}$$
(9)

where \(i_{smooth}^{\left( n \right)}\) denotes the mode of the smoothed binomial distribution [Eq. (6)] at the \(n\)th site, estimator of \(I_{s}\). Finally, the deterministic criterion measures the absolute discrepancy between observed and estimated intensities at a site:

$$diff_{bin} = \frac{1}{N}\mathop \sum \limits_{n = 1}^{N} \left| {i_{s}^{\left( n \right)} - i_{smooth}^{\left( n \right)} } \right|$$
(10)

It allows us to compare the reliability of the results between the probabilistic approach and the deterministic method which uses the logarithmic relationship [Eq. (1)] proposed in this study. The smaller the values, the better the performance of the model. As for the odds probabilistic criterion [Eq. (9)] we note that, being roughly \(p\left( A \right) \approx \exp \left( { - \mu_{odds} } \right)p\left( B \right)\) where \(\mu_{odds}\) is the mean of the odds values, the fitted model assigns on average to the observed intensity data about 83% of the probability of the predicted ones.

Table 4 shows the results of the validation analysis carried out on the two attenuation models proposed here. We express the average performance of the approaches through the mean and standard deviation of the values of absolute discrepancy diff [Eq. (10)]: as for the probabilistic model, the mean discrepancy is 0.64 and the standard deviation is 0.24, whereas for the deterministic method the mean discrepancy is 0.71 with standard deviation 0.19. Results appear similar and generally reliable, with a slightly better performance of the probabilistic model. The highest discrepancy diff is obtained for the 1883 earthquake; this event is the strongest among the analyzed ones and is also documented by a great number of IDPs, most of them being referred to the VIII and VII intensity degrees. The high value of diff is mainly due to the uneven distribution of IDPs as shown by the scattered and partially overlapping sets of sites with the same intensity decay, Δ = 2 and Δ = 3.

Table 4 Validation criteria adopted to evaluate retrospectively the forecasting performance of the deterministic versus probabilistic attenuation models
Full size table

Figure 5 compares the predicted intensity at a site (Is) according to the deterministic and probabilistic approaches expressed, respectively, by the expected intensity (blue lines) and the modal intensity (red lines). Shades of colours in the background correspond to different values of probability of intensity Is at any distance from the epicenter, as provided by the probabilistic model. The macroseismic attenuation trends are quite similar between the two approaches in the near-field. Conversely, they appear to diverge significantly in the far-field, largely reflecting the uncertainty due to the paucity of IDPs far from the epicenter.

Fig. 5
figure 5

Comparison of the intensity expected at a site (Iexp) calculated by the logarithm relation of Eq. (1) (blue lines) versus the mode of the beta-binomial probability distribution (red lines); all the distributions for each probability function (Prob.) of the intensity at a site IS at different epicentral-site distances, are also shown. *indicates the epicentral intensity class lacking macroseismic observations, for which we use the parameters from the prior distribution model

Full size image

5 Application to seismic scenarios

The most immediate and useful application for an intensity attenuation model, is reproducing in a reliable way the effects of an earthquake (past or future) in a given area. This target may be of particular complexity in volcanic zones, where each element leading to the definition of earthquake scenarios and risk analyses needs to be specifically calibrated. In Italy, methods and procedures to generate earthquake scenarios and to derive risk evaluations, have been proposed for Etna volcano (e.g. Azzaro et al. 2013; D’Amico et al. 2016; Langer et al. 2016; Pessina et al. 2021). In the following we describe the approach adopted for Ischia, and present results expressed in terms of intensity shake-maps.

The reason for this implementation was quite evident during the earthquake which struck Ischia in 2017. While the shock indeed caused in the epicentral area heavy impact—two casualties, many collapses and a number of homeless in Casamicciola and surroundings (Briseghella et al. 2019)—the automatic ShakeMap system (http://shakemap.ingv.it/shake4/index.html, see Michelini et al. 2020) running at the Osservatorio Sismico Nazionale of INGV Rome, produced an earthquake scenario with a maximum intensity reaching degree VI MCS (Fig. 6a). This estimate implies just slight damage and is two degrees lower than the intensity evaluated through the classic post-earthquake macroseismic survey (Azzaro et al. 2017b). Such a result has had obvious consequences in terms of seismic surveillance, since it prevented the prompt alert to civil protection authorities.

Fig. 6
figure 6

Comparison among different scenarios expressed in terms of macroseismic intensity, calculated for the 2017 Casamicciola earthquake starting from the same input parameters instrumentally determined (MW 3.9, star indicates the epicentral location). a Automatic shake-map derived from ground motions recorded by the Italian seismic network (modified from http://shakemap.ingv.it/shake4/index.html). Note that the maximum value calculated at the epicentre reaches intensity VI MCS, two degrees lower than the intensity determined from the macroseismic field survey (see small boxes in the other panels, data from Azzaro et al. 2017b); b Deterministic scenario obtained through the logarithmic regression (1); c Probabilistic scenario obtained from the mode of the distribution (expected intensity, Iexp); d–e the same, but expressed as 25th and 75th percentiles of the probability distribution

Full size image

The motivation for this poor performance is essentially due to the following two facts. Firstly, ShakeMap derives intensity from ground motion signals recorded by seismographs. Note that this step includes a twin passage: i) PGA registered at stations is attenuated over the territory by means of a ground motion model (GMM); ii) distribution of PGA values is converted into macroseismic intensity degrees through an empirical relationship (Faenza and Michelini 2010, 2011). Secondly, GMM and relationships used in the automatic ShakeMap (Michelini et al. 2020) are not specifically calibrated for the volcanic area of Ischia. Moreover, in the case of the 2017 earthquake there were only two stations recording the ground shaking, one at Casamicciola (epicentral area) and another at Pozzuoli (far field), in the mainland.

Here we propose a more direct approach not based on the conversion of ground motion instrumental parameters, but that exploits the attenuation models discussed above to generate earthquake scenarios expressed directly as macroseismic intensity. The computation procedure is implemented in a python plugin for QGIS® software (see Supplementary Information, https://www.ct.ingv.it/macro/download/software.html) that, given epicentre and intensity of the earthquake, applies the deterministic or probabilistic attenuation models and finally produces a shake-map on a 20 × 20 km grid centred on the island. The procedure may be also applied for real-time seismic surveillance by converting the instrumental value of magnitude into epicentral intensity I0 through the ensemble magnitudes estimations recently proposed for Ischia by Selva et al. (2021). This passage is quite straightforward for the shallow events characterising the island, and indeed results much less critical—in terms of associated uncertainties—than the application of a GMM and the conversion into macroseismic intensity degrees.

Figures 6b–e illustrate some examples of simulation carried out for the 2017 earthquake, adopting as input data the same epicentral instrumental parameters used in the automatic ShakeMap of Fig. 6a. Starting from a magnitude MW 3.9, through the relationship by Selva et al. (2021) we obtain an epicentral intensity I0 VIII MCS, corresponding to the value estimated from the field survey, which is the input for our scenarios. The maps show the results calculated on a grid with node distances of 0.5 km: for the probabilistic scenarios, the mode of the predictive distribution represents the intensity with the highest probability, which is assumed as the expected site intensity Is, while the 1st and 3rd quartiles provide an estimate of the uncertainties.

The main difference between the deterministic and probabilistic approaches is that the latter provides an assessment of the (Bayesian) uncertainty on the estimate of the macroseismic intensity at a site Is, which may be useful in applications at a very local scale; for example, in establishing priority in the retrofit interventions or preparing Civil Protection emergency plans. The deterministic and probabilistic shake maps (Fig. 6b, c) do not show substantial differences and are consistent with the distribution of the IDPs determined by the macroseismic survey, confirming that the severely hit area remains fairly limited in extension. Conversely, taking into account the uncertainties expressed in the maps of the 25th–75th percentiles (Fig. 6d, e), the differences are evident and imply a shift up to 2 km of the intermediate degrees (IV ≤ Is ≤ VI), particularly increasing in the far-field. For example, the locality of Barano (Fig. 6b) has experienced a macroseismic intensity degree V MCS during the 2017 earthquake; the predicted scenario is degree IV MCS for both deterministic and probabilistic approaches (Fig. 6b, c) but the probability distribution of the intensity value in Barano can range between degrees III and V with 50% of probability, where III and V correspond to the 25th and 75th percentiles (Fig. 6d, e). Note also that these maps significantly differ from the automatic ShakeMap (Fig. 6a).

The probabilistic approach therefore provides indication about the uncertainty associated with a seismic scenario. As an example, in Fig. 7a–e we show the probability distribution of having intensities at a site Is larger than a fixed value, for an event similar to the 1883 Casamicciola earthquake, which is reported in the historical catalogue as the largest shock to have occurred at Ischia (Selva et al. 2021). As input parameters, we assigned the same epicentre of the 2017 event, which is instrumentally well constrained (D’Auria et al. 2018), and an epicentral intensity I0 XI MCS (corresponding to a magnitude MW 5.2 by the relationship by Selva et al. 2021). The maps represent all the intensity classes relevant for a damage scenario (i.e. I ≥ VI MCS). In general, it is evident how the highest values of probability (Fig. 7a–c) significantly vary in short distances, being essentially confined to the near-field. In detail we note that for a 1883 type event, the probability of observing structural damage (i.e., Is ≥ VIII MCS) is higher than 70% in a large part of the northern sector of Ischia (Fig. 7c), while the probability of suffering slight to moderate damage (i.e., VI ≤ Is ≤ VII MCS) is at least 60% also in the southern sector of the island (Fig. 7e).

Fig. 7
figure 7

Scenarios for an event similar to the 1883 earthquake (I0 XI MCS, MW 5.2), located as the 2017 one (star indicates the epicentral location). a–e Distribution of the exceeding probabilities for fixed intensity values; f Shake-map obtained from the mode of the probability distribution (expected intensity, Iexp). The grid has a node distance of 0.5 km

Full size image

This different perspective of deaggregating the “standard” scenario represented by the mode of the probability distribution (Fig. 7f), may be used for statistical damage assessment in plans of pre-earthquake interventions for risk evaluations with an adequate level of accuracy.

6 Conclusions

The analysis presented here confirms that the characteristics of attenuation in the Ischia island are those typical of the volcanic zones, with an intensity decay even stronger than the one observed at Etna volcano. Thanks to a new revised dataset of macroseismic observations, much more rich and homogeneous than the ones available in the past, it has been possible to update the previous relationships and to calibrate new attenuation models through deterministic and probabilistic approaches. Both models consider an isotropic attenuation, in which the source is assumed as a point and the decay comparable to a symmetric spreading (circular). In particular, the probabilistic method based on the binomial-beta model allows a complete treatment of the uncertainty, so that the macroseismic intensity Iexp at any site as well as the entire probability distribution of Is are estimated. In practical terms, the seismic scenarios can be expressed as (i) the intensity that may be reached with a fixed probability threshold (i.e., mode of the distribution of Iexp values) or, (ii) the probability that the expected intensity exceeds a given degree.

In summary, the main findings of our analysis allow pointing out the following aspects:

  1. (a)

    the attenuation of intensity is extremely high, reaching a ΔI (difference between the epicentral intensity I0 and the intensity at a given site IS) of 4 degrees in 5 km of distance from the epicentre (double compared to Etna);

  2. (b)

    the performances of deterministic and probabilistic models are comparable, within the epistemic (observed intensity data) and aleatory (models) uncertainties;

  3. (c)

    the probabilistic model provides a more reliable statistical distribution of the expected effects in the near-field thanks to the uncertainty estimation represented by the probability distribution for fixed intensity degrees;

  4. (d)

    the procedure implemented in the plugin for QGIS® software to generate probabilistic earthquake scenarios in terms of intensity-based shake-maps may represent a concrete tool in risk analyses for estimating damage and exposure maps at a very local scale, for instance in establishing priority in the retrofit interventions or preparing Civil Protection emergency plans.

With all the limitations due to the nature of macroseismic data, considering the peculiar seismotectonic context and the scarcity of instrumental data of significant earthquakes recorded at Ischia, we believe that intensity can represent a valuable source of information to characterise seismic attenuation in an area, albeit small, exposed to a high seismic risk. The new attenuation models, obtained through the most updated macroseismic dataset, can also contribute to the seismic surveillance of this volcanic area, with more calibrated simulations for real-time applications supplementing the instrumental ShakeMap system used at a national scale.