1 Introduction

Macroseismic intensity is considered a classification of the severity of ground shaking on basis of observed effects in a limited area (Grünthal 1998), and it encompasses the effects of different factors that characterize the destructive potential, such as the peak parameters, the frequency content, and the duration of the ground-motion, the soil-structure interaction, the inelastic response of buildings, and so on (Trifunac 1991; Sokolov and Chernov 1998; Atkinson and Sonley 2000; Boatwright et al. 2001). However, since there are no physical models capable of fully describing this phenomenon, the comparison between qualitative and quantitative measures of the severity of the seismic ground shaking are commonly carried out empirically. However, several authors observed that such empirical relationships between macroseismic observation and instrumental measures of the ground shaking do not always have an good statistical correlation (Ritchter 1958; Ambraseys 1975; Decanini et al. 1995; Yih-Min et al. 2003; Fujimoto and Midorikawa 2005). The main issue relates to their high variability and is essentially due to the different spatial representativeness of the two ground shaking measures: the instrumental one is restricted to few hundreds of meters in the vicinity of the recording station and strongly depends on local site effects; on the other hand, the macroseismic observations that contribute to assigning to a locality an intensity level is carried out on an extended inhabited area (even several square kilometres), often placed on a composite substrate with different geological, geomorphological, and topographic characteristics (Trifunac and Westermo 1977; Trifunac and Lee 1992; Theodulis and Papazachos 1992).

Despite this limitation, empirical relationships between macroseismic intensity and instrumental ground motion parameters (GMPs) are largely used, since they are one of the key elements for comparing seismic hazard assessment (SHA) in GMP to SHA in terms of macroseismic intensities (Gomez Capera 2006; Gomez Capera et al. 2007) and for shakemaps implementation (Kaestli and Faeh 2006; Michelini et al. 2008; Wald et al. 2006; Allen and Wald 2009; Faenza and Michelini 2011).

Several relationships between macroseismic intensity and GMPs based on very different data sets and approaches have been published (Cua et al. 2010 and references therein). Table 1 shows a summary of such relationships proposed for California, the Euro-Mediterranean area and the Worldwide model by Caprio et al. (2015).

Table 1 Examples of empirical models proposed in previous studies to calibrate macroseismic intensity (I)—PGA relationships
Full size table

Various correlation models have been proposed in the past for Italy (Chiaruttini and Siro 1981; Margottini et al. 1987, 1992; Panza et al. 1997; Faccioli and Cauzzi 2006). In the last decade, the development of macroseismic intensity and GMP relationships took advantage from the cross-matching of the Italian Macroseismic Database (DBMI) and the ITalian ACceleration Archive (ITACA). Faenza and Michelini (2010, 2011) propose linear and orthogonal relationships between Mercalli–Cancani–Sieberg (MCS, Sieberg 1930) intensity (DBMI04, Stucchi et al. 2007) and related PGA, PGV and SA at 0.3, 1.0 and 2.0 s (ITACA1.0, Luzi et al. 2008).

Linear relationships between a set of GMPs (PGA, PGV, and SA at 0.2, 1 and 2 s) and MCS intensity have been proposed for Italy (Gomez Capera et al. 2015) in the frame of the Project S2—Constraining Observations into Seismic Hazard (DPC—INGV agreement 2014–2015, shorturl.at/gtu27), and subsequently updated with data coming from the major earthquakes of the 2016 Central Italy sequence (Gomez Capera et al. 2018). The calibration dataset has been compiled using ITACA2.0 (Luzi et al. 2008) and DBMI11 (Locati et al. 2011) and is constituted by 118 pairs of site Intensity and GMPs from 53 Italian earthquakes in the time window 1976–2009 with 3.9 ≤ Mw ≤ 6.9 and 3–4 ≤ IMCS ≤ 8–9 (Locati et al. 2017). Recently Zanini et al. (2019) propose reversible macroseismic intensity-GMPs (PGA, PGV, PGD, Arias intensity and Housner intensity) relationships on the base of Italian data at European Macroseismic Scale 1998 (EMS-98; Grünthal 1998). Finally, Masi et al. (2020) propose linear and bilinear relationships between macroseismic data, at scales EMS-98 and MCS, and GMPs such as PGA, PGV and Housner Intensity.

Due to its long historical record and the early start of macroseismic research, Italy has a large amount of macroseismic intensity data that can be used as an independent set for calibration purposes. Therefore, when comparing seismic hazard maps in PGA and in terms of macroseismic intensity in Italy (Boschi et al. 1995; Molin et al. 1996; Slejko et al. 1998; Albarello and D’Amico 2008; Gomez Capera et al. 2010; Stucchi et al. 2011), it is necessary to have available relationships between macroseismic intensity and GMPs that allow conversions for high macroseismic intensity levels to PGA values without having the saturation problem as observed in the linear correlations given in the literature in Italy (Faccioli and Cauzzi 2006; Gomez Capera et al. 2015, 2018; Zanini et al. 2019).

In the present study, we explore a non-linear correlation between GMPs and macroseismic intensity and vice versa using classical functional and separate regressions in the two directions. Non-linear empirical relationships between macroseismic intensity and GMPs (PGA, PGV, and SA at 0.2, 0.3, 1.0, and 2.0 s) have been developed by comparing the geometric mean of the horizontal components of the ground motion recorded by 150 accelerometric stations (ITACA3.0) to the related Mercalli–Cancani–Sieberg (MCS) macroseismic observations (DBMI15, Locati et al. 2019).

The calibration dataset is constituted by 240 macroseismic intensity-GMP pairs from moderate to large Italian earthquakes in the time-window 1972–2016. In order to account for the uneven distribution of GMPs corresponding to every macroseismic intensity level, the mean value of the GMP is assigned to each macroseismic intensity class (Tselentis and Danciu 2008; Atkinson and Kaka 2007; Faenza and Michelini 2010, 2011; Panjamani et al. 2016; Bilal and Askan 2014; Du et al. 2019; Zanini et al. 2019). The final product is a set of 6 empirical relationships predicting macroseismic intensity as a function of GMP (IMCS = f(LogGMP)) and 6 empirical relationships predicting GMP as a function of macroseismic intensity (LogGMP = g(IMCS)). The empirical relationship IMCS as a function of PGA is compared with similar relationships from previous studies among others in Italy, Greece, and California.

Finally, a preliminary application of the proposed relationship in PGA is used to compare seismic hazard in terms of macroseismic intensity (Gomez Capera et al. 2010) and PGA (Stucchi et al. 2011).

2 Data

A fundamental task of this study was to provide a well-qualified dataset for the calibration of macroseismic intensity-GMP relationships valid for the Italian territory. The compilation of the dataset was one of the activities planned for the next italian seismic hazard map (Meletti et al. 2017). Macroseismic intensity data mostly come from the Italian Macroseismic Database (DBMI15), which makes available intensity data related to earthquakes in the time-window 1000–2017 that is used to compile the parametric earthquake catalog of Italy (CPTI15, Rovida et al. 2019, 2020). Even if an updated version of the ITalian ACelerometric Archive (ITACA v3.1) has been recently published, the main source of accelerometric data is the previous version of the ITACA database (v3.0), which provide strong-motion records and related metadata of seismic events with M > 3.0 occurred in Italy in the time-window 1972–2018. The ITACA records are annually revised, hence data and metadata might differ among different versions. However, in order to make consistent the result of this study with what has already been produced in the framework of the next Italian seismic hazard map, we refer to the slightly earlier ITACA version which includes the last seismic crisis occurred in Central Italy (e.g. Mw6.5, 30th October 2016, Norcia earthquake). In addition, we have also considered the ESM strong-motion flat-file (Lanzano et al. 2018a, b; Bindi et al. 2018), a parametric table which contains metadata and intensity measures of manually processed waveforms included in the Engineering Strong Motion database (Luzi et al. 2016). The dataset used for the regressions is provided in xlsx format in the electronic supplement (ESUPP1, ESUPP2, ESUPP3, ESUPP4).

In order to compile the dataset of macroseismic intensity-GMPs pairs, we made a preliminary cross-matching of ITACA and DBMI records in the time-window 1972–2016 by keeping a threshold distance of about 3 km for the association between macroseismic localities and related accelerometric stations (Locati et al. 2017; Gomez Capera et al. 2018). After this first association, the similarity in terms of geological and topographic conditions between localities and accelerometric stations has been checked to provide a careful macroseismic intensity-GMPs association.

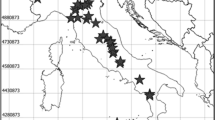
The cross-matching between macroseismic and accelerometric records is not a trivial issue. The DBMI15 localities are those well-delimited settlements where it was possible to classify the severity of the effects caused by the ground shaking on a statistically consistent sample of buildings. The concept of locality, that does not necessarily coincide with the entire urban area of a municipality, implies that the macroseismic classification of a more or less large area collapses into a point identified by geographic coordinates. The association between macroseismic data observed within an area and local measurements of the ground shaking induced by earthquakes need, moreover, a careful check in order to guarantee the similarity in terms of site response. Figure 1 shows two examples of macroseismic intensity-GMPs pairs, only defined on the base of the distance criterion. In the former case, the association can be judged reliable: the accelerometric station (IT.CDR), located in Codroipo (North-Eastern Italy), recorded the Mw6.45 Friuli 1976.05.06 earthquake and the site intensity (IMCS = 6) related to the same name locality in DBMI15 (Fig. 1a). In the latter case, the association is uncertain: the accelerometric station IT.ALT (Auletta) recorded the Mw6.81 Irpinia-Basilicata 1980.11.23 earthquake (Southern Italy) but it is located about 3 km far from two localities associated to different intensity levels (Auletta, IMCS = 8; Petina, IMCS = 7). In this case, the association is carried out preferring the locality with similar topographic conditions. For this reason, the locality of Petina (IMCS = 7) is linked with ALT Station.

Fig. 1
figure 1

a Example of accelerometric station (IT.CDR, blue triangle) well matching macroseismic observations in the built-up area of Codroipo for the Mw6.4 Friuli 1976.05.06 earthquake (North-Eastern Italy); b Example of linking accelerometric recording and macroseismic observation using an distance criteria and similar geological/topographic conditions between accelerometric station (IT.ALT) and two macroseismic localities (Auletta e Petina) for the Mw6.81 Irpinia-Basilicata 1980.11.23 earthquake (Southern Italy)

Full size image

After the additional check of geological and topographic conditions match, the final dataset consists of 240 macroseismic intensity-GMPs pairs from 67 Italian earthquakes occurred in the time interval 1972–2016 with 4.18 ≤ Mw ≤ 6.81 (CPTI15) characterized by macroseismic intensity values 2 ≤ IMCS ≤ 10–11. The maximum moment magnitude (Mw6.81) corresponds to the 1980.11.23 Irpinia Basilicata earthquake, whereas the minimum magnitude (Mw4.18) is for the 2003.12.07 Forvilese event (Northern Italy). As instrumental measures of the seismic shaking, we have considered the geometric mean between the two horizontal components of peak ground acceleration (PGA), peak ground velocity (PGV) and spectral accelerations (SA) at 0.2, 0.3, 1.0, and 2.0 s.

Figure 2a, b show the spatial distribution of 67 Italian earthquakes that provided the dataset used in this study and the location of the 150 acceleration station extracted from ITACA3.0, respectively. The 41% of the macroseismic intensity-GMP pairs is provided by the events of L’Aquila 2009.04.06 (Mw6.29), Irpinia 1980.11.23 (Mw6.81), Abruzzo Apennines 1984.05.07 (Mw5.86), Umbria-Marche Apennines 1997.09.26 (Mw5.97), and Amatrice 2016.08.24 (Mw6.00). For the 2016 Amatrice earthquake, we adopt the macroseismic study by Galli et al. (2016), rather than that adopted by the compilers of DBMI15 (Rossi et al. 2019). The reason for our choice relies on the different macroseismic scale used by the two studies, MCS in Galli et al. (2016) and EMS-98 in Rossi et al. (2019), and we opted to prioritise MCS for the sake of input data homogeneity. Additional intensity data provided from surveys performed after the earthquakes of the 30th October 2016 (mainshock Mw 6.5) and of the 18th January 2017 (mainshock 5.5) were not considered because of the cumulative damaging effects impacting the intensity estimation, as well as an incomplete intensity distribution (Rossi et al. 2019).

Fig. 2
figure 2

a Locations of the 67 earthquakes (CPTI15, Rovida et al. 2020) included in the dataset used in this study b location of the 150 acceleration stations (ITACA3.0, Luzi et al. 2019) associated with the macroseismic data points (DBMI15, Locati et al. 2019)

Full size image

Figure 3 shows the distribution of the macroseismic intensity levels as a function of the associated PGA and PGV (log10 unit) for three classes of magnitude. The 76% of the data falls within the range 5 ≤ IMCS ≤ 7, and the highest values of macroseismic intensity correspond to the events with Mw ≥ 6 (IMCS ≥ 5). The maximum macroseismic intensity (IMCS = 10–11) has been assigned to the Amatrice locality (Galli et al. 2016) after the Mw6.0 Central Italy earthquake (August 24th, 2016) and is correlated to the high level of ground shaking recorded by the station IT.AMT (PGA ~ 560 cm/s2, PGV ~ 42 cm/s). The list of the stations and the related number of events (ESUPP1), the list of 67 earthquakes for which at least one pair of GMP-I was found (ESUPP2), the data set of macroseismic localities and coupled accelerometric stations (ESUPP3), and the data set of macroseismic intensities and associated GMPs (ESUPP4) are provided in the electronic supplement of this paper.

Fig. 3
figure 3

Distribution of the 240 macroseismic a intensity (IMCS)—peak ground accelerations (PGAlog10) pairs, b intensity (IMCS)—peak ground accelerations (PGVlog10) pairs, divided in three class of Mw

Full size image

3 Methodology

The empirical relationships were obtained by ordinary least-squares regression between the macroseismic intensity and the average value of the GMPs (geometric mean of the horizontal components in log10 unit) for each macroseismic intensity level. The approach is to relate the logarithm of GMPs and macroseismic intensity as the only independent variable, because the relationships do not depend on the magnitude and/or distance (Bilal and Askan 2014). The functional form to be modelled was chosen so that the intensity is proportional to the exponential of the GMP (log10 unit).

Since the ground motion to intensity conversion equations are generally not reversible using traditional regression analyses, the assembled macroseismic intensity-GMPs pairs are also used to derive a corresponding macroseismic intensity to ground motion conversion equation by performing a separate regression using a logarithmic functional form.

3.1 Data set for regressions

The macroseismic intensity observations are generally scattered and the variation in intensity assignments at the same epicentral distance can be attributed to azimuthal variations in the radiated energy, differences in wave propagation through crustal and upper mantle structure, and near-site amplification factors, including the geologic foundation beneath the site and the sensitivity of the built environment and observers (Bakun and Wentworth 1997). For this reason, data bins are used to characterize the macroseismic intensity values, because wave propagation and site effects are minimized in the median hypocentral distance (Bakun et al. 2002; Bakun and Scotti 2006).

Following the same physical concept, we also found the same dispersion of the intensity data but this time with GMP. Several Authors (Atkinson and Sonley 2000; Atkinson and Kaka 2007; Tselentis and Danciu 2008; Faenza and Michelini 2010, 2011; Bilal and Askan 2014; Zanini et al. 2019; Du et al. 2019) used intensity-level binning, wherein the GMP averaged group, with different sample size, the same intensity is taken to represent the central tendency of the GMP assignments for that intensity level. As a result, the compiled data set is binned for computing the mean values (and the associated standard deviations) of the ground motion parameters, for each macroseismic intensity level, as reported in Table 2. The dataset is characterized by macroseismic intensities values in the interval 2 ≤ IMC ≤ 10–11 and PGA geometrical mean values in the range 0.9 ≤ PGA(cm/s2) ≤ 587.

Table 2 Mean and standard deviations of the bin (σbin) of PGA, PGV and SA at 0.2, 0.3, 1.0 and 2.0 s with the number of GMP observations for each macroseismic intensity class
Full size table

4 Empirical relationships

As already observed in past studies (Gomez Capera et al. 2007; Gomez Capera et al. 2015; Locati et al. 2017; Gomez Capera et al. 2018), the linear models do not always provide realistic correlations between the highest values of GMPs and the macroseismic intensity. In particular, the GMPs correlated to the highest levels of the macroseismic scale (i.e. IMCS > IX) cannot increase indefinitely; hence, it is advisable to adopt an exponential model with a vertical asymptote (e.g. around 1 g or above for PGA) to capture the observed trend. The exponential model is a monotonic function, continuous and easily derivable throughout the domain and grows in a way proportional to their size.

The regression form is an exponential model of the GMP (log10 unit):

$${\text{I}}_{\text{MCS}} = {\text{a}}\;{\text{e}}^{{ ( {\text{bLogGMP)}}}}$$
(1)

The inverse empirical conversion relations between the macroseismic intensity (I) and the mean value of the GMP (log10 unit) corresponds to:

$${\text{LogGMP}} = {\text{a}}^{{\prime }} + {\text{b}}^{{\prime }} \,{\text{Log}}\left( {{\text{I}}_{\text{MCS}} } \right)$$
(2)

The proposed coefficients (a, b; a′, b′) and the standard deviations (σ; σ′) are given in Tables 3 and 4.

Table 3 Regression coefficients (a, b), standard deviation of the bins (σ), standard deviation of the data (σc) and median values (μ) of the residuals and GMP range of the Eq. (1) for each GMP (σc and μ are computed from of whole dataset)
Full size table
Table 4 Regression coefficients (a′, b′), standard deviation of the bins (σ′), standard deviation of the data (σc′) and median values (μ′) of the residuals and GMP range of the Eq. (2) for each GMP (σc′ and μ′ are computed from of whole dataset)
Full size table

For the set of Eq. (1), the standard error (σ) is between 0.31 and 0.80 unit of macroseismic intensity. On the other hand, for the set of Eq. (2), the standard error is between 0.11 and 0.26 which are smaller than the standard error of Eq. (1). As expected, the standard deviation of the residuals of all data pairs (σc; σc′) is always higher than the standard errors of the set Eqs. (1) and (2), computed using the bins of the mean values.

The standard deviation (σc) is around one unit of MCS intensity for all the ground motion parameters of the set Eq. 1. However, the σc from SA2.0 s shows that the total scatter is the largest (1.42), that is in agreement with their higher standard error value given in the regression (σ = 0.80). The best correlation, to predict IMCS, is the Peak Ground Velocity, based on the fact that PGV provides the lowest uncertainty in prediction (σc = 1.04) using the whole dataset. Similar results are observed in Boatwright et al. (2001) and Kaka and Atkinson (2004), the peak ground velocity is directly related to the kinetic energy, which further influences the damage to structures. The GMPs can be predicted from IMCS (Eq. 2) within standard deviation values 0.35 ≤ σc′ ≤ 0.52. The 0.35 value corresponds to PGA and 0.52 corresponds to SA2.0 s.

The proposed models for PGA are also shown in Fig. 4. The standard deviation (σc and σc′), associated with IMCS (PGA) and LogPGA (IMCS), shows that the scatter is quite large and it is in agreement with the higher values of the standard deviation given for the bars for the mean value of LogPGA for each macroseismic intensity class.

Fig. 4
figure 4

a Proposed relationship from Eq. (1) and b proposed relationship from Eq. (2)

Full size image

Figures 5 and 6 show the residuals distribution of the intensity and the PGA (log10 observed/predicted) as a function of moment magnitude (Mw) and epicentral distance, respectively for the functional forms (1) and (2). Residual plots for LogPGV and LogSA at T = 0.2 s, 0.3 s, 1.0 s, 2.0 s are also available in the electronic supplement (ESUPP5). In general, no significant trends with Mw or epicentral distance are observed. Since there are no systematic biases in the predicted intensities with LogGMP and vice versa, the calibration can considered stable and results are reliable.

Fig. 5
figure 5

Residuals plots (observed–predicted) for IMCS from LogPGA using Eq. (1) (red squares) and for LogPGA from IMCS using Eq. (2) (blue squares) in function of the moment magnitude

Full size image
Fig. 6
figure 6

Residuals plots (observed–predicted) for IMCS from LogPGA using Eq. (1) (red squares) and for LogPGA from IMCS using Eq. (2) (blue squares) in function of the epicentral distance

Full size image

Some trial regressions (Fig. 7) were performed applying the functional forms of Eqs. (1) and (2) without binning the data (blue circles) and using the median (green diamonds) and the mean (red squares) of the empirical points. The tests were carried out both for the direct and the inverse empirical relations. In some cases the results are similar as the inverse relationship given by the logarithmic model of PGA (Fig. 7b), PGV and SA for T = 0.2 s, 0.3 s, 1.0 s, 2.0 s (ESUPP5).

Fig. 7
figure 7

Distribution of the calibration dataset (blue circles) and relationships between Intensity and PGA (log10 unit): a Direct, exponential model; b Inverse, logarithmic model. The calibration has been done by fitting all the 240 macroseismic intensity-GMPs pairs (blue line), as well as the mean (red line) and the median values (green line) for each beam of Intensity

Full size image

In order to further support our choice, linear and bilinear modeling was also explored for either the direct transformation equation (LogGMP to IMCS; Eq. 1) or for the inverse transformation (IMCS to LogGMP; Eq. 2), also evaluating the impact on the aleatory standard deviation. Figure 8a, b show the comparison between the exponential and vice versa (logarithmic model) with the linear and bilinear regressions. The bilinear model presents two different linear trends at low and high PGA as is plotted in Fig. 8a. Moreover, the bilinear model could be considered as an approximation of an exponential model as observed in the graphs, with the difference that the exponential model is continuous and differentiable throughout the entire domain. We can observe that the exponential and logarithmic models better capture the trend of PGA-IMCS-PGA pairs for the following reasons: (1) it exhibits lower standard error (σ, σ′) with respect to the linear and bilinear models; (2) it has a better predictive power since it provides more reliable predictions of macroseismic intensity with PGA higher.

Fig. 8
figure 8

Distribution of the calibration dataset (blue circles). The final calibration has been done by fitting the mean value of the LogPGA (red line) for each beam of Intensity. Comparison the linear and bilinear regression obtained in the present study with relationships between Intensity and PGA (log10 unit): a Direct, exponential model; b Inverse, logarithmic model (Log.). The standard error is given by σ and σ’

Full size image

Same results are observed between the mean values of the GMP–IMCS–GMP pairs for PGV, and SA at T = 0.2 s, 0.3 s, 1.0 s, 2.0 s. The plots and the coefficient regressions of the linear and bilinear empirical relationships are available in the electronic supplement (ESUPP5).

5 Comparison with previous studies

The empirical relationship proposed in the present study in terms LogPGA (Fig. 7a) is compared with Faenza and Michelini (2010), Gomez Capera et al. (2015, 2018), Zanini et al. (2019) and Masi et al. (2020) for the Italian territory, Wald et al. (1999) for California, Tselentis and Danciu (2008) for Greece and with the global model by Caprio et al. (2015) (see also Table 1).

In Fig. 9 it is observed that the Italian relationship in this study is in the range of the existing models. The model for PGA predicts macroseismic intensities higher than the relationship derived for California and Greece. However, both models are very close (IMCS = 6–7) to 100 cm/s2. The relationships proposed in Gomez Capera et al. (2015, 2018) are similar to the current model for 6 < IMCS < 9 because they have a common dataset. However, for Gomez Capera et al. (2018), part of the difference depend on the fact that the IMCS = 11 value, in Amatrice and Pescara del Tronto (Locati et al. 2019), of the Norcia earthquake (30th October 2016, Mw6.61; Rovida et al. 2020) was not included in the present study, due to the evidence of accumulated effects after other damaging events of the 2016 Central Italy sequence (Galli et al. 2016).

Fig. 9
figure 9

Comparison of the Macroseismic Intensity-PGA relationship obtained in the present study (Eq. 1) with relations from previous studies

Full size image

The relationship by Faenza and Michelini intersects the proposed model in correspondence of 3.3 cm/s2 (IMCS = 3) and 109.7 cm/s2 (IMCS = 7). It is observed that for 5 < PGA < 100 cm/s2 the relationship of Faenza and Michelini predicts macroseismic intensity values higher than the proposed model up to 1 MCS point. Similar intersections are found in Zanini et al. at 70.8 cm/s2 and 1.8 cm/s2. For PGA greater than 70.8 cm/s2 Zanini et al. (2019) show lower intensities compared with the present relationship; while Masi et al. (2020) provide lower macroseismic intensities compared to the our model for PGA greater than 22.1 cm/s2 (IMCS > 4–5). For PGA greater than 200 cm/s2 all the relationships show lower macroseismic intensities. The maximum intensity to Faenza and Michelini is IMCS = 8 that corresponds to around 316.2 cm/s2, for the same strong motion value our relationship predicts IMCS = 9. The model proposed in this study is valid until IMCS = 10–11, then it predicts IMCS = 11 for a value of PGA = 766 cm/s2.

The slope of each empirical relationship, I(LogGMP) and vice versa, is not constant. For Eq. (1), the slope (n) is given by the derivative of macroseismic intensity with respect to the LogPGA:

$${\text{n}} = 1. 2 4 3\;{\text{e}}^{{ ( 0. 5 4 6 {\text{LogPGA)}}}}$$
(3)

From Eq. (1) and (3), n can be expressed as a function of macroseismic intensity as follow:

$${\text{n}} = 0. 5 4 6\;{\text{I}}_{\text{MCS}}$$
(4)

The slope grows proportional to 0.5 of macroseismic intensity. Figure 10 shows the comparison between the slope n in function of LogPGA (Eq. 3), the slope n in function of macroseismic intensity (Eq. 4) and those of the literature equations in terms of PGA (Fig. 9; Table 1) that have a constant value because are linear and bilinear models. The damage threshold in this model (IMCS ≥ 5, PGA ≥ 28 cm/s2), corresponds to the trend of the slope n > 2.73 which is in good agreement at intersection points with Wald et al. (5 ≤ I ≤ 8), Caprio et al. (5 ≤ I ≤ 9), Masi et al. (5 ≤ IMCS ≤ 10–11) and Tselentis and Danciu which has reported that earthquakes in Greece cause damage when PGA exceeds 90 cm/s2 (I > VI). Our model has higher slope (n > 4.4) than those quoted in Fig. 9 (Table 1) from the trend observed for high macroseismic intensities (IMCS > 8) and PGA > 200 cm/s2.

Fig. 10
figure 10

Comparison of the slope n of the Macroseismic Intensity-PGA relationship obtained in the present study (Eq. 1; coefficients Table 3) with relationships from previous studies: a Equation (3); b Equation (4)

Full size image

Although several earthquakes are common with respect to the calibration dataset used in Faenza and Michelini (2010) and Zanini et al. (2019), the main differences are due to the addition of new and updated data (DBMI15, ITACA 3.0) (Table 1), and to the use of a nonlinear model which allows more reliable predictions of the macroseismic intensity in correspondence of the highest recorded PGAs.

6 Application to the probabilistic seismic hazard

The empirical relationships between macroseismic intensity and PGA can be used for converting the seismic hazard map in terms of intensity (Fig. 11a; Gomez Capera et al. 2010) with a probability of exceedance of 10% in 50 years, into PGA map using the empirical relationship given by Eq. 2 (Fig. 11b). The maximum value is equal to 0.33 g for a site located in Southern Italy, such value corresponds to Imax = 9 MCS in Fig. 11a.

Fig. 11
figure 11

a Official italian seismic hazard map in terms of macroseismic intensity for a probability of exceedance of 10% in 50 years (after Gomez Capera et al. 2010); b Seismic hazard map in terms of intensity (map a) converted in PGA (in g units) values using Eq. 2; c percentage differences between map (b) and map (d);  d Italian seismic hazard map (MPS04, Stucchi et al. 2011) in terms of PGA for a probability of exceedance of 10% in 50 years

Full size image

Figure 11d shows the national seismic hazard map for Italy (MPS04, Stucchi et al. 2011) in terms of PGA (10%/50 years), where the maximum value is equal to 0.28 g. Figure 11c shows the percentage of differences between the maps shown in Fig. 11b, d.

The positive values (shades of blue) indicate areas where the values of the converted map are greater than those of the MPS04. On the contrary, the negative values (shades of red) indicate areas where MPS04 values are greater than those of the seismic hazard map converted in PGA from Imax. The converted map (Fig. 10b) shows a similar range of PGA values of the map directly computed by MPS04 (Fig. 10d). The main differences are in Central and Southern Italy, where the average PGA values obtained from Imax are up to 30% greater than the values of MPS04: the intensity is a measure of ground shaking, independent of site conditions (stratigraphic and/or morphological), while the MPS04 has been derived specifically for rock conditions. On the other side, negative values (up to 30%) in North-East Italy and Northern Apennines could be due to the strong influence of the use of regional empirical ground-motion attenuation relations in MPS04, not accounted in the computation of the map in Fig. 11a.

The shape of the areas (Fig. 11a, b) is different because macroseismic intensity decreases less rapidly with distance compared to PGA (Gomez Capera 2006). However, the proposed seismic hazard map in terms of PGA concurs with the results obtained by MPS04, since the differences between the two maps lies within the range of the uncertainties associated with the hazard evaluation.

7 Discussion and conclusions

The aim of the present study was to provide an updated set of empirical relationships between macroseismic intensity and different ground motion parameters of engineering interest (i.e. PGA, PGV, and SA at T = 0.2 s, 0.3 s, 1.0 s, 2.0 s), valid for Italy.

This kind of empirical correlation is a challenging task, mainly due to the paucity of recording stations generally available nearby inhabited localities with macroseismic observations and the different nature of the data to be correlated. The macroseismic intensity associated to a locality can be considered as a footprint left by the ground shaking on a statistically consistent sample of buildings over a more or less wide area, whereas peak parameters inferred by earthquake time series or spectral amplitudes are instrumental measures of the ground motion recorded by a single station. In addition, the choice of a functional form to reproduce in a reliable way the correlation between the upper degrees of the macroseismic scales and the highest values of the recorded ground motion is a crucial issue.

One of the strengths of this study was the compilation of a well-qualified dataset of I-GMPs pairs available from the DBMI15 and the ITACA databases. The procedure started with a preliminary dataset compiled selecting accelerometric stations from ITACA and macroseismic localities from DBMI15 within 3 km. Subsequently, the similarity in terms of geological and topographical features between recording sites and macroseismic localities has been a posteriori checked to ensure that the macroseismic intensity and the accelerometric datum are, respectively, the qualitative and the quantitative measure of the ground motion due to the same earthquake. The final dataset is constituted by 240 macroseismic intensity-GMP pairs from 67 Italian earthquakes occurred in the time window 1972–2016, with Mw ranging from 4.2 to 6.8 and macroseismic intensity in MCS in the range [2, 10–11]. The 90% of the interdistance between macroseismic observations and strong-motion stations is within 2 km.

The set of empirical relationships between macroseismic intensity and GMPs (and vice versa) was calibrated using an exponential model that allows obtaining more realistic values of the recorded ground shaking in correspondence of the highest values of the macroseismic intensity scale (MCS), compared to other models already proposed in the literature. The choice of a non-linear model instead of linear or bi-linear models commonly employed to calibrate empirical relationships between observed and recorded ground-motion relies on the fact that these latter can be considered as approximations of an exponential functional.

Residual analysis between observed and predicted values of macroseismic intensities and GMPs concludes that the regressions do not depend significantly on either the moment magnitude or the epicentral distance. The standard deviations calculated over the complete dataset are between 1.0 for PGV and 1.4 for SA2.0 s and between 0.34 (SA0.3 s) and 0.52 (SA2.0 s), for direct I(LogGMP) and inverse LogGMP(I) models, respectively. Peak Ground Velocity (PGV) is the best predictive instrumental measure of macroseismic intensity (IMCS), because it provides the lowest uncertainty.

Although the approach adopted during this study aim at reducing the degree of subjectivity of the macroseismic localities and the recording station association, our future plan is to establish a more rigorous procedure to associate macroseismic and accelerometric data, taking also into account the possibility to attribute to each I-GMPs pair a quality index and to evaluate the influence of differently weighted I-GMPs on the calibration of empirical relationships.

The empirical relationships here proposed can be easily employed to convert already existent seismic hazard maps in terms of GMPs to macroseismic intensity (and vice versa) and for shakemaps implementation.

In the end, we recommend the use for the Italian territory of the relationships here presented as they are the most updated ones characterized by a wider applicability range in terms of macroseismic intensity compared to previous models.