Loss of support assessment for precast portal frames with friction connections and masonry infills

Abstract

The loss of support of beam elements in Italian precast buildings is one of the main vulnerabilities recorded in past earthquakes. The reason for beam falling is due to the absence of adequate structural details in the beam-column joints, which were typically relying on friction for buildings located in regions previously classified as non-seismic prone. To guarantee the structural safety of the whole existing building stock, this collapse mechanism must be further investigated; in this regard, it could be interesting to evaluate the level of safety achieved by simple beam-column friction connections to allow, for instance, the prioritization of the retrofit interventions to guarantee a minimum level of safety in a wide range of structures. The paper investigates the influence of the parameters governing the beam-column relative displacements in the case of friction connections to establish criteria for evaluating the seismic loss of support probability in existing precast buildings. A simplified analytical model is introduced to describe single and double portal frames with and without the presence of stiff masonry infills. The influence of the epicentral distance on the results obtained is also preliminary addressed. Nonlinear time history analyses are carried out on a 2D finite element model to validate the effectiveness of the simplified model taking as reference a building that experienced the loss of support of a main beam during a past earthquake.

1 Introduction

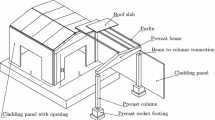
The high-quality control of the materials and the short construction time have led to the wide use of precast concrete structures in the Italian and European industrial and commercial building sectors. The typical structural layout of such buildings consists of a single story with a regular plan with reinforced concrete (RC) precast columns simply supporting prestressed beams and prestressed roof elements. A great share of these structures has been designed before the enforcement of modern anti-seismic regulation codes and their seismic vulnerability has dramatically been shown in the seismic events that occurred in 2012 in the Italian regions of Emilia-Romagna, Veneto, and Lombardia (Belleri et al. 2015a, b; Belleri 2017; Ercolino et al. 2016; Bournas et al. 2014; Magliulo et al. 2014, 2021; Minghini et al. 2012, 2016; Nastri et al. 2017; Palanci et al. 2017; Clementi et al. 2016).

Various inspections and research activities carried out after the aforementioned earthquake addressed the main collapse mechanisms (Brunesi et al. 2015; Belleri et al. 2016, 2017; Lago et al. 2018; Torquati et al. 2018; Iervolino et al. 2019; Ercolino et al. 2018; Bosio et al. 2020; Savoia et al. 2017; Bressanelli et al. 2021a). The loss of the beam-column support represents one of the main reasons of the building local collapse and a research topic to be further investigated; other local collapse mechanisms are associated with the failure of the RC out-of-plane restraints at top of the columns and subsequent out-of-plane overturning of the supported beam, the collapse of masonry infill panels, the failure of the cladding system, and the ultimate rotation of the column at the plastic hinge at the base (Toniolo and Colombo 2012; Biondini et al. 2013; Colombo et al. 2016; Menichini et al. 2020). A typical vulnerability for these old buildings is the absence of adequate structural details in the connections between the structural elements, which often rely solely on friction for the horizontal load transfer in the case of buildings located in sites not classified as seismic at the time of construction (Lago and Ferrara 2018; Dal Lago et al. 2016; Rodrigues et al. 2021; Zoubek et al. 2015).

In the literature, research works investigated the behaviour of precast structures with simple frictional beam-column connections through 2D and 3D nonlinear finite element models, as for instance assuming the influence of the amount of steel reinforcement (Liberatore et al. 2012; Bosio et al. 2021; Biondini and Toniolo 2009) or different values of the friction coefficient (Magliulo et al. 2008; Titi et al. 2018; Demartino et al. 2017). Other researchers have proposed the introduction of mechanical devices between the beam and the columns (Belleri et al. 2015b; Bressanelli et al. 2021b; Magliulo et al. 2017; Pollini et al. 2021; Martinelli and Mulas 2010; Belleri and Labò 2021; Sousa et al. 2020) to avoid the loss of support. Magliulo et al. (2014) and Belleri et al. (2015a) evaluated the minimum value of the friction coefficient required to avoid the sliding of the beam under the hypothesis of perfect correlation between the maximum values of the horizontal and vertical component of the seismic input. To investigate the most influential variables of the sliding condition in beam-column connections, (Demartino et al. 2017) introduced a simplified two degrees of freedom elastic rigid block model; furthermore, through 2D and 3D analyses developed with the software OpenSees, the risk of loss of support at frictional beam-column connections under seismic actions using typical characteristics of buildings was highlighted. The results showed that the loss of support depends on the friction coefficient, the horizontal and vertical fundamental periods of vibration of the structure, and the damping coefficient.

Although some research works investigated the influence of some parameters involved in the beam-column loss of support, other components not considered in the investigated simplified models may affect the behaviour of the structure. The evaluation of the influence of such parameters may help in addressing the risk of beam-column loss of support, the prioritization of the retrofit interventions, and it could provide useful information especially in low seismicity sites where, for example, the retrofit of the connection may not be everywhere necessary with the same priority level. This is the case, for instance, in which the length of the support is sufficiently wide to limit the loss-of-support risk.

The present paper proposes a new analytical and comprehensive model for the evaluation of the seismic response and provides indications on the influence of various parameters in relation to the loss of support. The main novelty introduced relies on the simplified model proposed which allows accounting for the column nonlinear behaviour, the friction coefficient, the horizontal and the vertical components of the seismic events, the presence of infills between the columns, and multiple layouts of precast portal frames. The precast portal frame is herein described by means of a dynamic system with four degrees of freedom (DOF): 3 horizontal and 1 vertical. The system could be further extended to a seven degrees of freedom model to account for the presence of an adjacent portal frame. The numerical model of the single portal frame is described in detail in Sect. 2, while the numerical description of the double portal frame is reported in "Appendix". In Sect. 3, parametric analyses are carried out to evaluate the influence of the main parameters on the beam-column relative displacement; preliminary considerations on the presence of asymmetries and the influence of the epicentral distance on the results are also drown. Monte Carlo analyses are carried out considering the most influencing parameters highlighted in the sensitivity analyses. Fragility curves are derived to assess the probability of the beam loss of support for different situations. In Sect. 4, the numerical model is validated by means of nonlinear time history analyses carried out on a selected case study resembling a portal frame of an existing building hit by the Emilia seismic sequence. The results of the analyses show the efficiency of the proposed simplified analytical formulation in addressing the possible risk of beam loss of support.

2 Simplified system development

This section describes the simplified 4 degrees of freedom (DOF) system used to describe the transverse response of a typical portal-like frame of single-storey precast industrial buildings (Fig. 1a). The proposed simplified model allows to analytically evaluate the equations of motion and it stems as an enhancement of previous research works in which few DOF system models were adopted (Demartino et al. 2017; Pompei et al. 1998; Taniguchi 2002; Lopez Garcia and Soong 2003a, b).

Fig. 1

a simplified 4-DOF system; b simplified 7-DOF system adopted to simulate the behaviour of the double portal frame; c, d layouts of a typical portal-like precast industrial building with and without infills highlighting the transfer of roof inertia force on the columns

Existing models consist of a rigid block model that is related to a single degree of freedom or a two-degree-of-freedom elastic model. In the first type, the behaviour of the friction beam-column connection is represented by a rigid block simply resting on a surface on which it can slide; in the second type, the portal frame is described through a system of equations which considers the elastic stiffness of the columns through an overall value. The two types of models are useful for describing the elastic behaviour of single portal frames for which the values of horizontal and vertical periods are assumed a priori; herein, the proposed model considers the case of multiple portal frames, non-linearity in the columns, the influence of the beam vertical modes of vibration and the presence of infills.

2.1 Simplified model setup

The simplified model considers the transverse response of single portal frames. In the case of a single portal frame (Fig. 1a), the lateral behaviour of the two columns (referred to as element 1 and element 3) and the horizontal beam (element 2) is described through a system characterized by three horizontal DOFs (u₁, u₂, u₃) plus one vertical DOF (v₂); the simplified system consists of three masses (m₁, m₂, m₃) connected by springs (k₁, k₁₂, k₂₃, k₃) and viscous dampers (c₁, c₃) and subjected to the ground horizontal and vertical accelerations ($\ddot{X}_{g} ,\ddot{Y}_{g}$).

Considering Fig. 1, the subscripts refer to the element considered or, in the case of connections, to the elements that are connected by the link (e.g., subscript-i refers to the element- i, while the subscript—ij refers to the link between the element-i and the element-j). Element 1 and element 3 (i.e., the two columns) are described by the masses m₁ and m₃ (i.e., corresponding to the participating mass of the columns and to the mass of possible supported elements such as gutter beams), the elastic lateral stiffnesses k₁ and k₃, the damping coefficients c₁ and c_3, and, to consider the nonlinear behaviour of the columns, the yielding forces F_y,1 and F_y,3, respectively. Element 2 (i.e., the beam), represented by the mass m₂ (i.e., corresponding to the beam mass and to the roof tributary mass), is connected to element 1 and element 3 through links representing herein a simple friction beam-column connection. The stiffnesses k₁₂ and k₂₃ describe the elastic stiffnesses of the connections (as for instance the stiffness of neoprene pads) before the friction forces (F_y,12 and F_y,13) are reached; the same friction coefficient was used for both static and dynamic behaviour. As for the vertical component, the generalized mass (M_n2) and the generalized stiffness (K_n2) are introduced to represent the participating mass and stiffness of the n-th vertical mode of this element (Chopra 1995).

In the case of an infill panel between the columns, its influence has been considered by introducing additional horizontal nonlinear springs whose behaviour is described by the function f(u_i); such function exhibits a stiffness equal to the elastic stiffness of the infill (k_Ii—for the infill; for the single portal frame, i is 1) in case the column moves inwards while a stiffness equal to zero when the column moves outwards (Fig. 1a) (i.e. supposing a compression-only contact). The nonlinear behaviour is accounted for by introducing the failure force of the infills (F_P,I1) as the maximum force reachable by the spring when the columns move inwards. A stiffness and force reduction factor can be eventually introduced to account for the presence of openings in the infill panels. Similar considerations can be extended for the double portal frame (Fig. 1b). In such case, the possible interaction between the two beams (element 2 and element 4) is accounted for by the spring k₂₄ (Fig. 1b). This spring exhibits similar behaviour to the infills one: it shows a high stiffness when the relative displacement between the two horizontal beams is less than zero, while a stiffness equal to zero otherwise. In general, the relative displacement between the DOF-j and the DOF-i is referred to as δ_ij (for instance, δ₁₂ is the difference between u₂ and u₁).

It is worth noting that under actual conditions (Fig. 1c) the roof horizontal inertia forces act at a higher level than the beam-column connections. Such an eccentricity generates an overturning moment that modifies the vertical reaction at the beam-column friction connections; these loads, which reduce as the span increases, are not accounted for in the proposed simplified approach.

2.2 Equations of motion and solving method

The free-body model of the 4-DOF system used to describe the single portal frame is represented in Fig. 2 while the double portal-frame case is provided in "Appendix".

Fig. 2

Free-body diagrams of the 4-DOF system

By enforcing balance to the horizontal translation of element 1, and element 3, it yields:

$$m_{1} \ddot{u}_{1} + k_{1} u_{1} + f\left( {u_{1} } \right) + c_{1} \dot{u}_{1} - k_{12} \left( {u_{2} - u_{1} } \right) = - m_{1} \ddot{X}_{g}$$

(1)

$$m_{3} \ddot{u}_{3} + k_{3} u_{3} - f\left( { - u_{3} } \right) + c_{3} \dot{u}_{3} + k_{23} \left( {u_{3} - u_{2} } \right) = - m_{3} \ddot{X}_{g}$$

(2)

The horizontal equilibrium on the element 2 is

$$m_{2} \ddot{u}_{2} + k_{12} \left( {u_{2} - u_{1} } \right) - k_{23} \left( {u_{3} - u_{2} } \right) = - m_{2} \ddot{X}_{g}$$

(3)

The vertical displacement of the element 2 (DOF-2), expressed through its time-derivative in principal coordinates (Chopra 1995), is

$${\raise0.7ex\hbox{${\partial v}$} \!\mathord{\left/ {\vphantom {{\partial v} {dt}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dt}$}} = \left[ { - K_{n2} v_{2} - c_{n2} \dot{v}_{2} - M_{n2} \ddot{v}_{2} } \right] \cdot \frac{1}{{M_{n2} }}$$

(4)

Considering the vertical modes of vibration of the beam (herein treated as a simply supported beam with uniformly distributed mass, i.e. the mass corresponding to the roof tributary area), the equation of the n-th mode of vibration can be derived by substituting in Eq. (4) the corresponding values of M_n2(n) and K_n2(n) (Chopra 1995):

$$\begin{gathered} M_{n2} = {\raise0.7ex\hbox{${m_{2} }$} \!\mathord{\left/ {\vphantom {{m_{2} } 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}} \hfill \\ K_{n2} = \frac{{n^{4} \pi^{4} EI}}{{2L^{3} }} \hfill \\ \end{gathered}$$

(5)

where n is the number of the vertical mode considered, E and I are the elastic modulus and the inertia moment of the horizontal beam, respectively, and L is the length of the beam. In this work, the damping coefficient (c) of the various elements is calculated according to a viscous damping model.

From the vertical displacement expressed in principal coordinate, the shear on the beam at each time instant V(x,t) can be derived for each vertical mode (n-th); the total shear that arises on the beam can be calculated as the sum of the contribution of each vertical mode:

$$\begin{gathered} V\left( {x,t} \right) = \mathop \sum \limits_{1}^{n} \left[ {EI\left( x \right)\Phi_{n}^{^{\prime\prime}} \left( x \right)} \right]^{^{\prime}} \cdot v\left( t \right) \hfill \\ \Phi_{n}^{^{\prime\prime}} \left( x \right) = {\raise0.7ex\hbox{${\partial^{2} \Phi }$} \!\mathord{\left/ {\vphantom {{\partial^{2} \Phi } {dx^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dx^{2} }$}} = - C_{1} \cdot \sin \left( {\frac{n\pi x}{L}} \right) \cdot \left( {\frac{n\pi }{L}} \right)^{2} \hfill \\ \end{gathered}$$

(6)

where C₁ is a constant that, for the considered case, is equal to 1 (Chopra 1995). The total vertical force on the column—i (N_i) can be calculated by the algebraic sum of V(x,t) and the shear related to the static load (i.e., $0.5 \cdot m_{2} g$).

The inelastic behaviour of the columns and the general link simulating the simple beam-column friction support is modelled by the Bouc-Wen hysteresis law (Wen 1976). Considering each column, its nonlinear behaviour is accounted for by substituting $k_{i} u_{i}$ in Eqs. (1 and 2) with $P\left( t \right)_{column}$:

$$P\left( t \right)_{column} = \alpha \cdot k_{i} \cdot u_{i} + \left( {1 - \alpha } \right)k_{i} \cdot \delta_{y,i} \cdot Z\left( t \right)$$

(7)

where -i refers to the element considered, α is the post yielding stiffness ratio, and Z is an internal variable whose behaviour is described by its derivative:

$$\frac{dZ}{{dt}} = \left( {\frac{1}{{\delta_{y,i} }}} \right) \cdot \left( {\dot{u}_{i} - \gamma \cdot \left| {\dot{u}_{i} } \right| \cdot Z\left( t \right) \cdot \left| {z\left( t \right)} \right|^{\eta - 1} - \upsilon \cdot \dot{u}_{i} \cdot \left| {z\left( t \right)} \right|^{\eta } } \right)$$

(8)

η, ν, and γ are dimensionless quantities: η governs the smoothness of the curve in the proximity of the yielding point (i.e., the lower the value of η, the smoother the transition between the elastic and post-yield branch); ν and γ control the size and the shape of the hysteretic loop with the constraint of |ν | +|γ|= 1. In this work ν = γ = 0.5. The interested reader is referred to, for instance, (Zhang et al. 2021) for a deeper insight of such parameters. In this case, the reference yielding force of the hysteretic model is derived as a function of the characteristics of the column, and it is introduced through the parameter $F_{y,i} = k_{i} \cdot \delta_{y,i}$ in (7).

A similar procedure is implemented for the nonlinear general link simulating the simple friction beam-column support as shown in Eq. (9):

$$P\left( t \right)_{friction} = \alpha \cdot k_{ij} \cdot u_{ij} + \left( {1 - \alpha } \right) \cdot \left( {\mu \cdot \left( { \pm V\left( {x,t} \right) + M_{n} g} \right)} \right) \cdot Z\left( t \right)$$

(9)

where the subscript − ij is equal to − 12 and − 23 for the left and the right connection, respectively, and u₁₂ and u₂₃ refer to the relative displacements between the beam and the columns (u₂–u₁ and u₃–u₂), respectively. Moreover, to simulate the simple friction support, the reference “yielding forces” of the links (F_y,ij) are derived according to Coulomb’s Law. Considering a friction coefficient μ at the column (element-i) and beam (element-j) interface, Coulomb’s Law defines the friction force (F_y,ij) as the product between μ and the total vertical force acting on the top of the column-i (N_i).

To account for the presence of an infill panel, a S-shaped (logistic) distribution $f\left( {u_{i} } \right)$ has been algebraically summed to P(t)_column:

$$f\left( {u_{i} } \right) = \frac{B}{{1 + e^{{ - s\left( {u_{i} - u_{0} } \right)}} }}$$

(10)

The considered curve is a function of the displacement of the element-i (u_i); its mean value (u₀), logistic growth rate (s), and scaling factor (B) have been selected to fit the considered infill curve (Eq. 10). The graphical representation of the considered hysteretic models is reported in Fig. 3.

Fig. 3

Reference hysteretic cycles for: a Bouc-Wen model used for the columns and the friction beam-column connection (friction parameters in square brackets); b logistic function used to model the infills

The differential equations of motion are solved with the function Ode45 (The MathWorks and Matlab 2017), a versatile ordinary differential equation solver that adopts the Runge–Kutta method with a variable time step. The algorithm requires the conversion of the second-order differential equations into an equivalent system of first-order equations. The nonlinear functions (Eqs. 7, 9, 10) were selected because they are continuous functions, as required by the solving algorithm. It is worth noting that the proposed simplified model is also suitable to represent beam-column dowel connections instead of simple friction connections by adapting the parameters of the Bouc-Wen hysteresis. Similar considerations apply for the case of a double portal frame ("Appendix").

Finally, it is highlighted that the degree of coupling between peripheral and inner portal frames due to a possible diaphragm behaviour of the roof is not directly captured herein. However, it is worth to note that in the case of precast roof elements laying on friction connections and not connected through each other, the degree of coupling provided by the roof is limited and the inner and peripheral frame could be preliminary approximated as uncoupled. On the other hand, in the case of a rigid roof diaphragm, as for instance by means of an additional RC topping on the roof, the higher lateral stiffness of the peripheral infilled frames compared to the inner ones would attract a higher seismic roof tributary area, as in the case of an elastic beam (roof diaphragm) laying on springs (portal frames). Therefore, by selecting the appropriate roof tributary area for the frames it would be possible to preliminary account for the influence of a roof diaphragm.

3 Sensitivity analysis

For the sensitivity analysis, the reference parameters used to represent the mean geometry of existing precast buildings (L_b = 10.64 m, L_i = 6.68 m, H = 5.27 m) are derived from Casotto et al. (2015), where L_b and L_i are the span of the main beam and the distance between two consecutive frames, respectively. Given the geometry of the building, the column cross-section is determined considering the load resulting from a roof dead-load and live-load equal to 2.4 (kN/m²) and 0.5 (kN/m²), respectively. It is worth noting that the live load is not considered in the seismic mass definition. The masses m₁ and m₃ are taken equal to half of the self-weight of each column; the elastic stiffnesses k₁ and k₃ are calculated from the geometry of the columns and account for a 50% reduction of the elastic modulus of the reinforced concrete due to cracking.

3.1 Parametric analyses and preliminary considerationsd

The input parameters considered in the parametric analyses are summarized in Table 1.

Table 1 Input parameters varied in the parametric analyses

Parametric analyses are conducted to account for various levels of seismic design. In this regard the factor q is introduced and defined as the ratio between the elastic seismic demand and the nonlinear lateral capacity. This factor could be thought as a behaviour factor in respect to the considered earthquakes. Higher values of q may also simulate the case of buildings not designed for seismic loads, provided that enough ductility is available. For the columns, the nonlinearity parameters of the Bouc-Wen model (Eqs. 7 and 8), i.e. η, ν, and γ, are set equal to 1, 0.5, 0.5, respectively, and the post yielding ratio is set equal to 0.001. The friction coefficient μ is varied among the values 0.13 to simulate a neoprene-concrete interface (Bosio et al. 2020) and 0.5 to consider a concrete-concrete interface (PCI design handbook, 1985). The parameters used to describe the Bouc-Wen hysteresis for the friction connections, i.e. η, ν, and γ, are set equal to 25, 0.5, 0.5, respectively, and the post yielding ratio is set equal to 0.001. The stiffness of the Bouc-Wen hysteresis of the friction support is set equal to 49,000 N/m (Bosio et al. 2020) for μ = 0.13, while it is assumed significantly higher (k_ij = 4,900,000 N/m) when the friction coefficient is set equal to 0.5. The cases with and without the vertical DOF are performed to evaluate the influence of the vertical component of the ground motion. When the vertical DOF is considered, the presence of higher modes of vibration is also investigated (2nd and 3rd modes). The damping ratio of the vertical mode of the beam (ξ₂) is set equal to 0.01 (Demartino et al. 2017); while the damping coefficients c₁ and c₃ are considered equal and they are calculated from the damping ratio ξ indicated in Table 1 (with − i equal to 1 or 3). In the cases with infill panels, the infill between the two columns is accounted for according to Eq. 10) in which the parameters B, u₀ and s are set equal to 350,000 N, 0.0104 m, and 250 (1/m), respectively, to fit a backbone curve obtained from Hak et al. (2012). It is worth noting that the considered backbone curve (Hak et al. 2012) represents herein an approximation of the actual behaviour because it is based on the results of infills fully enclosed by RC structural elements, while in existing industrial buildings a ribbon window may be present above the infill. The chosen fitting function (Eq. 10), which is continuous as required by the solving algorithm, allowed to capture the asymmetric behaviour of the infill, the elastic stiffness, and the capacity of the infill without discontinuities. The degrading branch after yielding was not modelled, however, it is worth noting that in all the cases evaluated, the loss of the support occurs before the infill panel yielding.

To evaluate the influence of an adjacent frame, the presence of both a bare portal frame (BF), and an infill-portal frame (IF) is investigated in adjacency to a portal frame either without (BF) and with infills (IF). Therefore, four different configurations are proposed: original frame with infills plus added frame with infills (IF-IF), original frame with infills plus added bare frame (IF-BF), original bare frame plus added frame with infills (BF-IF), original bare frame plus added bare frame (BF-BF). For these cases, only the first vertical mode of vibration is considered and the contact between the two horizontal beams is described by means of the same analytical function used for the infills Eq. (10) in which the parameters B is set equal to 5000 N, u₀ to 0.016 m and s to 312 (1/m).

For both the cases of single and double portal frame, the analyses are performed considering Italian seismic inputs: the ground motion recorded in L’Aquila during the 2008 seismic events (AQ: ref. IT-2009-0009, AVZ station, magnitude 6.10 and epicentral distance equal to 35.1 km), in Mirandola during the 2012 seismic events (MRN-1: ref. IT-2012-0008, MRN station, magnitude 6.10 and epicentral distance equal to 16.1 km; MRN-2: ref. IT-2012-0011, MRN station, magnitude 6.0 and epicentral distance equal to 4.1 km), in Amatrice during the 2016 seismic events (AM: ref. EMSC-20161030_0000029, MZ24 station, magnitude 6.50 and epicentral distance equal to 24.5 km). The records were selected among the last relevant Italian earthquakes which caused damage to industrial buildings. The records have different spectral shapes (Fig. 4), however, the assessment of the influence of the record characteristics is beyond the purpose of the paper, whose aim is to provide a tool suitable to preliminary assess the beam-column loss of support and to draw insights on the relevancy of infill panels. For such reasons the results will be presented for each seismic event separately.

Fig. 4

Elastic spectra of acceleration, velocity, and displacement of the selected seismic events. Note: horizontal and vertical direction on the left and right side, respectively. The vertical lines mark the first period of the bare portal frame (BF) and infill-frame (IF) with a neoprene-concrete interface (n–c) or concrete-concrete interface (c–c) at the beam-column joint

For the cases with a single portal frame (Fig. 5), the results are plotted as a function of q in terms of ratio of the maximum observed relative displacement at the friction connection (δ_ij = u_j–u_i) and the maximum relative displacement (δ_R) considering as reference the single portal frame without infill (BF), with ξ₁ = ξ₂ = 3%, μ = 0.13, q = 1, and without the vertical component.

Fig. 5

Parametric analysis results of a single portal frame for the different ground motions considered. Note: for all the ground motions the results are plotted as the ratio between the relative displacement at the friction connection (δ_ij) for the considered case and the reference case (δ_R) i.e., ξ₁ = ξ₃ = 3%, μ = 0.13, q = 1, BF

Considering the cases without infill (left column in Fig. 5), it is observed that the increase of the behaviour factor (q) leads to a decrease of the relative displacement (δ_ij) following an almost linear trend except in the case of Amatrice when the vertical component is considered; in the latter case, the relative displacement increases for higher values of q (up to + 50% with q = 4), probably due to the high value of the vertical acceleration component of this earthquake. In all cases, the reduction of relative displacements associated with increasing q values is lower when the vertical component is considered. The case of Mirandola shows the maximum reduction: − 57% and − 67% for q = 4 considering or not the vertical component, respectively.

The friction parameter (μ) is the parameter that mostly affects the relative displacement at the friction connection with an average reduction between − 70 and − 80% for all the cases investigated when the friction coefficient is increased from 0.13 to 0.50. The damping ratio (ξ) has a limited influence.

The relative displacement between the beam and the column increases for most of the analysed cases by considering the vertical component of the ground motion. The vertical component of the ground motion leads to a variation of the normal action at the sliding surface thus reducing the friction activation force in the case of reduction of the normal action, therefore fostering the activation of the sliding. The maximum increase is shown for Amatrice for q equal to 4 in which the relative displacement is 254% higher compared to the case without the vertical component. δ_ij increases up to + 30% and + 10% in the cases of Mirandola and L’Aquila, respectively (in both cases with q = 4).

Introducing the infill between the two columns (right side of Fig. 5), the relative displacements increase up to almost 3.5 times when the system is in Mirandola or Amatrice, and almost 3 times considering the ground motion of L’Aquila. This is the result of a non-homogeneous distribution of horizontal inertia forces at the connections when the infill panel is introduced: indeed, the presence of an infill constitutes a mono-lateral constraint to the column that moves inwards which forces the activation of the sliding in such column (Fig. 1d). As for the behaviour factor (q), a similar trend of the case without infill can be observed. Also in the case of infill, the friction coefficient (μ) is the most influencing parameter although the reductions observed are lower than the case without infill. The case of Amatrice does not follow the trend identified for the other cases; in this case, the introduction of a higher friction coefficient (μ = 0.50) leads to a higher relative displacement (δ_ij): 1.6 times the value obtained from μ = 0.13. The reason for this behaviour can be linked to a higher acceleration demand associated with the higher friction coefficient. The friction coefficient increase (from 0.13 to 0.5) leads to a fundamental period reduction from 1.12 s to 0.38 s which leads to an elastic acceleration demand from about 5 m/s² to 20 m/s². Similar considerations can be drawn from the velocity spectrum. The influence of the vertical component becomes less relevant in the cases with infills. The higher modes do not significantly affect the system response.

When the double portal frame case is analysed (Fig. 6), the results are reported taking as reference the results of a single portal frame. Both a bare frame (BF) and an infill-frame (IF) are considered for the left side frame, and both a bare frame and an infill-frame are considered for the right-side frame.

Fig. 6

Parametric analysis results of the double portal frame. Note: the results are plotted as the ratio between the relative displacement at the friction connection (δ_ij) for the considered case and the reference case, i.e., δ_R and δ_RI for the BF and IF cases, respectively

The results are reported in terms of the ratio between the maximum relative displacement (δ_ij) of the considered case study and the relative displacement of the single reference portal frame (δ_R when the reference case is a bare frame and δ_R^I when the reference case is an infill-frame). For the reference cases, ξ = 3% and μ = 0.13 are considered and, in all cases, the 1st vertical mode of vibration is accounted for.

When the reference case is a bare frame, a maximum increase of + 76% (with q = 1.0) is observed when an adjacent bare frame (BF-BF) is introduced and + 367% in the case of an adjacent infill-frame (BF-IF) for the case of Mirandola. Moreover, the influence of an adjacent infilled frame becomes more significant by increasing q; a similar trend is observed for L’Aquila. In the case of Amatrice, the influence of an adjacent portal frame is significant for values of q lower than 2.50, while becomes limitedly influent for values of q equal or higher than 2.50 (e.g., variation lower than + 10%).

When the reference case is an infill-portal frame, a well-defined trend cannot be outlined as in the single portal frame case. In general, the results show that the relative displacements in the infill-frame are not significantly affected by the presence of an adjacent portal, either a bare frame or an infill-frame, while the relative displacements of a bare frame increase both in the case of an additional bare frame or infill-frame.

As it concerns the bearing length of the support, specific considerations must be drawn since it determines the assessment of the loss of support. In this regard, the building codes provide different formulations to determine the length of the support; it is worth remembering that in a seismic zone the simple friction support provided by gravity loads was not allowed, however, the past seismic zonation did not include areas that are nowadays considered as seismic regions. Some reference minimum dimensions of the beam-column support are reported in CNR 10025/84 (1985) as (8 + L_b/200) and in DM/1987 (1988) as (8 + L_b/300), with the results in cm and L_b in cm; consequently, for the considered case (L_b = 10.65 m), the minimum dimension of the support would be 13.3 cm and 11.6 cm, respectively. Considering for instance the case of Mirandola, the relative displacement of the reference case (δ_R) is equal to 5.0 cm which is lower than the minimum dimension suggested by both building codes, however, in the presence of an infill panel, the relative displacements would become 15.5 cm, which would lead to the loss of support. Therefore, the presence of infills is detrimental in the case of friction connections.

3.1.1 Influence of asymmetries in the parameters of a single portal frame

The portal frame without infill, with μ = 0.13, ξ₁ = ξ₃ = 3%, accounting for the 1st vertical mode of vibration is considered as reference. Parametric analyses are carried out to investigate how asymmetry in the parameters may affect the relative displacement between the beam and the column (δ_ij); with this aim, only some parameters of the element 3 are changed (Fig. 1a): the elastic stiffness k₃, the mass m₃, the behaviour factor q₃ (therefore a change of the flexural capacity at the base of each column), the friction coefficient μ₃, and the damping coefficient ζ₃. The sensitivity analysis is carried out by changing only one parameter at a time, with respect to the reference parameters, in a range of variation of about ± 10%. The variation of δ_ij with respect to the reference case (i.e., the symmetric case) is represented by means of tornado plots (Fig. 7). The maximum absolute value between δ₁₂ and δ₂₃ is plotted.

Fig. 7

Tornado diagrams representing the variation of δ_ij with respect to the reference case (i.e., the symmetric case)

Similar considerations apply among the GM considered. Generally, asymmetric portal frames exhibit a higher relative displacement between the beam and the column. The stiffness k_i is the most influencing parameter for all the GM but Amatrice, especially for lower values of q, with an increase up to + 15%. In the case of Amatrice, an asymmetric mass leads to a variation of + 45% in the elastic case (i.e., with q equal to 1) while for q greater than 1, the most influencing parameter is k_i. Generally, the mass and the behaviour factor are the other most influencing parameters, although leading to variations of less than 10%. In the case of Amatrice, the other influencing parameter is the coefficient of friction.

3.1.2 Influence of the epicentral distance

Preliminary considerations on the influence of the epicentral distance are reported herein (Fig. 8) in terms of the maximum relative beam-column displacement evaluated through the single portal simplified model considering ξ = 3%, μ = 0.13 and the 1st vertical mode of vibration. The records of the same seismic event at various epicentral distances were retrieved considering a single record per epicentral distance in type C soil category according to EC8 (Eurocode 2004). The analyses were carried out with and without the vertical component of each seismic input.

Fig. 8

Relative beam-column displacement (δ_ij) as a function of the epicentral distance

Fig. 9

Maximum relative beam-column displacement (δ_ij) as a function of the epicentral distance

The results are reported in (Fig. 8) along with the beam-column bearing length according with the national standards DM1987 and CNR10025. A similar trend can be identified for all the considered earthquakes: the relative beam-column displacement decreases by increasing the epicentral distance. Moreover, the lower the epicentral distance, the higher is the spread of the values for a given q (Fig. 8). The relative displacement is higher that the beam-column bearing length defined according with the national standards only in the cases of infill-frame in Mirandola (MRN) and Amatrice (AM). The case of Amatrice (AM) shows the higher influence on the response of the vertical component (Fig. 8). Figure 9 shows the maximum values of the results of each considered earthquake in the case of bare and infill frames. A general influence of the epicentral distance on the loss of support is observed with a higher risk of beam falling for infill frames in the case of shorter epicentral distances, however this should be taken as a qualitative result due to the limited number of analyses and considered seismic events.

3.2 Monte Carlo simulations

Monte Carlo simulations have been also performed. The mean values used in the previous Section are herein expressed in terms of mean and standard deviation of a lognormal distribution taking as reference the distributions reported in Casotto et al. (2015): (10.65 m and 0.30 m), (6.68 m and 0.28 m), and (5.27 m and 0.25 m) for L_b, L_i, and H, respectively. The objective of this section is assessing the probability of loss of support for friction-based beam-column connections considering the aforementioned seismic events; in the case of Mirandola, both the 1st (20/05/2012) and the 2nd (29/05/2012) shocks have been considered. The sensitivity analysis is carried out taking as reference the following parameters: ξ₁ = ξ₃ = 3%, μ = 0.13, V1.

Figure 10 shows the influence of the behaviour factor and the seismic input expressed as the cumulative probability of 1000 realizations for the cases of the bare frame and the infill frame. The results are reported in terms of maximum beam-column relative displacement as a function of q. The reference length of the support in accordance with the CNR10025/84 and DM/87 (i.e., 13.32 cm and 11.55 cm) is represented as dashed and dotted vertical lines, respectively.

Fig. 10

Fragility curves of the single portal frame in terms of the maximum beam-column relative displacement (δ_ij). The vertical dashed and dotted lines represent the lengths of the support calculated according to CNR10025/84 and DM1987, respectively

The results (Fig. 10) well agree with the preliminary considerations drawn in the previous Section: in general, the relative displacement δ_ij decreases with the increase of the behaviour factor (q). With the introduction of the infill, the influence of q slightly decreases, and a large increase of the beam-column relative displacement (δ_ij) is observed. As for the case of Mirandola, the probability of loss of support increases by considering both the shocks, particularly in the case of infills: when an infill portal frame is considered, the probability of exceedance of the lowest target (DM1987) is more than 80% for the 1st shock; 20% for the sole 2nd shock and 100% when considering the whole seismic sequence (1st + 2nd shock). This highlights the importance of considering the whole seismic sequence. As for L’Aquila site, the relative displacements are lower than the limits for both the bare frame and the infill frame despite the curves are very close to the limit in the case of the infill frame. Similar considerations can be drawn for the Amatrice seismic input.

4 Validation through a reference case study

The effectiveness of the numerical model is assessed through the application to an industrial existing building which eventually experienced the beam-column loss of support during the Emilia seismic events of May 20th and 29th, 2012. The case study consists of a double portal-frame precast building located in the municipality of San Felice sul Panaro, in the province of Modena, Italy. The structural details and the post-earthquake damage state were derived from documents filled up after the seismic sequence by technicians and from other research works (Belleri et al. 2015b).

4.1 Description of the case study

The building has a total plan area of 25 × 32 m², each portal frame is 16 m wide and the height under the main beams is equal to 6.1 m (Fig. 11). The bearing structure is made of precast simply supported frames designed according to the regulation codes at that time. The main beam is a double-tapered beam with height assumed ranging between 0.60 and 1.95 m at the ridge (derived from the available post-earthquake pictures). The beams are simply supported and placed inside RC out-of-plane restraints at top of the columns; the portal-to-portal distance is about 6.25 m. The secondary roof system is made of RC precast elements and by panels made of RC beams and hollow bricks; the roof self-weight ranges between 2.40 ÷ 3.70 kN/m². The columns have a square cross-section of 0.40 × 0.35 m² with the higher inertia oriented along the portal frame. The longitudinal reinforcement ratio in the columns was not directly available, therefore it was obtained from a design simulation also considering the minimum prescriptions at that time: a value equal to 0.8% was considered. Infills made by precast panels were present all along the perimeter.

Fig. 11

Floor plan, transversal, and longitudinal section view of the case study building

4.2 Damage state observed after the earthquake

The case study was hit by the seismic events of May 20th and 29th, 2012, and severe damages were found on the structure, both in structural and non-structural elements such as infills. The columns exhibited some damage especially in correspondence of the ribbon glazing system due to the interaction with the infills.

Figure 12 shows the loss of support of the main beam on the perimeter and consequently the collapse of some portions of the roof. The other beam of the portal frame experienced a relative residual displacement of about 8 ÷ 10 cm.

Fig. 12

Selected pictures of the post-earthquake situation (29/05/2012)

4.3 Damage assessment through the analytical model and finite element simulations

The loss of support of the main beam on the perimeter (Fig. 12) is herein assessed through the developed simplified model. Based on the presence of huge entrance openings in the two portals, only the portions of infills in which compression struts may be developed are considered (Fig. 13). The fallen beam was not supported by the central column, which was considered effective only to carry the out-of-plane loads due to wind actions and placed to allow the adjacent driveway opening. For this reason, the central column of the left portal frame is not considered in the model. As for the columns, the mass and the stiffness are derived from the available documentation; the initial stiffness is reduced by 50% to consider concrete cracking. As it concerns the beams, a mean cross-section (0.2 × 0.96 m²) is assumed with a self-weight of 740 kg/m. C28/35 concrete with a characteristic cylindrical strength of 28 MPa and Feb38k steel with a characteristic yield strength of 38 MPa are assumed. The friction coefficient (µ) was assumed equal to 0.13 due to the presence of neoprene pads. The horizontal and vertical damping coefficients assumed in the models are 3% and 1%, respectively.

Fig. 13

Structural model scheme

The model was subjected to the sequence of the two main shocks whose main parameters are reported in Table 2. To adapt these registrations to the site of the case study, the first shock recorded in Mirandola was scaled by 86% according to shake maps. The ground motions were rotated of 19.5° around the vertical axis to meet the orientation of the case study; only a planar analysis of the perimeter portal frame is carried out.

Table 2 Characteristics of the seismic input

To validate the simplified analytical model, a nonlinear dynamic analysis was also carried out on a finite element (FE) model developed with the software MidasGEN (2020) with the same layout depicted in Fig. 13. Beam type elements are used for columns and beams while infills are modelled as truss elements converging in the column at 4.4 (m) height. The roof beams are modelled as elastic elements because damage under the seismic loads on these elements is not expected due to the friction connection. The nonlinear behaviour of the columns is accounted for by means of Takeda hysteresis. The non-linear behaviour of the infills is described by assigning a compression-only behaviour to the struts with a load–displacement relationship derived according to PCI design handbook (1985). The available slip-trilinear model (MidasGEN 2020) is considered; this model allows for energy dissipation and for a degrading branch after reaching the infill capacity.

As for the constraints, columns are fixed at the base while the beam-column connection is modelled using a “Friction Pendulum” general link due to the lack of Coulomb friction models in the considered software. The parameters of the friction pendulum model are the initial stiffness (490 kN/m), the friction coefficient (0.13), the radius of curvature (5 m), and the hysteretic loop parameters a and b (both equal to 0.5) (MidasGEN 2020). The FE model provides a slightly higher lateral stiffness compared to the simplified analytical model (1980 kN/m compared to 1690 kN/m), which leads to a corresponding fundamental period of vibration of 1.1 s, compared to 1.2 s of the simplified model. Figure 14 shows the results obtained from the FE model and the simplified analytical model in terms of relative and absolute maximum displacement of the main elements of the portal frame. The results are expressed in terms of displacements of the main elements of the left and right portal frames according to the nomenclature of the simplified model (Fig. 1a). The lowest displacement of the simplified analytical model is recorded in element 3 (u₃), which is reasonable considering that the column in common (element 3) has infills on both sides. The element 5 (right column of the right portal frame) moves only in a positive direction because inwards movements are prevented by the infill. Horizontal beams (u₂, u₄) display the highest displacements in the negative direction in accordance with the eventual collapse mechanism. It is worth noting also that if the beam of the right-side portal frame (u₄) has a significant displacement in the negative direction, it does not fall thanks to a large seating. The values of the beam-column relative displacements δ_ij occurring between the central column (element 3) and the horizontal beams is consistent with the damage detected after the earthquake on the case study for which a relative displacement of 8 ÷ 10 (cm) was associated with the loss of support. From the comparison of the results between the analytical and the finite element model, it is observed that the analytical model predicts the relative beam-column displacements of a double portal with an overall reasonable accuracy. Therefore, the developed analytical model is suitable for a preliminary check of the loss of support of bare and infill portal frames as for instance when addressing this vulnerability at a regional scale.

Fig. 14

Relative (a) and absolute (b) maximum displacement of the main elements of the portal frames

5 Conclusions

In this paper, a simplified model to evaluate the behaviour of precast portal frames with beam-column friction connections was presented. The model accounts for the actual column flexural capacity through the behaviour factor (q), the friction coefficient (μ), the horizontal and the vertical components of different seismic events, the presence of infill between the columns, and single and double portal frames. Parametric analyses were carried out. The results showed that the friction coefficient (μ) is the parameter that most significantly affects the relative displacement between the columns and the beam. The vertical component of the ground motion should be accurately considered in the evaluation of the beam loss of support: if the vertical component of the ground motion is not considered, the relative displacement would be underestimated especially when the vertical component of the seismic event is high (e.g., in the cases of Amatrice in which an increment of + 154% was obtained) and for high behaviour factors (q). The relative displacement (δ_ij) is significantly affected by the presence of infills between the columns; as an example, when an infill is introduced in the cases of Mirandola and Amatrice, the beam-column relative displacement increases up to 3.5 times with respect to the bare frame case.

The presence of an adjacent portal frame significantly affects the response in terms of relative displacements. When the reference case is a bare frame, the presence of an adjacent portal frame always increases the relative displacement between the beam and the column in the reference frame. Otherwise, for an infill-frame as reference, the presence of an adjacent portal frame does not always involve an increase of δ_ij. It is worth noting that this does not mean that the presence of an adjacent portal frame is beneficial for the reference one.

In addition, the presence of asymmetric parameters leads to an increase of the relative displacement; in most cases, mass, stiffness, and the behaviour factor are the most influencing parameters although, generally, such increases are not significant when the parameters are varied in the range ± 10% (up to + 15%). Only in the case of Amatrice, an asymmetric mass leads to a variation of + 45% in the elastic case (i.e., with q equal to 1).

Sensitivity analyses were performed to assess the probability of loss of the beam-column support associated with past earthquake events that hit Italy (Mirandola, L’Aquila, and Amatrice). The records were selected among the last relevant Italian earthquakes which caused damage to industrial buildings. However, the detailed assessment of the influence of the record characteristics was beyond the purpose of the paper. In general, the results highlighted that the earthquake of Mirandola is the most demanding earthquake in terms of beam-column relative displacements especially if the entire seismic sequence is considered. In addition, some preliminary considerations could be made on the influence of epicentral distance: the shorter the epicentral distance the higher the risk of loss of support particularly for the portal frame with infills.

The simplified model was validated taking as reference a case study hit by the seismic events of May 20th and 29th, 2012. A finite element model was also developed for comparison purposes. The comparison between the results of both the analytical and the numerical models and the damage observed after the earthquake suggest that the simplified analytical model is suitable for capturing the overall behaviour of the main structural elements during the earthquake. In particular, the order of magnitude of the maximum relative displacement in the beam-column connections is consistent with what observed from the actual damage.

It is worth noting that the simplified model provides a preliminary assessment tool for the beam-column loss of support in the case of industrial portal frames with and without infills. Such results could be used to draw preliminary considerations about the building seismic vulnerability and to address, for instance, the prioritization of the retrofit interventions. In addition, the model could be extended and applied for the fragility assessment of beam-column loss of support at a regional scale. As additional future developments, the model could be adapted to conduct fragility analyses also in the case of beam-column mechanical connections (e.g., dowel connections) as long as the Bouc-Wen hysteresis is suitable to represent the connection nonlinearity. Finally, the simplified model could be extended and adapted for the evaluation of the loss of support of roof elements from their supporting beams in the case of simple friction connections.

Appendix

The free-body model of the simplified system used to describe the double portal frame is represented in Fig. 

Fig. 15

Free-body diagrams of the 3DOF system

15.

By enforcing balance to horizontal translation to element 1, element 3, and element 5, it yields:

$$m_{1} \ddot{u}_{1} + k_{1} u_{1} + f\left( {u_{1} } \right) + c_{1} \dot{u}_{1} - k_{12} \left( {u_{2} - u_{1} } \right) = - m_{1} \ddot{X}_{g}$$

(A1)

$$m_{3} \ddot{u}_{3} + k_{3} u_{3} - f\left( { - u_{3} } \right) + f\left( {u_{3} } \right) + c_{3} \dot{u}_{3} + k_{23} \left( {u_{3} - u_{2} } \right) - k_{34} \left( {u_{4} - u_{3} } \right) = - m_{3} \ddot{X}_{g}$$

(A2)

$$m_{5} \ddot{u}_{5} + k_{5} u_{5} - f\left( { - u_{5} } \right) + c_{5} \dot{u}_{5} - k_{45} \left( {u_{5} - u_{4} } \right) = - m_{5} \ddot{X}_{g}$$

The horizontal equilibrium on the element 2 and element 4 is

$$m_{2} \ddot{u}_{2} + k_{12} \left( {u_{2} - u_{1} } \right) - k_{13} \left( {u_{3} - u_{2} } \right) + k_{24} \left( {u_{2} - u_{4} } \right) = - m_{2} \ddot{X}_{g}$$

(A3)

$$m_{4} \ddot{u}_{4} + k_{24} \left( {u_{4} - u_{2} } \right) + k_{34} \left( {u_{4} - u_{3} } \right) - k_{45} \left( {u_{5} - u_{4} } \right) = - m_{4} \ddot{X}_{g}$$

(A4)

The vertical DOF2 and DOF4, expressed through their time-derivative in principal coordinates (Chopra 1995), are

$${\raise0.7ex\hbox{${\partial v}$} \!\mathord{\left/ {\vphantom {{\partial v} {dt}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dt}$}} = \left[ { - K_{n2} v_{2} - M_{n2} \ddot{v}_{2} } \right] \cdot \frac{1}{{M_{n2} }}$$

(A5)

$${\raise0.7ex\hbox{${\partial v}$} \!\mathord{\left/ {\vphantom {{\partial v} {dt}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dt}$}} = \left[ { - K_{n4} v_{4} - M_{n4} \ddot{v}_{4} } \right] \cdot \frac{1}{{M_{n4} }}$$

(A6)

For a simply supported beam

$$M_{ni} = {\raise0.7ex\hbox{${m_{i} }$} \!\mathord{\left/ {\vphantom {{m_{i} } 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}$$

(A7)

$$K_{ni} = \frac{{n^{4} \pi^{4} EI}}{{2L^{3} }}$$

where i is equal to 2 and 4 for the DOF2 and DOF4, respectively, n is the vertical mode considered, E and I are the elastic modulus and the inertia moment of the horizontal beam, respectively, and L is the length of the beam. The damping coefficient is calculated according with a viscous damping model.

From the vertical displacement expressed in principal coordinate, the shear on the beam V(x) can be derived for each vertical mode (n-th); the total shear that arise on the beam can be calculated as the sum of the contribution of each vertical mode.

$$V\left( {x,t} \right) = \mathop \sum \limits_{1}^{n} \left[ {EI\left( x \right){\Phi }_{n}^{^{\prime\prime}} \left( x \right)} \right]^{^{\prime}} \cdot v\left( t \right)$$

(A8)

$${\Phi }_{n}^{^{\prime\prime}} \left( x \right) = {\raise0.7ex\hbox{${\partial^{2} {\Phi }}$} \!\mathord{\left/ {\vphantom {{\partial^{2} {\Phi }} {dx^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dx^{2} }$}} = - C_{1} \cdot {\text{sin}}\left( {\frac{n\pi x}{L}} \right) \cdot \left( {\frac{n\pi }{L}} \right)^{2}$$

where C₁ is a constant that, for the considered case, can be assumed equal to 1. It is worth noting that V(x, t) thus defined does not account for the mass m₂; the total vertical force on the column i (N_i) can be calculated by the algebraic sum of V(x,t) and the generalized mass multiplied by the gravity constant ($M_{n} g$).

The inelastic behaviour of the columns, the simple friction beam-to-column connection and the infills can be modelled in the same way of the single portal frame.