Displacement-based design of precast hinged portal frames with additional dissipating devices at beam-to-column joints

Abstract

The seismic performance of precast portal frames typical of the industrial and commercial sector could be generally improved by providing additional mechanical devices at the beam-to-column joint. Such devices could provide an additional degree of fixity and energy dissipation in a joint generally characterized by a dry hinged connection, adopted to speed-up the construction phase. Another advantage of placing additional devices at the beam-to-column joint is the possibility to act as a fuse, concentrating the seismic damage on few sacrificial and replaceable elements. A procedure to design precast portal frames adopting additional devices is provided herein. The procedure moves from the Displacement-Based Design methodology proposed by M.J.N. Priestley, and it is applicable for both the design of new structures and the retrofit of existing ones. After the derivation of the required analytical formulations, the procedure is applied to select the additional devices for a new and an existing structural system. The validation through non-linear time history analyses allows to highlight the advantages and drawbacks of the considered devices and to prove the effectiveness of the proposed design procedure.

1 Introduction

Precast structures have been widely adopted in the industrial and commercial sectors due to their ability to cover large surfaces by means of pre-stressing, to the high-quality control of materials and elements, and to the fast erection sequence if compared to traditional reinforced concrete (RC) structures. Besides these advantages, existing buildings designed before the enforcement of modern anti-seismic building codes may show several criticalities, particularly in the Italian territory (Magliulo et al. 2014a; Belleri et al. 2015a; Ercolino et al. 2016; Minghini et al. 2016), mainly related to the lack of efficient connections between structural elements and to the displacement incompatibility between structural and non-structural elements, such as cladding panels, arising as a consequence of the high flexibility of the building typology (Belleri et al. 2015b, 2016, 2018; Dal Lago et al. 2019; Scotta et al. 2015). The seismic assessment and risk analysis of such structural system highlight the influence of these vulnerabilities (Belleri et al. 2015b; Palanci et al. 2017; Torquati et al. 2018; Bosio et al. 2020).

The damage recorded during past earthquakes was related to a lack of seismic provisions of the damaged facilities rather than intrinsic deficiencies of precast structures. As a matter of fact, most of the severely damaged buildings were built before the enforcement of modern seismic codes and before an accurate seismic classification of the Italian territory. The current Italian building code (Italian Building Code 2018), in accordance to EN 1998–1:2004 (CEN 2004), prescribes the use of mechanical devices as connections between precast elements, although this prescription was mandatory in seismic areas only after the mid-80 s; therefore for old precast buildings or for buildings designed without the current seismic concepts and prescriptions, the horizontal load transfer mechanism of beam-to-column and beam-to-floor connections was left to shear friction with a consequent risk of loss of support (Belleri et al. 2015a; Casotto et al. 2015; Ercolino et al. 2016; Babic and Dolsek 2016; Demartino et al. 2018).

The considered industrial and commercial precast buildings are characterised by a typical structural layout consisting in cantilever columns placed inside cup footings or connected to the foundation by means of mechanical devices or grouted sleeves (Fernandes et al. 2009; Metelli et al. 2011; Belleri and Riva 2012; Dal Lago et al. 2016). The columns are pin-connected (Psycharis and Mouzakis 2012; Magliulo et al. 2014b; Zoubek et al. 2015; Clementi et al. 2016) to pre-stressed beams supporting roof joists made by pre-stressed precast elements. The connections are generally dry-assembled in place in order to speed up the construction sequence. The beam-to-column connections are usually made by dowels; as a result, the resulting joint stiffness is negligible if compared to the flexural stiffness of the connected elements.

In the case of single-storey or few-storey buildings, the columns represent the lateral force resisting system (LFRS) and provide energy dissipation by means of plastic hinges at their base; capacity design needs to be applied to avoid failure at other locations such as at the beam-to-column joint. The LFRS and the high inter-storey height of the considered building typology lead to more flexible structures compared to traditional RC systems. This, in turn, leads to a lower ductility demand and to a design of new buildings typically governed by lateral displacements rather than material strains. Another peculiar aspect is the presence of overhead cranes whose influence may be evaluated according to Belleri et al. (2017a).

The seismic displacement demand of the considered building typology could be reduced by placing additional mechanical devices at the beam-to-column joint for both new and existing buildings (Martinez Rueda 2002; Martinelli and Mulas 2010; Plumier 2007; Belleri et al. 2017b; Pollini et al. 2020; Francavilla et al. 2020; Bressanelli et al. 2021). The provision of additional devices is compatible with the dry-assembly construction system, being the devices put in place at the end of the erection sequence. Such devices can be designed to provide additional energy dissipation to the system and to increase the rotational stiffness of the beam-to-column joint. The latter is not to be sought for the reduction of internal actions in the main elements (particularly the bending moment distribution in the columns) but rather for the reduction of lateral displacements (i.e. reducing damages on nonstructural elements).

This paper provides a design procedure for the selection of additional devices at the beam-to-column joint for both new and existing buildings characterized by hinged beam-to-column connections. The procedure moves from the Displacement-Based Design (DBD) methodology described in Priestley et al. (2007) and represents an extension on the application to hinged frame precast structures (Belleri 2017). The additional devices considered herein are hysteretic dampers, linear or rotational friction devices, re-centring systems and viscous dampers. The proposed procedure is validated by means of non-linear time history analyses on finite element models resembling precast industrial buildings. In particular, the results allow deriving performance differences between each device in the case of new structural systems or as retrofit measure for existing buildings.

Although the sole performance of hinged portal frames with additional devices at the beam-to-column joint is considered herein, other local sources of energy dissipation are possible, for instance, at the roof level (Belleri et al. 2014) or at the building envelope (Scotta et al. 2015; Dal Lago et al. 2017; Nastri et al. 2017).

2 Precast frames with additional devices at the beam-to-column joint

2.1 Considered devices and structural typology

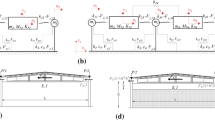
As mentioned before, the analysed structural typology is characterized by columns acting as fix-ended cantilevers hinge-connected to the supported beams; two typical configurations are considered herein: single portal frames and multi portal frames (Fig. 1). The additional devices are conceived to provide both energy dissipation and a degree of fixity at the beam-to-column joint to limit the system lateral displacements during a seismic event.

Fig. 1

Examples of the considered structural typologies

Figure 2 shows examples of the considered devices and their positioning at the beam-to-column joint. A not exhaustive list of possible devices is: linear dampers (viscous, friction or hysteretic), rotational dampers (friction or hysteretic) and stiffening/re-centring devices (cup springs, ring springs, shape memory alloys). A description of friction rotational dampers and re-centring springs is provided in Belleri et al. (2017b) along with a design procedure following a traditional force-based design approach. The devices are intended to be applied at joints either made by RC forks (Fig. 1a) or RC corbels (Fig. 1b). In the case of application to existing buildings, the beam-to-column joints might be reinforced with steel profiles (Belleri et al. 2015b) to carry the load resulting from the joint stiffening (Fig. 2).

Fig. 2

Examples of considered devices at the beam-to-column joint

2.2 General considerations

In this section, general considerations are derived based on the geometry and mechanical characteristics of the considered structural typology and beam-to-column devices. Such considerations will be used in the development of a design procedure in accordance with the displacement-based design methodology.

The devices analysed herein are activated by the relative rotation between beam and column at the beam-to-column joint. Considering the static schemes depicted in Fig. 3, representing the outer column (Case A) and inner column (Case B) of portal frames, the lateral stiffness (k^*) is obtained from the direct stiffness method (Appendix A), respectively:

$$k^{*} = \frac{{3(EI_{c} )}}{{H^{3} }} \cdot \frac{{12(EI_{b} )(EI_{c} ) + 12(EI_{b} )k \cdot H + 2(EI_{c} )k \cdot L}}{{12(EI_{b} )(EI_{c} ) + 3(EI_{b} )k \cdot H + 2(EI_{c} )k \cdot L}}$$

(1)

$$k^{*} = \frac{{3(EI_{c}) }}{{H^{3} }}\frac{{6(EI_{b} )(EI_{c} ) + 12(EI_{b} )k \cdot H + (EI_{c} )k \cdot L}}{{6(EI_{b} )(EI_{c} ) + 3(EI_{b} )k \cdot H + (EI_{c} )k \cdot L}}$$

(2)

where (EI_b) and (EI_c) are the flexural stiffness of the beam and column, respectively; L and H are the length of beam and column, respectively; k is the rotational stiffness of the joint associated with the considered additional device. The static schemes of Fig. 3a and Fig. 3b represent an approximation of the actual behaviour of the system (Fig. 3d), where the additional devices have been replaced by an ideal rotational spring lumped at the beam-to-column joint. As a result, the bending moment diagram on the column is in accordance with Fig. 3c: M_con is the bending moment arising at the connection due to additional beam-to-column devices.

Fig. 3

Beam-to-column representative static schemes: a and b represent an outer and inner column, respectively. c is the considered bending moment diagram on the column. d shows the actual bending moment diagram in the case of additional beam-to-column connections

The rotational stiffness k, ratio between the bending moment arising at the beam-to-column joint and the joint rotation, is derived applying a unit rotation at the beam-to-column joint for each of the considered devices. The flexibility of the beam and column portions is herein neglected owing to the lower stiffness of the devices. The rotational stiffness associated with the existing dowel connection is also neglected (i.e. herein considered as an ideal pin).

Considering the static schemes represented in Fig. 4, the rotational stiffness of the connection is expressed in the following equations, which are valid for one rotational device (Fig. 4a), three rotational devices (Fig. 4b), and one linear device (Fig. 4c), respectively:

$$k_{{rot\_1}} = \frac{{3EI_{{dev}} }}{{b^{3} \left( {2b + h_{b} + h_{c} } \right)}}\left[ {h_{b} \left( {b + h_{b} } \right)\left( {b + h_{b} + h_{c} } \right) + \left( {b + h_{c} } \right)^{2} \left( {b + h_{b} + h_{c} } \right)} \right]$$

(3)

$$k_{{rot\_3}} = \frac{{EI_{{dev}} }}{{4b^{3} }}\left( {56b^{2} + 30h_{b} ^{2} + 30h_{c} ^{2} + 36h_{b} h_{c} + 72bh_{b} + 72bh_{c} } \right)$$

(4)

$$k_{{lin}} = \frac{{EA_{{dev}} }}{{2\sqrt 2 _{{}} b}}\left( {b + h_{b} + h_{c} } \right)^{2}$$

(5)

where EI_dev and EA_dev are the flexural and axial stiffness of the device, respectively. In the case of coupled devices, the rotational stiffness of the connection is the sum of the stiffness of each device (i.e. the devices act as springs in parallel).

Fig. 4

Static schemes adopted for evaluating rotational stiffness of the joint

Given the activation moment of the rotational devices (i.e. M_y,dev,1 in Fig. 4a; M_y,dev,1 and M_y,dev,2 in Fig. 4b) and the activation load N_y,dev (Fig. 4c) of the linear device, the corresponding bending moment (M_con) at the beam-to-column joint, considering the static scheme of Fig. 3 (i.e. a rotational spring lumped at the joint), is respectively:

$$M_{{con,rot\_1}} = \frac{{M_{{y,dev,1}} }}{b}\left( {b + h_{b} + h_{c} } \right)$$

(6)

$$M_{{con,rot\_3}} = \frac{{M_{{y,dev,1}} + M_{{y,dev,2}} }}{b}\left( {b + h_{b} + h_{c} } \right) + M_{{y,dev,2}}$$

(7)

$$M_{{con,lin}} = \frac{{N_{{y,dev}} }}{{\sqrt 2 }}\left( {b + h_{b} + h_{c} } \right)$$

(8)

The corresponding load (F_joint) at the beam-to-column connection (as dowels or other types of mechanical connections) for each device in Fig. 4 is, respectively:

$$F_{{joint,rot\_1}} = \sqrt {\left( {V_{b} - \frac{{M_{{y,dev,1}} }}{b}} \right)^{2} + \left( {\frac{{M_{{con,rot\_1}} }}{{L/2}} - \frac{{M_{{y,dev,1}} }}{b}} \right)^{2} }$$

(9)

$$F_{{joint,rot\_3}} = \sqrt {\left( {V_{b} - \frac{{M_{{y,dev,1}} + M_{{y,dev,2}} }}{b}} \right)^{2} + \left( {\frac{{M_{{con,rot\_3}} }}{{L/2}} - \frac{{M_{{y,dev,1}} + M_{{y,dev,2}} }}{b}} \right)^{2} }$$

(10)

$$F_{{joint,lin}} = \sqrt {\left( {V_{b} - \frac{{N_{{y,dev}} }}{{\sqrt 2 }}} \right)^{2} + \left( {\frac{{M_{{con,lin}} }}{{L/2}} - \frac{{N_{{y,dev}} }}{{\sqrt 2 }}} \right)^{2} }$$

(11)

where L is the beam length. V_b is the column base shear for Case A (Fig. 3) and half the column base shear for Case B. The term in the first bracket corresponds to the axial load at the beam end, while the term in the second bracket corresponds to the shear load at the beam end. It is worth mentioning that Eqs. 9–11 refer to the load in each connection of the beam-to-column joint, therefore assuming one specific beam-to-column connection at the end of each beam.

The roof displacement associated with yielding at the column base (M_y,c), while the top connection is in the elastic range, is for Case A and Case B, respectively:

$$\Delta _{{y,c}}^{A} = \frac{{\phi _{{y,c}} H^{2} }}{3}\frac{{12(EI_{c}) (EI_{b}) + 3(EI_{b}) kH + 2(EI_{c}) kL}}{{12(EI_{c}) (EI_{b}) + 6(EI_{b}) kH + 2(EI_{c}) kL}}$$

(12)

$$\Delta _{{y,c}}^{B} = \frac{{\phi _{{y,c}} H^{2} }}{3}\frac{{12(EI_{c}) (EI_{b}) + 6(EI_{b}) kH + 2(EI_{c}) kL}}{{12(EI_{c}) (EI_{b}) + 12(EI_{b}) kH + 2(EI_{c}) kL}}$$

(13)

where ϕ_y,c is the column curvature at yield (ϕ_y,c = M_y,c/EI_c) and it is evaluated in accordance with available formulations (Priestley et al. 2007; Belleri 2017).

On the other side, while the column base is in the elastic range, the roof displacement associated with yielding at the ideal beam-to-column connection (M_con) is, for Case A and Case B:

$$\Delta _{{y,con}}^{A} = H\frac{{M_{{con}}^{{}} }}{k}\frac{{12(EI_{c}) (EI_{b}) + 3(EI_{b}) kH + 2(EI_{c}) kL}}{{18(EI_{c}) (EI_{b}) }}$$

(14)

$$\Delta _{{y,con}}^{B} = H\frac{{M_{{con}}^{{}} }}{k}\frac{{12(EI_{c}) (EI_{b}) + 6(EI_{b}) kH + 2(EI_{c}) kL}}{{18(EI_{c}) (EI_{b}) }}$$

(15)

The derivation of Eqs. 12–15 is reported in Appendix A. These formulations will be used later in another section. It is worth noting that M_con refers to a single beam-to-column connection; therefore, for Case B the bending moment at the column top is twice M_con.

3 DBD for single-storey frames with additional devices

3.1 Review of the displacement-based design procedure

A brief review of the fundamentals of the direct DBD methodology is reported herein. Priestley et al. (2007) provide a comprehensive description of the DBD procedure for various structural typologies. The DBD utilizes a substitute structure approach (Shibata and Sozen 1976) to define a linear elastic equivalent single degree of freedom system (SDOF) representative of the multi degree of freedom structure. The equivalent SDOF system is characterized by effective properties such as mass (m_eff), height (h_eff), stiffness (k_eff), period (T_eff), and equivalent viscous damping (ξ_eq) associated with a selected target displacement ($\Delta$_d). The effective mass, height and the target displacement are obtained directly from the MDOF-system deflected shape ($\Delta$_i), floor height (h_i) and floor mass (m_i):

$$m_{{eff}} = \frac{{\sum\nolimits_{{i = 1}}^{n} {m_{i} \Delta _{i} } }}{{\Delta _{d} }}$$

(16)

$$h_{{eff}} = \frac{{\sum\nolimits_{{i = 1}}^{n} {m_{i} \Delta _{i} h_{i} } }}{{\sum\nolimits_{{i = 1}}^{n} {m_{i} \Delta _{i} } }}$$

(17)

$$\Delta _{d} = \frac{{\sum\nolimits_{{i = 1}}^{n} {m_{i} \Delta _{i}^{2} } }}{{\sum\nolimits_{{i = 1}}^{n} {m_{i} \Delta _{i} } }}$$

(18)

The deflected shape ($\Delta$_i) represents the first inelastic vibration mode and it is typically obtained from non-linear time history analyses on finite element models of the same structural typology.

The next step is the evaluation of the equivalent viscous damping (ξ_eq), defined as the sum of elastic (ξ_el) and hysteretic (ξ_hy) damping. The former accounts for material viscous damping, radiation damping and nonlinear behaviour of the non-structural components; the latter is associated with the energy dissipation capacity of the system. Typical (ξ_eq) formulations (Grant and Priestley 2005; Dwairi and Kowalsky 2007; Priestley et al. 2007; Belleri 2017) consider the interdependency between (ξ_hy) and the displacement ductility demand (µ_Δ), which is defined as the ratio between the target ($\Delta$_d) and yield ($\Delta$_y) displacement. The equivalent viscous damping is used to scale the elastic displacement spectrum for damping values different from 5%. The substitute structure effective period (T_eff) is the period of the damped displacement spectrum corresponding to the target displacement ($\Delta$_d). The effective stiffness, defined as the secant stiffness at maximum displacement, is obtained from the effective period:

$$k_{{eff}} = 4\pi ^{2} \frac{{m_{{eff}} }}{{T_{{eff}}^{2} }}$$

(19)

The base shear of the MDOF system is the same as the base shear of the SDOF system (V_b). The lateral loads (F_i) on the MDOF system are derived considering the structural deflected shape ($\Delta$_i) and the capacity design is finally applied (Priestley et al. 2007). V_b and F_i are:

$$V_{b} = k_{{eff}} \Delta _{d}$$

(20)

$$F_{i} = V_{b} \frac{{m_{i} \Delta _{i} }}{{\sum\limits_{{i = 1}}^{n} {m_{i} \Delta _{i} } }}$$

(21)

3.2 DBD for hysteretic devices

The typical design approaches available in the case of additional hysteretic dampers have been derived for dampers with stiffness proportional to the main structural system (Lin et al. 2003; Oviedo et al. 2011; Mazza and Vulcano 2014); as a result, the same elastic mode shape is obtained from considering or not the dampers. It has also been shown (Oviedo et al. 2010) that hysteretic dampers with yield drift and strength proportional to the main structural system provide a relatively constant distribution of the ratio between maximum storey drifts. Such formulations are not suitable for the considered structural typology, where the additional devices are activated by the relative rotation between beam and column at the beam-to-column joint. From the general considerations derived in the previous section, a design procedure following the DBD approach is herein proposed according to Belleri (2017).

3.2.1 Step 1: initial data

Select a suitable target displacement, for example 2.5% inter-storey drift for damage control (Calvi and Sullivan 2009; FEMA 450, 2004). Select the column cross-section and the geometry of the additional beam-to-column devices. The latter choice may be based for instance on practical or aesthetic reasons or on available commercial devices. The column longitudinal reinforcement and the hysteretic characteristics of the additional devices will be obtained from the design procedure. The lateral stiffness of the resulting system is determined from Eq. 1 or Eq. 2. Such equations represent an alternative to the exact equations presented in Belleri et al. (2017b) which were derived for a force-based design procedure. The results of the comparison between the two sets of equations are reported in Appendix B.

3.2.2 Step 2: activation load and activation moment of the additional devices

The device should be activated before yielding of the column base to increase efficiency, both in terms of increase of the system dissipated energy and in terms of reduction of the column damage. This task is accomplished by imposing the lateral displacement at yielding of the top connection (Eqs. 14, 15) to be a factor of the lateral displacement at yielding of the column base (Eqs. 12, 13):

$$\Delta _{{y,con}}^{{}} = \gamma \cdot \Delta _{{y,c}}^{{}}$$

(22)

The coefficient γ is taken in the range 0.4–0.6 to assure the activation of the additional devices before the column yielding; such range represents the optimal values for selected devices to reduce damage at the column base, as reported in Belleri et al. (2017b).

Equation 22 allows determining the yield moment (M_con) of the beam-to-column connection for Case A and Case B (Fig. 3), respectively:

$$M_{{con}}^{A} = \gamma \frac{{\phi _{{y,c}} H}}{3}k\frac{{18(EI_{c}) (EI_{b}) }}{{12(EI_{c}) (EI_{b}) + 6(EI_{b}) kH + 2(EI_{c}) kL}}$$

(23)

$$M_{{con}}^{B} = \gamma \frac{{\phi _{{y,c}} H}}{3}k\frac{{18(EI_{c}) (EI_{b}) }}{{12(EI_{c}) (EI_{b}) + 12(EI_{b}) kH + 2(EI_{c}) kL}}$$

(24)

The activation load and activation moment of the additional devices (from Eqs. 6–8) is obtained from the yield moment of the beam-to-column connection. In the case of devices acting in parallel, the connection yield moment is distributed to each device in accordance with its stiffness.

3.2.3 Step 3: substitute structure

The substitute structure characteristics are obtained following the procedure proposed in Belleri (2017). The effective mass (m_eff) is equal to the roof mass, because the system is reduced to a SDOF system by static condensation. The effective height (H_eff) corresponds to the column inflection point (IP in Fig. 3C). It is essential to note that the effective height should be greater than 60% of the height of the column in order to avoid the development of a plastic hinge at the intersection between the column and the additional device. In the DBD procedure this aspect can be controlled by further reducing the coefficient γ in Eqs. 23 and 24.

The inter-storey drift (β) typically governs the design of the considered structural typology. The target displacement of the substitute structure and the displacement ductility are evaluated at a height equal to the column inflection point (Belleri 2017):

$$\Delta _{d}^{{IP}} = \frac{{\phi _{{y,c}}^{{}} H^{2} }}{3}\frac{{\alpha \left( {2\alpha - 1} \right)}}{{\left( {1 + 2\alpha } \right)^{2} }} + \frac{{\beta H}}{{1 + 2\alpha }}$$

(25)

$$\mu _{\Delta } = \alpha \left( {2\alpha - 1} \right) + \frac{{3\beta \left( {1 + 2\alpha } \right)}}{{\phi _{{y,c}}^{{}} H}}$$

(26)

where α is the ratio between the yield moment of the beam-to-column (M_con) and column-to-foundation (M_y,c) connection for Case B and half such value for Case A. For multiple bays the following weighted value is considered:

$$\alpha _{{weighted}} = \frac{{M_{{con}} }}{{M_{{y,c}} }}\frac{{0.5 \cdot n_{{per \ col}} + n_{{int \ col}} }}{{n_{{per \ col}} + n_{{int \ col}} }}$$

(27)

where n_{per col} and n_{int col} is the number of perimeter and interior columns, respectively.

Equation 26 represents the column ductility; the ductility associated with the device is higher owing to its activation before yielding of the column (Eq. 22). Therefore, the device ductility (µ_dev) is:

$$\mu _{{dev}} = \frac{{\beta H}}{{\Delta _{{y,con}} }}$$

(28)

3.2.4 Step 4: equivalent viscous damping

Before evaluating the equivalent viscous damping, it is worth highlighting the role of the beam-to-column connection in resisting the total overturning moment (OTM). Looking at Fig. 5, it is evident how the shear load (V_i) at each beam-end modifies the axial load in the columns, which contributes to counteract the seismic loads OTM. The other source of resistance of the OTM is the sum of the bending moment developed at each column base (M_OTM,col). The OTM contribution (M_OTM,con) provided by the beam-to-column connections is:

$$M_{{OTM,con}} = V_{i} \cdot L_{{tot}} = \frac{{2M_{{con}} }}{L} \cdot L_{{tot}}$$

(29)

Fig. 5

Contribution of beam-to-column connections in resisting the total overturning moment

Equation 29 is valid in the case of equal connections and equal spans with length equal to L. Indeed, in such conditions, the shear load at the left and right sides of the inner columns are equal and opposite. If the equal span and equal connection assumptions do not apply, the contribution of each span to M_OTM,con needs to be computed.

The evaluation of the Equivalent Viscous Damping (Priestley et al. 2007) in the case of various sources of energy dissipation is herein obtained from a weighted average of the hysteretic damping associated with the columns and the connections. Generally, the weights could be directly related to the dissipated energy at each source of energy dissipation (i.e. column base plastic hinges and beam-to-column connections as in Belleri 2017) or, as shown by Sullivan and Lago (2012) for wall-frame dual structures, to the overturning moment (or base-shear) associated with the various structural systems. The last approach is adopted herein.

In the case of the portal frame shown in Fig. 5, the total overturning moment can be calculated as the sum of the bending moment developed at each column base (M_OTM,col) and the OTM contribution (M_OTM,con) provided by the beam-to-column connections (Eq. 29):

$$M_{{OTM,TOT}} = \sum\limits_{{j = 1}}^{m} {M_{{OTM,col_{j} }} } + M_{{OTM,con}} = \sum\limits_{{j = 1}}^{m} {M_{{OTM,col_{j} }} } + \frac{{2M_{{con}} }}{L} \cdot L_{{tot}}$$

(30)

Therefore, the equivalent viscous damping can be evaluated as:

$$\xi _{{eq}} = \frac{{\sum\nolimits_{{j = 1}}^{m} {M_{{OTM,col_{j} }} } \cdot \xi {}_{{hy \ col}} + \frac{{2M_{{con}} }}{L} \cdot L_{{tot}} \cdot \xi {}_{{hy \ con}}}}{{\sum\nolimits_{{j = 1}}^{m} {M_{{OTM,col_{j} }} } + \frac{{2M_{{con}} }}{L} \cdot L_{{tot}} }}$$

(31)

The hysteretic damping for the columns and for the friction slider connections is (Priestley et al. 2007):

(a)

$$\xi _{{hy \ element}} = a \cdot \left( {1 - \frac{1}{{\mu _{\Delta }^{b} }}} \right) \cdot \left( {1 + \frac{1}{{\left( {T_{{eff}} + c} \right)^{d} }}} \right)$$

(32)

where the coefficients a, b, c, d depend on the nonlinear properties (i.e. hysteretic model) of the structural elements (Priestley et al. 2007, Belleri 2017).

3.2.5 Step 5: DBD performance point

Given these premises, it is possible to apply the DBD procedure shown before. The equivalent viscous damping is used to scale the elastic displacement spectrum. The damped displacement spectrum allows deriving the substitute structure effective period and from that the effective stiffness. The effective stiffness is used to determine the system base shear and from that the internal actions in the structural elements and in the devices. This procedure requires iterations, because α (Eqs. 25–26) is unknown at the beginning of the design process; α equal to 0 is suggested for the first iteration.

It is fundamental to note that the proposed procedure can be adopted also for the retrofitting of existing buildings. In the case of existing buildings, the geometry and the structural details are known at the beginning of the design process. In such conditions, the device characteristics and activation moment are selected in order to fulfil Eq. 22 and to obtain a column effective height (i.e. inflection point) at most equal to 65% of the column height. For the maximum exploitation of the devices such value is suggested. The roof drift β is tentatively selected and the same design procedure presented before is applied. The output of the procedure is the base moment demand of the column. The roof drift β is iteratively changed until the resulting base moment demand equals the available capacity. The load increase in the existing structural elements and connections due to the stiffness increase of the beam-to-column joint can be obtained from Eqs. 9–11 and from equilibrium, given the connection activation moment (Eqs. 6–8).

3.3 Design procedure in the case of viscous dampers

Various design procedures are available in the literature for viscous dampers (Ramirez et al. 2000; Filiatrault and Christopoulos 2006; Ribakov and Agranovich 2011; among others), also considering a DBD approach specifically (Sullivan and Lago 2012; Noruzvand et al. 2020). As for the hysteretic dampers, the available methodologies have been typically developed for the design of moment resisting frames with additional dampers acting in parallel to the main structural elements; consequently, the dampers carry directly a portion of the total seismic shear. In the present research, the adaptation of the procedure proposed by Ramirez et al. (2000) is proposed, along with design recommendations contained in Filiatrault and Christopoulos (2006). The procedure considers specifically the presence of viscous dampers activated by the relative rotation at the beam-to-column joint (Fig. 1). The design procedure is summarized in the following steps:

3.3.1 Step 1: target displacement definition

A displacement reduction of 30% is considered for the building implementing viscous dampers. Therefore, the target displacement $\Delta$_d corresponds to 70% of $\Delta$_u, where $\Delta$_u is the lateral displacement of the structure without additional devices.

3.3.2 Step 2: DBD procedure

The classical DBD procedure is applied to the bare frame (i.e. without additional devices) for a lateral displacement equal to $\Delta$_u. The base shear V_b is obtained.

3.3.3 Step 3: substitute structure characteristics

The effective stiffness (k_eff) and effective period (T_eff) associated with $\Delta$_d are respectively

$$k_{{eff}} = V_{b} /\Delta _{d}$$

(33)

$$T_{{eff}}^{{}} = 2\pi \sqrt {m_{{eff}} /k_{{eff}} }$$

(34)

3.3.4 Step 4: relative damping of the device

The damping ratio required by the additional dampers (ξ_damp) to reach the target displacement $\Delta$_d is obtained from (EN 1998–1:2004):

$$\frac{{\Delta _{d} }}{{\Delta _{{el}} }} = \sqrt {\frac{{10}}{{5 + \xi _{{hy \ col}} + \xi _{{damp}} }}} {\text{ }} \to {\text{ }}\xi _{{damp}} = 10\left( {\frac{{\Delta _{{el}} }}{{\Delta _{d} }}} \right)^{2} - \xi _{{hy \ col}} - 5$$

(35)

where $\Delta$_el is the elastic spectral displacement associated with T_eff (Eq. 34) and ξ_{hy col} is the hysteretic damping of the column considering the target displacement $\Delta$_d.

3.3.5 Step 5: damping coefficient of the device

The damping coefficient of the added dampers (C_damp) is obtained from the Jacobsen (1930) approach

$$\xi _{{damp}} = W_{D} /\left( {4\pi W_{S} } \right)$$

(36)

W_D is the viscous energy dissipated by the damper and W_S is the elastic energy stored by the structure. Considering the steady state response of an oscillating system under harmonic motion with period T_eff, the previous formula becomes

$$\xi _{{damp}} = \frac{{\pi \omega _{{eff}} C_{{damp}} u_{0}^{2} N}}{{4\pi \left( {\omega _{{eff}} ^{2} \Delta _{d} ^{2} m_{{eff}} /2} \right)}}{\text{ }} \to {\text{ }}C_{{damp}} {\text{ = 2}}\frac{{{\text{ }}\omega _{{eff}} \Delta _{d} ^{2} m_{{eff}} \xi _{{damp}} }}{{u_{0}^{2} N}}$$

(37)

ω_eff is the angular frequency, N is the number of dampers, u₀ is the maximum elongation of the damper. Taking as reference the device configuration depicted in Fig. 4c, the device elongation u₀ is

$$u_{0} {\text{ = }}\frac{{\Delta _{d} }}{H}\frac{{\text{b}}}{{\sqrt {\text{2}} }}$$

(38)

Substituting Eq. 38 into Eq. 37 and ω_eff with 2$\pi$/T_eff we obtain

$$C_{{damp}} {\text{ = 8}}\pi \frac{{{\text{ }}H^{2} m_{{eff}} \xi _{{damp}} }}{{b^{2} T_{{eff}} N}}$$

(39)

3.3.6 Step 6: force in the device

The maximum force expected in the damper (F_damp) is

$$F_{{damp}} {\text{ = }}C_{{damp}} {\text{u}}_{{\text{0}}} \frac{{2\pi }}{{T_{{eff}} }} = \sqrt {\text{2}} \pi C_{{damp}} \frac{{\Delta _{d} }}{H}\frac{{\text{b}}}{{T_{{eff}} }}$$

(40)

4 Procedure application to a selected case study

The developed procedure is applied to a selected case study resembling a portal-frame industrial building. Two sets of analyses are carried out considering the design of a new building and the retrofit of an existing one, respectively. The existing building has the same structural layout and given structural details. The main geometry of the portal-frame is shown in Fig. 6 along with a scheme of the finite element model used in the analysis. The portal-frame is composed of two 7.2 m height columns which support an inverted T pre-stressed beam 15 m long and 1.25 m high. In the existing building case, the columns are 50 × 50 cm square elements reinforced with 16 longitudinal rebars (16 mm diameter) equally distributed along the edges. The roof elements are double-T pre-stressed elements spanning in the transversal direction. The tributary roof mass (m_roof) is 110′000 kg. The assumed concrete cylindrical strength and steel reinforcement yield stress are 40 MPa and 450 MPa, respectively.

Fig. 6

a considered case study. b scheme of the finite element model

For both the new and the existing building, the following column-to-beam devices are considered (some of them according to Belleri et al. 2017b): rotation friction device with 1 active hinge (RF1), rotation friction device with 3 active hinges (RF3), linear friction device (LF), bi-linear elastic spring (BLS), coupled friction devices with bi-linear elastic spring, and viscous damper (VD).

The devices are placed following the scheme of Fig. 7, with b = 1 m. The frame of the friction devices is made by 2 UPN 240 steel profiles, while the BLS frame is made by a pipe with diameter 176 mm and thickness 8 mm. The considered hysteretic behaviour of the devices is: elastic perfectly plastic for the friction devices, bilinear elastic for the BLS device, and linear viscous for the VD device. In the case of coupled devices, the overall hysteretic behaviour is obtained from considering the single devices acting in parallel.

Fig. 7

Beam-to-column devices: a Rotation Friction device with 1 active hinge (RF1); b Rotation Friction device with 3 active hinges (RF3); c Linear Friction device (LF); d Bi-linear elastic spring (BLS); e Viscous device (VD)

The design procedures described in the previous sections are applied to the selected case study. In the case of a new building, a target roof drift ratio of 2.5% was chosen to control damage (Calvi and Sullivan, 2009; FEMA 450, 2004) under the life safety limit state, then the columns and the additional devices are designed following the proposed DBD procedure. Analogous considerations apply for the existing building case, with the exception that the column cross-section and the number of reinforcing bars are known (column flexural capacity equal to 421 kNm). The considered site seismicity for the life safety limit state is in accordance with EN 1998–1 type 1 spectrum, soil type C, and peak ground acceleration on rock equal to 0.30 g. The results of the proposed DBD procedure for the new and existing buildings are reported in Tables 1 and 2, respectively, where W/O refers to the case without devices.

Table 1 DBD procedure results for the new building case

Table 2 DBD procedure results for the existing building case

To validate the results, non-linear time history (NLTH) analyses were conducted (MidasGEN 2020) considering a set of seven ground motions¹ selected and scaled from the European strong motion database (Ambraseys et al. 2004) to be spectrum compatible with the considered spectrum (Fig. 8).

Fig. 8

Acceleration a and displacement b response spectra for the considered ground motions. GM-i is the response spectrum of each ground motion, AVG is the average spectrum of the considered ground motions, EC8 is the considered EN 1998–1 type 1 spectrum

As for the finite element model (Fig. 6b), the columns are modelled as fixed at the base and a Takeda lumped plastic hinge was introduced at each column base (Takeda et al. 1970). The horizontal girder is modelled as a pinned–pinned elastic inverted T-section element. The elements of the frame of the rotation friction devices are modelled as elastic beam elements while the hysteresis due to the friction is provided by a rigid-plastic rotational spring with activation moment equal to M_y,device (with reference to Tables 1 and 2). The linear friction and the bilinear spring devices are modelled with elasto-plastic springs with stiffness equal to the axial stiffness of the device (1256 kN/m) and activation load equal to N_y,device (with reference to Tables 1 and 2). The viscous damper device is modelled as a single exponential dashpot model with damping exponent (α) equal to 1 and damping coefficient equal to 425 kNm/s.

Figures 9 and 10 show an example of the hysteretic plots of the inelastic hinges at the devices considering a single ground motion (000333xa according to Ambraseys et al. 2004) for the new building case study; similar considerations apply for the existing building case. From Fig. 10, it is observed that for coupled devices a flag shape hysteresis is obtained.

Fig. 9

Example of the NLTH plots for the hysteretic response of: a RF1 device; b BLS device; c LF device d) VD device

Fig. 10

Example of base shear-roof displacement NLTH plots for: a RF1; b BLS; c LF; d RF1 + BLS; e LF + BLS

Figures 11, 12, 13and 14 show the boxplots of the NLTH results for both the new and existing buildings. The boxes are defined by the first and third quartiles and divided, in this case, by the mean value of the maximum results obtained from the 7 NLTH analyses; the ends of the vertical lines represent the maximum and the minimum values. The roof drift ratio, base shear, base moment, residual drift ratio (defined as the drift ratio at rest after the seismic event), and loads at the beam-to-column joint are thus graphically represented. Considering the new building case (Figs. 11, 12, 13, 14), it is observed a general good agreement between the target (2.5%) and the obtained average drift values, thus proving the effectiveness of the proposed design procedure. Figure 11b and c show the base shear and the base moment of a single column, respectively. It is observed how the bilinear system cases (BLS; RF1 + BLS; RF3 + BLS) are characterized by a higher base shear and bending moment demands; this is associated with the high stiffness of the device which leads to a lower fundamental period of vibration and consequently a higher spectral demand. Despite the high initial stiffness, the LF base shear and moment are lower than BLS because of the higher energy dissipation capacity of the former. The case with no device (referred to as “W/O”) shows a base shear lower than BLS but a higher base moment; this is due to the lower effective height of BLS. The VD device provides the lowest base shear and base moment values. As for the residual drift ratio, LF provides the highest value (0.32%); RF1 and RF3 show a residual drift ratio equal to about 0.1% while, as expected, the BLS residual drift ratio is almost zero due to the recentring system.

Fig. 11

Box plots of the results of the NLTH analyses for the new building case: a roof drift ratio of the portal frame (2.5% drift target in red); b base shear of the single column; c base moment of the single column; d residual drift ratio of the portal frame

Fig. 12

Nodal loads at the beam-to-column connection in the new building case: a column shear actions; b beam shear actions; c vectorial sum of the shear actions in the column and in the beam without considering gravity; d vectorial sum of the shear actions in the column and in the beam considering gravity

Fig. 13

Box plots of the results of the NLTH analyses related to the case of existing buildings; a roof drift of the portal frame (2.5% drift in red); b base shear of the single column; c base moment of the single column. In dotted red line the capacity base moment of the column; d residual drift ratio of the portal frame

Fig. 14

Nodal loads at the beam-to-column connection in the new building case: a column shear actions; b beam shear actions; c vectorial sum of the shear actions in the column and in the beam without considering gravity; d vectorial sum of the shear actions in the column and in the beam considering gravity

Figure 12a, b, c and d show the boxplots of the nodal loads at the beam-to-column joint. Figure 12a and b report the shear action in the column and in the beam, respectively. Figure 12c and d show the magnitude of the vectorial sum between the shear actions in the column and in the beam at the beam-to-column joint, thus representing the whole soliciting actions associated with the inclusion of additional devices: Fig. 12c does not include gravity loads (V_gl), i.e. considering that gravity loads are transferred directly as contact loads at the beam-to-column interface (only vertical uplift loads greater than gravity are included) and that the joint connection has been designed to transfer the sole horizontal loads; Fig. 12d includes gravity loads, i.e. it is assumed that the joint connection would transfer all the loads (gravity + seismic).

Figure 12a shows that the column shear at the beam-to-column connection reduces when additional rotational friction (RF1, RF3) or viscous (VD) devices are introduced: − 34%, − 49%, and − 59% reduction compared to the bare frame (W/O), respectively. For BLS and LF systems, such shear action is similar to the case without additional device. Figure 12b shows that the beam shear at the beam-to-column connection increases when additional devices are introduced; the most significant increases are associated with the introduction of BLS (BLS; RF1 + BLS; RF3 + BLS, LF + BLS): + 35%, + 34%, + 26%, and + 23% increase compared to the bare frame (W/O), respectively. Figure 12c shows that when gravity loads are not considered, the rotational friction devices (RF1; RF3) lead to similar results compared to the W/O case, while such loads significantly increase when a bilinear system is introduced (BLS; RF1 + BLS; RF3 + BLS, LF + BLS) reaching a maximum value of 190% of the W/O case for RF1 + BLS. The LF case is located between the RF and the BLS values (123% of the W/O case). A significant reduction is recorded in the VD case (− 55%). Figure 12d shows that when gravity loads are considered the use of VD devices does not involve a significant variation of the beam-to-column joint actions, while the maximum increase of joint loads is associated with BLS and RF1 + BLS (about 133%). In all the considered cases, the shear demand in the column is lower than the capacity provided by minimum stirrups (2 + 2Φ6/150 mm) (EC8).

As for the existing building, the geometry and capacity of the columns are known. The NLTH results are reported in Fig. 13. The base moment (Fig. 13c) does not exceed the bending moment capacity of the existing element (421 kNm). The maximum roof drift ratio (Fig. 13a) is observed in the bare frame (W/O) which is almost 4%. Among the cases with additional devices, the maximum value of roof drift ratio is associated with BLS (3.23%), i.e., for the case with no additional energy dissipation. The lowest drift ratio is associated with VD (2.15%); which proved to be the most effective device. Considering the residual drift ratio (Fig. 13d), LF devices are characterized by the highest value (0.63%).

Figure 14a, b, c and d show the boxplots of the nodal loads at the beam-to-column joint following the same approach adopted for the new building.

Figure 14a shows that the column shear at the beam-to-column connection is similar to the case without additional device (W/O) in most of the considered cases (RF1, RF3, RF3 + BLS, LF + BLS, VD). When BLS, LF, and RF1 + BLS devices are introduced, the shear action in the column increases up to 189%, 231%, 182% of the W/O case, respectively. Figure 14b shows that the beam shear at the beam-to-column connection increases when additional devices are introduced; the most significant increases are related to BLS, LF, and RF1 + BLS: + 25%, + 17%, and + 24% compared to the bare frame (W/O), respectively. Figure 14c shows that when gravity loads are not considered the RF3 and VD devices lead to similar results compared to the W/O case (actions increase at most of + 37% for the RF3). Such actions significantly increase for BLS, LF, RF1 + BLS, LF + BLS; in particular, up to + 250% for BLS. The RF1, RF3 + BLS, and the LF + BLS cases are located between the previous two ranges of values (200%, 182%, 259% of the W/O case, respectively). Figure 12d shows that when gravity loads are considered, the use of VD devices does not involve significant variations of the beam-column joint actions, while the maximum increase of joint loads is associated with BLS and RF1 + BLS (about 125% of the W/O case).

Considering the existing building features and the increase of the beam-to-column connection forces, retrofit measures could be required in the case the seismic demand exceeds the actual capacity. Such intervention can be for instance steel jacketing or fibre reinforced polymer retrofitting for the beam and column ends. Similarly, the beam-to-column joint can be strengthened for instance by mechanical connections such as the one represented in Fig. 2.

5 Conclusions

This paper examined a procedure to design precast portal frames with additional energy dissipation devices at the beam-to-column joint for both new and existing structures. The considered additional devices are hysteretic dampers activated by rotational or linear friction, bilinear elastic system, and viscous dampers. The procedure is based on the Displacement-Based Design methodology for all the considered hysteretic devices but the viscous dampers. After the development of the required analytical formulations, the procedure is applied to a case study resembling a precast portal frame of single-story industrial buildings; both the design of a new building and the retrofit of an existing one are considered.

The effectiveness of the proposed procedure was proven by means of non-linear time history analyses, whose results allow highlighting the advantages and drawbacks of the considered devices.

In the case of new buildings, the obtained roof drift ratio corresponds to the design value. The introduction of additional devices provides a general reduction of the column cross-section dimensions and of the column base moment. Among the analysed systems, the application of recentring devices (used as single devices or in parallel with other hysteretic devices) leads to higher values of the column base shear and moment. Considering residual displacements, the linear friction device provides the highest value (0.34%) while the bilinear systems the lowest value (0.006%). Regarding the additional load in the beam-to-column connection, the results show that the beam actions (V_beam) increase when additional devices are introduced (up to + 35% for the BLS case), while the columns shear action does not significantly increase (V_col increases by a maximum value of + 12% with re-centring devices, BLS). When the vectorial sums of the connection loads are plotted, it can be generally observed that with the rotational and linear friction devices the values do not significantly increase compared to the W/O case (up to + 23% for the linear friction case when the gravity loads are not considered). The magnitude of the vectorial sum increases when re-centring devices are introduced as a consequence of the associated shear increase in the beam.

In the case of the existing buildings, the additional devices lead to a reduction of the maximum roof drift ratio (from almost 4% to 2.5% for viscous dampers) and, generally, these results agree with the target drift ratio (2.5%). The introduction of a recentring system leads to an increase in the base shear of the column. As for the residual displacements, the linear friction device provides the highest value (0.63%) while the triple rotational friction device coupled with a recentring system provides the lowest value (0.012%).

As for the additional load in the beam-to-column connections, an increase of the shear actions in both the beam and the columns is recorded when additional devices are introduced. The magnitude of the vectorial sum does not significantly increase only for the triple rotational friction device and for viscous damping.

Generally, for both the cases (new and existing building), the linear friction device dissipates the highest amount of energy but with a greater residual displacement unless a recentring device is arranged to act in parallel. The viscous devices showed the lowest value of column base shear, base moment, and load in the beam-to-column connection in both the new and existing buildings, thus resulting in the best solution when the reduction of the soliciting actions (e.g. in an existing building) is the main barrier to overcome.

Appendices

Appendix A

Table 

Table 3 Linear equations governing the considered static schemes

3 reports the systems of linear equations associated with the static schemes of Fig. 3.

Let us consider Case A. From the third equation:

$$\theta _{2} = \frac{{kL}}{{6(EI_{b}) + kL}}\theta _{1}$$

(41)

Substituting into the second equation leads to

$$\theta _{1} = \Delta \frac{{6(EI_{c}) }}{H}\frac{{6(EI_{b}) + kL}}{{24(EI_{b} )(EI_{c}) + 4(EI_{c}) kL + 6(EI_{b}) kH}}$$

(42)

Which substituted back into the first equation leads to Eq. 1

$$k^{*} = \frac{{3(EI_{c}) }}{{H^{3} }}\frac{{12(EI_{b}) (EI_{c}) + 12(EI_{b}) kH + 2(EI_{c}) kL}}{{12(EI_{b}) (EI_{c}) + 3(EI_{b}) kH + 2(EI_{c}) kL}}$$

(43)

Equation 14 represents the roof displacement at yielding of the top connection considering the column elastic and it is obtained from the following expression and substituting Eqs. 41 and 42:

$$M_{{y,con}} = k\left( {\theta _{1} - \theta _{2} } \right)$$

(44)

Equation 12 represents the roof displacement at yielding of the column base considering the top connection elastic and it is obtained from the following expression and substituting Eq. 42:

$$M_{{y,c}} = \phi _{{y,c}} (EI_{c}) = \frac{{6(EI_{c}) }}{{H^{2} }}\Delta _{{y,c}} - \frac{{2(EI_{c}) }}{H}\theta _{1}$$

(45)

Analogous considerations apply for Case B. From the third and fourth equations (Table 3):

$$\theta _{2} = \frac{{kL}}{{6(EI_{b}) + kL}}\theta _{1}$$

(46)

$$\theta _{3} = \frac{{kL}}{{6(EI_{b}) + kL}}\theta _{1}$$

(47)

Substituting into the second equation leads to

$$\theta _{1} = \Delta \frac{{6(EI_{c}) }}{H}\frac{{6(EI_{b}) + kL}}{{24(EI_{b}) (EI_{c}) + 4(EI_{c}) kL + 12(EI_{b}) kH}}$$

(48)

which substituted back into the first equation leads to Eq. 2

$$k^{*} = \frac{{3(EI_{c}) }}{{H^{3} }}\frac{{6(EI_{b}) (EI_{c}) + 12(EI_{b}) kH + (EI_{c}) kL}}{{6(EI_{b}) (EI_{c}) + 3(EI_{b}) kH + (EI_{c}) kL}}$$

(49)

Equation 15 represents the roof displacement at yielding of top connection considering the column elastic and it is obtained from Eq. 44 and substituting Eqs. 46 and 48. Equation 13 represents the roof displacement at yielding of the column base considering the top connection elastic and it is obtained from Eq. 45 and substituting Eq. 48.

Appendix B

To evaluate the accuracy of the proposed simplified formulations to describe the lateral stiffness of the system, the comparison between Eq. 1 (Case A in Fig. 3) and the exact analytical solution reported in Belleri et al. (2017b) is shown in Table 

Table 4 Ratio between the lateral stiffness of the frame obtained from considering the simplified formulation of the paper and from considering the exact formulae

4. The results are expressed in terms of stiffness ratio between the exact and approximated formulation. The same 3 types of devices analysed in Belleri et al. (2017b) are considered: rotation friction device with 1 active hinge (RF1), stiffness re-centring device (in this paper referred to as bi-linear elastic spring, BLS), and coupled device with bi-linear elastic spring and rotation friction with 1 active hinge (BLS-RF1). Therefore Eqs. 3 and 5 and Eq. 3 + Eq. 5 are substituted in the variable k of Eq. 1 for RF1, BLS, and BLS-RF1 respectively. The same geometry of the portal-frame case study is considered (i.e. beam length L = 15 m, column height H = 7.2 m). Referring to Fig. 4, h_b = 0 and h_c = 0. The girder has an equivalent rectangular cross Sect. 0.3 m × 1.2 m. The flexural stiffness (EI) of the rotation friction device (RF1) is 15′120 kNm², which corresponds to the flexural stiffness of 2 UPN 240. The axial stiffness (EA) of the diagonal spring (BLS) is 887′000 kN, which corresponds to a pipe with diameter 176 mm and thickness 8 mm.

The results show a general good correspondence between the stiffness of the frame obtained from considering the simplified formulation of the paper and from considering the exact formulae. It is worth observing that the simplified formulation provides stiffer results (i.e. ratio below 1) and that the highest differences are recorded for low values of the ratio between the column cross-section and the column height and for high values of the ratio between the device arm and the column height.