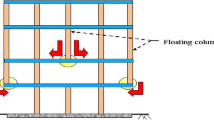
Abstract
Optimum intensity measures of ground motions have been extensively investigated in order to improve the quality of probabilistic seismic demand models. Common scalar-type intensity measures prevail in availability and computability but are less satisfactory when predicting seismic responses of systems with multiple contributing vibration modes and different forms of nonlinearity. For complex primary-secondary tuning structures, such as the modularized suspended building systems, optimal forms of scalar-type intensity measures have yet to be investigated. This study addresses this gap and particularly explores weighted arithmetic means of spectral accelerations or peak ground responses. Multi-objective optimizations of the weighting factors and the IM parameters are conducted for 5 performance indices and 10 targeted responses of a 10-story modularized suspended building on a shallow foundation when subjected to 660 ground motions. Frequency domain analysis and Pareto pattern analysis are used to interpret optimization results. It is shown that multiple elastic and elongated modes are attended to by the combination of spectral accelerations with various levels of modal periods and damping ratios, leading to a 0.22 proficiency index and a 0.96 correlation index which are 38% and 5% improvements from those of PGA. Optimal combinations of fractional order peak ground responses show distributions of derivative order between 0 and 3, achieving a 0.25 proficiency index and a 0.95 correlation index, but with notably fewer optimizing parameters.























Similar content being viewed by others
References
Adam C, Kampenhuber D, Ibarra LF, Tsantaki S (2017) Optimal spectral acceleration-based intensity measure for seismic collapse assessment of P-delta vulnerable frame structures. J Earthq Eng 21:1189–1195. https://doi.org/10.1080/13632469.2016.1210059
Akkar S, Özen Ö (2005) Effect of peak ground velocity on deformation demands for SDOF systems. Earthq Eng Struct Dyn 34:1551–1571. https://doi.org/10.1002/eqe.492
Asgarian B, Sadrinezhad A, Alanjari P (2010) Seismic performance evaluation of steel moment resisting frames through incremental dynamic analysis. J Constr Steel Res 66:178–190. https://doi.org/10.1016/j.jcsr.2009.09.001
Badillo-Almaraz H, Whittaker AS, Reinhorn AM (2007) Seismic fragility of suspended ceiling systems. Earthq Spectra 23:21–40. https://doi.org/10.1193/1.2357626
Baker JW, Cornell CA (2006) Spectral shape, epsilon and record selection. Earthq Eng Struct Dyn 35:1077–1095. https://doi.org/10.1002/eqe.571
Bindi D, Luzi L, Pacor F et al (2009) Towards a new reference ground motion prediction equation for Italy: update of the Sabetta-Pugliese (1996). Bull Earthq Eng 7:591–608. https://doi.org/10.1007/s10518-009-9107-8
Bojorquez E, Iervolino I (2011) Spectral shape proxies and nonlinear structural response. Soil Dyn Earthq Eng 31:996–1008. https://doi.org/10.1016/j.soildyn.2011.03.006
Buyco K, Heaton TH (2019) 70%-damped spectral acceleration as a ground motion intensity measure for predicting highly nonlinear response of structures. Earthq Spectra 35:589–610. https://doi.org/10.1193/111417EQS237M
Cardone D, Perrone G, Piesco V (2019) Developing collapse fragility curves for base-isolated buildings. Earthq Eng Struct Dyn 48:78–102. https://doi.org/10.1002/eqe.3126
Celarec D, Dolšek M (2013) The impact of modelling uncertainties on the seismic performance assessment of reinforced concrete frame buildings. Eng Struct 52:340–354. https://doi.org/10.1016/j.engstruct.2013.02.036
Cordova P, Deierlein G, Mehanny SF, Cornell C (2001) Development of a two-parameter seismic intensity measure and probabilistic assessment procedure. In: The second U.S.–Japan workshop on performance-based earthquake engineering methodology for reinforce concrete building structures, Sapporo, Hokkaido, pp 187–206
De Biasio M, Grange S, Dufour F et al (2014) A simple and efficient intensity measure to account for nonlinear structural behavior. Earthq Spectra 30:1403–1426. https://doi.org/10.1193/010614EQS006M
Du A, Padgett JE, Shafieezadeh A (2019) A posteriori optimal intensity measures for probabilistic seismic demand modeling. Bull Earthq Eng 17:681–706. https://doi.org/10.1007/s10518-018-0484-8
Eads L, Miranda E, Lignos DG (2015) Average spectral acceleration as an intensity measure for collapse risk assessment. Earthq Eng Struct Dyn 44:2057–2073. https://doi.org/10.1002/eqe.2575
Ebrahimian H, Jalayer F, Lucchini A et al (2015) Preliminary ranking of alternative scalar and vector intensity measures of ground shaking. Bull Earthq Eng 13:2805–2840. https://doi.org/10.1007/s10518-015-9755-9
Ellingwood B, MacGregor JG, Galambos TV, Cornell CA (1982) Probability based load criteria: load factors and load combinations. J Struct Div 108:978–997
FEMA (2009) FEMA P695: Quantification of building seismic performance factors | FEMA.gov. Federal Emergency Management Agency, Washington, D.C., US
Feng MQ, Mita A (1995) Vibration control of tall buildings using mega subconfiguration. J Eng Mech 121:1082–1088. https://doi.org/10.1061/(ASCE)0733-9399(1995)121:10(1082)
Garcia DL, Soong TT (2003) Sliding fragility of block-type non-structural components. Part 1: unrestrained components. Earthq Eng Struct Dyn 32:111–129. https://doi.org/10.1002/eqe.217
Ghotbi AR, Taciroglu E (2021) Ground motion selection based on a multi-intensity-measure conditioning approach with emphasis on diverse earthquake contents. Earthq Eng Struct Dyn 50(5):1378–1394. https://doi.org/10.1002/eqe.3383
Giovenale P, Cornell CA, Esteva L (2004) Comparing the adequacy of alternative ground motion intensity measures for the estimation of structural responses. Earthq Eng Struct Dyn 33:951–979. https://doi.org/10.1002/eqe.386
Giriunas K, Sezen H, Dupaix R (2012) Evaluation, modeling, and analysis of shipping container building structures. Eng Struct 43:48–57. https://doi.org/10.1016/j.engstruct.2012.05.001
Goodno BJ, Gere JM (1976) Earthquake behavior of suspended-floor buildings. J Struct Div 102:973–992
Jalayer F, Beck JL, Zareian F (2012) Analyzing the sufficiency of alternative scalar and vector intensity measures of ground shaking based on information theory. J Eng Mech 138:307–316. https://doi.org/10.1061/(ASCE)EM.1943-7889.0000327
Kale Ö, Padgett JE, Shafieezadeh A (2017) A ground motion prediction equation for novel peak ground fractional order response intensity measures. Bull Earthq Eng 15:3437–3461. https://doi.org/10.1007/s10518-017-0122-x
Lavan O, Avishur M (2013) Seismic behavior of viscously damped yielding frames under structural and damping uncertainties. Bull Earthq Eng 11:2309–2332. https://doi.org/10.1007/s10518-013-9479-7
Lawson M, Ogden R, Goodier C et al (2014) Design in modular construction. CRC Press, Boca Raton
Luco N, Cornell CA (2007) Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Earthq Spectra 23:357–392. https://doi.org/10.1193/1.2723158
Mackie K, Stojadinović B (2001) Probabilistic seismic demand model for california highway bridges. J Bridg Eng 6:468–481. https://doi.org/10.1061/(ASCE)1084-0702(2001)6:6(468)
Makris N, Black C (2004) Evaluation of peak ground velocity as a “Good” intensity measure for near-source ground motions. J Eng Mech 130:1032–1044. https://doi.org/10.1061/(ASCE)0733-9399(2004)130:9(1032)
Mollaioli F, Lucchini A, Cheng Y, Monti G (2013) Intensity measures for the seismic response prediction of base-isolated buildings. Bull Earthq Eng 11:1841–1866. https://doi.org/10.1007/s10518-013-9431-x
Nakamura Y, Saruta M, Wada A et al (2011) Development of the core-suspended isolation system. Earthq Eng Struct Dyn 40:429–447. https://doi.org/10.1002/eqe.1036
Nielson BG, DesRoches R (2007) Seismic fragility methodology for highway bridges using a component level approach. Earthq Eng Struct Dyn 36:823–839. https://doi.org/10.1002/eqe.655
O’Reilly GJ (2021) Limitations of Sa(T1) as an intensity measure when assessing non-ductile infilled RC frame structures. Bull Earthq Eng 19(6):2389–2417. https://doi.org/10.1007/s10518-021-01071-7
OpenSees Open system for earthquake engineering simulation - home page. http://opensees.berkeley.edu/. Accessed 4 Jul 2019
Padgett JE, Nielson BG, DesRoches R (2008) Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq Eng Struct Dyn 37:711–725. https://doi.org/10.1002/eqe.782
Pang Y, Wang X (2021) Cloud-IDA-MSA conversion of fragility curves for efficient and high-fidelity resilience assessment. J Struct Eng 147:04021049. https://doi.org/10.1061/(ASCE)ST.1943-541X.0002998
Riddell R (2007) On ground motion intensity indices. Earthq Spectra 23:147–173. https://doi.org/10.1193/1.2424748
Rigoni E, Poles S (2005) NBI and MOGA-II, two complementary algorithms for Multi-Objective optimizations. In: Branke J, Deb K, Miettinen K, Steuer RE (eds) Practical approaches to multi-objective optimization. Internationales Begegnungs- und Forschungszentrum für Informatik (IBFI), Schloss Dagstuhl, Germany, Dagstuhl, Germany
Sabetta F, Pugliese A (1996) Estimation of response spectra and simulation of nonstationary ground motions. Bull Seismol Soc Am 86(2):337–352
Saha A (2021) Synthesis of a vector-valued intensity measure for improved prediction of seismic demands in Inter-Story-Isolated (ISI) buildings subjected to near fault ground motions. Eng Struct. https://doi.org/10.1016/j.engstruct.2021.113241
Shafieezadeh A, Ramanathan K, Padgett JE, DesRoches R (2012) Fractional order intensity measures for probabilistic seismic demand modeling applied to highway bridges. Earthq Eng Struct Dyn 41:391–409. https://doi.org/10.1002/eqe.1135
Soroushian S, Rahmanishamsi E, Jenkins C, Maragakis EM (2019) Fragility analysis of suspended ceiling systems in a full-scale experiment. J Struct Eng 145:04019005. https://doi.org/10.1002/eqe.1135
Tang Y, Zhang J (2011) Probabilistic seismic demand analysis of a slender RC shear wall considering soil–structure interaction effects. Eng Struct 33:218–229. https://doi.org/10.1016/j.engstruct.2010.10.011
Val D, Bljuger F, Yankelevsky D (1997) Reliability evaluation in nonlinear analysis of reinforced concrete structures. Struct Saf 19:203–217. https://doi.org/10.1016/S0167-4730(96)00025-2
Vamvatsikos D, Cornell CA (2005) Developing efficient scalar and vector intensity measures for IDA capacity estimation by incorporating elastic spectral shape information. Earthq Eng Struct Dyn 34:1573–1600. https://doi.org/10.1002/eqe.496
Wang X, Shafieezadeh A, Padgett JE (2021) FOSID: a fractional order spectrum intensity for probabilistic seismic demand modeling of extended pile-shaft-supported highway bridges under liquefaction and transverse spreading. Bull Earthq Eng 19:2531–2559. https://doi.org/10.1007/s10518-021-01082-4
Wang X, Shafieezadeh A, Ye A (2018) Optimal intensity measures for probabilistic seismic demand modeling of extended pile-shaft-supported bridges in liquefied and laterally spreading ground. Bull Earthq Eng 16:229–257. https://doi.org/10.1007/s10518-017-0199-2
Ye Z, Feng D-C, Wu G (2019) Seismic control of modularized suspended structures with optimal vertical distributions of the secondary structure parameters. Eng Struct 183:160–179. https://doi.org/10.1016/j.engstruct.2018.12.099
Ye Z, Giriunas K, Sezen H et al (2021) State-of-the-art review and investigation of structural stability in multi-story modular buildings. J Build Eng 33:101844. https://doi.org/10.1016/j.jobe.2020.101844
Ye Z, Shafieezadeh A, Sezen H et al (2020a) (2020a) Cross-level fragility analysis of modularized suspended buildings based on experimentally validated numerical models. Struct Design Tall Spec Build 29(14):e1778. https://doi.org/10.1002/tal.1778
Ye Z, Wu G (2017) Optimal lateral aseismic performance analysis of mega-substructure system with modularized secondary structures. Struct Design Tall Spec Build 26:e1387. https://doi.org/10.1002/tal.1387
Ye Z, Wu G, Feng D-C (2020b) Shafieezadeh A (2020b) Shake table testing and computational investigation of the seismic performance of modularized suspended building systems. Bull Earthq Eng 18(11):5247–5279. https://doi.org/10.1007/s10518-020-00902-3
Zhang Y, Liang Q (2000) Asynchronous driving principle and its application to vibration control. Earthq Eng Struct Dyn 29:259–270. https://doi.org/10.1002/(SICI)1096-9845(200002)29:2%3c259::AID-EQE904%3e3.0.CO;2-7
Funding
This work was supported by the National Natural Science Foundation of China (51838004); Special Fund for Science and Technology of Guangdong Province, China (210719166874412); Scientific Foundation of Shantou University for Young Talents (NTF21020); Fundamental Research Funds for the Central University; and the Lichtenstein endowment fund at The Ohio State University.
Author information
Authors and Affiliations
Contributions
The contributions of authors are listed as follows: ZY: study conception and design; coding; computation; data analysis; first draft. AS: study conception and design; data analysis; comments on first draft. D-CF: study conception and design; computation; comments on first draft. GW: study conception; data analysis; comments on first draft. XW: study conception; coding; comments on first draft.
Corresponding author
Ethics declarations
Conflict of interest
All authors declare that they have no financial interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Ye, Z., Shafieezadeh, A., Feng, DC. et al. Optimum weighted arithmetic means of peak- and spectral-based intensity measures for probabilistic seismic demand modeling of modularized suspended buildings. Bull Earthquake Eng 20, 5383–5426 (2022). https://doi.org/10.1007/s10518-022-01410-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-022-01410-2