1 Introduction

Recent earthquakes have underlined the great importance of the seismic risk assessment for a well-organized emergency management and economic source allocations (Calvi et al. 2006). The significant number of casualties and economic losses registered after the last seismic events has induced many research groups to focus their attention on developing vulnerability models useful for the seismic scenario and risk assessments at large scale (Lagomarsino and Giovinazzi 2006; D’Ayala 2013; Molina Hutt et al. 2019). Then, the final goal is a refined evaluation of loss assessment (Aslani and Miranda 2005; Baker and Cornell 2008; Romano et al. 2018, 2021), for allocating the repair costs (Ramirez et al. 2012; Di Ludovico et al. 2017b; Del Vecchio et al. 2020) and the optimization of retrofit strategies (Polese et al. 2018; D’Amato et al. 2020; Ferracuti et al. 2020).

The main purpose of several models is developing damage fragility curves (e.g. Rota et al. 2008; Del Gaudio et al. 2019; Romano et al. 2019) or damage probability matrixes (e.g. Ferlito et al. 2013; Rosti et al. 2018; Biglari and Formisano 2020) for construction types characterized by homogeneous seismic behavior. The methods can be based on simplified mechanical models (Rota et al. 2010; Shabani et al. 2021) or empirical data collected after earthquakes (Braga et al. 1982; Drago et al. 2016; Colonna et al. 2017). Mechanical models became common only in the last years due to the increase of computational capacity, allowing the development of more refined numerical simulations (Erberik 2008; Rota et al. 2010; De Luca et al. 2015; AlShawa et al. 2017). Since the 1970s (e.g. Whitman et al. 1973), the empirical methods, based on observed damage data, were developed for typological classes (Rota et al. 2008; Del Gaudio et al. 2019; Romano et al. 2019) or considering a vulnerability index as a function of different structural parameters (Benedetti and Petrini 1984; Vicente et al. 2011; Zucconi et al. 2017, 2020; Chieffo et al. 2019). Besides, hybrid methods combined these two approaches using an observed damage database for the probabilistic assessment of vulnerability parameters, while using mechanical and structural considerations for statistical uncertainty treatment (Barbat et al. 1996; Kappos et al. 2006).

Recently, empirical methods were encouraged by the greater availability of observed data. In Italy, the National Civil Protection Department made public on the web platform Da.D.O. (Observed Damage Database) post-earthquake data collected in the last fifty years (Dolce et al. 2017), intending to promote the development of empirical fragility curves for typological classes representative of the Italian building stock. Different sets of fragility curves were developed for reinforced-concrete buildings (e.g. Del Gaudio et al. 2017, 2020; Romano et al. 2019) and unreinforced-masonry buildings (e.g. Rosti et al. 2018, 2021; Zucconi et al. 2021; Lagomarsino et al. 2021).

All previous works are based on the damage surveyed after seismic events; nevertheless, another important indicator for the building performance is the usability (Stannard et al. 2014), defined as the fitness for use of a building after a seismic event without risk for human life significantly increased compared to the pre-event condition (Di Ludovico et al. 2017a; Gebelein et al. 2017). In Italy, post-earthquake usability assessment is performed for a level of shaking comparable with that occurred at the building site during the seismic event. It requires an in situ survey to evaluate post-earthquake building conditions; thus, the usability assessment is not related to the hazard level considered in a formal vulnerability assessment resorting to geometric survey, material testing, and numerical modeling. The usability rating of a building is issued after a detailed inspection aimed at damage analysis. A specific usability form is filled by practitioners who had completed a specific course, were selected by emergency management public entities and underwrote a declaration that they would not be involved in possible later design and construction works.

In an initial phase of the reconstruction process after the 2009 L'Aquila earthquake, the usability rating was a criterion for allocating repair funding as described in Rossetto et al. (2014) and Di Ludovico et al. (2017b; c). Del Vecchio et al. (2020) analyzed the repair costs of reinforced-concrete structural components for residential buildings damaged by the 2009 L'Aquila earthquake, underlining the excellent correlation with usability performance. Additionally, loss of usability was directly linked to indirect costs related to the population's time for assistance (Mannella et al. 2017; Di Ludovico et al. 2022). Some authors analyzed the correlation between the usability performance and some structural and geometric characteristics, as Zucconi et al. (2018a) for 2009 L'Aquila earthquake and Sisti et al. (2018) for the 2016–2017 Central Italy seismic sequence. Moreover, Rosti et al. (2018) correlated different damage indexes with the usability classifications. Zucconi et al. (2017) developed an empirical usability assessment model for unreinforced-masonry buildings calibrated based on 2009 L'Aquila earthquake database. In particular, resorting to statistical techniques, a usability index was calculated as a weighted sum of seven structural parameters, given the macroseismic intensity. Then, in Zucconi et al. (2018b, 2020), the model was validated with data surveyed after the 2002 Molise earthquake in Italy, and a novel usability assessment model was calibrated, developing usability probability matrixes as a function of the peak ground velocity (PGV).

This work aims at developing fragility curves in terms of usability for Italian unreinforced-masonry buildings. The curves allow preventive scenario and risk analyses based only on vulnerability data already available in the census. However, such curves are not recommended for post-earthquake usability assessment, which is more robustly performed by means of on-site inspections and damage surveys. The 2009 L'Aquila earthquake database, accounting for almost 60,000 unreinforced-masonry inspected buildings, will be used to derive information about construction features and seismic performance. Typological classes will be defined considering parameters available both in the post-earthquake database and in the Italian census (ISTAT 2011). Although census information is less detailed than ad-hoc developed inventories (Marotta et al. 2015), it has the substantial advantage of covering the national territory systematically. Usability fragility curves will be defined as a function of peak ground acceleration (PGA), probably the most common intensity measure (IM) for practitioners (Çelebi et al. 2010; Mollaioli et al. 2019). The curves will account for uninspected buildings present in the affected seismic area. The results will be discussed in terms of the parameters most affecting loss-of-usability performance.

2 Ground motion description in terms of PGA

Fragility curves can be derived as a function of several IMs, e.g. macroseismic intensity, PGA, PGV or spectral acceleration for a given period of vibration. The first IM used since the 1980s is the macroseismic intensity because it is assigned observing building performance and it could be obtained from the historical seismicity without the need for instrumental data. In fact, the accelerometric network was largely developed only in the last two decades, while the density of instrumentation was inadequate in the past. As the years go by, instrumental IMs have replaced macroseismic intensity in defining fragility curves, because they are not influenced by the characteristics of the building portfolio affected by the earthquake as it happens for macroseismic intensities. Moreover, macroseismic intensity is not available for all settlements so this IM cannot be used everywhere. Conversely, nowadays, the accelerometric network is widespread in all Italian territory and instrumental data related to a seismic event are available as shakemaps (Michelini et al. 2008), published by the Italian National Institute of Geophysics and Volcanology.

In the present study, among all instrumental IMs available for past Italian earthquakes, PGA was chosen for deriving fragility curves in terms of usability, similarly to what done in other works in the literature. In fact, PGA is the most used IM in hazard studies and the Italian Civil Protection Department utilizes it for seismic vulnerability and risk scenarios (Dolce et al. 2019).

In particular, in the following sections, raw data related to the shakemap of the 2009 L'Aquila earthquake (Faenza et al. 2011) (http://shakemap.rm.ingv.it/shake/1895389/products.html) were considered to develop usability fragility curves. PGAs retrieved from the shakemap are discrete values characterized by a step of 0.04 g in the range 0.02–0.48 g and they were collected in bins with a 0.10 g step. The defined bins and the corresponding categorical values are shown in Table 1. The first bin is smaller and the last bin is slightly larger than the others, to be close to the mean of available data. The relevant categorical value of the bin was assigned to each building in the dataset.

Table 1 Peak ground acceleration bins and categorical values
Full size table

3 Usability inspections after the 2009 L'Aquila earthquake

The derivation of empirical usability functions relied on surveyed data to associate observed performance with building features. Hereinafter, information related to unreinforced-masonry buildings such as construction details and fitness-for-use tagging were obtained from damage and usability inspections performed after the 2009 L'Aquila, Abruzzo region, Italy earthquake. At that time, about 60,000 unreinforced-masonry constructions were surveyed from teams of trained practitioners and academics; they filled, for each construction, the AeDES "Level 1 Form for Post-Earthquake Damage and Usability Assessment and Emergency Countermeasures in Ordinary Buildings" (Baggio et al. 2007). A detailed explanation of the database, in terms of constructions characteristics and performance, was presented elsewhere (Zucconi et al. 2018a; Del Gaudio et al. 2019). In this section, only the information relevant for developing the model proposed hereinafter are briefly recalled.

The AeDES form is partitioned into nine sections, but those relevant for current goals are just five. In Sect. 1, the location of the building is given in terms of municipality, settlement, and address. Although fields for geographical coordinates are available, they are seldomly used. Both instances were adequate to associate a proper value of PGA to each building. In Sect. 2, the period of construction is given in terms of predefined timespan categories related to equivalent categories used by census. The total number of stories and number of basement stories are reported in this section as well. The latter is subtracted from the former to get the number of stories above ground, used by census. In Sect. 3 the type of structure is reported. Despite being rather detailed, with 30 structural categories for unreinforced-masonry constructions, in the following these information are used only to separate those structures from reinforced-concrete or steel ones. Section 4 is devoted to damage survey in terms of four severity categories (D0, D1, D2–D3, D4–D5) and three extension categories (< 1/3, 1/3–2/3, > 2/3 of building surfaces). The description is related to five individual structural components (i.e. vertical structures, floors, stairs, roof, infills and partitions) and to pre-existing damage, which is addressed in a global manner. This last piece of information is used in the following as a proxy of the state of repair of the building. Finally, Sect. 8 delivers one out of six fitness-for-use categories of the building, selected among: A rating: usable; B rating: temporarily unusable (i.e. usable after short-term interventions are implemented); C rating: partially unusable (i.e. the building can be compartmentalized and one portion is safe to use); D rating: requiring a more detailed investigation (e.g. necessitating an expert in steel structures or in geotechnical engineering); E rating: unusable; F rating: unusable due to external hazard (e.g. due to soil instability or collapse of a nearby construction). In the following, buildings requiring a more detailed investigation (D) and unusable buildings due to external hazard (F), which account for less than 5% of inspected buildings, were neglected because beyond the scope of this research. Additionally, B- and C-rating buildings were considered together because granted the same reparation contribution after the earthquake (Di Ludovico et al. 2017c), and were just referred to as B-rating, or partially-unusable, buildings hereinafter.

The interpretation of inspection data is greatly influenced by the total number of buildings present in a given area or, for the purposes of the proposed method, in a given PGA bin. In fact, an underestimation of this tally leads to an overestimation of the probability of exceeding a given performance level. The uncertainty in estimating the total number of buildings is particularly large for small PGA values because inspections are requested by landlords and they are prone to ask for one only if their property is damaged. Therefore, if the total number of buildings is estimated on AeDES forms alone an overrepresentation of damaged buildings occurs in far-field areas. Different authors have proposed alternative strategies to overcome this limitation, which can be sorted into four groups:

  1. (1)

    A reduced dataset is selected, considering only municipalities wherein the number of inspected buildings (from now on: AeDES buildings) overcomes a certain threshold of the number of the buildings listed in the census (from now on: census buildings). Such lower bound value was 65% for Goretti and Di Pasquale (2004) or 60% for Rota et al. (2008);

  2. (2)

    Data is considered only if belonging to a municipality that experienced a ground shaking large enough to ensure that systematic inspections were performed. For instance, Del Gaudio et al. (2017, 2019) took into account only settlements with PGA > 0.05 g and a Mercalli-Cancani-Sieberg macroseismic intensity greater than VI.

  3. (3)

    The observations database is increased to account for the number of buildings listed in census, with all additional buildings considered usable. Constructions are supplemented, if necessary, so that the number of inspected + additional buildings match the number of census buildings. This strategy was proposed by Zucconi et al. (2017) and then applied in other works (e.g. Romano et al. 2019; D’Amato et al. 2020; Zucconi et al. 2020).

  4. (4)

    A hybrid procedure considers, in each municipality, lower and upper bounds for the ratio of AeDES buildings by census buildings. As suggested by Del Gaudio et al. (2020) for reinforced-concrete structures and Rosti et al. (2021) for unreinforced-masonry structures, if the ratio is larger than 0.9 the municipality is included considering only AeDES data, if the ratio falls between 0.1 and 0.9 the municipality is removed from the database, because inspections are considered not systematic while uninspected buildings cannot be assumed as undamaged. If the ratio is less than 0.1, the municipality is included and the number of buildings is retrieved from census database.

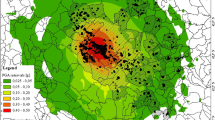
In this work, the total number of buildings was estimated as proposed in previous point 3. For the first two PGA categories (i.e. PGA < 0.15 g), additional buildings arised both from municipalities present in the AeDES database, complemented to match the number of census buildings, and from all other Abruzzo municipalities not present in the AeDES database. For PGA ≥ 0.15 g only the AeDES database was considered. The numbers of AeDES and total buildings considered for the following computations are presented in Table 2. In particular, Abruzzo is divided into 305 municipalities, of which only 129 are present in the AeDES database: 28 municipalities underwent systematic inspections, 101 municipalities were inspected but without full coverage, 176 municipalities were not inspected at all (Fig. 1). The increase of the database for the lowest PGA category was dramatic, while that of the second PGA category was relevant but less marked. No supplement was necessary for the other PGA categories because the more severe shaking entailed systematic inspections. Additional buildings were generated by means of a Monte Carlo simulation and were sorted in categories according to the building characteristic distributions computed from a sub-inventory of the AeDES database limited to macroseismic intensities greater than VI, a threshold above which inspections can be considered systematic. As already stated, all additional buildings were assumed usable.

Table 2 Number of AeDES and increased database buildings as a function of PGA (g) category
Full size table
Fig. 1
figure 1

Abruzzo municipalities wherein the number of buildings was estimated based on: AeDES database only, AeDES database complemented with census, census only. Location of municipalities superimposed on PGA shakemap. Shakemap base from: http://shakemap.rm.ingv.it/shake/1895389/products.html

Full size image

4 Italian census for residential constructions

Data collected with the AeDES form, or its previous versions, are available only for few areas where earthquakes occurred in the last 40 years. By contrast, the Italian statistics institute performs a systematic census survey over the full national territory, accounting for the resident population and the buildings. Therefore, census data constitute fundamental support for government decisions, allowing reference to the whole nation, or an individual region, province, municipality, settlement.

Census inspections do not require the internal visit of each building necessary in post-earthquake damage and usability assessment carried out with the AeDES form. In particular, the data collector makes an external rapid visual screening of the building, and the information collected is integrated with the use of administrative sources in support of field surveys. Moreover, the dwelling owner fills in a form received by mail, whose data are merged with those collected by the inspector. The building constitutes the census survey unit and represents the container of all the other surveyed entities, e.g. dwellings, families, individuals, etc.. However, it should be noted that the census definition of building is not exactly the same as in the AeDES form, because use is the most important census parameter, allowing grouping different structural units. At the same time, non-residential buildings, including those ancillary to dwellings (e.g., warehouses, stables, etc.) are not indexed by census. A direct consequence of the above considerations is that complementing the AeDES database with that of census introduces some uncertainties. Nevertheless, it should be noted that all census data have been added only in the first two PGA bins and they influence only the number of usable buildings, reducing the probability of exceeding for low values of the intensity measure. Moreover, although the total number of buildings estimated based on complementary census data could be affected by a bias, neglecting uninspected buildings would deliver unrealistic fragility curves.

For a residential building, the information collected by census are:

  • Structural material (e.g., unreinforced masonry, reinforced concrete, other);

  • Construction timespan;

  • Number of stories above ground;

  • State of repair, assigned based on a rapid visual assessment of general conditions;

  • Presence of adjacent buildings, on one or multiple sides;

  • Presence of underground stories;

  • Presence of a lift;

  • Number of stairs;

  • Number of dwellings.

The definition of all previous information is straightforward except for the state of repair. This parameter is evaluated based on the conditions of the following construction elements: plaster, window fixtures, vertical structures, and roof. Then, the evaluation can be traced back to four possible categories:

  • Excellent, if all construction elements present an excellent state, without damage to vertical structures or roof;

  • Good, if plaster is deteriorated, but other construction elements present an excellent state;

  • Mean, if plaster and window fixtures are deteriorated, vertical structures are damaged, but roof has no damage;

  • Poor, if plaster and window fixtures are deteriorated and vertical structures as well as roof are damaged.

5 Assumed typological classes

For the development of usability curves at territorial scale, a possible approach is defining typological classes combining buildings with similar seismic behavior. Parameters that can be gained both from AeDES and census forms were considered in order to calibrate usability fragility curves from post-earthquake data that can be used elsewhere resorting to census data.

In particular, the unreinforced-masonry building classification was defined according to two parameters: construction timespan and state of repair. Other parameters affecting the seismic behavior of unreinforced-masonry buildings, such as masonry quality, type of horizontal structures, presence of connections, co-existence of unreinforced-masonry and reinforced-concrete vertical structures, have not been considered because cannot be retrieved from census data. The number of stories above ground, available in census, will be shown to be relevant only in very specific cases, for which more detailed fragility curves will be developed nonetheless.

Census presents nine categories for construction timespan and four categories for state of repair. Disaggregating the database according to all such categories, as well as for PGA bins, would deliver very few or zero buildings in some instances, negatively affecting the robustness of fragility curves. Therefore, a reduced number of categories was considered in the following, using as identification criterion that of having well-separated single-parameter loss-of-usability regression lines. The construction timespan was described by three categories that follow the main changes in Italian standards for unreinforced-masonry constructions: < 1919, 1919–1961, > 1961 (Zucconi et al. 2018a).

An association between AeDES pre-existing damage and census state of repair is proposed in Table 3. First of all, the four census categories were combined in two, R1 for Excellent and Good, and R2 for Mean and Poor state of repair, because these last two categories were the only ones related to structural damage. Then, R1 was associated with pre-existing damage classification D0 and D1 with an extension less than 1/3 in the AeDES form, and R2 with all other damage classifications. This correspondence was selected in order to get a distribution of buildings similar in the two databases. Unfortunately, the public version of census data delivers the state of repair of all buildings, irrespective of structural material. Therefore, the distribution of R1 and R2 occurrence was evaluated for all Abruzzo municipalities with a percentage of masonry buildings greater than 75. In Table 3 the comparison between the distributions of pre-existing damage and state of repair is presented: percentage of no or very low pre-existing damage (87.8%) is somewhat larger than census R1 category (81.2%), while light to severe pre-existing damage (12.2%) is somewhat smaller than census R2 category (18.8%). Alternative associations, for instance D1 with extension < 2/3 corresponding to R1, delivered greater deviations. The census distribution in Table 3 was used to assign the state of repair to the additional buildings generated to increase the AeDES database.

Table 3 Association between AeDES pre-existing damage with census state of repair and corresponding building distributions
Full size table

For the above-mentioned parameters, loss-of-usability regressions were derived as shown in Fig. 2, where the percentage of unusable buildings, computed from the ratio between the number of E-rating buildings and the total number of buildings, is given as a function of PGA. It should be noted that the total number of buildings is the number of AeDES buildings possibly complemented resorting to census data as described in Sect. 3. In Fig. 2a and b the observed discrete values of unusable buildings as a function of construction timespan and the state of repair and corresponding regression lines are reported. As anticipated, loss-of-usability lines are well separated, whereas more detailed categories delivered regression lines close to each other (i.e. slightly affected the usability rating variation) and would have involved a disaggregation of the database in typological classes with few or zero buildings in several instances, especially those characterized by severe shaking.

Fig. 2
figure 2

Usability (E rating) regressions for census parameters: a construction timespan, b state of repair/pre-existing damage, c number of stories above ground

Full size image

In Fig. 2c the number of stories above ground is presented as well. Despite considering just two categories (1 story, more than 1 story), the lines are rather close one to the other and almost overlapped if categories commonly used in the literature are assumed, such as 1–2 stories and more than 2 stories. This trend was confirmed when developing fragility curves and led to a model based only on construction timespan and state of repair. However, an ad hoc discussion about number of stories will be presented in Sect. 6.2.

Although regression lines will not be used further in the following for the mathematical derivation of the fragility functions, they were instrumental to define the six census-based typological classes in Table 4, obtained by combining the categories of construction timespan and state of repair. The acronym of each class is TxRy: letter T is related to construction timespan (i.e. T1 for < 1919; T2 for 1919–1961; T3 for > 1961); letter R is related to the state of repair (R1 for Excellent and Good, and R2 for Mean and Poor). The relative frequency building distribution of the census-based typological classes is presented in Fig. 3, where the distribution of the AeDES database is compared with that of the increased database. A few small differences between the AeDES and AeDES complemented with census percentages of buildings belonging to each typological class depicted in Fig. 3 is due to the Monte Carlo simulation procedure used to generate the additional buildings.

Table 4 Census building typological classification
Full size table
Fig. 3
figure 3

Relative frequency distribution of census-based typological classes

Full size image

The relative frequency distributions of census-based typological classes with respect to usability categories (A rating: usable; B rating: partially unusable; E rating: unusable) are depicted in Figs. 4 and 5 with reference to the AeDES and increased database, respectively. The comparison between the two figures underlines the importance of properly assessing the total number of buildings, otherwise an overestimation of unusable buildings will occur.

Fig. 4
figure 4

Relative frequency distribution of usability categories for census-based typological classes (AeDES database only, 56,584 buildings)

Full size image
Fig. 5
figure 5

Relative frequency distribution of usability categories for census-based typological classes (AeDES database increased with census data, 375,053 buildings)

Full size image

6 Fragility curves in terms of usability

The main objective of this work was developing fragility curves in terms of usability, providing the probability of reaching and exceeding a specific building usability state. The first step was to evaluate the observed usability state relative frequency for each census-based typological class and each categorical PGA value, as defined in Table 1. In particular, three usability states US were considered: A rating: usable; B rating: partially unusable; E rating: unusable.

Then, similarly to several literature works on damage fragility curves (Rota et al. 2008; Rossetto et al. 2013; Del Gaudio et al. 2019), the lognormal distribution was selected to fit with an analytical function the discrete cumulative frequency distribution (Fig. 6) according to the following equation:

$$P\left[ {US \ge US_{i} |PGA} \right] = \Phi \left( {\frac{{\ln \left( {PGA} \right) - \mu }}{\beta }} \right)$$
(1)
Fig. 6
figure 6

Usability in terms of discrete observed data and continuous fragility functions for typological class T1R1: a AeDES database not accounting for uninspected buildings; b increased database accounting for uninspected buildings

Full size image

where \(P\left[ {US \ge US_{i} {|}PGA} \right]\) is the probability of exceeding a specific usability state \({US}_{i}\) given a \(PGA\) value;

\(\Phi (\bullet )\) is the standard normal cumulative distribution function, µ is the logarithmic mean and β is the logarithmic standard deviation.

The parameters µ and β were evaluated with the maximum likelihood estimation (e.g. Baker 2015; Buratti et al. 2017) method that searches the parameters by maximizing the likelihood function estimates for each US with the following equation:

$$Likelihood = \mathop \prod \limits_{j = 1}^{m} \left( {\begin{array}{*{20}c} {n_{j} } \\ {z_{j} } \\ \end{array} } \right)P\left( {US \ge US_{i} |PGA_{j} } \right)^{{z_{j} }} \left( {1 - P\left( {US \ge US_{i} |PGA_{j} } \right)} \right)^{{n_{j} - z_{j} }}$$
(2)

where \(\Pi\) is the product operator over values from 1 to m PGA categories and the binomial distribution is assumed to express the probability \({P}_{j}^{{z}_{j}}\) that, for the \(j\)-th category, \({z}_{j}\) buildings exceed the usability state USi, while \({n}_{j}-{z}_{j}\) buildings do not exceed that usability state with a probability \({\left(1-{P}_{j}\right)}^{{n}_{j}-{z}_{j}}\), with \({n}_{j}\) total number of buildings for the \(j\)-th PGA category. Finally, \(\left(\genfrac{}{}{0pt}{}{{n}_{j}}{{z}_{j}}\right)\) is the binomial coefficient defined as:

$$\left( {\begin{array}{*{20}c} {n_{j} } \\ {z_{j} } \\ \end{array} } \right) = \frac{{n_{j} !}}{{z_{j} !\left( {n_{j} - z_{j} } \right)!}}$$
(3)

The lognormal distribution of Eq. (1) was used to evaluate the probability \(P\), while the parameters were estimated maximizing the logarithm of the likelihood function (Baker 2015) with the following equation:

$$\hat{\mu }_{{US_{i} ,}} \hat{\beta } = {}_{{\hat{\mu }_{{US_{i} ,}} \hat{\beta }}}^{{{\text{argmax}}}} { }\mathop \sum \limits_{i = 1}^{2} \mathop \sum \limits_{j = 1}^{m} {\text{ln}}\left[ {\left( {\begin{array}{*{20}c} {n_{j} } \\ {z_{j} } \\ \end{array} } \right)\left( {{\Phi }\left( {\frac{{\ln \left( {PGA_{j} } \right) - \mu_{{US_{i} }} }}{\beta }} \right)} \right)^{{z_{i,j} }} { }\left( {1 - {\Phi }\left( {\frac{{\ln \left( {PGA_{j} } \right) - \mu_{{US_{i} }} }}{\beta }} \right)} \right)^{{n_{j} - z_{i,j} }} } \right]$$
(4)

The parameter β was assumed equal for all USi to avoid curves intersection as suggested by Porter (2020).

The fragility curve shape is greatly influenced by the total number of buildings falling in each PGA bin. If uninspected buildings are neglected (AeDES database only), the probability of exceeding a usability state is overestimated at low intensities and underestimated at high intensities, as shown in Fig. 6a in which fragility curves derived without accounting for census data are presented. By giving consideration to uninspected buildings belonging both to partially covered municipalities and to municipalities completely absent in the AeDES database (Fig. 1), Fig. 6b was obtained. In this way, the overestimation of the loss-of-usability occurrence for low PGA bins was avoided because fragility curves are less steep at low intensities.

6.1 Curves for construction timespan and state of repair

The parameters \(\theta ={e}^{\mu }\), median of PGA values, and \(\beta\), logarithmic standard deviation, for the proposed fragility curves are reported in Table 5 and depicted in Fig. 7 for each census-based typological class. Based on Table 5 and Fig. 7 it is possible to notice that:

  • The median values increase with the US, so that for the same typological class, the US = B always has a lower median than US = E; consequently, the partially-unusable buildings have always a greater probability of occurrence than unusable buildings for a given PGA value;

  • Older buildings always have a greater loss-of-usability than the newer ones, as it is possible to observe evaluating the influence of the construction timespan, for which the category T1 (< 1919) always shows higher loss-of-usability than T2 (1919–1961), which in turn is higher than that of T3 (> 1961);

  • The state of repair R2 always entails a higher loss of usability than the state of repair R1, for equal construction timespan and number of stories, as also shown by the fragility curve shape.

Table 5 Parameters of lognormal fragility curves in terms of usability for the census-based typological classes
Full size table
Fig. 7
figure 7

Median θ of usability curves for census-based typological classes

Full size image

As already mentioned, the usability fragility curves for US = B and US = E, of a given typological class, do not intersect each other even for PGA values larger than those plotted in the following, thanks to the logarithmic standard deviation constant for all usability states.

From Fig. 7 it is clearly evident the crucial relevance of the state of repair; furthermore, the usability rating B always leads to lower median values, even if this difference becomes less important for the state of repair R2.

The usability fragility curves for the six assumed typological classes are shown in Fig. 8. Similarly to previous comments related to Table 5, it is possible to observe that the state of repair R2 greatly influences the fragility curve shapes, which are steeper and with a higher probability of exceeding for a given intensity. A greater scatter in the observed discrete data can be noted in Fig. 8f, due to the limited number of buildings in these typological classes. In particular, for the 0.2 g PGA category, there are overall 18 buildings, of which 13 partially-unusable and 8 unusable.

Fig. 8
figure 8

Fragility curves in terms of usability fitting observed data for census-based typological classes: a T1R1, b T2R1, c T3R1, d T1R2, e T2R2, and f T3R2

Full size image

6.2 Curves for construction timespan, state of repair R1 and number of stories

Fragility curves accounting also for the number of stories above ground involve contradictory results in the case of state of repair R2, with taller buildings resulting slightly less vulnerable than shorter ones for equal construction timespan. This result led to adopting the presented model, relying only on construction timespan and state of repair. However, given that the information about the number of stories above ground is already available in census, in this subsection the fragility curves accounting for this parameter are also presented for R1, the only state of repair category for which the number of stories above ground is meaningful.

In Table 6 the relevant typological classes are identified, the parameters describing the corresponding fragility curves are delivered in Table 7, while the curves are plotted in Fig. 9. All other parameters being equal, taller buildings are always more vulnerable than shorter ones, both for B and E ratings. For equal construction timespan, median values in Table 5 always fall between the relevant values in Table 7. Moreover, it is confirmed that the number of stories is the parameter having the most limited effect on fragility. Finally, it is worth mentioning that just 16% of the sample is populated by 1 story (S1) and medium-good state of repair (R1) buildings, thus further justifying the adoption of a general model that neglects the number of stories above ground.

Table 6 Additional census-based typological classes, accounting for the number of stories above ground
Full size table
Table 7 Parameters of lognormal fragility curves in terms of usability for additional typological classes
Full size table
Fig. 9
figure 9

Fragility curves in terms of usability fitting observed data for additional typological classes with state of repair R1: a T1R1S1, b T2R1S1, c T3R1S1, d T1R1S2, e T2R1S2, and f T3R1S2

Full size image

7 Conclusions

Census performs the most systematic survey of residential buildings in Italy, covering all national territory, collecting information about structural material, construction timespan, and state of repair, as well as number of stories above ground. In the present work, census data related to unreinforced residential masonry buildings were compared to data gathered after the 2009 L’Aquila earthquake to derive fragility curves to forecast residential building usability, which is the fitness for use after a seismic event.

Based on single-parameter regressions, three categories were identified for construction timespan (< 1919; 1919–1961 and > 1961), and two categories for state of repair (R1 for excellent or good, and R2 for mean or poor state of repair). Whereas association between census data and post-earthquake data is straightforward for construction timespan, it is less direct in the case of the state of repair because the post-earthquake form registers the pre-existing damage in the building in terms of severity and extension. A correspondence criterion between pre-existing damage and state of repair was defined with the objective of delivering approximately equal percentages in the two building databases. Single-parameter regressions in terms of number of stories above ground delivered close lines anticipating that the number of stories has a minor impact on usability fragility curves, which therefore were derived only in terms of construction timespan and state of repair.

With the aim of avoiding an overestimation of unusable buildings, the original 2009 L’Aquila database was increased to account for far-field constructions not inspected because undamaged. The fragility curves were derived assuming as intensity measure the peak ground acceleration, adopted by the Italian Civil Protection Department for scenario and risk simulations and available for any national location for nine return periods between 30 and 2475 years.

Lognormal fragility curves for partially-unusable and unusable performance levels were defined, maximizing likelihood. Older and less maintained residential unreinforced-masonry buildings resulted most vulnerable, with state of repair being the predominant parameter. This result suggests that state of repair information should be implemented in scenario and risk platforms when forecasting post-earthquake fitness for use of buildings. Complementarily, fragility curves accounting for two number-of-stories categories were computed for R1 (excellent or good) state of repair buildings, the only ones showing a consistent, although limited, role of the number of stories. In the future, the use of multiple linear regressions or of principal component analysis will be investigated as an alternative to the typological class approach.

Developed fragility curves expressed in terms of partially-unusable and unusable performance levels of buildings can represent a crucial tool for preventive seismic scenario and risk assessments because usability is a suitable indicator for the allocation of economic funding after an earthquake. Indeed, usability has a strong correlation with both repair costs and time of population assistance, which account for the most significant portion of seismic direct and indirect losses. Finally, until specific studies are developed, proposed fragility curves can be used for preliminary estimations in countries having similar constructions. Even if a systematic census of buildings is missing, the much reduced number of parameters defining the proposed model are faster to collect than those required by more detailed alternatives. In fact, in most cases, they can be identified from on-line tools such as Google Street View and historical maps without the need of an on-site survey.