PRESSAFE-disp: a method for the fast in-plane seismic assessment of existing precast RC buildings after the Emilia earthquake of May 2012

Abstract

The existing precast reinforced concrete structures not specifically designed against earthquakes have proved to be very sensitive to seismic demands. After the lesson learnt from the Emilia earthquake of May 2012, causing many collapses and severe damage, reliable seismic design criteria have been established for the design of new precast structures and for the strengthening of the existing ones. Despite this, a large percentage of the existing precast buildings in the Italian territories actually has not been object of interventions and remains in an unsafe condition with regard to the seismic actions. In this context, the methods for a rapid seismic assessment can be very helpful both to estimate the current safety level of large building stocks and to plan the necessary strengthening interventions, possibly at the large scale of an industrial area. To this aim, the paper proposes the PRESSAFE-disp (PRecast Existing Structure Seismic Assessment by Fast Evaluation-displacements) method, useful for the fast evaluation of the fragility curves of precast structures. The damage criteria, applicable both to structural elements and non-structural cladding elements on the perimeter, have been selected in order to capture the damage mechanisms observed during the building inspections conducted by the authors in the aftermath of the 2012 Emilia earthquakes. The method allows a comprehensive explanation of the seismic in-plane behaviour of existing precast RC buildings and could be effectively adopted, for example, in earthquake loss estimations and seismic risk assessments of large Italian industrial areas, as well as of wide seismic-prone territories of the Mediterranean area.

1 Introduction

The seismic events which shook the northern Italy in May 2012, as well as several past seismic events in the Mediterranean area, have caused significant damage or even the collapse of buildings realized with precast technologies. The earthquake represents a serious test bench for existing precast reinforced concrete (RC) buildings since they were usually designed with non-redundant schemes in order to allow easy and fast assembling operations. In addition, even though the seismic activity of the Italian territory was well known since many years, wide areas of Italy, Emilia Romagna Region included, were considered non-seismic zones by national building codes until the re-classification proposed in 2003 (OPCM 2003). As a consequence, before 2003 the buildings were designed by means of static analyses by taking into account only vertical loads and wind action (Savoia et al. 2017). Thus, several precast buildings, built in the Italian territory before 2003, have simply-supported elements (beams and roof slab elements) with shear forces transmitted at the support level through friction resistance only. Indeed, steel connection devices, mandatory in seismic zones and fundamental to ensure the global safety of precast structures (Brunesi et al. 2015), usually were not adopted in those regions.

The lesson learnt after the 2012 Emilia sequence represented an occasion for engineers and researchers both for collecting data concerning structural damage on precast structures (Savoia et al. 2012, 2017; Liberatore et al. 2013; Belleri et al. 2014; Bournas et al. 2014; Magliulo et al. 2014) and developing reliable models to investigate the seismic behaviour of such buildings. Concerning the latter aspect, the possibility of having a large amount of data on the structural deficiencies of precast buildings boosted the investigations of many international researchers, with research and reports covering different aspects of these structures (Liberatore et al. 2013; Belleri et al. 2014; Bournas et al. 2014; Bovo and Savoia 2018, 2019; Ercolino et al. 2018). With specific reference to the seismic fragility functions, different authors focused on particular classes of precast buildings (e.g. considering specific types of connections or claddings, or considering only one type of collapse mechanism but neglecting the others). As a consequence, the outcomes of the various studies (Casotto et al. 2015; Buratti et al. 2017) are not simple to compare, thus the results cannot be generalized to a widespread stock of buildings. Furthermore, in other cases, the seismic fragility functions have been obtained for stocks that collect structures with very different dynamic features. In this way, the fragilities represent an average evaluation of seismic performances of a certain group of buildings but are not properly valid, in general, for an individual building or for narrow classes of buildings in the stock.

With the aim of providing a more uniform approach, Bovo and Savoia (2021) proposed a method for the fast seismic assessment of different classes of one-story precast RC buildings, selected on the basis of international reports and databases (Regione Emilia Romagna 2020). The PRESSAFE (PRecast Existing Structure Seismic Assessment by Fast Evaluation) methodology allows to define, in a simplified way, the seismic fragility curves of different existing precast RC structures not designed for seismic actions. The method, starting from the seismic deficiencies and weaknesses shown by the precast structures during past earthquakes, provides the fragility curves of different building typologies common in the Mediterranean area.

By following the approach proposed in Bovo and Savoia (2021), an alternative method called PRESSAFE-disp (PRecast Existing Structure Seismic Assessment by Fast Evaluation-displacements) is presented in this paper. Starting from the information collected in the numerous building inspections conducted by the authors in the aftermath of the 2012 Emilia earthquake, PRESSAFE-disp introduces different damage mechanisms taking into account the relative displacements and sliding between precast elements. The damage criteria have been properly selected and modelled in order to reproduce the mechanisms observed during the building surveys.

The main difference between the two methods, PRESSAFE and PRESSAFE-disp, relies in the definition of the collapse condition: in the first, the attainment of the plastic strength capacity in one of the sliding hinges (adopting a force-based collapse criterion) is considered; while in the latter, the attainment of the displacement capacity in one of the sliding hinges (adopting a displacement-based collapse criterion) is considered.

In both methods, under the hypothesis of flexible roof (i.e., no diaphragm effect), a frequent condition observed in many precast buildings in Emilia, the main frames of a building are studied separately. The horizontal force acting on a frame is considered to be proportional to its tributary vertical mass, thus the seismic in-plane behaviour is evaluated with dynamic analyses.

In this study, different precast frame typologies have been selected and investigated with incremental dynamic analyses (IDA) considering, for each building category, 8 vibrating periods ranging from 0.25 s to 3.0 s. The frames have been analysed by considering or excluding the presence of three common typologies of perimeter elements (i.e., RC horizontal cladding panels, RC vertical cladding panels and masonry infill walls), in order to simulate the perimeter frames or the internal bare frames of a precast building, respectively. Therefore, 120 different frame classes, 24 internal and 96 perimeter frames, have been analysed in the work. Two seismic fragility functions, related to severe damage and collapse state, have been obtained from the outcomes of the dynamic analyses. By interpolating the fragility functions over the set of the 8 periods of vibration, 3D fragility surfaces of each category have been derived, defining also the analytical expressions. The fragility surface provided in this work is a useful tool allowing to define the fragility curve of a frame starting from the knowledge of its structural category and the value of the first period of vibration T₁. Moreover, the fragility functions at failure of the different perimeter elements have been also obtained and reported.

Finally, the combined fragility function of the whole precast structure has been statistically derived by combining the fragility functions of its sub-elements (i.e. frames). As confirmed in recent studies (Silva and Horspool 2019), the availability of mathematical functions connecting vibrating period and fragility curves represents a powerful tool, not commonly provided in other studies concerning fragility functions. Indeed, it could be adopted to carry out statistical calculations based on vulnerability models, like seismic loss and damage assessments, considering the uncertainty in the period of vibration.

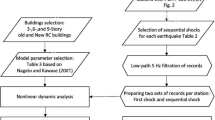
The simplified approach, introduced in the framework of this study, allows a fast evaluation of the fragility curves of a precast frame, starting from the knowledge of few structural information which can be collected through a building survey with a visual inspection and non-destructive tests. Hence, the direct approach, allowing to assess the fragility of the entire precast RC building, can be useful for performing rapid seismic risk evaluations. In particular, the methodology is deemed suitable for multiple applications at a territorial scale, for example in the case of large numbers of building stocks located in productive areas, and may be adopted for the identification of the most sensitive productive areas of a region. This may help to define specific economic measures for seismic risk reduction, or may be considered as a tool to support decision, for instance in the context of the Civil Protection seismic plan definition. A schematic overview of the main steps of the PRESSAFE-disp methodology, widely described in the following sections, is illustrated in Fig. 1.

Fig. 1

Overview of the application of the PRESSAFE-disp methodology

2 Main damage and collapse mechanisms observed in precast RC buildings after the 2012 Emilia earthquake

The 2012 Emilia earthquakes hit an area with many medium-to-large industrial and agrifood districts, causing extended damage and several collapses of the precast RC buildings (Liberatore et al. 2013; Bournas et al. 2014; Savoia et al. 2017). Figure 15 in Appendix shows some examples of the different damage mechanisms. From the outcomes of the building surveys in the earthquake aftermath, about 4000 production buildings, i.e. 45% of the total number in the area, were tagged as unsafe (equivalent to red-colour tag of ATC 1989), resulting in more than 3000 requests of regional funds for the retrofit and the reconstruction process (Agenzia Regionale per la ricostruzione 2018).

To this regard, also past earthquakes in other countries caused widespread structural collapses or serious damage to this building typology (Tzenov et al. 1978; Tapan et al. 2013), highlighting the international character of this criticality.

The seismic vulnerability of the Italian precast RC buildings has been largely acknowledged by engineers and researchers after the 2012 seismic events, as mentioned before. Due to the regular layout and the simple static scheme usually adopted for these highly standardised buildings (i.e., simply-supported horizontal elements above cantilever RC columns, with infilled masonry walls or precast cladding panels along the perimeter (Savoia et al. 2012; Bellotti et al. 2014)), the damage mechanisms observed in Emilia can be collected within a few common types, and summarized herein:

• The failure at the base of the columns due to the insufficient longitudinal and transverse reinforcement bars, resulting in inadequate flexural capacity (see Fig. 15a);

• The sliding of roof elements and, in several cases, even their fall, caused by the absence or inadequacy of steel connection devices between columns and beams or between beams and roof slab elements. Where the steel elements were absent, the sliding mechanism was even eased by the presence of neoprene pads between the precast RC elements (see Fig. 15b and c);

• The collapse of the non-structural walls along the perimeter of the buildings i.e., the detachment and the fall of the horizontal (Fig. 15d) and vertical cladding panels (Fig. 15e) and in-plane failure of masonry infills (Fig. 15f).

It is evident that, when precast RC buildings are subjected to a strong ground-motion, the damage may affect both the structural and the non-structural elements, and all these aspects should be taken into account in a consistent structural model. Moreover, the non-linear contribution due to second order effects should be considered since it may increase displacements and the corresponding damage for tall and flexible structures, like those considered in the present study. Accordingly, the method presented in this study has been developed considering suitable structural characteristics of the precast existing buildings, coherent with the in-field observations collected. Thus, various structural parameters have been selected, in order to model the seismic behaviour of the precast buildings in Emilia Romagna, as detailed in the next Section.

3 PRESSAFE-disp method

3.1 Description of the methodology

The aim of the methodology is to estimate the seismic vulnerability of one-story existing precast RC buildings, adopting mechanical models which must be simple but capable of reproducing the damage and collapse mechanisms described in Sect. 2.

The method is based on the following main steps:

• Classification of the building stock to be investigated, starting from the data of reports and building surveys in the aftermath of May 2012. This is achieved by identifying the most important parameters which mainly influence the response of these buildings when hit by the ground motion;

• Analysis of the behaviour of the internal frames and perimeter frames identified in the previous step. Considering the hypothesis of flexible diaphragm for this class of buildings, internal frames and perimeter frames are studied separately, the latter being characterized by the presence of cladding panels or masonry infills;

• Incremental dynamic (time-history) analyses with reference to the finite element models of internal and perimeter frames;

• Definition of the fragility curves and the fragility surfaces for each class of internal and perimeter frames. The fragility surfaces are defined as a function of the first vibrating period of the frames. Obviously, internal and perimeter frames could have different values of the period of vibration;

• Definition of the (combined) fragility curve for the entire building, statistically derived starting from the knowledge of the fragility functions of its frames.

Each step of the methodology is widely described in the following Sections.

3.2 Building features and typologies

The first step involves the identification and classification of the most widely used precast structural typologies not designed for the seismic actions, drawn from databases collecting the surveys of experts and engineers, carried out after the Emilia 2012 seismic event (Bellotti et al. 2014; Ongaretto et al. 2019).

The most common structural layout is constituted by cantilever columns supporting the horizontal roof elements, which are precast principal beams bearing perpendicular precast floor slab secondary elements. The foundations are usually isolated socket foundations, not linked by beams as presently mandatory in seismic zones. More complex (and rare) layouts, such as multi-storey buildings or structures with shed roof, are not considered.

The structure in elevation is quite slender since the typical height ranges from 6.0 to 9.0 m, and the square or rectangular column sectional dimensions are 40–80 cm. Most of the building mass is concentrated at the roof level, where monolithic prestressed beams are inserted in top forks above the columns or placed on thick corbels, so behaving as simply-supported elements, with or without steel connectors. If the steel elements are absent, the support strength against the horizontal forces relies on the frictional resistance, which can be negatively influenced by the presence of interposed neoprene pads. The floor slab elements sustained by the main beams constitute the top roof level, providing a flexible in-plane behaviour due to the lack of continuity and the insufficiency of the connections. The features of the most common roof elements (i.e. main beams and roof slab elements) have been collected and presented in Bovo and Savoia (2021).

In those few cases where mechanical devices connecting beams and columns were present, they were constituted by 2 steel dowels with Ø16 or Ø25 diameter, whereas the steel connections between slab elements and main beams were thin L-shaped plates. The connections proved to be stronger if compared with the friction-based support, since they have been able to prevent the horizontal sliding of the roof elements, as in many documented situations.

Masonry infill walls and precast cladding panels usually represent the building cladding elements on the perimeter, connected to the frames of the buildings. In more recent buildings, horizontal or vertical precast cladding panels are directly connected to the structural frame elements (columns and/or perimeter beams), while the older buildings have masonry walls placed between consecutive columns.

Among the connection typologies of the horizontal cladding panels, the two most frequently observed in the Emilia Romagna industrial areas are illustrated in Fig. 2. The first one is constituted by strong steel brackets, both supporting the horizontal panels and providing the connection to the columns. These steel profiles are usually designed to sustain the weight of the panel, with a slope that allows to prevent the out-of-plane displacement of the panel. The second type of panel-column connections consists of a steel channel placed in the column concrete cover and a hammer head strap fastened by means of a bolt in the panel (Colombo et al. 2016). In the case of a seismic action, this layout cannot guarantee the out-of-plane resistance of the panel because the shear deformation capacity of the connection is limited; as a result, this type of connection has proved to be very fragile during the Emilia seismic events.

Fig. 2

adapted from Reluis Report (2007): connection adopted for a The (h1) frame class and For the (h2) frame class

Schemes of two typical connections for horizontal cladding panels, b

Finally, the vertical panels are usually connected to the perimeter upper beams through a bolted angular profile, as illustrated in Fig. 3.

Fig. 3

adapted from Reluis Report (2007)

Scheme of a typical connection for vertical cladding panels,

All these characteristics have been selected from the in-situ surveys, and through the analysis of previous studies focused on the capacity of the frame elements and the different connections in precast buildings (ReLUIS 2007, Biondini et al. 2013; Bournas et al. 2013; Magliulo et al. 2015; Zoubek et al. 2016; Belleri et al. 2018). For details see Table 1.

Table 1 Materials and geometries assumed for the four different base column flexural capacity levels (f_cm: concrete mean cylindrical compressive strength; R_ck: concrete characteristic cubic compressive strength; f_ym: steel mean yielding stress; H: building height; L_b: beam spans; L_fs: span of the roof slab elements)

Therefore, the most common existing precast buildings of the Emilia Romagna region can be classified according to the four main criteria schematized in Fig. 4:

Fig. 4

Frame classification criteria adopted in the PRESSAFE-disp method

The first criterion is the value of the yielding moment at the column base, classified here through four reference values corresponding to four letters, from the lowest one (A) to the highest one (D). All the details for the calculation of the yielding moment values can be found in the paper Bovo and Savoia (2021) and are not reported here for the sake of brevity.

The second criterion is the beam-column connection, labelled with letters (L), (M) or (H), depending on the strength level of the typologies described above. This study concerns beams with tapered I cross-section.

The third criterion is the roof slab-beam connection defined as low strength typology (L) or high strength typology (H). This study concerns roof slab elements with double tee cross-section.

The fourth criterion is the type of perimeter panel, being one of the three aforementioned typologies, i.e. masonry infill walls (m), horizontal cladding panels (h) and vertical cladding panels (v). As far as perimeter frames with horizontal cladding panels are concerned, two different types of connections are considered in this study: the frames are labelled (h1) or (h2), when the steel corbel or the anchor channel connections are used, respectively.

Thus, 24 internal frame (I) categories and 96 perimeter frame (P) categories have been considered, the latter being further sub-classified according to the fourth criterion.

Each category for internal (bare frame) and perimeter frame of the buildings is thus labelled through 4 letters. The first 3 letters correspond to the first three criteria adopted. For example, one of the 24 internal frame categories is A-L-L-I, characterized by a column flexural capacity of 180 kNm (letter A), low strength of both beam-column and slab element-beam connections with neoprene pads (L-L). The final (I) stands for ‘internal frame’. Similarly, one of the 96 perimeter frames has the same first three letter classifications, plus a (P) that indicates a perimeter frame. For perimeter frames, the final letter defines the type of infill that can be (m) masonry wall, (h1) or (h2) horizontal cladding panels or (v) vertical cladding panels, according to the fourth criterion.

3.3 Finite element modelling

The seismic analyses of the frames belonging to the different categories have been performed on finite element (FE) models realized in OpenSees (OpenSees 2015) (see Fig. 5). Figure 5a depicts the FE model of an internal frame (I), whereas Fig. 5b, c and d show the models adopted for perimeter frames with the presence, respectively, of masonry infilled walls, horizontal and vertical precast RC cladding panels.

Fig. 5

FE modelling of the different frame typologies: a INTERNAL frame; Perimeter frame with b Masonry infill WALLS, c Horizontal cladding panels and d vertical cladding panels

3.3.1 Frames

The main elements of an internal frame (i.e. vertical columns and horizontal beams) have been modelled with 1-D elastic beam elements. The columns are fully clamped at the base and have pinned–pinned connections with upper beams.

The nonlinear behaviour of the columns has been accounted for by introducing plastic hinges at the column base, defined in terms of simplified trilinear moment-rotation laws (see sub-Figure a1 in Fig. 6), where: M_y is the yielding moment depending on the flexural capacity level (i.e. A, B, C or D); M_u is the ultimate moment assumed equal to 1.05 × M_y; θ_y and θ_u are the corresponding rotations evaluated according to EuroCode (2005). The plastic hinges have been defined by adopting the hysteretic uniaxial material in OpenSees (2015) with the following values for the damage parameters: pinchX = 1.0, pinchY = 1.0, damage1 = 0.0, damage2 = 0.08 and beta = 0.12 in order to consider the hysteretic degradation of the RC elements when subjected to cyclic loadings (Kurtman 2007; Bovo and Buratti 2019).

Fig. 6

Nonlinear laws adopted in the FE models. a Structural elements: (a1) Moment-rotation constitutive law for the plastic hinges at the base of the columns; (a2) Force–displacement shear law for zero-length sliding hinges simulating friction-based connections; (a3) Force–displacement shear law for zero-length sliding hinges simulating mechanical device-based connections. b Non-structural perimeter infill walls/panels: (b1) Force–displacement axial laws of the equivalent struts modelling the perimeter masonry infill walls; (b2) Force–displacement axial laws adopted for the column-panel connections of horizontal cladding panels; (b3) Force–displacement axial law adopted for the beam-panel connections of vertical cladding panels (top connection)

Moreover, the nonlinear behaviour of the beam-column connections has been modelled with a zero-length sliding hinge which is rigid-plastic if the connections are friction-based without mechanical devices (see sub-Figure a2 in Fig. 6), or elastic–plastic if dowels are present (see sub-Figure a3 in Fig. 6). In the friction-based connections, modelled with the Coulomb friction model implemented in OpenSees, the strength capacity is calculated by considering the current vertical force on the connection (due to the self-weight of the precast elements added to the vertical seismic action) multiplied by the friction coefficient μ assumed equal to 0.1. The value selected is in accordance with the experimental tests reported in Magliulo et al. (2011) considering the presence of a neoprene pad between two precast elements. The numerical parameters adopted to define the behaviour of the connections are summarized in Table 2. It is worth noting that the red circles in Fig. 6a represent the attainment of a collapse condition of the structural frame, as further explained in the following. Finally, the column cross-sections have been selected, for each building category, in order to obtain specific values of the period of vibration of the frame (i.e. Ť₁ = 0.25, 0.5, 0.75, 1.0, 1.5, 2.0, 2.5 and 3.0 s).

Table 2 Parameters defining the mechanical properties of connections and equivalent masonry struts adopted in the numerical models (F = force; d = displacement)

Regarding the masses considered in the analyses, the mass of columns and beams has been considered as a consistent mass along the length of the element. The masses of the roof slab elements have been added as lumped masses connected by zero-length elements to the beams (see Fig. 5). Moreover, the mass of the walls/panels in the plane of the perimeter frames has been introduced as a consistent mass along the finite elements simulating the panels or the struts. Finally, the mass of the walls/panels orthogonal to the plane of the internal and perimeter frames has been introduced as an equivalent consistent mass along the vertical finite elements of the columns.

3.3.2 Perimeter infill walls/panels

The infill walls considered in the study are 30 cm thick, and are unreinforced masonries with hollow clay bricks with mean compressive strength f_c = 3.5 MPa and hydraulic lime mortar with mean compressive strength f_c = 4.0 MPa. The masonry infill walls in the perimeter of the building have been modelled by means of two equivalent diagonal struts (see Fig. 5b). This strategy provides a suitable approximation of the global response of the frame (Crisafulli et al. 2000; Asteris et al. 2011). The axial behaviour of the equivalent struts has been modelled in OpenSees as hysteretic elements by using the Hysteretic Material (OpenSees 2015) and assuming the values indicated in Table 2, as suggested in Fardis (1996) and Celarec et al. (2012). Since the strut behaviour is a function of the frame geometry, four different curves are obtained and reported in sub-Figure b1 in Fig. 6, for the four aforementioned frame typologies (A), (B), (C) and (D). The failure for masonry infill walls has been assumed to be the crushing of the masonry struts. The results provided by these models are valid if the out-of-plane failure mechanisms of the masonry panels are prevented, or if these mechanisms are activated by higher horizontal accelerations than those causing structural collapse. If the out-of-plane failure mechanisms of slender masonry panels are expected to happen before the structure collapse, the results of the model may not be realistic.

On the other hand, the perimeter elements of the more recent buildings are typically constituted by precast cladding panels, horizontally or vertically arranged. The former panels may typically assume in two main configurations. In the first solution (h1), the panels are hung at the columns in four points by means of mechanical steel devices: usually the lower ones (bottom connections) bear the self-weight of the panels, whereas the upper (top connections) prevent the outward overturning and the horizontal column-panel slip. In the second solution (h2), the lowest series of panels directly leans on the foundation beams and the outward overturning is prevented by two top connections realized as in Fig. 2. Then, the upper series of panels directly leans on the lower one with analogous top connections. The FE model describing this typology of frames is reported in Fig. 5c. The behaviour of the connections both for (h1) and (h2) typologies is shown in sub-Figure b2 in Fig. 6. The values adopted in the FE models are reported in Table 2 and have been defined respectively for (h1) and (h2) connection typologies starting from the experimental outcomes reported in Belleri et al. (2016) and Del Monte et al. (2019). Three horizontal panel series have been considered in the models.

Lastly, the FE model simulating frames with vertical cladding panels (see Fig. 3) is reported in Fig. 5d. The vertical panel is clamped at the base and connected to the roof beam of the structure by means of the anchor–channel connections type HRC-U-M180 studied in Zoubek et al. (2016). The numerical law implemented for the top connection of the vertical panels is shown in sub-Figure b3 in Fig. 6, and the corresponding parameters are reported in Table 2. For each vertical panel, two anchor-channel devices have been considered. It is worth noting that the red circles in Figs. 6b correspond to the attainment of the failure of non-structural perimeter walls/panels. Since the dynamic analyses continue until the attainment of a collapse condition for the structural frame, also the post-failure behaviour of non-structural elements is defined.

Considering that all these are 2D simplified models, the out-of-plane behaviour of walls and panels in the direction orthogonal to the frame has not been taken into account. It is worth noting that this could entail a modification of the seismic demand to the columns adjacent to the cladding elements.

3.4 Definition of damage and collapse states

3.4.1 Frames

Following the indications reported in Sect. 2 regarding the observed damage, two limit states have been considered for the frames. They refer to a severe damage and a collapse condition of the main structural elements, respectively.

The severe damage condition has been set at the attainment of one of the following sub-conditions:

• The yielding bending moment of the base-section of a column;

• The strength capacity in a roof slab-beam connection or in a beam-column connection.

• The collapse condition has been defined at the attainment of one of the following sub-conditions:

• The ultimate rotation for a column;

• The displacement capacity in one of the sliding hinges shown in Fig. 5a, adopting a displacement-based collapse criterion for the connections.

• The second criterion, in both conditions, has been properly added in order to simulate the common damage and collapse mechanisms observed in the aftermath of the Emilia earthquake, where the horizontal sliding of heavy beams or roof slab elements, in several cases, caused the complete unseating and the subsequent fall of the elements.

The attainment of the element or connection failure, indicated by the red circles in Figs. 6a, identifies the collapse of the frame, at which the dynamic analyses have been interrupted. The possible attainment of a failure condition has been evaluated step-by-step during the dynamic time-history analysis. Moreover, in the IDA procedure, the second-order effects (P-∆) have been also considered. In particular, in very flexible structures, like those investigated here where cantilever columns support heavy masses, the non-linear second order effects may cause large displacements at the roof level and may increase the seismic damage anticipating the structural collapse.

3.4.2 Perimeter infill walls/panels

It seems worth highlighting that, in the aftermath of the Emilia earthquakes, the most commonly observed damage to non-structural elements concerned the perimeter walls/cladding panels. Hence, the failure of perimeter infill walls and cladding panels has been also considered and recorded in the dynamic analyses. For the masonry infill walls, the failure of the panels has been identified at the attainment of the peak point in the strut axial behaviour (see sub-Figure b1 in Fig. 6).

Analogously, the failure of the horizontal cladding panels has been identified with the attainment of the peak point in the behaviour of the connection supporting the panel (see sub-Figure b2 in Fig. 6). To this regard, it is to be highlighted that most of the precast buildings in the Emilia Romagna territories presents the (h2) connection typology described in Sect. 3. The (h2) type of connections showed a very high sensitivity to seismic actions, whereas the (h1) one resulted to be significantly less weak.

Finally, the failure of the vertical panels has been identified with the failure of the mechanical devices (top connections in Fig. 5d) connecting the panels to the structural elements (in this case the roof beam). Again, the failure of the connection has been registered at the attainment of the peak point of the constitutive law (see sub-Figure b3 in Fig. 6).

After the attainment of the failure point for non-structural perimeter walls/panels, the analyses continue according to the post-peak behaviour shown in Figs. 6b. The analyses have been then interrupted at the attainment of one of the aforementioned collapse conditions related to the structural frames. In all cases, the non-structural walls/panels failure condition has been evaluated independently from the structural collapse condition of the whole frame.

4 Incremental dynamic analysis

In order to evaluate the seismic response of the various frames, nonlinear time-histories analyses have been performed, considering as input the 30 ground motion records selected in Vamvatsikos and Fragiadakis (2010). Both the horizontal and vertical components of the ground motions have been considered, covering a wide range of frequency, time, duration and amplitude. The free field records have been extracted from PEER Strong Motion Database (PEER 2020), following the criteria of selection adopted by Vamvatsikos and Fragiadakis (2010).

The main characteristics of the records considered are collected in Table 3 and the 5%-damped acceleration response spectra of the 30 horizontal ground motions are reported in Fig. 7a. In the Figure, the 5% damped elastic spectra of the 30 recorded horizontal ground motions are represented together with their average spectrum (in red). No scaling factor have been used in the selection phase. The distance from the source, between 15.1 km and 32.6 km, has been selected to avoid the directivity effects. The dataset adopted has an average value of horizontal over vertical peak ground acceleration ratio, i.e. PGA_h/PGA_v (see Fig. 7b), comparable with that expected for seismic far fault records (PEER 2013). Following the criteria given in PEER (2013), the vertical records considered do not present pulse-velocity shape.

Table 3 Set of 30 horizontal ground motions adopted for time-history analyses as extracted from PEER Database (2020)

Fig. 7

Seismic inputs adopted for the dynamic analyses: (a) 5%-damped acceleration response spectra of the 30 horizontal ground motions and mean value (in red); b Horizontal/vertical peak ground acceleration vs. closest distance to fault rupture (R) for the records selected

The Incremental Dynamic Analyses (IDA) have been performed according to the methodology outlined by Vamvatsikos and Cornell (2002), to consider the record-to-record variability. The analyses have been carried out on 960 different FE models, considering, for each frame typology (i.e. 24 internal and 96 perimeter frames for a total of 120 frames), 8 different column cross-sections corresponding to 8 vibrating periods of the frames. The use of 8 periods of vibration allows to obtain a set with 8 fragility curves for each frame typology, which have been subsequently combined to determine one fragility surface considered as a function of the value of the first period of vibration (see the next Section).

The intensity measure (IM) considered in the IDA procedure is the 5%-damped first mode spectral acceleration, S_a(T₁,5%) or S_ain the following, and the engineering demand parameter (EDP) adopted is the maximum horizontal displacement at the roof level. In the IDA analyses, Rayleigh damping with damping matrix (D) proportional to the last computed stiffness matrix (K_current) has been considered. The damping matrix was calculated as D = ( 2ξ / ω₁) × K_current where the damping ratio ξ was assumed equal to 5% and ω₁ was the value of the first natural (circular) frequency of vibration.

In the IDA procedure, each record has been scaled up to the attainment of at least one collapse condition, considering also the P-∆effects. The results of the time-history analyses have been 28,800 IDA curves, statistically combined in order to generate 960 numerical fragility curves (see the procedures in Silva et al. 2019) and then 120 fragility surfaces in which the value of the first vibrating period T₁ has been also considered as a variable (see Sect. 5).

The introduction of the cladding elements causes a significant stiffening of the perimeter frame with respect to the bare frame, changing the original elastic vibrating periods. Hence, for the sake of clarity and to avoid misleading, the outcomes presented in the following will be referred to the first period of vibration of the bare frame T₁ even if the record scaling has been performed with reference to Sa(T₁*,5%) (where T₁* is the elastic vibrating period of a perimeter frame with cladding elements and, obviously, T₁* < T₁ for each category). Thus, the period of vibration for the perimeter frame has been calculated by removing the perimeter infills/panels from the FE model. Therefore, for the application of the method, the potential user should adopt the same procedure. This aspect makes the method more user-friendly since it simplifies considerably the procedure, especially for applications to existing buildings for which some structural parameters and details may be very complex to be determined through visual inspections only. Moreover, this allows a more direct comparison between frames with and without panels.

As an example, Fig. 8 provides the percentage of attainment of the two different collapse mechanisms (failure of columns or sliding of roof elements). The results are reported for the sake of brevity for some representative frame categories only, i.e. A-L-L-I, A-M-H-I, A-H–H-I, C-L-L-I, C-M-H-I and C-H–H-I, for T₁ = 1 s. The figure highlights that, for frames with friction-based support, i.e. A-L-L-I and C-L-L-I, most of the collapses can be attributed to sliding mechanisms. On the contrary, considering the frames with high-strength beam-column and roof slab element-beam connections, i.e. A-H–H-I and C-H–H-I, most of the collapses can be attributed to the failure of the columns. This confirms the reliability of the retrofitting criterion suggested by the Legislative Decree (2012) in the aftermath of the events. Indeed, the strengthening of the connections between precast elements has positive significant benefits preventing the fall of the roof elements, and can be considered the first effective retrofitting intervention to be introduced in order to reduce the vulnerability of these buildings.

Fig. 8

Percentage of attainment of the two collapse mechanisms for some frame typologies with two different base-column flexural capacity (for T₁ = 1 s). (a) LEVEL A; b Level C

5 Definition of fragility curves and surfaces of the frames

5.1 Fragility functions at collapse and severe damage

By means of the results of the IDA curves, for each frame typology, the cumulative fraction of structures reaching a specific damage state for the 30 accelerograms has been calculated, providing a set of points. An empirical IM-based fragility function has been thus derived, by interpolating the so obtained set of points expressing the cumulative number corresponding to each IM. In particular, the set of points, representing the fragility for a given damage state of a frame with a specific period of vibration, has been fitted with a log-normal cumulative distribution function having the following form:

$$\mathrm{F}\left(s\right)=\Phi \left[\frac{\mathrm{ln}\left(\frac{s}{\upmu }\right)}{\upsigma }\right]$$

(1)

where: s represents S_a, $\Phi$ [·] is the standardized normal distribution function, $\upmu$ and $\upsigma$ are the main descriptors of the fragility function (i.e., the mean and the standard deviation, respectively). These parameters have been calibrated through the maximum likelihood function (see Eq. (2)), imposing the maximisation of ln L (see Eq. (3)) in order to find the best fitting function for each numerical IDA dataset of points:

$$\mathrm{L}={\prod }_{i=1}^{N}{[\mathrm{F}({s}_{i})]}^{{x}_{i}}{\cdot [1-\mathrm{F}({s}_{i})]}^{{1-x}_{i}}$$

(2)

$$\frac{\partial \mathrm{lnL}}{\partial\upmu }=\frac{\partial \mathrm{lnL}}{\partial\upsigma }=0$$

(3)

where: s_i represents the i-th S_a value, x_i the corresponding probability of failure, N is the total number of points (i.e., 30 points) for a specific damage state, and a specific frame category.

In Figs. 16 and 17, the (best fitting) fragility curves resulting from the regression procedure are shown for some representative building categories and for three periods of vibration (i.e. 0.5 , 1.0 and 2.0 s), at collapse and severe damage limit states, respectively.

It is worth noting again, for the sake of the clarity, that the outcomes presented in the following, for perimeter frames, refer to the vibrating period of the bare frames T₁ (without the presence of non-structural walls/panels), in order to simplify the comparisons between the behaviour of different categories.

Considering a specific value of S_a (horizontal axis), the probability of exceedance (PoE) in both limit states (vertical axis of the fragility curves) increases with the increase of the period of vibration, meaning that the flexible frames (longer periods) are more likely to collapse or to be subjected to severe damage, due to large displacements and P-Δ effects. This effect is clearly visible for the internal frames, whereas it is not always valid for perimeter frames, in particular for those with masonry infill walls, which highly influence the structural behaviour (e.g. see sub-Figures a1, b1, c1, d1, e1, f1 in Figs. 16 and 17 in Appendix).

Moreover, as expected, for a specific value of S_a for each category, all the severe damage fragility curves (see Fig. 16) are characterized by higher PoE values with respect to the corresponding collapse fragility curves (see Fig. 17).

The increase of the flexural capacity at the base of the column, for instance from class A-L-L to class D-L-L, is reflected in a progressive decrease of the PoE for both limit states. Similarly, the benefit of having strong connections between the roof elements is evident by comparing the curves of frame category C-L-L and those of C-M-H.

For all frame categories, the presence of the perimeter elements on one hand has a positive effect in lowering the vulnerability of the frames if compared with that of the internal ones, on the other hand, it influences the shape of the fragility curves in a different way depending on the value of the period considered. This is only partially true for perimeter frames with vertical cladding panels, being the fragility curves very similar to those of the internal frames, due to the poor column-panel connections (see sub-Fig. 3a, b, c, d, e, f in Figs. 16 and 17).

As far as the different connection types of the horizontal cladding panels are concerned, the perimeter frame categories with the (h2) connections are significantly more vulnerable than those with (h1) connections. Indeed, the fragility curves of the frames with the (h1) connection typology have higher mean values than the ones with the (h2) typology (see sub-Fig. a2, b, c, d, e and f in Figs. 16 and 17).

In addition, in order to perform some general comparisons, the collapse fragility curves are plotted in Fig. 9 for the frame categories A-L-L, B-L-L and C-M-H, for various cladding typologies and different periods of vibration. The results obtained for the A-L-L category for frames with period of 1.5 s are shown in Fig. 9a. For a specific S_a value, the masonry infilled frames (A-L-L-P(m)) show lower values of PoE at collapse, followed by those with horizontal cladding panels with (h1) connection (A-L-L-P(h1)). As mentioned before, horizontal cladding panels with (h2) connection (A-L-L-P(h2)) and vertical panels (A-L-L-P(v)) do not produce a relevant modification of the internal frame (A-L-L-I) fragilities, resulting in a very slight decrease of the PoE. The C-M-H frame category, characterized by higher strength of both columns flexural capacity and connections, exhibits an analogous behaviour (see Fig. 9b).

Fig. 9

Collapse fragility functions of frames with perimeter walls. a Behavior of structures with different types of perimeter cladding elements (m: masonry walls; h1 and h2: horizontal cladding panels with different connections; v: vertical cladding panels) for frame category A-L-L-P with low flexural capacity and T₁ = 1.5 s and b for frame category C-M-H-P with high flexural capacity and T₁ = 1.5 s; c Effect of the variation of typology with the horizontal cladding panels (h1) and (h2) on the seismic capacity of A-L-L-P frames for three different vibrating periods. d Effect of the vibrating period on the fragility of the frame category B-L-L-P(h2) very common in the Emilia Romagna region

With reference again to the perimeter frame category A-L-L-P, in Fig. 9c the behaviour of frames with horizontal cladding panels and the (h2) connection (A-L-L-P(h2)) is compared with those with the (h1) connection typology (A-L-L-P(h1)). The figure confirms that the former frames are more vulnerable if compared with the latter, independently of the value of the vibrating period of the frames.

Finally, the fragility curves for the 8 periods investigated are reported in Fig. 9d for the frame typology B-L-L-P(h2). As expected, with the increase of the period, a general decrease in both the S_a value for a prescribed PoE (i.e. the collapse acceleration) and the S_a dispersion (i.e. scattered tendency of the collapse acceleration dataset) occurs.

5.2 Fragility surfaces at collapse and severe damage

The fragility curves have been defined, for each structural typology, for 8 different periods of vibration T₁ and for the two limit states selected, i.e. structural collapse and structural severe damage. In order to provide the vulnerability of the frames as a function of T₁, the 2D fragility curves F(S_a) have been assembled for the creation of 3D smoothed fragility surfaces, expressed in the form R(S_a,T₁). The mathematical functions expressing the variation of the statistical fragility curve parameters (μ, σ) with the value of the vibrating period have been firstly identified. In particular, the selected trend functions of the two fragility curve descriptors referring to collapse are the following:

$$\mathrm{for }\,0< T1 \le 2.0\mathrm{s }\,{\upmu }^{\mathrm{C}}({T}_{1})=\mathrm{a}1\cdot {{T}_{1}}^{2}+\mathrm{a}2\cdot {T}_{1}+\mathrm{a}3$$

(4a)

$${\mathrm{for }\,2.0\mathrm{s }< T1 < 3.0\mathrm{s\, \mu }}^{\mathrm{C}}({T}_{1})={\upmu }^{\mathrm{C}}(2.0)$$

(4b)

$${\mathrm{for }\,0< T1 < 3.0\mathrm{s\, \sigma }}^{\mathrm{C}}=\mathrm{b}1\cdot {{T}_{1}}^{3}+\mathrm{b}2\cdot {{T}_{1}}^{2}+\mathrm{b}3\cdot {T}_{1}+\mathrm{b}4$$

(4c)

Analogous functions for the severe damage limit state are:

$$\mathrm{for }\,0< T1 \le 2.0\mathrm{s}\, {\upmu }^{\mathrm{SD}}=\mathrm{c}1\cdot {{T}_{1}}^{2}+\mathrm{c}2\cdot {T}_{1}+\mathrm{c}3$$

(5a)

$$\mathrm{for }\,2.0\mathrm{s }< T1 < 3.0\mathrm{s}\, {\upmu }^{\mathrm{SD}}({T}_{1})={\upmu }^{\mathrm{SD}}(2.0)$$

(5b)

$$\mathrm{for }\,0< T1 \le 3.0\mathrm{s}\, {\upsigma }^{\mathrm{SD}}=\mathrm{d}1\cdot {{T}_{1}}^{3}+\mathrm{d}2\cdot {{T}_{1}}^{2}+\mathrm{d}3\cdot {T}_{1}+\mathrm{d}4$$

(5c)

where: T₁ (in seconds) is the first vibrating period of the bare frame, and the coefficients a1-d4 have been obtained by fitting the IDA data through a nonlinear regression procedure based on the least squares' method (see Tables 4 and 5, 6, 7 and 8 in the Appendix for internal and perimeter frames, respectively). The effectiveness of the regression is proved by the value of the coefficient of determination, being R² always greater than 0.9 and frequently over 0.95.

The fragility surfaces R(S_a,T₁) allow to consider the uncertainties in the value of T₁ in the estimation of the vulnerability of a precast frame. A similar tool was proposed by Crowley et al. (2004), with reference to ordinary RC buildings, for the derivation of relationships between the displacement capacity and the fundamental period of a building.

As a general example, a fragility surface for the category A-M-H-I is shown in Fig. 10, together with the IDA data adopted in the fitting procedure: for a value of T₁ ranging between 0.25 and 3.0 s, from the 3D fragility surface it is possible to extract the corresponding 2D fragility curve.

Fig. 10

Example of a fragility surface (for A-M-H-I frame category). Points obtained from IDA and best fitting approximation for the different periods

The plots of Eqs. 4 and 5 are illustrated for some relevant structural categories in Figs. 11 and 12, for collapse and severe damage state, respectively. While the trends related to σ are characterized by similar wavy shapes, the trend of μ presents some variations both in case of collapse and severe damage. In particular, for some categories (see sub-Fig. a1, c, d and e in Fig. 11) it has have a reversed bell shape, differently from those of the perimeter frame categories with masonry infill walls (sub-Fig. b1 in Fig. 11). This seems to be linked to the strong influence of the latter cladding typology on the frame response, as masonry infill walls influence, in particular, the highest vibrating periods.

Fig. 11

Trend of median value μ^C and standard deviation σ^C of lognormal distributions for different vibrating periods T₁ at collapse for some relevant frame typologies (see Eqs. (4)) for a Internal frames and perimeter frames with b Masonry infills, c Horizontal panels with (h1) connection, d Horizontal panels with (h2) connection and e Vertical panels

Fig. 12

Trend of median value μ^SD and standard deviation σ^SD of lognormal distributions for different vibrating period T₁ at severe damage condition for some relevant frame typologies (see Eqs. (5)) for a Internal frames and perimeter frames with b Masonry infills, c Horizontal panels with (h1) connection, d Horizontal panels with (h2) connection and e Vertical panels

The poor behaviour of the (h2) type of connection for horizontal cladding panels, with respect to the (h1) ones, is once again highlighted by lower values of the μ functions for both limit states (see sub-Fig. c1 and d in Fig. 11). The σ functions, related to the frames with the two different horizontal cladding panel connections, have similar trends for high periods, whereas they are very different for low periods (see sub-Fig. c2 and d in Fig. 11). In particular, the (h1) connection typology results in higher σ values for the more sensitive structural categories, i.e. A-L-L and A-M-H, at the low period values (see sub-Fig. c2 in Fig. 11). These different trends are justifiable because the weak (h2) connection, differently from the (h1) typology, is not able to modify considerably the seismic response and the collapse value of the perimeter frames with respect to the internal (bare) frames. Hence, for frames with (h2) connection type, in the whole range of periods investigated, the σ value is very similar to the case of internal frames. This effect is no more visible at higher periods for the frames with (h1) connections, because of the presence of remarkable P-Δ effects (in flexible frames). The same effects can be observed in the curves in Fig. 12.

5.3 Fragility surfaces of infill walls/panels (at failure)

Analogously to the procedure described in the previous Sections for the structural frames, the IDA outcomes related to the failure of perimeter infill walls and cladding panels have been elaborated to obtain fragility curves (i.e. fragility functions) of the various types of building perimeter elements.

The fragility curves for masonry infill walls have been defined considering the attainment of the peak point in the force–displacement curve of the equivalent struts (see sub-Fig. b1 in Fig. 6). For the precast RC cladding panels, instead, the failure condition has been set, conventionally, at the attainment of the peak point in the constitutive diagram of the connections hanging the panel (see the laws of the connections in sub-Figs. 2 and 3b in Fig. 6, and the red circles reporting the label “Failure”).

For some frame classes, the structural collapse anticipates the failure of the perimeter elements and, in those cases, i.e. for panels largely more robust than the frame, the IM value causing the collapse is not available. In other cases, the structural collapse and the failure of non-structural elements have comparable values and the walls/panels failure data are available just for some seismic inputs over the whole set investigated. Assuming the fragility functions of the walls/panels to be independent from the frame class, the fragilities of a given cladding element have been obtained, irrespective of the frame typology, by considering all the collapse data available (i.e. when the wall failure anticipated the frame structural collapse). In this way, it has been possible to establish, for the different cladding typologies and for each period investigated, the lognormal fragility functions. They have been provided assuming the same laws for the characteristic parameters of the distribution (i.e. μ and σ) as given in Eq. (4).

The values of μ and σ of the curves of the various perimeter elements are shown in Fig. 13 for the different periods of vibration. For the sake of brevity, Eqs 4a, 4c of the fitting curves are reported directly in Fig. 13. Obviously, the equations of μ reported in the figure are valid up to T₁ = 2.0 s whereas the trends for vibrating periods higher than 2.0 s follow Eq. (4b).

Fig. 13

Trend of median value μ and standard deviation σ of lognormal fragility curves at failure of non-structural elements for a Masonry infilled walls, b Horizontal cladding panels with (h1) connection, c Horizontal cladding panels with (h2) connection and d Vertical cladding panels

For masonry infill walls, a different trend has been obtained from the analyses of the different building categories, especially when comparing categories A-B and C-D. Hence, two different fitting procedures have been followed to obtain the parameters μ and σ of the lognormal collapse fragility surfaces, and the main results of the regression analyses are reported in sub-Figs 1 and 2 a in Fig. 13. The results confirm a lower capacity, in terms of median S_a, for frame categories C and D with respect to categories A and B, with median collapse spectral acceleration around 0.5–0.6 g for C-D frames and 0.7–0.8 g for A and B frames. The difference is probably due to the different geometries of frames A-B and C-D (see Table 1). Indeed, due to the higher column’s height of the C-D categories, top displacements are larger than those of A-B categories for analogous levels of horizontal forces. Anyway, the values of μ for a given category are quite similar as they seems to be rather insensitive to the period’s variation.

The coefficients of the equations obtained from the regression analyses are reported in the same figures. As far as σ is concerned, the values related to masonry infills in frame categories A-B and C-D have very similar trends, with the former having slightly bigger dispersion values (about 20% greater) than the latter.

The trends of μ for the two different horizontal cladding panel connections, at failure, are reported in sub-Fig. b1 b and c in Fig. 13, respectively. It is worth noting, as already emerged from the analyses at collapse of the structural frames, that horizontal panel connections (h1) can sustain a higher acceleration before collapse with respect to connections (h2), being μ about twice in the whole range of the periods investigated. Both panel connections show that their median acceleration value at failure is strongly period-dependent: it changes significantly, for instance for (h1) connection, from about 1–0.2 g by moving from 0.5–2.0 s of period values. The trends of σ parameter are very similar but with higher variability for (h1) cladding panel system (see sub-Fig. 2 band c in Fig. 13).

The very different acceleration capacities between (h1) and (h2) types of cladding panel connections is in fully agreement with the in situ observations in the aftermath of the Emilia earthquakes (Savoia et al. 2017), confirming the extended damage detected in the buildings with (h2) panel connection type and, on the other hand, very few cases of failure observed for the (h1) type.

A reasonable explanation of the numerous collapses of cladding panels with (h2) connection typology, observed during the Emilia earthquake, can be grasped by Fig. 14. Due to the cantilever behaviour of the columns, the highest horizontal inter-panel drift demand (i.e. relative horizontal displacements between two panels) is expected at the top of the columns, firstly involving the upper panel connections. The larger displacement capacity of the (h1) connection type, results in a less seismic-sensitive response of the panels, which are able to confer a considerable contribution to the capacity of the perimeter frames.

Fig. 14

Horizontal displacement demand for the (h2) connections supporting horizontal cladding panels positioned at different heights above the ground

Lastly, the outcomes obtained for the vertical RC cladding panels are reported in sub-Figs. d1 and d2 in Fig. 13. For this type of panels, both μ and σ distributions are intermediate between those of the (h1) and (h2) typologies. Also in this case, the μ value is strongly period-dependent and σ, representing the dispersion of the outcomes basically depending on the record-to-record variability, has the usual wavy trend already observed for the other cladding typologies. It is worth noting that the equations corresponding to the perimeter elements, reported in Fig. 13, could result useful also in the framework of a seismic loss evaluation and performance assessment of precast buildings subjected to earthquake (FEMA 2018). Indeed, they represent the component fragility curves of perimeter walls/panels which are necessary, together with the fragility curves of the structural elements, in order to perform a reliable and robust seismic loss estimation. Moreover, while a wide literature already exists with regard to the component fragility of masonry infill panels in cast in-situ RC frames (Del Gaudio et al. 2017; Rossetto et al. 2014), the component fragility of precast RC panels is not commonly provided.

6 Definition of fragility curves of the building

In this study, the precast RC building has been considered to be constituted by different main frames with distinct dynamic behaviours, due to the absence of a rigid diaphragm at the roof level. As mentioned, the 2012 earthquake has revealed the low in-plane stiffness of one-storey precast buildings, being them widely affected by partial collapses of the roof elements belonging to the internal frames, perimeter frames, or both.

Under this light, the fragilities of different frame categories (i.e. internal and perimeter) have been obtained separately, therefore the combined fragility function for the entire building can be statistically derived starting from the knowledge of the fragility functions of its frames (see Fig. 1).

Considering the repetitive layout of a precast RC building, it is typically possible to identify one frame category characterizing all the internal frames, and one frame category characterizing the perimeter frames of the building. Under the hypotheses that internal frames are assumed to be identical (in terms of geometry, materials, element dimensions and masses) since they belong to the same structural category, and the same is valid for perimeter frames, the collapse of the entire building can be described considering the combination of these two single events: the collapse of a internal (I) frame and/or the collapse of a perimeter (P) frame. In other words, the collapse of the precast building can be studied with the fundamental axioms of the algebra of sets (Benjamin and Cornell 1970) applied to the single events describing the collapse of the frames. Thus, assuming that the collapse of the internal frames does not affect the probability of occurrence of the collapse of the perimeter frames and vice-versa, the building collapse occurs when one of its frame categories, or both, collapse. Indeed, the events describing the attainment of the collapse of a frame typology can be considered (a) statistically compatible (or non-mutually exclusive) and (b) independent. Since the collapses of the two frame typologies are considered compatible events, named E_I and E_P, the following properties can be derived:

${\text{E}}_{{\text{I}}} \cap {\text{E}}_{{\text{P}}} \ne \varnothing$

(6)

$${\text{P}}({\text{E}}_{{\text{I}}} \cup {\text{E}}_{{\text{P}}} ) \, = {\text{ P}}\left( {{\text{E}}_{{\text{I}}} } \right) \, + {\text{ P}}\left( {{\text{E}}_{{\text{P}}} } \right) - {\text{P}}({\text{E}}_{{\text{I}}} \cap {\text{E}}_{{\text{P}}} )$$

(7)

where Ø is the empty set. Moreover, since the two events are considered independent, the following property is valid:

$${\text{P}}({\text{E}}_{{\text{I}}} \cup {\text{E}}_{{\text{P}}} ) \, = {\text{ P}}\left( {{\text{E}}_{{\text{I}}} } \right) \, + {\text{ P}}\left( {{\text{E}}_{{\text{P}}} } \right) - {\text{P}}\left( {{\text{E}}_{{\text{I}}} } \right) \cdot {\text{P}}({\text{E}}_{{\text{P}}} )$$

(8)

Hence, the values of the probabilities of collapse, at each S_a, are provided by the fragility functions of the two frame typologies. Under the aforementioned conditions, these probabilities can be combined through Eq. (8) at a specific value of seismic intensity in order to estimate the collapse probability of the entire building for that value. In other words, the fragility curve F_STR(s) of the entire building can be obtained in a discrete form at each value of S_a considered. Thus, for each i-th point (with i = 1,…, m) of a generic set S_a = (s₁,…, s_m) of m seismic intensity values,, the building collapse probability F_STR(s_i) can be obtained with the following equation:

$${F}_{STR}\left({s}_{i}\right)={F}_{I}\left({s}_{i}\right)+{F}_{P}\left({s}_{i}\right)-{F}_{I}\left({s}_{i}\right)\cdot {F}_{P}\left({s}_{i}\right)$$

(9)

where ${F}_{I}\left({s}_{i}\right)$ and ${F}_{P}\left({s}_{i}\right)$ are the values of the fragility curves of internal and perimeter frames, respectively. It is worth noting that, if ${F}_{I}\left(s\right)$ and ${F}_{P}\left(s\right)$ are lognormal distributions, the entire curve F_STR(s) is no longer a lognormal distribution since the lognormal functions do not have the additive regenerative property (Benjamin and Cornell 1970).

By generalizing to the case of n compatible and independent events E₁,…E_n, (i.e., n different typologies of frames belonging to the building), thus considering n different fragility functions, Eqs. 8 and 9 become respectively:

$$\mathrm{P}\left({\bigcup_{h=1}^{n}\mathrm{E}}_{h}\right)=\sum_{h=1}^{n}\mathrm{P}\left({\mathrm{E}}_{h}\right)-\sum_{h,\mathrm{k}}\mathrm{P}\left({\mathrm{E}}_{h}{\cap \mathrm{E}}_{k}\right)+\sum_{h,k,\mathrm{j}}\mathrm{P}\left({\mathrm{E}}_{h}{\cap \mathrm{E}}_{k}\cap {\mathrm{E}}_{j}\right){+(-1)}^{\mathrm{n}+1}\mathrm{P}(\bigcap_{h=1}^{n}{\mathrm{E}}_{h})$$

(10)

$${F}_{STR}\left({s}_{i}\right)=1-\prod_{f=1}^{n}\left(1-{F}_{f}\left({s}_{i}\right)\right)$$

(11)

with: $\sum_{h,k}$ and $\sum_{h,k,j}$ extended to all values 1 ≤ h < k < j < … ≤ n (Fisz 1963). Note that Eq. (11) is specifically valid under the hypothesis of independent events, and can be demonstrated (Fisz 1963).

The same approach can be applied in order to evaluate the fragility curve of the entire building at the severe damage limit state, by combining statistically the fragility curves of internal and perimeter frames.

7 Conclusions

The aim of the study is to provide a fast procedure, named PRESSAFE-disp (PRecast Existing Structure Seismic Assessment by Fast Evaluation-displacement), for the definition of the fragility curves of one-story precast RC buildings, typical of the European areas. In particular, PRESSAFE-disp is focused on the existing industrial buildings of the Emilia Romagna region, whose damage during the May 2012 seismic sequence is deeply described in the first part of the paper. The methodology allows to define the seismic fragilities in a simplified way, considering the hypothesis of flexible roof diaphragm, starting from the knowledge of few information that could be collected through a visual inspection or non-destructive tests.

The following conclusions were obtained:

• 1. The seismic in-plane performances of 120 different frame typologies of existing single-storey precast frames have been investigated, and the fragility curves have been obtained both for severe damage and collapse limit states. It is worth noting that the presence of the perimeter non-structural elements, typically, increases the in-plane seismic capacity of a precast frame and in general the perimeter frames result less vulnerable to the seismic action than the internal bare frames. This has been observed for almost all the frame categories at the severe damage state and, in several cases, also at the collapse state. Indeed, the increase of the collapse capacity is possible only if the non-structural walls/panels, at the attainment of the collapse of the frame, are still resisting. In general, the capacity increase is more evident for buildings with masonry infill walls.

• 2. The collapse condition has been defined at the attainment of one of the following: (i) the ultimate base rotation for a column or (ii) the displacement capacity in one of the sliding hinges, so adopting a displacement-based criterion for the connections. This assumption differentiates significantly the results of the PRESSAFE-disp method from the results of the alternative PRESSAFE method.

• 3. The analytical expressions of the fragility surfaces R(S_a,T₁) have been obtained for each frame typology, providing the PoE as a function of S_a and T₁for the limit state of interest.

• 4. The analytical expressions of the fragility curves defining the failure of different typologies of non-structural elements on the perimeter, i.e. masonry infill walls, horizontal precast cladding panels and vertical precast cladding panels, have been provided.

• 5. The procedure for the statistical derivation of the combined fragility function of the entire precast RC building has been outlined, starting from the fragility functions of the main frames.

In conclusion, the method and the outcomes made available from the paper allow a fast assessment of the fragilities which can be used for earthquake loss assessment and seismic risk analyses of large precast building stocks in seismic prone areas. It is worth saying that the results presented in this work are representative of common typologies of precast buildings and cladding elements observed in the Emilia Romagna territories, but they can be easily extended. Indeed, additional analyses following the same approach proposed here, but concerning other structural typologies of precast frames, or other damage mechanisms, can be conducted to widen the library of the categories included in the so called PRESSAFE method.

Appendix

See Figs. 15, 16 and 17. Tables 4, 5, 6, 7, 8.

Fig. 15

Details of the main damage typologies in precast RC buildings after the Emilia earthquake of 2012: (a) Damage at the column base; b Sliding and c Fall of precast beams and roof slab elements; collapse of d Horizontal and e vertical cladding panels; f Failure of masonry infill walls

Fig. 16

a Collapse fragilities for the frame category A-L-L (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). b Collapse fragilities for the frame category A-M-H (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). c Collapse fragilities for the frame category B-L-L (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). d Collapse fragilities for the frame category C-L-L (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). e Collapse fragilities for the frame category C-M-H (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). f Collapse fragilities for the frame category D-L-L (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively)

Fig. 17

a Severe damage fragilities for the frame category A-L-L (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively) b Severe damage fragilities for the frame category A-M-H (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). c Severe damage fragilities for the frame category B-L-L (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). d Severe damage fragilities for the frame category C-L-L (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). e. Severe damage fragilities for the frame category C-M-H (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively). f Severe damage fragilities for the frame category D-L-L (I: internal frame; P(m), P(h1), P(h2) and P(v): perimeter frame with masonry infill walls, vertical and horizontal panels, respectively)

Table 4 Coefficients of Eqs. 4, 5 for fragility surfaces of internal frames, as obtained by regression analysis

Table 5 Coefficients of Eqs. 4, 5 for fragility surfaces of perimeter frames with masonry infill walls, as obtained by regression analysis

Table 6 Coefficients of Eqs. 4, 5 for fragility surfaces of perimeter frames with precast horizontal cladding panels (h1), as obtained by regression analysis

Table 7 Coefficients of Eqs. 4, 5 for fragility surfaces of perimeter frames with precast horizontal cladding panels (h2), as obtained by regression analysis

Table 8 Coefficients of Eqs. 4, 5 for fragility surfaces of perimeter frames with precast vertical cladding panels, as obtained by regression analysis

.