1 Introduction

Nepal is an earthquake-prone country with a long history of devastating earthquakes located at the boundary between the Indian and Eurasian (Tibetan) tectonic plates. On 25 April 2015, at 11:56 (local time), Nepal was hit by a strong earthquake with a magnitude (Mw) of 7.8 with the epicenter at Barpak village, Gorkha district, located approximately 80 km northwest of the Nepal's capital city, Kathmandu (USGS 2018), which is known as the Gorkha earthquake. The hypocentral depth was approximately 8.2 km, and this was the largest earthquake in Nepal in recent time. The main shock caused intense ground shaking throughout Nepal, as well as in some parts of India, Bangladesh, and China. This earthquake affected thirty-one out of 75 districts in Nepal, 14 of which located in the Central and Western mountains and hills, including the Kathmandu Valley were categorized by the government of Nepal as the most affected areas (NPC 2015). The earthquake severely damaged properties like buildings, lands and civil engineering structures, and also caused infrastructural collapses in those most affected areas. A strong aftershock of magnitude (Mw) 7.3 also jolted central Nepal on 12 May, which further increased the damages and casualties. A total of 498,852 houses, 6,613 of which were reinforced concrete (RC) frame buildings, were categorized as fully collapsed or damaged beyond repair, and 256,697 houses (16,971 RC frame buildings) were partly damaged by this earthquake (NPC 2015). A study of seismic vulnerability of Nepal (NSET and GHI 1998) has shown that more than 60% of buildings in the Kathmandu Valley are vulnerable to large earthquakes. In addition, the seismic safety assessment conducted by Chaulagain et.al. (2015) based on the standard drift limits revealed that most of the existing RC frame buildings in Nepal exhibited inadequate seismic performance. Post-earthquake investigations after the Gorkha earthquake also indicated structural problems in Nepalese RC frame buildings (AIJ 2016; Gautam et al. 2016). To mitigate the damage to RC frame buildings due to earthquakes in the future, it is crucial to understand the specific characteristics of Nepalese RC frame buildings and their effects on the seismic performance. One of the specific characteristics of Nepalese RC frame buildings is that they always contain brick masonry infill walls. This kind of RC frame building is also widely used in other earthquake-prone countries worldwide. Easy construction, durability and low cost are known as the main reasons for using brick masonry infill walls as exterior and partition walls in RC frame buildings. Another specific characteristic of Nepalese RC frame buildings is that some of them have a higher number of stories than the design (hereafter conventional vertical extension), which may also be potentially common in other developing countries.

There is still a lack of knowledge in evaluating the failure modes of masonry infill walls and their interactions with the RC frames in perimeter mainly due to the different material properties, behavior, and capacity. Thus, masonry infill walls are mostly considered nonstructural elements and are often overlooked in structural analysis and design. The study performed by Murty and Jain (2000) revealed that the infill wall increased global stiffness, strength, ductility and energy dissipation of the building. The authors' previous study (Pradhan et al. 2020) has also shown that the presence of infill walls affects the vibration characteristics and increases the lateral strength of the RC frame building through a series of onsite studies in Kathmandu, Nepal. Moreover, Mostafaei and Kabeyasawa (2004) and Maidiawati and Sanada (2017) revealed that buildings showed better performance during earthquakes due to the presence of infill walls. In contrast, Paulay and Priestley (1992) explained that even though the masonry infills were relatively weak, it could drastically modify the intended structural response, attracting forces to parts of the structure that had not been designed to resist them. The masonry infill walls can interact with the bounding frames under seismic loads and alter the load resisting mechanism and failure pattern of the RC frames. In some cases, the interaction of masonry infill walls with the bounding frames induced brittle shear failure in the RC columns and thereby lead to catastrophic failures and undesired soft-story mechanisms (Talaat and Mosalam 2008). These literature review shows that the infill has both beneficial and ill effects on the seismic performance of RC frame buildings. Hence, designing and modeling a frame structure with masonry infill walls by neglecting the effects of the infill can lead to inaccurate predictions of the overall structural characteristics. Consequently, while designing, the omission of the masonry infill wall contributions may result in significant underestimation or overestimation of the seismic performance of the structure; thus, this study emphases the masonry infill effects on the seismic performance of RC frame buildings to minimize future damages and losses.

In general, Nepalese RC frame buildings need to be seismically designed according to detailed seismic demands provided by Nepal National Building Code (NBC: 105: 2020) or Indian Standards (IS 1893 (Part 1): 2016). On the other hand, Nepal building code with the Mandatory Rules of Thumb (NBC 201: 1994) on the prescriptive design recommends some dimensions and details regarding the structural and non-structural elements for up to 3-story RC frame buildings with brick masonry infill commonly built in Nepal. However, RC frame buildings with more than three stories are also often constructed following the NBC 201 (following the same rules for up to 3-story buildings). Furthermore, some of the RC frame buildings are originally designed for less number of stories, but the building stories are extended by the owners during construction or afterward. Such story extension is unauthorized and illegal but commonly practiced in Nepal. To the best of our knowledge, the reasons behind such illegal extension are as follows: 1) most of the Nepalese people have joint families, and due to the gradual increase in family members, the necessity for extra space leads to an increase in the number of stories; 2) land cost is getting high particularly in the urban areas; and 3) the number of stories sanctionable for residential buildings is limited (depends on place) in the country; thus, the building stories are vertically extended as per the owner's desire. Such vertical extension of the building not only increases the dead loads of the structure but also affects the seismic performance. This fact in RC frame buildings may lead to unexpected and severe damages in a manner quite different from the anticipated one during earthquakes. Nevertheless, to the authors' knowledge, such fact has not been investigated to date for Nepalese RC frame buildings. Hence, this study also focuses on the effects of conventional vertical extension on the seismic performance of RC frame buildings. Figure 1 shows samples of Nepalese RC frame buildings with brick masonry infill walls having conventionally extended stories. One of the present paper authors has previously proposed a theoretical model to quantitatively evaluate the in-plane interactions between masonry infill walls and RC frames (Maidiawati and Sanada 2017). Applying this model to typical Nepalese RC frame buildings, their seismic performance was examined according to the Japanese guidelines for seismic performance evaluation (AIJ 2004) of RC frame buildings considering the local material, structural characteristics and seismic demand in Kathmandu, Nepal.

Fig. 1
figure 1

RC frame buildings with brick masonry infill walls having conventional extended stories at Kathmandu, Nepal

Full size image

The present paper (1) briefly introduces the characteristics of a typical residential RC frame building in Kathmandu, designed by Nepalese engineers referring to Pradhan et al. (2020), (2) illustrates the numerical modeling parametrically considering three different contributions of brick masonry infill walls: Case A as a bare frame by completely neglecting the infill walls, Case B considering only the self-weight of the infill walls, and Case C considering the in-plane stiffness and strength as well as the self-weight of the infill walls, and (3) investigates the seismic performance of the RC frame building considering the effects of the infill wall modeling and the vertical extension through numerical analyses. The major objectives are to quantitatively clarify the positive and negative infill effects on the seismic performance of typical RC frame buildings, and to illustrate a detailed scheme for the seismic performance evaluation of RC frame buildings in different countries with similar problems. Modeling for the out-of-plane performance of the infill walls is out of scope in the present paper.

2 Case study

2.1 Study building

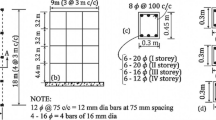
After the 2015 Gorkha earthquake, the authors conducted field investigations twice in Kathmandu to investigate the damage and to predict the seismic capacity of buildings (especially RC frame buildings) in Nepal (Pradhan et al., 2020). The investigations were performed by a team of researchers and were supported by many academics, local government officials, and young engineers of Nepal. A reinforced concrete residential building (hereafter study building) with brick masonry infill walls and conventionally extended stories in Shitapaila, Kathmandu, was selected as a typical residential RC frame building in Nepal; thus, detailed onsite investigations were carried out. This study building was designed by local engineer(s) which was confirmed through onsite interviews, while many buildings in Nepal are not designed by engineers. Figure 2 shows the location map of the building. The building was a typical reinforced concrete frame building with five stories, including the ground story and a penthouse at the top (superstructure) and one underground story (substructure) with a mat foundation, which was constructed after the Gorkha earthquake. Figure 3 shows the northwest, southeast, and interior views of the building, whereas Fig. 4 shows the building floor plans and sectional elevation along the X-X' axis. The building had 4 spans in the longitudinal direction and a single span in the transverse direction, as shown in Fig. 4. During the onsite survey and the microtremor measurements, the building was undergoing interior finishing work and no interior partition wall was constructed, as shown in Fig. 4. As shown in the figures, brick masonry infill walls were mainly implemented for exterior walls along the longitudinal direction of the building; thus, to investigate the effect of infill walls on the seismic performance of the building, the analyses presented in the current paper were performed in the longitudinal direction. Since almost no infill wall was installed in the transverse direction, the current paper doesn't account for the building's performance in the transverse direction even though the building might have lower performance in the direction. The exterior brick masonry infill walls on the northwest side in the longitudinal direction had plaster finishing on both sides (Fig. 3a and c), whereas the walls on the southeast side had plaster finishing only on the interior side (Fig. 3b and c). Local bricks with the dimensions of 220 mm × 110 mm × 55 mm were used for the masonry walls with masonry mortar and plaster mortar of cement-to-sand ratios of 1:4 and 1:5, respectively. The physical and mechanical properties are introduced in Sect. 2.3. The slab thickness was 160 mm. The cross-sectional details of the beams and columns of the building are shown in Fig. 5. The concrete strength of the building was evaluated as 39.8 N/mm2 by an onsite nondestructive (rebound hammer) test; the obtained value was close to the upper bound in Nepalese buildings referring to a past research (Aryal 2020). Since information about the reinforcement was not available, the yield stress of the reinforcement was considered 415 N/mm2 for the analyses from interviews to local engineers, which was widely used for residential RC frame buildings in Nepal.

Fig. 2
figure 2

Location map of the study building

Full size image
Fig. 3
figure 3

Overview of the study building

Full size image
Fig. 4
figure 4

Building floor plans and sectional elevation (Unit: mm)

Full size image
Fig. 5
figure 5

Beam and column cross-sections (Unit: mm)

Full size image

Originally, this building was designed as a 3-story (2-story and a penthouse) building but it was extended to 5-story (4-story and a penthouse) building during construction without redesigning by keeping the dimensions and the other structural properties of the structural members constant, as shown in Fig. 5. Hence, the details of the structural members were assumed to be common for all analytical cases (2–8 stories) in Sect. 4.4. Moreover, although RC frame buildings commonly built in Nepal do not often comply with requirements on material properties, rebar arrangement, or construction management, such uncertain errors were not considered in the following analyses.

2.2 Vibration characteristics from microtremor measurements

The onsite survey has been reported by Pradhan et al. (2020). The major findings are summarized in the following to be applied and compared to analytical results described later in the present paper.

2.2.1 Superstructure

To observe the mode shapes and natural periods of the building, three measuring instruments were installed: two fixed on the ground floor (G.F) and the top floor (4F) and the other one moved from the first floor to the rooftop (R.T), making four measurement cases for both longitudinal and transverse directions. The horizontal spectrum ratios of the upper floor to the ground floor in both directions were evaluated as shown in Fig. 6, which indicated that the natural frequencies and periods of the building were 7.3 to 9.4 Hz, 0.11 to 0.14 s in the longitudinal direction and 2.9 to 3.0 Hz, 0.33 to 0.34 s in the transverse direction, respectively. The natural period in the longitudinal direction was found to be shorter than that in the transverse direction. Almost no infill walls along the transverse direction, as shown in Fig. 4, were considered the main reason behind this phenomenon. Figure 7 shows the building fundamental mode shapes along the height from the measurement and analysis (Case C considering the infill effects, as described in Sect. 3.2). The building mode shapes from the measurement and analysis were standardized by using the standardization factor (β) (Shibata 2010) given in Eq. (1).

$$\beta =\frac{\sum_{i=1}^{N}{m}_{i}{u}_{i}}{\sum_{i=1}^{N}{m}_{i}{u}_{i}^{2}}$$
(1)

where mi and ui represent the mass and unstandardized mode value of the ith floor of the building.

Fig. 6
figure 6

H/H spectrum ratios of the study building

Full size image
Fig. 7
figure 7

Primary mode shapes of the building

Full size image

2.2.2 Ground

The horizontal/vertical (H/V) spectrum ratio is often used to evaluate the fundamental frequency of the ground. Microtremor measurements were performed at two relatively flat places (Grounds 1 and 2) on the ground approximately 30 m southwest of the study building, as shown in Fig. 8. Figure 9 represents the evaluated H/V spectrum ratios of the grounds. The peaks of the H/V spectrum ratios were observed at frequencies of 1.1 Hz and 1.0 Hz for Grounds 1 and 2, respectively. Consequently, the natural periods, which are reciprocal of the natural frequencies, were 0.9 s and 1.0 s, respectively, which were between 0.6 s and 1.0 s; hence, the underlying ground of the study building was categorized as soft soil sites according to the Nepal National Building Code (NBC: 105: 2020).

Fig. 8
figure 8

Microtremor measurements on the ground

Full size image
Fig. 9
figure 9

H/V Spectrum ratios of the ground

Full size image

2.3 Mechanical properties of the brick masonry walls

Estimation of the mechanical characteristics of the masonry wall is difficult due to the variations in materials, differences in quality and construction methods used, and the workmanship of the mason. Hence, the masonry prism specimens were prepared by engaging the same masons who constructed the study building, using similar materials, and following the same construction process; thus, which were the replicas of the infill walls used in the study building. The experimental results on the strengths, elastic moduli and weight density of the brick masonry walls were applied to the following numerical study.

As mentioned above, plaster finishing was applied to one side or both sides of the infill walls in the study building. Hence, two kinds of specimens with different types of plaster finishing (PO with plaster on one side, PB with plaster on both sides) were prepared by using burnt bricks (with dimensions of 220 mm × 110 mm × 55 mm in length × thickness × height), as shown in Fig. 10, to ascertain plaster finishing effects on the mechanical properties of brick masonry walls. Masonry mortar was prepared by hand mixing of cement, sand and water. The cement and sand were mixed with a volumetric cement-to-sand ratio of 1:4 under dry conditions till the mixture formed a uniform color and the water was gradually added with a volumetric water-to-cement ratio of approximately 0.85. Then the specimens were constructed by stacking the masonry mortar layer and brick layer alternatively following the same construction process of the infill wall in the study building. The plaster finishing was done one week after the specimen construction. The plaster mortar was prepared as above, however, with a different cement-to-sand ratio of 1:5.

Fig. 10
figure 10

Specimens

Full size image

Figure 11 shows the test setup. The experiments were conducted at the Material Laboratory at Tribhuvan University, Pulchowk Campus, Kathmandu, using a universal testing machine (UTM) following Indian Standards (IS:1905–1987 1989). Multiple vertical cracks were visually observed on the bricks, while little cracks appeared on the plaster finishing. Considering separations under the plaster finishing observed after testing, such separation might have occurred at early loading stages. Table 1 shows the average values and coefficients of variation of the compressive strength and the elastic modulus along with the measured weight density of the brick masonry prism specimens. No obvious effect of plaster finishing was observed on the compressive strength within this series of tests, which might have resulted from the separation of plaster finishing from the prism side surface(s) as mentioned above, while the averaged elastic modulus of the PB series was higher than that of the PO series.

Fig. 11
figure 11

Test setup

Full size image
Table 1 Mechanical properties and weight density of brick masonry specimens
Full size table

3 Numerical seismic performance evaluation of buildings with different considerations on brick masonry infill walls

Numerical analyses were performed for the 5-story study building representing the existing building using macromodeling by replacing each column and beam with a line element. Three analytical cases (Case A, Case B, and Case C) with different contribution of the brick masonry infill walls were considered to investigate the effects of the infill walls on the structural characteristics of the overall building, as summarized in Table 2. Since the building was under construction during the field investigation, as explained in Sect. 2.1, only the dead loads of the structure (weight of column, beam, slab, brick wall) were considered for the analyses. The weight densities for brick walls were the experimental values in Table 1, while that for RC members were assumed to be 25 kN/m3. The building was analyzed as a bare frame, completely neglecting the brick masonry infill walls for Case A, which represented the case in which the infill walls were completely removed or replaced by alternative lightweight walls. For Case B, only the weight of the brick masonry infill walls was considered, which represented a practical building design in Nepal, whereas for Case C, the in-plane stiffness, strength and weight of the infill walls were considered, replacing each infill wall with a compression strut. In the authors' previous study (Pradhan et al. 2020), the stiffness and strength of the struts replacing the infill walls were evaluated considering the widths given by Smith and Carter (1969) and Mainstone (1971), respectively. However, both methods provided empirical equations for the strut width evaluation; thus, there was no evidence for their reliable application to Nepalese brick masonry walls. Therefore, the present study focused on the Maidiawati and Sanada model (2017) which was a theoretical modeling for the infill effects considering force equilibrium and lateral displacement compatibility at the interface of the infill wall and the perimeter frame, and adopted for the infill wall modeling for Case C. The model also provided a theoretical scheme to evaluate the deformability of the infilled frame, as presented in Sect. 3.3.2.1, which was essential for the seismic performance evaluation. The structural characteristics of the brick masonry infill walls referred to the experimental results are presented in Sect. 2.3.

Table 2 Analytical cases with different consideration of the brick masonry infill walls
Full size table

3.1 Modeling of the building

The building was numerically modeled according to the following methods and assumptions:

  1. (1)

    The 5-story superstructure above ground level was represented by line elements and supported by pins below the ground-story beam elements neglecting the basement. The weight consideration for each case are as illustrated in Table 2.

  2. (2)

    Each column and beam was replaced by a line element considering rigid zones at both ends with a length of D/4 (D: depth of each member) from the critical member section to the node. The restoring force characteristics of the columns and the beams were evaluated based on different spring models, as summarized in Table 3. The modeling for the columns and beams is illustrated in Fig. 12.

  3. (3)

    A model called the multispring model (MS model) was used to evaluate the restoring force characteristics of the column with an assumed plastic hinge length of half of the column depth. The hysteresis characteristics of the steel spring element considering the Bauschinger effect were represented by a bilinear model, as shown in Fig. 13. Figure 14 shows the trilinear model that represents the hysteresis characteristics of the concrete spring element.

  4. (4)

    The restoring force characteristics of the beam during bending were represented by a trilinear model called the Takeda model, as shown in Fig. 15, which considered the cracking strength (bMc), yield strength (bMu), and rigidity reduction after cracking (bαy), which were evaluated using Eqs. (2), (3) and (4) based on Japanese guidelines (AIJ 2018).

    $${}_{b}{M}_{c}=0.56 \sqrt{{f}_{c}^{{{^\prime}}}} Z$$
    (2)
    $${}_{b}{M}_{u}=0.9{\cdot a}_{bt}\cdot {\sigma }_{by}\cdot d$$
    (3)
    $${{}_{b}\alpha }_{y}=\left(0.043+1.64\cdot {n\cdot p}_{bt}+0.043{a}_{b}\right){\left(\frac{d}{{D}_{b}}\right)}^{2}$$
    (4)

    where \(f^{\prime}_{c}\) is the compressive strength of concrete (in N/mm2); Z is section modulus of the beam (=BbDb2/6); abt and σby are the total cross-sectional area and yield stress of tensile reinforcing bars of the beam (in N/mm2), respectively; d and Db are effective depth and total depth of beam; n is the reinforcement to concrete Young's modulus ratio; pbt is tensile reinforcement ratio of the beam; ab is shear span to depth ratio of beam. The member properties of the beam were based on the gross section properties

  5. (5)

    For Case C, the weight and in-plane stiffness and strength of the infill walls were considered as shown in Table 2. Each infill wall was replaced by a compression strut with pins at both ends based on the proposal by Maidiawati and Sanada (2017). The mechanical properties and the thickness of the strut were identical to those of the infill wall, whereas the width (W) and the compressive strength (Cs) of the strut were evaluated based on Eqs. (5) and (6) (Maidiawati and Sanada 2017), respectively.

    $$W=2\cdot {h}_{s}\cdot cos\theta$$
    (5)
    $${C}_{s}=W\cdot t\cdot \alpha \cdot {\sigma }_{m}$$
    (6)

    where hs is the minimum column-infill contact length between Ths for the tensile column and Bhs for the compressive column, as shown in Fig. 16, which was evaluated through the iteration presented in the reference (Maidiawati and Sanada 2017); θ is the infill diagonal angle; t is the thickness of the infill wall; σm is the uniaxial compressive strength of the infill wall (= 2.5 N/mm2 and 3.2 N/mm2 for one side and both sides plaster infill walls, respectively) from Section 2.3; and α is a reduction factor (= 0.65~0.66) to evaluate the averaged compressive strength of the strut to σm (Maidiawati and Sanada 2017). The symbols can be referred to in Fig. 16.

    For the strut's restoring force characteristics, a bilinear model linking the origin to the yield point was applied (Maidiawati and Sanada 2017), as shown in Fig. 17. The drift angles at yield point in Fig. 17 were 0.0034 ~ 0.0040 rad and 0.0016 ~ 0.0021 rad for one side and both sides plaster infill walls, respectively. The postyield stiffness was assumed to be 0.1% of the elastic modulus

  6. (6)

    However, infill walls with openings were represented as equivalent walls without openings and replaced with struts having reduced wall thickness so that the wall volumes were equal. Appropriateness of this modeling has not been experimentally validated, however, the openings in the longitudinal direction were very small with the ratios to the wall panel area of less than 3%, as shown in Fig. 3, resulting in the limited effects.

Table 3 Spring models adopted for the column and beam
Full size table
Fig. 12
figure 12

Modeling of the columns and beams

Full size image
Fig. 13
figure 13

Bilinear model for steel element

Full size image
Fig. 14
figure 14

Trilinear model for concrete element

Full size image
Fig. 15
figure 15

Takeda model

Full size image
Fig. 16
figure 16

Symbol reference diagram for the infill wall modeling (Maidiawati and Sanada 2017)

Full size image
Fig. 17
figure 17

Bilinear model for the strut

Full size image

The global analytical models based on the above assumptions are shown in Fig. 18. In the figure, black, blue, and green lines represent the columns, beams, and compression struts replacing the infill walls for Case C, respectively.

Fig. 18
figure 18

Global modeling

Full size image

3.2 Comparison of the building vibration characteristics from analyses and measurements

Eigenvalue analyses were performed for all three cases in both the longitudinal and transverse directions, and the results were compared with those obtained from the microtremor measurements described in Sect. 2.2.1. Table 4 compares the results obtained from the analytical cases and the microtremor measurements. The natural periods of Case B were longer than those of Case A because of the considered weight of the infill walls. Among all three cases, the natural periods of Case C were minimum and showed the closest values to the microtremor measurements. However, the value in the longitudinal direction of Case C was still longer than that from the measurements, which was due to the infill modeling on the initial stiffness, as shown in Fig. 17, that was simplified as the secant stiffness at yielding as suggested in the past study (Maidiawati and Sanada 2017). It was also confirmed that the effects of such simplified modeling on the building performance close to and beyond the yield point were limited. The mode shapes of the building from Case C and the microtremor measurements were compared in Fig. 7. The analytical mode shapes had good agreement with those from the measurements in both the longitudinal and transverse directions.

Table 4 Comparison of the elastic natural periods
Full size table

Considering the minimum natural periods from Case C, which were approximately consistent with those from the microtremor measurements, the brick masonry infill walls increased the overall stiffness of the building. Additionally, reminding that Case B is common for practical building design in Nepal, as stated at the beginning of this section, the neglect of the stiffness of infill walls is likely to mislead seismic forces applied to the building. Hence, the seismic performance evaluation was carried out as follows.

3.3 Masonry infill wall effects on seismic behavior/performance

Strength and deformability are two crucial properties of a structure to understand its seismic behavior/performance, as both affect the capacity and seismic demands; hence, it is inevitable to evaluate the effects of brick masonry infill walls on the strength and deformability of the study building. Most of the infill walls were located along the longitudinal direction of the study building, as shown in Fig. 4; thus, pushover analyses were performed only in the longitudinal direction by applying lateral loads proportional to the primary mode shape of the building, up to a maximum inter-story drift angle of 0.05 rad.

3.3.1 Infill wall effects on the building strength

Figures 19 and 20 compare the story shear force versus inter-story drift angle relationship and the story shear force coefficient (ratio of story shear force to the seismic weight) versus inter-story drift angle relationship among the three cases. Figures 21 and 22 compare the base shear force and the base shear coefficient versus the ground story's inter-story drift angle. As shown in Fig. 21, Case B showed a slightly higher base shear strength than Case A because the axial-flexural interactions were considered in the MS model for the column behavior/strength evaluation, as shown in Table 3. However, as shown in Fig. 22, the story shear force coefficient was higher in Case A than in Case B. Case C with the struts representing brick masonry infill walls exhibited the highest strength (base shear coefficient) among the three cases: approximately 2.4 times higher than that of Case A and 3.6 times higher than that of Case B from Fig. 22. This indicates a significant increase in the building strength upon considering the effects of brick masonry infill walls (i.e., their weight, stiffness, and strength) as in Case C.

Fig. 19
figure 19

Story shear force-inter-story drift angle relationships

Full size image
Fig. 20
figure 20

Story shear force coefficient-inter-story drift angle relationships

Full size image
Fig. 21
figure 21

Comparison of the base shear forces

Full size image
Fig. 22
figure 22

Comparison of the base shear coefficients

Full size image

3.3.2 Infill wall effects on the building deformability

3.3.2.1 Deformation capacity of the columns

In this study, it was assumed that once the columns in the building attained their deformation capacity, they no longer contributed to the building performance (JBDPA 2005). Hence, to evaluate the effects of the infill walls on the deformability of the building, the deformation capacity of the individual columns for all analytical cases were evaluated by defining a drift angle RD when the flexural and shear capacity curves of the column intersected, as shown in Fig. 23. Moreover, the maximum column deformation capacity was taken as 1/30 rad according to the Japanese seismic performance evaluation guidelines (JBDPA 2005).

Fig. 23
figure 23

Deformation capacity of the column

Full size image

For Cases A and B, the strength and stiffness contribution of infill walls were neglected, and the flexural capacity curve was represented by a bilinear curve with a yield point (Qy, Ry) evaluated using Eqs. (7) and (8) (Kabeysawa et al. 1983). The shear capacity (Vu) of the column was evaluated by superposition of truss action (Vt) and strut action (Vs) using Eq. (9) (Ichinose 1992).

$${Q}_{y}=\frac{2{M}_{u}}{{H}_{0}}$$
(7)
$${M}_{u}=0.8.{a}_{t}\cdot {\sigma }_{y}\cdot D+0.5\cdot N\cdot D\cdot \left(1-\frac{N}{b\cdot D\cdot {f}_{c}^{^{\prime}}}\right)$$
(7a)
$${R}_{y}=\frac{{Q}_{y}}{{{\alpha }_{y}\cdot K\cdot H}_{0}}$$
(8)
$${\alpha }_{y}=\left(0.043+1.64\cdot {n\cdot p}_{t}+0.043a+0.33\eta \right){\left(\frac{{D}_{e}}{D}\right)}^{2}$$
(8a)

where Mu is ultimate flexural strength of column; at and σy are the total cross-sectional area and yield stress of tensile reinforcing bars (in N/mm2), respectively; b and D are the width and depth of the column; N is the axial load on the column; H0 is clear height of column; K is the lateral stiffness of column (= 12EI/H03); EI is the flexural rigidity of column; αy is the reduction factor for the secant stiffness at yielding; pt is the tensile reinforcement ratio; a is the shear span to depth ratio (= M/(QD)); η is the axial compression ratio (= N/(bDfc')); De is the effective depth of the column.

$${V}_{u}={V}_{t}+{V}_{s}$$
(9)
$${V_u} = b \cdot {j_t} \cdot {p_{wm}} \cdot {\sigma _{wy}} \cdot \cot \phi + \frac{{\tan \theta \cdot\left( {1 - \beta } \right) \cdot b \cdot D \cdot \nu \cdot f_c^\prime }}{2}$$
(9a)
$$cot\phi =\left\{\begin{array}{l}2.0 \quad for \quad {R}_{p}=0 \\ 2-50{R}_{p} \quad for \quad {0<R}_{p}<0.02 \\ 1.0 \quad for \quad {R}_{p}\ge 0.02\end{array}\right.$$
(9b)
$$tan\theta =\sqrt{{\left(\frac{H}{D}\right)}^{2}+1 }-\frac{H}{D}$$
(9c)
$$\beta =\frac{{p}_{wm}\cdot {\sigma }_{wy}\cdot \left(1+co{t}^{2}\phi \right)}{\nu \cdot {f}_{c}^{^{\prime}}}$$
(9d)
$$\nu = \left\{ {\begin{array}{*{20}l} {\nu_{0} = 0.7 - \frac{{f_{c}^{\prime } }}{200}} & {for \quad R_{p} = 0 } \\ {\left( {1 - 15R_{p} } \right)\cdot\nu_{0} } & { for \quad 0 < R_{p} < 0.05} \\ {0.25\cdot\nu_{0} } & { for \quad R_{p} \ge 0.05} \\ \end{array} } \right.$$
(9e)

where jt is the center-to-center distance of the main reinforcements; pwm is the shear reinforcement ratio; ϕ is the angle of truss action; and cotϕ is a coefficient that depends on the plastic hinge rotation (Rp) given by Eq. (9b); θ is the angle of the concrete compressive stress of the truss action to the member axis; and the relations for tanθ and β are given in Eqs. (9c) and (9d), respectively; ν is the effectiveness factor of the concrete compressive strength depending on the plastic hinge rotation (Rp) given by Eq. (9e); \(f_{c}^{\prime }\) is concrete compressive strength in N/mm2.

Focusing on the boundary columns of the infilled frame, a previous study (Maidiawati and Sanada 2017) evaluated the shear force applied to the bottom and top of the column on the compressive and tensile side Qyi as the average (average of Qain Eq. (10)) over the height of the column depth (D) from the column end and then showed good agreement with the experimental results. The present study also evaluated the applied shear force for analytical Case C in the same manner and compared it with the capacity by Eq. (9) to find the deformation capacity. Moreover, the yield drift (Ryi) was evaluated by using Eq. (11) (Maidiawati and Sanada 2017), considering the displacement compatibility between the infill wall and the column at the member ends.

$${Q}_{a}={Q}_{u}-{c}_{h}y$$
(10)
$${Q}_{u}=\frac{2{M}_{u}}{H}+{c}_{h}{h}_{s}-\frac{{c}_{h}{h}_{s}^{2}}{H}$$
(10a)
$${Q}_{u}=\frac{2{M}_{u}}{H}+{c}_{h}{h}_{s}-\frac{{c}_{h}{h}_{s}^{2}}{H}+\frac{{c}_{h}{h}_{s}^{3}}{3{H}^{2}}$$
(10b)
$${R}_{yi}=\frac{{\varepsilon }_{i}d/cos\theta }{H}$$
(11)

where ch is the horizontal component of the infill diagonal compressive strength per unit length; y varies from 0 to D; Qu is the shear force on the column given by Eqs. (10a) and (10b) for interior and exterior columns, respectively; εi is the strain at compressive strength of the infill wall; d and H are the diagonal length and the height of the infill wall (Fig. 16).

Figure 24 shows the deformation capacity of column E of the ground story (refer to Figs. 4 and 5d), which has the smallest deformation capacity compared to the other columns, in the longitudinal direction for all cases. For Cases A and B, the column failure mode was a flexural-shear failure (shear failure after reaching the flexural strength), whereas, for Case C, it was a brittle shear failure. This figure illustrates that the failure mode of the column may change due to the infill wall effects. Table 5 summarizes the deformation capacity of each column of the ground story for all cases in the longitudinal direction.

Fig. 24
figure 24

Deformation capacity of column E for all cases

Full size image
Table 5 Deformation capacity of each column (× 10–2 rad)
Full size table
3.3.2.2 Deformation capacity of the building

To evaluate the relationship between base shear and inter-story drift considering the column deformation capacity, the following analytical procedure was adopted:

Step 1: Pushover analysis of the whole building was performed until the inter-story drift attained the lowest deformation capacity (see R1 in Fig. 25) of the column evaluated from Sect. 3.3.2.1. The base shear vs. inter-story drift relationship is drawn, as shown in Fig. 25 (see Step 1 in Fig. 25).

Fig. 25
figure 25

Visual flowchart to evaluate the deformation capacity of the building

Full size image

Step 2: The following i+1-th pushover analysis was performed for the building, in which the column that failed in the previous i-th pushover analysis was removed (see Column_Ri in Fig. 25). For Case C, where each infill was replaced by a strut, both the failed column and the adjacent struts were removed since it was assumed in the original model (Maidiawati and Sanada 2017) that once one of the columns supporting the strut reached its deformability, the strut also lost the reaction from the column. Although this assumption was likely to be conservative, no modification was applied to the original model in the present study because such post-peak behavior of infill walls is still unclear. The i+1-th analytical result follows that of the i-th analysis, as shown in Fig. 25 (see Step 2 in Fig. 25).

Step 3: Then, the whole building's deformation capacity was judged to determine whether the base shear (Q) deteriorated by 80% of the maximum strength. When the base shear was lower than the criteria, the pushover analysis was stopped, finding the deformation capacity of Ri. Otherwise, the relationship is drawn up to a drift when the column with the i+1-th lowest deformation capacity fails at Ri+1.

Step 4: The procedure from Step 2 to Step 3 was repeated until the deformation capacity (R2 in the case of Fig. 25) of the whole building was found.

Figure 25 illustrates the overall procedure to evaluate the deformation capacity of the building. Applying the above procedure, the relation between the base shear and the ground inter-story drift angle and the building's deformation capacity was evaluated for each analytical case, as shown in Fig. 26. This shows that the deformation capacity of Case B (0.0174 rad) was smaller than that of Case A (0.0226 rad) because of the increased axial load on each column due to the considered weight of the infill walls. Due to the stiffness and strength contributions of the infill walls in Case C, the deformation capacity was the smallest (0.0015 rad) among the three cases: only 7% and 9% of Case A and Case B, respectively. Consequently, the infill effects increased the strength but decreased the deformation capacity of the building, revealing both positive and negative impacts on the building's capacity. The seismic performance should be evaluated considering not only the capacity but also the demand, which is discussed in the following section.

Fig. 26
figure 26

Deformation capacity of the building

Full size image

4 General seismic performance evaluation of RC frame buildings in Nepal and risk assessment considering conventional vertical extension

Section 3.3 revealed that the presence of infill walls increased the strength while it decreased the deformation capacity of the building, which may affect both the capacity and demand, and ultimately the seismic performance of the building. Hence, to mainly discuss the infill effects on the seismic performance of the building, it is essential to compare the building capacity to the seismic demand; thus, Japanese guidelines for the seismic performance evaluation (AIJ 2004) is applied in the following. The evaluation scheme itself can be applied to similar type of buildings in other countries.

4.1 Replacement to equivalent single degree of freedom systems

To directly compare the design response spectrum and the building performance evaluated in Sect. 3, the results of the pushover analyses were replaced with static performance curves (Sa–Sd relationships) in the form of equivalent single-degree-of-freedom systems based on Eqs. (12) and (13) (Kuramoto et al. 2000). Furthermore, the obtained performance curve was idealized by an elastoplastic bilinear curve so that the bilinear curve had the equivalent energy dissipation capacity (area enclosed by the curve) to that of the static performance curve. The results of the replacement are shown as the "capacity spectrum" in Fig. 29 illustrated later in Sect. 4.3.

$${S}_{a}=\frac{\sum_{j=1}^{N}{m}_{j}\hspace{0.33em}{{\delta }_{j}}^{2}}{{\left(\sum_{j=1}^{N}{m}_{j}\hspace{0.33em}{\delta }_{j}\right)}^{2}}\hspace{0.33em}{Q}_{B}$$
(12)
$${S}_{d}=\frac{\sum_{j=1}^{N}{m}_{j}\hspace{0.33em}{{\delta }_{j}}^{2}}{\sum_{j=1}^{N}{P}_{j}\hspace{0.33em}{\delta }_{j}}\hspace{0.33em}{S}_{a}$$
(13)

where Sa is the spectral acceleration; Sd is the spectral displacement; mj, δj, and Pj are the mass, displacement, and external force on the jth story, respectively; and N and QB are the number of building stories and the base shear force, respectively.

4.2 Design response spectrum used in Nepal

In response to the 1988 earthquake (Bothara et al. 2018) and in recognition of the high seismic hazard in Nepal, the Government of Nepal developed the first National Building Code (NBC) in 1994. The technology and construction practices in India and Nepal are similar; hence, before the introduction of NBC in 1994, structural design in Nepal was performed by referring to Indian Standards (IS). Even after the introduction of NBC, IS code is widely used and accepted throughout the country (Neupane and Shrestha 2015). Hence, in this study, an acceleration response spectrum for the study building was evaluated according to IS (IS 1893 (Part 1): 2016), and that from the NBC was not considered within this study.

According to the IS code, soil type is categorized into three different types, i.e., Type I (rock or hard soil), Type II (medium soil), and Type III (soft soil). The acceleration response spectrum as per IS (IS 1893 (Part 1): 2016) for different categories of soil is shown in Table 6. Equation (14) gives the relation for the design horizontal seismic coefficient (Ah) in IS (IS 1893 (Part 1): 2016). Figure 27 shows the acceleration-displacement (Sa–Sd) response spectrum considering the highest zone factor (Z) for Kathmandu, Nepal, as Kathmandu was categorized as the highest zone (Z = V) according to IS (IS:1893–1984 1986). From the microtremor measurement results of immediate ground in the vicinity of the study building in Sect. 2.2.2, the underneath soil of the building was categorized as soft soil. Hence, the building capacity was compared to the design spectrum corresponding to Type III (soft soil).

Table 6 Average response acceleration in (IS 1893 (Part 1): 2016)
Full size table
Fig. 27
figure 27

Design spectrum for Nepal (IS 1893 (Part 1): 2016)

Full size image

Furthermore, Fig. 28 shows the response spectrum of ground motion of the Gorkha earthquake in Kathmandu (Motra 2015; Sharma et al. 2016). Comparing the peak of the design spectrum for Nepal based on IS (IS 1893 (Part 1): 2016) and that of the ground response spectrum of the Gorkha earthquake, the ground response spectrum (peak of 360 deg component in Fig. 28) is approximately 1.5 times the design response spectrum. This reveals that the design spectrum used in Nepal based on IS (IS 1893 (Part 1): 2016) is being significantly underestimated.

$${A}_{h}=\frac{ZI{S}_{a}}{2Rg}$$
(14)

where Z is the zone factor (Z = 0.36 for seismic zone V for Nepal), I represents the importance factor (I = 1 for residential buildings), R is the response reduction factor (which is explained in the “Appendix”), and Sa and g can be found in Table 6.

Fig. 28
figure 28

Response spectrum of ground motion of the Gorkha earthquake 2015 (Motra 2015)

Full size image

4.3 Comparison of the seismic performance of the study building in terms of the masonry infill effects

The seismic performance of the study building was evaluated according to the Japanese guidelines (AIJ 2004) and was compared among the three analytical cases considered in Sect. 3. The seismic performance evaluation was performed in the following procedures:

Step I: Pushover analysis with a lateral load distribution proportional to the primary mode shape of the building (as explained in Sect. 3.3) was performed to obtain the relation between the shear force and inter-story drift angle of each story (see Fig. 29a)).

Fig. 29
figure 29

Evaluation procedure of the seismic performance of the building

Full size image

Step II: The equivalent performance curve (Sa–Sd relationship) of the building was obtained as explained in Sect. 4.1 using Eqs. (12) and (13) (Kuramoto et al. 2000) based on the outputs in each loading step from the pushover analysis (see Fig. 29 b)).

Step III: The response point corresponding to the deformation capacity of the building for each analytical case (evaluated in Sect. 3.3.2.2) was preset on a respective equivalent performance curve (see Fig. 29c)).

Step IV: The obtained equivalent performance curve in Step II was replaced by an elastoplastic bilinear curve (capacity spectrum) having equivalent energy dissipation capacity at the response point (so that the enclosed areas up to the response point are equivalent, as shown in the grey and blue areas in Fig. 29c) and d)).

Step V: The corresponding ductility factor (µ), which was defined by the ratio of response displacement (Δ) to the yield displacement (Δy) for each analytical case was evaluated (see Fig. 29e)).

Step VI: The response reduction factor (R) (which is explained in the “Appendix”) for Eq. (14) for each analytical case was evaluated based on the ductility factor (µ) in Step V and the natural period of the building (T) (R= 2.73, 2.38, and 1.00 for Case A, Case B, and Case C, respectively) (see Fig. 29f)).

Step VII: The demand spectrum was obtained by reducing the elastic spectrum (design spectrum) by the respective response reduction factor (R) for each case (see Fig. 29f)).

Step VIII: Finally, the demand spectrum was amplified by a suitable amplification factor (hereafter amplification level, α) so that the resulting amplified spectrum intersects the capacity spectrum at the preset response point (in Step III) (see Fig. 29g)).

Namely, the value of amplification level (α) 1 represents that the demand and capacity of the building are equal. Likewise, when α is 2, the capacity is twice the demand. Hence, buildings with a higher value of α have a better resistance capacity to earthquake demand.

Applying the above procedure, α was evaluated as 3.95, 2.73, and 2.12 for Case A, Case B, and Case C, respectively, as shown in Fig. 30. The evaluated absolute values were generally higher than the design spectrum based on IS (IS 1893 (Part 1): 2016) because the building weight was evaluated considering only the dead loads of the building (weight of column, beam, slab, and brick wall), as described in Sect. 3, and the design spectrum itself was underestimated, as shown in Fig. 28; thus, the values should be compared in terms of the relative relations among the three analytical cases in the following. Case A had the highest value of α, indicating better seismic performance among all cases. This result mainly attributed to the higher reduction factor (R), as shown in Fig. 30, based on the higher deformation capacity in Fig. 26. Case A represents a building where masonry infill walls are completely removed or replaced by alternative lightweight walls as explained in Sect. 3; thus, the case may not be realistic in Nepal in spite of the effectiveness in terms of the seismic performance. On the other hand, Case C had the lowest value of α, indicating poorer seismic performance than that of Case B. These results were from the positive and negative infill effects that increased the stiffness and strength and decreased the deformation capacity, respectively, for Case C, which also lead the higher acceleration demand for the case, as shown in Fig. 30. Consequently, this comparison revealed that the infill effects negatively affected the seismic performance of the study building.

Fig. 30
figure 30

Comparison of seismic performance of each case (5-story)

Full size image

Regardless of the above discussion, the infill effects on the seismic performance of RC frame buildings were likely to vary under different numbers of stories. Hence, to justify this, additional analytical works were performed in the following section.

4.4 Risk assessment on conventional vertical extension

As mentioned above, the study building had conventionally extended stories without considering the consequences on the seismic performance (including any increase in gravity loads) of the building. The previous sections revealed that the seismic performance of the study building was significantly affected by the infill walls; hence, for the risk assessment of conventional vertical extension, a comparative study was performed considering all analytical cases (Case A, Case B, and Case C) by changing the numbers of stories of the study building, i.e., from 2 stories (one story with a penthouse) to 8 stories (7 stories with a penthouse). For all analytical cases, however, the same cross-sections, positions and material properties of the columns, beams and infill walls were assumed as those of the study building, as explained in Sect. 2.1. The analytical cases with 6 to 8 stories were assumed to have the same floor plans as that of the ground to 3rd floor of the study building shown in Fig. 4 and to have the same penthouse on the top floor. The seismic performance for each analytical case was evaluated in the form of amplification level (α), as summarized in Table 7, by applying the same procedure as explained in the previous section. From the table, the values of α for Case A were the highest compared to those for Cases B and C regardless of the numbers of stories, which indicated the common conclusion that the complete removal of the infill walls or replacement by lightweight walls were effective to seismically upgrade the building performance, as mentioned in the previous section. Since such solution was not realistic in Nepal, the seismic performance of Cases B and C were also compared. As a result, Case C had comparatively higher values of α when the building stories were equal to or lower than three. Figure 31 compares the evaluation results on the Cases A, B and C with three stories in the same manner as Fig. 30, clarifying the evaluation procedures for the values of α. The comparisons between the seismic performance of Cases B and C concluded that the infill effects positively affected the seismic performance for low-rise buildings, while they negatively affected that for medium-rise buildings with more than three stories.

Table 7 Amplification level (α) for buildings with different numbers of stories
Full size table
Fig. 31
figure 31

Comparison of seismic performance of each case (3-story)

Full size image

Focusing on α in Table 7 for Case C, the 5-story building representing the existing building exhibited a lower α of approximately 0.6 times than the originally designed 3-story building. The assumed 8-story building with an additional 3 stories extension decreased α approximately 0.5 and 0.3 times the 5-story and the designed 3-story buildings, respectively. This result indicates that the conventional vertical extension of RC frame buildings causes a substantial decline in seismic performance. Hence, this analysis reveals that conventional vertical extension results in a significant decrease in the seismic performance of RC frame buildings, which may lead to severe damage and catastrophic failure during earthquakes.

5 Limitations, future works, and recommendations

In this study, the infill out-of-plane effects were not considered as explained in Sect. 1. If all the infill walls collapsed in the out-of-plane direction, the building performance would be similar to Case B, whereas it would remain the same as Case C without the out-of-plane failure. In contrast, the building performance under partial out-of-plane failure would be different from the above three analytical cases (Cases A, B and C). Considering such estimates, a detailed investigation on the out-of-plane performance of the infill wall is planned to perform, which will investigate the infill out-of-plane effects on the seismic performance of the RC frame building. Moreover, the other possible infill effects as reported in NZSEE (2017): for instance, short column effect, torsional effect, and soft story effect were not comprehensively covered within the current study. The seismic performance of the building with masonry infill is likely to be affected due to the mechanical properties, density, thickness etc. of the masonry infill wall and its distribution on the building. However, in this research, those factors were not considered and the infill effects on the seismic performance of the buildings with different numbers of stories were investigated under the common specifications of the study building. Furthermore, the study building was limited to one well-designed building by the local engineer(s) assumed no uncertain construction errors. Non-engineered RC buildings often observed in developing countries are out-of-scope within the present study.

The comparative study in Sect. 4.4 revealed that the infill wall reduces the seismic performance for medium-rise buildings with more than three stories. Hence, this study suggests that when applying a brick masonry infill wall to such medium-rise buildings, its contribution should be restricted by separating it from the RC frame (e.g., by using seismic slits at the interface of the infill and RC frame) for better seismic performance; however, this solution should be implemented preventing the out-of-plane failure of the infill wall. Moreover, the analytical study in the above section revealed that the conventional vertical extension significantly decreases the seismic performance of RC frame buildings. Hence, this study revealed that the vertical extension should be put to an end to mitigate severe damage to buildings. Regarding the point where such extension is unavoidable, engineers are advised to heed the fact that the conventional vertical extension has a negative effect on the seismic performance of buildings; hence, proper strengthening or retrofitting of buildings or building elements to meet seismic demands correspond to extended numbers of stories should be carried out.

6 Conclusions

The present paper summarized the characteristics of a typical residential RC frame building with brick masonry infill walls and conventional vertical extension in Kathmandu, Nepal. The analytical studies were conducted in the longitudinal direction of the study building to mainly investigate the in-plane effects of infill walls. The seismic performance of the building with different contribution of the infill walls along with the conventional vertical extension was evaluated based on Japanese guidelines (AIJ 2004) under an acceleration response spectrum according to IS (IS 1893 (Part 1): 2016). Moreover, based on the research findings, future suggestions were presented for the practical design and seismic performance evaluation of RC frame buildings in Nepal, considering the common practice in the country. The major findings of this study are summarized below.

  1. (1)

    The eigenvalue analyses and static elastoplastic pushover analyses were carried out by replacing the study building with a three-dimensional model for three analytical cases with different considerations of the infill walls. When the in-plane stiffness, strength and self-weight of brick masonry infill walls were considered (Case C), the natural periods and the vibration characteristics agreed well with the microtremor measurement results. Case C showed maximum strength and minimum deformation capacity compared to other analytical cases (Case A and Case B). This exemplifies that the presence of the infill walls significantly affects the structural characteristics and capacity of typical RC frame buildings.

  2. (2)

    The results of pushover analyses were replaced by the performance curves in the equivalent single degree of freedom systems and compared with the design spectrum used in Nepal according to IS (IS 1893 (Part 1): 2016). It was found that the seismic performance was highest for Case A that ignored the presence of infill walls; however, this case is not realistic in Nepal. On comparison between two analytical cases neglecting/considering the infill effects (Case B/Case C), it was found that the seismic performance increased for low-rise buildings (equal to or less than three stories) due to the infill effects; in contrast, it decreased for medium-rise buildings (more than three stories). The latter result indicates that when using a brick masonry infill wall in medium-rise buildings, separating it from the RC frame (e.g., by using seismic slits at the interface of the infill and RC frame) can be one solution for better seismic performance; however, the possible out-of-plane failure of the infill wall should be prevented while separating the infill from the surrounding RC frame.

  3. (3)

    To investigate the consequences on the seismic performance of the building caused by the conventional vertical extension in Nepal, comparative studies were performed by changing the numbers of building stories (focusing on Case C). This comparison revealed that the conventional extension of the building stories without reconsidering the structural design causes significant decrease in the seismic performance of the building.

  4. (4)

    In Nepal, brick masonry infill walls are currently partially neglected, i.e., the in-plane stiffness and strength of the infill are neglected except for the self-weight, as they are being treated as nonstructural elements. However, the outcomes from the present research supported previous studies indicating that brick masonry infill walls significantly affect the stiffness and strength of typical RC frame buildings. Hence, while designing new buildings or evaluating the seismic performance of existing buildings, the structural effects of masonry infill walls should be considered (by Case C).

The above findings contribute to evaluating and mitigating the possible damages from future earthquake disasters on typical RC frame buildings with masonry infill walls not only in Nepal but also in other countries with similar backgrounds. The limitations, future works and recommendations of/from the present study have been discussed in the paper.