1 Introduction

Seismic risk assessment studies are an effective support for investigating the consequences of earthquakes in a region of interest, allowing understanding the potential impact and economic losses and the risk-informed planning and preparation of long-term risk reduction policies.

The development of building inventory at the territorial scale is a fundamental step in the framework of earthquake risk analysis. Indeed, the knowledge of the geographical distribution of building vulnerability classes, that is building inventory, is a pre-requisite to perform realistic risk estimations in a region of interest.

Depending on the scale of the analysis, as well as on the data availability and resources, variable level building inventories databases can be developed. Building-by-building surveys may provide high quality vulnerability information and are generally the most complete source towards vulnerability classification. Due to the elevated costs and time required, these kinds of surveys are generally only available after post-earthquake usability and damage evaluation campaigns or for small scale vulnerability studies conducted for limited areas in a country, such as urban districts or small municipalities. To cover larger geographical areas at comparatively low costs, satellite remote sensing shows great potential for rapid vulnerability assessment capturing some buildings’ features, that are visible from the outside, remotely by images. Several studies have explored techniques for extracting buildings footprints from high resolution optical satellite imagery (e.g. Taubenböck et al., 2006; Saito et al. 2004) and on the possibility of combining multiple imaging sources (Wieland et al. 2012; Ploeger et al. 2016). However, this technique based on image processing allow to gather only spatial type building features (building shape, position and height) while the features that are crucial for vulnerability assessment (e.g. building material or age of construction) cannot be easily derived. To overcome this issue, within GEM project (Pagani et al., 2018) remote sensing are combined with local expertise and field observations to estimate the distribution of building types for urban areas (Foulser-Piggott et al. 2014)). The resulting inventory can be input into the Global Exposure Database (GED), a global building inventory focused on people and residential buildings with global coverage at national and sub-national (province, municipality) level (Gamba2014). Another global approach to inventory is presented in Jaiswal et al. 2010, within PAGER program. The global inventory presented is built combining available data sources (e.g. World Housing Encyclopaedia, Census of Housing) and published literature, such as research articles and reports, that provide country-specific building-stock data. Yepes-Estrada et al. (2017) proposed a residential building inventory for South America, relying only on public sources of information and adopting a judgment-based mapping of the available (census) data to the distribution of building classes. In Europe, a similar effort was conducted within the NERA project by Spence et al. (2012), making a first attempt to harmonise the available data in each of the European countries (e.g. census data and data collected through building-by-building field surveys) to create the first single uniform database of the European building stock. A more recent European exposure model was developed within SERA project and presented in Crowley et al. (2020). This model describes the distribution of the main residential, industrial and commercial building classes across all countries in Europe inferred from census data further informed by the local experts judgment and a number of different public sources of data (e.g. World Housing Encyclopedia, PAGER building inventory, TABULA—Typology Approach for Building Stock Energy Assessment and NERA project).

The above-mentioned global inventory databases can be adopted for large scale risk assessment in the framework of supranational studies, also usefully applied in comparative evaluations among different countries. However, when dealing with national or sub-national risk assessment, the vulnerability and exposure characterization can be improved, allowing for a description of the building stock features and geographical distribution that is more adherent to the region under investigation. The recent effort for the national risk assessment NRA 2018 in Italy (Italian Civil Protection Department 2018; Dolce et al. 2021; da Porto et al. 2021) has shown the application of several vulnerability and exposure models VEMs that were specifically tested and validated for the residential building stock in Italy.

As happens for several exposure models, also for the exposure models adopted in the NRA 2018 the primary source of information are national housing census databases. For each vulnerability model, after definition of fragility functions for building classes, suitable rules to map the census data to building classes are proposed, that is an exposure model specific for each vulnerability model. The next section presents some relevant exposure models that were developed in Italy starting from census data as primary source of information. Most of such models are calibrated based on building typological data available from post-earthquake surveys in Italy. This approach has the advantage of allowing an implicitly validated association of typology to vulnerability classes. However, it has the drawback of being based on data from specific geographic areas, namely the ones that have been hit by damaging earthquakes, despite the buildings’ characteristics can vary greatly for different areas of a country. For example, in several vulnerability models for unreinforced masonry buildings (Braga et al. 1982, Di Pasquale et al. 2005; Rota et al. 2008; Del Gaudio et al. 2019; Rosti et al. 2021), the type of vertical structure (e.g. regular, irregular, round stone, regular stone etc.) or of horizontal structure (flexible, rigid, semirigid and vaults) has a clear influence on seismic vulnerability. However, the distribution of building typologies in a country may vary significantly depending on the availability of construction material in the area, the evolution of construction techniques, the seismic history and the codes in force at the time of construction, also depending on the seismic classification. The type of available stones to be employed in the construction of masonry buildings is influenced by the geography of the territory, by the presence of quarries, waterways and volcanic areas. Construction techniques are closely related to the type of stone, as well: for example, tuff and travertine, commonly used in Italy, can be cut into square blocks, while limestone is used for irregular blocks. Similarly, the presence of cobblestones, that can be found in historical centre built near rivers, can determine the presence of irregular masonry structures. In Italy, limestone can be found mainly in the internal Apennine areas, tuff is typical of volcanic areas and bricks are typical of the Adriatic coast and many northern towns, due to the large presence of alluvial deposits (Salmoiraghi 1892; Rodolico 1965; Zuccaro et al. 1999). Thus, for example, the city of L’Aquila, in Abruzzi region, in which limestone is widespread, is characterized by the presence of irregular masonry buildings. In Naples, Campania region, masonry buildings are mostly regular masonry, due to the large diffusion of tuff; however, in Benevento, an inland city of the same region, cobblestones are widespread due to the nearness to rivers (Sabato and Calore), that lead the presence of irregular masonry buildings. Table 1 shows some examples of different layout of masonry vertical structures spread on the Italian territory and how the use of different type of elements can affect the building type (regular or irregular layout).

Table 1 Examples of different masonry vertical structure types present in three Italian regions
Full size table

The classification criteria used in the development of empirical fragility and vulnerability functions are very coarse (e.g. based on vertical and horizonal structure types) and might not grasp substantial differences in local building typologies (e.g. irregular layout structures for masonry buildings could represent both a limestone construction with poor quality mortar and/or a granite or volcanic stone construction with compact texture which constitutes structures with considerably different seismic resistance). This makes the empirical functions highly related to the specific location where damage data are available, introducing a bias about their use for the vulnerability assessment in other locations and pointing out another limit to the application of empirical methods in large scale analysis.

Acknowledging the variability of building typological distribution at the territorial scale, recently the Italian Civil Protection Department financed the “Territorial Themes” ReLUIS project; in such a framework, a specific survey form “Cartis” was developed. Thanks to the speediness of the form compilation for relatively large areas, the interview-based form Cartis (Zuccaro et al. 2015) represents an alternative source towards the assemblage of large-scale inventories, allowing to rapidly collect information on relevant buildings features at urban level. As discussed in (Polese et al. 2019a, b, 2020), based on the availability of Cartis survey, an improved “integrated building inventory” can be obtained, coupling the largely spread data based on census surveys with more detailed typological data collected through the Cartis form. This paper investigates on the effects of an improved exposure modelling, adopting a building inventory based on Cartis data, on the vulnerability characterization and on the consequent risk assessment at the territorial scale. To this aim, two empirical models recently proposed by Del Gaudio et al. (2019) and Rosti et al. (2021) are used. Both models propose empirical based fragility curves for masonry building vulnerability classes defined based on typological features such as masonry type (e.g. regular or irregular) and horizontal type structures (e.g. deformable or rigid). They also introduce exposure models to allow building classification based on census data. In this paper, based on the Cartis survey available for several municipalities in three regions in Italy, an improved building inventory for such areas is built. This allowed to take into account local typological features that are variable in different parts of the country. Starting from such inventories, the exposure models relative to both vulnerability models are updated. It will be shown that the damage and risk assessment obtained from the original vulnerability/exposure models and from the ones updated through the improved inventory and exposure models vary depending on the analyzed region.

2 Census -based exposure modeling in Italy

In Italy census campaigns on population and buildings are carried out by ISTAT, the National Statistical Institute dealing with general censuses of the population, services and industry, and agriculture, sample surveys on households and general economic surveys at a national level. For each census tract, ISTAT database provides the number of buildings and information on building characteristics such as the construction material (masonry, reinforced concrete, other), the number of storeys, construction age. For privacy reason, such data are generally available in aggregated form, while they are disaggregated at the municipality level or larger scales. As clearly described in (Dolce et al. 2021), given disaggregated census data on buildings, it is possible to determine the distribution of building typologies in terms of material, construction age and storey number. However, in order to define the building inventory according to most refined vulnerability models, additional information is required, such as type of vertical and horizontal structures for masonry buildings. To this end, census data may be integrated by others source of information.

In general, in large scale seismic risk assessment, fragility functions refer to different vulnerability classes, for which different seismic behaviour is expected. The definition of the vulnerability classes usually involves the type of construction material (masonry, reinforced concrete, steel, wood) and could take into account other structural and non-structural features (Braga et al., 1982; Karababa and Pomonis, 2011; Yamazaki and Murao, 2000). A commonly used vulnerability classification is that defined by the European Macroseismic Scale EMS’98 (Grünthal 1998), according to which buildings are clustered into six classes (from A to F) of decreasing vulnerability based on the type of structures (i.e. the construction material and the earthquake-resistant design level).

Thus, in order to compile building inventory starting from census data, the association of building typology inferred by ISTAT to vulnerability classes through the definition of a suitable exposure model is required. The exposure model establishes the class assignment rules for associating each building typology to one or more vulnerability classes. This procedure may be calibrated on available survey data and/or expert judgment, analysing the correlation between the main vulnerability parameters for buildings and the census information.

In Lucantoni et al. (2001), the observed damage data from 1980 Irpinia and 1984 Lazio-Abruzzi earthquakes were used to integrate 1991 ISTAT data and define the distribution of national building stocks in 4 vulnerability classes of decreasing vulnerability A, B and C1 and C2, with masonry buildings divided into classes A, B and C1 based on the combination of quality of the vertical structures (poor, medium and good) and the type of horizontal system (wooden floors, floors with iron beams, reinforced concrete floors) and RC buildings grouped in C2 class.

In Di Pasquale et al. (2005), a first pattern of exposure matrix for masonry buildings was presented. The correlation between the structural elements and the age of masonry buildings was obtained through a statistical study of a sample of about 50,000 dwellings after the 1980 Irpinia M 6.9 earthquake. The structural types were grouped in vulnerability classes as defined by Braga et al. (1982) and the occurrence percentages of vulnerability classes was assigned as a function of the construction age.

In Bernardini et al. (2010), an expert judgment guided the probabilities assignment of membership to the EMS type as a function of the years of construction, considering some available information on construction techniques for masonry buildings in different areas, the seismic classification of the area and the level of seismic protection imposed by the rules in force, according to the seismic building code in the year of construction. These approaches allow to convert the original ISTAT classification by building construction material and age to a classification relevant to vulnerability.

Cacace et al. (2018) adopted the BINC procedure to estimate the vulnerability classes distribution for some Italian regions, starting from national Census data. The BINC method is based on the analysis of statistical correlations between available data at national scale and PLINIVS survey database, in which georeferenced data related to buildings typologies are collected in site through building-by-building survey activities on about 800 Italian municipalities.

Acknowledging its usefulness to compile building inventory, in the methodology adopted in the last National Risk Assessment (NRA) for Italy, the role of the exposure modelling is formally recognized (Dolce et al. 2021). To evaluate the seismic risk of Italian residential buildings and display the results, in terms of damage or impact, a WebGis platform IRMA (Italian Risk Maps) was specifically developed by EUCENTRE (Borzi et al. 2020). In IRMA different models for vulnerability assessment and related exposure characterization may be used for risk calculation. Each vulnerability/exposure model employed towards NRA defines specific rules to assign the percentage of each building typology, identified starting from ISTAT 2001 or 2011 census database, to relevant vulnerability classes adopted in the model. However, as previously observed, the distribution of the building typologies in the Italian territory is not homogeneous due to several factors that may affect the use of certain materials in a given areas, such as the geography of the territory, the seismic history and codes. Thus, as also outlined in Masi et al. (2021), the use of a regional specific  exposure model may improve the risk assessment.

With the scope to investigate on the effect on the vulnerability assessment of the different typological distribution at the regional scale, in this paper we analyse specifically two empirical vulnerability/exposure models that were recently proposed for masonry type buildings. The former one by Del Gaudio et al. (2019), was derived based on the statistical treatment of typological and damage data for 22,618 masonry buildings damaged after the 2009 L’Aquila earthquake; this model will be referred to as DG2019. The second model, proposed by Rosti et al. (2021) and also employed in the framework of the recent national risk assessment (Dolce et al. 2021), was derived considering the damage data available in the Da.D.O. database (Dolce et al. 2019) and specifically considering the L’Aquila 2009 and Irpinia 1980 earthquakes; this model will be referred to as RO2021. Both vulnerability models proposed different exposure models so to be employable with publicly available data such as those of ISTAT census databases, specifically construction age for DG2019 and construction age + height class for RO2021.

Next, the DG2019 and RO2021 vulnerability and exposure models are briefly described.

2.1 DG2019 model

The DG2019 approach is based on L’Aquila 2009 post-earthquake survey data. After the L’Aquila earthquake, the AeDES form (Baggio et al. 2007; Goretti and Di Pasquale 2002), a first-level survey form for post-earthquake damage and usability assessment in Italy, was compiled for a large number of buildings by means of in situ inspections performed by teams of experts and practitioners. However, only the municipalities classified with MCS intensities (Sieberg 1930) IMCS higher than VI and characterized by high PGA value were completely investigated and they were included in the dataset used for the calibration of DG2019 exposure model. The model proposes empirical based lognormal fragility curves for 14 masonry buildings classes. Through observed data, the authors identified four vertical structural types (i.e. regular layout or good quality, irregular layout or poor quality structure with or without tie rods/beams), and five horizontal structural types (i.e. vaults with or without tie rods, beams with flexible, semi-rigid or rigid slabs). The combination of vertical and horizontal structure types (e.g. irregular layout structure without tie rods or tie beams and flexible slabs) were grouped into 14 vulnerability classes, reported in Table 12 (“Appendix”). According to the European Macroseismic Scale (Grunthal 1998), the measure of the observed damage to each building is based on (5 + 1) damage grades and PGA was used as intensity measure to represent the seismic intensity. To allow building classification based on poor level data, the authors also proposed to build fragility curves directly referred to construction age intervals, the same as identified by census returns. To this end, based on the data derived from the sample of 22,618 residential masonry buildings surveyed after L’Aquila earthquake, the authors inferred the percentage of occurrence of each of the 14 classes within the 8 times intervals (< 1919, 1919–1945, 1946–1961, 1962–1971, 1972–1981, 1982–1991, 1991–2001, > 2001), defined by ISTAT (2001), as reported in Table 12. Looking at the distribution of buildings belonging to different age ranges, it can be noted that the older buildings (< 1919) are mainly poor quality masonry buildings with vaults (Class 23BC) or beams with flexible (4B or 4C) or semi-rigid slabs (5B or 5C). This percentage gradually decreases over the years in favour of good quality masonry buildings with rigid slabs (6D or 6E). The percentages of occurrence of Table 12 were used to build age-dependent fragility curves, i.e. fragility defined for census-compatible age intervals. Such curves were derived as weighted averages of the 14 sets of typological fragility curves with the percentage of occurrence of each class, as reported in Table 12.

2.2 RO2021 model

In Rosti et al. (2021) the Observed Damage Database Da.D.O. (Dolce et al. 2019), storing and sharing data from large post-earthquake damage surveys carried out in the aftermath of the most significant earthquakes occurred in Italy from 1976 to 2013, was exploited to derive empirical based fragility curves for masonry buildings. In particular, the data relative to the events of 1980 Irpinia and the 2009 L’Aquila earthquakes were used, due to the availability of complete post-earthquake field surveys and of shake-maps. For the calibration of this model the authors considered all the Abruzzi’s municipalities. The ones surveyed by AeDES form and exhibiting completeness ratio (i.e. number of inspected buildings over the total number of buildings retrieved from national census) higher than 90% were selected for creating an unbiased damage dataset, i.e. the same municipalities considered for the calibration of DG2019 model. The damage dataset was then enlarged by including non-surveyed and partially-surveyed municipalities of the Abruzzi region, which buildings could be reasonably assumed to be undamaged. The number of masonry buildings site in non-surveyed and partially-surveyed municipalities was retrieved from the national building census (ISTAT 2001) and their structural features are assigned based on the frequency of occurrence of each building structural typology considered by the model within the unbiased damage dataset.

Based on their structural characteristics, masonry buildings are classified into eight building typologies representative of the Italian built environment, according to the typological classification proposed by Rota et al. (2008). They depend on: quality of the masonry fabric (i.e. irregular layout or poor-quality masonry, regular layout and good-quality masonry); in-plane flexibility of diaphragms (i.e. flexible, rigid); presence (or absence) of connecting devices, such as tie-rods and tie-beams. These buildings typologies were merged into three vulnerability classes of decreasing vulnerability (i.e. A: high vulnerability, B: medium vulnerability, C1: low vulnerability), based on the similarity of the observed seismic fragility, using a hierarchical agglomerative clustering technique. Table 2 reports the classification rules proposed by Rota et al. (2008) to assign the vulnerability classes based on combination of vertical (poor or good quality masonry) and horizontal structures (rigid or flexible) and presence of connection device.

Table 2 Definition of vulnerability classes based on type of vertical and horizontal structures and presence of connection devices, according to Rota et al. 2008 and Rosti et al. 2020
Full size table

These vulnerability classes are further specified based on the building height, Low L: 1–2 storeys and Medium High MH: > 2 storeys. The aim of the study was to implement the model within the IRMA platform (Borzi et al. 2020) and its possible application for national risk assessment in Italy (Dolce et al. 2021). The exposure model in RO2021 subdivides census-based typologies for masonry buildings (defined based on construction age—< 1919, 1919–1945, 1946–1961, 1962–1971, 1972–1981, > 1981- and height level—L and MH) into the three vulnerability classes A, B and C1. While the vulnerability model was developed considering data from 1980 Irpinia and the 2009 L’Aquila earthquakes, the exposure model is built starting from the sole dataset of masonry buildings damaged after 2009 L’Aquila earthquake. To this end, a set of fragility curves was obtained by empirical damage data for each typology of masonry buildings.

Then, through an optimisation problem and by minimising the difference among the empirically derived fragility curves of a given typology and the fragility curves previously derived for A, B and C1 vulnerability classes, the percentages of each typology belonging to the predefined vulnerability classes were derived, as reported in Table 16. Table 16 represents the exposure matrix describing the RO2021 exposure model. For example, low-rise (L = 1–2 storeys) masonry buildings constructed before 1919 are subdivided with the following percentage: 86% belong to vulnerability class A and 14% to C1.

3 A methodology for regional-scale vulnerability assessment

For the purpose of employing solely census-based data to build the exposure model, the two models DG2019 and RO2021 adopt two slightly different approaches. Indeed, in DG2019 the fragility curves relative to the 14 vulnerability classes defined based on building construction features are re-arranged in age-dependent fragility curves considering the 7 age ranges available in ISTAT 2001; in this way, the building classification may be directly based on age considering the data available in ISTAT.

RO2021 adopts 6 vulnerability classes (i.e. three macro-classes A, B and C1, for two height ranges, L and MH) and the exposure matrix in Table 16 is suitably developed so to allow assignment of buildings to each one of these classes simply based on 6 age ranges (available in ISTAT 2001 but up to 82–91 range) and building height. It should be noted that the exposure matrices in DG2019 and RO2021, see Tables 12, 16, were obtained by statistical analysis of typological data relative to the sole buildings that were inspected after the 2009 L’Aquila earthquake. Thus, these matrices are strictly representative of the typological distribution in only one region (i.e. Abruzzo region). Similarly, also other exposure models were calibrated considering typological data available for a specific region (e.g. Di Pasquale et al. (2005) model that was calibrated on Irpinia earthquakes data). However, a relevant exposure matrix at regional scale could lead to improved evaluation of vulnerability distribution and consequently to a different estimate of expected damage and impacts.

In this paper, we propose to use the information collected through the Cartis form to re-calibrate the exposure model in different Italian regions. The Cartis approach allows to detect many of the distinctive masonry buildings elements that have significant influence on seismic behaviour and are strongly incisive for vulnerability classification for buildings. For example, the type of masonry (e.g. irregular layout masonry or regular layout with square stones or bricks), horizontal slab type (e.g. flexible, rigid or semi-rigid slabs), type of vaults (if present) and the presence of tie rods or tie beams are some of the vulnerability factors considered. On the other hand, for RC buildings no information leading to a substantial difference in vulnerability classification is inferred. Indeed, although Cartis form provides useful information on features that may influence the seismic behaviour (e.g. plan and elevation irregularity, the presence of moment resisting frame only in one direction, type of infill elements), generally the vulnerability classification for RC buildings is defined based on information easily obtainable also by census data, such as the building height and the building’s age. The latter parameter strongly affects the type of design (e.g. the buildings built before seismic classification of an area are designed only for gravity loads). Thus, for the present study, only masonry structures are considered.

These re-calibrated exposure matrices can be used to create the regional building inventory starting from the sole census data toward regional risk assessment.

The next Sect. 3.1 illustrates the methodology to compile the building inventory starting from Cartis database with an example applied for both DG2019 and RO2021 models.

3.1 Cartis approach

The 1st level “Cartis” form (Zuccaro et al. 2015) was recently implemented in Italy within “Territorial Themes” ReLUIS project, a project financed by the Department of Civil Protection with the scope of improving the exposure assessment at territorial scale, investigating the construction types in Italy and identifying local construction characteristics.

The Cartis approach aims at the survey of ordinary building typologies in sub-areas of the town denominated Town Compartments TC, characterized by homogeneity of the building stock in terms of construction age and construction techniques and/or structural types. The subdivision of the municipal area into TCs depend on bibliographic and documentary sources and historical investigations. It allows to define the main areas of the town interested by the different construction phases, such as first building erection of the historical centre and expansion areas of later stages. For each investigated municipality, the form is compiled through an interview with a technician belonging to the local Public authority (Region, Province, Municipality) and / or a technician who carries out a private profession in the area subjected to study that has proved experience on local building typologies. The form consists of 4 sections, in which the main constructive and structural characteristics of the prevailing typologies present in each TC are detected. They involve the number of storeys, the age of construction, the vertical and horizontal structure types (for masonry buildings), the type of reinforced concrete structures and infill types, the roof types and, if any, presence of structural interventions.

As for today, more than 350 municipalities were investigated with Cartis, with information on about 1,550 Town compartments and 708,100 buildings. The Italian regions with the highest completeness rate (number of surveyed municipalities versus the total number of municipalities in the region) are Basilicata (18%), Tuscany (15%), Umbria (14%) and Campania (13%). At the current state, the whole database covers about the 10% of national territory.

3.2 Cartis-based inventory: an example application

The Cartis database can be used to inform urban scale building inventory. For each municipality and each town compartment TC, the Cartis form provides the total number of buildings and the distribution belonging to different masonry or RC typologies at TC level. In particular, the form allows to detect up to four different typologies for masonry buildings (MUR1, MUR2, MUR3, MUR4) and four for RC buildings (CAR1, CAR2, CAR3, CAR4) in a single TC. For each typology, all the crucial elements in the characterization of seismic behaviour are identified. The main features concerning masonry typologies are, in addition to age of construction and number of storeys, the quality of vertical structures (e.g. regular or irregular), the type of horizontal structures (flexible, semi-rigid and rigid slabs and vaults), the building position in the block (corner, external, internal, insulated) and the presence of tie rods or tie beams. For RC typologies, other features are considered such as e.g. the presence of squat/brittle elements, the infill panel regularity, the presence of moment resisting frame in only one direction. Thus, given the number of buildings in a TC and the incidence percentages of the different typologies, the number of buildings characterized by certain vulnerability features can be obtained (e.g. the number of irregular masonry buildings built before 1919, having two storeys and flexible slabs).

An example of procedure to compile the building inventory starting from Cartis database is reported in the following. We consider a generic municipality, having about 25,000 inhabitants and 2500 residential buildings. According to Cartis approach, two Town Compartments are identified: the first is the historical centre of the town TC1, while the second is the expansion area TC2, as shown in Fig. 1. TC1, the most densely built, hosts most of buildings (1,700 buildings), distributed in different typologies according to the following percentages: MUR 1 (50%), MUR2 (30%), CAR 1 (20%). In Fig. 2 an example of buildings distribution considering the TC1 typologies is shown: starting from the total number of buildings belonging to each typology, the specific structural features are assigned based on relative distribution percentages. The MUR 1 typology includes masonry buildings built before 1919, with regular layout and having 2 storeys; the 25% of such buildings are characterized by vaults, while the 75% have flexible slabs, without tie rods or tie beams. The MUR2 typology includes masonry buildings with regular layout, built between 1920 and 1945, having 3 storeys, with semi-rigid (80%) and rigid (20%) slabs and the 50% of the buildings with tie rods or tie beams. CAR 1 typology includes RC buildings built between 1946 and 1961, having 5 storeys and characterized by the presence of geometric irregularities in elevation. In TC2 (800 buildings) only two typologies are identified: MUR 1 (20%), that includes masonry buildings with regular layout, built between 1946 and 1961, having 3 storeys and characterized by rigid slabs (100%); CAR 1 (80%), that includes RC buildings built after 1981, having 6 storeys; the 20% of this typology is characterized by irregularities in elevation.

Fig. 1
figure 1

Town Compartments for the municipality taken as an example and the building typologies idetified for TC 1, representing the historical centre. The characteristics of a building typology in the TC are also reported as example

Full size image
Fig. 2
figure 2

Example of buildings distribution for TC1, based on the related percentages, and the attribution in the relative vulnerability classes, according to DG2019 and RO2021 models

Full size image

Once the number of buildings belonging to defined structural types is obtained, it is possible to group them into vulnerability classes, according to the adopted vulnerability model. For example, starting from MUR1 typology, the two storeys masonry buildings with regular layout, with vaults and without tie rods or tie beams are assigned to 23DE vulnerability class, according DG2019 model, and to C1 L vulnerability class according to RO2021 model (Fig. 2). If the data of the total number of buildings in the TCs is missing for Cartis database, the procedure proposed by Polese et al. (2019a, b) to build the inventory, integrating census and Cartis data, can be used. The latter procedure is based on the possibility to assign Cartis specific features to census data through a GIS based overlapping technique that allows to define the census tracts (and the relative number of buildings) belonging to a given TC; in this way it is possible to assign to census tracts’ buildings the relevant Cartis typologies.

Finally, assembling all the TCs in a municipality, the building inventory at urban scale can be defined. The Cartis-based inventory of masonry buildings for the considered municipality, according to the DG2019 and RO2021 models, is reported in Table 3.

Table 3 Example of inventory of masonry buildings starting from Cartis data for the considered municipality
Full size table

In this study, the procedure introduced above is applied to evaluate the Cartis-based inventory at municipality scale, for the towns where Cartis form is available. Starting from the inventory in these towns, new statistics concerning the occurrence percentage of building typologies at regional scale are derived and employed to re-calibrate regional based exposure models.

4 Application to Italian regions

The application is proposed for three Italian regions: Abruzzi, Campania and Emilia-Romagna. In Abruzzi region 31 towns were surveyed with the Cartis approach; they represent about 10% of Abruzzi municipalities and 23% of regional inhabitants (see Fig. 3a, b). Municipalities are subdivided in demographic classes (from 1 to 7) according to the number of inhabitants (< 500, 500–2000, 2000–5000, 5000–10,000, 10,000–50,000, 50,000–250,000, > 250,000). In Campania region, 68 municipalities were surveyed with Cartis form, representing the 13% of municipalities and covering approximately the 17% of regional population, see Fig. 4. The number of buildings investigated by Cartis approach is estimated around the 18% of Campania’s buildings (about 144.000 buildings of which 67.000 are masonry buildings). In Emilia- Romagna, 29 municipalities were surveyed with Cartis approach, about the 9% of the municipalities, covering the 14% of the population of the region, see Fig. 5.

Fig. 3
figure 3

Distribution of municipalities (a) and number of inhabitants (b) as a function of demographic classes for Abruzzi region and Cartis’ municipalities surveyed. The red dashed lines represent the cumulative frequency

Full size image
Fig. 4
figure 4

Distribution of municipalities (a) and population (b) in Demographic classes for Campania region and Cartis’ municipalities surveyed. The red dashed lines represent the cumulative frequency

Full size image
Fig. 5
figure 5

Distribution of municipalities (a) and population (b) in Demographic classes for Emilia-Romagna region and Cartis’ municipalities surveyed. The red dashed lines represent the cumulative frequency

Full size image

For all the towns where Cartis information is available, the Cartis-based inventory is compiled, according to the procedure described in Sect. 3. These inventories are used to derive the statistical distribution of building typologies at regional level.

Although the database does not cover the whole regional territory, the municipalities surveyed by Cartis are considered as representative of the entire region. Obviously, this is a simplifying hypothesis that may lead to inaccurate estimations at the regional scale. As observed in (Polese et al. 2020), the mean vulnerability at municipality level tends to be higher for smaller towns, belonging to lower demographic class, that have generally a higher percentage of masonry buildings. To have a balanced covering of municipalities within different demographic classes, indications for proper selection of municipalities to investigate with Cartis approach for each region were given in the “Territorial Themes” ReLUIS project, mentioned in Sect. 3.1. Actually, the municipality belonging to demographic classes 5 and 6 are the most investigated in percentage for the considered regions, while lower percental covering is guaranteed for other demographic classes. While this aspect could potentially lead to an unbalanced estimation of vulnerability trends according to Cartis survey, the demographic classes 5 and 6 are also the ones covering a significant part of buildings (almost 40%, 50% and 70% in Abruzzo, Campania and Emilia Romagna, respectively) and the larger part of population in each region.

Another relevant aspect to consider is that the assumption that the regional administrative boundaries defines the areas with a homogeneous distribution of building typologies may be not the most suitable option. Still, the present study is conducted with the scope to perform a first application of a methodology for vulnerability characterization at regional level, being aware that the results can be updated and refined as more data become available.

Considering ISTAT 2001 age ranges, the occurrence percentages of the building typologies, derived based on Cartis data, into seven time-intervals (< 1919, 1919–1945, 1946–1961, 1962–1971, 1972–1981, 1982–1991, 1991–2001) are used to re-calibrate the DG2019 and RO2021 exposure models. Adopting the procedure already described, age-dependent fragility curves adapted for each region are also built for DG2019 model, that can be directly used with ISTAT 2001 data to evaluate the risk. Then, the exposure models and the sets of age-dependent fragility curves are used to implement damage and risk assessment with the aid of IRMA platform.

The proposed procedure is applied to the three Italian regions listed above (Abruzzo, Campania, Emilia- Romagna), in order to evaluate the variation of the exposure models due to the presence of different local building typologies. With the aid of IRMA platform, the risk analysis is performed with reference to unconditional damage assessment in a 50 years time-frame. Considering both the original vulnerability/exposure models DG2019 and RO2021 and the re-calibrated models in each region under investigation, the expected damage distribution is derived and compared. Finally, the risk assessment is carried out, providing a further comparison also in terms of direct economic losses.

4.1 Application in Abruzzi, Campania and Emilia Romagna regions

Adopting the previously described procedure, the building inventory based on Cartis data was assembled for all the municipalities investigated with Cartis approach in Abruzzi, Campania and Emilia-Romagna regions. This allows to obtain, for each town, the number of buildings with specific structural features (e.g. the number of masonry buildings with irregular layout and flexible slab without tie rods) and to group them into vulnerability classes, according to DG2019 and RO2021 models.

Figure 6 shows the percentage of irregular/regular layout of masonry vertical structures in the regions under investigation; in Abruzzi region irregular layout structures are widespread, while in Campania only the 12% of masonry buildings have irregular layout, mostly typical of the inland towns, and in Emilia-Romagna this typology is almost absent.

Fig. 6
figure 6

Diffusion of the vertical (irregular or regular layout) types on masonry building stock at regional scale, derived by Cartis-based inventory

Full size image

Figure 7 shows the incidence percentages of the horizontal structures for the two types of vertical structure, irregular and regular layout. It shows that in Abruzzi region only the 1% of irregular structures and the 26% of regular structures have rigid slabs while in Emilia-Romagna the vaults and semi-rigid slabs are almost absent. This confirms the variability of masonry building typologies distribution in different regions and its potential significant influence on damage and risk assessment.

Fig. 7
figure 7

Diffusion of horizontal structure types for irregular layout buildings (a) and regular layout masonry buildings (b), according to Cartis-based inventory

Full size image

Considering the municipalities surveyed by Cartis as representative of the whole region, the statistical distribution of building classes is detected for all towns and used to build the exposure matrix at regional level. Although this is a simplifying hypothesis, the statistical incidence can be updated as more data become available.

4.1.1 Results for DG2019 model

The percentage distribution of typologies into relevant age ranges, derived for the Abruzzi, Campania and Emilia-Romagna regions, are reported in Table 13, 14 and 15 in “Appendix”. It can be noted that in these tables the very last interval (> 2001) percentages were not evaluated because the exposure database used for following application is the ISTAT 2001 database, thus buildings built after 2001 are not included. However, being Italy a nation where the trend to build new constructions is limited, the percentage of buildings erected after 2001 is very low with respect to the other time intervals.

For the Abruzzi region, the comparison with the DG2019 exposure model reported in Table 12 shows a considerable decrement of irregular layout masonry buildings for the second time interval (1919–1945 buildings).In particular, the poor-quality masonry buildings with worst features are lower than in case of Table 12 (absence of tie rods or tie beams), while it becomes significant the percentage of regular layout structures with semi-rigid slab with or without tie rods or tie beams, respectively 43% and 17% against the 9% and 4% of original percentages. This evidence is graphically summarized in Fig. 9 (see red and orange histograms).

It may be worth to note that not so negligible differences can be highlighted between the exposure model of DG2019 and the one defined based on Cartis data, despite Abruzzi is the region where the data of the original model come from. This could find explanation in the different areas covered by the two different survey form, the AeDES form, from which DG2019 dataset was derived, and the Cartis one. Indeed, the area hit by the L’Aquila 2009 earthquake and were AeDES survey was available is mainly inland, while the Cartis survey considers also different areas of the same region (e.g. coastal area, that may be characterized by some different construction features). Figure 8 shows Abruzzi’s municipalities included in the DG2019 dataset (DATASET), those surveyed by Cartis and the ones belonging to both databases (CARTIS-DATASET).

Fig. 8
figure 8

Abruzzi’s municipalities included in the DG2019 Dataset (green) and in the Cartis database (light red) and the indication of which of them are in common between the two databases

Full size image

The comparison between the two inventories over all the municipalities for which both Cartis and AeDES form was available (see Fig. 8) shows similar percentages of buildings in each vulnerability class, while a significant discrepancy can be observed only for class 23 BC (30% of AeDES and only 3% according to Cartis).

It is worth noting that the aim of this study is not to assert a preference in using Cartis form rather than buildings by buildings survey, whose higher reliability is recognized and not questioned, but it is to show the large variability of building typological distribution at the territorial scale and how the latter can be easily captured thanks to Cartis approach, that is less time consuming and allows to rapidly investigate main building features in wider areas.

In Campania and Emilia—Romagna, a considerable difference with data reported in Table 12, which are generally adopted for the whole national territory but calibrated on data coming from Abruzzo region, can be recognized. The difference is significant especially for buildings belonging to construction age < 1919 and 1919–1945 (i.e. a greater number of buildings in regular layout classes for Campania + 13% and + 15% in 23DE and 4D classes; for Emilia-Romagna up to60% more buildings in 4D class, see Fig. 9). It can be observed a predominance of buildings without tie rods or tie beams for all time intervals (on average + 28% and + 53% of buildings in class 6D respectively for Campania and Emilia-Romagna). Moreover, the poor presence of vaults is recorded mostly for Emilia-Romagna region, with a reduction of 22% of irregular buildings with vaults (23BC class) with a small increase of regular buildings with vaults (+ 3% of 23 DE class).

Fig. 9
figure 9

Comparison of some relevant DG2019 vulnerability classes distribution for 1919–1945 time intervals for the three regions analysed

Full size image

The percentages reported in the tables of “Appendix” are used as linear combination’s coefficient to obtain the age-dependent fragility curves for each region analysed; they have been determined according to the approach illustrated in Sect. 2.1. The change of exposure matrix leads the change of the combination coefficient and, consequently, a different set of fragility curves. Note that, for the case of Abruzzi region, the resulting building typologies in age range’92–2001 derived from Cartis data are absent (all 0% in Table 13). The absence of data should mean that in the opinion of the interviewed technician the buildings built in this time period represent a neglectable percentage (lower than 5%). This finding is coherent with census-based data (ISTAT, 2001), according to which masonry buildings built between 1992 and 2001, in all the region, are less than 2%. In such a case, the age-dependent fragility curves for buildings constructed in’92–2001 are assumed equal to the ones relative to the prior age interval (’82–’91).

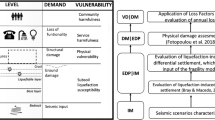
To evaluate the effect of the re-calibration procedure, damage assessment at regional scale is performed with the aid of IRMA platform (Borzi et al. 2020). With the scope to evaluate conditional risk, i.e. referring to a selected return period, or unconditional risk, i.e. referring to an observation time window, IRMA employs the OpenQuake calculation engine (Pagani et al., 2014), developed as part of the Global Earthquake Model (GEM), to perform damage and risk calculations. Figure 10 illustrates the Probabilistic Seismic Hazard Analysis (PSHA) based methodology to calculate unconditional risk in terms of expected number of damaged buildings in a region.

Fig. 10
figure 10

PSHA based methodology to calculate unconditional risk at the regional scale

Full size image

In Fig. 10, seismic hazard, obtained by PSHA, is represented at territorial scale through hazard maps, showing the spatial distribution of expected intensity at assigned return periods (Tr). Seismic vulnerability is represented by fragility curves for relevant building classes, while the exposure considers the building inventory (the distribution of building vulnerability classes at the territorial scale according to the adopted vulnerability model). For each town (site) in a region, the calculation of seismic risk involves the convolution of the seismic hazard at the site with vulnerability and exposure of the assets at risk. This means that for each vulnerability class, the mean annual rate λk of attaining damage state Dk may be obtained as in Eq. (1):

$$\lambda_{k} = \int\limits_{0}^{\infty } {P(D_{k} |im) \cdot \left| {d\lambda_{IM} (im)} \right|}$$
(1)

where P(Dk|im) represents the fragility of the considered building class, i.e. the probability that the buildings in such class will attain damage state Dk when subjected to an earthquake with ground motion intensity level im, and λIM represents the mean annual frequency of exceedance of the ground motion intensity im (obtained through the hazard maps for the generic Tr).

The probability pk of attaining damage state Dk in t years (i.e. the unconditional seismic risk in t years referred to damage state Dk) may be calculated as in the Eq. (2):

$$p_{k} = 1 - e^{{\lambda_{k} *t}}$$
(2)

Repeating the calculation for each building class, the number of damaged building (for each damage level) in a given time period can be obtained considering the proportion of each class in the considered building inventory, that is the exposure. Note that calculation is performed for each town (point-wise calculation) to which both hazard and exposure data are referred; y summing up for all the towns in a region the regional results are obtained.

Considering the different sets of fragility curves for each region analysed (the original ones and the ones calculated based on re-calibrated exposure), unconditional risk assessment for 50 years time-frame is performed.

In IRMA the exposure data is pre-loaded and represented by census data (ISTAT, Italian National Institute of Statistics 2001 or 2011), but different vulnerability/exposure models (VEM) can be employed for risk calculation. The VEM is defined by an exposure matrix and the associated set of fragility curves; the exposure matrix provides the rules to classify the building type (as derived by census data) into vulnerability classes and allows to complete the building inventory. Moreover, the user can choose the region of Italy to investigate, allowing the definition of different VEMs for different regions. For the purpose of this application, using DG2019 approach, the VEM is defined by considering building classes defined by age of construction, derived by ISTAT 2001 census data, and the associated age-dependent fragility curves. In particular, in order to test the proposed procedure to account for regional building features, two sets of age-dependent fragility curves are adopted: the original ones and the curves obtained from the re-calibration procedure. The results of unconditional risk assessment in 50 years time frame, in terms of number of buildings for each damage state (from DS0, no damage, to DS5, destruction) for the regions under investigation are reported in Tables 4, 5, 6 and Fig. 11. The number of buildings for each damage state employing the original DG2019 model and the updated exposure model starting from Cartis are reported in columns “DG” and “CARTIS” of the tables, respectively. The difference between CARTIS and DG is indicated as Δ and the Regionalization factor RF is calculated as the ratio of Δ versus DG. RF may be considered as a parameter representing the variation due to the different vulnerability characterization at regional scale.

Table 4 Number of masonry buildings for each damage state for 50 years time-frame, adopting the original exposure matrix DG2019 (DG) and the re-calibrated one based on Cartis data (CARTIS) for Abruzzi region
Full size table
Table 5 Number of masonry buildings for each damage state for 50 years time-frame, adopting the original exposure matrix DG2019 (DG) and the re-calibrated one based on Cartis data (CARTIS) for Campania region
Full size table
Table 6 Number of masonry buildings for each damage state for 50 years time-frame, adopting the original exposure matrix DG2019 (DG) and the re-calibrated one based on Cartis data (CARTIS) for Emilia-Romagna region
Full size table
Fig. 11
figure 11

Number of masonry buildings in each damage state for Abruzzi (a), Campania (b) and Emilia-Romagna (c). The cumulative frequency distributions are also reported

Full size image

A decrease of number of buildings for medium (DS3) and high damage state (DS4 and DS5) can be observed by using Cartis data; vice versa, it results in an increase of number of buildings in the damage state DS0, DS1 and DS2. The RF for Abruzzi region varies between the 10% and the 34%, showing that also in the same region the exposure can vary simply by considering different municipalities compared to the ones employed to calibrate the original DG2019 model. In Campania and Emilia-Romagna higher values of the RF are obtained with respect to Abruzzi, with a maximum value of 47% in Campania and of 60% in Emilia-Romagna.

It is worth noting that the variation in vulnerability observed with the adoption of Cartis-based approach may not occur for other Italian regions, as shown in Polese et al. (2021) where another application of the proposed procedure is presented. Basically, the higher or lower vulnerability observed with respect to the original model depends on the higher or lower diffusion of certain building typologies in the considered region, detected though Cartis inventory, and how these ones differ from those detected in the post-earthquake survey areas and used to calibrate fragility curves.

Once the risk results in terms of expected damage are available, expressing the probability of attaining the different damage states k (k = 1,…5) in a given time period, other impact quantities relevant for civil protection purposes can be calculated (e.g. fatalities, injured, homeless, direct economic losses, number of unusable or collapsed buildings). Indeed, the impact quantities can be determined as a function of expected number of buildings affected by different damage level. The damage-to-impact conversion criteria adopted in the recent national risk assessment for Italy are reported in (Dolce et al. 2021). For example, referring to the economic losses L, the Eq. (3), adapted from (Dolce et al. 2021) referring to only masonry buildings, is employed:

$$L = CU\left( {\mathop \sum \limits_{j = 1}^{{n_{M} }} \mathop \sum \limits_{k = 1}^{5} A_{Mj} p_{Mj,k} c_{k} } \right)$$
(3)

In Eq. (3) nM is the number of masonry (M) building classes; AMj is the built area of the jth M building class, respectively; CU is the Unit cost (Euro/m2) of a building, including technical expenses and VAT; pMj,k, is the probability, in the considered time period t for risk estimation, for the jth M building class to experience structural damage state k; ck is the percentage cost of repair or replacement (with respect to CU) for each structural damage state k. The default unit cost proposed in IRMA is assumed 1.350 euro/m2 and the cost parameters (DS1 2%, DS2 10%, DS3 30%, DS4 60%, DS5 100%) are calibrated on the actual repair costs that were monitored in the reconstruction process following recent Italian earthquakes (Di Ludovico et al. 2017a, b).

The seismic risk in term of economic losses L is calculated for each town of the three considered regions; note that only masonry buildings are considered for loss estimation. In particular, for each town in each region, two different results are obtained: the losses obtained using the age-dependent fragility curves derived by re-calibrated exposure matrices; and those resulting from the original DG2019 age-dependent fragility curves. The mean value of losses/m2 among all the municipalities in each region is selected as regional loss indicator. The ratio between the modified loss indicator derived by the re-calibration process (L_CARTIS) and the one obtained starting from the original VEM (L_DG), indicates the variation due to the different vulnerability characterization. The ratio between the differences Δ (= L_CARTIS—L_DG) versus the loss indicator relative to original model L_DG is defined as the regionalization factor due to losses RF_L and represents the influence on loss estimation of improved vulnerability characterization at regional scale.

The values of loss indicators for 50 years time-frame and the relevant RF_L are reported in Table 7. The RF_L is the lowest for Abruzzi region (22%). In Campania and Emilia-Romagna, RF_L is 40% and 51%, respectively, pointing out the considerable influence of the use of different exposure model at regional level. In particular, for the region under investigation the use of refined regional data led to a significant reduction in loss predictions. Moreover, RF_L assumes a higher value than the average value, RF_average estimated on the base of damage assessment (see Tables 4, 5, 6). Thus, the regionalization’s influence on the economic losses could be more incisive than the influence on the consequences in terms of damaged buildings. It is worth noting that the results in terms of damaged buildings and the ones in terms of economic losses are in strong correlation, due to the consequence model adopted. As a matter of fact, the model defines a cost ratio (cost of repair to cost of replacement) for each damage state, assuming higher values for the heaviest damage levels, that are also the ones for which the major discrepancies can be observed between the original approach and the Cartis-based one. However, the approach to give a major weight (cost ratio) to losses associated to heaviest damage levels is adopted in most existing loss models, e.g. HAZUS (FEMA, 2003), Maeviz (Karaman et al. 2008), SELENA (Molina et al. 2010), Global Earthquake Model GEM (Crowley et al. 2019). For example, the GEM model assumes as cost ratios for slight, moderate, extensive, and collapse damage states the following values: 5%, 25%, 60%, and 100%, respectively. Despite the damage levels in GEM are not the ones defined by EMS'98 scale, a correlation law is proposed in Lagomarsino and Giovinazzi (2006), based on which a direct correspondence of the first three damage levels and the first three EMS’98 damage grades can be assumed, while the fourth damage level is representative of both very serious damage (D4) and of the building destruction (D5). According to these assumptions, the adoption of the GEM consequence model to the above results in terms of damage leads to a very similar values of RFs, with results differing of less than 4% with respect to the ones obtained with the previously adopted loss model.

Table 7 Values of economic losses for each region analysed for 50 years time-frame, according to the different models adopted (the DG2019 and the one re-calibrated by the use of Cartis)
Full size table

4.1.2 Results for RO2021 model

The masonry buildings of Cartis-based inventory are grouped into vulnerability classes based on their structural features. In Cartis form the type of horizontal structures that can be detected are subdivided in Flexible, Semi-rigid, Rigid and Vaults. While for DG2019 vulnerability model these types of horizontal structures are identified, in RO2021 these structures are distinguished between rigid floors (reinforced concrete slabs and vaults) and flexible floors (wood, steel, etc.), according to Rota et al. (2008). Considering that the flexible and the semi-rigid slabs are mainly represented by wood and steel slabs, they can be considered as flexible floors, while the rigid ones is represented by reinforced concrete slabs and so they are considered as rigid floors. The classification rules proposed by Rosti et al. (2020), reported in Table 2, allows to determine the vulnerability classes based on combination of vertical (poor or good quality masonry) and horizontal structures (rigid or flexible) and presence of connection device.

The occurrence percentage of macro-category of buildings, considering six time intervals (< 1919, 1919–1945, 1946–1961, 1962–1971, 1972–1981, 1982–1991) and two height classes (Low (L) for buildings having 1 or 2 storeys, and medium height (MH) for buildings having more of 2 storeys), are inferred from Cartis-based inventory at regional scale, obtained using the approach presented in Sect. 3.1. The exposure matrices obtained for the three regions analysed are reported in Tables 17, 18 and 19 in “Appendix”.

Compared to original RO2021, in Abruzzi the re-calibrated model shows a similar percentage distribution for masonry buildings built after 1946, for both the L and the MH classes. On the other hand, a significant difference is observed for older buildings (< 1919; 1919–1945), whit a considerable reduction of buildings in the class A-L (38% and 10% instead of original 86% and 45% of RO2021 exposure matrix, see Table 16); furthermore a larger number of buildings in C1 for MH classes is found with respect to original RO2021 (18% and 36% instead of 3% and 0% of original RO2021, Table 16). For Campania region, a significant reduction of the number of buildings in vulnerability class A can be observed, especially for buildings built < 1919 and between 1919 and 1945. In the original RO2021 model, almost all the buildings built before 1919 are in vulnerability class A (86% and 97% for A-L and A-MH buildings, respectively), while they become less than 50% according to the new exposure matrix (24% and 18% for A -L and A-MH class, respectively). This reduction is even more marked for Emilia-Romagna (i.e. 3% of buildings in class A-MH buildings against 97% of the original model). For the building built after the 1972, characterized by low vulnerability, no substantial differences are observed by comparing the two exposure matrices.

Figure 12 shows the comparison of RO2021 building class distribution for the three regions analysed. It can be noted that the most significant differences can be observed for Low high classes (A-L, B-L, C1-L).

Fig. 12
figure 12

Comparison of RO2021 vulnerability classes distribution for 1919–1945 time intervals for the three regions analysed

Full size image

These exposure matrices are employed in IRMA platform and they are combined with the fragility curves proposed by Rosti et al. (2021). The results of damage and risk assessment are shown in Tables 8, 9, 10 and Fig. 13; the figure shows a comparison of the results obtained by the original model with the ones derived considering the Cartis-based exposure.

Table 8 Number of buildings for each damage state for 50 years time-frame, adopting the original exposure matrix RO2021 (RO) and the re-calibrated one based on Cartis data (CARTIS) for Abruzzi region
Full size table
Table 9 Number of buildings for each damage state for 50 years time-frame, adopting the original exposure matrix RO2021 (RO) and the re-calibrated one based on Cartis data (CARTIS) for Campania region
Full size table
Table 10 Number of buildings for each damage state for 50 years time-frame, adopting the original exposure matrix RO2021 (RO) and the re-calibrated one based on Cartis data (CARTIS) for Emilia-Romagna region
Full size table
Fig. 13
figure 13

Number of buildings in each damage state for Abruzzi (a), Campania (b) and Emilia-Romagna (c). The cumulative frequency distributions are also reported

Full size image

For all the regions under investigation, a decrease in the number of buildings for medium and high damage state can be observed with the use of Cartis, with the highest variations corresponding to the highest damage state, DS5. Consequently, the RF assumes increasing values as the damage state increases, with maximum values of 33% for Abruzzi, 45% for Campania and 58% for Emilia- Romagna, without significant differences compared to DG2019 model (i.e. 21%, 28%, and 40%, respectively). In terms of graphical output, it may seem that the differences in vulnerability between the original model and the Cartis-based one (Fig. 13) are lower than the differences observed adopting DG2019 model. This happens because, as observed in Sect. 4.2.2, the RO2021 model allows to capture more realistically the number of undamaged buildings and consequently according to RO2021 most buildings result undamaged (more than 70% in Campania and Emilia-Romagna and about 60% in Abruzzi), with high bars representing DS0 in the chart. This implies that also buildings in other damage states are re-distributed differently with respect to DG2019. Nevertheless, the maximum percentage changes of the recalibrated model (i.e. the RFs) are very similar with respect to DG2019 model.

It should be noted that the differences in the results achieved by using the two original methods of DG2019 and RO2021 may be even higher than those produced by the use of refined exposure data, especially referring to the estimated number of buildings attaining DS0. This circumstance is due to the different approach adopted in DG2019 and RO2021 models for the selection of dataset used for the fragility curves derivation. Indeed, for the DG2019 model only the completely surveyed municipalities were included in the dataset (i.e. the municipalities most hit to the earthquake, with a high number of damaged buildings), while RO2021 model was developed using also buildings sited in non-surveyed and partially-surveyed municipalities. As observed in Del Gaudio et al. (2020), the latter approach, including in the dataset also municipalities that are not “completely” surveyed, is adopted towards a more reliable estimation of the expected damage for low seismic intensities, that have a significant weight in the convolution for risk and losses computation. The comparison of results for the original methods of DG219 and RO2021 highlights the important issue associated to the strong epistemic uncertainty in the derivation of empirical fragility curves. Still, the differences due to more accurate exposure assessment at the territorial scale may be relevant, as it is shown in the scope of this study.

The same procedure described in Sect. 4.2.2 is employed for calculation of economic losses L in the three regions and the results are reported in Table 11. As observed before, the RO2021 model and DG2019 model produce significantly different results, especially considering the estimate of number of undamaged buildings, i.e. buildings in DS0; consequently, the losses estimated with RO2021 are very different with respect to the ones predicted by DG2019. Nevertheless, the estimation in terms of variation of the losses due to the adoption of more refined inventory, which represents the final goal of the work, are similar. As it can be seen, also for RO2021 model, the average results of RF estimated on the base of damage assessment, RF_average in Tables 8, 9 and 10, are lower than relevant RF_L reported in Table 11. As observed for DG2019 model, this result is correlated to the adopted consequence model employed to calculate the losses, that gives higher weight to most severe damage levels in computation of economic losses. Nevertheless, similar trend would be obtained also with other loss models; adopting the loss model employed in GEM (Crowley et al. 2020) similar direct economic losses are derived, with RF_L differing of less than 3% with respect to previously calculated one.

Table 11 Values of economic losses for each region analysed for 50 years time-frame, according to the different models adopted (the RO2021 and the one re-calibrated by the use of Cartis)
Full size table

5 Conclusions

The recently proposed interview-based Cartis approach allows to rapidly assemble building inventory at the municipality level. It allows taking into account building typological features crucial for vulnerability classification as regular or irregular vertical structures masonry types and deformable, rigid, semi-rigid horizontal structure types.

Relying on the availability of the Cartis-based survey for a significant number of towns in different regions in Italy, this study proposes a methodology to evaluate the effect of adopting improved building inventory and exposure assessment, taking into account relevant typological features recognised at regional scale, towards risk and loss analysis. The methodology accounts for different distribution of building typologies on the territory and allows overcoming one of the most critical aspect of available exposure models commonly calibrated on the base of empirical data derived on areas recently struck by an earthquake.

The Cartis based inventory for a percentage of municipalities in three regions in Italy, Abruzzo (10%), Campania (12%) and Emilia-Romagna (9%), is used to re-calibrate the exposure models relative to two existing empirical vulnerability models (Del Gaudio et al. (2019), DG2019, and Rosti et al. (2021), RO2021) recently developed for masonry type buildings in Italy. Original exposure models were developed based on typological distributions derived from post-earthquake damage and vulnerability survey after the L’Aquila 2009 earthquake, while the re-calibrated exposure models account for different distribution of building typologies derived from the Cartis-based inventory.

The study demonstrates that the different distribution of building typologies on the territory may have a significant influence on the exposure models and therefore it affects the building inventory that can be assembled based on available census data.

The proposed procedure to improve the exposure modelling through the Cartis based statistics allows to assess the effect of the different typological distribution at regional scale on damage and risk assessment. In particular, the unconditional damage and risk in terms of direct economic losses, relative to a 50 year time frame, were computed with the aid of IRMA platform (Borzi et al. 2020). The ratio between the difference of damage (i.e. the number of buildings that reach a certain damage level, DS) resulting by the use of re-calibrated models and the damage obtained starting from the original vulnerability/exposure models, indicated as Regionalization factor (RF), represents the variation due to the different vulnerability characterization at regional scale. Also, a regionalization factor associated to economic losses was evaluated, RF_L.

The main outcomes obtained by applying the proposed methodology to three Italian regions are:

the use of Cartis leads to different exposure matrices at regional scale;

the use of different exposure models at regional level can influence considerably the damage assessment. The exposure model can significantly vary simply by considering different municipalities compared to the ones employed to calibrate the original models, as shown for Abruzzi region for which RF_average is about 0.20 according to both models adopted; in other regions it varied between 0.28 and 0.40;

although the two original considered VEMs, DG2019 and RO2021, produce significantly different damage distribution, the maximum percentage changes of the recalibrated model (i.e. the RFs) are very similar.

a considerable influence of the use of different exposure models at regional level can also be observed by the comparison in terms of economic losses; in particular, a reduction of loss indicator in the range 22–51% has been evaluated, referring to DG2019 and RO2021 model respectively.

The reliability of the proposed exposure models is obviously influenced by the amount of the Cartis data available at regional level and could be improved considering a higher percentage of municipalities within a region. Nevertheless, this study represents a first application toward the regional exposure assessment, allowing to have a first quantitative estimation of the effect, in terms of damage and risk assessment, of adoption of different exposure model for different regions of a country.