Fragility functions for local failure mechanisms in unreinforced masonry buildings: a typological study in Ferrara, Italy

Abstract

Unreinforced masonry buildings undergoing seismic actions often exhibit local failure mechanisms which represent a serious life-safety hazard, as recent strong earthquakes have shown. Compared to new buildings, older unreinforced masonry buildings are more vulnerable, not only because they have been designed without or with limited seismic loading requirements, but also because horizontal structures and connections amid the walls are not always effective. Also, Out-Of-Plane (OOP) mechanisms can be caused by significant slenderness of the walls even if connections are effective. The purpose of this paper is to derive typological fragility functions for unreinforced masonry walls considering OOP local failure mechanisms. In the case of slender walls with good material properties, the OOP response can be modeled with reference to an assembly of rigid bodies undergoing rocking motion. In particular, depending on its configuration, a wall is assumed either as a single rigid body undergoing simple one-sided rocking or a system of two coupled rigid bodies rocking along their common edge. A set of 44 ground motions from earthquake events occurred from 1972 to 2017 in Italy is used in this study. The likelihood of collapse is calculated via Multiple Stripe Analysis (MSA) from a given wall undergoing a specific ground motion. Then, the single fragility functions are suitably combined to define a typological fragility function for a class of buildings. The procedure is applied to a historical aggregate in the city center of Ferrara (Italy) as a case study. The fragility functions developed in this research can be a helpful tool for assessing seismic damage and economic losses in unreinforced masonry buildings on a regional scale.

Introduction

UnReinforced Masonry (URM) buildings represent a large part of the Italian building stock. Compared to new buildings, existing URM buildings tend to be even more vulnerable to earthquakes. In Italian historical centers, this is essentially due to the following causes:

• (i) Old buildings may have been strongly altered over time, often resulting in a reduction of cross-section areas of masonry walls, a general weakening of mutual connections between walls and floors, and sometimes a significant increase in the seismic masses.

• (ii) Materials may be seriously degraded due to weathering, rising damp, and poor maintenance.

• (iii) In some territories, such as a large part of the Po River plain, seismic design has become mandatory only since 2005, and most of the buildings have been designed in the absence of specific provisions for earthquake resistance.

Recent seismic events (Decanini et al. 2004; Indirli et al. 2013; Penna et al. 2014; Sorrentino et al. 2019) have provided evidence that Out-Of-Plane (OOP) collapse mechanisms in URM structures still represent a serious life-safety hazard. In fact, under seismic actions, existing URM buildings are often subjected to local collapse mechanisms involving partial or whole OOP failure of façade walls (D’Ayala and Speranza 2003; D’Ayala 2005, 2013; Maio et al. 2016). Both activation and evolution up to collapse of these mechanisms strictly depend on stiffness and strength of connections between facade walls and other structural elements such as partition walls, floors and roof.

It is worth observing that, despite the recalled vulnerability of existing URM buildings to OOP collapse mechanisms, the European standard (CEN 2005) lacks information about the procedure to be used to assess the OOP behaviour of masonry walls.

In Italy, the seismic analysis of historical URM buildings based on the assessment of collapse mechanisms starts with Giuffrè (1996). Linear kinematic analysis is considered one of the most reliable tools to assess the activation of OOP failure of masonry walls, and it is currently adopted by the Italian building code (IMIT 2018). It is based on the use of the kinematic theorem of limit analysis to select, among various OOP mechanisms, that leading to the minimum seismic load multiplier (α₀). This multiplier may be rewritten in terms of acceleration capacity (a₀). In fact, if W = Mg indicates the generic gravitational load associated to mass M and gravity g, the activation load is given by α₀W = a₀Mg/g = a₀M. Then, for the safety check, acceleration capacity a₀ is compared with acceleration demand a_ref provided by the building code for the selected limit state. Yet, when the mechanism evolution is of interest, a displacement-based (nonlinear) approach should be used. This approach, usually referred to as kinematic nonlinear analysis, is based on the following steps (IMIT 2018):

• (i) imposition, for the selected mechanism, of equilibrium conditions corresponding to a generic, deformed configuration;

• (ii) evaluation of the capacity curve for the mechanism as a continuous function of the horizontal displacement of a control point;

• (iii) transformation of the capacity curve for the mechanism into the capacity curve corresponding to an equivalent Single Degree-Of-Freedom (SDOF) system;

• (iv) location, on the SDOF curve, of a limiting displacement corresponding to the considered limit state and comparison with the displacement demand.

This analysis method is intended to provide an approximation of the envelope of acceleration-displacement rocking cycles for the mechanism, and results then to be more suitable to catch the Ultimate Limit State (ULS) conditions of masonry walls than the linear method. It can happen, for example, that the mechanism with the smallest displacement capacity does not coincide with the mechanism with the minimum activation acceleration. It can be the case of vertical bending mechanisms of slender walls, which usually provide activation loads significantly larger than simple overturning mechanisms, but tend to experience a very low displacement capacity prior to collapse. That said, the rocking behaviour of rigid blocks is highly influenced by ground motion characteristics, which cannot be taken into due account without a nonlinear time-history analysis. Various authors showed the drawbacks related with the use of kinematic analysis methods, which often underestimate the actual capacity of URM walls (Shawa et al. 2012; Giresini et al. 2015; Sorrentino et al. 2016).

As for nonlinear dynamic analyses, there are several numerical methods that allow to evaluate the structural response employing FEM with different constitutive relationships (e.g., Concrete Damage Plasticity (CDP), Total strain-based crack (TSC)), discontinuous methods (e.g., Non-Smooth Contact Dynamics (NSCD), Discrete Element Method (DEM)) (Clementi et al. 2019; Clementi 2021; Ferrante et al. 2021) and Discrete Macro-Element Modeling (DMEM) (Chácara et al. 2019). One of the better performing approaches appears to be the nonlinear dynamic analysis of the walls considered as rocking rigid blocks. The study of rocking oscillators began with the seminal paper by Housner (1963), that derived a SDOF equation of motion for the OOP response of a parapet wall. Following that study, the research focused on the description of the dynamic response of rocking blocks subjected to either earthquake excitations or pulse (Yim et al. 1980; Spanos and Koh 1984). It has been found that this response may be characterized by dynamic instability and strong nonlinearity. Later, other models were adopted introducing equivalent SDOF models to govern the dynamic behaviour of complex multi-block rocking systems (Sorrentino et al. 2008; DeJong and Dimitrakopoulos 2014). A SDOF force–displacement idealization of the rocking behavior of URM walls was proposed by Doherty et al. (2002).

A unified probabilistic approach taking account of uncertainties, vulnerability, and risk can provide, with the use of nonlinear dynamic analysis, a better estimate of structural safety levels. One of the main tools in PEER—PBEE framework (Deierlein et al. 2003; Krawinkler and Miranda 2004) is the fragility function. For the rocking block, various studies provided fragility functions in terms of different intensity measures (Dimitrakopoulos and Paraskeva 2015; Lagomarsino 2015; Chiozzi et al. 2017). The methods available in the literature to derive fragility functions can be divided into four categories (Pitilakis et al. 2014; Silva et al. 2019): analytical, empirical, expert judgment, and hybrid. Fragility functions have also been proposed to describe the global behavior of masonry structures (Lagomarsino and Giovinazzi 2006; Rota et al. 2010; Spillatura et al. 2014). Most of these researches consider only the in-plane response of masonry walls (Chiozzi and Miranda 2017). More recent studies propose fragility functions for OOP mechanisms based on kinematic limit analysis (Zuccaro et al. 2017). Simões et al. (2019a, b, 2020) developed fragility functions for URM buildings combining in- and out-of-plane wall responses. In particular, for the OOP response, nonlinear kinematic analyses were used in that work. In addition, Ferreira et al. 2017 developed fragility curves for OOP walls calibrated with observed damage.

This paper presents a procedure to derive fragility functions for OOP mechanisms in URM buildings based on nonlinear dynamic analyses. A rigid block model is adopted for a given load-bearing wall. Fragility functions are derived considering the uncertainties associated with the peculiarities of masonry structures. These uncertainties are both aleatory and epistemic. The aleatory variables involved, such as wall geometry, masonry mass density, loads transferred from floors and roof, are treated by the Monte Carlo method (Zio 2013). Epistemic uncertainty is treated through the use of logical trees (Simões et al. 2019b). In the end, the individual fragility functions obtained are combined to define a typological fragility function for a class of masonry buildings. The approach adopted for the derivation of fragility functions is described in detail in the following sections. The method is then applied to a case study concerning a historical aggregate in the city center of Ferrara (Italy). Some preliminary results of this research have been recently presented by Nale et al. (2020).

Buildings database

CARTIS database

The structural-Typological and Seismic ChARacterization database, referred to in the following as CARTIS (Zuccaro et al. 2016), is an inventory of building typologies funded by the Italian National Civil Protection Department and implemented by the Italian University Network of Seismic Engineering Laboratories (ReLUIS) with the purpose of a seismic vulnerability assessment at a territorial scale. To date, the database collects information on 506 municipalities. For any given municipality involved, the data collection is mainly based on an interview to municipality technicians informed on historical events of city planning. This generally allows subdividing the urban center into homogeneous building compartments, and filling out a form with data (i.e., age of structures, types of vertical structures, floor slabs and roofs, geometrical data) on the various structural typologies contained into them. To validate the datasets, several buildings for each structural typology are also accurately surveyed on site. The resulting information is more detailed than that provided by available standard methods (ISTAT data, Census Database) and can more effectively support the creation of vulnerability models. In this paper, CARTIS database is used to develop typological fragility functions for local failure mechanisms in URM structures.

Case study

The historic center of Ferrara is made up of 92% masonry buildings and the remainder is made up of reinforced concrete and mixed structures. The structures are of less than three  storeys for 83%, albeit unevenly distributed concerning the construction periods of the city from the 14th to the 19th century (Dolce et al. 2015). In addition to the data extrapolated from the CARTIS database, it was decided to survey a historical aggregate of buildings in the center of Ferrara to improve the knowledge of masonry buildings. Table 1 shows the main parameters of the buildings in the historic center of Ferrara from CARTIS Database.

Table 1 Buildings parameters

For the selected compartment there are two typologies of masonry buildings in the city center of Ferrara (MUR 1 and MUR 2) (Fig. 1). The MUR1 typology refers to buildings from two to four stories, belonging to the oldest part of the historic center (medieval area) but also to the Renaissance area up to the 1800s and early 1900s (Fig. 2). The MUR2 typology is more recent (from 1920 to 1945) and has a variable percentage of tie rods, even though it also has wooden floors and a wooden roof (Table 1). The buildings of these types are for residential, commercial, tourist-accommodation, and office use (Fig. 3). The structural behavior of URM buildings is directly dependent on the materials and constructive details and indirectly dependent on the usage and state of conservation. One of the main challenges when assessing existing buildings is the definition of the mechanical properties of the materials (e.g. quality of clay brick walls, see Fig. 4). In general, poor mutual connections (Fig. 5) and limited stiffness of (timber) floors are major weaknesses of URM buildings.

Fig. 1

The historical aggregate in the center of Ferrara, Italy (aerial view)

Fig. 2

Example of buildings MUR1 class

Fig. 3

Example of buildings MUR 2 class

Fig. 4

Types of clay brick wall in Ferrara for MUR1 and MUR2 class

Fig. 5

Out-of-plane collapse mechanisms taking into account connections with transversal walls (de Felice and Giannini 2001)

Seismic assessment

Description of the approach

Under seismic actions, the local response is related to the activation of OOP collapse mechanisms (Fig. 6) of parts of the building insufficiently connected to the rest of the structure. Furthermore, fragility curves were used to describe the local response in a probabilistic context. These curves are useful for defining related vulnerability models. The intensity measure (IM) adopted in this work is the peak ground acceleration (PGA) as required by Italian building code (IMIT 2018) and which represents a common choice in the case of URM buildings. Epistemic uncertainty was treated using a logic tree approach that allows describing the vulnerability of each mechanism (Sect. 4.1). The aleatory uncertainty of each mechanism deriving from the properties of the materials, the geometry of the elements, and the loads applied on the mechanism have been treated with the Monte Carlo method (Sect. 4.2). The input parameters for a given mechanism were treated as one of the possible combinations of existing walls. To create a group of walls representative of the type of structures considered, a number of 1000 walls have been created. Such walls are the final result of all the uncertainties considered deriving from the epistemic and aleatory ones.

Fig. 6

Example of out-of-plane wall overturning in unreinforced masonry buildings a overturning of a wall at first-floor b partial overturning of the facade, c total overturning of the facade, d flexural mechanism of a wall, e flexural mechanism of the facade

To create the topological fragility curves, we proceeded as follows:

• (i) Identification of all possible configurations of the collapse mechanisms and relative weights (Sect. 4.1).

• (ii) Extrapolation of the main collapse mechanisms from the logic tree (Sect. 4.1).

• (iii) Generation of walls for the various mechanisms (Sect. 4.2).

• (iv) Multiple stripe analysis and creation of fragility curves (Sect. 5.2.4).

• (v) Typological fragility curves by combining the weights of mechanisms (Sect. 5.3).

Dynamic analysis of local collapse mechanisms

Modeling unreinforced masonry walls, subjected to seismic loads, represents an important challenge for both engineers and researchers because of its complexity of being described with nonlinear dynamic analysis. In this study, a single degree of freedom (SDOF) numerical model is used for the analysis of their dynamic behavior under seismic action.

Modeling strategy

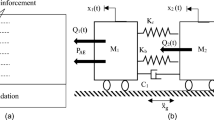
The equation of motion for a rocking block associated with a given local mechanism can be derived using Lagrange’s equation (DeJong and Dimitrakopoulos 2014):

$$\frac{d}{dt}\left( {\frac{{\partial T\left( {\phi ,\dot{\phi }} \right)}}{{\partial \dot{\phi }}}} \right) - \frac{{\partial T\left( {\phi ,\dot{\phi }} \right)}}{{\partial \dot{\phi }}} + \frac{\partial V\left( \phi \right)}{{\partial \dot{\phi }}} = - B\left( \phi \right)\ddot{u}_{g} + Q\left( \phi \right)$$

(1)

where $\phi$ is the lagrangian parameter that describes the motion, $T$ and V indicate kinetic and potential energy, respectively, $- B\left( \phi \right)\ddot{u}_{g}$ is the generalized inertial force induced by earthquake ground accelerarion ü_g, Q is the generalized force provided by static loads and overdot stands, as usual, for time derivative. Equation 1 can be rewritten in the following form:

$$I\left( \phi \right)\ddot{\phi } + J\left( \phi \right)\dot{\phi }^{2} + G\left( \phi \right) = - B\left( \phi \right)\ddot{u}_{g} + Q\left( \phi \right)$$

(2)

where $I\left( \phi \right)$,$J\left( \phi \right)$,$G\left( \phi \right)$ and $B\left( \phi \right)$ are nonlinear functions of $\phi$. It is also possible to derive from Eq. 2, for different local mechanisms, the load multiplier that activates the rocking motion from a resting position, i.e. from a state with null acceleration and velocity ($\ddot{\phi } = 0, \, \dot{\phi } = 0, \, \phi = 0$):

$$\lambda = - \frac{{\left. Q \right|_{\phi = 0} - \left. G \right|_{\phi = 0} }}{{g\left. B \right|_{\phi = 0} }}$$

(3)

where g is the gravity acceleration. The same load multiplier can be obtained by the limit analysis approach. In rocking systems, the energy dissipation is associated with the impact of the blocks at the base (Housner 1963; Yim et al. 1980; Spanos and Koh 1984). The restitution coefficient is defined, indeed, as the ratio of angular velocity after and before the nth impact. This formulation, reported in Sects. 3.2.2. and 3.2.3, is widely used in the literature (Liberatore and Spera 2001; Makris and Konstantinidis 2003; Sorrentino et al. 2011). In the adopted models it is assumed that the rigid block is rocking on a rigid foundation (this is not completely true). The coefficient strongly depends on the contact interface as shown in experimental tests (ElGawady et al. 2011). If the role of the base is considered, a possible shifting rotation point defined on the basis of the interface (compressive behavior of interface and accounting of crushing effects) should be considered (Mehrotra and DeJong 2018).

One-sided rocking

A one-sided rocking can be assumed for a wall even though the presence of internal constraints such as transverse walls and floor slabs. The governing equation for one-sided rocking of a rigid body can be written similarly to that for two-sided rocking:

$$I_{0} \ddot{\phi } + gM_{b} R\sin \left( {\alpha - \phi } \right) = - M_{b} R\ddot{u}_{g} \cos \left( {\alpha - \phi } \right)$$

(4)

where I₀ is the polar moment of inertia with the pivot point 0, M_b is the mass of the block and α is the internal angle and R is the length of the half-diagonal. In the case of vertical restraint, the rotation ϕ of the system remains positive (Fig. 7). For one-sided cases, the experimental evidence shows that energy dissipation depends on the interface between rigid block and its external constraint through the coefficient (Sorrentino et al. 2011):

$$\eta_{1s} = \left( {1 - \frac{3}{2}\sin^{2} \alpha } \right)^{2} \left( {1 - \frac{3}{2}\cos^{2} \alpha } \right)$$

(5)

Fig. 7

a Geometry of a rigid block under the one-sided rocking under ground motion, b normalized moment-rotation relationship

For a more accurate modeling of the seismic behavior of the wall, a tri-linear moment–curvature relationship with finite initial stiffness can be assumed on the basis of experimental test (Doherty et al. 2002). The tri-linear law takes account of initial imperfections, nonlinear material behavior, and the second-order effects. If this law is transformed into a tri-linear moment-rotation relationship, the motion equations can be written as follows (Boscato et al. 2014):

$$\begin{aligned} \ddot{\phi } & = - \frac{WR}{{I_{0} }}\left[ {\frac{{k_{i} }}{WR}\phi + \frac{{\ddot{x}_{g} (t)}}{g}\cos \left( {\alpha - \left| \phi \right|} \right)} \right]\quad \quad \quad \quad \quad \quad \quad {\text{if }}\left| \phi \right| \le \alpha_{1} \\ \ddot{\phi } & = - \frac{WR}{{I_{0} }}\left[ {{\text{sgn}} \left( \phi \right)\frac{{k_{i} }}{WR}\alpha_{1} + \frac{{\ddot{x}_{g} (t)}}{g}\cos \left( {\alpha - \left| \phi \right|} \right)} \right]\quad \quad \quad \quad \;{\text{if }}\alpha_{1} < \left| \phi \right| \le \alpha_{2} \\ \ddot{\phi } & = - \frac{WR}{{I_{0} }}\left[ {{\text{sgn}} (\phi )\frac{{k_{f} }}{WR}\left( {\alpha - \left| \phi \right|} \right) + \frac{{\ddot{x}_{g} (t)}}{g}\cos \left( {\alpha - \left| \phi \right|} \right)} \right]\quad \quad {\text{if }}\left| \phi \right| > \alpha_{2} \\ \end{aligned}$$

(6)

where R is the distance of the center of gravity from the rotation pivot, k_i is the initial stiffness ($k_{i} = \frac{WR\sin \left( \alpha \right)}{\alpha } \cdot \frac{{\alpha - \alpha_{2} }}{{\alpha_{1} }}$); and k_f is the final stiffness $k_{f} = \frac{WR\sin \left( \alpha \right)}{\alpha }$ with parameter $\alpha_{1} = \tan^{ - 1} \left( {3\frac{{\Delta_{1} }}{2H}} \right)$ (Table 2). The ultimate normalized rotation ($\Delta_{u}$) of the SDOF system is equal to 1. The ultimate normalized rotation corresponds to the Engineering Demand Parameter (EDP, see Sect. 5.2.3).

Table 2 The trilateral moment rotation curves parameters

Two block mechanism

The two-block mechanism can be used to describe the dynamic behavior of a wall that is characterized by the formation of the classical pivot interface at the wall top, bottom, and mid-height. The top and bottom pivot can rotate if they are under a ground motion excitation. The mechanism is described by these main parameters: α₁ and α₂ the describe the slenderness of the two blocks; I₀₁ and I₀₂ that are the polar moment of inertia regarding the relative mass centers M_b1 and M_b2 that are the masses of the bottom and the top blocks (Fig. 8). The resulting equation of motion is equivalent to those proposed in the literature (Sorrentino et al. 2008; DeJong and Dimitrakopoulos 2014; Mauro et al. 2015) and can be written as follows:

$$\begin{gathered} \left( {I_{01} + B_{1} I_{02} + B_{2} M_{b2} R_{2}^{2} } \right)\ddot{\phi } + \left( {C_{1} I_{02} + C_{2} M_{b2} R_{2}^{2} } \right)\dot{\phi }^{2} + gAR_{2} \left[ {M_{b1} + M_{b2} \left( {1 + \frac{{B_{2} }}{{4A^{2} }}} \right)} \right] = \hfill \\ - A\left( {M_{b1} + M_{b2} } \right)R_{2} \cot \left( {\alpha_{1} - \phi } \right)\ddot{u}_{g} + Q \hfill \\ \end{gathered}$$

(7)

Fig. 8

a Wall parameters, b cracked vertical spanning strip wall parameters, c displaced configuration and ground acceleration component acting in the mass centers of the two bodies

with the following system coefficients that are not constant but are functions of rotation $\phi$.

$$\begin{aligned} A & = \frac{{\sin \left( {\alpha_{2} } \right)}}{{\sin \left( {\alpha_{1} } \right)}}\sin \left( {\alpha_{1} - \phi } \right) \\ B_{1} & = \frac{{A^{2} \cot^{2} \left( {\alpha_{1} - \phi } \right)}}{{1 - A^{2} }} \\ B_{2} & = 4A^{2} \left[ {1 + \sqrt {B1} } \right] \\ C_{1} & = \left[ {1 - \frac{{A^{2} }}{{\sin^{2} \left( {\alpha_{1} - \phi } \right)}}} \right]\left( {\frac{A}{{1 - A^{2} }}} \right)^{2} \cot \left( {\alpha_{1} - \phi } \right) \\ C_{2} & = \frac{{B_{2} }}{2}\left[ {\frac{A}{{\sqrt {1 - A^{2} } }} - \frac{{A^{2} - 2}}{{\left( {1 - A^{2} } \right)}}\cot \left( {\alpha_{1} - \phi } \right)} \right] \\ Q & = - 2ANR_{2} \sqrt {B_{2} } \cos^{2} \left( {\alpha_{2} } \right)\left[ {\frac{1}{{\sqrt {B_{2} } \cos^{2} \left( {\alpha_{2} } \right)}} + 1 + \xi \tan^{2} \left( {\alpha_{2} } \right) + \frac{{\left( {\xi - 1} \right)\tan \left( {\alpha_{2} } \right)\sqrt {1 - A^{2} } }}{A}} \right] \\ \end{aligned}$$

(8)

The critical rotation and the horizontal load multiplier of the system become:

$$\begin{aligned} \phi_{cr,0} = & \alpha_{1} \\ \lambda = & \tan \left( {\alpha_{1} } \right)\frac{{M_{b1} + \left( {M_{b2} + \frac{N}{g}} \right)\left( {2 + \frac{{\tan \left( {\alpha_{2} } \right)}}{{\tan \left( {\alpha_{1} } \right)}}} \right) + \left( {2\xi - 1} \right)\frac{N}{g}\frac{{\tan \left( {\alpha_{2} } \right)}}{{\tan \left( {\alpha_{1} } \right)}}}}{{M_{b1} + M_{b2} }} \\ \end{aligned}$$

(9)

and the coefficient of restitution $\eta_{tb}$ is defined as follows:

$$\eta_{tb} = \frac{{M_{b1} R_{1}^{2} + I_{01} \frac{{\tan \alpha_{2} }}{{\tan \alpha_{1} }} - 2M_{b1} R_{1}^{2} \sin^{2} \alpha_{1} + M_{b2} R_{1}^{2} \left[ {2 + \frac{{\sin \alpha_{1} \cos \alpha_{1} }}{{\tan \alpha_{2} }} - \sin^{2} \alpha_{1} \left( {4 + \frac{{\tan \alpha_{2} }}{{\tan \alpha_{1} }}} \right)} \right]}}{{M_{b1} R_{1}^{2} + I_{01} - I_{02} \frac{{\tan \alpha_{2} }}{{\tan \alpha_{1} }} + M_{b2} R_{1}^{2} \left[ {2 + \sin \alpha_{1} \cos \alpha_{1} \left( {\frac{1}{{\tan \alpha_{2} }} + \tan \alpha_{2} } \right)} \right]}}$$

(10)

The coefficient of restitution depends on the slenderness of the wall and the position of the hinge. For the stockier wall and lower intermediate hinge, the energy dissipation will decrease. For this type of mechanism, the value of the coefficient of restitution is between 0.84 and 0.90 from experimental tests (Graziotti et al. 2016). This model, does neither include progressive damage (Doherty et al. 2002) nor an energy damping term (Tomassetti et al. 2019). In this paper, the analytical formulation (Eq. 10) is used for the analyses.

The rocking response results are obtained from a MATLAB code that numerically solves the nonlinear equations by means of a 4th–5th order Runge–Kutta integration technique (The Mathworks Inc. 2016).

Comparison between linear and nonlinear kinematic approaches and nonlinear dynamic analysis

In this section, a critical review of seismic response assessment techniques for local collapse mechanisms in existing masonry structures is discussed. To have statistically robust results, three types of walls with the two different configurations of constraints are subjected to nonlinear dynamic analyses (Table 3). Each wall was subjected to 44 accelerograms with 2 constraint configurations for 10 different amplitude scales of ground motion. A total of 1320 nonlinear dynamic analyses were performed. The results of the dynamic analysis are expressed by the ratio between energy demand (E_D) and capacity (E_C) (Shawa et al. 2012; Sorrentino et al. 2016). The energy demand (E_D) is calculated as the maximum potential energy during the seismic action or as the sum of the potential and kinetic energy at instability. The capacity energy (E_C) is calculated as the difference in the potential energy of the system. In Fig. 9, the results obtained from the nonlinear dynamic analyses are compared with the methods proposed by the Italian code (IMIT 2018). In the Italian code, the evaluation of local collapse mechanisms is recommended with two approaches: the force-based approach and the displacement-based approach. The force-based approach defines the acceleration capacity (a₀*). The acceleration demand is defined as the peak ground acceleration (PGA) divided by behavior factor q = 2.0 according to Eurocode 8 (CEN 2004, Table 4.4). This behavior factor is suitable for partitions and facades. The ratio between demand acceleration (PGA at the base of the block) and capacity acceleration is used to compare the force-based approach to the ratio of energy demands and capacity from dynamic approach that are presented in Fig. 9a–c. The displacement-based approach, on the other hand, defines a displacement capacity (d_u*). The corresponding demand displacement is evaluated using the spectral displacement (S_De(T_S)) at the secant period (T_S) of the local mechanism. The secant period of mechanism is defined as:

$$T_{S} = 2\pi \sqrt {\frac{{d_{s}^{*} }}{{a_{s}^{*} }}}$$

(11)

where $d_{s}^{*} = 0.4 \cdot d_{u}^{*}$ and $a_{s}^{*}$ is the relative pseudo-acceleration of the bilinear response curve (Sorrentino et al. 2016). The ratio between displacement demand and capacity is used to compare the displacement-based approach to the ratio of energy demands and capacity from the dynamic approach that are presented in Fig. 9b–d. As it can be observed in Fig. 9, the number of non-conservative cases is less for the one-sided mechanism, while it increases in the case of two-blocks mechanism. Furthermore, it is possible to see how displacement-based approach can reduce the number of non-conservative cases. Both code approaches confirm that they are in some cases unconservative. This evidence is due to several factors, for more details see (Shawa et al. 2012; Mauro et al. 2015; Sorrentino et al. 2016).

Table 3 Block used in the analysis, b is the thickness of the wall whereas h is the height of the wall

Fig. 9

Comparison between Italian code (IMIT 2018) and nonlinear dynamic analysis: a static force-based approach for one-sided rocking, b displacement-based approach for one-sided rocking, c static force-based approach for vertical bending, b displacement-based approach for vertical bending

Evaluation of uncertainties

To assess the seismic behavior of buildings, the epistemic and aleatory uncertainties are briefly defined in the next sections to account for the possible variations within a given class of buildings. The geometry of the building is not considered an uncertainty as the layout of the buildings is similar. Aleatory uncertainty is classified as irreducible uncertainty and refers to a property of the system associated with variability, whereas epistemic uncertainty can be reduced and it is associated with a lack of knowledge by the analyst (Beer et al. 2013).

Epistemic uncertainties

The epistemic uncertainties for the analysis of the local behavior are related to the incomplete knowledge about the structure of the buildings. These features are treated by the logic-tree approach (Simões et al. 2020). Figure 10 presents the logic-tree for the URM buildings in Ferrara for different categories of buildings (MUR1 and MUR2). Each branch of the tree is given a weight based on expert judgment. The end of a branch of the tree represents a class of possible mechanisms with specific features and the final weights. The weight attributed to the class of mechanisms is determined by multiplying the weights of all the component branches of the tree. More in detail, from the logic tree it is possible to obtain the weights associated with the various collapse mechanisms for the two main classes of masonry buildings (Fig. 11). The main mechanisms obtain from the logic tree are: overturning 1 floor, overturning 2 floor, overturning 3 floor, overturning 4 floor and vertical bending. With the expression overturning n floor, we mean a one-sided rocking with a height of the block corresponding to n floors. The final weight for any given mechanism is obtained from the sum of the partial weights referred to that mechanism. For the two-block mechanism, we consider a mechanism restricted to the top floor only. The vertical bending in the lower floors have been excluded a priori because there the walls are comparatively much less vulnerable to this mechanism (Mauro et al. 2015). These weights will be used to create the typological curve for OOP mechanisms.

Fig. 10

Logic-tree for URM buildings in Ferrara of the possible local mechanisms with relative weights (green for the MUR 1 typology and blue for MUR2 typology)

Fig. 11

Diagram of the relative weights for each type of collapse mechanism

Aleatory uncertainties

Aleatory uncertainties are related to the randomness of a certain phenomenon. For the analysis of the global behavior, the aleatory variables account for variations on the mechanical properties of masonry and geometrical properties of the wall. It is proposed to treat these aleatory variables by the Monte Carlo Method (Zio 2013) to define, in a random way, the properties to be assigned to the numerical models. The parameter ranges were chosen using the ranges extrapolated from the CARTIS database and possible mechanisms. The random generation of the parameters was done considering an interval set described by a lower and higher value. Generation occurs assuming a uniform distribution. This choice was made due to the fact that the information about the parameters was vague. The possible choice of a normal or lognormal probability distribution was not compliant because there were not enough tests for the relative parameters. The specific weight of the masonry is assumed constant to 18 kN/m³. The facade walls vary with a height between 2.5 m and 12.50 m and the thickness between 0.28 and 0.43 m. The thickness was also defined considering random values compatible with the possible combination of the bricks (i.e. single-leaf wall). Table 4 shows all parameters that are used to generate the samples. A total of 1000 simulations are assumed to have a sufficient number of results to reach a good convergence in the estimation. In the random generation of the walls, the variability of the loads, the percentages of openings in the walls (Fig. 12) and the presence of transverse connections were considered. Openings in the walls are taken into account in the form of variations in the position of the center of mass.

Table 4 Categorization of aleatory variables

Fig. 12

Different possible combinations of wall with different types of openings

Fragility analysis

General approach

A fragility function is defined as a lognormal cumulative distribution function:

$$P\left( {C\left| {IM = x} \right.} \right) = \Phi \left( {\frac{{\ln \left( {{x \mathord{\left/ {\vphantom {x \theta }} \right. \kern-\nulldelimiterspace} \theta }} \right)}}{\beta }} \right)$$

(12)

where $P\left( {C\left| {IM = x} \right.} \right)$ is the probability that a ground motion with $IM = x$ will cause the collapse of the wall, Φ() is the standard normal cumulative distribution function (CDF), θ is the mean of the fragility function and β is the standard deviation of $\ln IM$. To create a fragility curve, it is necessary to estimate the parameters that describe the curve, in particular the mean value and the standard deviation for a lognormal cumulative distribution function. The parameters of the fragility curves can be estimated by various methods. The two most common are the incremental dynamic analysis (IDA) and multiple stripe analysis (MSA). The first method consists in performing analyses from a series of ground motions that are repeatedly incremented to find the IM causing the collapse (Vamvatsikos and Cornell 2002). The second method entails performing analyzes for each of the levels of IM from a ground motion set (Jalayer 2003). A multi-stripe analysis (MSA) is used in this work.

Derivation of fragility curves

Selection of ground motions

In this paper, we used ground motion records from the ESM and ITACA databases (Bindi et al. 2011). The 46 ground motion records used for this study have been derived from 22 different events, recorded in different regions of the Italian territory between 1972 and 2017 (Table 5). These ground motions are within a specified range: magnitude M_w between 5.0 and 7.0, Joyner-Boore distance R_jb between 0 and 30 km, EC8 soil classification from B to E, and strike-slip, reverse or reverse-oblique faults. The number of ground motions is in accordance with NEHRP Guidelines (Whittaker et al. 2011). The ground motions are mainly obtained by the Italian accelerometric network (Rete Accelerometrica Nazionale, RAN) managed by the Italian Civil Protection Department (DPC) and the national seismic network managed by Istituto Nazionale di Geofisica e Vulcanologia (INGV). The selected ground motions take into account a wide range of PGA as well as PGV (Suzuki and Iervolino 2017).

Table 5 Italian ground motion records with important recorded PGA and PGV (^†EC8 classification (CEN 2004), *Epicentral distance, [I] = ITACA, [E] = ESM)

Intensity measure (IM)

The intensity measure is a parameter that quantifies the intensity of ground motion and serves as a connection between probabilistic seismic hazard analysis and probabilistic structural response analysis. The choice of this parameter has significant effects on structural response. In the Italian Building code (IMIT 2018), the use of Peak Ground Acceleration (PGA) is recommended for safety checks of mechanisms related with walls supported on ground. For mechanisms located at higher floors, Peak Spectral Acceleration (PSA) is more appropriate. It is well known that the use of PGA may lead to some inconsistencies (Housner 1965). Other intensity measures such as Peak Ground Velocity (PGV) may sometimes result in more reliable fragility curves (Dimitrakopoulos and Paraskeva 2015). However, PGA is the most used intensity measure in post-quake damage surveys, because its records are less sensitive than PSA to scarsity of operating seismic stations. As a consequence, several empirical fragility functions are based on PGA (Buratti et al. 2017). Moreover, the use of PGA turns out to be useful when the global behavior of low-rise masonry buildings is of interest (Lagomarsino and Giovinazzi 2006). For these reasons, the PGA is adopted as intensity measure in this study.

Engineering demand parameter (EDP)

For the correct evaluation of the fragility curve, an appropriate engineering demand parameter (EDP) is necessary for association with the damage state. In this paper, the damage state considered is the collapse damage state that corresponds to the complete overturn of the block. The absolute peak rocking rotation $\left| {\phi_{\max } } \right|$ divided with the slenderness α is the EDP:

$$EDP = \frac{{\left| {\phi_{\max } } \right|}}{\alpha }$$

(13)

The choice of this dimensionless EDP is physically explained: the large value of EDP implies that the block starts rocking (EDP > 0), high values (e.g. EDP > 1.0) show overturning as a consequence of rocking (Table 6). The parameter α for the vertical bending is assumed equal to the slenderness α₁ of lower block (Sorrentino et al. 2008). The collapse is considered with a EDP = 1.0 (Fig. 13a). This choice is conventional. In fact, this value occurs when there is a static instability. It is possible that the block rocking without overturning with EDP > 1 because the problem is strongly nonlinear (Dimitrakopoulos and Paraskeva 2015).

Table 6 Performance criteria for rocking behavior

Fig. 13

Example MSA analysis results; a analyses causing collapse are plotted at a critical angle of greater than 1.0 and are offset from each other to aid in visualizing the number of collapses. b Observed fractions of collapse as a function of IM, and a fragility function estimated using Eq. 17

Multiple stripe analysis (MSA)

The parameter estimators were obtained using the maximum likelihood method (Baker 2015). This method is widely used in literature as an alternative to the moments method to estimate the parameters because the estimators are asymptotically unbiased and efficient (Benjamin and Cornell 1970). This method is briefly described hereinafter.

The rocking analyses are performed for a level of intensity $IM = x_{j}$ which will give a number of collapses over the total number of the ground motions set. The probability of having z_j collapses in n_j ground motion per fixed intensity level is expressed as follows

$$P\left( {z_{j} {\text{ collapses in }}n_{j} {\text{ ground motions}}} \right) = \left( {\begin{array}{*{20}c} {n_{j} } \\ {z_{j} } \\ \end{array} } \right)p_{j}^{{z_{j} }} \left( {1 - p_{j} } \right)^{{n_{j} - z_{j} }}$$

(14)

where the collapse of the block can be caused with a probability p_j for a certain level of intensity IM = x_j. The observations of non-collapse and collapse can be assumed as ground motion independent of each other. The purpose of deriving the various collapse probabilities for different intensity levels is to derive a function with the highest probability from the collapse data observed by the rocking analysis. This is possible due to the likelihood method. The likelihood for the entire set of data obtained from multiple levels of IM is expressed by the product of the binomial probabilities (Eq. 14) and is described as follows.

$${\text{Likelihood}} = \prod\limits_{j = 1}^{m} {\left( {\begin{array}{*{20}c} {n_{j} } \\ {z_{j} } \\ \end{array} } \right)} p_{j}^{{z_{j} }} \left( {1 - p_{j} } \right)^{{n_{j} - z_{j} }}$$

(15)

where П indicates the product of all m level of IM. The probability function is made explicit by substituting Eq. 12 for p_j

$${\text{Likelihood}} = \prod\limits_{j = 1}^{m} {\left( {\begin{array}{*{20}c} {n_{j} } \\ {z_{j} } \\ \end{array} } \right)} \Phi \left( {\frac{{\ln \left( {{{x_{j} } \mathord{\left/ {\vphantom {{x_{j} } \theta }} \right. \kern-\nulldelimiterspace} \theta }} \right)}}{\beta }} \right)^{{z_{j} }} \left( {1 - \Phi \left( {\frac{{\ln \left( {{{x_{j} } \mathord{\left/ {\vphantom {{x_{j} } \theta }} \right. \kern-\nulldelimiterspace} \theta }} \right)}}{\beta }} \right)} \right)^{{n_{j} - z_{j} }}$$

(16)

Maximizing the likelihood function, it is possible to obtain the estimator parameters of the fragility curve that can be written:

$$\left\{ {\hat{\theta },\hat{\beta }} \right\} = \mathop {\arg \max }\limits_{\theta ,\beta } \sum\limits_{j = 1}^{m} {\left\{ {\ln \left( {\begin{array}{*{20}c} {n_{i} } \\ {z_{j} } \\ \end{array} } \right) + z_{j} \ln \Phi \left( {\frac{{\ln \left( {{{x_{j} } \mathord{\left/ {\vphantom {{x_{j} } \theta }} \right. \kern-\nulldelimiterspace} \theta }} \right)}}{\beta }} \right) + \left( {n_{j} - z_{j} } \right)\ln \left( {1 - \Phi \left( {\frac{{\ln \left( {{{x_{j} } \mathord{\left/ {\vphantom {{x_{j} } \theta }} \right. \kern-\nulldelimiterspace} \theta }} \right)}}{\beta }} \right)} \right)} \right\}}$$

(17)

Figure 13 shows an example of a fragility curve obtained from the approach just described.

Proposed typology fragility curves

The creation of typological fragility curves allows to include all uncertainties and describe a general behavior of the structure or element. Figure 14 shows the sensitivity analysis made for the mechanism of vertical bending. The parameters considered are the position of the formation of the hinge (Fig. 14a) and the influence of the vertical force N (Fig. 14b). In our case, we consider a wall $0.3 \times 3.0$ m. The position of the hinge has been changed considering the $h_{1} /h$ ratio which varies from 0.5 to 0.8 (ABK 1981; Graziotti et al. 2016), which constitutes an input parameter for the nonlinear dynamic analyzes. This parameter has little influence on the variation of the fragility curve. Instead, the vertical force affects the vulnerability of the wall. The vertical force was considered as the effect of the load due to the span of the slab. This force was applied in the center of the wall thickness. The type of floor chosen is a wooden slab at the roof of the structure (load of 2.5 kN/m²). The span of the slab varies from 1.0 to 5.0 m, as found in Ferrara masonry structures (Table 1). In Fig. 14b, the span of the floor L varies from 0.0 m (where the floor does not discharge on the wall) to 5.0 m. It can be seen that the vertical force at the top is a stabilizing component for the wall and, therefore, lowers the vulnerability. This can also be seen with static and dynamic analyses (Mauro et al. 2015).

Fig. 14

Sensitivity of the fragility parameters for vertical bending mechanism: a variation of the position of hinge (h₁/h from 0.5 to 0.8), b variation of the vertical force N as effect of the span of the slab (L from 0 to 5 m)

Subsequently, the fragility curves for the various mechanisms were created by varying the parameters. Each fragility curve was obtained by carrying out 44 nonlinear dynamic analyses for 9 different levels of intensity. For each curve, 396 nonlinear dynamic analyses were carried out for each wall considered. From the data extrapolated from CARTIS, we obtained intervals of parameters that were used as input for the analysis. The distributions could not be extrapolated due to the lack of information on the individual buildings. The database allows us to provide general data on a group of buildings. For each mechanism identified, a population of walls was created with randomly generated geometric parameters (Table 4). This choice is the most reasonable given the availability of data. For the mechanisms, a Monte Carlo method was applied with a population of 1000 walls. The population is subdivided according to the various weights associated with the mechanisms (Fig. 11) from which it is possible to obtain the relative fragility curves (Fig. 15). Figure 15 shows the curves of the various mechanisms obtained from the population (gray curves) and their relative average curves (black curves). The fragility curves for the overturning mechanism of the first floor and the vertical bending mechanism are the same for both the MUR1 and MUR2 classes, because the range of geometric parameters is the same. The curves are distinguished by a great variability of mean values and dispersions (Table 7). This is appreciable for simple overturning mechanisms (Fig. 15c–h). In fact, the presence of loads, openings and wedges (it has been assumed 25% of the population with wedges), influences fragility curves. In particular, the position of the center of gravity changes and loads and wedges tend to make the block more stable, so that greater accelerations are required to induce collapse.

Fig. 15

Fragility curves from CARTIS database: a top floor vertical bending, b overturning of the first floor, c overturning of two floors for MUR1, d overturning of two floors for MUR2 class, e overturning of three floors for MUR1 class f overturning of three floors for MUR2 class, g overturning of four floors for MUR1 class, h overturning of four floors for MUR2 class

Table 7 Lower and upper bound of mean (θ) and standard deviation (β) for fragility curves with Monte Carlo Simulation

The fragility curves for the mechanisms present in the survey (Fig. 16) have been obtained from 98 possible mechanisms for the aggregate. Figure 16 shows the curves of the various mechanisms obtained from the population (gray curves) and their relative average curves (black curves). The average curves for the single mechanism are generated using the arithmetic mean of the means and variances of the single curve.

Fig. 16

Fragility curves from the survey of the historical aggregate in the center of Ferrara (black average curve, grey survey curves): a vertical bending, b overturning of the first floor, c overturning of two floors, d overturning of three floors

The overall global typological curves for OOP mechanisms are shown in Fig. 17. All the curves are obtained by weighted arithmetic mean of the mean values and variances of fragility curves previously obtained from the individual class of mechanisms. The curves of each class of mechanism are the mean curves of the mechanisms (Fig. 16). These weights are obtained from the logical trees created from the possible collapse configurations (Fig. 11). Each class of mechanism (e.g. vertical bending) is summarized by a mean fragility curve. This fragility curve is defined by two parameters: the mean value and the standard deviation. Each class of mechanism is also associated with its weight (e.g. 0.36 for vertical bending (Fig. 11)). These parameters are obtained for all the mechanism classes and are aggregated to create the overall global typological curve using the weighted arithmetic mean.

Fig. 17

Comparison between the average curves obtained from the population created from the CARTIS database and the average curves obtained from the survey of the historical aggregate: difference between the typological survey curve (back line), the typological curve MUR1 (blue line) and the typological curve MUR2 (red line)

The most significant comparison is between the average curve obtained from the population of MUR1 class (this category constitutes 90% of the total of the buildings surveyed) with the curve obtained from the survey of the compartment. For completeness, the comparison between the curves of the MUR2 population is also reported. The typological fragility curves MUR1 and MUR2 are very similar despite the different age of construction which has little influence on the likelihood of overturning. The quality of the connections, slenderness and mass of the walls, load and span of the floors influences the fragility curves. The variation of the parameters between typologies MUR 1 and MUR 2 is small (Table 1), leading to fragility curves which are close to one another. Also, the buildings have good masonry qualities and textures (Fig. 4), good transversal connections, and the presence of tie rods or tie beams. Some indications on the masonry quality are reported in the CARTIS manual for the MUR1 and MUR2 typologies. Furthermore, supplementary assessments were made by evaluating the masonry quality in a qualitative way (e.g. visual inspection, expert judgement) through the survey. It is possible to say in general that under seismic action, buildings from different historical periods do not show great differences in our case study. It can be seen how the average population curves are more conservative than that obtained from the survey. This evidence is due to the greater number of walls analyzed for the various mechanisms obtained by the population than the number of walls obtained from the survey. The difference between the obtained curves is due to the level of knowledge of the walls. The survey increases the level of knowledge about the walls therefore the curve reduces the uncertainty associated with the geometry of the wall and provides a more detailed description of the walls for the historic aggregate. Moreover, the curves obtained from the survey consider the good masonry quality of the walls and the connection with the transverse walls The MUR1 and MUR2 classes derived from CARTIS have within themselves the variability of an entire type of building, while the aggregate has more homogeneous characteristics and less dispersed geometric and mechanical properties (e.g. buildings built in a specific period, similar masonry quality). In this comparison, the most influencing parameter is the quality of connections between the investigated wall and orthogonal walls. Indeed, transversal connections help to greater stability of the wall compared to its absence. The transversal connections between walls detected in the survey are relatively good in most of the buildings of the aggregate. Conversely, these connections are present in lower rate in the building typologies provided by the CARTIS database. The higher quality of data on geometry and loads allows us to generate curves more representative than those obtained from CARTIS. Anyway, the adopted approach shows how, with less detailed information (CARTIS), it is possible to obtain appreciable (and on the safe side) results in terms of probabilistic vulnerability assessment for masonry typologies typical of the Po valley.

Conclusions

This paper presents a procedure for the derivation of typological fragility functions for OOP local failure mechanisms in unreinforced masonry buildings. The proposed method starts with the data processing of the CARTIS database. A qualitative description of the building stock and associated relevant uncertainties (material, geometrical, loads) are initially considered. Epistemic uncertainties are included through the use of logical trees. Mechanical models, the validity of which is documented in the literature also from results of experimental campaigns, are introduced to analyze the OOP response of masonry walls. A dynamic approach is used, adopting a multiple stripe analysis method to derive fragility curves estimators. Finally, fragility functions are fitted to the computed fragilities.

The method is applied to historical aggregates of URM buildings. For the selected compartment in the city center of Ferrara, two building typologies (MUR 1 and MUR 2) are identified. MUR1 typology refers to buildings belonging to the oldest part of the historic center (medieval area) but also to the Renaissance area up to the 1800s and early 1900s, whereas MUR2 typology is more recent (from 1920 to 1945) and has a different percentage of tie rods on the total of the buildings.

The final fragility functions provide an overall assessment of the seismic vulnerability for these classes of buildings. The fragility curves for the MUR1 and MUR2 classes are not very different from each other although the buildings are of different construction periods. What distinguishes the two types is the presence of tie rods or tie beams and connections. The masonry quality is good for both classes. The fragility curves obtained by the two classes are different from the survey. The survey increases the level of knowledge about the walls therefore the curve reduces the uncertainty associated with the geometry of the wall and provides a more detailed description of the walls for the historic aggregate. The results show the moderate quality of the building stock and the important role of the connections in the vulnerability of the aggregates of masonry buildings. Indeed, the introduction of effective tie rods, modifying the OOP failure mechanisms from rocking to vertical bending, can dramatically reduce the vulnerability of aggregates, keeping the streets of historic centers operational even after strong earthquakes. The proposed approach, due to its computational efficiency, may be useful for identifying the seismically most fragile typologies of the urban context. Therefore, it is a tool capable of orienting targeted retrofit strategies.

Typological fragility curves for these local mechanisms then provide a first step for the evaluation of damages and the assessment of economic losses on an urban scale. This can help to identify possible scenarios for civil protection. In future researches, we would like to analyse other aggregates present in Italy, including building typologies similar to those of the Po Valley. This will also have to consider the uncertainties relating to the geometry of macro-elements and loads. The influence of the interaction between the floor effect of masonry structures and the local collapse mechanisms can be a further aspect to be explored. Finally, we will hopefully integrate these results into a comprehensive assessment method including the global behavior of masonry structures.