Fast simulation of railway bridge dynamics accounting for soil–structure interaction

Abstract

A novel numerical methodology is presented to solve the dynamic response of railway bridges under the passage of running trains, considering soil–structure interaction. It is advantageous compared to alternative approaches because it permits, (i) consideration of complex geometries for the bridge and foundations, (ii) simulation of stratified soils, and, (iii) solving the train-bridge dynamic problem at minimal computational cost. The approach uses sub-structuring to split the problem into two coupled interaction problems: the soil–foundation, and the soil–foundation–bridge systems. In the former, the foundation and surrounding soil are discretized with Finite Elements (FE), and padded with Perfectly Match Layers to avoid boundary reflections. Considering this domain, the equivalent frequency dependent dynamic stiffness and damping characteristics of the soil–foundation system are computed. For the second sub-system, the dynamic response of the structure under railway traffic is computed using a FE model with spring and dashpot elements at the support locations, which have the equivalent properties determined using the first sub-system. This soil–foundation–bridge model is solved using complex modal superposition, considering the equivalent dynamic stiffness and damping of the soil–foundation corresponding to each natural frequency. The proposed approach is then validated using both experimental measurements and an alternative Finite Element–Boundary Element (FE–BE) methodology. A strong match is found and the results discussed.

1 Introduction

The response of railway bridges is strongly affected by soil–structure interaction (SSI), especially under resonance conditions (Romero et al. 2013). Radiation and material soil damping influence the modal parameters and usually mitigate the structural vibration levels. However, the interaction between the sub-structure and the soil is seldom considered in numerical models when solving the dynamic problem. In order to predict realistically the vibrational response of bridges under railway traffic, or to asses the structural integrity for new operational situations, SSI should be considered. In the design of new structures this may lead to optimized alternatives and in the case of existing ones, it will permit to assess the bridge performance when facing operational challenges (e.g. increase in the speed or capacity of services) and improve model calibration procedures.

Several researchers have investigated the dynamic response of the bridge accounting for SSI. The soil surrounding the bridge foundations can be modelled applying the Boundary Element method (Domínguez 1993) or the FE method adding non-reflecting boundaries (Lysmer and Drake 1972). Galvín and Domínguez (2007) studied the vibrations induced by high-speed trains crossing a curvlet-type railroad underpass using a three-dimensional (3D) BE model. Báez et al. (2018) analysed the aforementioned structures following a sub-structuring approach, and Zangeneh et al. (2018) by means of a FE model. In all cases, the authors found the influence of SSI relevant. Romero et al. (2012, 2013) studied the effect of SSI on the resonant response of railway bridges. They concluded that the bridge fundamental periods and damping ratios increase when soil interaction is taken into account. Later, Doménech et al. (2016) and Martínez-Rodrigo et al. (2018) analysed SSI effects over an extensive catalogue of bridge typologies prone to experience high transverse accelerations at resonance for modern trains and high design velocities. They studied the structural response using a coupled 3D BE–FE model and concluded that incorporating SSI effects in the analysis of new simply supported (SS) bridges or in the analysis of existing ones for retrofitting purposes could be of great importance in the assessment of the Serviceability Limit Sate (SLS) associated to traffic safety. González et al. (2020) studied the performance of inclined pile foundations on the seismic response of bridges. The authors computed impedance functions and kinematic interaction factors of the pile foundations and compared them with the results of two different approaches: a Winkler-type model and a BE–FE model. Zangeneh et al. (2019) presented a simplified discrete model for calculating the modal parameters of the fundamental bending mode of railway beam bridges on viscoelastic supports. They proposed exact, closed-form expressions for the fundamental frequency and modal damping ratio, considering the effect of the dynamic stiffness and dissipation capacity of the foundation–soil system. Recently, Zangeneh (2021) investigated the effect of the foundation mass on the fundamental modal properties of the beam bridges. Gara et al. (2019) studied the effect of the foundation–soil system on the interpretation of experimental ambient vibration tests and on the calibration of numerical models. They concluded that the common practice of updating fixed base numerical models to fit experimental results should be prudently evaluated in the case of bridges where SSI is significant.

In the aforementioned research, simplified foundation geometries are mostly considered due to the high computational cost of the chosen numerical approaches. However, the computational effort could be reduced to a certain extent during SSI simulations using Perfectly Matched Layers (PML) to limit the size of the soil domain (Basu and Chopra 2003a, b, 2004; Basu 2009; Kausel and de Oliveira Barbosa 2012). For example, Davoodi et al. (2018) studied the response of simplified geometries of different foundations using the absorbing layers provided by the PML incorporated in a FE model. Lopes et al. (2014) studied the problem of a track-tunnel-ground system using a two-and-a-half-dimensional (2.5D) FE-PML approach. Esmaeilzadeh Seylabi et al. (2017) solved the wave propagation problem in the frequency-domain on a FE model applying PML to numerically simulate measured dynamic impedances of soil–pile systems. Zangeneh et al. (2021) investigated the effect of dynamic SSI on the resonant response of portal frame bridges founded on a rigid base, and the parameters governing their interaction. The authors compare the results given by a simplified model with those from a full 3D FE-PML model.

Fig. 1

Schematic representation of soil–foundation–bridge coupled system

Figure 1 shows a schematic representation of the railway beam-bridge coupled problem. The problem is usually divided into two sub-domains. First the bridge deck, supports and foundations are commonly represented using FEs. Then this structural domain is coupled to the soil subspace. Alternatively, if the complete problem is modelled, and therefore modal superposition is not applied, the corresponding dynamic equilibrium equations can be solved using either implicit or explicit integration schemes, in the time or frequency domains. These approaches require large amounts of computational resources and time since, in addition, it is usually required to obtain the bridge response under several train types and speeds. An alternative and faster approach is to decouple the problem and to compute the structural response as the superposition of the first modal contributions. However, this transformation is not straightforward when the soil is accounted for, due to the presence of non-proportional damping.

Fig. 2

Schematic representation of the soil–foundation decoupled system

In this paper a general approach is proposed to solve the SSI problem in railway bridges applying modal superposition. A sub-structuring approach involving PML permits the modelling of arbitrary foundation geometries. First, the problem in Fig. 1 is decoupled into (i) the soil–foundation problem (Fig. 2), and, (ii) the soil–foundation–bridge interaction problem (Fig. 3). In the first, the equivalent frequency dependent dynamic stiffness and damping characteristics of the soil–foundation system are computed using the FE-PML method. In the second, the dynamic response of the structure under railway traffic is computed using a FE model that includes spring/dashpot elements at the supports, where the equivalent properties at the bridge–foundation connection points are extracted from the first problem. This soil–foundation–bridge model is solved by modal superposition considering the equivalent dynamic stiffness and damping of the soil–foundation corresponding to each natural frequency. To do so, a model updating procedure is implemented. As the model presents non-proportional damping, the complex eigenvalue problem is solved in order to compute the natural frequencies and mode shapes.

The study considers the vertical force transmission between the deck and the foundation, as the aim of the investigation is to develop and present the methodology. Nevertheless, the approach could easily be extended to more complex bridge–foundation–soil systems.

Fig. 3

Schematic representation of soil–foundation–bridge decoupled system

The outline of the paper is as follows. In Sect. 2, the numerical formulation is presented. In Sect. 3 the modal properties and dynamic response of a particular soil–foundation–bridge system are validated and compared to those from previous publications which are computed applying different numerical techniques. In Sect. 4 the response of a real bridge is reproduced and compared to experimental measurements. Finally, in Sect. 5 the main conclusions are summarized.

2 Numerical formulation

The soil–foundation–bridge interaction problem (Fig. 1) is decoupled (Figs. 2, 3) with the aim of implementing a fast and accurate analysis tool that can be used in practice for the design and performance evaluation of these types of structures.

2.1 Soil–foundation interaction problem

The dynamic stiffness of the soil–foundation system is computed applying the FE method. In order to represent the absorbing boundaries for the wave equation, PML is used. Following, the formulation of the PML is briefly summarized (Basu and Chopra 2003b; Bindel and Govindjee 2005; ANSYS, Inc. 2021).

Fig. 4

Attenuation function

The PML layers absorb and attenuate the arriving waves. In the frequency domain, the PML medium is formulated assuming a harmonic time dependence of the displacement, stress and strain, e.g. ${\mathbf{u}}({\mathbf{x}},t)=\overline{{\mathbf{u}}}({\mathbf{x}})\exp {\iota \omega t}$, where $\iota =\sqrt{-1}$ and $\omega$ is the frequency of excitation. The waves are attenuated along the local coordinate system ${\mathbf{x}}'$ inside the PML domain. Figure 4 shows a schematic representation of the attenuation function at each spatial direction j, with $L_{Pj}$ being the PML thickness. The frequency-domain equations for the PML medium are obtained by applying nonzero complex-valued coordinate stretching functions in the $x_j'$ direction denoted as $s_j$:

$$\begin{aligned} \frac{1}{s_j(x_j')}\frac{\partial {\overline{\sigma }}_{ij}'}{\partial x_j'}=-\omega ^2\rho {\overline{u}}_i' \end{aligned}$$

(1)

where ${\overline{\sigma }}_{ij}'$ are the components of the stress tensor in the local coordinate system, and $\rho$ is the density of the medium.

The components of the strain tensor in the local coordinate system are:

$$\begin{aligned} {\overline{\varepsilon }}_{ij}'=\frac{1}{2}\left[ \frac{1}{s_j(x_j')}\frac{\partial {\overline{u}}_{i}'}{\partial x_j'}+\frac{1}{s_i(x_i')}\frac{\partial {\overline{u}}_{j}'}{\partial x_i'}\right] \end{aligned}$$

(2)

The stretching function is $s_j(x_j')=[1+f^e_j(x_j')/\omega ]-\iota f^p_{j}(x_j')/\omega$, where the functions $f^e_j$ and $f^p_{j}$ attenuate evanescent and propagating waves, respectively. If evanescent waves are not present, the stretching function results $s_j(x_j')=1-\iota f^p_{j}(x_j')/\omega$. The attenuation functions used in this work and referred to in Fig. 4 are:

$$\begin{aligned} f_{j}(x_j')=f_{0j}\left( \frac{x_j'}{L_{Pj}}\right) ^2 \end{aligned}$$

(3)

The parameters $f_{0j}$ and $L_{Pj}$ are set to obtain a normal reflection coefficient of $-60\,\text{ dB }$, i.e.:

$$\begin{aligned} 20\log _{10}\left( \frac{{\overline{u}}_{j}'(L_{Pj})}{{\overline{u}}_{j}'(0)}\right) =20\log _{10}10^{-3}=-60 \end{aligned}$$

(4)

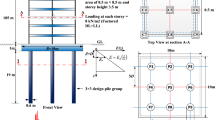
The versatility of the FE methodology allows the simulation of different foundation types and soil stratigraphies. Firstly the soil–foundation system shown in Fig. 2 is considered in order to compare the proposed methodology with the results presented in Doménech et al. (2016) and Martínez-Rodrigo et al. (2018).

Three homogeneous soil types are defined with flexibilities covering the AASHTO classification (AASHTO 2012). In particular s and p-wave speeds of $c_s=\left\{ 150, 220, 365\right\} \,\text{ m/s }$ and $c_p=2c_s$ are admitted, meaning that Poisson’s ratio $\nu _s=1/3$. Soil density and material damping are $\rho _s=1800\,\text{ kg/m}^3$ and $\zeta _s=0.05$, respectively, for all cases. Identical $2B\times 2B$ rigid foundation plates with $B=2.5\,\text{ m }$ are considered in all the cases initially.

The soil–foundation system is analysed using the FE model shown in Fig. 2 implemented in ANSYS. In this figure only volumes are indicated for simplicity, and not the actual mesh. A massless foundation plate is considered for a better comparison with the cited works, which is modelled with four-node shell elements with six degrees of freedom (dof) per node. The plate is surrounded by a volume of soil represented with eight-node solid elements with three dof per node. At the boundaries of the soil elements, additional solid elements are created incorporating the PML formulation in order to act as absorbing boundaries.

The number of PML layers determines the absorbing efficiency of the PML region. The absorbing efficiency depends on the excitation frequency, the distance between the source and the PML domain, the PML domain thickness $L_{Pj}$, and the wave propagation velocity. The number of layers of the PML region is obtained from the PML thickness and the required element size. It is recommended a number of layers higher than 2 to reproduce the attenuation distribution. Moreover, it is advisable to model the near-field soil, at least, by two elements (ANSYS, Inc. 2021).

A total soil volume of $20\,\text{ m }\times 20\,\text{ m }\times 10\,\text{ m }$ is generated, where the thickness of the PML boundary equals $5\,\text{ m }$, according to the mentioned requeriments. Therefore, the distance between the PML region and the foundation is $2.5\,\text{ m }$. The size of the elements is selected based on the frequency. In particular, the mesh is discretized in 10 elements per wave length $\lambda =2\pi c_{s}/\omega$ (Coronado and Gidwani 2016) with a minimum element size of $0.5\,\text{ m }$.

When a harmonic vertical force $F_s(\omega )$ is applied at the center of the foundation plate with frequency $\omega$, the dynamic stiffness is defined as Domínguez (1993):

$$\begin{aligned} K_v^{d}(\omega )=F_s(\omega )/v_s(\omega ) \end{aligned}$$

(5)

where $v_s$ is the vertical displacement of the foundation. $K_v^{d}(\omega )$ can be expressed as:

$$\begin{aligned} K_v^{d}(\omega )={\mathrm {Re}}\{K_v^{d}(\omega )\}+\iota {\mathrm {Im}}\{K_v^{d}(\omega )\} \end{aligned}$$

(6)

The real and imaginary parts of the previous equations are related to the stiffness and inertia, and to the damping properties of the soil, respectively. Therefore,

$$\begin{aligned} K_v^{d}(\omega )=K_v(\omega )+\iota \omega C_v(\omega ) \end{aligned}$$

(7)

where $K_v(\omega )={\mathrm {Re}}\{K_v^{d}(\omega )\}$ stands for the stiffness, and $C_v={\mathrm {Im}}\{K_v^{d}(\omega )\}/\omega$ represents the damping of the system in terms of the frequency.

Figure 5 shows the vertical compliance for the surface square foundation. The results are normalised to $a_0=\omega B/c_{s}$ and to the compliance $F_0=B c_{s}^2 \rho _s/K_v^{d}$ as in Domínguez (1993). The normalised results for the three different soils types with $c_s=\left\{ 150, 220, 365\right\} \,\text{ m/s }$ match as indicated in Domínguez (1993). The agreement with the results computed with a BE model, shown in the same figure in solid black trace, is good.

Fig. 5

a Real and b imaginary parts of the vertical compliance for surface square foundation. BE results are represented in black trace

Figure 6 presents the soil–foundation system stiffness and damping for the same soils. Moreover, the results presented in Gazetas (1991) are superimposed with circles. Gazetas (1991) provided results in the dimensionless frequency range $a_0$ from 0 to 2, i. e., 0–$19\,\text{ Hz }$, 0–$28\,\text{ Hz }$ and 0–$46\,\text{ Hz }$, respectively, for the three soils considered. In the cited research, the stiffness decreases approximately $40\%$ percent and the radiation damping remains fairly constant while the material damping decreases with the frequency in the considered range. The agreement between the proposed methodology and the results presented in Gazetas (1991) is good. At low frequencies, the FE-PML model predicts slightly higher values for the stiffness, and lower for the damping for the two stiffest soils. As the frequency increases, both properties decrease. The decrement of the material damping is higher in Gazetas (1991).

The advantage of the methodology presented herein is that it permits the representation and analysis of any type of foundation (abutments, piles, etc.) and soil stratigraphy. This study focuses on the numerical validation of the approach based on previous results. Cases dealing with more complex geometries will be presented in future works.

Fig. 6

a Stiffness $K_v$ and b damping $C_v$ of the foundation–soil system. The results presented in Gazetas (1991) are superimposed with circles

2.2 Soil–foundation–bridge interaction problem

Figure 3 shows the soil–foundation–bridge decoupled model. Beam bridges of length L, cross-section bending stiffness $EI_{z}$, mass per unit length $m_b$, and structural damping $\zeta$ are discretized using two-node Bernoulli-Euler beam elements, well suited for the analysis of railway bridges in this study given the slenderness ratios and the frequency range of interest from 0 to $30\,\text{ Hz }$ (Doménech et al. 2016). The spring/dashpot elements at the bridge–foundation connection points, with equivalent stiffness and damping values $K_v$ and $C_v$, are obtained from the FE-PML model as explained in Sect. 2.1. Therefore, the cross-interaction between the two foundations of the bridge is neglected.

The bridge FE model with N dof is solved using complex modal superposition (Hurty and Rubinstein 1965). The equilibrium equation of the system is:

$$\begin{aligned}&\varvec{M}\ddot{\varvec{u}}(t)+\varvec{C}\dot{\varvec{u}}(t)+\varvec{K}{\varvec{u}}(t)=\varvec{F}(t)\nonumber \\&\varvec{u}(0)=\varvec{u}_0\nonumber \\&\dot{\varvec{u}}(0)=\dot{\varvec{u}}_0 \end{aligned}$$

(8)

where $\varvec{M}$, $\varvec{C}$, and $\varvec{K}$ are the mass, damping and stiffness matrices, respectively. Due to the SSI effect, represented by the spring/dashpot elements at the supports, damping in the problem is non-proportional, i.e., $(\varvec{M}^{-1}\varvec{C})(\varvec{M}^{-1}\varvec{K})\ne (\varvec{M}^{-1}\varvec{K})(\varvec{M}^{-1}\varvec{C})$. In the case of non-proportional damping, the position of each dof in each mode shape is defined by the amplitude and the phase, which requires 2N equations to determine the solution of the N dof structure. Equation 8 can be rewritten as a system of 2N equations to be solved in this case as:

$$\begin{aligned} \begin{bmatrix} \varvec{C} &{} \varvec{M}\\ \varvec{M} &{} \varvec{0} \end{bmatrix}\begin{bmatrix} \dot{\varvec{u}}(t)\\ \ddot{\varvec{u}}(t) \end{bmatrix}+ \begin{bmatrix} \varvec{K} &{} \varvec{0}\\ \varvec{0} &{} -\varvec{M} \end{bmatrix}\begin{bmatrix} \varvec{u}(t)\\ \dot{\varvec{u}}(t) \end{bmatrix}=\begin{bmatrix} \varvec{F}(t)\\ \varvec{0} \end{bmatrix} \end{aligned}$$

(9)

Equation 9 is expressed as a first order matrix equation:

$$\begin{aligned} \varvec{A}\dot{\varvec{y}}(t)+\varvec{B}\varvec{y}(t)=\varvec{P}(t) \end{aligned}$$

(10)

where

$$\begin{aligned} \varvec{A}=\begin{bmatrix} \varvec{C} &{} \varvec{M}\\ \varvec{M} &{} \varvec{0} \end{bmatrix} \qquad \varvec{B}=\begin{bmatrix} \varvec{K} &{} \varvec{0}\\ \varvec{0} &{} -\varvec{M} \end{bmatrix} \qquad \varvec{P}=\begin{bmatrix} \varvec{F}(t)\\ \varvec{0} \end{bmatrix} \qquad \varvec{y}(t)=\begin{bmatrix} \varvec{u}(t)\\ \dot{\varvec{u}}(t) \end{bmatrix} \end{aligned}$$

(11)

In the previous equations, $\varvec{A}$ and $\varvec{B}$ are real symmetric matrices with dimensions 2N by 2N, and $\varvec{y}$ is the state vector.

2.2.1 Free vibration response

In the free vibration case, Eq. 10 takes the form

$$\begin{aligned} \varvec{A}\dot{\varvec{y}}(t)+\varvec{B}\varvec{y}(t)=\varvec{0} \end{aligned}$$

(12)

The non trivial solution of this linear system of equations may be expressed as

$$\begin{aligned} \varvec{y}(t)=\varvec{\Psi }_j e^{s_j t} \end{aligned}$$

(13)

where $s_j$ represents the j-th element of a set of 2N eigenvalues, and $\varvec{\Psi }_j$ are the corresponding eigenvectors:

$$\begin{aligned} \varvec{\Psi }_j=\begin{bmatrix} \varvec{\phi }_j\\ s_j\varvec{\phi }_j \end{bmatrix} \end{aligned}$$

(14)

The natural frequencies, damped natural frequencies and the modal dampings may be obtained from the eigenvalues $s_j$ as $\omega _j=|s_j|$, $\omega _{dj}=|{\mathrm {Im}}\{s_j\}|$ and $\zeta _j=-{\mathrm {Re}}\{s_j\}/|s_j |$. Therefore, in the problem analysed, ${\mathrm {Re}}\{s_j\}$ should be negative and ${\mathrm {Im}}\{s_j\}\ne 0$. Moreover, orthogonality conditions $\varvec{\Psi }_j^T\varvec{A}\varvec{\Psi }_k=0$ and $\varvec{\Psi }_j^T\varvec{B}\varvec{\Psi }_k=0$ for $j\ne k$ apply as proven in Hurty and Rubinstein (1965), where the superscript T indicates transpose.

The natural frequencies of the soil–foundation–bridge system are computed as per Eq. 12. First, the values of $K_v$ and $C_v$ obtained from Fig. 6 for the j-th natural frequency of the SS beam are selected as an initial solution. Then, an iterative problem is solved by updating the values of $K_v$ and $C_v$ for the damped natural frequencies of the bridge, upto the relative error in the n-th iteration, $(f_j^n-f_j^{n-1})/f_j^{n-1}<0.01$. The convergence of the problem is very efficient, involving generally only a few iterations.

2.2.2 Forced vibration response of non-proportional damped structures

The solution to Eq. 10 can be expressed as:

$$\begin{aligned} \varvec{y}(t)=\sum _{j^=1}^{2N}\varvec{\Psi }_j \xi _j(t) \end{aligned}$$

(15)

Applying orthogonality conditions and normalising the eigenvectors to the matrix $\varvec{A}$, i. e., $\varvec{\Psi }_j^T\varvec{A}\varvec{\Psi }_j=1$, Eq. 10 can be uncoupled in a set of 2N equations as (Hurty and Rubinstein 1965)

$$\begin{aligned} {\dot{\xi }}_j(t)+\alpha _j\xi _j(t)=p_j(t) \end{aligned}$$

(16)

where $\alpha _j=\varvec{\Psi }_j^T\varvec{B}\varvec{\Psi }_j=-s_j$ and $p_j(t)=\varvec{\Psi }_j^T\varvec{P}(t)$.

Taking into account that the eigenvalues and eigenvectors for the structures analysed are pairs of complex conjugates, the displacements in the bridge can be computed from

$$\begin{aligned} \varvec{u}(t)=\sum _{j^=1}^{N}2{\mathrm {Re}}\{\varvec{\phi }_j \xi _j(t)\} \end{aligned}$$

(17)

Equation 16 may be solved numerically. It corresponds to a non-stiff differential equation that, in what follows, is solved using a Runge–Kuta (4,5) explicit algorithm (Dormand and Prince 1980; Shampine and Reichelt 1997).

The effects of SSI on the seismic structural response are large and they should be accounted for. Carbonari et al. (2011) used lumped parameter models to approximate the frequency-dependent behaviour of the SSI in multi-span bridges and to evaluate their seismic responses. Poul and Zerva (2019) implemented the PML for modeling the unbounded domain in the seismic response evaluation of a concrete gravity dam. Chen et al. (2021) computed the frequency response of offshore monopile foundations to seismic excitation using the PML as an absorbing boundary condition. The present methodology can be extended to seismic problems applying the corresponding accelerograms ($\ddot{u}_g(t)$) in the force term of Eq. 9, by an additional term $-{\mathbf{M}}\ddot{u}_g(t)$. Then, $\varvec{u}(t)=\varvec{u}^{t}(t)-u_g(t)$, where $\varvec{u}^{t}(t)$ represents the total displacement of the structure. The proposed approach allows the computing of the displacements and the stresses in the bridge.

3 Numerical analysis

Several of the cases presented by Doménech et al. (2016) and Martínez-Rodrigo et al. (2018) are undertaken following the approach presented in Sect. 2, with the aim of performing a numerical validation and comparing the results with those obtained by applying a different numerical procedure. In the aforementioned works, the authors analyse SSI in beam bridges with the same superficial rigid plate foundations using a fully coupled 3D BE–FE model integrated in the time domain. In this case, the Green’s function for an elastic half-space is used as the fundamental solution for the soil, and material damping is approximated as a constant value. In order to compare with the results presented in Doménech et al. (2016), the same structure studied in the mentioned reference consists of a beam bridge of length $L=17.5\,\text{ m }$, mass per unit length $m=17{,}500\,\text{ kg/m }$, and fundamental frequency equal to $35\%$ of the simplified method frequency band in Eurocode 1, is analysed under the circulation of the HSLM trains from these standards. A structural Rayleigh damping of $1.18\%$ is assigned according to the design recommendations of Eurocode 1 for prestressed concrete bridges. The three soil types presented in Sect. 2.1 are studied. $5.00\,\%$ soil material damping is used in all cases.

A modal analysis of the bridge is performed as per Eq. 12. Non-oscillatory modes with real eigenvalues are excluded from the analysis. The first vertical bending frequency of the bridge in the simply supported (SS) case is $f_1^{SS}=6.87\,\text{ Hz }$. When the interaction with the soil is taken into account, the fundamental frequencies resulting from the proposed approach for the three soil types are: $f_{1}^{150}=6.13\,\text{ Hz }$, $f_{1}^{220}=6.43\,\text{ Hz }$, and $f_{1}^{365}= 6.69\,\text{ Hz }$, where the superindices indicate the soil shear wave velocity. Moreover, the modal damping ratios, which include the effect of both material and radiation damping, in addition to structural damping, computed from the complex eigenvalue problem are: $\zeta _{1}^{150}=9.44\%$, $\zeta _{1}^{220}=3.94\%$, $\zeta _{1}^{365}=1.97\%$. The increment in the modal damping corresponding to the softer soil numerically identified in Martínez-Rodrigo et al. (2018) from BE–FE analyses is reproduced with the present approach, although the soil damping decreases with the shear-wave velocity according to Fig. 6. The second vertical bending frequency of the bridge is modified from $f_2^{SS}=27.48\,\text{ Hz }$, to $f_{2}^{150}=27.43\,\text{ Hz }$, $f_{2}^{220}=26.59\,\text{ Hz }$, and $f_{2}^{365}= 26.24\,\text{ Hz }$, while the modal damping ratios corresponding to the second vertical bending mode shape are: $\zeta _{2}^{150}=20.18\%$, $\zeta _{2}^{220}=14.64\%$, $\zeta _{2}^{365}=7.14\%$. This mode is highly damped, mainly for the softer soil. The soil–foundation system stiffness and damping obtained from the iterative process are shown in Fig. 7 for these particular cases.

Fig. 7

a Stiffness $K_v$ and b damping $C_v$ of the foundation–soil system for the $17.5\,\text{ m }$ beam type bridge first (circle) and second (asterisk) vertical bending frequencies and different soil properties

It should be also remarked that the second bending natural frequency for the system, accounting for these damping and stiffness values, decreases as the shear wave velocity increases. It can be explained by the parametric analysis shown in Fig. 8. The frequencies corresponding to modes 1 and 2 for the stiffness values shown in Fig. 7a and different $C_v/K_v$ ratios are plotted in solid trace. The frequency values obtained for the $C_v$ values obtained from the iterative procedure and presented in Fig. 7b are superimposed with circles.

Fig. 8

Frequencies corresponding to a mode 1 and b mode 2 for the stiffness values shown in Fig. 7a and different $C_v/K_v$ ratio. The frequencies computed for the numerical case considered are superimposed with circles

Figure 9 shows the mode shapes of the soil–bridge systems corresponding to the first and second natural frequencies. The real and imaginary parts are plotted, and in the complex mode shapes, each degree of freedom has a different phase angle.

Fig. 9

a, c Real and b, d imaginary part of the a, b first, and c, d second bending mode shapes for different soil properties

Figure 10 shows the free vibration response of the beam at mid-span after the passage of a single load in terms of the non-dimensional speed $K_1^{SS}=v/(2f_1^{SS}L)$ for different soil properties. These free vibration envelopes permit the identification of velocities leading to either local maxima or cancellation conditions (minima of free vibrations). The amplification of the response to be expected at resonance, depends on the amplitude of these free vibrations, which will add in phase in the resonant case.

Figure 11 presents the maximum bridge acceleration at mid-span under the loading of HSLM-A1 and HSLM-A6 trains (Eurocode 1 2002). The characteristic distances of these trains are $d =18\,\text{ m }$ and $d=23\,\text{ m }$, respectively. HSLM-A1 and HSLM-A6 theoretically induce a second resonance of the fundamental mode of the bridge at $v_{1,2}=f_1^{SS}\times d/2=6.87\times 18/2\times 3.6= 222.59\,\text{ km/h }$, and $v_{1,2}=f_1^{SS}\times d/2=6.87\times 23/2\times 3.6= 284.42\,\text{ km/h }$, respectively (non-dimensional speed 0.26 and 0.33). The dashed horizontal line indicates the SLS of the vertical acceleration for ballasted track bridges ($0.35g=3.43\,\text{ m/s}^2$).

In Fig. 11a, b the response of the bridge under the two aforementioned trains computed following the present approach is compared with the results from Doménech et al. (2016). The HSLM-A1 train induces a second resonance on the bridge at approximately $222\,\text{ km/h }$, close to the theoretical resonant velocity. The resonant velocity decreases with the soil stiffness, as a consequence of the reduction in the bridge fundamental frequency. In the case of the HSLM-A6 train, resonance does not take place because the span length and characteristic distance $L/d=0.76$, is close to a cancellation condition. This phenomenon of cancellation of resonance occurs even in the case of the soil with $c_s=150\,\text{ m/s }$. From the figures it can be seen that when SSI is considered, the natural frequencies of the bridge computed following the present approach are very close to the results from the BE–FE model in Doménech et al. (2016). Nevertheless, the overall damping exhibited by the bridge–foundation–soil system is higher, especially for soils with very low values of $c_s$.

Fig. 10

Maximum free vibration displacement at mid-span as a function of non-dimensional speed for different soil properties: single moving load, $L=17.5\,\text{ m }$, $f_{1,035}$, $m=17{,}500\,\text{ kg/m }$, and $\zeta =1.18\%$

Fig. 11

Maximum acceleration at mid-span as a function of the speed parameter v/d for different soil properties: $L=17.5\,\text{ m }$, $f_{1,035}$, $m=17{,}500\,\text{ kg/m }$, $\zeta =1.18\%$, and a HSLM-A1 and b HSLM-A6 trains. The vertical dashed line indicates the theoretical resonant speed for the SS case. The dashed horizontal line indicates the SLS. The results presented in Doménech et al. (2016) are plotted in dotted traces

4 Case study

In this section the dynamic response of Old Guadiana bridge (Fig. 12), from Madrid-Alcázar de San Juan-Jaén conventional railway line in Spain, is reproduced and compared with experimental measurements. It is a SS bridge with two identical spans of approximately $12\,\text{ m }$ of length. The deck is composed of two single track independent decks of $5.075\,\text{ m }$ width. Each deck consists of a $25\,\text{ cm }$ thickness concrete slab resting on five pre-stressed concrete beams with a $75\,\text{ cm }$ height rectangular cross-section (Fig. 13a). This bridge was monitored by the authors in 2019.

A portable acquisition system LAN-XI of Brüel & Kjaer was used. The acquisition system fed the sensors (accelerometers) and an instrumented impact hammer in the case of the soil tests. LAN-XI also performed the Analog/Digital conversion (A/D). The A/D was carried out at a high sampling frequency, $f_s=4096\,\text{ Hz }$, that avoided aliasing effects. The acquisition equipment was connected to a laptop for data storage. Endevco model 86 piezoelectric accelerometers were used with a nominal sensitivity of $10\,\text{ V/g }$ and a lower frequency limit of approximately $0.1\,\text{ Hz }$. Structural response recordings were decimated (order 16) to carry out data analysis in the frequency range of interest. Structural responses were filtered applying two third-order Chebyshev filters with high-pass and low-pass frequencies of $1\,\text{ Hz }$ and $30\,\text{ Hz }$, respectively. The modal parameters of the bridges were identified from ambient vibration data by the stochastic subspace identification technique (Reynders 2012). The dynamic characterisation of the soil was carried out by the seismic refraction and the Spectral Analysis of Surface Waves (SASW) tests. More details of the experimental campaign, the identified properties of the bridge and surrounding soil and the dynamic response under several train passages may be consulted in Galvín et al. (2021).

Fig. 12

a Old Guadiana bridge and b soil test set-up

Fig. 13

Railway bridge cross section

The site has two upper soil layers with a shear wave velocity close to $300\,\text{ m/s }$ resting on a halfspace with $c_s=250\,\text{ m/s }$ (Fig. 13b and Table 1). According to Eurocode 8 (1998), the soil profile is approximated as a homogeneous stratum with average shear wave velocity $V_{s30}=303\,\text{ m/s }$. Likewise, a material damping ratio of $7.85\%$ is admitted. Following, the results obtained from the actual stratigraphy and the equivalent homogeneous soil are compared.

Table 1 Identified soil properties at Old Guadiana Bridge

A first vertical bending mode (see Fig. 14) with a natural frequency of $9.8\,\text{ Hz }$ is identified from ambient vibrations. The modal damping corresponding to this mode obtained under traffic conditions reaches $2.8\%$, which is higher than the value prescribed by standards for design purposes for this particular length and bridge typology (1.5% as per Eurocode 1 2002). A beam model of the bridge is considered in order to show the application of the previously proposed approach. $5\,\text{ m }\times 5\,\text{ m }$ rigid massless foundations are included. The value for the fundamental frequency of the beam model in the SS case is $10.06\,\text{ Hz }$. This frequency reduces to $9.8\,\text{ Hz }$ due to SSI effects. Figure 15 shows the corresponding numerical mode shape which is the only bending mode of the beam bridge below $30\,\text{ Hz }$. The MAC value (Allemang and Brown 1982) between the experimental mode shape corresponding to the longitudinal middle section and the numerical mode shape is 0.99. As part of the initial approach, only the contribution of this mode is taken into account as it dominates the vertical response at mid-span along the centre line. Nevertheless the first torsion and transverse bending modes with frequencies $11.0\,\text{ Hz }$ and $12.8\,\text{ Hz }$ were also identified.

Fig. 14

Experimentally identified first mode shape in Old Guadiana Bridge at $9.8\,\text{ Hz }$

Fig. 15

a Real and b imaginary parts of the first bending mode at $9.8\,\text{ Hz }$ with modal damping $2.8\%$

The response of the bridge is presented under the circulation of the Renfe Altaria train with 9 coaches crossing the bridge at $v=160\,\text{ km/h }$. Table 2 summarizes the train coach distribution and axle distances. Figure 16 shows the bridge acceleration response at the mid-span section, measured under the track and its comparison with the numerical predictions obtained with the proposed methodology. The agreement between numerical and experimental results is good given the simplicity of the beam model used for the deck. The response contains peaks associated with the excitation (i.e. ratio of train speed v to the characteristic distance $v/d=3.38\,\text{ Hz }$), corresponding harmonics and with the bridge lowest natural frequency. The experimental response shows certain participation of modes between 10 and $20\,\text{ Hz }$ that cannot be reproduced with the beam model. The train speed is close to a third resonance of the fundamental mode of the bridge: $v_{1,3}=f_1\times d/3=9.8\times 13.14/3\times 3.6= 154\,\text{ km/h }$. This justifies the dominant contribution of this mode in the frequency domain. The numerical prediction overestimates the response at the resonant frequency, which is expected because dissipation mechanisms such as vehicle-structure and track-structure interaction are not included, and are particularly relevant under these conditions. In this case, the actual stratigraphy is well represented by the equivalent homogeneous soil. The comparison between both results presents very small differences in the frequency range analysed.

The time used by a laptop computer with $1.9\,\text{ GHz }$ processor and $16\,\text{ GB }$ of RAM in order to solve the complete problem is $26.69\,\text{ s }$: the homogeneous soil–foundation problem required $24.02\,\text{ s }$ (two frequencies were computed in this case), the eigenvalue problem required $0.92\,\text{ s }$, and the modal superposition required $1.75\,\text{ s }$, for one train speed. A speed sweep from $[150{:}1{:}400]\,\text{ km/h }$ was solved in $439.2\,\text{ s }$ for this particular train and soil–foundation–bridge system. This is considerably lower than the time required if the same problem is solved using BE–FE methods in the time domain.

Table 2 Renfe Altaria train with 9 coaches

Fig. 16

Old Guadiana Bridge: a time history and b frequency content of the acceleration at the midspan induced by Renfe Altaria train with 9 coaches at $v=160\,\text{ km/h }$ circulating on track 2: (black line) experimental and numerical results. The results obtained using the actual stratigraphy are plotted in blue trace, and those obtained from the equivalent homogeneous soil are represented in red. For interpretation of the references to colour in this figure, the reader is referred to the web version of this article

5 Conclusions

A fast numerical methodology to determine the dynamic response of railway bridges under the passage of running trains including the effect of soil–structure interaction is proposed. The coupled problem is sub-structured into a soil–foundation and a soil–foundation–bridge interaction problems. In the first step, the foundation and surrounding soil are simulated via a FE-PML model. Using this approach, equivalent frequency dependent dynamic stiffness and damping characteristics of the soil–foundation system are computed. In the second step, the dynamic response of the structure under railway traffic is calculated using a FE model that includes spring/dashpot elements at the supports, using the equivalent properties extracted from the first problem. This model is solved by complex modal superposition considering the equivalent dynamic stiffness and damping of the soil–foundation corresponding to each natural frequency. The complex modal parameters are obtained iteratively and the dynamic complex modal equations are solved using a Runge–Kutta explicit algorithm. The benefits of the proposed approach increase dramatically with the problem complexity since it allows exploiting dedicated analysis tools for addressing the soil–foundation and the superstructure domain.

From the analyses performed the following is concluded:

• The proposed approach can be used to obtain the dynamic response of railway bridges under running trains considering SSI, with minimal computational effort. However, it is remarked that soil–foundation impedances should be previously calculated.

• The results obtained in terms of the bridge deck vertical displacements and accelerations are similar to those given by BE–FE analyses.

• Resonance and cancellation phenomena, which are often responsible for the maximum bridge acceleration, are accurately reproduced.

• In this particular study, the structural model is simplified to a beam bridge and superficial infinitely rigid plate foundations, because the main objective of the work is to present the method and to compare with previous results. However, the consideration of more complex geometries for the bridge and the foundations, and the simulation of stratified soils is also straightforward to implement. In particular, the effect of the foundation mass should be further analysed.

• Using the proposed approach it is possible to solve the dynamic problem taking into account high modal contributions of the structure, with minimal computational cost.

• The results are compared with those given by a fully coupled 3D BE–FE model solved in the time domain, where the Green’s function for an elastic half-space is used as the fundamental solution for the soil, and material damping is assumed to be constant. In this case similar resonant speeds are determined, and close to the resonant frequency, a more highly damped response is obtained using the present method, particularly for soils with very low shear wave velocities.

• Using the proposed model the experimental response of a real beam-type bridge under train loading is reproduced, capturing the frequency contributions of the first structural bending mode and the loading frequency contributions.