In-plane and out-of-plane seismic damage of masonry infills in existing r.c. structures: the case study of De Gasperi-Battaglia school in Norcia

Abstract

A significant correlation between the in-plane (IP) and out-of-plane (OOP) damage propagation of masonry infills (MIs) is frequently observed after strong earthquakes, posing a serious problem as regards vulnerability of public buildings such as schools. The present work is aimed at identifying the effects of different IP and OOP modelling assumptions of MIs on their seismic damage. To this end, the state secondary school De Gasperi-Battaglia in Norcia (Italy), object of monitoring by the Department of Civil Protection since 2000, is investigated for the heterogeneity of infill typologies. The school is composed of a basement and three storeys above ground level, with a reinforced concrete (r.c.) framed structure having a long-shaped rectangular plan. Two typologies can be identified in terms of transverse layout of MIs: (i) double-leaf interior partitions, made of hollow clay bricks; (ii) double-leaf exterior infill walls, constituted by facade solid bricks paired with hollow clay bricks. In addition, partial height infills in the longitudinal direction, due to classroom windows, make the columns susceptible to short column effects. MIs are represented by a five-element macro-model predicting both in-plane (IP) and out-of-plane (OOP) behaviour through a horizontal nonlinear truss and four diagonal nonlinear beam elements, respectively. Stiffness and strength values in the OOP direction are also reduced considering the evolution of the IP damage. Three assumptions are investigated for the behaviour of structural MIs: i.e. elastic both IP and OOP; inelastic IP and elastic OOP; inelastic both IP and OOP. Bare and infilled test structures are subjected to biaxial spectrum-compatible accelerograms, to evaluate the IP and OOP damage levels and effectiveness of the OOP simplified verification proposed by seismic codes.

1 Introduction

Simplified methods are generally used for the out-of-plane verification of masonry infills (MIs) placed at different floor levels of a building, specifying equivalent static design forces on the basis of floor response spectra of acceleration (e.g. NTC18 in Italy, Eurocode 8 in Europe and FEMA 356 in USA). However, recent ground motions (e.g. L’Aquila 2009) have highlighted that seismic codes may lead to erroneous safety estimations. Unreinforced MIs can be typically found in reinforced concrete (r.c.) framed buildings, but they are commonly neglected in design practice. As a result, many existing r.c. buildings suffered severe damage to their structural parts also reaching an early collapse condition due to a soft-storey mechanism. These effects are typically studied through in-plane (IP) elastic and inelastic models of MIs (Braga et al. 2011). The increase of lateral stiffness, reduction of structural vibration periods, soft-storey and torsional effects have a global impact on the structure. On the other hand, the detrimental interaction with beam-column joints and short-column effects triggered by partial height of infill walls can be classified as local problems. In-plan and in-elevation irregular distributions of MIs are responsible for the global effects described above, which are also related to the number of storeys and the period of construction (Dolce and Goretti 2015). On the other hand, the OOP collapse of MIs happens when the connection with the frame or between the leaves is partial or absent. The OOP collapse represents a source of risk, in terms of economic loss and protection of human life, so it should be properly addressed in the assessment of the seismic vulnerability of school buildings (e.g. Di Domenico et al. 2019; Mazza and Donnici 2019).

The typical cracking pattern of MIs is a combination between the effects of both IP and OOP mechanisms. The IP failure generally happens at the lower storeys, where high values of the IP drift ratio are expected, while OOP collapse of MIs occurs at the upper storeys because of the amplification of seismic acceleration. However, the IP-OOP interaction can result in severe OOP damage even at the lower storeys where the IP drift ratio is prevailing (Hak et al. 2012). The first simplified but still widely used macro-model of MIs is represented by a strut element, able to reproduce the global IP effects on the structure. Its low computational demand allowed the development of many multi-strut models, in order to reproduce local interaction effects between the infill and r.c. frame members (Noh et al. 2017).

The OOP response of MIs has been investigated only in recent years giving rise to the development of two main categories of macro-models (Asteris et al. 2017; Pasca et al. 2017): i.e. models with fibre-section and beam/truss elements. Besides the first model considering IP and OOP nonlinear behaviour (Hashemi and Mosalam 2007), with eight compression-only nonlinear struts connected with a tension-only elastic-linear tie, the following proposals belong to the first category: (i) the model of Kadysiewski and Mosalam (2009), subsequently updated in 2015 (Mosalam and Gunay) and 2017 (Donà et al.), where two beam-column elements are placed along a single diagonal and joined at the midpoint node where a lumped mass in the OOP direction is assumed; (ii) the four-strut model of Oliaee and Magenes (2016), with two left diagonal halves controlling the IP response and other two right diagonal halves delivering OOP inelasticity; (iii) the four-strut model of Di Trapani et al. (2018), with two diagonal struts to describe the IP behaviour and horizontal and vertical beam-column elements contributing to the OOP response, and its recent evolution (Pradan and Cavaleri 2020). These macro-models are effective for describing the nonlinear response of MIs but considered more expensive for analysis of multi-storey structures when compared to macro-models based on beam/truss elements only. The five-element model proposed by Furtado et al. (2016a) falls into this second category, with four diagonal OOP elastic beams linked to a central (horizontal) strut  with non-linear IP behaviour. The OOP nonlinear behaviour of MIs and its interaction with the IP response are accounted for by using the model of Ricci et al. (2017, 2018), in which V-shaped bi-diagonal rigid struts are linked in the central node with two set of zero-length link elements. In the present work an improved version of the Furtado model is assumed (Mazza 2019a; Mazza and Donnici 2019), which includes nonlinear behaviour of MIs in the OOP direction and takes into account the reduction in OOP capacity produced by simultaneous or prior IP seismic damage. However, this modelling approach, having struts directly connected to the centroid of beam-columns joints, does not represent accurately the internal actions distribution deriving from the infill-frame interaction (Di Trapani et al. 2015; Basha and Kaushik 2018; Gentile et al. 2019), so requiring that shear strength of r.c. columns is checked a posteriori considering maximum loads transmitted by MIs.

The present study is focused on the assessment of seismic damage in r.c. framed structures due to the presence of MIs: i.e. damage scenarios of non-structural infill elements, taking into account different modelling approaches for their IP and OOP behaviour; effectiveness of the OOP verifications of MIs provided by the Italian (NTC18), European (EC8) and American (FEMA356) seismic codes; a posteriori estimation of the effects of MIs on r.c. structural elements, on the basis of shear failure mechanisms. The attention is drawn to school buildings, where MIs can reduce human safety and increase economic losses. The secondary school De Gasperi-Battaglia in Norcia (Italy), composed of a four storeys, is assumed as test structure for the nonlinear dynamic analyses. This decision was based on the satisfactory level of knowledge of its geometrical and mechanical properties, collected by the Department of Civil Protection, and availability of different typologies of masonry infills, as well as the possibilities of future studies on effectiveness of the buckling-restrained braces retrofitting system, dating back to 2010, as indirect protection strategy of MIs. Specifically, two infill typologies can be identified in terms of transverse layout: (i) double-leaf interior partitions, with a thickness of (8 + 8) cm, made of hollow clay bricks; (ii) double-leaf exterior infill walls, constituted by 12 cm facade solid bricks paired with 8 cm hollow clay ones. In addition, partial height infills in the longitudinal direction, due to classroom windows, make the columns along the perimeter prone to short column effects. Three-dimensional models of bare and infilled structures are subjected to real accelerograms, scaled at the life-safety limit state in compliance with the current Italian building code (NTC, 2018). MIs are represented by a five-element macro-model that is able to predict both in-plane (IP) and out-of-plane (OOP) behaviour through a horizontal nonlinear truss and four diagonal nonlinear beam elements. Three hypotheses are considered for the behaviour of MIs: i.e. elastic both IP and OOP; inelastic IP and elastic OOP; inelastic both IP and OOP.

2 Layout and simulated design of the De Gasperi-Battaglia school

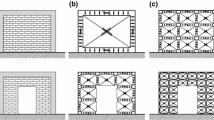
The secondary school De Gasperi-Battaglia of Norcia is assumed as test structure (Fig. 1a), in order to describe the nonlinear seismic behaviour of different typologies of masonry infills and their interaction with the framed part. This four-storey r.c. building can be considered as representative of typical school buildings built in the 1960s, with regard to the design philosophy of the frame and the layout of MIs (Iacovino et al. 2019; Nuzzo et al. 2019). Seventeen bays with constant length of 3.5 m are placed along the longitudinal direction, while two bays with a length of  5.55 m and 6.65 m are considered in the transversal direction where the central block (i.e. block #2) has a third bay of 2.15 m. The inter-storey height is equal to 3.5 m in the basement while a constant value of 3.3 m is assumed for the upper floors. Since the Umbria-Marche earthquake of 1997, the school has been monitored and deeply analysed through geometrical surveys and materials testing. The building is composed of three parts (Fig. 1b), initially separated by Gerber saddles at the interfaces that were totally closed in 2005. The structure was statically and seismically improved following the approval of two projects, dating back to 2003 and 2010. The retrofitting consisted of steel braces placed at the basement level and buckling-restrained braces on the upper storeys. The 2016 Central Italy earthquake caused severe damage to structural and especially non-structural parts, some of which fell over and made inoperative one of the two lateral fire-escape steel staircases.

Fig. 1

Picture of De Gasperi-Battaglia school (Norcia, Italy)

All data necessary for structural modelling are collected from the surveys of the Department of Civil Protection, complemented by a simulated design. The r.c. framed structure is composed by five typologies of beams (B_i, i = 1–5) and three of columns (C_i, i = 1–5), which differ in terms of geometry and/or reinforcement ratio (Fig. 2). Dimensions of the cross-sections are reported in Table 1. Destructive and non-destructive tests led to a cylindrical compressive strength f_ck = 25.2 MPa and an elastic secant modulus E_c = 22,000 MPa, while the longitudinal steel reinforcement showed a yield strength f_yk = 375 MPa. The level of knowledge of the structure is assumed to be LC2 (NTC, 2018), given the number and spatial distribution of the tests. A simulated design supports available data of the structure where shortcomings are identified (e.g. lack of information about the longitudinal steel reinforcement of some structural members). The simulated design is carried out in accordance with the Royal Decree Law n. 2229 (RDL, 1939), with the assumptions of medium class of seismic intensity (C = 0.05) and medium typology of subsoil ($\varepsilon$ = 1.0). The seismic load combination is evaluated considering dead and live floor loads equal to 5.20 kN/m² and 3.00 kN/m², respectively, except for the fourth level, where the dead load also includes the weight of the roof (8.48 kN/m²) and a live load of 1.00 kN/m² is considered.

Fig. 2

In-plan distribution of beams (B_i, i = 1–5) and columns (C_i, i = 1–3)

Table 1 Cross-section dimensions of beams and columns (unit in cm)

Only relevant MIs are taken into account, being able to be classified into four typologies (Fig. 1b): i.e. partial height infills MI.1, along the X-direction; full height MI.2a (external), MI.2b (internal) and MI.3 (stair enclosure), along the Y-direction. MI.2a and MI2b panels have the same aspect ratio, but consist of different leaves. Specifically, two leaves of hollow clay bricks, with thickness t_w,ext = t_w,int = 8 cm, characterize MI.2b infills, while the exterior leaf is made with solid bricks (t_w,ext = 12 cm) as regards MI.1, MI.2a and MI.3 typologies. Note that only MIs represented in full colour (see Fig. 1b) can be found at all levels.

Strength and stiffness of MIs are calculated starting from two formulations of the equivalent diagonal strut having width b_w, with the aim of representing the highest and lowest contribution of MIs to the structural response as well as collecting results about two limit non-structural damage conditions. The lower bound value of b_w can be described by the expression proposed by Mainstone (1974):

$$\frac{{b_{w,M} }}{{d_{w} }} = 0.175 \cdot \left( {\lambda \cdot h} \right)^{0.4} ,\,\lambda = \sqrt[4]{{\frac{{E_{w\theta } \cdot t_{w} \cdot \sin \left( {2\theta } \right)}}{{4E_{c} \cdot I_{c} \cdot h_{w} }}}}$$

(1)

where d_w and h are the diagonal length of the panel and the distance between the centrelines of the enclosing beams, respectively. The relative stiffness parameter $\lambda$ depends on: the mean moment of inertia of the columns (I_c); the diagonal Young’s moduli of masonry (E_wθ) and concrete (E_c); the height of the infill h_w; the inclination θ of the strut with respect to the horizontal direction. The upper bound value of b_w is evaluated through the formulation presented by Papia et al. (2003):

$$\frac{{b_{w,P} }}{{d_{w} }} = \frac{c}{z} \cdot \frac{1}{{\left( {\lambda^{*} } \right)^{\beta } }},\,\lambda^{*} = \frac{{E_{w\theta } \cdot t_{w} \cdot h}}{{E_{c} \cdot A_{c} }} \cdot \left( {\frac{{h^{2} }}{{l^{2} }} + \frac{1}{4} \cdot \frac{{A_{c} }}{{A_{b} }} \cdot \frac{l}{h}} \right),\,z=1+0.25 \cdot (\frac{{l_{w} }}{{h_{w} }}-1)$$

(2)

$\lambda$* being a parameter that depends on some parameters of the infilled frame, such as the mean cross-section area of beams (A_b) and columns (A_c) and the length (l) between the centrelines of the columns. The coefficients c and $\beta$ are interpolated with respect to the diagonal Poisson’s ratio $\nu$_d of the MI:

$$c = 0.249 - 0.0116 \cdot \nu_{d} + 0.567 \cdot \nu_{d}^{2}$$

(3)

$$\beta = 0.146 + 0.0073 \cdot \nu_{d} + 0.126 \cdot \nu_{d}^{2}$$

(4)

Geometry of MIs and width of the equivalent struts for the four infill typologies are summarized in Table 2. The aspect ratio of each typology is calculated referring to the panel length l_w and height h_w.

Table 2 Geometric properties of masonry infills and equivalent diagonal struts (unit in cm)

The interior leaf consists of an 8.0 cm thick leaf with horizontally hollowed bricks (unit weight of 11 kN/m³), while the exterior one is made with a 12 cm thick leaf of solid bricks (unit weight of 18 kN/m³). There is no transversal connection between the leaves, which are divided by an intermediate cavity ranging from 5 to 13 cm in thickness.

Literature values of mechanical properties considered for MIs of the De Gasperi-Battaglia school are summarized in Table 3, where: f_wh and f_wv are the compression strengths in the horizontal and vertical directions; f_wu is the sliding shear resistance of the mortar joints; f_ws is the shear resistance under diagonal compression; E_wh and E_wv are the secant moduli of elasticity in the horizontal and vertical directions; G is the shear modulus. Specifically, mechanical properties of the hollow clay bricks are those suggested in (Hak et al. 2012) for weak infill typology, while mean values among those proposed by NTC18 are assumed for solid clay bricks.

Table 3 Mechanical properties for masonry infills of De Gasperi-Battaglia school (unit in MPa, apart from $\nu$)

The influence of the MIs on the first two modal shapes and their respective participating mass ratio, along the X and Y horizontal directions, is shown in Table 4.

Table 4 Dynamic properties of De Gasperi-Battaglia school (m_tot = 36,687 kN)

Results for bare structure (BS) are also reported as a comparison, pointing out the reduction of the vibration periods in both directions when MIs are considered. Two infilled models are considered, in accordance with the Mainstone (IS.M) and Papia (IS.P) formulations. It is worth noting that the percentage of the total mass m_tot participating along the Y-direction is reduced when the IS.P formulation is adopted, because the first torsional mode becomes progressively more relevant.

Two pictures collected in the immediate aftermath of the 2016 Central Italy earthquake are reported in Fig. 3, as remarkable examples of the OOP damage of external MI.2a infill panels at the second level (Fig. 3a) and IP damage of internal partitions walls with a 8.0 cm thickness (Fig. 3b), while MI.1 and MI.3 typologies did not exhibit significant IP and OOP damage. It should be noted that internal single leaf partitions with openings are neglected in the present work.

Fig. 3

Damage of masonry infills of De Gasperi-Battaglia school after the 2016 Central Italy earthquake

3 Layout and nonlinear modelling of masonry infills

Each masonry panel is modelled through a five-element macro-model (Mazza 2019a) that is able to represent both the in-plane (IP) and out-of-plane (OOP) nonlinear responses as well as the IP-OOP interaction (Fig. 4). The model is constituted by a horizontal truss element, flexurally rigid, representing the IP behaviour (Fig. 4a) and four diagonal beam elements, axially rigid and with inclination θ with respect to the horizontal direction, describing the OOP response (Fig. 4b). As regards the interaction with the surrounding frame, on every corner a spherical hinge allows the transmission of axial forces only.

Fig. 4

Nonlinear modelling of a masonry infill panel

Moreover, two cylindrical hinges are placed between the horizontal and diagonal elements restraining the OOP rotations, so that OOP flexural behaviour of the diagonal elements is obtained, but enabling the in-plane rotations, consistently with the IP axial behaviour of the horizontal element. The IP mass ($\mu$^(IP)) is uniformly distributed on the beam supporting the infill panel, while OOP masses equal to 0.5 m^(OOP) = 0.405m_MI,tot, where m_MI,tot is the total mass of the panel, are lumped in two central nodes. These equivalent masses correspond to the same natural frequency of the infill wall assumed as a simply supported vertical beam (Mosalam and Gunay 2015).

The IP cyclic response corresponds to the lateral force-storey drift (F^(IP)-$\Delta$^(IP)) tri-linear backbone curve (Fig. 5a) proposed by Cavaleri and Di Trapani (2014). This formulation is preferred because the authors also provide the calibrated parameters to apply the pivot hysteretic model, although other recent backbone models are available in literature on the basis of a large number of experimental data (Liberatore et al. 2018; De Risi et al. 2018). The first branch represents the elastic behaviour of the infill

$$F_{wC}^{(IP)} = 0.4 \cdot F_{w}^{(IP)} ,\Delta_{wC}^{(IP)} = F_{wC}^{(IP)} /k_{w1}^{(IP)} ,k_{w1}^{(IP)} = E_{w\theta } \cdot b_{w} \cdot t_{w} \cdot \cos^{2} \theta /d_{w}$$

(5)

where anisotropy of the brick infills is reflected in the diagonal elastic modulus (Cavaleri et al., 2014)

$$E_{w\theta } = \left[ {\frac{{\cos^{4} \theta }}{{E_{wh} }} + \frac{{\sin^{4} \theta }}{{E_{wv} }} + \cos^{2} \theta \cdot\sin^{2} \theta \cdot \left( {\frac{1}{G} - \frac{2\nu }{{E_{wv } }}} \right)} \right]^{{{ - }1}}$$

(6)

Fig. 5

Monotonic and hysteretic (pivot) curves of a masonry infill panel

The post-cracking branch shows a significant reduction of stiffness and reaches the maximum IP strength

$$F_{wFC}^{(IP)} = F_{w}^{(IP)} ,\Delta^{(IP)}_{wFC} = \Delta_{wC}^{(IP)} + \left( {F_{wFC}^{(IP)} } \right)/k_{w2}^{(IP)} ,k_{w2}^{(IP)} = 0.15 \cdot k_{w1}^{(IP)}$$

(7)

The assigned post-peak softening stiffness leads to a conventional collapse point, defined by the residual strength ratio

$$F_{wRS}^{(IP)} = 0.7 \cdot F_{wFC}^{(IP)} ,\Delta_{wRS}^{(IP)} = \frac{1}{0.02}\ln \left( {\frac{{F_{wFC}^{(IP)} }}{{F_{wRS}^{(IP)} }} \cdot e^{{0.02 \cdot \Delta_{wFC}^{(IP)} }} } \right),k_{w3} (IP) = \frac{{F_{wRS}^{(IP)} { - }F_{wFC}^{(IP)} }}{{\Delta_{wRS}^{(IP)} { - }\Delta_{wFC}^{(IP)} }}$$

(8)

The transversal force-OOP drift (F^(OOP)-$\Delta$^(OOP)) backbone curve is simplified in two branches (Fig. 5b). The secant-to-peak stiffness proposed by Kadysiewski and Mosalam (2009) is used to represent the infill arching action that takes place until the maximum OOP strength is reached:

$$F_{{wFAA}}^{{(OOP)}} = q_{u} \cdot l_{w} \cdot h_{w} ,\quad \Delta _{{wFAA}}^{{(OOP)}} = {{F_{{wFAA}}^{{(OOP)}} } \mathord{\left/ {\vphantom {{F_{{wFAA}}^{{(OOP)}} } {k_{{w1}}^{{(OOP)}} }}} \right. \kern-\nulldelimiterspace} {k_{{w1}}^{{(OOP)}} }},\quad k_{{w1}}^{{(OOP)}} = {{48 \cdot E_{{eq}} \cdot I_{{eq}} } \mathord{\left/ {\vphantom {{48 \cdot E_{{eq}} \cdot I_{{eq}} } {d_{w}^{3} }}} \right. \kern-\nulldelimiterspace} {d_{w}^{3} }}$$

(9)

where q_u represents the OOP maximum capacity, in terms of pressure acting on the panel, while E_eq and I_eq are the equivalent elasticity modulus and moment of inertia assigned to the model:

$$E_{eq} = \frac{{k_{p} \cdot d_{w}^{3} }}{{48 \cdot I_{eq} }}; \, I_{eq} = 1.644 \cdot I \cdot \left( {\frac{{d_{w} }}{{h_{w} }}} \right)^{3} , \, I = \frac{{l_{w} \cdot t_{w}^{3} }}{12}$$

(10)

with k_p obtained by imposing the equivalence of the stiffness between simply supported bi-diagonal beams and cracked plate (Mazza 2019a). The value of q_u [kPa] is calculated through the empirical relations proposed by Dawe and Seah (1989), assuming that the panel is supported on four sides:

$$q_{u} = 4.5 \cdot \left( {f_{wv} } \right)^{0.75} \cdot t_{w}^{2} \cdot \left[ {\frac{\alpha }{{\left( {l_{w} } \right)^{2.5} }} + \frac{\beta }{{\left( {h_{w} } \right)^{2.5} }}} \right]$$

(11)

where the infill height (h_w) and width (l_w) are expressed in mm. Moreover, the parameters $\alpha$ and $\beta$ take into account the restraining effect due to columns and beams, respectively, through the following expressions

$${\upalpha } = \frac{{1}}{{{\text{h}}_{{\text{w}}} }} \cdot \left( {{\text{E}}_{{\text{c}}} \cdot {\text{I}}_{{{\text{col}}}} \cdot {\text{h}}_{{\text{w}}}^{{2}} + {\text{G}}_{{\text{c}}} \cdot {\text{J}}_{{\text{t,col}}} \cdot {\text{t}}_{{\text{w}}} \cdot {\text{h}}_{{\text{w}}} } \right)^{0.25} \le 50$$

(12)

$${\upbeta } = \frac{{1}}{{{\text{l}}_{{\text{w}}} }} \cdot \left( {{\text{E}}_{{\text{c}}} \cdot {\text{I}}_{{{\text{beam}}}} \cdot {\text{l}}_{{\text{w}}}^{{2}} + {\text{G}}_{{\text{c}}} \cdot {\text{J}}_{{\text{t,beam}}} \cdot {\text{t}}_{{\text{w}}} \cdot {\text{l}}_{{\text{w}}} } \right)^{0.25} \le 50$$

(13)

being: E_c and G_c the Young and shear moduli of concrete expressed in MPa; I_col(I_beam) and J_t,col(J_t,beam) the moment of inertia and torsional constant of the column (beam), expressed in mm⁴. Note that this formulation accounts for two-way arching action occurring for infills bounded along four edges, so resulting suitable on the assumption that MI.2a, MI.2b and MI.3 typologies of De Gasperi-Battaglia school are not detached from the confining frame along the upper edge, while a simplified law expression (Dawe and Seah 1989)

$${\text{q}}_{{\text{u}}} = 4.5 \cdot \left( {{\text{f}}_{{{\text{wv}}}} } \right)^{0.75} \cdot {\text{t}}_{{\text{w}}}^{{2}} \cdot \left[ {\frac{{\upalpha }}{{\left( {{\text{l}}_{{\text{w}}} } \right)^{{{2}{\text{.5}}}} }}} \right]$$

(14)

needs to be considered for MIs in full contact along three edges (i.e. MI.1 typology).

A softening branch until a conventional OOP collapse point, where the arching action shall be deemed null, is considered on the assumption that the panel is adequately connected to the surrounding frame

$$F_{wRS}^{(OOP)} = 0.6 \cdot F_{wFAA}^{(OOP)} ,\Delta_{wRS}^{(OOP)} = \Delta_{wFAA}^{(OOP)} + 0.015,k_{w2}^{(OOP)} = \frac{{F_{wRS}^{(OOP)} - F_{wFAA}^{(OOP)} }}{{\Delta_{wRS}^{(OOP)} - \Delta_{wFAA}^{(OOP)} }}$$

(15)

assuming the ultimate displacement expressed in m.

Based on the backbone curves described above, the IP and OOP cyclic behaviour of the infill panel is simulated through two pivot hysteretic models (Fig. 5). The unloading and reloading branches are governed by a pivot point, expressed as a fraction of the IP cracking strength (F^(IP)_wC in Fig. 5a) and OOP maximum strength (F^(OOP)_wFAA in Fig. 5b) and placed on the first branch direction. Specifically, the coefficient $\alpha_{2}^{(IP)}$⁾ and $\alpha$₂^(OOP) are assumed equal to 0.25 and 0.95, respectively, referring to a calibration on experimental data. The ordinate of the point PP referring to the IP behaviour is assumed equal to the value proposed by (Cavaleri and Di Trapani 2014), while the analogous ordinate corresponding to the OOP response is calibrated in a previous work (Mazza 2019a) on the basis of available experimental results (Hak et al. 2014; Furtado et al. 2017).

The effect of the previous or concurrent in-plane damage on the OOP response is described by two relations, interpolated on the basis of experimental tests available in the literature. The OOP strength and stiffness decay begins when the IP drift $\Delta$^(IP)/h exceeds a fixed threshold, keeping the backbone curve bilinear. The effects of the OOP damage on the IP response are neglected. Two expressions normalized to the corresponding undamaged value are proposed for degrading and residual values of the maximum OOP strength

$$r_{F,weak} [\% ] = \frac{{F_{wFAA,damaged}^{(OOP)} }}{{F_{wFAA,undamaged} (OOP)}} = 17.163 \cdot \left( {\Delta_{h}^{(IP)} } \right)^{ - 0.9617} ,\quad for\;\left( {\frac{\Delta (IP)}{h}} \right) \le 0.8\%$$

(16a)

$$r_{F,weak} [\% ] = \frac{{F_{wFAA,damaged}^{(OOP)} }}{{F_{wFAA,undamaged} (OOP)}} = 21.25,\,\;for\;\left( {\frac{{\Delta^{(IP)} }}{h}} \right) > 0.8\%$$

(16b)

and OOP stiffness of the first branch

$$_{{r_{F,weak} [\% ] = \frac{{k_{wFAA,damaged}^{(OOP)} }}{{k_{wFAA,undamaged} (OOP)}} = 1.962 \cdot \left( {\frac{{\Delta^{(IP)} }}{h}} \right)^{ - 2.145} ,\,\quad for\;\left( {\frac{{\Delta^{(IP)} }}{h}} \right) \le 0.8\% }}$$

(17a)

$$r_{F,weak} [\% ] = \frac{{k_{wFAA,damaged}^{(OOP)} }}{{k_{wFAA,undamaged} (OOP)}} = 3.1,\,\quad for\;\left( {\frac{{\Delta^{(IP)} }}{h}} \right) > 0.8\%$$

(17b)

as function of the IP drift ratio. The OOP reduction of strength and stiffness is activated when the displacement corresponding to the maximum IP strength is exceeded and continues up to a fixed drift threshold (i.e. $\Delta$ ^(IP)/h)_upper = 0.8%, in the case of weak infills), keeping the OOP backbone unaltered from this point on (Mazza 2019a). These expressions are calibrated on the basis of experimental results available in literature, with reference to weak infill panels (i.e. 8–15 cm thick leaf) with horizontal hollow clay bricks. The first experimental campaign (Furtado et al. 2016b) refers to double-leaf panels first damaged in the IP direction, after which the internal leaf is removed leaving the external leaf to be cyclically tested in the OOP direction. The second experimental campaign (Ricci et al. 2018) is characterized by IP cyclic loading up to three drift levels, followed by monotonic OOP tests on MIs with a single leaf.

Four IP compressions strengths are considered for MIs (Bertoldi et al. 1993), taking four failure modes: i.e. diagonal compression (σ_w1); corner crushing (σ_w2); sliding shear (σ_w3); diagonal tension ($\sigma$ _w4). The minimum value determines the maximum lateral strength of the strut:

$$F_{w}^{(IP)} = \sigma_{w,\min } \cdot b_{w} \cdot t_{w} \cdot \cos \theta ,\sigma_{w,\min } = \min \{ \sigma_{w1} ,\sigma_{w2} ,\sigma_{w3} ,\sigma_{w4} \}$$

(18)

The transition between OOP curves corresponding to different levels of IP damage is governed by geometric rules described in a previous work (Mazza 2019a), where other modelling details are presented. The IP backbone curves corresponding to the infill typologies described in Sect. 2 are shown in Fig. 6a, assuming lower (Mainstone 1974) and upper (Papia et al. 2003) values for the width of the equivalent strut. It should be noted these backbones are obtained by adding the curves referred to each leaf until the collapse point of the weakest leaf is attained. As expected, the highest values of cracking (C), full cracking (FC) and residual strength (RS) are obtained with the Papia formulation, while full height MI.2a and MI.2b infills are stronger than partial height MI.1 ones. The exterior and interior leaves are modelled separately when the OOP behaviour is considered (Fig. 6b), distinguishing solid (SB, t_w,ext = 12 cm) and hollow (HB, t_w,int = 8 cm) bricks. As can be observed, the exterior leaf shows the highest values of full arching action (FAA) and residual strength (RS). Moreover, MI.1 and MI.3 are less susceptible to the OOP collapse than MI.2, depending on the OOP maximum capacity (see Eqs. 11, 14) decreasing for increasing values of the infill height (h_w) and width (l_w) reported in Table 2. Experimental values available in literature confirm a high variability of the displacement capacity in terms of storey drift ratio, generally including the values selected for the infill types of the De Gasperi-Battaglia school: i.e. IP drift ratios (Del Gaudio et al. 2019) equal to $\Delta$_wC/h_w = 0.02–0.35%, $\Delta$_wFC/h_w = 0.12–1.33% and $\Delta$_wRS/h_w = 0.35–1.87%; OOP drift ratios (Ricci et al. 2018) equal to 2 $\Delta$_wFAA/h_w = 0.40–2.00% and 2 $\Delta$_wRS/h_w = 1.00–8.00%.

Fig. 6

Monotonic backbone curves of masonry infills for De Gasperi-Battaglia school

4 Numerical results

The infill macro-model, briefly described in Sect. 3 and detailed in a previous work (Mazza 2019a), is implemented in a homemade code for the nonlinear seismic analysis of three-dimensional frames. Specific functions handle the in-plane effects on the out-of-plane behaviour of a MI, checking the IP drift ratio of the nonlinear horizontal truss element, computing the new branches of the OOP backbone and assigning the modified mechanical properties to the diagonal nonlinear beams. This reassignment occurs at the end of every step, if the last maximum recorded IP drift is exceeded. Three assumptions about the response of MIs of the De Gasperi-Battaglia school are compared: (i) elastic both IP and OOP; (ii) inelastic IP and elastic OOP; (iii) inelastic both IP and OOP. Given that MI.1, MI.2a and MI.3 typologies of MIs are composed of two leaves, each nonlinear dynamic analysis is split in two sub-analyses, in order to correctly evaluate the independent OOP behaviour of each layer. Following a macroscopic approach, the r.c. framed structure is discretized in member-type-lumped-plasticity elements for simulation of the hysteretic behaviour. Specifically, the central part of each element is assumed elastic while a lumped plasticity model describes the nonlinear behaviour at the end sections where inelastic deformations are expected (Mazza 2019b). A piecewise linearization of the axial load-biaxial bending moment elastic domain is assumed for r.c. cross-sections, once geometry of the concrete section and diameter and position of the longitudinal steel reinforcement are defined (Mazza 2014). Twenty-six flat surfaces are used for each section, including: six surfaces normal to the principal axes; twelve surfaces normal to the bisections of the principal planes; eight surfaces normal to the bisections of the octants. Elasto-plastic constitutive laws are considered for concrete and steel, and, for concrete, tensile resistance is neglected. It should be noted that buckling restrained braces are not modelled on the upper storeys of De Gasperi-Battaglia school, so the structural behaviour before the retrofitting intervention is investigated. The step-by-step procedure is based on an implicit integration scheme and an initial-stress like iterative procedure. Time integration proves to be optimal in reducing numerical instability, round-off error effects and beat phenomena between spurious solutions (Mazza et al. 2012). The scheme operates by dividing the time axis in successive intervals, employing for each interval two parameters depending on time step and maximum and minimum vibration periods of the structure. The two main periods of vibration, related to the horizontal modal shapes having the highest participating mass, contribute to the definition of the Rayleigh damping matrix. Specifically, the viscous damping ratio ($\xi$) is set equal to 5% when considering the bare structure or the infilled structures with elastic MIs. In order to avoid an overestimation of the energy dissipation, $\xi$ = 1% is assumed when at least one type of inelasticity (IP or OOP) is considered for MIs. Next, seven pairs of seismic acceleration histories are selected from the European Strong Motion (ESD) database (Luzi et al. 2016). The selection is mainly focused on local earthquakes (Central Italy 2016) in order to make comparisons with the observed damage patterns of the De Gasperi-Battaglia school. Records are scaled to match, on average, the life-safety (LS) elastic response spectrum provided by current Italian seismic code (NTC, 2018), with reference to the geographical coordinates (longitude 13.0963° and latitude 42.7941°) of the building site and a subsoil class B. A building usage class III and a nominal design life V_R = 50 years are also assumed. The modified acceleration spectrum intensity measure (Mazza and Labernarda 2017) is assumed as matching parameter, whose values are evaluated on a suitable range of vibration periods. Moreover, the In-Spector software (Acunzo et al. 2014) is used to calculate the parameter D_rms (i.e. a root mean square difference of the spectral ordinates of acceleration), representing a measure of the similarity between real and design elastic response spectra. In Table 5, the key information of the selected ground motions are reported: i.e. place and date of the seismic event, seismic station, magnitude (M_w), peak ground acceleration in the horizontal directions (i.e. PGA_H1 and PGA_H2); root mean square differences with NTC18 design spectrum (D_rms,H1 and D_rms,H2) and scale factors (i.e. SF_H1 and SF_H2). Two seismic directions (i.e. $\alpha$ = 0° and $\alpha$ = 90°) and corresponding maximum results are considered for each earthquake. In order to have a more accurate estimation of the inelastic structural and non-structural response in nonlinear dynamic analysis, results are expressed as mean of the maximum values evaluated for the whole set of seven records (Iervolino et al. 2009). The only exception are the overview of the IP and OOP damage levels of masonry infill panels along the building height, where envelope of maximum results is considered, and time histories of the IP and OOP response parameters, which are referred to specific earthquakes. It should be noted that only records whose spectrum matches the target design spectrum to a certain value of the root mean square difference (D_rms) are selected, so avoiding that the variability of individual spectra within the set may affect the assessment of the seismic response (Reyes and Kalkan 2012).

Table 5 Main data of the selected far-fault earthquakes (Luzi et al. 2016)

Recent studies define and quantify damage states for masonry infill panel based on the analysis of a wide set of experimental data, suggesting thresholds of the storey drift ratio as function of significant properties of MIs (Cardone and Perrone 2015; De Risi et al. 2018; Del Gaudio et al. 2019). In the present work, four IP damage states (DSi, i = 1–4) are considered for the masonry infills, distinguishing different ranges for the storey drift ratio in line with limit values of the IP backbone curve presented in Sect. 3: i.e. DS1, elastic range; DS2, progressive cracking of the panel until its maximum lateral contribution; DS3, post-peak softening with extensive damage; DS4, collapse. Since the OOP curve does not account for an initial elastic behaviour, only three OOP damage states are considered. Specifically, the DS1 represents the OOP damage development until the attainment of the full arching action, while DS2 and DS3 are referred to the plastic redistribution of stresses and panel expulsion, respectively. Moreover, capacities of r.c. frame members for ductile and brittle mechanisms are evaluated in line with empirical formulations proposed by the Italian (NTC, 2018) and European (EC8 2004) seismic codes. The ductile mechanism is reached when the chord-rotation demand ($\theta_{max}$) is more than 0.75 $\theta_{u}$. The brittle mechanism verification is carried out comparing maximum shear demand (V_max) and corresponding capacity (V_u), the latter evaluated assuming a shear span length L_S = L/2, L being the length of each structural member.

4.1 In-plane response of masonry infills

Drift and acceleration ratios are assumed as IP reference parameters, as plotted in Fig. 7 with reference to all floors of the De Gasperi-Battaglia school. The first is calculated as the percentage ratio between the maximum interstorey displacement (Δ_max) and the storey height (h), while the latter as the maximum floor acceleration (a_max) normalized by the gravity value (g).

Fig. 7

IP drift and acceleration ratios for MI typologies of De Gasperi-Battaglia school

Three pairs of graphs are plotted with reference to a specific typology of MIs: i.e. MI.1 (Fig. 7a, b), representing partial height infill walls along the X direction; MI.2a (Fig. 7c, d) and MI.3 (Fig. 7e, f) along the Y direction. These MIs differ in the aspect ratio, defined as width-to-height ratio (see l_w/h_w values reported in Table 2). For the sake of brevity, MI.2b is not reported because results similar to those obtained for MI.2a are attained. Different curves are plotted for the bare structure (BS), where infills are only considered as weights, and the infilled ones modelled with the lower (Mainstone, IS.M) and upper (Papia, IS.P) bound formulations of the equivalent diagonal strut. Nonlinear dynamic analyses are carried out three times, assuming the following behaviour of MIs and considering the IP-OOP interaction: (i) elastic both in-plane and out-of-plane (IS_{E.IP_E.OOP}); (ii) inelastic in-plane and elastic out-of-plane (IS_{I.IP_E.OOP}); inelastic both in-plane and out-of-plane (IS_{I.IP_I.OOP}). As expected, the IP drift ratios are more significant in the X direction (Fig. 7a), even if comparable values of acceleration are obtained in the X (Fig. 7b) and Y (Fig. 7d, f) directions. Moreover, drift ratios of MI.2a (Fig. 7c) and MI.3 (Fig. 7e) decrease along the building height, while the opposite behaviour is observed for MI.1 (Fig. 7a) due to the combination between roof masses and higher deformability of the columns in the longitudinal direction. The IS.P structures are characterized by lower drift ratios and higher acceleration demands than those observed for the IS.M ones. In addition, the IS.M_{E.IP_E.OOP} and IS.P_{E.IP_E.OOP} structures show an overestimation of the stiffness, while drift values increase when the IP nonlinear behaviour is considered for both the elastic (IS.M_{I.IP_E.OOP} and IS.P_{I.IP_E.OOP}) and inelastic (IS.M_{I.IP_I.OOP} and IS.P_{I.IP_I.OOP}) OOP responses. Drift ratios of the BS structure are comparable to those of the IS structures with IP inelastic behaviour of MIs, while acceleration ratios are lower than those obtained for the IS.M_{E.IP_E.OOP} and IS.P_{E.IP_E.OOP} structures.

Afterwards, an overview of the IP damage level of masonry infill panels along the building height is reported in Fig. 8. Specifically, the IS.M_{I.IP_I.OOP} and IS.P_{I.IP_I.OOP} structures are compared in Fig. 8a, b, respectively, considering only perimetral MIs along the X and Y directions. Maximum damage state of the opposite couples of facades is plotted for each typology of MIs and marked with a different colour: i.e. DS1, yellow; DS2, orange; DS3, dark orange; DS4, red. As can be observed, MIs along the X direction (i.e. MI.1 typology) highlight the highest level of IP damage when the Mainstone formulation, characterized by the lowest strength, is adopted (Fig. 8a). In detail, a widespread collapse mechanism (DS4) affects MI.1 at the second and third level, while only DS2 and DS3 are attained with the Papia formulation (Fig. 8b).

Fig. 8

IP damage states for MIs of De Gasperi-Battaglia school: a Mainstone and b Papia formulations

On the other hand, the MI.3 typology, along the Y direction, exhibits increased damage at the first two levels where DS3 is attained for the Papia formulation (Fig. 8b). This can be explained by the increased torsional response induced by the asymmetric layout of MIs along the Y direction, which leads to an increase of lateral stiffness and corresponding in-plane forces acting on them. Finally, DS2 is observed for the other two typologies of infill panels along the Y direction (i.e. MI.2a and MI.2b), with negligible differences when the Mainstone and Papia formulations are compared. These results highlight that a simplified but reasonable accurate IP and OOP modelling of MIs is significant to reproduce main aspects of their influence in the design and assessment of r.c. infilled framed structures. Specifically, dynamic properties and seismic loads are notable modified with the addition of the infill panels to the bare frame (see Table 4). Moreover, a proper evaluation of the damage states of MIs makes possible the selection of suitable design choices and strengthening strategies in order to avoid their collapse in new and existing structures, respectively. Finally, as further discussed below, partial modelling (e.g. only inelastic IP behaviour) could lead to an incorrect forecast of the distribution of the non-structural damage.

4.2 Out-of-plane response of masonry infills

Curves of the OOP drift ratio, defined as the ratio between the relative OOP displacement of an infill panel (see $\Delta$^(OOP) in Fig. 4b) and half of the infill height (h_w/2), and acceleration ratio, evaluated with reference to the central points of each MIs, are reported in Fig. 9. As shown, the adoption of an OOP elastic model (i.e. IS.M_{E.IP_E.OOP} and IS.P_{E.IP_E.OOP} structures) induces an underestimation of drift and accelerations ratios for MI.1 (Fig. 9a, b), while an increase of the OOP drift is observed for IS.M_{I.IP_I.OOP} due to the notable IP-OOP interaction (Fig. 9a). This is not evident for MI.2a typology, which highlights an early OOP collapse (Figs. 9c, d) when the IS.M_{I.IP_I.OOP} is considered, although slightly damaged in the IP direction (Fig. 7c). Moreover, similar response is obtained for elastic and inelastic OOP models of MI.3 at the upper levels (Fig. 9e), where low values of IP drift (Fig. 7e) slightly affect the OOP degradation in case of the IS.M_{I.IP_I.OOP}, with the only exception at the first level where IP drift induces reduction of OOP strength and stiffness. For all typologies of MIs, the IS.P_{I.IP_I.OOP} is the preferred one because it enables to represent an early OOP collapse and/or highlights the highest values of the OOP drift and acceleration demands. As expected, an elastic IP and OOP modelling of MIs (i.e. IS.M_{E.IP_E.OOP} and IS.P_{E.IP_E.OOP} structures) corresponds to an underestimation of damage. Based on the results obtained for MI.2a, the IS.M_{I.IP_E.OOP} and IS.P_{I.IP_E.OOP} structures highlight inability in reproducing the OOP collapse at the lower levels, reaching OOP demands unrealistically higher than those obtained for the IS.M_{I.IP_I.OOP} and IS.P_{I.IP_I.OOP} structures. Moreover, MI.1 and MI.3 panels are not prone to OOP collapses even when the interaction process is triggered. This can be justified by the low mass of MI.1 and high OOP stiffness and strength of both MI.1 and MI.3, these latter depending on equivalent elasticity modulus and moment of inertia (Eq. 10) and ultimate load (Eqs. 11 and 14).

Fig. 9

OOP drift and acceleration ratios for MI typologies of De Gasperi-Battaglia school

Next, mean percentage loss of the OOP strength and stiffness is shown in Fig. 10a, b, c, d, respectively, for MIs along the building height. Hollow (i.e. HB, t_w = 8 cm) and solid (i.e. SB, t_w = 12 cm) bricks are distinguished, with reference to the lower (Mainstone) and upper (Papia) bound estimations of the IP width of the equivalent strut. The focus is on the MI.1 (Fig. 10a, b) and MI.3 (Fig. 10c, d) typologies of the IS.M_{I.IP_I.OOP} and IS.P_{I.IP_I.OOP} structures, suffering degradation of the OOP force–displacement law as a result of the high values of IP drifts. In detail, MI.1 typology exhibits a loss shape similar to the OOP drift (see Fig. 9a), with OOP stiffness decay (Fig. 10b) more marked than that observed for the OOP strength (Fig. 10a), thereby confirming the degradation laws (see Eqs. 16a, b and 17a, b). This result confirms the close relation between increase of OOP deformability and IP damage, with the most evident effects in the case of hollow bricks. At the first two levels degradation is found for the MI.3 only (Fig. 10c, d), with the Papia formulation corresponding to the highest losses for both hollow and solid bricks.

Fig. 10

Percentage loss of OOP strength and stiffness for MI typologies of De Gasperi-Battaglia school

As with to the above, a picture of OOP damage distribution of MIs along the building height is reported in Fig. 11, always with reference to the IS.M_{I.IP_I.OOP} (Fig. 11a) and IS.P_{I.IP_I.OOP} (Fig. 11b) structures. The damage state of MI.1, MI.2a,b and MI.3 typologies is separately evaluated for their interior and exterior leaves having different thickness, assuming different shades of blue (hollow brick for the interior leaf) and green (solid brick for the exterior leaf) colours.

Fig. 11

OOP damage states for MIs of De Gasperi-Battaglia school: a Mainstone and b Papia formulations

The results refer to damage states with (i.e. DSi_D) and without (i.e. DSi_UD) OOP degradation induced by the IP-OOP interaction. In detail, MI.2a and MI.2b typologies are subjected to the highest OOP forces because their mass is greater than that of MI.1 and MI.3 ones, generally leading to collapse at the second level regardless to the IP-OOP interaction and thickness of the leaf. The IP damage produces an OOP weakening of the MI.1 and MI.3 typologies, even if the damage is only slight as a result of the low OOP forces mainly dependent on their low mass. Specifically, the hollow leaf of the infill panels MI.1 is degraded at all levels, unlike the solid leaf highlighting only damage at the upper two floors where the additional mass of the roof amplifies the IP drift. Finally, the only difference between the Mainstone and Papia formulations appears for the MI.3 typology, in which the degradation also affects the solid leaf of the second level as a result of the greater IP force in the case of Papia formulation (Fig. 11b).

Next, the effectiveness of the OOP verification of stability currently adopted by some seismic codes is tested by comparing the simplified approaches followed for the calculation of the horizontal forces, at the centre of mass of MIs placed at each floor level, with the mean of the maximum OOP forces resulting from nonlinear seismic analysis of the IS.M_{I.IP_I.OOP} and IS.P_{I.IP_I.OOP} structures. As a general comment, it appears that OOP degradation induced by the interaction with IP response is responsible for a notable increase of OOP deformability and, at the same time, a decrease of OOP strength that can induce an anticipated collapse. This effect is unforeseeable by current seismic codes using a simplified model of non-structural element in order to obtain the OOP floor spectral accelerations.

Specifically, the horizontal forces provided by the Italian (i.e. F_{a_NTC18}), European (i.e. F_{a_EC8}) and American (i.e. F_{a_FEMA}) seismic codes and the corresponding difference in percentage terms ($\Delta$) from results achieved by means of nonlinear seismic analysis (i.e. F_max,OOP) are reported in Table 6a, b , c with reference to the MI.1, MI.2a and MI.3 typologies, respectively.

Table 6 Comparison of horizontal forces for the OOP verification of (a) MI.1 typology (unit in kN), (b) MI.2a typology (unit in kN), (c) MI.3 typology (unit in kN)

Floor response acceleration spectrum proposed by NTC18 take into account the elongation of the vibration period of the infilled structure due to inelastic deformations, as well as height and fundamental vibration period of the infill panel in the OOP direction, which are the only parameters considered by EC8 and FEMA356. It should be noted that NTC18 proposal allows capturing, at least partially, the effect of structural higher modes because it is characterized by a plateau, so extending the range of maximum amplification to periods shorter than the fundamental vibration period of the structure (Petrone et al. 2015). Moreover, the behaviour factor of non-structural MIs is assumed equal to 2 by NTC18 and EC8 while a value equal to 1.5 is proposed by FEMA356. To understand the difference in behaviour resulting from different thickness of a leaf, results obtained for hollow (HB) and solid (SB) bricks are distinguished along the building height, but no clear trend emerges. The maximum horizontal force acting on MI.1 is generally underestimated by NTC18 and EC8 (Table 6a), while values close to F_max,OOP are obtained by applying the American code, which is characterized by the lowest reduction of the elastic OOP force. Regardless of the seismic code, the horizontal forces are underestimated for MI.2 placed at the first two levels (Table 6b), where OOP collapse appears without IP damage. Finally, a general trend towards very conservative estimations is obtained for MI.2a and MI.3 at the third level. This kind of behaviour can be interpreted observing that floor acceleration provided by seismic codes increases along the building height, while a reduction of OOP acceleration is observed at the third level when the numerical simulation is carried out, as a result of the increased top dead load that includes the weight of the roof. To sum up, significant deviations between seismic code formulations and results from nonlinear seismic analysis are observed, but additional studies are needed before any firm conclusion is drawn. Specifically, variability of main structural parameters (e.g. behaviour factor, ratio between vibration periods of MIs and supporting structure and number of storeys) as well as further nonlinear modelling assumptions (e.g. the OOP-IP interaction, with damage in the OOP direction affecting the progression of the IP damage) need to be examined.

4.3 Interaction between in-plane and out-of-plane response of masonry infills

The global infill damage of the MI.1, MI.2 and MI.3 typologies is plotted in Fig. 12, in terms of the percentage ratio between number of infills exhibiting an assigned damage level (n_MIs,DSi) and total number of MIs (n_MIs). The previously defined IP (DSi, i = 1–4) and OOP (DSi, i = 1–3) damage states are considered with reference to coupled leaves and single leaf, respectively. Note that DS1 is omitted for the IP, given that a small number of panels remains in the elastic range. Regardless of the infill typology, IP damage patterns are not influenced by the assumption made on the OOP behaviour. Specifically, the highest percentage of infills reaches the IP cracked stage DS2, while only a low number of MI.1 (Fig. 12a) and MI.3 (Fig. 12e) is heavily damaged (i.e. DS3). Only MI.1_M panels placed at the third level exceed the IP collapse point (i.e. DS4), while this damage state is not attained for MI.1_P (Fig. 12a). There are no significant differences between MI.3_M and MI.3_P (Fig. 12e) in terms of maximum damage state (i.e. DS_max = DS3), but moderate torsional effects slightly increase the percentage of MI.3_P falling within this range. Specifically, the percentage ratio ranges from about 10% to 20% when MI3.M and MI3.P are considered, respectively, for both elastic and inelastic OOP assumptions.

Fig. 12

IP and OOP damage states for exterior MI.1, MI.2a and MI.3 infill panels

With the same thickness and mechanical properties, main parameters affecting the OOP response are the other two dimensions of the infill panel (i.e. l_w and h_w) and height at which it is placed. The OOP strength decreases for increasing values of the in-plan geometric dimensions (Dawe and Seah 1989), also producing an increase of the OOP demand. Moreover, the OOP acceleration changes along the height and depends on the OOP vibration period of the panel. In view of these factors, the OOP response of MI.1 and MI.3 typologies is characterized by high strength and low demand, while the opposite behaviour happens for MI.2a typology where OOP collapse is expected. The OOP damage states of the interior leaf with hollow bricks (HBs, t_w,int = 8 cm) and exterior leaf with solid bricks (SBs, t_w,ext = 12 cm) are separately represented in Fig. 12b, d, f, with reference to the IS.M_{I.IP_I.OOP} and IS.P_{I.IP_I.OOP} structures involving their inelastic OOP response. In detail, percentages of degraded (D, dashed bars) and undegraded (UD, solid bars) infill panels falling within each OOP damage state are reported, distinguishing the IP stiffness modelling proposed by Mainstone (M_D and M_UD) and Papia (P_D and P_UD). As shown, MI.2a panels result vulnerable to OOP collapses (Fig. 12d), without IP-OOP interaction because the in-plane DS3 is not reached. This is evident for the HB, highlighting a percentage of panels falling in the DS2 and DS3 greater than that observed for the SB. Similar results, omitted for the sake of brevity, are obtained for MI.2b panels.

The percentage of MI.2a_P_UD which lies in the DS2 and DS3 is slightly higher than that of MI.2a_M_UD, while the opposite happens with reference to DS1. Effects of the IP response are quite relevant for MI.1 and MI.3, even though their mass holds them back from damage states higher than DS1 with only few cases of MI.3 achieving DS2 (Fig. 12f). Moreover, MI.1 highlights about 50% of HBs and 10% of SBs with OOP damage influenced by the IP response (Fig. 12b), while similar values can be found for the exterior and interior leaves of MI.3 (Fig. 12f).

The IP-OOP drift domains of MIs at all three levels are shown in Figs. 13 and 14, with reference to time-histories that do not (IS.M_{I.IP_E.OOP}) or do consider (IS.M_{I.IP_I.OOP} with IP-OOP interaction) the OOP inelasticity, respectively. As a reference, the IP-OOP limit curves prescribed by FEMA 356 at the life-safety ultimate state are also plotted with a red line, where the IP threshold is related to the aspect ratio (l_w/h_w) of each typology of MIs and strength ratio between the infill and the surrounding r.c. frame members, while the OOP threshold is assumed equal to 3% for all typologies of MIs. Results correspond to the most severe earthquake separately selected for each typology of MIs: i.e. the Irpinia earthquake for MI.1 (Figs. 13a, b, c and 14a, b, c) and MI.3 (Figs. 13g, h, i and 14g, h, i) and Norcia earthquake for MI.2 (Figs. 13d, e, f and 14d, e, f).

Fig. 13

Inelastic IP and elastic OOP drift domains for MI typologies of De Gasperi-Battaglia school

Fig. 14

Inelastic IP and inelastic OOP drift domains for MI typologies of De Gasperi-Battaglia school

It should be noted that some plots are terminated before the end of the simulation because the ultimate value of the IP (red circle) or OOP (red square) drift is attained. The MI.1 typology is affected by large IP loads that exceed the IP threshold imposed by FEMA and collapse at the upper two levels (Fig. 13b, c), while extremely low values of OOP drift are observed when the IP-OOP interaction is neglected (Fig. 13a, b, c). A substantial worsening of the OOP response happens if the latter is taken into account, with peak values exceeding 1% despite the prevailing IP response (Fig. 14b, c). The MI.3 typology satisfies both IP and OOP limit drifts prescribed by FEMA, with maximum IP drift increasing at the first two levels (Fig. 13g, h) and low values of OOP drift as for the MI.1. OOP degradation under IP loading occurs only at the first level and leads to a substantial increase of the OOP deformation (Fig. 14g). On the other hand, the MI.2 typology differs from the other two for the most significant OOP loads. An elastic OOP response highlights a marked vulnerability of MIs at the second floor (Fig. 13e), while FEMA thresholds are fulfilled at the first floor (Fig. 13d). The OOP collapse of the first two levels arises when the nonlinear OOP behaviour is taken into account (Fig. 14d, e). As noted above, IP-OOP interaction is not present for this type of MI, in the sense that the OOP collapse happens before the IP activation drift is exceeded (i.e. in-plane DS3 is not attained for MI.2a). The OOP damage of MIs observed in-situ for the MI.2a typology is well captured by the implemented macro-model (see Fig. 14d, e), while the IP damage on MI.1 and MI.3 overestimates the effects produced by the Norcia earthquake that struck the school in 2016. This result can be due to the fact that buckling restrained braces of the retrofitting intervention are not modelled, referring to the original structural model of De Gasperi-Battaglia school.

Finally, curves representing time histories of OOP drift and acceleration are plotted in Fig. 15, in order to emphasize the significance of the inelastic OOP response combined with the IP-OOP interaction over the simplified OOP elastic response.

Fig. 15

OOP drift and acceleration time-histories for MI typologies of De Gasperi-Battaglia school

As can be observed, MI.1 (Fig. 15a, b) and MI.3 (Fig. 15e, f) show an identical OOP response up to the time when the IP drift exceeds the value corresponding to the beginning of OOP damage. From that point onwards there is an amplification of the OOP response, particularly marked in terms of displacement because of the reduction of stiffness (Fig. 15a, e). It should be noted that MI.1 infill panels of the second floor collapse a few seconds after the IP-OOP interaction is triggered (red lines in Fig. 15a, b). Moreover, MI.1 infill panels of the first level do not collapse but the OOP drifts are amplified for the duration of the time history (Fig. 15e, f). Finally, MI.2 typology is not affected by the IP-OOP interaction: the OOP response of IS.M_{I.IP_I.OOP} matches the elastic time history obtained for IS.M_{I.IP_E.OOP} until the maximum OOP strength is reached, then it degrades following the OOP backbone softening branch and becomes zero at collapse.

4.4 Effects of masonry infills response on r.c. frame members

Finally, absolute value of the maximum shear force demand along the building height is reported in Fig. 16, with reference to exterior columns where a brittle failure mechanism is expected. In order to take into account the plastic hinges at intermediate column height and the short column effect, due to partial infill walls connected to the columns (see MI.1 typology along the X direction), the latter are discretized in two sub-elements. The focus is on perimeter columns enclosing infills with partial height (i.e. MI.1 in the X direction, Fig. 16a, b), and perimeter (i.e. MI.2a in the Y direction, Fig. 16c, d) and corner (i.e. MI.3 in the Y direction, Fig. 16e, f) columns where one-sided imbalanced contact with an infill panel exists. Along the storey height, two values of shear demand are obtained for columns adjacent to MI.1, depending on their discretization in two subelements, with a sudden variation highlighting the short column effect. Comparisons are made between the elastic (IS.M_{E.IP_E.OOP} and IS.P_{E.IP_E.OOP}), inelastic (IS.M_{I.IP_I.OOP} and IS.P_{I.IP_I.OOP}) and mixed (IS.M_{I.IP_E.OOP} and IS.P_{I.IP_E.OOP}) assumptions for the response of MIs. Further observations are related to the Mainstone and Papia formulations. Shear demands on the bare frame are evaluated too, together with thresholds imposed by NTC18 and EC8 seismic standards. Both formulations decrease the shear strength when cyclic inelastic deformations increase, considering brittle and ductile shear behaviour when the ultimate shear failure occurs before and after flexural yielding, respectively. Moreover, the shear capacity for short columns should not be larger than the value corresponding to web crushing failure along the diagonal, in line with the formulation proposed by EC8. Assumption of elastic IP and OOP response of MIs leads to unrealistic evaluation of the shear demand due to the absence of a limit value of the lateral strength and an unexpected overestimation below the short column for the MI.1 (Fig. 16a, b). The OOP modelling does not significantly influence shear demand, as confirmed by similar results obtained when inelastic IP behaviour is combined with elastic or inelastic OOP response. Shear demands do not satisfy NTC18 and EC8 limit values for columns corresponding to MI.2a (Fig. 16c, d), as opposed to MI.1 (Fig. 16a, b) and MI.3 (Fig. 16e, f) cases. Finally, the Papia formulation generally leads to more conservative prediction of shear demand than that corresponding to Mainstone formulation. Further results, omitted for the sake of brevity, confirm the secondary importance of ductile mechanism for the De Gasperi-Battaglia school.

Fig. 16

Shear force demand for exterior columns of De Gasperi-Battaglia school

5 Conclusions

An improved five-element macro-model able to represent both the IP and OOP nonlinear responses of unreinforced MIs, as well as their interaction, is presented in this work. Given its variety of infill types, the secondary school De Gasperi-Battaglia of Norcia (Italy) is considered as test structure in order to evaluate the influence of nonstructural modelling in a nonlinear dynamic framework. Three assumptions are investigated for the behaviour of MI.1, MI.2a, MI.2b and MI.3 typologies of structural MIs: i.e. elastic both IP and OOP; inelastic IP and elastic OOP; inelastic both IP and OOP. Moreover, two expressions are used to evaluate the IP width of the diagonal strut equivalent to the MI, selected as representative of lower and upper bound estimations available in the literature. Results are presented as mean values over the set of seven spectrum-compatible earthquakes, except for the overview of the IP and OOP damage levels of masonry infill panels along the building height, where envelope of maximum results is considered, and time histories of the IP and OOP response parameters, which are referred to specific earthquakes.

The formulation used to evaluate the width of the equivalent strut affects the IP backbone curve and is crucial for both the IP vulnerability of MIs and failure mechanism of r.c. columns. It is clear from the above results that Mainstone formulation can be considered conservative as regards the IP damage of MIs, while Papia formulation leads to higher and more realistic shear demands on r.c. columns, sometimes exceeding the NTC18 and EC8 thresholds. The OOP behaviour is strongly affected by the IP level of damage experienced by the panel, resulting in significant loss of strength and stiffness. In this respect, both formulations of the width of the equivalent strut could be considered. Moreover, a proper modelling of the IP and OOP behaviour of MIs has proved to be of paramount importance. An elastic IP model induces unrealistic overestimation of the IP response, while an elastic OOP behaviour is not able to represent the OOP collapse of MIs. Both hypotheses make less reliability of time history analyses from the instant corresponding to the IP or OOP collapse. In addition, the IP-OOP interaction has a significant effect on the OOP vulnerability of the infill panels, increasing the OOP drift demand. Specifically, MI.1 and MI.3 panels of the De Gasperi-Battaglia school are heavily affected by the interaction but only slightly damaged in the OOP direction given their low mass. On the other hand, OOP collapse is observed for MI.2, with lower OOP strength and higher OOP mass compared to the previous typologies of MIs. This suggests that vulnerability to the OOP collapse mainly affects panels with comparable in-plane dimensions and low thickness. The OOP damage of MIs observed in-situ for the MI.2 typology is well captured by the implemented macro-model, and this is confirmed by results referred to the Norcia earthquake that struck the school in 2016. However, the IP damage on MI.1 and MI.3 is overestimated. This can be due to the fact that buckling restrained braces are not modelled, only referring to the structural model of De Gasperi-Battaglia school before the retrofitting intervention. Time histories of the OOP displacement and acceleration emphasize the significance of the inelastic OOP response combined with the IP-OOP interaction, vis-à-vis the simplified OOP elastic response verified through simplified interaction domains. All examined seismic codes underestimate the horizontal forces acting on MI.2 placed at the first two levels, while very conservative values are obtained for MI.2a and MI.3 at the third level. However, definitive conclusions cannot be drawn about the effectiveness of force-based verifications. This topic will be analysed in detail in a future study. The use of a simple yet complete macro-model of MIs has proved to be essential for a more accurate description of structural response and a more realistic estimation of the non-structural damage pattern, which can be useful to ensure the safety of escape routes in school buildings.