Numerical simulation of the seismic response and soil–structure interaction for a monitored masonry school building damaged by the 2016 Central Italy earthquake

Abstract

Despite significant research advances on the seismic response analysis, there is still an urgent need for validation of numerical simulation methods for prediction of earthquake response and damage. In this respect, seismic monitoring networks and proper modelling can further support validation studies, allowing more realistic simulations of what earthquakes can produce. This paper discusses the seismic response of the “Pietro Capuzi” school in Visso, a village located in the Marche region (Italy) that was severely damaged by the 2016–2017 Central Italy earthquake sequence. The school was a two-story masonry structure founded on simple enlargements of its load-bearing walls, partially embedded in the alluvial loose soils of the Nera river. The structure was monitored as a strategic building by the Italian Seismic Observatory of Structures (OSS), which provided acceleration records under both ambient noise and the three mainshocks of the seismic sequence. The evolution of the damage pattern following each one of the three mainshocks was provided by on-site survey integrated by OSS data. Data on the dynamic soil properties was available from the seismic microzonation study of the Visso village and proved useful in the development of a reliable geotechnical model of the subsoil. The equivalent frame (EF) approach was adopted to simulate the nonlinear response of the school building through both fixed-base and compliant-base models, to assess the likely influence of soil–structure interaction on the building performance. The ambient noise records allowed for an accurate calibration of the soil–structure model. The seismic response of the masonry building to the whole sequence of the three mainshocks was then simulated by nonlinear time history analyses by using the horizontal accelerations recorded at the underground floor as input motions. Numerical results are validated against the evidence on structural response in terms of both incremental damage and global shear force–displacement relationships. The comparisons are satisfactory, corroborating the reliability of the compliant-base approach as applied to the EF model and its computational efficiency to simulate the soil–foundation–structure interaction in the case of masonry buildings.

1 Introduction

Seismic events that hit Italy in the last 20 years produced not only dramatic social and economic consequences, but also major data to understand various engineering issues (Dolce and Di Bucci 2017). In 2002, Molise earthquake caused the collapse of San Giuliano di Puglia school, highlighting the significant role of site amplification on damage to buildings and strategic structures (e.g., Puglia et al. 2013) and promoting national research programs to assess their safety level and support the updating of building codes (Dolce et al. 2019). L’Aquila earthquake in 2009 demonstrated the role of near-fault seismic motion and vulnerability of non-structural components in losses, providing unique data supporting the reconstruction process (Di Ludovico et al. 2017a, b). In 2012, Emilia earthquake pointed out the existence of soil liquefaction hazard in Italy (Lai et al. 2015) and its potential damage to buildings and provided data on the seismic response of specific assets particularly spread in that area, such as fortresses (Cattari et al. 2014; Parisi and Augenti 2013a) or industrial buildings (Bournas et al. 2014). During 2016 and 2017, the historical seismicity of Italy was further marked by a sequence of strong earthquakes that hit the central regions of the country, causing once again heavy damages and loss of lives. Those earthquakes struck numerous historical urban centres, involving an area even larger than those mentioned above and producing cumulative damage particularly to unreinforced masonry (URM) constructions (Di Ludovico et al. 2019).

Focusing on the 2016–2017 Central Italy earthquake, reports (GEER 2016, 2017) and papers (e.g. Sextos et al. 2018; Stewart et al. 2018; Sorrentino et al. 2019) following post-earthquake field missions highlighted a distinct variability of damage throughout the affected area, due to site-by-site differences in structural vulnerability and local amplification of seismic ground motion produced by subsoil response. A significant amount of accurate data collected during and after seismic events on real buildings, in terms of seismic motion, structural features and soil properties, were useful to minimize the uncertainties involved in the validation process of predictive models. Within this context, since 1993 the Italian Department of Civil Protection through the OSS (acronym of the Italian name “Osservatorio Sismico delle Strutture”) installed a network of permanent seismic monitoring systems on public buildings, bridges and dams (Dolce et al. 2017), particularly those located in highly hazardous areas.

This paper presents a numerical simulation and validation study for a real masonry structure monitored by OSS through permanent accelerometers, which were able to record its motion under both weak-to-strong earthquakes and ambient noise (ReLUIS 2018a; Cattari et al. 2019a). The case-study building is an URM school located in Visso village, which was settled in a depressed area between the Nera and Ussita rivers of the Marche region, very close to the epicentres of 26th October and 30th October 2016 earthquakes (see Fig. 1a). The school was progressively damaged under the mainshocks of the Central Italy seismic sequence, resulting in a severe damage accumulation that motivated its demolition.

Fig. 1

a Location of the 2016 seismic events versus the Italian hazard map in terms of peak ground acceleration with a probability of exceedance equal to 10% in 50 years; b amplification factors estimated in Visso for buildings with periods between 0.1 and 0.5 s and H/V peaks (MZS3 2018); c pictures of differently damaged buildings after event E3

Several factors make the Visso school an interesting, if not even singular, case-study according to the following remarks:

• (1) Monitoring data on the seismic behaviour of a real building that developed a strong nonlinear response is available for a detailed validation of numerical models. This is an almost unique occurrence, being the amount and accuracy of the digital data recorded comparable only to that typically produced by shaking table tests, which however necessarily imply simplifications with respect to the prototype testing (e.g. Senaldi et al. 2020; Magenes et al. 2014; Pitilakis et al. 2018a).

• (2) The building had a T-shaped plan that is a recurrent characteristic of Italian school buildings, typically producing an irregular seismic response, damage concentrations or even a premature collapse (see e.g. Augenti and Parisi 2010).

• (3) The building was accurately inspected after the last mainshock occurred in 2016, but data related to previous shocks was collected as well, allowing damage accumulation to be assessed in terms of location, typology, and incremental severity rating.

• (4) The main periods obtained from the interpretation of the dynamic structural behaviour under ambient noise (Cattari et al. 2019a; Lorenzoni et al. 2019) resulted unexpectedly high, evidencing possible effects of the inertial interaction with the soft foundation soil (Cattari et al. 2019b; Ferrero et al. 2020). The available strong motion records represent a unique chance to observe such effects on a real case study, overcoming the physical limitations or the unavoidable assumptions that usually characterize both laboratory and field tests on simplified prototypes (e.g. Gajan and Kutter 2008; Tileylioglu et al. 2011; Jabary and Madabhushi 2017; Pitilakis et al. 2018b; Star et al. 2019). Moreover, until today most of evidences or studies on soil structure interaction on URM structures were focused on slender or monumental buildings (e.g. Karatzetzou et al. 2015; de Silva et al. 2018; de Silva 2020)

In this study, the potential effects of soil–structure interaction (SSI) are examined through a compliant-base numerical model, which was characterized through experimental investigations performed on the structure (Sect. 2) and the soil (Sect. 3). The dynamic response of the school was compared to the results of the on-site dynamic identification (Sect. 4). Then, the seismic response of the building was simulated through nonlinear time history analyses on both fixed-base (FB) and compliant-base (CB) models under the sequence of the mainshocks (Sect. 5), recorded at the underground level of the school. The simulated response through the FB and CB models was compared to the observed behaviour, first at a local scale (i.e. motion recorded by single sensors) and thereafter as a global performance. The scope of such a comparison was twofold: (1) to assess the capability of equivalent frame (EF) models to reproduce the observed cumulative damage, and (2) to evaluate the potential impact of soil–structure interaction on nonlinear behaviour and damage of the URM buildings through CB models.

2 Main features of the case study

The school masonry building was located in the near field region of the Central Italy seismic sequence. Figure 1a shows the position of epicentres of the three mainshocks that struck Central Italy in 2016, with moment magnitude M_W equal to 6.0, 5.9 and 6.5 on 24th August, 26th October and 30th October, respectively (hereafter tagged as E1, E2 and E3). Figure 1b shows the location of the Visso village in a depressed area at the confluence of the alluvial valleys of Nera and Ussita rivers. The soil fundamental frequency identified from ambient noise recorded in the middle of the depression falls in the typical range of the predominant frequencies of URM buildings (i.e. 2 to 5 Hz). Moving toward the valley borders, higher soil frequency values are caused by a shallower bedrock.

The effect of the variable bedrock depth on the site response is reflected by the amplification factors of spectral accelerations at periods between 0.1 and 0.5 s (see contours re-drawn in Fig. 1b as resulting from the seismic microzonation studies of the village), which are representative of the seismic response of most URM buildings in that area. In fact, the highest amplification values involve almost the whole valley (except the North-West border), consistently with the distribution of the observed damage. As an example, Fig. 1c shows three different damage levels detected on various buildings in three different zones of Visso. Collapses (see left-hand side picture) and huge damages (see central picture) occurred in the most recently urbanized area, which was settled in the middle of the valley where loose soil deposits reach their maximum thickness. By contrast, more ancient buildings laying closer to the valley edges, i.e. where the geological bedrock outcrops, survived the seismic sequence with none-to-slight damage (see right-hand side picture in Fig. 1c).

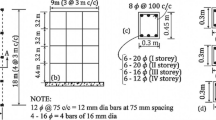
Figure 1b also indicates the position of the case study analysed in this paper: the “Pietro Capuzi” school, which was built around 1930 and extended over a 620 m² floor surface with T shape (Fig. 2a). The building consisted of two stories above ground and an attic covered by a pitched timber roof. The load-bearing walls were characterized by a two-leaf stone masonry with a rather regular bond scheme; there were also four internal pillars made of brick masonry. Floor diaphragms were composed by a mixed concrete-masonry system, with an exception for the attic floor system that was made of iron beams and thin, hollow clay bricks. The timber roof was a typical “Piemontese” type system, with the covering consisting of hollow flat tiles and a thin reinforced concrete (RC) slab. The foundation system was barely an enlargement of the load-bearing walls, slightly embedded in the soil, except for the North-East side where there was a partially underground additional storey. After the 1997–1998 Umbria-Marche earthquake sequence, the building was subjected to seismic retrofitting that mainly consisted of: mortar injections through some internal load-bearing walls; insertion of some tie-rods; improvement of roof-to-wall connections; and partial replacement of the timber roof structure, the latter deteriorated due to aging. The position of most of those retrofitting interventions is shown in Fig. 2a. More details can be found in Cattari et al. (2019a) and de Silva et al. (2019).

Fig. 2

a Plan view of the building; b damage to different structural components (walls and diaphragms) observed after event E3; c cumulative damage observed on a pier of load-bearing wall W7; d cumulative damage observed on a pier of load-bearing wall W9

The municipality decided to demolish the building due to the severe damage observed after event E3, including the partial collapse of a façade that contributed to that of the upper floors (Fig. 2b). Damage was firstly produced by shock E1 and was further aggravated by shocks E2 and E3. Figure 2c, d show the cumulative damage to two different piers that suffered an in-plane shear failure mode.

A detailed description of the building structure and damage observed after each single earthquake is included in the ReLUIS—Task 4.1 Workgroup report (ReLUIS 2018a). Figure 3 summarizes the damage level attained by each wall (DL_W) after the three mainshocks, which was rated as follows: DL0–1: none to negligible; DL2: moderate; DL3: severe; DL4: very severe to near collapse; DL5: collapse.

Fig. 3

Reconstruction of the cumulative damage suffered by the load-bearing walls after the three mainshocks E1, E2 and E3. For E2, photos were available only for exterior walls

A damage level DL_E was firstly assigned to the single structural elements in terms of type and severity of failure, based on the interpretation of photos made available by OSS thanks to various investigators after the first two mainshocks (E1 and E2) and the direct on-site survey carried out by the University of Genova (ReLUIS 2018a) after the third mainshock (E3). Then, the overall damage level DL_W at wall scale was computed as weighted average of the levels DL_E assigned to the individual piers of the wall under consideration, by assuming their sectional areas as weights. In such a way, single damage peaks in some piers are lost, but a more effective overview of damage at building scale is provided. That computation considered only piers because of their primary importance in the seismic resistance of URM buildings, like the P. Capuzi school, which have strong spandrels due to the systematic presence of RC tie beams. The final step of damage assessment was aimed at transforming the DL_W value into a synthetic information to map the damage distribution over the building plan, as shown in Fig. 3. For each wall, the DL_W value was converted into an integer degree (as depicted in Fig. 3) by conventionally assuming a binominal distribution, leading to the following ranges: 0‒0.7 for DL0; 0.7‒1.6 for DL1; 1.6‒2.5 for DL2; 2.5‒3.4 for DL3; 3.4‒4.3 for DL4; 4.3‒5 for DL5. Figure 3 provides evidence of significant damage accumulation with the highest damage severity occurred along Y rather than X direction. The collapse of diaphragms was surveyed after mainshock E3, but it probably occurred during mainshock E2, together with the activation of the out-of-plane collapse mechanism of load-bearing wall W6. Apart the activation of that local mechanism (also probably favoured by the accumulated damage), the seismic behaviour of the building was dominated by the in-plane response of walls.

3 Geotechnical subsoil model and seismic site response

The geological section drawn in Fig. 4a shows the location of the school in the middle of the valley, above an almost 40-m-thick layer of loose soil deposits covering the geological bedrock made of Scaglia Variegata (VAS) and Scaglia Cinerea (SCC).

Fig. 4

a Geological cross section of the Visso village area (modified after Sextos et al. 2018); b variation of normalized shear stiffness and damping ratio with shear strain; c soil layering; d V_S profiles measured by DH and MASW tests; e, f back-figured profiles of shear strain and normalized stiffness mobilized along the building plan directions under the three mainshocks

The soil closely below the P. Capuzi school was investigated through a borehole drilled down to 35 m and a down-hole test performed during the seismic microzonation study of the Visso village (MZS3 2018). In the frame of the ReLUIS research activities (ReLUIS 2018a), the OSS made available the data of a MASW test committed by the Italian Civil Protection Department when the monitoring system was installed. Figure 4c, d show the layered soil profile and the associated values of shear wave velocity V_S, respectively. The predominance of a sandy gravel layer (SG), covered and locally interbedded by clayey silt (CS) and silty clay (SC) lenses, was recognized. Both DH and MASW tests reveal that the V_S of the SG deposit increases with depth, exceeding the V_S values measured in the fine-grained lenses.

The one-dimensional seismic response of the subsoil profile under the three mainshocks of the Central Italy sequence was investigated through the EERA numerical code (Bardet et al. 2000).

Table 1 summarizes physical and mechanical soil properties assigned to each layer (ReLUIS 2018b): the values of V_S derive from the downhole test, whereas those of unit weight (γ), Poisson’s ratio (ν) and shear wave velocity of the bedrock half-space were inferred from measurements on similar materials collected and adopted during the seismic microzonation study (MZS3 2018). In the same table, z_min and z_max indicate the minimum and maximum depths of each soil layer, whereas G stands for the initial shear modulus of soil. As a matter of fact, neither P-wave measurements nor laboratory tests were included in the investigations at this site.

Table 1 Physical and mechanical properties of soils

A strain-dependent visco-elastic behaviour was assigned to all materials except for the bedrock, through the curves in Fig. 4b that reproduce the decay of the shear modulus normalized with respect to its small-strain value (G/G₀) and the increase of the damping ratio (D) with the shear strain amplitude (γ).

The curves adopted for the fine-grained soils (CS, SC) were obtained on the basis of a comprehensive model calibrated on the results of laboratory tests, which were performed on comparable materials in the seismic microzonation studies for Central Italy (ReLUIS 2018c; Ciancimino et al. 2019). The functional expressions of the curves were defined assuming a plasticity index (I_P) equal to 17%, based on laboratory tests on samples taken on site.

The G/G₀-γ curves obtained by Liao et al. (2013), through laboratory tests on silty sandy gravel samples consolidated at confining stress σ ^′_c  = 52 kPa and σ ^′_c  = 207 kPa, were associated to the shallower SGa and deeper SGb and SGc layers, respectively, in order to reproduce the dependence of nonlinear soil behaviour on the lithostatic stress. The corresponding D-γ curves were calculated by applying the Ramberg and Osgood (1943) model and the Masing (1926) criteria to the above G/G₀-γ curves taken from the literature.

A validation of the soil model is reported by Cattari et al. (2019b), who demonstrated that the resonance frequency characterizing the dynamic response of the one-dimensional soil model under a low-amplitude input motion is very close to the value measured on site (MZS3 2018; Gaudiosi et al. 2016) by interpreting noise records through horizontal-to-vertical spectral ratio (HVSR in Fig. 4a).

In this study, the accelerograms recorded at the underground floor during the E1, E2 and E3 seismic events were deconvolved to the bedrock depth. The analyses were performed through the linear equivalent approach, in which materials are assumed to be visco-elastic with shear stiffness and damping ratio iteratively updated according to the strain level achieved in each soil layer throughout the shaking time history. In these deconvolution analyses, the accelerograms recorded at the underground floor level were assumed to be representative of the free-field motion.

Figure 4e, f show the profiles of both shear strain and normalized shear modulus provided by the deconvolution of the ground motions recorded under the three main events along the two directions, i.e. X and Y. The profile in Fig. 4e shows larger shear strains along the Y-direction, particularly during event E2 that was the mainshock with the closest epicentre to Visso (see Fig. 1a). In the shallowest fine soil layers, the reduction of shear modulus with the mobilized strain is moderate (G/G₀ > 0.6), and even in the underlying gravel the shear strain is well below 1%. Consequently, soil plastic straining in free-field conditions is not expected to have occurred.

Figure 5a compares the response spectra (for 5% structural damping ratio) obtained from the accelerograms recorded at the base of the school against those provided by the Italian Building Code (NTC 2018) for soil type C, being V_S30 = 281 m/s as shown in Fig. 4d. Two return periods were considered, i.e. T_R = 475 years (adopted for ordinary buildings) and T_R = 712 years (corresponding to highly important buildings such as schools). The same comparison is reported in Fig. 5b between the spectra at the bedrock depth resulting from the deconvolution and the reference code spectrum corresponding to a rock outcrop (type A ground, T_R = 475 years). The vertical lines plotted in Fig. 5 indicate the fundamental periods estimated for the school from the ambient vibration measurements before the seismic events (T_x and T_y, see Sect. 4.3) and for the subsoil (T_soil).

Fig. 5

Acceleration response spectra specified by the Italian National Technical Code versus a spectra derived from seismic motion recorded at school building and b spectra back-figured through deconvolution

The comparison highlights that the spectral accelerations predicted by NTC 2018 are generally lower than those recorded on site, especially under the strongest event E2; such a phenomenon was already recognized in epicentral area (Iervolino et al. 2019). Peaks of the recorded spectra occur at periods longer than those measured at school under ambient noise. Indeed, resonance might have occurred due to the close values of soil and structural periods, leading the school to suffer the spectral accelerations mostly amplified by site- effects. Moreover, the plausible increase of the fundamental period of the structure in its damaged state could have enhanced these effects.

4 Setting and calibration of the numerical SSI model

4.1 Equivalent frame building model

The structural knowledge acquired from survey, together with some pre-existing results regarding the mechanical properties of masonry (ReLUIS 2018a; Cattari et al. 2019a), permitted the authors to develop a 3D model of the structure based on the equivalent frame (EF) approach (see Fig. 6). This choice is justified by the regular pattern of wall openings in P. Capuzi school and by the evidence on the actual response, with cracks mainly developed in piers and spandrels as assumed by the EF idealization that concentrates the nonlinear response in those elements of load-bearing masonry walls (see e.g. Parisi and Augenti 2013b).

The structural model was realized with the Tremuri software package (Lagomarsino et al. 2013) that is particularly effective in performing nonlinear dynamic analyses (Cattari et al. 2018). In the capacity model, both pier and spandrel panels were idealized through nonlinear beams with lumped inelasticity, whereas floor diaphragms were modelled as 3- or 4-node finite elements with linear orthotropic membrane formulation in plane stress conditions. The in-plane behaviour of the diaphragms and the out-of-plane response of walls were not considered, assuming a global building response mainly governed by the in-plane behaviour of walls. This assumption is consistent with the main behaviour exhibited by the building (as described in Sect. 2) and rigorous at least until the mainshock E2 that activated a local mechanism only in the rear body, that is, in a small portion of the building.

The dimensions of piers and spandrels were assumed on basis of the criteria proposed by Lagomarsino et al. (2013); the accuracy of this choice was directly validated, since the actual pattern of seismic damage was observed on the P. Capuzi school. The role of other possible epistemic uncertainties in the modelling process was already deepened in Cattari et al. (2019a), leading to the following assumptions: length of RC beams intermediate between that of the opening span and the distance between two consecutive nodes; effective height of piers of the ground level varying with the actual foundation level; attic and roof modelled as equivalent mass.

Two structural models were analysed in the paper, i.e. a fixed-base (FB) model and a compliant-base (CB) model in which the soil-foundation impedance was simulated with equivalent linear springs at the base of each pier (see Fig. 6b). The underground story located in Area II (see Fig. 2a) was not explicitly modelled, but its presence was taken into account in the computation of the spring stiffness, as described in Sect. 4.2.

Fig. 6

a Plan position of accelerometers installed by OSS and area attributed to each sensor (SF is the sensor located at the basement level, while brackets indicate sensors located at the first floor); b 3D equivalent frame model with springs implemented in the CB model

A full factorial analysis was carried out to assess the role of aleatory uncertainties on mechanical properties of the masonry typologies detected in the structure and on the diaphragm stiffness. The following variables or groups of variables have been singled out:

• X₁—Young’s and shear moduli of the unreinforced masonry (E_URM1, G_URM1);

• X₂—Young’s and shear moduli of the strengthened masonry (E_URM2, G_URM2);

• X₃—Shear modulus of the equivalent membrane assumed for diaphragms of floor level 1 (G_D,1);

• X₄—Shear modulus of the equivalent membrane assumed for diaphragms of floor level 2 (G_D,2).

For the groups X₁ and X₂, the variables were considered as fully correlated to each other, by assuming a fixed ratio between them (G = E/3, i.e. uncompressible material) as proposed also in the Italian Building Code Commentary (MIT 2019). This deepening permitted the definition of the more plausible combination of values (i.e. minimum, maximum or another) to be assumed for the aleatory variables for reproduction of target frequencies identified on site. The results are in the following illustrated only referring to the FB model, having checked that substantially analogous conclusions could have obtained from CB model.

Figure 7 shows the range of variation assumed in the factorial analysis for the variables which have been selected to be compatible with the reference interval proposed in the Italian Building Code Commentary (MIT 2009, then recently updated into MIT 2019) for the “cut stone masonry with good bonding”. The range of variation also accounts for some modification coefficients proposed in (MIT 2019) to consider beneficial effects of construction features on mechanical properties of masonry (e.g. the presence of good-quality mortar joints or transverse connections). The maximum value assumed for URM2 is higher than that of URM1, being the former strengthened by a mortar injection intervention. The shear stiffness properties of floor diaphragms (X₃, X₄) were assumed to be compatible with those of a RC slab with thickness equal to 0.05 m. Then, the apparently huge range of variation accounted for both the possible effects of material degradation and quality of floor-to-wall connections. Conversely, the brick masonry type was assumed as deterministic since it characterizes very few elements in the buildings (not able to significantly influence the overall response); the values are consistent with the mean value of the range of variation proposed in the Italian Building Code Commentary (MIT 2019) amplified by 1.5, in order to consider the presence of a good-quality mortar.

Fig. 7

Results of the full factorial analysis carried out in the calibration process and ranges of variation assumed for the aleatory variables

Figure 7 also summarizes the results of the full factorial analysis in terms of variable β_i, expressed as follows:

$$\beta_{i} = \left( {{\mathbf{Z}}^{\rm T} {\mathbf{Z}}} \right)^{ - 1} {\mathbf{Z}}^{\rm T} {\mathbf{T}}$$

(1)

where

• Z is the matrix of normalized variables (i.e. by assigning − 1 and + 1 to the minimum and maximum value attributed to each variable, as reported in Fig. 7);

• T is the array collecting the structural response parameters, in this case the periods associated with the first 10 modes.

These results highlight that X₁ group significantly affects the first three vibration modes that mainly activated the flexural behaviour of walls (in X and Y directions). By contrast, the role of diaphragms at the first floor level (X₃ group) and second floor level (X₄ group) becomes more significant for the highest and intermediate vibration modes, respectively.

On such a basis, a final reference model was set up, through which the SSI phenomena were investigated by considering both the FB and CB models and the final refinement of aleatory variables was carried out. In particular, Table 2 outlines the values of the stiffness properties adopted in the models, which were calibrated to achieve a satisfactory agreement of the simulated dynamic behaviour of the structure against the observations, as illustrated in Sect. 4.3. For both masonry types URM1 and URM2, the maximum value of the initial range of variation was assumed. Moreover, the values assigned to the cut stone masonry (URM1) are also compatible—even higher—with some results of double flat-jack tests performed on the structure by OSS before the seismic events (ReLUIS 2018a).

Table 2 Mechanical parameters adopted for piers and spandrels

Table 2 also shows the strength parameters adopted in nonlinear dynamic analyses. In the nonlinear field, the response of piers and spandrels (in orange and green respectively in Fig. 6b) was simulated through the piecewise-linear formulation proposed by Cattari and Lagomarsino (2013) and illustrated in Fig. 8. The constitutive law allows for describing the nonlinear response until very severe damage levels at element scale (i.e. DL_E from 1 to 5) through progressive strength degradation corresponding to assigned drift values. The values assumed for the latter drifts and the corresponding strength decay are consistent with experimental data in the literature (Vanin et al. 2017; Graziotti et al. 2012; Beyer and Dazio 2012). The hysteretic response is formulated through a phenomenological approach to capture the differences among the possible failure modes (flexural type—Fig. 8a, shear type –Fig. 8b, or even hybrid) and the different response of piers (Fig. 8a, b) and spandrels (Fig. 8c).

Fig. 8

Backbone and hysteretic response of masonry elements: a piers under flexure; b piers under shear; c spandrels. In c δ₃ was defined starting from drift corresponding to the yielding point of the element and assuming a ductility factor equal to 4, similarly to what suggested in Beyer and Mangalathu (2014)

As far as the strength criteria concern, the flexural behaviour was interpreted according to those proposed in NTC (2018), whereas the shear behaviour according to the diagonal cracking failure mode proposed by Turnšek and Sheppard (1980) (proposed as reference in MIT 2019 for existing masonry). In the case of spandrels, the development of a strut mechanism was assumed likely to occur due to the presence of RC tie beams and it was interpreted according to the criterion proposed in NTC (2018). Strength parameters are consistent for the masonry typology that characterized the building and are compatible with those proposed in the Italian Building Code Commentary (MIT 2019). They were set to the same reference value (mean eventually amplified by some modification factors) similarly to what defined for the Young’s and shear moduli, as resulting from the calibration process in the elastic phase. Strength values are also consistent with some evidences from experimental results available in the literature (Vanin et al. 2017; Kržan et al. 2015). Indeed, in line of principle, it is evident that also the strength parameters reported in Table 2 and the factors that characterize the nonlinear behaviour shown in Fig. 8 should be considered as uncertain variables.

Despite this, they were considered as deterministic properties in the nonlinear dynamic analyses described in Sect. 5. The motivation behind that choice was to carry out a blind prediction similarly to what a common and expert analyst can do by calibrating the model against on-site dynamic identification data and then by defining the other parameters through expert judgment. In engineering practice, it is indeed not possible to make further modelling refinements in the absence of evidence from the actual response, as that kind of data is typically not available to professionals.

4.2 Setting of foundation impedance functions

Following the so-called ‘substructure approach’ (e.g. Wolf 1985; Mylonakis et al. 2006), the soil–structure interaction should be modelled accounting for both ‘kinematic’ and ‘inertial’ mechanisms. As usually suggested in the literature for shallow foundations (e.g. Elsabee and Morray 1977; Kim and Stewart 2003; Conti et al. 2017), in this case the kinematic interaction can be neglected, being the stiffness of masonry foundations comparable to that of the surrounding soil (Pitilakis and Karatzetzou 2015) and the embedment of load-bearing walls relatively low. Consequently, SSI analysis was reduced to the inertial mechanisms only.

In the substructure approach, the dynamic soil compliance is represented through springs and dashpots assigned to the base of the structural model. The relevant dynamic stiffness and damping properties are respectively based on the real and imaginary parts of the impedance functions (Gazetas 1991). The reliability of such a soil–structure model was already assessed for URM buildings by de Silva et al. (2018) and Piro et al. (2020) against predictions of more refined numerical methods, in which a unique soil–foundation–structure continuum system was simulated.

Since the adopted structural software package is not capable to implement base-supporting dashpots, the radiation damping was implemented in the nonlinear analyses through the procedure described in Sect. 5.1, whereas, only the real part of dynamic soil compliance was considered at this stage of the work. The latter was computed for each degree of freedom of the foundation piers through the formulas proposed by Gazetas (1991) for a rectangular rigid foundation embedded in an elastic half-space. To get consistency between the structural and geotechnical models, the foundation length (2L) was defined by adding the half-length of the spandrel panel to the size of the load-bearing wall. Moreover, an enlargement of 0.15 m at each side of the load-bearing wall was considered, leading to a foundation width 2B = 0.90 m. The value of the embedment (D) was set to 0.6 m for Area I and 2.95 m for Area II, where the underground level was present (see Fig. 2a).

For the dynamic impedance computation, the assumption of a homogeneous half-space for the subsoil is reliable enough. In fact, the depth—where the uppermost stiff layer is intercepted (around 18 m below the ground level, as shown in Fig. 4c)—is much higher than that affecting the foundation motion, which is approximately equal to once to twice its width (Stewart et al. 2003; Mylonakis et al. 2006).

In the ambient noise records adopted for the dynamic identification analysis (Sect. 4.3), a full contact was supposed between the foundation and surrounding soil, where small strain levels are expected to be mobilized. For the same reason, in such analyses the static stiffness (K_stat) was computed considering the small-strain shear stiffness (G₀) derived from the mean shear wave velocity measured in the shallowest 3 m of the first soil layer, corresponding to the depth of the soil volume expected to affect the foundation motion (de Silva 2020). Each dynamic impedance component turned out approximately equal to the corresponding static stiffness, since the frequency-dependent dynamic stiffness coefficients associated to the experimental fundamental frequency were close to unity. The results of the deconvolution analyses reported in Sect. 3 revealed that the strain levels mobilized in the shallowest soil layer are significantly lower than those associated with the plastic behaviour. Accordingly, it appeared reasonable to exclude soil plasticity without neglecting nonlinear effects. Thus, the soil nonlinearity was considered by computing the impedance functions through a ‘degraded’ stiffness value (G_deg) consistent with the shear strain levels induced in the soil by the three mainshocks. From the seismic response analyses, a mean shear stiffness G_deg = 26.25 MPa resulted as mobilized in the shallowest 3 m of subsoil, corresponding to about 70% of the initial small strain value (G₀).

The impedance values relevant to axial (K_z), swaying (K_x, K_y) and rocking (K_r,x, K_r,y) foundation motion components were computed considering the variability of the pier length (2L) with the position in the building. Table 3 summarizes the mean value (μ) and the coefficient of variation (COV) of the data computed in Areas I and II of the structure, accounting for the different depths of the embedment. In Area II, the embedment depth induces a significant increase of the mean values along with a decrease of the statistical variation, more apparently for the rocking stiffness terms.

Table 3 Mean value and coefficient of variation of the real part of the impedance functions of load-bearing walls adopted in the dynamic identification procedure and in the back-analysis of the recorded seismic response

4.3 Numerical model assessment through dynamic identification data

The dynamic identification data herein adopted as target for the calibration were available from the studies carried out by other researchers involved in the ReLUIS Workgroup (2018a), thanks to the data on ambient noise tests provided by OSS (e.g. as reported in Lorenzoni et al. 2019). Indeed, the interpretation of the recordings turned out to be quite complex, providing distinct results from different teams involved in such a research. Despite that, the different results agree on the fact the first modal shape suggests a combined effect of torsional and flexural behaviour along the Y direction, whereas the second mode reflects a significant torsional component and the third mode a purely flexural behaviour along the X direction.

The differences between the two available interpretations were investigated by computing the Modal Assurance Criterion (MAC)  for the first three modal shapes; in particular, those identified by OSS (solution Ψ₂, available from ReLUIS 2018a) and those obtained by the research group from the University of Padua (solution Ψ₁, available from Lorenzoni et al. 2019) have been assumed as reference. As well known, the MAC index increases from zero to unity as the match improves. Figure 9a shows the results, highlighting a significant uncertainty on the second modal shape.

Fig. 9

MAC matrix between: a two alternative interpretations of experimental data (Ψ₁ or Ψ₂); the CB model against the b Ψ₁ and c Ψ₂ interpretations of experimental data

The left part of Table 4 summarizes the experimental periods associated with the first three modes. The experimental periods appear to be significantly affected by the interaction with the soil being significantly higher than those expected for a URM building characterized by the structural details and the geometrical configuration of P.Capuzi school when assumed fixed at the base (as discussed for example in Graziotti et al. 2019; Ferrero et al. 2020).

Table 4 Reference values of periods estimated through ambient noise measurements (ReLUIS 2018a) and modal analysis results for numerical models

Figure 10 shows the natural periods identified from the ambient noise records compared to those resulting from modal analysis of both the FB and CB equivalent frame models adopted in this study and based on the material properties characterized as described in Sects. 4.1 and 4.2. For the CB model, only the springs resulting from the adoption of G₀ were assumed as reference, since nonlinearity is not expected to be induced by ambient noise. The numerical values are also reported in the right-hand side of Table 4 together with the estimates of the participating mass from the FB model.

Fig. 10

Comparison between the experimental and numerical periods according to a Ψ₁ and b Ψ₂

The plots in Fig. 10a, b show that the periods predicted by the CB model are much closer to the target experimental values with respect to those relevant to the FB-model, that conversely are too short for all the first three modes identified by both Ψ₁ and Ψ₂. Also the sensitivity to the epistemic uncertainties examined in Cattari et al. (2019b) on the FB model (shown by the whisker symbols in Fig. 10a, b) and an alteration of the values of aleatory variables are not enough to explain such a high mismatch of the fixed-base modelling, unless making unrealistic assumptions as also discussed by Ferrero et al. (2020). This result indicates a significant effect of SSI on the building dynamic response, coherently with some evidence from the survey at the scale of the whole historical centre (Sextos et al. 2018) and from other numerical simulations (Ferrero et al. 2020).

A final model assessment is further provided by Fig. 9, showing even the MAC values obtained by comparing the numerical modal shapes to their experimental counterparts, i.e. CB model with impedance based on G₀ versus Ψ₁ or Ψ₂ in Fig. 9b, c, respectively. Even though the relevant MAC values are not very close to unity, the calibration can be considered globally satisfactory, also taking into account the aforementioned huge uncertainty in the interpretation of experimental data.

5 Numerical simulation of seismic response

For simulating the seismic performance of the P. Capuzi school to the series of strong-motion events (E1, E2, E3), the sequence of acceleration time histories recorded along both horizontal directions X and Y at the basement together with the vertical component were applied to nonlinear EF models with both fixed and compliant base.

While the dissipation associated with the nonlinear response of URM panels was directly taken into account through the hysteretic formulation introduced in Sect. 4.1, the soil-footing radiation damping was approximately introduced by calibrating the equivalent viscous damping of the well-known Rayleigh formulation through the method described in Sect. 5.1.

The results of the nonlinear dynamic analyses are reported in the subsequent sections, where different types of comparisons are presented as follows:

• At the local scale (Sect. 5.2), in terms of acceleration time histories recorded by each single sensor versus those resulting from the analyses at the same points;

• At the global scale (Sect. 5.3), in terms of activated inertia forces versus the average top displacement, attributing to each sensor a pertinent mass estimated from the model;

• In terms of damage mechanisms (Sect. 5.4), to assess the accuracy of the model also in describing the main failure modes observed and their localization.

5.1 Evaluation of SSI effects through the replacement oscillator

The total horizontal displacement of a structure on soft soil can be expressed as the sum of three contributions, with the first one associated with the oscillation of the structure (i.e. soil assumed as rigid) and the others associated with the swaying and rocking oscillations of the base (i.e. structure assumed as rigid). From such a conceptual basis, Maravas et al. (2014) demonstrated that the fundamental period $\tilde{T}$ and the total damping $\tilde{\zeta }$ of an equivalent single-degree-of-freedom (SDOF) system (the so-called ‘replacement oscillator’), characterized by the same total displacement of an actual soil–structure system, can be obtained from the real and imaginary parts of the following equation:

$$\frac{{\tilde{T}^{2} (1 - 2i\tilde{\zeta })}}{{1 + 4\tilde{\zeta }^{2} }} = \frac{{T_{x}^{2} (1 - 2i\zeta_{x} )}}{{1 + 4\zeta_{x}^{2} }} + \frac{{T_{\theta }^{2} (1 - 2i\zeta_{\theta } )}}{{1 + 4\zeta_{\theta }^{2} }} + \frac{{T_{c}^{2} (1 - 2i\zeta )}}{{1 + 4\zeta^{2} }}$$

(2)

where

• T_c is the oscillation period of the structure in the fixed-base conditions;

• ζ is the structural viscous damping ratio;

• T_x and T_θ are the uncoupled (fictitious) natural periods of the system under swaying and rocking oscillation of the base, respectively;

• ζ_x and ζ_θ are energy loss coefficients relevant to the swaying and rocking modes.

T_c increases with the ratio between the mass and the lateral stiffness of the FB structure. Similarly, periods T_x and T_θ are proportional to the ratio between the structural mass and the real part of the translational and rotational impedance functions (Wolf 1985) respectively, whereas ζ_x and ζ_θ depend on the ratio between the imaginary and real parts of the same functions. Since the impedances are frequency-dependent, Eq. (2) needs to be solved iteratively until the resulting $\tilde{T}$ is equal to the value adopted for the computation of the impedance functions. This approach was applied to the case-study building by firstly approximating the structure through a SDOF system with viscous damping ratio ζ = 3% and dynamic properties associated with the first vibration modes of the FB configuration, as resulting from the modal analysis (see Table 4). Being the replacement oscillator motion expressed in terms of horizontal in-plane displacement, reference was made to the first and third vibration modes, neglecting the second one, identified as mainly torsional and with lower participating mass (see Sect. 4.3).

The SDOF system was therefore considered to be placed on a foundation characterized by the sum of the impedances of the Y-oriented load-bearing walls to evaluate the SSI effects on the first mode. Similarly, the sum of the impedances of the X-oriented load-bearing walls was considered in the approximation regarding the third mode of vibration.

Consistently with the approaches described in Sect. 4.2, the soil shear stiffness was assumed equal to the following values:

• The small-strain value (G₀), to predict the fundamental periods provided by on-site dynamic identification;

• G_deg = 0.7G₀, to approximate the nonlinear seismic response under the strong-motion records.

In this latter case, the footing might even detach from the soil. Thus, two extreme hypotheses were formulated, i.e. full connection and total loss of lateral soil-foundation contact.

The values of period and damping ratio resulting for all the analysed cases are reported in Table 5, where the symbol $\tilde{\zeta }$ _m indicates the mean total damping ratio mobilized by the 1^st and 3^rd modes.

Table 5 Period and damping ratio predicted by the replacement oscillator

Assuming the small-strain soil stiffness (G₀), the periods predicted by the replacement oscillator are very close to those resulting from numerical analyses (see right-hand side of Table 5), with a difference equal to − 12% for the 1^st mode and only − 6% for the 3^rd mode. It is noted that the 1^st mode is partially torsional and consequently more difficult to be reproduced through the simplified replacement oscillator approach. An expected period elongation occurs if the soil stiffness degradation and soil-footing detachment are incorporated.

Being the radiation damping proportional to the extension of the soil-footing contact area, higher values of $\tilde{\zeta }$ result for the 3^rd mode, since the X-oriented load-bearing walls participating to such a structural motion are longer than those oriented along Y direction, involved in the 1^st mode. For the same reason, the loss of soil-foundation contact produces a reduction of $\tilde{\zeta }$.

In order to account for both structural viscous damping ratio and foundation radiation damping ratio, the nonlinear analyses under the three mainshocks were then performed by assigning an additional Rayleigh damping ratio to the EF model, calibrated to be almost constant in the frequency range from 1.41 Hz to 3.45 Hz. The upper bound of such a range is equal to the initial main vibration frequency of the CB model, whereas the lower bound was set to include the expected frequency reduction associated with the structural damages, i.e. 1.41 = 3.45/(6)^1/2, where 6 is the ductility factor. A value of $\tilde{\zeta }$ = 6% was inferred from the replacement oscillator model as an intermediate estimate between those computed by assuming G_deg in both contact conditions (7.31 and 5.06 in Table 5).

5.2 Comparisons at local scale: recorded versus numerical accelerations at sensor locations

The model capability to reproduce the seismic response of different parts of the building was quantitatively evaluated through the covariance (COV) between the numerical accelerogram and the signal recorded by all the available sensors. The COV computation was repeated also by considering a time lag and then by assuming as reference the highest value obtained. Figure 11a highlights the time lag associated with the COV values shown in Fig. 11b expressed as n times a conventional reference time τ = 0.024 s (corresponding to the sampling time of the signal). Indeed, apart very few cases (e.g. sensor #6), the time shift is not decisive in improving the agreement and in all cases can be considered very small compared to the main periods of the structure. Therefore, the time shift has a negligible effect. In Fig. 11b, the outcome of the numerical-experimental comparison is tagged in green, yellow and red according to high, moderate and low agreement levels, which were defined in terms of COV ranges as COV ≥ 0.7, 0.4 ≤ COV < 0.7 and COV < 0.4, respectively.

Fig. 11

Numerical-experimental matching of accelerations at each sensor expressed in terms of a time lag and b COV (indicated as percentage) for all selected mainshocks, floor levels, building plan directions and equivalent frame models

Even if both models provide a fair agreement during the first mainshock, the CB model reproduces the best overall consistency over all three mainshocks, significantly improving the response simulation of the Y component of sensor #2. For some measurement locations, the COV values associated with the FB and CB models gradually reduce starting from the mainshock E2 and E3, respectively. Referring to the CB model, the increase in the mismatch is particularly evident for both components of sensor #1 and appreciable for the Y component of further sensors located at the ground floor. To explain such a result, it is worth to recall that during the mainshock E2 the following damage occurrences were detected (see Figs. 2, 3): (1) a local collapse mechanism activated on Wall 6 where sensor #1 was placed; and (2) a significant damage—reaching collapse—reasonably involved the floors of Area I. As a matter of fact, both failures cannot be captured by the numerical model, which neglects the out-of-plane response of URM walls and assumes a linear behaviour of the floor diaphragms. Despite the above approximations, the general agreement between numerical results and monitoring data appears satisfactory.

The evolution of the school response along the two horizontal directions of the building plan was investigated in detail through a time–frequency analysis using the Stockwell transform (see e.g. Sundar 2019). That transform was carried out on the recorded acceleration time histories (including the input motion) and those obtained from numerical simulations through the FB and CB models. Figure 12a shows the time–frequency contours relevant to the motion along X direction, using data from sensor #8 installed at the centre of the first floor and poorly affected by the local failure of curtain walls. The visual comparison between the contours obtained from the time–frequency analysis shows a good overall agreement of both numerical models with the on-site recorded data, evidencing a more significant high-frequency content in the response of the FB model.

Fig. 12

a Stockwell transform of the X-acceleration recorded on site by sensor #8 and simulated through the FB and CB models; b time histories of the X-acceleration and normalised Arias intensity recorded at the underground level of the school during the Central Italy seismic sequence; c, d comparison between the experimental and numerical frequencies during the three mainshocks along X and Y directions

The frequency response was analytically assessed by computing the mean predominant frequency of the experimental records and numerical results throughout the significant duration (D_5–95) of each one of the three mainshocks and during the ‘quiet’ pauses between two subsequent events. The latter intervals are indicated in Fig. 12b with reference to the time history and cumulative Arias intensity (normalised to its final maximum value for each event) of the X-acceleration recorded at the underground level of the school, i.e. that applied as input motion in the simulations. Figure 12c, d compare the resulting frequencies, clearly highlighting a satisfactory agreement with the experimental data during the three mainshocks (full markers). On the other hand, differences are recognized during the quiet intervals between the earthquakes (hollow markers), where motion tends to a free vibration and the response of the FB model resets to higher frequency values.

The vertical dashed lines in Fig. 12c, d indicate the mean predominant frequencies of the input motions, again computed in the time-window of the significant duration (D_5–95).

For each event, full markers remain close to the associated vertical line, indicating that the seismic response of both the real structure and the numerical model is controlled by the frequency content of the strong input motion. Such an effect is clearly recognized during the first event (E1) in both directions and the following earthquakes (E2 and E3) along the X direction. As a matter of fact, the lower frequency response along the Y direction could have been induced by a higher amount of structural permanent damage along that direction, detected during the in situ survey (see Sect. 2, Figs. 2, 3), as further discussed in Sect. 5.4. Furthermore, the reduction of experimental and numerical frequency in the quiet intervals between the couples of mainshocks (E1-E2 and E2-E3) as well as after mainshock E3 confirms the structural stiffness degradation related to damage accumulation and progression of nonlinear response (de Silva et al. 2019). As a further corroboration of the relevance of soil–structure interaction, the degradation in the experimental frequency is better captured by the numerical CB model with respect to its FB counterpart.

5.3 Comparisons at global scale: inertia forces

Figure 13 shows the experimental building response and the numerical simulations by the FB and CB models under the three mainshocks, in terms of horizontal components of base shear (V) versus the average top displacement (d) of the building.

Fig. 13

Comparison between experimental and numerical base shear–top displacement curves (numerical curves are derived from nonlinear time history analyses under the sequence of consecutive mainshocks)

The experimental behaviour was evaluated by approximating the building as an equivalent multi-degree-of-freedom (MDOF) system, having the amount of DOFs equal to the number of stories. The base shear V was computed as total inertia force at the base of the structure, i.e. the sum of recorded accelerations multiplied by corresponding inertia masses. These latter were estimated on the basis of the tributary floor area of each sensor, as shown in Fig. 6a (see also Cattari et al. 2019a). Similarly, the top displacement d was computed as weighted average of the nodal displacements on roof level, assuming inertia masses as weights. Starting from the mainshock E2, recordings of sensor #6 were not considered, since its response was affected by the activation of the local mechanism in Wall 6. It is worth recalling that the analyses were performed under the sequence of three mainshock signals. Nonetheless, the force–displacement curves in Fig. 13 are plotted for each mainshock for sake of clearness.

The experimental increase of both displacement amplitude and energy dissipated in the hysteresis loops highlights a progressive development of the nonlinear response of the school building, which was more pronounced in the Y direction. Such unbalanced structural behaviour can be explained by the stronger ground motion recorded starting from the mainshock E2 along the Y direction (see Fig. 5) and is consistent with the uneven evolution of observed damage discussed in Sect. 2 (see Fig. 3). In fact, Fig. 3 allows deducing that, moving from the mainshock E1 to E2, the damage to the load-bearing walls oriented in the X direction mostly moved from DL0–1 to DL2 (in few cases from DL2-3 to DL4-5). By contrast, most walls oriented in the Y direction experienced a damage transition from either DL0–1 to DL3 or DL2 to DL4.

The numerical results show that the difference between the FB and CB models is less evident than in the elastic field (as discussed in Sect. 4.3), since the effect of nonlinear structural response prevails on soil–structure interaction. In the case of CB model, a slight overestimation of top displacement can be observed in the X direction after mainshock E1. This can be explained by the lower value of equivalent damping ratio adopted in the simulation with respect to the value predicted by the replacement oscillator approach along X (see Table 5). Along the Y direction, both models tend to overestimate the peak displacement even during mainshock E1. Thereafter, the FB model strongly overestimates the top displacement, due to the apparent attainment of the collapse condition in piers that were only partially damaged in the reality (see also Fig. 16b in the following Sect. 5.4). In this respect, the simulation results of the CB model are more consistent with the recorded response. The hysteresis loops produced by mainshock E3 (characterized by a lower intensity than E2; see also Fig. 5) indicate that the numerical models tend to underestimate a bit the response. This can be due to a slight model deficiency to reproduce the effects of damage accumulation (as pointed out by Fig. 17 passing from E2 to E3). Despite this, results appear quite satisfactory, particularly for the CB model.

5.4 Real versus simulated damage

The comparison between recorded and numerical data in terms of damage was carried out at different scales, to verify the following validation aspects:

• For each pier element, the ability of the numerical simulation to capture the failure mode (i.e. flexural, shear or hybrid, herein respectively abbreviated as F, S and H), the damage level and its evolution during the seismic sequence (Figs. 14, 15);

  Fig. 14

  

  Damage comparison at single element scale in terms of a severity and b failure mode after mainshock E3 (F = flexural, S = shear, H = hybrid; for the element numbering refer to Fig. 15). c Damage level computed at wall scale

  Fig. 15

  

  Comparison between observed and simulated damage on CB model for Wall 7 after mainshock E3

• At wall scale, the correspondence in the prevailing activated in-plane mechanism (Fig. 16);

  Fig. 16

  

  Comparison between simulated and observed damage levels after mainshock E3 for load-bearing walls oriented along a X and b Y directions

• At building scale, the overall consistency in the extension and damage level throughout several load-bearing walls and parts of the structure (Fig. 17).

  Fig. 17

  

  Comparison between the cumulative rate of pier damage as simulated and observed after each mainshock: a FB model; b CB model

Figures 14 and 15 summarize how the data from numerical simulations were post-processed, considering Wall 7 oriented in the Y direction as an example. The damage level (Fig. 14a) and failure modes (Fig. 14b) were firstly compared for each pier element and mainshock. Then, consistently with the observed damage (see Sect. 2), the reference damage level of the wall was computed as the average value of the piers weighted by their gross sectional area (Fig. 14c). The comparison in Fig. 14a shows a more satisfactory agreement between damage simulated by the CB model and damage observed after the whole sequence. Figure 14b shows that, whatever the base condition, both models predict the occurrence of the flexural failure mode more frequently than in reality. Finally, Fig. 14c suggests that both numerical models tend to overestimate the damage severity at the wall scale under the mainshock E1, with the CB model better predicting the subsequent cumulated damage at both floor levels.

Figure 15 shows a detailed, element-by-element, comparison between the observed and simulated damage to Wall 7 after mainshock E3, considering the numerical results associated with the CB model. Such a comparison shows a good agreement on the distribution of failure modes activated throughout the wall, with a higher overall damage at ground floor. As expected, a higher damage level affects piers rather than spandrels, being these latter strengthened by the RC tie beams.

Figure 16 shows an overview of the damage level simulated at scale of each wall after mainshock E3. In general, a quite overall good agreement can be observed but, on average, the FB model is too over-conservative at the ground floor and the numerical simulations overestimate the damage at the first floor. Overall, the CB model is found to allow the best simulation of the observed damage.

Finally, Fig. 17 depicts the cumulative rate of pier damage (CD_DLi,piers), computed as the percentage of piers that reached or exceeded a given DL, weighted by the corresponding gross sectional area, as originally proposed by Lagomarsino and Cattari (2015). The damage evolution was reconstructed also for the observed damage, as reported in Sect. 2. It is worth to recall that the increase of the observed damage moving from mainshock E2 to E3 is affected by more uncertainty with respect to that related to the transition from mainshock E1 to E3, due to less accurate information available after mainshock E2.

Notwithstanding the already mentioned inconsistency about the initial overestimation of damage following mainshock E1, the models appear able to satisfactorily reproduce the subsequent accumulation. In general, it can be observed that both numerical models tend to overestimate the occurrence of moderate damage (i.e. DL2), whereas a quite good agreement is found for the higher severity degrees (i.e. DL3 through to DL5), particularly for the CB model at the end of seismic sequence. Indeed, it should be recalled that a reliable assignment of DL2 at the pier scale is more difficult to make in reality, being that damage level associated with the attainment of a yielding condition that is complex to be detected by visual inspection.

6 Conclusions

The paper investigated the seismic response of the P. Capuzi school in Visso, which was monitored during the 2016–2017 Central Italy earthquake sequence. The school represented almost a unicum for the amount of data available not only on the structural response but also on the soil characterization. The availability of both qualitative information on damage accumulation phenomena (as reconstructed by photos and in situ surveys) and quantitative data (as provided by the permanent monitoring system) formed a valuable and indispensable source for a comprehensive validation of equivalent frame models with and without consideration of soil–foundation–structure interaction.

The fundamental periods of the structure, as identified from the interpretation of ambient noise measurements, resulted very close to the soil predominant period, evidencing that the spectral accelerations affecting the building performance are those mostly amplified by the soil. Such an occurrence, together with the intensity and frequency content of the seismic events, justified the high damage level observed on the school structure, which did not present significant deficiencies nor vulnerability factors (apart the in-plan irregularity) from a structural point of view.

Nonlinear time history analyses were performed by applying the accelerograms recorded at the school basement to fixed-base (FB) and compliant-base (CB) three-dimensional models of the building, which were developed according to the equivalent frame approach. Periods and modal shapes of both models were compared to the results of the on-site dynamic identification of the school. The comparison revealed a strong influence of the soil compliance in the linear range, so that the match between experimental and numerical frequencies is much better in the case of the CB model.

Conversely, the nonlinear response of the FB and CB models is more similar during the three strong motions, because (1) the mobilization of structural nonlinearity prevails on the soil–structure interaction effects and (2) the seismic structural response is mainly governed by the frequency content of the input motions. As a matter of fact, more significant differences between the responses of the two models were recognized through a time–frequency analysis during the low-amplitude stages of the input motions. Both the experimental and numerical predominant periods of the school increase over time, highlighting a stiffness degradation of the structure and the relevant progression of nonlinear response, as proven by the damage accumulation detected by the in situ survey.

It must be underlined that the soil–structure model was calibrated in the linear field thanks to the availability of dynamic identification data, whereas nonlinear analyses were performed as a ‘blind prediction’. In fact, nonlinear material properties, such as the masonry strength and the strain-dependency of soil stiffness and damping, were set on the basis of reference literature data, without altering or back-figuring them in order to achieve the best match with the experimental records. This choice firstly reflects the will to test the effectiveness of the equivalent frame modelling in a representative application as it might be managed by a common, even if expert, analyst. The simulation demonstrates satisfactory results, validating the accuracy of such a structural modelling strategy that is widespread in engineering practice. Moreover, the uncoupled approach based on proper impedance functions appeared quite promising to simulate the SSI interaction, if carefully calibrated by duly considering soil nonlinearity and radiation damping. As a perspective, coupled advanced approaches accounting for the explicit modelling of the soil as a continuum will be very useful to confirm the role of SSI interaction and to corroborate the use of more simplified strategies, such as the uncoupled approach, also in the case of URM buildings.