Seismic effectiveness and robustness of tuned mass dampers versus nonlinear energy sinks in a lifecycle cost perspective

Abstract

Tuned mass dampers (TMDs) and nonlinear energy sinks (NESs) are two viable options for passively absorbing structural vibrations. In seismic applications, a trade-off exists in their performance, because TMDs’ effectiveness varies with the structural stiffness while NESs’ effectiveness varies with the earthquake intensity. To investigate this trade-off systematically, a lifecycle cost- (LCC-) oriented robust analysis and design method is here proposed, in which the effectiveness of a solution is measured by the reduction it entails in the expected cost of future seismic losses. In it, structural stiffness variability is modelled using a worst-case approach with lower and upper bounds, while seismic intensity variability is inherently captured by the incremental dynamic analyses underlying every LCC evaluation. The resulting worst-case lifetime cost provides a rational metric for discussing pros and cons of TMDs and NESs, and becomes the objective function for their robust optimization. The method is applied to the design of TMDs and NESs on a variety of single- and multi-story linear building models, located in a moderate-to-high seismic hazard region. Mass ratios from 1 to 10% and structural stiffness reductions up to 4 times are considered. Results show that TMDs are consistently more effective than NESs even in the presence of large stiffness reductions, provided that structural stiffness uncertainty is considered in design. They also show that a conventional robust H_∞ design provides for TMDs a solution which is very close to that obtained by minimizing the proposed LCC metric.

1 Introduction

Dynamic vibration absorbers (DVAs) are passive control devices widely used in vibration mitigation of civil structures (Housner et al. 1997). Most applications are meant to improve serviceability conditions of slender low-damped structures under quasi-stationary excitation. Seismic applications are less common, mainly because the efficacy of passive absorption diminishes with the impulsiveness of the input and with the excursions of the structural response in the inelastic range. Nevertheless, considerable effort has been made in the last decades to assess the seismic effectiveness of DVAs and to enhance it through improving existing types of device and their optimal design criteria (Luo et al. 2014a; Greco et al. 2016; Lu et al. 2018; Matta 2019a).

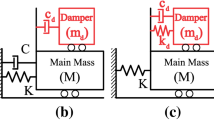
Typically, a DVA is a single-degree-of-freedom (SDOF) mass-spring-damper system appended to the primary structure. Driven by the motion of its structural support, the DVA absorbs vibration energy from the structure and locally dissipates it. Various types of DVA exist, characterized by different types of spring and damper components.

Linear DVAs, known as tuned mass dampers (TMDs), use a linear spring and a linear viscous damper arranged in parallel. Dating back to the first half of the twentieth century (Den Hartog 1956), TMDs absorb vibration energy through resonating with the target structural mode (typically the most energetic one) by means of frequency tuning. Because the natural frequency of the TMD is fixed, its suppression bandwidth is relatively narrow, and its effectiveness diminishes if detuning occurs due to changes in the natural frequency of either the target mode or the absorber (Taflanidis et al. 2009; Marano and Greco 2009).

As an alternative to TMDs, nonlinear DVAs have been proposed, known as nonlinear energy sinks (NESs), which combine a linear viscous damper with a smooth nonlinear spring (Roberson 1952; Gendelman et al. 2001). The nonlinear spring is typically conceived to provide a restoring force that is cubic in the displacement; this can be practically achieved through different arrangements, including the track NES (Wang et al. 2015b), the wire NES (McFarland et al. 2005), and the bumper NES (Luo et al. 2014b). Because of the cubic spring, NESs are “essentially nonlinear” devices, with no fixed natural frequency (Vakakis et al. 2003). Unlike TMDs, they do not need tuning to a specific structural frequency, and can suppress energy over a broader bandwidth through targeted energy transfer (TET), i.e. the nearly one-way, irreversible transfer of vibration energy from the primary structure to the absorber, in which energy is confined and dissipated without backscattering (Nucera et al. 2007). NESs can resonantly interact with one or more structural modes through isolated resonance capture or resonance capture cascades (Vakakis et al. 2003). They can also redistribute vibration energy from lower modes to higher modes, whose contribution to structural displacement is usually less significant (Wang et al. 2019). On the other hand, NESs’ nonlinearity makes their effectiveness depend on the structural vibration amplitude, and therefore on the excitation level. Under harmonic or impulse loads, an activation input threshold exists, below which energy is not efficiently dissipated, and above which the vibration suppression capabilities progressively decrease (Vakakis et al. 2009).

Comparing TMDs and NESs, a performance trade-off seems immediately recognizable, whereby TMDs appear more sensitive to detuning, but independent from the input level as long as the structure remains linear, while NESs appear sensitive to changes of the excitation intensity, but less affected by shifts in the structural modal frequencies.

To the aim of seismic mitigation, TMDs’ sensitivity to detuning and NESs’ sensitivity to the input amplitude may largely influence their effectiveness. Structural frequency shifts often occur during seismic events, as the equivalent linear stiffness of the primary structure (including contributions from soil and nonstructural components) tends to decrease because of reversible or irreversible response nonlinear excursions (Clinton 2006). On the other hand, performance-based earthquake engineering requires that an entire set of seismic intensities be considered in evaluation and design, each contributing to future seismic damages and losses.

A conspicuous literature exists on the seismic effectiveness of TMDs and, to a lesser extent, of NESs, including a few papers comparing the two types. In Gourdon et al. (2007) NESs’ robustness to structural frequency shifts is examined under sinusoidal loads. NESs are proven effective against two impulsive seismic records, but no comparison with TMDs is provided, as well as no investigation of NESs’ performance under a varying seismic amplitude. In Wang et al. (2015b) a TMD and two variants of NES are compared under impulse and seismic loading. Impulse analyses show the robustness of the TMD to amplitude scaling and of the NESs to stiffness variations. Seismic analyses under a scaled set of records show the superior performance of the TMD when the structural stiffness is nominal, and of the NESs when the structural stiffness is reduced to 50%. No seismic analysis is repeated using a different amplitude scaling. In Luo et al. (2014b) six NES devices (including smooth and non-smooth types) are simultaneously operated on a nine-story large-scale model of a building structure under ground motions. Experimental tests show that a rapid mitigation of the structural response is achieved. Numerical simulations show the efficacy of the system against two sets of records representing two distinct earthquake intensities. No comparison with TMDs is reported. Simulating numerically the same benchmark building under earthquake records, in Luo et al. (2014a) structural stiffness reductions are shown to more heavily reduce the seismic effectiveness of TMDs than that of NESs. However, no comparison is reported under varying seismic amplitudes. In Lu et al. (2017) a NES is tested on a large-scale five-story building model. Significant reductions of structural displacements and accelerations are reported, involving multiple vibration modes. No comparison with a TMD is presented. In Boroson et al. (2017) robustly optimized multiple NESs are studied on structures subjected to impulse loading. They are shown to widen the range of input amplitudes over which the single NES is efficient, and to improve its nominal and robust performance. No seismic action is considered and no comparison with TMDs is reported. In Oliva et al. (2017) a NES is numerically tested on a SDOF structure under white noise base excitation. An approximate optimization based on statistical linearization is proposed, resulting in design formulas providing NES’s optimal parameters as a function of the input intensity. No comparison with a TMD is reported. In Wang et al. (2019) a TMD, a smooth NES and a non-smooth NES are compared on a tall building under impulse and seismic loading. Various objectives are considered for optimization and assessment, some incorporating economic factors. As far as the response mitigation is concerned, the three optimal devices achieve a similar performance under impulse loads, the TMD proving superior against amplitude variations and the two NESs against stiffness variations. Under seismic loading, the TMD proves the best option when structural stiffness is nominal, the worst when this latter is reduced to 50%. No uncertainty is considered in design.

Throughout the aforesaid studies, the trade-off in seismic efficacy between TMDs and NESs, although ascertained qualitatively, seems not yet completely clarified in quantitative terms. In most studies, the comparison between TMDs and NESs resolves in a sensitivity analysis of their respective performance versus arbitrary variations in the structural stiffness and in the input intensity. In no case the expectation of stiffness shifts is exploited in design to enhance the absorbers’ robustness and, at the same time, the economic impact of different seismic intensities is used to evaluate and maximize their lifetime benefits.

The main goal of this paper is to fill in this gap and to investigate that trade-off systematically, for single TMDs and single NESs applied on linear building structures susceptible to stiffness variations under earthquake loading. To this purpose, a lifecycle cost- (LCC-) oriented robust analysis and design method is proposed, in which the effectiveness of a solution is measured by the reduction it entails in the expected cost of future seismic losses. Structural stiffness variability is modelled using a worst-case approach with lower and upper bounds, while seismic intensity variability is inherently captured by the incremental dynamic analyses underlying every LCC evaluation. The resulting worst-case lifetime cost provides a rational metric for discussing pros and cons of TMDs and NESs, and becomes the objective function for their robust optimization. Different components of the total lifecycle cost are also specifically addressed, including the cost of drift-dependent and acceleration-dependent damages as well as the cost of human losses, throwing some light on other trade-offs existing between alternative control objectives. The method is applied to the design of TMDs and NESs of varying mass ratio on single- and multi-story building structures, located in a moderate-to-high Italian seismic hazard region. The results offer a quantitative comparison of two devices in multiple design scenarios, which seems to be lacking in the existing literature.

2 The structural model

Single- and multi-story building models are considered in this study, representing existing reinforced concrete (RC) frame building structures. For simplicity, they are planar models, with only one lateral DOF per story in the x direction, and they are linear models. Regarding this latter aspect, although existing RC structures approaching collapse may exhibit an inelastic response with potentially ductile behavior, a linear elastic response is here assumed, and potential inelastic excursions are simplistically modelled as a reduction in the equivalent structural stiffness, assumed constant throughout the seismic event, and uniform along the structure. These simplifying modelling assumptions are clearly inadequate to closely reproduce the several degradation mechanisms potentially occurring in RC frames under severe seismic shaking. Their adoption cannot generally ensure unbiased estimations of peak structural response quantities (on which LCC is made to depend), particularly in dissipative inelastic structures. These modelling assumptions strictly delimit the scope of this paper, whose conclusions have therefore no claim of general validity for all categories of RC frames. An in-depth investigation of how sensitive such conclusions are to modelling assumptions is left for future works. In any case, because most modelling assumptions, with the exception of those reflecting in structural frequency shifts (here specifically accounted for), are likely to affect the performance of both absorbers in a similar way, with only minor influence on their relative cost-effectiveness, which is indeed the main focus of this paper, it is believed that the main conclusions of this work will achieve an acceptable level of generality. Additionally, it should be noticed that exactly the same modelling assumptions (elastic model with uniform stiffness scaling) are quite common in TMDs’ and NESs’ literature (Matta 2011; Luo et al. 2014a; Wang et al. 2015b, 2019). Their simplicity accounts for the issue of detuning in a more succinct way than a rigorous nonlinear model would do, implicitly addressing other potential causes of structural frequency variation, not directly related with seismic damage (long-term material degradation, environmental loads, random fluctuations of mechanical properties, …). Their greater clarity establishes a common ground to compare the results of different studies. Their reduced computational burden allows for an easier incorporation in a design procedure, particularly if robustly oriented.

Atop these planar models a TMD or a NES is alternatively mounted for improving the seismic structural response. Three configurations are thus compared: the uncontrolled one, the TMD-controlled one and the NES-controlled one.

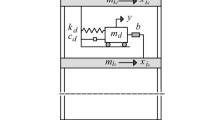
Denoting as N_s the number of stories of the building, the equations of motion for the combined structure-absorber system subjected to a ground acceleration input are expressed as follows (Fig. 1):

$$ {\mathbf{M\ddot{u}}} + {\mathbf{C\dot{u}}} + {\mathbf{Ku}} = - {\mathbf{Mt}}_{g} \ddot{u}_{g} + {\mathbf{t}}_{a} p_{a} $$

(1)

$$ m_{a} \ddot{u}_{a} + p_{a} = - m_{a} \ddot{u}_{g} $$

(2)

where ${\mathbf{u}} = [u_{1} \, u_{2} \, \ldots \, u_{{N_{S} }} ]^{T}$ is the horizontal displacement vector of the structure relative to the ground; ${\mathbf{M}}$, ${\mathbf{C}}$ and ${\mathbf{K}}$ are the mass, damping and stiffness matrices of the structure; $\ddot{u}_{g}$ is the ground acceleration; ${\mathbf{t}}_{g} = [ 1 { 1 } \ldots { 1}]^{T}$ is the topological vector related to the ground acceleration; $p_{a}$ is the absorber reaction force; ${\mathbf{t}}_{a} = [ 0 { } \ldots { 0 1}]^{T}$ is the topological vector corresponding to the absorber location; $u_{a}$ is the horizontal displacement of the absorber relative to the ground; and $m_{a}$ is the mass of the absorber (TMD or NES).

In Eqs. 1 and 2 the absorber reaction force p_a is expressed, respectively for the TMD and for the NES, by

$$ p_{a} = c_{a} (\dot{u}_{a} - \dot{u}_{{N_{S} }} ) + k_{a} (u_{a} - u_{{N_{S} }} ) $$

(3)

$$ p_{a} = c_{a} (\dot{u}_{a} - \dot{u}_{{N_{S} }} ) + \chi_{a} (u_{a} - u_{{N_{S} }} )^{3} $$

(4)

where $c_{a}$ is the damping coefficient of the absorber (TMD or NES); $k_{a}$ is the linear stiffness coefficient of the TMD; and $\chi_{a}$ is the nonlinear stiffness coefficient of the NES.

Fig. 1

Schematics of the planar model of the N_S-story building structure with either a TMD or a NES atop

To account for structural stiffness variations, the (actual) stiffness matrix K in Eq. 1 is taken as

$$ {\mathbf{K}} = {\mathbf{K}}_{0} /\delta $$

(5)

where K₀ is the nominal stiffness matrix and δ is the stiffness reduction factor, scaling all matrix coefficients in the same way.

Complemented by Eqs. 3 and 4, Eqs. 1 and 2 are linear when the absorber is a TMD and nonlinear when the absorber is a NES. They are both numerically solved herein using Matlab Simulink, in accelerator mode so as to shorten the run time (Gidaris and Taflanidis 2013). Each absorber is fully described by three independent design parameters. Denoting by m the total mass of the structure, and by ω₁, ω₁₀ and ζ₁ respectively the (actual) circular frequency, the nominal circular frequency and the damping ratio of its fundamental mode, those three parameters are defined as follows:

• for the TMD as: (1) the mass ratio µ = m_a/m; (2) the (nominal) frequency ratio r = ω_a/ω₁₀, ω_a being the TMD natural frequency; and (3) the TMD damping ratio ζ = c_a/(2ω_a m_a);

• for the NES as: (1) the mass ratio µ = m_a/m; (2) the (nominal) nonlinear stiffness ratio ρ = χ_a/(ω ⁵₁₀ m_a); and (3) the (nominal) NES damping ratio ξ = c_a/(2ω₁₀ m_a).

All said parameters are dimensionless except ρ, measured in s³ m⁻² in the I.S. The mass ratio µ is identically defined for the two absorbers. For the TMD, r and ζ are classically defined. For the NES, ξ is defined like ζ, except that ω₁₀ replaces ω_a (inexistent for a NES), and ρ is defined so that its optimal value would be nearly independent from ω₁₀ if the seismic input were a zero-mean stationary Gaussian white noise process (Oliva et al. 2017).

3 The lifecycle cost performance

3.1 Conventional versus LCC performance measures

The seismic performance of passive control systems is generally evaluated by comparing the controlled and the uncontrolled values of some measurable response quantities, called the engineering demand parameters (EDPs). Various EDPs can be chosen, depending on the deterministic or stochastic nature of the models used to describe the structural system and the seismic action, or on the particular design objective.

Conventional EDPs include the peak value over time of some relevant system output, deterministically computed under one or more selected seismic records (Ohtori et al. 2004). Preferably, a set of records is often used, representing a certain intensity level at the site, and the EDP is averaged over the set. If the system is nonlinear, repeating the procedure for multiple intensity levels reveals how the performance of the control system depends on the seismic intensity (Matta 2019b).

Alternatively, LCC performance evaluation criteria are increasingly used in earthquake engineering to quantify the economic advantages of a mitigation system, on either new or existing constructions (Ang and Lee 2001). Unlike conventional EDPs, which cannot weigh the relative impact of different seismic intensities, the LCC provides a concise and rational scalar measure of the cost-effectiveness of a solution, expressed in monetary units and directly useable by asset managers.

Several recent studies have adopted a LCC perspective to analyze or design control systems for seismic or wind mitigation. A systematic probabilistic framework for LCC evaluation and optimization is presented in Taflanidis and Beck (2009) and later improved in Gidaris and Taflanidis (2015), generally applicable to any engineering system under seismic hazard and specifically demonstrated on RC frame buildings retrofitted with fluid viscous dampers. In Hahm et al. (2013) LCC is used to evaluate the cost-effectiveness of semi-active magneto-rheological dampers on cable-stayed bridges under earthquake loading. In Micheli et al. (2019) LCC is used to discuss the cost-effectiveness of viscous and friction dampers designed to ensure performance-based code-compliant accelerations in steel frame tall buildings under wind loading. In Beheshti and Asadi (2020) LCC is used as the minimization objective for the optimal seismic retrofit of steel frames with viscoelastic dampers, while accounting for their temperature dependence. In Jiang et al. (2020) a new seismic LCC assessment methodology relying on cost-based fragility analysis is proposed to measure the effectiveness of steel panel walls installed in steel frame buildings.

More specifically, LCC concepts have also been used to analyze and design TMDs, for the purposes of either wind mitigation (Wang et al. 2015a; Ierimonti et al. 2018) or seismic mitigation (Lee et al. 2012; Matta 2015; Ruiz et al. 2016; Matta 2018). Conversely, to the best of the author’s knowledge, no application of LCC concepts to NESs is reported in the literature, though the amplitude dependence of their performance should make them ideal candidates for LCC assessment.

In this paper, LCC is used to evaluate and compare the seismic effectiveness of TMDs and NESs. The remaining of this Section provides the details of the adopted criterion for LCC analysis.

3.2 Engineering demand parameters for LCC analysis

In seismic engineering, LCC assessment requires the analysis of the structure under multiple levels of earthquake intensity. To this aim, incremental static or dynamic analyses can be used (Vamvatsikos and Cornell 2002). When applied to structures controlled through VDAs, LCC methods implementing nonlinear dynamic analysis are required. Among these, multiple-stripe dynamic analysis (MSDA) is widely adopted. It consists in performing multiple suites of nonlinear dynamic analysis at different seismic levels, each level corresponding to a given return period, or equivalently to a given exceedance probability in a given time, according to the seismic hazard at the site. The result is the correlation between the seismic intensity and the corresponding structural response, described by one or more EDPs (Lagaros et al. 2006).

Selecting the appropriate EDP is crucial in LCC analysis. Among the various EDPs proposed in the literature for evaluating the seismic performance of frame building structures, the peak interstory drift ratio θ is by far the most used (Ghobarah et al. 1999). Consolidated relations exist between θ and performance conditions (immediate occupancy, life safety and collapse prevention), as well as between θ and damage states, in the academic literature (Wen and Kang 2001; Ghobarah 2004; Su et al. 2016) and in building codes (SEAOC Vision 2000; FEMA-273 1997; FEMA-350 2000; CSA A23.3-04 2004; PEER Report 2010/05). Additionally, because damage to building contents may be sensitive not only to θ but also to the acceleration of their supports, another significant EDP is the peak story acceleration A. θ-sensitive contents are typically claddings and partitions in their in-plane mode. A-sensitive contents are typically furniture and equipment (Elenas and Meskouris 2001), suspended ceilings and automatic sprinklers (Ramirez et al. 2012; Ierimonti et al. 2018), as well as claddings and partitions in their out-of-plane mode.

In this paper, MSDA is used for performing LCC analyses. It is applied to the planar model presented in Sect. 2, by considering N_L = 8 intensity levels, each described by a suite of N_R = 14 spectrum-compatible records. θ and A, separately computed at each story, are used as the significant EDPs, and their relation with damage is taken as proposed for RC frame structures in Mitropoulou et al. (2010) based on the works by Ghobarah (2004) and by Elenas and Meskouris (2001), according to the N_D = 7 damage states reported in Table 1.

Table 1 Damage states as a function of the selected EDPs (Mitropoulou et al. 2010)

3.3 LCC evaluation model

The expected earthquake-related total cost $C_{TOT}$ of an existing building over its residual lifetime t can be defined as

$$ C_{TOT} (t) = C_{a} + C(t) $$

(6)

where $C_{a}$ is the initial cost of the absorber, comprising its material and labor costs, and C(t) is the present value of future seismic damages and losses, accounting for various cost categories: the cost of structural and non-structural repair, the cost of loss of contents, the cost of injury recovery, the cost of human fatality, and other direct or indirect economic losses (e.g. rental and income costs) (Wen and Kang 2001; Lagaros et al. 2006).

Because the aim of this paper is the comparison of TMDs and NESs in terms of their damage cost savings, rather than in terms of their construction and installation cost (which, in the lack of more accurate cost models, can be in fact deemed approximately equal for the two absorbers), attention will be mainly focused on the damage cost C, whose minimization provides the LCC-optimal solution. For the existing building with no absorber, C coincides with the uncontrolled building damage cost, C_unc. For the controlled building, the more C decreases with respect to C_unc, the more cost-effective the absorber is.

According to its dependence on the two relevant EDPs, the damage cost C can be defined as

$$ C = C_{\theta } + C_{A} $$

(7)

where $C_{\theta }$ is the drift-dependent damage cost and $C_{A}$ is the acceleration-dependent damage cost.

Assuming a Poisson model of earthquake occurrences, and an immediate restoration of damaged buildings to their original intact state after every significant earthquake, $C_{\theta }$ and $C_{A}$ are given (Wen and Kang 2001) respectively by

$$ C_{\theta } = t_{a} \sum\limits_{i = 1}^{{N_{D} }} {C_{\theta }^{i} \phi_{o,\theta }^{i} } $$

(8a)

$$ C_{A} = t_{a} \sum\limits_{i = 1}^{{N_{D} }} {C_{A}^{i} \phi_{o,A}^{i} } $$

(8b)

where $\phi_{o,\theta }^{i}$ and $\phi_{o,A}^{i}$ are the mean frequencies of occurrence of the ith damage state, respectively for θ-dependent and A-dependent damages; $t_{a} = (1 - e^{ - \lambda t} )/\lambda$ is the actualized time period, with λ being the momentary discount rate; and $C_{\theta }^{i}$ and $C_{A}^{i}$ are the θ-dependent and the A-dependent costs of the ith damage state, respectively given as

$$ C_{\theta }^{i} = C_{dam}^{i} + C_{con,\theta }^{i} + C_{ren}^{i} + C_{inc}^{i} + C_{inj,m}^{i} + C_{inj,s}^{i} + C_{fat}^{i} $$

(9a)

$$ C_{A}^{i} = C_{con,A}^{i} $$

(9b)

where $C_{dam}^{i}$ is the damage repair cost, $C_{con,\theta }^{i}$ is the cost for the loss of θ-sensitive contents, $C_{con,A}^{i}$ is the cost for the loss of A-sensitive contents, $C_{ren}^{i}$ is the rental loss cost, $C_{inc}^{i}$ is the income loss cost, $C_{inj,m}^{i}$ is the minor injury cost, $C_{inj,s}^{i}$ is the serious injury cost, and $C_{fat}^{i}$ is the human fatality cost (Mitropoulou et al. 2010). Noticeably, 7 cost categories provide $C_{\theta }^{i}$ in Eq. 9a, and only one cost category provides $C_{A}^{i}$ in Eq. 9b.

For the ith damage state, the cost of each category is computed according to Table 2, where the basic costs, reported in the third column, provide the first component of the calculation formulas reported in the second column. The damage state parameters, providing the last component of the calculation formulas, are reported in Table 3 (Mitropoulou et al. 2010).

Table 2 Damage state cost calculation formulas (Mitropoulou et al. 2010)

Table 3 Damage state parameters for cost evaluation (Mitropoulou et al. 2010)

Following Wen and Kang (2001), the occurrence of each damage state is governed by the drift ratio intervals and the acceleration intervals reported in Table 1, according if drift-dependent or acceleration-dependent damages are concerned.

Referring to drift-dependent damages, and denoting as $\theta^{i}$ the lower bound for the ith damage state, $\phi_{o,\theta }^{i}$ in Eq. 8a is given by

$$ \phi_{o,\theta }^{i} = \phi_{e,\theta }^{i} - \phi_{e,\theta }^{i + 1} $$

(10)

where $\phi_{e,\theta }^{i}$ is the mean frequency of exceedance of $\theta^{i}$ and can be obtained as

$$ \phi_{e,\theta }^{i} = f(\theta^{i} ) $$

(11)

In Eq. 11, f is an appropriately shaped function, whose parameters are determined by exactly fitting the N_L known $\phi_{e}^{j} \,$ – $\, \theta^{j}$ pairs, each pair corresponding to a specific intensity level, having probability of exceedance $P_{e}^{j}$ in a given time period τ ^j. For each intensity, $\phi_{e}^{j}$ is derived, according to Poisson’s law, as

$$ \phi_{e}^{j} = - \frac{1}{{\tau^{j} }}\ln (1 - P_{e}^{j} ) $$

(12)

while $\theta^{j}$ is the average value of θ obtained through nonlinear dynamic analyses under the corresponding suite of records. In this paper, f is expressed as the weighted sum of a piecewise hyperbolic function and a piecewise linear function, as in Matta (2015). A graphical representation of f will be shown later, in Fig. 3.

Similarly, referring to acceleration-dependent damages, and denoting as $A^{i}$ the lower bound for the ith damage state, $\phi_{o,A}^{i}$ in Eq. 8b is given by

$$ \phi_{o,A}^{i} = \phi_{e,A}^{i} - \phi_{e,A}^{i + 1} $$

(13)

where $\phi_{e,A}^{i}$ is the mean frequency of exceedance of $A^{i}$ and can be obtained as

$$ \phi_{e,A}^{i} = f(A^{i} ) $$

(14)

In Eq. 14, f has the same expression as in Eq. 11, and its parameters are determined by fitting the N_L known $\phi_{e}^{j} \,$ – $A^{j}$ pairs, where $\phi_{e}^{j}$ is still given by Eq. 12 and $A^{j}$ is the average value from nonlinear dynamic analyses.

Admitting that damage and cost at each story depend only on the EDPs computed at that story, the procedure described above is separately conducted for every story to determine the individual story cost, and finally the overall building cost is derived by summing over the building height. The only exception are the costs related to the collapse damage state (“7-Destroyed”), which is supposed to be governed, for every story, by the largest θ along the building height, because the collapse of any story is admitted to imply the collapse of the whole building.

4 The robust lifecycle cost design

Based on the LCC evaluation procedure exposed in Sect. 3, multiple objective functions can be identified, which will be used in this paper to investigate the trade-off between the two absorbers. For convenience, all said objectives are defined by normalizing the controlled value of a predefined quantity to its corresponding uncontrolled value.

The main objective is the normalized overall LCC, defined as $C^{*} = C/C_{unc}$ (the “*” superscript denoting normalization). This appears the most rational and objective performance metric, regarded in this paper as the preferential and decisive optimality criterion for designing a dynamic absorber.

Three other secondary objectives are proposed as partial LCC metrics. They are defined, respectively, as $C_{\theta }^{*} = C_{\theta } /C_{\theta ,unc}$(normalized θ-dependent LCC), $C_{A}^{*} = C_{A} /C_{A,unc}$ (normalized A-dependent LCC), and $C_{h}^{*} = C_{h} /C_{h,unc}$(normalized human LCC), where $C_{h}$ is the lifecycle cost of injuries and fatalities, obtained by summing up categories 5–7 in Table 2. Compared with $C^{*}$, these three objectives allow discussing the trade-offs that exist between cost- oriented and safety-oriented design strategies, as well as between displacement and acceleration reduction approaches.

Two further objectives are finally introduced for each seismic level and for each story, respectively defined as $\theta^{j*} = \theta^{j} /\theta_{unc}^{j}$ (normalized θ) and as $A^{j*} = A^{j} /A_{unc}^{j}$ (normalized A). These objectives allow measuring absorbers’ performance in a more conventional way, and discussing its amplitude dependence.

Because the structural stiffness is uncertain, and variable with the stiffness reduction factor δ according to Eq. 5, both the uncontrolled and controlled quantities defining the abovementioned objectives, and therefore the objectives themselves, are dependent on δ. To avoid the need of an accurate probabilistic uncertainty description, a worst-case approach is here adopted in which δ can take any possible value between a lower bound and an upper bound. The lower bound is taken as 1 (nominal stiffness) and the upper bound, denoted as d, is variously assigned.

For both absorbers, once the mass ratio µ is chosen, the search domain is two-dimensional, the design variables being r and ζ for the TMD, ρ and ξ for the NES. Consequently, depending on the assigned values of µ and d, and referring independently to any of the objective functions defined above, here generically denoted as F_ob, each single-objective robust optimization problem can be formulated, respectively for the TMD and the NES, as

$$ F_{ob,opt} = \mathop {\hbox{min} }\limits_{r,\varsigma } \mathop {\hbox{max} }\limits_{\delta } F_{ob} ,\quad [r_{opt} ,\varsigma_{opt} ] = \arg \mathop {\hbox{min} }\limits_{r,\varsigma } \mathop {\hbox{max} }\limits_{\delta } F_{ob} ,\quad 1 \le \delta \le d $$

(15a)

$$ F_{ob,opt} = \mathop {\hbox{min} }\limits_{\rho ,\xi } \mathop {\hbox{max} }\limits_{\delta } F_{ob} ,\quad [\rho_{opt} ,\xi_{opt} ] = \arg \mathop {\hbox{min} }\limits_{\rho ,\xi } \mathop {\hbox{max} }\limits_{\delta } F_{ob} ,\quad 1 \le \delta \le d $$

(15b)

The solution of Eqs. 15a and 15b is obtained, simultaneously for all the objectives, by exploring the two-dimensional search space over a unique, sufficiently large, domain, so to encompass the global minima of every F_ob, and with a sufficiently dense mesh, so to achieve the desired accuracy. More efficient optimization algorithms might be used, but hardly any so simple and controllable. This criterion provides not only the multiple individual optima but also the trade-off among different objectives, representable in the classical form of Pareto fronts, thus offering a view into the solution of the multi-objective optimization problem (Goldberg 1988). At the same time, this criterion also provides an immediate understanding of the sensitivity of each objective function to the design variables.

5 The case studies

The robust optimization methodology exposed in Sect. 4 is applied to the optimal design of a TMD and a NES on four different models of existing RC frame building structures, located in a moderate-to-high seismic region. The main features of the proposed case studies are reported in this section.

5.1 The seismic input

The four buildings are located in L’Aquila (Central Italy), at geographic coordinates 42°21′57.60″ N and 13°23′39.84″ E, on a Type B soil according to Eurocode 8 (EN 1998-1:2004). The site seismic hazard is defined according to the INGV seismic hazard maps adopted by the Italian building code (NTC MIT 2018). Eight hazard levels of increasing return period T_R are considered, whose main characteristics are reported in Table 4. For each level, 14 spectrum-compatible natural seismic records are selected, compliant with the 5%-damped pseudo-acceleration horizontal elastic spectrum specified by NTC (MIT 2018) (Fig. 2). They are extracted from the European Strong-Motion Database, for sites on Type B soil. They are chosen so that their moment magnitude M and their source-to-site distance R approach those representative of the seismic hazard at the site, and they are scaled to match the elastic response spectra at the site. The complete list of records in each set is reported in the “Appendix”.

Table 4 The N_L = 8 multiple intensity levels

Fig. 2

Horizontal pseudo-acceleration 5%-damped elastic spectra: a Set 6 (T_R = 475 years): individual spectra and their average, compared with the target normative spectrum; b Sets 1–8: average and target spectra

5.2 The uncontrolled structure

5.2.1 The nominal model

The four buildings are modelled as planar linear frame structures according to Sect. 1, having respectively 1, 3, 8 and 15 stories, and accordingly denoted as B01, B03, B08 and B15. Regular in elevation, they have constant interstory height of 3.5 m, and equal mass in every story. Their stiffness matrix is shear-type, and their damping ratio is 0.03 in every vibration mode. Their nominal stiffness matrix K₀ is assigned so that:

• the nominal fundamental period is $T_{10} = C_{1} H^{0.75}$, where H is the building height and C₁ is 0.075, as suggested for RC frame buildings (Su et al. 2016; Eurocode 8; NTC MIT 2018);

• the interstory stiffness is distributed along the height in proportion to the design shear force computed for the reference return period T_R = 475 years (BSE hazard level), as obtained through a multi-modal spectral analysis using the corresponding elastic spectrum and the SRSS combination rule; this condition entails, along the building height, a uniform design value of the interstory drift, and an approximately parabolic interstory stiffness.

The main structural features of the four nominal models are reported in Table 5, showing for each building: (1) the distribution of the nominal interstory stiffness along the height, normalized to the story mass; (2) the nominal natural frequencies of the first three modes; (3) the percentage modal masses of the first three modes.

Table 5 The main features of the four nominal building models

For the sake of the LCC evaluation, a surface of 1000 m² and a mass of 560 kg/m² (comprising 500 kg/m² due to permanent loads and 0.3 times 200 kg/m² due to residential live loads) is conventionally assumed for each floor of every building. Additionally, the lifetime t is assumed as 50 years and the annual discount rate λ as 0.02.

With these data, the LCC of the four uncontrolled nominal buildings can be computed. Figure 3a, b exemplify, for the 8th story of building B08, the determination of the annual frequencies of exceedance of the different damage states, respectively in terms of drift-sensitive (a) and acceleration-sensitive damages (b). The black circles represent the “forward step” of the procedure, corresponding to the N_L EDP–frequency pairs coming from time-history analyses. The continuous line represents their interpolation by f in Eqs. 11 and 14. The white circles represent the “backward step” of the procedure, providing the N_D EDP–frequency pairs, from which the annual frequencies of occurrence are derived according to Eqs. 10 and 13 (as exemplified in Fig. 3a for the 5th damage state).

Fig. 3

Uncontrolled nominal building B08. Annual frequency of exceedance for the 8th story, as a function of: a the drift ratio; b the floor acceleration. Black circles: from analyses; white circles: from fitting

For the four uncontrolled nominal buildings, the lifecycle cost $C_{unc}$ is reported in Fig. 4a, b, respectively decomposed among cost categories (a) and damage states (b), and in both cases normalized to the initial building cost $C_{0}$, computed as the replacement cost of all structural components and contents. It results that $C_{unc}$ ranges from 4.36% (for B01) to 8.53% (for B03) of the initial building cost, expectedly for a moderate-to-high seismic hazard. Referring to the cost categories (Fig. 4a), for building B01 the acceleration-dependent cost (8th category, yellow) largely prevails over the drift-dependent cost (the other 7 categories), while for buildings B03, B08 and B15 the acceleration-dependent cost is second after structural damage cost (1st category, dark blue). Injury costs are nearly irrelevant, while the fatality cost increases with the building height, ranging from 0.26% (for B01) to 3.92% (for B15), in percentage of $C_{unc}$. Referring to the damage states (Fig. 4b), most damage appears to be inflicted in the “4-Moderate” damage state, followed by the “3-Light”. Collapse damage costs range from 2.89% (for B08) to 4.96% (for B01).

Fig. 4

Lifecycle cost $C_{unc}$ for the four uncontrolled nominal buildings, normalized to the initial building cost $C_{0}$: a decomposition in cost categories; b decomposition in damage states

5.2.2 The uncertain model

The four nominal building models are turned into their corresponding uncertain models by incorporating into the stiffness matrix the stiffness reduction factor δ. The structural performance, in terms of both EDPs and costs, becomes a function of δ. Various values of δ will be considered in this paper, ranging from 1 to 4.

5.3 The absorber and the controlled structure

A single TMD and a single NES are separately mounted atop each building. Three mass ratios µ are considered for each absorber, respectively equal to 1%, 5% and 10%. The two design variables of each absorber are determined by solving the minimization problem in Eqs. 15a and 15b. Because δ affects any objective function in those equations, its upper bound d determines the worst-case optimal solution.

6 The results

The results of applying the proposed design methodology to the selected case studies are reported in this Section, respectively for the nominal and the uncertain models.

6.1 The nominal LCC design

The nominal design is accomplished by solving Eqs. 15a and 15b with d = 1, respectively for the TMD and the NES. Many design scenarios are addressed, according to all possible combinations of: (1) the four buildings; (2) the three mass ratios; and (3) the various objectives introduced in Sect. 4. The adoption of a unique large search space permits the simultaneous optimization of several objectives. For example, Fig. 5a, b, referring to a NES having µ = 5% on building B01, show how the same search grid can simultaneously minimize multiple objectives: two LCC objectives, $C_{\theta }^{*}$ and $C_{A}^{*}$ (in Fig. 5a), and two EDP objectives, $\theta^{1*}$ and $A^{8*}$ (in Fig. 5b). The trade-off among the different objectives is immediately understood, as well as the sensitivity of each F_ob to the design variables.

Fig. 5

Optimization of a NES on nominal building B01 (µ = 5%). Dependence of some objectives on the NES’s parameters: a LCC-type objectives ($C_{\theta }^{*}$ and $C_{A}^{*}$); b EDP-type objectives ($\theta^{1*}$ and $A^{8*}$)

In Fig. 6, still considering building B01 but adopting $\theta^{j*}$ as the F_ob (with j = 1–8), the optimal solution is plotted versus the seismic level for both TMD and NES, and for the three mass ratios. Figure 6a–c show the TMD’s optimal parameters, $r_{opt}$ and $\varsigma_{opt}$, and the corresponding $\theta_{opt}^{j*}$. Figure 6d–f show the NES’s optimal parameters, $\rho_{opt}$ (in log scale) and $\xi_{opt}$, and the corresponding $\theta_{opt}^{j*}$. Figure 6g compares the same curves already plotted in Fig. 6c, f, for better clarity. Focusing on the absorbers’ optimal parameters, it appears that these are nearly amplitude independent for the TMD but not for the NES, whose optimal stiffness ratio $\rho_{opt}$ largely decreases with the seismic level. Focusing on the absorbers’ optimal performance, it appears that: (1) this is nearly amplitude independent for both absorbers; (2) the TMD is systematically superior to the NES. Similar results might be shown for $A^{j*}$, omitted for brevity.

Fig. 6

Optimal $\theta^{j*}$ and corresponding optimal parameters for a TMD and a NES installed on building B01 in nominal conditions, as a function of the seismic intensity level

Clearly, the nearly amplitude independent performance recognized in Fig. 6g is conditioned on the assumption that, at each seismic level, the absorbers’ parameters should be equal to their respective optimal values corresponding to that level, i.e. should vary with the seismic intensity according to Fig. 6a, b, d, e. Because this adjustability is impossible for passive devices, the actual performance shall be optimal only at a certain intensity level, and degraded at all others. The proposed LCC approach will identify the best compromise among different intensities, thus minimizing the overall extent of that degradation.

To better focus on the LCC design approach, the EDP objectives can be conveniently replaced by the four LCC objectives, i.e. the main objective $C^{*}$ and the partial objectives $C_{\theta }^{*}$, $C_{A}^{*}$ and $C_{h}^{*}$. The corresponding nominal optimal solution is then reported in Table 6 for the TMD and in Table 7 for the NES, covering all combinations of the four buildings and the three mass ratios.

Table 6 Nominal TMD design according to the 4 LCC objectives, for the 4 buildings and the 3 mass ratios

Table 7 Nominal NES design according to the 4 LCC objectives, for the 4 buildings and the 3 mass ratios

Tables 6 and 7 suggest the following considerations, valid in the absence of stiffness uncertainty:

• Among the three partial objectives, $C_{h,opt}^{*}$ is consistently the smaller, followed by $C_{\theta ,opt}^{*}$ and then by $C_{A,opt}^{*}$, while the main objective $C_{opt}^{*}$ is intermediate between $C_{\theta ,opt}^{*}$ and $C_{A,opt}^{*}$. In other words, if optimized for a partial objective at a time, absorbers are more efficient in reducing drift-related costs than acceleration-related costs, and human costs more than any other cost. This difference is caused by the nonlinear relation existing between the reduction of costs and the reduction of EDPs: an equal reduction in drifts and accelerations at all seismic levels produces cost reductions that differ among the various damage states, and between θ-dependent and A-dependent costs. For example, the first row of Table 6 (TMD on building B01 with µ = 1%) shows four optimal solutions which are very close to each other in terms of $r_{opt}$ and $\varsigma_{opt}$; in fact, they are all characterized by reductions of about 12% in drifts and 14% in accelerations at every seismic intensity; yet their optimal objectives are quite different, ranging from 33 to 84%.

• The TMD proves consistently superior to the NES, for all buildings, mass ratios and objectives (a total of 48 cases), with only one exception (building B08, µ = 10% and $C_{h,opt}^{*}$, where the NES is slightly better). On geometric average, the value of $C_{opt}^{*}$ obtained with the TMD is 84% of the value obtained with the NES. This percentage is nearly invariant with µ; it decreases to about 80% for B01 and B03, and increases to about 90% for B08 and B15. Referring to $C_{h,opt}^{*}$, the percentage drops to 73%.

• Regarding TMD’s optimal parameters, $r_{opt}$ tends to decrease with µ (as typical of TMDs) and with the building height. More confused is the trend for $\varsigma_{opt}$, which tends to increase with µ but shows no clear relation with the building height. For B08 and B15, the TMD optimized for $C_{A}^{*}$ tunes to the second structural mode instead of the first one, with $r_{opt}$ much higher than 1 and $\varsigma_{opt}$ much increased. The TMD optimized for $C_{h}^{*}$ differs significantly from the TMD optimized for $C^{*}$, in an apparently random way.

• Regarding NES’s optimal parameters, $\rho_{opt}$ tends to decrease and $\xi_{opt}$ tends to increase with µ, both showing no clear relation with the building height.

• Comparing the optimal damping ratios of TMD and NES, $\varsigma_{opt}$ appears basically smaller than $\xi_{opt}$, particularly for small building heights. Consequently, the optimal value of the damping coefficient $c_{a}$ is significantly smaller, on average, for the TMD than for the NES.

One interesting result in Tables 6 and 7 is the difference among the optimal solutions corresponding to different objectives. The trade-off among the four objectives is partially shown in Fig. 7. Namely, the $C^{*}$ – $C_{h}^{*}$ trade-off is shown in Fig. 7a÷d, and the $C_{\theta }^{*}$ – $C_{A}^{*}$ trade-off in Fig. 7e÷h, for the four buildings. In each figure, Pareto fronts are shown (Goldberg 1988), composed by all non-dominated solutions encountered along the search grid. Obviously, these Pareto fronts include, at their ends, the individual optimal solutions already met in Tables 6 and 7.

Fig. 7

TMD and NES Pareto fronts of the non-dominated solutions in the nominal case, for the 4 buildings and the 3 mass ratios: (a÷d) $C^{*}$ – $C_{h}^{*}$ trade-off for the 4 buildings; (e÷h) $C_{\theta }^{*}$ – $C_{A}^{*}$ trade-off for the 4 buildings

Figure 7 shows that, in the absence of stiffness uncertainty:

• NESs’ Pareto fronts are entirely dominated by TMDs’ Pareto fronts, for all buildings and for all mass ratios; i.e. the TMD is systematically superior to the NES.

• Increasing µ always improves performance: Pareto fronts drawn for µ = 1% are entirely dominated by Pareto fronts drawn for µ = 5%, and these by Pareto fronts drawn for µ = 10%.

• Referring to the TMD, Pareto fronts have a limited extension and a convex shape, showing small competitiveness between alternative objectives. In some cases, the front is nearly punctual, indicating that the same solution is optimal w.r.t. both objectives. This is the case, e.g., of the TMD on building B01 (Figs. 7a and e). This small trade-off ensures, for a TMD, that the most cost-effective solution is also nearly the safest for life protection. Only on B08 and B15 the TMD presents a relatively large $C_{\theta }^{*}$ – $C_{A}^{*}$ Pareto front (Fig. 6g, h), which indeed becomes concave for building B15 when µ = 1%. The two objectives are truly competing in these cases, because, for building B08 and, even more, for building B15, $C_{\theta }^{*}$ is governed by the first structural mode whilst $C_{A}^{*}$ by the second, as already mentioned in commenting Table 6.

• Referring to the NES, although few Pareto fronts may be relatively narrow (Fig. 7c), the others generally appear wide and sometimes concave (Fig. 7a, b, e). This phenomenon does not seem due, as for the TMD, to an attempt of the NES to control higher modes (it appears also on building B01, which has a single mode), but rather to the inability of the NES to effectively control a large range of seismic intensities. Because $C^{*}$ is governed by intermediate intensities and $C_{h}^{*}$ by the highest ones, a trade-off between cost-effectiveness and safety necessarily arises for the NES.

In particular, if the TMD and the NES are nominally designed assuming $C^{*}$ as the only objective function, the two normalized EDPs, expressed by their mean value along the building height, are as shown in Table 8. For brevity, results are reported only for the BSE (T_R = 475 years) and MSE hazard levels (T_R = 2475 years). The superiority of the TMD is evident, larger in terms of θ than in terms of A, and scarcely influenced by the hazard level. Namely, in geometric average, $\bar{\theta }^{*}$ and $\bar{A}^{*}$ result, for the TMD, 0.91 and 0.94 times the respective values obtained for the NES.

Table 8 Normalized mean EDPs, as provided by the nominally designed TMD and NES in case of T_R = 475 years and T_R = 2475 years, for the 4 buildings and the 3 mass ratios

6.2 The robust LCC design

The robust design is accomplished by solving Eqs. 15a and 15b with d > 1, respectively for the TMD and the NES. For example, d = 2 is assumed. For brevity, $C^{*}$ is the only objective function used for optimization. To reduce the computational effort, the values of δ over which the maximum of F_ob is evaluated in Eqs. 15a and 15b are limited to the two bounds of the assigned interval, i.e. to 1 and d.

Results are reported in Tables 9 and 10, and can be commented as follows:

• $C_{opt}^{*}$ obviously increases w.r.t. the nominal case. For the TMD, the increase is of 1.11 times on average. For the NES, of 1.04 times. In the end, $C_{opt}^{*}$ obtained for the TMD is 0.90 times the value obtained for the NES.

• For the TMD $r_{opt}$ systematically decreases w.r.t. the nominal case (by 0.74 times on average), as expected (Matta 2011). For the NES $\rho_{opt}$ reduces on average (by 0.31 times) but not systematically. For both absorbers the average reductions are more conspicuous as µ gets larger.

• For the TMD $\varsigma_{opt}$ systematically increases w.r.t. the nominal case (by 1.88 times on average), as expected (Matta and De Stefano 2009). For the NES $\xi_{opt}$ reduces on average (by 0.77 times) but not systematically. For the TMD the increase is less conspicuous as µ gets larger, while for the NES the decrease shows no clear correlation with µ. At the end, the gap between $\varsigma_{opt}$ and $\xi_{opt}$ reduces, the former being on average 0.95 times the latter.

• The normalized mean EDPs computed for T_R = 475 years and T_R = 2475 years confirm the superiority of the TMD already recognized in Table 8, although here reduced by structural stiffness variations. In geometric average, $\bar{\theta }^{*}$ and $\bar{A}^{*}$ are, for the TMD, 0.93 and 0.98 times the respective values obtained for the NES.

To compare the robust solution obtained in this Subsection with the nominal solution obtained in the previous one, a robust analysis can be run, in which the LCC performance of the two solutions is evaluated under structural stiffness variations, with δ ranging from 1 to d = 2. Focusing on $C^{*}$ and $C_{h}^{*}$, their dependence on δ is shown in Fig. 8, for the two absorbers, the 4 buildings and the 3 mass ratios. Unlike in Fig. 7a÷d, the Pareto fronts are now replaced, for each value of δ, by a single sample corresponding to $C_{opt}^{*}$.

Table 9 Robust TMD and NES design with d = 2 and F_ob = $C^{*}$, for the 4 buildings and the 3 mass ratios

Table 10 Normalized mean EDPs, as provided by the robustly designed TMD and NES (d = 2) in case of T_R = 475 yrs and T_R = 2475 yrs, for the 4 buildings and the 3 mass ratios

Fig. 8

Evolution of $C^{*}$ (ordinates) and $C_{h}^{*}$ (abscissas) as a function of δ, for the 4 buildings (in columns) and the 3 mass ratios (in rows). Comparison of the TMD and NES, both nominal and robust, with $C^{*}$ the only design objective. Each circle corresponds to a different value of δ, ranging from 1 (rimmed circle) to 2 with 0.1 spacing

Figure 8 can be commented as follows:

• For the nominal TMD (blue curves), $C^{*}$ tends naturally to increase with δ. For δ = 2, most of the nominal performance is lost in the case of small mass ratios, whilst a certain effectiveness survives in the case of large mass ratios (particularly for the multi-story buildings, because of their larger effective mass ratio). Also $C_{h}^{*}$ (here no longer the objective of design) tends to increase with δ, until generally exceeding 1 at some point. These trends are not exactly monotonic with δ, because the absorber effectiveness fluctuates as stiffness reductions randomly alter the “tuning” of the structure to the seismic loadings.

• For the robust TMD (green curves), $C^{*}$ tends to be maximum at the two ends of the δ interval (δ = 1 and δ = 2). This proves that these values of δ are the most difficult to simultaneously minimize, and indeed the only two over which the maximum in Eqs. 15a and b deserves to be computed. In any case, not only $C^{*}$ but also $C_{h}^{*}$ (here not optimized) prove scarcely sensitive to δ. In the absence of stiffness reductions (δ = 1), the disadvantage of the robust TMD over the nominal TMD is generally minor (Fig. 8f, j). As a result, the robust green cluster generally appears more compact than the nominal blue cluster, and favorably located more to the left and below.

• For both the nominal and the robust NES (red and magenta curves, respectively), the relation of $C^{*}$ and $C_{h}^{*}$ with δ is less clearly recognizable, because of the lesser sensitivity of the NES to detuning. Yet, significant fluctuations of $C^{*}$ and $C_{h}^{*}$ with δ appear for the nominal NES, which the robust design helps to reduce. This is particularly apparent for large mass ratios, in which case the magenta cluster appears more compact and decentered, whereas for small mass ratios the red and magenta clusters tend to coincide.

• Comparing the nominal TMD and the nominal NES, a typical trade-off appears between the blue and the red clusters, showing that the TMD is preferable below a certain δ threshold, and the NES above it. Focusing on $C^{*}$, the threshold tends to increase with the building height and with the mass ratio, ranging from 1.5 to more than 2 (for building B15 and for μ = 5% or μ = 10%, the TMD is superior for any considered δ).

• Comparing the robust TMD with both the nominal and the robust NESs, the green cluster appears to entirely dominate both the magenta and the red ones. So, as long as δ ≤ 2, the robust TMD proves superior to all possible NESs, sometimes by a large extent, in terms of both $C^{*}$ and $C_{h}^{*}$.

To check if the superiority of the robust TMD continues to hold under larger stiffness variations than those assumed in design, Fig. 9 plots $C^{*}$ as a function of δ in the range from 1 to 4. The same four optimal cases described above are compared (i.e. nominal TMD and NES, robust TMD and NES optimized for d = 2), plus two new ones that will be explained in Sect. 7.

Fig. 9

Evolution of $C^{*}$ as a function of δ, for the 4 buildings (in columns) and the 3 mass ratios (in rows). Comparison of: (i) the nominal TMD and NES, designed by minimizing $C^{*}$; (ii) the robust TMD and NES, designed by minimizing $C^{*}$; (iii) the nominal and robust TMD, designed by minimizing the worst-case H_∞ transfer function (see Sect. 7 next). All robust designs are conducted assuming d = 2

Focusing on the first four cases, the corresponding $C^{*}$ – δ curves confirm, up to δ = 2, the results obtained in Fig. 8: the nominal TMD is the best option for small values of δ, and the robust TMD is better than any NES.

As δ further increases, the lesser sensitivity of NES to detuning makes the TMD worsen more rapidly, until the performance of the robust TMD (green curve) intercepts that of the robust NES (magenta curve) at some δ threshold. Because the respective curves are not monotonic, an entire δ bandwidth exists (shown in grey), over which the performances of the robust TMD and of the robust NES are equivalent. Before that band the robust TMD is better, after it the robust NES is. The band tends to move rightward as the building height and the mass ratio increase. In 4 out of 12 cases (B08 and B15 for μ = 5% or μ = 10%) the band is absent, indicating that the TMD is always better in the explored δ interval. In the other 8 cases, on average, the band is centered at δ = 3. This means that the robust TMD, designed assuming as the worst possible case d = 2, has so large an advantage over the robust NES to still be preferable up to d ≥ 4 in 4 cases out of 12, and up to about d = 3 in the others. Obviously, if d = 4 were indeed a credible option, this value might be incorporated in the design, and the grey bands would consequently move even further to the right.

These results definitely prove that, in all the cases examined in this paper, the TMD is more convenient than the NES for seismic purposes, even under large fluctuations of the structural stiffness.

7 The robust TF-based TMD design

Section 6 shows that, in all the examined cases, the TMD is seismically superior to the NES. This Section focuses on the TMD alone, to understand if conventional TMD design criteria, based on the optimal manipulation of input–output transfer functions (TFs) of the building-TMD system, can acceptably approximate the results of a LCC design.

To this purpose, the H_∞ design proposed in Matta (2011) is here reformulated in a worst-case robust variant. Namely, denoting as TF = TF(ω) and TF_unc = TF_unc(ω) the controlled and uncontrolled TFs from the ground acceleration to the maximum interstory drift (through the interposition of an appropriate Kanai-Tajimi filter centered on the first structural frequency), and subsequently introducing the normalized transfer function as $TF^{*} = TF/\mathop {\hbox{max} }\limits_{\omega } TF_{unc}$, then the worst-case robust minimization of the H_∞ norm of the latter, defined by $H_{\infty }^{*} = \mathop {\hbox{max} }\limits_{\omega } TF^{*}$, can be formalized as

$$ H_{\infty ,opt}^{*} = \mathop {\hbox{min} }\limits_{r,\varsigma } \mathop {\hbox{max} }\limits_{\delta } H_{\infty }^{*} ,\quad \quad [r_{opt} ,\varsigma_{opt} ] = \arg \mathop {\hbox{min} }\limits_{r,\varsigma } \mathop {\hbox{max} }\limits_{\delta } H_{\infty }^{*} ,\quad 1 \le \delta \le d $$

(16)

The solution of Eq. 16 is reported, for the 4 buildings and the 3 mass ratios, in Table 11 and in Fig. 10, for both the nominal case (d = 1) and the robust case (d = 2).

Table 11 Nominal and robust TMDs designed according to F_ob = $H_{\infty }^{*}$, for the 4 buildings and the 3 mass ratios

Fig. 10

Worst-case normalized TFs for the H_∞-designed TMD, for the 4 buildings and the 3 mass ratios: a nominal case (d = 1); b robust case (d = 2)

Table 11 reports the optimal parameters $r_{opt}$ and $\varsigma_{opt}$, and the corresponding optimal objective function $H_{\infty ,opt}^{*}$. On average, the robust $r_{opt}$ is about 0.8 times the nominal $r_{opt}$, and the robust $\varsigma_{opt}$ is about 2.67, 1.64 and 1.45 times the nominal $\varsigma_{opt}$, respectively for μ = 1%, 5% and 10%.

Figure 10 shows the optimal worst-case normalized TFs. Each TF in Fig. 10b is the envelope of 11 curves, corresponding to the 11 equally spaced values of δ here used to span the interval from 0 to d. The two highest, lateral peaks of each TF derive from the curves corresponding to the upper and lower bounds of that interval. This shows that the maximum in Eq. 16 can be indeed obtained by sampling the δ domain only at its two ends, thus saving computational time.

Comparing Table 11 with Tables 6 and 9 shows that the LCC design and the H_∞ design provide similar optimal solutions. The nominal H_∞ design gives a slightly increased $r_{opt}$ (1.03 times), the robust H_∞ design a slightly decreased $r_{opt}$ (0.96 times), while both H_∞ designs give an increased $\varsigma_{opt}$ (1.35 times on average).

By subjecting the H_∞-designed solutions to the robust analysis already applied in Sect. 6.2, the two aforementioned additional curves in Fig. 9 are obtained. They are the H_∞ counterpart of the dotted curves of equal color obtained with the LCC design. Compared to the LCC-designed TMDs, the H_∞-designed TMDs approximate them well. Their advantage over the NESs is remarkable, especially because they are designed independently from any assumption on the seismic action.

8 Identification of the optimal mass ratio based on the absorber cost

The main focus of this paper is on the relative advantage of TMDs and NESs, measured by the reduction that either option achieves in terms of building damage costs. Accordingly, of the two components making the total cost $C_{TOT}$ in Eq. 6, no attention has been paid in previous sections to the cost of the absorber $C_{a}$, and all has been directed to the building damage cost C.

However, in moderate-to-high seismic hazard regions like the one here examined, particularly on linear or weakly nonlinear structures, C may be relatively small with respect to the initial building cost $C_{0}$, and potentially of the same order of $C_{a}$, if ordinary values of µ are considered. The cost of the absorber, strictly related to µ and possibly to other absorber parameters, becomes then a decisive term for assessing costs and benefits of the control system, i.e. its actual cost effectiveness. To this aim, performance shall be evaluated no longer in terms of C but in terms of $C_{TOT}$ (the new, augmented objective function of design), and µ shall be no longer a fixed datum of the problem (as in Eqs. 15a and 15b) but indeed an independent design variable to be optimally identified (Matta 2018).

With no ambition to solve this augmented optimization problem comprehensively, this final section just briefly touches upon it, broadening the perspective and paving the way for future investigations. Naturally, such reformulation requires a cost model for the absorber. In the lack of more plausible alternatives, the simple cost model proposed for TMDs in Matta (2018) is here adopted for both devices. Such model, drawn from the analysis of previous work (e.g. Taflanidis and Beck 2009; Wang et al. 2015a; Ruiz et al. 2016; Greco et al. 2016), establishes a proportionality between the mass and the cost of the absorber, according to $C_{a}$ = $c_{u}$ · $m_{a}$. Because there is no evidence, in the literature or from the present study, that the unit cost $c_{u}$ should be significantly different for the two devices (for example, the optimal damping coefficients are similar for the two devices, particularly in the case of a robust design), the same value of $c_{u}$ = 1500 €/ton, taken from the range of values suggested for TMDs in Matta (2018), is here assumed for both devices.

With this assumption, and denoting with $C_{a}^{*} = C_{a} /C_{unc}$ and with $C_{TOT}^{*} = C_{TOT} /C_{unc}$ respectively the normalized absorber cost and the normalized total cost, Table 12 reports $C_{a}^{*}$, $C^{*}$ and $C_{TOT}^{*}$ = $C_{a}^{*}$ + $C^{*}$, for the nominal (d = 1) and the robust (d = 2) optimal TMD and NES obtained in previous sections, for the 4 buildings and the 3 mass ratios. Obviously, $C_{TOT}^{*}$ equals 1 in the uncontrolled case. Smaller values mean a profitable investment, larger values a wrong one. Results show that TMDs are much superior to NESs, even more in the light of $C_{TOT}^{*}$ than of $C^{*}$. For both devices, building B03 is the one that is more cost-effectively controlled, followed by B08. In all cases, the smallest $C_{TOT}^{*}$ is obtained using µ = 1%, followed by µ = 5% and finally by µ = 10% (with the only exception of B03 for the TMD and for d = 2, in which case the smallest $C_{TOT}^{*}$ is obtained using µ = 5%). This is the effect of the moderate seismicity of the site, which produces relatively limited damage costs, making large values of µ not economically acceptable, in that more expensive than their corresponding damage cost savings. In this circumstances the optimal µ, that minimizes $C_{TOT}^{*}$ by sufficiently reducing $C^{*}$ without excessively increasing $C_{a}^{*}$, tends to be small, in the order of 1% or less.

Table 12 Absorber, damage and total costs for the nominal (d = 1) and robust (d = 2) optimal TMD and NES as designed in previous sections, for the 4 buildings and the 3 mass ratios (optimal solutions in bold character)

Of course, Table 12 does not exactly identify the optimal µ, but merely compares three values of it, for each combination of building and absorber type. Among these three values, µ = 1% seems reasonably close to optimal for the TMD, on average; it always ensures values of $C_{TOT}^{*}$ smaller than 1, in both the nominal and the robust scenarios. Regarding the NES, µ = 1% seems reasonably close to optimal for buildings B03 and B08, but larger than optimal for buildings B01 and B15, where its cost nullifies or even exceeds its benefits. To rigorously identify the optimal µ for each case, the LCC optimal design procedure illustrated in previous sections should be repeated over a range of µ around the expected optimum. Considering for example the TMD on building B03, this search for the optimal µ would provide (1) µ = 2.5% in the nominal case (d = 1), corresponding to $C_{a}^{*}$ = 0.11, $C^{*}$ = 0.66 and $C_{TOT}^{*}$ = 0.77, and (2) µ = 3.0% in the robust case (d = 2), corresponding to $C_{a}^{*}$ = 0.13, $C^{*}$ = 0.73 and $C_{TOT}^{*}$ = 0.86.

Obviously, the results of Table 12 and of any search for the optimal µ strictly depend on the chosen absorber cost model. For example, a larger value of $c_{u}$ would further increase $C_{TOT}^{*}$ and decrease the optimal value of µ, and viceversa. To achieve conclusive results about the absolute cost-effectiveness of the control, a more accurate cost model would be needed, especially in the present case, where the cost of the optimal absorber is comparable with the cost savings it produces. Following previous proposals of absorbers capable of integrating additional non-structural functions, for example pursuing environmental objectives (Matta and De Stefano 2009), this cost model might appropriately consider other cost advantages of the intervention, to be included in the final budget.

In conclusion, with all the limits of the adopted absorber cost model, and despite having chosen a moderate seismicity site, the installation of a TMD of appropriate mass still appears a profitable investment for all the examined buildings, systematically more convenient than the installation of a NES. Its absolute cost advantages would certainly increase if the seismic damage costs were a larger percentage of the initial building cost, i.e. if a higher seismicity at the site was considered, and maybe also if an inelastic building model was adopted. Investigations on these specific issues are left for future work.

9 Conclusions

The TMD and the NES are compared in this paper in the light of the building LCC and of other metrics, chosen as the design objectives. Uncertainty in the structural stiffness is assumed for performance optimization and assessment. A simplified H_∞ design is also proposed.

The main conclusions, resulting from simulating different design scenarios (various buildings and mass ratios) in moderate-to-high seismic hazard conditions, can be summarized as follows:

• Proper account of seismic intensity variability is required for a reliable evaluation of NESs’ performance, which can be concisely achieved by adopting a LCC performance metric.

• Proper account of structural stiffness variability is required for a reliable evaluation of TMDs’ performance, which can be simply achieved by adopting a worst-case uncertainty approach, for instance letting the stiffness reduction factor δ assume any possible value in a given range (from 1 to d).

• By accounting for both seismic intensity and structural stiffness variability, the proposed LCC analysis and design methodology is a fair tool for comparing the two absorbers, exploiting their full potential.

• If a nominal LCC design is performed, the TMD proves largely superior to the NES as long as δ remains small. In fact, as long as δ = 1 and on geometric average, the LCC obtained with the TMD ($C_{opt}^{*}$ equal to 0.81, 0.64 and 0.56 for µ respectively equal to 1%, 5% and 10%) is 0.84 times the value obtained with the NES ($C_{opt}^{*}$ equal to 0.93, 0.77 and 0.67 for µ respectively equal to 1%, 5% and 10%). As δ increases, TMD’s performance worsens more rapidly than NES’s performance, until for δ > 1.5÷2 the NES becomes preferable. The larger the mass ratio of the TMD, the slower its performance degradation.

• If a robust LCC design is performed assuming d = 2, the TMD loses little of its nominal performance as long as δ remains small, continuing to be much superior to the NES. In fact, as long as δ ≤ 2 and on geometric average, the LCC obtained with the TMD ($C_{opt}^{*}$ equal to 0.89, 0.72 and 0.63 for µ respectively equal to 1%, 5% and 10%) is 0.90 times the value obtained with the NES ($C_{opt}^{*}$ equal to 0.94, 0.81 and 0.72 for µ respectively equal to 1%, 5% and 10%). As δ increases, TMD’s performance degradation is delayed, so that the TMD continues to be preferable until δ > 3÷4, i.e. under stiffness variations which are nearly double their expected design value.

• In summary, in all the examined cases the NES does not appear seismically advantageous with respect to the TMD, at least when uncertainty is incorporated in design.

Other conclusions can be listed as follows:

• A limited trade-off exists between drift-dependent and acceleration-dependent costs. For the TMD the trade-off is virtually absent on the single-story building but increases with the number of stories, as drifts remain governed by the first mode while accelerations by the second.

• A limited trade-off exists for the TMD between the overall damage cost (including injuries and fatalities) and the life safety cost alone, ensuring that the most cost-effective solution is also nearly the safest for life protection. A larger trade-off exists for the NES, because the overall damage cost is governed by intermediate seismic intensities, whilst the life safety cost by the highest ones.

• The proposed H_∞ design method proves a practical and reliable way to approximate the LCC-optimal TMD.

• In all examined case studies, because of the moderate-to-high seismicity of the site, damage costs are relatively small with respect to initial building costs. The cost of the absorber proves therefore of the same order of magnitude of the damage cost savings. The optimal mass ratios are then small, resulting in a limited damage cost reduction. A more advantageous performance would be achieved by considering a more severe seismic hazard.

Appendix

The 8 sets of seismic records used for the analyses are reported in the following Tables 13, 14, 15, 16, 17, 18 and 19, as extracted from the European Strong Motion database.

Table 13 The 14 records in Set 1 (return period T_R = 1 year) and Set 2 (return period T_R = 10 years)

Table 14 The 14 records in Set 3 (return period T_R = 30 years)

Table 15 The 14 records in Set 4 (return period T_R = 101 years)

Table 16 The 14 records in Set 5 (return period T_R = 201 years)

Table 17 The 14 records in Set 6 (return period T_R = 475 years)

Table 18 The 14 records in Set 7 (return period T_R = 975 years)

Table 19 The 14 records in Set 8 (return period T_R = 2475 years)