A theoretical and experimental exploration of the seismic dynamics of multi-span bridges

Abstract

A generalized reduced-order model of a multi-span continuous bridge, on flexible discrete supports, that is subjected to multi-support seismic excitation is presented. This model highlights the key non-dimensional system parameters. Real spatiotemporal ground motion time-series (from the SMART-1 array, Taiwan) are used, as an alternative to employing artificial ground motion based on some spatial incoherence kernels. Benchmark experimental test data, using the multiple support excitation rig of a four-span bridge and SMART-1 array excitation, is used to validate/calibrate the proposed reduced-order model. An operational modal analysis is conducted to obtain least-square estimates of these key dynamic parameters using a Levenberg–Marquardt algorithm. The computationally efficient reduced-order model is then employed for a parametric study that explores the effect of spatial incoherence, bridge alignment and archetypal symmetrical and asymmetrical bridge geometries. A comparison of identical and multi-support excitation cases indicate the likely range of beneficial/adverse errors in neglecting the spatiotemporal nature of ground motions in design analyses.

1 Introduction

The incorporation of spatially variable seismic excitation in the design of life-line structures has received much attention over the last few decades (Zanardo et al. 2002; Lin et al. 2004; Lupoi et al. 2005; Ye et al. 2011; Camara et al. 2014). The influence of multi-input seismic excitation on long structures is complex. This has resulted in a few antithetical study outcomes that have dissimilar assumed structural models and ground motion inputs (Bogdanoff et al. 1965; Masri 1976; Hao and Duan 1995; Loh and Ku 1995; Der Kiureghian et al. 1997). In the design of artifacts such as multi-span bridges, the structural engineer would like to know whether, and when, it is necessary to model the spatial variation in ground motion (Nazmy and Abdel-Ghaffar 1992; Zerva 2016). There are extensive databases of accelerogram records for singleton stations. However, there exist far fewer record sets that have enough spatially distributed stations, that are close enough together, to accurately estimate the complete spatiotemporal surficial ground motion (Loh et al. 1982). Thus, the structural engineer is often left with the choice of artificially generating spatiotemporal ground motion (Harichandran and Vanmarcke 1986; Harichandran et al. 1996) or neglecting the spatial variation by using identical ground motions inputs at all supports (Fardis 2005).

Real earthquakes produce spatially heterogeneous, surficial, ground motions. Wavelengths of shear waves at the surface (in granite) are typically between 0.3 and 3 km [for 10 Hz and 1 Hz component frequencies respectively (Bolt 2001)]. Thus, long structures can suffer from differential excitations along their length. Nuti and Vanzi (2005) discussed many important parameters showing for example spatial incoherence is very influential even for medium span bridges. This spatial variation in ground motion can be more pronounced over even shorter distances in the case where the superficial geology exhibits heterogeneity (Lavorato et al. 2017, 2018).

The artificial spatiotemporal models of ground motion, such as Harichandran and Vanmarcke (1986), define the variation in ground motion expected between any arbitrary stations. These models tend to assume some exponential approximation for the absolute coherency and a linear function for the phase variation between stations. Using ground motion models whose spatial variability are parametrically stochastic is attractive as they enable the use and extension of recorded singleton station records to the generalized spatiotemporal case. This allows a sensitivity analyses to be performed with respect to these stochastic model parameters. However, and unfortunately, it is well-known that these models are only able to summarize underlying trends (the low-order statistics) and do not preserve the high-order statistics of real spatially heterogeneous ground motions; see Alexander (2008) and Lavorato et al. (2018). These parametric models assume a particular spatial coherence which may not be valid in the general case of heterogeneous ground in anything other than an approximate sense. An alternative is to make use of real spatiotemporal ground motions, from multi-station arrays. These significantly reduce the uncertainty of spatial ground motion variation at a particular site, but are unfortunately limited to only a few particular locations where these arrays exist. Therefore, we are faced with a choice between imposing uncertain variation caused by a priori assumptions implied by parametric stochastic ground motion models or the uncertainty of a small sample of real spatio-temporal ground motions at a limited number of locations. In this paper we chose to adopt the latter rather than the former, i.e. we make use of real recorded data over multi-station arrays to generate spatiotemporal characteristics of the motions rather than assume a priori a particular coherency model.

Varied studies concluded different seismic response patterns for spatially support excitations (Zanardo et al. 2002). In the design of nuclear structures (American Society of Civil 1987) recommended specific seismic reduction factors that account for the effect of spatially varying ground motion. For suspension and cable-stayed bridges, Nazmy and Abdel-Ghaffar (1992) proposes the use of simulated ground excitations for analyses of multi-support excitation problems. However, in the design of highway bridges, an equivalent uniform excitation, that simulates the effect of spatially variable ground motion, is suggested in Fardis (2005).

Owing to the simplicity of its structural configuration, the majority of investigations are on the effect of spatially varying ground motion on highway bridges (Johnson and Galletly 1972; Kiureghian and Neuenhofer 1992; Zerva 2016). One of the early studies to evaluate the seismic response of highway bridges under a range of multi-support excitations was Monti et al. (1996). They concluded that, in general, using identical support excitation (ISE), rather than multi-support excitation (MSE), led to a conservative design. However, Tzanetos et al. (2000) drew different conclusions. They questioned the scope and generality of the conclusions (Monti et al. 1996) by pointing out the symmetric bridge configuration and characteristics of the ground motions employed in the study.

Zerva (1990, 1991) carried out comprehensive analyses of two-span and three-span continuous beams, of varying span lengths, under different arrangements of spatially varying ground motions. She concluded that, for symmetrical structural configuration, ISE could only excite the symmetric modes, while MSE could excite all modes, i.e. symmetrical and anti-symmetrical modes. Furthermore, spatially variable excitation increases the modal response for higher modes more considerably than uniform excitation. Price and Eberhard (1998) conducted the comprehensive analysis on a two-span bridge under incoherent excitation. In their study, for spatially varying excitation, the significant increase of anti-symmetrical modal responses was observed although the contribution of symmetrical modes tended to decrease. Sextos et al. (2003a, b) performed parametric analyses on 20 various bridge models and suggested that the spatially varying excitation increases the seismic response quantities significantly where the total bridge length exceed more than 400 m.

In this paper, we derive a reduced-order model for the analysis of seismically excited multi-span continuous bridges. The dynamics of these bridges is based on the multi-input–multi-output (MIMO) system that is designed to allow great computational efficiency. Therefore, extensive subsequent parametric studies can be achieved. Additionally, we identify the key non-dimensional parameter groups that govern the system responses. For ground excitation, we do not use artificial records but employ real spatiotemporal ground motions recorded at the SMART-1 array, Taiwan. For the purpose of validation, we use results from a physical scale model benchmark test. This physical scale model of a bridge with five independently actuated supports was designed and tested previously (Norman et al. 2006; Norman 2006; Norman and Crewe 2008). These tests were carried out at the University of Bristol. We make use of the reduced-order MIMO formulation to perform inverse system identification of the physical benchmark tests. Finally, we make use of the validated/calibrated reduced-order bridge model to explore parametrically the likely errors (both over and under estimations) when using identical support excitation (ISE) rather than real multi-support excitation (MSE).

2 A reduced order model for lateral responses of multi-span bridges

The typical method of setting up the equations of motion for the multi-support excitation of multi-span bridges involves the finite element method as described in Chopra and Chopra (2007) and Zerva (2016). However, in this paper, we are seeking a novel reduced order model (1) that is highly computationally efficient so that large-scale future parametric studies can be performed, and it additionally can enable future real-time sub-structuring tests of nonlinear columns (Wagg and Neild 2010) (2) that helps to identify the key system parameter groups for this problem and (3) that is readily extendable to include nonlinear hysteretic phenomenological of soil and columns (Bouc 1967; Wen 1976).

2.1 Defining kinetic and potential energies

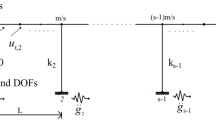
Consider a general multi-span bridge subjected to lateral ground excitation shown in Fig. 1. This reduced order model can be likened to the dynamics of a beam on a discrete elastic foundation that is subjected to spatiotemporal support excitation. This figure is a 3D view of the deformations in the horizontal xy plane. The kinetic energy for the deck is as follows

$$ T = \tfrac{1}{2}\int_{0}^{{\left( {n - 1} \right)L}} {m_{d} } \dot{y}_{d}^{2} {\text{d}}x $$

(1)

where n is the number of piers and ($n - 1)L$ is the total bridge length for equal spans, m_d mass per unit length and y_d is the deck lateral displacement in the horizontal xy plane. Pier masses are neglected in this analysis. Note the Newtonian prime notation indicates differentiation with respect to a spatial variable, hence $y^{\prime} = {{{\text{d}}y} \mathord{\left/ {\vphantom {{{\text{d}}y} {{\text{d}}x}}} \right. \kern-0pt} {{\text{d}}x}}$, while the dot notation indicates differentiation with respect to a temporal variable, hence $\dot{y} = {{{\text{d}}y} \mathord{\left/ {\vphantom {{{\text{d}}y} {{\text{d}}t}}} \right. \kern-0pt} {{\text{d}}t}}$.

Fig. 1

Schematic of the dynamic horizontal motion of bridge during lateral seismic ground motion

The potential energy is given as follows

$$ U = \tfrac{1}{2}\int_{0}^{{\left( {n - 1} \right)L}} {EI_{z} y_{d}^{\prime \prime 2} } {\text{d}}x + \tfrac{1}{2}\sum\limits_{i = 1}^{n} {k_{i} \left( {y_{d} \left( {x_{i} } \right) - y_{g} \left( {x_{i} } \right)} \right)^{2} } - \sum\limits_{i = 1}^{n} {R_{i} y_{g} \left( {x_{i} } \right)} , $$

(2)

where $EI_{z}$ is the deck flexural rigidity, R_i is ground reaction underneath the pier, x_i and k_i are the ith pier locations and its lateral flexural stiffness and y_g is the seismically induced free field displacement of the ground surface. The first term in (2) is the flexural strain energy of the deck, the second term is the flexural strain energy of the pier/soil springs, and the final term is the work done by the horizontal ground reactions. The connection between piers and deck is assumed to be moment-less i.e. pinned.

2.2 Employing discrete spatiotemporal Rayleigh–Ritz vectors

By introducing a Rayleigh–Ritz type spatiotemporal function for integral Eqs. (1) and (2) we can convert these continuous equations into discrete ones.

$$ y_{d} \left( {x,t} \right) = L{\mathbf{u}}\left( t \right)^{T} {\varvec{\uppsi}}\left( x \right),\quad y_{g} \left( {x,t} \right) = L{\mathbf{g}}\left( t \right)^{T} {\varvec{\uppsi}}_{g} \left( x \right) $$

(3)

The degrees of freedom (dofs) on the deck are ${\mathbf{u}} \in {\mathbb{R}}^{m \times 1}$ and constrained dofs on the ground are ${\mathbf{g}} \in {\mathbb{R}}^{n \times 1}$. In this paper the number of deck dofs $m \ge n$. The introduction of L in Eq. (3) results in both dofs vectors u and g being dimensionless. The Ritz vector basis are ${\varvec{\uppsi}} \in {\mathbb{R}}^{m \times 1}$ and ${\varvec{\uppsi}}_{g} \in {\mathbb{R}}^{n \times 1}$ for deck and ground respectively. Lagrangian interpolants are employed, for these Ritz vectors, because they have certain orthogonal properties that diagonalize all subsequent pier/soil stiffness block matrices. This useful feature makes it simpler to deal with the end constraints of the deck through later partitioning and condensation. These are defined later, in the “Appendices 1 and 2”. Both ${\varvec{\uppsi}}_{g}$ and ${\varvec{\uppsi}}$ are dimensionless.

Hence, we can write the Lagrangian (Kinetic minus Potential Energies) as follows

$$ \begin{aligned} \varPi & = \tfrac{1}{2}{\dot{\mathbf{u}}}^{T} \left[ {L^{2} \int_{0}^{{\left( {n - 1} \right)L}} {m_{d} {\varvec{\uppsi \uppsi }}^{T} {\text{d}}x} } \right]{\dot{\mathbf{u}}} - \tfrac{1}{2}{\mathbf{u}}^{T} \left[ {L^{2} \int_{0}^{{\left( {n - 1} \right)L}} {EI_{z} {\varvec{\uppsi}}^{\prime \prime } {\varvec{\uppsi}}^{\prime \prime T} } {\text{d}}x} \right]{\mathbf{u}} - \tfrac{1}{2}{\mathbf{u}}^{T} \left[ {L^{2} \sum\limits_{i = 1}^{n} {k_{i} } {\varvec{\uppsi}}\left( {x_{i} } \right){\varvec{\uppsi}}\left( {x_{i} } \right)^{T} } \right]{\mathbf{u}} \\ & \quad + {\mathbf{u}}^{T} \left[ {L^{2} \sum\limits_{i = 1}^{n} {k_{i} } {\varvec{\uppsi}}\left( {x_{i} } \right){\varvec{\uppsi}}_{g}^{T} \left( {x_{i} } \right)} \right]{\mathbf{g}} - \tfrac{1}{2}{\mathbf{g}}^{T} \left[ {L^{2} \sum\limits_{i = 1}^{n} {k_{i} } {\varvec{\uppsi}}_{g} \left( {x_{i} } \right){\varvec{\uppsi}}_{g}^{T} \left( {x_{i} } \right)} \right]{\mathbf{g}} + L{\mathbf{g}}^{T} \sum\limits_{i = 1}^{n} {R_{i} {\varvec{\uppsi}}_{g} \left( {x_{i} } \right)} \\ \end{aligned} $$

(4)

where the first term in the above equations is from the Kinetic energy and all subsequent terms are from the Potential energy. Note that all stiffness and inertia terms are in a quadratic form.

2.3 Dimensionless Lagrangian

By introducing a dimensionless coordinate $x = \xi L$ and assuming constant deck mass per unit length and flexural rigidity, the Lagrangian can be re-written as follows,

$$ \begin{aligned} \varPi & = \tfrac{1}{2}m_{d} L^{3} {\dot{\mathbf{u}}}^{T} \left[ {\int_{0}^{n - 1} {{\varvec{\uppsi \uppsi }}^{T} {\text{d}}\xi } } \right]{\dot{\mathbf{u}}} - \tfrac{1}{2}\frac{{EI_{z} }}{L}{\mathbf{u}}^{T} \left[ {\int_{0}^{n - 1} {{\varvec{\uppsi}}^{\prime \prime } {\varvec{\uppsi}}^{\prime \prime T} } {\text{d}}\xi } \right]{\mathbf{u}} - \tfrac{1}{2}L^{2} {\mathbf{u}}^{T} \left[ {\sum\limits_{i = 1}^{n} {k_{i} } {\varvec{\uppsi}}\left( {\xi_{i} } \right){\varvec{\uppsi}}\left( {\xi_{i} } \right)^{T} } \right]{\mathbf{u}} \\ & \quad + L^{2} {\mathbf{u}}^{T} \left[ {\sum\limits_{i = 1}^{n} {k_{i} } {\varvec{\uppsi}}\left( {\xi_{i} } \right){\varvec{\uppsi}}_{g}^{T} \left( {\xi_{i} } \right)} \right]{\mathbf{g}} - \tfrac{1}{2}L^{2} {\mathbf{g}}^{T} \left[ {\sum\limits_{i = 1}^{n} {k_{i} } {\varvec{\uppsi}}_{g} \left( {\xi_{i} } \right){\varvec{\uppsi}}_{g}^{T} \left( {\xi_{i} } \right)} \right]{\mathbf{g}} + L{\mathbf{g}}^{T} \sum\limits_{i = 1}^{n} {R_{i} {\varvec{\uppsi}}_{g} \left( {\xi_{i} } \right)} \\ \end{aligned} $$

(5)

In the above Eq. (5), we re-define the prime to be differentiation with respect to $\xi$ hence, $y^{\prime\prime} = {{{\text{d}}^{2} y} \mathord{\left/ {\vphantom {{{\text{d}}^{2} y} {{\text{d}}\xi^{2} }}} \right. \kern-0pt} {{\text{d}}\xi^{2} }}$ and therefore ${{{\text{d}}^{2} y} \mathord{\left/ {\vphantom {{{\text{d}}^{2} y} {{\text{d}}x^{2} }}} \right. \kern-0pt} {{\text{d}}x^{2} }} = \left( {{1 \mathord{\left/ {\vphantom {1 {L^{2} }}} \right. \kern-0pt} {L^{2} }}} \right)y^{\prime\prime}$. We now introduce a change in time-scale $t = {\tau \mathord{\left/ {\vphantom {\tau \omega }} \right. \kern-0pt} \omega }$ where $\tau$ is a dimensionless time-scale. Thus,${{{\text{d}}{\mathbf{u}}} \mathord{\left/ {\vphantom {{{\text{d}}{\mathbf{u}}} {{\text{d}}t}}} \right. \kern-0pt} {{\text{d}}t}} = {{\omega {\text{d}}{\mathbf{u}}} \mathord{\left/ {\vphantom {{\omega {\text{d}}{\mathbf{u}}} {{\text{d}}\tau }}} \right. \kern-0pt} {{\text{d}}\tau }}$. By dividing Eq. (5) by $\omega^{2} m_{d} L^{3}$ we obtain

$$ \frac{\varPi }{{\omega_{{}}^{2} m_{d} L^{3} }} = \tfrac{1}{2}{\dot{\mathbf{u}}}^{T} {\mathbf{M\dot{u}}} - \tfrac{1}{2}\left( {{\mathbf{u}}^{T} {\mathbf{Ku}} + {\mathbf{u}}^{T} {\mathbf{K}}_{1} {\mathbf{u}} - 2{\mathbf{u}}^{T} {\mathbf{K}}_{2} {\mathbf{g}} + {\mathbf{g}}^{T} {\mathbf{K}}_{3} {\mathbf{g}} - 2{\mathbf{g}}^{T} {\mathbf{r}}} \right) $$

(6)

The non-dimensional matrices in Eq. (6) are define as follows.

$$ \begin{aligned} {\mathbf{M}} & = \int_{0}^{n - 1} {{\varvec{\uppsi \uppsi }}^{T} {\text{d}}\xi } \in {\mathbb{R}}^{m \times m} ,\quad {\mathbf{K}}{ = }\int_{0}^{n - 1} {{\varvec{\uppsi}}^{\prime \prime } {\varvec{\uppsi}}^{\prime \prime T} } {\text{d}}\xi \in {\mathbb{R}}^{m \times m} ,\quad {\mathbf{K}}_{1} { = }\sum\limits_{i = 1}^{n} {\eta_{i} } {\varvec{\uppsi}}\left( {\xi_{i} } \right){\varvec{\uppsi}}\left( {\xi_{i} } \right)^{T} \in {\mathbb{R}}^{m \times m} , \\ {\mathbf{K}}_{2} & { = }\sum\limits_{i = 1}^{n} {\eta_{i} } {\varvec{\uppsi}}\left( {\xi_{i} } \right){\varvec{\uppsi}}_{g}^{T} \left( {\xi_{i} } \right) \in {\mathbb{R}}^{m \times n} ,\quad {\mathbf{K}}_{3} { = }\sum\limits_{i = 1}^{n} {\eta_{i} } {\varvec{\uppsi}}_{g} \left( {\xi_{i} } \right){\varvec{\uppsi}}_{g}^{T} \left( {\xi_{i} } \right) \in {\mathbb{R}}^{n \times n} ,\quad {\mathbf{r}} = \sum\limits_{i = 1}^{n} {r_{i} {\varvec{\uppsi}}_{g} \left( {\xi_{i} } \right)} \in {\mathbb{R}}^{n \times 1} \\ \end{aligned} $$

(7)

The system parameters are defined as follows

$$ \omega^{2} = \frac{{EI_{z} }}{{m_{d} L^{4} }},\quad \eta_{i} = \frac{{k_{i} L^{3} }}{{EI_{z} }},\quad r_{i} = \frac{{R_{i} L^{2} }}{{EI_{z} }} $$

(8)

where $\eta_{i}$ is the non-dimensional ith pier to deck stiffness ratio and $r_{i}$ is a non-dimensional horizontal reaction. $\omega$ is a system frequency parameter (rad/s) appears to have been removed from the equations of motion (6). However, the support ground motion time-series are defined by g and these are now defined in terms of a time-scale $\tau = \omega t$. Therefore, the sampling interval (of the time-series) must be multiplied by $\omega$ before performing time history analyses. So $\omega$ is still a key system parameter. It has been removed from system matrices and is now located within the system excitation vector g.

2.4 Euler–Lagrange equations of motion

The Euler–Lagrange equations are as follows

$$ \frac{\text{d}}{{{\text{d}}t}}\left( {\frac{\partial \varPi }{{\partial {\dot{\mathbf{u}}}}}} \right) - \left( {\frac{\partial \varPi }{{\partial {\mathbf{u}}}}} \right) = 0 = \tfrac{1}{2}{\mathbf{M\ddot{u}}} - \left( {{\mathbf{Ku}} + {\mathbf{K}}_{1} {\mathbf{u}} - {\mathbf{K}}_{2} {\mathbf{g}}} \right) $$

(9)

$$ \frac{\text{d}}{{{\text{d}}t}}\left( {\frac{\partial \varPi }{{\partial {\dot{\mathbf{g}}}}}} \right) - \left( {\frac{\partial \varPi }{{\partial {\mathbf{g}}}}} \right) = 0 = \left( { - {\mathbf{K}}_{2}^{T} {\mathbf{u}} + {\mathbf{K}}_{3} {\mathbf{g}} - {\mathbf{r}}} \right) $$

(10)

Hence, the full dimensionless equations of motion (including a dimensionless orthogonal Rayleigh damping matrix (Clough and Penzien 1995) are as follows

$$ \left[ {\begin{array}{*{20}c} {\mathbf{M}} & {\mathbf{0}} \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{u}}}} \\ {{\mathbf{\ddot{g}}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\mathbf{C}} & { - {\mathbf{C}}_{12} } \\ { - {\mathbf{C}}_{12}^{T} } & {{\mathbf{C}}_{22}^{{}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}} \\ {{\dot{\mathbf{g}}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{K}} + {\mathbf{K}}_{1} } & { - {\mathbf{K}}_{2} } \\ { - {\mathbf{K}}_{2}^{T} } & {{\mathbf{K}}_{3} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\mathbf{u}} \\ {\mathbf{g}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {\mathbf{r}} \\ \end{array} } \right] $$

(11)

where the first row of block matrix equations (11) (i.e. Eq. (9)) are the dynamic equilibrium equations of the deck and the second row of block matrix equations (11) (i.e. Eq. (10)) are the equilibrium equations at the supports of piers. The viscous damping block matrices in the above equation are defined as follows;

$$ {\mathbf{C}} = \beta_{m} {\mathbf{M}} + \beta_{k} \left( {{\mathbf{K}} + {\mathbf{K}}_{1} } \right),\quad {\mathbf{C}}_{12} = \beta_{k} {\mathbf{K}}_{2} $$

(12)

where $\beta_{m}$ and $\beta_{k}$ are defined in the standard way (Clough and Penzien 1995; Chopra and Chopra 2007) by using modal frequencies, damping ratios, and mode shapes.

Hence, the dynamic equations of motion are complete and defined by the first m rows thus;

$$ {\mathbf{M\ddot{u}}} + {\mathbf{C\dot{u}}} + \left( {{\mathbf{K}} + {\mathbf{K}}_{1} } \right){\mathbf{u}} = {\mathbf{C}}_{12} {\dot{\mathbf{g}}} + {\mathbf{K}}_{2} {\mathbf{g}} $$

(13)

2.5 Employing matrix partitioning and condensation to accommodate end constraints

At this point, we introduce a set of constraint equations for the two ends of the deck. It is assumed that the deck meets the ground at the two ends and therefore must have the same displacement, i.e. $y\left( {0,t} \right) = y_{g} \left( {0,t} \right)$ and $y\left( {\left( {n - 1} \right)L,t} \right) = y_{g} \left( {\left( {n - 1} \right)L,t} \right)$. These two boundary conditions can be dealt with by either (1) assuming very stiff piers at the two ends, or (2) introducing Lagrange multipliers constraint equations or (3) by matrix partitioning and condensation. We chose the latter approach here as it appears to be the most numerically stable and efficient approach. To achieve this matrix partitioning we re-order the dofs thus,

$$ {\mathbf{u}} = \left[ {\begin{array}{*{20}c} {u_{1} = g_{1} } \\ {u_{m} = g_{n} } \\ \hline {u_{2} } \\ \vdots \\ {u_{m - 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{E} } \\ {\mathbf{w}} \\ \end{array} } \right],\quad {\mathbf{g}} = \left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{n} } \\ \hline {g_{2} } \\ \vdots \\ {g_{n - 1} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{E} } \\ {{\mathbf{g}}_{I} } \\ \end{array} } \right] $$

(14)

where ${\mathbf{g}}_{E} \in {\mathbb{R}}^{2 \times 1}$ is the ground displacements timeseries at the exterior ends of the bridge, ${\mathbf{g}}_{I} \in {\mathbb{R}}^{{\left( {n - 2} \right) \times 1}}$ is the ground displacements timeseries at the interior pier supports, and ${\mathbf{w}} \in {\mathbb{R}}^{{\left( {m - 2} \right) \times 1}}$ is the vector of non-constrained bridge deck displacement dofs.

The matrix Eq. (13) can now be re-written as follows

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{m}}_{11} } & {{\mathbf{m}}_{12} } \\ {{\mathbf{m}}_{12}^{T} } & {{\mathbf{m}}_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{g}}}_{E} } \\ {{\mathbf{\ddot{w}}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{c}}_{11} } & {{\mathbf{c}}_{12} } \\ {{\mathbf{c}}_{12}^{T} } & {{\mathbf{c}}_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{g}}}_{E} } \\ {{\dot{\mathbf{w}}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{k}}_{11} } & {{\mathbf{k}}_{12} } \\ {{\mathbf{k}}_{12}^{T} } & {{\mathbf{k}}_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{E} } \\ {\mathbf{w}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{c}}_{12a} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{c}}_{12b} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{g}}}_{E} } \\ {{\dot{\mathbf{g}}}_{I} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{k}}_{2a} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{k}}_{2b} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{g}}_{E} } \\ {{\mathbf{g}}_{I} } \\ \end{array} } \right] $$

(15)

Note that because we have employed Lagrangian interpolants, the matrices ${\mathbf{K}}_{2}$ and ${\mathbf{C}}_{12}$ are diagonal (in block matrix form) with off-diagonal zero block matrices. Therefore, the second row of the block matrix equation above leads us to the final form of the partitioned and condensed equation of motion. We employ a MIMO representation of system equations of motion, as follows,

$$ {\mathbf{m}}_{22} {\mathbf{\ddot{w}}} + {\mathbf{c}}_{22} {\dot{\mathbf{w}}} + {\mathbf{k}}_{22} {\mathbf{w}} = {\mathbf{P}}\;{\mathbf{f}} $$

(16)

$$ {\mathbf{f}}\left( \tau \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\mathbf{\ddot{g}}}_{E} } \\ {{\dot{\mathbf{g}}}_{E} } \\ \end{array} } \\ {{\mathbf{g}}_{E} } \\ {{\dot{\mathbf{g}}}_{I} } \\ {{\mathbf{g}}_{I} } \\ \end{array} } \right]{\kern 1pt} ,\quad {\mathbf{P}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - {\mathbf{m}}_{12}^{T} } & { - {\mathbf{c}}_{12}^{T} } \\ \end{array} } & { - {\mathbf{k}}_{12}^{T} } & {{\mathbf{c}}_{12b} } & {{\mathbf{k}}_{2b} } \\ \end{array} } \right] $$

(17)

where ${\mathbf{f}}\left( \tau \right) \in {\mathbb{R}}^{{\left( {2n + 2} \right) \times 1}}$ denotes the seismic input vector, ${\mathbf{w}} \in {\mathbb{R}}^{{\left( {m - 2} \right) \times 1}}$ is the unconstrained dofs vector and ${\mathbf{P}} \in {\mathbb{R}}^{{\left( {m - 2} \right) \times \left( {2n + 2} \right)}}$ is the participation matrix.

3 Experimental multi-support bridge tests

Equations (16) and (17) represent the dynamics of a multi-span continuous bridge with n − 1 spans of span length L. These equations of motion represent a reduced order non-dimensional model and this is expressed in terms of system parameters, (1) frequency parameter $\omega$, (2) pier to deck lateral stiffness ratios $\eta_{i}$ and (3) damping coefficients $\beta_{k} ,\beta_{m}$ that are determined by assuming modal ratios of critical damping.

Validation of these equations of motion is achieved by comparing numerical results from time-history analyses and a benchmark experimental physical bridge model that was subjected to multi-support excitation. These benchmark tests were independently performed over a decade ago therefore are favourable, for the purposes of validation, to our own numerical FEA simulations.

3.1 Physical experimental model

The bridge model is a 1:50 scale model of a prototype 200 m long bridge. The bridge has 4 spans 50 m long and is supported by two abutments and three piers. In this experimental study, the piers are of an equal length of 1 m. A 200 m long bridge was chosen because similar bridges have been used in studies by Zapico et al. (2003) and Lupoi et al. (2005) and these studies have shown that bridges of this size may be susceptible to a significant increase in response when considering MSE. The length was also chosen because a large proportion of bridges on major road projects are of a similar length. For example, on the new Egnatia Motorway in Greece, 103 of the 612 bridges were between 100 m and 300 m long, whilst only 4 were longer than 600 m (Ahmadi-Kashani 2004).

The bridge model was constructed from a 4 m, 60 × 60 × 3.2 mm box section. The piers are 420 mm long and have a 20 × 25 mm solid section. The abutments are pinned in plan but fixed in elevation. This is achieved by having a smooth/greased sliding bearing. All the bridge components are made from S275 grade steel. 160 added masses were attached to the bridge deck, increasing the mass of the bridge model to 500 kg. The masses are attached in groups of four and are isolated from each other so as not to change the flexural properties of the bridge deck. The ground excitations were simulated by use of five-single axis, actuators, see Fig. 2a. Each actuator is mounted on a pair of bearings, which move over a single steel shaft. The shaft is attached at each end to a stiff frame. The beam is connected to the piers with a semi-rigid connection shown in Fig. 2b. The bolted connection provides a negligible moment restraint. The Details of Bridge parameters for the experimental bridge model are summarized in Table 1. For further performance specification, see Norman et al. (2006). While the connections were designed as pinned, they did act as imperfect pins, i.e. some small stiffening of the piers was implied through inverse system identification. The optimal estimate of the pier to deck stiffness ratio $\eta$ for these experimental piers is discussed in Sect. 3.4.

Fig. 2

a The five, single axis, actuators with the bridge model, b pier support fixity arrangement

Table 1 Structural parameters and estimated model parameters for the experimental bridge

3.2 Real ground motions from the SMART-1 array are employed

Ground motions used in this study are not based on artificial spatial incoherence estimates; they are obtained from real recording at the SMART-1 Array, Taiwan. The SMART-1 Array was one of the first large arrays of digital accelerometers specially designed to investigate the near-field properties of earthquake ground motion (Abrahamson et al. 1987). It was located in the northeast corner of Taiwan near the city of Lotung on the Lanyang Plain. The near-surface geology under the array is predominantly recently laid alluvial deposits; the water table was at or near the surface. The topology of the surface was very flat. Records from event 43 (IES 1980–1990) are employed in this paper. Correction of these records is discussed in Alexander et al. (2001) and Chanerley and Alexander (2007, 2008). In order to produce ground displacements, the corrected ground acceleration are numerically integrated twice by a Simpson’s 1/3rd rule. Low-cut filtering is performed on the acceleration and the velocity timehistories to reduce to the influence of spurious increasing trends in the displacement timehistories. Very low-frequency Fling components (Chanerley and Alexander 2010) were not extracted.

Figure 3 depicts the location of the prototype bridge. Twelve radial alignments of the bridge were considered in this paper. The ground motion time-series at the two ends ${\mathbf{\ddot{g}}}_{E}$ of the bridge were the real time-series recorded at the stations of the inner ring [I01] to [I12] and centre [C00]. Albeit, these station recordings are rotationally transformed through the appropriate angle to obtain the ground motion time-series normal to the bridge longitudinal alignment. The intermediate bridge support ground motion time-series ${\mathbf{\ddot{g}}}_{I}$ are obtained by a full spatial interpolation across the whole array using a biharmonic cubic spline interpolant, see Alexander (2008). Figure 4 displays the elastic response spectra for station accelerograms for north–south and east–west directions. These plots are suggestive of significant spatial incoherence, particularly in the east–west directions (at 6 Hz).

Fig. 3

Bridges positioned along radii between centre [C00] and inner ring stations [I01] to [I12] of SMART-1 array

Fig. 4

Elastic response spectra for SMART-1 Array inner ring stations I00 to I12 for event 43 for a east–west component and b north–south component

3.3 Numerical model of the physical test bridge

The generalised mathematical model shown in Fig. 1 is adapted for the specific case of the benchmark 4 span bridge shown in Fig. 4. Our aim here is to derive the simplest, most computationally efficient, reduced order model. This bridge has four equal spans L and is of total length 4L. To explore the influence effect of the number of dof m on the system accuracy we consider two cases.

• (1) Using $m = n = 5$ resulting in a 3-dof reduced order model. In this case only the displacement at the top of piers are included.

• (2) Using $m = 9,n = 5,$ which results in a 7-dof reduced order model. In this case displacements at the top of piers and at the mid-span of beams are included.

Figure 5 displays graphically the bridge. The beam dofs shown in black are associated with 3-dofs system (1) and those in blue are the dofs for case (2) the 7-dofs system.

Fig. 5

A four-span continuous-beam on three flexible supports

Note that the beam degrees of freedom at edge supports $({\text{u}}_{1} ,{\text{u}}_{5} )$ for the 3-dofs system and $({\text{u}}_{1} ,{\text{u}}_{9} )$ for the 7-dofs system are restrained completely. Therefore, those displacements are equal to the ground displacements at these points.

3.4 System identification of model parameters from experimental responses

The validation of the mathematical model for a dynamical structure is a vital step in the process of structural analysis (Alvin et al. 2003; Zapico-Valle et al. 2010). The innovation of State-space models provides explicit techniques of linear multiple input multiple output (MIMO). This representation allows the direct estimation of unknown parameters if explicit equations demonstrating physics of the dynamical system can be expressed mathematically. These methods known as Grey-Box Modeling (Ljung 1987) require that the equation of the dynamical system is expressed in the framework of ordinary differential or difference equations (ODEs).

In this section, we aim to re-cast the equations of motion (16) in a form that permits system identification of a MIMO system. A general linear time-invariant (LTI) system typically has a state space form as follows

$$ \left[ {\begin{array}{*{20}c} {{\dot{\mathbf{x}}}(\tau )} \\ {{\mathbf{y}}\left( \tau \right)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{A}}\left( \varvec{\uptheta } \right)} & {{\mathbf{B}}\left( \varvec{\uptheta } \right)} \\ {{\mathbf{C}}\left( \varvec{\uptheta } \right) } & {{\mathbf{D}}\left( \varvec{\uptheta } \right)} \\ \end{array} } \right] \;\;\left[ {\begin{array}{*{20}c} {{\mathbf{x}}(\tau )} \\ {{\mathbf{f}}\left( \tau \right)} \\ \end{array} } \right],\quad {\mathbf{x}}(\tau ) = \left[ {\begin{array}{*{20}c} {{\mathbf{w}}(\tau )} \\ {{\dot{\mathbf{w}}}\left( \tau \right)} \\ \end{array} } \right] $$

(18)

where ${\mathbf{f}}\left( {\text{t}} \right)\varvec{ }$, ${\mathbf{x}}\left( {\text{t}} \right)$ and ${\mathbf{y}}\left( {\text{t}} \right)$ are system input, state and observed output (measured displacement) respectively. The block matrices in Eq. (18) are defined as follows

$$ {\mathbf{A}}\left( \varvec{\uptheta } \right) = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - {\mathbf{m}}_{22}^{ - 1} {\mathbf{k}}_{22} } & { - {\mathbf{m}}_{22}^{ - 1} {\mathbf{c}}_{22} } \\ \end{array} } \right]{\kern 1pt} ,\quad {\mathbf{B}}\left( \varvec{\uptheta } \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\mathbf{0}} \\ { - {\mathbf{m}}_{12}^{T} } \\ \end{array} } & {\begin{array}{*{20}c} {\mathbf{0}} \\ { - {\mathbf{c}}_{12}^{T} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\mathbf{0}} \\ { - {\mathbf{k}}_{12}^{T} } \\ \end{array} } & {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{c}}_{12b} } \\ \end{array} } & {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{k}}_{2b} } \\ \end{array} } \\ \end{array} } \right]{\kern 1pt} , $$

(19)

$$ {\mathbf{C}}\left( \varvec{\uptheta }\right) = \left[ {{\mathbf{j}}\;\;{\mathbf{0}}} \right],\quad {\mathbf{D}}\left( \varvec{\uptheta }\right) = {\mathbf{0}} $$

(20)

where matrices 0, I and j denote null, identity and all-ones matrices respectively. The vector θ is a set of system parameters that are optimization arguments. For this problem, the parameter vector θ is defined as follows

$$ {\varvec{\uptheta}} = \left[ {\gamma_{1} ,\gamma_{2} ,\omega ,\eta_{1} ,\eta_{2} ,\eta_{3} } \right]^{T} $$

(21)

Thus, given the recorded inputs and responses we seek the optimal system parameters θ that minimise the least square errors in Eq. (18). In this case, we employ (Matlab system identification toolbox, Grey-Box Model Estimation (Ljung 1995) that makes use of the Levenberg–Marquardt algorithm (LMA). For well-behaved mathematical formulations, this LMA is a powerful method to obtaining an optimal solution even if initial state is selected far away from the final optimum.

The MIMO optimization of the 3-dof and 7-dof models (equations) are performed for both free vibration and forced (MSE) vibration cases. The part of the time-series after the end of the seismic ground excitation is used for the free vibration case. The summary of these optimal analyses is shown in Table 2. In this table, the success ratio percentage is used as a goodness-of-fit statistic (Ljung 1987). This statistic measures the correlation between observed output responses and predicted responses using Eq. (16). The finite element results were obtained with Diana FEA package (Norman 2006; DIANA 2010). Experimental white-noise tests, at low excitation amplitudes, were performed to estimate the first three modes of vibration using a classical frequency domain linear input/output inverse system identification (Norman 2006). The performance of the 7-dof system shows some slight improvement over the 3-dof system in terms of success ratio. That is, overall, for both forced and unforced cases the 7-dof model seems to perform marginally better. However, it should be stated that the reduced order 3-dof system performs remarkably well given that it only contains 3-dofs. The optimal solution for the 3-dof system suggests that the piers have marginally varying stiffnesses, which should not have been the case as they are constructed with identical geometries and materials. Although it was difficult to estimate experimentally the fixity of the top of the piers (shown in Fig. 6b) precisely. The 7-dof optimal solution suggests that these piers are identical. Does the 7-Dof system over fit the test results predicting equal pier stiffnesses and/or is the 3-Dof model too simple to completely capture the higher modal behaviour? Without recourse to the physical specimen and further tests it is not clear which of 7-Dof or 3-Dof system are truer to reality. However, the main aim here is to confirm the robustness and fidelity of the reduced order models, therefore this discussion is not critical for this paper.

Table 2 Comparison of MIMO optimal dynamical parameters and system frequency estimates

Fig. 6

a 7-Dof system under multi-support excitation, b 7-Dof system under free-vibration, c 3-Dof system under multi-support excitation and d 3-Dof system under free-vibration

The equivalent viscous damping for this experimental model was very low as shown in Table 2. An interesting result that emerges from the MIMO optimal analyses is that there is significantly more damping under forced vibrations than there is under free (unforced) vibrations. This suggests that there is an amplitude dependent frictional mechanism active in this physical model.

Figure 6 shows, graphically, a comparison of the model-updated numerical solution to the system in Eq. (18) with the experimentally recorded results. This figure compares the displacement time-histories at the top of the central column for both 3-Dof and 7-Dof system. Both these numerical models time-histories match experimental model extremely well; this confirms that the low order system is a reasonable model of a multi-support excited multi-span bridge.

4 Numerical parametric study using the validated reduced order model

In this section, we seek to compare ISE and MSE analyses. The main scientific question is to explore what factors make it more likely that ISE analyses will be non-conservative? In particular, we consider the influence of (1) pier to deck stiffness ratio $\eta_{i}$ (2) bridge frequency parameter $\omega$ (3) bridge alignment (4) archetypal symmetrical and asymmetrical bridge geometries and (5) real spatiotemporal ground motions.

4.1 Performance measures

To make a direct comparison we compare the responses of a bridge when analysed using ISE and then using MSE. Hence, we proposed the following simple performance measures,

$$ \varepsilon_{d} \left( {\eta ,\alpha ,i,j} \right) = 100\left\{ {\frac{{\mathop {\hbox{max} }\limits_{t} \left| {u_{i} (t) - g_{i} (t)} \right|_{MSE} - \mathop {\hbox{max} }\limits_{t} \left| {u_{i} (t) - g_{i} (t)} \right|_{ISE} }}{{\mathop {\hbox{max} }\limits_{t} \left| {u_{i} (t) - g_{i} (t)} \right|_{ISE} }}} \right\} $$

(22)

$$ \varepsilon_{a} \left( {\eta ,\alpha ,i,j} \right) = 100\left\{ {\frac{{\mathop {\hbox{max} }\limits_{t} \left| {\ddot{u}_{i} (t)} \right|_{MSE} - \mathop {\hbox{max} }\limits_{t} \left| {\ddot{u}_{i} (t)} \right|_{ISE} }}{{\mathop {\hbox{max} }\limits_{t} \left| {\ddot{u}_{i} (t)} \right|_{ISE} }}} \right\} $$

(23)

where $\varepsilon_{d} \left( {\eta ,\alpha ,i,j} \right)$ is the percentage difference (error) in pier deformation, for a bridge with (1) parameters $\eta$ and $\alpha$ and (2) pier i and bridge orientation j, between MSE and ISE simulations. Similarly, $\varepsilon_{a} \left( {\eta ,\alpha ,i,j} \right)$ is the percentage difference (error) in pier total acceleration between MSE and ISE simulations. The MSE simulations make use of real spatiotemporal SMART-1 array ground excitation for event 43. In this case, abutments and pier supports have different ground excitation time-series. The ISE simulations employed the ground motion from the centre station I00 applied (at the appropriate rotation angle) to the supports of abutments and piers. Hence, these performance measures estimate what is the likely percentage error in employing ISE rather than the more correct MSE. As we are interested in the statistical range of these errors, with respect to pier i and bridge orientation j, we state the following

$$ \mathop {\hbox{min} }\limits_{\forall i,\forall j} \left\{ {\varepsilon_{d} } \right\} \le \varepsilon_{d} \le \mathop {\hbox{max} }\limits_{\forall i,\forall j} \left\{ {\varepsilon_{d} } \right\} $$

(24)

$$ \mathop {\hbox{min} }\limits_{\forall i,\forall j} \left\{ {\varepsilon_{a} } \right\} \le \varepsilon_{a} \le \mathop {\hbox{max} }\limits_{\forall i,\forall j} \left\{ {\varepsilon_{a} } \right\} $$

(25)

The negative of these ranges identifies the cases where ISE is conservative. The positive of these ranges identifies the cases where ISE is non-conservative. We shall graphically display these statistical ranges in the figures in Sects. 4.3 and 4.4.

4.2 Estimating reasonable parameter values

The key numerical parameters in Eq. (16) are (1) system frequency parameter: $\omega$ and (2) the pier to deck stiffness ratios $\eta_{i}$. In the experimental section of this paper, we have determined by rigorous experimental inverse system identification the values for these parameters. In this section, we aim to choose parameter values that are appropriate for real bridge structures. In the paper, Dusseau and Dubaisi (1993) measured the vertical and lateral fundamental frequencies for a set of concrete bridges in the Pacific Northwest, USA. Data collected from this paper is used to propose a new empirical formula for of generic concrete bridges

$$ f_{1} = \frac{996.3}{{L_{t}^{1.19} H^{0.194} }} $$

(26)

where $f_{1}$ (Hz) is the fundamental lateral frequency, $L_{t}$ (m) is the total length of the bridge and H (m) is the maximum pier height. Figure 7a displays the experimental data collected by Dusseau and Dubaisi (1993) and the empirical formula (26). The empirical fit was obtained by using Matlab curve fitting toolbox and had an $R^{2} = 0.96$.

Fig. 7

a Experimental lateral frequencies vs total bridge length for concrete bridges in the Pacific Northwest, USA (Dusseau and Dubaisi 1993). b Theoretical lateral frequencies versus pier to deck stiffness ratio from Eq. (16) with equal piers $\eta_{2} = \eta_{3} = \eta_{4} = \eta$

Figure 7b display the fundamental lateral frequency from the reduced order model, Eq. (16). At $\omega = 18.5$[rad/s] and pier to deck stiffness ratio $\eta = 3.5$ the natural frequency is about $f_{1} = 6$ (Hz). The 200 m long prototype structure, that was used to design the experimental model bridge, should have a frequency in the range 2.7 to 0.43 (Hz) (from Eq. (26)). This analysis suggests that the experimental model was a little stiffer than ideal if the aim was to parametrically match this prototype. A more reasonable value of $\omega$ would be about $\omega = 5$ (rad/s), if we are to place the parametric analysis within the scope of real structures. Therefore, we shall adopt $\omega = 5$ (rad/s) for the subsequent parametric studies.

4.3 An archetypal symmetrical multi-span bridge model

Figure 8 displays the general form of an archetypal symmetrical multi-span bridge model. By inducing symmetry, we reduce the system to key parameters the pier to deck stiffness ratios $\eta = \eta_{2} = \eta_{4}$ for the outer piers, and $\alpha = {{\eta_{3} } \mathord{\left/ {\vphantom {{\eta_{3} } \eta }} \right. \kern-0pt} \eta }_{2}$ the ratio of stiffness ratios between central and outer piers. A shorter central column would result in a stiffer column, hence $\alpha > 1$. The suggestion here is that when the central column is stiff enough the fundamental mode must become anti-symmetric about the central pier. This is a key feature of the parametric analyses in this section. Archetypally symmetrical (in geometry) bridges need not have symmetrical first modes of vibration. In this case, when $\alpha$ is large, the first mode is anti-symmetrical. This may induce larger differences between MSE and ISE analyses for larger $\alpha$.

Fig. 8

An archetypal symmetrical multi-span bridge model

In this structure, we also assume $L = 200$ (m) and $\omega = 5$ (rad/s). Additionally, we assume a 0.05 ratio of critical damping for modes 1 and 3 in the Rayleigh damping matrices, Eq. (12). Modes 1 and 3 are used because it is possible for modes 1 and 2 to have identical modal frequencies in this system. In these cases, the conventional Rayleigh damping formulae become singular, hence a more stable numerical process is obtained by avoiding this scenario. These damping ratios are larger than the experimentally observed ones but more realistic of large amplitude seismic oscillations in real bridges.

Figure 9 displays examples of time-history analyses for pier 4 for two orthogonal alignments of the bridge. The response total acceleration of the top of pier 4 is displayed for both MSE and ISE cases. Figure 9a shows MSE peak responses are 23% greater than the ISE peak responses. This indicates ISE is non-conservative in this case. Figure 9b shows an error of − 13.9% indicating that MSE peak responses smaller than the ISE peak responses. This indicates ISE is conservative in this case. The larger spatial scatter in the east–west components (see Fig. 4a) compared with the north–south components (Fig. 4b) induces significant differences in error for some alignments. These features are not typically present in artificially generated spatiotemporal ground motions.

Fig. 9

Examples of total acceleration responses for parameters $\eta = 25,\alpha = 5$. a Alignment 11 with an error of $\varepsilon_{a} = 23\%$, b alignment 4 with an error of $\varepsilon_{a} = - 13.9\%$

Figure 9 are examples at a specific parameter set $\left\{ {\alpha ,\eta } \right\}$. To generalize these results, we explore a range of $\left\{ {\alpha ,\eta } \right\}$. Figures 10 and 11 display the error estimates $\varepsilon_{a}$ and $\varepsilon_{d}$, respectively. These figures require 12,000 unique time-history analyses, with 192 different ground motion time-series. Figure 10a displays the lower bound for the error in total acceleration (using Eq. (22)). These represent the cases where, at some alignment of the bridge, the ISE analyses are conservative (i.e. greater than the MSE analyses). Figure 10b displays the upper bound for the error in total acceleration (using Eq. (23)). These represent the cases where, at some alignment of the bridge, the ISE analyses are non-conservative (i.e. less than the MSE analyses).

Fig. 10

Error range in pier total acceleration $\varepsilon_{a}$ for archetypal symmetrical bridges. a Lower bound of errors, b upper bound of errors

Fig. 11

Error range in pier deformation $\varepsilon_{d}$ for archetypal symmetrical bridges. a Lower bound of errors, b upper bound of errors

Figure 11 displays the errors pier deformation $\varepsilon_{d}$. As before the lower and upper bound plot estimate confidence bounds for the error in ISE analyses. What is clear from these analyses is that for any given symmetrical bridge ISE could be conservative or non-conservative. This is dependent on system parameters, bridge orientation, and the ground motion time-series. Therefore, studies based on limit parametric explorations of the problem could easily produce antithetical conclusions, as in the literature.

It is worth reflecting on a possible physical interpretation of pier to deck stiffness ratio $\eta$ in Figs. 10 and 11. Consider the case where the flexural stiffness of the deck is considered relatively invariant. Then $\eta$ is governed predominantly by the inverse of pier height which is a function of valley profile. Hence, very shallow valleys are likely to have larger values of $\eta$ and very deep valleys are likely to have lower values of $\eta$. Hence, it appears, qualitatively, from the results in Figs. 10 and 11, that bridges over shallow valleys are far more susceptible to the spatial incoherent effect of ground motions than bridges over deep valleys.

4.4 An archetypal asymmetrical multi-span bridge model

Figure 12 displays the general form of an archetypal asymmetrical multi-span bridge model. By inducing a simple asymmetry, we reduce the system to key parameters the pier to deck stiffness ratios $\eta = \eta_{3} = \eta_{4}$ for the outer and central pier, and $\alpha = {{\eta_{2} } \mathord{\left/ {\vphantom {{\eta_{2} } \eta }} \right. \kern-0pt} \eta }_{3}$ the ratio of stiffness ratios between outer piers. In this structure we also assume $L = 200$ (m) and $\omega = 5$ (rad/s). The damping model assumes 0.05 ratio of critical damping as before.

Fig. 12

An archetypal asymmetrical multi-span bridge model

Figures 13 and 14 show the estimated errors in employing ISE analyses for pier total acceleration $\varepsilon_{a}$ and deformation $\varepsilon_{d}$. Figure 13 particularly demonstrates that these archetypal symmetrical bridges have a much larger range of error, from − 60.0621 to 168.3720. This suggests quite clearly that symmetric bridges can be more vulnerable to non-conservative ISE analyses estimates.

Fig. 13

Error range in pier total acceleration $\varepsilon_{a}$ for archetypal asymmetric bridges. a Lower bound of errors, b upper bound of errors

Fig. 14

Error range in pier deformation $\varepsilon_{d}$ for archetypal asymmetric bridges. a Lower bound of errors, b upper bound of errors

However, it should also be noted that comparing Fig. 13 (for asymmetrical bridges) and Fig. 10 (for symmetrical bridges) it is also clear that for many parameters sets $\left( {\alpha ,\eta } \right)$ the performance of ISE is not that much worse for asymmetrical bridges. The mean maximal error in Fig. 13 (for asymmetrical bridges) is 29.8% while it is 29.03% in Fig. 10 (for symmetrical bridges). This again highlights the need for extensive parametrical studies.

5 Conclusions

In this paper, we derive a reduced order model for the lateral vibrations of a continuous multi-span bridge. This model is based on linear elastic system behaviour and makes use of a real multi-station ground motion array records. Linearity limits the scope to small magnitude seismic events, and using the SMART-1 array data reduces the sample size of the seismic data. Therefore, results obtained should be viewed as contingent on the scope of the assumptions employed. The reduced order model employed highlights the key system parameters, namely pier to deck stiffness ratio, inter-pier stiffness ratio, and the system fundamental frequency parameter. It makes use of a MIMO system formulation to simulate the dynamic behaviour of multi-span bridges. Validation of this reduced order model was conducted using an operational modal analysis on experimental benchmark tests conducted previously at the University of Bristol. The results of this grey-box inverse system identification demonstrate that a 3-dof model can accurately capture the significant lateral system responses. Results suggest that this approach could be used on the inverse system identification of real bridges.

In the extensive parametric study, we explore the bridge responses for differing bridge longitudinal alignment in a spatiotemporal superficial ground displacement field. The aims were to (1) determine whether or not, an identical support excitation (ISE) assumption is conservative and (2) identify the cases where it is not and (3) to determine the statistical range of the non-conservatism of ISE.

The results can be conceptually divided up into (a) alignment effects (ground motion variability) and (b) geometry parameter effects (structural variability). The influence of alignment, on the question (1), was significant for all geometry parameter sets. The alignment effect is probably more significant than the effect of geometry.

This is to say if one selected a particular bridge (symmetrical or asymmetrical) and varied its alignment in a superficial ground displacement field. Then you could obtain either conservative or non-conservative ISE analysis estimates. Additionally, it is easy to find an example of an asymmetrical bridge that is not prone to the negative effects of ground motion spatial incoherence. This is made clear in Figs. 10, 11, 12, 13 and 14, that show a conservative ISE at some alignment and unconservative ISE at other alignments. Thus, the effect of anisotropy (at the surface) of real spatiotemporal ground motion fields is large on the system dynamical responses of long structures.

The maximal (non-conservative) errors in ISE analyses are found for asymmetrical structural systems at particular, localised, geometric parameter sets. Archetypally asymmetrical bridges exhibit smaller maximal errors than for archetypally symmetrical bridges. However, it is worth noting that the mean maximal error (across the entire geometric parameter set range explored in this paper) shows little significant difference between symmetrical and asymmetrical bridge geometries. The reason for this is that these maximal errors occur when input system power (ground motion spectral content) is aligned (in frequency) unfavourably with the system transfer function peaks.

Within the scope of the analyses presented in this paper, the influence of alignment (and hence ground motion spatial variability) was found to be more significant than the influences of various bridge geometries. Although there is some evidence to suggest that bridges over shallow valleys (with stiffer, shorter, piers) may be more susceptible to unconservative ISE analysis estimates than bridges over deep valleys (with taller, more flexible, piers). This conclusion needs to be validated with base ground motions which include the orographical effects caused by valleys which is not currently the case in this paper. The effect of alignment caused by anisotropic spatially varying real ground motion at the SMART-1 array highlights the persistent requirement for a larger database of real recorded spatiotemporal ground motions.

Appendices

Appendix 1: 3 dof formulation of 4 span bridge test case

The general form of Lagrangian interpolating polynomials is as follows

$$ {\varvec{\uppsi}}^{\text{T}} = \left[ {\begin{array}{*{20}c} {\uppsi_{1} } & {\uppsi_{2} } & \cdots & {\uppsi_{m} } \\ \end{array} } \right] ,\quad\uppsi_{i} \left( \xi \right) = \frac{{\ell_{i} \left( \xi \right)}}{{\ell_{i} \left( {\xi_{i} } \right)}},\quad \ell_{i} \left( \xi \right) = \frac{{\prod\nolimits_{q = 1}^{m} {\left( {\xi - \xi_{q} } \right)} }}{{\left( {\xi - \xi_{i} } \right)}} $$

where the interpolating polynomial $\psi_{i} \left( \xi \right) = 0$ for all integer $\xi$ not equal to i and $\psi_{i} \left( i \right) = 1$. The interesting feature of this interpolant is that it results in diagonalization of system matrices ${\mathbf{K}}_{1} ,{\mathbf{K}}_{2}$ and ${\mathbf{K}}_{3}$ that in turn enables a more simplified form of the final system equations.

A set of 4th order Lagrangian interpolating function for both the ground and deck deformation Ritz vectors defined below.

$$ {\varvec{\uppsi}} = {\varvec{\uppsi}}_{g} = \left[ {\begin{array}{*{20}c} {\frac{{\left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - 4} \right)}}{24}} \\ {\frac{{\xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right)}}{24}} \\ { - \frac{{\xi {\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - 4} \right)}}{6}} \\ {\frac{{\xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - 4} \right)}}{4}} \\ { - \frac{{\xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 4} \right)}}{6}} \\ \end{array} } \right],\quad {\mathbf{u}} = \left[ {\begin{array}{*{20}c} {u_{1} = g_{1} } \\ {u_{5} = g_{5} } \\ \hline {u_{2} } \\ {u_{3} } \\ {u_{4} } \\ \end{array} } \right],\quad {\mathbf{g}} = \left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{5} } \\ \hline {g_{2} } \\ {g_{3} } \\ {g_{4} } \\ \end{array} } \right], $$

Thus, the number ground dofs n is the same as the number deck dofs m. After partitioning the system condenses to a 3dof system i.e. u₂ to u₄. Using the symbolic algebra toolbox in Matlab the system matrices can be determined.

Appendix 2: 7 dof formulation of 4 span bridge test case

A set of 8th order Lagrangian interpolating function for deck deformations Ritz vector ${\varvec{\uppsi}}$ and a 4th order for the ground Lagrangian interpolating function Ritz vector ${\varvec{\uppsi}}_{g}$ show below

$$ {\varvec{\uppsi}} = \left[ {\begin{array}{*{20}c} {\frac{{2{\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - \frac{1}{2}} \right){\mkern 1mu} \left( {\xi - 4} \right){\mkern 1mu} \left( {\xi - \frac{3}{2}} \right){\mkern 1mu} \left( {\xi - \frac{5}{2}} \right){\mkern 1mu} \left( {\xi - \frac{7}{2}} \right)}}{315}} \\ {\frac{{2{\mkern 1mu} \xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - \frac{1}{2}} \right){\mkern 1mu} \left( {\xi - \frac{3}{2}} \right){\mkern 1mu} \left( {\xi - \frac{5}{2}} \right){\mkern 1mu} \left( {\xi - \frac{7}{2}} \right)}}{315}} \\ { - \frac{{16{\mkern 1mu} \xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - 4} \right){\mkern 1mu} \left( {\xi - \frac{3}{2}} \right){\mkern 1mu} \left( {\xi - \frac{5}{2}} \right){\mkern 1mu} \left( {\xi - \frac{7}{2}} \right)}}{315}} \\ {\frac{{8{\mkern 1mu} \xi {\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - \frac{1}{2}} \right){\mkern 1mu} \left( {\xi - 4} \right){\mkern 1mu} \left( {\xi - \frac{3}{2}} \right){\mkern 1mu} \left( {\xi - \frac{5}{2}} \right){\mkern 1mu} \left( {\xi - \frac{7}{2}} \right)}}{45}} \\ { - \frac{{16{\mkern 1mu} \xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - \frac{1}{2}} \right){\mkern 1mu} \left( {\xi - 4} \right){\mkern 1mu} \left( {\xi - \frac{5}{2}} \right){\mkern 1mu} \left( {\xi - \frac{7}{2}} \right)}}{45}} \\ {\frac{{4{\mkern 1mu} \xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - \frac{1}{2}} \right){\mkern 1mu} \left( {\xi - 4} \right){\mkern 1mu} \left( {\xi - \frac{3}{2}} \right){\mkern 1mu} \left( {\xi - \frac{5}{2}} \right){\mkern 1mu} \left( {\xi - \frac{7}{2}} \right)}}{9}} \\ { - \frac{{16{\mkern 1mu} \xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - \frac{1}{2}} \right){\mkern 1mu} \left( {\xi - 4} \right){\mkern 1mu} \left( {\xi - \frac{3}{2}} \right){\mkern 1mu} \left( {\xi - \frac{7}{2}} \right)}}{45}} \\ {\frac{{8{\mkern 1mu} \xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - \frac{1}{2}} \right){\mkern 1mu} \left( {\xi - 4} \right){\mkern 1mu} \left( {\xi - \frac{3}{2}} \right){\mkern 1mu} \left( {\xi - \frac{5}{2}} \right){\mkern 1mu} \left( {\xi - \frac{7}{2}} \right)}}{45}} \\ { - \frac{{16{\mkern 1mu} \xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - \frac{1}{2}} \right){\mkern 1mu} \left( {\xi - 4} \right){\mkern 1mu} \left( {\xi - \frac{3}{2}} \right){\mkern 1mu} \left( {\xi - \frac{5}{2}} \right)}}{315}} \\ \end{array} } \right],\quad {\varvec{\uppsi}}_{g} = \left[ {\begin{array}{*{20}c} {\frac{{\left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - 4} \right)}}{24}} \\ {\frac{{\xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right)}}{24}} \\ { - \frac{{\xi {\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - 4} \right)}}{6}} \\ {\frac{{\xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 3} \right){\mkern 1mu} \left( {\xi - 4} \right)}}{4}} \\ { - \frac{{\xi {\mkern 1mu} \left( {\xi - 1} \right){\mkern 1mu} \left( {\xi - 2} \right){\mkern 1mu} \left( {\xi - 4} \right)}}{6}} \\ \end{array} } \right],\quad {\mathbf{u}} = \left[ {\begin{array}{*{20}c} {u_{1} = g_{1} } \\ {u_{9} = g_{5} } \\ \hline {u_{2} } \\ {u_{3} } \\ {u_{4} } \\ {u_{5} } \\ {u_{6} } \\ {u_{7} } \\ {u_{8} } \\ \end{array} } \right],\quad {\mathbf{g}} = \left[ {\begin{array}{*{20}c} {g_{1} } \\ {g_{5} } \\ \hline {g_{2} } \\ {g_{3} } \\ {g_{4} } \\ \end{array} } \right], $$

Thus, the number ground dofs n is less than the number of deck dofs m. After partitioning the system condenses to a 7dof system, i.e. u₂ to u₈. Using the symbolic algebra toolbox in Matlab the system matrices can be determined.