Spatiotemporal seismic excitation of bridges with an anti-symmetrical first mode

Abstract

This study uses a generalized and parametrized reduced-order model in the frequency-domain to evaluate the effects of asynchronous excitation on the lateral response of bridge structures. Bridge geometry parametric regions, corresponding conceptually to valley profile shapes, are explored. Both modal and bounding analyses, that are dependent on bridge geometry alone, are employed to highlight regions where the first mode is anti-symmetrical and the likely error between identical support excitation (ISE) and multi-support excitation (MSE) analyses is large. Numerical time history analyses, using a heuristic bridge case and spatiotemporal ground motion from the SMART-1 array, are employed. These analyses confirm that in parametric configurations where the first mode is anti-symmetrical the error between MSE and ISE is often larger. This confirms the utility of geometry only modal and bounding analyses in identifying critical regions. These critical parametric cases of a first mode that is anti-symmetrical correspond to shallow valleys with a central rise. In these cases it is recommended that both ISE and MSE analyses should be employed to be conservative.

1 Introduction

Many attempts have been made (Leger and Ide et al. 1990; Monti and Nuti et al. 1996; Lin and Zhang et al. 2004; Soyluk 2004), among others, to examine the effect of spatially varying earthquake ground motion (SVEGM) on the response of long, extended, structures. Over the last two decades, the approach using random vibration techniques, in the frequency domain, for example (Abdel-Ghaffar and Rubin 1982), has frequently been employed as the uncertainty of seismic inputs can be easily modelled and interpreted by structural engineers (Abdel-Ghaffar and Rubin 1982; Ding and Lin et al. 2007). These techniques are generally limited to a linear elastic problem domain. Time-domain analyses (Fajfar 2000; Lou and Zerva 2005; Bardakis and Fardis 2011; Konakli and Der Kiureghian 2014), that account for spatial ground motions, can be considered in two forms (1) a modal decomposition that makes use of spectral responses and modal combination rules and (2) a full nonlinear time-history analysis that uses spatiotemporal ground motion timeseries. Methodology (1) is an approximate method for the case of nonlinear systems as modal decomposition/superposition is no longer a mathematically valid concept in this case. Nevertheless, some researchers have still proposed extending spectrum-oriented methods into the nonlinear regime by using a statistical linearization technique (Guyader and Iwan 2006; Spanos and Giaralis 2013; Mitseas and Kougioumtzoglou et al. 2018).

The influence of spatial heterogeneity in the ground excitation input is primarily categorized by (Kiureghian 1996): (a) wave-passage effect due to the time lag of the arriving wave between two arbitrary stations i and j; (b) loss of coherency due to consecutive reflections and refractions of earthquake waves as they scatter in heterogeneous soil media (c) the local site effects due to variation in local soil conditions underneath each stations which propagate seismic wave with different frequency and amplitude content. All the above effects could be described through modifying the amplitude and phase of seismic ground motions at stations. These modifications are modelled generally through (1) general empirical formulae which are fitted using regression (Harichandran and Vanmarcke 1986; Hao and Oliveira et al. 1989; Loh and Lin 1990; Abrahamson and Schneider et al. 1991; Oliveira and Hao et al. 1991), (2) semi-empirical approaches where the exponential parameters of the analytical form are estimated from real seismic records (Luco and Wong 1986; Kiureghian 1996; Zerva and Harada 1997; Konakli and Der Kiureghian 2012) and (3) completely theoretical models (Zerva and Shinozuka 1991; Liao and Li 2002).

In addition to the above advancements, the real seismic ground motion records from digital accelerometer arrays located all over the world like the SMART-1 array in Taiwan (Abrahamson and Bolt et al. 1987) and Imperial Valley in California (Joyner and Boore 1981) provide very important sources of information for exploring spatially heterogeneous ground motions.

The structural configuration (symmetry, overall length, regularity, abutment condition, etc.) coupling with ground motion characteristic determines the dynamic response pattern. A parametric study of 27 different bridge conducted by Sextos et al. (2003a, b) reveals that the limit, of an overall length of the bridge, for consideration of spatial variability in the dynamic analysis is in the range of 200–400 m for different ground categories which are reconcilable with EC8 classification. Lou and Zerva (2005) highlighted the significance of SVEGM effects for a shorter bridge with supports which soil conditions at their bases differ considerably. Recent studies primarily examined the response of symmetrical and unsymmetrical structures (Zerva 1990; Hao 1991; Hahn and Liu 1994); investigated the spatial variability effect on suspension and cable bridges (Nazmy and Abdel‐Ghaffar 1992; Camara and Astiz 2012); evaluated the effect of the anti-symmetrical mode on the bridge responses (Price and Eberhard 1998; Lee and Poon et al. 2006; Papadopoulos and Sextos 2018); exploring the effect of valley profile on the accuracy of ISE analyses for linear and nonlinear cases (Meibodi Alexander et al. 2020) and developed the nonlinear dynamic analysis to incorporate SVEGM effects (Wen 1976; Guyader and Iwan 2006; Sextos and Kappos 2009; Mitseas and Kougioumtzoglou et al. 2018).

In this context, the objective of this paper is first to understand and explore the mathematical features on a generalized reduced-order model to calculate the dynamic response of the multi-support bridge when spatial variability of the ground motion is taken into account. This proposed linear model is then transformed to a frequency-domain with the specific aim of quantifying the plausible bounds on the error between MSE and ISE analysis. These bounds are expressed in terms of the (a) Auto Modal Participation (AMP) and (b) Cross Modal participation (CMP) factors. They are only dependent of bridge geometry and hence can be evaluated before any time history analysis. To confirm the utility of these geometry only bounds an extensive parametric analysis scheme (that made use of tens of thousands of timehistory analyses) is undertaken where the geometrical configuration of a heuristic bridge is altered due to valley profile. Therefore, this study aims:

• 1. To explore whether certain geometry only bounds (proposed in this paper) can help to identify critical bridge configurations where identical support excitation (ISE) and multiple support excitation (MSE) analyses produce significantly different answers.

• 2. To evaluate, quantitively, the role that symmetric and anti-symmetric modes play in the bridge responses for these critical configurations.

• 3. To assess the relative importance of proposed geometrical parameters, the Auto Modal Participation factor (AMP) and Cross Modal Participation factor (CMP) and investigate its correlation with bridge responses from large-scale parametric studies conducted in the companion papers.

2 Dynamic response of MDOF bridge under multi-support excitation

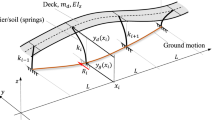
Consider an MDOF bridge subjected to the lateral seismic ground motion shown in Fig. 1. The total number of deck dofs is m but the two abutments are constraints hence there are n free DOFs (unknowns) of the deck which are $n = m - 2$. The system degree of freedom consists of two parts: (1) the n deck DOFs (unknowns) and (2) the s ground DOFs (knowns) which is equal to the number of supports.

Fig. 1

General MDOFs Bridge with n unconstrained DOFs (where n = m − 2) of deck resting on s supports. Ground motions are applied in the outof-plane direction

The equation of motion for the bridge system subjected to earthquake excitation is given by:

$$\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{11} } & {{\mathbf{M}}_{12} } \\ {{\mathbf{M}}_{21} } & {{\mathbf{M}}_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{u}}}_{t} } \\ {{\mathbf{\ddot{u}}}_{g} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{11} } & {{\mathbf{C}}_{12} } \\ {{\mathbf{C}}_{21} } & {{\mathbf{C}}_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{u}}}_{t} } \\ {{\dot{\mathbf{u}}}_{g} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{11} } & {{\mathbf{K}}_{12} } \\ {{\mathbf{K}}_{21} } & {{\mathbf{K}}_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{u}}_{t} } \\ {{\mathbf{u}}_{g} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ {\mathbf{r}} \\ \end{array} } \right]$$

(1)

where ${\mathbf{u}}_{t} = [u_{t,1} , \cdots ,u_{t,n} ]^{T} \in {\mathbb{R}}^{n \times 1}$ and ${\mathbf{u}}_{g} = \left[ {g_{1} , \cdots ,g_{s} } \right]^{T} \in {\mathbb{R}}^{s \times 1}$. A more detailed derivation of system is described in (Meibodi, Alexander et al. 2020) The first block row of Eq. (1) is defined as follows:

$${\mathbf{M}}_{11} {\mathbf{\ddot{u}}}_{t} + {\mathbf{C}}_{11} {\dot{\mathbf{u}}}_{t} + {\mathbf{K}}_{11} {\mathbf{u}}_{t} = - {\mathbf{M}}_{12} {\mathbf{\ddot{u}}}_{g} - {\mathbf{C}}_{12} {\dot{\mathbf{u}}}_{g} - {\mathbf{K}}_{12} {\mathbf{u}}_{g}$$

(2)

These Eqs. (1) and (2) are defined in terms of a fixed coordinate frame (i.e. so-called total displacements, velocities, and accelerations). Typically, in earthquake engineering, we seek a change of coordinates that switches to a moving coordinate frame (i.e. relative coordinates). Thus, we introduce the following

$${\mathbf{u}}_{t} = {\mathbf{u}}_{s} + {\mathbf{u}}$$

(3)

Hence, the Eq. (2) becomes

$${\mathbf{M}}_{11} {\mathbf{\ddot{u}}} + {\mathbf{C}}_{11} {\dot{\mathbf{u}}} + {\mathbf{K}}_{11} {\mathbf{u}} = - {\mathbf{M}}_{11} {\mathbf{\ddot{u}}}_{s} - {\mathbf{M}}_{12} {\mathbf{\ddot{u}}}_{g} - {\mathbf{C}}_{11} {\dot{\mathbf{u}}}_{s} - {\mathbf{C}}_{12} {\dot{\mathbf{u}}}_{g} - {\mathbf{K}}_{11} {\mathbf{u}}_{s} - {\mathbf{K}}_{12} {\mathbf{u}}_{g}$$

(4)

We seek to simplify the above by removing the ground displacement terms from the right hand side of the Eq. (4). So, if we assign

$${\mathbf{u}}_{s} = - {\mathbf{Ru}}_{g} ,\quad \quad {\mathbf{R}} = {\mathbf{K}}_{11}^{ - 1} {\mathbf{K}}_{12}^{{}} \in {\mathbb{R}}^{n \times s}$$

(5)

Note that displacements ${\mathbf{u}}_{s}$ can be viewed as the quasi-static displacement imposed on the system by the ground displacements. These impose a quasi-static set of stiffness forces on the system ${\mathbf{f}}_{s}$

$${\mathbf{f}}_{s} = {\mathbf{K}}_{11} {\mathbf{u}}_{s} = - {\mathbf{K}}_{12} {\mathbf{u}}_{g}$$

(6)

Thus, we can cancel out displacement terms on the right hand side of the Eq. (4) and simplify to

$${\mathbf{M}}_{11} {\mathbf{\ddot{u}}} + {\mathbf{C}}_{11} {\dot{\mathbf{u}}} + {\mathbf{K}}_{11} {\mathbf{u}} = {\mathbf{N}}_{a} {\mathbf{\ddot{u}}}_{g} + {\mathbf{N}}_{v} {\dot{\mathbf{u}}}_{g}$$

(7)

where

$${\mathbf{N}}_{a} = \left( {{\mathbf{M}}_{11} {\mathbf{R}} - {\mathbf{M}}_{12} } \right) \in {\mathbb{R}}^{n \times s} ,\quad {\mathbf{N}}_{v} = \left( {{\mathbf{C}}_{11} {\mathbf{R}} - {\mathbf{C}}_{12} } \right) \in {\mathbb{R}}^{n \times s}$$

(8)

Note if the damping matrix is proportional to the stiffness matrix only, then ${\mathbf{C}} = \alpha {\mathbf{K}}$ and therefore ${\mathbf{N}}_{v} = {\mathbf{0}}$. In the more general case, where damping matrix ${\mathbf{C}}$ is orthogonal (i.e. a Caughey damping model) we can determine the undamped homogeneous solutions to (1) by solving the resulting generalized eigenvalue problem. Nevertheless, these forcing terms ${\mathbf{N}}_{v} {\dot{\mathbf{u}}}_{g}$ are relatively small due to the low values of the damping ratios, henceforth we neglect this term.

2.1 Modal frequency domain analysis

Let’s consider, k modes participate in dynamic analysis. By employing generalized coordinates ${\mathbf{q}}$ defined as:

$${\mathbf{u}} ={\varvec{\Phi}}{\kern 1pt} {\kern 1pt} {\mathbf{q}}{\kern 1pt}$$

(9)

$${\varvec{\Phi}}= \left[ {{\varvec{\Phi}}_{1} \cdots {\varvec{\Phi}}_{k} } \right] \in {\mathbb{R}}^{n \times k} ,\quad {\mathbf{q}} = \left[ {q_{1} ; \cdots ;q_{k} } \right] \in {\mathbb{R}}^{k \times 1} ,\quad {\mathbf{u}} = \left[ {u_{1} ; \cdots ;u_{n} } \right] \in {\mathbb{R}}^{n \times 1}$$

(10)

where, ${\varvec{\Phi}}$, the partial eigenvector matrix that spans the first k modes (each column is an individual eigenvector $\varvec{\Phi }_{i}$). By pre-multiplying Eq. (7) by ${\varvec{\Phi}}^{T}$ and using the orthogonality principle we obtain the following uncoupled 2nd order ordinary differential system for each mode,

$$\ddot{q}_{i} + 2\gamma_{i} \omega_{i} \dot{q}_{i} + \omega_{i}^{2} q_{i} = \varvec{\Phi }_{i}^{T} {\mathbf{N}}_{a} \,{\mathbf{\ddot{u}}}_{g}$$

(11)

By taking the Fourier transform of the Eq. (11) we convert this ordinary differential equation into an algebraic equation (in the frequency domain, where $\omega$ is the Fourier frequency) as:

$${q}_{i} \left( \omega \right){ = h}_{i} \left( \omega \right){{\varvec{\Gamma}}}_{i}^{T} {\mathbf{\ddot{u}}}_{g} \left( \omega \right)$$

(12)

where the modal participation vector is defined as follows,

$${{\varvec{\Gamma}}}_{i}^{T} \left( \omega \right)=\varvec{\Phi }_{i}^{T} {\mathbf{N}}_{a} = \left[ {\Gamma_{i1} , \cdots ,\Gamma_{is} } \right] \in {\mathbb{R}}^{1 \times s}$$

(13)

and the scalar modal transfer function $\varvec{h}_{\varvec{i}} \left( \omega \right)$ is now defined for mode k as:

$${\text{h}}_{i} \left( \omega \right)=\left( {\left( {\omega_{i}^{\varvec{2}} -\omega_{{}}^{\varvec{2}} } \right) + {\mathbf{i}}{2}\gamma_{i} \omega_{i}^{{}} \omega } \right)^{ - 1} ,\quad {\mathbf{i}} = \sqrt { - 1}$$

(14)

Now let us consider a general ground motion for the p-th support,

$${\ddot{{g}}}_{p} \left( \omega \right) = {R}_{p} \left( \omega \right)\exp \left( {{\mathbf{i}}\theta_{p} \left( \omega \right)} \right)$$

(15)

Therefore, the Power Spectral Density (PSD) of modal response in Eq. (12) can be stated in general as

$$\left| {{q}_{i} \left( \omega \right)} \right|^{{2}} = \left| {{h}_{i} \left( \omega \right)} \right|^{{2}} \left| {\sum\limits_{{{p }= 1}}^{s} {\Gamma_{{{ip}}} {R}_{p} \left( \omega \right){e}^{{{\mathbf{i}}\theta_{{p}} \left( \omega \right)}} } } \right|^{2}$$

(16)

Further expansion and re-arrangement of Eq. 16 (using Appendix) results in the generalised MSE case

$$\left| {{q}_{i} \left( \omega \right)} \right|_{\text{MSE}}^{2} = \left| {{h}_{i} \left( \omega \right)} \right|^{{2}} \left\{ {\sum\limits_{{{p} = 1}}^{s} {\left( {\Gamma_{{{ip}}}^{{}} {R}_{p} \left( \omega \right)} \right)^{2} } + 2\sum\limits_{{{p} = 1}}^{{{s} - 1}} {\sum\limits_{{{l = p + 1}}}^{s} {\Gamma_{{{il}}} \Gamma_{ip} } {R}_{p} \left( \omega \right){R}_{l} \left( \omega \right)\,\cos \left( {\theta_{l} \left( \omega \right) - \theta_{p} \left( \omega \right)} \right)} } \right\}$$

(17)

Consider the ISE case where $R_{p} {\kern 1pt} e^{{{\text{i}}\theta_{p} }} = R_{l} {\kern 1pt} e^{{{\text{i}}\theta_{l} }} = R{\kern 1pt} e^{{{\text{i}}\theta }}$ for $\forall p,l$ then

$$\left| {{q}_{i} \left( \omega \right)} \right|_{{{\text{ISE}}}}^{2} = \left| {{h}_{i} \left( \omega \right)} \right|^{{2}} {R}\left( \omega \right)^{2} \left\{ {\sum\limits_{{{p} = 1}}^{s} {\Gamma_{{{ip}}}^{2} } + 2\sum\limits_{{{p} = 1}}^{{{s} - 1}} {\sum\limits_{{{l = p + 1}}}^{s} {\Gamma_{{{il}}} \Gamma_{ip} } } } \right\}$$

(18)

2.2 Total responses

Hence, the dynamic responses of Eq. (9) (and using Eq. (12)) in the nodal coordinate can be represented as a linear function of modal displacement as:

$${\mathbf{u}}\left( \omega \right) = \sum\limits_{i = 1}^{k} {{{\varvec{\upphi}}}_{i} } {h}_{{i}}{\varvec{\Gamma}}_{{i}}^{\varvec{T}} {\mathbf{\ddot{u}}}_{{{g}}} \left( \omega \right)$$

(19)

The power spectral density (PSD) of dynamic response vector ${\mathbf{S}}\left( \omega \right)$ can be evaluated as:

$${\mathbf{S}}\left( \omega \right) = {\mathbf{u}} \circ {\overline{\mathbf{u}}} = \left[ {S_{11} \left( \omega \right),S_{22} \left( \omega \right), \cdots ,S_{nn} \left( \omega \right)} \right]^{T}$$

(20)

where symbol $\circ$ indicates the Hadamard product (element-wise vector multiply), ${\overline{\mathbf{u}}}$ is the complex conjugate of ${\mathbf{u}}$ and $S_{pp}$ is the power spectral density of the response of the p-th dof.

2.3 Determining the error between MSE and ISE solutions.

It is clear from consideration of the equation of motion that we do not know a priori whether ISE analysis will be conservative or unconservative. Therefore, the first question here is, for what bridge/valley configurations does the ISE assumption produce an over conservative estimate of the bridge’s lateral responses? And, secondly, what is the magnitude of this error (the difference between MSE and ISE estimates)?

The modal error (the difference between MSE and ISE estimates) is defined as follows

$$\varepsilon_{u,i} \left( \omega \right) = \phi_{u,i}^{2} \left( {\left| {{q}_{i} } \right|_{{\text{MSE}}}^{2} - \left| {{q}_{i} } \right|_{\text{ISE}}^{2} } \right) = \left| {{h}_{i} \left( \omega \right)} \right|^{{2}} {R}\left( \omega \right)^{2} \left\{ {\alpha_{u,i} \left( \omega \right) + \beta_{u,i} \left( \omega \right)} \right\}$$

(21)

where $\varepsilon_{u,i} \left( \omega \right)$ is the error for the u-th dof due to the i-th mode, and the i-th eigenvector $\varvec{\phi }_{i}^{T} = \left[ {\phi_{1,i} , \cdots ,\phi_{n,i} } \right]$ and hence $\phi_{u,i}^{{}}$ its u-th element. Terms, $\alpha_{u,i} \left( \omega \right)$ and $\beta_{u,i} \left( \omega \right)$ are defined as follows

$$\alpha_{u,i} \left( \omega \right) = \phi_{u,i}^{2} \sum\limits_{{{p} = 1}}^{s} {\Gamma_{{{ip}}}^{2} } \left( {\frac{{{R}_{p}^{{}} \left( \omega \right)_{{}}^{2} }}{{{R}\left( \omega \right)^{2} }} - 1} \right)\,,\;$$

(22)

$$\beta_{u,i} \left( \omega \right) = 2\phi_{u,i}^{2} \sum\limits_{{{p} = 1}}^{{{s} - 1}} {\sum\limits_{{{l = p + 1}}}^{s} {\Gamma_{{{il}}} \Gamma_{ip} \left( {\frac{{{R}_{p} \left( \omega \right){R}_{l} \left( \omega \right)\,\cos \left( {\theta_{l} \left( \omega \right) - \theta_{p} \left( \omega \right)} \right)}}{{{R}\left( \omega \right)^{2} }} - 1} \right)} }$$

(23)

These two terms in the modal error are (1) $\alpha_{u,i} \left( \omega \right)$ (the summation of support ground motion power terms) ignores the affect of arrival timing of the peaks in the ground motion and (2) $\beta_{u,i} \left( \omega \right)$ (the summation of cross-terms and phases) includes the effect of arrival timing of the peaks in the ground motion. The power term, $\alpha_{u,i} \left( \omega \right)$, is dependent solely on the amplitude contents of the ground motions, although the cross term, $\beta_{u,i} \left( \omega \right)$, is dependent on amplitude and phase-difference content of the ground motions.

2.4 An estimate of a geometry only bound on $\alpha_{u,i} \left( \omega \right)$ and $\beta_{u,i} \left( \omega \right)$

The terms $\alpha_{u,i} \left( \omega \right)$ and $\beta_{u,i} \left( \omega \right)$ are dependant both on bridge geometry and ground motion characteristics. We seek to obtain a proxy (and in this case a bound) for these terms that is independent of ground motion characteristics and dependent on geometry alone. To achieve this we introduce the following assumption. We assume that there exists a singleton station (that was used for ISE) who’s power is greater or equal to the power of any of the stations used for MSE, that is

$$R\left( \omega \right) \ge \left\{ {R_{p} \left( \omega \right){ : }\forall p} \right\}$$

(24)

With this assumption, considering the Eq. (22), the last bracketed term ranges from zero (when all ground motions are equal in power) to minus one (when all ground motions other than $R\left( \omega \right)$ are zero). Similarly, consider Eq. (23), the last bracketed term ranges from zero (when all seismic inputs are equal in power) to minus two (when the phase difference ${\theta }_{l}\left(\omega \right)-{\theta }_{p}\left(\omega \right)$ between stations is exactly$\pi$). Additionally, the term ${\Gamma }_{il}{\Gamma }_{ip}$ can be positive or negative. Hence the term in Eq. (23) (which is double summed) must range between $- 2\left| {\Gamma_{{{il}}} \Gamma_{ip} } \right|$ and $2\left| {\Gamma_{{{il}}} \Gamma_{ip} } \right|$ and hence we obtain the strict mathematical bounds that are defined in Eq. (26) below.

Therefore, we obtain an estimated bound of terms $\alpha_{u,i} \left( \omega \right)$ and $\beta_{u,i} \left( \omega \right)$

$$\begin{gathered} - {\rm A}_{u,i} \le \alpha_{u,i} \left( \omega \right) \le 0 \hfill \\ - 2\left| {{\rm B}_{u,i} } \right| \le \beta_{u,i} \left( \omega \right) \le 2\left| {{\rm B}_{u,i} } \right| \hfill \\ \end{gathered}$$

(25)

where the positive term ${\rm A}_{u,i}$ is designated, in this paper, as the Auto Modal Participation (AMP) factor and positive/negative term ${\rm B}_{{{u},{i}}}$ is designated, in this paper, as the Cross-Modal Participation (CMP) factor, and are defined as follows

$$\quad {\rm A}_{u,i} = \phi_{u,i}^{2} \sum\limits_{{{p} = 1}}^{s} {\Gamma_{{{ip}}}^{2} } ,\quad {\rm B}_{{{u},{i}}} =\phi_{u,i}^{2} \sum\limits_{{{p} = 1}}^{{{s} - 1}} {\sum\limits_{{{l = p + 1}}}^{{s}} {\Gamma_{{{ip}}} \Gamma_{{{il}}} } }$$

(26)

And therefore, we estimate the bound of the modal error (between ISE and MSE), using the triangle inequality, which is given by the following

$$\left| {\varepsilon_{u,i} \left( \omega \right)} \right| \le \left| {{h}_{i} \left( \omega \right)} \right|^{{2}} {R}\left( \omega \right)^{2} \left\{ {{\text{A}}_{u,i}^{{}} + 2\left| {{\text{B}}_{u,i} } \right|} \right\}$$

(27)

Thus, as the magnitude of ${\rm A}_{u,i}$ and ${\rm B}_{{{u},{i}}}$ reduces this suggests that the error (between ISE and MSE) will also reduce. And note that this magnitude of ${\rm A}_{u,i}$ and ${\rm B}_{{{u},{i}}}$ is dependent on geometry alone.

It is worth pointing out that Eq. 24, while often satisfied for stocastic ground (artifical) spatially varying ground motions, may not be always satisfied in the case of real ground motions. Therefore the bounds in Eqs. (25) and (27) must be considered, in practice, as approximations rather than universally valid ones.

3 Seismic ground motion input from SMART1 array

In this paper, we employ an actual seismic dataset from the SMART1 array rather than some artificially constructed spatiotemporal ground motion. The SMART-1 Array was one of the biggest seismic databases specifically used to explore the near-field characteristics of ground excitation (Abrahamson and Bolt et al. 1987). The records from event 43 (IES 1980-1990) are used in this study. This seismic event with the epicenter close to the array is the largest event recorded at the SMART-1 Array. It occurred on 30/ 7/86 at 11:31:47.5 (UTC), it had a magnitude of 6.2M_L. The epicenter of the event was at depth and distance of around 2 km and 5 km (from the centre of the array), respectively. The epicenter was discovered at an estimated bearing of 150° from the center of the array.

The correction processing of seismic data is fully explained in (Alexander and Chanerley et al. 2001; Chanerley and Alexander 2007, 2008). The location of the center station (C00) and inner (I00-I12) in a concentric circle with radii 200 m are illustrated in Fig. 2. The array components are recorded in three directions: north, east and vertical. The easterly and northerly components are rotationally transformed into a local coordinate system corresponding to the bridge longitudinal alignment. The fully spatiotemporal ground motion time-series across the array is estimated using a biharmonic interpolation (Alexander 2008; Vicencio and Alexander 2019). Thus, using these interpolating functions we can estimate the two horizontal components of the ground motion anywhere in the inner circle of the SMART-1 array. From these two components we estimate the transversal (to the bridge) ground motion at the abutments and bridge pier supports for any bridge in any of 12 radial alignments as shown in Fig. 2.

Fig. 2

Example of radial bridge orientation and the configuration of SMART-1 array including center (C00) and inner ring station (I01-I12)

Figure 3a shows the power spectrum of the corrected seismic data at the centre and inner ring station and co-spectrum between origin station C00 and selected inner ring stations. Note that in this figure the seismic data are rotated to be orthogonal to the bridge longitudinal orientation. The spectra are obtained using the Welch method (Welch 1967) and a Hanning (Gruber 1997) smoothing window function. It can be suggested from Fig. 3 that the PSD at the chosen stations has closely analogous frequency contents in which, the peaks of the PSD curve for all stations occurs at roughly 0.8 and 2 Hz.

Fig. 3

a Power Spectrum of acceleration time-series at selected inner ring station. PSD of station C00 is aligned with the orintation C00-I03. b Cospectrum between C00 and selected inner ring stations of SMART-1 array for event 43

The co-spectrum is derived from the cross-spectrum which provides helpful details to interpret seismic data. The co-spectrum is the real part of the cross-spectral density function at two different stations.. Figure 3b indicates that in the range of dominant frequency (up to 5 Hz), the phase difference spectra are primarily positive. From 5 Hz onwards, the co-spectrum starts to fluctuate around the x-axis and reach the negative values at some frequencies. However, the amplitude of seismic waves in this range is small.

4 Parametric study

In this section, we aim to provide insight into the parametric analysis carried out in studies (Meibodi and Alexander 2020; Meibodi and Alexander et al. 2020). The studied bridge (Lupoi and Franchin et al. 2005; Crewe and Norman 2006) was selected as a reference bridge for the parametric analysis and is shown in Fig. 4. Note that a numerical/experimental validation of the equations of motion used in this paper was previously presented in (Meibodi and Alexander 2020).

Fig. 4

symmetrical bridge arrangement for parametric study

In this heuristic case, shown in Fig. 4, we shall numerically explore various bridge configurations with different dynamic properties. To further reduce the parameter space complexity was shall assume that the profile of the valley varies so that the bridge arrangement remains symmetrical. The application of equations of motion (7) to this bridge case is explicitly derived in (Meibodi and Alexander et al. 2020). For this case four system level parameters are defined; namely, a bridge frequency parameter $\varpi$ and three non-dimensional pier to deck stiffness ratios $\eta_{i}$. The bridge frequency parameter $\varpi$ is defined as follows

$$\varpi^{2} = \frac{{EI_{z} }}{{m_{d} L^{4} }}$$

(28)

where $EI_{z}$ is the lateral flexural rigidity of the deck, $L$ is the length of a span and $m_{d}$ is the mass per unit length of the deck. An empirical estimate of this system frequency parameter $\varpi$ is defined (Meibodi and Alexander 2020).For this reference bridge (with 50 m spans) it was estimated as 5. Thus, we do not explore this parameter in this paper. The pier to deck stiffness ratios $\eta_{i}$ are defined as follows

$$\eta_{i} = \frac{{k_{i} L^{3} }}{{EI_{z} }}$$

(29)

where $k_{i}$ is the elastic lateral stiffness of the i-th bridge pier. We further reduce this number of parameters by assuming bridge symmetry and this results in just two parameters, $\alpha$ and $\eta$ that are defined as follows

$$\alpha = {{\eta_{3} } \mathord{\left/ {\vphantom {{\eta_{3} } \eta }} \right. \kern-\nulldelimiterspace} \eta }_{2} \,,\quad \quad \quad \eta = \eta_{2} = \eta_{4}$$

(30)

where α is a ratio of stiffness between the central and outer pier and η is the deck to pier stiffness ratios for outer piers.

As the central pier becomes shorter (due to a central valley rise for example) $\alpha$ becomes greater than 1 it is possible for the first mode to become anti-symmetric. This is a key feature in this parametric analysis. This suggests that Archetypally symmetrical bridges do not necessarily possess a symmetrical fundamental mode. It is worth mentioning that dynamic parameter η is inversely proportional to column height. The low values of η correspond to bridge constructed on the deep valleys and high values of η correspond to bridge constructed on shallow valleys. The physically admissible range for η can be inferred from the lateral frequency of the bridge, which are depicted Fig. 7 of (Meibodi, Alexander et al. 2020). Thus we explore those values of η that are compatible with the lateral frequencies of real bridges.

The ratio of critical damping for all modes is assumed to equal to 0.05 in this study.

4.1 Modal analysis: is the first mode symmetrical or anti-symmetrical?

The natural frequencies and mode shapes for the 9-DOFs system are calculated from Eq. (7). The eigenvalue problem for this system is $\left(\mathbf{D}-{\upomega }_{\mathrm{i}}^{2}\mathbf{I} \right){{\varvec{\upphi}}}_{i}=0$. The dynamic matrix $\mathbf{D}$ is equal to ${\mathbf{M}}_{11}^{-1}{\mathbf{K}}_{11}$. In general, $\mathbf{D}$ is a function of four system parameters (pier-to-deck stiffness ratios ${\upeta }_{1},{\upeta }_{2},{\upeta }_{3}$ for the 1st to 3th piers respectively and the frequency parameter $\varpi$).

A graphical representation of these Eigen solutions is shown in Fig. 5 for bridges in the parametric study. Notations S1 and S2 represent the first and second symmetric modes while A1 and A2 represent the first and second anti-symmetric modes. Figure 5a shows the variation of modal circular frequencies ${\omega }_{\mathrm{i}}$ with pier-to-deck stiffness ratio η. In this case α = 1, thus all three support piers are identical.

Fig. 5

Variation of modal frequencies and mode shapes with structural geometry a α = 1 b α = 3

At low values of η, this would be for long slender piers, the natural frequencies of lateral horizontal modes are well separated. However, at the larger values of η (on this graph), this would be for shorter stockier piers, the natural frequencies are not so well separated. The first and second modes cross (are equal in frequency) at $\upeta =110.1$ (in Fig. 5a). Consider, also, the changes in mode shapes that are displayed in Fig. 5a. For low values $\eta <110$, as modes are well-separated, the first mode is always symmetrical. However, with $\eta >110$, the first mode is now always anti-symmetrical. Therefore, this raises the question, will spatially incoherent ground motions (MSE) be more problematic by exciting this anti-symmetrical first mode?

Consider now another case where α = 3 (Fig. 5b) implying the central pier has triple the lateral flexural stiffness of the first and third piers. This could be due to a larger flexural rigidity, a shorter pier height and/or stiffer foundations. The first and second eigen solutions, for $\alpha =1$, only intersect at $\eta \approx$ 110 as shown in Fig. 5a. This is not the case where $\alpha =3$. The first two eigensolutions intersected and cross at $\eta \approx 7$ and again at $\eta \approx 75$ and $\eta \approx 110$. Between the first two intersections, for $7<\eta <$ 75, the first mode is anti-symmetrical. Continuing the argument proposed in the previous paragraph it is likely that analysis of a bridge, for $7<\eta <$ 75 and $110<\eta$, the ISE analysis case will not be able to excite the first mode that is anti-symmetrical.

The locus of the frequency intersection points of the first symmetric and anti-symmetric modal frequencies is displayed in Fig. 6. In this figure, ${\omega }_{s}$ and ${\omega }_{A}$ denote the first circular frequency of symmetrical and anti-symmetrical modes respectively. The red lines correspond to the cases in Fig. 5.

Fig. 6

locus of frequencies where first symmetric and anti-symmetric modes are equal. ω_s and ω_A denote the first circular frequency of symmetric and anti-symmetric mode respectively. The red lines correspond to the cases in Fig. 5

For a case where $\eta >109$, the first mode is anti-symmetrical for all values of α. When $\alpha >1.26$ and $\eta <109$ then there exist values of η such that the first mode is anti-symmetrical. While for $\alpha <1.26$ and $\eta <109$ there exists no region in which this first mode is anti-symmetrical. Thus, increasing the height of the central pier, relative to the other piers, will reduce its stiffness and hence reduce α below 1 and tend to increase the separation of the symmetrical and anti-symmetrical modal frequencies; with the first symmetrical mode always being the fundamental mode.

4.2 Bounding analysis: numerical examples of geometry only bounds ${\rm A}_{u,i}$,${\rm B}_{u,i}$

Previously, in Sect. 2.4, we defined geometry only parameters, the auto-modal participation (AMP) factor ${\rm A}_{u,i}$ and cross-modal participation (CMP) factor ${\rm B}_{u,i}$. These helped to define bounds on the error between MSE and ISE analyses, see equation (27). To explore their effect, let’s consider the (CMP) factor of pier (C1) for the first mode ${\rm B}_{2,1}$ and the second mode ${\rm B}_{2,2}$ (note that the suffix numbering for ${\rm B}_{u,i}$ is for the u-th dof, and i-th mode), Fig. 7 depicts the CMP factor (${\rm B}_{2,1}$ and ${\rm B}_{2,2}$) for the bridge with various dynamic parameters α and η. It is entirely consistent with the locus plot in Fig. 6.

Fig. 7

CMP factor for the studied bridge with various dynamic parameters α and η at outer Pier C1 a First mode cross modal participation (CMP) B_2,1 b Second mode cross model participation (CMP) B_2,2

The area with positive values represents the cases where the mode shape is symmetrical. Contrarily, the region with negative values shows that the mode shape is anti-symmetrical. In these regions only MSE ground motion input can properly excite this mode. Therefore, it seems that bridge cases in the area with a first anti-symmetrical mode, would be excited considerably by MSE seismic input and they cannot be excited by ISE inputs.

While Fig. 7 uses the conventional mode numbering (ranked in ascending frequency) it is also instructive to number the modes by their characteristics, i.e. symmetrical and anti-symmetrical. Therefore, exploring the value of AMP and CMP factors for Pier (C1) in Figs. 8 and 9 respectively reveals an interesting result. The values of A_2,S1 and B_2,S1 are pronounced where the anti-symmetrical mode is fundamental. This suggests that the effect of the first symmetrical mode (mode 2) may also be significant although the first mode is anti-symmetrical. The values of A_2,A1 (in Fig. 8b) and B_2,A1 (in Fig. 9b) appears surprisingly constant and hence of little utility in distinguishing those regions of geometric parameter space susceptible to significant errors between ISE and MSE analyses. As AMP and CMP represent geometry only bound estimates we need to also explore what happens when we include ground excitation.

Fig. 8

AMP factor for the studied bridge with various dynamic parameters α and η at outer Pier C1 a First symmetrical mode’s Auto Modal Participation A_2,S1 b First anti-symmetrical mode’s Auto Modal Participation A_2,A1

Fig. 9

CMP factor for the studied bridge with various dynamic parameters α and η at outer Pier C1 a First symmetrical modes’s cross model participation (CMP) B_2,S1 b First anti-symmetrical mode’s cross model participation (CMP) B_2,A1

4.3 Dynamical analysis including both geometry and loading

In the previous Sects. 4.2 (modal analysis) and 4.3 (bounding analysis) we suggest a hypothesis that in the regions where the first mode is anti-symmetrical there may be greater errors between MSE and ISE. Numerical analysis that includes explicitly ground excitation is necessary to confirm these suggestions. Therefore, this section explores the validity of the above observations by comparing with numerical analysis of the heuristic bridge when subjected to real ground motion excitations from the SMART-1 Array. To quantify dynamic responses in the frequency domain, the ‘mean-squared’ dynamic response of the u-th dof of the structure is defined as (Zerva 1990):

$$\sigma_{u}^{2} = \int_{ - \infty }^{ + \infty } {S_{{{uu}}} \left( \omega \right){\kern 1pt} {\kern 1pt} {\text{d}} {\kern 1pt} \omega }$$

(31)

where $S_{uu} \left( \omega \right)$ is the power spectrum of the responses of the u-th dof and is defined from the total response solution in equation (20) (Fig.10).

Fig. 10

illustration of PSD of dynamic response and mean square $\sigma_{u}^{2}$ of Pier 3 for the reference bridge with dynamic parameters η = 2.4, α = 1

For the sake of comparison between the MSE and ISE analysis cases, the following performance measure is introduced in this study:

$$\chi_{u} \left( {\eta ,\alpha ,j} \right) = 100\left\{ {\frac{{\left( {\sigma_{u}^{2} } \right)_{\text{MSE}} - \left( {\sigma_{u}^{2} } \right)_{\text{ISE}} }}{{\left( {\sigma_{u}^{2} } \right)_{\text{ISE}} }}} \right\}$$

(32)

where the dynamic error, $\chi_{u} \left( {\eta ,\alpha ,j} \right)$ is the difference (percentage error) in dynamic response between MSE and ISE cases for specific values of parameters $\alpha$ and $\eta$. The number $1 \le j \le 12$ determines the bridge orientation. The MSE simulations make use of real spatiotemporal SMART-1 array ground excitation for event 43. In this case, abutments and pier supports have different ground excitation time-series, see Sect. 3. The ISE simulations employ the seismic ground input from the centre station C00 (aligned with appropriate rotation angle) to the base of all abutments and piers. Due to the symmetrical configuration of the bridge, The middle piers (C2) become the rest point (for anti-symmetrical modes) and can only be affected by a symmetric mode as it is concluded in the study (Price and Eberhard 1998). Therefore, we focus on the response of the first outer pier (C1) in this study. The maximum and minimum of the range of the dynamic error $\chi_{u}$ for all bridge orientation are defined as:

$$\mathop {\min }\limits_{\forall j} \left\{ {\chi_{u} } \right\} \le \chi_{u} \le \mathop {\max }\limits_{\forall j} \left\{ {\chi_{u} } \right\}$$

(33)

The negative values of these ranges identifies the cases where ISE is conservative. The positive of these ranges identifies the cases where ISE is non-conservative.

The contribution of i-th mode to the dynamic error can be calculated from the modal analysis error as follows:

$$\chi_{u,i} = 100\frac{{\int_{ - \infty }^{ + \infty } {\varepsilon_{u,i} \left( \omega \right)d{\kern 1pt} \omega } }}{{\left( {\sigma_{u}^{2} } \right)_{\text{ISE}} }}$$

(34)

Figure 11 shows the dynamic error range for various parameters $\alpha$ and $\eta$. This plot represents tens of thousands of different parametric/ground excitation configurations and their numerical solutions. Note that varying both parameters $\alpha$ and $\eta$ conceptually allows us to explore both deep valleys (high values of $\eta$) and shallow valleys (low values of $\eta$). In addition values of $\alpha$ greater than 1 start to introduce a central rise profile in the valley.

Fig. 11

Dynamic error $\chi_{u} (\eta ,\alpha ,j)$ (for top outer pier (C1) in Fig. 4) for studied bridges in a lower bound error b upper bound error

This is compared with the proposed analytical curves from the previous sections, Fig. 6 (modal analysis) and Figs. 8 and 9 (bounding analysis). The results suggest that for each bridge configuration with a specific set of geometric parameters $\alpha$ and $\eta$, it is conceivable to find an input motion combination that the ISE case is either conservative (down to −20%) or non-conservative (up to 40%). Figure 11 shows a close correlation between numerical results (geometry and forcing) and the analytical results (Fig. 6 based on geometry alone). Therefore, it appears possible to identify some regions where MSE and ISE analyses could produce very different results based on geometry alone.

Thus, results from this dynamic analysis (including geometry and loading) and geometry alone (modal and bounding analyses) appear to show a corroboration if a large enough sample of records is chosen.

This confirms that when the first mode is anti-symmetrical one should avoid just employing ISE analysis. However, the question remains: is this due to the contribution of this anti-symmetrical mode?

4.4 Forensic analysis of modal contributions

To explore the effects of certain modes, we expand the dynamic error due to the i-th mode given in equation (34). This dynamic error is plotted in Fig. 12. This case is for parameters ($\eta = 30,\alpha = 10$) chosen from the critical area where the first mode is anti-symmetrical. This bridge case has A1 (first mode) and S1 (second mode) modes within the significant frequency range of 3–5 Hz as shown in Fig. 12c (which is the transfer function estimate).

Fig. 12

The modal analysis error normalized by $\sigma_{\text{ISE}}^{2}$ for parameters η = 30, α = 10. a Alignment 1 (C00-I01), b Alignment 9 (C00-I09). c Frequency transfer function $\gamma_{1} = \gamma_{2} = 5\%$.

The area under the curve of the modal analysis error in the figures illustrates the total contribution of the i-th mode to the percentage error $\chi_{u,i}$ in Fig. 12. The maximal positive (MSE > ISE) and maximal negative dynamic error are presented in Fig. 12a and Fig. 12b respectively. The magnitude of the modal dynamic error for the anti-symmetrical modes is always positive as these modes would only be excited in the MSE cases.

An interesting result that emerges from Fig. 12 is that mode 1, the first anti-symmetrical mode (A1), is excited considerably in alignment 1 (C00-I01) while its response is marginal in alignment 9 (C00-I09). Thus, even though the transfer function for mode 1 has a higher peak value, this is not necessarily sufficient to result in larger responses for mode 1 (A1).

However, the response pattern is different for mode 2, the first symmetrical mode (S1). In alignment 1, S1 has a large positive error indicating the MSE analysis induces a substantially larger response than ISE. For the case of alignment 9 the large negative error indicates that MSE results are far smaller than the ISE analysis results.

These results highlight the importance of the power/phasing of ground motion inputs. To forensically analyse such effects, we take a closer look at the correlation of ground motion data of the stations at the inner ring with central station C00. Figure 13 represents the acceleration power spectra of the time-series in bridge alignments 1 and 9.

Fig. 13

Power Spectrum of acceleration time-series of station at a Alignment 1 b Alignment 9

Figure 13 suggests that for orientations with higher values of power-spectrum, for the central station (C00) at a bridge significant frequency range (of 3–5 Hz), the symmetrical mode would be excited substantially in the ISE analysis case. This situation can be seen in alignment 9 (Fig. 12) where the error of the symmetrical mode is negative. This is due to the seismic input at the central station C00 (chosen for the ISE case) having higher overall power to the MSE case inputs. Contrarily, for alignment 1, the lower value of the power-spectrum at the central station (at bridge frequency range of 3–5 Hz) indicates that the symmetrical mode can be more induced by MSE cases. In this case, the dynamic error for both A1 and S1 mode is significant and positive.

Consider now the case where the first mode is now symmetrical, shown in Fig. 14 where ($\eta = 30,\alpha = 1$). This bridge has a very similar transfer function, shown in Fig. 14c, where the bridge significant frequency range is again between 3-5 Hz. Thus, we have very similar frequency ranges filtered by the transfer functions in both cases Figs. 13 and 14. However, the errors between MSE and ISE are far lower because of the smaller values of $\alpha_{u,i} \left( \omega \right)$ and $\beta_{u,i} \left( \omega \right)$ in equation (21) that where predicted by the geometry only bounds ${\rm A}_{u,i} ,{\rm B}_{u,i}$.

Fig. 14

The modal analysis error normalized by $\sigma_{\text{ISE}}^{2}$ for parameters η = 30, α = 1. a Alignment C00-I01, b alignment C00-I09. c Frequency transfer function $\gamma_{1} = \gamma_{2} = 5\%$

5 Conclusion remarks

A large-scale parametric study was presented herein to explore the sensitivity of the responses to asynchronous excitation of a heuristic bridge where geometry parameters of the bridge differed conceptually due to valley profile.

Firstly, we explore the regions of the geometry only parameter space where the first mode of the system is anti-symmetrical (modal analysis). Second, we derive bounds on the modal error between MSE and ISE analyses cases (a bounding analysis) and demonstrate that the errors are likely larger for the cases where the first mode is anti-symmetrical. Both, modal and bounding analyses are geometry only analyses that neglect any ground motion characteristics. Therefore, finally, we compare and contrast these predictions with actual time-history analysis (in the frequency domain) that is predicated on both geometry and loading. Results from time-history analysis agree that the error between MSE and ISE analyses could be far larger for the cases where the first mode is anti-symmetrical. It is worth noting that while the maximal/minimal error range between MSE and ISE is larger for the case when the first mode is anti-symmetrical this does not guarantee that for a specific individual loading set that the error will be large. This feature was highlighted by noting that the variation in the bridge system’s responses caused by just changing its spatial radial orientation was significant.

Therefore, we concluded that a larger error range between MSE and ISE analyses is likely to occur when the first mode is anti-symmetrical. But is this due to a larger magnitude of the anti-symmetrical mode in the responses? For these bridge configurations, numerical time-history results indicate that the anti-symmetrical mode may occasionally play some significant role in the responses, with a specific ground motion content. However, the main component in the response seems due to the symmetrical mode even when it is not the first mode.

The geometry only modal analysis is able to highlight parameter regions where the first mode is anti-symmetrical, and the geometry only bounding analysis is able to estimate the likely relative magnitude of the errors between MSE and ISE analyses. Both analyses have some utility in highlighting the cases where it is expedient to perform both MSE and ISE analyses to ensure a conservative analysis estimate of the responses.

Finally, we highlight that the critical parametric cases of larger error ranges between MSE and ISE occurs when the valley profile is shallow with a central rise. This case results in a first mode that is anti-symmetrical but it is still the case that most of this error is due to the first symmetrical mode (mode 2 here).

Appendix: expansion of a sum of n complex numbers

Consider $z_{r}$, the sum of n complex numbers:

$$\begin{gathered} z_{r} = \sum\limits_{i = 1}^{n} {a_{ir} } e^{{\varvec{i}\theta_{iq} }} = \sum\limits_{i = 1}^{n} {a_{ir} } \cos \left( {\theta_{ir} } \right) + \varvec{i}a_{ir} \sin \left( {\theta_{ir} } \right) \\ = \sum\limits_{i = 1}^{n} {a_{ir} c_{ir} } + \varvec{i}\sum\limits_{i = 1}^{n} {a_{ir} s_{ir} } = A_{r} + \varvec{i}B_{r} \\ \end{gathered}$$

(A.1)

The modulus/amplitude of this sum is

$$\begin{gathered} \left| {z_{r} } \right|^{2} = \left( {\sum\limits_{i = 1}^{n} {a_{ir} c_{ir} } } \right)^{2} + \left( {\sum\limits_{i = 1}^{n} {a_{ir} s_{ir} } } \right)^{2} \\ = \left\{ \begin{gathered} a_{1r}^{2} c_{1r}^{2} + a_{2r}^{2} c_{2r}^{2} + \cdots \\ + a_{1r}^{2} s_{1r}^{2} + a_{2r}^{2} s_{2r}^{2} + \cdots \\ \end{gathered} \right\} + 2\left\{ \begin{gathered} a_{1r} c_{1r} a_{2r} c_{2r} + a_{1r} c_{1r} a_{3r} c_{3r} + \cdots \hfill \\ + a_{1r} s_{1r} a_{2r} s_{2r} + a_{1r} s_{1r} a_{3r} s_{3r} + \cdots \hfill \\ \end{gathered} \right\} \\ = \sum\limits_{i = 1}^{n} {a_{ir}^{2} } + 2\sum\limits_{j = 1}^{n - 1} {\sum\limits_{i = j + 1}^{n} {a_{ir} } } a_{jr} \cos \left( {\theta_{jr} - \theta_{ir} } \right). \\ \end{gathered}$$

(A.2)