Abstract
The current design approach recommended by seismic codes is often based on the use of uniform-hazard response spectra, reduced to account for inelastic structural behaviour. This approach has some strong limitations that have been highlighted in many studies, including not allowing a direct control of the seismic risk and losses. This study aims at quantifying the levels of safety and the costs associated with this design approach, and to investigate alternative design approaches that have been developed in the last decades. In particular, a risk-targeting approach and a minimum-cost approach are considered. The first one, allowed by US codes, aims at designing structures with the same risk of collapse throughout regions of different seismicity. The second one aims to minimize the sum of the initial construction cost and the cost of expected losses due to future earthquakes. The comparison of the three approaches is performed by considering, as an example structure, a four-storey reinforced concrete frame building located in different areas in Europe, and by looking at the implications in terms of achieved safety levels, initial costs, and future losses. The study’s results provide useful information on how the design criteria and the different hazard levels throughout Europe affect the cost and safety levels of seismic design.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Current seismic design regulations are often based on a uniform-hazard philosophy. This simplified design practice is essentially deterministic and employs a uniform-hazard spectrum, with predefined exceedance frequency depending on the performance objectives, to define the seismic action. Although this approach is simple, well established, and results in overall satisfactory performance (e.g. Jeong et al. 2012; Rivera and Petrini 2011; Panagiotakos and Fardis 2004; Mwafy 2001; Kappos 1997), it comes with the drawback of uncontrollable distribution of the risk levels in different locations (e.g. Collins et al. 1996; Tubaldi et al. 2012; Silva et al. 2016; Iervolino et al. 2017). This means that, although the structures are designed using the same regulation, they are exposed to different risk levels.
Acknowledging this, modern design philosophies have introduced the use of fully probabilistic approaches in the design stage to account explicitly for the risk level of the designed structure. A first official attempt to control the seismic risk across regions of different seismicity at a national level was made in the US, with regulations (ASCE 7-16 2017; FEMA P-750 2009) that proposed the use of risk-targeted ground motion maps. This risk-targeting methodology has been investigated and applied by many researchers (e.g. Douglas and Gkimprixis 2018; Silva et al. 2016; Tsang and Wenzel 2016; Douglas et al. 2013; Luco et al. 2007), while alternative techniques of risk targeting have also been proposed in the literature (Gkimprixis et al. 2019; Tsang et al. 2020).
Observations on the effects of past historical earthquakes have shown that, while life safety is usually ensured by compliance with design codes, the economic losses due to damage in structural and non-structural components can be large (e.g. Perrone et al. 2019; Braga et al. 2011). This is mainly because structures are designed to undergo significant inelastic behaviour under major earthquakes to dissipate seismic energy, and there is insufficient attention paid to the behaviour of non-structural components in the design stage. Moreover, the behaviour of building components such as masonry infills, interacting with the frame structural components, is usually disregarded in the design stage, and very often these elements experience damage even under moderate earthquakes, leading to significant losses (e.g. De Risi et al. 2019; De Luca et al. 2014; Ricci et al. 2011; Romão et al. 2013; Braga et al. 2011).
It is understandable that seismic design has to serve a double goal and provide not only safe, but also economic design solutions. The two objectives can be conflicting, because in order to reduce the risk of loss of life the construction costs generally need to increase. Thus, there should be a compromise between construction costs and target levels of safety. This has motivated intense research in the development of design techniques that consider the benefit from the future losses reduction when the seismic design level, and consequently the initial construction cost, is increased (Cardone et al. 2019; Ordaz et al. 2017; Crowley et al. 2012; Padgett et al. 2010; Kappos and Dimitrakopoulos 2008; Lagaros 2007; Ellingwood and Wen 2005; Wen and Kang 2001).
The aim of this study is to quantify the levels of safety and the costs associated with the code design approach, and to investigate the effectiveness of the risk-targeted and minimum-cost design approaches, by considering a benchmark case study. This case study consists of a four-storey reinforced concrete (RC) frame building located in different regions in Europe, which exhibit a wide range of hazard levels. After reviewing briefly the alternative design approaches, the RC structure is designed following the Eurocodes (ECs) for different values of the design peak ground acceleration (PGA). Using a nonlinear finite element model developed in Seismostruct (Seismosoft 2020), time-history analyses are carried out to evaluate the performance of the building and establish a link between the seismic fragility and the design PGA. The distribution of the collapse risk rates obtained across Europe considering the uniform hazard PGA as design input is then assessed. Risk targeting is subsequently applied, followed by an evaluation of the design PGA levels minimizing the total costs of the building across Europe. In the calculations, the initial construction costs, the future losses due to damage of both structural and non-structural components of the building and additional losses are considered. Finally, some comparisons are made among the results of the different approaches.
2 Review of design approaches
This section illustrates briefly the three design approaches considered in this study. Each approach provides a different value of the design seismic intensity at the site of interest, which is synthetically represented here by the design peak ground acceleration, PGAd.
2.1 Uniform-hazard design
Modern seismic design codes generally follow a force-based approach in which the earthquake input is defined in terms of an acceleration response spectrum to be used in conjunction with simplified elastic analyses. The ductile behaviour of the structure is taken into account through the application of a reduction factor to transform the elastic spectrum into an inelastic design spectrum. In EC8 (CEN 2004b), this spectrum is anchored to a PGA value obtained from the hazard curve of the structure’s site for a predefined probability of exceedance (e.g. 10% in 50 years for the ‘no-collapse’ objective associated with the ‘ultimate limit state’), while the spectral shape is assumed to depend only on the local soil conditions. The application of this design framework establishes uniform hazard levels between different locations, meaning that the ‘uniform-hazard’ design PGA values, \(PGA_{d}^{UH}\), share the same exceedance probability at every location. It is noteworthy that this approach leads to non-uniform levels of risk for different locations, as discussed in e.g. Gkimprixis et al. (2019).
2.2 Risk-targeted design
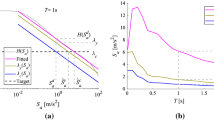
This method aims to design a structure that will be exposed to an acceptable and controlled risk level, expressed as the mean annual frequency (MAF) of collapse, \(\lambda_{C}\). This depends on the design acceleration,\(PGA_{d}\), through the following expression (Kennedy 2011):
where \(H(IM)\) is the hazard curve, obtained from PSHA (Cornell 1968; McGuire 2008; Baker 2015), providing the MAF of exceeding the seismic intensity measure (IM) used for risk assessment, and \(P\left( {\left. C \right|IM} \right)\) denotes the probability of collapse conditional on the IM level.
The solution of the risk-targeting problem requires an iterative approach (see Fig. 1) that eventually leads to the risk-targeted design peak ground acceleration, \(PGA_{d}^{RT}\), corresponding to the target risk level \(\lambda_{C}\).
2.3 Minimum-cost design
This approach aims to design a structure such that the total life-cycle cost is minimized. The costs of construction and seismic damage to structural and non-structural components are considered, while additional losses can be included. The methodology discussed herein is based mainly on the work of Wen and Kang (2001), while other articles have been considered as well (e.g. Kappos and Dimitrakopoulos 2008; Lagaros 2007; Ordaz et al. 2017; Crowley et al. 2012; Padgett et al. 2010). The variable to be minimized is the expected value of the life-cycle cost, E[LCC], over the time period t, which can be expressed as:
where \(C_{0}\) is the initial construction cost and \(E[FL]\) is the expected cost due to future losses. The latter stems from the sum of the losses incurred for repairing (or replacing) the damaged structure and additional losses (e.g. from personal property damage, injuries or fatalities, and loss of function of the building).
The expected cost due to the future losses over a time period t is calculated as:
where λ is a constant discount rate/year, which converts the future losses into present monetary value. The expected value of the annual losses, \(E[AL]\), is equal to:
where \(E[AL|IM]\) is the expected value of the losses given an IM level, usually referred to as vulnerability. The total vulnerability of the building derives from the sum of the vulnerability of each component at every storey, which is based on the fragility curves of the component for the various damage states and the costs associated with each damage state. If the collapse criterion is met at any storey, then it is assumed that the whole building has collapsed (‘global collapse’ case), and consequently it has to be replaced.
Following Ramirez et al. (2012), the collapse (C) and no-collapse (NC) cases are considered explicitly in the derivation of the vulnerability according to the following expression:
where the probability of collapse given the IM, \(P(C|IM)\), is the fragility curve for the case of ‘global collapse’, and \(C_{r}\) is the associated cost.
The value of E[LCC] depends on the PGAd, which influences both the initial costs and the losses. An optimization technique can be employed to minimize E[LCC], as shown schematically in the flowchart of Fig. 2. Starting with a trial PGAd, the corresponding fragility curves of each component (structural and non-structural) of every storey are calculated, together with their cost. Based on the fragility curves and the costs associated with the various damage states, the vulnerability curves of the building are derived using Eq. (5), by assembling the vulnerability of the various components and taking into account the building collapse events. Then, E[LCC] is calculated from Eq. (2). This procedure is repeated for a range of trial PGAd levels and the minimum-cost design acceleration, \(PGA_{d}^{MC}\), is obtained as the one that minimizes E[LCC].
3 Applications
A benchmark RC building is considered to evaluate and compare the design PGAs, risk levels, and losses corresponding to the application of the alternative design approaches illustrated in the previous section. The case study is representative of many structures built across Europe, and consists in a 4-storey 3-bay RC frame building, symmetrical in plan and elevation, with span length and column height respectively equal to 5 m and 3 m (Fig. 3).
3.1 Seismic design according to Eurocodes
The building is designed following EC2 (CEN 2004a) and EC8 (CEN 2004b). Both the columns and the beams have the same section in all storeys. The concrete strength class is C25/30, corresponding to a characteristic compressive strength of 25 MPa, a mean compressive strength of 33 MPa, a mean tensile strength of 2.6 MPa, and a modulus of elasticity of 3.1 × 104 MPa. A B450C steel is assumed for the reinforcement, corresponding to a characteristic yield strength of 450 MPa, a mean strength of 517.5 MPa, and a modulus of elasticity of 2.0 × 105 MPa.
The self-weights of the concrete elements are derived assuming a specific weight of 25 KN/m3. Regarding the permanent loads, 1 KN/m2 is assumed for the floor finishing weight and 7 KN/m3 for the weight of the masonry infills of the external frames. The influence of the structural elements dimensions and the presence of openings was considered in the calculation of the weight of the panel. An additional uniformly distributed load of 0.4 KN/m2 is added to the floor loads to account for internal partitions, as per NTC-3.1.3 (NTC 2018). The live load (Q) is taken equal to 2 KN/m2. The following load combinations are considered, according to EC8 (CEN 2004b) and EC0 (CEN 2002): 1.35·G + 1.50·Q (gravity loads only), G + 0.30·Q ± Ex ± 0.30·Ey, G + 0.30·Q ± 0.30·Ex ± Ey, where G, Q and E are the permanent, live and earthquake loads respectively and x and y refer to the two horizontal directions.
Rather than considering the design spectra defined by national codes, the Type 1 horizontal design acceleration spectrum (EC8-1-3.2.2.2) is used for every location across Europe. The seismic design is carried out considering different design acceleration values, namely 0.0 g, 0.1 g, 0.3 g and 0.5 g, an importance class II, and a medium ductility class (EC8-1), corresponding to a behaviour factor q = 3.9 (EC8-1-5.2.2.2). Class B is assumed for the soil conditions and 5% for the damping ratio. It should be noted that the EC8 Type 1 spectrum employed for the design is not strictly a uniform-hazard spectrum as its shape is constant for different locations (Tsang 2015).
Two performance objectives are considered: ‘no-collapse’ under the seismic design action, and ‘damage limitation’ for a more frequent seismic event. Starting with ‘the no-collapse’ requirements, first an elastic analysis is performed, using the elastic response spectrum, modified by q. The contribution of the infills to the stiffness and strength of the frames is disregarded in the design stage, an approach usually followed in design practice. A modal response spectrum analysis is performed [EC8-1-4.3.3.1(2)P] to find the required reinforcement area for beams and columns. In the numerical model, a 50% reduction of the materials’ modulus of elasticity is considered to account for the effect of cracking [EC8-1-4.3.1(7)]. Rigid diaphragms are considered at floor levels and the contribution of the slab (15 mm thick) to the lateral stiffness is taken into account by assuming T-shaped beams (EC2-1.1-5.3.2.1). The accidental eccentricity (EC8-1-4.3.2) is considered equal to ± 0.05·Li, where i is the floor-dimension perpendicular to the direction of the seismic action.
Capacity design rules are applied to design the required reinforcement area for beams and columns. This is to ensure that in every joint the sum of the moments of resistance of the columns are at least 1.3 times higher than that of the beams of the joint (EC8-1-5.2.3.3). Following EC8-1-4.4.2.2(2), an additional check is made to ensure that second-order (P-δ) effects are not excessively high.
The ‘damage limitation’ criterion is satisfied by checking that the inter-storey drifts (ISDs) are less than 0.5% of the storey height (non-structural elements of brittle materials attached to the structure), in accordance with the criterion of paragraph EC8-1-4.4.3.2. To account for the reduced return period of the seismic action associated with this criterion, the design action is multiplied by a reduction factor of 0.5.
If the structure fails any of the above criteria, the sections are increased, otherwise the design procedure is complete. The results of this design procedure, in terms of RC member dimensions and total reinforcement, are summarized in Table 1, and are comparable to those of similar research works (e.g. Fardis et al. 2012; Ulrich et al. 2014).
It is clarified that wind and snow loads are not considered in the design because they may vary significantly from location to location and, therefore, they could complicate interpretation of the effect of the seismic hazard on the structural design. Thus, the case of PGAd = 0.0 g refers to a design executed only under the gravity load combination. Further analyses have been carried out for the case-study building to confirm that the results are not significantly altered if the wind action is taken into account (for velocities up to 25 m/s).
3.2 Numerical models for nonlinear analyses
The finite element software Seismostruct (Seismosoft 2020) is used to perform the nonlinear analyses. The inelastic plastic hinge force-based frame element type is used to describe the inelastic behaviour of beam and column elements. The plastic hinge properties are derived based on the cross-sections at the extremes of the elements, employing 150 fibres to discretize the section (Calabrese et al. 2010; Scott and Fenves 2006). The length of the plastic hinge (Lp) is calculated according to Paulay and Priestley (1992), based on the element’s length as well as the yield strength and the diameter of the longitudinal reinforcing steel. Beam–column joints are assumed to be rigid and their degradation is not explicitly taken into account, assuming that in newly-designed buildings these elements are not expected to be as critical as in existing buildings.
For the constitutive law of the RC members, the Mander et al. (1988) nonlinear concrete model and the Menegotto and Pinto (1973) steel model are used. While in the design approach the characteristic values were used, for the nonlinear analyses the mean values of Table 1 are used instead, as stated in EC8-1-4.3.3.4.1(4). A Rayleigh damping matrix with the tangent stiffness approach is employed to model the damping inherent to the structure and its contribution to the seismic energy dissipation (Chopra 1995). A 5% damping ratio is considered for the first two transitional modal periods (estimated via eigenvalue analysis). Finally, the seismic excitation is applied only along the horizontal direction, while the permanent and live loads are considered with the combination G + 0.30·Q.
The frames of the perimeter of the building are infilled with masonry panels made of 30 cm-thick hollow bricks. Following the RINTC project (RINTC Workgroup 2018), the following properties of the infill are considered: σ0 = 0 MPa (vertical stress), σm0 = 6 MPa (vertical compression strength), τm0 = 0.775 MPa (shear strength), fsr = 0.542 MPa (slide resistance in the joints), and Em = 4312 MPa (elastic modulus of the infills).
The diagonal strut approach (Decanini et al. 2004) is followed to simulate the infills, using the above parameters to define the various failure mechanisms and the resulting constitutive law of the struts representing the infill panels. In order to account for the openings in the panels (doors or windows), the strut strength values are reduced by the factor proposed in Decanini et al. (2014). Generally, an opening of area 2.4 m2 is assumed, (e.g. height 1.2 m and width 2 m for windows) corresponding to a 60% strength reduction. More specifically, the reduction factor is equal to 0.44, 0.42, 0.40, and 0.38, for PGAd equal to 0.0 g, 0.1 g, 0.3 g and 0.5 g, respectively. A further modification of the Decanini et al. (2004) model is introduced, to achieve a better agreement between predicted and observed ISD corresponding to infill damage, by using the drift values provided in the RINTC project. Recent researchers (Sassun et al. 2016; Hak et al. 2012) have investigated the relation between the drift capacity of an infill panel and the strain capacity of the equivalent strut. Using the analytical formulae of these works, the drift thresholds are used together with the geometry of the panel to obtain the strain values for the constitutive law of the strut. The constitutive laws of the struts and of the other materials are shown in Fig. 4, together with the numerical model of the case-study buildings.
It is noteworthy that increasing the PGAd levels leads to a decrease of the contribution/impact of the infills. This is mainly because the columns section increases with PGAd and thus the ratio of the infilled area to the area of the columns reduces. This ratio is one of the main parameters that controls the infill-frame interaction. In Seismostruct (Seismosoft 2020), the infills are modelled with inelastic truss elements, using a trilinear concrete model with no residual strength.
3.3 Modal and pushover analyses
Modal analyses have been carried out on the numerical models corresponding to the various PGAd levels considered. In the case of bare frames, the contribution of the infills to the lateral strength is disregarded, while the mass is the same as in the infilled case. The fundamental vibration periods for the bare models are 0.73 s, 0.47 s, 0.29 s and 0.22 s, for PGAd equal to 0.0 g, 0.1 g, 0.3 g and 0.5 g, respectively. These periods are reduced to 0.36 s, 0.32 s, 0.25 s and 0.20 s in the case of the infilled models. In general, the fundamental period of vibration reduces for increasing design acceleration levels, due to higher stiffness of the resisting components. Moreover, accounting for the stiffness of the infills results in a reduction of the fundamental period of vibration, as expected. This reduction is more significant for the frames designed for lower PGA levels, due to the higher infill-frame stiffness ratio, as discussed in the previous section.
Static pushover analyses are also performed and the resulting capacity curves, in terms of total base shear versus maximum (across the various storeys) ISD, are presented in Fig. 5. It can be observed that the strength and stiffness of the infilled models are significantly higher than those of the corresponding bare models for low ISD levels. For high ISD levels, the infills are damaged and their contribution to the resistance reduces. The capacity curves of the models with and without infills coincide at high ISD levels, where all the infill frames are extensively damaged. The contribution of the infills to the global strength and stiffness of the buildings is rather low, in line with other studies on masonry infilled frames (see e.g. RINTC Workgroup 2018). This is mainly due to the use of hollow bricks for the infills, and the effect of the openings, which significantly reduce the infill capacity. It is noteworthy that the ISD levels at which the capacity curves of the infilled models attain their peak values tend to increase with the PGAd levels. Moreover, the differences in terms of stiffness and strength between the infilled and bare frame models are more significant for low PGAd levels, which is consistent with the observation of the previous subsection that the stiffness and strength of the strut elements modelling the infills reduces for increasing PGAd. The ultimate ISD values of the capacity curves (3%) correspond to the failure of the RC members, as discussed below. Overall, the ductility capacity of the designed models is high, demonstrating the effectiveness of the employed capacity design criteria. Nonlinear geometric effects have been considered, but they are not significant for these buildings and the post-peak behaviour of the pushover curve is strongly affected by the constitutive law of the confined concrete.
3.4 Incremental dynamic analyses
Incremental dynamic analyses (IDAs) (Vamvatsikos and Cornell 2002) are performed to derive fragility curves for the various models considered. To capture the uncertainties inherent to record-to-record variability effects, 22 records selected from RESORCE (Akkar et al. 2014) are considered. Since using a different set of records for each location of Europe would be too time-consuming, the considered records are not representative of any specific site, but have been selected based on generic criteria: epicentral distance between 0 and 30 km, moment magnitude between 5 and 7, and focal depth less than or equal to 30 km. It is noteworthy that the choice of the records selected to represent record-to-record variability effects may have an influence on the performance assessment, and other record sets, intensity measures, and nonlinear demand estimation methods may lead to different results. There is no perfect method for selecting the input ground motions for a Europe-wide study.
Figure 6 shows the linear elastic pseudo-spectral acceleration and displacement response spectra (Chopra 1995) of the records scaled to a common PGA value of 0.1 g, for a damping ratio of 5%. In the same figure, the mean spectrum and the first modal periods of the designed structures are also plotted. It can be seen that increasing the design acceleration and/or accounting for the presence of infills, results in lower displacement demand and higher accelerations levels, due to the shortening of the building period.
IDAs are performed by scaling the records to 29 different PGA levels, between 0.015 g and 4 g. Whenever numerical convergence issues arise, the structure is assumed to have failed. Figure 7 shows the IDA curves obtained for each record, in terms of PGA values versus maximum ISDs and maximum absolute accelerations observed across the storeys. The 50th, 16th and 84th percentile IDA curves are also shown in the same figures. It can be observed that increasing the design acceleration results in decreased ISDs, and in higher absolute accelerations, since the structure becomes stiffer.
3.5 Fragility analyses
The results of the IDAs are used in this section to derive fragility curves for every component of each storey. The fragility curves are assumed to have a lognormal distribution and maximum-likelihood estimation (Shinozuka et al. 2000) is used for the fitting of the IDA results. This approach, treating the IDA results as binary variables (corresponding to exceedance or not exceedance of the considered damage threshold), is particularly convenient for dealing with numerical convergence issues (e.g. Gehl et al. 2015).
All the components of the structure, have to be categorized in fragility groups (ATC 2012a, b; Cardone et al. 2019; O’Reilly and Sullivan 2018; Cardone and Perrone 2017; O’Reilly et al. 2018). The RC members (columns, beams and slabs) are regarded as structural components, while the rest are defined as non-structural components. For the structural components, six damage states are considered, which are controlled by the ISD. For simplicity, the same ISD thresholds are considered for the different structures rather than use other criteria. These thresholds are based on the limits provided by Ghobarah (2004) for moment-resisting frames (Ductile MRF) and these limits have been employed in many other research works on RC building fragility assessment (Gkimprixis et al. 2018; Manoukas and Athanatopoulou 2018; Martins et al. 2018; Ulrich et al. 2014; Lagaros 2007).
Based on the RINTC project, four damage states are defined for the damage of the infills explicitly, using ISD thresholds. In particular, the drift value at the peak strength of the panel is assumed equal to 0.334%. The cracking point is calculated at 80% of the peak strength, corresponding to a drift of 0.267%. Finally, it is considered that the infills reach the ultimate condition at a 50% drop of strength (Cardone and Perrone 2015), leading to a value of 1.439% for the drift threshold. The number and distribution of the internal partitions is estimated based on their distributed load assumed at the design stage, and the three limit states of Cardone and Perrone (2015) for partitions with doors are used.
The fragility of the rest of the non-structural components is evaluated by subdividing them into drift-sensitive and acceleration-sensitive ones, following FEMA P-58 (ATC 2012a, b). Table 2 summarizes the components considered in the study together with the assumptions made for the damage state definition.
Based on the results of the IDA and the damage state definition of Table 2, fragility curves are generated by considering explicitly the structural (S), non-structural drift-sensitive (N/D) and non-structural acceleration-sensitive (N/A) components at each storey (76 different fragility curves for each model). While the fragility of each components of every storey is considered separately, the case of collapse is defined ‘globally’. This means that when the 3% ISD limit is exceeded in any storey, then the whole building is assumed to collapse, and consequently both structural and non-structural components have to be replaced.
Due to space limitations, only the results for the ‘global collapse’ condition for the four analysed models are presented in Fig. 8. It can be observed that by increasing the PGAd, the median value of the lognormal fragility increases roughly linearly.
3.6 Risk analyses
In this subsection, the collapse risk levels corresponding to the uniform hazard design approach are evaluated across Europe. Then, the risk-targeting design approach is implemented to evaluate the design accelerations that will lead to a tolerable risk level. Finally, a comparison is made between the risk-targeted PGA levels and the uniform-hazard PGAs across Europe.
3.6.1 Risk levels associated with code-based design
The hazard curves for the different locations are based on the PGA values that correspond to 1%-, 2%-, 5%,- 10%-, 39%- and 50%-in-50-years exceedance probabilities according to the 2013 European Seismic Hazard Model (ESHM13, Giardini et al. 2013; Woessner et al. 2015). The second-order polynomial function in log-space proposed by Vamvatsikos (2013) is used to extrapolate the hazard data to a wider range of PGA. Figure 9 presents the PGA values for site class A that correspond to a 10%-in-50-years exceedance probability (MAF of exceedance 2.1 × 10−3). As the seismic designs were undertaken using the EC8 spectrum for site class B, the PGAs for site class A from the ESHM13 hazard curves were multiplied by the soil factor 1.2, expressing the ratio between PGAs on site classes B and A in EC8.
Using the values of Fig. 9 as the design acceleration, \(PGA_{d}^{UH}\), a risk analysis is then performed to assess the levels of collapse risk obtained if the RC building is designed with the uniform-hazard (UH) approach. In future studies the design for each country could be done individually using the national design code. The parameters of the global-collapse fragility curves for a given \(PGA_{d}^{UH}\) value are obtained by interpolating the fragility parameter results of Fig. 8. The annual collapse risk is obtained by convolution of the fragility and the hazard curves at each location, using Eq. (1).
Figure 10 illustrates the obtained values of the collapse risk across Europe. In general, the probability of collapse is significantly lower than the probability of exceedance of the design hazard level (2.1 × 10−3), due to the various safety margins (e.g. safety factors, capacity design, minimum member size and detailing requirements) considered in the design. In areas of high seismicity, such as Italy and Greece, the values of the risk are generally between 10−5 and 10−4. This figure confirms the findings of other studies (e.g. Martins et al. 2018; Silva et al. 2016; Luco et al. 2007) that applying the UH approach leads to inconsistent risk levels.
3.6.2 Comparisons with risk-targeting results
One of the key aspects of any risk-targeting framework is the choice of an acceptable collapse risk. Different values for this have been suggested in the regulations (Fajfar 2018) while other criteria (e.g. societal risk) have been proposed too (Tsang et al. 2020). First, following the recommendations of ASCE 7-16 (2017), the risk targeting design approach of paragraph 2.2 is applied considering a target annual collapse risk of 2 × 10−4. Figure 11a presents the values of \(PGA_{d}^{RT}\) that lead to a uniform distribution of risk across Europe. These values are lower, except in the areas of highest hazard where they are the same or slightly higher, than those corresponding to the uniform-hazard approach, since the targeted risk value is higher than the actual risk levels obtained by designing with \(PGA_{d}^{UH}\) for almost all locations (Fig. 10). It is noteworthy that the obtained results may change significantly by considering different risk targets and structural systems. For instance, adopting the lower risk target of 5 × 10−5 (following Silva et al. 2016) the \(PGA_{d}^{RT}\) values are significantly increased (Fig. 11b).
3.7 Initial construction costs
This subsection investigates the effect of the seismic design on the total construction costs. First, the cost of the structural members, i.e. columns, beams and slabs, is estimated based on the dimensions resulting from the application of the code design procedure (Table 1). Following Manoukas and Athanatopoulou (2018), the costs per unit weight of concrete and steel are assumed equal to 150 €/m3 and 875 €/t, respectively. These costs include materials, labour cost and social security expenses. The costs of non-structural components are based on data collected using personal contacts with engineers, construction price indices, as well as expert judgement, while they can be taken as a percentage of the replacement cost (Martins et al. 2016; Manoukas and Athanatopoulou 2018). Following FEMA P-58 (ATC 2012a, b), the cost of the foundations is not included in the analysis.
Table 3 reports the cost per m2 (of the total area) of the building components for each PGAd level considered. In addition, these costs are expressed as a percentage of the total construction cost (of each PGAd level) in the same table. Similar to other research works (Taghavi and Miranda 2003; Porter 2016) the structural elements are found to contribute to only 17–23% of the total cost, depending on the design level. The total construction cost of the structural and the non-structural components is found to be equal to 655,840 €, 656,778 €, 675,161 € and 693,205 € for PGAd equal to 0.0 g, 0.1 g, 0.3 g and 0.5 g, respectively. With the total area of the building being equal to 900 m2, this gives a range of the total cost between 729 €/m2 and 770 €/m2, which is similar to the values considered in other studies (Manoukas and Athanatopoulou 2018; Kappos and Dimitrakopoulos 2008; Lagaros 2007). An idea of the cost of seismic design is obtained by normalizing the costs for different PGAd levels by the cost for PGAd = 0.0 g. This gives a relative difference of 0.1%, 2.9% and 5.7% for the models designed for 0.1 g, 0.3 g and 0.5 g, respectively, when compared to the total cost of the non-seismically-designed one (i.e. PGAd = 0.0 g).
The obtained values show that the cost of seismic design is not significant, compared to the total construction cost. Similar conclusions were made in the past by other researchers. Almost 5 decades ago, Whitman et al. (1975) investigated the change of initial cost for different seismic design levels. For low-rise RC buildings, it was found that the cost of seismic design was less than 5%. In NEHRP (2013), a construction cost increase of up to 3% with respect to the design for wind loads only was reported for six buildings in Memphis, Tennessee. In Porter (2016) a 50% upgrade from the life-safety minimum of the US codes increased the construction cost by only 1%.
Figure 12 presents a disaggregation of the total costs into the various components, classified as structural (S), non-structural drift-sensitive (N/D), and non-structural acceleration-sensitive (N/A). It is evident that the majority of the cost is attributed to the non-structural drift-sensitive components (for the case study and the considered assumptions), while the cost of the acceleration-sensitive components is comparable to the cost of the structural elements.
Figure 13 presents the initial construction cost across Europe, when the building of the case study is designed using the \(PGA_{d}^{UH}\) values for the 475-years return period. The values are normalized to the initial cost at the site with the highest hazard (i.e. 707,609 €), and the difference at the site with lowest hazard is below 7%. This normalization is made because possible differences in construction costs across Europe are disregarded in this article.
3.8 Future losses
According to Eq. (4), the losses due to future earthquakes are a function of the vulnerability of the structural and non-structural components (probability of exceeding a given amount of loss conditional on the PGA level) and the hazard of the location. Thus, the fragility curves of each component are transformed into vulnerability curves with Eq. (5), using the cost data of the previous sections and the damage percentages of Table 2, while, alternatively, specific repair interventions can be costed (Martins et al. 2016). The replacement cost is considered herein equal to the initial construction cost. The resulting vulnerability curves (normalized to the construction cost of each model) are presented in Fig. 14a–d, together with the contribution of the S, N/D, and N/A components. Generally, the N/D components contribute most to the total vulnerability, while S and N/A have almost the same impact.
In Fig. 14e–h, the vulnerability is disaggregated into the two contributions of the non-collapse (NC) and collapse (C) cases, according to Eq. (5). For low seismic intensities, the losses are dominated by the NC scenario, while at high intensities the losses are mainly dominated by the collapse scenario. As expected, by increasing the design acceleration the contribution of the C cases to the total vulnerability decreases. For instance, for PGA = 2 g, the percentage of the total losses that is attributed to the collapse cases is equal to 88%, 75%, 59% and 48% when the structure is designed with a PGAd equal to 0.0 g, 0.1 g, 0.3 g and 0.5 g, respectively. Also, it is interesting to observe that the PGA level at which the C and NC cases contribute equally to the total losses increases for increasing PGAd (i.e. PGA equal to 0.6 g, 1.1 g, 1.5 g and 2.1 g for PGAd equal to 0.0 g, 0.1 g, 0.3 g and 0.5 g, respectively).
The expected annual losses (EAL) for the structure built considering different PGAd at a particular location can be obtained via convolution of the hazard curve for the site and the vulnerability curves. Figure 15a shows the EAL obtained for Patras (21.75° E, 38.24° N), a Greek city of high seismicity. The EAL are normalized by dividing them by the EAL for PGAd = 0.0 g, i.e., 4850 €. A disaggregation of the losses at different levels of ground motion intensities, indicated that 90% of the total EAL losses derive from PGA levels lower than 0.4 g, 0.4 g, 0.5 g and 0.7 g for the models designed with PGAd equal to 0.0 g, 0.1 g, 0.3 g and 0.5 g, respectively. It can be observed that while the losses due to the drift sensitive components damage are decreased when increasing the PGAd level, that is not the case for the acceleration sensitive components (see also Fig. 14a–d). This is reasonable, since the structure becomes stiffer and thus undergoes higher absolute accelerations (and lower displacements), as already observed in the response spectra of Fig. 6. The loss disaggregation of Fig. 15b highlights the importance of considering the NC case in the loss assessment process, since the contribution of the collapse scenario which is less frequent is only a small percentage of the total losses.
Additional losses can also be considered when estimating future losses, usually from the following contributions (Lagaros 2007): loss of contents (unit contents cost · floor area · mean damage index); rental loss (rental rate · gross leasable area · loss of function), which refers to the loss of rental income to the owner until functionality is restored; income loss (rental rate · gross leasable area · down time), which refers to buildings that are used for commercial reasons; cost of minor injuries, cost of serious injuries, and cost of human fatalities (cost per person · floor area · occupancy rate · expected rate).
It is noted that usually the losses are categorized as direct and indirect, but the terms can have different meanings within various projects [see e.g. the difference between Kappos and Dimitrakopoulos (2008) and Kircher et al. (2006)]. Also, different stakeholders (e.g. engineers, homeowners, insurance companies) may focus on different types of losses (e.g. contents loss considered or studied separately). To avoid confusion, two extreme cases are studied herein: losses due to repair/replacement costs and additional losses.
The previous vulnerability analysis is repeated considering the repair/replacement costs and the additional losses in the minimum-cost design. Similarly to Lagaros (2007), 250 €/m2 is assumed for the loss of contents, while the rates for the calculation of the rental and income losses are 7 €/m2/month and 2000 €/m2/year, respectively. For the minor injury, serious injury and fatality cost rates, 5000 €/person, 50,000 €/person and 2.5 × 106 €/person, are used, together with the assumption of 2 persons per 100 m2. It is also assumed that the down time required in the extreme case of collapse is 18 months, based on Manoukas and Athanatopoulou (2018).
The contents are treated as acceleration sensitive components (FEMA P-58), and thus their damage states are defined based on acceleration thresholds. For simplicity, it is assumed that half of the losses are reached at a level of 0.55 g, and the rest for accelerations higher than 1.2 g. The rest of the additional losses are attributed to the structural damage, and thus they are calculated using the cost rates of Table 4, based on the damage state thresholds of the RC members.
The vulnerability curves of the case-study models considering both the repair/replacement costs and the additional losses are presented in Fig. 16, disaggregated into C and NC cases. The EAL are divided by the initial construction cost of each model.
The result of the loss analyses for the building located in Patras are shown in Fig. 17a, where the repair cost and additional losses are presented separately, for each PGAd (normalized to the total EAL for the 0.0 g case, i.e. 28,603 €). In this example, it can be observed that the fatalities, the income loss, and the repair cost contribute most to the overall EAL.
Figure 17b shows the contribution of the collapse and non-collapse scenarios to the total EAL. It can be observed that for a building designed with no seismic provisions the collapse scenario dominates the losses with a contribution of about 70%, whereas in the case of seismic design acceleration of 0.5 g, the losses from the collapse scenario are about a third of the EAL. This is attributed to the fact that the annual collapse risk levels for the two cases have an order of magnitude difference (10−3 and 10−4) and the fatalities and income losses that contribute most (see Fig. 17a) are linked with the collapse scenario, as mentioned above. A further disaggregation of the losses at different levels of ground motion intensities, indicates that 90% of the total expected annual losses derive from PGA levels lower than 0.8 g, 0.8 g, 0.9 g, and 1 g, for a PGAd equal to 0.0 g, 0.1 g, 0.3 g, 0.5 g, respectively.
Figure 18a shows the EAL for repair/replacement across Europe for the building designed following the uniform hazard approach, i.e., based on the \(PGA_{d}^{UH}\) level that corresponds to a probability of exceedance of 10%-in-50-years. The EAL obtained considering also the additional losses are shown in Fig. 18b. The areas with highest EAL are mainly in southern Europe (e.g. Greece, Turkey, Italy and Romania) and the maximum values for the EAL when considering only the repair cost is 2455 €, which is increased to 7609 €, when additional losses are included.
The future losses for a period of \(t\) years and a discount factor \(\lambda\) can be easily estimated by multiplying the EAL of Fig. 18 with the factor \((1 - e^{ - \lambda \cdot t} )/\lambda\), according to Eq. (3), and the expected life-cycle cost, E[LCC], can then be obtained by adding the initial construction costs, following Eq. (2). Figure 19 shows the results obtained considering a design period of 50 years and a 3% discount rate. The maximum value of the E[LCC] calculated only with the repair/replacement costs is found to be 766,246 €. This increases to 898,912 € when additional losses are considered.
3.9 Minimum-cost analyses
This subsection shows the application of the minimum-cost design approach of Fig. 2 for the example building placed in different locations across Europe. Figure 20a shows the initial costs, the future losses and their sum, E[LCC], for Patras for different values of PGAd. The expected losses refer to a period of 50 years, while a discount factor 3% is applied. The minimum-cost design acceleration, \(PGA_{d}^{MC}\), is the one that minimizes the total cost, which is lower than the one that minimizes the total losses.
Figure 20a shows the effect of accounting for additional losses (see previous section) in the minimum-cost design, which results in an increase of the design PGA. In fact, when only the repair cost is considered, \(PGA_{d}^{MC}\) equals 0.42 g, whereas a value of 0.67 g is obtained if additional losses are considered. It is noteworthy that in the vicinity of \(PGA_{d}^{MC}\), the losses have a small variation with PGAd, which leads to small difference of the total costs obtained designing with UH and the minimum-cost approaches. The reduced variation of the total costs with the PGAd is due to fact that they depend on the initial costs, which also exhibit a reduced variation. Also, while the losses attributed to the drift sensitive components are reduced when increasing the design level, this is not the case for the acceleration sensitive ones (see e.g. Fig. 15).
Figure 20b provides an alternative illustration of the application of the method, where the cost of ‘seismic design’ is considered instead of the initial construction cost. The cost of seismic design is defined as the additional money one must invest to make the structure resistant to a given PGAd level, compared to the case with no seismic provisions (0.0 g). Of course, the representation of Fig. 20b provides the same value of \(PGA_{d}^{MC}\) as the representation of Fig. 20a, since the location of the minimum value of the total costs is not affected by a constant translation along the vertical axis.
The minimum-cost design is carried out for every location across Europe, and the obtained \(PGA_{d}^{MC}\) values are shown in Fig. 21a. Comparing the results with the \(PGA_{d}^{UH}\) of Fig. 9, a general reduction of the design acceleration values is observed when considering only the repair costs, while on the contrary the values are increased if the additional losses are included.
It is highlighted that designing with \(PGA_{d}^{MC}\) does not guarantee that the MAF of collapse of the structure is below the predefined acceptable risk level. In this regard, it could be useful to combine the results of the minimum-cost and the risk-targeting approaches to find the acceleration that minimizes the total building costs, while also satisfying the constraint on the acceptable risk level. This ‘minimum-cost risk-targeted’ design acceleration corresponds for a given location to the maximum of the risk-targeted (Fig. 11) and the minimum-cost value (Fig. 21).
When only the repair costs are considered, the E[LCC] with the minimum-cost approach is almost the same as that obtained with the UH approach (Fig. 19). This is mainly the result of the reduced variation of the total cost in the surrounding of \(PGA_{d}^{MC}\), as discussed above in the example for Patras (Fig. 20a). Even when the additional losses are also included together with the repair costs, the differences are still lower than 6%. This can be observed in Fig. 22, which illustrates the ratio of the E[LCC] obtained when designing with the minimum-cost approach over that obtained with the uniform-hazard approach (Fig. 19).
Studies on retrofit measures for existing structures consider the benefit-to-cost ratio (Calvi 2013; Padgett et al. 2010; Kappos and Dimitrakopoulos 2008) to compare the benefit from the loss reduction due to retrofitting to the cost of the intervention. The same concept can be used to evaluate the economic significance of minimum-cost design. The benefit to cost ratio in this case can be defined as the change of future losses when increasing the design acceleration from 0 to the \(PGA_{d}^{MC}\), divided by the seismic design cost (increase in the initial construction cost due to this change). It is understandable that the higher the value of the ratio, the more beneficial is the implementation of minimum-cost design. In the example for the repair costs in Patras (Fig. 20b) this ratio is roughly equal to 3, and is 4 times higher when additional losses are considered, too.
Figure 23 shows the values of benefit-to-cost ratios across Europe, considering a period of 50 years and a 3% discount rate. These ratios can provide decision makers with information on the benefit of seismic design, compared to the design carried out disregarding the seismic loads. It is noteworthy that for very low values of \(PGA_{d}^{MC}\) (close to 0.1 g), the initial cost is not significantly increased compared to the no-seismic provision case. This explains why high values of the ratios are obtained for some regions (e.g. Belgium, Slovakia) with relatively low \(PGA_{d}^{MC}\) (see Fig. 21). For the rest of Europe, it can be concluded that these ratios have roughly a maximum value of 10 for the repair costs case, and 25 if the additional losses are included.
A similar comparison between the results of the MC and UH approaches, not shown due to space constraints, gives much lower values of these ratios. For the areas of interest (\(PGA_{d}^{MC}\) higher than 0.2 g), the ratios are close to unity when only the repair/replacement costs are considered and less than 2.5 when the additional losses are included as well.
4 Conclusions
The aim of this article is to review and compare three different approaches for seismic design, namely the uniform-hazard (UH), the risk-targeted (RT), and the minimum-cost (MC) approaches. For this purpose, an example 4-storey 3-bay reinforced concrete frame building placed in different locations across Europe is considered. First, the methodologies for implementing the three approaches are briefly reviewed. Then, a comparison of the effectiveness of the approaches is carried out based on safety and costs considerations. The evaluation presented in this article is case-specific and therefore future studies on different building types are necessary to generalize the following conclusions:
-
Using the UH design acceleration results in inconsistent levels of the risk across Europe, as already observed in past studies. The attained risk levels for the case-study building are generally within the acceptable risk limits proposed by the US regulations (except for some high hazard areas).
-
The impact of the design seismic intensity (PGAd) on the initial construction cost is small, due to the high contribution of the non-structural components, the cost of which is not dependent on the PGAd.
-
A small variation of the losses with the PGAd levels has been noticed when only the damage of the structure is assessed. This variation is increased when additional losses are also included in the analysis.
-
The life-cycle cost when designing with the UH approach is not far from that obtained using the MC method.
-
A benefit-to-cost analysis has shown that there are many areas in Europe where seismic design is highly cost-beneficial in terms of life-cycle cost, compared to no seismic provisions.
The fact that the initial construction costs do not increase significantly by increasing the design PGA may suggest that higher performance levels could be targeted by seismic codes, since this would allow an increased safety to be achieved without increasing greatly the costs of the design. However, the economic benefits stemming from considering the optimal design PGA that minimizes the total life cycles costs instead of the PGA levels currently considered by seismic codes are not significant. Thus, a revision of design approaches in seismic codes is not warranted on the basis of the results of this study, given the fact that considering life-cycle cost analysis concepts in the design would make the design process more complicated to practicing engineers. It is recalled, however, that this conclusion is based on only a single example building type and hence it may not hold for other buildings.
References
Akkar S, Sandikkaya MA, Senyurt M, Azari Sisi A, Ay BÖ, Traversa P, Douglas J, Cotton F, Luzi L, Hernandez B, Godey S (2014) Reference database for seismic ground-motion in Europe (RESORCE). Bull Earthq Eng 12(1):311–339. https://doi.org/10.1007/s10518-013-9506-8
ASCE (2017) Minimum design loads and associated criteria for buildings and other structures, ASCE/SEI 7-16. American Society of Civil Engineers, Reston
ATC—Applied Technology Council, FEMA P-58 (2012a) Seismic performance assessment for buildings, volume 1—methodology. Federal Emergency Management Agency, Washington, D.C
ATC—Applied Technology Council, FEMA P-58 (2012b) Seismic performance assessment for buildings, volume 2—implementation guide. Federal Emergency Management Agency, Washington, D.C
Baker JW (2015) Introduction to probabilistic seismic hazard analysis. White Paper Version 2:1
Braga F, Manfredi V, Masi A, Salvatori A, Vona M (2011) Performance of non-structural elements in RC buildings during the L’Aquila, 2009 earthquake. Bull Earthq Eng 9(1):307–324
Calabrese A, Almeida JP, Pinho R (2010) Numerical issues in distributed inelasticity modeling of RC frame elements for seismic analysis. J Earthq Eng 14(S1):38–68. https://doi.org/10.1080/13632461003651869
Calvi GM (2013) Choices and criteria for seismic strengthening. J Earthq Eng 17:769–802
Cardone D, Perrone G (2015) Developing fragility curves and loss functions for masonry infill walls. Earthq Struct 9(1):257–279
Cardone D, Perrone G (2017) Damage and loss assessment of pre-70 RC frame buildings with FEMA P-58. J Earthq Eng 21(1):23–61
Cardone D, Gesualdi G, Perrone G (2019) Cost–benefit analysis of alternative retrofit strategies for RC frame buildings. J Earthq Eng 23(2):208–241
CEN (2002) EN 1990:2002+A1 Eurocode—basis of structural design. European Committee for Standardization, Brussels
CEN (2004a) EN 1992-1-1:2004 Eurocode 2: design of concrete structures—part 1-1: general rules and rules for buildings. European Committee for Standardization, Brussels
CEN (2004b) EN 1998-1:2004 Eurocode 8: design of structures for earthquake resistance—part 1: general rules, seismic actions and rules for buildings. European Committee for Standardization, Brussels
Chopra AK (1995) Dynamics of structures: theory and applications to earthquake engineering. Prentice-Hall, Upper Saddle River
Collins KR, Wen YK, Foutch DA (1996) Dual-level seismic design: a reliability-based methodology. Earthq Eng Struct Dy 25(12):1433–1467
Cornell CA (1968) Engineering seismic risk analysis. Bull Seismol Soc Am 58(5):1583–1606
Crowley H, Silva V, Bal IE, Pinho R (2012) Calibration of seismic design codes using loss estimation. In: Proceedings of 15th world conference on earthquake engineering, Lisbon, Portugal
De Luca F, Verderame GM, Gómez-Martínez F, Pérez-García A (2014) The structural role played by masonry infills on RC building performances after the 2011 Lorca, Spain, earthquake. Bull Earthq Eng 12:1999–2026. https://doi.org/10.1007/s10518-013-9500-1
De Risi MT, Del Gaudio C, Verderame GM (2019) Evaluation of repair costs for masonry infills in RC buildings from observed damage data: the case-study of the 2009 L’Aquila Earthquake. Buildings 9(5):122
Decanini L, Mollaioli F, Mura A, Saragoni R (2004) Seismic performance of masonry infilled R/C frames. In: 13th world conference on earthquake engineering (No. 165)
Decanini LD, Liberatore L, Mollaioli F (2014) Strength and stiffness reduction factors for infilled frames with openings. Earthq Eng Eng Vib 13(3):437–454
Douglas J, Gkimprixis A (2018) Risk targeting in seismic design codes: the state of the art, outstanding issues and possible paths forward. In: Vacareanu R, Ionescu C (eds) Seismic hazard and risk assessment—updated overview with emphasis on Romania. Springer, Berlin. https://doi.org/10.1007/978-3-319-74724-8_14
Douglas J, Ulrich T, Negulescu C (2013) Risk-targeted seismic design maps for mainland France. Nat Hazards 65(3):1999–2013
Ellingwood BR, Wen YK (2005) Risk-benefit-based design decisions for low-probability/high consequence earthquake events in Mid-America. Prog Struct Mat Eng 7(2):56–70
Fajfar P (2018) Analysis in seismic provisions for buildings: past, present and future. Bull Earthq Eng 16:2567–2608. https://doi.org/10.1007/s10518-017-0290-8
Fardis MN, Papailia A, Tsionis G (2012) Seismic fragility of RC framed and wall-frame buildings designed to the EN-Eurocodes. Bull Earthq Eng 10(6):1767–1793
FEMA (2009) NEHRP recommended seismic provisions for new buildings and other structures (FEMA P750). Federal Emergency Management Agency
Gehl P, Douglas J, Seyedi D (2015) Influence of the number of dynamic analyses on the accuracy of structural response estimates. Earthq Spectra 31(1):97–113. https://doi.org/10.1193/102912EQS320M
Ghobarah A (2004) On drift limits associated with different damage levels. In: Proceedings of international workshop on performance-based seismic design concepts and implementation, June 28th–July 1st, 2004, Bled, Slovenia
Giardini D et al (2013) Seismic hazard harmonization in Europe (SHARE). Online Data Resource. https://doi.org/10.12686/sed-00000001-share
Gkimprixis A, Douglas J, Tubaldi E, Zonta D (2018) Development of fragility curves for use in seismic risk targeting. In: 16th European conference on earthquake engineering
Gkimprixis A, Tubaldi E, Douglas J (2019) Comparison of methods to develop risk-targeted seismic design maps. Bull Earthquake Eng 17:3727–3752. https://doi.org/10.1007/s10518-019-00629-w
Hak S, Morandi P, Magenes G, Sullivan TJ (2012) Damage control for clay masonry infills in the design of RC frame structures. J Earthq Eng 16(sup1):1–35
Iervolino I, Spillatura A, Bazzurro P (2017) RINTC Project-assessing the (implicit) seismic risk of code-conforming structures in Italy. In: COMPDYN 2017-6th ECCOMAS thematic conference on computational methods in structural dynamics and earthquake engineering, Rhodes Island, Greece
Jeong SH, Mwafy AM, Elnashai AS (2012) Probabilistic seismic performance assessment of code-compliant multi-story RC buildings. Eng Struct 34:527–537
Kappos AJ (1997) A comparative assessment of R/C structures designed to the 1995 Eurocode 8 and the 1985 CEB seismic code. Struct Des Tall Build 6(1):59–83
Kappos AJ, Dimitrakopoulos EG (2008) Feasibility of pre-earthquake strengthening of buildings based on cost-benefit and life-cycle cost analysis, with the aid of fragility curves. Nat Hazards 45(1):33–54
Kennedy RP (2011) Performance-goal based (risk informed) approach for establishing the SSE site specific response spectrum for future nuclear power plants. Nucl Eng Des 241:648–656
Kircher CA, Whitman RV, Holmes WT (2006) HAZUS earthquake loss estimation methods. Nat Hazards Rev 7(2):45–59
Lagaros ND (2007) Life-cycle cost analysis of design practices for RC framed structures. Bull Earthq Eng 5(3):425–442
Luco N, Ellingwood BR, Hamburger RO, Hooper JD, Kimball JK, Kircher CA (2007) Risk-targeted versus current seismic design maps for the conterminous United States. In: SEAOC 2007 convention proceedings
Mander JB, Priestley MJN, Park R (1988) Theoretical stress–strain model for confined concrete. J Struct Eng 114(8):1804–1826
Manoukas GE, Athanatopoulou AM (2018) Safety vs. economy in performance-based design of buildings: inevitable compromise or false dilemma? J Earthq Eng 22(4):687–707
Martins L, Silva V, Marques M, Crowley H, Delgado R (2016) Development and assessment of damage-to-loss models for moment-frame reinforced concrete buildings. Earthq Eng Struct Dyn 45(5):797–817
Martins L, Silva V, Bazzurro P, Marques M (2018) Advances in the derivation of fragility functions for the development of risk-targeted hazard maps. Eng Struct 173:669–680
McGuire RK (2008) Probabilistic seismic hazard analysis: early history. Earthq Eng Struct Dyn 37:329–338. https://doi.org/10.1002/eqe.765
Menegotto M, Pinto PE (1973) Method of analysis for cyclically loaded R.C. plane frames including changes in geometry and non-elastic behaviour of elements under combined normal force and bending. In: Symposium on the resistance and ultimate deformability of structures acted on by well defined repeated loads, International Association for Bridge and Structural Engineering, Zurich, Switzerland
Mwafy AM (2001) Seismic performance of code-designed RC buildings. Ph.D. thesis, Imperial College, London
NEHRP Consultants Joint Venture (2013) Cost analyses and benefit studies for earthquake-resistant construction in Memphis, Tennessee. NIST GCR 14-917-26. National Institute of Standards and Technology, Gaithersburg, MD
NTC—Norme Tecniche per le Costruzione (2018) Aggiornamento delle Norme tecniche per le costruzioni, decreto 17-1-2018, Gazzetta Ufficiale 42, 20-02-2018, Ordinary Suppl. n. 8 (in Italian)
O’Reilly GJ, Sullivan TJ (2018) Probabilistic seismic assessment and retrofit considerations for Italian RC frame buildings. Bull Earthq Eng 16(3):1447–1485
Ordaz M, Salgado-Gálvez MA, Pérez-Rocha LE, Cardona OD, Mena-Hernández U (2017) Optimum earthquake design coefficients based on probabilistic seismic hazard analyses: theory and applications. Earthq Spectra 33(4):1455–1474. https://doi.org/10.1193/110116eqs189m
O’Reilly GJ, Perrone D, Fox M, Monteiro R, Filiatrault A (2018) Seismic assessment and loss estimation of existing school buildings in Italy. Eng Struct 168:142–162
Padgett JE, Dennemann K, Ghosh J (2010) Risk-based seismic life-cycle cost–benefit (LCC-B) analysis for bridge retrofit assessment. Struct Saf 32(3):165–173
Panagiotakos TB, Fardis MN (2004) Seismic performance of RC frames designed to Eurocode 8 or to the Greek codes 2000. Bull Earthq Eng 2(2):221–259
Paulay T, Priestley MJN (1992) Seismic design of reinforced concrete and masonry buildings. Wiley, New York
Perrone D, Calvi PM, Nascimbene R, Fischer EC, Magliulo G (2019) Seismic performance of non-structural elements during the 2016 Central Italy earthquake. Bull Earthq Eng 17(10):5655–5677
Porter K (2016) Not safe enough: the case for resilient seismic design. In: Proceedings of 2016 SEAOC convention
Ramirez CM, Liel AB, Mitrani-Reiser J, Haselton CB, Spear AD, Steiner J, Deierlein GG, Miranda E (2012) Expected earthquake damage and repair costs in reinforced concrete frame buildings. Earthq Eng Struct Dyn 41(11):1455–1475
Ricci P, De Luca F, Verderame GM (2011) 6th April 2009 L’Aquila earthquake, Italy: reinforced concrete building performance. Bull Earthq Eng 9:285–305. https://doi.org/10.1007/s10518-010-9204-8
RINTC Workgroup (2018) Results of the 2015–2017 Implicit seismic risk of code-conforming structures in Italy (RINTC) project. ReLUIS report, Rete dei Laboratori Universitari di Ingegneria Sismica (ReLUIS), Naples, Italy. http://www.reluis.it/. Accessed May 2020
Rivera JA, Petrini L (2011) On the design and seismic response of RC frame buildings designed with Eurocode 8. Bull Earthq Eng 9(5):1593–1616
Romão X, Costa AA, Paupério E, Rodrigues H, Vicente R, Varum H, Costa A (2013) Field observations and interpretation of the structural performance of constructions after the 11 May 2011 Lorca earthquake. Eng Fail Anal 34:670–692
Sassun K, Sullivan TJ, Morandi P, Cardone D (2016) Characterising the in-plane seismic performance of infill masonry. Bull N Z Soc Earthq Eng 49(1):100–117
Scott MH, Fenves GL (2006) Plastic hinge integration methods for force-based beam–column elements. ASCE J Struct Eng 132(2):244–252
Seismosoft (2020) SeismoStruct 2020—a computer program for static and dynamic nonlinear analysis of framed structures. https://seismosoft.com/. Accessed May 2020
Shinozuka M, Feng Q, Lee J, Naganuma T (2000) Statistical analysis of fragility curves. J Eng Mech 126:1224–1231
Silva V, Crowley H, Bazzurro P (2016) Exploring risk-targeted hazard maps for Europe. Earthq Spectra 32(2):1165–1186
Taghavi S, Miranda E (2003) Response assessment of nonstructural building elements. Pacific Earthquake Engineering Research Center, Berkeley
Tsang HH (2015) Evaluation of codified elastic design spectrum models for regions of low-to-moderate seismicity. Soil Dyn Earthq Eng 70:148–152
Tsang HH, Wenzel F (2016) Setting structural safety requirement for controlling earthquake mortality risk. Saf Sci 86:174–183
Tsang HH, Daniell JE, Wenzel F, Wilson JL (2020) A universal approach for evaluating earthquake safety level based on societal fatality risk. Bull Earthq Eng 18(1):273–296
Tubaldi E, Barbato M, Ghazizadeh S (2012) A probabilistic performance-based risk assessment approach for seismic pounding with efficient application to linear systems. Struct Saf 36:14–22
Ulrich T, Negulescu C, Douglas J (2014) Fragility curves for risk-targeted seismic design maps. Bull Earthq Eng 12(4):1479–1491
Vamvatsikos D (2013) Derivation of new SAC/FEMA performance evaluation solutions with second-order hazard approximation. Earthq Eng Struct Dyn 42(8):1171–1188
Vamvatsikos D, Cornell CA (2002) Incremental dynamic analysis. Earthq Eng Struct Dyn 31(3):491–514
Wen YK, Kang YJ (2001) Minimum building life-cycle cost design criteria. II: applications. J Struct Eng 127(3):338–346
Whitman RV, Biggs JM, Brennan JE III, Cornell CA, de Neufville RL, Vanmarcke EH (1975) Seismic design decision analysis. J Struct Div 101:1067–1084
Woessner J, Danciu L, Giardini D, Crowley H, Cotton F, Grunthal G, Valensise G, Arvidsson R, Basili R, Demircioglu MB, Hiemer S, Meletti C, Musson RW, Rovida AN, Sesetyan K, Stucchi M, The SHARE Consortium (2015) The 2013 European seismic hazard model: key components and results. Bull Earthq Eng 13(12):3553–3596. https://doi.org/10.1007/s10518-015-9795-1
Acknowledgements
The first author is undertaking a PhD funded by the University of Strathclyde “Engineering The Future” studentship, for which we are grateful. The authors would like to thank Dr. Hing-Ho Tsang and Dr. Vitor Silva for reviewing an early version of this article and providing many useful suggestions that helped to improve this article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gkimprixis, A., Tubaldi, E. & Douglas, J. Evaluating alternative approaches for the seismic design of structures. Bull Earthquake Eng 18, 4331–4361 (2020). https://doi.org/10.1007/s10518-020-00858-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-020-00858-4