Optimal intensity measure based on spectral acceleration for P-delta vulnerable deteriorating frame structures in the collapse limit state

Abstract

This study proposes an “optimal” spectral acceleration based intensity measure (IM) to assess the collapse capacity of generic moment frames vulnerable to the P-delta effect. The IM is derived from the geometric mean of the spectral pseudo-acceleration over a certain period interval. The optimized IM includes for first time a flexible lower limit for the period interval, corresponding to the structural period associated with the exceedance of 95% of the total effective mass. This flexible lower limit bound provides an efficient IM, independently of the contribution of higher modes to the total response. The upper bound period is 1.6 times the fundamental period to account for period elongation due to inelastic deformations and gravity loads. In a parametric study on generic frames, structural parameters are varied to quantify the performance of this IM compared to classical benchmark IMs. The “optimal” IM provides minimum, or close to the minimum, dispersion for the entire set of frames with different fundamental periods of vibration, number of stories, and P-delta vulnerability.

1 Introduction

In earthquake engineering analysis the intensity measure (IM), i.e., one parameter or a couple of parameters associated with a set of ground motion records, quantifies the severity of a seismic event and characterizes the uncertainty related to earthquake excitation. For the definition of the intensity of an earthquake record various approaches have been proposed. In its simplest form the IM is a scalar quantity directly related to the recorded ground motion, such as the peak ground acceleration (PGA) and peak ground velocity (PGV). A second group of frequently used scalar IMs comprises elastic and inelastic spectral values, such as the spectral acceleration and spectral displacement at the fundamental structural period. Advanced definitions may include the effects of higher modes and period elongation due to inelastic deformation (e.g., Cordova et al. 2001; Haselton and Baker 2006; Luco and Cornell 2007; Bianchini et al. 2009; Kadas et al. 2011; Vamvatsikos and Cornell 2005; Bojórquez and Iervolino 2011; Adam et al. 2014; Eads et al. 2015). Vector valued IMs (e.g., Vamvatsikos and Cornell 2005; Baker and Cornell 2005) combine several intensity related parameters, and thus, when appropriately defined they capture more comprehensively the intensity of earthquake excitation. The applicability of an IM, however, is limited to the availability of appropriate attenuation relations, as well as its validation for a wider class of structural systems. Thus, one of the main challenges other IMs face is the lack of relationships between earthquake characteristics, and IM magnitudes at different distances, and soil conditions, among other factors. For instance, Baker and Cornell (2006) revealed the significance of the spectral shape on the IM. Jalayer et al. (2012) examined the suitability of commonly used IMs compared to some others, using concepts of information theory. Most of these studies have not focused on earthquake excited structures in the collapse limit state. Currently, the most widely accepted IM for this limit state is the 5% damped pseudo-spectral acceleration at the (fundamental) period of the structure, $T_{1}$, which serves in the present study as the benchmark IM.

According to Luco and Cornell (2007) and Bianchini et al. (2009) an appropriate IM should comply with the following properties:

• Hazard computability (practicability), i.e., for the IM appropriate ground motion prediction equations must be available to quantify the ground motion hazard at the site.

• Efficiency, i.e., the record-to-record (RTR) variability of peak structural response, measured by an appropriate Engineering Demand Parameter (EDP), should be low at any level of the IM. The more efficient an IM is, the smaller the number of ground motion records required to predict the structural response within a certain confidence level.

• Sufficiency, i.e., the distribution of the IM given the EDP is conditionally independent of seismological characteristics, such as the magnitude, $M_{w}$, and the source-to-site distance, $R$, or alternatively, the distribution of the EDP given the IM is independent on those characteristics (Kazantzi and Vamvatsikos 2015a).

• Scaling robustness, i.e., the independence of the IM from scaling factors.

Most studies were mainly focused on the efficiency of the considered IMs. The properties of sufficiency, scaling robustness and hazard compatibility have also been studied (e.g., Shome and Cornell 1999; Luco and Cornell 2007; Bianchini et al. 2009; Bojórquez and Iervolino 2011; Eads et al. 2015).

More recently, IMs based on the geometric mean of spectral pseudo-acceleration over a specific period interval have attracted the attention of several researchers. The studies of Tsantaki (2014) and Tsantaki et al. (2017) have shown that for P-delta vulnerable single-degree-of-freedom (SDOF) systems this IM based on the geometric mean concept of spectral accelerations satisfies better the properties of efficiency and sufficiency, compared with outcomes of benchmark studies (Adam and Jäger 2012a; Jäger and Adam 2013; Tsantaki et al. 2015), where the 5% damped spectral pseudo-acceleration at the structural period has been used as IM. In Eads et al. (2015) the efficiency and sufficiency of a similar IM for collapse prediction of about 700 moment-resisting frame and shear wall structures has been evaluated. In this investigation for the IMs a lower bound period of 20% of $T_{1}$ and an upper bound of three times $T_{1}$ was used. Kazantzi and Vamvatsikos (2015a) compared the effectiveness of various geometric mean based IMs superposing the spectral acceleration read at different linearly equally and logarithmically spaced periods. In their study an IM that combines the spectral acceleration read at five periods ranging from the second-mode period to twice the first-mode period was found to perform best in terms of efficiency and sufficiency across the practical range of peak floor acceleration and interstory drift values of low-rise and high-rise structures.

For selection and modification of earthquake records, several codes consider the elongated period interval due to nonlinear behavior, as well as to higher mode effects associated to shorter periods of vibration. For instance, spectral matching period intervals of 0.2$T_{1}$ to 2.0$T_{1}$ (Eurocode 8, 2004), 0.4$T_{1}$ to 1.5$T_{1}$ (NZSEE 2006) and 0.2$T_{1}$ to 1.5 $T_{1}$ (ASCE/SEI 41-13, 2014) are specified in current codes, where $T_{1}$ denotes the fundamental period of vibration. Katsanos et al. (2012) suggested to reduce the period interval specified in Eurocode 8 (2004) to 0.2$T_{1}$ < $T_{1}$ < 1.5$T_{1}$ at least for new buildings designed for low or moderate levels of ductility and low-to-medium stiffness degradation. However, most of the proposed code-bounds of the period intervals are based on expert elicitation, without being referred to specific research studies.

In this paper, the choice of an appropriate IM is investigated based on the geometric mean of spectral pseudo-acceleration over a specific period interval for defining the collapse capacity of multi-story moment-resisting frames vulnerable to the destabilizing effect of gravity loads (i.e., global P-delta effect). Thus, in the first part of this study the efficiency of this IM for various lower and upper bound periods, depending on the fundamental period and for various structural configurations of P-delta sensitive generic frame structures, is studied. Based on these analyses, an “optimal” IM based on the geometric mean of spectral accelerations is proposed, which renders minimum dispersion due to RTR variability for all the evaluated frames. This “optimized” IM includes a flexible lower bound period interval that corresponds to the structural period associated with the exceedance of 95% of the total effective mass, to efficiently consider small or large high mode contributions. It follows a quantitative and qualitative evaluation of the efficiency property of this IM in the collapse limit state with respect to the characteristic structural parameters. After that, the sufficiency of the identified “optimal” IM is studied.

2 Spectral acceleration based intensity measures

2.1 Definitions

Nowadays a single target spectral value is commonly used as IM. In its simplest form, the spectral acceleration is read at an “arbitrary” period, such as 1.0 s, i.e., $S_{a} (T = 1.0\;{\text{s}})$. A more elaborated IM is the 5% damped spectral acceleration at the fundamental period, $T_{1}$, of the structure, $S_{a} (T = T_{1} )$, see Fig. 1a. This IM is correlated to ground motion and building information. Thus, for an elastic structure that is first mode dominated it is generally more efficient than IMs such as $S_{a} (T = 1.0\;{\text{s}})$ or the peak ground acceleration (PGA).

Fig. 1

Pseudo-spectral acceleration of a ground motion record. a Spectral acceleration at the fundamental mode $T_{1}$, b at $T_{1}$ and higher mode periods, c at $T_{1}$ and $2T_{1}$, d at equally spaced periods between a lower bound period $T^{(1)}$ and an upper bound period $T^{(n)}$

For tall buildings, where higher modes contribute significantly to the seismic response, the efficiency of the IM is improved by superposition of the spectral value at the first mode with the spectral values of the first $m$ higher modes (see Fig. 1b),

$$IM = \left( {\prod\limits_{j = 1}^{m} {S_{a} (T_{j} )} } \right)^{1/m}$$

(1)

The superposition is based on the geometric mean, and $T_{j}$ is the jth mode period of the structure. For example, Shome and Cornell (1999) found that inclusion of the spectral accelerations at the second and the third mode, $S_{a} (T_{2} )$ and $S_{a} (T_{3} )$, respectively, reduces the RTR dispersion of the elastic EDP demand of high-rise structures. At this point it should be noted that in the collapse limit state only one failure mode dominates the response, as it has been shown in Brozovič and Dolšek (2014). This failure mode can be very different from the mode shapes obtained from modal analysis of the elastic structure, however, it is triggered by the fundamental as well higher modal modes in combination with the given ground motion record (Brozovič and Dolšek 2014). Thus, subsequently the generic expression higher mode effect refers to the effect of higher modes on the failure mode. However, in particular in taller structure the shape of the failure mode close to collapse significantly depends on the ground motion used (Brozovič and Dolšek 2014).

When a structure responds inelastically, the structural periods elongate depending on the plastic deformation. The first studies considering period elongation (Mehanny and Deierlein 2000; Cordova et al. 2001) included a second spectral value at a period longer than the first mode, leading to an IM of the form $IM = S_{a} (T_{1} )^{(1 - \beta )} S_{a} (cT_{1} )^{\beta }$. With the suggested values $\beta = 0.5$ and $c = 2$, this IM represents the geometric mean of the two spectral accelerations read at the periods $T_{1}$ and $2T_{1}$, i.e., $IM = \left( {S_{a} (T_{1} )S_{a} (2T_{1} )} \right)^{1/2}$, see Fig. 1c.

In an effort to capture both higher mode effects and period elongation due to plastic deformations Vamvatsikos and Cornell (2005) conducted a parametric Incremental Dynamic Analysis (IDA) study up to collapse to identify the optimal periods $T_{a}$, $T_{b}$, $T_{c}$ and exponents $\beta$ and $\gamma$ of a similar IM composed of three spectral values according to $IM = S_{a} (T_{a} )^{(1 - \beta - \gamma )} S_{a} (T_{b} )^{\beta } S_{a} (T_{c} )^{\gamma }$, where $\alpha < 1$, $\beta < 1$, and $1 - \alpha - \beta \ge 0$. They found that the optimal parameters depend strongly on the actual deformation of the structure, i.e., elastic, moderately inelastic, or at onset of collapse.

Bianchini et al. (2009) proposed to calculate the geometric mean of discrete spectral acceleration values $S_{a} (T^{(i)} )$ ($i = 1, \ldots ,n$) as,

$$S_{a,gm} (T^{(1)} ,T^{(n)} ) = \left( {\prod\limits_{i = 1}^{n} {S_{a} (T^{(i)} )} } \right)^{1/n}$$

(2)

within the period interval $\Delta T$

$$\Delta T = T^{(n)} - T^{(1)} ,\,\,\,\,\,T^{(n)} > T^{(1)} \,$$

(3)

The period interval ΔT has a lower bound period $T^{(1)} \,$ and an elongated upper bound period $T^{(n)}$. Also, $T^{(i)}$ is the ith period of the set of n periods $T^{(1)} , \ldots ,T^{(i)} , \ldots ,T^{(n)}$. In general, $T^{(i)}$ does not comply with a system period $T_{j}$. In contrast to Bianchini et al. (2009), where $S_{a}$ is discretized at 10 log-spaced periods within $\Delta T$, Tsantaki et al. (2017) discretized $S_{a}$ at equally spaced periods $T^{(i)}$ within $\Delta T$ (Fig. 1d),

$$T^{(i)} = T^{(1)} + \left( {i - 1} \right)\delta T,\quad i = 1, \ldots ,n,\quad \delta T = \frac{\Delta T}{n - 1} = \frac{{T^{(n)} - T^{(1)} }}{n - 1}$$

(4)

Based on parametric IDAs on P-delta vulnerable highly inelastic SDOF systems, Tsantaki et al. (2017) found that the upper elongated period $T^{(n)}$ leading to the minimum RTR dispersion of the collapse capacity is around $1.6T_{SDOF}$, fluctuating between $1.4T_{SDOF}$ and $2.0T_{SDOF}$. According to this study, for these SDOF systems the “optimal” lower bound period $T^{(1)}$ corresponds to the elastic period, i.e., $T^{(1)} = T_{SDOF}$. The collapse capacity dispersion due to RTR variability of SDOF systems based on the IM $S_{a,gm} (T_{SDOF} ,1.6T_{SDOF} )$ is 50% lower than that obtained from the common IM $S_{a} (T_{SDOF} )$.

In a preliminary study on collapse capacity dispersion due to RTR variability of multi-story frame structures sensitive to P-delta, Adam et al. (2014) proposed as IM $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$. In this IM, the lower bound interval is 20% of the fundamental period, i.e., $T^{(1)} = 0.2T_{1}$, to account for higher mode effects, in agreement with Eurocode 8 (2004) and ASCE/SEI 41-13 (2014) specifications.

Another possibility is to superpose discrete spectral accelerations that are weighed with respect to their importance with a period dependent shape function $\varphi (T)$,

$$\bar{S}_{a,gm} (T^{(1)} ,T^{(n)} ) = \left( {\prod\limits_{i = 1}^{n} {\varphi (T^{(i)} )S_{a} (T^{(i)} )} } \right)^{1/n} ,\quad 0 \le \varphi (T) \le 1$$

(5)

It is reasonable to assume that at the fundamental period the function $\varphi (T)$ is 1, $\varphi (T = T_{1} ) = 1$, and then decreases on both sides up to 0 when the lower and upper bound period is reached, i.e., $\varphi (T = T^{(1)} ) = \varphi (T = T^{(n)} ) = 0$. The appropriate shape of $\varphi (T)$ for IM $\bar{S}_{a,gm} (T^{(1)} ,T^{(n)} )$ must be identified in a parametric investigation, but it is not part of the scope of this paper.

Recently, Kazantzi and Vamvatsikos (2015b) proposed for seismic vulnerability studies a new scalar IM that combines the geometric mean concept of spectral accelerations with a significant duration property of the ground motions based on the Arias Intensity.

2.2 Studied intensity measures

Subsequently, the choice of an appropriate IM, $S_{a,gm}$ according to Eq. (2), is evaluated based on the geometric mean of fifty 5% damped spectral pseudo-accelerations at equally spaced periods between predefined lower and upper bound periods. The appropriateness of the IM is associated to the collapse capacity dispersion of moment-resisting frames (MRFs) vulnerable to the P-delta effect due to RTR variability. The single target 5% damped spectral pseudo-acceleration, $S_{a} (T_{1} )$ serves as the benchmark IM. This IM fulfills the hazard computability property since attenuation relationships describing the probability distribution of spectral pseudo-accelerations at single target periods are widely available. Seismic hazard analysis for the geometric mean based IMs, $S_{a,gm}$, can also be applied based on correlation equations between spectral accelerations at multiple periods derived by Baker and Jayaram (2008). According to Bianchini et al. (2009) the choice of a period interval has never been comprehensibly evaluated. In their study of collapse limit state, for instance, Eads et al. (2015) fixed the lower bound period to $T^{(1)} = 0.2T_{1}$ and the upper bound period to $T^{(n)} = 3.0T_{1}$. A first attempt to assess the appropriate period interval has been conducted in Adam et al. (2014). Subsequently, the efficiency of IM $S_{a,gm}$ at collapse is studied for various lower and upper bound periods and various structural configurations of P-delta sensitive generic frame structures to identify an “optimal” IM.

3 Testbed generic frame structures

3.1 General set-up

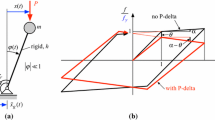
Generic multi-story frames as shown in Fig. 2a, similar to the ones evaluated by Medina and Krawinkler (2003), are used to assess collapse capacity dispersion. All stories of these moment-resisting single-bay frame structures of N stories are of uniform height h, and they are composed of elastic flexible columns and rigid beams. Inelastic rotational springs are located at the base of the first floor columns and at both ends of the beams, according to the weak beam-strong column design philosophy. Thus, the computed collapse capacity of frames exhibiting column yielding, other than at the base of first floor columns, will be overestimated (Ibarra and Krawinkler 2005). To each joint of the frames an identical lumped mass $m_{s} /2$ is assigned. The desired straight-line fundamental mode shape is the governing condition for adjusting the bending stiffness of the columns and the initial stiffness of the springs. The rotational springs are modeled with a bilinear backbone curve. The inelastic branch of this backbone curve with reduced stiffness is characterized by the strain-hardening coefficient, $\alpha$, which is the same for all springs. The initial strength of the springs is tuned such that yielding is initiated simultaneously at all spring locations in a static pushover analysis (without gravity loads) based on a first mode design load pattern.

Fig. 2

a Generic test-bed frame. b Global pushover curve of a considered generic P-delta vulnerable multi-story frame structure (red curve), and the corresponding outcome disregarding gravity loads (black curve). [modified from Adam and Jäger (2012b)]

The hysteretic response of the springs is assumed to be bilinear. Since the focus of this study is on purely P-delta vulnerable structures, a post-capping stiffness is not considered. That is, the deformation associated with the post-capping strength is set to infinity. However, unloading stiffness and strength cyclic deterioration is simulated with the modified Ibarra-Medina-Krawinkler deterioration model (Ibarra and Krawinkler 2011; Lignos and Krawinkler 2012). The controlling unloading stiffness deterioration and cyclic strength deterioration parameters, $\varLambda_{K}$ and $\varLambda_{S}$, respectively, are assumed to be equal to each other for all springs of the frame, $\varLambda_{K} = \varLambda_{S}$. Three material deterioration levels are used to represent slow, medium, and rapid deterioration based on Lignos and Krawinkler (2012) database.

Rayleigh type damping is set at 5% viscous damping for the first mode and the mode in which the sum of modal masses exceeds 95% of the total mass. The damping matrix is proportional to the mass matrix and the tangent stiffness matrix.

3.2 Modeling of the P-Delta effect

The P-delta effect on the studied frame structures is quantified by means of two base shear-roof drift relations (global pushover curves) resulting from two different pushover analyses based on a fundamental mode design load pattern, as outlined in Adam and Jäger (2012b). In the first pushover analysis identical gravity loads are assigned to each story joint to simulate P-delta effects. The second pushover analysis is conducted without gravity loads. Since in the evaluated frames all springs yield simultaneously, both pushover curves are bilinear, as illustrated in Fig. 2b. The P-delta effect reduces for a given roof displacement, $x_{N}$, the base shear, V, and consequently, the elastic and post-yield stiffness become apparently smaller. According to Medina and Krawinkler (2003) the stability coefficient of a multi-story frame structure is non-uniform in the elastic and inelastic branch of deformation, in contrast to a single-degree-of-freedom (SDOF) oscillator. If the pushover curves are bilinear, two stability coefficients can be identified, i.e., a stability coefficient in the elastic range of deformation ($\theta_{e}$) and a stability coefficient in the post-yield range of deformation ($\theta_{i}$), as observed in Fig. 2b. It has been shown in Medina and Krawinkler (2003) that $\theta_{i}$ is larger than $\theta_{e}$, and with increasing P-delta vulnerability also the difference between the elastic and the inelastic stability coefficient is increasing, i.e., $\theta_{i} > (>)\theta_{e}$. In many flexible frame structures the collapse capacity is not significantly affected by cyclic deterioration of its structural components. In those structures a negative post-yield stiffness is a precondition for seismic collapse. This precondition can be expressed as $\theta_{i} - \alpha_{S} > 0$, i.e., the difference of inelastic stability coefficient $\theta_{i}$ and lateral global hardening ratio $\alpha_{S}$ must be larger than zero, as it is illustrated in Fig. 2b (Adam and Ibarra 2015). It should be noted that the strain hardening coefficient assigned to each rotational spring, $\alpha$, and the global hardening coefficient, $\alpha_{S}$, are generally different.

3.3 Characteristic structural parameters

Collapse capacity dispersion due to RTR variability of the considered P-delta vulnerable MDOF systems is primarily influenced by

• the fundamental period $T_{1}$ (without gravity loads),

• the negative slope of the post-yield stiffness $\theta_{i} - \alpha_{S}$ in the capacity curve,

• the period elongation due to inelastic deformations,

• higher modes correlated with the number of stories N and the structural periods.

In this study the elastic fundamental period $T_{1}$, the negative post-yield stiffness ratio $\theta_{i} - \alpha_{S}$, and the number of stories N serve as variables. Variation of these parameters affects the fundamental period including the effect of gravity loads, which is subsequently denoted as $T_{1}^{P\Delta }$. The period elongation at collapse is largely controlled through $\theta_{i} - \alpha_{S}$, and deterioration of the unloading stiffness and strength. Thus, results are presented for frames with non-deteriorating springs, and springs subjected to slow, medium, and rapid deterioration.

In total 2048 generic frame structures are studied. All predefined basic model parameters of the considered generic frame structures are summarized in Table 1.

Table 1 Range of basic model parameters of the considered generic frame structures

4 Incremental dynamic analysis and ground motions

4.1 The seismic collapse capacity and its record-to-record variability

The IDA procedure (Vamvatsikos and Cornell 2002) is used to predict collapse capacity of the testbed structures. An IDA consists of a series of time history analyses, in which the intensity of a particular ground motion is monotonically increased. As a result, the IM is plotted against the EDP (here the roof drift), and the procedure is stopped when this parameter grows unbounded, indicating that structural failure occurs. The corresponding IM, $\left. {IM_{i} } \right|_{collapse}$, is referred to as the structural collapse capacity $CC_{i}$ of the structure subjected to ground motion record i,

$$CC_{i} = \left. {IM_{i} } \right|_{collapse}$$

(6)

Collapse capacities are computed for all records of the selected bin, and subsequently evaluated statistically given that RTR variability leads to different collapse capacities for different ground motion records. Shome and Cornell (1999) and Ibarra and Krawinkler (2011) provide good arguments for representing a set of corresponding collapse capacities by a log-normal distribution. The log-normal distribution is characterized by the median $\mu_{\ln CC}$ of the natural logarithm and the standard deviation $\beta$ of the logarithm of individual collapse capacities (FEMA-350 2000),

$$\beta = \sqrt {\sum\limits_{i = 1}^{r} {\frac{{(\ln CC_{i} - \mu_{\ln CC} )^{2} }}{r - 1}} }$$

(7)

where r is the number of ground motion records, and thus, of individual collapse capacities, $CC_{i}$, $i = 1, \ldots ,r$.

4.2 Utilized ground motion sets

The uncertainty in the frames collapse capacity caused by RTR variability is computed employing the far-field ground motions of both the FEMA P-695 far-field record set (FEMA P-695 2009), referred to as FEMA P-695-FF, and the LMSR-N record set (Medina and Krawinkler 2003). The FEMA P-695-FF records include seismic events of magnitude $M_{w}$ between 6.5 and 7.6, and closest distance to the fault rupture larger than 10 km. The Joyner-Boore distance is between 7.1 and 26 km. Only strike-slip and reverse sources are considered. The 44 records of this set were recorded on NEHRP site classes C (soft rock) and D (stiff soil) (FEMA P-695 2009). The second bin, LMSR-N, contains 40 ground motions recorded in California on NEHRP site class D during earthquakes of moment magnitude $M_{w}$ between 6.5 and 7 and closest distance to the fault rupture between 13 km and 40 km. This set of records has strong motion duration characteristics insensitive to magnitude and distance (Medina and Krawinkler 2003).

5 Identification of an optimal intensity measure

To identify the optimal IM, three evaluations are performed varying the period interval bounds. The first evaluation focuses on the effect of upper bound variations on collapse capacity dispersion, whereas the second evaluation considers the effect of different lower bounds on this dispersion. The third evaluation simultaneously analyzes the effect of lower and upper bound variations on collapse capacity dispersion.

5.1 Intensity measures covering the effect of period elongation

In the first evaluation the effect of period elongation due to the presence of gravity loads and the potential of inelastic deformations on the efficiency of IM $S_{a,gm}$ is investigated. The lower bound period $T^{(1)}$ is the fundamental period $T_{1}$ (unaffected by P-delta), whereas $T^{(n)}$ values of $1.6T_{1}$, $2.0T_{1}$, and $1.3T_{1}$ are assigned to the upper bound period. The resulting period intervals $\Delta T$ are $S_{a,gm} (T_{1} ,1.6T_{1} )$, $S_{a,gm} (T_{1} ,2.0T_{1} )$, and $S_{a,gm} (T_{1} ,1.3T_{1} )$. Tsantaki et al. (2017) found that the period interval from $T^{(1)} = T_{1}$ to $T^{(n)} = 1.6T_{1}$ leads on average to the smallest collapse capacity dispersion of P-delta vulnerable SDOF systems.

For this evaluation three sets of generic frames that do not exhibit cyclic deterioration are assessed. Each set includes 1-, 3-, 9-, and 18-story structures. The frames of the first set exhibit a fundamental period of $T_{1} = 0.5\;{\text{s}}$, and a small negative post yield-stiffness ratio of $\theta_{i} - \alpha_{S} = 0.03$. The frames of the second and third set are more flexible, $T_{1} = 2.0\;{\text{s}}$ and $T_{1} = 3.5\;{\text{s}}$, respectively. These second and third sets also exhibit larger post-yield stiffness ratios of $\theta_{i} - \alpha_{S} = 0.10$ and $\theta_{i} - \alpha_{S} = 0.20$, respectively; and therefore are more prone to collapse.

Figure 3 shows the collapse capacity dispersion $\beta$ (as defined in Eq. 7) of these frames when subjected to the 44 records of FEMA P-695-FF set, based on the discussed averaged IMs and the $S_{a} (T_{1} )$ benchmark IM. As observed, IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ is more efficient than IM $S_{a} (T_{1} )$ for all structural configurations. For stiff structures with $T_{1} = 0.5s$, IM $S_{a,gm} (T_{1} ,2.0T_{1} )$ is slightly more efficient than IM $S_{a,gm} (T_{1} ,1.6T_{1} )$. However, for the most flexible structures with $T_{1} = 3.5s$, IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ leads to the smallest collapse capacity dispersion, whereas for the 3-, 9-, and 18-story structures IM $S_{a,gm} (T_{1} ,2.0T_{1} )$ is even less efficient than benchmark IM $S_{a} (T_{1} )$. A statistical analysis of dispersion $\beta$ of all considered structures shows that, in general, IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ performs better than IM $S_{a,gm} (T_{1} ,2.0T_{1} )$, and better than all other IMs that only consider period elongation.

Fig. 3

Dispersion of the collapse capacity for three frame sets with parameters as specified. No material deterioration. Four IMs considering period elongation as specified, and benchmark IM $S_{a} (T_{1} )$. FEMA P-695-FF record set

5.2 Intensity measures covering higher mode effects

Subsequently, two average IMs are utilized to investigate the effect of using period intervals that account only for higher modes on collapse capacity dispersion. The evaluated period intervals are $S_{a,gm} (0.2T_{1} ,T_{1} )$ and $S_{a,gm} (0.4T_{1} ,T_{1} )$. Six different frame sets are considered, including the three sets of the previous evaluation. The fourth set consists of six flexible ($T_{1} = 3.5\;{\text{s}}$) 18-story frames with $\theta_{i} - \alpha_{S}$ varying from 0.03 to 0.40. The fifth set considers six 9-story frames with constant $\theta_{i} - \alpha_{S}$ = 0.10, and $T_{1}$ varying from 0.5 to 3.5 s. The sixth set has six 18-story frames with $\theta_{i} - \alpha_{S}$ = 0.20, and $T_{1}$ also varies from 0.5 to 3.5 s. All frames are subjected to FEMA P-695-FF ground motion set.

The results shown in Fig. 4 reveal that IMs that only consider the effect of higher modes in the period range definition lead to a larger collapse capacity dispersion (even for multi-story structures) compared to the traditional IM $S_{a} (T_{1} )$. This can be attributed to the large influence of first mode contributions to the response. It is, thus, more useful to reduce the RTR variability in the first mode than using an average interval that only considers higher modes. There is no significant or consistent difference whether the lower bound period is $T^{(1)} = 0.2T_{1}$ or $T^{(1)} = 0.4T_{1}$. Thus, it can be concluded that these IMs are not useful, and are no longer evaluated.

Fig. 4

Dispersion of the collapse capacity for six frame sets with parameters as specified. No material deterioration. Two IMs considering period elongation as specified, and benchmark IM $S_{a} (T_{1} )$. FEMA P-695-FF record set

5.3 Intensity measures covering the effect of period elongation and higher modes

In the third set of analyses, two IMs $S_{a,gm}$ are defined to cover the range of periods associated to higher modes and period elongation: $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$ and $S_{a,gm} (0.4T_{1} ,1.6T_{1} )$. A $T^{(1)}$ of $0.2T_{1}$ corresponds to the lower bound period suggested in Eurocode 8 (2004) and ASCE/SEI 41-13 (2014), and $T^{(1)} = 0.4T_{1}$ is provided in the standard NZSEE (2006). The collapse capacity dispersion based on these two IMs is compared to the outcomes based on IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ and on the two single target IMs $S_{a} (T_{1} )$ and $S_{a} (T_{1}^{P\Delta } )$.

Six frame sets exhibiting non-deteriorating material properties subjected to FEMA P-695-FF bin are assessed. The results for the first two frame sets of 1-, 3-, 9- and 18-story frames are depicted in Fig. 5a, b. The first set includes stiff frames with $T_{1} = 0.5\;{\text{s}}$ and a small $\theta_{i} - \alpha_{S}$ = 0.03. The frames of the second set are more flexible, $T_{1} = 3.5\;{\text{s}}$, and have a steeper $\theta_{i} - \alpha_{S} = 0.20$. As observed, stiffer frames ($T_{1} = 0.5\;{\text{s}}$) with IMs $S_{a,gm} (T_{1} ,1.6T_{1} )$, $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$ and $S_{a,gm} (0.4T_{1} ,1.6T_{1} )$ lead to a dispersion of the same order. In contrast, the dispersion for IMs $S_{a} (T_{1} )$ and $S_{a} (T_{1}^{P\Delta } )$ is significantly larger. IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ is, however, most efficient for all frames of this set, see Fig. 5a. According to Fig. 5b, IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ yields the smallest collapse capacity dispersion for the 3.5 s one-story structure, while for the multi-story frames IMs $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$ and $S_{a,gm} (0.4T_{1} ,1.6T_{1} )$ are more efficient.

Fig. 5

Dispersion of the collapse capacity for six frame sets with parameters as specified. No material deterioration. Benchmark IM $S_{a} (T_{1} )$, IM $S_{a} (T_{1}^{P\Delta } )$, one IM considering period elongation, and two IMs considering both period elongation and higher mode effects as specified. FEMA P-695-FF record set

This outcome is confirmed by the studies on four additional frame sets. Figure 5c, d shows the collapse capacity dispersion $\beta$ for sets of 1- and 9-story frames, respectively. In both figures, the negative post-yield stiffness ratio $\theta_{i} - \alpha_{S}$ is varied from 0.03 to 0.40, keeping the period $T_{1} = 2.0\;{\text{s}}$ (without gravity load) constant. Figure 5e, f presents 1- and 18-story frames, respectively, in which $\theta_{i} - \alpha_{S} = 0.20$, and fundamental periods of 0.5, 1.0, 1.5, 2.5, and 3.5 s are investigated. The one-story systems with $\theta_{i} - \alpha_{S}$ > 0.20 (Fig. 5c) are the only structural configurations where the dispersion based on IM $S_{a} (T_{1} )$ is different than the dispersion based on $S_{a} (T_{1}^{P\Delta } )$. This can be attributed to the fact that SDOF one-story frames exhibit only one stability coefficient $\theta$ uniform in both elastic and post-yield branches of deformation (MacRae 1994). This “global” stability coefficient $\theta$ is of the same order as the inelastic stability coefficient $\theta_{i}$ of the multi-story frames. In the one-story frame the period elongation due to P-delta is associated with $\theta$, i.e., $T_{1}^{P\Delta }$ = $T_{1}^{{}} \sqrt {{1 \mathord{\left/ {\vphantom {1 {(1 - \theta }}} \right. \kern-0pt} {(1 - \theta }})}$, and therefore, is larger than the corresponding elongation of a multi-story frame associated with the elastic stability coefficient $\theta_{e} ( \ll \theta_{i} )$, see Fig. 2. For this reason, for the one-story frame the target spectral acceleration $S_{a} (T_{1} )$, based on the period $T_{1}$, differs from $S_{a} (T_{1}^{P\Delta } )$ based on the period considering gravity loads, $T_{1}^{P\Delta }$, by 14% if $\theta$ = 0.20. With increasing number stories the difference between the inelastic stability coefficient $\theta_{i}$ and the elastic one $\theta_{e}$ becomes larger. Consequently, for a given $\theta_{i} - \alpha_{S}$ the elastic stiffness considering P-delta approaches the stiffness unaffected by P-delta, and also the difference between periods $T_{1}^{P\Delta }$ and $T_{1}$ becomes smaller. Thus, with increasing number of stories the superior performance of IM $S_{a} (T_{1}^{P\Delta } )$ over IM $S_{a} (T_{1} )$ decreases for a given $\theta_{i} - \alpha_{S}$, as observed when comparing Fig. 5c with Fig. 5d, and Fig. 5e with Fig. 5f.

It is worth to note that in all one-story structures of Fig. 5c, e IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ is more efficient than IMs $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$ and $S_{a,gm} (0.4T_{1} ,1.6T_{1} )$ because SDOF systems have no higher mode effects. However, the superior performance of IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ over IM $S_{a} (T_{1} )$ for SDOF systems is already drastically reduced for the three-story buildings, as observed in Fig. 5b. Further increase of the story number diminishes the positive effect of this average IM for the collapse capacity dispersion $\beta$.

The IMs $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$ and $S_{a,gm} (0.4T_{1} ,1.6T_{1} )$ lead to the smallest collapse capacity dispersion $\beta$ for the flexible 3-, 9-, and 18-story frames of Fig. 5b, d, f, except for $T_{1}$  = 0.5 s frames of Fig. 5a, in which the IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ is slightly more efficient. Also, IMs $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$ and $S_{a,gm} (0.4T_{1} ,1.6T_{1} )$ lead to almost the same efficiency for different MDOF systems, which according to Table 2 implies that the effect of the third mode on collapse capacity dispersion is very small. This table presents the ratios of second and third periods to the fundamental period, i.e., $T_{2} /T_{1}$ and $T_{3} /T_{1}$, respectively; and the ratio of effective modal mass to total effective mass for the first three modes, i.e., $M_{i} /M,\;i = 1, \ldots ,4$. As observed, $T_{2} /T_{1}$ is around 0.4 for most frames, whereas $T_{3} /T_{1}$ is close to 0.2 in most cases. Thus, the lower bound $0.4T_{1}$ captures second mode effects, whereas the lower bound $0.2T_{1}$ includes second and third mode effects.

Table 2 Period ratios for the first four modes; period associated with the exceedance of 95% of the cumulative effective modal mass T _0.95M ; effective modal mass ratios for the first four modes; ratio cumulative effective modal mass at T _0.95M  to total mass

5.4 Optimal intensity measure

Based on the findings for the entire frame set defined in Table 1, it is concluded that the lower bound period of an “optimal” IM should not be a fixed fraction of the fundamental period $T_{1}$ (such as $0.2T_{1}$ or $0.4T_{1}$), because such an IM reduces the efficiency for SDOF systems, or systems with low high mode contributions. As a solution it is proposed to relate the lower bound period of averaging interval $\Delta T$ in analogy to Rayleigh damping with 95% of the total effective modal mass $M$, leading to the following IM

$$IM_{opt} = S_{a,gm} (T_{0.95M} ,1.6T_{1} )$$

(8)

which is subsequently referred to as “optimal” IM. Table 2 also shows the period associated with exceedance of 95% of the cumulative effective modal mass, $T_{0.95M}$, and the ratio cumulative effective modal mass to total mass $M_{95cum} /M$ at this period. Clearly, for an SDOF system the lower bound period corresponds to the fundamental period $T_{1}$, i.e., $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$. For the three-story system the lower bound $T^{(1)}$ corresponds to the second period $T_{2}$, $T^{(1)} = T_{2}$, or expressed in terms of the fundamental period, $T^{(1)} = 0.34T_{1}$. For an 18-story structure the lower bound period is related to the fourth mode, i.e., $T^{(1)} = T_{4} = 0.17T_{1}$. For the sake of completeness it is noted here that for the considered generic frames period $T_{0.95M}$ can roughly estimated as

$$T_{0.95M} \approx T_{1} /\left[ {1 + 3(m_{0.95M} - 1)/2} \right]$$

(9)

where $m_{0.95M}$ is the mode associated with the exceedance of 95% of the total mass,

$$m_{0.95M} = {\text{ceil}}\sqrt N$$

(10)

Equation (10) applies for all frames and does not depend on the fundamental period. It yields for all frames the correct mode number except for 18-story frame, where the fifth mode instead of the fourth mode is obtained.

In a recent study (Adam et al. publ. online 2016) a preliminary evaluation of this IM has been conducted.

It should be noted here that the definition of a new IM requires hazard curves expressed in terms of this IM to comply with the property of practicability. For the proposed IM, hazard curves can be determined in a similar fashion as for the single target spectral IM $S_{a} (T_{1} )$. However, since for $IM_{opt}$ spectral acceleration $S_{a}$ is not read at a single period, but depends additionally on the lower and upper bound period range of the averaging interval, a matrix (or set) of hazard curves needs to be derived including the information of these quantities (i.e., $S_{a}$ at the fundamental period, and lower and upper limit of the considered period range). Consequently, many more combinations of hazard curves do exist, but when stored in a database the application is straightforward. The derivation of such a set of hazard curves is, however, out of the scope of the present study.

6 Efficiency of optimal intensity measure

In this section the efficiency of the “optimal” intensity measure $IM_{opt}$ is qualitatively and quantitatively assessed. Figure 6 shows dispersion parameter $\beta$ for nine sets of frames with non-deteriorating material properties subjected to the 44 FEMA P-695-FF ground motions based on IM $IM_{opt}$, and for comparison also for the IMs $S_{a} (T_{1} )$, $S_{a} (T_{1}^{P\Delta } )$, $S_{a,gm} (T_{1} ,1.6T_{1} )$, and $S_{a,gm} (0.2T_{1} ,1.6T_{1} )$. As observed, for all structures $IM_{opt}$ is more efficient than single target IMs $S_{a} (T_{1} )$ and $S_{a} (T_{1}^{P\Delta } )$. Moreover, for most structures it is the most efficient IM, and in the remaining cases, the deviation to the most efficient one is 5% at most. To quantify the efficiency enhancement of the alternative IMs with respect to the benchmark IM $S_{a} (T_{1} )$, Fig. 7 represents the ratio of the dispersion of the four alternative IMs with respect to $\beta$ based on IM $S_{a} (T_{1} )$.

Fig. 6

Dispersion of the collapse capacity for nine frame sets with parameters as specified. No material deterioration. Benchmark IM $S_{a} (T_{1} )$, IM $S_{a} (T_{1}^{P\Delta } )$, one IM considering period elongation, one IM considering both period elongation and higher mode effects as specified, and “optimal” IM $IM_{opt}$. FEMA P-695-FF record set

Fig. 7

Dispersion of the collapse capacity based on alternative IMs over the dispersion for benchmark IM $S_{a} (T_{1} )$. Nine frame sets with parameters as specified. No material deterioration. FEMA P-695-FF record set

In Fig. 6a, b, c the collapse capacity variability is depicted for three groups of frames, as a function of the number of stories. The period $T_{1} = 3.5\;{\text{s}}$ is constant, but $\theta_{i} - \alpha_{S}$ is different in each figure. As observed, the collapse capacity dispersion increases as the number of stories increases. It is also observed that in structures exposed to moderate P-delta effect, i.e., $\theta_{i} - \alpha_{S} = 0.03$, the $IM_{opt}$ efficiency only increases 5–9% as compared to benchmark IM $S_{a} (T_{1} )$, see Fig. 7a. However, for the two other frame sets the dispersion based on $IM_{opt}$ is up to 30% smaller than for IM $S_{a} (T_{1} )$. Here it is referred to Fig. 7b, c.

Figure 6d, e, f show the collapse variability for flexible frames with a fundamental period of 3.5 s as a function of the negative post-yield stiffness ratio for frames of one (Fig. 6d), nine (Fig. 6e), and 18 (Fig. 6f) stories. For a steeper $\theta_{i} - \alpha_{S}$ the collapse capacity dispersion decreases, because the structures are more prone to collapse and less dependent on RTR variability. For instance, for $IM_{opt}$ the nine-story structure with $\theta_{i} - \alpha_{S} = 0.03$ exhibits dispersion $\beta = 0.58$, for $\theta_{i} - \alpha_{S} = 0.40$ it decreases to $\beta = 0.30$, as can be seen in Fig. 6e. Also, for SDOF frames with a large negative post-yield stiffness ratio, the efficiency enhancement related to $IM_{opt}$ is most pronounced: for $\theta_{i} - \alpha_{S} = 0.40$ the dispersion for $IM_{opt}$ is only 48% of the dispersion based on IM $S_{a} (T_{1} )$, see Fig. 6d. For this structural configuration the dispersion based on the single-target IM $S_{a} (T_{1}^{P\Delta } )$ is of the same order as for IM $S_{a} (T_{1} )$. On average the reduction of the dispersion based on $IM_{opt}$ is about 20% compared to benchmark IM $S_{a} (T_{1} )$.

The effect of different fundamental periods of vibration in 1-, 9-, and 18-story frames is presented in Fig. 6g, h, i, respectively. The parameter $\theta_{i} - \alpha_{S} = 0.20$ is constant, and periods $T_{1}$ between 0.5 and 4.0 s spaced at 0.5 s in the three frame sets. Figure 6g, h, i show that the dispersion is not significantly affected by period $T_{1}$. More important for dispersion is the number of stories. While for one-story structures and $IM_{opt}$ the variability $\beta$ fluctuates around 0.20, for the nine-story and 18-story frames it is on average 0.28. According to Fig. 7g, h, i the efficiency enhancement of $IM_{opt}$ with respect to IM $S_{a} (T_{1} )$ does not follow a uniform trend. However, it is more pronounced for SDOF systems than for the multi-story frames, as discussed before. The collapse capacity dispersion associated with IM $S_{a} (T_{1} )$ is similar to outcomes reported in the literature. For instance, Haselton et al. (2011) obtained for a set of thirty 1- to 20-story RC frame structures collapse capacity dispersions based on IM $S_{a} (T_{1} )$ between 0.36 and 0.48. In the studies of Lazar and Dolšek (2014a, b) the collapse capacity dispersion of six RC frames varied from 0.35 to 0.44. As it can be observed from Fig. 6, in the current study the $S_{a} (T_{1} )$ related collapse capacity dispersions vary in a larger bandwidth, from $\beta$ = 0.27 (N = 1, T = 0.50 s, $\theta_{i} - \alpha_{S} = 0.20$) to $\beta$ = 0.64 (N = 18, $T_{1}$ = 3.5 s, $\theta_{i} - \alpha_{S} = 0.03$). It must be noted here that in particular the structural configuration corresponding to the upper bound dispersion is not realistic. However, when narrowing down the comparison to generic frames with similar fundamental periods and number of stories, and moderate stiffness ratios, the bandwidth of variation becomes smaller [i.e., from 0.27 (N = 1, T = 0.50 s, $\theta_{i} - \alpha_{S} = 0.20$) to 0.42 (N = 18, $T_{1}$ = 2.0 s, $\theta_{i} - \alpha_{S} = 0.20$)] and agrees better with the ones of Haselton et al. (2011) and Lazar and Dolšek (2014a,b).

Subsequently, it is investigated whether the findings for material non-deteriorating P-delta vulnerable frames can be transferred to structures that are also exposed to rapid material deterioration, as defined in Table 1. Figure 8 shows the collapse capacity dispersion for similar generic frames to those of Fig. 6, but with rapid deterioration of strength and stiffness. A comparison of the outcomes of these two figures reveals that the general trend of $\beta$ with respect to the number of stories N, negative post-yield stiffness ratio $\theta_{i} - \alpha_{S}$, and fundamental period $T_{1}$ is the same.

Fig. 8

Dispersion of the collapse capacity for nine frame sets with parameters as specified. Rapid material deterioration. Benchmark IM $S_{a} (T_{1} )$, IM $S_{a} (T_{1}^{P\Delta } )$, one IM considering period elongation, one IM considering both period elongation and higher mode effects as specified, and “optimal” IM $IM_{opt}$. FEMA P-695-FF record set

Moreover, the superior efficiency of $IM_{opt}$ is confirmed. However, the magnitude of $\beta$ becomes (much) smaller compared to the non-deteriorating counterparts, in particular, if the negative post-yield stiffness ratio is small, i.e., $\theta_{i} - \alpha_{S} = 0.03$. For instance, for the first frame set, whose results are shown in Figs. 6a and 8a, consideration of rapid material deterioration reduces the dispersion $\beta$ by 50% compared to the non-deteriorating systems.

Another important observation is that the efficiency of $IM_{opt}$ with respect to the benchmark IM $S_{a} (T_{1} )$ is significantly improved. The corresponding plots of the collapse capacity ratios of Fig. 9 show that the efficiency enhancement is on average about 30%, compared to 20% for non-deteriorating frames, see Fig. 7.

Fig. 9

Dispersion of the collapse capacity based on alternative IMs over the dispersion for benchmark IM $S_{a} (T_{1} )$. Nine frame sets with parameters as specified. Rapid material deterioration. FEMA P-695-FF record set

The three-dimensional bar plots of Figs. 10 and 11 provide a global overview of collapse capacity dispersion and its trends with respect to period $T_{1}$, number of stories N and negative post-yield-stiffness ratio $\theta_{i} - \alpha_{S}$. Figure 10 shows the dispersion based on IMs $S_{a} (T_{1} )$ and $IM_{opt}$ for a set of rapidly deteriorating frames with $\theta_{i} - \alpha_{S} = 0.20$ as a function of period $T_{1}$ and number of stories $N$. Additionally, the dispersion ratio for these two IMs is depicted. The structures of Fig. 11 have a period of $T_{1} = 3.5\;{\text{s}}$, and the dispersion is plotted against $\theta_{i} - \alpha_{S}$ and $N$. As observed before, there is a general trend of larger dispersion with increasing N. Also, with increasing period $T_{1}$ the dispersion increases in most cases, however, not uniformly. With respect to the negative post-yield stiffness ratio, a coherent trend can be observed.

Fig. 10

Dispersion of the collapse capacity for 72 frames with $\theta_{i} - \alpha_{S} = 0.20$ plotted against the number of stories and the fundamental period. a IM $S_{a} (T_{1} )$, b IM $IM_{opt}$, c dispersion ratio. Rapid material deterioration. FEMA-P695-FF set

Fig. 11

Dispersion of the collapse capacity for 64 frames with $T_{1} = 3.50\;{\text{s}}$ plotted against the number of stories and the negative post-yield stiffness ratio. a IM $S_{a} (T_{1} )$, b IM $IM_{opt}$, c dispersion ratio. Rapid material deterioration. FEMA-P695-FF set

In a final efficiency study the material deteriorating frame sets are subjected to the 40 ordinary ground motions of the LMSR-N record set. In Fig. 12 the corresponding dispersion parameter $\beta$ of the collapse capacities are depicted. Comparing these results with the outcomes of the same frame set subjected to the records of the FEMA P-695-FF bin presented in Fig. 8, shows that the findings based on the FEMA P-695-FF bin can be generalized to other ground motion sets with similar overall properties. For all frames the general trend of the collapse capacity in magnitude and efficiency is similar for the FEMA P-695-FF and the LMSR-N ground motions. Detailed inspection reveals that $IM_{opt}$ is for LMSR-N record set slightly more efficient than for the FEMA P-695-FF record set.

Fig. 12

Dispersion of the collapse capacity for nine frame sets with parameters as specified. Rapid material deterioration. Benchmark IM $S_{a} (T_{1} )$, IM $S_{a} (T_{1}^{P\Delta } )$, one IM considering period elongation, on IM considering both period elongation and higher mode effects as specified, and “optimal” IM $IM_{opt}$. LMSR-N record set

From the entire efficiency study it can be concluded that $IM_{opt}$ is both efficient for SDOF and MDOF systems vulnerable to P-delta.

7 Sufficiency study

The trend and magnitude of $\beta$ for the FEMA-P695-FF and the LMSR-N bin is similar, and thus it provides first evidence of sufficiency of the discussed IMs, because the ground motion parameters of these sets are different.

Subsequently, the sufficiency of the evaluated IMs at collapse capacity is examined for the testbed structures subjected to FEMA P-695-FF ground motions. Sufficiency is examined against several ground motion parameters, such as earthquake magnitude, $M_{w}$, and the Joyner-Boore distance $R_{JB}$. As discussed in Kazantzi and Vamvatsikos (2015a), in the collapse limit state of a structure it is advantageous to check the sufficiency based on the IM given EDP. Consequently, this study relies on a standard linear regression of the natural logarithm of the collapse capacities, $\ln CC_{i}$, with the considered ground motion parameters according to (e.g., Eads et al. 2015),

$$E[\left. {\ln CC_{i} } \right|M_{w} = x] = a_{1} + b_{1} x,\quad E[\left. {\ln CC_{i} } \right|R_{jb} = y] = a_{2} + b_{2} y$$

(11)

where x (y) is the value of $M_{w}$ ($R_{JB}$), $a_{1}$ ($a_{2}$) and $b_{1}$ ($b_{2}$) are the regression coefficients, and $E[\left. {\ln CC_{i} } \right|M_{w} = x]$ ($E[\left. {\ln CC_{i} } \right|R_{jb} = y]$) is the expected value of $\ln CC_{i}$ given x (y). For each IM and each structural configuration slopes $b_{1}$ and $b_{2}$ are identified. In the present study, a hypothesis test is conducted, applying the null hypothesis that $b_{1} (b_{2} ) = 0$ (i.e., the expected value of $\ln CC_{i}$ does not depend on x (y)). The decision about whether the null hypothesis can be rejected at some predefined significance level is based on the so-called p value. The p-value is the probability of observing a $b_{1} (b_{2} )$ value at least as large as the $b_{1} (b_{2} )$ value found by the regression given that the true value of $b_{1} (b_{2} )$ equals 0. Here, a 5% significance value is utilized to judge the sufficiency of the IMs (Eads et al. 2015; Tsantaki et al. 2017). This means that a p-value less than 0.05 leads to a rejection of the null hypothesis, and the IM is deemed not sufficient with respect to the ground motion parameter of interest (Eads et al. 2015). However, a non-rejection of the null hypothesis is not equivalent to an acceptance of it. Recently Kazantzi and Vamvatsikos (2015a) conducted a more elaborated sufficiency study on IMs based on the geometric mean concept.

Tables 3 and 4 summarize the results of the sufficiency evaluations of the 2048 analyzed P-delta vulnerable generic frame structures for different material deterioration levels. In Table 3 for each considered IM the percentage of structures with p-values greater or equal 0.05 for the relationship of the collapse intensity and magnitude $M_{w}$ is presented. It is observed that for IMs $S_{a} (T_{1} )$, $S_{a} (T_{1}^{P\Delta } )$, and $IM_{opt}$ at least 91% of the structures exhibit p values $\ge$0.05, suggesting that these IMs are sufficient with respect to the earthquake magnitude $M_{w}$. It is furthermore indicated that the sufficiency performance of IM $S_{a,gm} (T_{1} ,1.6T_{1} )$ is less satisfactory, because only 84% of the frames exhibiting rapid material deterioration pass the test. The results summarized in Table 4 show that also sufficiency of all studied IMs with respect to the Joyner-Boore distance is indicated.

Table 3 Percentage of structures with p values $\ge$0.05 for the relationship between collapse capacity and magnitude $M_{w}$ based on IMs as specified. FEMA-P695-FF ground motion set

Table 4 Percentage of structures with p values $\ge$ 0.05 for the relationship between collapse capacity and distance $R_{jb}$ based on IMs as specified. FEMA-P695-FF ground motion set

8 Conclusions

This research proposes an “optimized” average spectral acceleration based intensity measure (IM) for P-delta vulnerable frames, which leads to the smallest RTR collapse capacity dispersion. The optimized IM, $IM_{opt}$, includes for first time a flexible lower limit for the period interval in which the average spectral pseudo-acceleration, $S_{a,gm}$, is computed. A parametric study has been carried out considering a set of 2048 generic moment resisting frames subjected to two ground motion sets to account for the effect of record-to-record (RTR) variability on collapse capacity uncertainty. Several “average” IMs based on the geometric mean of $S_{a,gm}$ over a certain period interval are evaluated. These average IMs have different lower and upper bounds for the period interval. The lower bound is usually smaller than the fundamental period of vibration ($T_{1}$) to account for the influence of higher modes, and the upper bound is larger than $T_{1}$ to consider period elongation due to structural nonlinear behavior. However, the use of a fixed lower bound (e.g. 0.2 $T_{1}$) increases the dispersion of systems in which higher mode effects are smaller, or nonexistent, like SDOF systems. The $IM_{opt}$ flexible lower bound period corresponds to the structural period associated with the exceedance of 95% of the cumulative effective modal mass. The efficiency of the evaluated IMs to reduce collapse capacity dispersion due to RTR variability, and their sufficiency with respect to ground motion parameters is compared to two single target spectral IMs: the 5% damped spectral pseudo-acceleration $S_{a} (T_{1} )$ and $S_{a} (T_{1}^{P\Delta } )$ at the elastic fundamental period with and without consideration of gravity loads, $T_{1}$ and $T_{1}^{P\Delta }$, respectively. The following conclusions can be drawn:

• The “optimal” upper bound of the period interval for the geometric mean IM is about 1.6 times the system period without consideration of gravity loads. The period elongation is a result of large inelastic deformations and gravity loads. This upper bound applies to one-story and multi-story systems.

• For SDOF systems the “optimal” lower bound of the period interval corresponds precisely to the SDOF period of vibration. In multi-story structures, however, a lower bound period interval shorter than $T_{1}$ (e.g. 0.2$T_{1}$, 0.4$T_{1}$) increases the IM efficiency because higher mode effects are taken into account.

• Consequently, an “optimal” IM, $IM_{opt}$, is defined based on a flexible lower bound period corresponding to the structural period associated with the exceedance of 95% of the total effective mass: $IM_{opt} = S_{a,gm} (T_{0.95M} ,1.6T_{1} )$. This allows a consistent representation of an IM, both “optimal” for SDOF and MDOF systems.

• “Average” IMs with a period interval that only considers higher mode effects (no period elongation) increases the collapse capacity dispersion.

• For material non-deteriorating systems $IM_{opt}$ is on average about 20% more efficient than the traditional benchmark IM $S_{a} (T_{1} )$. For structures subjected to material deterioration the efficiency of $IM_{opt}$ increases on average up to 30%.

• For non-deteriorating systems with a small negative stiffness ratio $\theta_{i} - \alpha_{S} = 0.03$ the efficiency enhancement of IM $IM_{opt}$ compared to IM $S_{a} (T_{1} )$ is minor.

• A larger $\theta_{i} - \alpha_{S}$ and the consideration of material deterioration reduce the collapse capacity dispersion. In both cases, the systems become more prone to collapse and less dependent on RTR variability.

• Analyses based on IMs $S_{a} (T_{1} )$ and $IM_{opt}$ show that the collapse capacity dispersion due to RTR variability increases with a longer fundamental period.

• As the number of stories increases, the collapse capacity dispersion increases due to the contribution of the higher modes.

• For material non-deteriorating frames and the FEMA-P695-FF record set, $IM_{opt}$ exhibits a bandwidth of dispersion between 0.092 ($T = 3.0\;{\text{s}}$, $N = 1$, $\theta_{i} - \alpha_{S} = 0.4$) and 0.78 ($T = 4.0\;{\text{s}}$, $N = 18$, $\theta_{i} - \alpha_{S} = 0.03$). In the case of the single-target IM $S_{a} (T_{1} )$, the dispersion limits are between 0.26 ($T = 0.5\;{\text{s}}$, $N = 9$, $\theta_{i} - \alpha_{S} = 0.3$) and 0.82 ($T = 4.0\;{\text{s}}$, $N = 18$, $\theta_{i} - \alpha_{S} = 0.03$).

• For material deteriorating frames and the FEMA-P695-FF record set, $IM_{opt}$ exhibits a bandwidth of dispersion between 0.095 ($T = 3.0s$,$N = 1$,$\theta_{i} - \alpha_{S} = 0.4$) and 0.37 ($T = 2.0\;{\text{s}}$, $N = 18$, $\theta_{i} - \alpha_{S} = 0.03$). For IM $S_{a} (T_{1} )$ the dispersion is between 0.25 ($T = 4.0\;{\text{s}}$, $N = 1$, $\theta_{i} - \alpha_{S} = 0.03$) and 0.44 ($T = 4.0s$, $N = 20$, $\theta_{i} - \alpha_{S} = 0.03$).

• Magnitude of trends of the collapse capacity dispersion and its efficiency with respect to the characteristic structural parameters was confirmed utilizing two different ground motion sets with similar far-field ground motion characteristics. Then, the results of this study need to be corroborated for records with other characteristics, such as near-field and long-duration records.

• The “optimal” $IM_{opt}$ and benchmark IM $S_{a} (T_{1} )$ meet the sufficiency criterion, and are adequate to compute the collapse limit state of the considered structures.

The results and conclusions of this study are valid only for P-delta vulnerable hysteretic systems, where the post-capping range of deformation is not attained.