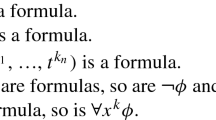Existential Quantifier and Ontological Pluralism

Abstract

Within the context of the debate between ontological monists and pluralists the paper discusses a number of argumentative strategies that the latter can apply to answer the “there can be only one” argument. I show here that the reply to this argument suggested by J. Turner has its disadvantages and suggest a number of adjustments thereof. In particular, I develop a concept of domain-specific quantifiers that allow the pluralist to elaborate his or her ontological position.

1 Introduction

It is currently the standard view in analytical philosophy that existence can be adequately captured by means of the existential quantifier of formal logic. In consequence philosophers usually accept ontological monism, which has it that “existence” is univocal. After all, one, well-defined, logical symbol cannot express different ways of existence. If you are not persuaded by this argumentative metaphor, there is one or two arguments that purport to show the untenability of the ontological pluralism. In his recent papers Jason Turner demonstrated how the main available arguments of this sort can be answered by the ontological pluralist (Turner 2010). I will focus here on the so-called “there can be only one” argument and the reply Turner recommends for the pluralist. I will argue that (1) Turner’s solution implies a number of consequences that the ontological pluralist may not be willing to accept and that (2) there is an alternative, “epistemologically cheaper”, position the pluralist may take in order to meet the argument.

2 The “There Can be Only One” Argument

The “there can be only one” argument (aka the argument here) is to show the untenability of the pluralist’s craving for multiple existential quantifiers, say just two: “$\exists _1$” and “$\exists _2$”. This need is based on a more general requirement to speak in a metaphysically perspicuous way, i.e., to make it plain what the reality ultimately is. In the case of the pluralist this principle implies the requirement that we should be able to state that objects from different ontological categories exist in different ways—for example to state the difference between existence of lakes and the existence of inaccessible cardinal numbers. The ontologist intends to make this difference explicit by means of the conceptual tools at hand.

The argument shows that “$\exists _1$” is equivalent to “$\exists _2$” (in the sense to be explained below), so the difference therebetween, if any, is not enough to support ontological pluralism. If there exist abstract objects and there exists concrete particulars, then the former exists in the same way as the latter.

In my opinion the most crucial implicit assumption of the argument concerns the meaning of the equivalence in question. Suppose that there is a language L whose alphabet contains both “$\exists _1$” and “$\exists _2$”, and predicate “A”. Suppose also that the pluralist employs a consequence relation “$\vdash$” (over L) to say what entails what. Now “$\exists _1$” is assumed to be equivalent to “$\exists _2$” iff $[\exists _1 x ~A(x) \vdash \exists _2 x ~A(x)]$ and $[\exists _2 x~ A(x) \vdash \exists _1 x ~A(x)]$.

The explicit assumption of the argument claims that if “$\exists _1$” and “$\exists _2$” were existential quantifiers, then the rules of inference we know from classical logic should be valid also for them. In particular, the rule existential generalisation—state as 1 below—and the rule of existential instantiation—2—would be valid for both.

• 1. $\varPhi (a) \vdash \exists _i x ~\varPhi (x)$.

• 2. If $\varDelta ,\varPhi (a) \vdash \psi$ and “a” does not occur in $\varPhi (x)$ or in any formula from $\varDelta$, then $\varDelta , \exists _i x~ \varPhi (x) \vdash \psi$, where:

  • (a) “a” is a constant and “$\varPhi (a)$” stands for any propositional expression from L that contains it;

  • (b) “$\varPhi (x)$” stands for any propositional formula from L that contains “x” as a free variable;

  • (c) $\psi \in L$ and $\varDelta \subseteq L$.¹

It can be shown that given these rules “$\exists _1$” is equivalent to “$\exists _2$”.

Why is this significant for the pluralist? Notice that even if “$\exists _1$” is equivalent to “$\exists _2$”, one can still maintain that “$\exists _1 x~ A(x)$” means something different than “$\exists _2 x~ A(x)$”, so the pluralist can still speak about two modes of existence using these quantifiers. Consider the following analogue. Again let L be a language of first-order predicate logic. Suppose we define in L the relation of (syntactic) consequence “$\vdash$“ by means of, say, any complete Hilbert-style axiomatisation of classical logic. And suppose that “$\vDash$” denotes the relation of semantic consequence for this logic. Since we can prove that $\vdash \phi$ if and only if $\vDash \phi$, so “$\vdash$“ is equivalent to “$\vDash$“ in the sense analogous to the sense defined above. But this fact does not make “$\vdash$“ and “$\vDash$“ synonyms: “$\vdash \phi$” means something different than “$\vDash \phi$”. Analogously, “$\exists _1 x~ A(x)$” may mean something else then “$\exists _2 x ~A(x)$” despite the fact that $\exists _1 x~ A(x) \vdash \exists _2 x~ A(x)$ and $\exists _2 x ~A(x) \vdash \exists _1 x ~ A(x)$.

If “$\exists _1$” and “$\exists _2$” are not proved to be synonyms, why should the pluralist be bothered by their equivalence? Turner answers rather succinctly:

If the pluralist’s quantifiers are indeed provably equivalent, she is in trouble: if whatever one quantifier ranges over is also ranged over by the other, she will find it hard to justify the claim that we really have two ways of being here. (Turner 2010, p. 25)

As it stands, this remark needs some more elaboration because, prima facie, the argument has the proof-theoretic nature and the aforementioned role of the quantifier is semantic and may be traced back to the respective satisfaction condition. However, the argument also shows that for any constant $b\in L$,

$$\exists _1 x ~x=b \vdash \exists _2 x ~ x=b$$

and

$$\exists _2 x ~ x=b \vdash \exists _1 x ~ x=b.$$

Then following the route set by W. van O. Quine (in: van Orman Quine 1969) we can show that b exists$_1$ if and only if b exists$_2$, which consequence undermines the tenability of ontological pluralism. At best the pluralist can maintain then that any object enjoys all modes of existence, which, for some reason or other, are nevertheless different from one another.

Turner argues that in order to refute the argument the ontological pluralist may need to reject the explicit assumption and claim that the rules of existential generalisation and existential instantiation are not necessary for being a quantifier. He recommends that the pluralist replace them with the following counterparts:

• 3. $\varPhi (a), \exists _i x ~x=a \vdash \exists _i x ~\varPhi (x)$.

• 4. If $\varDelta , \varPhi (a), \exists _i x ~x=a \vdash \psi$ and “a” does not occur in $\varPhi (x)$ or in any formula from $\varDelta$, then $\varDelta , \exists _i x ~\varPhi (x) \vdash \psi$.²

Given these rules it can be shown that “$\exists _1$” is not equivalent to “$\exists _2$”.

3 The Argument’s Aftermath

In this section I would like to argue that accepting this line of defence the pluralist has to pay a hefty epistemological price. Namely, he or she needs to give up the fundamental principles of classical logic that concern quantifiers. For instance, he or she cannot reason any longer: “$A(a) \vdash \exists _i A(x)$” (for any i!). In particular, the following inference is no longer valid:

Jason is an ontological pluralist.

therefore:

There $\hbox {exists}_i$ someone who is an ontological pluralist.

The general issue at stake has a different, more devastating, exemplification. Let us assume that our pluralist requires two existential quantifiers: “$\exists _A$” and “$\exists _P$” to make explicit his or her belief that there are two kinds of existence: “$\exists _A$” characterises the way in which any abstract object exists and “$\exists _P$” characterises the mode of existence specific to the particular entities. Then, 3 and 4 do not support the validity of the following inference:

The empty set is an abstract object.

therefore:

There exist$_A$ abstract objects.³

The general issue is then that Turner’s solution conceals the conceptual links between the ontological categories and the ways of existence associated with them. This makes them inaccessible to the pluralist. So although the pluralist’s quantifiers are meant to range over the extensions of some, perhaps the most fundamental or general, predicates, this intention is not expressible in the language.

It seems then that the new rules, although making enough room for any number of quantifiers, deprive them of their basic conceptual capabilities required both by the monist and by the pluralist. In what follows I intend to show that if such consequences are too revisionary for the pluralist, he or she may adopt a different strategy to refute the argument.

4 Domain Specific Quantifiers

If the main goal of the pluralist is to show that different ontological categories exhibits different modes of existence and if he or she persists in expressing this difference by means of existential quantifiers, then the solution to the problem revealed by the argument seems to be obvious. The pluralist should use the domain specific quantifiers: say “$\exists _A$” for the category of abstract objects, “$\exists _P$” for the category of particular objects, etc., where the formula “$\exists _A B(x)$” means “There abstractly exist objects that are B”.⁴

In order to introduce such quantifiers I employ the following domain-specific rules for existential generalisation 5 and the existential instantiation the latter by means of two schemata 6 and 7

• 5. $\varPhi (a), \varPsi (a) \vdash \exists _\varPsi x~ \varPhi (x)$.

• 6. If $\varDelta$, $\varPhi (a) \vdash \psi$ and “a” does not occur in $\varPhi (x)$ or in any formula from $\varDelta$, then $\varDelta$, $\exists _\varPsi x~ \varPhi (x) \vdash \psi$.

• 7. If $\varDelta$, $\varPsi (a) \vdash \psi$ and “a” does not occur in any formula from $\varDelta$, then $\varDelta , \exists _\varPsi x \varPhi (x) \vdash \psi,$⁵ where besides the conventions mentioned earlier:

  • (a) “$\varPsi (a)$” is an atomic propositional formula built by means of the predicate represented by “$\varPsi$” and the constant “a”.

It is easy to verify that “$\exists _\varPhi$” is not equivalent to “$\exists _\varPsi$” provided that $\not \vdash [\forall _{\varPhi } x~ \varPhi (x) \equiv \varPsi (x)]$ and $\not \vdash \forall _\varPsi x~ [\varPhi (x) \equiv \varPsi (x)]$.⁶ Also 6 implies that $\varPsi (a) \vdash \exists _\varPsi x \varPsi (x)$, so the “empty-set reasoning” mentioned above is now valid. The first reasoning may be also validated if we consider it as an enthymeme with an implicit assumption to the effect that Jason is, say, a particular. Then we can render it as:

Ontological$\_$Pluralist(Jason), P(Jason) $\vdash \exists _P x$ Ontological$\_$Pluralist(x),

which is an exemplification of 5. Incidentally, note that $\forall _\varPsi x [\varPhi (x) \rightarrow \varPsi (x)] \wedge \varPhi (a) \vdash \exists _\varPsi \varPhi (x).$

Obviously, “$\varPhi (a) \vdash \exists _\varPsi \varPhi (x)$” does not represent a valid inference, but this is what the pluralist should expect. After all, it may happen that “$\varPhi$” represents an ontological category whose instance do not exhibit the mode of existence represented by “$\exists _\varPsi$”.

I should emphasise that rules 5–7 should be considered in the context of the language which the pluralist uses for the sake of his or her ontological research (denoted here by “L”). I take it for granted that this assumption defines the list of predicates that can occur in the predicate position of the quantifiers at stake. For instance, rules 5–7 are to be understood in such a way that “$\varPsi$” ranges only over such predicates.

Without this constraint one can show that

$$\exists _\varPsi x \varPhi (x) \vdash \exists _\varPhi x~ \varPsi (x)$$

and

$$\exists _\varPhi x \varPsi (x) \vdash \exists _\varPsi x~ \varPhi (x)$$

provided that both “$\varPhi$” and “$\varPsi$” are atomic predicates.

Within the current framework we can block such inferences by constraining the language in such a way that, say, “$\exists _\varPhi x~ \varPsi (x)$” is not a well-formed formula. I propound that each predicate that performs such role within a given language be called a domain predicate and its quantifier be dubbed as domain specific.⁷

5 Beyond Domain Specific Quantifiers

Is the difference between the standard quantifier of the first-order logic and the pluralist’s quantifiers substantial enough to separate ontological monism from ontological pluralism? To answer this question, I will compare the respective Tarskian satisfaction conditions for the quantifiers in question.

Let L be a first-order language with the standard quantifier “$\exists$” and let Q be a set of Turner’s quantifiers $\{\exists _1, \exists _2, \dots \}$. Suppose that $M = <D, I>$ is a model for language L and let v be a variable assignment in this model. The quantifier for the monist is defined in the usual way:

• 8. $M, v \vDash \exists x \phi$ iff for some variable assignment $v'$ that differs from v at most at “x”: $M, v' \vDash \phi$.

To characterise Turner’s quantifiers, we need a mapping d from Q to a subset D of the powerset of D. Having this mapping in place we can state:

• 9. $M, v \vDash \exists _i x \phi$ iff for some variable assignment $v'$ that differs from v at most at “x” and such that $v'(x) \in d(\exists _i), M, v'\vDash \phi$.

Condition 9 is a slight modification of the clause ($\forall _i$ T) from (Turner 2012, p. 432). In the basic system there, dubbed “Ontologically Plural and Free”, variable assignments are restricted so that $v(x) \in \bigcup \{d(\exists _i) : \exists _i \in Q\}$. This restriction may be dropped by the pluralist, which results in another system described there.

In the case of my domain specific quantifiers set Q contains quantifiers indexed by a subset of unary predicates of L, e.g., $Q=\{\exists _A, \exists _B, \dots \}$. Then we do not need the mapping d to state the satisfaction conditions:

• 10. $M, v \vDash \exists _\varPsi x \varPhi (x)$ iff for some variable assignment $v'$ that differs from v at most at “x” and such that $v'(x) \in I(\varPsi ), M, v' \vDash \phi$.

Obviously, when for every predicate “$\varPsi$”, $I(\varPsi )=D$, 10 is equivalent to 8.

It can be easily shown that 10 matches rules 5–7 in the sense that they are sound with respect to the relation of semantic consequence the former defines.

If we assume that these conditions provide sufficient descriptions of the respective quantifiers, then the difference between 8 and 9 (or 10) boils down to the difference in the scope of variable assignments. Ultimately the difference concerns a set of objects over which the quantifier ranges over: the pluralist’s quantifiers range over (proper) subsets of those objects over which the standard quantifier ranges over. In other words, the difference between ways of being amounts to the difference between the extensions of the respective ontological categories: the abstract way of existence boils down to falling under the category of abstract objects, the particular way of existence boils down to falling under the category of particular objects, etc. Although not being viciously circular this account implies that a way of existence is something brute: the abstract way of existence is the way of existence enjoyed by abstract objects, the particular way of existence is the way of existence enjoyed by particular objects, etc.

Now there are many strains of ontological pluralism as Ben Caplan has recently demonstrated (Caplan 2011). Some of them, e.g., Russell’s distinction between being and existence, may not require more sophisticated quantifiers than those characterised by 1–2 (or my 5–7). Other views, however, may imply that the difference between two modes of existence cannot be adequately expressed in the set-theoretical terms. The meaning of mode of existence is far too rich for such simple definitions. Turner envisages this objection and says:

[...] models in logic ostensibly have a different job: investigating the nature of logical consequence, given inferential constraints on logical terms. Not assigning meanings. (Turner 2012, p. 433)

But even if you accept this metalogical position, you may wonder whether it is possible to provide a more accurate formal account of the difference between modes of existence. In other words, can we modify the model-theoretic semantics so that it will correspond more closely to a given pluralist’s viewpoint?

One possibility to be considered here concerns a way in which a quantifier ranges over a set of objects. Suppose that the ontological pluralist intends to express a position that the domain of artefacts, as opposed to the domain of other concrete objects, exhibits a peculiar type of existence. The existence of the latter is peculiar because it somehow involves ontological dependence between pairs of objects: a constituting natural object, e.g., a piece of matter, and a constituted artefact. It may happen that when constituting objects spatiotemporarily coincide with constituted objects, some proper names we use within this domain refer not to single objects but indiscriminately denote two objects. For instance, “Michelangelo’s David” may refer both to a piece of marble, i.e., a constituting object, and to a statue, i.e., a constituted object. Then in certain contexts the so-called paradoxes of material constitution may arise. On the other hand, the domain of the natural is, supposedly, free from this semantic ambiguity and each proper name in this domain, e.g., “Moon”, denotes exactly one particular. Following Schaffer (2009) I generalise the relation of constitution to the relation of dependence. This is to say, I will investigate those theories of logical pluralism that imply that the notion of mode of existence can be defined in terms of the notion of ontological dependence. Schaffer seems to claim that the ontological system of Aristotle may belong to this group. Another ontologist worth to be mentioned in this context is Ingarden (2013)

Is it possible then to incorporate the notion of ontological dependence as a component of the satisfaction condition for quantifiers of logic? In what follows I will exemplify a positive answer to this question. Namely, I will stipulate that the quantifier specific to a given domain of dependent objects does not range over single objects from this domain but ranges over (ordered) pairs of such objects, where the first element is a dependent object and the second is an object on which the former depends (“depending object”). For the sake of uniformity I will let the quantifier range over reflexive couples ($<x, x>$) when its domain contains only independent objects. Since this is just a preliminary attempt, I will make a number of simplifying assumptions.

First, each object is assumed to depend on at most one object. Secondly, all objects from each domain exhibit the same type of dependence relations:

• 11. All objects from one domain are either independent (from any other object) or depend on objects that belong to one and the same domain.

So the instance-level relation of dependence is represented at the level of domains: one domain depends on another if every object from the former depends on some object from the latter. Thirdly, following most accounts of ontological dependence, I take it for granted that the relation of dependence is asymmetric. Finally, I will focus only on unary predicates, i.e., I will outline the satisfaction conditions for formulas built out of unary predicates. Note that even if these assumptions are relaxed, the resulting theory of quantifiers may still oversimplify the tenets of your favourite version of ontological pluralism.

In order to capture these assumptions, we need a deeper modification of the pluralist’s toolbox than the adjustments required by 1–2 (or my 5–7). First we need another change to our thinking about quantifiers. Instead of the domain specific quantifiers I propound that we should resort to dependence specific quantifiers, where the dependence relation will be represented by couples <dependent domain, depending domain>. For instance, if you want to refer to the mode of existence exhibited by Michelangelo’s David, you should use the quantifier, say, “$\exists _{Art, Nat}$”, where “Art” stands for the domain of artefacts and “Nat” stands for the domain of natural objects.

Let L be a unary first-order language whose domain specific quantifiers are included in set Q=$\{\exists _{A_1, B_1}, \exists _{A_2,B_2}, \dots \}$. In what follows it will be convenient to use the following abbreviation:

• 12. $\varDelta = \{\varPsi _1 : \exists _{\varPsi _1, \varPsi _2} \in Q \vee \exists _{\varPsi _2, \varPsi _1} \in Q\}$.

Let D be a non-empty set. The function of interpretation I is now a mapping from the union of L’s set of individual constants and L’s set of predicates such that (i) if $\alpha$ is a constant, then $I(\alpha ) \in D \times D$ and (ii) if $\alpha$ is a predicate, then $I(\alpha ) \subseteq D \times D$. In addition let $\delta$ be an endomorphism on $\varDelta$ whose role is to represent the dependency relation between domains, so “$\delta (\varPsi _1)= \varPsi _2$“ means that the domain denoted by predicate “$\varPsi _1$” depends on the domain represented by predicate “$\varPsi _2$”. If the domain denoted by “$\varPsi$” contains independent objects, then $\delta (\varPsi )=\varPsi$. Since the relation of dependence is assumed to be asymmetric, it holds that

• 13. if $\delta (\varPsi$)=$\varPsi$, then $\delta (\delta (\varPsi$))=$\varPsi$.

Furthermore, in order to meet condition 13 we need also:

• 14. If $\varPsi \in \varDelta$ and $<i, j> \in I(\varPsi )$, then for some $k \in D, <j, k> \in I(\delta (\varPsi ))$.

A model M for language L is now a triple $<D, I, \delta>$. A variable assignment, v, in this model is a mapping from the set of L’s variables to $D \times D$. I will say that variable assignment v$\varPsi$-differs from variable assignment $v'$ at most at “x” if v(“x”$) \in I(\varPsi )$ and for every other variable “y”, $v(y)=v'(y)$.

• 15. $M, v \vDash \varPhi (a)$ iff I(“a”$) \in I(\varPhi )$.

• 16. $M, v \vDash \varPhi (x)$ iff v(“x”$) \in I(\varPhi )$.

• 17. $M, v \vDash \exists _{\varPsi _1, \varPsi _2} x ~\phi$ iff $\varPsi _2=\delta (\varPsi _1)$ and for some variable assignment $v'$ that $\varPsi _1$-differs from v at most at “x”, $M, v' \vDash \phi$.

Having these conditions in place one can define the relation of semantic consequence $\vDash$ in the usual way.

It can be easily shown that the above model-theoretic characteristic matches rules 18–20 in the sense that the rules are sound with respect to $\vDash$.

• 18. $\varPhi (a), \varPsi _1(a) \vdash \exists _{\varPsi _1, \varPsi _2} x~ \varPhi (x)$, for some predicate “$\varPsi _2$”.

• 19. If $\varDelta , \varPhi (a) \vdash \psi$ and “a” does not occur in $\varPhi (x)$ or in any formula from $\varDelta$, then $\varDelta$, $\exists _{\varPsi _1, \varPsi _2} x~ \varPhi (x) \vdash \psi$.

• 20. If $\varDelta , \varPsi (a) \vdash \psi$ and “a” does not occur in any formula from $\varDelta$, then $\varDelta , \exists _{\varPsi _1, \varPsi _2} x~ \varPhi (x) \vdash \psi$ , for some predicate “$\varPsi _2$”.

Moreover, clause 20 is equivalent to 10 when for each predicate “$\varPsi$” from $\varDelta$, it holds that $\delta (\varPsi )=\varPsi$ (and provided that we use only such dependence specific quantifiers as “$\exists _{\varPsi , \varPsi }$”).

6 Conclusions

Although the idea of quantification we find in formal logic does not quite fit the philosophical intuitions of the ontological pluralist, it is possible to adjust the classical notion of existential quantifier and one can still claim that “We may indeed take “$\exists x~ x=a$” as explicating “a exists”” (van Orman Quine 1969, p. 94). Nevertheless, the “there can be only one argument” shows that this adjustment comes at a price, which in this case is the loss of the validity of some rules of inference. Then a care is needed so that this loss will be minimised. But when we intend to stay close to the classical notion of existential quantifier, an average ontological pluralism is philosophically too sophisticated to be fully expressible within these limits. On the other hand, if we want to accommodate the pluralist’s intuitions, the resulting formalism appears to be fairly distant from classical logic. This is attested, I hope, by the last example above. Given the peculiar character of this formalism one may doubt then whether the aforementioned standard view on quantification is congruent with these philosophical views that find the notion of existence inseparable from the notion of mode of existence. Perhaps the claim that “existence can be adequately captured by means of the existential quantifier of formal logic” is incongruous with ontological pluralism after all.