A perturbative approach to complexity during dissipative collapse

Abstract

Radiative gravitational collapse is an important and much studied phenomenon in astrophysics. Einstein’s theory of general relativity (GR) is well suited to describing such processes provided closure of the system of nonlinear differential equations is achieved. Within a perturbative scheme, the property of vanishing complexity factor is used in order to complete the description of the radiative, self-gravitating system. We show that a physically viable model may be obtained which reflects the absence of energy inhomogeneities for lower density systems, in contrast to what might be expected for more aggressive collapse processes.

1 Introduction

Gravitational collapse remains an ongoing subject of research due to its many challenging and often exciting implications in relativistic astrophysics. In the seminal paper on gravitational collapse, produced by Oppenheimer and Snyder (1939), the first solution for the non-adiabatic collapse of a spherically symmetric system was found. It is believed that this phenomenon of gravitational collapse plays a fundamental role in shaping the universe by way of its influence on structure formation and destruction. A result of the end state of a collapsing star is the formation of a black hole – a system whose gravity is so strong that nothing can escape from it, and inside which resides a place of infinite density, a place where all laws of physics break down – a singularity. Roger Penrose, in his paper of 1969, famously proposed, by way of what is now known as the Cosmic Censorship Conjecture (CCC), that every singularity in the universe is hidden behind the event horizon of a black hole. He refuted the occurrence of a naked singularity – one that is visible to an outside observer – on the basis that, while naked singularities comply with general relativity, in a physically reasonable situation they will never form. Whilst many researchers agree with Penrose, not all have expressed excitement, with some providing counter-examples to prove the existence of naked singularities (Joshi 1993, 2002; Joshi et al. 2004), and so the CCC remains an open problem.

Discovery of the Vaidya metric (1953) allows for the study of dissipative gravitational collapse. Given that a radiating collapsing mass distribution undergoes loss of energy, its exterior spacetime is no longer a vacuum but contains null radiation. Vaidya obtained an exact solution of the Einstein field equations which describes the exterior field of a radiating spherically symmetric fluid. Santos (1985) derived the first set of junction conditions for a collapsing spherically symmetric shear-free non-adiabatic fluid with heat flow. This pioneering work addressed the question of matching a spherically symmetric interior matter distribution with the exterior Vaidya spacetime, thus paving the way for the study of dissipative gravitational collapse. Early work on radiating models has been considered by many authors, some of which are referenced in this article (Herrera et al. 1989; Chan et al. 1993). Models of collapsing systems have evolved over time, with studies being extended to include aspects such as the cosmological constant (Govender and Thirukkanesh 2009; Thirukkanesh et al. 2012), electromagnetic field (de Oliviera and Santos 1987; Maharaj and Govender 2000) and the presence of non-zero shear (Chan 2000; Naidu et al. 2006) to name a few. In recent studies, for the shear-free case, Paliathanasis et al. (2021) explored the junction condition arising from the matching of a spherically symmetric interior undergoing dissipative collapse to the Vaidya exterior. This boundary condition is a second order non-linear differential equation governing the temporal behaviour of the model. They used the method of Lie symmetries to produce, for the first time, a general solution to this equation.

A system which is initially in static equilibrium may undergo a disturbance or perturbation which is likely to render it dynamic, thus impacting on the stability of that system. Dynamical stability is the characteristic of a system to retain its stable state under perturbation. The dynamical stability of self-gravitating bodies is an important property in modelling, since a static stellar model offers little insight into a study if it proves to be unstable under collapse. Herrera et al. (1989) studied the instability ranges for a non-adiabatic sphere and showed that when relativistic corrections were imposed to address heat flow, the instability range of the model decreased, suggesting that the outcome was a fluid that was less unstable. Chan et al. (1993) investigated the stability criteria by deviating from the perfect fluid configuration in two ways: they considered dissipation in the free-streaming approximation and, secondly, they assumed the fluid to be locally anisotropic. In more recent studies, Govender et al. (2019) conducted research on the influence of an equation of state on the gravitational behaviour of a collapsing star. The study then explored, with great success, the stability ranges in the Newtonian and post-Newtonian regimes using the adiabatic index $\Gamma$, introduced in 1964 by Chandrasekhar (1964), where he showed that for a system to remain stable under collapse, the value of $\Gamma$ must exceed $\frac{4}{3}$. Govender et al. (2021) also examined gravitational collapse of a shear-free radiating star with an initial static core which satisfied the time-independent Karmarkar condition. Invoking a perturbative approach, they were able to find a new radiating model with simple time dependence. In this work, we employ the perturbative method as an inquiry into complexity during radiative collapse.

There have been many attempts at defining complexity in the various fields of science (Kolmogorov 1965; Crutchfield and Young 1989; Anderson 1991; Lopez-Ruiz et al. 1995; Sanudo and Pacheco 2009; de Avellar et al. 2014), with little consensus reached on a specific definition. Herrera (2018) proposed a new definition of complexity for static and spherically symmetric self-gravitating fluid distributions. In this pioneering work, he established a scalar quantity which he referred to as the ‘complexity factor’ denoted by $Y_{TF}$. The complexity factor was obtained by the orthogonal splitting of the Riemann tensor within general relativity. In the analysis conducted by Herrera, he commenced by defining a simplest (least complex) system as one possessing isotropic pressure and homogenous energy density, and for which $Y_{TF}$ vanishes. He then proceeded to show that a complexity factor of value zero may also arise in systems with the properties of pressure anisotropy and energy density inhomogeneity, where these two quantities cancel each other, thus concluding that there existed systems of varying distributions which satisfy the vanishing complexity condition. Starting off with a general spherically symmetric static metric, Contreras and Stuchlik (2022) imposed the condition of vanishing complexity and were able to complete the integration and in doing so, reduced the problem of finding exact solutions to a single-generating metric function. Abbas and Nazar (2018) studied the complexity factor for a static anisotropic self-gravitating system in the $f(R)$ gravity theory. In their findings, the anisotropic pressure and inhomogeneous energy density cancelled each other, and the zero-complexity condition was achieved. Extended gravitational decoupling and complexity were employed to anisotropise the Buchdahl static solution. In order to completely describe the gravitational behaviour of the seed solution and the secondary source, an equation of state and the complexity-free condition were imposed. It was shown that stability of the anisotropic Buchdahl sphere was sensitive to the decoupling parameter (Maurya et al. 2023).

Bogadi and Govender (2022) explored the dynamics of the complexity factor as the collapse of a shear-free radiating sphere proceeded. They were able to show that the complexity factor could, in future work on gravitational collapse, form an essential part in justifying the physical viability of relativistic models. Bogadi et al. (2022) considered the implications of vanishing complexity in radiative self-gravitating fluids of spherical configuration, and found that imposing the constraint of a vanishing complexity results in metric forms which are similar to those of Maiti and Bergmann (Maiti 1982; Bergmann 1981). Complexity and the departure from spherical symmetry was studied by Govender et al. (2022). They found that a departure from spherical symmetry lead to a higher degree of complexity within the stellar structure. A recent detailed article by Herrera (2023) addresses the complexity and simplicity of self-gravitating fluids. This work builds on his proposed definition of complexity from 2018 (Herrera 2018). In an attempt to arrive at a reliable definition for complexity, the study begins with a static spherically symmetric case, is then extended to the static axially symmetric case, followed by the non-static spherically symmetric case and then a fluid with hyperbolic symmetry is considered. The grading of complexity is established from the simplest Minkowski spacetime to the most complex systems undergoing gravitational radiation.

This paper is structured as follows: In Sect. 2 we introduce the interior spacetime of a collapsing star by way of a spherically symmetric, shear-free metric, and the associated field equations. The exterior spacetime and junction conditions required for the smooth matching between the interior and Vaidya exterior are presented in Sect. 3. In Sect. 4 the perturbative scheme is described and the field equations for the static and perturbed configurations are given. Section 5 introduces the complexity factor which is utilised to obtain forms for the gravitational potentials. A perturbative analysis is performed on $Y_{TF}$ in Sect. 6, allowing the complexity factor to be split into static and non-static parts, and leading to the solutions for the material functions which completes the description of the model via a perturbative scheme. The matching of the interior spacetime with the Schwarzschild exterior is done in Sect. 7 after which the physical viability of the model is interrogated in Sect. 8, followed by a discussion in Sect. 9. We make some concluding remarks in Sect. 10.

2 Interior spacetime

The interior of the collapsing star is described by the general spherically symmetric, shear-free metric in comoving coordinates

$$ ds^{2} = -A^{2}dt^{2} + B^{2}[dr^{2} + r^{2}(d\theta ^{2} + \sin ^{2}{ \theta}d\phi ^{2})], $$

(1)

where $A = A(r,t)$ and $B = B(r,t)$ are the unspecified metric potentials. We assume that the interior stellar fluid is characterised by anisotropic pressures and heat flux.

$$\begin{aligned} T_{ab} =& (\mu + p_{t})w_{a} w_{b} + p_{t}g_{ab} + (p_{r} - p_{t})X_{a}X_{b} \\ & + q_{a}w_{b} + q_{b} w_{a}, \end{aligned}$$

(2)

where $\mu$ is the energy density, $p_{r}$ the radial pressure, $p_{t}$ the tangential pressure and $q_{a}$ the heat flux, vector $w_{a}$ is the four-velocity of the fluid and $X_{a}$ is a unit four-vector along the radial direction. These quantities must satisfy $w_{a}w^{a} = -1$, $w_{a}q^{a} = 0$, $X_{a}X^{a} = 1$ and $X_{a}w^{a} = 0$. Furthermore, in comoving coordinates we have

$$ w^{a} = A^{-1}\delta ^{a}_{0} , $$

(3)

$$ q^{a} = q\delta ^{a}_{1} , $$

(4)

and

$$ X^{a} = B^{-1}\delta ^{a}_{1} . $$

(5)

The nonzero components of the Einstein field equations for the line element (1) and the energy momentum (2) are

$$\begin{aligned} \mu =& - \frac{1}{B^{2}}\left [2\frac{B^{\prime \prime}}{B} - \left ( \frac{B^{\prime}}{B}\right )^{2} +\frac{4}{r}\frac{B^{\prime}}{B} \right ] +\frac{3}{A^{2}}\left (\frac{{\dot{B}}}{B}\right )^{2} , \end{aligned}$$

(6)

$$\begin{aligned} p_{r} =& \frac{1}{B^{2}}\left [\left (\frac{B^{\prime}}{B}\right )^{2} + \frac{2}{r}\left (\frac{A^{\prime}}{A}+ \frac{B^{\prime}}{B}\right ) + 2\frac{A^{\prime}}{A}\frac{B^{\prime}}{B}\right ] \\ \\ &+ \frac{1}{A^{2}}\left [-2\frac{\ddot{B}}{B} - \left ( \frac{\dot{B}}{B}\right )^{2} + 2\frac{\dot{A}}{A}\frac{\dot{B}}{B} \right ] , \end{aligned}$$

(7)

$$\begin{aligned} p_{t} =& \frac{1}{A^{2}}\left [-2\frac{\ddot{B}}{B} -\left ( \frac{\dot{B}}{B}\right )^{2} +2 \frac{\dot{A}}{A}\frac{\dot{B}}{B} \right ] \\ \\ & + \frac{1}{B^{2}}\left [\frac{B^{\prime \prime}}{B}-\left ( \frac{B^{\prime}}{B}\right )^{2}+\frac{1}{r}\left ( \frac{A^{\prime}}{A}+\frac{B^{\prime}}{B}\right )+ \frac{A^{\prime \prime}}{A}\right ] , \end{aligned}$$

(8)

$$\begin{aligned} q =& \frac{2}{AB^{2}}\left [\frac{{\dot{B}}^{\prime}}{B}- \frac{\dot{B}}{B}\left (\frac{B^{\prime}}{B}+\frac{A^{\prime}}{A} \right )\right ] , \end{aligned}$$

(9)

where the dots and primes represent the partial derivatives with respect to $t$ and $r$ respectively.

3 Exterior spacetime and junction conditions

The spacetime consists of two seperate regions, the interior spacetime which is described by the metric (1) and the exterior spacetime. Due to the star radiating energy, the exterior spacetime is not a vacuum and can be described by Vaidya’s metric (Vaidya 1951)

$$\begin{aligned} ds^{2}_{+} =& -\left [1 - \frac{2m(v)}{\mathtt{r}}\right ]dv^{2} - 2dvd \mathtt{r} + \mathtt{r}^{2} d\theta ^{2} \\ & + \mathtt{r}^{2}\sin ^{2}\theta d\phi ^{2} , \end{aligned}$$

(10)

where $m(v)$, the total energy inside $\Sigma$, is a function of the retarded time $v$, and $\mathtt{r}$ is the radial coordinate for the exterior.

The junction conditions that are required to be satisfied across the boundary are

$$ \left (K^{+}_{ij} - K^{-}_{ij}\right )_{\Sigma} = 0, $$

(11)

and

$$ \left (ds^{2}_{+} - ds^{2}_{-}\right )_{\Sigma} =0, $$

(12)

where $K_{ij}$ is the extrinsic curvature on the two sides of the boundary. The calculations carried out by de Oliviera and Santos (1987) is utilized and we obtain the following

$$ \left (p_{r}\right )_{\Sigma} = \left (qB\right )_{\Sigma}, $$

(13)

$$ \left (qB\right )_{\Sigma} = -\left (\frac{2}{\mathtt{r}^{2}}{{\dot{v}}^{2}} \frac{dm}{dv}\right )_{\Sigma} , $$

(14)

$$ \left (rB\right )_{\Sigma} = \mathtt{r}_{\Sigma} , $$

(15)

$$ m(v) = \left (\frac{r^{3}B{\dot{B}}^{2}}{2A^{2}} - r^{2}{B^{\prime}} - \frac{r^{3}{{B^{\prime}}^{2}}}{2B}\right )_{\Sigma} , $$

(16)

and

$$ \left (A dt\right )_{\Sigma} = \left (1 - \frac{2m}{\mathtt{r}} + 2 \frac{d\mathtt{r}}{dv}\right )^{1/2}_{\Sigma} dv . $$

(17)

In the above equations ie: (13)-(17), the following conditions are given across the boundary ${\Sigma}$ respectively: the radius of the bounding surface, $\Sigma$ in both coordinate systems, the conservation of momentum flux, conservation of radiation flux, the total energy inside $\Sigma$ and the relationship between each of the times $t$ and $v$. We are in a position to give the total energy entrapped up to a radius of $r$ inside $\Sigma$ given by

$$ m(r,t) = \frac{r^{3}B{\dot{B}}^{2}}{2A^{2}} - r^{2}{B^{\prime}} - \frac{r^{3}{{B^{\prime}}^{2}}}{2B}, $$

(18)

which is refered to as the Misner and Sharp mass (Misner and Sharp 1964).

4 The perturbative scheme

We assume that the fluid is initially in static equilibrium, hence the fluid is described by quantities that have radial dependence only. We then assert that the static system is perturbed, undergoing slow shear-free collapse and producing pure radiation. We denote the quantities such as energy density, radial pressure and tangential pressure of the static system by a zero subscript and those of the perturbed fluid by an overhead bar. We further assume that the metric functions $A(r,t)$ and $B(r,t)$ have the same time dependence in their perturbations. This assumption would imply that the perturbed material functions also have the same time dependence. Therefore the metric functions and the material functions are given by Naidu et al. (2020)

$$\begin{aligned} A(r,t) =& A_{0}(r) + \epsilon a(r)T(t), \end{aligned}$$

(19)

$$\begin{aligned} B(r,t) =& B_{0}(r) + \epsilon b(r)T(t) , \end{aligned}$$

(20)

$$\begin{aligned} \mu (r,t) =& \mu _{0}(r) + \epsilon \bar{\mu}(r,t) , \end{aligned}$$

(21)

$$\begin{aligned} p_{r}(r,t) =& p_{r0}(r) + \epsilon {\bar{p}}_{r}(r,t) , \end{aligned}$$

(22)

$$\begin{aligned} p_{t}(r,t) =& p_{t0}(r) + \epsilon {\bar{p}}_{t}(r,t) , \end{aligned}$$

(23)

$$\begin{aligned} m(r,t) =& m_{0}(r) + \epsilon \bar{m}(r,t) , \end{aligned}$$

(24)

where we assume that $0<\epsilon \ll 1$.

Einstein’s field equations for the static configuration are

$$\begin{aligned} \mu _{0} =& - \frac{1}{B_{0}^{2}}\left [2 \frac{B_{0}^{\prime \prime}}{B_{0}} - \left ( \frac{B_{0}^{\prime}}{B_{0}}\right )^{2} +\frac{4}{r} \frac{B_{0}^{\prime}}{B_{0}}\right ], \end{aligned}$$

(25)

$$\begin{aligned} p_{r0} =& \frac{1}{B_{0}^{2}}\left [\left ( \frac{B_{0}^{\prime}}{B_{0}}\right )^{2} + \frac{2}{r}\left ( \frac{A_{0}^{\prime}}{A_{0}}+ \frac{B_{0}^{\prime}}{B_{0}}\right ) + 2 \frac{A_{0}^{\prime}}{A_{0}}\frac{B_{0}^{\prime}}{B_{0}}\right ] , \end{aligned}$$

(26)

$$\begin{aligned} p_{t0} =& \frac{1}{B_{0}^{2}}\left [ \frac{B_{0}^{\prime \prime}}{B_{0}}-\left ( \frac{B_{0}^{\prime}}{B_{0}}\right )^{2}+\frac{1}{r}\left ( \frac{A_{0}^{\prime}}{A_{0}}+\frac{B_{0}^{\prime}}{B_{0}}\right )+ \frac{A_{0}^{\prime \prime}}{A_{0}}\right ] . \end{aligned}$$

(27)

whereas the perturbed field equations up to first order in $\epsilon$ can be cast as

$$\begin{aligned} \bar{\mu} =&-3\mu _{0}\frac{b}{B_{0}}T + \frac{1}{B_{0}^{3}} \\ &\times \biggl[-\left (\frac{B_{0}^{\prime}}{B_{0}}\right )^{2} b + 2 \left (\frac{B_{0}^{\prime}}{B_{0}} -\frac{2}{r}\right )b^{\prime} -2b^{ \prime \prime}\biggr]T , \end{aligned}$$

(28)

$$\begin{aligned} \bar{p}_{r} =& -2p_{r0}\frac{b}{B_{0}}T + \frac{2}{B_{0}^{2}}\biggl[ \left (\frac{B_{0}^{\prime}}{B_{0}} + \frac{1}{r} + \frac{A_{0}^{\prime}}{A_{0}}\right )\left (\frac{b}{B_{0}}\right )^{ \prime} \\ &+\left (\frac{B_{0}^{\prime}}{B_{0}}+ \frac{1}{r}\right )\left ( \frac{a}{A_{0}}\right )^{\prime}\biggr]T- 2\frac{b}{{A_{0}^{2}}B_{0}}{ \ddot{T}} , \end{aligned}$$

(29)

$$\begin{aligned} \bar{p}_{t} =& -2p_{t0}\frac{b}{B_{0}}T \\ & + \frac{1}{B_{0}^{2}}\biggl[\left (\frac{b}{B_{0}}\right )^{ \prime \prime} + \frac{1}{r}\left (\frac{b}{B_{0}}\right )^{\prime} + 2 \frac{A_{0}^{\prime}}{A_{0}}\left (\frac{a}{A_{0}}\right )^{\prime} + \left (\frac{a}{A_{0}}\right )^{\prime \prime} \\ &+ \frac{1}{r}\left (\frac{a}{A_{0}}\right )^{\prime}\biggr]T - 2 \frac{b}{{A_{0}^{2}}B_{0}}{\ddot{T}} , \end{aligned}$$

(30)

$$\begin{aligned} qB =& \frac{2}{B_{0}}\left (\frac{b}{A_{0} B_{0}}\right )^{\prime}{ \dot{T}} . \end{aligned}$$

(31)

The total energy entrapped up to radius $r$ inside $\Sigma$ for the static and perturbed configurations are respectively given by

$$\begin{aligned} m_{0}(r_{\Sigma}) =& -\left ( r^{2}{B_{0}^{\prime}} + \frac{r^{3}{{B_{0}^{\prime}}^{2}}}{2B_{0}}\right )_{\Sigma}, \end{aligned}$$

(32)

$$\begin{aligned} \bar{m}(r_{\Sigma},t) =& -\left (\left [{r^{2}}b^{\prime} + \frac{r^{3}{{B_{0}^{\prime}}^{2}}}{2B_{0}} \left (2 \frac{b^{\prime}}{B_{0}^{\prime}}-\frac{b}{B_{0}}\right )\right ]T(t) \right )_{\Sigma} . \end{aligned}$$

(33)

The smooth matching of the interior spacetime to the Vaidya exterior is facilitated by using the junction conditions derived by Santos (1985), and we may rewrite equations (29) and (31) as

$$ \bar{p}_{r} = -2p_{r0}\frac{b}{B_{0}}T +\frac{2b}{{A_{0}^{2}}B_{0}} \left ({\alpha}T - {\ddot{T}}\right ), $$

(34)

and

$$ qB = \frac{4b}{{A_{0}^{2}}B_{0}}{\beta}{\dot{T}}, $$

(35)

where

$$\begin{aligned} \alpha (r) =& \frac{A_{0}^{2}}{B_{0} b}\biggl[\left ( \frac{B_{0}^{\prime}}{B_{0}} + \frac{1}{r} + \frac{A_{0}^{\prime}}{A_{0}}\right )\left (\frac{b}{B_{0}}\right )^{ \prime} \\ & + \left (\frac{B_{0}^{\prime}}{B_{0}}+ \frac{1}{r}\right ) \left ( \frac{a}{A_{0}}\right )^{\prime}\biggr], \end{aligned}$$

(36)

and

$$ \beta (r) = \frac{A_{0}^{2}}{2b}\left (\frac{b}{A_{0}B_{0}}\right )^{ \prime}, $$

(37)

are constants at the boundary.

The explicit form of the temporal function is obtained by integrating (35),

$$ T(t) = -\exp \left [\left (-\beta _{\Sigma }+ \sqrt{\alpha _{\Sigma }+ \beta _{\Sigma}^{2}}\right ) t \right ], $$

(38)

where $\alpha _{\Sigma }= \alpha (r_{\Sigma})$ and $\beta _{\Sigma }= \beta (r_{\Sigma})$. The above result has been extensively used by numerous authors in modeling radiating spheres in quasi-static equilibrium (Govender and Govinder 2002; Pretel and da Silva 2020; Govender et al. 2021).

5 Complexity

The complexity factor for radiating, self-gravitating systems, is well defined by Herrera et al. (2018) and is given by

$$ Y_{TF} = 8\pi \delta + \frac{4\pi}{(r B)^{3}}\int _{0}^{r} (r B)^{3} \left ( \rho ' - 3q B \frac{\dot{B}}{A}\right ) dr, $$

(39)

where $\delta = p_{t} - p_{r}$ is a measure of the anisotropic stresses and the first and second terms in the integral are contributions from the density inhomogeneity and dissipative fluxes respectively. By utilizing the corresponding field equations (6)–(9) we determine

$$\begin{aligned} Y_{TF} =& 8\pi \delta - \frac{1}{(r B)^{3}}\int _{0}^{r} 2r\bigg[r \left (B'' + \frac{r}{2} B''' \right ) \\ & - \frac{r B'}{B} \left (3 B' +2 r B'' \right ) - B' + \frac{r^{2} (B')^{3}}{B^{2}} \bigg] dr . \end{aligned}$$

(40)

The integration of (40) can be completed to yield

$$ Y_{TF} = 8\pi \delta - \frac{1}{B^{2}}\left [\frac{B ''}{B} - 2\left ( \frac{B '}{B}\right )^{2} - \frac{1}{r}\frac{B '}{B} \right ]. $$

(41)

The reader is directed to the works of Bogadi and Govender (2022) for more insight into the $Y_{TF}$ function. After inspection of (41), two cases arise. By setting $\delta = 0$, we have the isotropic case for vanishing complexity which enables us to have the following form for $B '$

$$ B ' = C(t) B^{2} r, $$

(42)

where $C(t)$ is a constant of integration. Upon integration, the form for $B(r,t)$ is achieved

$$ B(r,t) = \frac{R(t)}{1 + k(t) r^{2}}, $$

(43)

where $R(t)$ and $k(t)$ are once again integration constants.

By utilizing (43) in the Einstein field equations for pressure isotropy, a form for $A(r,t)$ is obtained

$$ A(r,t) = \xi (t) + \frac{\zeta (t)}{1 + k(t) r^{2}} $$

(44)

where $\xi (t)$ and $\zeta (t)$ are constants of integration.

The alternative is that of the anisotropic case, which is obtained by ensuring that $\delta$ is nonzero, thus the complexity factor is reduced to

$$ Y_{TF} = \frac{1}{B^{2}}\left [ \frac{1}{A}\left (A '' - \frac{A '}{r} \right ) - 2\frac{A '}{A}\frac{B '}{B}\right ]. $$

(45)

Considering the case of vanishing complexity, upon integration, we obtain

$$ A ' = C(t) B^{2} r $$

(46)

which reduces the problem of finding solutions to a single-generating function.

6 Perturbative analysis on $Y_{TF}$

Using the perturbative scheme (19) in (45), we obtain

$$\begin{aligned} Y_{TF} =& \frac{1}{r \left (A_{0} + \epsilon a T \right )\left (B_{0} + \epsilon b T \right )^{3}} \\ &\times \bigg[B_{0} (r A_{0}'' - A_{0}') - 2 r A_{0}' B_{0}' \\ &\qquad + \epsilon T \bigg( B_{0} (r a'' - a') - 2 r (A_{0}' b' + B_{0}' a' ) \\ & \qquad + b( r A_{0}'' - A_{0}') \bigg)\bigg]. \end{aligned}$$

(47)

Equation (47) can be split into a static and non-static part.

$$\begin{aligned} Y_{TF} =& \frac{1}{r \left (\epsilon a T+A_{0}\right ) \left (\epsilon b T+B_{0}\right ){}^{3}} \\ & \times \bigg[\text{static} + \text{dynamic} \bigg], \end{aligned}$$

(48)

where

$$\begin{aligned} \text{static} = r B_{0} A_{0}'' - B_{0} A_{0}' - 2 r A_{0}' B_{0}' \end{aligned}$$

(49)

and

$$\begin{aligned} \text{dynamic} =& \epsilon T \bigg( B_{0} (r a'' - a') - 2 r (A_{0}' b' + B_{0}' a' ) \\ & + b( r A_{0}'' - A_{0}') \bigg). \end{aligned}$$

(50)

Setting $Y_{TF} = 0$ in equation (48), i.e. for vanishing complexity, the static component (49) integrates to

$$ A_{0}' = C\left ( r B_{0}^{2}\right ), $$

(51)

where $C$ is a constant of integration. In addition, the dynamic part yields a differential equation in $a(r)$ or $b(r)$ by equating (50) to zero,

$$ B_{0} (r a'' - a') - 2 r (A_{0}' b' + B_{0}' a' ) + b( r A_{0}'' - A_{0}') = 0. $$

(52)

The static configuration is determined by specifying $B_{0}(r)$ and employing (51). A functional form for $b(r)$, widely used by researchers to study dissipative collapse in perturbation models (Chan et al. 1993; Govender et al. 2021; Naidu et al. 2020), is used which then allows the determination of $a(r)$ via (52).

Following Pant et al. (2014), we assume the ansatz,

$$ B_{0}(r) = {\mathcal{B}} \left (1 + C r^{2}\right )^{-k}, $$

(53)

where ℬ and $k$ are constants. This potential formulation has been successfully employed by Murad and Pant (2014) and Tewari (2013). Using equation (51), we then obtain

$$ A_{0}(r) = \frac{{\mathcal{A}} {\mathcal{B}}^{2} \left (1 + C r^{2}\right )^{1-2 k}}{2(1 - 2 k)}, $$

(54)

where ${\mathcal{A}}$ is a constant. For the non-static part, the functional form for $b(r)$ is given by

$$ b(r) = A_{0}(r)B_{0}(r)\left [1 + \zeta f(r)\right ], $$

(55)

where $f(r) = r^{2}$. This functional form for $b(r)$ was used to study dissiative collapse of shear-free radiating stars in the Newtonian and Post-Newtoninan regimes (Chan et al. 1993).

Substituting (55) into equation (52) then yields

$$\begin{aligned} 0 =& a''(r) - \frac{\left (1 + (1-4k )C r^{2} \right )}{r \left (1 + C r^{2}\right )}a'(r) \\ & - \frac{2 {\mathcal{A}}^{2} {\mathcal{B}}^{4} C r^{2} \left (\zeta + C \left (1 -2k +2 \left (1 - k\right )\zeta r^{2} \right ) \right )}{\left (1 + C r^{2}\right )^{4 k }(1-2 k)} \end{aligned}$$

(56)

which can be integrated to give

$$\begin{aligned} a(r) =& \frac{{\mathcal{A}}^{2} {\mathcal{B}}^{4}}{2 C (1 - 2 k)} \bigg( \frac{(C - \zeta )(1 + C r^{2})^{2 - 4k}}{2 (1-2 k)} \\ & +\frac{\zeta \left (1 + C r^{2}\right )^{3 - 4 k}}{3-4 k}\bigg) \\ &+ \frac{\omega _{1} \left (1 + C r^{2}\right )^{1-2 k}}{2C(1-2k ) }+ \omega _{2}, \end{aligned}$$

(57)

where $\omega _{1}$ and $\omega _{2}$ are integration constants. This completes the description of our model via the perturbative scheme.

7 Junction conditions

The smooth matching of the static interior spacetime to that of the Schwarzschild exterior, is facilitated by using the junction conditions,

$$\begin{aligned} ({A_{0}})_{\Sigma} =& \frac{2(1 - 2 k) \left (1-\frac{M}{2 \mathtt{r}_{\Sigma}}\right )}{{\mathcal{B}}^{2}\left (1 + C r_{\Sigma}^{2}\right )^{1 - 2 k} \left (1 + \frac{M}{2 \mathtt{r}_{\Sigma}}\right )}, \end{aligned}$$

(58)

$$\begin{aligned} ({B_{0}})_{\Sigma} =& \left (1 + C r_{\Sigma}^{2}\right )^{k} \left (1 + \frac{M}{2 \mathtt{r}_{\Sigma}}\right )^{2}, \end{aligned}$$

(59)

where $\mathtt{r}_{\Sigma} = r_{\Sigma }B_{0}(r_{\Sigma})$. By considering the static part for which the pressure at the boundary must vanish ($(p_{r0})_{ \Sigma} = 0$), we obtain

$$\begin{aligned} r_{\Sigma} = \frac{\sqrt{3 k-1}}{\sqrt{5 C k^{2}-5 C k+C}}, \end{aligned}$$

(60)

where $k-1>0$ and $k>\frac{1}{3}$, which sets the boundary of the star.

8 Physical application

In order to test the physical viability of our model we firstly set the parameters for the static configuration. The initial mass is chosen to be $M = 5\text{ M}_{\odot}$ with a radius of $r_{\Sigma }= 2159\text{ km}$ as considered by Bonnor et al. (1989). This introduces an initial setup for a supernova which then collapses to form a black hole.

Simultaneous equations in parameters $C$ and $k$ are obtained and solved via (32) and (60), which completes the specification of the static configuration. We obtain Table 1.

Table 1 Parameters for the static configuration

The perturbation part is now considered. The parameters for $b(r)$ are chosen to be,

$$ \zeta = 3\times 10^{-10} \text{ km}^{-2}, \epsilon = 0.01, $$

(61)

whereby $\zeta$ was chosen such that $\zeta f(r_{\Sigma}) \approx 0.1\%$. The perturbation parameter $\epsilon$ is consistent with the requirement $\epsilon \ll 1$. In order to set the integration constants for $a(r)$, we make use of the special case where $a(r)/A_{0}(r) = b(r)/B_{0}(r)$ (Govender et al. 2003). These are then computed to be,

$$ (\omega _{1} = 5.94394\times 10^{-10} \text{ km}^{-2} ;\ \omega _{2} = -0.644838). $$

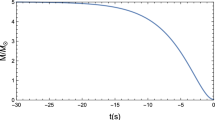
This allows for the gravitational collapse of the $5M_{\odot}$ stellar object in which a mass loss of about $15\%$ occurs before horizon formation. Plots of mass and luminosity are shown in Figs. 1 and 2 respectively.

Fig. 1

Progression of mass

Fig. 2

Luminosity at infinity

9 Discussion

We now turn our attention to the physical viability of our complexity-free model. To this end, we have plotted the mass function in Fig. 1. Since the star is always close to quasi-static equilibrium, there is a small decrease in mass as time evolves. One expects this decrease in mass as the star is radiating energy to the exterior. The luminosity profile is shown in Fig. 2 and is typical of that found in other studies (Pretel et al. (2020)). Here we see that initially the luminosity is zero (no dissipation for early times) and then increases steadily, reaching a peak in some finite time after which it decreases to zero as the horizon is reached. The duration of the process, of the order of half a second, is typically longer than that expected. This is attributed to imposing the vanishing complexity condition. Progression of the energy density (Fig. 3) is somewhat unexpected as it decreases as the collapse proceeds. This must be due to loss in energy over an extended time frame in contrast to more aggressive collapse processes which occur within fractions of a millisecond. Figure 4 shows that the radial pressure is continuous at each interior point of the collapsing core and increases as the collapse proceeds as would be expected. Heat generation within the collapsing body can be seen in Fig. 5. For early times, the production of heat is small (the star is close to hydrostatic equilibrium). As the star departs from equilibrium it begins to radiate energy in the form of a radial heat flux which peaks for some finite time and decreases smoothly as the horizon is formed.

Fig. 3

Progression of energy density

Fig. 4

Progression of radial pressure

Fig. 5

Heat flux

10 Conclusion

In this work we have employed a perturbative scheme to model a star undergoing dissipative collapse in the form of a radial heat flux. In order to complete the gravitational behaviour of the initially static configuration and the collapsing core, we employed the condition of vanishing complexity factor and the Pant et al. (2014) ansatz. Since the star is radiating energy, the exterior spacetime is described by Vaidya’s outgoing solution. The matching of the interior spacetime and the exterior Vaidya atmosphere determined the temporal evolution of the perturbed quantities. The vanishing of the complexity factor splits the evolution equation for the metric functions into static and non-static components. The static part was easily integrated which enabled us to write one metric function in terms of the other. The dynamic component of the complexity-free condition involved the perturbation functions and their derivatives. By specifying the behaviour of one of these functions, we were able to obtain the full radial perturbative behaviour for our model. The physical viability of our radiating solution was studied in the context of regularity and stability as the collapse proceeded. We believe that the perturbative approach to vanishing complexity is novel and lends more insight into the evolution of a star which loses hydrostatic equilibrium and moves into the dissipative regime.

Appendices

Appendix A: Static quantities

$$\begin{aligned} \mu _{0} =& -\frac{1}{{\mathcal{B}}^{2}} \biggl[\left (Z\right )^{2 k} \biggl( \frac{1}{{\mathcal{B}}} \biggl[ 2 \left (Z\right )^{k} \biggl(-4 { \mathcal{B}} C^{2} \\ & (-k-1) k r^{2} \left (Z\right )^{-k-2} \\ & -2 {\mathcal{B}} C k \left (Z\right )^{-k-1}\biggr) \biggr] - \frac{4 C^{2} k^{2} r^{2}}{\left (Z\right )^{2}} -\frac{8 C k}{Z} \biggr) \biggr] , \end{aligned}$$

(A1)

$$\begin{aligned} p_{r0} =& \frac{1}{{\mathcal{B}}^{2}} \biggl[\left (Z\right )^{2 k} \biggl(\frac{4 C^{2} k^{2} r^{2}}{\left (Z\right )^{2}} - \frac{8 C^{2} (1-2 k) k r^{2}}{\left (Z\right )^{2}} \\ & + \frac{2 \left (\frac{2 C (1-2 k) r}{Z}-\frac{2 C k r}{Z}\right )}{r}\biggr) \biggr] , \end{aligned}$$

(A2)

$$\begin{aligned} p_{t0} =& \frac{1}{{\mathcal{B}}^{2}} \biggl[ \left (Z\right )^{2 k} \biggl( \frac{1}{{\mathcal{A}} {\mathcal{B}}^{2}} \biggl[ (2-4 k) \left (Z\right )^{2 k-1} \\ & \biggl( \frac{1}{2-4 k} \biggl[ 2 {\mathcal{A}} {\mathcal{B}}^{2} C (1-2 k) \left (Z\right )^{-2 k} \biggr] \\ & - \frac{8 {\mathcal{A}} {\mathcal{B}}^{2} C^{2} (1-2 k) k r^{2} \left (Z\right )^{-2 k-1}}{2-4 k}\biggr) \biggr] \\ & + \frac{1}{{\mathcal{B}}} \biggl[ \left (Z\right )^{k} \biggl(-4 {\mathcal{B}} C^{2} (-k-1) k r^{2} \\ & \left (Z\right )^{-k-2}-2 {\mathcal{B}} C k \left (Z\right )^{-k-1} \biggr) \biggr] \\ & -\frac{4 C^{2} k^{2} r^{2}}{\left (Z\right )^{2}}+ \frac{\frac{2 C (1-2 k) r}{Z}-\frac{2 C k r}{Z}}{r}\biggr) \biggr] , \end{aligned}$$

(A3)

$$\begin{aligned} m_{0} =& -2 {\mathcal{B}} C k r^{3} (Z)^{-2 - k} \\ & (-1 + C (-1 + k) r^{2}) , \end{aligned}$$

(A4)

where $Z = Cr^{2}+1$

Appendix B: Perturbed quantities

$$\begin{aligned} \bar{\mu} =& - \frac{1}{(2 k-1) \left (Z\right )} \\ & \biggl[ 2 {\mathcal{A}} \biggl(C \biggl(r^{2} \biggl(\zeta \left (10 C (k-1)^{2} r^{2}-10 k+13\right ) \\ & +C (10 (k-1) k+3)\biggr)+3\biggr)+3 \zeta \biggr) \\ & \exp \biggl(t \biggl( \biggl[ \frac{1}{{\mathcal{B}}^{2} (2-4 k)^{2} \left (\zeta r_{0}^{2}+1\right ){}^{2}} \\ & \biggl[ \left (Z_{1}\right ){}^{-2 (k+1)} \biggl({\mathcal{A}}^{2} \zeta ^{2} r_{0}^{2} \left ({\mathcal{B}} C r_{0}^{2}+{\mathcal{B}}\right ){}^{4} \\ & +(2-4 k) \left (\zeta r_{0}^{2}+1\right ) \biggl( \frac{1}{C^{2} (4 k-3)} \\ & \biggl[ \left (C (2 k-1) r_{0}^{2}-1\right ) \biggl(4 C^{3} (1-2 k)^{2} (4 k-3) \omega _{2} \\ & \left (Z_{1}\right ){}^{4 k}-{\mathcal{B}}^{4} {\mathcal{A}}^{2} \left (Z_{1} \right ){}^{2} \biggl(4 C \zeta (k-1) r_{0}^{2} \\ & +C (4 k-3)-\zeta \biggr)\biggr) \biggr] - \frac{1}{2 k-1} \biggl[ {\mathcal{B}}^{4} {\mathcal{A}}^{2} \left (Z_{1}\right ){}^{2} \\ & \left (3 C (2 k-1) r_{0}^{2}-1\right ) \biggl(2 C \zeta (k-1) r_{0}^{2}+C (2 k-1) \\ & -\zeta \biggr) \biggr] \biggr)\biggr) \biggr] \biggr]^{\frac{1}{2}} - \frac{{\mathcal{A}} {\mathcal{B}} \zeta r_{0} \left (Z_{1}\right ){}^{1-k}}{(2-4 k) \left (\zeta r_{0}^{2}+1\right )} \biggr)\biggr) \biggr] , \end{aligned}$$

(B1)

$$\begin{aligned} \bar{p}_{r} =& \frac{1}{{\mathcal{A}} \left (Z\right )^{3}} \biggl[ 2 \exp \biggl[ t \biggl( \biggl[ \frac{1}{{\mathcal{B}}^{2} (2-4 k)^{2} \left (\zeta r_{0}^{2}+1\right ){}^{2}} \\ & \biggl[ \left (Z_{1}\right ){}^{-2 (k+1)} \biggl({\mathcal{A}}^{2} \zeta ^{2} r_{0}^{2} {\mathcal{B}}^{4} \left (Z_{1}\right ){}^{4} \\ &+(2-4 k) \left (\zeta r_{0}^{2}+1\right ) \biggl( \frac{1}{C^{2} (4 k-3)} \\ & \biggl[ \left (C (2 k-1) r_{0}^{2}-1\right ) \\ & \biggl(4 C^{3} (1-2 k)^{2} (4 k-3) \omega _{2} \left (Z_{1}\right ){}^{4 k}-4 {\mathcal{A}}^{2} { \mathcal{B}}^{4} C^{3} \\ & (k-1) \zeta r_{0}^{6} +{\mathcal{A}}^{2} {\mathcal{B}}^{4} C^{2} (C (3-4 k)+(9-8 k) \zeta ) r_{0}^{4} \\ &+2 {\mathcal{A}}^{2} {\mathcal{B}}^{4} C (C (3-4 k)+(3-2 k) \zeta ) r_{0}^{2} \\ &+{ \mathcal{A}}^{2} {\mathcal{B}}^{4} (C (3-4 k)+\zeta )\biggr) \biggr] \\ & - \frac{1}{2 k-1} \biggl[ {\mathcal{B}}^{4} {\mathcal{A}}^{2} \left ( Z_{1} \right ){}^{2} \left (3 C (2 k-1) r_{0}^{2}-1\right ) \\ & \left (2 C (k-1) \zeta r_{0}^{2}+C (2 k-1)-\zeta \right ) \biggr] \biggr)\biggr) \biggr] \biggr]^{\frac{1}{2}} \\ &- \frac{{\mathcal{A}} {\mathcal{B}} \zeta r_{0} \left (Z_{1}\right ){}^{1-k}}{(2-4 k) \left (\zeta r_{0}^{2}+1\right )}\biggr) \biggr] \\ & \biggl( \frac{1}{{\mathcal{B}}^{2}} \biggl[ (2-4 k) \left (\zeta r^{2}+1 \right ) \biggl( \biggl[ \frac{1}{{\mathcal{B}}^{2} (2-4 k)^{2} \left (\zeta r_{0}^{2}+1\right ){}^{2}} \\ & \biggl[ \left (Z_{1}\right ){}^{-2 (k+1)} \biggl({\mathcal{A}}^{2} \zeta ^{2} r_{0}^{2} {\mathcal{B}}^{4} \left (Z_{1}\right ){}^{4} +(2-4 k) \left (\zeta r_{0}^{2}+1\right ) \\ &\biggl( \frac{1}{C^{2} (4 k-3)} \biggl[ \left (C (2 k-1) r_{0}^{2}-1\right ) \\ &\biggl(4 C^{3} (1-2 k)^{2} (4 k-3) \omega _{2} \left (Z_{1}\right ){}^{4 k}-4 {\mathcal{A}}^{2} { \mathcal{B}}^{4} C^{3} (k-1) \\ & \zeta r_{0}^{6} +{\mathcal{A}}^{2} {\mathcal{B}}^{4} C^{2} (C (3-4 k)+(9-8 k) \zeta ) r_{0}^{4} \\ &+2 {\mathcal{A}}^{2} {\mathcal{B}}^{4} C (C (3-4 k) \\ & +(3-2 k) \zeta ) r_{0}^{2}+{\mathcal{A}}^{2} {\mathcal{B}}^{4} (C (3-4 k)+ \zeta )\biggr) \biggr] - \frac{1}{2 k-1} \\ & \biggl[ {\mathcal{B}}^{4} {\mathcal{A}}^{2} \left ( Z_{1}\right ){}^{2} \left (3 C (2 k-1) r_{0}^{2}-1\right ) \\ &\biggl(2 C (k-1) \zeta r_{0}^{2}+C (2 k-1) -\zeta \biggr) \biggr] \biggr)\biggr) \biggr] \biggr]^{\frac{1}{2}} \\ &- \frac{{\mathcal{A}} {\mathcal{B}} \zeta r_{0} \left (Z_{1}\right ){}^{1-k}}{(2-4 k) \left (\zeta r_{0}^{2}+1\right )} \biggr){}^{2} \left (Z\right )^{2 k+2} \biggr] - \frac{1}{2 k-1} \\ & \biggl[ 2 C {\mathcal{A}}^{2} \left (Z\right )^{2} \biggl(5 C k^{2} r^{2}+C r^{2} \\ &-k \left (5 C r^{2}+3\right )+1\biggr) \left (\zeta r^{2}+1 \right ) \biggr] \\ & - \frac{1}{{\mathcal{B}}^{4}} \biggl[ \frac{1}{C^{2} (4 k-3)} \biggl[ \left (C (2 k-1) r^{2}-1\right ) \\ & \biggl(4 C^{3} (1-2 k)^{2} (4 k-3) \left (Z\right )^{4 k} \omega _{2} \\ & -{\mathcal{B}}^{4} {\mathcal{A}}^{2} \left ( Z\right )^{2} \biggl(C \biggl(-4 \zeta r^{2}+4 k \left (\zeta r^{2}+1\right ) -3\biggr) \\ &-\zeta \biggr) \biggr) \biggr] - \frac{1}{2 k-1} \biggl[ {\mathcal{B}}^{4} {\mathcal{A}}^{2} \left (Z\right )^{2} \left (3 C (2 k-1) r^{2}-1\right ) \\ &\biggl(C \biggl(-2 \zeta r^{2}+2 k \left (\zeta r^{2}+1\right )-1\biggr)-\zeta \biggr) \biggr] \biggr] \biggr) \biggr] , \end{aligned}$$

(B2)

$$\begin{aligned} \bar{p}_{t} =& \frac{1}{{\mathcal{A}} \left (Z\right )^{3}} \biggl[ 2 \exp \biggl[t \biggl( \biggl[ \frac{1}{{\mathcal{B}}^{2} (2-4 k)^{2} \left (\zeta r_{0}^{2}+1\right ){}^{2}} \\ & \biggl[ \left (Z_{1}\right ){}^{-2 (k+1)} \biggl({\mathcal{A}}^{2} \zeta ^{2} r_{0}^{2} {\mathcal{B}}^{4} \left (Z_{1}\right ){}^{4} +(2-4 k) \left (\zeta r_{0}^{2}+1\right ) \\ & \biggl( \frac{1}{C^{2} (4 k-3)} \biggl[\left (C (2 k-1) r_{0}^{2}-1 \right ) \\ &\biggl(4 C^{3} (1-2 k)^{2} (4 k-3) \omega _{2} \left (Z_{1} \right ){}^{4 k} \\ & -4 {\mathcal{A}}^{2} {\mathcal{B}}^{4} C^{3} (k-1) \zeta r_{0}^{6}+{\mathcal{A}}^{2} {\mathcal{B}}^{4} C^{2} (C (3-4 k) \\ &+(9-8 k) \zeta ) r_{0}^{4}+2 {\mathcal{A}}^{2} {\mathcal{B}}^{4} C (C (3-4 k) +(3-2 k) \zeta ) r_{0}^{2} \\ &+{\mathcal{A}}^{2} {\mathcal{B}}^{4} (C (3-4 k)+\zeta )\biggr)\biggr] \\ &- \frac{1}{2 k-1} \biggl[ {\mathcal{B}}^{4} {\mathcal{A}}^{2} \left (Z_{1}\right ){}^{2} \left (3 C (2 k-1) r_{0}^{2}-1\right ) \\ &\biggl(2 C (k-1) \zeta r_{0}^{2}+C (2 k-1)-\zeta \biggr) \biggr] \biggr)\biggr) \biggr] \biggr]^{ \frac{1}{2}} \\ & - \frac{1}{(2-4 k) \left (\zeta r_{0}^{2}+1\right )} \biggl[ {\mathcal{A}} {\mathcal{B}} \zeta r_{0} \left (Z_{1}\right ){}^{1-k}\biggr]\biggr) \biggr] \\ & \biggl( \biggl[ \frac{1}{{\mathcal{B}}^{2} (2-4 k)^{2} \left (\zeta r_{0}^{2}+1\right ){}^{2}} \\ & \biggl[ \left (Z_{1}\right ){}^{-2 (k+1)} \biggl({\mathcal{A}}^{2} \zeta ^{2} r_{0}^{2} {\mathcal{B}}^{4} \left (Z_{1}\right ){}^{4} \\ &+(2-4 k) \left (\zeta r_{0}^{2}+1\right )\biggl( \frac{1}{C^{2} (4 k-3)} \\ & \biggl[ \left (C (2 k-1) r_{0}^{2}-1\right ) \\ &\biggl(4 C^{3} (1-2 k)^{2} (4 k-3) \omega _{2} \left (Z_{1}\right ){}^{4 k} \\ &-4 {\mathcal{A}}^{2} { \mathcal{B}}^{4} C^{3} (k-1) \zeta r_{0}^{6} \\ &+{\mathcal{A}}^{2} {\mathcal{B}}^{4} C^{2} (C (3-4 k) +(9-8 k) \zeta ) r_{0}^{4} \\ &+2 {\mathcal{A}}^{2} {\mathcal{B}}^{4} C (C (3-4 k)+(3-2 k) \zeta ) r_{0}^{2} \\ & +{\mathcal{A}}^{2} {\mathcal{B}}^{4} (C (3-4 k)+\zeta )\biggr)\biggr] \\ &- \frac{1}{2 k-1} \biggl[{\mathcal{B}}^{4} {\mathcal{A}}^{2} \left (Z_{1}\right ){}^{2} \left (3 C (2 k-1) r_{0}^{2}-1\right ) \\ & \left (2 C (k-1) \zeta r_{0}^{2}+C (2 k-1)-\zeta \right ) \biggr] \biggr)\biggr) \biggr] \biggr]^{\frac{1}{2}} \\ &- \frac{{\mathcal{A}} {\mathcal{B}} \zeta r_{0} \left (Z_{1}\right ){}^{1-k}}{(2-4 k) \left (\zeta r_{0}^{2}+1\right )} \biggr){}^{2} \left (Z\right )^{2 k+2} \biggr] - \frac{1}{2 k-1} \\ & \biggl[ 2 C {\mathcal{A}}^{2} \left ( Z\right )^{2} \biggl(4 C k^{2} r^{2}+C r^{2} \\ &-k \left (4 C r^{2}+3\right )+1\biggr) \left (\zeta r^{2}+1 \right ) \biggr] \\ & + \frac{1}{{\mathcal{B}}^{4} C^{2} \left (8 k^{2}-10 k+3\right )} \\ & \biggl[ {\mathcal{B}}^{4} \left ({\mathcal{A}} C r^{2}+{\mathcal{A}}\right )^{2} \biggl((4 k-3) r^{2} \bigl(4 \left (\zeta r^{2}+1\right ) k^{2} \\ &-4 \left (2 \zeta r^{2}+1\right ) k+4 r^{2} \zeta +1\bigr) C^{4} \\ & -(4 k-3) \left (-5 \zeta r^{2}+k \left (6 \zeta r^{2}+2\right )-1 \right ) C^{3} \\ &+\biggl(8 \biggl(6 k^{3}-13 k^{2}+9 k-2\biggr) \zeta r^{4}+3 (1-2 k)^{2} \\ & (4 k-3) r^{2}+(4 k-3) \zeta \biggr) C^{2} \\ &-(2 k-1 \left (-11 \zeta r^{2}+2 k \left (7 \zeta r^{2}+2\right )-3\right ) C \\ &+(2 k-1) \zeta \biggr) -4 C^{3} (2 k-1)^{3} (4 k-3) \left (Z\right )^{4 k} \\ &\biggl(C (2 k-1) r^{2}-1\biggr) \omega _{2} \biggr] \biggr) \biggr] , \end{aligned}$$

(B3)

where $Z = Cr^{2}+1$, $Z_{1}=Cr_{0}^{2}+1$.