Study of the $^{3}He(\alpha ,\gamma )^{7}Be$ reaction using effective field theory

Abstract

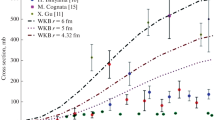
The $^{3}He(\alpha ,\gamma )^{7}Be$ reaction as one of the twelve reactions in Big-Bang Nucleosynthesis (BBN) has an important role in making light nuclei. Measuring its cross section within the range of astrophysical energies can answer many questions in astrophysics. In this work, we used the Effective Field Theory (EFT) method to find the radiative capture cross section of the $^{3}He(\alpha ,\gamma )^{7}Be$ reaction in the astrophysical energy range. We calculated the astrophysical $S$-factor in the $E_{1}$ and $E_{2}$ transitions to the ground state ($l_{f}=1$, $J_{f}=3/2$), at Leading Order (LO). The results of this procedure are in good agreement with the other theoretical methods and the available experimental results.

Appendix: How to calculate Kernel functions

To calculate the kernel functions, we must take the following steps:

$$\begin{aligned} Z_{ij}(q,q^{\prime };E) =&\iint p^{2} \,dp p^{\prime \,2}\, dp^{ \prime }\quad g_{l_{i}}(p) G_{0}^{(i)}(p,q;E) \\ \times & g_{l_{j}}(p^{\prime }) _{i}< p,q;\Omega _{i}\mid {p^{ \prime },q^{\prime };\Omega _{j}}>_{j}. \end{aligned}$$

(38)

1) Two complete sets of Jacobian momentum $p$ and $q$ should be inserted into $Z_{ij}$ function as follows:

$$\begin{aligned} &\iint \, d^{3}p_{1}\, d^{3}q_{1}\, \mid {p_{1}q_{1}}> < p_{1}q_{1} \mid ,\\ &\iint \, d^{3}p_{2}\, d^{3}q_{2}\, \mid {p_{2}q_{2}}> < p_{2}q_{2} \mid , \end{aligned}$$

$$\begin{aligned} Z_{ij}(q,q^{\prime };E) =&\iint p^{2} \,dp p^{\prime \,2}\, dp^{ \prime }\quad g_{l_{i}}(p) G_{0}^{(i)}(p,q;E) \\ \times &\,g_{l_{j}}(p^{\prime }) \iint \, d^{3}p_{1}\, d^{3}q_{1} \, \iint \, d^{3}p_{2}\, d^{3}q_{2} \\ \times &\, _{i}< p,q;(l_{i},\lambda _{i})\, , (L_{i},M_{i})\mid {p_{1} \, q_{1}}>_{i} \\ \times & \, _{i}< p_{1}\, q_{1}\mid {p_{2}\, q_{2}}>_{j} \\ \times &_{j}< p_{2}\, q_{2}\mid {p{\prime },q{\prime };(l_{i},\lambda _{i}) \, , (L_{i},M_{i})}>_{j}. \end{aligned}$$

(39)

2) Matrix elements including spin and orbital angular momentum quantum numbers are defined as follows:

$$\begin{aligned} &_{i}< p,q;(l_{i},\lambda _{i})\, , (L_{i},M_{i})\mid {p_{1}\, q_{1}}>_{i}= \\ &\frac{1}{p_{1}^{2}}\, \delta (p_{1}-p)\, \frac{1}{q_{1}^{2}}\, \delta (q_{1}-q)\, y_{l_{i}\, \lambda _{i}}^{*\, L_{i}\, M_{i}}\, ( \hat{p_{1}}\, \hat{q_{1}}), \\ &_{j}< p_{2}\, q_{2}\mid {p,q;(l_{j},\lambda _{j})\, , (L_{j},M_{j})}>_{j} = \\ &\frac{1}{p_{2}^{2}}\, \delta (p_{2}-p)\, \frac{1}{q_{2}^{2}}\, \delta (q_{2}-q)\, y_{l_{j}\, \lambda _{j}}^{\, L_{j}\, M_{j}}\, ( \hat{p_{2}}\, \hat{q_{2}}). \end{aligned}$$

(40)

Using the following equation, we can separate the variables $p$ and $q$ in the $y_{l_{i}\, \lambda _{i}}^{\, L_{i}\, M_{i}}$ functions:

$$\begin{aligned} y_{l_{j}\, \lambda _{j}}^{\, L_{j}\, M_{j}}\, (\hat{p_{2}}\, \hat{q_{2}}) =&\sum _{m_{l_{i}}}\sum _{m_{\lambda _{i}}}\, C(l_{i}, \lambda _{i},L\mid {m_{l_{i}},m_{\lambda _{i}},M_{L_{i}}}) \\ \times & y_{l_{i}\, m_{l_{i}}}(\hat{p})\, y_{\lambda _{i}\, m_{l_{i}}}( \hat{q}). \end{aligned}$$

(41)

Also, the projection of the eigenstate of momentum $i$ on the eigenstate of momentum $j$ is defined as:

$$\begin{aligned} _{i}< p_{1}\, q_{1}\mid {p_{2}\, q_{2}}>_{j}=\delta ^{(3)}(p_{1}+p_{ij}) \, \delta ^{(3)}(p_{2}+p_{ij}^{\prime }), \end{aligned}$$

(42)

where $p_{ij}$, $p_{ij}^{\prime }$ are the Jacobian coordinates and are defined by the following general relations. For the three particles $(i, j, k)$ in which $(k)$ is the observer and $(i,j)$ are the pair, relative momentum of the pair, represented by $p_{ij}$, and the relative momentum of the observer and pair, $p_{k}^{\prime }=p_{ij}^{\prime }$, are;

$$\begin{aligned} &p_{ij}=\frac{m_{j}\, \hat{q_{i}}-m_{i}\, \hat{q_{j}}}{m_{i}+m_{j}}, \\ &p_{ij}^{\prime }= \frac{m_{k}(\hat{q_{i}}+\hat{q_{j}})-(m_{i}+m_{j})\hat{q_{k}}}{m_{i}+m_{j}+m_{k}}. \end{aligned}$$

(43)

The quantities $\hat{q_{i}}$, $\hat{q_{j}}$, $\hat{q_{k}}$ are the particles’ momenta in the center-of-mass framework, and the indices change for different pairs and observers.

3) After substituting the above relations into $Z_{ij} (q.q^{\prime };E)$;

$$\begin{aligned} Z_{ij}(q,q^{\prime };E) =&\iint p^{2} \,dp p^{\prime \,2}\, dp^{ \prime } g_{l_{i}}(p) G_{0}^{(i)}(p,q;E) \\ \times & g_{l_{j}}(p^{\prime }) \, \iint \, d^{3}p_{1}\, d^{3}q_{1}\, \iint \, d^{3}p_{2}\, d^{3}q_{2} \\ \times &\, \frac{1}{p_{1}^{2}}\, \delta (p_{1}-p)\, \frac{1}{q_{1}^{2}}\, \delta (q_{1}-q) \\ \times &\, \sum _{m_{l_{i}}}\sum _{m_{\lambda _{i}}}\, C(l_{i}, \lambda _{i},L\mid {m_{l_{i}},m_{\lambda _{i}},M_{L_{i}}}) \\ \times & y_{l_{i}\, m_{l_{i}}}^{*}(\hat{p}_{1})\, y_{\lambda _{i}\, m_{l_{i}}}^{*}( \hat{q}_{1}) \\ \times &\, \delta ^{(3)}(p_{1}+p_{ij})\, \delta ^{(3)}(p_{2}+p_{ij}^{ \prime }) \\ \times &\, \frac{1}{p_{2}^{2}}\, \delta (p_{2}-p)\, \frac{1}{q_{2}^{2}}\, \delta (q_{2}-q) \\ \times &\, \sum _{m_{l_{j}}}\sum _{m_{\lambda _{j}}}\, C(l_{j}, \lambda _{j},L\mid {m_{l_{j}},m_{\lambda _{j}},M_{L_{j}}}) \\ \times & y_{l_{j}\, m_{l_{j}}}(\hat{p}_{2})\, y_{\lambda _{j}\, m_{l_{j}}}( \hat{q}_{2}). \end{aligned}$$

(44)

Using the delta functions, the number of variables is reduced and the integral is converted in the following way:

$$\begin{aligned} Z_{ij}(q,q^{\prime };E) =&\iint \frac{1}{q^{2}} d^{3}q \frac{1}{q^{\prime 2}} d^{3}q^{\prime } \\ \times & g_{l_{i}}(-p_{ij}) G_{0}^{(i)}(-p_{ij},q;E) g_{l_{j}}(p_{ij}^{ \prime }) \\ \times &\, \sum _{m_{l_{i}}}\sum _{m_{\lambda _{i}}}\, C(l_{i}, \lambda _{i},L\mid {m_{l_{i}},m_{\lambda _{i}},M_{L_{i}}}) \\ \times &y_{l_{i}\, m_{l_{i}}}^{*}(-p_{ij})\, y_{\lambda _{i}\, m_{l_{i}}}^{*}(q) \\ \times &\, \sum _{m_{l_{j}}}\sum _{m_{\lambda _{j}}}\, C(l_{j}, \lambda _{j},L\mid {m_{l_{j}},m_{\lambda _{j}},M_{L_{j}}}) \\ \times & y_{l_{j}\, m_{l_{j}}}( p_{ij}^{\prime })\, y_{\lambda _{j}\, m_{l_{j}}}(q^{ \prime }). \end{aligned}$$

(45)

4) After expanding the sigma and calculating the Clebsch–Gordan coefficients, we can convert $p_{ij}$ and $p_{ij}^{\prime }$ in terms of particle mass and momentum $q$ and $q^{\prime }$. In this case $y_{l_{i} m_{l_{i}}}^{*} (-p_{ij})$ and $y_{l_{j} m_{l_{j}}} (p_{ij}^{\prime })$ will be as a combination of $q$ and $q{\prime }$. Using Eq. (45) we can convert them to the single-variable Legendre functions:

$$\begin{aligned} y_{lm}(\widehat{q_{1}+q_{2}}) =& \sum _{l_{1}+l_{2}=l} \sqrt{ \frac{4\pi (2l+1)!}{(2l_{1}+1)!\, (2l_{2}+1)!}} \\ \times & \frac{q_{1}^{l_{1}}\, q_{2}^{l_{2}}}{\mid {q_{1}+q_{2}}\mid ^{2}} \\ \times &\, \sum _{m_{1}m_{2} }\, C(l_{1}\, l_{2}\, l\mid {m_{1}\, m_{2} \, m}) \\ \times & y_{l_{1}m_{1}}(q_{1})\, y_{l_{2}m_{2}}(q_{2}). \end{aligned}$$

(46)

5) The parts consisting of Green functions and form factors, $g_{l_{i}} (-p_{ij} )\, G_{0}^{(i)} (-p_{ij},q;E)\, g_{l_{j}} (p_{ij}^{ \prime } )$, with the assumption of $g_{l_{i}} (-p_{ij} )=-p_{ij}$ and $g_{l_{j}} (p_{ij}^{\prime })=p_{ij}^{\prime }$, are rewritten in terms of Legendre functions:

$$\begin{aligned} &g_{l_{i}} (-p_{ij} )\, G_{0}^{(i)} (-p_{ij},q;E)\, g_{l_{j}} (p_{ij}^{ \prime }) \\ &=-p_{ij}\, p_{ij}^{\prime }\, G_{0}^{(i)} (-p_{ij},q;E) \\ &=-4\pi \, p_{ij}\, p_{ij}^{\prime }\, \sum _{l\, m_{l}}\, Q_{ij}^{ \prime }(q,q^{\prime };E)\, y_{l\,m_{l}}^{*}(\hat{q})\, y_{l\,m_{l}}( \hat{q}^{\prime }), \end{aligned}$$

(47)

where the function $Q_{ij}^{\prime }$ is defined as follows:

$$\begin{aligned} Q_{ij}^{\prime }(q,q^{\prime };E)=\frac{1}{2}\, \int _{-1}^{1}\, dx\, p_{l}(x) \, G_{0}^{(i)} (p,q;E), \end{aligned}$$

(48)

where

$$ G_{0}^{(i)} (p,q;E)=\left (E-\frac{p^{2}}{\mu _{jk}}- \frac{q^{2}}{\mu _{i(jk)}}\right )^{-1}, \quad p=-p_{ij}. $$

(49)

6) In this part, the Green function is computed by inserting the $-p_{ij}$ in terms of the particle momentum and entering the reduced mass into the above expression:

$$\begin{aligned} G_{0}^{(i)}(p,q;E) =&\{E-\left (\frac{m_{j}+m_{k}}{2m_{j}m_{k}}\right )\left ( \frac{m_{i}q^{\prime }+m_{k}q}{m_{i}+m_{k}}\right )^{2} \\ -&\frac{1}{2}\, q^{2}\left ( \frac{m_{i}m_{j}+m_{j}m_{k}+m_{k}m_{i}}{m_{i}m_{j}m_{k}}\right )\}^{-1}. \end{aligned}$$

(50)

By simplifying and separating the expressions in terms of $q$ and $q'$, by multiplying and dividing it by $\frac{m_{j}}{qq^{\prime }}$:

$$\begin{aligned} &G_{0}^{(i)} (p,q;E)=\frac{m_{j}}{qq^{\prime }}\, \{ \frac{1}{qq^{\prime }}\, [\, m_{j}\, E \\ &-\left (\frac{(m_{j}+m_{k})\, m_{k}}{2(m_{i}+m_{k})^{2}}+ \frac{m_{i}m_{j}+m_{j}m_{k}+m_{k}m_{i}}{2\, m_{i}m_{k}}\right )\, q^{2} \\ &-\left (\frac{(m_{j}+m_{k})\, m_{i}^{2}}{2(m_{i}+m_{k})^{2}m_{k}} \right )\,q^{\prime 2}\, ] - \left ( \frac{(m_{j}+m_{k})m_{i}}{(m_{i}+m_{k})^{2}}\right ) \}^{-1}. \end{aligned}$$

(51)

By substituting Eq. (50) into Eq. (47):

$$ Q_{ij}^{\prime }(q,q^{\prime };E)=\frac{1}{2}\, \frac{m_{j}}{qq^{\prime }}\, \int _{-1}^{1}\, dx\, p_{l}(x)\, \{z_{ik}-x \}^{-1}, $$

(52)

where

$$\begin{aligned} &z_{ik}= \frac{1}{qq^{\prime }}\, \{\, m_{j}\, E \\ &-\left (\frac{(m_{j}+m_{k})\, m_{k}}{2(m_{i}+m_{k})^{2}}+ \frac{m_{i}m_{j}+m_{j}m_{k}+m_{k}m_{i}}{2\, m_{i}m_{k}}\right )\, q^{2} \\ &-\left (\frac{(m_{j}+m_{k})\, m_{i}^{2}}{2(m_{i}+m_{k})^{2}m_{k}} \right )\,q^{\prime 2}\, \}, \end{aligned}$$

and

$$ x=\left (\frac{(m_{j}+m_{k})m_{i}}{(m_{i}+m_{k})^{2}}\right ). $$

(53)

By definition

$$ Q_{l}(z)=\frac{1}{2}\, \int _{-1}^{1}\, dx\, \frac{p_{l}(x)}{z_{ik}-x} , $$

and by substituting Eq. (51) into Eq. (46):

$$\begin{aligned} &g_{l_{i}} (-p_{ij} )\, G_{0}^{(i)} (-p_{ij},q;E)\, g_{l_{j}} (p_{ij}^{ \prime }) \\ &=-p_{ij}\, p_{ij}^{\prime }\, G_{0}^{(i)} (-p_{ij},q;E), \\ &=-4\pi \, p_{ij}\, p_{ij}^{\prime }\, \sum _{l\, m_{l}}\, Q_{ij}^{ \prime }(q,q^{\prime };E)\, y_{l\,m_{l}}^{*}(\hat{q})\, y_{l\,m_{l}}( \hat{q}^{\prime }) \\ &=-4\pi \, \frac{m_{j}}{qq^{\prime }}\, p_{ij}\, p_{ij}^{\prime }\, \sum _{l\, m_{l}}\, Q_{l}(z)\, y_{l\,m_{l}}^{*}(\hat{q})\, y_{l\,m_{l}}( \hat{q}^{\prime }). \end{aligned}$$

(54)

The functions $Q_{l} (z)$, are defined for different values of $I$, as follows:

$$\begin{aligned} &Q_{0}(z)=\frac{1}{2}\, \ln (\frac{z+1}{z-1}), \\ &Q_{1}(z)=\frac{1}{2}\, z \ln (\frac{z+1}{z-1})-1, \\ &Q_{2}(z)=\frac{1}{2}\, (-\frac{1}{2}+\frac{3}{2}\, z^{2})\ln ( \frac{z+1}{z-1})-\frac{3}{2}\, z . \end{aligned}$$

(55)

Following a review of the above six steps, the relation (37) will be completed in terms of $q$ and $q'$, which by subsequent integration, an expression will be obtained in terms of $q$ and $q'$.