LES of Premixed Turbulent Combustion Using Filtered Tabulated Chemistry

Abstract

The filtered tabulated chemistry (FTACLES) approach utilizes data from pre-tabulated explicitly filtered 1D flame profiles for closure of the LES-filtered transport terms. Different methodologies are discussed to obtain a suitable progress variable c from detailed chemistry calculations of a methane/air flame. In this context, special focus is placed on the analytical modeling of the reaction source term using series of parameterized Gaussians. For increasing effective filter sizes in LES (i.e. including the flame thickening) the precise shape of the reaction rate profile becomes less and less relevant. In particular, it is shown that for one-step chemistry, a single Gaussian is sufficient to derive an explicitly expressible 1D flame profile with a prescribed laminar flame speed and thermal flame thickness. The resulting artificial flame profile is shown to have similarities with profiles based on carbon chemistry and detailed reaction mechanisms. Next, the behavior of the filtered c-transport equation is analyzed and several possible closure methods are compared for a wide range of filter widths. It is shown that the unclosed contribution of the filtered diffusion term can be combined with the subgrid convection term, thus simplifying the FTACLES formulation. The model is implemented in OpenFOAM and validated in 1D for a variety of LES filter sizes in combination with artificial flame thickening. A power-law-based wrinkling model is modified for use with artificial flame thickening and combined with the FTACLES model to enable 3D simulations of a premixed turbulent Bunsen burner. The comparison of 3D Large Eddy Bunsen flame simulations at increasing levels of turbulence intensity shows a good match to experimental results for most investigated cases. In addition, the results are mostly insensitive to the variation of the mesh size.

1 Introduction

Synthetically produced fuels, such as hydrogen ($\textrm{H}_2$) or methane ($\textrm{CH}_\textrm{4}$), could become an important part of the future energy infrastructure (Agnolucci and McDowall 2013; Balat 2008; Biswas et al. 2020). Production (assuming a renewable energy source) and combustion of synthetic fuels constitute a closed carbon cycle, which makes the process inherently carbon neutral (“green”). These green fuels can be used as storage for excess renewable energy (power-to-X concepts (Biswas et al. 2020; Foit et al. 2017)), for power generation (electricity or transportation), and as a resource in industrial processes (Kohse-Höinghaus 2021).

Accurate computational fluid dynamic (CFD) simulations of reactive flows not only support the design of safe and efficient technical systems, but also provide deep insights into the physics of combustion itself. Direct numerical simulation (DNS) coupled with detailed chemistry reaction mechanisms aims at resolving all turbulent and chemical length and timescales and is therefore usually limited to small-scale experiments or simplified academic cases. DNS of practical application cases (which usually involve high Reynolds numbers) however, are presently mostly unfeasible because of the enormous computational demand. In terms of computational costs, Reynolds-averaged Navier–Stokes (RANS) simulations are several orders of magnitude cheaper than DNS, making RANS often the preferred method in industrial applications. The downside of RANS is the sometimes strong dependence of results on the utilized turbulence model, since the entire range of turbulent scales has to be modeled. With the growing availability of cheap computational resources, the usage of large eddy simulation (LES) is becoming increasingly attractive for application oriented combustion CFD. Due to the resolution of large- and medium-scale structures of the reactive flow, modeling efforts can be concentrated on small-scale effects, which are usually more universal and therefore more likely to be case independent (Janicka and Sadiki 2005).

A compilation and detailed explanation of the well-known modeling approaches for filtered transport equations (and the filtered reaction source term) for LES of turbulent premixed combustion can be found in Veynante and Vervisch (2002). This includes flame-surface-density (FSD) based approaches (Boger et al. 1998), the G-equation model (Williams 1985) and the Bray–Moss–Libby (BML) model (Libby and Williams 1994; Bray 1996). Also worth mentioning is the artificially thickened flame (ATF) model by Colin et al. (2000). The main common feature of the filtered tabulated chemistry model and the ATF model is the utilization of artificial flame thickening to ensure sufficient resolution of the flame front on the numerical grid. The main difference is that the ATF model does not utilize filtered tabulated closures based on 1D flames, since the filtered source term is explicitly defined by an Arrhenius expression. In the model presented in this work, all terms are filtered, which includes a model for the unclosed diffusion term based on tabulation.

The FTACLES (Filtered Tabulated Chemistry for Large Eddy Simulation) method proposed by Fiorina et al. (2010) closes the filtered transport equations by using pre-tabulated data from explicitly filtered 1D flames. Subsequent work has extended the FTACLES approach to stratified non-adiabatic flames (Auzillon et al. 2012; Fiorina et al. 2015), counter-flow flames (Coussement et al. 2015) and sprays (Chatelier et al. 2019). This work builds on the general approach of the original FTACLES model (Fiorina et al. 2010) for the LES of turbulent premixed methane/air flames. The objective of this paper is to investigate and compare different closure approaches for the filtered transport terms used in the context of the classic FTACLES formulation (Fiorina et al. 2010). After choosing a set of suitable closures, the modified FTACLES formulation is implemented in OpenFOAM, including a power-law-based wrinkling approach and a one-equation turbulence closure. This model formulation is shown to be suitable for the LES of premixed turbulent combustion by performing 3D simulations of turbulent Bunsen flames at different turbulence intensities and comparing the results to experimental data. Since the FTACLES-closures are based on filtered 1D flames, a thorough discussion on the modeling of 1D flame profiles is included. Here, a special focus is placed on analytical methods that allow the modeling of a well-defined global reaction source term based on Gaussians.

2 Modeling of 1D Flame Profiles

The stationary profile of a freely propagating premixed flame is calculated in 1D using the open source chemical kinetics and thermodynamics library Cantera (Goodwin et al. 2018) and the GRI-Mech 3.0 chemical mechanism (Frenklach et al. 2022). The diffusive fluxes are modeled using the mixture-averaged formulation implemented in Cantera. To facilitate comparisons with the turbulent Bunsen burner database of Kobayashi et al. (1996, 1997, 1998), a methane/air mixture with an equivalence ratio of $\phi =0.9$ is chosen. A grid spacing of $\Delta x = 1/20 \delta _\textrm{th}$ is selected to ensure a sufficient resolution of the flame reaction zone. The complete set of input parameters for detailed chemistry calculations with Cantera is shown in Table 1.

Table 1 Input parameters for the detailed chemistry calculations with Cantera

The temperature (T), density ($\rho$) and velocity (u) profiles for the converged stationary flame are shown in Fig. 1. The position of the reaction zone is centered around the maximum of the source term $\dot{\omega }$ (see Eq. (3)), the axial coordinate x is normalized with the thermal flame thickness $\delta _\textrm{th}$ which is defined as:

$$\begin{aligned} \delta _\textrm{th} = \frac{T_\textrm{ad}-T_0}{\textrm{max}(|\nabla T|)} \end{aligned}$$

(1)

Fig. 1

Velocity, density and temperature profiles of the stationary methane/air flame at $\phi =0.9$

The flame reaches an adiabatic flame temperature of $T_\textrm{ad}={2139}\,{\hbox {K}}$ and propagates with a laminar flame speed of $S_\textrm{L}={0.34}\,{\hbox {m}\,\hbox {s}^{-1}}$ (see Table 2 for flame parameters). A characteristic feature of many hydrocarbon flames is the pronounced tail of the temperature distribution in the post-active-reaction zone (Law 2006). This behavior is also apparent in the present result, as the temperature profile reaches its burned equilibrium value after a significant distance ($>10\delta _\textrm{th}$) away from the main reaction zone. More specifically, $T>90\%T_\textrm{ad}$ occurs at $\approx 3\delta _\textrm{th}$ (measured from $x=-1.5\delta _\textrm{th}$ to $x=1.5\delta _\textrm{th}$), while $T>99\%T_\textrm{ad}$ is only reached deep in the post-reaction zone at $x\approx 11.5\delta _\textrm{th}$.

Table 2 Flame parameters for the laminar methane/air flame at $\phi =0.9$

Due to the high computational demand associated with detailed chemistry computations (Lu and Law 2009), LES applications often model the combustion process as an irreversible one-step reaction. The transport equation for the reaction progress variable c and the global reaction source term $\dot{\omega }$ is as follows:

$$\begin{aligned} \frac{\partial \rho c}{\partial t} + \frac{\partial \rho u_i c}{\partial x_i} = \frac{\partial }{\partial x_i}\left( \rho D \frac{\partial c}{\partial x_i}\right) + \dot{\omega } \end{aligned}$$

(2)

For a stationary 1D case ($\partial /\partial t = 0$) and using mass conservation ($\rho u = \mathrm {const.}=\rho _0 S_\textrm{L}$) Eq. 2 can be simplified to:

$$\begin{aligned} \dot{\omega } = \rho _0 S_\textrm{L} \frac{\partial c}{\partial x} - \frac{\partial }{\partial x}\left( \rho D \frac{\partial c}{\partial x}\right) ~. \end{aligned}$$

(3)

For a Lewis number close to unity ($\textrm{Le}\approx 1$), the diffusivity $\rho D$ (with the diffusion coefficient D) can be calculated directly from the thermal conductivity (temperature-dependent) $\lambda (c)$ and the specific heat capacity $c_\textrm{p}(c)$ with $\rho D = \lambda /c_\textrm{p}$. Figure 2 shows the resulting profiles of $\rho D$ plotted vs. the normalized coordinate $x/\delta _{th}$ and vs. the reaction progress variable c.

Fig. 2

Normalized diffusivity $\rho D/\rho D_0$ over the normalized position (left) and over the reaction progress variable (right) for the methane/air flame at $\phi =0.9$

From the detailed chemistry solution, a temperature-based reaction progress variable $c_\textrm{T}$ (Pfitzner and Klein 2021) for use in an equivalent one-step reaction mechanism is derived as

$$\begin{aligned} c_\textrm{T} = \frac{T-T_\textrm{0}}{T_\textrm{ad}-T_0} ~, \end{aligned}$$

(4)

resulting in the flame-profile shown in Fig. 3. As an alternative to the temperature-based $c_\textrm{T}$-approach, the progress variable can also be defined by a suitable combination of species concentrations. Species-based progress variables can be defined using specific mole numbers $n=Y_k/W_k$ of $\textrm{CO}_2$, $\textrm{CO}$, $\textrm{H}_2$ and $\textrm{H}_2\textrm{O}$, where $Y_k$ and $W_k$ represent the respective mass fractions and molecular weights of the species k. With $n_\textrm{C}=n_\textrm{CO}+n_\textrm{CO2}$ and $n_\textrm{H}=n_\textrm{H2}+n_\textrm{H2O}$ the reaction progress variables based on carbon chemistry ($c_\textrm{C}$) and hydrogen chemistry ($c_\textrm{H}$) are defined as:

$$\begin{aligned} c_\textrm{C} = \frac{n_\textrm{C}-n_\textrm{C,0}}{n_{\textrm{C},\infty }-n_\textrm{C,0}} \qquad&c_\textrm{H} = \frac{n_\textrm{H}-n_\textrm{H,0}}{n_{\textrm{H},\infty }-n_\textrm{H,0}} \end{aligned}$$

(5)

Figure 3 compares the flame profiles obtained for $c_\textrm{T}$, $c_\textrm{C}$ and $c_\textrm{H}$. The $c_\textrm{T}$ profile inherits its pronounced tail from the detailed temperature profile. The tail is significantly reduced for $c_\textrm{H}$ and completely vanishes for $c_\textrm{C}$. Very similar findings have been made by Pfitzner and Breda (2021), who also find that the $c_\textrm{C}$ progress variable agrees well with an analytical single-step progress variable profile derived from Arrhenius-chemistry (Pfitzner 2021). The definitions for $c_\textrm{C}$ and $c_\textrm{H}$ have been chosen specifically due to their differences from $c_\textrm{T}$. If the goal is to maintain the tail in the post-reaction region as accurately as possible, then $c_\textrm{T}$ would certainly be the right choice.

Fig. 3

Reaction progress variables based on temperature ($c_\textrm{T}$), carbon-chemistry ($c_\textrm{C}$) and hydrogen-chemistry ($c_\textrm{H}$) for the methane/air flame at $\phi =0.9$

Having determined $\rho _0$, $S_\textrm{L}$ and $\rho D$ from the detailed chemistry calculations, the corresponding source terms $\dot{\omega }_\textrm{T}$, $\dot{\omega }_\textrm{C}$ and $\dot{\omega }_\textrm{H}$ are calculated from Eq. (3) and shown in Fig. 4. Depending on the definition of $\rho D$, the diffusion term on the right hand side of Eq. (3) can surpass the convective term, resulting in negative values of $\dot{\omega }$ over a limited range of c. In the present work, this is the case for $\dot{\omega }_\textrm{C}$ for $c<0.5$ and is (in general) an undesired behavior for single-step chemistry source terms. This problem is avoided by the approach suggested in Sect. 2.2.

Fig. 4

Chemical source term $\dot{\omega }$ for temperature based progress variable (subscript T), carbon-chemistry (C) and hydrogen-chemistry (H) for the methane/air flame at $\phi =0.9$

For a data-driven approach, the flame profiles determined in this section may be filtered numerically and used directly to create the tables for the filtered tabulated chemistry model (see Sect. 3.3). The following sections explore a function-driven approach by modeling $\dot{\omega }$ using Gaussians. First, Sect. 2.1 investigates the approximation of $\dot{\omega }$-curves obtained from detailed chemistry (for example $\dot{\omega }_\textrm{T}$) through a series of Gaussians. Second, in Sect. 2.2 a new analytic formulation for $\dot{\omega }$ is presented, which utilizes a single parameterized Gaussian and prescribed values for $S_\textrm{L}$ and $\delta _\textrm{th}$.

2.1 Laminar Flame Profile from Gauss-Based Source Term

In principle, the one-step reaction source terms obtained from detailed chemistry (for example $\dot{\omega }_\textrm{T}$ or $\dot{\omega }_\mathrm {C/H}$) can be approximated by a sum of parameterized Gaussians (Pfitzner et al. 2022):

$$\begin{aligned} \dot{\omega }_\textrm{gN}(x) = \sum _{n=1}^{N} \frac{A_n}{C_n\sqrt{\pi }} \exp \left[ -\left( \frac{x-B_n}{C_n}\right) ^2\right] ~. \end{aligned}$$

(6)

The Gauss coefficients $A_n$, $B_n$, and $C_n$ can be found by performing a least-squares curve fit on the $\dot{\omega }$-profile for a given number (N) of Gaussians. Figure 5 (left) shows the resulting fitted curves with $N=1$ to $N=7$ for the example of the source term $\dot{\omega }_\textrm{T}$, where the curve-fitted source terms are designated as $\dot{\omega }_\textrm{gN}$.

As expected, the agreement of the resulting $\dot{\omega }_\textrm{gN}$ and the original $\dot{\omega }_\textrm{T}$ improves with an increasing number of Gaussians N. The largest discrepancies at low N are found at the beginning and tail of the flame. A more quantitative evaluation can be made by comparing the integrals of the source terms. Defining $x=L_-$ as an arbitrary coordinate in the completely unburned ($c=0$) region of the flame and $x=L_+$ as an arbitrary coordinate in the completely burned ($c=1$) region, the definite integral of both sides of Eq. (3) can be evaluated as

$$\begin{aligned} \int _{L_-}^{L_+}\dot{\omega }\textrm{d}x=\rho _0 S_\textrm{L} ~, \end{aligned}$$

(7)

since the definite integral of the diffusion term from $x=L_-$ to $x=L_+$ always vanishes and $\int _{L_-}^{L_+} \partial c / \partial x ~\textrm{d}x = 1$.

Fig. 5

Comparison of the source term development over the normalized position (left) and source term integrals (right) for detailed chemistry $\dot{\omega }_\textrm{T}$ and Gauss-fit $\dot{\omega }_\textrm{gN}$

Comparing the normalized integrals of the source terms in Fig. 5 (right) reveals that for $N=1$ the overall integral reaction rate is under-predicted by $\approx 27\%$. The error decreases to $<1\%$ for $N=7$, a further increase in the number of Gaussians (with a reasonable number of additional terms) did not show further improvement. Next, the different c-profiles that result from the fitted source terms need to be determined. Using the derivative product rule, Eq. (3) can be rewritten as:

$$\begin{aligned} \frac{\partial ^2c}{\partial x^2} = - \frac{f_{\rho D}}{F_{\rho D}} \left( \frac{\partial c}{\partial x}\right) ^2 + \frac{\rho _0 S_\textrm{L}}{F_{\rho D}} \frac{\partial c}{\partial x} - \frac{\dot{\omega }}{F_{\rho D}} \end{aligned}$$

(8)

Here, we define $F_{\rho D}(c)=\rho D$ and $f_{\rho D}(c) = \partial F_{\rho D}/\partial c$. The functional dependencies of $F_{\rho D}(c)$ and $f_{\rho D}(c)$ on the progress variable c can be obtained from the detailed chemistry results, which are shown in Fig. 6 and are used in the present cases. It is seen that $F_{\rho D}$ can be fitted very well as a linear function (shown in Fig. 6), which leads to a constant $f_{\rho D}$. If a constant $F_{\rho D}$ is assumed, the function $f_{\rho D}=0$, which allows Eq. (8) to be solved analytically (see “Appendix 1”), but only for the special assumption of a Gaussian source term. A similiar Gauss-based analytical closure has been proposed by Duwig (2007) for flamelet LES and an analytical approach using Gauss-fitted Ansatz functions is also demonstrated in Pfitzner et al. (2022).

Fig. 6

Development of $F_{\rho D}$ (left) and $f_{\rho D }$ (right) over c for the detailed results obtained with Cantera (cant.) and a linear fit (lin.)

If $F_{\rho D}$ is not assumed as constant, Eq. (8) can be solved numerically. This has been done in this work using the “HYBRD” algorithm (Powell 1970; Moré et al. 1980), which is implemented in Python’s scipy.optimize.fsolve function (Virtanen et al. 2020). The resulting c-profiles are shown in Fig. 7. For $0\le c \le 0.75$ the c-profiles from the Gauss-fitted and detailed chemistry source terms show good agreement (even at $N=1$). The maximum attainable c is limited by the total integral reaction rate (see Fig. 5, right) and therefore $c \approx 1$ is only reached with $\dot{\omega }_\textrm{g7}$. Since the thermal flame thickness is determined from the maximum gradient of c, rather than its maximum value, all cases show good agreement in $\delta _\textrm{th}$, even for low N. In general, the number of summands (see Eq. (6)) needed may vary significantly depending on the definition of the source term from detailed chemistry (for example from temperature or species fractions). Nevertheless, the Gauss-fitting method provides an interesting approach, because it allows to analytically prescribe the source term and the corresponding 1D flame profile obtained from a flamelet solution with very good accuracy. In the context of an LES, the results from a sufficiently good approximation (through Gauss fitting) and tabulation would be identical. In Sect. 2.2 the idea of a Gaussian-based source term is modified, maintaining only a single Gaussian for simplicity.

Fig. 7

Comparison of reaction progress variable development (left) and thermal flame thickness (right) for c-profiles from detailed chemistry $\dot{\omega }_\textrm{T}$ and Gauss-fit $\dot{\omega }_\textrm{gN}$

2.2 Optimized Gaussian

A common approach to model the source term in irreversible single-step chemistry (Eq. (2)) is to use an Arrhenius-type expression of the form

$$\begin{aligned} \dot{\omega }_\textrm{A} = \rho B_\textrm{A} (1-c) \exp \left[ \frac{-E_\textrm{ac}}{R_\textrm{s}T}\right] ~, \end{aligned}$$

(9)

where $B_\textrm{A}$ denotes the pre-exponential Arrhenius factor, $E_\textrm{ac}$ the activation energy and $R_\textrm{s}$ the specific gas constant. Finding the values of $B_\textrm{A}$ and $E_\textrm{ac}$ is not a trivial task, particularly since analytic solutions of the 1D steady-state c transport equation do only exist for special cases. As a mathematical generalization of Eq. (9), the source term can be expressed as a single parameterized Gaussian $\dot{\omega }_\textrm{opt}$ with

$$\begin{aligned} \dot{\omega }_\textrm{opt} =\frac{A_\textrm{opt}}{C_\textrm{opt}\sqrt{\pi }} \exp \left[ -\left( \frac{x-B_\textrm{opt}}{C_\textrm{opt}}\right) ^2\right] ~. \end{aligned}$$

(10)

The goal is to find the parameters $A_\textrm{opt}$, $B_\textrm{opt}$ and $C_\textrm{opt}$, which represent a flame profile that has been optimized to achieve a specific, targeted (prescribed) laminar flame speed $S_\textrm{L}$ and flame thickness $\delta _\textrm{th,0}$. Since the laminar flame speed is defined by Eq. (7), the optimized Gaussian must meet the following condition (with adjusted limits $L^*_\pm =L_\pm \cdot C_\textrm{opt}+B_\textrm{opt}$):

$$\begin{aligned} \int _{L_-}^{L_+}\dot{\omega }\textrm{d}x=\int _{L^*_-}^{L^*_+}\frac{A_\textrm{opt}}{C_\textrm{opt}\sqrt{\pi }} \exp \left[ -\left( \frac{x-B_\textrm{opt}}{C_\textrm{opt}}\right) ^2\right] \textrm{d}x= \rho _0 S_\textrm{L} ~. \end{aligned}$$

(11)

The definite integral in Eq. (11) can be evaluated as

$$\begin{aligned} \frac{2}{\sqrt{\pi }C_\textrm{opt}}\int \exp \left[ -\left( \frac{x-B_\textrm{opt}}{C_\textrm{opt}}\right) ^2\right] = \textrm{erf}\left( \frac{x-B_\textrm{opt}}{C_\textrm{opt}}\right) + C_\textrm{I} ~, \end{aligned}$$

(12)

where $C_\textrm{I}$ is an integration constant and the error-function is defined as $\textrm{erf}(x)=2/\sqrt{\pi }\int _0^x \exp \left[ -\tau ^2\right] \textrm{d}\tau$. After inserting Eq. (12) into Eq. (11) we get:

$$\begin{aligned} \frac{A_\textrm{opt}}{2}\left[ \textrm{erf}\left( \frac{L_+^*-B_\textrm{opt}}{C_\textrm{opt}}\right) - \textrm{erf}\left( \frac{L_-^*-B_\textrm{opt}}{C_\textrm{opt}}\right) \right] =\frac{A_\textrm{opt}}{2}\left[ \textrm{erf}\left( L_+\right) - \textrm{erf}\left( L_{-}\right) \right] =\rho _0 S_\textrm{L} \end{aligned}$$

(13)

From $\textrm{erf}(L_\pm )=\pm 1$ follows $A_\textrm{opt}=\rho _0 S_\textrm{L}$. Since the maximum of $\dot{\omega }_\textrm{opt}$ is located (by definition) at $x=0$, it follows that $B_\textrm{opt}=0$. For a constant $F_{\rho D}$, the analytical solution given in “Appendix 1” is obtained. For a nonconstant $F_{\rho D}$ the coefficient $C_\textrm{opt}$ must be determined iteratively from Eq. (8), under the condition that $\textrm{max}(\partial c/\partial x)=1/\delta _\textrm{th}$.

Comparisons of $\dot{\omega }$ and c obtained with the optimized Gauss method ($\dot{\omega }_\textrm{opt}$), from a temperature-based progress variable ($\dot{\omega }_\textrm{T}$) and a carbon-based progress variable ($\dot{\omega }_\textrm{C}$) are shown in Fig. 8. Comparison of the integrals of $\dot{\omega }$ shows that all methods produce the correct flame speed $S_\textrm{L}$. It should be noted here that the $\dot{\omega }_\textrm{C}$ result obtained in Pfitzner and Breda (2021) does not show any negative values, since a different diffusion model ($\textrm{Le}_i=\mathrm {const.}$) is used to obtain their results. At first glance, the profiles of $c_\textrm{C}$ and $c_\textrm{opt}$ look very similar, since both do not have the distinct post-reaction tail seen for $c_\textrm{T}$. However, in detail, comparison of the flame thicknesses (evaluated from $\delta _\textrm{th}=1/\textrm{max}(\nabla c)$) reveals that the reference flame thickness $\delta _\textrm{th,0}$ (from Eq. 1) is reduced by about $30\%$ when using carbon-based chemistry, while the optimized Gauss method captures $\delta _\textrm{th,0}$ perfectly. While the approaches for $\dot{\omega }_\textrm{opt}$ and $\dot{\omega }_\textrm{g1}$ (Eq. (6) with $N=1$) both utilize a single Gaussian, the resulting profiles differ substantially (compare Fig. 5 and Fig. 8) since the parameters for $\dot{\omega }_\textrm{g1}$ are derived from a curve fit of $\dot{\omega }_\textrm{T}$, whereas $A_\textrm{opt}$, $B_\textrm{opt}$ and $C_\textrm{opt}$ are derived analytically.

In summary, while the Gauss optimization method produces a flame profile similar to the carbon-based method, the flame (by definition) maintains the prescribed reference values for both $S_\textrm{L}$ and $\delta _\textrm{th}$ and maintains $\dot{\omega }_\textrm{opt}\ge 0$. From comparisons with 3D results (see Sect. 5.3) the inclusion of the tail in $c_\textrm{T}$ has been found to be of very little influence in the case of the investigated LES configurations. For the present work the goal was to explore the possibilities of modeling the source term in an explicit mathematical way, without reconstructing it from the temperature or species distributions, and to investigate how this model could influence the behavior of the flame in the presence of turbulence. Using an analytically defined flame profile also allows for the analysis of very particular effects, such as the influence of the post-reaction tail by comparing results obtained from $c_\textrm{opt}$ and $c_\textrm{T}$, while keeping other characteristics such as $S_\textrm{L}$ and $\delta _\textrm{th}$ constant. Therefore, the results presented in the following sections are based on $\dot{\omega }_\textrm{opt}$ and $c_\textrm{opt}$ unless explicitly stated otherwise.

Fig. 8

Comparison of source term (top) and reaction progress variable (bottom) for profiles based on temperature $\dot{\omega }_\textrm{T}$, carbon-chemistry $\dot{\omega }_\textrm{C}$ and the optimized Gaussian $\dot{\omega }_\textrm{opt}$

3 A-Priori Analysis of Filtered Transport Equation

The 1D filtering operation to obtain the filtered quantity $\overline{z}(x)$ from the original quantity z(x) and a filter kernel r(x) can be expressed by the convolution integral

$$\begin{aligned} \overline{z}(x) = (z *r)(x) = \int _{-\infty }^{\infty }z(\tau )r(x-\tau ) \textrm{d}\tau ~, \end{aligned}$$

(14)

where 3D-filtering can be achieved by consecutively performing the 1-D filtering operation in all three spatial directions. The filter kernel r(x) with the filter width $\Delta$ is defined by the following Gaussian

$$\begin{aligned} r(x) = \frac{1}{\Delta }\sqrt{\frac{5}{\pi }}\exp \left[ -5\left( \frac{x}{\Delta }\right) ^2\right] ~, \end{aligned}$$

(15)

which has been derived by Pfitzner et al. (2022) based on the area-variation of planar flame fronts moving through filter volumes at different angles. From Eq. (14) the Favre-filtered (density weighted) quantity $\tilde{z}$ can be defined as:

$$\begin{aligned} \tilde{z} = \frac{\overline{\rho z}}{\overline{\rho }} \end{aligned}$$

(16)

By spatially filtering Eq. (2) one can obtain the following Favre-filtered transport equation for $\tilde{c}$:

$$\begin{aligned} \frac{\partial \overline{\rho } \tilde{c}}{\partial t} + \frac{\partial \overline{\rho }\tilde{u}_i\tilde{c}}{\partial x_i} = \frac{\partial }{\partial x_i}\left( \overline{\rho D \frac{\partial c}{\partial x_i}}\right) - \frac{\partial }{\partial x_i}\left( \overline{\rho }(\widetilde{u_i c}-\tilde{u}_i \tilde{c})\right) + \overline{\dot{\omega }} \end{aligned}$$

(17)

For the following 1D analysis the filtered values are based on $\overline{\dot{\omega }} = (\dot{\omega }_\textrm{opt} *r)$ and $\overline{c} = (c_\textrm{opt} *r)$, respectively. For this work, Eq. (14) was numerically evaluated to obtain the filtered values $\overline{z}(x)$ at the respective filter widths. Figure 9 shows $\overline{c}$ and $\tilde{c}$ evaluated at various filter sizes. The difference between $\overline{c}$ and $\tilde{c}$ is negligible for small filters, but becomes clearly noticeable with increasing $\Delta$. For very large filter sizes, the relation between $\overline{c}$ and $\tilde{c}$ converges to the flamelet expression (Peters 2000)

$$\begin{aligned} \overline{c} = \frac{\tilde{c}(1+\tau )}{1+\tau \tilde{c}} ~, \end{aligned}$$

(18)

which is derived from the Bray–Moss–Libby (BML) model (Libby and Williams 1994; Bray 1996). The heat release parameter $\tau$ in Eq. (18) is defined as $\tau =(T_\textrm{ad}-T_\textrm{0})/T_0$.

Fig. 9

Comparison of $\overline{c}$ and $\tilde{c}$ for different filter sizes $\Delta$ vs. normalized position (left) and vs. $\tilde{c}$ (right)

As clearly evident from Fig. 9 (left), the filtered flame thickness $\overline{\delta }_\textrm{th}$ increases significantly for larger $\Delta$, which is evaluated in detail in Fig. 10. For $\Delta \ge 2\delta _\textrm{th}$ the filtered flame thickness increases linearly as $\overline{\delta }_\textrm{th,l}\approx 0.8\Delta +0.3\delta _\textrm{th}$. As the filter size decreases to $\Delta \ll \delta _\textrm{th}$, the flame is fully resolved and $\overline{\delta }_\textrm{th}\approx \delta _\textrm{th}$. The nonlinear behavior between $0<\Delta \le 2\delta _\textrm{th}$ can be approximated by $\overline{\delta }_\textrm{th,nl}\approx 0.18 \Delta ^2/\delta _\textrm{th} + 0.09 \Delta + \delta _\textrm{th}$. The fits are meant to emphasize the linear and nonlinear behavior of $\overline{\delta }_\textrm{th}$ with varying $\Delta$. It cannot be expected that these fits work equally well for a wide range of operating conditions and fuel/oxidizer mixtures, as these factors can strongly affect the flame thickness. However, qualitatively, the behavior (first nonlinear then linear growth) should be the same for other cases as well, since this is mainly an effect caused by the filtering itself.

Fig. 10

Development of filtered flame thickness $\overline{\delta }_\textrm{th}$ with increasing filter size $\Delta$, with zoomed view of nonlinear section (left) and whole investigated range from $0<\Delta \le 100 \delta _\textrm{th}$ (right)

Since $\int _{-\infty }^{\infty }r(x)\textrm{d}x=1$ the area below the filtered and unfiltered source terms remains constant:

$$\begin{aligned} \int _{-\infty }^{\infty }\dot{\omega }\textrm{d}x = \int _{-\infty }^{\infty }\overline{\dot{\omega }}\textrm{d}x= \rho _0 S_\textrm{L} \end{aligned}$$

(19)

Therefore, with increasing filter size, the filtered reaction rate $\overline{\dot{\omega }}(x)$ is flattened and distributed over a wider region (see Fig. 11, left). The source term conditioned on $\tilde{c}$ (Fig. 11 (right)) shows a decrease and a shift of the maximum of $\overline{\dot{\omega }}$ to smaller values of $\tilde{c}$ with increasing filter size. The large gradient in the region between $0<\tilde{c}<0.1$ needs to be taken into account when creating the tables for $\overline{\dot{\omega }}(\tilde{c},\Delta )$, by choosing an appropriate step size for $\tilde{c}$.

Fig. 11

Comparison of $\dot{\omega }$ and $\overline{\dot{\omega }}$ for different filter sizes $\Delta$ over normalized position (left) and over $\tilde{c}$ (right)

Figure 12 compares the relative sizes of the filtered source term $\overline{\dot{\omega }}$, the filtered diffusion term $\partial (\overline{\rho D \partial c/\partial x})/\partial x$ and the SGS-flux term $\Omega =-\partial (\overline{\rho }(\widetilde{u c}-\tilde{u}\tilde{c}))/\partial x$. Normalization with the filtered flame thickness $\overline{\delta }_\textrm{th}$ (see Fig. 10) yields a maximum of the source term of $\textrm{max}(\overline{\dot{\omega }})\approx 1$.

For small filter sizes the SGS-flux term can be neglected, while the diffusion term reaches its peak at $\approx 60\%$ of the maximum source term value. When the filter size is increased, the relative sizes of the diffusion and SGS terms switch, as the influence of the diffusion term approaches 0, while the SGS-flux term reaches $\approx 60\%-70\%$ of the maximum value of the source term.

Fig. 12

Relative size-comparison of normalized filtered source term ($\overline{\dot{\omega }}$), the diffusion term (Diff.) and the SGS flux-term ($\Omega$) for different filter sizes $\Delta$ over normalized position

Figure 13 shows a comparison of $\tilde{c}_\textrm{opt}$ with the temperature-based Favre-filtered profiles of $\tilde{c}_\textrm{T}$. Interestingly, the influence of the post-reaction tail diminishes with increasing filter sizes, until there is only a negligible difference left for $\Delta = 10 \delta _\textrm{th}$. This indicates that for LES applications with a filter width exceeding $\approx 3\delta _\textrm{th}$ the overall results should change little when $\tilde{c}_\textrm{opt}$ or $\tilde{c}_\textrm{T}$ is used. This will be further investigated in Sect. 5.3.

Fig. 13

Comparison of $\tilde{c}_\textrm{opt}$ and $\tilde{c}_\textrm{T}$ for different filter sizes $\Delta$

3.1 Analysis and Modeling of the Diffusion Term

The filtered diffusion term (in 1D) is often modeled (Fiorina et al. 2010) as

$$\begin{aligned} \frac{\partial }{\partial x}\left( \overline{\rho D \frac{\partial c}{\partial x}}\right) \approx \frac{\partial }{\partial x}\left( \overline{\rho D} \frac{\partial \tilde{c}}{\partial x}\right) ~, \end{aligned}$$

(20)

which works well from a computational standpoint, since $\tilde{c}$ is readily available and $\overline{\rho D}$ can be modeled as a function of temperature and therefore, of $\tilde{c}$.

Fig. 14

Comparison of the $\overline{c}$ (left) and $\tilde{c}$ (right) diffusion term model with exact solution (reference) for different filter sizes $\Delta$ over $\tilde{c}$

Figure 14 (right) compares the exactly filtered LHS (left-hand side) and model expression on the RHS (right-hand side) of Eq. (20) for the 1D flame profile, revealing a large modeling error at higher filter widths. The modeling error is mainly due to the use of $\partial \tilde{c} /\partial x$ and can be significantly reduced using $\partial \overline{c} /\partial x$

$$\begin{aligned} \frac{\partial }{\partial x}\left( \overline{\rho D \frac{\partial c}{\partial x}}\right) \approx \frac{\partial }{\partial x}\left( \overline{\rho D} \frac{\partial \overline{c}}{\partial x}\right) ~, \end{aligned}$$

(21)

which is shown in Fig. 14 (left). Please note that in the case of $\rho D=const.=\overline{\rho D}$, the RHS of Eq. (21) becomes an exact expression, while the RHS of Eq. (20) produces an error proportional to the difference between the second derivatives of $\overline{c}$ and $\tilde{c}$. To further improve the agreement between the (exact) filtered diffusion term and the modeled diffusion term, Fiorina et al. (2010) introduces the correction factor $\alpha _\textrm{c}$, which is defined as

$$\begin{aligned} \frac{\partial }{\partial x}\left( \overline{\rho D \frac{\partial c}{\partial x}}\right) = \frac{\partial }{\partial x}\left( \alpha _{\tilde{c}}~ \overline{\rho D} \frac{\partial \tilde{c}}{\partial x}\right) ~. \end{aligned}$$

(22)

The correction factor $\alpha _{\tilde{c}}$ can then be written as

$$\begin{aligned} \alpha _{\tilde{c}} = \frac{\overline{\rho D \frac{\partial c}{\partial x}}}{\overline{\rho D} \frac{\partial \tilde{c}}{\partial x}} ~. \end{aligned}$$

(23)

For the approach based on $\bar{c}$ in Eq. (21) the correction factor $\alpha _{\overline{c}}$ can be calculated simply by replacing $\tilde{c}$ with $\overline{c}$ in Eq. (23). The resulting correction factors $\alpha _{\tilde{c}}$ and $\alpha _{\overline{c}}$ are shown in Fig. 15 for a range of filter sizes $\Delta$.

Fig. 15

Diffusion term correction factors $\alpha _{\tilde{c}}$ (left) and $\alpha _{\overline{c}}$ (right) for different filter sizes $\Delta$ over $\tilde{c}$

Since the correction factor can also be interpreted as a measurement of the modelling error, the values reached for $\alpha _{\tilde{c}}$ are substantially higher than for $\alpha _{\overline{c}}$, especially at large filter widths. In both cases, the largest values are reached between $0<\tilde{c}<0.2$, as the peak of the diffusion term is shifted to smaller $\tilde{c}$ values for increasing filter sizes (similar to the source term in Fig. 11, left).

Based solely on the a-priori assessment, the usage of $\partial \overline{c}/\partial x$ seems to be clearly advantageous. However, $\overline{c}$ is generally not known in a simulation that solves a transport equation for $\tilde{c}$, so a model of $\overline{c}(\tilde{c},\Delta )$ is required. Simulations using a filtered diffusion term using a tabulated $\overline{c}(\tilde{c},\Delta )$ derived from the 1D filtered flame profiles (see Fig. 9) unfortunately yielded inconclusive results regarding the numerical stability of this approach.

Overall, it is found that the model can be quite sensitive to small errors in the numerical tabulation of the closure terms (causing large deviations in the flame speed), which makes it important to obtain numerically precise values for $\alpha _{\tilde{c}}$. This is complicated by its limiting behavior, with $\alpha _{\tilde{c}}$ approaching 0/0 as $\tilde{c}\rightarrow 0$. Furthermore, while $\alpha _{\tilde{c}}$ has its peak close to $\tilde{c}=0$, it must approach $\alpha _{\tilde{c}}=1$ exactly at $\tilde{c}=0$, since there $\overline{\rho D \partial c /\partial x}=\overline{\rho D}\partial \tilde{c} /\partial x$. In the following section, an alternative to the $\alpha _{\tilde{c}}$ based approach is presented, which combines the modeling uncertainty of the filtered diffusion term and the subgrid-scale flux term (SGS-flux), thus eliminating the need for the $\alpha _c$ correction factor altogether.

3.2 Analysis and Modeling of the Subgrid-Scale Flux Term

Considering mass conservation ($\rho u = \rho _0 S_\textrm{L})$ in a steady laminar premixed flame (in 1D), the SGS-flux term can be simplified to:

$$\begin{aligned} \frac{\partial }{\partial x}(\overline{\rho }(\widetilde{u c}-\tilde{u}\tilde{c})) = \frac{\partial }{\partial x}(\overline{\rho u c} - \overline{\rho } \tilde{u}\tilde{c}) = \rho _0 S_\textrm{L}\frac{\partial }{\partial x}(\overline{c}-\tilde{c})~. \end{aligned}$$

(24)

Following the procedure presented by Fiorina et al. (2010) the SGS-flux can be modeled by tabulating Eq. (24) as $\Omega (\tilde{c},\Delta ) =\rho _0 S_\textrm{L}\partial (\overline{c}-\tilde{c})/\partial x$ and including $\Omega (\tilde{c},\Delta )$ in the $\tilde{c}$ transport equation as a source term. If the SGS-flux is modeled according to Eq. (24) the diffusion term in Eq. (17) must be corrected using the correction factors $\alpha _{\tilde{c}}$ or $\alpha _{\overline{c}}$, as explained in Sect. 3.1. The difference $\tilde{c}-\overline{c}$ can be interpreted as the normalized SGS-flux $-\rho _0 S_\textrm{L}(\overline{c}-\tilde{c})/(\rho _0 S_\textrm{L})$ and is shown in Fig. 16 (left).

Fig. 16

Normalized SGS-flux (left) and normalized diffusion error-term (right) over $\tilde{c}$ for different filter sizes $\Delta$

The normalized SGS term will approach the following limit for very large filter sizes, which can be calculated by the BML-theory introduced with Eq. (18):

$$\begin{aligned} (\tilde{c}-\overline{c})_\textrm{lim}=\tilde{c}\left( 1-\frac{1+\tau }{1+\tau \tilde{c}}\right) \end{aligned}$$

(25)

In contrast, the diffusion “error term” $(\overline{\rho D \partial c/\partial x})- (\overline{\rho D} \partial \tilde{c}/\partial x)$ shown in Fig. 16 (right) does not approach such a limit, but rather reaches a maximum for intermediate filter sizes of $\Delta \approx 1\delta _\textrm{th}-3\delta _\textrm{th}$. For larger filter sizes, the error term shrinks significantly and approaches 0. This behavior can be explained using the following estimate of the error-term

$$\begin{aligned} \overline{\rho D \frac{\partial c}{\partial x}} - \overline{\rho D} \frac{\partial \tilde{c}}{\partial x} \approx \overline{\rho D}\frac{\partial \overline{c}}{\partial x} - \overline{\rho D} \frac{\partial \tilde{c}}{\partial x} = -\overline{\rho D}\frac{\partial (\tilde{c}-\overline{c})}{\partial x} ~. \end{aligned}$$

(26)

For small filter sizes, up to $\approx 3\delta _\textrm{th}$, the difference $(\tilde{c}-\overline{c})$ will grow rapidly (see Fig. 16, left), while the flame thickness stays comparably small (see Fig. 10). This leads to an overall increase of the gradient on the right-hand side of Eq. (26) and therefore to a growing error term. As the filter size increases further, the difference $(\tilde{c}-\overline{c})$ approaches the BML-limit, while at the same time the flame thickness continues to grow linearly, leading to an overall decrease in the error term (due to the reduction of the x gradients of filtered quantities with growing filter size).

Here, we propose to combine the filtered diffusion term and the SGS-subgrid flux into the following modified flux term:

$$\begin{aligned} \Omega ^* = \frac{\partial }{\partial x}\left( \overline{\rho D \frac{\partial c}{\partial x}} - \overline{\rho D} \frac{\partial \tilde{c}}{\partial x} - \rho _0 S_\textrm{L} (\overline{c}-\tilde{c})\right) \end{aligned}$$

(27)

In this case, only one combined modelling error occurs and the resulting model equation appears to be more numerically robust as shown below. Note, that the integral across the flame of Eq. (27) must vanish. This is shown in Fig. 16, where the difference $(\overline{c}-\tilde{c})$ and the gradient term $(\overline{\rho D\partial c/\partial x} - \overline{\rho D} \partial \tilde{c}/\partial x)$ approach 0 as $\tilde{c}$ approaches the limits 0 and 1. A similar closure, which models the individual contribution of the unresolved diffusion and convection as source terms, is demonstrated by Coussement et al. (2015) in the context of non-premixed counter-flow flames.

In Fig. 17 the flux terms $\Omega$ and $\Omega ^*$, evaluated from filtering the 1D flame profiles, are compared.

Fig. 17

Comparison of normalized $\Omega ^*$ (solid lines) and normalized $\Omega$ (dashed lines) SGS-flux terms over $\tilde{c}$ for different filter sizes $\Delta$

Generally, the modification leads to a shift of the SGS-flux curves (or their minima) towards higher levels of $\tilde{c}$. Consistent with the findings in Fig. 16 (right), the effect of adding the modeling error of the diffusion term is largest for intermediate filter sizes $\Delta \approx 1\delta _\textrm{th}-3\delta _\textrm{th}$, while there is only a slight shift of the profiles at larger filters. For very large filter sizes, the modified term $\Omega ^*$ will approach the BML-limit of the unmodified term $\Omega$ as the diffusion error approaches zero (see Fig. 16). Although the relative difference between modified and unmodified terms seems large for the $\Delta =0.5\delta _\textrm{th}$ case, the size of the SGS term is insignificant for small filter sizes compared to the other terms in the c transport equation, as shown in Fig. 12.

3.3 Definition of Filtered Tabulated Chemistry Model for LES

In the LES context, the transport equations for the momentum, absolute enthalpy $\tilde{h}_\textrm{a}$ and the Favre-filtered reaction progress variable $\tilde{c}$ can be modeled in the following way:

$$\begin{aligned} \frac{\partial \overline{\rho }}{\partial t} + \frac{\partial (\overline{\rho } \tilde{u}_k)}{\partial x_k}&=0 \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial (\overline{\rho } \tilde{u}_i)}{\partial t} + \frac{\partial (\overline{\rho } \tilde{u}_k \tilde{u}_i)}{\partial x_k}&= \frac{\partial \tilde{\tau }_{\textrm{eff,}{ki}}}{\partial x_k} - \frac{\partial \overline{p}}{\partial x_i} \end{aligned}$$

(29)

$$\begin{aligned} \frac{\partial (\overline{\rho } \tilde{h}_\textrm{a})}{\partial t} + \frac{\partial (\overline{\rho } \tilde{u}_k \tilde{h}_\textrm{a})}{\partial x_k}&= -\frac{\partial (\overline{\rho } \tilde{K})}{\partial t} - \frac{\partial (\overline{\rho } \tilde{u}_k \tilde{K})}{\partial x_k} \nonumber \\ {}&\quad -\frac{\partial \overline{p}}{\partial t} + \frac{\partial }{\partial x_k} \left( \left( \overline{\rho D}[\tilde{c},\Delta ^{\prime }] + \frac{\mu _\textrm{t}}{\textrm{Pr}_\textrm{t}}\right) \frac{\partial \tilde{h}_\textrm{a}}{\partial x_k} \right) \end{aligned}$$

(30)

$$\begin{aligned} \frac{\partial \overline{\rho } \tilde{c}}{\partial t} + \frac{\partial \overline{\rho }\tilde{u}_k\tilde{c}}{\partial x_k}&= \Xi \frac{\partial }{\partial x_k}\left( \overline{\rho D}[\tilde{c},\Delta ^{\prime }] \frac{\partial \tilde{c}}{\partial x_k}\right) + \Xi \Omega ^*[\tilde{c},\Delta ^{\prime }] + \Xi \overline{\dot{\omega }}[\tilde{c},\Delta ^{\prime }] ~. \end{aligned}$$

(31)

The effective stress-rate tensor $\tau _\textrm{eff}$ in Eq. (30) includes both the resolved stress-rate and the subgrid-scale Reynolds-stresses, which are modeled using a Boussinesq Eddy Viscosity approach. A thorough derivation of $\tau _\textrm{eff}$ (and its OpenFOAM implementation) can be found in the work of Holzmann (2019). The energy transport equation in Eq. (30) is expressed in terms of the filtered absolute enthalpy $\tilde{h}_\textrm{a}$, which contains the sensible enthalpy and the heat of formation. The filtered specific kinetic energy $\tilde{K}$ is defined as $\tilde{K}=0.5 |\varvec{\tilde{u}}|^2$. The unresolved turbulent fluxes are modeled by a gradient closure approach

$$\begin{aligned} \widetilde{u_k h_\textrm{a}} - \tilde{u}_k \tilde{h}_a = - \frac{\mu _\textrm{t}}{\textrm{Pr}_\textrm{t}}\frac{\partial \tilde{h}_\textrm{a}}{\partial x_k} ~, \end{aligned}$$

(32)

where the turbulent Prandtl number is set to $\textrm{Pr}_\textrm{t}=1$ and the turbulent viscosity is determined from Eq. (33). For unity Lewis numbers and adiabatic flow, the total enthalpy remains constant and Eq. (30) can be omitted. Therefore, the particular closures used in Eq. (30) do not have a significant impact on the $\tilde{c}$ field.

Finally, the transport equation for the filtered reaction progress variable $\tilde{c}$ utilizes the filtered tabulated chemistry approach. The 2D table interpolations of the respective quantities $\overline{\rho D}[\tilde{c},\Delta ^{\prime }]$, $\Omega ^*[\tilde{c},\Delta ^{\prime }]$ (see Eq. (27)) and $\overline{\dot{{\omega }}}[\tilde{c},\Delta ^{\prime }]$ (see Eq. (10)) can be obtained from the previously discussed filtered 1D-solution (Sect. 2.2) of the optimized Gaussian flame profile.

The tables are evaluated at the effective filter size $\Delta ^{\prime }=\Delta c_\Delta$ (Fiorina et al. 2010), where $c_\Delta$ can be interpreted as a flame thickening parameter. Choosing a flame thickening factor $c_\Delta >1$ ensures that the flame can be resolved sufficiently even on coarser meshes, where the LES filter size $\Delta$ is typically larger than the thermal flame thickness. A similar approach can be found in the well-known artificial thickened flame model (Colin et al. 2000). The implementation of the wrinkling factor $\Xi$ in Eq. (31) ensures that the filtered flame propagates at a turbulent flame speed $S_\textrm{t}=\Xi S_\textrm{L}$ (see also Fiorina et al. 2010). The wrinkling factor takes into account that the subgrid filtered chemical source term increases proportionally to the area of the reaction front folded by turbulent eddies, which is not explicitly resolved by the LES. The modeling of the subgrid scale turbulence (including the turbulent viscosity $\mu _\textrm{t}$) and the subgrid flame wrinkling $\Xi$ are discussed in the following subsections.

3.3.1 Modelling of Subgrid Scale Turbulence

According to Yoshizawa and Horiuti (1985), the turbulent viscosity can be calculated from

$$\begin{aligned} \mu _\textrm{t}=C_\textrm{k} \Delta \sqrt{k_\textrm{sgs}} ~, \end{aligned}$$

(33)

where the model coefficient $C_\textrm{k}$ is approximated as $C_\textrm{k}\approx 0.094$ (Schumann 1975). In the present work, the one-equation eddy-viscosity model, derived by Yoshizawa and Horiuti (1985), is utilized to evaluate the subgrid turbulent energy $k_\textrm{sgs}$ (see also Huang and Li 2009 and Schumann (1975) for further context). In this model, $k_\textrm{sgs}$ is described by the following transport equation:

$$\begin{aligned} \frac{\partial \overline{\rho } k_\textrm{sgs}}{\partial t} +\frac{\partial \overline{\rho }\tilde{u}_k k_\textrm{sgs}}{\partial x_k} = \frac{\partial }{\partial x_k} \left( \overline{\rho }(\mu + \mu _\textrm{t}) \frac{\partial k_\textrm{sgs}}{\partial x_k}\right) - \frac{C_\textrm{e} \overline{\rho } k_\textrm{sgs}^{3/2}}{\Delta } - \tilde{\tau }_{{ki},\textrm{sgs}} \overline{S}_{ki} ~. \end{aligned}$$

(34)

The model coefficient $C_\textrm{e}$ is approximated as $C_\textrm{e}\approx 1$ (Schumann 1975) and the subgrid tensor $\tilde{\tau }_{{ki},\textrm{sgs}}$ can be determined from

$$\begin{aligned} \tilde{\tau }_{{ki},\textrm{sgs}}=\frac{2}{3}k_\textrm{sgs}\delta _{ki}-2\mu _\textrm{t}\overline{S}_{ki} ~, \end{aligned}$$

(35)

with the filtered deformation rate tensor:

$$\begin{aligned} \overline{S}_{ki}=\frac{1}{2}\left( \frac{\partial \tilde{u}_k}{\partial x_i} + \frac{\partial \tilde{u}_i}{\partial x_k}\right) ~. \end{aligned}$$

(36)

3.3.2 Wrinkling Factor Modeling

The flame wrinkling factor $\Xi =\Sigma _\textrm{gen}/|\nabla \overline{c}|$ is defined by the ratio of the generalized flame surface density $\Sigma _\textrm{gen}=\overline{|\nabla c|}$ and the resolved flame surface density $|\nabla \overline{c}|$. With the turbulent flame surface area $A_\textrm{t}=\int _V \Sigma _\textrm{gen}\textrm{d}V$ and the projected flame area $A_\perp = \int _V |\nabla \overline{c}| \textrm{d}V$, the wrinkling factor can also be interpreted as the ratio of the turbulent and the resolved flame surface area $\Xi =A_\textrm{t}/A_\perp$.

For small LES-filter sizes up to roughly $\Delta /\delta _\textrm{th}\approx 1$ the wrinkled flame is well resolved and the wrinkling factor should remain close to unity ($\Xi \approx 1$) (Pfitzner et al. 2022). For filter sizes $\Delta >\delta _\textrm{th}$, the wrinkling factor can increase significantly and must be modeled. A well-known approach (Fureby 2005; Charlette et al. 2002) is to model the wrinkling factor using a power-law equation resulting from the assumption of fractal flame folding.

$$\begin{aligned} \Xi = \Gamma ^{D-2} \end{aligned}$$

(37)

where D denotes the fractal dimension and $\Gamma = \eta _\textrm{o}/\eta _\textrm{i}$ is the ratio of outer ($\eta _\textrm{o}$) to inner ($\eta _\textrm{i}$) cut-off scales. The following expression for the fractal dimension, which depends on the subgrid Karlovitz number $\textrm{Ka}_\Delta$ has been proposed by Keppeler et al. (2014):

$$\begin{aligned} D_\textrm{K} = \frac{8/3 \textrm{Ka}_\Delta + 2c_\textrm{K}}{\textrm{Ka}_\Delta + c_\textrm{K}} ~, \end{aligned}$$

(38)

where $\textrm{Ka}_\Delta$ can be calculated from

$$\begin{aligned} \textrm{Ka}_\Delta = \left( \frac{u^{\prime }_\Delta }{S_\textrm{L}}\right) ^{3/2} \left( \frac{\Delta }{\delta _\textrm{th}}\right) ^{-1/2} ~. \end{aligned}$$

(39)

The velocity fluctuation $u^{\prime }_\Delta$ can be determined from the definition of the subgrid kinetic energy with $u^{\prime }_\Delta =\sqrt{2 k_\textrm{sgs}/3}$. With the model parameter $c_\textrm{K}$, the scaling behavior of Eq.(38) can be adjusted. For the present cases, $c_\textrm{K}=0.2$ is found to lead to a reasonable scaling of $D_\textrm{K}$.

A simple model of the inner cut-off scale is provided by $\eta _\textrm{i}=\delta _\textrm{th}$ (Driscoll 2008). Since the present model utilizes a flame-thickening approach, the outer cut-off scale is not only governed by the LES filter size $\Delta$, but rather by the effective filter size $\Delta ^{\prime }=c_\Delta \Delta$. The easiest approach is to define the outer cut-off scale as $\eta _\textrm{o}=c_\Delta \Delta$. This approach is only valid for comparably small values of flame thickening ($c_\Delta =5$), as is the case in this work. For very large values of $c_\Delta$, $\eta _\textrm{o}$ should approach a RANS-like limit of the order of the integral length scale, where none of the flame wrinkling is resolved. These cases would require a more sophisticated modeling of $\eta _\textrm{o}$, limiting its maximum value, which is not needed in this work. With the cut-off scales defined, Eq. (37) to Eq. (39) can be combined to obtain the wrinkling factor

$$\begin{aligned} \Xi _\textrm{K} = \textrm{max}\left[ 1, \left( c_\Delta \frac{\Delta }{\delta _\textrm{th}}\right) ^{D_\textrm{K}-2} \right] ~. \end{aligned}$$

(40)

4 Simulation of 1D Stationary Flames

4.1 1D Simulation Setup

The LES-model defined in Eq. (31) is implemented using the open-source software package OpenFOAM (Weller et al. 1998; Greenshields 2019). A pressure-based solver (modified version of the “XiFoam” solver) is applied. It should be noted here that while technically “XiFoam” solves a transport equation of the regression variable $\tilde{b}=1-\tilde{c}$, this does not have an effect on the results and therefore the following analysis will only refer to the reaction progress variable $\tilde{c}$. The unburnt mixture is assumed to be homogeneous (constant equivalence ratio $\phi$) and the ideal gas equation of state is applied. A temperature-dependent heat capacity $c_\textrm{p}(T)$ is defined via JANAF polynomials (Stull 1965). The filtered temperature $\tilde{T}$ can then be directly obtained by solving for the root of:

$$\begin{aligned} \tilde{h} = \int _{T_0}^{\tilde{T}}c_\textrm{p}(T)\textrm{d}T \end{aligned}$$

(41)

4.2 1D Simulation Results

To enable the capturing of thick flames at very large filter sizes $\Delta$, the total length of the computational domain $L_x$ is always adjusted to $L_\textrm{x}=50\overline{\delta }_\textrm{th}$, using the filtered flame thickness $\overline{\delta }_\textrm{th}$ obtained from Fig. 10 for a particular $\Delta$. To enable a smooth convergence to a steady state, the flame is initialized using a generic error function,

$$\begin{aligned} \Psi (x) = \Psi _0 + \frac{1}{2} a_\textrm{ini} \left( \mathrm {erf\left( \frac{x-b_\textrm{ini}}{c_\textrm{ini}}\right) } +1 \right) \end{aligned}$$

(42)

where the placeholder value $\Psi (x)$ can be replaced by the temperature $\tilde{T}$, reaction progress $\tilde{c}$ and velocity $\tilde{U}$ fields. The parameter $a_\textrm{ini}$ is simply defined by the unburned ($\Psi _0=\Psi (\tilde{c}=0)$) and burned ($\Psi (\tilde{c}=1)$) values of the respective quantity, with $a_\textrm{ini} = \Psi (\tilde{c}=1) - \Psi (\tilde{c}=0)$. Since the flame is in the center of the domain, $b_\textrm{ini}=L_\textrm{x}/2$ is valid. Finally, the parameter $c_\textrm{ini}$ controls the thickness of the flame. Using the definition of the flame thickness from Eq. (1) with the derivative of Eq. (42) it can be found that $c_\textrm{ini}=\overline{\delta }_\textrm{th}/\sqrt{\pi }$. The non-dimensional run-time for the simulations is $t_\textrm{run}=50\overline{\delta }_\textrm{th}/S_\textrm{L}$.

Fig. 18

Results of the 1D simulations for the normalized laminar flame speed over the normalized LES filter size for different values of the flame thickening parameter $c_\Delta$

Figure 18 shows the dependence of the normalized filtered flame speed (which ideally should be equal to one if $S_{\textrm{L},\Delta } = S_\textrm{L,0}$) on LES filter size $\Delta _\textrm{LES}$. For small filter sizes $\Delta _\textrm{LES}<0.5\delta _\textrm{th}$, the grid is sufficiently fine to resolve the flame profile even when no artificial flame thickening is applied ($c_\Delta = 1$). When no ($c_\Delta =1$) or insufficient ($c_\Delta =3$) flame thickening is applied, increasing deviations in the calculated $S_\textrm{L}$ from the nominal value become apparent for $\Delta _\textrm{LES} > 0.5\delta _\textrm{th}$. Interestingly, for both $c_\Delta = 1$ and $c_\Delta =3$ the laminar flame speed (and therefore the area below $\overline{\dot{\omega }}(x)$) is first overestimated and later underestimated for very large filter sizes. The overestimation for small $c_\Delta$ and small $\Delta _\textrm{LES}$ has also been reported by Fiorina et al. (2010).

After a certain filter size is reached, the error becomes independent of $\Delta _\textrm{LES}$, as the number of grid points inside the flame is only governed by the solver’s numerics and $c_\Delta$. This is also the case for $c_\Delta =1$, but the point is reached only for $\Delta _\textrm{LES} \ge 10 \delta _\textrm{th}$, which is not a value range of concern for the present work.

Fig. 19

Comparison of normalized filtered reaction source term over $\tilde{c}$ (left) and normalized position (right) for $\Delta =10\delta _\textrm{th}$ (at $c_\Delta =1$) and the reference result

Figure 18 appears to suggest that for $c_\Delta =1$ the error reduces between $\Delta _\textrm{LES}=2\delta _\textrm{th}$ and $\Delta _\textrm{LES}=10\delta _\textrm{th}$. An explanation of this counter-intuitive behavior can be found in Fig. 19. It can be seen that the correct values of $\overline{\dot{{\omega }}}$ are interpolated for each discrete value of $\tilde{c}$. However, the actual shape of $\overline{\dot{{\omega }}}(\tilde{c})$ is not reproduced due to a too low number of grid points inside the flame. Even if the shape is not matched, the area below the resolved curve of $\overline{\dot{{\omega }}}$ may be approximately correct, explaining the trend seen in Fig. 18 for $c_\Delta =1$.

Fig. 20

Comparison of the filtered reaction source term with the explicitly filtered a-priori data (ref.) for different filter widths. Note the change in scale of the x- and y-axes between the first and second rows

By increasing the flame thickening factor to $c_\Delta \ge 5$, the laminar flame speed is correctly predicted over the entire analyzed range of filter sizes with a maximum error of $+4.2\%$ ($c_\Delta =5$), $+2.5\%$ ($c_\Delta =7$) and $+1.5\%$ ($c_\Delta =9$). To minimize the modeling error introduced by the wrinkling model, artificial flame thickening should be minimized. Therefore, the smallest stable value $c_\Delta =5$ is chosen for this work.

Figure 20 shows that the shape of the filtered chemical source term for $c_\Delta =5$ matches the a-priori filtered Cantera data very well, both as a function of $\tilde{c}$ and when plotted vs. x.

Fig. 21

Comparison of the $\tilde{c}$-profile with the filtered reference result for different filter widths

The adequacy of the choice of $c_\Delta =5$ is confirmed by comparing the filtered flame profiles $\tilde{c}(x)$. As shown in Fig. 21, the $\tilde{c}$-curves match the a-priori results (ref.) very well.

Fig. 22

Normalized laminar flame speed over normalized LES filter size for different approaches of the diffusion term correction (left) and for different wrinkling factors $\Xi$ (right). For the dotted lines the data points at $\Xi =1$ have been directly multiplied by the given value of $\Xi$

In addition to ensuring a sufficient resolution of the flame by setting $c_\Delta =5$, an accurate flame profile and therefore an accurate laminar flame speed can only be obtained by correcting the modeling error of the diffusion term. In this work, this is achieved by utilizing the modified flux term $\Omega ^*$ (see Eq. (27)).

As shown in Fig. 22 the laminar flame speed is severely underestimated for filter sizes $\Delta _\textrm{LES}>0.5 \delta _\textrm{th}$ if the RHS of Eq. (21) is used as an approximation of the diffusion term. In contrast, the flux term $\Omega$ with correction factor $\alpha _{\tilde{c}}$ (see Eq.(23)) yields approximately the correct laminar flame speed (see Fiorina et al. 2010 for details). A similar behavior is seen when using the newly proposed $\Omega ^*$ approximation. While both methods ($\Omega ^*$ and $\Omega$ combined with $\alpha _{\tilde{c}}$) should be equivalent in theory, the resulting flame speeds can differ slightly due to numerical effects.

Lastly, a test of the effect of the flame wrinkling factor in Eq. (31) is performed by setting $\Xi >1$ in the 1D calculations. Note that, in contrast to FSD models, in the FTACLES model the entire right-hand side of Eq. (31) is scaled with $\Xi$ to ensure that $S_\textrm{t}=\Xi S_\textrm{L,0}$. Figure 22 (right) shows that the intended scaling behavior can indeed be achieved in this way.

5 Simulation of a Turbulent 3D Bunsen Flame

The 3D simulation setup is designed to emulate the Bunsen flame experiments performed by Kobayashi et al. (1996, 1997, 1998). In the context of FSD model development and validation, similar LES studies using the Kobayashi database have been performed by Keppeler et al. (2014) and Aluri et al. (2008). RANS studies were also performed by Brandl et al. (2005) and Muppala et al. (2005).

5.1 3D Numerical Setup

Fig. 23

Computational mesh and dimensions of Bunsen flame simulations

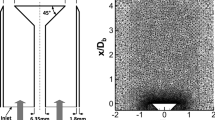
Figure 23 depicts the computational mesh and the overall dimensions of the Bunsen flame simulation setup. The cylindrical domain has an overall length of $L_\textrm{x}={120}\,{\hbox {mm}}$ and an outer radius of $r_\textrm{o}={40}\,{\hbox {mm}}$. The nozzle itself has a radius of $r_\textrm{i}={10}\,{\hbox {mm}}$. The reference mesh shown in Fig. 23 consists of a total of $n\approx 630000$ cells, with an average cell size of $\Delta ={0.4}\,{\hbox {mm}}\approx \delta _\textrm{th}$ in the region near the flame front (see Sect. 5.3.1 for resolution study). A detailed analysis of the mesh quality and sensitivity was performed by Keppeler et al. (2014), where it is concluded that for meshes similar to the present one approximately $75\%$ to $85\%$ of the total turbulent kinetic energy is resolved in the flame-containing region ($x={0}\,{\hbox {mm}}$ to $x={60}\,{\hbox {mm}}$).

At the outer surface of the cylinder and the outlet plane of the cylindrical domain (opposite to the flame), outflow boundary conditions are specified. At the flame inlet (bounded by $r_\textrm{i}$) a Dirichlet boundary condition is applied for all values except U, k and p. The pressure p satisfies a zero-gradient Neumann boundary at the inlet. In the area surrounding the flame inlet, an adiabatic wall boundary condition is applied.

A time-dependent turbulent velocity field $\textbf{U}(t)$ is realized on the inlet patch using a diffusion-based turbulence generator by Kempf et al. (2005). The method has been successfully applied by Tangermann et al. (2010) and Keppeler et al. (2014) in the context of the Kobayashi Bunsen flame simulations and emulates the experimentally measured turbulence intensities and integral length scales (see Table 3). The time-dependent inlet values of the turbulent kinetic energy $k_\textrm{sgs}$ are determined from $\textbf{U}(t)$ at the inlet patch using $k_\textrm{sgs}=3/2(I |\textbf{U}|)^2$, where $I=u^{\prime }/U_\textrm{in}$ is the turbulence intensity. For all simulations the flame thickening parameter is set to $c_\Delta =5$.

Table 3 Simulation parameters for the investigated methane/air Bunsen burner flames (from Kobayashi et al. 1996)

5.2 Verification of Numerical Algorithm with Laminar Bunsen Flame

The laminar Bunsen flame (case 1 in Table 3) is utilized to validate the implementation of the presented model in 3D, without the influence of a specific wrinkling model ($\Xi =1$). The resulting stationary flame is depicted in Fig. 23.

Fig. 24

Averaged $\langle \tilde{c} \rangle$-slice of the laminar Bunsen flame with flame cone angle $\beta$

Following the method described by Kobayashi et al. (1996), the (turbulent) flame speed $S_\textrm{t}$ of a conical Bunsen flame can be calculated from $S_\textrm{t}=U_\textrm{in}\textrm{sin}(\beta )$, where $\beta$ is the angle of the flame cone, excluding the base and flame tip regions. The averaged flame cone angle is calculated here from a line fit of the points between $0.45\le \langle \tilde{c}\rangle \le 0.55$ contours in the region between $40\%$ to $80\%$ of the flame height, as shown in Fig. 24. The basis is a $\langle \tilde{c}\rangle$ field which is averaged with respect to time and with respect to the circumferential angle. This averaging method will become especially important in the analysis of the turbulent cases to obtain a well-defined average flame cone angle.

The cone angle shown in Fig. 24 yields a laminar flame speed $S_\textrm{t}={0.32}\,\hbox {m}\,\hbox {s}^{-1}\approx 0.95 S_\textrm{L,0}$. It should be stressed here again that $S_\textrm{L,0}$ is not explicitly prescribed anywhere in the numerical model. Rather, the laminar flame speed emerges naturally from the solution of Eq. (31) and therefore a certain deviation from $S_\textrm{L,0}$ ($5\%$ in this case) due to interaction of numerical effects can be expected. In addition, the laminar flame speed can be affected by curvature effects, which do not occur in the planar case.

The flame speed can also be calculated using the assumption that the massflow through the inlet and over the flame cone has to remain constant:

$$\begin{aligned} \rho _0 U_\textrm{in} A_\textrm{in} = \rho _\textrm{out} S_\textrm{t} A_\textrm{out} \end{aligned}$$

(43)

The isosurface at $\langle \tilde{c} \rangle = 0.05$ is chosen for $A_\textrm{out}$ (Peters 2000; Griebel et al. 2007), since the gas is still mostly unburned and therefore $\rho _\textrm{out} \approx \rho _0$. Next, the turbulent flame speed can be evaluated from $S_\textrm{t}=U_\textrm{in}A_\textrm{in}/A_{\langle \tilde{c}\rangle =0.05}$. For the laminar Bunsen case, this analysis method leads to a flame speed of $S_\textrm{t}={0.323}\,\hbox {m} \hbox {s}^{-1}$, which matches the value obtained with the cone angle method.

5.3 Analysis of Turbulent Flame Speed

Next, the results of the simulations of turbulent cases 2 to 5 are analyzed and compared with the experimental data of Kobayashi et al. (1996). The main metric used for the comparison is the turbulent flame speed, which is determined in a similar way to the previously discussed laminar case.

Fig. 25

Instantaneous xy-slice of the $\tilde{c}$ field at $t={0.4}\,{\hbox {s}}$ (left) and time and rotationally averaged $\langle \tilde{c} \rangle$ slice with fitted flame cone angle (right) for the no-wrinkling-model ($\Xi =1$) case 5

Figure 25 shows a xy-slice of the $\tilde{c}$-field (left) and a slice of the averaged field $\langle \tilde{c} \rangle$ and the fitted cone angle (right) for case 5 at $t={0.4}\,\hbox {s}$ (no wrinkling model: $\Xi =1$). In contrast to the laminar case, the angle of the flame cone is clearly not constant throughout its entire length. The part of the flame cone where the time-averaged flame contour in a cut plane can be considered linear starts at a distance of $\approx 40-50\%$ from the flame base and ends at a distance of $\approx 10-20\%$ from the flame tip.

In the simulations it is found that the region where the flame cone angle can be considered constant shifts towards the tip of the flame with increasing $S_\textrm{t}$. This adds a significant amount of uncertainty to the measurement of the flame cone angle $\beta$, since the calculated $S_\textrm{t}$ is found to change up to $\pm 20\%$, depending on which section of the averaged flame is used to determine $\beta$. The cone angle and area method are also compared by Keppeler (2013), who reports differences of $\approx 10\%$ between both methods depending on $u^{\prime }$. Therefore, the following investigations are based on the area method (Eq. (43)), as it is found to be much more robust, since the area of a particular isosurface of $\langle \tilde{c}\rangle$ is always well defined, independent of the turbulence level.

Fig. 26

Normalized flame speed over relative velocity fluctuation for the Kobayashi experiments (“kob96”), simulations without wrinkling model ($\Xi =1$) and the modified Keppeler model ($\Xi _\textrm{K}$). For the last data set (rectangle), the FTACLES tables are calculated with the temperature-based progress variable $c_\textrm{T}$

Figure 26 shows the comparison of the normalized turbulent flame speeds obtained for the experimental flame (“kob96”) (Kobayashi et al. 1996), the simulations without the wrinkling model ($\Xi =1$) and the simulations using the wrinkling factor model ($\Xi =\Xi _\textrm{K}$). Since $\textrm{Ka}=0$ for $u^{\prime }=0$, the wrinkling factor model reverts to $\Xi _\textrm{K}\approx 1$ when there is no turbulence.

Table 4 Turbulent flame speeds $S_\textrm{t}[\hbox {m}\,\hbox {s}^{-1}]$ obtained in experiment (kob96) and in the simulation ($\Xi =1$ and $\Xi =\Xi _\textrm{K}$)

Table 4 presents the turbulent flame speeds obtained from the simulations and the relative deviation from the experimental results. While theoretically $u^{\prime }=0$ (case 1) should result in $\Xi _\textrm{K}=1$ globally, this is not forced in the solver and locally $\Xi _\textrm{K}>1$ can still occur due to $u_\Delta ^{\prime }>0$. This results in a slightly elevated flame speed when using $\Xi _\textrm{K}$ in case 1. With the exception of case 2 ($u^{\prime }/S_\textrm{L}\approx 0.3$), the predictions of the modified FTACLES chemistry model in combination with the wrinkling model show very good agreement with the experimental results with an average deviation of 2.3%. The biggest outlier is case 2, the lowest turbulence intensity tested. Since the turbulent flame speed is already overpredicted for this case when no subgrid flame wrinkling is applied at all ($\Xi =1$), it is not surprising that the addition of subgrid wrinkling through the wrinkling factor model causes a relatively large deviation.

The same overprediction for low turbulence intensities was found in LES (with a chemistry model based on flame-surface-density) and also RANS performed by Tangermann et al. (2010) for the same case. This seems to suggest that the problem is not related to the usage of the FTACLES model, but is caused by a too fast increase of flame subgrid wrinkling by the wrinkling model, or by the turbulence model at low turbulence intensities. Due to possible measurement errors and inaccuracies in using the flame angle method to determine $S_\textrm{t}$, the experimental results may also be subject to a non-negligible amount of uncertainty. The experimenters did not provide uncertainty bars.

Fig. 27

Schlieren image of the Kobayashi Bunsen flame (Kobayashi et al. 1996) (left) and numerical Schlieren (right) of the simulated flame ($\Xi =1$) for case 2

In Fig. 27 a Schlieren image of case 2 [found in Kobayashi et al. (1996)] is compared to a numerical Schlieren image (Samtaney et al. 2000) of the simulation with $\Xi =1$ at $t={0.25}\,\hbox {s}$. While the total flame length of the simulated flame appears to be slightly larger than the experimental one, the size, shape and distribution of the turbulent wrinkles compare very well to the snapshot from the experiment. Obviously, due to turbulent fluctuations the shape of the flame will vary over time. Nevertheless, it can be concluded that the overall look of the flame is captured very well by the simulation.

When simulations are performed with tables based on $c_\textrm{T}$ (instead of $c_\textrm{opt}$), the influence of the post-reaction tail can be identified. The inclusion of a post-reaction tail might increase the effective flame thickness and therefore reduce flame wrinkling. The results of this study can also be seen in Fig. 26, which clearly shows only a negligible difference between the simulations based on $c_\textrm{opt}$ and $c_\textrm{T}$. A possible explanation can be found by going back to Fig. 13, where it was shown that the difference between the two progress variables decreases with increasing filter size. For the present LES, which has an effective filter size of $\Delta ^{\prime }=5\delta _\textrm{th}$, the results are therefore expected to be very similar (see also “Appendix 2”).

5.3.1 Resolution Study

Figure 28 shows the normalized turbulent flame speed for the experimental flame (“kob96”) and the simulations at three different resolution levels. The simulations at $\Delta _\textrm{LES} \approx 1 \delta _\textrm{th}$ correspond to the setup introduced in Sect. 5, where $\Delta _\textrm{LES}$ denotes the average cell size close to the flame. For the “coarse” and “fine” simulations, the cell size was doubled to $\Delta _\textrm{LES}=2\delta _\textrm{th}$ and halved to $\Delta _\textrm{LES}=0.5\delta _\textrm{th}$, respectively. Ideally, $S_\textrm{t}$ should remain approximately constant between changing mesh resolutions, since the change in resolved flame wrinkling should be captured by the $\Xi _\textrm{K}$ model. For the fine mesh, the wrinkling model scales very well, as there is only a negligible difference between the results for $\Delta _\textrm{LES}=0.5\delta _\textrm{th}$ and $\Delta _\textrm{LES}=1\delta _\textrm{th}$ (with the exception of the second case). For the coarse mesh, the deviations are slightly larger due to the increasing modeling errors, as most of the wrinkling has to be captured by $\Xi _\textrm{k}$. The influence of changes in $\Delta _\textrm{LES}$ on the resolved wrinkling is further shown in Fig. 29, which compares the $\tilde{c}=0.5$ isosurfaces for the three cases.

Fig. 28

Normalized flame speed over relative velocity fluctuation for the Kobayashi experiments (“kob96”) and simulations at different LES mesh sizes

Fig. 29

Isosurfaces of $\tilde{c}=0.5$ for case 5 at different resolutions

6 Discussion

The definition of the 1D laminar flame profiles (defined by c and $\dot{\omega }$) is a central part of the FTACLES formalism, since the filtered profiles are used to systematically derive the model closures. One of the main characteristics of the FTACLES model is that the resulting filtered flame profiles match the reference (numerically filtered) profiles almost exactly (see Figs. 20 and 21). A common definition for c (for example Pfitzner and Breda 2021) is discussed in Sect. 2, where the progress variable is derived from the detailed chemistry result by using either the temperature profile to define $c_\textrm{T}$ or the species fractions to define $c_\textrm{C}$ and $c_\textrm{H}$. For species-based progress variables, the solution of Eq. 3 also yielded regions of $\dot{\omega }$ with negative values, as demonstrated for $\dot{\omega }_\textrm{C}$ and $\dot{\omega }_\textrm{H}$. Although this is not the case in this work, depending on the mixture and the choice of $\rho D$, negative values of $\dot{\omega }_\textrm{T}$ can also not be ruled out. An analytical representation (shown in Sect. 2.1) of the flame profiles can be obtained by using a series of Gaussians to approximate and explicitly express the source terms derived from detailed chemistry. Finally in Sect. 2.2, an explicit mathematical model for a one-step chemistry source term $\dot{\omega }_\textrm{opt}$ is derived, which uses a single optimized Gaussian to prescribe the laminar flame speed, flame thickness and $\rho D$. While the flame profile $c_\textrm{opt}$ obtained using this model matches well with $c_\textrm{C}$, it does not show the characteristic post-reaction tail seen in $c_\textrm{T}$. The analysis of the 1D filtered progress variables in Fig. 13 and the results of the 3D simulation in Fig. 18 suggest that for higher LES filter widths the impact of the post-reaction tail is negligible.

The second part of the paper addresses the closure of the filtered diffusion term (Sects. 3.1 and 3.2). An alternative closure of the diffusion term is proposed that eliminates the need for the correction factor $\alpha _{\tilde{c}}$, by introducing a modified sgs-flux term $\Omega ^*$ (Eq. (27)). This new $\Omega ^*$-term is composed of the counter-gradient term $\Omega$ and an sgs-closure of the diffusion term and tabulated from the 1D laminar profiles. Because $\alpha _{\tilde{c}}$ approaches 0/0 for $\tilde{c}\rightarrow 0$ (Eq. (23)), it can be numerically challenging to obtain precise values close to $\tilde{c} = 0$. This can be problematic, since (as shown in Fig. 14 (left)) the maximum deviations of the ideal filtered and modeled diffusion terms and therefore the maximum values of $\alpha _{\tilde{c}}$ also move toward $\tilde{c}= 0$ with growing filter size (Fig. 15). The modified sgs flux term $\Omega ^*$ behaves very similar to $\Omega$ for growing filter sizes $\Delta$ (Fig. 17), avoiding the boundary problem encountered with $\alpha _{\tilde{c}}$. Lastly, this change simplifies the closure of the $\tilde{c}$-transport equation, since the subgrid models of the filtered diffusion and the subgrid flux terms are combined into one.

The last part of the paper presents results of the combination of the modified FTACLES closure with models that account for subgrid flame wrinkling and subgrid turbulence effects (Sects. 3.3.1 and 3.3.2). The 1D-results (Sect. 4.2) show clearly that an accurate (filtered) flame profile, laminar flame speed and flame thickness are obtained. In the application of the fractal power-law wrinkling model, it is suggested that the effective filter size $\Delta ^{\prime }=c_\Delta \Delta$ used for artificial flame thickening can also be used as an outer cut-off scale (Eq. 40), to take into account the reduction in wrinkling due to the lower amount of resolved flame wrinkling of the thickened flame. The good agreement between the experiment and the 3D simulations (Fig. 26) supports this approach.

7 Conclusion and Outlook

In this work, a modified filtered tabulated chemistry approach (FTACLES) is proposed to be used in Large-Eddy-Simulations of turbulent premixed flames. The FTACLES model ingredients are derived from an explicitly filtered stationary 1D methane/air flame profile, which is generated using detailed chemistry in CANTERA. In this work the chemical source term $\dot{\omega }(x)$ in the transport equation of a single progress variable is represented by a single Gaussian with parameters adapted to yield the same laminar flame speed and flame thickness as derived from the detailed chemistry 1D calculation. It is shown that for large filter sizes, the shape of the reaction rate profile becomes less and less important.

The unclosed contributions of the filtered laminar diffusion term and the filtered SGS-flux term are modeled together in a modified SGS-flux term, which is calculated and tabulated directly from the 1D filtered flame profile data. It is shown that using this modeling approach, a correction term to the filtered diffusion term as proposed in the original FTACLES model is not required. For large filter sizes, the new SGS-flux term can be expressed by an algebraic BML-based formulation.

The modified FTACLES model is combined with a one-equation model for turbulence closure and a power-law-based wrinkling model and implemented into OpenFOAM. 1D simulations at different LES filter sizes show that artificial flame thickening is required on coarse LES-meshes in order to obtain the correct laminar flame profile and laminar flame speed. A premixed turbulent Bunsen flame is simulated in 3D for different turbulence intensities and compared to experimental results. With the exception of one case at very low turbulence intensities, the turbulent flame speeds obtained in simulation and experiment match very well.

Future work can include the application of the model to high-pressure Bunsen flames and investigation of improved flame wrinkling models.

Appendices

Appendix 1: Analytical Solution for Progress Variable and Source Term

For $F_{\rho D}=F=\mathrm {const.}$ ($f_{\rho D}=0$) and assuming that $\dot{\omega }$ can be approximated by a single parameterized Gaussian (see Eq. (6)), the transport Eq. (8) can be expressed as

$$\begin{aligned} \frac{\partial ^2c}{\partial x^2} = \frac{\rho _0 S_\textrm{L}}{F} \frac{\partial c}{\partial x} - \frac{A}{F C\sqrt{\pi }} \exp \left[ -\left( \frac{x-B}{C}\right) ^2\right] ~. \end{aligned}$$

(44)

Following the arguments made in the context of Eqs. (11) to (13) it can be concluded that $A=\rho _0 S_\textrm{L}$ and $B=0$ if $\dot{\omega }$ is centered around $x=0$, leading to the following expression:

$$\begin{aligned} \frac{\partial ^2c}{\partial x^2} = \frac{A}{F} \frac{\partial c}{\partial x} - \frac{A}{F C\sqrt{\pi }} \exp \left[ -\left( \frac{x}{C}\right) ^2\right] \end{aligned}$$

(45)

Assuming that at $x=x_\textrm{max}$ the c-gradient reaches its maximum with $\partial ^2 c/\partial x^2 = 0$, we can write:

$$\begin{aligned} \left. \frac{\partial c}{\partial x}\right| _{x_\textrm{max}} = \frac{1}{C\sqrt{\pi }}\exp \left[ -\left( \frac{x_\textrm{max}}{C}\right) ^2\right] \end{aligned}$$

(46)

The maximum gradient is reached for $x_\textrm{max}=0$ and with $\textrm{max}(\partial c/\partial x) = \delta _\textrm{th}^{-1}$ we obtain $C = \delta _\textrm{th}/\sqrt{\pi }$. Under the condition that $c(x)\rightarrow 0,1$ for $x\rightarrow \mp \infty$ Eq. (45) can be solved analytically to obtain $c_\textrm{a}(x)$:

$$\begin{aligned} c_\textrm{a}(x) = \frac{1}{2}\left( \textrm{exp}\left[ \frac{Ax}{F}+\left( \frac{AC}{2F}\right) ^2\right] \left( 1-\textrm{erf}\left[ \frac{AC}{2F}+\frac{x}{C}\right] \right) +\textrm{erf}\left[ \frac{x}{C}\right] +1\right) \end{aligned}$$

(47)

Figure 30 (left) shows the analytical solution $c_\textrm{a}(x)$ with $A=\rho _0 S_\textrm{L}$, $F=\rho _0 D_0$ and $C=\delta _\textrm{th}/\sqrt{\pi }$ in comparison to the temperature based progress variable $c_\textrm{T}$ from detailed chemistry and the result obtained using the optimized Gaussian and a non-constant $F_{\rho D}$ (Sect. 2.2). The corresponding analytical solution to the source term is defined by

$$\begin{aligned} \dot{\omega }_\textrm{a} = \frac{A}{C\sqrt{\pi }}\exp \left[ -\left( \frac{x}{C}\right) ^2\right] \end{aligned}$$

(48)

and shown in Fig. 30(right).

Fig. 30

Comparison of reaction progress variable (left) and source term (right) for profiles obtained from detailed chemistry $c_\textrm{T}$, optimized Gauss-fit $c_\textrm{opt}$ (non-constant $\rho D$) and analytical solution $c_\textrm{a}$ (constant $\rho D$)

Appendix 2: Comparison of 3D Bunsen Isosurfaces

Figure 31 shows $\tilde{c}$-isosurfaces for simulations of case 5 (see Table 3) with tables based on $c_\textrm{opt}$ (top) and $c_\textrm{T}$ (bottom). The wrinkled structures of both flames are almost identical for $\tilde{c}=0.1$ and $\tilde{c}=0.5$, the greatest difference being the slightly increased thickness visible at $\tilde{c}=0.9$ for $\tilde{c}_\textrm{T}$. This is due to the small influence of the post-reaction tail in $\tilde{c}_\textrm{T}$, which is still present for high values of $\tilde{c}$.

Fig. 31

Isosurfaces for simulations of case 5 with tables from $\tilde{c}_\textrm{opt}$ (top) and $\tilde{c}_\textrm{T}$ (bottom)