Assessment of Laws of the Wall During Flame–Wall Interaction of Premixed Flames Within Turbulent Boundary Layers

Abstract

The validity of the usual laws of the wall for Favre mean values of the streamwise velocity component and temperature for non-reacting flows has been assessed for turbulent premixed flame-wall interaction using Direct Numerical Simulation (DNS) data. Two different DNS databases corresponding to friction velocity-based Reynolds number of 110 and 180 representing unsteady head-on quenching of statistically planar flames within turbulent boundary layers have been considered. The usual log-law based expressions for the Favre mean values of the streamwise velocity and temperature for the inertial layer have been found to be inadequate at capturing the corresponding variations obtained from DNS data. The underlying assumptions of constant shear stress and the equilibrium of production and dissipation of turbulent kinetic energy underpinning the derivation of the usual log-law for the mean streamwise velocity have been found to be rendered invalid within the usual inertial layer during flame-wall interaction for both cases considered here. The heat flux does not remain constant within the usual inertial layer, and the turbulent flux of temperature exhibits counter-gradient transport within the so-called inertial layer for the cases considered in this work. These render the assumptions behind the derivation of the usual log-law for temperature to be invalid for application to turbulent flame-wall interaction. It has been found that previously proposed empirical modifications to the existing laws of the wall, which account for density and kinematic viscosity variations with temperature, do not significantly improve the agreement with the corresponding DNS data in the inertial layer and the inaccurate approximations for the kinematic viscosity compensated wall normal distance and the density compensated streamwise velocity component contribute to this disagreement. The DNS data has been utilised here to propose new expressions for the kinematic viscosity compensated wall normal distance and the density compensated streamwise velocity component, which upon using in the empirically modified law of wall expressions have been demonstrated to provide reasonable agreement with DNS data.

1 Introduction

Flame-wall interaction (FWI) is of fundamental importance for the analysis of heat transfer rates and thermal stresses experienced by combustor walls, and it is particularly important for the design process of modern downsized combustors and micro combustors where FWI takes place more readily than conventional combustors. Several studies have contributed to the fundamental understanding and modelling of FWI for premixed combustion using both experimental (Jainski et al. 2017a, b, 2018; Mann et al. 2014; Rißmann et al. 2016) and computational (Ahmed et al. 2018; Ahmed et al. 2019, 2020; Ahmed et al. 2021a, 2021b, 2021c, 2021d; Ahmed et al. 2023a, b; Ahmed et al. 2023b; Alshaalan and Rutland 2002; Alshaalan and Rutland 1998; Bruneaux et al. 1996; Bruneaux et al. 1997; Ghai et al. 2022b; Ghai et al. 2022c; Ghai et al. 2023c; Gruber et al. 2010; Gruber et al. 2012; Kitano et al. 2015; Lai and Chakraborty 2016a, 2016b; Lai et al. 2017a, b, c; Lai et al. 2017a; Lai et al. 2017b; Lai et al. 2018a; Poinsot et al. 1993; Sellmann et al. 2017) means. The advancements in high-performance computing have enabled Direct Numerical Simulations (DNS) of premixed FWI which can provide three-dimensional temporally and spatially resolved data which are either difficult or impossible to obtain using experimental diagnostics. These DNS studies provided important insights into the statistics of wall heat flux (Ahmed et al. 2023a, b; Alshaalan and Rutland 2002; Bruneaux et al. 1996; Bruneaux et al. 1997; Ghai et al. 2023a; Jiang et al. 2019; Lai et al. 2018a; Lai et al. 2022; Poinsot et al. 1993; Zhao et al. 2018a, b), near-wall flow dynamics and species distributions (Ahmed et al. 2018; Ahmed et al. 2019; Ahmed et al. 2021b; Gruber et al. 2010; Gruber et al. 2012; Jiang et al. 2019; Jiang et al. 2021; Kitano et al. 2015; Lai et al. 2017a, b, c; Lai et al. 2017b; Lai et al. 2018a; Zhao et al. 2018a, 2018b, 2021), reactive scalar gradient (Ahmed et al. 2020; Ahmed et al. 2021c; Gruber et al. 2010; Gruber et al. 2012; Konstantinou et al. 2020; Lai and Chakraborty 2016a, 2016b; Lai et al. 2018a; Lai et al. 2022; Sellmann et al. 2017; Zhao et al. 2018b, 2019), flame propagation during turbulent premixed FWI (Ahmed et al. 2020, 2021c; Konstantinou et al. 2020; Lai et al. 2017a; Zhao et al. 2018a, b, 2021) and contributed to the understanding and development of turbulent scalar flux (Ahmed et al. 2021b; Lai et al. 2017a) and mean reaction rate closures (Ahmed et al. 2021a, b, c, d; Ghai et al. 2023b; Lai and Chakraborty 2016a; Lai et al. 2018a; Lai et al. 2022; Sellmann et al. 2017; Zhao et al. 2018a, b) during turbulent premixed FWI. The engineering simulations of FWI using Reynolds Averaged Navier–Stokes (RANS) and hybrid RANS-Large Eddy Simulations (LES) methodologies need highly accurate wall-functions for mean velocity and temperature predictions in turbulent reacting boundary layers. However, the existing wall functions for turbulent boundary layers are proposed for small changes in temperature and density (Durbin and Pettersson Reif 2010; Hanjalić and Launder 2011; Wilcox 1998) but density, viscosity and temperature change significantly within the turbulent boundary layer during FWI. Angelberger et al. (1997) and Han et al. (1996) proposed some modifications to the wall functions of mean velocity and temperature to account for the effects of the changes in thermophysical properties because of the temperature rise within turbulent reacting flow boundary layers. However, to date, limited effort has been directed to the assessment of the performances of the existing (Durbin and Pettersson Reif 2010; Hanjalić and Launder 2011; Wilcox 1998) and modified (Angelberger et al. 1997; Han et al. 1996) wall functions using DNS data of premixed FWI. In this work the performances of wall functions of mean values of streamwise velocity and temperature have been assessed for unsteady head-on quenching (HOQ) of statistically planar flames across turbulent boundary layers for friction Reynolds numbers of $Re_{\tau } = 110$ and 180. In this respect, the main objectives of the current study are:

• (1) To assess the performance of the standard wall functions for mean streamwise velocity and temperature at two different Reynolds numbers.

• (2) To provide physical explanations for the statistical behaviours of the performances of the standard wall functions analysed in 1.

• (3) To propose modifications to the wall functions of mean streamwise velocity and temperature for FWI, if necessary, and validate them using DNS data.

The rest of the paper is organised as follows. The mathematical background and numerical implementation pertaining to the current analysis are presented in Sects. 2 and 3, respectively. The results are presented and discussed in Sect. 4. The main findings are summarised, and conclusions are drawn in the final section.

2 Mathematical Background

The mean wall shear stress in the viscous sub-layer region of a constant density non-reacting turbulent boundary layer is expressed as $\overline{\tau }_{w} = \mu \left( {\partial \tilde{u}/\partial y} \right)_{w}$ (Pope 2000). Here $\tilde{u}$ is the Favre-mean streamwise velocity component, $\overline{\tau }_{w}$ is the mean wall shear stress, $\mu$ is the dynamic viscosity, and $y -$ direction aligns with the wall-normal direction and the streamwise direction is aligned with $x$. The terms, $\overline{q},\tilde{q} = \overline{\rho q} /\overline{\rho }$ and $q^{\prime\prime} = q - \tilde{q}$ are the Reynolds averaged, Favre-averaged and Favre fluctuations of a general quantity $q$, respectively and $\rho$ is the gas density. Although density is constant in a boundary layer of a non-reacting incompressible flow, the expressions are still written in terms of Favre averages and $\overline{\rho }$ are used in these expressions because these expressions are often adopted for specifying wall conditions during FWI. The equation representing $\overline{\tau }_{w}$ leads to:

$$\frac{{\tilde{u}}}{{u_{\tau } }} = \frac{{u_{\tau } y}}{{\nu_{w} }}\,\,\,{\text{or}}\,\,\,u^{ + } = y^{ + }$$

(1)

where $u_{\tau } = \sqrt {\left| {\overline{\tau }_{w} } \right|/\overline{\rho }_{w} }$ is the friction velocity, $\nu$ is the kinematic viscosity and $y^{ + } = u_{\tau } y/\nu_{w}$ is the normalised wall normal distance $y$. The subscript ‘$w$’ is used to refer to wall values. Equation 1 is valid within the viscous sub-layer (i.e. $y^{ + } \le 10.8$) where the viscous effects dominate over the inertial effects (Durbin and Pettersson Reif 2010; Hanjalić and Launder 2011; Pope 2000).

It is important to consider the turbulent kinetic energy transport in order to understand the theoretical framework underpinning the wall functions for velocity in the case of turbulent boundary layers. The transport equation for the Favre averaged turbulent kinetic energy, $\tilde{k} = 0.5\overline{{\rho u_{i}^{^{\prime\prime}} u_{i}^{^{\prime\prime}} }} {/}\overline{\rho }$ is expressed as follows (Chakraborty et al. 2011a, b; Ghai et al. 2023c; Nishiki et al. 2002):

$$\begin{aligned} \frac{{\partial \left( {\overline{\rho }\tilde{k}} \right)}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\tilde{u}_{j} \tilde{k}} \right)}}{{\partial x_{j} }} = & \underbrace {{ - \overline{{\rho u_{i}^{^{\prime\prime}} u_{j}^{^{\prime\prime}} }} \frac{{\partial \tilde{u}_{i} }}{{\partial x_{j} }}}}_{{P_{k} }} - \underbrace {{\overline{{u_{i}^{^{\prime\prime}} }} \frac{{\partial \overline{p}}}{{\partial x_{i} }} }}_{{P_{w} }} + \underbrace {{\overline{{p^{\prime}\frac{{\partial u_{k}^{^{\prime\prime}} }}{{\partial x_{k} }} }} }}_{{P_{D} }} - \underbrace {{\frac{{\partial \left( {\overline{{p^{\prime}u_{i}^{^{\prime\prime}} }} } \right)}}{{\partial x_{i} }}}}_{{P_{T} }} - \underbrace {{\frac{{\partial \left( {\overline{{0.5u_{i}^{^{\prime\prime}} u_{k}^{^{\prime\prime}} u_{k}^{^{\prime\prime}} }} } \right)}}{{\partial x_{i} }}}}_{{T_{T} }} \\ & - \underbrace {{\overline{\rho }\tilde{\varepsilon } }}_{D} + \underbrace {{\nabla \cdot \left( {\mu \nabla { }\tilde{k} } \right)}}_{{M_{D} }} + \underbrace {{\overline{{u_{i}^{^{\prime\prime}} \frac{\partial }{{\partial x_{k} }}\left( {\mu \frac{{\partial u_{k}^{^{\prime\prime}} }}{{\partial x_{i} }}} \right)}} - \frac{2}{3}\overline{{u_{i}^{^{\prime\prime}} \frac{\partial }{{\partial x_{i} }}\left( {\mu \frac{{\partial u_{k}^{^{\prime\prime}} }}{{\partial x_{k} }}} \right)}} }}_{V} \\ \end{aligned}$$

(2)

The terms on the right-hand side of Eq. 2 are as follows: (i) $P_{k} =$ production term, (ii) $P_{w} =$ pressure work term, (iii) $P_{D} =$ pressure dilatation term$,$ (iv) $P_{T} =$ pressure transport term$,$ (v) $T_{T} =$ turbulent transport term, (vi) $D = \overline{{\mu \left( {\partial u_{i}^{^{\prime\prime}} /\partial x_{j} } \right)\left( {\partial u_{i}^{^{\prime\prime}} /\partial x_{j} } \right)}} =$ dissipation term where $\tilde{\varepsilon } = D/\overline{\rho }$ is the dissipation rate of turbulent kinetic energy, (vii) $M_{D} =$ molecular diffusion term, and (viii) $V =$ viscous dissipation term related to dilatation rate.

The equilibrium of the production, $P_{k} ,$ and dissipation, $D,$ in the $\tilde{k}$ transport equation within the inertial layer (i.e. $y^{ + } \gg 10.8$ and $\mu \left( {\partial \tilde{u}/\partial y} \right) \ll - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}}$ where $v^{\prime\prime}$ is the Favre-fluctuation of the wall normal velocity component) leads to the following relation for a non-reacting constant density boundary layer over a flat plate (Durbin and Pettersson Reif 2010; Hanjalić and Launder 2011; Pope 2000):

$$- \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} \left( {\frac{{\partial \tilde{u}}}{\partial y}} \right) = D$$

(3)

According to Boussinesq’s hypothesis $- \overline{{\rho u^{\prime\prime}v^{\prime\prime}}}$ can be modelled as: $- \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} = \overline{\rho }\nu_{t} (\partial \tilde{u}/\partial y)$ where $\nu_{t}$ is the kinematic eddy viscosity. As the inertial layer is assumed to have constant shear stress, this leads to the following expression for constant density non-reacting turbulent boundary layer (Durbin and Pettersson Reif 2010; Hanjalić and Launder 2011; Pope 2000):

$$\overline{\rho }\nu_{t} (\partial \tilde{u}/\partial y) = \overline{\tau }_{w}\, \text{or} \,\,\nu_{t} (\partial \tilde{u}/\partial y) = u_{\tau }^{2} \,\,$$

(4)

The inertial range scaling $(\partial \tilde{u}/\partial y)\,\sim\,u^{\prime } /l$ and $\nu_{t} \,\sim\,u^{\prime } l$ with $u^{\prime }$ and $l$ being the root-mean-square turbulent velocity and mixing length scale, respectively, give rise to $u^{\prime } \,\sim\,u_{\tau }$. For turbulent non-reacting flow boundary layers $\nu_{t}$ is found to be: $\nu_{t} = \kappa u_{\tau } y$ where $\kappa = 0.41$ is the von-Karman’s constant (Durbin and Pettersson Reif 2010; Hanjalić and Launder 2011; Pope 2000). This leads to $\tilde{\varepsilon } = u_{\tau }^{3} /\left( {\kappa y} \right)$ in the inertial layer and using this relation in Eq. 3 yields:

$$u^{ + } = \frac{{\tilde{u}}}{{u_{\tau } }} = \frac{1}{\kappa }\ln y^{ + } + \underbrace {{C_{1} - \frac{1}{\kappa }\ln \frac{{u_{\tau } }}{\nu }}}_{B} = \frac{1}{\kappa }\ln y^{ + } + B$$

(5)

In Eq. 5, $B$ depends on Reynolds number but assumes a value ranging from 5.0 to 6.5 (Durbin and Pettersson Reif 2010; Pope 2000; Wilcox 1998).

Similarly, in the corresponding turbulent thermal boundary layer, the following expression is obtained for the mean wall heat flux $\overline{q}_{w}$:

$$\overline{q}_{w} = - \lambda \left. {\frac{{\partial \tilde{T}}}{\partial y}} \right|_{w} - \overline{{\rho v^{\prime\prime}T^{\prime\prime}}}$$

(6)

where $\lambda$ is the thermal conductivity. For an isothermal wall, a non-dimensional temperature can be defined as (Hanjalić and Launder 2011; Kays and Crawford 1993):

$$T^{ + } = \frac{{\rho_{w} c_{p} u_{\tau } \left( {T_{w} - \tilde{T}} \right)}}{{\overline{q}_{w} }}$$

(7)

where $T_{w}$ is the wall temperature. Using Eq. 7 and the gradient hypothesis closure for the Reynolds flux of temperature $- \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} = \left( {\overline{\rho }\nu_{t} /Pr_{t} } \right)(\partial \tilde{T}/\partial y)$ yields (Hanjalić and Launder 2011; Kays and Crawford 1993):

$$\left( {\frac{1}{Pr} + \frac{{\nu_{t} }}{\nu }\frac{1}{{Pr_{t} }}} \right)\frac{{\partial T^{ + } }}{{\partial y^{ + } }} = 1.0$$

(8)

Equation 8, in turn, leads to (Hanjalić and Launder 2011; Kays and Crawford 1993):

$$T^{ + } = \mathop \int \limits_{0}^{{y^{ + } }} \frac{{dy^{^{\prime} + } }}{{\left( {\frac{1}{\Pr } + \frac{{\nu_{t} }}{\nu }\frac{1}{{\Pr_{t} }}} \right)}}$$

(9)

In order to evaluate Eq. 9, the combination of Eqs. 1 and 4 provides (Hanjalić and Launder 2011; Kays and Crawford 1993):

$$u^{ + } = \mathop \int \limits_{0}^{{y^{ + } }} \frac{{dy^{^{\prime} + } }}{{\left( {1 + \frac{{\nu_{t} }}{\nu }} \right)}}$$

(10)

A combination of Eqs.9 and 10 gives rise to:

$$T^{ + } = Pr_{t} u^{ + } + B_{c} \left( {Pr,Pr_{t} } \right)$$

(11)

where $B_{c} \left( {Pr,Pr_{t} } \right)$ is given by:

$$B_{c} \left( {\Pr ,\Pr_{t} } \right) = \mathop \int \limits_{0}^{{y^{ + } }} \frac{{\Pr_{t} dy^{^{\prime} + } }}{{\left( {\frac{{\Pr_{t} }}{\Pr } + \frac{{\nu_{t} }}{\nu }} \right)}} - \mathop \int \limits_{0}^{{y^{ + } }} \frac{{\Pr_{t} dy^{^{\prime} + } }}{{\left( {1 + \frac{{\nu_{t} }}{\nu }} \right)}}$$

(12)

In the viscous-sublayer (i.e. $y^{ + } \le 10.8$), Eq. 1 can be used in Eq. 11 to yield (Hanjalić and Launder 2011; Kays and Crawford 1993):

$$T^{ + } = Pr y^{ + }$$

(13)

whereas in the inertial sub-layer (i.e. $y^{ + } > 10.8$), the following expression is obtained (Hanjalić and Launder 2011; Kays and Crawford 1993):

$$T^{ + } = \frac{{Pr_{t} }}{\kappa }\ln y^{ + } + Pr_{t} B + B_{c} \left( {Pr,Pr_{t} } \right)$$

(14)

Equation 14 has been approximated by Kays and Crawford (1993) as:

$$T^{ + } = 2.075\ln y^{ + } + 3.9$$

(15)

The relations given by Eqs. 1,5, 13, 14 and 15 were derived for non-reacting constant density flows and they have been applied successfully for heat transfer problems where the temperature change is not large enough to change density and kinematic viscosity by an order of magnitude. However, these relations may not be valid in the presence of significant changes in density and kinematic viscosity during FWI.

To account for changes in density and kinematic viscosity there are a number of different transformations available in the literature for velocity and wall distance in the case of compressible or variable density flows and all these transformations can be cast in terms of the mapping functions $S_{1}$ and $S_{2}$ for wall normal distance and mean velocity defined as:

$$\eta^{ + } = \mathop \int \limits_{0}^{{y^{ + } }} S_{1} dy^{ + } \,\,\,{\text{and}}\,\,\, \,\psi^{ + } = \mathop \int \limits_{0}^{{u^{ + } }} S_{2} du^{ + }$$

(16)

The summary of the different proposed transformations can be found in Table 1.

Table 1 Transformation for wall normal distance and mean velocity according to Eq. 16 with $G$ = $\overline{\rho }/\overline{\rho }_{w}$ and $H = \tilde{\nu }/\nu_{w}$

To satisfy the inner layer similarly, mapping functions must satisfy this relation, $S_{1} = S_{2} /\left( {G \times H} \right)$ (Volpiani et al. 2020). The above relation can be derived either by enforcing universality of the viscous sublayer or by enforcing universality in the Morkovin-scaled Reynolds shear stress throughout the inner layer. The transformations that satisfy the above relation can predict reasonable results until the edge of the viscous sublayer. Only few transformations that are listed in Table 1 can satisfy this relation (Angelberger et al. 1997; Han et al. 1996; Trettel and Larsson 2016; Volpiani et al. 2020). However, for non-adiabatic turbulent boundary layer flows, the transformations proposed by Angelberger et al. (1997) and Han et al. (1996) provide reasonable results within the whole domain and these wall functions were proposed in the context of FWI. Therefore, in this work modifications have been suggested to the transformation given by Angelberger et al. (1997) and Han et al. (1996) to account for changes in density and kinematic viscosity in the reacting flow boundary layer. The interested readers are referred to Sect. 4 of this paper for further information in this regard. However, the predictions of other transformations (Howarth and Taylor 1997; Trettel and Larsson 2016; Van Driest 1951; Volpiani et al. 2020) are also shown in the Appendix A of this paper for the sake of completeness.

Angelberger et al. (1997) and Han et al. (1996) proposed empirical modifications to the laws of the wall (i.e., Eqs. 1, 5, 13, 15) using following transformations:

$$d\eta^{ + } = \frac{{\nu_{w} }}{{\tilde{\nu }}}dy^{ + } ;\,\,\,d\psi^{ + } = \frac{{\overline{\rho }}}{{\rho_{w} }}du^{ + } \,\,\,{\text{and}}\,\,\,d{\Theta }^{ + } = \frac{{\overline{\rho }}}{{\rho_{w} }}dT^{ + }$$

(17)

Based on Eq. 17, the kinematic viscosity compensated non-dimensional wall normal distance $\eta^{ + }$ at a location corresponding to $y_{1}^{ + }$ is approximated as (Angelberger et al. 1997; Han et al. 1996; Poinsot and Veynante 2005):

$$\eta^{ + } = \mathop \int \limits_{0}^{{y_{1}^{ + } }} \frac{{\nu_{w} }}{{\tilde{\nu }}}dy^{ + } \approx \frac{{\nu_{w} }}{{\tilde{\nu }}}y_{1}^{ + }$$

(18)

Similarly, the density compensated non-dimensional streamwise velocity $\psi^{ + }$ corresponding to $u_{1}^{ + } = u^{ + } \left( {y_{1}^{ + } } \right)$ is approximated as (Angelberger et al. 1997; Han et al. 1996; Poinsot and Veynante 2005):

$$\psi^{ + } = \mathop \int \limits_{0}^{{u_{1}^{ + } }} \frac{{\overline{\rho }}}{{\rho_{w} }}du^{ + } \approx \frac{{\overline{\rho }u_{1}^{ + } }}{{\rho_{w} }}$$

(19)

Using $\tilde{T} = T_{w} \left( {1 + \xi T^{ + } } \right)$ with $\xi$ being $\xi = - \overline{q}_{w} /\left( {\rho_{w} c_{p} u_{\tau } T_{w} } \right)$ allows for expressing the mean density as $\overline{\rho }/\rho_{w} = 1/\left( {1 + \xi T^{ + } } \right)$ for constant pressure, which upon using in Eq. 17 yields (Angelberger et al. 1997; Han et al. 1996; Poinsot and Veynante 2005):

$$\Theta^{ + } = \mathop \int \limits_{0}^{{T^{ + } }} \frac{{dT^{^{\prime} + } }}{{\left( {1 + \xi T^{^{\prime} + } } \right)}} = \frac{{\ln \left( {1 + \xi T^{ + } } \right)}}{\xi } = \frac{1}{\xi }\ln \left( {\frac{{\tilde{T}}}{{T_{w} }}} \right)$$

(20)

According to Angelberger et al. (1997) and Han et al. (1996) $y^{ + } ,u^{ + }$ and $T^{ + }$ in Eqs. 1, 5, 13 and 15 are substituted by $\eta^{ + } ,\psi^{ + }$ and ${\Theta }^{ + }$, respectively to obtain revised ‘laws of the wall’ in the following manner (Poinsot and Veynante 2005):

$$\psi^{ + } = \eta^{ + } \,\,\,{\text{and}}\,\,\,{\Theta }^{ + } = Pr \eta^{ + } \,\,\,{\text{for}}\,\,\,\eta^{ + } \le 10.8$$

(21)

$$\psi^{ + } = \frac{1}{\kappa }\ln \eta^{ + } + B\,\,\,{\text{and}}\,\,\,{\Theta }^{ + } = 2.075\ln \eta^{ + } + 3.9\,\,\,{\text{for}}\,\,\,\eta^{ + } > 10.8$$

(22)

However, it is worthwhile to note that the success of Eqs. 21 and 22 also depends on the modelled expressions of $\eta^{ + }$ and $\psi^{ + }$ given by Eqs. 18 and 19, respectively. The applicability of Eqs. 1, 5, 13, 15, 18, 19, 21 and 22 during FWI in turbulent boundary layers will be assessed in Sect. 4 of this paper.

3 Numerical Implementation

In this work, DNS databases of unsteady HOQ of statistically planar flames across turbulent boundary layers due to interaction with isothermal inert walls have been considered for friction velocity-based Reynolds numbers $Re_{\tau }$ of 110 and 180. In the existing literature, the friction velocity $Re_{\tau }$ of 180 is often regarded as a benchmark case for DNS of fully developed turbulent channel flows (Kawamura et al. 1998; Kim et al. 1987) because all the turbulence statistics for this friction Reynolds number is qualitatively similar to those for higher values of $Re_{\tau }$ (Kawamura et al. 1998; Kim et al. 1987) but can be afforded without exorbitant computational cost. It is worth noting that turbulent boundary layers in internal combustion engines are characteristic of low $Re_{\tau }$ values (e.g., $Re_{\tau }$ ranging from 100 to 200). Therefore, $Re_{\tau }$ of 110 is considered in this analysis to ensure that the findings for $Re_{\tau } =$ 180 also remain valid for weakly turbulent boundary layers. Moreover, the computational requirement of the DNS considered here, with a maximum mesh size of 1.536 billion, also played a crucial role in determining the Reynolds numbers. Higher Reynolds numbers demand finer meshes and thus are more computationally expensive. Thus, the chosen $Re_{\tau }$ values are deemed appropriate to ensure a reasonable compromise between computational cost and required physical insights within the constraints of available computational resources.

The simulations have been conducted using a compressible DNS code SENGA + (Jenkins and Cant 1999), which solves conservation equations of mass, momentum, energy and species in non-dimensional form. In SENGA+, spatial derivatives for internal grid points are systematically computed utilising a 10th-order central difference scheme. However, it is noteworthy that the order of accuracy gradually diminishes to a one-sided 2nd-order scheme at the non-periodic boundaries, as explained by Jenkins and Cant (1999). Temporal progression in these simulations is achieved through the utilisation of a low storage explicit 3rd-order Runge–Kutta scheme.

A generic single step irreversible chemical reaction representing fuel and oxidiser is considered in the present work: $1$ unit mass of Fuel + $s$ unit mass of Oxidiser → ($1 + s$⁠) unit mass of Products, where $s$ is the stoichiometric oxidiser-fuel mass ratio. Here, fuel is methane ${\text{CH}}_{4}$, oxidiser is ${\text{O}}_{2}$ and products is ${\text{CO}}_{2}$ and ${\text{N}}_{2}$ in the air is considered to be inert. This yields a value of $s = 4.0$ for methane-air combustion. The reactants of the stoichiometric methane-air mixture in their unburned state undergo preheating to a temperature of 730 K. This preheating condition results in the determination of the heat release parameter $\tau$, expressed as the ratio $\left( {T_{ad} - T_{0} } \right)/T_{0}$, where $T_{0}$ denotes the unburned gas temperature, and $T_{ad}$ represents the adiabatic flame temperature. Specifically, in this scenario, the calculated value for $\tau$ is 2.3. It is pertinent to note that standard values are employed for the Prandtl number $Pr$ and the ratio of specific heats $\gamma$, with $Pr$ assigned a value of 0.7 and $\gamma$ set at 1.4. The Lewis number $Le$ of all the species are taken to be unity for the sake of simplicity as the fuel and oxidiser for the present analysis (i.e. methane and oxygen) have Lewis numbers close to unity (= 0.96 and 1.10 for methane and oxygen, respectively) (Smooke and Giovangigli 1991). It is important to note that the present analysis focuses principally on the statistics related to turbulent fluid motion, which are only affected by the density change and dilatation rate arising from chemical heat release. Thus, the exact nature of chemical mechanism is not expected to have a major impact on the statistics presented here. Moreover, it has been demonstrated elsewhere (Ahmed et al. 2018, 2021b; Lai et al. 2022; Zhao et al. 2018a, b) that the statistics of vorticity, reactive scalar gradient, maximum wall heat flux magnitude and the flame quenching distance obtained from single step chemistry (Ahmed et al. 2018; Ahmed et al. 2021c; Lai and Chakraborty 2016a; Lai et al. 2018a; Poinsot et al. 1993; Sellmann et al. 2017) are in good qualitative and quantitative agreement with the corresponding detailed chemistry results (Ahmed et al. 2018; Ahmed et al. 2021b; Lai et al. 2018a; Lai et al. 2022). Thus, it can be expected that the findings of the current analysis will be at least qualitatively valid in the presence of detailed chemistry. The aforementioned studies, encompassing both single-step irreversible chemical reactions representing fuel and oxidiser, as well as those employing detailed chemistry, serve as representations of stoichiometric methane-air (Ahmed et al. 2018, 2021b; Lai et al. 2018a) and stoichiometric hydrogen-air (Lai et al. 2022) mixtures.

The bulk Reynolds number for the non-reacting fully developed channel flow simulations which are used to initilise the reacting flow simulations are $Re_{b} = 2\rho_{0} u_{b} h/\mu_{0} = 3285$ and $5665$ for $Re_{\tau } = 110$ and 180, respectively where $u_{b} = 1/2h\mathop \int \limits_{0}^{2h} udy$ is the bulk mean velocity, $\rho_{0}$ is the unburned gas density, $h$ is the half channel height, and $\mu_{0}$ is the unburned gas viscosity. The ratio of unstretched laminar burning velocity to the non-reacting flow friction velocity, denoted as $S_{L} /u_{\tau ,NR}$, is taken to be 0.7. The Mach number based on $u_{\tau ,NR}$, represented as $Ma = u_{\tau ,NR} /a_{0}$ (where $a_{0}$ is the acoustic speed in the unburned gas), is $3 \times 10^{ - 3}$ for all cases considered. Validation of the non-reacting flow simulation results has been undertaken by comparing them to prior research findings, specifically those presented by Tsukahara et al. (2005). The achieved agreement, as reported in studies by Ahmed et al. (2021a, 2021b, 2021c, 2021d), attests to the reliability and accuracy of the simulations in capturing the fundamental flow features. For these simulations, key parameters such as the longitudinal integral length scale $L_{11}$ and the root-mean-square velocity fluctuation exhibit scaling relationships with $h$ and $u_{\tau ,NR}$ respectively, as shown by Ahmed et al. (2021a), which yield a Damköhler number $Da = L_{11} S_{L} /u^{\prime}\delta_{th}$ of 15.80 and 26, and a Karlovitz number $Ka = \left( {u^{\prime}/S_{L} } \right)^{3/2} \left( {L_{11} /\delta_{th} } \right)^{ - 1/2}$ of 0.36 and 0.28 for $Re_{\tau }$ of $110$ and $180$, respectively. These values are representative of the corrugated flamelets regime combustion when the flame is away from the wall (Peters 2000).

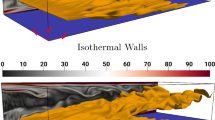
The schematic diagram for the HOQ configuration is shown in Fig. 1. The computational domain size and the corresponding grid size are listed in Table 2 for the cases considered in the present work. The grid resolution employed in these simulations guarantees a minimum of 8 grid points within the thermal flame thickness, denoted as $\delta_{th} = \left( {T_{ad} - T_{0} } \right)/\max \left| {\nabla T} \right|_{L}$, where $T$ represents the instantaneous temperature. Additionally, a stringent criterion is imposed to maintain a maximum value of $y^{ + }$ (dimensionless distance from the wall) not exceeding 0.6 for the grid points adjacent to the wall. Periodic boundary conditions are specified for the streamwise ($x -$direction) and spanwise ($z -$direction) dimensions, while the mean pressure gradient, expressed as $- \partial \overline{p}/\partial x = \overline{\rho }u_{\tau ,NR}^{2} /h$ (where $p$ denotes pressure), is applied in the streamwise flow direction. A no-slip boundary condition is implemented at $y = 0$, and the wall temperature $T_{w}$ is equal to the unburned gas temperature $T_{0}$, which is specified, $T_{w} = T_{0} = 730K$ as isothermal wall boundary condition. The wall-normal mass flux is constrained to zero at the wall. At $y/h = 1.33$, a partially non-reflecting boundary is prescribed based on the NSCBC conditions proposed by Yoo and Im (2007). Initialisation of the reacting flow field is carried out such that the reaction progress variable, denoted as $c$, attains a value of 0.5 at $y/h \approx 0.85$. In this context, the reaction progress variable $c$ is defined in terms of the fuel mass fraction $Y_{F}$, given by $c = (Y_{FR} - Y_{F} )/(Y_{FR} - Y_{FP} )$ where subscripts $R$ and $P$ represent the fresh reactant and fully burned products, respectively. This formulation ensures that $c$ ranges from 0.0 in the unburned gas to 1.0 in the fully burned gas. The initialisation of the reacting scalar field is designed such that the reactant side of the flame faces the wall, while the product side of the flame consistently orients towards the outflow side of the boundary in the $y -$direction. The simulation duration spans a maximum of 2.0 flow-through times, corresponding to $21.30t_{f}$ and $30.3t_{f}$ for $Re_{\tau }$ values of 110 and 180, respectively, where $t_{f}$ is the chemical timescale, defined as $t_{f} = \delta_{th} /S_{L}$. During the simulation period, the flame propagates towards the wall and interacts with it, although the boundary layer exhibits minimal evolution, as corroborated by the corresponding non-reacting flow simulation (Ahmed et al. 2021a, 2021b, 2021c, 2021d). The Reynolds and Favre averaged quantities, involving correlations of Reynolds and Favre fluctuations in the HOQ configuration under consideration, are determined by spatial averaging the relevant parameters within the periodic directions (i.e., $x - z$ planes) at a given time instant.

Fig. 1

Schematic diagram of the HOQ configuration

Table 2 Simulation parameters for the HOQ configuration for $Re_{\tau }$ = 110 and 180

4 Results and Discussion

4.1 Instantaneous and Mean Scalar Fields

The isosurfaces of reaction progress variable $c = 0.8$ at the different stages of HOQ (i.e., for different values of $t/t_{f}$) of the statistically planar flame are shown in Fig. 2a, b at $t/t_{f} = 3.99, 10.92, 13.12, 16.27$ for $Re_{\tau } = 110$ and at $t/t_{f} = 7.89, 14.38, 16.75, 20.11$ for $180$, respectively along with the distributions of normalised vorticity magnitude ${\Omega } = \sqrt {w_{i} w_{i} } \times h/u_{\tau ,NR}$ on the $x - y$ plane at $z/h = 4$, where $w_{i}$ is the ith component of vorticity. The aforementioned time instants with increasing values of $t/t_{f}$ correspond to the normalised wall normal distance of $y/h = 0.72, 0.22, 0.06$ and $0.03$ of non-dimensional temperature $\tilde{\theta } = \left( {\tilde{T} - T_{0} } \right)/\left( {T_{ad} - T_{0} } \right) = 0.5$ isosurface, respectively for both values of $Re_{\tau }$. The vortical flow structures close to the wall, as can be seen from Fig. 2a, b, affect the flame wrinkling and the interaction of the flame surface with the wall leads to eventual flame quenching due to heat loss through the cold isothermal wall. The effect of the increase in the $Re_{\tau }$ is reflected in the higher extent of wrinkling of the $c = 0.8$ isosurface in Fig. 2b than in Fig. 2a. At higher $Re_{\tau }$ values, the flame wrinkling increases due to stronger turbulent activity within the boundary layer, which is reflected in the higher magnitudes of turbulent burning velocity $S_{T} = \int \dot{\omega }_{c} dV/\rho_{0} A_{p}$ (where $A_{p}$ is the projected flame area in the direction of mean flame propagation, $\dot{\omega }_{c}$ is the reaction rate of progress variable and $\rho_{o}$ is the unburnt gas density) for a given wall-normal distance of $\tilde{\theta } = 0.5$ isosurfaces in the $Re_{\tau } = 180$ case than in the $Re_{\tau } = 110$ case, which can be substantiated from the Table 3. Therefore, the interaction between flame and wall surface becomes stronger for higher values of $Re_{\tau }$ where the flame elements are convected more strongly towards the wall by the turbulent fluid motion.

Fig. 2

Isosurfaces of reaction progress variable $c = 0.8$ at the different stages of HOQ of the statistically planar flame in terms of $t/t_{f}$ at (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$. The distributions of normalised vorticity magnitude ${\Omega } = \sqrt {w_{i} w_{i} } \times h/u_{\tau ,NR}$ is shown on the $x - y$ plane at $z/h = 4$

Table 3 The values of the normalised turbulent burning velocity $S_{T} /S_{L}$ for the $Re_{\tau }$ = 110 and 180 case of HOQ configuration at different $t/t_{f}$ and $y_{{\tilde{\theta } = 0.5}} /h.$

In the case of low Mach number globally adiabatic premixed flames, $c = \theta$ (where $\theta = \left( {T - T_{0} } \right)/\left( {T_{ad} - T_{0} } \right)$ is the non-dimensional temperature) is maintained without any significant heat loss but the requirements of $c = \theta$ are not met in the vicinity of an isothermal wall boundary condition. The instantaneous distributions of $\left( {c - \theta } \right)$ at the central midplane for both cases are shown in Fig. 3. Initially, away from the wall, there is a coherent maintenance of the relationship $c = \theta$, indicating a coupling between progress variable, $c$ and non-dimensional temperature $\theta$. However, in close proximity to the wall, a pronounced decoupling between $c$ and $\theta$ is evident. This decoupling originates due to the imposed boundary conditions at the wall. The non-dimensional temperature $\theta$ at the wall is maintained to a constant value of 0.0 due to an imposed isothermal wall boundary condition. By contrast, the progress variable $c$ undergoes an increase from 0.0 as the flame quenching progresses due to the zero wall normal gradient boundary condition. This increase in $c$ is attributed to the diffusion of unburned gas from the vicinity of the wall towards the interior of the domain. Therefore, the value of $\left( {c - \theta } \right)$ emerges as a distinctive marker of FWI, providing valuable insights into the progress of flame quenching. (Ahmed et al. 2021a, b, c, d; Ahmed et al. 2023a, b; Ghai et al. 2022a, b, c). This can be substantiated from Fig. 4, which shows that the evolutions of $\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right)$ (where the subscript $w$ is used for wall values) and the mean normalised wall heat flux magnitude ${\overline{\Phi }} = \left| {\overline{q}_{w} } \right|/\left[ {\rho_{0} c_{p0} S_{L} \left( {T_{ad} - T_{0} } \right)} \right]$ with normalised time $t/t_{f}$, where $c_{p0}$ and $q_{w}$ are the specific heat at constant pressure in the unburned gas, and wall heat flux respectively. It can be seen from Fig. 4 that $\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right)$ starts to assume significant non-zero values when ${\overline{\Phi }}$ takes non-zero values, which can be considered as the marker of the initiation of FWI. The magnitude of ${\overline{\Phi }}$ starts to drop once the flame is quenched but $\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right)$ continues to increase until it assumes a value of 1.0. The normalised maximum heat flux magnitude ${\Phi }_{max} = |q_{w} |_{max} /\left[ {\rho_{0} c_{p0} S_{L} \left( {T_{ad} - T_{0} } \right)} \right]$, minimum Peclet number $Pe_{min} = \delta_{Q} /\delta_{z}$ (i.e. the minimum wall normal distance $\delta_{Q}$ of the $\theta = 0.75$ isosurface normalised by the Zel’dovich flame thickness $\delta_{z} = \alpha_{T0} /S_{L}$ with $\alpha_{T0}$ being the thermal diffusivity in the unburned gas) are often used to characterise the FWI process. Note that the maximum heat release rate in the unstretched freely propagating laminar premixed flame occurs at $\theta = 0.75$ for the present thermochemistry. The ${\Phi }_{max}$ and $Pe_{min}$ values for this turbulent boundary layer HOQ case are 0.47 and 1.71 for $Re_{\tau } = 110$ and 0.46 and 1.72 for $Re_{\tau } = 180$. The distributions of ${\Phi }$ and normalised vorticity magnitude ${\Omega }$ on the wall when the minimum Peclet number is observed are shown in Fig. 5a, b, for $Re_{\tau } = 110$ and $180$, respectively, which show the signatures of heat flux streaks induced by vortical motions. The occurrence of heat flux streaks is intimately connected to the dynamic behaviour of vortical structures within the turbulent boundary layer. Vortical motions, characterised by the presence of coherent structures, play a pivotal role in the heat transfer to the wall (Ghai et al. 2023a).

Fig. 3

Instantaneous distributions of $\left( {c - \theta } \right)$ is shown in the central midplane at the different stages of HOQ (i.e. for different values of $t/t_{f}$) of the statistically planar flame for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$

Fig. 4

Distributions of $\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right)$ (1st row) and the mean normalised wall heat flux magnitude ${\overline{\Phi }} = \left| {\overline{q}_{w} } \right|/\left[ {\rho_{0} c_{p0} S_{L} \left( {T_{ad} - T_{0} } \right)} \right]$ (2nd row) with normalised time $t/t_{f}$ for statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$

Fig. 5

Instantaneous distributions of ${\Phi }$ (left) and normalised vorticity magnitude ${\Omega }$ (right) on the wall at the time when the maximum heat flux magnitude is obtained for HOQ of statistically planar flame for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$

It is not only the wall heat flux but also the wall shear stress $\tau_{w}$ which is affected during FWI. Figure 6 shows the variations of $\overline{\tau }_{w} /\overline{\tau }_{w,NR}$ and $\overline{u}_{\tau } /\overline{u}_{\tau ,NR} = \sqrt {|\overline{\tau }_{w} |/\overline{\rho }_{w} } /\overline{u}_{\tau ,NR}$ with the normalised time $t/t_{f}$ for the statistical planar flame HOQ case, where $\overline{\tau }_{w}$ is the mean wall shear stress and the subscript NR is used for the corresponding non-reacting values for $Re_{\tau } = 110$ and $180$. The gas density drops with an increase in temperature as the thermodynamic pressure remains almost constant in the cases considered here. Accordingly, density increases as the cold wall is approached and at the wall the density becomes comparable to the unburned gas density (i.e. $\rho_{w} \approx \rho_{0}$). In this configuration, the mean direction of flame propagation is perpendicularly aligned with the wall and thus the thermal expansion effects are mostly felt in the wall-normal direction. The redistribution of momentum due to thermal expansion leads to reductions in $\left( {\partial u/\partial y} \right)_{y = 0}$ and $\tau_{w}$ during FWI in the HOQ configuration considered here (Ahmed et al. 2023a, b). This leads to a drop in $u_{\tau }$ during FWI in comparison to the non-reacting channel flow value for the cases considered here (Ahmed et al. 2023a, b). Figures 4 and 6 indicate that both $\overline{q}_{w}$ and $\overline{\tau }_{w}$ change during FWI, which, in turn, can affect $T^{ + }$, $u^{ + }$ and $y^{ + }$ values. Therefore, the values of $y^{ + }$ at a given value of $y/h$ can be different during FWI in both cases considered here.

Fig. 6

Variations of $\overline{\tau }_{w} /\overline{\tau }_{w,NR}$ (1st row) and $\overline{u}_{\tau } /\overline{u}_{\tau ,NR} = \sqrt {|\overline{\tau }_{w} |/\rho_{w} } /\overline{u}_{\tau ,NR}$ (2nd row) with normalised time $t/t_{f}$ for statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$

4.2 Evaluation of Existing Wall Functions

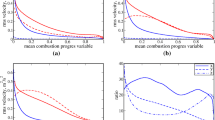
Figure 7 represents the variation of $y^{ + }$ with $y/h$ and it can be seen from Fig. 7a, b that the range of $y^{ + }$ values within the region given by $0 < y/h < 1.0$ changes with time. The dynamic changes in $y^{ + }$ values are indicative of the evolving flow conditions near the wall during FWI. The wall shear stress changes with the progress of FWI in this configuration due to the redistribution of momentum in the near-wall region because of flame normal acceleration indued by thermal expansion, which was discussed in detail by Ahmed et al. (2023a, b) and thus is not repeated here. The time-dependent variation in $y^{ + }$ values in the unsteady head-on quenching across turbulent boundary layers underscore the need for a nuanced understanding of turbulent boundary layer dynamics during FWI. Moreover, it suggests that wall functions for FWI need to capture the dynamic nature of the near-wall flow dynamics. Furthermore, this has a major implication on the applicability of Eqs. 1, 5, 13 and 15 within turbulent boundary layers during FWI. Figure 8 shows the variations of normalised Favre mean streamwise velocity $u^{ + }$ and normalised mean temperature $T^{ + }$ with normalised wall-normal distance $y^{ + }$. The variation of $u^{ + }$ with $y^{ + }$ in a non-reacting channel flow corresponding to $Re_{\tau } = 110$ and $180$ are also shown in Fig. 8 and it is found that the predictions of Eqs. 1 and 5 agree well with DNS data and the observed variation of $u^{ + }$ with $y^{ + }$ is consistent with previous findings (Tsukahara et al. 2005). In Fig. 8, the time instants for the simulations are chosen in such a manner that it ranges from the time when the flame is away from the wall (i.e., $t/t_{f} < 8.0$) to when it interacts with the wall (i.e., $t/t_{f} > 10.0$). The predictions of the standard relations for viscous sub-layer (i.e. Equation 2 for $y^{ + } < 10.8$) and inertial layer (i.e. Equation 5 for $y^{ + } > 10.8$) are also compared with the variation of $u^{ + }$ with $y^{ + }$ extracted from DNS data in Fig. 8 where the predictions of the temperature wall functions for viscous sublayer (i.e. Equation 13) and inertial layer (i.e. Equation 15) are also shown. Figure 8 shows that the variation of $u^{ + }$ with $y^{ + }$ from DNS matches reasonably well with $u^{ + } = y^{ + }$ for $y^{ + } < 10.8$ for both $Re_{\tau }$ cases, but the agreement with log-law remains unsatisfactory for $y^{ + } > 10.8$, and the disagreement increases with increasing $t/t_{f}$. Moreover, Eqs. 13 and 15 do not capture the variation of $T^{ + }$ both in the viscous sub-layer and inertial layers.

Fig. 7

Variations of $y^{ + }$ with $y/h$ at different normalised time instants $t/t_{f}$ for the statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$. The background colour in Figs. 6, 7, 8, 9, 10, 11, 12, 13 provides the value of $\tilde{c}$

Fig. 8

Variations of (a) $u^{ + }$ and (b) $T^{ + }$ with $y^{ + }$ at different normalised time $t/t_{f}$ for the statistical planar flame HOQ case

It is worth noting that Eqs. 1 and 5 assume that $\mu \left( {\partial \tilde{u}/\partial y} \right) - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}}$ remain unchanged and is equal to $\overline{\tau }_{w}$ in the wall normal direction. The variations of $\mu \left( {\partial \tilde{u}/\partial y} \right)/\overline{\tau }_{w}$, $- \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} /\overline{\tau }_{w}$ and $\left[ {\mu \left( {\partial \tilde{u}/\partial y} \right) - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} } \right]/\overline{\tau }_{w}$ with $y/h$ at different time instants for the HOQ of the statistically planar flame are shown in Fig. 9. It can be seen from Fig. 9 that $\mu \left( {\partial \tilde{u}/\partial y} \right)_{{\text{w}}} = \overline{\tau }_{w}$ is maintained at the wall because $\overline{{\rho u^{\prime\prime}v^{\prime\prime}}}$ vanishes at the wall, whereas the magnitude of the contribution of $\left( { - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} } \right)$ increases in the wall normal direction. However, the net contribution of $\left[ {\mu \left( {\partial \tilde{u}/\partial y} \right) - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} } \right]$ does not remain equal to $\overline{\tau }_{w}$ but remains always smaller than $\overline{\tau }_{w}$ away from the wall for both cases. Therefore, the assumption $\left[ {\mu \left( {\partial \tilde{u}/\partial y} \right) - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} } \right] = \overline{\tau }_{w}$ that underpins Eq. 4 is rendered invalid in the reacting flow turbulent boundary layers considered in the current analysis. Moreover, the equilibrium between $P_{k} = - \overline{{\rho u_{i}^{^{\prime\prime}} u_{j}^{^{\prime\prime}} }} \left( {\partial \tilde{u}_{i} /\partial x_{j} } \right)$ and $\overline{\rho }\tilde{\varepsilon }$ is invoked while deriving the log-law (i.e., Eq. 5) in the inertial layer. The ratio of $P_{k} /\overline{\rho }\tilde{\varepsilon }$ in the wall-normal distance $y/h$ at different time instants for the HOQ of the statistically planar flame are shown in Fig. 10. Figure 10 further shows that $P_{k} /\overline{\rho }\tilde{\varepsilon }$ assumes locally negative values for $y^{ + } > 10.8$ in the HOQ of statistically planar flame. According to the Boussinesq hypothesis, $- \overline{{\rho u^{\prime\prime}v^{\prime\prime}}}$ can be modelled as: $- \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} = \overline{\rho }\nu_{t} \left( {\partial \tilde{u}/\partial y} \right)$, which leads to $P_{k} = - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} \left( {\partial \tilde{u}/\partial y} \right) = \overline{\rho }\nu_{t} \left( {\partial \tilde{u}/\partial y} \right)^{2}$ for boundary layer flows considered here. This suggests that $P_{k} /\overline{\rho }\tilde{\varepsilon }$ becomes equal to $P_{k} /\overline{\rho }\tilde{\varepsilon } = \nu_{t} \left( {\partial \tilde{u}/\partial y} \right)^{2} /\tilde{\varepsilon }$, which is a positive value. However, negative values of $P_{k} /\overline{\rho }\tilde{\varepsilon }$ in the region of the flame brush where the effects of heat release rate are strong, shown in Fig. 10, suggests that the Boussinesq hypothesis might not even be qualitatively valid within the flame brush. Figure 10 further shows that $P_{k} /\overline{\rho }\tilde{\varepsilon }$ assumes positive values in the unburned and burned gases where the thermal expansion effects are not strong, which indicates that the Boussinesq hypothesis at least predicts the correct sign of $\overline{{\rho u^{\prime\prime}v^{\prime\prime}}}$ both in the fully unburned and fully burned gases. However, the value of $P_{k} /\overline{\rho }\tilde{\varepsilon }$ remains considerably different from unity even when the value is positive. Interested readers are referred to (Ahmed et al. 2019; Ghai et al. 2023c; Lai et al. 2017a, b, c) for further discussion into the turbulent kinetic energy $\tilde{k} = 0.5\overline{{\rho u_{i}^{^{\prime\prime}} u_{i}^{^{\prime\prime}} }} /\overline{\rho }$ transport equation during FWI in turbulent boundary layers where the physical reasons for the lack of equilibrium between $P_{k}$ and $\overline{\rho }\tilde{\varepsilon }$ and the invalidity of Boussinesq’s assumption in premixed turbulent FWI were discussed in detail.

Fig. 9

Variations of $\mu \left( {\partial \tilde{u}/\partial y} \right)/\overline{\tau }_{w}$, $- \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} /\overline{\tau }_{w}$ and $\left[ {\mu \left( {\partial \tilde{u}/\partial y} \right) - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} } \right]/\overline{\tau }_{w}$ at different normalised time instants $t/t_{f}$ for the statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$. The location corresponding to $y^{ + } = 10.8$ is shown by the blue vertical line

Fig. 10

Variations of $P_{k} /\overline{\rho }\tilde{\varepsilon }$ at different normalised time instants $t/t_{f}$ for the statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$. The location corresponding to $y^{ + } = 10.8$ is shown by the blue vertical line

The observations made from Fig. 10 suggest that Eq. 3, which was invoked during the derivation of the log-law (i.e., Eq. 5), is also rendered invalid during FWI with the reacting flow boundary layers considered here. Figures 9 and 10 show that the fundamental assumptions underpinning the derivation of the log-law (i.e., Eq. 5) are not valid during FWI within turbulent boundary layers and thus Eq. 5 is not expected to predict the variation of $u^{ + }$ with $y^{ + }$ accurately within the inertial layer (i.e., $y^{ + } > 10.8$).

The variations of $- \lambda \left( {\partial \tilde{T}/\partial y} \right)/\overline{q}_{w}$, $- \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} /\overline{q}_{w}$ and $\left[ { - \lambda \left( {\partial \tilde{T}/\partial y} \right) - \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} } \right]/\overline{q}_{w}$ at different time instants for the HOQ of the statistically planar flame are shown in Fig. 11. The mean heat fluxes $\overline{q}_{w}$ are negligibly small at early times when the flame remains away from the wall (see Fig. 4) and thus the variations of $- \lambda \left( {\partial \tilde{T}/\partial y} \right)/\overline{q}_{w}$, $- \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} /\overline{q}_{w}$ and $\left[ { - \lambda \left( {\partial \tilde{T}/\partial y} \right) - \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} } \right]/\overline{q}_{w}$ at $t/t_{f} = 3.99$ and $7.89$ for $Re_{\tau } = 110$ and 180, respectively are not shown in Fig. 11 to avoid any confusion. It is evident from Fig. 11 that the contribution $- \lambda \left( {\partial \tilde{T}/\partial y} \right)_{w} = \overline{q}_{w}$ is maintained at the wall, whereas the magnitude of $- \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} /\overline{q}_{w}$ increases in the wall normal direction. However, the magnitude of $- \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} /\overline{q}_{w}$ is significant in the intertial layer only during the initial stages of FWI, and this contribution vanishes when the flame starts to quench. Moreover, $- \lambda (\partial \tilde{T}/\partial y)$ and $- \overline{{\rho v^{\prime\prime}T^{\prime\prime}}}$ exhibit same signs for a major part of the inertial layer (i.e., $y^{ + } > 10.8$). This suggests that the gradient hypothesis (i.e., $- \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} = \left( {\overline{\rho }\nu_{t} /Pr_{t} } \right)(\partial \tilde{T}/\partial y$)), which was assumed for the derivation of Eqs. 8 and 15 is rendered invalid for both FWI cases considered here. Furthermore, the magnitude of $\left[ { - \lambda \left( {\partial \tilde{T}/\partial y} \right) - \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} } \right]/\overline{q}_{w}$ remains smaller than unity for a major part of the inertial layer (i.e., $y^{ + } > 10.8$) so the assumption of constant heat flux layer is rendered invalid in the case of FWI within turbulent boundary layers considered here. A comparison between Figs. 9 and 11 reveals that $\left( { - \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} } \right)$ and $- \lambda (\partial \tilde{T}/\partial y$) exhibit the same signs (i.e. counter-gradient transport) in the regions where $\left( { - \overline{{\rho u^{\prime\prime}v^{\prime\prime}}} } \right)$ and $\mu (\partial \tilde{u}/\partial y)$ also exhibit same signs (i.e. counter-gradient behaviour). Subject to the assumption of counter-gradient transport of both momentum and temperature, it is possible to obtain a log-law based relation for the mean temperature in the inertial layer if a log-law holds for the Favre-mean values of the streamwise velocity component.

Fig. 11

Variations of $- \lambda \left( {\partial \tilde{T}/\partial y} \right)/\overline{q}_{w}$, $- \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} /\overline{q}_{w}$ and $\left[ { - \lambda \left( {\partial \tilde{T}/\partial y} \right) - \overline{{\rho v^{\prime\prime}T^{\prime\prime}}} } \right]/\overline{q}_{w}$ at different normalised time instants $t/t_{f}$ for the statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$. The location corresponding to $y^{ + } = 10.8$ is shown by the blue vertical line

4.3 Assessment of Proposed Wall Functions

Angelberger et al. (1997) and Han et al. (1996) modified the usual laws of the wall based on empirical relations given by Eqs. 21 and 22 for the purpose of FWI. The predictions of Eqs. 21 and 22 relating $\psi^{ + }$ and ${\Theta }^{ + }$ in terms of $\eta^{ + }$ are shown in Fig. 12 for the sake of completeness. The quantities $\eta^{ + }$ and $\psi^{ + }$ are approximated as $\eta_{{Model_{1} }}^{ + } = \left( {\nu_{w} /\tilde{\nu }} \right)y_{1}^{ + }$ (i.e. right hand side of Eq. 17) and $\psi_{{Model_{1} }}^{ + } = \overline{\rho }u^{ + } /\rho_{w}$ (i.e. right hand side of Eq. 19) (Angelberger et al. 1997; Han et al. 1996; Poinsot and Veynante 2005) and thus the variations of $\psi_{{Model_{1} }}^{ + }$ and ${\Theta }^{ + }$ with $\eta_{{Model_{1} }}^{ + }$ are also shown in Fig. 12 to assess the practical implications of these approximations. Figure 12 shows that there are significant differences between the variations of $\psi^{ + }$ and ${\Theta }^{ + }$ with $\eta^{ + }$ with the corresponding variations of $\psi_{{Model_{1} }}^{ + }$ and ${\Theta }^{ + }$ with $\eta_{{Model_{1} }}^{ + }$ especially for large values of $\eta^{ + }$. Thus, $\eta^{ + } \approx \eta_{{Model_{1} }}^{ + }$ and $\psi^{ + } \approx \psi_{{Model_{1} }}^{ + }$ are rendered invalid for large values of $\eta^{ + }$. A comparison between Figs. 8 and 12 reveals that the modified wall functions given by Eqs. 20 and 21 do not offer any appreciable benefit over the standard wall functions (Eqs. 5 and 15) for the inertial layer when $\eta^{ + }$ and $\psi^{ + }$ are approximated by Eqs. 18 and 19, respectively but the predictions remain in reasonable agreement with DNS data in the viscous sublayer. The variations of $\eta_{{Model_{1} }}^{ + }$ (i.e., right hand side of Eq. 18) with $\eta^{ + }$ obtained from DNS (i.e., left hand side of Eq. 18) for different normalised times $t/t_{f}$ are shown in Fig. 13. The corresponding variations of $\psi_{{Model_{1} }}^{ + }$ (i.e., right hand side of Eq. 19) with $\psi^{ + }$ obtained from DNS (i.e., left hand side of Eq. 19) are shown in Fig. 14. It can be seen from Figs. 13 and 14 that $\eta_{{Model_{1} }}^{ + }$ and $\psi_{{Model_{1} }}^{ + }$ do not adequately capture the integrals $\eta^{ + } = \mathop \int \limits_{0}^{{y^{ + } }} \nu_{w} /\tilde{\nu }dy^{ + }$ and $\psi^{ + } = \mathop \int \limits_{0}^{{u^{ + } }} \overline{\rho }/\rho_{w} du^{ + }$. Here, $\eta^{ + } = \mathop \int \limits_{0}^{{y^{ + } }} \nu_{w} /\tilde{\nu }dy^{ + }$ and $\psi^{ + } = \mathop \int \limits_{0}^{{u^{ + } }} \overline{\rho }/\rho_{w} du^{ + }$ are modelled in the following manner:

$$\eta^{ + } = \mathop \int \limits_{0}^{{y^{ + } }} \frac{{\nu_{w} }}{{\tilde{\nu }}}dy^{ + } \approx \left( {1 - \alpha_{1} } \right)y^{ + } + \alpha_{1} \nu_{w} y^{ + } /\tilde{\nu } = \eta_{{Model_{2} }}^{ + }$$

(23)

$$\psi^{ + } = \mathop \int \limits_{0}^{{u^{ + } }} \frac{{\overline{\rho }}}{{\rho_{w} }}du^{ + } \approx \left( {1 - \alpha_{2} } \right)u^{ + } + \alpha_{2} \overline{\rho }u^{ + } /\rho_{w} = \psi_{{Model_{2} }}^{ + }$$

(24)

where, $\alpha_{1} = \frac{{\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right)}}{{\left[ {\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right) + \epsilon } \right]}}\left[ {0.5 + 0.5{\text{erf}}\left\{ {\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right)^{0.2} } \right\}} \right]$ and

$$\alpha_{2} = \frac{{\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right)}}{{\left[ {\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right) + \epsilon } \right]}}\left[ {0.45 + 0.4{\text{erf}}\left\{ {\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right)} \right\}} \right]$$

(25)

Fig. 12

Variations of (a) $\psi^{ + }$ and (b) ${\Theta }^{ + }$ with $\eta^{ + }$ at different normalised time instants $t/t_{f}$ for the statistical planar flame HOQ case. The predictions of Eqs. 21 and 22 based on quantities extracted from DNS data, $\eta^{ + }$ estimation based on Eq. 18 and $\eta^{ + }$ estimation based on Eq. 23

Fig. 13

Variations of $\eta^{ + }$ obtained from Eqs. 18 and 23 (i.e. $\eta_{{Model_{1} }}^{ + }$ and $\eta_{{Model_{2} }}^{ + }$, respectively) with $\eta^{ + }$ obtained from DNS data at different normalised time instants $t/t_{f}$ for the statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$

Fig. 14

Variations of $\psi^{ + }$ obtained from Eqs. 19 and 24 (i.e. $\psi_{{Model_{1} }}^{ + }$ and $\psi_{{Model_{2} }}^{ + }$, respectively) with $\psi^{ + }$ obtained from DNS data at different normalised time instants $t{/}t_{f}$ for the statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$

In Eq. 25, $\epsilon$ is a small number (i.e., $\epsilon < 0.0001$) to avoid division by zero. According to Eqs. 23–25, $\eta_{{Model_{2} }}^{ + }$ and $\psi_{{Model_{2} }}^{ + }$ approach $y^{ + }$ and $u^{ + }$, respectively when $\left( {\tilde{c}_{w} - \tilde{\theta }_{w} } \right) = 0$, which physically represents a condition when the FWI does not take place and/or when the flame remains sufficiently away from the wall to impart any influence on the near-wall dynamics. It can be seen from Figs. 13 and 14 that $\eta_{{Model_{2} }}^{ + }$ and $\psi_{{Model_{2} }}^{ + }$ approximate $\eta^{ + } = \mathop \int \limits_{0}^{{y^{ + } }} \nu_{w} /\tilde{\nu }dy^{ + }$ and $\psi^{ + } = \mathop \int \limits_{0}^{{u^{ + } }} \overline{\rho }/\rho_{w} du^{ + }$ more accurately than Eqs. 18 and 19, respectively. Furthermore, the predictions of Eqs. 21 and 22, when $\eta^{ + }$ is approximated by $\eta_{{Model_{2} }}^{ + }$, are also shown in Fig. 13, which show that they agree with $\psi^{ + }$ and ${\Theta }^{ + }$ evaluated from DNS data. This implies that Eq. 21 and 22 can be used in RANS simulations of FWI when $\eta^{ + }$ is approximated by Eq. 23 using $y^{ + }$ to obtain $\psi^{ + }$ and ${\Theta }^{ + }$ and Eq. 24 can be used to obtain $u^{ + }$ from $\psi^{ + }$. Similarly, Eq. 20 can be used to obtain the Favre-mean temperature $\tilde{T}$ from ${\Theta }^{ + }$. It is worth noting that all the transformations for wall normal distance and mean velocity presented in Table 1 involve some degree of empiricism and the approach adopted here is no different to the earlier propositions of wall laws for the variable density flows. A degree of empiricism is not unusual in turbulence and turbulent combustion modelling and such empirical fits have a value like any new experimental or DNS result that shows an effect, which is yet to be analysed. Moreover, it has been found that Eqs. 23–25 also work well for a database of oblique wall-quenching of a V-shaped flame within a channel (Ghai et al. 2023a), which is not presented here for the sake of brevity.

5 Conclusions

The validity of the laws of the wall for Favre mean streamwise velocity component and Favre mean temperature, which are usually used for RANS simulations of non-reacting flows, has been assessed for turbulent premixed flame-wall interaction using DNS data representing unsteady head-on quenching of statistically planar flames across turbulent boundary layers. It has been found that the usual log-law based expressions for the Favre mean values of streamwise velocity and temperature for the inertial layer do not adequately capture the corresponding variations obtained from DNS data in the reacting flow turbulent boundary layers considered here. The underlying assumptions of constant shear stress and the equilibrium of production and dissipation of turbulent kinetic energy underpinning the usual log-law for the mean streamwise velocity are rendered invalid within the so-called inertial layer of the turbulent boundary layer during flame-wall interaction. Moreover, the heat flux does not remain constant within the so-called inertial layer, which along with the counter-gradient transport of temperature within the inertial layer makes the assumptions underpinning the derivation of the usual log-law for temperature to be invalid during flame-wall interaction. As several underlying assumptions are rendered invalid during FWI, a comprehensive review of various wall models is undertaken in this paper in order to assess their predictive capabilities in the presence of flame-wall interaction. It has been found that that the modified wall laws proposed by Angelberger et al. (1997) and Han et al. (1996) provided the best qualitative agreement with the variations obtained from DNS data although these expressions, which account for density and kinematic viscosity variations with temperature are empirical in nature. However, the modified wall law expressions by Angelberger et al. (1997) and Han et al. (1996) do not appreciably improve the agreement with the corresponding DNS data in the inertial layer in the reacting flow turbulent boundary layers considered here, and there is a scope for improving the way the integrations are performed while computing density-compensated velocity and kinematic viscosity compensated wall-normal coordinate in this modelling flamework. The inadequacies of the empirical modifications to the existing laws of the wall are a result of the inaccurate approximations for the kinematic viscosity compensated wall normal distance and the density compensated streamwise velocity component. The DNS data has been utilised here to propose new expressions for the kinematic viscosity compensated wall normal distance and the density compensated streamwise velocity component, which upon using in the empirically modified law of wall expressions provide reasonable agreement with DNS data.

While the proposed modifications are incorporated in an empirical modelling framework, the modelling choices are informed by the physics extracted from the DNS data. Considering the limited information available on wall laws for flame-wall interaction, it is encouraging that the proposed modifications enhanced the predictive capabilities of wall laws for both streamwise velocity component and temperature but a theoretical framework of wall laws for flame-wall interaction based on first principles will be necessary, which will form the basis of future studies. It is also worth noting that the unity Lewis number assumption is made in this paper as a starting point because laws of the walls for FWI are rarely addressed in the existing literature. However, it has been recent demonstrated that the lack of validity of standard log-laws for streamwise velocity component and temperature for flame-wall interaction with non-unity Lewis number flames are qualitatively similar to the corresponding unity Lewis number flame (Chakraborty et al. 2023). Moreover, the modifications suggested in the current analysis in the form of Eqs. 23 and 24 do not invoke any assumptions regarding the Lewis number. Nevertheless, the predictive capabilities of the revised wall functions need to be assessed for flame-wall interaction with non-unity Lewis numbers in the future. Furthermore, the performance of newly modified wall functions needs to be assessed based on RANS simulations of premixed turbulent flame-wall interaction. Finally, the current findings need to be confirmed in the presence of detailed chemistry for the sake of completeness, although the chemical mechanism is not expected to affect turbulent flow statistics in FWI because the chemical reaction rate effects are felt through the changes in density and kinematic viscosity in turbulent flow statistics.

Appendix A

The variations of $\psi_{ }^{ + }$ with $\eta_{ }^{ + }$ at different normalised time instants $t/t_{f}$ for the statistically planar flame HOQ case at $Re_{\tau } = 110$ and $Re_{\tau } = 180$ are shown in Fig. 

Fig. 15

Variations of $\psi^{ + }$ with $\eta^{ + }$ at different normalised time instants $t{/}t_{f}$ for the statistical planar flame HOQ case for (a) $Re_{\tau } = 110$ and (b) $Re_{\tau } = 180$. The predictions of Eqs. 21 and 22 based on quantities extracted from DNS data, $\eta^{ + }$ estimation based on Eq. 18 and $\eta^{ + }$ estimation based on Eq. 23

15. The predictions from the different transformation given in Table 1 and the model approximations given by Eqs. 18, 19, 23 and 24 are also shown in Fig. 15. It can be seen from the results that within the viscous sublayer the predictions from the different transformations and the model approximations provide reasonable agreement with the standard relation i.e., given by Eq. 21. However, outside the viscous sublayer, there are significant variations in the predictions obtained from the different transformations and model approximations. The transformation proposed by Van Driest (1951) is widely used and is a classic example of density weighted velocity scaling which is based on dimensional reasoning around the mean velocity gradient in the log-layer. However, it is known to be inaccurate for non-adiabatic walls (Volpiani et al. 2020). Along with the transformation proposed by Van Driest (1951), the transformation proposed by Howarth and Taylor (1997) does not follow the inner layer similarity law given by $S_{1} = S_{2} /\left( {G \times H} \right)$ (Trettel and Larsson 2016). In reacting turbulent boundary layer flows, the transformation proposed by Trettel and Larsson (2016) gives inaccurate predictions when there is a sharp change in the density ratio. The transformation given by Volpiani et al. (2020) yields satisfactorily results by collapsing mean velocity profiles with incompressible flows but their validity for the non-adiabatic turbulent boundary layer reacting flows is still questionable. However, the transformations proposed by Angelberger et al. (1997) and Han et al. (1996) provide reasonable agreement for the non-adiabatic turbulent boundary layer reacting flows. Therefore, the transformations proposed by Angelberger et al. (1997) and Han et al. (1996) are used in this work as a platform to propose model modifications. The model approximations given by Eqs. 18 and 19 do not provide good collapse with the transformations proposed by Angelberger et al. (1997) and Han et al. (1996). Therefore, the new modifications given by Eqs. 23 and 24 are used which provide a reasonable collapse of mean velocity and mean temperature with the transformations proposed by Angelberger et al. (1997) and Han et al. (1996), as shown in Fig. 12.