Statistical Behaviour and Modelling of Variances of Reaction Progress Variable and Temperature During Flame-Wall Interaction of Premixed Flames Within Turbulent Boundary Layers

Abstract

The statistical behaviour of the transport of reaction progress variable variance, $\widetilde{{c^{^{\prime\prime}2} }},$ and non-dimensional temperature variance, $\widetilde{{T^{^{\prime\prime}2} }},$ have been analysed using three-dimensional Direct Numerical Simulation (DNS) data of turbulent premixed flame-wall interaction with isothermal inert walls within turbulent boundary layers for (i) an unsteady head-on quenching of a statistically planar flame propagating across the boundary layer, and (ii) a statistically stationary oblique wall quenching of a V-flame. It has been found that the reaction rate contribution acts as a leading order source term to the transport of both reaction progress variable variance, $\widetilde{{c^{^{\prime\prime}2} }},$ and non-dimensional temperature variance, $\widetilde{{T^{^{\prime\prime}2} }},$ whereas the molecular dissipation term remains the leading order sink term for both configurations analysed here. With the progress of flame wall interaction, the magnitude of all the source terms for the transport equations of both reaction progress variable and non-dimensional temperature variances vanish in the near-wall region with the onset of flame quenching. However, the molecular dissipation term continues to act as a sink term. The performances of the existing models for turbulent scalar flux, reaction rate and scalar dissipation rate contributions have been assessed for both flame-wall interaction configurations based on a priori DNS analysis. The existing available models for scalar dissipation rate for temperature and the reaction rate contribution in the variance transport equations even with the previously proposed wall corrections do not adequately predict the behaviour in the near-wall region. Modifications have been suggested to the existing closure models for the scalar dissipation rate and the reaction rate contribution to the scalar variance transport equations to improve the predictions in the near-wall region. Furthermore, the recommended closures for the unclosed terms of both reaction progress variable variance, $\widetilde{{c^{^{\prime\prime}2} }},$ and non-dimensional temperature variance, $\widetilde{{T^{^{\prime\prime}2} }},$ are shown to accurately capture the corresponding variations obtained from DNS data for both near to and away from the wall.

1 Introduction

Development of efficient, reliable, and robust models for turbulent combustion is indispensable for the design and optimization of modern combustion systems. Currently, many industrial combustors are being redesigned to increase their energy density and to make them compatible for electric powertrains (IEA 2015). The decrease in the size of the combustors increases the chances of flame-wall interactions (FWI) and quenching of the flame due to the heat loss to the combustor wall. To date, most existing studies on turbulent premixed combustion have focused on the development of models by neglecting the influence of the walls and turbulent boundary layers. In the last two decades, several studies used Direct Numerical Simulation (DNS) data to analyse FWI for turbulent premixed combustion which revealed valuable insights into the flame structure and flow dynamics (Ghai et al. 2022a, 2022c; Lai et al. 2017c; Zhao et al. 2018a), kinetic energy (Ahmed et al. 2019; Ghai et al. 2022d; Lai et al. 2017a), wall heat flux (Konstantinou et al. 2021; Zhao et al. 2018a), reactive scalar gradient (Konstantinou et al. 2021; Sellmann et al. 2017; Zhao et al. 2018b) and displacement speed (Zhao et al. 2018a, 2021) statistics. Moreover, these studies gave rise to the development of high-fidelity models for turbulent kinetic energy (Lai et al. 2017a), turbulent scalar flux (Lai et al. 2017d), scalar variance (Lai and Chakraborty 2016b), FSD (Bruneaux et al. 1997; Lai et al. 2018; Sellmann et al. 2017) and scalar dissipation rate (SDR) (Lai and Chakraborty 2016a, 2016d; Lai et al. 2018) methodologies. The laminar premixed FWI has been extensively analysed using numerical (Popp and Baum 1997; Wichman & Bruneaux 1995) simulations and experimental (Huang et al. 1988; Vosen et al. 1985) means and these studies revealed valuable information regarding the maximum wall heat flux, quenching distance and the modification of chemical pathways due to the heat loss close to the wall. Poinsot et al. (1993) conducted two-dimensional DNS to analyse head-on quenching (HOQ) in premixed turbulent flames under isotropic turbulence. On a similar note, Chakraborty and co-workers (Ahmed et al. 2018; Lai and Chakraborty 2016c, 2016d; Lai et al. 2017b) investigated HOQ configuration using three-dimensional DNS data for flames with both unity and non-unity Lewis numbers. In this HOQ configuration, the flame is wrinkled by the initial isotropic turbulence and propagates towards the wall, where it eventually extinguishes. In this configuration, there is no mean flow and turbulence rapidly decays during the FWI process. Nonetheless, these studies provide valuable insights in terms of flame quenching distance and wall heat flux in FWI. Lai et al. (2018) used both single-step and skeletal multi-step chemical mechanisms using three-dimensional DNS of HOQ of both laminar and turbulent statistically planar CH₄—air premixed flames by an isothermal inert wall and subsequently Lai et al. (2022) used three-dimensional DNS data to compare the wall heat flux and flame quenching distance statistics between HOQ of stoichiometric CH₄—air and H₂—air premixed flames. Lai et al. (2018) and Lai et al. (2022) demonstrated that both the heat release rate and reaction rate of progress variable based on fuel mass fraction vanish at the wall for simple chemistry simulations, but the heat release rate does not vanish at the wall for the detailed chemistry simulations due to low-temperature chemistry involving HO₂ and H₂O₂. Lai et al. (2018) also found that the absence of OH in the near-wall region leads to a high concentration of CO in the vicinity of the cold wall for HOQ of CH₄—air premixed flames. Jiang et al. (2019) simulated a constant pressure unsteady HOQ configuration in 2D involving a mixture of CH₄/air diluted with hot combustion products using detailed chemistry and transport properties. This study focused on investigating the impact of dilution levels, wall temperature, and pressure on the distribution of CO and other species in the near-wall region. Palulli et al. (2019) also considered CO accumulation in the near-wall region and wall heat flux behaviour based on two-dimensional detailed chemistry for unsteady HOQ simulations of CH₄-air mixtures. The near-wall CO production obtained from DNS results (Jiang et al. 2019; Palulli et al. 2019; Lai et al. 2018) was found to be consistent with recent experimental findings (Jainski et al. 2017a, 2017b; Kosaka et al. 2020; Mann et al. 2014). Recently, Gupta et al. (2022) performed a priori analyses of HOQ of statistically planar turbulent premixed flames to explore the effectiveness of LES sub-grid scale modelling methods in determining the near-wall CO distribution. This study demonstrated the potential of using pre-tabulated CO lookup tables parameterised with specific variables as a promising approach for non-adiabatic CO concentration modelling within the framework of LES. Zhao et al. (2018a, 2021) conducted simple chemistry DNS of a statistically steady FWI configuration which is representative of an impinging flow on the wall where the burned gas products are in contact with the wall. The studies by Zhao et al. (2018a, 2021) have been used to analyse wall heat flux, reactive scalar gradient alignment and flame propagation, and the influence of thermo-diffusive effects due to non-unity fuel Lewis number on these aspects were analysed by Konstantinou et al. (2021). This configuration was recently analysed by Zhao et al. (2023) based on detailed chemistry DNS for H₂—air premixed flames and it was found that the wall heat flux model based on simple chemistry DNS (Zhao et al. 2018a) holds reasonably well even in the presence of detailed chemistry. Zhao et al. (2022) also compared the effects of the chemical activity of the wall on FWI with the corresponding FWI for inert isothermal wall for turbulent H₂—air premixed flame impingement on the wall and reported based on detailed chemistry DNS that the wall-normal temperature profile and wall heat flux do not change significantly between the cases with the absence and presence of the wall heat release. However, all the aforementioned studies were done for configurations without any well-characterised turbulent boundary layer.

In most practical engineering devices premixed FWI occurs within the turbulent boundary layer and thus it is worthwhile to analyse the effects of wall-induced shear and vorticity on premixed FWI in well-characterised boundary layers. Bruneaux et al. (1996; 1997) conducted DNS studies of FWI in a turbulent channel flow configuration under constant density assumption. These investigations revealed that the near-wall structures strongly influence the flame when it is in the vicinity of the wall and Bruneaux et al. (1997) used the physical information extracted from DNS data to propose near-wall modifications to the models for the unclosed terms of the FSD transport equation. Gruber et al. (2010), Alshaalan and Rutland (2002) and Ahmed et al. (2021b, 2021c) performed 3D DNS studies of statistically stationary oblique wall flame-quenching (OWQ) of V-shaped turbulent premixed flames within a turbulent channel flow configuration. Alshaalan and Rutland (2002) used their DNS data to analyse turbulent scalar characteristics and their impact on the FSD-based mean reaction rate closure during FWI. The alteration of the flame structure and species distribution within the flame during the progress of OWQ was analysed by Gruber et al. (2010) using DNS data. Ahmed et al. (2021c) analysed the evolution of the reactive scalar gradient magnitude during FWI for a V-flame for both isothermal and adiabatic wall boundary conditions. The statistics of scalar flux and scalar dissipation rate during FWI in different turbulent boundary layer configurations for both isothermal and adiabatic wall boundary conditions were analysed by Ahmed et al. (2021b), which revealed that the wall boundary condition and the orientation of flame normal direction with respect to the wall normal direction have a significant influence on scalar statistics in FWI within turbulent boundary layers. Ahmed et al. (2021d) used the data reported in Ahmed et al. (2021b) for the purpose of the assessment of turbulent premixed models in the case of FWI. The findings of these studies remain qualitatively similar for a much higher friction Reynolds number, which was recently demonstrated by Kai et al. (2022) for OWQ of a V-shaped turbulent premixed flame within a turbulent channel flow configuration. These studies demonstrate that the turbulent structures significantly affect the behaviour of FWI, which in turn influence wall heat fluxes and localised flame quenching within turbulent boundary layers. Jiang et al. (2021) reported the accumulation of CO in the near-wall region in the case of OWQ of V-shaped CH₄/air premixed flames within a turbulent boundary layer which is consistent with the findings for the HOQ configuration (Jiang et al. 2019; Palulli et al. 2019; Lai et al. 2018). Steinhausen et al. (2022) used a fully resolved simulation incorporating detailed chemistry to examine the thermodynamic state of a turbulent methane-air flame as it interacts with a cold wall and demonstrated the role of flame-vortex interaction during OWQ. During the flame vortex interaction, the entrainment of the burnt gases into the fresh gas mixture occurs near the quenching point of the flame. Similar behaviour has been reported recently by Ghai et al. (2023) for the OWQ of V-shaped premixed flame in turbulent channel flows. The effects of heat loss on curvature dependence of heat release rate and mixture fraction variation in OWQ of a V-shaped lean dimethyl-ether premixed flame in a turbulent channel flow have been analysed by Kaddar et al. (2022) and it was found that the correlations of heat release rate and mixture fraction with curvature weaken with decreasing wall normal distance as the heat loss effects strengthen.

Gruber et al. (2012), Kitano et al. (2015), Ahmed et al. (2019, 2020) and Bailey and Richardson (2021) investigated flashback within turbulent boundary layers using DNS data. The global features for flashback of hydrogen-rich premixed combustion within the boundary layer of a turbulent channel flow were analysed based on DNS data by Gruber et al. (2012) who reported that Darrieus–Landau instability can play a significant role during flashback within turbulent boundary layers. In a subsequent analysis Gruber et al. (2018) analysed the transient upstream flame propagation through homogeneous and fuel-stratified hydrogen-air mixtures transported in fully developed turbulent channel flows and reported a change in combustion regime in the regions away from the wall to the vicinity of the wall in the stratified mixture case. Bailey and Richardson (2021) focussed on the effects of swirl on the flashback process for lean hydrogen-air mixture and used the DNS data to develop a model for swirl effects on the flashback speed. Kitano et al. (2015) used DNS data to demonstrate the role of pressure oscillations in the flashback of a fuel-rich hydrogen-air mixture in a turbulent channel flow. Ahmed et al. (2019, 2020) analysed statistical behaviours of turbulent kinetic energy transport (Ahmed et al. 2019) and displacement speed (Ahmed et al. 2020) during the flashback of hydrogen-rich flames within turbulent boundary layers using the DNS dataset by Kitano et al. (2015). Recently experiments (Jainski et al. 2017a, 2017b) were also conducted in turbulent boundary layer flows to analyse the OWQ of turbulent V-shaped flame. They assessed the performance of the FSD and mean reaction rate models in the near-wall regions using experimental data (Jainski et al. 2017a) along with providing important physical insights into the near-wall species distribution as a result of flame quenching ((Jainski et al. 2017a, 2017b; Kosaka et al. 2020; Mann et al. 2014).

Although the aforementioned analyses on FWI provided useful physical insights into the premixed FWI for a range of different flow configurations and thermal wall boundary conditions, the modelling effort of the unclosed terms for Reynolds Averaged Navier-Stokes (RANS) simulations has mostly been limited to HOQ of premixed flames in a canonical configuration (Lai and Chakraborty 2016a, 2016b, 2016d; Lai et al. 2017a, 2017d, 2018; Sellmann et al. 2017) without any fully developed boundary layer and in the absence of mean shear. Thus, these models need to be assessed further in FWI within turbulent boundary layers in the presence of mean wall-induced shear in order to develop a robust modelling strategy in the context of RANS or hybrid RANS/Large Eddy Simulations (LES). The scalar variance is one of the key unclosed quantities, which plays an important role in turbulent premixed combustion modelling (Ahmed and Prosser 2016, 2018; Domingo and Bray 2000; Ghai and De 2019; Klimenko and Bilger 1999; Kolla et al. 2009; Lindstedt and Vaos 1999; Swaminathan and Bray 2005; Varma et al. 2022a) and thus it is necessary to assess the existing closures of scalar variance and its transport for premixed combustion without walls (Chakraborty and Swaminathan 2010) and HOQ in canonical configuration (Lai and Chakraborty 2016b) in premixed FWI within turbulent boundary layers. This provides the main motivation for the analysis presented in this paper.

The closure of the mean chemical reaction rate plays a crucial role in the modelling of turbulent reacting flows. The evaluation of the mean chemical reaction rate is challenging due to its non-linear temperature dependence. In turbulent premixed flames, the modelling of mean chemical reaction rate often requires the knowledge of the variance of reactive scalars such as reaction progress variable, temperature, etc. (Ahmed and Prosser 2016, 2018; Ghai and De 2019; Klimenko and Bilger 1999; Klimenko and Pope 2003; Pope 2012). The reaction progress variable, $c,$ and non-dimensional temperature, $T,$ can be defined in such a manner that it increases monotonically from zero in the unburned gas mixture to unity in the fully burned gas for low Mach number, unity Lewis number and adiabatic conditions:

$$c=\frac{{Y}_{Ru}-{Y}_{R}}{{Y}_{Ru}-{Y}_{Rb}};\quad T=\frac{\widehat{T}-{\widehat{T}}_{u}}{{\widehat{T}}_{b}-{\widehat{T}}_{u}}$$

(1)

where ${Y}_{R}$ is the appropriate reactant mass fraction, $\widehat{T}$ is the dimensional instantaneous temperature with subscripts $u$ and $b$ representing the values in unburned and burned gas mixture, respectively. In the modelling of turbulent premixed combustion, the variance of the reaction progress variable, $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}},$ (where $\widetilde{q}=\overline{\rho q}/\overline{\rho }$ and $q^{\prime\prime} = q - \tilde{q}$ represents the Favre average and Favre fluctuations of a general quantity $q,$ respectively, the overbar denotes the Reynolds averaging and $\rho$ is the gas density) is one of the key parameters in turbulent combustion modelling using flamelet (Domingo and Bray 2000), conditional moment closure (Klimenko and Bilger 1999), multiple mapping conditioning (Ghai and De 2019) and Eddy Break Up (EBU) (Lindstedt and Vaos 1999) approaches. Furthermore, the variance of the progress variable, $\widetilde{{c^{^{\prime\prime}2} }},$ is also required in the tabulated chemistry framework of modelling premixed flames to calculate the marginal probability density function (PDF) $P(c)$, of the reaction progress variable (Bray et al. 2006). Besides these, the variance of reaction progress variable, $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}},$ is used for the algebraic closure of scalar dissipation rate (Ahmed and Prosser 2016, 2018; Kolla et al. 2009; Swaminathan and Bray 2005) and the turbulent scalar flux of the Flame Surface Density (FSD) (Varma et al. 2021).

According to the Bray-Moss-Libby (BML) modelling framework (Bray et al. 1985), in the absence of differential diffusion of mass and heat, the variance of the reaction progress variable can be expressed as:

$$\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}=\widetilde{c}\left(1-\widetilde{c}\right)+O({\gamma }_{c})$$

(2)

where $O({\gamma }_{c})$ is the contribution of the burning mixture. A similar expression (i.e., $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}=\widetilde{T}\left(1-\widetilde{T}\right)+O({\gamma }_{c})$) can be obtained between non-dimensional temperature variance $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{T}\left(1-\widetilde{T}\right)$ for unity Lewis number, globally adiabatic low Mach number conditions. The contribution of $O({\gamma }_{c})$ can be usually neglected when the flame front is thinner than the Kolmogorov length scale and the turbulent eddies do not affect the inner flame structure and this corresponds to the corrugated flamelet regime combustion characterised by high values of Damkӧhler number (${\text{i.e.}}, Da\gg 1)$ (Peters 2000). The variance of the reaction progress variable, $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}},$ for $Da\gg 1$ assumes its maximum possible value which is realised when $P\left(c\right)$ can be approximated as a bimodal PDF with impulses at $c=0.0$ and $c=1.0$. However, for small values of Damkӧhler (${\text{i.e.}}, Da<1)$, the contribution of $O({\gamma }_{c})$ cannot be neglected and subsequently $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ remains smaller than the $\widetilde{c}\left(1-\widetilde{c}\right)$ (Chakraborty and Cant 2009). As a result, the bimodal distribution for $P(c)$ is not sufficient to capture the non-negligible probabilities of burning mode. In this case, the transport equation for the reaction progress variable variance, $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}},$ needs to be solved along with other modelled conservation equations in the context of RANS simulations.

For low Mach number flows, the non-dimensional temperature, $\widetilde{T},$ and reaction progress variable, $\widetilde{c},$ are identical to each other for unity Lewis number when combustion occurs under adiabatic conditions. For the isothermal wall boundary condition, there is a decoupling between $\widetilde{T}$ and $\widetilde{c}$ when the flame approaches the wall even under unity Lewis number conditions, and under that condition both the non-dimensional temperature and the reaction progress are needed to represent the scalar field in turbulent premixed flames (Ahmed et al. 2021b). This suggests that the modelling of both non-dimensional temperature variance $\widetilde{{{T}^{{^{\prime}}{^{\prime}}}}^{2}}$ and reaction progress variable variance $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ are needed. However, to date, limited efforts have been made in this respect to study the statistical analysis of the transport characteristics for reaction progress variable and non-dimensional temperature variances in turbulent boundary layer flows using DNS data for turbulent premixed FWI. This gap is addressed in the present study by analysing the statistical behaviour of these two variances in detail using their transport equation for two different flow configurations under isothermal wall boundary conditions. The first configuration deals with unsteady HOQ of the statistical planer flame propagating into a fully developed turbulent boundary layer with a frictional velocity-based Reynolds number of $R{e}_{\tau }=110$. The other configuration is the statistically stationary OWQ of a V-shaped flame in a turbulent channel flow with $R{e}_{\tau }=110.$ Thus the main objectives of the present study are:

• (1) To investigate the statistical behaviours of the unclosed terms of the reaction progress variable variance, $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}},$ and non-dimensional temperature, $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}},$ variance transport equations during FWI.

• (2) To propose the modifications to the existing models and propose new models, where necessary, for the unclosed terms of these variance transport equations to account for the near-wall behaviour during FWI within turbulent boundary layers.

The remainder of the paper is organised as follows. The mathematical background and numerical implementation are provided in Sects. 2 and 3, respectively. The results are presented and discussed in Sect. 4. Finally, the main findings are summarised, and conclusions are drawn in the final section of this paper.

2 Mathematical Background

The present study considers a single-step Arrhenius based irreversible chemical reaction for the sake of computational economy because 3-D DNS simulations with detailed chemical kinetics are still computationally prohibitive for turbulent boundary layer flows of premixed FWI. Single step simplified chemistry was used to analyse the premixed FWI in several DNS studies (Alshaalan and Rutland 2002; Bruneaux et al. 1997) in the past. Moreover, the turbulent flow structures in FWI simulations based on single step chemistry are found to be qualitatively similar to the detailed chemistry DNS results (Lai et al. 2018, 2022). Earlier proposed closures for the mean reaction rate and the models for the FSD and SDR for FWI using single-step chemistry (Lai et al. 2017b, 2017d; Sellmann et al. 2017) are found to perform well also for hydrocarbon-air flame DNS based on detailed chemistry (Lai et al. 2018, 2022). Recently, Jainski et al. (2017a) reported that the FSD model based on simple chemistry is found to work satisfactorily in the flame-wall interaction when compared to experimental data. Thus, FWI for hydrocarbon-air flames within turbulent boundary layers can be at least qualitatively captured using simple chemistry.

The instantaneous transport equation for the reaction progress variable, $c,$ is given, as follows:

$$\frac{\partial (\rho c)}{\partial t}+\frac{\partial (\rho {u}_{j}c)}{\partial {x}_{j}}=\frac{\partial }{\partial {x}_{j}}\left(\rho D\frac{\partial c}{\partial {x}_{j}}\right)+\dot{\omega }$$

(3)

where ${u}_{j}$ is the $j$th component of velocity, $D$ is the reaction progress variable diffusivity and $\dot{\omega }$ is the reaction rate of the reaction progress variable. Reynolds averaging of Eq. 3 yields the following transport equations for the Favre averaged reaction progress variable:

$$\frac{\partial (\bar{\rho }\widetilde{c})}{\partial t}+\frac{\partial (\bar{\rho }{\widetilde{u}}_{j}\widetilde{c})}{\partial {x}_{j}}=\frac{\partial }{\partial {x}_{j}}\overline{\left(\rho D\frac{\partial c}{\partial {x}_{j}}\right)}+\overline{\dot{\omega } }-\frac{\partial (\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}}})}{\partial {x}_{j}}$$

(4)

Using this relation $\overline{\rho {c}^{{^{\prime}}{^{\prime}}}}=\overline{\rho {c}^{2}}-\overline{\rho }{\widetilde{c}}^{2}$ along with Eqs. 3 and 4, the transport equation for the reaction progress variable variance, $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ can be obtained in the following manner:

$$ \frac{{\partial \left( {\bar{\rho }\widetilde{{c^{{''2}} }}} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar{\rho }\tilde{u}_{j} \widetilde{{c^{{''2}} }}} \right)}}{{\partial x_{j} }} = \underbrace {{\frac{\partial }{{\partial x_{j} }}\left[ {\rho D\frac{{\partial \widetilde{{c^{{''2}} }}}}{{\partial x_{j} }}} \right]}}_{{D_{{1c}} }}\underbrace {{ - \frac{{\partial \left( {\overline{{\rho u_{j}^{{''}} c''^{2} }} ^{~} } \right)}}{{\partial x_{j} }}}}_{{T_{{1c}} }}\underbrace {{ - 2\overline{{\rho u_{j}^{{''}} c''}} \frac{{\partial \tilde{c}}}{{\partial x_{j} }}}}_{{T_{{2c}} }} + \underbrace {{2\left( {\overline{{\mathop {\omega ~}\limits^{ \cdot } c}} - \overline{{\mathop {\omega ~}\limits^{ \cdot } }} \tilde{c}} \right)}}_{{T_{{3c}} }}\underbrace {{ - 2\bar{\rho }\tilde{\varepsilon }_{c} }}_{{D_{{2c}} }} $$

(5)

where, $\widetilde{{\varepsilon }_{c}}=\overline{\rho D\nabla {c}^{{^{\prime}}{^{\prime}}}\cdot \nabla {c}^{{^{\prime}}{^{\prime}}} }/\overline{\rho }$ is the SDR of the reaction progress variable. Following the same procedure, it is possible to derive the transport equation for the normalised temperature variance, $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$, which takes the following form:

$$ \frac{{\partial \left( {\bar{\rho }\widetilde{{T^{{''2}} }}} \right)}}{{\partial t}} + \frac{{\partial \left( {\bar{\rho }\tilde{u}_{j} \widetilde{{T^{{''2}} }}} \right)}}{{\partial x_{j} }} = \underbrace {{\frac{\partial }{{\partial x_{j} }}\left[ {\rho \alpha _{T} \frac{{\partial \widetilde{{T^{{''2}} }}}}{{\partial x_{j} }}} \right]}}_{{D_{{1t}} }}\underbrace {{ - \frac{{\partial \left( {\overline{{\rho u_{j}^{{''}} T''^{2} }} ^{~} } \right)}}{{\partial x_{j} }}}}_{{T_{{1t}} }}\underbrace {{ - 2\overline{{\rho u_{j}^{{''}} T''}} \frac{{\partial \tilde{T}}}{{\partial x_{j} }}}}_{{T_{{2t}} }} + \underbrace {{2\left( {\overline{{\mathop {\omega ~}\limits^{ \cdot } T}} - \overline{{\mathop {\omega ~}\limits^{ \cdot } }} \tilde{T}} \right)}}_{{T_{{3t}} }}\underbrace {{ - 2\bar{\rho }\tilde{\varepsilon }_{T} }}_{{D_{{2t}} }} $$

(6)

where, $\widetilde{{\varepsilon }_{T}}=\overline{\rho {\alpha }_{T}\nabla {T}^{{^{\prime}}{^{\prime}}}\cdot \nabla {T}^{{^{\prime}}{^{\prime}}} }/\overline{\rho }$ is the SDR of the normalised temperature and ${\alpha }_{T}$ is the thermal diffusivity.

The first terms on the RHS of Eqs. 5 and 6, ${ D}_{1c}$ and ${D}_{1t}$ denote the molecular diffusion of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$, respectively and the second terms on the RHS (i.e. ${T}_{1c}$ and ${T}_{1t}$) represent the turbulent transport of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$, respectively. The terms ${T}_{2c}$ and ${T}_{2t}$ will be referred to the production/destruction of variances $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ by the mean scalar gradients $\partial \widetilde{c}/\partial {x}_{j}$ and $\partial \widetilde{T}/\partial {x}_{j}$ respectively, whereas the terms ${T}_{3c}$ and ${T}_{3t}$ denote the reaction rate contributions to the transports of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ respectively. Finally, the terms ${-D}_{2c}$ and ${-D}_{2t}$ represents the molecular dissipation to the transports of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$, respectively. The terms ${T}_{1c}, {T}_{2c}, {T}_{3c}$ and ${-D}_{2c}$ in Eq. 5 and terms ${T}_{1t}, {T}_{2t}, {T}_{3t}$ and ${-D}_{2t}$ in Eq. 6 are unclosed and need modelling. The terms ${T}_{2c}$ and ${T}_{2t}$ involve turbulent scalar fluxes which are closed in the framework of second order moment closure and therefore, these terms can be treated to be closed. The statistical behaviour of all the terms and modelling of the unclosed terms will be discussed later in Sect. 4 of this paper using 3D DNS data of HOQ of a statistical planer flame and OWQ of a V-shaped flame in a turbulent channel flow under isothermal wall boundary conditions.

3 Numerical Implementation

In this paper, the simulations have been conducted using a three-dimensional compressible code called SENGA + (Jenkins and Cant 1999). The conservation equations of mass, momentum, energy and species are solved in non-dimensional form. In SENGA + , all the spatial derivatives for the internal grid points are evaluated using a 10th order finite difference central scheme where the order of accuracy gradually drops to second order for the non-periodic boundaries (Jenkins and Cant 1999). A low storage explicit third order Runge-Kutta scheme has been employed for the time advancement. The stoichiometric methane air mixture is considered as the reactant in this study and the unburned reactants are heated to 730 K (i.e., ${\widehat{T}}_{u}=730\mathrm{K}$), which yields a heat release rate parameter $\tau =({\widehat{T}}_{b}-{\widehat{T}}_{u})/{\widehat{T}}_{u}=2.3$. The standard values of Prandtl number, $Pr,$ and the ratio of specific heat, $\gamma,$ are chosen (i.e., $Pr=0.7$ and $\gamma =1.4$) for this analysis. The Lewis number $Le$ for all the species in both cases are assumed to be unity for the sake of simplicity. A non-reacting turbulent channel flow solution corresponding to $R{e}_{\tau }={\rho }_{0}{u}_{\tau ,NR}h/{\mu }_{0}=110$ (where ${\mu }_{0}$ is the unburned gas viscosity, ${u}_{\tau ,NR}=\sqrt{\left|{\tau }_{w.NR}\right|/\rho }$ is the friction velocity for the non-reacting channel flow, ${\tau }_{w,NR}$ is the mean wall shear stress for the non-reacting channel flow, ${\rho }_{0}$ is the unburned gas density and $h$ is the channel half height) under a mean pressure gradient (i.e., $-\partial p/\partial x=\rho {u}_{\tau ,NR}^{2}/h$ where $p$ is the pressure) has been applied in the streamwise flow direction for specifying the initial conditions for the reacting flow simulation for the HOQ configuration and also for the inlet boundary conditions for the OWQ configuration. The bulk Reynolds number, $R{e}_{b}={2\rho }_{0}{u}_{b}h/{\mu }_{0}=3285$ (where ${u}_{b}=1/2h{\int }_{0}^{2h}udy$ is the bulk mean velocity) is taken for these simulations. For the channel flow configuration, the longitudinal integral length scale ${L}_{11}$ remains of the order of $h$ and the root-mean-square velocity fluctuation scales with ${u}_{\tau ,NR}$ (Ahmed et al. 2021a), which give rise to a Damköhler number $Da={L}_{11}{S}_{L}/{u}^{^{\prime}}{\delta }_{th}$ of 15.80 and a Karlovitz number $Ka={\left({u}^{^{\prime}}/{S}_{L}\right)}^{3/2}{\left({L}_{11}/{\delta }_{th}\right)}^{-1/2}$ of 0.36. These values indicate that turbulent premixed combustion in these cases takes place in the corrugated flamelet regime (Peters 2000). It has previously been demonstrated that the variations of the normalised dissipation rate of kinetic energy and enstrophy in terms of wall units in non-reacting flows for $R{e}_{\tau }=110$ are in good agreement (Ghai et al. 2022c) with the computational results of (Gorski et al. 1994) at $R{e}_{\tau }=145$ and with experimental data of (Balint et al. 1990) at $R{e}_{\tau }=890$.

For the unsteady HOQ statistically planer flame, the computational domain size is taken to be $10.69h\times 1.33h\times 4h$ which is discretised by an equidistant Cartesian grid of $1920\times 240\times 720$ which ensures at least 8 grid points within the thermal flame thickness ${\delta }_{th}=({\widehat{T}}_{b}-{\widehat{T}}_{u})/{\mathrm{max}\left|\nabla \widehat{T}\right|}_{L}$ for ${S}_{L}/{u}_{\tau ,NR}=0.7$ where ${S}_{L}$, being the unstretched laminar burning velocity. The maximum value of the non-dimensional distance from the wall ${y}^{+}= {\rho }_{0}{u}_{\tau ,NR}y/{\mu }_{0}$ for the wall adjacent grid point remains close to 0.6, where $y$ is the distance from the wall. For this case, periodic boundary conditions are imposed in the streamwise (i.e., $x-$ direction) and spanwise (i.e., $z$ directions) directions. No slip boundary condition is specified in the wall-tangential direction and impenetrability (i.e., zero wall normal velocity and zero wall normal mass flux) is imposed in the wall-normal direction (i.e., $y$-direction) on the wall and Dirichlet boundary condition is imposed (i.e., ${T}_{w}={T}_{u}$) for the temperature at the wall. According to Yoo and Im (2007), a partially non-reflecting Navier-Stokes Characteristic Boundary condition (NSCBC) is specified at $y/h=1.33$. In this case, the solution from the 1-D laminar flame simulation is interpolated to a 3-D grid ensuring that $c$ $=0.5$ is obtained at $y/h\approx 0.85$. The solution is initialised in such a manner that the reactant side of the flame is always facing the wall, whereas the product side of the flame is always facing towards the outflow side of the boundary in the $y$ direction. The simulations are run for the 2.0 flow through times based on the maximum axial streamwise velocity which is equivalent to $21.3{u}_{\tau, NR}$. Within this time, the flame propagates and moves towards the wall and ultimately quenches while interacting with the isothermal wall due to the wall heat loss. The turbulent boundary layer does not evolve significantly during the simulation duration (Ahmed et al. 2021d). Reynolds and Favre averaged quantities involving correlations of Reynolds and Favre fluctuations have been calculated by spatial averaging the quantities of interest in the periodic directions (i.e., $x- z$ planes) for a given time instant in this HOQ configuration case. Further details for this configuration are provided in (Ahmed et al. 2021b, 2021d).

In the case of OWQ of a V-flame in a channel flow, the numerical domain size is taken to be ${L}_{x}\times {L}_{y}\times {L}_{z}=22.22h\times 2h\times 4h$, which is discretised by using an equidistant Cartesian grid of $4000\times 360\times 720.$ The grid spacing ensures at least 8 grid points are present within the flame thermal thickness, ${\delta }_{th}$ with a maximum value of ${y}^{+}$ smaller than 0.6 adjacent to the wall. In this case the laminar flame speed to friction velocity ratio, ${S}_{L}/{u}_{\tau ,NR}$=0.7. The flame holder is placed at the centre of the fully developed turbulent channel flow at $x/h=0.83$ from the inlet of the channel. The radius of the flame holder is approximately $0.2{\delta }_{th}$. The flow and scalar conditions (such as velocity, temperature, and species) at the flame holder are imposed using a presumed Gaussian function following Dunstan et al. (2010) and further details about the flame holder setup can be found elsewhere (Ahmed et al. 2021c). Boundary conditions are specified following an improved version of NSCBC by Yoo and Im (2007). The inflow velocity conditions for this simulation have been generated by solving a separate non-reacting turbulent channel flow simulation and instantaneous velocity is recorded at a fixed streamwise location to be used in the reacting flow simulations. The time step chosen for the non-reacting simulation, while the data is being sampled, is the same as that of the reacting flow simulation. In this case, a partially non-reflecting outflow boundary condition is specified at $x/h=22.22$. The isothermal inert walls for OWQ have been maintained at a temperature similar to the reactant temperature (i.e., ${T}_{y=0}={T}_{y=2h}={T}_{0})$ and walls are assumed to be impenetrable, therefore mass flux for all the species at the wall is zero. The boundaries in the $z$-direction are treated as periodic. The simulation has been performed for two flow-through times and data has been extracted after one flow-through time when the initial transience has decayed. The Reynolds and Favre averaged quantities involving correlations of Reynolds and Favre fluctuations are evaluated by time averaging and afterwards spatial averaging has been performed in the periodic $(z)$ direction.

4 Results and Discussion

4.1 Instantaneous and Mean Behaviour

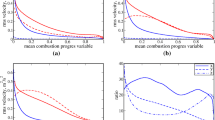
The instantaneous distribution of the non-dimensional temperature, $T$, on the $x-y$ midplane is shown in Fig. 1a and 1b for turbulent boundary layer HOQ and for V-flame OWQ configurations, respectively and the contours of the reaction progress variable, c $=0.1, 0.5$ and $0.9$ (from bottom to top) are superimposed on top of the non-dimensional temperature field. In HOQ, when the flame is away from the wall $($ i.e., $t/{t}_{f}=3.99$ where ${t}_{f}={\delta }_{th}/{S}_{L}$ is the chemical timescale), the turbulence-flame interactions in the fully developed boundary layer wrinkles the flame structure and the observed flame behaviour is akin to the statistically planar flame in the corrugated flamelet regime. As the time progresses in the HOQ case, the flame moves forward towards the wall and interacts with it leading to the reduction in the reaction rate of the progress variable due to the wall heat loss and ultimately leads to the quenching of the flame. The formation of the thermal boundary layer during the FWI can be seen in Fig. 1a at the later stages of FWI and the downstream of the FWI in Fig. 1b. A clear decoupling between the instantaneous non-dimensional temperature and the reaction progress variable can be noticed in the zone where FWI takes place in both configurations from Fig. 1a and 1b. This behaviour arises due to different boundary conditions for the species mass fraction and temperature in the case of an isothermal wall. A Dirichlet boundary condition is specified for temperature, whereas a Neumann boundary condition is implemented for the reaction progress variable. As a result of flame quenching, the mass fraction of the unburned reactants decreases at the wall due to its diffusion away from the wall. Thus, the value of the reaction progress variable increases at the wall with the progress of flame quenching, whereas the temperature at the wall remains unchanged. This observation is consistent with the previously reported DNS (Ahmed et al. 2021b, 2021c, 2021d; Alshaalan and Rutland 2002; Bruneaux et al. 1996; Gruber et al. 2010) results and recently reported experimental observations (Jainski et al. 2017a, 2017b). The mean profiles for the reaction progress variable, $\widetilde{c},$ and the non-dimensional temperature, $\widetilde{T},$ with normalised wall-normal distance $y/h$ for turbulent boundary layer HOQ configuration and V-flame OWQ configuration are shown in Fig. 2a and 2b, respectively. In the HOQ configuration, at $t/{t}_{f}=3.99$, the flame remains away from the wall, therefore there is no interaction of the flame with the wall, and hence the profiles of $\widetilde{c}$ and $\widetilde{T}$ are similar to each other. As the time progresses, the flame starts interacting with the wall and an appreciable difference between the profiles of $\widetilde{c}$ and $\widetilde{T}$ can be seen (see Fig. 2a). At the advanced stages of HOQ, when the flame is on the verge of quenching, significant differences between the profiles of $\widetilde{c}$ and $\widetilde{T}$ are obtained due to decoupling between reaction progress variable and non-dimensional temperature. The similar discrepancy between the profiles of $\widetilde{c}$ and $\widetilde{T}$ are observed in the OWQ of V-flame with an increase in $x/h$, which can be seen from Fig. 2b.

Fig. 1

Instantaneous distribution of the non-dimensional temperature, $T$, along with the $c = 0.1, 0.5$ and $0.9$ isolines (black solid lines) for a HOQ configuration at different time instants and b V-flame OWQ configuration

Fig. 2

Profiles of Favre mean reaction progress variable, $\widetilde{c}$ and non-dimensional temperature, $\widetilde{T}$ with normalised wall-normal distance $y/h$, a at different normalised time instants $t/{t}_{f}$ for the HOQ case. b at different normalised streamwise distances $x/h$ for the V-flame OWQ case

The variations of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$, $\widetilde{c}\left(1-\widetilde{c}\right)$, $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ and $\tilde{T}\left( {1 - \tilde{T}} \right)$ with normalised wall-normal distance $y/h$ at different normalised time instants $t/{t}_{f}$ for the statistical planar flame HOQ case and at different normalised streamwise distances $x/h$ for the V-flame OWQ case are shown in Figs. 3 and 4, respectively. According to Bray et al. (1985) $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ becomes equal to $\widetilde{c}\left(1-\widetilde{c}\right)$ for the flames with $Da>>1$ within the corrugated flamelet regime where the PDF of $c$ can be approximated by a presumed bimodal distribution of $c$ with impulses at $c=0$ and $c=1.0$. The extent of the difference between $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{c}\left(1-\widetilde{c}\right)$ is the measure of the deviation of $P(c)$ from the presumed bimodal distribution of $c$ with impulses at $c=0.0$ and $c=1.0$. It is evident from Fig. 3 that $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ remains smaller than the $\widetilde{c}\left(1-\widetilde{c}\right)$ for both the cases considered here. In the HOQ case, even when the flame is away from the wall, the magnitude of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ is significantly smaller than the $\widetilde{c}\left(1-\widetilde{c}\right)$. As time progresses and the flame starts to quench as a result of FWI, the magnitude of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ significantly decreases at the wall and ultimately vanishes, whereas the magnitude of $\widetilde{c}\left(1-\widetilde{c}\right)$ still assumes non-zero values at the wall. Lai and Chakraborty (2016a) based on the DNS of HOQ in a canonical configuration demonstrated that $P(c)$ does not resemble to the bimodal distribution in the near-wall region. Therefore, it is impossible to model $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ by $\widetilde{c}\left(1-\widetilde{c}\right)$ in the presence of FWI.

Fig. 3

Variation of $\widetilde{{c^{^{\prime\prime}2} }}$ (black dashed lines), $\widetilde{{T^{^{\prime\prime}2} }}$ (black dashed lines), $\tilde{c}\left( {1 - \tilde{c}} \right)$ (black solid lines) and $\tilde{T}\left( {1 - \tilde{T}} \right)$ (black solid lines) with normalised wall-normal distance $y/h$ at different normalised time $t/t_{f}$ for the statistical planar flame HOQ case

Fig. 4

Variation of $\widetilde{{c^{^{\prime\prime}2} }}{ }\left( {\text{black dashed lines}} \right)$, $\widetilde{{T^{^{\prime\prime}2} }}$ (black dashed lines), $\tilde{c}\left( {1 - \tilde{c}} \right)$ (black solid lines) and $\tilde{T}\left( {1 - \tilde{T}} \right)$ (black solid lines) with normalised wall-normal distance $y/h$ at different normalised streamwise distances $x/h$ for the V-flame OWQ case

The variations of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ (and also $\widetilde{c}\left(1-\widetilde{c}\right)$ and $\widetilde{T}\left(1-\widetilde{T}\right)$) are similar to each other away from the wall where heat loss effects are weak, and the reaction progress variable and non-dimensional temperature remain coupled. However, $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{T}\left(1-\widetilde{T}\right)$ are identically zero at the wall in the case of isothermal wall boundary condition for both configurations. However, $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}<$ $\widetilde{T}\left(1-\widetilde{T}\right)$ is obtained at all stages of flame-turbulence interaction in both configurations and thus $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}=$ $\widetilde{T}\left(1-\widetilde{T}\right)$ is rendered invalid for the cases considered in this analysis. Hence, it is necessary to solve the transport equations for the variances to evaluate $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ for these configurations.

4.2 Statistical Behaviour of the Variance $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ Transport

The variation of the terms ${T}_{1c}, {T}_{2c}, {T}_{3c}$ and ${-D}_{2c}$ in the transport equation of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ (Eq. 5) and terms ${T}_{1t}, {T}_{2t}, {T}_{3t}$ and ${-D}_{2t}$ in the transport equation of $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ (Eq. 6) with normalised wall-normal distance $y/h$ at different normalised time instants $t/{t}_{f}$ for the statistically planar flame HOQ case and at different normalised streamwise distances $x/h$ for the V-flame OWQ case are shown in Figs. 5 and 6, respectively. For both cases considered here, the reaction rate term ${T}_{3c}$ remains the leading order source term, whereas the molecular dissipation term ${-D}_{2c}$ acts as a sink term in the transport equation of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$, when the flame is away from the wall. The magnitudes of both of these terms start to drop with the progress of time in the HOQ case and with increasing downstream distance in the OWQ case. Term ${T}_{3c}$ eventually vanishes during FWI due to the flame quenching but the term ${-D}_{2c}$ continues to act as a leading order sink. However, $({-D}_{2c})$ eventually disappears when the flame is completely quenched in the HOQ configuration. Similarly, ${T}_{3t}$ and ${-D}_{2t}$ are the leading order source and sink terms, respectively in the transport equation of $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ and behave approximately similar to ${T}_{3c}$ and ${-D}_{2c}$, respectively. However, term ${T}_{3t}$ decreases rapidly and term ${-D}_{2t}$ assumes higher negative values at the wall with the progress of time for the HOQ case and with increasing streamwise distance in the OWQ case of V-flame as compared to ${T}_{3c}$ and ${-D}_{2c}$, respectively due to the high temperature gradient at the wall as a result of isothermal wall boundary condition. The mean scalar gradient terms ${T}_{2c}$ and ${T}_{2t}$ act as sink terms for both cases considered here when the flame is away from the wall. However, during the advanced stages of flame quenching, these terms act as source terms near the wall but their magnitudes remain small compared to leading order source terms (${T}_{3c}$ and ${T}_{3t}$). The sink contribution of ${T}_{2c}$ and ${T}_{2t}$ is a consequence of counter-gradient transport (i.e. $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{{c{^{\prime}}{^{\prime}}}}}\partial \widetilde{c}/\partial {x}_{j}>0$ and $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{{T{^{\prime}}{^{\prime}}}}}\partial \widetilde{T}/\partial {x}_{j}>0$) which takes place when the flame normal acceleration dominates over the transport processes induced by turbulent velocity fluctuations (Veynante et al. 1997). However, at the advanced stages of flame quenching, the flame normal acceleration effects become weak in the absence of chemical reaction and heat release, and this gives rise to a gradient transport (i.e. $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{{c{^{\prime}}{^{\prime}}}}}\partial \widetilde{c}/\partial {x}_{j}<0$ and $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{{T{^{\prime}}{^{\prime}}}}}\partial \widetilde{T}/\partial {x}_{j}<0$), which in turn leads to positive values of ${T}_{3c}$ and ${T}_{3t}$. The scalar fluxes are either modelled by algebraic relations or by solving transport equations in the context of RANS. Modelling of these scalar fluxes has been discussed elsewhere (Lai and Chakraborty 2016b; Lai et al. 2017d; Varma et al. 2022b; Veynante et al. 1997) and will not be discussed further in this paper. Turbulent transport terms ${T}_{1c}$ and ${T}_{1t}$ assume negative values close to the wall and positive values away from the wall for both the cases considered here when the flame is away from the wall for the HOQ case and during the early stages of FWI in the OWQ case. At the later stages of FWI, the turbulent transport terms assume positive values at the wall and negative values away from the wall. The behaviours of turbulent transport terms are determined by turbulent fluxes of the variances $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}$ and $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$, which will be analysed in detail in the subsequent part of this paper. The molecular diffusion terms ${D}_{1c}$ and ${D}_{1t}$ are small in magnitude when the flame is away from the wall and assumes negative values. During the early stages of FWI, the molecular diffusion terms assume significant positive values at the wall and negative values away from the wall. With the progress in FWI, the magnitudes of ${D}_{1c}$ and ${D}_{1t}$ decrease at the wall and ultimately, they assume negative values when the flame begins to quench. Using the scaling arguments given by Swaminathan and Bray (2005), the scaling estimation of the terms presented in Figs. 5 and 6, when the flame is away from the wall, can be summarised as:

$$ D_{1c} \sim D_{1t} \sim O\left( {\frac{{\rho_{o} S_{L} }}{{\delta_{th} }};\frac{1}{{Re_{\tau } .Da }}} \right); T_{1c} \sim T_{1t} \sim O\left( {\frac{{\rho_{o} S_{L} }}{{\delta_{th} }};\frac{1}{{\sqrt {Re_{\tau } .Da} }}} \right);\;T_{2c} \sim T_{2t} \sim O\left( {\frac{{\rho_{o} S_{L} }}{{\delta_{th} }};\frac{1}{{\sqrt {Re_{\tau } .Da} }}} \right); T_{3c} \sim T_{3t} \sim O\left( {\frac{{\rho_{o} S_{L} }}{{\delta_{th} }};1} \right); D_{2c} \sim D_{2t} \sim O\left( {\frac{{\rho_{o} S_{L} }}{{\delta_{th} }};1} \right) $$

(7)

where the mean gradients are scaled with the integral length scale $l$ and the length scale associated with the gradient of fluctuating quantities is scaled using the thermal flame thickness ${\delta }_{th}$. The density of the gas is scaled using the unburned gas density ${\rho }_{o}$, the turbulent burning velocity fluctuations are scaled using the unstrained laminar burning velocity ${S}_{L}$ and the reaction rate is scaled as $\dot{\omega }\sim {\rho }_{o}{S}_{L}/{\delta }_{th}$. It can be seen from the above scaling arguments in Eq. 7 that terms ${T}_{3c}$, ${T}_{3t}$, ${-D}_{2c}$ and ${-D}_{2t}$ are the leading order terms in the transport equations of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$. This can be substantiated by Figs. 5 and 6 when the flame is away from the wall as discussed before. Modelling of the unclosed terms will be discussed next in this paper.

Fig. 5

Variation of the terms on the RHS of the $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ transport equation (i.e., ${T}_{1c}, {T}_{2c}, {T}_{3c}$ and ${-D}_{2c}$) and the $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ transport equation (i.e., ${T}_{1t}, {T}_{2t}, {T}_{3t}$ and ${-D}_{2t}$) with normalised wall-normal distance $y/h$ at different normalised time $t/{t}_{f}$ for the statistical planar flame HOQ case

Fig. 6

Variation of the terms on the RHS of the $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ transport equation (i.e., ${T}_{1c}, {T}_{2c}, {T}_{3c}$ and ${-D}_{2c}$) and the $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ transport equation (i.e., ${T}_{1t}, {T}_{2t}, {T}_{3t}$ and ${-D}_{2t}$) with normalised wall-normal distance $y/h$ at different normalised streamwise distances $x/h$ for the V-flame OWQ case

4.3 Modelling of the Turbulent Fluxes of Scalar Variances $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}$ and $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$

The closure of turbulent transport terms ${T}_{1c}$ and ${T}_{1t}$ in Eqs. 5 and 6, respectively requires the modelling of the turbulent fluxes of scalar variances, $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}$ and $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$. Following the BML analysis (Bray et al. 1985), the turbulent scalar flux of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ can be represented in the following manner:

$$\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}=\overline{\rho }{\left({\overline {\left({u}_{j}\right)}_{P}}-\overline{{\left({u}_{j}\right)}}_{R}\right)}\cdot \widetilde{c}\left(1-\widetilde{c}\right)\left(1-2\widetilde{c}\right)+O({\gamma }_{c})$$

(8)

where ${\overline{\left({u}_{j}\right)}}_{P}$ and ${\overline{\left({u}_{j}\right)}}_{R}$ are the jth components of the conditional mean velocities of products and reactants, respectively. Moreover, the turbulent scalar flux, $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}}}$ following the BML analysis (Bray et al. 1985) can also be written as:

$$\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}}}=\overline{\rho }{\left({\overline{\left({u}_{j}\right)}}_{P}-{\overline{\left({u}_{j}\right)}}_{R}\right)}\cdot \widetilde{c}\left(1-\widetilde{c}\right)+O({\gamma }_{c})$$

(9)

The last term on the R.H.S of Eqs. 8 and 9 can be neglected for flames with $Da\gg 1$. Then Eq. 8 can be rewritten as:

$$\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}=\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}}}\cdot \left(1-2\widetilde{c}\right)$$

(10)

For low Damkӧhler number combustion (i.e., $Da<1$), Eq. 10 does not adequately predict the variation of $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}$ (Chakraborty and Swaminathan 2010). Therefore, Chakraborty and Swaminathan (2010) proposed an alternative model which also accounts for low Damkӧhler number combustion. Following Chakraborty and Swaminathan (2010), the turbulent scalar flux, $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}$ can be modelled as:

$$\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}=\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}}}\cdot \left(1-2\widetilde{c}\cdot {\left[\frac{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{c}\cdot \left(1-\widetilde{c}\right)}\right]}^{m}\right)\cdot \frac{2\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}+\widetilde{c}\cdot \left(1-\widetilde{c}\right)}$$

(11)

where $m=0.3$, is a model parameter. Equation 11 accounts for the contribution arising from the interior of the flame for low Damkӧhler number combustion, which is represented by the $2\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}/[\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}+\widetilde{c}\cdot \left(1-\widetilde{c}\right)]$. The term ${\left[\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}/\widetilde{c}\cdot \left(1-\widetilde{c}\right)\right]}^{m}$, becomes unity according to Eq. 2 for high Damkӧhler number combustion. However, it accounts for the transition of $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}/\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}}}$ from positive to negative value at an appropriate value of $\widetilde{c}.$ Eq. 11 provides satisfactory agreements for flames over a wide range of operating conditions. However, in the case of HOQ in a canonical configuration, Eq. 11 leads to an underprediction in the near-wall region (Lai and Chakraborty 2016b). Therefore, Lai and Chakraborty (2016b) modified Eq. 11 to account for the near-wall behaviour and the modified version of Eq. 11 can be written as:

$$\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}=\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}}}\cdot \left({A}_{w}^{3}-2\widetilde{c}\cdot {\left[\frac{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{c}\cdot \left(1-\widetilde{c}\right)}\right]}^{m}\right)\cdot \frac{2\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}+\widetilde{c}\cdot \left(1-\widetilde{c}\right)}$$

(12)

where ${A}_{w}=-exp\left[\left(\widetilde{c}-\widetilde{T}\right)\right]+2.0$ is the model parameter to account for the near-wall behaviour, which comes into play near the wall during FWI where the value of $\widetilde{c}\ne \widetilde{T}$, while $\widetilde{c}=\widetilde{T}$ is maintained away from the wall giving rise to ${A}_{w}=1.0$.

Following Eq. 12 the model for the term $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$ can also be constructed in the following manner:

$$\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}=\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}}}\cdot \left({A}_{w}^{3}-2\widetilde{T}\cdot {\left[\frac{\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{T}\cdot \left(1-\widetilde{T}\right)}\right]}^{m}\right)\cdot \frac{2\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}+\widetilde{T}\cdot \left(1-\widetilde{T}\right)}$$

(13)

For HOQ of the statistical planar flame, $\overline{\rho {u}_{2}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}$ and $\overline{\rho {u}_{2}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$, and for V-flame OWQ case, $\overline{\rho {u}_{1}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}, \overline{\rho {u}_{2}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}, \overline{\rho {u}_{1}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$ and $\overline{\rho {u}_{2}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$ are the only non-zero components of turbulent fluxes of scalar variances $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$. Figures 7 and 8 show the variations of the non-zero components of $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}$ and $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$ with normalised wall-normal distance $y/h$ for HOQ and OWQ cases, respectively. The values obtained from the DNS along with the predictions of Eqs. 12 and 13 are shown in Figs. 7 and 8. It can be seen from Figs. 7 and 8 that Eqs. 12 and 13 are in good agreement with the DNS data. However, small quantitative discrepancies are observed for the peak values of the turbulent variance fluxes. It is evident from Figs. 7 and 8 that the transition from positive to negative values for $\overline{\rho {u}_{2}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}$ and $\overline{\rho {u}_{2}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}$ takes place in the wall normal direction towards the product side. However, for V-flame OWQ case, the components of the variance fluxes in the streamwise direction assume negative values close to the wall at the early stages of FWI, but they take positive (negative) values close to (away from) the wall with the progress of flame quenching.

Fig. 7

Variation of $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}/{\rho }_{o}{S}_{L}$ and $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}/{\rho }_{o}{S}_{L}$ extracted from DNS data and along with the predictions of Eqs. 12 and 13, respectively with normalised wall-normal distance $y/h$ at different normalised time $t/{t}_{f}$ for the statistical planar flame HOQ case

Fig. 8

Variation of $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{c}^{{^{\prime}}{^{\prime}}2}}/{\rho }_{o}{S}_{L}$ and $\overline{\rho {u}_{j}^{{^{\prime}}{^{\prime}}}{T}^{{^{\prime}}{^{\prime}}2}}/{\rho }_{o}{S}_{L}$ extracted from DNS data and along with the predictions of Eqs. 12 and 13, respectively with normalised wall-normal distance $y/h$ at different normalised streamwise distances $x/h$ for the V-flame OWQ case

4.4 Modelling of Reaction Rate Terms ${{\varvec{T}}}_{3{\varvec{c}}}$ and ${{\varvec{T}}}_{3{\varvec{t}}}$

The variation of ${T}_{3c}$ and ${T}_{3t}$ with normalised wall-normal distance $y/h$ at different normalised times $t/{t}_{f}$ for the statistical planar flame HOQ case and at different normalised streamwise distances $x/h$ for the V-flame OWQ case are shown in Figs. 9 and 10, respectively. It is evident from the results shown in Figs. 9 and 10 that both ${T}_{3c}$ and ${T}_{3t}$ assume positive values towards the unburned side of the reactants, and show a weakly negative contribution towards the burned gas side, which is consistent with the previous findings (Chakraborty and Swaminathan 2010; Lai and Chakraborty 2016b). However, at the wall, the reaction rate terms do not have any contribution. Following the scaling arguments of Swaminathan and Bray (2005), ${T}_{3c}$ and ${T}_{3t}$ can be scaled as: ${T}_{3c}\sim O({\rho }_{0}{S}_{L}\sqrt{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}/{\delta }_{th})$ and ${T}_{3t}\sim O({\rho }_{0}{S}_{L}\sqrt{\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}}/{\delta }_{th})$. Therefore, ${T}_{3t}$ can be expressed in terms of ${T}_{3c}$ in the following manner (Chakraborty and Swaminathan 2010):

Fig. 9

Variation of ${T}_{3c}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ and ${T}_{3t}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ extracted from DNS data and along with the predictions of ${T}_{3c}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ using Eqs. 18 ($Mode{l}_{1}$) and 23 (parameters of Eqs. 21 ($Mode{l}_{2}$) and 22 ($Mode{l}_{3}$)), and ${T}_{3t}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ using Eqs. 19 ($Mode{l}_{1}$) and 24 (parameters of Eqs. 21 ($Mode{l}_{2}$) and 22 ($Mode{l}_{3}$)) with normalised wall-normal distance $y/h$ at different normalised time $t/{t}_{f}$ for the statistical planar flame HOQ case

Fig. 10

Variation of ${T}_{3c}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ and ${T}_{3t}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ extracted from DNS data and along with the predictions of ${T}_{3c}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ using Eqs. 18 ($Mode{l}_{1}$) and 23 (parameters of Eqs. 21 ($Mode{l}_{2}$) and 22 ($Mode{l}_{3}$)), and ${T}_{3t}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ using Eqs. 19 ($Mode{l}_{1}$) and 24 (parameters of Eqs. 21 ($Mode{l}_{2}$) and 22 ($Mode{l}_{3}$)) with normalised wall-normal distance $y/h$ at different normalised streamwise distances $x/h$ for the V-flame OWQ case

$${T}_{3t}=\sqrt{\frac{\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}}\cdot {T}_{3c}$$

(14)

Following Bray et al. (1985), term ${T}_{3c}$ can be modelled in the following manner (Chakraborty and Swaminathan 2010; Lai and Chakraborty 2016b):

$${T}_{3c}=2\overline{\dot{\omega } }({c}_{m}-\widetilde{c})$$

(15)

where ${c}_{m}$ is the thermochemical parameter given by ${c}_{m}={\int }_{0}^{1}{\left[\dot{\omega }c\right]}_{L}f\left(c\right)dc/{\int }_{0}^{1}{\left[\dot{\omega }\right]}_{L}f\left(c\right)dc$, the subscript $L,$ referring to the unstretched laminar flame quantity and $f\left(c\right)$ is the probability of the burning mode. Bray (1980) suggests that any continuous function can be used for approximating $f(c)$ and it does not have any impact on the value of the ${c}_{m}.$ In the present set of thermochemistry, the value of ${c}_{m}$ is found to be 0.78. Using Eq. 14, the model for ${T}_{3t}$ can also be obtained as follows (Chakraborty and Swaminathan 2010):

$${T}_{3t}=2\overline{\dot{\omega }}\sqrt{\frac{\widetilde{{T }^{{^{\prime}}{^{\prime}}2}}}{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}}\cdot ({c}_{m}-\widetilde{c})$$

(16)

The predictions of Eqs. 15 and 16 depending on the accurate modelling of the mean reaction rate, $\overline{\dot{\omega } }$ and Bray (1980) proposed the closure for the mean reaction rate, $\overline{\dot{\omega } }$ in terms of the scalar dissipation rate ${\widetilde{\varepsilon }}_{c}$ for flames with $Da\gg 1$. Further, Chakraborty and Swaminathan (2010) and Chakraborty and Cant (2011) demonstrated that the earlier proposed closure for the mean reaction rate by Bray (1980) remains valid for the thin reaction zones regime for small values of Damköhler number (i.e. $Ka>1 \mathrm\,{{\text{and}}}\,Da<1$) as long as the flamelet assumption holds. Therefore, the closure for the mean reaction rate $\overline{\dot{\omega } }$ and the modelled reaction rate terms ${T}_{3c}$ and ${T}_{3t}$ can be expressed as follows:

$$\overline{\dot{\omega } }=\frac{2\overline{\rho }{\widetilde{\varepsilon }}_{c}}{2{c}_{m}-1}$$

(17)

$${T}_{3c}=\frac{4\overline{\rho }{\widetilde{\varepsilon }}_{c}({c}_{m}-\widetilde{c})}{2{c}_{m}-1}$$

(18)

$${T}_{3t}=\frac{4\overline{\rho }{\widetilde{\varepsilon }}_{c}({c}_{m}-\widetilde{c})}{2{c}_{m}-1}\cdot \sqrt{\frac{\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}}$$

(19)

The model predictions from Eqs. 18 and 19 are also shown in Figs. 9 and 10, respectively. Figures 9 and 10 show that the model predictions are in good agreement with DNS data when, the flame is away from the wall. However, when the flame interacts with the wall, the agreement of the model predictions with the DNS data deteriorates due to the incorrect prediction of the mean reaction rate at the wall and in the near-wall region, which can be substantiated by Fig. 11 where the predictions obtained from Eq. 17 are compared to the mean reaction rate $\overline{\dot{\omega } }$ obtained from DNS data. It can be seen from Fig. 11 that Eq. 17 predicts the non-zero values at the wall and in the near-wall region, where $\overline{\dot{\omega } }$ vanishes due to the flame quenching. Lai and Chakraborty (2016b) modified the mean reaction rate $\overline{\dot{\omega } }$ closure given by Eq. 17 to account for the near-wall behaviour in the following manner based on a priori DNS assessment of HOQ of statistically planar flames in canonical configurations:

Fig. 11

Variation of  $\overline{\dot{\omega }}\times {\delta }_{th}/{\rho }_{o}{S}_{L}$ extracted from DNS data and along with the predictions of Eqs. 17 ($Mode{l}_{1}$) and 20 using parameters given by Eqs. 21 ($Mode{l}_{2}$) and 22 ($Mode{l}_{3}$) with normalised wall-normal distance $y/h$ at different normalised time $t/{t}_{f}$ for the statistical planar flame HOQ case and different normalised streamwise distances $x/h$ for the V-flame OWQ case

$$\overline{\dot{\omega } }=\frac{2\overline{\rho }{\widetilde{\varepsilon }}_{c}}{2{c}_{m}-1}{A}_{1}{e}^{Le(\widetilde{c}-\widetilde{T})}+{A}_{2}{A}_{3}\frac{{\rho }_{0}{S}_{L}}{L{e}^{B}}\sqrt{\frac{{\widetilde{\varepsilon }}_{c}}{\widetilde{D}}}{e}^{-0.5{\left(\frac{y}{{\delta }_{Z}}-\Pi \right)}^{2}}$$

(20)

The parameters ${A}_{1}, {A}_{2}, {A}_{3},\Pi$ and $B$ in Eq. 20 are given by (Lai and Chakraborty 2016b, 2016c):

$${A}_{1}=0.5\left\{erf\left[3.0\left(\frac{y}{{\delta }_{z}}-\Pi \right)\right]+1\right\}, {A}_{2}=0.5\left[erf\left(\frac{y}{{\delta }_{z}}-\psi\Pi \right)+1\right], {A}_{3}=2.31erf\left[2.6\left(\widetilde{c}-\widetilde{T} \right)\right], B=-6\left(Le-1\right), \mathrm{where}, \psi =ma{x\left[5\left(\widetilde{{c}_{w}}-\widetilde{{T}_{w} } \right),1\right]}^{0.3}\quad \mathrm{ and}\quad \Pi ={\left(P{e}_{min} \right)}_{L} erf(8Le-6)/2$$

(21)

In Eq. 21, $\widetilde{{c}_{w}}$ and $\widetilde{{T}_{w}}$ are the Favre averaged value of reaction progress variable and temperature at the wall, $Le$ is the Lewis number of the reaction progress variable and ${\left(P{e}_{min} \right)}_{L}={y}_{Q}/{\delta }_{z}$ is the minimum Peclet number for the HOQ of laminar premixed flame with ${y}_{Q}$ and ${\delta }_{z}$ being the minimum quenching distance and Zel’dovich flame thickness, ${\delta }_{z}={\alpha }_{T0}/{S}_{L}$, respectively where ${\alpha }_{T0}$ is the thermal diffusivity of the unburned gas. Interested readers are referred to the Lai and Chakraborty (2016b, 2016c) for further information related to the above model.

The predictions of Eq. 20 are also shown in Fig. 11. The predictions of Eq. 20 converge to the prediction of Eq. 17 when the flame is away from the wall, which is consistent with the previous findings (Lai and Chakraborty 2016b, 2016c). The predictions of Eq. 20 in the early stages of FWI remains satisfactory but this model provides overpredictions during the advanced stages of FWI for both HOQ and OWQ cases considered here. Similarly, the same trend is observed for the ${T}_{3c}$ and ${T}_{3t}$ predictions when Eq. 20 is used for $\overline{\dot{\omega } }$ closure in Eqs. 15 and 16. This is perhaps not surprising because the model parameters in Eq. 21 were not originally calibrated for turbulent boundary layer flows. Therefore, small modifications have been suggested here to the parameters used in Eq. 21. The parameter ${A}_{1}$ and ${A}_{3}$ has been modified and their modified expressions are given below:

$${A}_{1}=0.5\left\{erf\left[\left(\frac{y}{{\delta }_{z}}-\Pi \right)\right]+1\right\}, {A}_{3}=1.5erf\left[\left(\widetilde{c}-\widetilde{T}\right)\right]$$

(22)

The predictions of Eq. 20 with modified expressions given by Eq. 22 are also shown in Fig. 11, which reveal satisfactory agreement with $\overline{\dot{\omega } }$ obtained from DNS data at all stages of FWI for both HOQ and OWQ cases considered here. Substituting, $\overline{\dot{\omega } }$ model using Eq. 20 with model parameters given by Eq. 22 in Eqs. 15 and 16 yields the following model for the ${T}_{3c}$ and ${T}_{3t}$:

$${T}_{3c}=2\left[\frac{2\overline{\rho }{\widetilde{\varepsilon }}_{c}}{2{c}_{m}-1}{A}_{1}{e}^{Le(\widetilde{c}-\widetilde{T})}+{A}_{2}{A}_{3}\frac{{\rho }_{0}{S}_{L}}{L{e}^{B}}\sqrt{\frac{\widetilde{{\varepsilon }_{c}}}{\widetilde{D}}}{e}^{-0.5{\left(y/{\delta }_{z}-\Pi \right)}^{2}}\right]({c}_{m}-\widetilde{c})$$

(23)

$${T}_{3t}=2\left[\frac{2\overline{\rho }{\widetilde{\varepsilon }}_{c}}{2{c}_{m}-1}{A}_{1}{e}^{Le(\widetilde{c}-\widetilde{T})}+{A}_{2}{A}_{3}\frac{{\rho }_{0}{S}_{L}}{L{e}^{B}}\sqrt{\frac{\widetilde{{\varepsilon }_{c}}}{\widetilde{D}}}{e}^{-0.5{\left(y/{\delta }_{z}-\Pi \right)}^{2}}\right]({c}_{m}-\widetilde{c})\cdot \sqrt{\frac{\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}}{\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}}}$$

(24)

The predictions of Eqs. 23 and 24 with modified parameters given by Eq. 22, are also shown in Figs. 9 and 10 which indicate that the overall model predictions remain satisfactory in the near-wall region as well as away from the wall for both HOQ and OWQ cases considered in this work. Furthermore, the predictions of $\overline{\dot{\omega } }$, ${T}_{3c}$ and ${T}_{3t}$ depend upon the accurate evaluation of the SDR $\widetilde{{\varepsilon }_{c}}$ and $\widetilde{{\varepsilon }_{t}}$. Therefore, the modelling of SDR $\widetilde{{\varepsilon }_{c}}$ and $\widetilde{{\varepsilon }_{t}}$ will be discussed in the next subsection of this paper.

4.5 Modelling of Scalar Dissipation Rates $\widetilde{{{\varvec{\varepsilon}}}_{{\varvec{c}}}}$ and $\widetilde{{{\varvec{\varepsilon}}}_{{\varvec{t}}}}$

The modelling of the scalar dissipation rate terms $\widetilde{{\varepsilon }_{c}}$ and $\widetilde{{\varepsilon }_{t}}$ are required in order to obtain the closure for the terms ${D}_{2c}$ and ${D}_{2t}$ in Eqs. 5 and 6, respectively. The linear relaxation model (i.e. $\widetilde{{\varepsilon }_{c}}\approx {C}_{\varepsilon }\left(\widetilde{\varepsilon }/\widetilde{k}\right)\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ where $\widetilde{k}=\overline{\rho {u }_{j}^{{^{\prime}}{^{\prime}}}{u}_{j}^{{^{\prime}}{^{\prime}}}}/2\overline{\rho }$ is the turbulent kinetic energy and $\widetilde{\varepsilon }=\overline{{\mu \left(\partial {u}_{i}^{{^{\prime}}{^{\prime}}}/\partial {x}_{j}\right)\left(\partial {u}_{i}^{{^{\prime}}{^{\prime}}}/\partial {x}_{j}\right)}}/\bar{\rho }$ is the dissipation rate of turbulent kinetic energy $\widetilde{k}$), which is usually used for passive scalar mixing, does not give satisfactory outcomes for the SDR modelling of reactive scalars (Kolla et al. 2009). Therefore, Kolla et al. (2009) suggested an alternate algebraic closure for the $\widetilde{{\varepsilon }_{c}}$ for flames in the corrugated flamelet regime (i.e., $Da\gg 1$) using the equilibrium between the leading order contributors in the transport equation of $\widetilde{{\varepsilon }_{c}}:$

$$\widetilde{{\varepsilon }_{c}}=\left(\frac{2{K}_{c}^{*}{S}_{L}}{{\delta }_{th}}+{C}_{1}\frac{\widetilde{\varepsilon }}{\widetilde{k}}-\tau {\cdot C}_{2}\frac{{S}_{L}}{{\delta }_{th}}\right)\frac{\widetilde{c}(1-\widetilde{c})}{{\beta }_{\varepsilon }}$$

(25)

where ${\beta }_{\varepsilon }=6.7$, ${C}_{1}=1.5\sqrt{K{a}_{L}}/(1+\sqrt{K{a}_{L}})$ and ${C}_{2}=1.1/{\left(1+K{a}_{L}\right)}^{0.4}$ are the model parameters and $K{a}_{L}={\left({\delta }_{th}\widetilde{\varepsilon }/{S}_{L}^{3}\right)}^{1/2}$ is the local Karlovitz number. The thermochemical parameter ${K}_{c}^{*}$ is related to the flame front structure, ${K}_{c}^{*}=\left({\delta }_{th}/{S}_{L}\right){\int }_{0}^{1}{\left[\left(\rho D\nabla \mathrm{c}\cdot \nabla c\right)\nabla .\overrightarrow{u}f\left(c\right)\right]}_{L}dc/{\int }_{0}^{1}{\left[\left(\rho D\nabla \mathrm{c}\cdot \nabla c\right)f\left(c\right)\right]}_{L}dc$, which is 0.78 $\tau$ for the present thermochemistry.

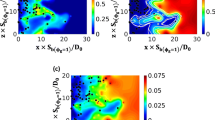
The variations of $\widetilde{{\varepsilon }_{c}}$ extracted from the DNS data and along with the predictions of Eq. 25 with normalised wall-normal distance $y/h$ at different normalised time instants $t/{t}_{f}$ for the statistical planar flame HOQ case and at different normalised streamwise distances $x/h$ for the V-flame OWQ case are shown in Figs. 12 and 13, respectively. It can be seen from Figs. 12 and 13 that the model predictions are in satisfactory agreement in the region away from the wall for both HOQ and OWQ cases considered here. In the near-wall region and at the wall, Eq. 25 significantly overpredicts the $\widetilde{{\varepsilon }_{c}}$, which can be seen from Figs. 12 and 13. Therefore, Eq. 25 yields an incorrect value for the dissipation rate term ${D}_{2c}$ and SDR $\widetilde{{\varepsilon }_{c}}$ in the near-wall region. Lai and Chakraborty (2016b) also corroborated a similar phenomenon using Eq. 25 in the near-wall region in the case of HOQ of statistically planar flames in canonical configurations. Therefore, Lai and Chakraborty (2016b) suggested a modification to Eq. 25 to account for the near-wall behaviour in the near-wall region ($y/{\delta }_{z}\le {\left(P{e}_{min}\right)}_{L}$):

$$\widetilde{{\varepsilon }_{c}}={A}_{\varepsilon}{e}^{-1.2Le{\left(\widetilde{{c}_{w}}-\widetilde{{T}_{w}}\right)}^{3}}\left(\frac{2{K}_{c}^{*}{S}_{L}}{{\delta }_{th}}+{C}_{3}\frac{\widetilde{\varepsilon }}{\widetilde{k}}-\tau {\cdot C}_{4}\frac{{S}_{L}}{{\delta }_{th}}\right)\frac{\widetilde{c}(1-\widetilde{c})}{{\beta }_{\varepsilon }}$$

(26)

where ${A}_{\varepsilon }=0.5[\mathrm{erf}(y/{\delta }_{z}-\Pi )]$ and $\mathrm{exp}(-1.2Le{\left(\widetilde{{c}_{w}}-\widetilde{{T}_{w}}\right)}^{3})$ are the model parameters, which remain active close to the wall during FWI and asymptotically approach unity away from the wall. The quantity $(\widetilde{{c}_{w}}-\widetilde{{T}_{w}})$ remains zero when the flame is away from the wall (i.e., $y/{\delta }_{z}\gg\Pi$) and under that condition Eq. 26 converges to Eq. 25. The predictions of Eq. 26 are also shown in Figs. 12 and 13 and significant improvements in the agreement with DNS data can be observed in the near-wall region as compared to the model predictions of Eq. 25.

Fig. 12

Variation of $\widetilde{{\varepsilon }_{c}}\times {\delta }_{th}/{S}_{L}$ and ${\widetilde{\varepsilon }}_{t}\times {\delta }_{th}/{S}_{L}$ extracted from DNS data and along with the model predictions of ${\widetilde{\varepsilon }}_{c}\times {\delta }_{th}/{S}_{L}$ using Eqs. 25 ($Mode{l}_{1}$) and 26 ($Mode{l}_{2}$), and ${\widetilde{\varepsilon }}_{t}\times {\delta }_{th}/{S}_{L}$ using Eqs. 27 ($Mode{l}_{1}$) and 28 ($Mode{l}_{2}$) with normalised wall-normal distance $y/h$ at different normalised time $t/{t}_{f}$ for the statistical planar flame HOQ case

Fig. 13

Variation of $\widetilde{{\varepsilon }_{c}}\times {\delta }_{th}/{S}_{L}$ and $\widetilde{{\varepsilon }_{t}}\times {\delta }_{th}/{S}_{L}$ extracted from DNS data and along with the model predictions of $\widetilde{{\varepsilon }_{c}}\times {\delta }_{th}/{S}_{L}$ using Eqs. 25 ($Mode{l}_{1}$) and 26 ($Mode{l}_{2}$), and $\widetilde{{\varepsilon }_{t}}\times {\delta }_{th}/{S}_{L}$ using Eqs. 27 ($Mode{l}_{1}$) and 28 ($Mode{l}_{2}$) with normalised wall-normal distance $y/h$ at different normalised streamwise distances $x/h$ for the V-flame OWQ case

A model, similar to Eq. 25, can also be constructed for $\widetilde{{\varepsilon }_{t}}$ in the following manner for low Mach number, globally adiabatic, unity Lewis number flames:

$$\widetilde{{\varepsilon }_{t}}=\left(\frac{2{K}_{c}^{*}{S}_{L}}{{\delta }_{th}}+{C}_{1}\frac{\widetilde{\varepsilon }}{\widetilde{k}}-\tau {\cdot C}_{2}\frac{{S}_{L}}{{\delta }_{th}}\right)\frac{\widetilde{T}(1-\widetilde{T})}{{\beta }_{\varepsilon }}$$

(27)

The model predictions of Eq. 27 along with the DNS data are also shown in Figs. 12 and 13 for $\widetilde{{\varepsilon }_{t}}$ for the statistical planar flame HOQ and the V-flame OWQ cases, respectively. Similar to the prediction of $\widetilde{{\varepsilon }_{c}}$ using Eq. 25, the predictions of $\widetilde{{\varepsilon }_{t}}$ using Eq. 27 significantly overpredicts the $\widetilde{{\varepsilon }_{t}}$ in the near-wall region. Therefore, the following near-wall modification to the $\widetilde{{\varepsilon }_{t}}$ model is suggested here to account for the near-wall behaviour in the following manner:

$$\widetilde{{\varepsilon }_{t}}={(1-{\mathrm{erf}\left(\widetilde{{c}_{w}}-\widetilde{{T}_{w}}\right)}^{0.3})}A_{\varepsilon }{e}^{-1.2Le{\left(\widetilde{{c}_{w}}-\widetilde{{T}_{w}}\right)}^{3}}\left(\frac{2{K}_{c}^{*}{S}_{L}}{{\delta }_{th}}+{C}_{3}\frac{\widetilde{\varepsilon }}{\widetilde{k}}-\tau {\cdot C}_{4}\frac{{S}_{L}}{{\delta }_{th}}\right)\frac{\widetilde{T}(1-\widetilde{T})}{{\beta }_{\varepsilon }}+{\mathrm{erf}\left(\widetilde{{c}_{w}}-\widetilde{{T}_{w}}\right)}^{0.3}\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}\frac{\widetilde{\varepsilon }}{\widetilde{k}}$$

(28)

In Eq. 28, along with the near-wall corrections, the linear relaxation contribution (i.e., the third term on the right-hand side) has been added to account for SDR prediction in the thermal boundary layer after flame quenching (e.g. when $(\widetilde{{c}_{w}}-\widetilde{{T}_{w}})$ approaches unity). It is worth noting that $\widetilde{{\varepsilon }_{t}}$ assumes higher values than $\widetilde{{\varepsilon }_{c}}$ in the near-wall region during FWI in isothermal wall boundary condition (Ghai et al. 2022b) (see Figs. 12 and 13) because of high temperature gradient close to the wall, whereas the wall normal species gradient goes to zero. The last term on the right-hand side of Eq. 28 (i.e., linear relaxation contribution) accounts for $\widetilde{{\varepsilon }_{t}}>\widetilde{{\varepsilon }_{c}}$ in the near-wall region during FWI when $(\widetilde{{c}_{w}}-\widetilde{{T}_{w}})\ne 0$. The predictions of Eq. 28 are also shown in Figs. 12 and 13, which reveal that this model significantly improves the predictions of $\widetilde{{\varepsilon }_{t}}$ in the near-wall region but slight underpredictions can be discerned away from the wall.

5 Conclusions

The statistical behaviour of the unclosed terms and their modelling in the reaction progress variable variance, $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and non-dimensional temperature variance, $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}$ transport equations have been analysed for the turbulent premixed flame-wall interaction using two different DNS databases representing an unsteady HOQ of a statistically planar flame across a turbulent boundary layer and a statistically stationary OWQ of a V-flame. It has been found that the reaction rate contribution (${T}_{3c}$ and ${T}_{3t})$ and the molecular dissipation term (${-D}_{2c}$ and ${-D}_{2t}$) are the leading order source and sink terms, respectively in the transport equations of $\widetilde{{c}^{{^{\prime}}{^{\prime}}2}}$ and $\widetilde{{T}^{{^{\prime}}{^{\prime}}2}}.$ However, in the near-wall region, the reaction rate gradually vanishes with the progress in the FWI due to the quenching of the flame, whereas the molecular dissipation terms continue to act as major sink terms. The performances of previously proposed models for turbulent variance flux, reaction rate contribution to the variance transport and scalar dissipation rate have been assessed with respect to the corresponding quantities extracted from the DNS data for both configurations considered here. The existing models for turbulent reaction progress variable and non-dimensional temperature variance fluxes and scalar dissipation rates of reaction progress variable and temperature with near-wall corrections adequately predict the behaviour of the corresponding quantities, whereas some modifications have been suggested to the reaction rate contribution to the scalar variance transport equation. The SDR-based mean reaction rate closure has been modified based on a priori DNS analysis, which significantly improves the agreement of the model predictions with the DNS data in the near-wall region. An existing algebraic closure for $\widetilde{{\varepsilon }_{c}}$ has been modified to suggest a model for $\widetilde{{\varepsilon }_{t}}$ both within the flame brush and also to account for the thermal boundary layer transport. Further validations of these models are required for high values of friction Reynold number, and the proposed models need to be implemented in the actual RANS setting to further assessment of their predictive capabilities.