Turbulence and Interface Waves in Stratified Oil–Water Channel Flow at Large Viscosity Ratio

Abstract

We investigate the dynamics of turbulence and interfacial waves in an oil–water channel flow. We consider a stratified configuration, in which a thin layer of oil flows on top of a thick layer of water. The oil–water interface that separates the two layers mutually interacts with the surrounding flow field, and is characterized by the formation and propagation of interfacial waves. We perform direct numerical simulation of the Navier-Stokes equations coupled with a phase field method to describe the interface dynamics. For a given shear Reynolds number, $Re_\tau =300$, and Weber number, $We=0.5$, we consider three different types of oils, characterized by different viscosities, and thus different oil-to-water viscosity ratios $\mu _r=\mu _o/\mu _w$ (being $\mu _o$ and $\mu _w$ oil and water viscosities). Starting from a matched viscosity case, $\mu _r=1$, we increase the oil-to-water viscosity ratio up to $\mu _r=100$. By increasing $\mu _r$, we observe significant changes both in turbulence and in the dynamics of the oil–water interface. In particular, the large viscosity of oil controls the flow regime in the thin oil layer, as well as the turbulence activity in the thick water layer, with direct consequences on the overall channel flow rate, which decreases when the oil viscosity is increased. Correspondingly, we observe remarkable changes in the dynamics of waves that propagate at the oil–water interface. In particular, increasing the viscosity ratio from $\mu _r=1$ to $\mu _r=100$, waves change from a two-dimensional, nearly-isotropic pattern, to an almost monochromatic one.

1 Introduction

Oil–water flows are observed in a number of energy applications and environmental phenomena, from the transport of oil and water over long distances in pipelines (Preziosi et al. 1989; Joseph et al. 2003; Huang and Joseph 1995) to the prevention and mitigation of pollution in oil spill accidents (Kujawinski et al.2011; Beyer et al. 2016). An important feature of oil–water flows is the small density difference between the two fluids. If, on one side, this density difference does not significantly alter the exchange of momentum and energy in oil–water interactions, on the other side, it promotes the occurrence of stratified configurations in which the oil—which is slightly lighter—flows on top of water. This aspect has a huge impact on the resulting flow and on its control and manipulation (to design efficient oil/water separators, or to devise strategies to mitigate pollution from oil-spill risks). Indeed, the presence of a thin layer of oil, characterized by a density similar to water, but by a much larger viscosity, can largely modify the pressure drop required to drive the flow inside pipelines in industrial applications (Bannwart 2001), or can lead to strong modifications of the waves and turbulence dynamics at the water surface in environmental/marine applications (Alpers and Hühnerfuss 1989; Al Wahaibi and Angeli 2011; Barral and Angeli 2013; Cheng et al. 2017).

For all these reasons, the oil–water stratified flow has gathered the attention of many researchers. Several investigations have been performed employing different analytical, experimental, and numerical techniques (Bannwart 2001; Deike et al. 2014; Li et al. 2021; Kim and Choi 2018; Barmak et al. 2016; Bochio and Rodriguez 2022), as well as targeting different flow configurations, from pipe/channel flows to more environmental-oriented setups. Experimental techniques often represent an important tool to investigate the physics of turbulent flows, but also to validate analytical or simplified mathematical models. However, accurate experimental measurements, which usually rely on optical techniques, are difficult to realize in oil/water flows because of the fluid turbidity. It is therefore not surprising that, to obtain precise space- and time-resolved data on the entire flow field and also on the dynamics of the oil/water interface, direct numerical simulations are being used in this field more and more frequently in the recent years (Fulgosi et al. 2003; Zonta et al. 2015; Kim and Choi 2018; Giamagas et al. 2023). Also in this case, accurate and reliable numerical methodologies capable of describing the interface position and deformation in time are required (Scardovelli and Zaleski 1999; Elghobashi 2019; Soligo et al. 2021). An additional difficulty arises when large oil-to-water viscosity ratios are considered, since the resulting flow structure might be characterized by laminar-turbulent patches and by a high degree of intermittency, depending on the local flow characteristics and on the interface-flow interactions.

In this work, we use Direct Numerical Simulation (DNS) of the Navier-Stokes (NS) equations coupled with a Phase-Field Method (PFM) to investigate the channel flow of a thin layer of oil flowing on top of a thick layer of water. In contrast with our previous works (Ahmadi et al. 2018a, 2018b; Roccon et al. 2019, 2021), where the focus was mainly on elucidating the Drag-Reduction (DR) mechanisms observed in lubricating channels (i.e. when a thin layer of small viscosity fluid is used to lubricate the flow of a large viscosity fluid), here we move to the opposite situation in which a thin layer of a much more viscous fluid (50 or 100 times more viscous) flows on top of a thick layer of water. This configuration aims at mimicking oil–water flows in pipelines, as well as free-surface flows in which a thin oil film, being very viscous, behaves as a boundary for the liquid flow beneath it. The main goal of the paper is to characterize the flow field as well as the structure and properties of the waves that propagate at the oil–water interface.

The paper is organized as follows: in Sect. 2 we present the numerical methodology and the setup employed to perform the simulations, while in Sect. 3 we present and discuss the results of the simulations in terms of turbulence behavior and wave dynamics. Finally, in Sect. 4 we draw the conclusions.

2 Methodology

We consider a flow configuration consisting of two immiscible fluid layers driven by an imposed mean pressure gradient along the horizontal direction. Channel dimensions are $L_x \times L_y \times L_z=4 \pi h \times 2 \pi h \times 2 h$, with h the half-channel height and x, y, z the streamwise, spanwise and wall-normal directions, respectively. A thin oil layer, $0.15 h$ thick, flows over a thick water layer, $1.85 h$ thick. To mimic a realistic oil–water configuration, we consider that the two layers have the same density $\rho _o=\rho _w=\rho$, but different viscosity, $\mu _o$ and $\mu _w$. The deformable interface separating the two fluid layers is characterized by a constant and uniform value of the surface tension, $\sigma$. The dynamics of the system is described by coupling the Navier–Stokes equations (used to describe the flow field), with a Cahn-Hilliard equation (used to describe the interface dynamics). The resulting set of governing equations in non-dimensional form reads as follows (Jacqmin 1999; Badalassi et al. 2003):

$$\begin{aligned} \nabla \cdot \textbf{u}\,\,=\,\, &{} 0 \,, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \textbf{u}}{\partial t} + \textbf{u} \cdot \nabla \textbf{u}= & {} -\nabla p + \frac{1}{Re_{\tau }} \nabla \cdot \left[ \mu (\phi )\big {(} \nabla \textbf{u} + \nabla \textbf{u}^{T} \big {)} \right] + \frac{3 Ch}{\sqrt{8} We} {\nabla \cdot \textbf{T}_c} \,, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial {\phi }}{\partial t}+\textbf{u}\cdot \nabla \phi= & {} \frac{1}{Pe}\nabla ^2 (\phi ^3-\phi - Ch^2 \nabla ^2 \phi )\,, \end{aligned}$$

(3)

where $\textbf{u}=(u,v,w)$ is the velocity vector, p is pressure, $\phi$ is the phase-field, $\mu (\phi )$ is the viscosity map and $\textbf{T}_c$ is the Korteweg stress tensor. In the Navier–Stokes Eq. (2), the term $\mu (\phi )$ defines the non-dimensional viscosity distribution inside the domain, here assumed to be a linear function of the phase-field (Ding et al. 2007; Kim 2012; Roccon et al. 2019) while the last term represents the contribution of surface tension forces, where the Korteweg stress tensor (Korteweg 1901) is defined as:

$$\begin{aligned} \textbf{T}_c=\mid \nabla \phi \mid ^2 \textbf{I} - \nabla \phi \otimes \nabla \phi \,. \end{aligned}$$

(4)

The Cahn-Hilliard Eq. (3) describes the transport of the phase field $\phi$ used to identify the two phases: $\phi$ is constant in the bulk of the two phases ($\phi =\pm 1$ inside the oil and water layer, respectively) and changes smoothly across the interface. The diffusive flux at the right-hand side of the CH Eq. (3) governs the behavior of the thin transition layer.

The following dimensionless numbers appear in Eqs. (1–3): the shear Reynolds number, the Weber number, the Péclet number, and the Cahn number. The shear Reynolds number, $Re_\tau =\rho u_\tau h /\mu _w$, represents the ratio between inertial and viscous forces; it is computed using the friction velocity $u_{\tau }=\sqrt{\tau _w/\rho }$, with $\tau _w$ the shear stress at the wall and the water viscosity $\mu _w$ as reference. The Weber number, $We=\rho u_\tau ^2 h / \sigma$, is the ratio between inertial and surface tension forces and controls the interface deformability (which is larger for larger We). The Péclet number, $Pe=u_\tau h / {\mathcal {M}} \beta$, is a parameter that controls the interface relaxation time and is defined in terms of ${\mathcal {M}}$, the Onsager coefficient or mobility, and of $\beta$, a numerical factor used during the dimensionless procedure of the Cahn-Hilliard equation. Finally, the Cahn number, $Ch=\xi /h$, represents the characteristic length scale of the transition layer.

The governing equations are solved using a pseudo-spectral method, which employs Fourier series along the periodic directions (streamwise and spanwise) and Chebyshev polynomials along the wall-normal direction. The Navier–Stokes and continuity equations are solved using the velocity-vorticity formulation: Eq. (2) is rewritten as a 4th order equation for the wall-normal component of the velocity $u_z$ and a 2nd order equation for the wall-normal component of the vorticity $\omega _z$ (Kim et al. 1987; Speziale 1987). The 4th order equation for the wall-normal velocity is then split into two equivalent 2nd order equations. Similarly, the Cahn-Hilliard equation is also split into two 2nd order equations (Badalassi et al. 2003). In this way, all the governing equations are recasted as a coupled system of Helmholtz equations, which can be readily solved. The governing equations are advanced in time using an IMplicit-EXplicit (IMEX) scheme. In particular, the linear terms of the governing equations are integrated using an implicit scheme, while the non-linear terms with an explicit scheme. The computation of all the non-linear terms is performed in two steps: First, the variables, which are defined in the wavenumber space, are back-transformed to the physical space, where the products that represent the nonlinear terms are computed. These products are re-transformed to the wavenumber space, where the derivatives can be evaluated. Standard dealiasing procedure (e.g., using the 2/3 rule, see Canuto et al. (2007) is then applied to avoid the generation of unphysical frequencies. Note that, for the Navier–Stokes equations, the non-linear viscous term is first rewritten as the sum of a linear and a non-linear contribution (Zonta et al. 2012). Then, the linear part is integrated using a Crank-Nicolson implicit scheme, while the non-linear part is integrated explicitly using an Adams-Bashforth explicit scheme. Likewise, for the Cahn-Hilliard equation, the linear term is integrated using an implicit Euler scheme, while the non-linear term is integrated in time using an Adams-Bashforth scheme. The adoption of the implicit Euler scheme helps damping unphysical high-frequency oscillations that could arise from the steep gradients of the phase field (Badalassi et al. 2003; Yue et al. 2004). Further details on the numerical method can be found in Soligo et al. (2019, 2021).

2.1 Simulation Setup

We considered the benchmark case of a single-phase turbulent channel flow, and three different cases of oil–water two-phase flow, each characterized by a different value of the oil-to-water viscosity ratio $\mu _r=\mu _o/\mu _w$. In particular, we consider the following viscosity ratios: $\mu _r=1$, $\mu _r=50$ and $\mu _r=100$. All simulations are run at the given reference value of the shear Reynolds number $Re_\tau =300$ and Weber number $We=0.5$. For all cases, the domain is discretized using $N_x \times N_y \times N_z=512 \times 256 \times 513$ grid points. The Cahn number is set to $Ch=0.02$, while the Péclet number is obtained according to the scaling $Pe=3/Ch$ (Magaletti et al. 2013; Jacqmin 1999). An overview of the simulation parameters, together with the resulting grid spacing is reported in Table 1. The initial condition for all simulations is taken from a preliminary direct numerical simulation of a single-phase turbulent channel flow at $Re_\tau =300$, complemented by a proper definition of the initial distribution of the order parameter $\phi$ so that the liquid-liquid interface is at the beginning flat and located at distance $0.15 h$ from one wall.

Fig. 1

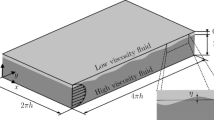
Sketch of the computational domain employed for the simulations. The channel has dimensions $L_x \times L_y \times L_z = 4 \pi h \times 2 \pi h \times 2 h$. The nominal thickness of the oil layer (located at the top) is $0.15 h$ while the nominal thickness of the water layer (located at the bottom) is $1.85 h$. The close-up view shows the definition of the interface elevation $\eta$, i.e. the vertical distance from the nominal position of the interface

Table 1 Overview of the main simulation parameters for the reference single-phase (SP) flow and for the oil–water flows characterized by different values of the viscosity ratio. The resulting grid spacing in wall units is also reported

3 Results

In the following, we discuss the results obtained from the numerical simulations. We focus first on the flow field, investigating the turbulence behavior from both a qualitative and quantitative viewpoint, and then we move to the characterization of the oil–water interface.

3.1 Flow Field Characterization

3.1.1 Qualitative Description of the Flow Field

Figure 2 shows the instantaneous distribution of turbulent kinetic energy, $TKE = \left( u'^2 + v'^2 + w'^2 \right) /2$, on a $y-z$ plane located at $x=0$, for the different cases considered in this study: single-phase (panel a), $\mu _r=1$ (panel b), $\mu _r=50$ (panel c) and $\mu _r=100$ (panel d). The instantaneous position of the interface (identified as the iso-level $\phi =0$) is also shown by a white line. We notice that— compared to the reference single-phase case—the presence of the interface, no matter the value of $\mu _r$, induces an asymmetry in the flow. In particular, by increasing $\mu _r$, turbulence is progressively damped inside the thin oil layer (located near the top wall). In addition, we note that by increasing $\mu _r$ turbulence is damped also in the thick water layer, near the bottom wall. This behavior can be explained by looking at the value of the local Reynolds number. At the bottom wall, considering that the friction velocity is $u_{\tau ,bot}=\sqrt{\tau _{w,bot}/\rho }$, the semi-local Reynolds number becomes (Pecnik and Patel 2017; Roccon et al. 2019):

$$\begin{aligned} Re_{\tau ,bot}=Re_\tau \sqrt{\frac{2 \mid \tau _{w,bot} \mid }{\mid \tau _{w,bot}\mid +\mid \tau _{w,top}\mid }}\,, \end{aligned}$$

(5)

from which we obtain: $Re_{\tau ,bot}=364$ ($\mu _r=1$), $Re_{\tau ,bot}=255$ ($\mu _r=50$) and $Re_{\tau ,bot}=251$ ($\mu _r=100$). As a consequence, turbulence becomes progressively attenuated near the bottom wall. It is also interesting to observe that the turbulent intensity just below the interface, in the water layer, is higher for $\mu _r=50$ and $\mu _r=100$ compared to the case with $\mu _r=1$. This effect suggests that the interface behaves for the water layer similarly to a solid boundary, whereas it behaves like a compliant surface for $\mu _r=1$.

Fig. 2

Instantaneous distribution of turbulent kinetic energy, $TKE = \left( u'^2 + v'^2 + w'^2 \right) /2$ on an $y-z$ plane located at $x=0$ for the different cases considered in this study: single-phase (panel a), $\mu _r=1$ (panel b), $\mu _r=50$ (panel c), $\mu _r=100$ (panel d)

3.1.2 Mean Velocity Profiles and Flow Rates

The change of the flow structure described above clearly results into a corresponding change of the mean velocity profiles. Figure 3a shows the mean streamwise velocity profile, $\langle u \rangle$, as a function of the wall-normal coordinate, z, for all cases considered here. We observe that, compared to the single-phase case—for which the velocity profile is symmetric, the introduction of the thin oil layer breaks the symmetry of the velocity profile. While for $\mu _r=1$ the velocity profile is skewed towards the upper part of the channel, for $\mu _r=50$ and $\mu _r=100$ it is skewed towards the bottom part. The main reason for this different behavior is, as anticipated above, the different character of the liquid-liquid interface depending on the value of $\mu _r$: while for $\mu _r=1$ the interface is compliant, and actively adapts to vertical momentum, for $\mu _r=50$ and $\mu _r=100$ the interface acts essentially as a wall, hence giving a velocity profile with a maximum located roughly halfway between the interface and the bottom wall (i.e. shifted towards the bottom wall compared to the channel centerline). Rescaling the velocity profile by the actual value of the friction velocity at the bottom wall, $u_{\tau ,{bot}}$ (as done to compute the semi-local Reynolds number in Eq. 5), it is possible to evaluate the behavior of the velocity field in wall units, and compare it with the law of the wall: $u = z^+$ and $u = (1/k) \log (z^+) + 5$ (where $k = 0.41$ is the von Kármán constant (Von Kármán 1931). The single-phase turbulent flow (black) shows a good agreement with the law of the wall (represented by the dashed line). Even for the case $\mu _r=1$ the results of the simulation follow fairly well the behavior of the law of the wall. The situation is slightly different for $\mu _r=50$ and $\mu _r=100$, for which we notice a reduction of the flow velocity, in particular in the viscous sub-layer. This indicates that the introduction of the thin oil layer in the top part of the channel induces a general attenuation of turbulence, which reflects into a corresponding modulation of the turbulence regeneration cycle even at the bottom wall. The flow rate of the oil and the water layer, $Q_o$ and $Q_w$, as well as the total flow rate, $Q_{t}$, are shown—normalized by the single-phase flow rate, $Q_{SP}$—in Table 2. As it can be observed, the introduction of a thin liquid layer with the same viscosity of the thick layer ($\mu _r=1$) leads to a significant increase in the total flow rate, which amounts to about $27\%$ compared to the single-phase case. In contrast, when the thin layer has a much larger viscosity than the thick layer, i.e. $\mu _r=50$ and $\mu _r=100$, the flow rate is reduced by about 30 and $34\%$, respectively. Given that the mean pressure gradient is constant for all simulations, the modification of the flow rate can be associated with a reduction of drag for the matched viscosity case (Roccon et al. 2019) and an increase of drag for the other two cases with a more viscous fluid in the thin layer.

Fig. 3

Panel a: wall-normal behavior of the mean streamwise velocity $\langle u \rangle$ as a function of z/h. The nominal interface position is shown with a dotted line, while the position of the channel centerline is shown with a dash-dotted line. Panel b: wall-normal behavior of the mean streamwise velocity $\langle u \rangle$ in the water layer, rescaled based on the actual value of the friction velocity at the bottom wall, $u_{\tau ,bot}$. Also shown in panel b is the law of the wall: $u^+ = z^+$ and $u^+ = (1/k) \log (z^+) + 5$ (where $k = 0.41$ is the von Kármán constant (Von Kármán 1931). The different cases are reported with different colors: single-phase (black), $\mu _r=1$ (blue), $\mu _r=50$ (violet), $\mu _r=100$ (green)

Table 2 Flow rate measurement for the different simulations: $Q_o$, $Q_w$ and $Q_{t}$ correspond to the flow rates of the thin layer (oil), of the thick layer (water), and of the entire flow oil–water flow, respectively, while $Q_{SP}$ is the flow rate of the reference single-phase case. The quantity ΔQ represents the increase (in percentage) of the total flow rate between the two-phase and the single-phase flow simulations

3.1.3 Stress Budget

To analyze in more detail the modifications produced by the introduction of a thin viscous layer in the flow, we look at the stress behavior as a function of the wall-normal coordinate z. The mean stress can be expressed as

$$\begin{aligned} \tau _{tot} = \underset{\tau _{v}}{\underbrace{\frac{\langle \mu (z) \rangle }{Re_\tau } \frac{\partial \langle u \rangle }{\partial z}}} - \underset{\tau _t}{\underbrace{\langle u' w' \rangle }} + \underset{\tau _c}{\underbrace{ \frac{3}{\sqrt{8}} \frac{Ch}{We} \left\langle \frac{\partial \phi }{\partial x} \frac{\partial \phi }{\partial z} \right\rangle }}\,, \end{aligned}$$

(6)

indicating that the total stress $\tau _{tot}$ is the sum of three contributions: the viscous stress, $\tau _v$, the Reynolds or turbulent stress, $\tau _t$, and the capillary stress, $\tau _c$. The wall-normal behavior of the stresses averaged along the two homogeneous directions x and y and in time is shown in Fig. 4. For all considered cases, the total stress—shown in Fig. 4a with a dashed line—is a linear function of z. The sum of the absolute values of the stress evaluated at the two walls is constant and equal to 2 for all cases, since the wall-shear stress balances the mean pressure gradient used to drive the flow, which is kept constant and equal to ${\overline{\nabla p} }=-1$. In Fig. 4a, we also show the wall-normal behavior of the Reynolds stress, $\tau _t$, for all cases (continuous line). Compared to the single-phase case, for which $\tau _t$ is anti-symmetric about the channel centerline, the introduction of thin layer near the top wall induces remarkable changes. For $\mu _r=1$, there is a significant reduction of $\tau _t$ around the liquid-liquid interface and in the thin layer, due to the blockage effect induced by the presence of the compliant liquid-liquid interface (Roccon et al. 2019). By contrast, in the bottom part of the channel, we observe an opposite behavior, with $\tau _t$ much larger than the single-phase case, as a consequence of the increased turbulence activity. For $\mu _r=50$ and $\mu _r=100$, $\tau _t$ is almost vanishing inside the thin viscous layer, due to the large fluid viscosity, while it becomes larger below the liquid-liquid interface, which in this case is perceived as a solid boundary by the flow, hence actively contributing to the turbulence production (larger $\tau _t$). On the other hand, $\tau _t$ decreases near the bottom wall, because of the already observed turbulence reduction there.

Considering now the capillary stress, shown in the inset of Fig. 4a, we observe that is larger for $\mu _r=1$, and smaller for $\mu _r=50$ and $\mu _r=100$. Given that the flow in the thin layer tends to be laminar, the liquid-liquid interface acts– via the capillary stress—as an active barrier against momentum transport between the thick and the thin layer.

The wall-normal behavior of the viscous stress $\tau _v$ is shown in Fig. 4b. For $\mu _r=1$, the viscous stress at the top wall is lower than the reference single-phase flow and is characterized by a non-monotonic transition across the interface, while it decreases towards zero below the interface, similarly to the single-phase case at the same distance from the wall. At the bottom wall, the viscous stress is $\sim 50\%$ higher, due to the increase of the mean velocity gradient in that region (see Fig. 3a). For $\mu _r=50$ and $\mu _r=100$, the viscous stress is significantly higher at the top wall, because of the high viscosity, and remains high over a much larger distance from the wall–down to $z/h \approx 0.5$. The large extent of the region in which the viscous stress is considerably higher, observed for $\mu _r=50$ and $\mu _r=100$, seems to suggest that for these cases the thin viscous layer present near the top wall has a direct influence also on the turbulence behavior near the bottom wall, where the canonical single-phase turbulence is not fully recovered (and the viscous stress is smaller than the single phase case).

In summary, the presence of the thin layer leads to a sharp gradient in the mean velocity profile below the interface, which is associated with an increased shear stress between the two fluid layers. This is true in particular for $\mu _r=50$ and $\mu _r=100$, and is also the reason behind the increased production of turbulent kinetic energy in that region, where turbulence intensity can be even higher compared to the region near the bottom wall (see Fig. 2d). Therefore, when high viscosity ratios are considered, the thick layer perceives the liquid-liquid interface as an almost rigid boundary, which is a situation that is not observed for $\mu _r=1$. However, strictly speaking, the behavior of the thin liquid layer differes from that of a rigid boundary: The liquid layer, which is slightly compliant, can absorb/release energy via surface tension forces, and can also dissipate additional energy because of the larger viscosity.

Fig. 4

Panel a: wall-normal behavior of the Reynolds stress (solid lines), total stress (dashed lines) and capillary stress (inset) as a function of the wall-normal coordinate z/h. Panel b: wall-normal behavior of the viscous stress as a function of the wall-normal coordinate z/h. The different cases are reported with different colors: single-phase (black), $\mu _r=1$ (blue), $\mu _r=50$ (violet), $\mu _r=100$ (green). The dotted line marks the mean interface  position

3.2 Interface Statistics

In this section, we present a space-time characterization of the interface that separates the two liquid layers, for the different cases considered in this study.

3.2.1 Spatial Characterization of the Interface Deformation

In Fig. 5 we show the instantaneous shape of the liquid-liquid interface for the three different two-phase flow cases considered here: Fig. 5a refers to $\mu _r=1$, Fig. 5b refers to $\mu _r=50$ and Fig. 5c refers to $\mu _r=100$. Together with a three dimensional rendering of the liquid-liquid interface (left column), we also show—for each case—a close-up view of the interface elevation $\eta /h$ (as defined in Fig. 1) along the streamwise direction x/h, and measured at spanwise location $y=0$. At a first glance, the interface shape, regardless of the value of $\mu _r$, seems characterized by the presence of waves. In our setting, in which the two fluid layers have the same density and the role of gravity is ruled out, these waves are pure capillary waves in which the restoring force is the surface tension. We notice also that the interface deformation shows remarkable differences for the high viscosity ratio cases, $\mu _r=50$ and $\mu _r=100$, compared to the matched viscosity case, $\mu _r=1$. In particular, instead of multiple different wavelengths of moderate wave amplitudes observed for the matched viscosity case, the interface deformation for the two cases at large viscosity ratio is characterized by a regular wave pattern. This pattern is very pronounced at $\mu _r=100$, and is characterized by a steep windward side (up to the crest), followed by a much less steep lee side (down to the trough). The values of the root mean square elevation for each case are: $\sqrt{\langle {\eta ^2} \rangle } = 2.7 \times 10^{-2}$ ($\mu _r=1$), $\sqrt{\langle {\eta ^2} \rangle } = 3.6 \times 10^{-2}$ ($\mu _r=50$), $\sqrt{\langle {\eta ^2} \rangle } = 4.0 \times 10^{-2}$ ($\mu _r=100$), and indicates that waves grow in amplitude as the viscosity ratio increases. It is interesting to note that the shape of the interface elevation at large viscosity ratio looks similar to the so-called bamboo wave structure observed in oil–water core annular flows in pipes (Kouris and Tsamopoulos 2001; Joseph et al. 2003).

Fig. 5

Three-dimensional rendering of the instantaneous interface deformation (left), and corresponding profiles of the interface elevation $\eta$ (right), measured as a function of the streamwise direction x at a given y position. Each panel refers to a different case: $\mu _r=1$ (panel a), $\mu _r=50$ (panel b) and $\mu _r=100$ (panel c)

To quantify the influence of the viscosity ratio on the deformation of the liquid-liquid interface, we look at the Probability Density Function (PDF) of the interface elevation normalized by its root mean square value, for each case. Results are shown in Fig. 6. We can observe that, for $\mu _r=1$, the probability density is maximum near the mean interface location $\langle \eta \rangle =0$, and it is negatively skewed due to the effect of wall confinement (waves are larger towards the center of the channel than towards the wall). Note indeed that the wall is located at a distance of 0.15h from the nominal interface position, and therefore there is a vanishing probability of extreme events with positive interface elevations compared to extreme events with negative interface elevations. For the high viscosity ratio cases, the probability density function is bimodal, and the major mode is positive. This suggest a larger presence of wave crests than troughs. The bimodal distribution also indicates the persistence of wave crests and troughs with specific amplitudes, corresponding to the two modes of the distribution.

Fig. 6

Probability Density Functions (PDF) of the interface elevation, $\eta$, normalized by the root mean square (RMS) of the interface elevation $\sqrt{\langle \eta ^2 \rangle }$. The different cases are reported with different colors: $\mu _r=1$ (blue), $\mu _r=50$ (violet) and $\mu _r=100$ (green)

Naturally, the interface deformation is two-dimensional, and waves propagate at the interface along x and y. This is visualized in Fig. 7 for the three different cases: Fig. 7a refers to $\mu _r=1$, Fig. 7b refers to $\mu _r=50$ and Fig. 7c refers to $\mu _r=100$. Beside the three dimensional rendering of the liquid-liquid interface (left column) we now show the contour maps of the entire interface elevation, $\eta (x,y)$ (right column), for the three different values of the viscosity ratio. Compared to the case $\mu _r=1$, for which the interface deformation does not show a regular pattern, for the cases $\mu _r=50$ and $\mu _r=100$ the interface deformation looks much more regular and quasi-1D (along x), with only little perturbations along y. This is properly quantified in Fig. 8, by looking at the two-dimensional time-averaged wavenumber power spectra of wave elevation $\overline{S_\eta \left( k_x, k_y \right) }$. This quantity represents the distribution of energy at the different wavenumbers $k_x$–$k_y$. For $\mu _r=1$, the power spectrum appears isotropic, with almost no sign of preferential distribution. On the other hand, for $\mu _r=50$ the energy distribution is more focused along the streamwise direction, $k_x$. This effect is even more pronounced for $\mu _r=100$, where we can also observe the presence of spectral peaks at certain discrete wavenumbers.

Fig. 7

Three-dimensional rendering of the instantaneous interface deformation $\eta$ (left), and corresponding two-dimensional contour maps of $\eta$ (right). Each panel refers to a different case: $\mu _r=1$ (panel a), $\mu _r=50$ (panel b) and $\mu _r=100$ (panel c)

To compare more closely the structure of the interface deformation for the three different $\mu _r$, we average the two-dimensional power spectra of wave elevation, $\overline{S_\eta \left( k_x, k_y \right) }$, along the y direction, so to obtain the streamwise spectra of the interface elevation, $\overline{ \langle S_\eta \left( k_x \right) \rangle }$. Results are shown in Fig. 9. We observe that, unlike the smooth distribution of energy as a function of the streamwise wavenumber $k_x$ at $\mu _r=1$, the wave energy for the cases $\mu _r=50$ and $\mu _r=100$ is concentrated at specific discrete wavenumbers. This suggests that the wave field is dominated by the presence of a "parent" wave, on top of which other less energetic waves (having wavenumber that is a multiple of that of the parent wave) can propagate. The peak wavenumber is $k_{x,{peak}}=1.5$ for $\mu _r=50$ and $\mu _r=100$ (or, in terms of wavelength, $\lambda _{peak}=4 \pi /3$) and corresponds to the presence of $N \approx 3$ waves inside a domain of length $L_x=4 \pi$. This is in agreement with the patterns shown in Fig. 5b, c and 7b, c. This suggests a highly anisotropic situation and agrees with the qualitative observation of waves developing only across the streamwise direction and being self-similar across the channel span.

Fig. 8

Two-dimensional time-averaged wavenumber power spectra of the interface elevation, $\overline{S_\eta \left( k_x, k_y \right) }$. Each panel refers to a different case: $\mu _r=1$ (panel a), $\mu _r=50$ (panel b), $\mu _r=100$ (panel c)

Fig. 9

Streamwise wavenumber power spectra of the interface elevation, $\overline{\langle S_\eta \left( k_x\right) \rangle }$, averaged in space (over the spanwise direction) and in time. Results are shown for $\mu _r=1$ (blue), $\mu _r=50$ (violet) and $\mu _r=100$ (green)

3.2.2 Temporal Characterization of Interface Deformation

So far, we examined the spatial behavior of interface waves. We now move to the time characterization of waves.

Note that, since the interface is advected at a mean velocity (see Fig. 3a) wave frequencies are Doppler shifted to higher frequencies. The mean advection velocities for the three cases are: $\langle u_i \rangle \approx 16.5$ ($\mu _r=1$), $\langle u_i \rangle \approx 1.9$ ($\mu _r=50$) and $\langle u_i \rangle \approx 0.9$ ($\mu _r=100$). Therefore, in order to isolate the wave frequencies, a shift of the interface elevation signal is applied as $\eta '(x,t)=\eta (x+dx_{shift},t)$, where $dx_{shift} =\langle {u}_i \rangle / df_{samp}$ and $df_{samp}$ is the frequency at which the interface elevation is sampled (Giamagas et al. 2023). Space-averaged frequency power spectra of wave elevation $\langle S_\eta \left( \omega \right) \rangle$ of the shifted wave signals for each case are reported in Fig. 10. The minimum angular frequency on the x-axis ($\omega _{min}=0.628$) corresponds to the overall duration of the recorded wave signal. We note even here a remarkable difference between the case $\mu _r=1$ and the other two cases at higher viscosity ratio. In particular, while for $\mu _r=1$ energy is evenly distributed over a broad range of frequencies – before it starts diminishing at higher frequencies – for $\mu _r=50$ and $\mu _r=100$ the energy is concentrated over a narrow range in the low-frequency region of the spectrum, and it vanishes rapidly as the frequency increases. This suggests that at large viscosity ratio the waves oscillate so slowly that their oscillation is not even perceived, and waves seem rigidly advected by the flow. This can also be appreciated by looking at the animations of the time-resolved rendering of the interface dynamics included in the supplementary material.

Fig. 10

Space-averaged frequency power spectra of wave elevation, $\langle S_\eta \left( \omega \right) \rangle$ computed using the shifted wave signal. The different cases are reported with different colors: $\mu _r=1$ (blue), $\mu _r=50$ (violet) and $\mu _r=100$ (green)

4 Conclusions

We have performed direct numerical simulations of a pressure-driven oil–water turbulent channel flow. We have considered a stratified flow configuration, in which a thin layer of oil flows on top of a thick layer of water. Three different values of the oil-to-water viscosity ratio, $\mu _r=1$, $\mu _r=50$ and $\mu _r=100$ are used, and their influence on the turbulence modulation and on the dynamics of the liquid-liquid interface is considered. Results show that, compared to the reference single-phase turbulent flow, the introduction of a thin fluid layer, characterized by a viscosity equal or larger than that of the thick layer, modifies the overall velocity profiles and the turbulence behavior. In particular, the mean flow rate increases significantly for $\mu _r=1$ and decreases significantly for $\mu _r=50$ and $\mu _r=100$. This is associated to a corresponding change of the drag coefficient. When the viscosity contrast between the two fluids is large, the liquid-liquid interface is perceived as a solid boundary by the thick water layer, leading to high shear stress and a local increase in turbulent kinetic energy production around it. In addition, we also observe that the near-wall turbulent cycle at the bottom wall (at the bottom of the thick layer) is influenced as well by the thin layer viscosity. In addition, the structure and the dynamics of the liquid-liquid interface show remarkable changes by changing the viscosity ratio between the two fluids. Specifically, we observe a transition from a regime characterized by the presence of an almost isotropic wave field for the matched viscosity case $\mu _r=1$, to a regime characterized by regular long waves with short crests and longer troughs for high viscosity ratios. The wave structure in these latter cases seems to resemble the so-called bamboo waves observed in oil–water pipe flows. Finally, the temporal analysis of the wave signals reveals that while for the matched viscosity case $\mu _r=1$ waves oscillate at different frequencies over a rather broad range of values, for high viscosity ratios waves oscillate at a specific very low frequency, thus generating an interface deformation that seems purely advected by the mean flow velocity.