1 Introduction

In several combustion devices, the combustion process occurs under inhomogeneous fuel–air conditions within the flammability limits of the mixture, commonly referred to as stratified combustion (Lipatnikov 2017). The imperfect mixing offers some benefits compared to premixed combustion, such as enabling leaner burning conditions, manipulation of flammability limits, flame propagation and reduced pollutant emission rates (Lipatnikov 2017). Mixture stratification can also occur unintentionally due to inadequate mixing in combustors designed to operate in the premixed mode of combustion. Interested readers are referred to the review paper by Lipatnikov (2017) for an extensive review of the experimental and numerical investigations into stratified mixture combustion. The advances in high-performance computing have enabled Direct Numerical Simulations (DNS) of stratified mixture combustion (Hélie and Trouvé, 1998; Haworth et al. 2000; Malkeson and Chakraborty 2010a, b, c; 2011a, b, c, 2012, 2013a, b; Richardson and Chen 2017; Proch et al. 2017a, b; Inanc et al. 2022), but the vast majority of these studies have been conducted for statistically planar flames (Hélie and Trouvé, 1998; Haworth et al. 2000; Malkeson and Chakraborty 2010a, b, c; 2011a, b, c, 2012, 2013a, b; Brearley et al. 2020, 2022). Moreover, one-dimensional laminar flame analyses (Egolfopoulos and Campbell 1996; Da Cruz et al. 2000; Lauvergne et al. 2000; Sankaran and Chen 2002; Kang and Kyritsis 2007; Richardson et al. 2010; Vena et al. 2011; Inanc et al. 2020) also provided important physical insights into stratified mixture combustion. The laboratory-scale stratified flame burners are mostly analysed numerically based on Reynolds-averaged Navier–Stokes/Large Eddy Simulations (Ribert et al. 2005; Robin et al. 2006; Darbyshire et al. 2010; Marincola et al. 2013; Proch and Kempf 2014; Mercier et al. 2015; Shi et al. 2016; Proch et al. 2017b; Turkeri et al. 2019; Zhang et al. 2021) but recently, Proch et al. (2017a, b) and Inanc et al. (2022) carried out flame-resolved three-dimensional flame-resolved high-fidelity simulations for turbulent stratified mixture combustion of a laboratory-scale configuration, which was analysed extensively using experiments (Barlow et al. 2009; Sweeney et al. 2012a, b). The aforementioned DNS and flame-resolved high-fidelity simulation studies provided important physical insights into the stratified flame structure (Hélie and Trouvé, 1998; Haworth et al. 2000; Malkeson and Chakraborty 2010a, c, 2011b; Richardson and Chen 2017; Brearley et al. 2020, 2022; Inanc et al. 2022) and flame propagation rate (Malkeson and Chakraborty 2010a, c; Richardson and Chen 2017; Inanc et al. 2022), which gave rise to closure methodologies for scalar variances and co-variances (Malkeson and Chakraborty 2010a, b; 2013b), turbulent scalar flux (Malkeson and Chakraborty 2012), Flame Surface Density (Malkeson and Chakraborty 2013a), and scalar dissipation and cross-scalar dissipation rates (Malkeson and Chakraborty 2011a, c). The effects of different types of mixture stratification in the presence of shear in non-canonical flow configurations were analysed recently by Richardson and Chen (2017) based on three-dimensional DNS, where the effects of the relative alignments of mixture fraction and reaction progress variable gradients (i.e. \(\nabla \xi \) and \(\nabla c\), respectively) on the global behaviours of burning, flame propagation rate and flame surface area were studied. However, the effects of the relative alignment between mixture fraction and reaction progress variable gradients (i.e. \(\nabla \xi \) and \(\nabla c\), respectively) on modelling assumptions related to the burning rate, flame surface area and scalar gradients are yet to be analysed in detail. This gap in the existing literature is addressed in this paper by extending the analysis by Richardson and Chen (2017) by performing a three-dimensional DNS of turbulent slot jets for stratified methane-air mixture combustion under three different relative alignments of \(\nabla \xi \) and \(\nabla c\): (a) when the flame propagates from the richer to leaner mixture characterised by \(\nabla \xi \cdot \nabla c>0\), (b) when the flame propagates from the leaner to richer mixture characterised by \(\nabla \xi \cdot \nabla c<0\) and (c) when the mixture fraction gradient is orthogonal to the flame in a mean sense (i.e. \(\nabla \xi \cdot \nabla c\approx 0\)). For comparison, DNS of a turbulent premixed flame is also conducted for the mixture fraction which is the arithmetic mean of maximum and minimum values of \(\xi \) in stratified mixture cases. The DNS data has been utilised to analyse the effects of the relative alignment of \(\nabla \xi \) and \(\nabla c\) on the flame evolution. In this respect, the main objectives of the current analysis are:

  1. (1)

    To demonstrate and explain the effects of the relative alignments of \(\nabla \xi \) and \(\nabla c\) on the flame height, flame surface area and overall burning rate.

  2. (2)

    To analyse the effects of the global nature of mixture stratification on burning rate and flame propagation characteristics, and modelling of reaction rate in the context of Reynolds Averaged Navier–Stokes (RANS) simulations.

The rest of this paper is organised as follows. The mathematical background and the relevant definitions are provided in the next section. This is followed by a discussion of the numerical implementation pertinent to this work. Following this, the results are presented and subsequently discussed. The main findings are summarised, and conclusions are drawn in the final section of this paper.

2 Mathematical Background

A two-step methane-air chemical mechanism presented by Westbrook and Dryer (1981) has been used for the present analysis for computational economy. This chemical mechanism accounts for 6 species (\({\mathrm{CH}}_{4}, {\mathrm{O}}_{2},\mathrm{ C}{\mathrm{O}}_{2}, {\mathrm{H}}_{2}\mathrm{O},\mathrm{ CO}\) and \({\mathrm{N}}_{2}\)) and is a compromise between single-step chemistry and more complex mechanisms. The values of the coefficients in this reaction are following those proposed by the CERFACS 2s_CM2 mechanism (Bibrzycki and Poinsot 2010). Pre-exponential adjustment (PEA) proposed by Bibrzycki and Poinsot (2010) is used to accurately capture the laminar burning velocity dependence on the equivalence ratio and is designed to capture the laminar burning velocity obtained from GRI-Mech 3.0 (Smith et al. 2018) across the whole of the \({\mathrm{CH}}_{4}\) flammability range (\(0.55\le \phi \le 1.55\)), which can be substantiated from Fig. 1. All the species are assumed to have unity Lewis number, which was shown to be a reasonable assumption for fuel-lean flames (Marincola et al. 2013; Proch et al. 2017a; Inanc et al. 2022). Standard values are taken for Prandtl number \(Pr=0.7\) and the ratio of specific heats \(\gamma ={C}_{p}/{C}_{v}=1.4\).

Fig. 1
figure 1

Variation of laminar burning velocity \(S_{L\left( \phi \right)}\) with equivalence ratio \(\phi\) for the present thermochemistry alongside the corresponding variation obtained from GRI-Mech 3.0 (Smith et al. 2018)

Full size image

In stratified combustion, the mixture inhomogeneity is characterised in terms of mixture fraction \(\xi \), which can be defined as (Bilger 1980):

$$\xi =\frac{\beta -{\beta }_{O}}{{\beta }_{F}-{\beta }_{O}}$$
(3)

where \(\beta =2{Y}_{C}/{W}_{C}+{Y}_{H}/2{W}_{H}-{Y}_{O}/{W}_{O}\) with \({\beta }_{O}\) and \({\beta }_{F}\) being the values of \(\beta \) in the oxidiser (i.e. air) and fuel streams respectively, with \({Y}_{k}\) and \({W}_{k}\) denoting the atomic mass fractions and molecular weights. For \({\mathrm{CH}}_{4}\)-air mixtures, \({\beta }_{F}=0.25\) and \({\beta }_{O}=-0.01456\). The stoichiometric mixture fraction value is expressed as (Bilger 1980):

$${\xi }_{st}= -\frac{{\beta }_{O}}{{\beta }_{F}-{\beta }_{O}}$$
(4)

The local equivalence ratio \(\phi \) can be defined in terms of \(\xi \) and \({\xi }_{st}\) as (Bilger 1980):

$$\phi =\frac{\xi (1-{\xi }_{st})}{{\xi }_{st}(1-\xi )}$$
(5)

The extent of the completion of the chemical reaction can be quantified by a reaction progress variable \(c\) that increases monotonically from zero in the unburned mixture to unity in the products. It is defined here based on the fuel mass fraction as

$$c=\frac{{Y}_{Fu}^{eq}-{Y}_{F}}{{Y}_{Fu}^{eq}-{Y}_{Fb}^{eq}}$$
(6)

where \({Y}_{Fu}^{eq}\) and \({Y}_{Fb}^{eq}\) are the equilibrium fuel mass fraction values in the unburned gas and fully burned gas, respectively. The reaction progress variable can also be defined in terms of the \({\mathrm{O}}_{2}\) mass fraction, however, the choice of progress variable definition does not affect the conclusions drawn in this paper. The local gradients of \(c\) and \(\xi \) determine whether the local mode of flame propagation and the relative alignments of \(\nabla c\) and \(\nabla \xi \) can be characterised by (Marincola et al. 2013):

$$\mathrm{cos}{\theta }_{c\xi }=\frac{\nabla c\cdot \nabla \xi }{\left|\nabla c\right||\nabla \xi |}$$
(7)

For back-supported flames, where flame propagates into a progressively leaner mixture, \(\mathrm{cos}{\theta }_{c\xi }\) takes positive values, whereas in front-supported flames, \(\mathrm{cos}{\theta }_{c\xi }\) takes negative values. Finally, the transport equation of \(c\) takes the following form (Bray et al. 2005; Malkeson and Chakraborty 2010b):

$$\rho \left[\frac{\partial c}{\partial t}+{u}_{j}\frac{\partial c}{\partial {x}_{j}}\right]={\dot{\omega }}_{c}+\nabla \cdot \left(\rho D\nabla c\right)+{A}_{\xi }$$
(8)

where \(D\) is the diffusivity of the reaction progress variable and \({\dot{\omega }}_{c}\) is the reaction rate of the reaction progress variable, which takes the following form (Bray et al. 2005; Malkeson and Chakraborty 2010c):

$${\dot{\omega }}_{c}=-{\dot{\omega }}_{F}/[{Y}_{Fu}^{eq}] \, \mathrm{ for } \, \xi \le {\xi }_{st},{\dot{\omega }}_{c}=-{\dot{\omega }}_{F}/[{Y}_{Fu}^{eq}-{Y}_{Fb}^{eq}] \, \mathrm{ for } \, \xi >{\xi }_{st}$$
(9)

with \({\dot{\omega }}_{F}\) being the reaction rate of the fuel and \({A}_{\xi }\) being the cross-scalar dissipation contribution, which is defined as (Bray et al. 2005; Malkeson and Chakraborty 2010c):

$${A}_{\xi }=2\rho D(\nabla c\cdot \nabla \xi )/\xi \, \mathrm{ for }\,\xi \le {\xi }_{st}\mathrm{ and }{A}_{\xi }=-2\rho D(\nabla c\cdot \nabla \xi )/(1-\xi )\mathrm{ for }\xi >{\xi }_{st}$$
(10)

Equation 8 can be written in the kinematic form for a given \(c\)-isosurface (Bray et al. 2005; Malkeson and Chakraborty 2010c):

$$\frac{\partial c}{\partial t}+{u}_{j}\frac{\partial c}{\partial {x}_{j}}={S}_{d}|\nabla c|$$
(11)

where \({S}_{d}\) is the flame displacement speed, which is defined as:

$${S}_{d}=\frac{{\dot{\omega }}_{c}+\nabla \cdot \left(\rho D\nabla c\right)+{A}_{\xi }}{\rho |\nabla c|}$$
(12)

Based on Eq. 12, it is possible to write (Trouvé and Poinsot 1994; Boger et al. 1998; Malkeson and Chakraborty 2010c):

$$\overline{{\dot{\omega } }_{c}}+{\overline{\nabla \cdot \left(\rho D\nabla c\right)}}+\overline{{A }_{\xi }}={\overline{\left(\rho {S}_{d}\right)}}_{s}{\Sigma }_{\mathrm{gen}}$$
(13)

where \(\overline{Q }\) refers to the Reynolds/LES filtered value of a general quantity \(Q\) and \({\overline{\left(Q\right)}}_{s}=\overline{Q\left|\nabla c\right|}/{\Sigma }_{\mathrm{gen}}\) is the surface averaged/filtered value of the general quantity \(Q\) with \({\Sigma }_{\mathrm{gen}}=\overline{\left|\nabla c\right|}\) being the generalised Flame Surface Density (FSD) (Boger et al. 1998). It can be appreciated from Eqs. 10–13 that the statistical behaviours of \(|\nabla c|\) and \(|\nabla \xi |\) and the relative alignments of \(\nabla c\) and \(\nabla \xi \) play key roles in determining the flame propagation rate and overall burning rate, which will be discussed in detail in Sect. 4 of this paper.

3 Numerical Implementation

The simulations for the current analysis have been carried out using a well-known DNS code SENGA+ (Jenkins and Cant 1999) where the standard conservation equations for mass, momentum, energy and species are solved in a non-dimensional form. In SENGA+, the spatial discretisation is approximated using a 10th-order central difference scheme for the internal grid points and the order of accuracy gradually decreases to a single-sided 2nd-order scheme at the non-periodic boundaries (Jenkins and Cant 1999). The time advancement has been carried out using an explicit 3rd-order low storage Runge–Kutta scheme (Wray 1990). The schematic diagrams of the simulation configurations are shown in Fig. 2. The slot width \(h\) of the planar jet shown in Fig. 2 is taken to be \(4.6{\delta }_{st}\) where \({\delta }_{st}={\delta }_{th(\phi =1.0)}=({T}_{ad\left(\phi =1\right)}-{T}_{0})/{\mathrm{max}\left|\nabla T\right|}_{L}\) is the thermal flame thickness of the stoichiometric mixture with \({T,T}_{ad\left(\phi =1\right)}\) and \({T}_{0}\) being the dimensional temperature, the adiabatic flame temperature of the stoichiometric \({\mathrm{CH}}_{4}\)-air mixture and the unburned gas temperature, respectively. The computational domain is taken to be a parallelepiped with dimensions of \({L}_{x}\times {L}_{y}\times {L}_{z}=37 {h}\times 19 {h}\times 4.3 {h}\) with the longest side aligned with the streamwise direction (i.e. \(x\)-direction) and the smallest side is aligned to the spanwise direction (i.e. \(z\)-direction). These dimensions allow for the development of both non-reacting and reacting jet flows. The transverse boundaries are taken to be periodic, and partially non-reflecting boundary conditions are imposed for the outflow boundary in the streamwise direction. The turbulent velocity components and density are imposed at the inflow boundary opposite the outlet. The domain of \(37h\times 19h\times 4.3h\) is discretised using a uniform cartesian grid of \(1920\times 990\times 225\), which ensures 11 grid points within \({\delta }_{st}\) and 52 grid points within the slot width \(h\). The grid spacing also remains smaller than the Kolmogorov length scale throughout the domain. It was shown elsewhere (Turquand d’Auzay and Chakraborty 2021) that the mixture fraction \(\xi \) and streamwise velocity \({u}_{1}\) statistics for a non-reacting flow show self-similar behaviour for \(9\le x/h\le 30\) and the confinement effects due to the periodic boundary conditions are felt only for \(x/h>30\). For these simulations, the bulk velocity of the jet is \({U}_{\mathrm{jet}}=40 {S}_{L(\phi =1)}\), whereas the coflow velocity is \({U}_{\mathrm{coflow}}=4{S}_{L(\phi =1)}=0.1{U}_{\mathrm{jet}}\). Under these conditions, the jet Reynolds number is \(\rho {U}_{\mathrm{jet}}h/\mu =650\). The coflow is assumed to be laminar at the inlet and no turbulent velocity fluctuations are imposed. The turbulent velocity fluctuations at the jet inlet are specified by scanning a plane through a frozen periodic channel flow with a scanning velocity of \({U}_{\mathrm{jet}}\). The turbulent velocity fluctuations at the inlet are specified based on \({u}_{i}^{^{\prime}}/{U}_{\mathrm{bulk}}\) values obtained from a fully-developed channel flow with friction Reynolds number \(R{e}_{\tau }\) of 395 (i.e. \(R{e}_{\tau }=2\rho {U}_{\tau}H/\mu =395\)) where the \({u}_{i}^{^{\prime}}\) is the fluctuating component of velocity in the \(i\)th direction, \({U}_{\mathrm{bulk}}\) is the bulk mean velocity, \(u_{\tau}\) is the mean friction velocity in the channel and \(H\) is the channel half height. The choice of \(R{e}_{\tau }=395\) for the turbulent inflow specification is motivated by the fact that the \({u}_{i}^{^{\prime}}/{U}_{\mathrm{bulk}}\) profile reaches a self-similar pattern for \(R{e}_{\tau }\ge 395\) (Moser et al. 1999).

Fig. 2
figure 2

Schematic diagram of the flame configurations analysed in this paper

Full size image

For initialisation of the flame, the non-dimensional temperature \({c}_{T}=[T-{T}_{u}\left(\xi \right)]/[{T}_{b}\left(\xi \right)-{T}_{u}\left(\xi \right)]\) is specified as (Richardson and Chen 2017):

$${c}_{T}=1-\frac{1}{4}\left(1-\mathrm{tanh}\left[\frac{2{y}^{^{\prime}}-\left(h+3\delta \right)}{\delta }\right]\right)\left(1+\mathrm{tanh}\left[\frac{2{y}^{^{\prime}}+(h+3\delta )}{\delta }\right]\right)$$
(14)

where \({y}^{^{\prime}}=y-{y}_{c}\) with \({y}_{c}\) being the \(y\) coordinate at the centre of the slot, \(\delta \) is representative of the flame thickness for initialisation, which is taken to be \(\delta =1.5{\delta }_{st}\) for the present analysis. In Eq. 14, \({T}_{u}\left(\xi \right)\) and \({T}_{b}\left(\xi \right)\) are the unburned gas temperature and the adiabatic flame temperature corresponding to the mixture fraction \(\xi \). For all simulations the unburned gas temperature \({T}_{u}(\xi )={T}_{0}\) is taken to be 415 K, which yields a heat release parameter \(\tau =({T}_{ad\left(\phi =1\right)}-{T}_{0})/{T}_{0}\) of 4.5 (i.e. \(\tau =({T}_{ad\left(\phi =1\right)}-{T}_{0})/{T}_{0}=4.5\)) for the present database.

In the case of turbulent stratified jet flame simulations, the mixture fraction \(\xi \) is initialised as (Richardson and Chen 2017):

$$\xi ={\xi }_{0}+Z({\xi }_{1}-{\xi }_{0})$$
(15)

where \({\xi }_{0}\) and \({\xi }_{1}\) refer to the smallest and the largest values of mixture fraction which are taken to be 0.034 and 0.055, respectively, which correspond to \(\phi =0.6\) and 1.0 for the present analysis. Here, \(Z\) is a normalised variable representative of the mixture fraction, which is used for initialisation of \(\xi \). For the back-supported and front-supported stratified cases, the initial distribution of \(Z\) is specified as (Richardson and Chen 2017):

$$Z=1-\frac{1}{4}\left(1-\mathrm{tanh}\left[\frac{2{y}^{^{\prime}}-h}{\delta }\right]\right)\left(1+\mathrm{tanh}\left[\frac{2{y}^{^{\prime}}+h}{\delta }\right]\right)\mathrm{for \, back\!\!-\!\!supported \, case}$$
(16i)
$$Z=\frac{1}{4}\left(1-\mathrm{tanh}\left[\frac{2{y}^{^{\prime}}-h}{\delta }\right]\right)\left(1+\mathrm{tanh}\left[\frac{2{y}^{^{\prime}}+h}{\delta }\right]\right)\mathrm{for \, front\!\!-\!\!supported \, case}$$
(16ii)

In the misaligned case (i.e. where \(\nabla \xi \cdot \nabla c=0\) is specified), \(Z\) is initialised as (Richardson and Chen 2017):

$$Z=1-\frac{1}{4}\left(1-\mathrm{tanh}\left[\frac{{z}^{^{\prime}}-0.25{L}_{z}}{h/2}\right]\right)\left(1+\mathrm{tanh}\left[\frac{{z}^{^{\prime}}+0.25{L}_{z}}{h/2}\right]\right)\mathrm{for \, misaligned \, case}$$
(16iii)

where \({z}^{^{\prime}}=z-{z}_{c}\) with \({z}_{c}\) being the \(z\) coordinates at the centre of the slot. This imparts a regularly repeating wave in the \(z\) direction when considering the periodic boundary conditions, with equal volumes of lean and stoichiometric mixture. For comparison, the mixture fraction for the premixed flame case is taken to be \(\xi =0.044\), which corresponds to an equivalence ratio \(\phi =0.8\) everywhere in the domain.

All the species mass fractions, temperature and density are initialised as a function of local values of \({c}_{T}\) and \(\xi \) based on tabulated laminar flame simulations. The simulations have been conducted for 2.0 flow through times (i.e. \(2{t}_{fl}=4{L}_{x}/({U}_{\mathrm{jet}}+{U}_{\mathrm{coflow}})\)) and statistics presented in Sect. 4 are evaluated based on the time series after one flow through time when the initial transience has disappeared. The Reynolds and Favre averaged values of a general quantity \(Q\) (i.e. represented by \(\overline{Q }\) and \(\widetilde{Q}=\overline{\rho Q }/\overline{\rho }\), respectively) by time-averaging the quantity in question after one throughpass time.

4 Results and Discussion

4.1 General Behaviours

The instantaneous views of \(c=0.5\) isosurface coloured by local values of equivalence ratio \(\phi \) are shown in Fig. 3a. It can be seen that in the globally back-supported case, the local equivalence ratio on the given \(c\) isosurface decreases as the flame develops in the streamwise direction. By contrast, the flame in the globally front-supported case develops in such a manner that the local equivalence ratio on the \(c=0.5\) isosurface increases in the streamwise direction. The equivalence ratio variation between \(\phi =0.6\) and 1.0 persists on the \(c=0.5\) isosurface for a major part of the flame length in the misaligned scalar gradient case. As expected, the equivalence ratio does not change in the premixed flame case. Due to the periodic boundary conditions in the \(z\) direction, it appears as if the centre of the jet in the misaligned scalar gradient case is fuel-lean as in the back-supported case. However, this is not true as the mixture could be shifted by \({L}_{z}/2\) in the \(z\) direction such that the centre of the jet is stoichiometric. In this scenario, the flame tip would appear on either side of the periodic boundary conditions and would be physically unaffected. The mixture fraction imposed at the inlet \(\xi (z)\) has a consistent wavelength with equal amounts of lean and rich mixture, so there are no biases towards either state.

Fig. 3
figure 3

a Instantaneous views of \(c = 0.5\) isosurface coloured by local equivalence ratio \(\phi\) for globally back-supported, globally front-supported, misaligned gradient stratified flames and premixed flame (1st–4th column). b Distributions of Reynolds averaged reaction progress variable \(\overline{c}\) with the contours of Reynolds averaged equivalence ratio \(\overline{\phi }\) superimposed (solid line: \(\phi = 1.0\), dotted line: \(\phi = 0.87\), dashed line: \(\phi = 0.73\), dash-dot line: \(\phi = 0.6\)) for globally back-supported, globally front-supported, misaligned gradient stratified mixture cases and premixed flame cases (1st–4th column)

Full size image

It can be seen from Fig. 3a that the height of the back-supported and misaligned gradient flames are comparable, and their heights are both greater than the front-supported flame. The height of the premixed flame remains in between the front-supported and back-supported flames. This can further be substantiated from the distributions of the Reynolds-averaged reaction progress variable \(\overline{c }\) in Fig. 3b, where the Reynolds averaged values of equivalence ratio \(\overline{\phi }\) are superimposed. The highest distance of the \(\overline{c }=0.5\) contour from the slot is shown in Fig. 4a, which shows that the tallest flame is obtained for the misaligned case. To explain this behaviour, the variations of the mean values of equivalence ratio \({\langle \phi \rangle }_{f}\) within the flame (i.e. in the region given by \(0.01\le c\le 0.99\)) along the normalised distance from the nozzle inlet \(x/h\), are shown in Fig. 4b. It can be seen that \({\langle \phi \rangle }_{f}\) for the back-supported case starts close to 1.0 at the inlet and decreases with increasing \(x/h\) before settling to a value close to 0.65 for \(x/h\ge 10\). By contrast, \({\langle \phi \rangle }_{f}\) increases from a value close to 0.6 in the vicinity of the inlet before settling to a value close to 0.95 for \(x/h\ge 15\) in the front-supported case. In the misaligned gradient case, \({\langle \phi \rangle }_{f}\approx 0.8\) is maintained close to the inlet but \({\langle \phi \rangle }_{f}\) decreases with increasing \(x/h\) for \(x/h>15\) and eventually reaches \({\langle \phi \rangle }_{f}\approx 0.65\) towards the flame tip. The corresponding probability density functions (PDFs) of \(\phi \) within \(0.01\le c\le 0.99\) are shown in Fig. 4c, which shows the widths of the PDFs decrease in the downstream direction suggesting that combustion progressively takes place in an increasingly homogeneous mixture away from the slot and towards the flame tip. The PDFs of \(\phi \) for the globally back-supported case show that the mean value of \(\phi \) decreases with increasing distance from the nozzle inlet and the same qualitative behaviour is observed for the misaligned scalar gradient case, but this tendency in the misaligned scalar gradient case is weaker than the globally back-supported case. The opposite behaviour is observed for the globally front-supported case where the PDFs of \(\phi \) peak at greater values as the jet develops away from the slot inlet. The aforementioned behaviour of the PDFs of \(\phi \) in Fig. 4c is consistent with the variations of \({\langle \phi \rangle }_{f}\) with \(x/h\) shown in Fig. 4b. The narrowing of \(\phi \) PDFs away from the inlet (see Fig. 4c) is consistent with the levelling of \({\langle \phi \rangle }_{f}\) values away from the slot (see Fig. 4b).

Fig. 4
figure 4

a The highest normalised distance of \(\overline{c} = 0.5\) contour from the slot; b variation of the mean values of equivalence ratio \(\phi_{f}\) within the flame (i.e. in the region given by \(0.01 \le c \le 0.99\)) along the normalised distance from the nozzle inlet \(x/h\); c PDFs of \(\phi\) within \(0.01 \le c \le 0.99\) for different values of \(x/h\)

Full size image

It can be seen from Fig. 4b, c that the flame experiences less reactive mixture than \(\phi =0.8\) for a major part of the flame development for the globally back-supported and misaligned gradient cases which leads to a smaller overall burning rate \({\Omega }_{c,O}={\int }_{V}{\dot{\omega }}_{c}dV\) than the premixed flame case where \(\phi =0.8\). By contrast, a major part of the flame develops in a more reactive mixture than \(\phi =0.8\) in the globally front-supported stratified case and thus \({\Omega }_{c,O}\) assumes greater values than the premixed flame case with \(\phi =0.8\).

It can indeed be verified from Table 1 that \({\Omega }_{c,O}^{+}={\int }_{V}{\dot{\omega }}_{c}dV/\left[{\rho }_{0(\phi =0.8)}{S}_{L(\phi =0.8)}{\delta }_{th(\phi =0.8)}^{2}\right]\) (where the unburned gas density \({\rho }_{0(\phi )}\), laminar flame speed \({S}_{L\left(\phi \right)}\) and thermal flame thickness \({\delta }_{th(\phi )}\) all correspond to the equivalence ratio \(\phi \), and the superscript + indicates a normalised quantity) the stratified globally back-supported and misaligned gradient cases assume smaller values than the corresponding value for the premixed flame case with \(\phi =0.8\). As the mass inflow rate remains comparable for all cases, the higher overall burning rate for the globally front-supported stratified flame gives rise to smaller flame height than the premixed flame. By contrast, the smaller overall burning rate in the stratified globally back-supported and misaligned gradient flames leads to greater flame heights than the premixed flame case. Table 1 also reports the mean equivalence ratio on the \(c=0.5\) isosurface (shown in Fig. 3), \({\langle \phi \rangle }_{c=0.5}\), which shows the same overall trend as \({\Omega }_{c,O}^{+}\). Although the stratified flames have been initialised between \(\phi =0.6\) and \(\phi =1.0\) mixture, it is not guaranteed that the mean equivalence ratio within the flame will be maintained at 0.8. An alternative approach would be to initialise the flames to foster a global flame average of \({\langle \phi \rangle }_{c=0.5}=0.8\). However, flame propagation through stratified mixtures is complex and depends not only on the local values of \(\xi \) but also on the gradient \(\nabla \xi \) and consequently the temperature of the burned gas, and such an approach may impart inconsistencies in these values. This study follows a similar methodology to that of Richardson and Chen (2017).

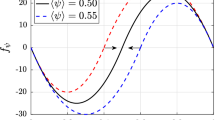
Table 1 Values of the normalised overall burning rate \({\Omega }_{c,O}^{ + } = \mathop \smallint \limits_{V} \dot{\omega }_{c} dV/\left[ {\rho_{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} \delta_{{th\left( {\phi = 0.8} \right)}}^{2} } \right]\) and the mean equivalence ratio on the \(c = 0.5\) isosurface \(\phi_{c = 0.5}\) flame for all cases
Full size table

The variations of time-averaged values of normalised burning rate \({\Omega }_{c}^{+}(x)={\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }\overline{{\dot{\omega } }_{c}} dxdydz/\left[{\rho }_{0(\phi =0.8)}{S}_{L(\phi =0.8)}{\delta }_{th(\phi =0.8)}^{2}\right]\) and normalised flame surface area \({A}_{T}^{+}\left(x\right)={A}_{T}/{\delta }_{th\left(\phi =0.8\right)}^{2}={\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }\overline{|\nabla c|}dxdydz/{\delta }_{th(\phi =0.8)}^{2}\) with \(x/h\) are shown in Fig. 5a, b, respectively with \(\epsilon \) being a small length scale, which is taken to be two times the DNS grid size \(\Delta x\) (i.e. \(\epsilon =2\Delta x\approx 0.04h\)) for this analysis. In the premixed flame case, \({\Omega }_{c}^{+}\) increases mildly until \(x/h \approx 22\) before decreasing and eventually vanishing at around \(x/h \approx 32\). The increase in \({\Omega }_{c}^{+}\) for \(0<x/h <22\) in the premixed case is driven by the increase in flame surface area due to the increased flame wrinkling, which can be substantiated by the increasing trends of \({A}_{T}^{+}\) for \(0<x/h <22\). The flame surface area drops for \(x/h>22\) in the premixed flame case due to the decrease in the area close to the flame tip, which is also reflected by the drop in values of \({\Omega }_{c}^{+}\) in this region. The variations of \({\Omega }_{c}^{+}\) and \({A}_{T}^{+}\) with \(x/h\) for the misaligned gradient stratified flames are qualitatively similar to the premixed flame, but the peak values of \({\Omega }_{c}^{+}\) and \({A}_{T}^{+}\) are obtained closer to the slot (e.g. \(x/h\approx 16\)) than that in the premixed flame. A comparison between Figs. 4 and 5 reveals that \({\Omega }_{c}^{+}\) and \({A}_{T}^{+}\) for the misaligned stratified flame starts to deviate significantly from the premixed flame from \(x/h\approx 16\) where \({\langle \phi \rangle }_{f}\) starts to assume values smaller than 0.8. The flame thickness \({\delta }_{th(\phi )}\) scales with \({\alpha }_{T0}/{S}_{L(\phi )}\) where \({\alpha }_{T0}\) is the unburned gas thermal diffusivity, and the variation of \({\delta }_{th(\phi )}/{\delta }_{th(\phi =1)}\) with \(\phi \) for the present thermochemistry can be found in Fig. 6. Predominance of the relatively less reactive mixture and thereby thicker flame in the misaligned gradient case give rise to smaller \({\Omega }_{c}^{+}\) and \({A}_{T}^{+}\) values than those in the premixed flame case. Figure 5a, b indicate that both \({\Omega }_{c}^{+}\) and \({A}_{T}^{+}\) decrease with increasing \(x/h\) for the globally back-supported flame and these values remain smaller than the corresponding premixed flame values for a major part of the flame because \({\langle \phi \rangle }_{f}\) in the back-supported case remains smaller than \(\phi =0.8\) (see Fig. 4a, b). The predominant availability of less reactive mixture in the globally back-supported flame than in the premixed flame (i.e. \({\langle \phi \rangle }_{f}<0.8\)) leads to smaller values of \({\Omega }_{c}^{+}\) than that found in the premixed flame. Thicker flame elements for the leaner mixtures reduce the likelihood of obtaining high values of \(|\nabla c|\) in the globally back-supported flame when compared to the premixed flame, and as a result, \({A}_{T}^{+}\) assumes smaller values in the back-supported flame than in the premixed flame. By contrast, \({\langle \phi \rangle }_{f}>0.8\) is obtained for a major part of the flame length in the globally front-supported flame and thus the greater availability of more reactive mixture and smaller flame thickness associated with it give rise to higher values of \({\Omega }_{c}^{+}\) and \({A}_{T}^{+}\) than the corresponding values in the premixed flame for a major part of the flame length. The extent of flame wrinkling also determines the magnitudes of \({\Omega }_{c}^{+}\) and \({A}_{T}^{+}\). The extent of flame wrinkling can be quantified in terms of a wrinkling factor defined as \({\Xi }_{v}={\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }\overline{|\nabla c|}dxdydz/{\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }|\nabla \overline{c }|dxdydz\) and its variation in the streamwise distance is shown in Fig. 5c. The data in Fig. 5c is plotted up to the calculated flame height shown in Fig. 2a, beyond which data becomes not representative of the overall flame due to the limited samples. It can be seen from Fig. 5c that \({\Xi }_{v}\) increases with increasing \(x/h\) for all cases and high values are obtained close to the flame tip. However, the peak value of \({\Xi }_{v}\) in the globally front-supported case remains greater than the premixed flame, and the opposite behaviour is observed in the globally back-supported flame. The wrinkling factor \({\Xi }_{v}\) for the misaligned gradient flame is found to increase with increasing \(x/h\) for the region given by \(0<x/h<16\) but \({\Xi }_{v}\) does not change appreciably for \(x/h>16\) and the peak value of \({\Xi }_{v}\) remains comparable to that in the globally back-supported flame. Moreover, the peak value of \({\Xi }_{v}\) is obtained closer to the slot in the globally front-supported flame than in other cases because of the smaller flame height (see Fig. 4a).

Fig. 5
figure 5

Variations of a normalised burning rate \({{\Omega }}_{c}^{ + } \left( x \right) = \mathop \smallint \nolimits_{0}^{{L_{z} }} \mathop \smallint \nolimits_{0}^{{L_{y} }} \mathop \smallint \nolimits_{{x - \varepsilon }}^{{x + \varepsilon}} \overline{{\dot{\omega }_{c} }} dxdydz/\left[ {\rho _{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} \delta _{{th\left( {\phi = 0.8} \right)}}^{2} } \right]\), b normalised flame surface area \( A_{T}^{ + } \left( x \right) = A_{T} /\delta _{{th\left( {\phi = 0.8} \right)}}^{2} = \mathop \smallint \nolimits_{0}^{{L_{z} }} \mathop \smallint \nolimits_{0}^{{L_{y} }} \mathop \smallint \nolimits_{{x - \varepsilon}}^{{x + \varepsilon}} \overline{{\left| {\nabla c} \right|}} dxdydz/\delta _{{th\left( {\phi = 0.8} \right)}}^{2} \), c wrinkling factor \({{\Xi }}_{v} = \mathop \smallint \nolimits_{0}^{{L_{z} }} \mathop \smallint \nolimits_{0}^{{L_{y} }} mathop \smallint \nolimits_{{x - \varepsilon}}^{{x + \varepsilon}} \overline{{\left| {\nabla c} \right|}} dxdydz/\mathop \smallint \nolimits_{0}^{{L_{z} }} \mathop \smallint \nolimits_{0}^{{L_{y} }} \mathop \smallint \nolimits_{{x - \varepsilon}}^{{x + \varepsilon}} \left| {\nabla \bar{c}} \right|dxdydz\), d burning intensity \(I\) with normalised streamwise distance \(x/h\)

Full size image
Fig. 6
figure 6

Variation of the normalised thermal flame thickness \(\delta_{th} /\delta_{{th\left( {\phi = 1} \right)}}\) with \(\phi\) for the present thermochemistry (black ‘x’s) with a fitted spline

Full size image

A comparison of Fig. 5a, b shows that \({A}_{T}^{+}\) values at the slot inlet are close to each other, but \({\Omega }_{c}^{+}\) values close to the inlet are different because of the differences in mixture composition coming through the slot. As the local equivalence ratio changes within the flame, it is important to analyse the consumption rate per unit flame area, which can be quantified with the help of burning intensity \(I\) (Richardson and Chen 2017):

$$I=\frac{{\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }\overline{{\dot{\omega } }_{c}}dxdydz}{{\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }\overline{{\rho }_{0}\left(\xi \right){S}_{L}(\xi )|\nabla c|}dxdydz}$$
(17)

where \({\rho }_{0}\left(\xi \right)\) and \({S}_{L}(\xi )\) are the unburned gas temperature and laminar burning velocity corresponding to local mixture fraction \(\xi \). The variations of local values of \(I\) with \(x/h\) are shown in Fig. 5d up to the calculated flame height, which shows that \(I\) remains close to unity (i.e. \(I\approx 1.0\)) for a major part of the flame length but \(I\) deviates from unity towards the flame tip and assumes a value greater than unity. This is consistent with previous detailed chemistry DNS results by Richardson and Chen (2017).

Using Eq. 13 it is possible to write:

$${\Omega }_{c}+{M}_{D}+{M}_{\xi }=\int_{0}^{{L}_{z}}\int _{0}^{{L}_{y}}\int_{x-\epsilon }^{x+\epsilon }{\overline{\left(\rho {S}_{d}\right)}}_{s}{\Sigma }_{gen} dxdydz$$
(18)

The magnitudes of \({M}_{D}=\int_{0}^{{L}_{z}}\int_{0}^{{L}_{y}}\int_{x-\epsilon }^{x+\epsilon }\overline{\nabla \bullet (\rho D\nabla c)}dxdydz\) and \({M}_{\xi }=\int_{0}^{{L}_{z}}\int_{0}^{{L}_{y}}\int_{x-\epsilon }^{x+\epsilon }\overline{{A }_{\xi }}dxdydz\) are mostly negligible in comparison to \({\Omega }_{c}\) for all cases, which is consistent with previous findings (Malkeson and Chakraborty 2010b; Inanc et al. 2022) for stratified mixture combustion and is not repeated here. The right-hand side of Eq. 18 can further be split using different components of displacement speed as:

$$\int_{0}^{{L}_{z}}\int_{0}^{{L}_{y}}\int_{x-\epsilon }^{x+\epsilon }{\overline{\left(\rho {S}_{d}\right)}}_{s}{\Sigma }_{gen}dxdydz=\int_{0}^{{L}_{z}}\int_{0}^{{L}_{y}}\int_{x-\epsilon }^{x+\epsilon }{\overline{\left({\rho S}_{r}+\rho {S}_{n}+{\rho S}_{t}+{\rho S}_{\xi }\right)}}_{s}{\Sigma }_{gen}dxdydz$$
(19)

where \({S}_{r}={\dot{\omega }}_{c}/\rho |\nabla c|\), \({S}_{n}={\varvec{N}}\cdot \nabla (\rho D{\varvec{N}}\cdot\nabla c)/\rho |\nabla c|\), \({S}_{t}=-2D{\kappa }_{m}\) and \({S}_{\xi }={A}_{\xi }/\rho |\nabla c|\) are the reaction, normal diffusion, tangential diffusion and mixture inhomogeneity contributions to the displacement speed with \({\varvec{N}}=-\nabla c/|\nabla c|\) and \({\kappa }_{m}=0.5\nabla \cdot {\varvec{N}}\) being the local flame normal vector and flame curvature, respectively. According to this definition, the flame curvature \({\kappa }_{m}\) assumes a positive (negative) value when the flame surface is convex (concave) to the reactants. The assumption \({\overline{\left({\rho S}_{r}+{\rho S}_{n}\right)}}_{s}\approx {\overline{{(\rho }_{0}\left(\xi \right){S}_{L}(\xi ))}}_{s}\) allows for the manipulation of Eq. 18 in the following manner:

$$I=\frac{{\Omega }_{c}}{{\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }\overline{{\rho }_{0}\left(\xi \right){S}_{L}(\xi )|\nabla c|}dxdydz}\approx 1.0+\frac{{\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }{\overline{\left({\rho S}_{t}\right)}}_{s}{\Sigma }_{gen}dxdydz}{{\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }\overline{{\rho }_{0}\left(\xi \right){S}_{L}(\xi )|\nabla c|}dxdydz}$$
(20)

The variations of \({\overline{\left({\rho S}_{d}\right)}}_{s}/ {\overline{{(\rho }_{0}\left(\xi \right){S}_{L}(\xi ))}}_{s}\), \({\overline{\left({\rho S}_{r}+{\rho S}_{n}\right)}}_{s}/ {\overline{{(\rho }_{0}\left(\xi \right){S}_{L}(\xi ))}}_{s}\) and \({\overline{\left({\rho S}_{t}\right)}}_{s}/ {\overline{{(\rho }_{0}\left(\xi \right){S}_{L}(\xi ))}}_{s}\) with Favre-averaged reaction progress variable \(\widetilde{c}\) for different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c }=0.5\) contour from the inlet, and the corresponding \(x/h\) values can be extracted from Fig. 4a) are shown in Fig. 7a–c, respectively. It is worth noting the flame heights are significantly different and thus the globally front-supported case does not have any samples if identical values of \(x/h\) are considered for the statistics presented in Fig. 7 and subsequent figures. Therefore, the statistics are presented for 25%, 50%, 75% and 90% of the furthest point of \(\overline{c }=0.5\) contour from the inlet but it is recognised that the flow conditions are likely to be different for different cases, which can be substantiated from Table 2.

Fig. 7
figure 7

Variations of a \(\overline{{\left( {\rho S_{d} } \right)}}_{s} /{ }\overline{{(\rho_{0} \left( \xi \right)S_{L} \left( \xi \right))}}_{s}\), b \(\overline{{\left( {\rho S_{r} + \rho S_{n} } \right)}}_{s} /{ }\overline{{(\rho_{0} \left( \xi \right)S_{L} \left( \xi \right))}}_{s}\) and c \(\overline{{\left( {\rho S_{t} } \right)}}_{s} /{ }\overline{{(\rho_{0} \left( \xi \right)S_{L} \left( \xi \right))}}_{s}\) with Favre-averaged reaction progress variable \(\tilde{c}\) for i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet)

Full size image
Table 2 The normalised distance \(x/h\) from the inlet for 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet
Full size table

4.2 Displacement Speed Statistics

It can be seen from Fig. 7a–c that \({\overline{\left({\rho S}_{r}+{\rho S}_{n}\right)}}_{s}/ {\overline{{(\rho }_{0}\left(\xi \right){S}_{L}(\xi ))}}_{s}\) assumes values close to unity throughout the flame length for all cases and this is also true for \({\overline{\left({\rho S}_{d}\right)}}_{s}\) up to 50% of the flame height, but \({\overline{\left({\rho S}_{d}\right)}}_{s}\) assumes greater values than \({\overline{{(\rho }_{0}\left(\xi \right){S}_{L}(\xi ))}}_{s}\) near the flame tip. This behaviour originates principally because of the positive contribution of \({\overline{\left({\rho S}_{t}\right)}}_{s}/ {\overline{{(\rho }_{0}\left(\xi \right){S}_{L}(\xi ))}}_{s}\) which increases from the slot inlet to the flame tip. The PDFs of normalised curvature \({\kappa }_{m}\times {\delta }_{th(\phi =0.8)}\) of the \(c=0.8\) isosurface at different \(x/h\) values for all cases are shown in Fig. 8. Here, the \(c=0.8\) isosurface is chosen because the maximum heat release rate occurs at this reaction progress variable value but the curvature PDFs for other \(c\) isosurfaces behave qualitatively similar to the results shown in Fig. 8. The curvature PDFs show an almost equal likelihood of obtaining \({\kappa }_{m}>0\) and \({\kappa }_{m}<0\) close to the slot and for a major part of the flame length but the most probable value of \({\kappa }_{m}\) becomes negative and the probability of finding \({\kappa }_{m}<0\) overwhelms that of finding \({\kappa }_{m}>0\) close to the flame tip. This suggests that \({\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }{\overline{\left({\rho S}_{t}\right)}}_{s}{\Sigma }_{gen}dxdydz=-{\int }_{0}^{{L}_{z}}{\int }_{0}^{{L}_{y}}{\int }_{x-\epsilon }^{x+\epsilon }\overline{2\rho D {\kappa }_{m}|\nabla c|} dxdydz\) is expected to yield a positive value close to the flame tip and that gives rise to \(I>1.0\) according to Eq. 20. In the premixed flame case, \(I=1.0\) is indicative of the validity of Damköhler’s first hypothesis but \(I>1.0\) at the flame tip is consistent with previous DNS for Bunsen burner flames (Chakraborty et al. 2019) and experimental findings (e.g. Gulder 2007) involving flames with globally negative flame curvatures.

Fig. 8
figure 8

PDFs of normalised curvature \(\kappa_{m}^{ + } = \kappa_{m} \times \delta_{{th\left( {\phi = 0.8} \right)}}\) of the \(c = 0.8\) isosurface at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for a globally back-supported, b globally front-supported, c misaligned gradient stratified mixture and d premixed flames

Full size image

For quantitative comparison, the variations of \({\overline{\left({\rho S}_{d}\right)}}_{s}^{+}={\overline{\left({\rho S}_{d}\right)}}_{s}/[{\rho }_{0\left(\phi =0.8\right)}{S}_{L\left(\phi =0.8\right)}]\) with \(\widetilde{c}\) for different percentages of flame heights (i.e. 25%, 50%, 75% and 90%) are shown in Fig. 9a, which shows that \({\overline{\left({\rho S}_{d}\right)}}_{s}\) increases from the inlet in the globally front-supported flame due to the availability of a more reactive mixture with increasing distance from the inlet. By contrast, \({\overline{\left({\rho S}_{d}\right)}}_{s}\) decreases from the inlet in the globally back-supported flame before increasing again close to the flame tip. The decrease in \({\overline{\left({\rho S}_{d}\right)}}_{s}\) from the slot in the globally back-supported flame is driven by the availability of an increasingly fuel-lean mixture with \(x/h\). The same qualitative behaviour has been observed for the misaligned scalar gradient flame, but the mixture encountered here is mostly more reactive (i.e., higher values of \({\langle \phi \rangle }_{f}\), see Fig. 4b) than the globally back-supported flame for \(x/h<16\). Thus, \({\overline{\left({\rho S}_{d}\right)}}_{s}\) for the misaligned flame assumes greater values than in the globally back-supported flame up to 50% of the flame height. In order to explain the qualitative similarities between the globally back-supported and misaligned gradient cases, it is worthwhile to consider the percentage contribution of the overall heat release rate locally by the back-supported mode (i.e. \(\mathrm{cos}{\theta }_{c\xi }>0\)) of combustion because local turbulent mixing characteristics can alter the relative alignments of \(\nabla c\) and \(\nabla \xi \) in comparison to the initial distribution. Figure 9b shows that the entire heat release occurs in the back-supported mode for the globally back-supported flame, as expected, but the extent of the back-supported mode of combustion increases in the streamwise direction for the misaligned gradient flame and this increase becomes more prominent for \(x/h>16\) (i.e. \(>50\%\) of the flame height) where the \(\phi >0.8\) mixture is completely consumed and the flame develops into \(\phi <0.8\) mixtures. The local flame wrinkling also induces a locally back-supported mode of heat release close to the flame tip in the globally front-supported flame, but the heat release mostly takes place the under front-supported mode.

Fig. 9
figure 9

a Variations of (a) \(\overline{{\left( {\rho S_{d} } \right)}}_{s}^{ + } = \overline{{\left( {\rho S_{d} } \right)}}_{s} /\left[ {\rho_{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} } \right]{ }\) with \(\tilde{c}\) at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for globally back-supported, globally front-supported, misaligned gradient stratified mixture and premixed flame cases (1st–4th column); b Percentage of heat release rate in back-supported mode with \(x/h\)

Full size image

4.3 Modelling Implications

The distributions of the estimated values of local Karlovitz number \(K{a}_{L}={S}_{L}{\left(\widetilde{\xi }\right)}^{-3/2}{\left[\widetilde{\varepsilon }{\delta }_{th}\left(\widetilde{\xi }\right)\right]}^{1/2}\) and local Damköhler number \(D{a}_{L}=\widetilde{k}{S}_{L}(\widetilde{\xi })/\widetilde{\varepsilon }{\delta }_{th}(\widetilde{\xi })\) within \(0.1\le \widetilde{c}\le 0.9\) are shown in Fig. 10a, b, respectively. It can be seen from Fig. 10a, b that \(K{a}_{L}\) remains greater than unity throughout the flame brush for all cases. Figure 10b shows that \(D{a}_{L}\) remains smaller than unity close to the inlet for all cases. For the premixed and globally back-supported cases, \(D{a}_{L}\) assumes values greater than unity towards the burned gas side of the flame brush from 50% to 100% of their heights. This behaviour is obtained at 50% of the flame height for the globally misaligned case but \(D{a}_{L}\) remains mostly smaller than unity both close to the nozzle inlet and flame tip. In the premixed, globally back-supported and globally front-supported flames, \(K{a}_{L}\) decreases and \(D{a}_{L}\) rise with increasing flame height but an opposite trend is observed for the misaligned case for the latter half of the flame length towards the flame tip (i.e. \(x/h>16\)). This is due to the combination of decreasing \({S}_{L}(\widetilde{\xi })\) and increasing \({\delta }_{th}(\widetilde{\xi })\) with streamwise distance because of the greater availability of mixture leaner than \(\phi =0.8\). The values of \({Ka}_{L}\) and \(D{a}_{L}\) observed in Fig. 10 are representative of the thin reaction zones regime of combustion (Peters 2000) throughout the flame brush. This has implications for the modelling of the mean reaction rate in stratified combustion in this configuration. Thus, it is worthwhile to consider the validity of the combustion modelling methodologies based on flamelet assumption, such as Flame Surface Density (FSD) (Vervisch et al. 2011) and Scalar Dissipation Rate (SDR) (Chakraborty et al. 2011) based mean reaction rate \(\overline{{\dot{\omega } }_{c}}\) closures.

Fig. 10
figure 10

Variations of the estimated values of a local Karlovitz number \(Ka_{L} = S_{L} \left( {\tilde{\xi }} \right)^{ - 3/2} \left[ {\tilde{\varepsilon }\delta_{th} \left( {\tilde{\xi }} \right)} \right]^{1/2}\) and b local Damköhler number \(Da_{L} = \tilde{k}S_{L} \left( {\tilde{\xi }} \right)/\tilde{\varepsilon }\delta_{th} \left( {\tilde{\xi }} \right)\) within \(0.1 \le \tilde{c} \le 0.9\) with \(\tilde{c}\) at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for globally back-supported, globally front-supported, misaligned gradient stratified mixture and premixed flames (1st–4th row)

Full size image

According to the FSD-based closure \(\overline{{\dot{\omega } }_{c}}\) is modelled using Eq. 13 and \({\overline{\left({\rho S}_{d}\right)}}_{s}\) is often modelled as \({\overline{\left({\rho S}_{d}\right)}}_{s}\approx {\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}(\widetilde{\xi })\) [28,30]. For RANS, \(\overline{{\dot{\omega } }_{c}}\gg \overline{\nabla \cdot \left(\rho D\nabla c\right)}\) is assumed and \(\overline{{A }_{\xi }}\) for fuel-lean/stoichiometric mixture is usually modelled as (Marincola et al. 2013; Proch and Kempf et al. 2014):

$$\overline{{A }_{\xi }}=2\overline{\left[\rho D\frac{(\nabla c\cdot \nabla \xi )}{\xi }\right]}=2\overline{\rho }\widetilde{D}\nabla \widetilde{c}\cdot \nabla \widetilde{\xi }/\widetilde{\xi }$$
(22)

In the context of SDR-based closure, \(\overline{{\dot{\omega } }_{c}}\) is modelled for \(D{a}_{L}\gg 1\) in the following manner (Bray 1980):

$$\overline{{\dot{\omega } }_{c}}=2\overline{\rho }{\widetilde{N}}_{c}/(2{c}_{m}-1)$$
(23)

where \({\widetilde{N}}_{c}=\overline{\rho D\nabla c\bullet \nabla c }/\overline{\rho }\) is the Favre-averaged SDR and \({c}_{m}\) is a thermochemical parameter, which is given as (Bray 1980):

$${c}_{m}={\int }_{0}^{1}[\dot{{\omega }}_{c}c{]}_{L}f\left(c\right)dc/{\int }_{0}^{1}[{\dot{\omega }}_{c}{]}_{L}f\left(c\right)dc$$
(24)

Here the subscript ‘L’ refers to the laminar flame value for a given mixture fraction \(\xi \) and \(f\left(c\right)\) represents the burning mode PDF. Bray (1980) demonstrated that any continuous function of \(c\) should suffice for the evaluation of \({c}_{m}\) for premixed flames. It is worth noting that \({c}_{m}\) depends on the mixture composition and thus depends on mixture fraction (i.e. \({c}_{m}=f(\xi )\)). Although Eq. 23 was originally proposed for \(K{a}_{L}<1\) and \(D{a}_{L}>1\) (Bray et al. 1980), it was shown by Chakraborty and Cant (2011) that this relation remains valid in the thin reaction zones regime for premixed flames with moderate values of\(K{a}_{L}\). However, in order to apply Eq. 23 for the mean reaction rate closure in turbulent stratified mixture combustion (e.g. Butz et al. 2015), \({c}_{m}\) needs to be approximated based on the local value of \(\widetilde{\xi }\) (i.e.\({c}_{m}=f(\widetilde{\xi })\)) and this gives rise to uncertainties in the prediction of \(\overline{{\dot{\omega } }_{c}}\) using Eq. 23 in turbulent stratified flames. The variations of \({\left\{\overline{{\dot{\omega } }_{c}}\right\}}^{+}, {\left\{\overline{\nabla \cdot \left(\rho D\nabla c\right)}\right\}}^{+}, {\left\{\overline{{A }_{\xi }}\right\}}^{+}=\left\{\overline{{\dot{\omega } }_{c}} , \overline{\nabla \cdot \left(\rho D\nabla c\right)}, \overline{{A }_{\xi }}\right\}\times {\delta }_{th\left(\phi =0.8\right)}/[{\rho }_{0\left(\phi =0.8\right)}{S}_{L\left(\phi =0.8\right)}]\) with \(\widetilde{c}\) for different percentages of flame heights (i.e. 25%, 50%, 75% and 90%) are shown in Fig. 11. Figure 11 shows that \(\overline{\nabla \cdot \left(\rho D\nabla c\right)}\) assumes comparable magnitudes of \(\overline{{\dot{\omega } }_{c}}\) close to the nozzle (e.g., at 25% of the flame height) where the extent of flame wrinkling remains small (see Fig. 5c) but the magnitudes of \(\overline{\nabla \cdot \left(\rho D\nabla c\right)}\) in comparison to the magnitudes of \(\overline{{\dot{\omega } }_{c}}\) decreases progressively with increasing \(x/h\). Moderate values of the Reynolds number for these cases contribute to the non-negligible magnitude of \(\overline{\nabla \cdot \left(\rho D\nabla c\right)}\) in comparison to \(\overline{{\dot{\omega } }_{c}}\). As the Reynolds number increases, the contribution of \(\overline{\nabla \cdot \left(\rho D\nabla c\right)}\) in comparison with \(\overline{{\dot{\omega }}_{c}}\) becomes negligible away from the inlet as the reaction rate is augmented by increased flame wrinkling (Bray 1990). It can be seen from Fig. 11 that the magnitudes of \(\overline{{A }_{\xi }}\) remain small in comparison to those of \(\overline{{\dot{\omega } }_{c}}\) and \(\overline{\nabla \cdot \left(\rho D\nabla c\right)}\) at all locations.

Fig. 11
figure 11

Variations of \(\left\{ {\overline{{\dot{\omega }_{c} }} } \right\}^{ + } , \left\{ {\overline{{\nabla \cdot \left( {\rho D\nabla c} \right)}} } \right\}^{ + } , \left\{ {\overline{{A_{\xi } }} } \right\}^{ + } = \left\{ {\overline{{\dot{\omega }_{c} }} , \overline{{\nabla \cdot \left( {\rho D\nabla c} \right)}} , \overline{{A_{\xi } }} } \right\} \times \delta_{{th\left( {\phi = 0.8} \right)}} /\left[ {\rho_{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} } \right]\) with \(\tilde{c}\) at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for globally back-supported, globally front-supported, misaligned gradient stratified mixture and premixed flames (1st–4th column)

Full size image

The predictions of FSD and scalar dissipation rate based mean reaction rate closures (i.e. \({\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}\left(\widetilde{\xi }\right){\Sigma }_{\mathrm{gen}}\) and \(2\overline{\rho }{\widetilde{N}}_{c}/(2{c}_{m}-1)\)) are compared to \(\overline{{\dot{\omega } }_{c}}\) extracted from DNS data in Fig. 12. It can be seen from Fig. 12 that both \({\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}\left(\widetilde{\xi }\right){\Sigma }_{\mathrm{gen}}\) and \(2\overline{\rho }{\widetilde{N}}_{c}/(2{c}_{m}-1)\)) do not adequately capture the qualitative behaviour of \(\overline{{\dot{\omega } }_{c}}\) close to the nozzle inlet (e.g. 25% of the flame height). The qualitative agreement between \(\overline{{\dot{\omega } }_{c}}\) and \({\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}\left(\widetilde{\xi }\right){\Sigma }_{\mathrm{gen}}\) improves with increasing distance from the nozzle inlet. It can be seen from Eq. 13\({\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}\left(\widetilde{\xi }\right){\Sigma }_{\mathrm{gen}}\) is supposed to model \(\overline{{\dot{\omega } }_{c}}+\overline{\nabla \cdot \left(\rho D\nabla c\right)}+\overline{{A }_{\xi }}\) subject to the assumption of \({\overline{\left({\rho S}_{d}\right)}}_{s}\approx {\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}(\widetilde{\xi })\). It can be seen from Fig. 11 that \(\overline{{A }_{\xi }}\) is negligible in comparison to \(\overline{{\dot{\omega } }_{c}}\). The size of \(\overline{\nabla \cdot (\rho D\nabla c)}\) is often small in comparison to \(\overline{{\dot{\omega }}_{c}}\), but it can be seen from Fig. 11 that this is only realised away from the nozzle (e.g. 75% and 90% of the flame height) and thus, \({\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}\left(\widetilde{\xi }\right){\Sigma }_{\mathrm{gen}}\) does not predict the qualitative behaviour of \(\overline{{\dot{\omega } }_{c}}\) (but captures the qualitative behaviour of \(\overline{{\dot{\omega } }_{c}}+\overline{\nabla \cdot \left(\rho D\nabla c\right)}+\overline{{A }_{\xi }}\), not shown for brevity) close to the inlet (e.g. 25% of the flame height). The qualitative behaviour of \(\overline{{\dot{\omega } }_{c}}\) is captured by \({\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}\left(\widetilde{\xi }\right){\Sigma }_{\mathrm{gen}}\) for 75% and 90% flame height locations but there are quantitative discrepancies. These discrepancies partially originate due to the small but non-negligible values of \(\overline{\nabla \cdot \left(\rho D\nabla c\right)}\) and also due to limitations of the assumption \({\overline{\left({\rho S}_{d}\right)}}_{s}\approx {\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}(\widetilde{\xi })\), which was reported previously for turbulent premixed flames (Sabelnikov et al. 2017; Papapostolou et al. 2019; Varma et al. 2022). Moreover, \(I\) is implicitly assumed to be unity when the assumption \({\overline{\left({\rho S}_{d}\right)}}_{s}\approx {\rho }_{0}\left(\widetilde{\xi }\right){S}_{L}(\widetilde{\xi })\) is invoked but this assumption is not valid close to the flame tip due to \(I>1\) (see Fig. 5c).

Fig. 12
figure 12

Variations of a \(\left\{ {\overline{{\dot{\omega }_{c} }} } \right\}^{ + } = \overline{{\dot{\omega }_{c} }} \times \delta_{{th\left( {\phi = 0.8} \right)}} /\left[ {\rho_{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} } \right]\) (broken line) and \( \left\{ {\rho_{0} \left( {\tilde{\xi }} \right)S_{L} \left( {\tilde{\xi }} \right){\Sigma }_{{{\text{gen}}}} } \right\}^{ + } = \rho_{0} \left( {\tilde{\xi }} \right)S_{L} \left( {\tilde{\xi }} \right){\Sigma }_{{{\text{gen}}}} \times \delta_{{th\left( {\phi = 0.8} \right)}} /\left[ {\rho_{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} } \right]\) (line with symbols), b \(\left\{ {\overline{{\dot{\omega }_{c} }} } \right\}^{ + } = \overline{{\dot{\omega }_{c} }} \times \delta_{{th\left( {\phi = 0.8} \right)}} /\left[ {\rho_{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} } \right]\) (broken line) and \( \left\{ {2\overline{\rho }\tilde{N}_{c} /\left( {2c_{m} - 1} \right)} \right\}^{ + } = 2\overline{\rho }\tilde{N}_{c} /\left( {2c_{m} - 1} \right) \times \delta_{{th\left( {\phi = 0.8} \right)}} /\left[ {\rho_{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} } \right]\) (line with symbols) with \(\tilde{c}\) at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for globally back-supported, globally front-supported, misaligned gradient stratified mixture and premixed flames (1st–4th column)

Full size image

The model given by Eq. 13 was originally proposed for turbulent conditions with highly wrinkled flames (Bray 1980; Chakraborty et al. 2011) but all the flames retain quasi-laminar structure with a reduced level of flame wrinkling (see Fig. 5c) and thus these models do not adequately capture \(\overline{{\dot{\omega } }_{c}}\) extracted from DNS data close to the inlet. However, \(2\overline{\rho }{\widetilde{N}}_{c}/(2{c}_{m}-1)\) satisfactorily captures both the qualitative and quantitative behaviours of \(\overline{{\dot{\omega } }_{c}}\) for 50%, 75% and 90% of the flame heights for all cases.

The variations of \(\left\{\overline{{A }_{\xi }} ,2\overline{\rho }\widetilde{D}\nabla \widetilde{c}\cdot \nabla \widetilde{\xi }/\widetilde{\xi } \right\}\times {\delta }_{th\left(\phi =0.8\right)}/[{\rho }_{0\left(\phi =0.8\right)}{S}_{L\left(\phi =0.8\right)}]\) with \(\widetilde{c}\) at different percentages of flame heights (i.e. 25%, 50%, 75% and 90%) are shown in Fig. 13. Figure 13 shows that \(\overline{{A }_{\xi }}\) exhibits positive values for the globally back-supported flame (where \(\mathrm{cos}{\theta }_{c\xi }>0\)), whereas negative values are obtained for the globally front-supported flame (where \(\mathrm{cos}{\theta }_{c\xi }<0\)). In the misaligned gradient flame, \(\overline{{A }_{\xi }}\) remains small close to the slot but becomes positive in the downstream which is consistent with previous findings based on Fig. 9. It can further be seen from Fig. 13 that \(2\overline{\rho }\widetilde{D}\nabla \widetilde{c}\cdot \nabla \widetilde{\xi }/\widetilde{\xi }\) captures the correct qualitative trend of \(\overline{{A }_{\xi }}\) but exhibits quantitative discrepancies. As the magnitudes of \(\overline{{A }_{\xi }}\) and \(2\overline{\rho }\widetilde{D}\nabla \widetilde{c}\bullet \nabla \widetilde{\xi }/\widetilde{\xi }\) remain much smaller than \(\overline{{\dot{\omega } }_{c}}\) (see Fig. 11), the quantitative discrepancies between \(\overline{{A }_{\xi }}\) and \(2\overline{\rho }\widetilde{D}\nabla \widetilde{c}\cdot \nabla \widetilde{\xi }/\widetilde{\xi }\) are unlikely to affect RANS simulation predictions.

Fig. 13
figure 13

Variations of \(\left\{ {\overline{{A_{\xi } }} ,2\overline{\rho }\tilde{D}\nabla \tilde{c} \cdot \nabla \tilde{\xi }/\tilde{\xi } } \right\} \times \delta_{{th\left( {\phi = 0.8} \right)}} /\left[ {\rho_{{0\left( {\phi = 0.8} \right)}} S_{{L\left( {\phi = 0.8} \right)}} } \right]{ }\) with \(\tilde{c}\) at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for globally back-supported, globally front-supported and misaligned gradient stratified flames (1st–3rd column)

Full size image

It is also possible to model \(\overline{{\dot{\omega }_{c} }}\) based on a tabulated chemistry approach under the flamelet assumption (Proch et al. 2017a,b; Inanc et al. 2022; De Swart et al. 2010; Darbyshire and Swaminathan 2012):

$$ \overline{{\dot{\omega }_{c} }} = \mathop \smallint \limits_{0}^{1} \mathop \smallint \limits_{0}^{1} \left[ {\dot{\omega }_{c} \left( {c,\xi } \right)} \right]_{{{\text{Tab}}}} P\left( {c,\xi } \right)dcd\xi $$
(25)

where \(\left[ {\dot{\omega }_{c} \left( {c,\xi } \right)} \right]_{{{\text{Tab}}}}\) is the tabulated value of reaction rate and \(P\left( {c,\xi } \right)\) is the joint probability density function of reaction progress variable and mixture fraction. The contours of the joint PDFs of \(P\left( {c,\xi } \right)\) for \(\tilde{c} = 0.5\) at different locations are exemplarily shown in Fig. 14, and the same qualitative behaviour is observed for other values of \(\tilde{c}\). It can be seen from Fig. 14 that a positive (negative) correlation is observed in the globally back-supported (front-supported) case, but this correlation weakens with increasing streamwise distance as the variation of \(\xi\) weakens with increasing \(x/h\) (see Fig. 4). By contrast, the correlation between \(c\) and \(\xi\) remains weakly positive close to the inlet due to the configuration in the misaligned case but this positive correlation strengthens with increasing streamwise distance as this case shows predominantly back-supported behaviour away from the inlet (see Fig. 9b). The correlations between \(c\) and \(\xi\) are reflected in the non-zero values of \(\widetilde{c^{\prime\prime}\xi ^{\prime\prime}}\), which can be substantiated from Fig. 15 where the variations of \(\widetilde{c^{\prime\prime}\xi ^{\prime\prime}}\) with \(\tilde{c}\) are shown at different streamwise distances. There have been attempts to model the joint PDFs of \(P\left( {c,\xi } \right)\) by different approaches which involved approximating the marginal PDFs of \(c\) and \(\xi\) by presumed functions and also the modelling of \(\widetilde{c^{\prime\prime}\xi ^{\prime\prime}}\). Usually, marginal Favre-PDFs of \(c\) and \(\xi\) are often modelled by presumed \(\beta\)-PDF (Poinsot and Veynante, 2001; Darbyshire and Swaminathan 2012), which is given by:

$$ \tilde{P}\left( q \right) = \frac{{\Gamma \left( {a + b} \right)}}{{\Gamma \left( a \right)\Gamma \left( b \right)}}~q^{{a - 1}} \left( {1 - q} \right)^{{b - 1}} $$
(26i)

where \(\Gamma \left( x \right) = \mathop \smallint \limits_{0}^{\infty } e^{{ - t}} t^{{x - 1}} dt\) is the gamma function and \(a\) and \(b\) are defined as (Poinsot and Veynante 2005; Darbyshire and Swaminathan 2012):

$$ a = { }\tilde{q}\left[ {\tilde{q}{ }\left( {1 - \tilde{q}} \right)/\widetilde{{q^{{\prime\prime}{2}} }}{ } - 1} \right]; \, b = { }a/\tilde{q}{ } - a $$
(26ii)

where \(q\) is the variable in question, which can be \(c\) and \(\xi\), as applicable. It can be seen from Fig. 16 that the presumed \(\beta\)-PDF mostly captures the qualitative behaviour of the Favre-PDFs of \(c\) and \(\xi\) reasonably well for back-supported and front-supported cases but the quantitative agreement is relatively better for mixture fraction PDFs. Figure 16 shows that the presumed \(\beta -\) PDF does not adequately capture the qualitative behaviour of the PDF of mixture fraction close to the inlet for the misaligned gradient case but both the qualitative and quantitative agreement between \(\tilde{P}\left( \xi \right)\) and \(\beta -\) PDF improves in the downstream direction.

Fig. 14
figure 14

Joint PDFs \(P\left( {c,\xi } \right)\) for \(\tilde{c} = 0.5\) at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% (1st–4th row) of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for globally back-supported, globally front-supported, misaligned gradient stratified flames (1st–3rd column)

Full size image
Fig. 15
figure 15

Variations of \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}}\) and \(\nabla \tilde{c} \cdot \nabla \tilde{\xi }/\left[ {\left| {\nabla \tilde{c}} \right|\left| {\nabla \tilde{\xi }} \right|} \right]\sqrt {\widetilde{{c^{{{^{\prime\prime}}2}} }}} \sqrt {\widetilde{{\xi^{{{^{\prime\prime}}2}} }}}\) (‘model’ in the figure legend) with \(\tilde{c}\) at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for globally back-supported, front-supported, misaligned gradient stratified flames (1st–3rd column)

Full size image
Fig. 16
figure 16

Favre-PDFs of a \(c\) and b \(\xi\) for \(\tilde{c} = 0.3\), 0.5 and 0.7 at different percentages of flame heights (i.e. 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) alongside the predictions of the presumed \(\beta -\) PDF

Full size image

It is worth noting that the predictions of the presumed \(\beta\)-PDF depend on the evaluations of \(a\) and \(b\) which involve scalar variances (i.e. \(\widetilde{{c^{{\prime\prime}{2}} }}\) and \(\widetilde{{\xi^{^{\prime\prime}2} }}\)), which are unclosed quantities and thus need closures. For high Damköhler number values (i.e. \(Da_{L} \gg 1\)), \(\widetilde{{c^{{\prime\prime}{2}} }}\) can be approximated as \(\widetilde{{c^{{\prime\prime}{2}} }} = \tilde{c}{ }\left( {1 - \tilde{c}} \right) + O\left( {\gamma_{c} } \right)\) in the context of Bray-Moss-Libby (BML) modelling where the PDF of \(c\) is approximated by a bimodal distribution with impulses at \(c = 0\) and \(c = 1.0\) (Bray et al. 1985). The contribution \({\text{O}}\left( {\gamma_{c} } \right)\) arises due to the burning mixture from the interior of the flame. Moreover, the departure of \(\widetilde{{c^{{\prime\prime}{2}} }}\) from \(\tilde{c}{ }\left( {1 - \tilde{c}} \right)\) provides a measure of the deviation of the reaction progress variable PDF from a bimodal distribution. The variations of \(\widetilde{{c^{^{\prime\prime}2} }}\) and \(\tilde{c}\left( {1 - \tilde{c}} \right)\) with \(\tilde{c}\) for different streamwise distances are shown in Fig. 17. Figure 17 shows that \(\widetilde{{c^{^{\prime\prime}2} }}\) remains smaller than \(\tilde{c}\left( {1 - \tilde{c}} \right)\) at all locations for all cases, which suggests that \(Da_{L}\) values are not large enough to approximate the PDF of \(c\) by a bimodal distribution. Moreover, \(\widetilde{{c^{^{\prime\prime}2} }}\) values remain particularly small close to the inlet due to the limited extent of reaction progress variable fluctuation as a result of weak flame wrinkling in this region (see Fig. 5c). A similar behaviour was reported by Rasool et al. (2022) for turbulent premixed Bunsen burner flames. The findings from Fig. 17 indicate that \(\widetilde{{c^{^{\prime\prime}2} }} = \tilde{c}{ }\left( {1 - \tilde{c}} \right)\) cannot be used for the closure of \(\widetilde{{c^{^{\prime\prime}2} }},\) and it is necessary to solve a modelled transport equation for \(\widetilde{{c^{^{\prime\prime}2} }} \) alongside a modelled transport equation of \(\widetilde{{\xi^{^{\prime\prime}2} }}.\) However, this approach needs closures of scalar dissipation rates \(\tilde{N}_{c} = \overline{\rho D\nabla c \cdot \nabla c} /\overline{\rho }\) and \(\tilde{N}_{\xi } = \overline{\rho D\nabla \xi \cdot \nabla \xi } /\overline{\rho }\), which have been discussed elsewhere for turbulent stratified mixture combustion (Mura et al. 2007; Malkeson and Chakraborty 2010b; 2011a) and these aspects are kept beyond the scope of the current analysis.

Fig. 17
figure 17

Variations of \(\widetilde{{c^{{\prime\prime}{2}} }}\) and \(\tilde{c}\left( {1 - \tilde{c}} \right)\) with \(\tilde{c}\) at different percentages of flame heights (i.e., 25%, 50%, 75% and 90% of the furthest point of \(\overline{c} = 0.5\) contour from the inlet) for the globally back-supported, front-supported, misaligned gradient stratified mixture and premixed flames (1st–4th column)

Full size image

The modelling of the joint PDF \(P\left( {c,\xi } \right)\) with correlations either by correlated \(\beta\)-PDFs or by copula (Darbyshire and Swaminathan 2012) also needs the closure of \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}}\). Ribert et al. (2005) proposed a model for \(\widetilde{{Y_{F}^{^{\prime\prime}} \xi ^{\prime\prime}}} = \sqrt {\widetilde{{Y_{F}^{^{\prime\prime}2} }}} \sqrt {\widetilde{{\xi^{^{\prime\prime}2} }}}\) in the context of the Libby-Williams (2000) model for partially premixed combustion and following this methodology, a model for \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}}\) can be considered in the following manner:

$$ \widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}} = \sqrt {\widetilde{{c^{^{\prime\prime}2} }}} \sqrt {\widetilde{{\xi^{^{\prime\prime}2} }}} $$
(27)

However, it is impossible to capture negative values of \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}}\) for the globally front-supported case (see Fig. 14) using \(\sqrt {\widetilde{{c^{^{\prime\prime}2} }}} \sqrt {\widetilde{{\xi^{^{\prime\prime}2} }}}\) although the correct qualitative behaviour of \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}}\) can be captured using Eq. 27 in the globally back-supported and the misaligned gradient cases.

In order to capture the correct sign and qualitative behaviour of \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}}\), Eq. 27 can be modified in the following manner:

$$ \widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}} = \frac{{\nabla \tilde{c} \cdot \nabla \tilde{\xi }}}{{\left| {\nabla \tilde{c}} \right||\nabla \widetilde{\xi |}}}\sqrt {\widetilde{{c^{^{\prime\prime}2} }}} \sqrt {\widetilde{{\xi^{^{\prime\prime}2} }}} $$
(28)

It can indeed be seen from Fig. 14 that the prediction of Eq. 28 captures the correct sign of \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}}\) but overpredicts its magnitude, and this overprediction arises due to the correlation between the reaction progress variable and mixture fraction fluctuations, which is ignored in the algebraic closures given by Eqs. 27 and 28. Thus, a modelled transport equation of \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}} \) may need to be solved in RANS simulations of turbulent stratified mixture combustion. This approach also necessitates a closure for the cross-scalar dissipation rate \(\widetilde{{N_{c\xi } }} = \overline{\rho D\nabla c \cdot \nabla \xi } /\overline{\rho }\), which is addressed elsewhere (Brearley et al. 2022; Inanc et al. 2022) and thus is not discussed here.

The results presented in Figs. 11, 12, 13, 14, 15, 16, 17 reveal that the global nature of mixture stratification does not have a major influence on the performance of the mean reaction rate closures, and parameterisation of marginal PDFs of scalars. However, the influence of the global nature of stratification on the closures of variances (i.e. \(\widetilde{{c^{{\prime\prime}{2}} }}{ }\) and \(\widetilde{{\xi^{^{\prime\prime}2} }}\)), co-variance (i.e. \(\widetilde{{c^{\prime\prime}\xi ^{\prime\prime}}}\)) and the terms related to scalar gradients (e.g. \({\Sigma }_{gen} ,\widetilde{{N_{c} }}\), \(\widetilde{{N_{\xi } }}\) and \(\widetilde{{N_{c\xi } }}\)) need to be ascertained, which will be addressed in future investigations.

5 Conclusions

The effects of the global nature of mixture stratification on flame properties (e.g. flame surface area, flame height, flame wrinkling and flame brush thickness) and overall burning rate (along with its modelling in the context of RANS) in a turbulent slot jet configuration have been analysed based on three-dimensional Direct Numerical Simulations where the chemistry is simplified by a two-step mechanism for CH4-air combustion calibrated to yield the correct laminar burning velocity variation with equivalence ratio. Three different configurations representative of globally back-supported (where the gradients of reaction progress variable and mixture fraction are in the same direction), globally front-supported (where the gradients of reaction progress variable and mixture fraction are in opposite directions) and misaligned gradients (where the gradients of reaction progress variable and mixture fraction are in perpendicular directions) have been considered with equivalence ratio ranging from 0.6 to 1.0. Moreover, a premixed flame corresponding to the equivalence ratio of 0.8 (which is the arithmetic mean of maximum and minimum equivalence ratio values for the stratified cases) has also been simulated for the sake of comparison. It has been found that the globally front-supported case exhibits the smallest flame height. The flame heights for the globally back-supported and misaligned gradient cases remain comparable and greater than the length of the premixed flame case. This behaviour has been explained in terms of the mean equivalence ratio within the flame during the flame development in the streamwise direction. It has been found that the mean equivalence ratio within the flame for the back-supported case starts close to 1.0 at the inlet and decreases with increasing streamwise distance before settling to a value close to 0.65. By contrast, the mean equivalence ratio within the flame increases from a value close to 0.6 close to the inlet before settling to a value close to 0.95 in the front-supported case. In the misaligned gradient case, the mean equivalence ratio within the flame remains about 0.8 close to the inlet but eventually decays and reaches 0.65 close to the flame tip. The aforementioned equivalence ratio variations lead to the highest value of volume-integrated reaction rate for the front-supported case, whereas this value remains comparable for the back-supported and misaligned gradient cases but the overall burning rates for these cases are found to be smaller than the premixed flame case. Variations in the mixture composition within the flame lead to significant differences with the evolutions of the flame area and flame wrinkling in the streamwise direction. The highest flame wrinkling is obtained for the globally front-supported case, whereas the smallest value is obtained in the back-supported case. The burning intensity is unity for a major part of the flame length, but it assumes values greater than unity close to the flame tip where the flame curvature effects become strong. This behaviour has been explained using the surface averaged values of different components of density-weighted displacement speed. All cases predominantly exhibit the premixed mode of combustion, which occurs locally in the back-supported (front-supported) mode for the globally back-supported (front-supported) case, but the combustion in the misaligned gradient case shows predominantly back-supported behaviour. The combustion process in all cases represents high values of Damköhler number away from the slot, and Karlovitz number values for all cases remain marginally greater than unity. Thus, the flamelet assumption is expected to hold for these cases. Therefore, the FSD and SDR-based mean reaction rate closures, which were originally proposed for premixed turbulent combustion under flamelet assumption, have been assessed for turbulent stratified mixture combustion. It has been found that the closure of surface averaged density-weighted displacement speed plays a key role in the accuracy of the FSD closure, whereas the uncertainty in terms of parameterisation of the thermochemical parameter in the SDR-based reaction rate closure is crucial for the accuracy of the mean reaction rate closure in turbulent stratified mixture combustion. The cross-scalar dissipation rate contribution to the Favre-averaged reaction progress variable transport is found to be negligible in comparison to the mean reaction rate term and the modelling inaccuracy in evaluating the cross-scalar dissipation rate contribution is unlikely to affect the performance of RANS simulations. The reaction progress variance for all cases has been found to exhibit significant departures from the algebraic expression obtained from the BML analysis (Bray et al. 1985) even where the local Damköhler number values remain greater than unity. Therefore, modelled transport equations for scalar variances in RANS/LES will be needed even when the local Damköhler number is greater than unity for turbulent stratified mixture combustion. It has been found that \(\beta\)-PDF parameterisation is reasonably successful in capturing marginal PDFs of both reaction progress variable and mixture fraction. Moreover, the joint PDFs of the reaction progress variable and mixture fraction exhibit correlations to yield non-zero covariance, and algebraic closures of covariance in terms of the product of the square roots of variances of reaction progress variable and mixture fraction are not sufficiently accurate. Thus, an improved closure of covariance is necessary for accurate parameterisation of the joint PDF of the reaction progress variable and mixture fraction. The present simulation results suggest that the global nature of mixture stratification does not have a major effect on the performance of the mean reaction rate closures, and parameterisation of marginal PDFs of scalars. However, the influence of the global nature of stratification on the closures of variances, covariance, scalar dissipation rate and cross-scalar dissipation rate needs to be ascertained, which will the basis of future investigations.