Scalar Forcing Methodology for Direct Numerical Simulations of Turbulent Stratified Mixture Combustion

Abstract

Scalar forcing in the context of turbulent stratified flame simulations aims to maintain the fuel-air inhomogeneity in the unburned gas. With scalar forcing, stratified flame simulations have the potential to reach a statistically stationary state with a prescribed mixture fraction distribution and root-mean-square value in the unburned gas, irrespective of the turbulence intensity. The applicability of scalar forcing for Direct Numerical Simulations of stratified mixture combustion is assessed by considering a recently developed scalar forcing scheme, known as the reaction analogy method, applied to both passive scalar mixing and the imperfectly mixed unburned reactants of statistically planar stratified flames under low Mach number conditions. The newly developed method enables statistically symmetric scalar distributions between bell-shaped and bimodal to be maintained without any significant departure from the specified bounds of the scalar. Moreover, the performance of the newly proposed scalar forcing methodology has been assessed for a range of different velocity forcing schemes (Lundgren forcing and modified bandwidth forcing) and also without any velocity forcing. It has been found that the scalar forcing scheme has no adverse impact on flame-turbulence interaction and it only maintains the prescribed root-mean-square value of the scalar fluctuation, and its distribution. The scalar integral length scale evolution is shown to be unaffected by the scalar forcing scheme studied in this paper. Thus, the scalar forcing scheme has a high potential to provide a valuable computational tool to enable analysis of the effects of unburned mixture stratification on turbulent flame dynamics.

1 Introduction

Direct Numerical Simulations (DNS) often use numerical velocity forcing schemes (Eswaran and Pope 1988a; Alvelius 1999; Lundgren 2003; Klein et al. 2017) in order to maintain the root-mean-square (rms) value of the turbulent velocity field and obtain a statistically stationary state. This forcing, when applied to DNS of turbulent reacting flows, enables the analysis of flame-turbulence interaction under sustained turbulent conditions, which is not possible under decaying turbulence. Moreover, in the absence of any inherent turbulence generation mechanism, the forcing of the turbulent velocity field enables turbulent premixed flames to reach a statistically stationary state in a ‘flame in a box’ type canonical configuration. This leads to well-grounded scientific conclusions resulting from converged statistics achieved by ensemble averaging in time (Ahmed et al. 2019; Brearley et al. 2019). In the context of stratified mixture combustion, where the flame propagates through an inhomogeneous mixture, DNS studies have not yet employed turbulence forcing schemes since this only accelerates the rate of mixing and makes the analysis of the influence of mixture stratification a challenging task. The extent of stratification decays with time as the simulation progresses in the absence of any scalar fluctuation generating mechanisms. This aspect further exacerbates if turbulence forcing is used because the sustained turbulence level accelerates the mixing of the scalars. Under this situation, the statistical stationarity is only achieved once the mixture reaches a homogeneous, fully mixed state. Thus, exclusively forcing the turbulent flow velocities in DNS of stratified mixture combustion is highly counterproductive. It is therefore desirable to have a scalar forcing mechanism employed in conjunction with turbulent velocity forcing in order to maintain both turbulence intensity and the scalar rms value during the simulation of stratified mixture combustion. This obtains a statistically stationary state of turbulent stratified mixture combustion in a canonical configuration where no other mechanism is available to maintain scalar fluctuations. A turbulent flame propagating into a stratified unburned mixture subject to both velocity and scalar forcing can eventually reach a statistically stationary state even under highly stratified and turbulent conditions. Thus, the scalar forcing has the potential to become a valuable research tool for isolating mixture stratification effects on turbulent flame dynamics. Since turbulent stratified flames are often modelled as a departure from premixed flames, scalar forcing that can maintain not only the rms scalar fluctuation, but also ensures a prescribed distribution, is of interest.

A passive scalar quantity $\psi$, which does not have any influence on the velocity and density fields (e.g. mixture fraction), can be forced to maintain its rms value $\psi ^\prime$ by including a source term in the following transport equation:

$$\begin{aligned} \frac{\partial\, \left( \rho \psi \right) }{\partial\, t}+\frac{\partial \left( \rho u_k\psi \right) }{\partial x_k}=\frac{\partial }{\partial x_k}\left( \rho D\frac{\partial \psi }{\partial x_k}\right) +\rho f_\psi \end{aligned}$$

(1)

where $f_\psi$ is the scalar forcing term. To date, three generally recognised scalar forcing approaches have been used in the literature. The most prevalent is the mean gradient (MG) technique which has been used in many studies (Overholt and Pope 1996; Yeung and Xu 2002; Yeung et al. 2004; Watanabe and Gotoh 2004; O’Gorman and Pullin 2005; Donzis et al. 2005, 2008, 2010; Gotoh and Watanabe 2012; Iyer and Yeung 2014; Yeung and Sreenivasan 2014) and was first used in a numerical study by Overholt and Pope (1996). The MG method maintains the mixture inhomogeneity by mimicking the mixing produced by an imposed constant mean scalar gradient e.g. $\nabla \left\langle \psi \right\rangle =\left[ G,0,0\right]$ across the flow, where the angled brackets are used to denote the mean value over the whole domain. The forcing term in the MG method takes the form of $f_\psi =\mathbf {u}\cdot \nabla \left\langle \psi \right\rangle$. The scalar field resulting from MG forcing reaches a homogeneous but anisotropic state due to the directionality of the imposed scalar gradient. The linear scalar (LS) method (Carroll et al. 2013) is an alternative scalar forcing scheme. The LS method has taken inspiration from the successful linear velocity forcing approaches (Lundgren 2003) by multiplying the scalar field with a coefficient C derived from the scalar dissipation and rms information, such as to maintain the desired scalar rms. The LS method imposes no directionality, so the forced scalar fields can reach a homogeneous, isotropic state.

The two aforementioned scalar forcing schemes are both linear since they consist of a coefficient (i.e. G in the case of MG forcing, and C in the case of LS forcing) multiplied by a velocity component (in the case of MG forcing) or a scalar (in the case of LS forcing). Linear forcing schemes give little flexibility in controlling the distribution of the resulting scalar field. The consequence of this problem lessens when turbulent velocity fields are forced, as they often exhibit bell-shaped distributions which linear forcing can maintain effectively. However, particularly in the case of turbulent stratified combustion, velocity and scalar fields can exhibit fundamentally different characteristics depending on the source of mixture stratification in the unburned gas. The distribution of a passive scalar, such as the mixture fraction $\xi$, in the unburned mixture of stratified flames can take on many forms such as bell-shaped, bimodal and asymmetric distributions. In addition, scalar fields are often subject to strict bounds. For example, the mass fraction of a given species must lie between zero and unity, whereas a component of the velocity has no such limits. Linear forcing schemes cannot satisfy this boundedness without imposing unnatural additional constraints, and therefore, such linear forcing schemes are not suitable for maintaining mixture inhomogeneity in turbulent stratified mixture combustion.

Addressing the clear lack of scalar forcing schemes suitable for use in combustion, Daniel et al. (2018) more recently introduced the reaction analogy (RA) scalar forcing method that can produce a wide range of probability density functions (PDFs) that respect the scalar’s naturally occurring bounds. The forcing term was derived by considering a hypothetical chemical reaction converting partially mixed fluid (the hypothetical reactants) into one of its two unmixed states (the hypothetical products). The desired bounds of the scalar are specified, and the resulting scalar distribution between those bounds is determined by selecting the desired scalar dissipation rate. Due to its clear applicability for sustaining physical unburned mixture inhomogeneity in stratified combustion, the RA method has been identified as the primary scalar forcing scheme of interest in this work.

To date, scalar forcing schemes have not been implemented in chemically reacting combustion simulations. This study addresses this gap in the existing literature and provides a commentary on the prospects of scalar forcing for the use in DNS analysis of stratified mixture combustion. The RA method has been modified in this analysis for the purpose of testing and validation in the case of passive scalar mixing in a triply periodic cube before applying to reacting flow simulations.

The following section (i.e. Sect. 2) provides the mathematical description of the forcing methodology. Section 3 describes the numerical implementation of the cases investigated. The results are presented, and associated interpretations are discussed in Section 4. The summary of the main findings is provided, and the potential usage of the scalar forcing in the future research into turbulent stratified mixture combustion is discussed in the final section (i.e. Sect. 5) of this paper.

2 The Forcing Methodology

The forcing method proposed by Daniel et al. (2018), capable of satisfying characteristics of fuel-air stratification, considers a hypothetical chemical reaction that converts mixed fluid into its unmixed states. The forcing term is given as:

$$\begin{aligned} f_\psi = {\left\{ \begin{array}{ll} -\left( \psi _u-\psi _l\right) mK\left( \frac{\psi _u+\psi _l-2\psi }{\psi _u-\psi _l}\right) ^n\left( \frac{\psi -\psi _l}{\psi _u-\psi _l}\right) ^m &{} \text {when }\psi \le \psi _\text {mean} \\ +\left( \psi _u-\psi _l\right) mK\left( \frac{2\psi -\psi _u-\psi _l}{\psi _u-\psi _l}\right) ^n\left( \frac{\psi _u-\psi }{\psi _u-\psi _l}\right) ^m &{} \text {when }\psi >\psi _\text {mean} \end{array}\right. } \end{aligned}$$

(2)

where $\psi _l$ and $\psi _u$ are the chosen lower and upper bounds of a generic scalar $\psi$ (which is to be forced) respectively with a target mean $\psi _\text {mean}=(\psi _u+\psi _l)/2$ assuming a symmetrical scalar distribution. The reaction rate constant of the hypothetical chemical reaction is given by K, with m and n being the stoichiometric coefficients. The hypothetical chemical reaction equation is given by:

$$\begin{aligned} mM+nE_l&\rightarrow \left( 2m+n\right) E_l \quad \text {when } \psi \le \psi _\text {mean} \end{aligned}$$

(3a)

$$\begin{aligned} mM+nE_u&\rightarrow \left( 2m+n\right) E_u \quad \text {when } \psi >\psi _\text {mean} \end{aligned}$$

(3b)

where M is a hypothetical chemical species representing the mixed fluid state, $E_l$ and $E_u$ are hypothetical chemical species representing the extra molecules of unmixed fluid towards the lower or upper bounds of the scalar respectively.

In this analysis, modifications have been made to Eq. (2) to make it more robust in a chemically reacting configuration. Daniel et al. (2018) proposed selecting the K value that corresponds to the desired steady state scalar dissipation rate, which controls the scalar PDF distribution. This analysis intends to maintain the prescribed rms value of scalar fluctuation $\psi _0^\prime$, so introduces a rms error signal term $\left( \psi _0^\prime -\psi ^\prime \right)$ to Eq. 2 to simplify the matter. Then, K is considered as the constant in the proportional control system to maintain $\psi ^\prime$. The forcing term with these modifications therefore takes the following form:

$$\begin{aligned} f_\psi = {\left\{ \begin{array}{ll} -\left( \psi _0^\prime -\psi ^\prime \right) \left( \psi _u-\psi _l\right) mK\left( \frac{\psi _u+\psi _l-2\psi }{\psi _u-\psi _l}\right) ^n\left( \frac{\psi -\psi _l}{\psi _u-\psi _l}\right) ^m &{} \text {when } \psi \le \psi _\text {mean} \\ +\left( \psi _0^\prime -\psi ^\prime \right) \left( \psi _u-\psi _l\right) mK\left( \frac{2\psi -\psi _u-\psi _l}{\psi _u-\psi _l}\right) ^n\left( \frac{\psi _u-\psi }{\psi _u-\psi _l}\right) ^m &{} \text {when } \psi >\psi _\text {mean} \end{array}\right. } \end{aligned}$$

(4)

If the scalar field is subject to asymmetries the above forcing scheme would eventually convert all the fluid into a uniform field of either $\psi =\psi _u$ or $\psi =\psi _l$. Such asymmetries could be introduced in the initial conditions, or due to the flame preferentially propagating through certain mixture compositions. To counter this, Eq. 4 must be modified further to allow for a robust self-correction mechanism. The instantaneous mean scalar $\left\langle \psi \right\rangle$, not to be confused with the target mean $\psi _\text {mean}$, is calculated and fed back to the forcing equation to allow for self-balancing of the PDF of $\psi$. The updated $\psi _\text {mean}$ to be used in the forcing equation is thus given as:

$$\begin{aligned} \psi _\text {mean}^*=K^*\left( \left\langle \psi \right\rangle -\psi _\text {mean}\right) +\psi _\text {mean} \end{aligned}$$

(5)

where $K^*$ is the proportional control constant to maintain $\psi _\text {mean}$. In addition, hypothetical lower and upper limits $\psi _l^*$ and $\psi _u^*$ corresponding to $\psi _\text {mean}^*$ should be evaluated in the following manner:

$$\begin{aligned} \psi _l^*&=\psi _u-2\left( \psi _u-\psi _\text {mean}^*\right) \end{aligned}$$

(6a)

$$\begin{aligned} \psi _u^*&=\psi _l+2\left( \psi _\text {mean}^*-\psi _l\right) \end{aligned}$$

(6b)

Note that these limits do not change the location of the specified upper and lower bounds $\psi _u$ and $\psi _l$. Rather, $\psi _u^*$ is only used in the calculation of the forcing term for $\psi \le \psi _\text {mean}^*$, and $\psi _l^*$ is only used in the calculation for $\psi >\psi _\text {mean}^*$. Finally, the forcing term used in this study takes the following form:

$$\begin{aligned} f_\psi = {\left\{ \begin{array}{ll} -\left( \psi _0^\prime -\psi ^\prime \right) \left( \psi _u^*-\psi _l\right) mK\left( \frac{\psi _u^*+\psi _l-2\psi }{\psi _u^*-\psi _l}\right) ^n\left( \frac{\psi -\psi _l}{\psi _u^*-\psi _l}\right) ^m &{} \text {when } \psi \le \psi _\text {mean}^*\\ +\left( \psi _0^\prime -\psi ^\prime \right) \left( \psi _u-\psi _l^*\right) mK\left( \frac{2\psi -\psi _u-\psi _l^*}{\psi _u-\psi _l^*}\right) ^n\left( \frac{\psi _u-\psi }{\psi _u-\psi _l^*}\right) ^m &{} \text {when } \psi >\psi _\text {mean}^*\end{array}\right. } \end{aligned}$$

(7)

A plot of $f_\psi \left( \psi \right)$ with different instantaneous values of global mean $\left\langle \psi \right\rangle$ with $\psi _l=0$ and $\psi _u=1$ is shown in Fig. 1. The forcing term naturally reduces to zero at the specified bounds under all conditions. The effects of modifying the stoichiometric coefficients (m and n) change the shape of the forcing term and consequently the resulting scalar PDF. In this analysis, only $m=n=1$ is considered, and to avoid repetition, the reader is referred to Daniel et al. (2018) for a detailed account of the effects of these parameters. Figure 1 schematically shows the forcing term when $\left\langle \psi \right\rangle =\psi _\text {mean}$, and the self correction control system when $\left\langle \psi \right\rangle <\psi _\text {mean}$ and $\left\langle \psi \right\rangle >\psi _\text {mean}$.

Fig. 1

The forcing term $f_{\psi }$ considered in this analysis under different values of global mean scalar $\left\langle \psi \right\rangle$ with $\psi _l=0$, $\psi _u=1$, $K (\ell _0/u'_0)=1.71 \times 10^3$ and $K^*=2.0$

The distribution of the scalar field is controlled by setting the input parameters $\psi _l$, $\psi _u$, and $\psi ^\prime$ to match the desired symmetrical distribution. Once the desired bounds are specified, setting the desired value of $\psi '$ will control the distribution between those bounds (i.e. a high value will result in a bimodal distribution, and a low value will result in a bell-shaped distribution). Thus, this forcing scheme enables controlled numerical experiments to analyse the influence of the mixture inhomogeneity distribution on stratified mixture combustion.

It is worth noting that although the forcing term diminishes to zero at the scalar bounds, overshoots and undershoots in the scalar field can still occur with a very low probability, and as such, boundedness cannot strictly be guaranteed. However, these statistically insignificant overshoots and undershoots are unlikely to have major implications in the case of equivalence ratio/mixture fraction forcing in the unburned gas for DNS of stratified mixture combustion where only the initial mean equivalence ratio $\langle \phi \rangle$ and rms equivalence ratio $\phi '$ are prescribed as the initial condition. Strict boundedness can be enforced by using a simple limiting condition in the code (e.g. an if statement) without any detrimental effects.

Like all existing scalar forcing schemes, (Pope 2000; Carroll et al. 2013; Daniel et al. 2018) the proposed modified RA forcing scheme has no provision of maintaining a specific scalar length scale. This decision has been taken because maintaining a scalar length scale independently of turbulent velocity length scale raises fundamental issues regarding the physicality of the solution since the scalar field naturally aligns with the velocity field throughout the evolution of the flow for gaseous mixtures where the Schmidt number is expected to be of the order of unity.

3 Numerical Implementation

A three-dimensional DNS code SENGA+ Jenkins and Cant (1999) was used for the simulations where the conservation equations of mass, momentum, energy, and species for compressible flows are solved in non-dimensional form. This code uses a 10th order central difference scheme to calculate spatial derivatives of internal grid points, and the order of accuracy of the discretisation scheme gradually reduces to a one-sided 2nd order scheme at non-periodic boundaries. The time advancement has been carried out using an explicit low storage 3rd order Runge-Kutta scheme (Wray 1990).

In all simulations, turbulent velocity fluctuations have been initialised by a divergence-free homogeneous isotropic field using the well-established pseudo-spectral method by Rogallo (1981) for a set of prescribed values of rms velocity $u^\prime$ and the longitudinal integral length scale $\ell$. Mixture inhomogeneity has been initialised with a bimodal distribution according to a different pseudo-spectral method proposed by Eswaran and Pope (1988b) for a prescribed rms value of scalar fluctuation $\psi ^\prime$. Bell-shaped scalar fields are also initialised using Rogallo’s pseudo-spectral method (Rogallo 1981). For the assessment of the newly devised scalar forcing methodology, non-reacting simulations of constant-density passive scalar mixing have been conducted in a triply periodic cube. The scalar fields were generated according to an initial ratio of scalar to turbulence integral length scales of $\ell _{\psi }/\ell =0.5$, 1.0 and 1.5.

The simulation parameters for the triply periodic cases are shown in Table 1. The table shows, from left to right, the case number, the turbulent Reynolds number $Re_t=u^\prime \ell _0/\nu$ (where $\nu$ is the kinematic viscosity), the initial type of scalar distribution (bimodal, bell-shaped, or roughly flat), the initial scalar to turbulence longitudinal integral length scale ratio $\ell _{\psi 0}/\ell _0$, the mean scalar value $\psi _\text {mean}$, the rms scalar fluctuation $\psi ^\prime$, the physical size of the domain in terms of the initial longitudinal integral length scale $\ell$, the size of the Cartesian grid, the velocity forcing scheme used in the simulations (none, Lundgren, 2003 or modified bandwidth Klein et al. 2017), the type of scalar forcing (reaction analogy Daniel et al. 2018 or linear scalar Carroll et al. 2013), and the value of the constants in the scalar forcing Eqs. (4) and (5). In all of the simulations, the Schmidt number $Sc=\nu /D$ of the mixture is taken to be 0.7 (where D is the mass diffusivity). These simulations have been carried out for a Mach number $Ma_{NR}=\nu /(\ell _0 a)=2.33 \times 10^{-4}$ with a being the acoustic speed.

Table 1 Parameters of triply periodic cube forced scalar simulations for passive scalar mixing

All simulations have been conducted with and without scalar forcing for comparison. Simulations A(i-iii) have no velocity forcing, simulations B(i-iii) and D–H are subject to Lundgren velocity forcing (Lundgren 2003) where the momentum equation includes a forcing term equalling $\rho \left( \varepsilon /2k\right) u_i$, where $k=0.5\left\langle u_j^\prime u_j^\prime \right\rangle$ is the mean turbulent kinetic energy in the domain and $\langle \nu \partial u'_i/\partial x_j\partial u'_i/\partial x_j\rangle$ is the dissipation rate of turbulent kinetic energy. Simulations C(i-iii) use a more recently proposed physical-space modified bandwidth filtered forcing term for the momentum equations (Klein et al. 2017). Advantages of Lundgren physical space forcing approach are its simplicity of implementation and it produces more physical velocity fields than many of its alternatives, as argued by previous analyses (Eswaran and Pope 1988b; Rosales and Meneveau 2005). However, a caveat of Lundgren forcing is that the turbulence length scale eventually reaches around 35% of the domain size (Rosales and Meneveau 2005). The modified bandwidth filtered forcing approach was derived as an extension to Lundgren forcing for its ability to maintain the specified length scale $\ell _T = k^{3/2}/\varepsilon$ (Klein et al. 2017). The velocity forcing term takes the following form:

$$\begin{aligned} \mathbf {f}=\max {\left[ 0,\frac{k_{target}-k}{\varDelta t k_{target}}\right] }{\bar{\mathbf {u}}}^{HP} \end{aligned}$$

(8)

where $k_{target}$ is the desired turbulent kinetic energy value, $\varDelta t$ is the timestep size, and k is the current level of turbulent kinetic energy, ${{\bar{u}}_i}^{HP}=u_i-\bar{u_i}$ a high pass filtered velocity fluctuation with $\overline{\left( \ldots \right) }$ being a conventional low pass filter typically used in the context of LES with a 1D Gaussian filter kernel given by $G\left( x\right) =\left( 6/\pi \ell _f^2\right) ^{1/2}\exp {\left( -6x^2/\ell _f^2\right) }$ and where $\ell _f$ is a filter length scale of the order of $\ell$. The value of $\ell _f$ is gradually adjusted to control $\ell _T$ such that it reaches the target value (given in Table 2). The final value of $\ell _f$ is $\ell _f=\ell _T/4$ for the simulation reported in this work. This is consistent with the previous analyses by Klein et al. (2017).

The reacting simulations consist of statistically planar flames propagating into an inhomogeneous methane-air mixture. A single-step Arrhenius irreversible chemical reaction (1 unit mass of Fuel $+$ s unit mass of Oxidiser $\rightarrow (1+s)$ unit mass of Products) has been considered for the present analysis. The activation energy $E_{ac}$ is calculated depending on the equivalence ratio, $\phi$ following the model proposed by Tarrazo et al. (2006) which can capture main flame features (i.e. accurate equivalence ratio $\phi$ dependence of the unstrained laminar burning velocity $S_{b(\phi _g)}$ and adiabatic flame temperature $T_{ad(\phi )}$) for hydrocarbon fuel-air mixtures. As suggested by Tarrazo et al. (2006), the Zel’dovich number $\beta$, can be expressed as: $\beta = E_{ac} (T_{ad(\phi =1)}-T_0)/RT_{ad(\phi =1)}^2 =6f(\phi )$ (with R and $E_{ac}$ being the gas constant and activation energy, respectively, and $T_{ad(\phi )}$ is the adiabatic flame temperature for the equivalence ratio $\phi$ and $T_0$ is the unburned gas temperature) where $f(\phi )$ is taken to be a function of the gaseous phase equivalence ratio $\phi$ in the following manner (Tarrazo et al. 2006):

$$\begin{aligned} f(\phi _g) = {\left\{ \begin{array}{ll} 1.0+8.250(\phi - 0.64)^2, &{} \phi \le 0.64 \\ 1.0, &{} 0.64< \phi < 1.07 \\ 1.0 + 1.443(\phi - 1.07)^2, &{} \phi \ge 1.07 \end{array}\right. } \end{aligned}$$

(9)

The heat of combustion per unit mass of fuel consumption $H_\phi = (T_{ad(\phi )}-T_0)C_p/(Y_{Fu(\phi _g)}-Y_{Fb(\phi )})$ is expressed as Tarrazo et al. (2006):

$$\begin{aligned} \frac{H_\phi }{H_{\phi =1}} = {\left\{ \begin{array}{ll} 1, &{} \phi \le 1 \\ 1-\alpha _H(\phi -1), &{} \phi >1 \end{array}\right. } \end{aligned}$$

(10)

where $\alpha _H=0.21$, $C_p$ is the specific heat at constant pressure, and $Y_{Fu(\phi )}$ and $Y_{Fb(\phi )}$ denote the fuel mass fractions in the unburned and burned gases, respectively for a premixed flame of equivalence ratio $\phi$ (Tarrazo et al. 2006). It has been shown by Malkeson and Chakraborty (2010) that this chemical mechanism captures the equivalence ratio $\phi$ dependence of the normalised laminar burning velocity $S_{b(\phi )}/S_L$ (where $S_L=S_{b(\phi =1)}$) obtained from experimental data, which is not repeated here for the sake of conciseness.

Since this study focuses on the viability of the scalar forcing methodology in the case of stratified mixture combustion, the choice of chemical mechanism is of secondary importance, thus a modified single-step chemistry has been chosen for computational economy. In the case of reacting flow simulations, the boundaries in the direction of the mean flame propagation are taken to be partially non-reflecting, while the transverse boundaries are considered to be periodic. The non-periodic boundaries are specified according to the Navier-Stokes characteristic boundary conditions (NSCBC) technique (Poinsot and Lele 1992). The scalar fluctuations with a specified mean value equal to the global mean in the 3D domain and the turbulent velocity fluctuations corresponding to the required root-mean-square values are supplied from a time-evolving triply periodic box. The mean inlet velocity is gradually adjusted to match the turbulent flame speed to keep the flame within the computational domain.

The forced scalar was chosen to be the mixture fraction $\xi$ in the unburned gas of the reacting simulation (i.e. $\psi = \xi$ in Eq. 1), given by Bilger (1989)

$$\begin{aligned} \xi =\frac{Y_F-Y_O/s+Y_{O\infty }/s}{Y_{F\infty }+Y_{O\infty }/s} \end{aligned}$$

(11)

which rises from zero in pure air to unity in pure fuel, where $Y_F$ and $Y_O$ are the fuel and oxidiser (i.e. oxygen) mass fractions, $Y_{F\infty }=1$ and $Y_{O\infty }=0.233$ are their values in the pure fuel and air respectively, and $s=4.0$ is the mass stoichiometric ratio for methane-air mixtures. The equivalence ratio $\phi$ is related to the mixture fraction $\xi$ and is given by:

$$\begin{aligned} \phi =\frac{Y_F/Y_O}{\left( Y_F/Y_O\right) _{st}}=\frac{\xi \left( 1-\xi _{st}\right) }{\xi _{st}\left( 1-\xi \right) } \end{aligned}$$

(12)

The values of the lower and upper bounds of the scalar were chosen to be $\xi _l=0.0337$ and $\xi _u=0.0753$ since these values correspond to an equivalence ratio $\phi _l=0.6$ and $\phi _u=1.4$ which lie close to the flammability limits for methane-air combustion. Thus, strong manifestations of the effects due to stratified combustion are expected to be observed. The target mean value of mixture fraction is $\xi _\text {mean}=0.055$ corresponding to the globally stoichiometric mixture (i.e. $\phi _m=1.0$).

Scalar forcing is applied only in the unburned gas because artificially modifying the species mass fractions within the flame is likely to produce unphysical results. This is achieved by defining a reaction progress variable c and applying the scalar forcing only where $c<\epsilon _c$ where $\epsilon _c$ is a small number, which is taken to be 0.001 in this analysis (and $\epsilon _c$ ranging from 0.0001 to 0.01 was tested and was found to have marginal impact on the results). In stratified mixtures, the reaction progress variable c can be defined as (Hélie and Trouvé 1998; Malkeson and Chakraborty 2010):

$$\begin{aligned} c=\frac{\xi Y_{F\infty }-Y_F}{\xi Y_{F\infty }-\max {\left[ 0,\frac{\xi -\xi _{st}}{1-\xi _{st}}\right] }Y_{F\infty }} \end{aligned}$$

(13)

Then, the species mass fractions in the unburned gas are updated at the end of each time step from the mixture fraction according to the expressions

$$\begin{aligned}&Y_F=\xi Y_{F\infty }-c\left[ \xi Y_{F\infty }-\max \left( 0,\frac{\xi -\xi _{st}}{1-\xi _{st}}\right) Y_{F\infty }\right] \end{aligned}$$

(14)

$$\begin{aligned}&Y_O = (1-\xi )Y_{O\infty } - c\left[ (1-\xi )Y_{O\infty }-\max \left( 0, \frac{\xi _{st}-\xi }{\xi _{st}}\right) Y_{O\infty }\right] \end{aligned}$$

(15)

As a result, $\langle Y_F'Y_F'\rangle =\langle \xi '^2\rangle Y_{F\infty }^2$and $\langle Y_O'Y_O'\rangle =\langle \xi '^2\rangle Y_{O\infty }^2$ are maintained in the fully unburned gas. Whilst, in principle, the turbulent velocity field can be forced throughout the domain, the same conclusions cannot be automatically applied to scalar forcing. It is the purpose of the scalar forcing scheme to deliver inhomogeneous unburned fuel-air mixture with prescribed values of mean and rms equivalence ratio to the flame. Scalar forcing within the flame will artificially alter the fuel and oxidiser concentrations, which, in turn, will affect the burning rate and subsequent mixing of species within the burned gas. Moreover, forcing of an active scalar forcing into the flame induces additional complexity (e.g. scalar fluctuations introduced by forcing cannot be separated from the fluctuations due to chemical reaction), particularly for more detailed chemical mechanisms, for little benefit.

For this analysis, the reactants are considered to be calorifically perfect gas for the purpose of simplicity in order to prove the concept of scalar forcing. In most stratified flame DNS simulations in canonical configuration, the unburned reactants are considered to be in an isothermal state and under this condition, the species mass fractions in the unburned gas can be tabulated in terms of mixture fraction, as used in the past for detailed chemistry DNS (Minamoto et al. 2014) and flame-resolved simulations (Sandeep et al. 2018). It is important to note that in principle it is possible to force the mean and variances of all the species mass fractions irrespective of the molecular weights because the molecular weight does not feature in the mathematical formulation of the proposed scalar forcing technique. In this respect, it is worthwhile to consider that the mixture fraction $\xi$ is a linear function of species mass fractions (e.g. fuel and oxidiser mass fractions in the context of simple chemistry and atomic mass fractions in the context of more detailed chemistry (Bilger 1989)), forcing of individual scalars so that their mean values are retained will automatically retain the mean value of mixture fraction $\langle \xi \rangle$. For example, the desired values of $\langle \xi \rangle =(\langle Y_F \rangle -\langle Y_O \rangle /s+Y_{O\infty }/s)/(Y_{F\infty }+Y_{O\infty }/s)$ can be retained by forcing $Y_F$ and $Y_O$ individually such that $\langle Y_F \rangle = Y_{F\infty } \langle \xi \rangle$ and $\langle Y_O \rangle = Y_{O\infty } (1- \langle \xi \rangle )$ are retained for the case of passive scalar mixing according to the mixing line on the Burke-Schumann diagram irrespective of the value of the stoichiometric coefficient s which is a function of the molecular weights of the constituents. Moreover, forcing $Y_F$ and $Y_O$ in the manner than $\langle {Y'_F}^2 \rangle =Y_{F\infty }^2\langle \xi '^2\rangle$ and $\langle {Y'_O}^2\rangle =Y_{O\infty }^2\langle \xi '^2 \rangle$ based on the desired value of $\langle \xi '^2 \rangle$ yields the same results as that of forcing $\xi$ to retain desired values of $\langle \xi \rangle$ and $\langle \xi '^2 \rangle$. This is not explicitly shown here because the PDFs of $\xi$ are indistinguishable between these two methodologies. This is also qualitatively valid for reacting cases because the scalar forcing is applied only for the unburned reactants. In the numerical methodology used here, the conservation equations of mass and energy are solved alongside the conservation equations of momentum and species along with an ideal gas law. As the forcing term acts as a reaction term (see Eqs. (2) and (7)) in the species conservation equation, no further adjustments are needed in the mass and energy (i.e. total specific internal energy including the chemical part) conservation equations similarly to the conventional low Mach number single-phase reacting flows (where the temperature field is obtained from the solution of the specific internal energy, which inherently accounts for the species field contributions through the specific heat and enthalpies of formation). However, further analyses will be needed to assess if this procedure works for high Mach number multiphase flows.

Modified bandwidth filtered velocity forcing (Klein et al. 2017) is used for all chemically reacting simulations. A factor of $(1-c)$ is included in Eq. 8 to ensure that the forcing is not active in the burned gas (i.e. $c=1.0$) to allow for the flame to naturally influence the evolution of the velocity field from the unburned to the burned side of the flame. The level of turbulence in flames within the thin reaction zones regime often decays from the unburned gas side to the burned gas side of the flame brush and the integral length scale of turbulence increases due to dilatation and a rise in viscosity with heat release (Chakraborty 2021; Chakraborty and Cant 2011), By contrast, turbulence intensity may increase from the leading edge to somewhere within the flame brush in the corrugated flamelets regime (Chakraborty 2021; Chakraborty and Cant 2011). However, forcing everywhere in the domain tries to enforce a constant level of turbulence on both sides of the flame brush. In this sense, the flame-turbulence interaction will not be physical if the forcing is applied to the whole computational domain. This is explained in detail in Klein et al. (2017) and therefore the approach advocated in Klein et al. (2017) is followed in this analysis.

Table 2 Parameters of the reacting, forced scalar simulation

Table 2 lists the simulation parameters for the reacting cases. From left to right, the table shows the case number, values of the rms turbulent velocity fluctuation normalised by laminar burning velocity in a stoichiometric premixed flame $u^\prime /S_L$, integral length scale of turbulence normalised by the thermal flame thickness of the stoichiometric laminar flame $\ell _T/\delta _{st}$, initial scalar to turbulence integral length scale ratio $\ell _{\xi 0}/\ell _0$, global mean of mixture fraction $\xi _\text {mean}$, rms mixture fraction fluctuation $\xi ^\prime$, Damköhler number $Da=\ell _TS_L/u^\prime \delta _{st}$, Karlovitz number $Ka=\left( u^\prime /S_L\right) ^{1.5} \left( \ell _T/\delta _{st}\right) ^{-0.5}$, heat release parameter $\tau =(T_{ad(\phi =1)}-T_0)/T_0$ along with the size of the domain in terms of $\delta _{st}$ and the Cartesian grid with uniform grid spacing used for discretisation. The terms appearing in these quantities are the thermal flame thickness of the stoichiometric mixture $\delta _{st} = (T_{ad(\phi =1)}-T_0)/\max |\nabla T|_L$, where $T_{ad\left( \phi =1\right) }$, $T_0$ and T are the adiabatic flame temperature of the stoichiometric mixture, unburned gas temperature and the instantaneous dimensional temperature, respectively with the subscript L referring to the unstretched steady stoichiometric laminar flame value. The grid spacing ensures 10 grid points within $\delta _{st}$ and at least 2 grid points within the Kolmogorov length scale $\eta$. Standard values are taken for Prandtl number (i.e. $Pr=0.7$) and the ratio of specific heats (i.e. $\gamma =1.4$) and all the species are assumed to have a Lewis number of unity (i.e. $Le=Sc/Pr=1.0$). For the reacting flow cases, the Mach number $Ma_R$ was taken to be $Ma_R=\nu _0/(\ell _{T0} a_0)=1.633 \times 10^{-3}$ with $\nu _0$ and $a_0$ being the kinematic viscosity and acoustic speed in the unburned gas, respectively. The differences in Mach number between non-reacting and reacting simulations originates from the fact that smaller value of turbulent Reynolds number is obtained for the same grid resolution in the reacting case because of the extra requirement of resolving the flame thickness in addition to the Kolmogorov length scale. However, the Mach number is much smaller than unity for both reacting and non-reacting cases that this variation makes no substantial difference. Most industrially relevant stratified mixture combustion takes place under small Mach numbers and that is why no Mach number sensitivity was conducted in this analysis.

4 Results and Discussion

Fig. 2

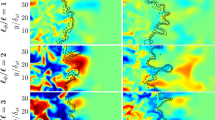
Distributions of the passive scalar $\psi$ in a forced scalar, non-reacting, triply periodic cube configuration after 17.5 initial eddy turnover times (i.e. $t_{sim}=17.5T_{turb}$). Columns 1-3 show initial $\ell _{\psi 0}/\ell _0=0.5$, 1.0, 1.5 respectively, while rows 1-3 show simulations without velocity forcing, with Lundgren forcing, and with modified bandwidth filtered forcing respectively

Fig. 3

Evolutions of the mean value of $\left\langle \psi \right\rangle$ (top row) and rms scalar fluctuation $\psi ^\prime$ (bottom row) in cases A–C for different initial values of normalised scalar length scale $\ell _{\psi 0}/\ell _0$ under decaying turbulence (left), Lundgren forced turbulence (middle), and modified bandwidth forced turbulence (right)

Fig. 4

Evolution of the PDF of the passive scalar $\psi$ in cases A–C. Columns 1–3 show initial $\ell _{\psi 0}/\ell _0=0.5$, 1.0 and 1.5 respectively, while rows 1–3 show simulations without velocity forcing, with Lundgren forcing, and with modified bandwidth filtered forcing respectively

Figure 2 shows the distributions of $\psi$ for cases A–C after 17.5 initial eddy turn over times (i.e. $t_{sim}=17.5 T_{turb}=17.5\ell _T/u^\prime )$ by which the statistically stationary state has been achieved. It can be seen from Fig. 2 that the mixture remains highly stratified even after a long simulation time, and the regions of low scalar concentrations (i.e. $\psi <\psi _\text {mean}$) appear to have similar volume as that of high scalar concentrations (i.e. $\psi >\psi _\text {mean}$), indicating the effectiveness of the scalar forcing scheme. This behaviour can be observed both with and without velocity forcing although velocity forcing significantly alters the instantaneous distribution of the passive scalar $\psi$. Figure 3 shows the temporal evolutions of the mean scalar value $\left\langle \psi \right\rangle$ and rms scalar fluctuation $\psi ^\prime$ for the same cases, which demonstrate that the target values of the mean $\left\langle \psi \right\rangle$ (i.e.$=1.0$) and rms $\psi ^\prime$ (i.e. $=0.28$) are well-maintained throughout the simulation irrespective of the velocity forcing method. It can further be seen from Fig. 4 that the forcing scheme appears to do a good job at maintaining the bimodal $\psi$ distribution irrespective of the nature of velocity forcing, and the initial bimodal distribution is very closely maintained throughout the simulation. Figure 4 also shows that the probability of finding scalar exceeding the specified lower and upper bounds of $\psi _l=0.6$ and $\psi _u=1.4$ is negligible. The initialisation process of $\psi$ following the bimodal distribution according to Eswaran and Pope (1988b) routinely gives rise to the overshoots comparable to the ones shown in the case of forcing. The use of limiting conditions in conjunction with the newly proposed scalar forcing methodology avoids any overshoots, which is demonstrated for cases shown in Fig. 17 in the Appendix.

Returning to Fig. 2 for further qualitative analysis of the scalar field, it can be seen that the length scale of scalar distribution at the end of simulation time (i.e. $t_{sim}=17.5T_{turb}$) appears independent of the initial value of $\ell _\psi$ and is only dependent on the nature of the velocity forcing scheme. These simulations have been run for long enough for the turbulence to have a strong influence on the scalar length scale. This observation is quantitatively depicted in Figs. 5a and 6a, which show the scalar integral length scale evolution normalised by the initial velocity length scale for non-reacting cases subject to scalar field forcing. Figure 5a indicates that for all cases the scalar integral length scale converges to comparable values (because the initial longitudinal length scale of turbulence $\ell _0$ remains the same for all cases), regardless of the velocity forcing scheme or initial scalar integral length scale. The cases subject to velocity forcing but not scalar forcing mix rapidly, and as such, the integral length scale rises sharply to the size of the domain once complete mixing has occurred at around $t_\text {sim}=15T_\text {turb}$.

Fig. 5

Evolution of the scalar integral length scale normalised by the initial velocity scalar length scale $\ell _\psi /\ell _0$ (first row) and the instantaneous velocity length scale $\ell _\psi /\ell$ (second row) for cases A–C with scalar forcing. Plots are shown under decaying turbulence (left column), Lundgren forced turbulence (middle column), and modified bandwidth forced turbulence (right column)

Fig. 6

Evolution of the scalar integral length scale normalised by the initial velocity scalar length scale $\ell _\psi /\ell _0$ (first row) and the instantaneous velocity length scale $\ell _\psi /\ell$ (second row) for cases A–C without scalar forcing. Plots are shown under decaying turbulence (left column), Lundgren forced turbulence (middle column), and modified bandwidth forced turbulence (right column)

Fig. 7

Evolution of the normalised scalar dissipation rate $N_\xi \times (\ell _0/u'_0)$ in cases A–C. Columns 1–3 show initial $\ell _{\psi 0}/\ell _0=0.5$, 1.0 and 1.5 respectively, while rows 1–3 show simulations without velocity forcing, with Lundgren forcing, and with modified bandwidth filtered forcing respectively

In the case of small initial values of $\ell _\psi$, the small-scale inhomogeneities are rapidly mixed due to high values of initial scalar dissipation rate $N_\psi =D\nabla \psi \cdot \nabla \psi$, and thus the resulting scalar inhomogeneity with the progression of time leads to a mixture distribution with an integral length scale of mixture inhomogeneity $\ell _\psi$, which is comparable to the integral length scale of turbulence $\ell$. In the cases with large initial values of $\ell _\psi$ with $\ell _\psi >\ell$, the initial scalar dissipation rate $N_\psi$ remains small so initial mixing rate remains small, but background fluid turbulence breaks the large-scale islands of mixture inhomogeneities to smaller pockets, and therefore the length scale of mixture inhomogeneity approaches to a value comparable to the integral length scale of turbulence $\ell$, as time progresses.

Ideally, the scalar forcing should only influence the rms scalar value and the underlying scalar distribution, but should not interfere with the flow physics. Therefore, the evolution of the scalar to turbulence integral length scale, as shown for the forced cases A–C in Fig. 5, should be determined by turbulent mixing for passive scalars and should not be unduly influenced by the scalar forcing scheme.

Figure 6 shows the scalar to turbulence integral length scale ratio evolution for cases A–C without any scalar forcing. A comparison between Figs. 5 and 6 under decaying turbulence shows that the scalar forcing has an almost negligible influence on the scalar length scale evolution, and the same qualitative behaviours are observed under Lundgren velocity forcing and modified bandwidth forcing throughout the simulation time. However, it can be seen from Fig. 5b that $\ell _\psi /\ell$ for the modified bandwidth forcing settles to a higher value than in the case for Lundgren forcing. Although $\ell _\psi$ converges to comparable values irrespective of the turbulence forcing method (see Fig. 5a), $\ell$ settles to about 35% of the transverse domain length for Lundgren forcing, whereas $\ell$ is maintained at the desired level in the case of bandwidth forcing, which in this case remains smaller than 35% of the transverse domain length. This leads to higher values of $\ell _\psi /\ell$ in the case of bandwidth forcing in comparison to that for Lundgren forcing.

The mean values of the normalised scalar dissipation rate $N_\psi = D\nabla \psi \cdot \nabla \psi \times (\ell _0/u'_0)$ conditional upon $\psi$ for the cases shown in Figs. 4 and 5 are presented in Fig. 7. It can be seen from Fig. 7 that the peak mean value of $N_\psi$ increases from its initial value for scalar forcing irrespective of the nature of turbulent flow forcing. This behaviour is consistent with the visual impression obtained from Fig. 2, which shows the scalar gradient increases in comparison to the initial distribution because of scalar forcing, as the forcing splits the blobs of mixture inhomogeneity into small filaments with high magnitudes of $\nabla \psi$. This trend is obtained also for decaying turbulence but is the strongest for Lundgren forcing, while the bandwidth forcing yields a behaviour comparable to the decaying turbulence case. It can also be seen from Fig. 7 that the profiles of $N_\psi$ converge to a state which is comparable for different values of $\ell _{\psi 0}/\ell _0$ under the quasi-stationary state.

Figure 8 shows the ability of the forcing scheme to maintain other distributions different from a bimodal distribution. Figure 8 (left) shows the $\psi$ PDF evolution of the initially bell-shaped case D, and Fig. 8 (right) shows the corresponding plot for the initially roughly flat PDF distribution case E. It is worth noting that the distribution for case E is obtained if an initial bimodal distribution is allowed to evolve in the absence of forcing for passive scalar mixing before it eventually assumes a bell-shaped distribution (Hélie and Trouvé 1998; Brearley et al. 2020). Figure 8 illustrates that the reaction analogy (Daniel et al. 2018) method maintains both distributions of $\psi$ with reasonable accuracy during the course of the simulation until the quasi-steady condition is obtained. The overshoots in the PDFs of $\psi$ in Fig. 8 in comparison to their initial shapes remain negligible and these overshoots can also be eliminated completely by using limiting conditions, as demonstrated for the bimodal distribution in the Appendix. The PDFs corresponding to Fig. 8 upon using limiting conditions are not explicitly shown here for the sake of conciseness. The variation of mean values of scalar dissipation rate $N_\psi$ conditional on $\psi$ for cases D and E follow the same qualitative trends, as those shown in Fig. 7, and thus are not explicitly shown here for the sake of conciseness.

Table 3 Values of the rms, skewness, and kurtosis of the scalar field in case D at different time instances

In order to demonstrate the capability of the newly proposed scalar forcing methodology to preserve the bell-shaped $\psi$ PDF, Table 3 shows the rms, skewness and kurtosis of the scalar forced bell-shaped case D for different time instances. It can be seen from Table 3 that the PDF corresponding to the initial condition is almost truly Gaussian (i.e. skewness is almost zero and the kurtosis is close to 3.0 and this deviation is not unexpected for moderate sized samples). Table 3 shows that the root-mean-square value of scalar fluctuation is faithfully maintained by the newly proposed scalar forcing and the skewness of the PDFs remains almost zero throughout the simulation but the kurtosis comes down from the theoretical limit for Gaussian distribution (i.e. 3.0) and is maintained at 2.2, indicating that there are fewer low-probability scalar values far from the mean. The values have been compared to a Gaussian distribution as a well-known benchmark, but the preservation of a near-Gaussian PDF kurtosis is not critically important since the probability of these events revealed by the high-order moment are usually negligible.

Fig. 8

Evolution of the PDF of the passive scalar $\psi$ for bell-shaped distribution case D (left) and roughly flat distribution case E (right). Both simulations use the same scalar limit parameters $\psi _l = 0.6$ and $\psi _u = 1.4$, but the bell-shaped distribution uses $\psi ' = 0.11$ and the roughly flat distribution uses $\psi ' = 0.19$

Fig. 9

Evolution of the PDF of the passive scalar $\psi$ for case E

Fig. 10

Evolutions of the mean (left) and the rms scalar fluctuation (right) with the normalised scalar forcing parameter $K(\ell _0/u'_0)=1.71$ (red), $1.71 \times 10^3$ (blue) and $1.71 \times 10^5$ (yellow) for $K^*=2.0$ (i.e.cases G, B(ii) and H, respectively)

Fig. 11

Evolutions of the scalar PDF (top row) and the mean value $\left\langle \psi \right\rangle$ (bottom row) for scalar forcing parameter $K^* = 0$ (left), 2.0 (middle) and 10.0 (right) in the case of $K(\ell _0/u'_0)=1.71 \times 10^3$

Figure 9 shows the temporal evolution of scalar PDF for case F with an initial bimodal distribution of $\psi$ under the linear scalar forcing method (Carroll et al. 2013). It can be seen from Fig. 9 that the linear scalar forcing scheme rapidly transforms the scalar field to a bell-shaped distribution by the time the statistically stationary state is obtained. Thus, if scalar field characteristics other than bell-shaped are desired, the linear scalar method is not appropriate.

Based on the above information, it is worthwhile to demonstrate the effects of scalar forcing parameters K and $K^*$ on the simulation results. It is worth noting that the scalar forcing methodology depends on the parameters K and $K^*$ , where the appropriate value of K is necessary to ensure the scalar variance is retained, whereas $K^*$ retains the desired mean value through a proportional controller (see Eq. (7)). The sensitivity of the scalar forcing scheme on the forcing parameters K and $K^*$ are demonstrated in Figs. 10 and 11. Figure 10 shows the sensitivity of the scalar forcing to the parameter K in Eq. (7) by considering cases B(ii), G and H. It can be seen from Fig. 10 that a significant steady-state error occurs in $\psi '$ when K is not high enough (e.g. $K = (1.71 \times 10)u'_0/\ell _0$ in this case). The forcing scheme is shown not to be sensitive to the values of $K(\ell _0/u'_0) \ge 10^3$ tested in this analysis, and no overshoots are observed for $K(\ell _0/u'_0) \ge 10^3$ in Fig. 10.

Likewise, Figure 11 shows the sensitivity of the scalar forcing to the parameter $K^*$. Figure 11 shows the necessity of this parameter to keep the scalar field in balance. It is important that this parameter is greater than unity so the forcing term will take the same sign immediately on either side of $\langle \psi \rangle$. Otherwise, similar effects as that of $K^*=0$ in Fig. 11 will be observed, only it will take longer for this to occur. Similar to K, no adverse effects are observed for the large values of $K^*$ (i.e., $K^*>>1$) tested.

Figure 11 demonstrates that $K^*$ has a strong influence in terms of retaining the desired mean value $\left\langle \psi \right\rangle$ and an increase in $K^*$ maintains the mean value closely but slight oscillations around the desired mean value can be discerned. These oscillations occur due to slight overshoots in the PDFs of the scalar, but in a stratified flame, the range of equivalence ratio remains within the flammability range and thus small overshoots in the mixture fraction or equivalence ratio is not expected to affect the accuracy of the simulations provided the flow is sufficiently resolved. Although K does not significantly influence $\left\langle \psi \right\rangle$ but an increase in K allows one to achieve the desired value of $\psi '$ more faithfully in a short duration of time. This can be improved further by modifying the proportional controller to a more complex one because it is well-known that the proportional controller is prone to overshoots but here a proportional controller is used, as a first attempt, as done previously by other authors (Carroll and Blanquart 2013; Ketterl and Klein 2018). As the parameter K is inverse of a timescale, it can in principle be parameterised in terms of the volume-averaged scalar dissipation rate $\left\langle N_{\psi }\right\rangle$. However, this presents several practical challenges. Providing K as a function of $\left\langle N_{\psi }\right\rangle$ can potentially affect the scalar integral length scale $\ell _\psi$ independent of the evolution of the scalar field under turbulent fluid motion. Moreover, the evaluation of $\left\langle N_{\psi }\right\rangle$ in the unburned gas for the reacting flow simulation in a dynamic manner may not be straightforward especially for complex geometries, and this may give rise to complex feedback which may increase the time duration to obtain a statistically stationary state. Therefore, further consideration is needed to parameterise K in terms of scalar dissipation rate, which is beyond the scope of current analysis but worth investigating in the future.

Fig. 12

Coloured contours of the fuel mass fraction $Y_F$ (first row) and mixture fraction $\xi$ (second row). Superimposed is the reaction progress variable c (defined in Eq. 12) white contours equalling 0.1, 0.5 and 0.9 (left to right), and black dash contours indicating the stochiometric mixture ($\xi _{st}=0.055$). Contours are shown for initial integral length scale ratios of $\ell _{\xi 0}/\ell _0=0.5$ (left column) and 2.0 (right column). Contours are shown on the midplane of the 3D domain

Finally, the newly developed scalar forcing has been applied to DNS of turbulent stratified flames in a domain comprising of a parallelepiped. Figure 12 shows the coloured contours of the fuel mass fraction and the mixture fraction, with additional contours for the reaction progress variable c and stoichiometric mixture fraction $\xi _{st}$ on the central midplane for the chemically reacting cases I(i,ii). It can be observed from Fig. 12 that, similar to the non-reacting configurations, the mixture inhomogeneity is maintained with a seemingly bimodal distribution in the unburned gas. The $\xi$ contours show that the bimodal distribution is not maintained into the burned gas since the scalar forcing is switched off, and thus, the hot gases can mix freely. Figure 13 confirms that the desired values of $\left\langle \xi \right\rangle$ and $\xi '$ are faithfully maintained in the unburned gas (i.e. $c<\epsilon _c = 0.001$) throughout the simulation, and its distribution in the unburned gas is given in Fig. 14. Figure 14 shows the same qualitative behaviour as that of Fig. 4, exhibiting that the scalar forcing, and the mean self-correcting mechanism is effective in retaining the PDF shape of $\xi$ and the mean and rms values of mixture fraction in the unburned gas (i.e. $c<\epsilon _c = 0.001$) throughout the simulation even for chemically reacting flows. Figure 15 shows the temporal evolution of the scalar-turbulence integral length scale ratio $\ell _{\xi }/\ell$ in the unburned gas for the stratified flame cases, and it can be seen from Fig. 15 that $\ell _\xi$ eventually assumes a value of the order of $\ell$ in the unburned gas under the statistically stationary state, and this behaviour is qualitatively similar to the observed behaviour in Fig. 5 for the non-reacting cases. The evolutions of the turbulent flame speed normalised by the laminar flame speed $S_T/S_L$, and the flame surface area normalised by the area of the laminar flame $A_T/A_L$ for both reacting cases are shown in Fig. 16, where the turbulent burning velocity and flame surface area are defined as $S_T=1/(\rho _0A_P)\int _{V}^{}{\dot{\omega }}_cdV$ and $A_T=\int _{V}^{}\left| \nabla c\right| dV$, respectively with $A_{\text{P}}$ being the projected flame surface area in the direction of mean flame propagation. Both the flame speed and area reach a statistically stationary value at $t\approx 2.5T_{turb}$. Note that the parameter defining the unburned gas cut-off point $\epsilon _c$ (where $c<\epsilon _c$) was tested with $\epsilon _c = 0.0001$, 0.001 and 0.01 and it was found that there was no notable influence on the values of $S_T/S_L$ and $A_T/A_L$. Recently, Brearley et al. (2020) investigated a similar stratified flame DNS database to that considered here, without any scalar or turbulence forcing mechanisms, and found that $S_T/S_L$ and $A_T/A_L$ remained comparable to each other, and the results presented in Fig. 16 under scalar forcing are consistent with the previous findings by Brearley et al. (2020).

Fig. 13

Evolution of mean $\left\langle \xi \right\rangle$ (left) and the rms value $\xi '$ (right) of mixture fraction in the unburned gas for for the reacting cases I(i,ii)

Fig. 14

Evolution of the PDF of $\xi$ in the unburned gas (defined by $c<0.001$) for initial integral length scale ratios of $\ell _{\xi 0}/\ell _0=0.5$ (left) and 2.0 (right)

Fig. 15

Evolution of the scalar to turbulence integral length scale ratio $\ell _\xi /\ell$ in the unburned gas for initial integral length scale ratios of $\ell _{\xi 0}/\ell _0=0.5$ (left) and 2.0 (right)

Fig. 16

Evolution of the turbulent flame speed normalised by the laminar flame speed $S_T/S_L$ and the turbulent flame surface area normalised by the laminar flame surface area $A_T/A_L$ for initial integral length scale ratios of $\ell _{\xi 0}/\ell _0=0.5$ (left) and 2.0 (right)

The nature of the mixture inhomogeneity distribution can have significant effects on the turbulent flame speed, and as such, there are no tabulated flame speeds that can be used to validate these results. Furthermore, there have not been any statistically stationary DNS data for stratified mixture combustion for the canonical configuration considered in this analysis. This serves as the motivation for the development of a scalar forcing scheme for obtaining statistically stationary stratified flame simulations. It is also important to note that there is no experimental data corresponding to the canonical configuration available in the literature for comparison purposes.

The slight difference between the steady state values of $S_T/S_L$ for the two cases with $\ell _{\xi }/\ell _0 = 0.5$ and 2.0 cases arises due to the differences in the scalar length scale evolutions for these cases. This can also be observed in Fig. 15, which shows that $\ell _\xi /\ell _0$ increases from its initial value with time for the case with $\ell _{\xi }/\ell _0=0.5$, whereas an opposite behaviour is observed for $\ell _{\xi }/\ell _0=2.0$. However, $\ell _\xi /\ell _0$ for these cases eventually assumes comparable values under statistically stationary state. These differences give rise to differences in the scalar dissipation rates $N_\xi =D\nabla \xi \cdot \nabla \xi$, $N_c=D\nabla c\cdot \nabla c$ and cross-scalar dissipation $N_{c\xi }=D\nabla c\cdot \nabla \xi$ rates which affects the value of $\dot{\omega }_c = [\dot{\omega }_F + N_\xi \partial ^2Y_F/\partial \xi ^2 + N_c \partial ^2 Y_F/\partial c^2 + 2N_{c\xi }\partial ^2Y_F/\partial \xi \partial c]$ (Ruan et al. 2012; Malkeson et al. 2013), which in turn affects the evolution of $S_T/S_L$. A detailed discussion on the turbulent burning velocity and flame surface area behaviours under combined actions of turbulence and scalar forcing is beyond the scope of this analysis and will form the basis of future investigations.

5 Conclusions

The present analysis focuses on the development of scalar forcing methodology to maintain the mixture inhomogeneity in the unburned gas region in Direct Numerical Simulations (DNS) of turbulent stratified flames in canonical configurations without any mechanism for the generation of scalar and velocity fluctuations. The scalar forcing identified in this paper not only maintains both the mean and rms of the scalar, but also retains the initial specified scalar PDF along with upper and lower bounds of the scalar in question for both passive scalar mixing and turbulent stratified mixture combustion subjected to a variety of different turbulent velocity forcing schemes. In particular, it has been demonstrated that the scalar forcing scheme identified in this paper can, in principle, reasonably maintain any symmetrical inhomogeneity distributions between bell-shaped and bimodal, and thus it has the potential to become a useful research tool for turbulent stratified mixture combustion using DNS especially for large turbulence intensities and rms values of scalar fluctuations. The newly proposed scalar forcing does not artificially affect the evolution of the scalar integral length scale. The integral length scale of mixture inhomogeneity has been found to be driven by the turbulent fluid motion and the integral length scales associated with the respective scalar and velocity fields eventually assume comparable values in the order of magnitude sense due to the similarity of scalar and velocity spectra for Schmidt numbers of the order of unity.

In the present analysis, the application of scalar forcing for turbulent stratified flame simulation has been demonstrated for single step chemistry as a proof of concept but this methodology needs to be extended for detailed chemistry and transport. In addition, the scalar forcing methodology has been assessed in this analysis for small Mach numbers but the applicability of the proposed forcing methodology for large Mach number values need to be assessed. Moreover, the identification of differences in stratified combustion process due to forced and unforced scalar mixing is beyond the scope of current analysis because the current study deals with the proof of the concept of scalar forcing for DNS of stratified mixture combustion. It is also worth noting that a simple proportional feedback control is used in this analysis for the purpose of simplicity. However, there is further scope for improvement of the error correcting mechanism for the mean value by employing a more complex controller. Furthermore, the forcing parameter can be taken to be a function of scalar dissipation rate which may have an impact on the scalar length scale evolution but this aspect is kept beyond the scope of current analysis. Note that the implications of scalar forcing within the flame are yet to be analysed and some of these issues will form the platform for future investigations.

Appendix

Figure 17 shows the evolution of the scalar field PDF in the non-reacting cases where the scalar bounds are strictly enforced by a limiting condition (i.e. if $\psi < \psi _l$ then $\psi = \psi _{l}$, and if $\psi > \psi _u$ then $\psi = \psi _{u}$). The simulations are identical to that in Fig. 4 aside from these conditions. Such a method of strictly enforcing the scalar bounds is effective for bimodal distributions since a high probability of finding the scalar value near to the bounds is desirable. For other distributions, such as the bell-shaped and roughly flat distributions shown in Fig. 8, the likelihood of the scalar exceeding the bounds is substantially lower than for a bimodal distribution, which is already very low. For example, in Fig. 8, the scalar stays within its specified bounds naturally without the need for any external intervention. If methodology to strictly enforce the boundedness is required, using the same methodology to maintain bimodal distributions is perhaps not a good solution since it will cause a small increase in probability of finding scalar at its desired extreme limits (i.e. minimum and maximum values). In practice, this solution would be adequate since the probability of the scalar exceeding the limits remains small (see Fig. 8). Alternatively, a low-pass filtering operation can be applied to the scalar field to achieve the desired bounded behaviour. In a stratified flame, the range of equivalence ratio remains within the flammability limit and thus small overshoots in the mixture fraction or equivalence ratio is not expected to affect the accuracy of the simulations provided the flow is sufficiently resolved.

Fig. 17

Evolution of the PDF of the passive scalar $\psi$ in cases A–C where strict boundedness has been enforced using a limiting condition. Columns 1–3 show initial $\ell _{\psi 0}/\ell _0=0.5$, 1.0 and 1.5 respectively, while rows 1–3 show simulations without velocity forcing, with Lundgren forcing, and with modified bandwidth filtered forcing respectively