1 Introduction

Liquid atomization is an essential unit operation that has applications in various industrial processes, such as combustion, surface coatings, and spray drying. Its objective is to increase the surface area between the liquid phase that is being atomized and the surrounding gas, which promotes the rate of heat and mass transfer (Lee and Abraham 2011). The enlargement of the surface area requires energy, which must be transferred to the liquid using a suitable atomizer (Lefebvre and McDonell 2017). Due to the wide range of applications, there is a vast number of different types of atomizers, each with their own strengths and weaknesses.

This particular study focused on understanding the behavior and performance of the Air-Core-Liquid-Ring (ACLR) nozzle (Stähle et al. 2017), which is a type of internal-mixing pneumatic nozzle. In pneumatic nozzles, the atomization energy is transferred via a compressed gas stream (Omer and Ashgriz 2011), which enables the atomizer to handle liquids with higher viscosities than other common nozzle types, such as pressure swirl nozzles (Stähle et al. 2017). As an internal-mixing atomizer, the gas and liquid flows are combined inside of the nozzle (Wozniak 2003). This allows for a more efficient transfer of energy from gas to liquid, so lower gas flow rates are necessary than in external-mixing atomizers (Hammad et al. 2020).

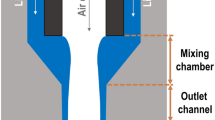
The ability to handle higher viscosities makes the ACLR-nozzle of special importance for spray drying, since it also means that higher solid concentrations can be handled (Rao 2014). Based on a model calculation by Fox et al. (2010), Wittner et al. (2020) showed that the ACLR-nozzle can potentially reduce the total energy consumption in spray-drying processes up to 29% compared with the utilization of a standard pressure swirl nozzle. A schematic of the ACLR-nozzle is shown in Fig. 1. The device is composed of two concentric tubes. The outer tube is where the liquid feed flows, while a capillary at the center carries the gas, which for spray drying processes is compressed air, and injects it at the core of the liquid phase in the mixing chamber. This forms an annular flow, with a liquid lamella (or ring) around the air core. As this two-phase flow exits the nozzle, the air phase expands, and the liquid film forms a cone that breaks up into droplets (Wittner et al. 2018b).

Fig. 1
figure 1

Schematic of the Air-Core-Liquid-Ring (ACLR) atomizer. The nozzle is composed of a casing where the liquid flows in, and a capillary that injects the compressed air into the middle of the liquid phase, which causes the formation of an annular flow

Full size image

However, as with most internal-mixing pneumatic nozzles, the free-surface interaction between air and liquid inside the nozzle causes the flow conditions to be unstable. Combined with the highly turbulent flow of the air core, this may lead to fluctuations of the thickness of the liquid film and consequently to a wide droplet size distribution during atomization (Zaremba et al. 2017). Additionally, air and liquid flow cannot be set entirely independently of each other (Wittner et al. 2018b), as the interaction between the liquid volume flowrate and the inlet air pressure defines the resulting air flowrate. In order to be able to design the flow conditions in the ACLR-atomizer and ensure a stable spray with narrow droplet size distribution, the internal flow needs to be fully comprehended. This knowledge is essential to formulate the process function of the ACLR-nozzle and to be able to tailor the nozzle design for specific industrial applications.

Since it is not feasible to measure pressure and velocity profiles inside the nozzle, this study focuses on building a computational fluid dynamics (CFD) model that allows the investigation of the fluid behavior inside the ACLR-atomizer. With such a model, we could then predict the effect of different process conditions and of the geometric design of the nozzle on the flow variables inside the nozzle and the spray performance outside of it.

While there are some computational studies of pneumatic internal-mixing atomizers, most of them modelled only water-air mixtures or executed very limited experimental validation of the model (Alizadeh Kaklar and Ansari 2019; Mousavi and Dolatabadi 2018; Mohammadi et al. 2022). There is one former study from Wittner et al. (2019) which focused on the ACLR nozzle. However, they assumed a constant density for the air phase, instead of using a compressible gas model, which can increase simulation error (Alizadeh Kaklar and Ansari 2019). They also identified that optical distortions, caused by refraction from the curved geometry and from the refraction indexes of the materials, had to be considered in the experimental measurements. The purpose of this study was to assemble an efficient and reliable CFD model on ANSYS Fluent that could represent the flow conditions inside the ACLR nozzle, and to validate this model with experimental data with a highly viscous liquid, since it is the main application for this type of nozzle.

2 Nozzle Design

Figure 2 displays the design used for the ACLR-nozzle. It consists of two parts: a metal capillary tube, which injects the compressed air, and a clear acrylic block around it, which receives the liquid feed and houses both the mixing chamber (with a length of 2.4 mm) and the outlet channel (with a length and diameter of 1.5 mm). The clear material was chosen to allow the visualization of the flow inside the nozzle.

Fig. 2
figure 2

Nozzle geometry, which is composed of a central steel capillary (dark grey) surrounded by PMMA block (light grey). Dimensions for the designated mixing chamber and outlet channel are shown

Full size image

3 Experimental Setup

As in former studies (Wittner et al. 2019; Taboada et al. 2021), a spray test rig was used for the atomization experiments, with various model solutions and operating conditions.

3.1 Spray Test Rig

A schematic of the spray test rig is shown in Fig. 3. The liquid flow was supplied and maintained by an eccentric screw pump (NM011BY, Erich Netzsch GmbH and Co. Holding KG, Waldkraiburg, Germany) and measured by a flow meter (VSI 044/16, VSE GmbH, Neuenrade, Germany). Air was used as atomizing gas, which was supplied by a compressor (Renner RSF-Top 7.5, Renner GmbH, Güglingen, Germany). Gas pressure was adjusted with a pressure regulator. The resulting gas volume flow was measured by a gas flow meter (ifm SD6000, ifm electronic, Essen, Germany). The liquid pressure was not monitored in the performed investigations. The spray mist was collected by a vessel below the measurement zone. The collector vessel was equipped with a filter and connected to an exhaust fan to prevent recirculation of small droplets into the measurement zone. All trials were performed at room temperature, which was assumed to average 25 \(^\circ\)C for all calculations and simulations.

Flow conditions inside the exit orifice of the atomizer were optically analyzed. For that purpose,a high-speed video camera (OS3-V3-S3, Integrated Design Tools Inc., Tallahassee, FL, USA) was used. It was equipped with a 150 mm macro lens (150 mm F2.8 EX DG OS HSM, Sigma, Kawasaki, Japan) with a polarizing filter. The exit orifice of the atomizer was illuminated from the opposite side of the camera with diffused light from a high performance light-emitting diode system (constellation 120 E, Imaging Solution GmbH, Eningen unter Achalm, Germany).

Fig. 3
figure 3

Setup of the atomization test rig. The elements in the schematic are not shown in scale

Full size image

3.2 Visualization of Internal Liquid Lamella

The high-speed camera recorded the internal flow of the nozzle at a rate of 20 kHz. Each measurement was composed of 10,000 images, which amounts of a measurement time of 0.5 s. The exposure time was 5 µs, and the resolution was around 10 µm/pixel. An example of the recorded images is shown on Fig. 4a. Each image was processed following the algorithm described by Wittner et al. (2019), which is programmed on Matlab (The MathWorks Inc., Natick, MA, USA). An example of the processed image can be seen on Fig. 4b. The algorithm effectively uses grayscale analysis to track the interface between gas and liquid, as the pixel with the largest intensity gradient. The tracked interface can be seen on the image as a red contour. The program then calculates the lamella thickness in the middle section of the channel, i.e. where the three green horizontal lines are located. The lamella thickness at the middle line was used when analyzing the average lamella thickness. The other two measurements of the lamella thickness where used to validate that the tracking did not have unexpected jumps in lamella thickness.

Fig. 4
figure 4

a Sample flow profile at the outlet channel. The liquid phase on both sides of the outlet is noticeably lighter than the gas core at the center, which allows the gradient method to be used. The dotted orange rectangle exemplifies the near-wall region obscured by light refraction. b Same sample profile processed by the Matlab code. The channel wall and the interface are determined, and the lamella thickness is calculated in the middle region of the channel, i. e. at the green horizontal cross-sections

Full size image

Wittner et al. (2019) mentioned that optical distortions may cause some underestimation of the lamella thickness. This possibility was evaluated by running simplified models of the system on the raytracing program TracePro (Lambda Research Corporation, Littleton, Massachusetts, USA), with different liquid lamella thicknesses. The theoretical calculations were also corroborated by measuring the apparent width of single-thread Nylon lines (Maxima Fishing Lines, Geretsried, Germany) of known diameter, after they were inserted inside of a replica of the nozzle that was filled with model solution. Both methods led to the conclusion that the distortion of the lamella thickness and that of the diameter of the outlet channel are proportional. Since the lamella thickness is calculated proportional to the channel diameter, the distortion is already corrected by the algorithm.

However, the curvature at the nozzle wall casts a shadow that begins to interfere with measurements for lamella thicknesses below 0.08 mm (see the dotted rectangle on Fig. 4a) and completely obscures measurements below 0.05 mm. Since the code identifies the highest intensity gradients, the shadow at the wall may reduce the gradient value at the interface, when it is close to the wall. This may lead to a misidentification of the liquid/gas interface. To fix this, we had to limit the gradient recognition in the code to only the pixels that were more than 0.05 mm away from the wall. That means, only lamella thicknesses above this value can be measured. Additionally, we altered the original code to compare all local maxima, starting with the one closest to the wall. Based on some threshold values of the gradient and the actual intensity value of each maximum, the interface was then chosen. These threshold values were refined based on preliminary testing with sample recordings of the liquid lamella, to ensure that the interface was being tracked correctly.

3.3 Model Solutions

Experiments were carried out with water and with a 47% m/m maltodextrin solution (Cargill C*DryTM MD 01910, Germany). The fluid properties of these model solutions were also introduced into the simulations (see Table 1), to recreate the experimental validation. The air properties in the table are averaged, since they change with pressure between measurements and even along the nozzle. The properties of air and water were taken from the database of ANSYS, Inc. (2019). The viscosity of the maltodextrin solution was measured with a rotational rheometer (Physica MCR 301, Geometry DG26.7, Anton Paar, Austria) at shear rates between 10 and 10\(^3\) s\(^{-1}\). Its density was measured by use of a 25 cm\(^3\) pycnometer (Blaubrand, Brand, Wertheim, Germany).

Table 1 Average properties of the simulated phases
Full size table

It is important to note that the model selection was performed using the experimental data from Wittner et al. (2019) who used a 0.39 Pa∙s maltodextrin solution. This was done because it was carried out simultaneously with the experiments. Nonetheless, the time-dependent and time-averaged analysis (Sects. 5.3 and 5.5) were carried out using our own experimental data for comparison.

3.4 Operating Nozzle Conditions

Three different gas pressures were used for the experimental investigation and the simulations, at a fixed liquid flowrate. Taking into account that also two viscosities were analyzed, six configurations were evaluated in total, and they are summarized on Table 2. It should be noted that the model selection was done with fixed operating conditions of 0.3 MPa and 40 L/h because it was based on previous experimental data from Wittner et al. (2019).

Table 2 Analyzed variables in the experiments and simulations
Full size table

4 Numerical Model

The numerical model was implemented on ANSYS Fluent 2019 R3 (Ansys, Inc., Canonsburg, Pennsylvania, USA). Several steps were followed to build the model that best represented the physical system. Different approximations to the governing equations and numerical methods were evaluated in order to select the ones that could better capture the complex multiphase flow behavior inside of the nozzle. The simulating and boundary conditions of the model were defined to approximate the experimental conditions. Additionally, a polyhedral mesh was generated to represent the geometry of the nozzle design.

4.1 Governing Equations and Models

The internal flow of the nozzle is an immiscible mixture of two phases: an incompressible Newtonian liquid, and a gas phase, for which three equations-of-state were evaluated (incompressible, ideal gas, and the Redlich–Kwong model for a real gas Aungier 1995). The multiphase flow was modelled using the Volume Of Fluid (VOF) method. VOF assumes that all fluid phases share the same pressure and velocity fields. This means that the two-phase system is numerically treated as a single-phase fluid, whose physical properties are calculated from the volume-averaged properties of the actual phases (Sun and Zhang 2020). This means that only one momentum equation, like the one shown in Eq. 1, is solved to predict the velocity and pressure fields of the mixture.

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} \int _{V} \rho \textbf{u}\textrm{d}V + \int _{A} \rho \textbf{u}\otimes \textbf{u} \cdot \textrm{d}\textbf{A} = - \int _{A} p \textbf{I}\cdot \textrm{d}\textbf{A} + \int _{A} \varvec{\tau } \cdot \textrm{d}\textbf{A} +\int _{V} {\mathbf {f_b}}\textrm{d}V \end{aligned}$$
(1)

On the left side of the equation are the terms for transient and convective transport. \(\textbf{u}\) represents the velocity vector, while \(\rho\) is the volume-averaged density. On the right side of the equation are the pressure gradient term, the viscous flux term, and external body force term. p is the local pressure, while \(\varvec{\tau }\) is the stress tensor, and \({\mathbf {f_b}}\) is the body force vector. It should be noted that \(\textbf{I}\) is the identity matrix (Alizadeh Kaklar and Ansari 2019; Ballesteros Martínez et al. 2020). As for the integrals and differentials, V represents the volume; \(\textbf{A}\) is the area vector of the surface that encloses the volume, and t is time.

The VOF method requires the introduction of additional differential transport equations for the volume fraction of the phases. The conservation equation that describes the transport of the volume fraction (\(\alpha\)) of each phase i is shown in Eq. 2.

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t} \int _{V} \rho _{i}\alpha _{i}\textrm{d}V + \int _{A} \rho _{i}\alpha _{i} \textbf{u} \cdot \textrm{d}\textbf{A} = S_{i} + \sum _{j}(\dot{m}_{ji}-\dot{m}_{ji}) \end{aligned}$$
(2)

On the left side of the equation are again the terms for the transient and convective transport. On the right side of the equation, the first term takes into account the sources or sinks (S) of the phase; the second term accounts for mass transfer between phase i and any other existing phase j (ANSYS, Inc. 2019; Ballesteros Martínez et al. 2020). In this study there are no sources or sinks as there are neither reactions nor phase changes. In each cell of the mesh, the sum of the volume fractions of all phases must always be one, so only one extra independent equation has to be solved when dealing with a two-phase flow.

This additional equation requires a specific scheme that can handle the discontinuity of the phases at the interface. There are different available options for such type of schemes (ANSYS, Inc. 2019). Geometric schemes, such as Geo-Reconstruct, track the discontinuities in the volume fraction field and reconstruct a linear interface plane in each cell, which can be very computationally expensive (Denner and van Wachem 2014). Compressive methods, such as CICSAM and HRIC, skip the explicit geometrical reconstruction of the interface and focus on solving the volume fraction gradient with high-resolution numerical schemes. This makes these methods more efficient, but can lead to diffuse or distorted interfaces (Di Zhang et al. 2014). It was therefore necessary to examine which scheme works better when simulating the annular flow inside the nozzle. Two possible models were pre-selected (Geo-Reconstruct and CICSAM) based on previous studies on multiphase flow simulation, particularly for high-viscosity liquids, as well as literature recommendation (ANSYS, Inc. 2019; Waclawczyk and Koronowicz 2008; Jabbari et al. 2014). Both schemes were used with an explicit formulation of the volume fraction equation, which means that the solver directly uses the known quantities from the previous timestep without requiring additional iterations. For our case, where there is no mass transfer between the phases nor any sources or sinks, the explicit formulation utilized is the one shown on Eq. 3 (ANSYS, Inc. 2019).

$$\begin{aligned} \frac{\rho _i^{n+1}\alpha _i^{n+1} - \rho _i^{n}\alpha _i^{n}}{{\Delta }t} V = -\sum _f\left( \rho _i^{n}\alpha _{i}^{n}u_f^n A_f\right) \end{aligned}$$
(3)

This formulation is comparable with Eq. 2, especially with the terms on the left of the integrated equation. The left term on Eq. 3 represents the time derivative discretized between the previous timestep n and the next timestep \(n+1\). The right term represents the convective transport, which is summed up for every face f of the cell, taking into account the normal volumetric flux u and the area of the face A. This formulation was only used for the liquid phase. The air was designated as the primary phase, which means that its volume fraction is calculated in each cell by subtracting the liquid volume fraction from one (ANSYS, Inc. 2019).

The internal flow was modelled as transient because of the unstable free surface between the phases. A first order implicit formulation was used for the time discretization, since an explicit scheme could not be coupled with the explicit formulation used for VOF (ANSYS, Inc. 2019). In addition, the implicit formulation provides a larger numerical stability and allows the use of larger timesteps (Pulliam 1993). A pressure-based solver was implemented, using the Pressure Implicit with Splitting of Operators (PISO) algorithm for the velocity-pressure coupling. With this algorithm, the velocity and pressure fields are iteratively and consecutively calculated within each timestep (i.e. the velocity field is updated on the previous pressure field and vice versa) until convergence is reached (Xiao and Jenny 2012). A schematic of the general solver algorithm of this iteration with a VOF formulation can be seen on Ballesteros Martínez et al. (2020).

All equations were spatially discretized with a second order upwind scheme, except for the pressure and the volume fraction. The options evaluated for the volume fraction were discussed before already. For the pressure, we utilized the PREssure STaggering Option (PRESTO!) scheme. All discretization schemes were chosen following recommendations by ANSYS, Inc. (2019).

Along the gas-liquid interface, the fluid immiscibility generates a tensile tangential force known as surface tension force. This force (\({\mathbf {f_b}}\)) is modelled by the VOF method using the Continuum Surface Force (CSF) method developed by Brackbill et al. (1992). The model considers surface tension as a body force that depends on the interfacial tension coefficient (\(\sigma _{ij}\)) between phase i and j, the phase densities (\(\rho _i\), \(\rho _j\)), as well as the volume-averaged density of the mixture \(\rho\) (see Eq. 4).

$$\begin{aligned} {\mathbf {f_b}} = \sigma _{ij} \frac{\rho \kappa _i \varvec{\nabla }\alpha _i}{\frac{1}{2} (\rho _i+\rho _j)} \end{aligned}$$
(4)

The model also takes into account the gradient of the volume fraction (\(\varvec{\nabla }\alpha _i\)), and the curvature of the interface (\(\kappa _i\)). This curvature is calculated as the divergence of the normalized gradient vector (ANSYS, Inc. 2019). The calculated body force is then incorporated into the body force term of the momentum equation (Eq. 1).

Because of the nature of the multiphase flow, the model has to handle the velocity and viscosity differences between the liquid and gas phases. This impacts how the turbulence in the internal flow has to be resolved. Using the common Reynolds number (Re) estimations used for annular flows (Ramsey 2019; Zeigarnik 2006), we expected the aircore to experience a highly-turbulent flow regime with Re numbers of up to \(10^5\), while we expected the liquid lamella to remain in the laminar regime with Re numbers of up to \(5\times 10^2\). These estimations were corroborated with the liquid properties and velocities obtained in this study. Because our study case involved a wall-bounded flow with a high Reynolds number, this study was centered on evaluating and choosing an appropriate Reynolds-Averaged approach for modelling the turbulence. No additional option, such as implementing a Large Eddy Simulation method, was considered. This decision was made in order to maintain the CFD model and the mesh as simple and efficient as possible, since LES (or even hybrid variations of it) scale strongly with the Re number of the flow and are very sensitive to the mesh density (Xiao and Jenny 2012; Blocken 2018).

With a Reynolds-Averaging approach, the instantaneous flow velocity is decomposed into a time-averaged and a time-fluctuating component. Substituting this decomposition into Eq. 1, results in the Reynolds-Averaged Navier–Stokes (RANS) equation, which has the same general form of the normal Navier–stokes equation, apart from an additional term for the divergence of the Reynolds stresses (Baker et al. 2019). When simulating transient flows, the equations are averaged over small time scales, so that the time derivative remains in the equation. This variation of the approach is known as Unsteady RANS, or URANS (Baker et al. 2019).

On principle, there are six Reynolds stress tensor components that represent the turbulence effects in all directions. These must be calculated with additional turbulence closure equations, for which there is a wide variety of models (ANSYS, Inc. 2019). Three URANS options were evaluated for this study, based on accuracy and computational cost. The first two, the k-\(\omega\) SST and the standard k-\(\epsilon\) turbulence viscosity models, are fairly similar. Both are computationally efficient, because they assume that Reynolds stresses are isotropic, which reduces the closure equations that need to be solved to just two. A k-\(\epsilon\) model solves the turbulent kinetic energy (k) and the turbulent dissipation rate (\(\epsilon\)), while an k-\(\omega\) model replace the \(\epsilon\) for the dissipation rate per unit turbulent kinetic energy (\(\omega\) = k/\(\epsilon\)). The third option we evaluated was the Reynolds Stress Model (RSM). RSM uses a set of seven equations. This causes the model to be quite computationally expensive, but it can simulate anisotropic and rotational phenomena that cannot be modelled with the previous models. A more thorough explanation of what the equations that compose these models are and how they are implemented into the governing equations is presented in Baker et al. (2019). No additional wall treatment was coupled with the models apart from the one already incorporated by ANSYS, Inc. (2019).

The mesh and physics model tests were performed using a base CFD model, which initially used the k-\(\omega\) SST turbulence model, the Geo-Reconstruct scheme for interface capturing, and the ideal gas equation-of-state. First, the three possible turbulence models were tested, while maintaining the rest of the CFD model unaltered. The base model was then updated with the selected turbulence model, before using it to determine the interface scheme. This process was repeated once more in order to choose a gas equations-of-state. The model configuration that resulted from this step-by-step analysis was then used for the experimental validation.

4.2 Boundary and Simulating Conditions

Just as in the experimental setup, the gas pressure and the liquid flowrate were the inlet boundary conditions set in the simulations. The nozzle exit was set as an atmospheric pressure outlet, while two symmetry planes were set in the faces where the nozzle was divided into quarters. A graphical representation of these boundaries can be seen in Fig. 5a. Gravity was set in the direction of the outlet (the z-direction on Fig. 5b). For the initialization the mixing chamber and the liquid feed ring were filled with liquid and the capillary and outlet channel were filled with gas. Figure 5b shows the initial phase distribution.

Fig. 5
figure 5

a Boundary conditions implemented into the nozzle simulation. b Initialization of liquid and gas phases

Full size image

As for the turbulent inlet conditions, these were set following the recommendations from ANSYS, Inc. (2019). The turbulent viscosity ratio was left at its default value of 10. On the other hand, the turbulent intensity I was estimated using Eq. 5.

$$\begin{aligned} I = 0.16(\textrm{Re})^{-1/8} \end{aligned}$$
(5)

The Reynolds number Re was estimated from the velocity profiles from Wittner et al. (2019) but was later corroborated with our own simulation results. The hydraulic diameter of each phase inlet was used as characteristic length of the Reynolds calculations. No further investigation was done on the turbulent boundary conditions because there were no means available to validate them experimentally, and the turbulence model chosen has a low sensitivity to turbulent inlet conditions (see Sect. 5.2).

The simulations were initially run with a fixed timestep that was chosen using the Courant–Friedrichs–Lewy (CFL) criterion. This criterion relates the flow velocity with the spatial and temporal discretizations. A CFL value below one indicates that no change in the flow variables can be advected through more than one cell of the mesh in one timestep, which is considered a necessary condition for convergence. With this in mind, the timestep was calculated with the maximum velocity observed in the results of the numerical model utilized by Wittner et al. (2019) and the reference cell size of the finest mesh evaluated in the mesh independence test (see Sect. 4.4). The resulting timestep was of 0.5 \(\upmu\)s. This means that there might have been local CFL numbers in some cells that reached values over one, because some cells might be refined by the mesh solver to slightly smaller sizes than the reference size. However, according to ANSYS, Inc. (2019), CFL values of up to 5 can be handled by the solver without affecting convergence, so these local high values were considered acceptable. This assumption was later reevaluated during the model selection (see Sect. 5.2).

All simulations were run for at least 8 ms. This minimum run-time was decided based on two main criteria. On the one hand, the flow variations were observed to occur every 1–2 ms, both in the results from Wittner et al. (2019) as well as in our experimental profiles (see Fig. 13). On the other hand, we considered an approximated time that the slowest phase (the liquid) would require to flow all throughout the nozzle, which also amounted to 2 ms. Based on this information, we accounted for 4 ms of initialization time and used the other 4 ms of simulated time for the time-dependent and time-averaged analysis. We corroborated this by plotting the Air-to-Liquid ratio (ALR) and ensuring that it was oscillating within a stable range, which would be expected in the physical system. For every timestep, the convergence criteria was to reach absolute residual values below \(10^{-3}\), which was usually achieved within 20 iterations.

4.3 Calculation of Lamella Thickness

To make the simulation results as comparable as possible, the lamella thickness was determined replicating the measuring methodology used in the experiments (see Sect. 3.2). This meant that a linear probe was created in the middle of the outlet channel, with the same length as the radius of the channel. This is equivalent to the middle green cross-section shown on Fig. 4 for the experimental measurements. The liquid volume fraction \(\alpha _{liquid}\) was measured along the length of the linear probe. The resulting profile was then turned into a step function following the criteria shown in Eq. 6.

$$\begin{aligned} {\left\{ \begin{array}{ll} 0 &{} \alpha _{liquid}\le 0.5 \\ 1 &{} \alpha _{liquid}>0.5 \end{array}\right. } \end{aligned}$$
(6)

Using a line integral and the aforementioned step function, we calculated the portion of the line probe that was occupied by the liquid phase. This is is equivalent to the linear lamella thickness that is measured with the high-speed camera. The conversion to a step function was not considered to affect the calculations significantly, since the phases remain mostly segregated and with a sharp interface (see Fig. 14a).

4.4 Mesh Generation

Some simplifications were considered when creating the geometry and mesh for the system. First, only a quarter of the internal volume of the nozzle was simulated, in order to reduce computation cost. This type of simplification is common in multiphase computational analysis and has been found in other studies with segregated and annular flows, where bilateral or even axi-symmetry (Alizadeh Kaklar and Ansari 2019; Ballesteros Martínez et al. 2020) has been assumed for vertical flows. It is important to note that the simplification does not mean that each quarter of the nozzle behaves exactly the same, but rather that there is no consistent difference between each quarter of the nozzle. This means that, though there may be local and temporal differences and perturbations in the flow on each side, the average nozzle behavior can still be deduced from modelling a quarter of it.

Additionally, since the aim of the study was to understand the two-phase flow inside the nozzle, we did not mesh all of the geometry with the same fineness and grid type. The regions of interest, i.e. the mixing chamber and the outlet channel, have a fine polyhedral grid, while the inlet regions, where there is only either gas or liquid, were fitted with a coarser hexahedral grid. Figure 6 shows the final mesh obtained for the geometry.

Fig. 6
figure 6

Mesh representation of a quarter of the nozzle. Close-ups of the two types of meshes utilized (hexahedral and polyhedral) are shown; the prism layers generated in the near-wall region are also indicated

Full size image

Since polyhedral cells are multi-faceted, they are connected to a high number of neighboring cells, which allows a better and more robust approximation of transport gradients (Sosnowski et al. 2017). They do tend to form, however, high-density meshes, which is why the hexahedral cells were used in the single-phase inlet regions. It should be noted that thin prismatic cells were generated near the wall all around the geometry to better approximate the boundary layer (Okumura 2000).

A mesh independence test was carried out to define the optimal cell density. Such a test is based on running several simulations of the same system under the same conditions with increasing mesh densities, until a convergence criterion reached a stable value (Versteeg and Malalasekera 2007). With that in mind, we generated four meshes (M1–M4) using the parameters shown in Table 3. They all differed in reference cell size, while the number of prism layers was kept constant. The thickness of the first layer was calculated following good practice recommendations by White (2016), to make sure that its y+ [i.e. the dimensionless wall distance relative to the viscous wall layer as defined by Schlichting and Gersten (2017)] was below one. For that calculation, we used the maximum velocity observed in the results of the numerical model utilized by Wittner et al. (2019).

Table 3 Mesh parameters for the four grids (M1–M4) evaluated in the mesh independence test
Full size table

The convergence criteria were the lamella average thickness (our main flow parameter of interest) and the Air-to-Liquid Ratio (ALR), as it can be seen on Fig. 7a. The ALR is the ratio between the air and liquid mass flows, and it has been identified in previous studies as an important process parameter for pneumatic nozzles (Wittner et al. 2018a, b). More details of the independence test are shown in our past conference proceeding (Ballesteros and Gaukel 2022).

Fig. 7
figure 7

Effect of the number of grid cells on: a predicted liquid film thickness (left axis and gray straight line) and Air-to-Liquid-Ratio ALR (right axis and green dashed line). b Required CPU time (left axis and gray straight line) and simulating efficiency (right axis and green dashed line), which is defined as physical simulated time in \(\upmu\)s per core-hour of CPU Time. All simulations were performed for a quarter of the ACLR nozzle with a maltodextrin solution (of 0.39 Pa∙s), at a gas pressure of 0.3 MPa and liquid flow of 40 L/h

Full size image

Since mesh density affects both simulation accuracy and computational efficiency, Fig. 7b shows how the cell count impacted the total CPU time required for each mesh. In addition, we estimated how efficiently we could simulate the system: this meant determining the physical time, for which the system can be simulated, per every core-hour of CPU time. Because parallelization is not necessarily linear (Xu et al. 2007), it should be noted that these simulations were all run with 32 cores at the high-performance computer system BwUnicluster 2.0 (Baden-Württemberg, Germany).

After considering the convergence test and the simulation efficiency, we concluded that a mesh M3 is appropriate to simulate a quarter of the nozzle. This corresponds to a cell reference size of 36 \(\upmu\)m. With such mesh density, the numerical error caused by the spatial discretization seems to have been reduced as much as possible. Therefore, refining the mesh above this value would bring no benefit and only negatively affect the simulation efficiency. This is evident when looking at the finest mesh, which has around 20% more cells than the chosen mesh. The refinement caused only a 2% change in both convergence criteria but reduced simulation efficiency by around 60%.

Based on mesh independence tests observed in other studies (Alessandro et al. 2019), we decided to plot the velocity profile in the outlet channel of the nozzle. This allowed us to evaluate the spatial resolution of the grid. The resulting profiles are shown in Fig. 8, and they were taken from a cross-sectional line located in the middle of the outlet channel after 8 ms of simulation. The location of the air-liquid interface is also indicated, so that air-core velocity can be distinguished from the velocity of the liquid film. The behavior of the profiles corresponds with our conclusions from the convergence test, in that there is very little difference when comparing the finer meshes. This corroborates our decision of using mesh M3.

Fig. 8
figure 8

Effect of the number of the reference cell size (CS) on the instantaneous phase velocity profile on a cross-section in the middle of the outlet channel after simulating for 8 ms a quarter of the ACLR nozzle with a maltodextrin solution (of 0.39 Pa∙s), at a gas pressure of 0.3 MPa and liquid flow of 40 L/h. The vertical reference lines indicate the position of air-liquid interface: the cyan dotted line indicates the interface for all evaluated meshes apart for the coarsest mesh (CS = 42 \(\upmu\)m), whose interface is indicated by the gray dashed line

Full size image

Lastly, we evaluated the quality of the mesh with respect to convergence and numerical stability issues. The evaluated mesh statistics are shown on Table 4. Orthogonal quality measures the geometric distribution and validity of the cells. Flat cells with faces whose normal vectors point inwards have low-quality indexes (Ballesteros Martínez et al. 2020). Comparing both the average and the minimum values of the mesh with recommended values (ANSYS, Inc. 2019) shows that the cell orthogonal quality is within the expected range. Another parameter that is well within the recommended range is the skewness index. Highly skewed cells can decrease accuracy and destabilize the solution convergence (ANSYS, Inc. 2019). We ensured that both the average and the maximum skewness in the mesh were below the 0.95 limit.

The aspect ratio refers to how stretched the cells are. For the cells in the bulk region of the mesh, this value does not exceed the maximum recommended 5:1 ratio (ANSYS, Inc. 2019). On the other hand, cells in the prismatic layers near the wall are flat, which leads to the 100:1 aspect ratio in the maximum value. Because these cells are supposed to model the thin viscous layer near the wall, the high aspect ratio was intended and no critical maximum limit was considered. Finally, we considered the volume change ratio between neighboring cells. Values below 0.01 can indicate badly meshed regions with differently sized cells (ANSYS, Inc. 2019), but no region in the created mesh showed such small values. With this in mind, the general quality of the mesh M3 proved more than adequate to represent the system.

Table 4 Mesh quality statistics
Full size table

5 Results and Discussion

As mentioned before, the investigation was divided into an experimental and a computational study. Since the focus was to simulate the internal flow conditions of the ACLR nozzle, so that it could later be correlated with the droplet size distribution of the sprayed liquid, the investigations from both parts of the investigation centered on the liquid film thickness. For the experimental analyzes, we measured the lamella thickness and evaluated the limitations the measuring method. From the computational side, a numerical model was implemented, in order to predict the liquid lamella thickness. Finally, the results from experiments and simulations were compared, both to validate the CFD model and to analyze how the internal flow conditions change with different operating conditions. This comparison was done for time-averaged values of the lamella thickness as well as for the moment-to-moment lamella profile. In order to ensure that the operating conditions were correctly replicated in the simulations, we also used the ALR as a secondary validation parameter.

5.1 Experimental Visualization of the Internal Flow

The experimental measurement of the liquid film thickness for the six evaluated configurations can be seen on Fig. 9. As observed in previous studies (Wittner et al. 2019), the film thickness varies significantly during the atomization. However, both and the range of variation and the median lamella thickness become smaller as the operating pressure increases. Also as expected, at constant pressure, higher viscosities lead to a larger median liquid film thickness and a wider thickness variation. Complete gas core collapses (when the whole nozzle fills with liquid) are also less frequent with higher pressure and lower viscosities, which can be seen in Fig. 9 when the lamella thickness measurements reach the nozzle radius.

Fig. 9
figure 9

Liquid film thickness for water (W) and the 47% m/m maltodextrin solution (MD), at different \(p_{gas}\) and \(Q_L=40\) L/h, during 0.5 s of atomization. The region between the dotted lines represents the range between percentiles \(x_{5,0}\) and \(x_{95,0}\), while the solid line represents the median \(x_{50,0}\). The nozzle radius is represented as a dashed black line; a film thickness of this value means the nozzle outlet is filled completely with liquid

Full size image

It is important to note that the characteristic values for the distribution of the liquid film thickness do not change equally with viscosity and pressure. The median thickness for both liquids decreased around 30% when doubling the pressure, but the \(x_{95,0}\) percentile decreased twice as much for water than for the maltodextrin solution. The aforementioned lower frequency of gas core collapses may be largely responsible, but the fact that this decrease happens for water and not the maltodextrin solution indicates that liquid properties play a role on flow behavior, beyond just increasing the lamella thickness.

The measured distribution is also highly skewed, as there is a wider range of points above the median, than below. This skewedness can be seen clearly on the results shown in Fig. 10, which are fitted by a lognormal shape. We expected this distribution shape due to the nature of an annular flow. However, the errors generated by the channel curvature, as well as the measuring limit, cause a compression of the measured points between 0.05 and 0.08 mm, which appears in the distribution as a peak. This is more evident with larger pressures, as the median lamella thickness decreases and approaches the limit. Nonetheless, we considered that this compression would not affect the analysis of the inner flow for two reasons: First, it would only become significant when the median approaches the lower limit (Hartwig et al. 2020), which is typically not the case for high-viscosity liquids for which the ACLR nozzle is designed. Second, the peak is restricted to a narrow band near the lower measuring limit of the experimental setup. This means that, even when the median approaches the range of the measuring error, it is also close to the lower limit of measurement. Therefore, even if the compression of the measured data would not be there, there would be no fundamental change in any of the correlations and trends we concluded from the measurements.

Fig. 10
figure 10

Frequency density of the lamella thickness inside the nozzle for the 47% m/m maltodextrin solution (\(Q_L\) = 40 L/h) at different \(p_{gas}\). The bars represent the data frequency, while the curves are fitted lognormal distributions. The dashed black line marks the 0.08 mm threshold, below which the optical refraction begins to obscure the experimental measurement. This is what causes the peak seen in the shaded region

Full size image

As for the air-to-liquid ratio, the ALR was calculated for each of the six tested configurations. The values can be seen in Table 7 as validation of the process conditions in the simulations. The ALR follows the same trends identified already by Wittner et al. (2018b). It increases, as expected, with gas pressure and decreases slightly with increasing viscosities. The effect of pressure seems, however, to be more significant.

5.2 Numerical Model Selection

Implementing the CFD model was divided into three critical selection steps: the turbulence modelling, the interface-capturing scheme, and the gas equation-of-state. It should be noted that no real change was observed in the ALR in the simulations run for this section. They all approached the value shown on Fig. 7a for mesh M3. Because of that, it was not taken into account when choosing the physics models.

With respect to the turbulence model, each of the three options was run with the base CFD model configuration (see Sect. 4.1) until the film thickness stabilized, as shown in Fig. 11. This stabilization, which did not occur in the experimental results (see Fig. 9), was noticed but analyzed only after the model selection was finished, since the models themselves did not seem to be the reason for the stabilization. Once they stabilized, all turbulence models predict similar values for liquid film thickness. In addition, they all converge to values within a range of 10% of each other, although the behavior during the stabilization is quite different. The RSM model stabilizes quickly and with very little overshoot. In contrast, the two turbulence viscosity models took a lot more time to converge, and the k-\(\omega\) SST simulation particularly presented a large amount of variation after initialization. However, as mentioned, the stabilization was a point of contention, since it was not observed in the experiments. As a consequence, the difference in the behavior right after initializing was disregarded, and only the converged value of the lamella thickness was taken into account.

Fig. 11
figure 11

Turbulence model comparison using operating and fluid conditions from Wittner et al. (2019) (\(\mu\) = 0.39 Pa∙s, \(Q_L\) = 40 L/h and \(p_{gas}\) = 0.3 MPa)

Full size image

With that in mind, all three models perform similarly. This means that the model choice was based on the computational efficiency instead. RSM was much more computationally expensive than the turbulence viscosity (k-\(\omega\) SST and k-\(\epsilon\)) models, as it required around four times more computational time than the simpler two-equation models. Nonetheless, it still presented the same artificial stabilization. The two turbulence viscosity models required similar computational times and predicted similar values. Each calculation method has its own advantages: the k-\(\omega\) method can model the viscous regions near the channel wall with good accuracy, while the k-\(\epsilon\) method is more robust with respect to inlet condition parameters (Menter 1992). The used k-\(\omega\) SST model already uses a combination of both methods. It implements the k-\(\epsilon\) method in the free-stream region and the k-\(\omega\) method for the flow near the wall (Zahedi et al. 2017). Therefore, the k-\(\omega\) SST model was chosen as the most appropriate turbulence model for the CFD model, at least when considering the stabilized lamella thickness and the computational cost.

After an appropriate turbulence model was determined, we proceeded to evaluate the most suitable interface-capturing scheme. The two investigated models produced effectively the same lamella thickness profiles (see k-\(\omega\) SST profile in Fig. 11), but the Geo-Reconstruct method required around twice the time to run than the CICSAM scheme. Taking into account that the latter scheme is also recommended when the phases have a high viscosity ratio (ANSYS, Inc. 2019), the CICSAM method was chosen. The base CFD model configuration was updated accordingly.

Finally, the three different equations-of-state for the gas phase were evaluated. Figure 12 shows the lamella thickness profiles with the different models, as well as the experimental data from Wittner et al. (2019), for comparison. Surprisingly, the incompressible gas phase model did not present the artificial stabilization that occurred with the ideal gas model or the real gas model. Instead, it presented a flow variation quite similar to the one observed in the experiments. However, when comparing the average values with the experimental average, the error was larger with the incompressible model, with a difference of 15%. In comparison, the ideal gas model provided an error as low as 5%.

Fig. 12
figure 12

Gas equation-of-state analysis using operating and fluid conditions from Wittner et al. (2019) (\(\mu\) = 0.39 Pa∙s, \(Q_L\) = 40 L/h and \(p_{gas}\) = 0.3 MPa)

Full size image

However, computational time and ease of computation had to be considered, too. The real gas model required about 150% more time to run than the other options and still provided the same results than the ideal gas model. In addition, it required multiple attempts to converge, so we discarded it. Moreover, assuming gas incompressibility is only considered valid with gas velocities of less than 0.3 Mach (Anderson 2017), which is not the case for the investigated nozzle. From the simulation results, we expected average air velocities of around 0.7 Mach. This was later confirmed with the gas velocities that we calculated from the experimental gas flow and liquid lamella thickness (see Table 3). From the simulation results, we also observed local Mach numbers in the outlet channel as high as 1.2, which has been reported as well in previous studies on pneumatic nozzles (Park et al. 1996). This made the ideal-gas model a more suitable and reliable option, which is why it was chosen.

With the derived model configuration, we focused on the possible reasons for the stabilization of the liquid film thickness in the simulations. From the experimental point of view, this meant looking at possible sources of flow variation that were not yet included in the simulation. From the numerical side, this meant revising boundary conditions and model parameters to see if the solution was being over-restricted, or under-resolved. Table 5 summarizes the possible causes that were evaluated, from which all except for the time discretization were discarded.

Table 5 Possible sources of error for the artificial stabilization
Full size table

An adaptative timestep was therefore introduced to better capture the flow variations. This ensured that the local CFL number across all the cells of the mixing chamber and outlet channel was always below one. The timestep \(\Delta t_{step}\) was then calculated in every iteration following Eq. 7.

$$\Delta t_{{step}} = \frac{{CFL_{{global}} }}{{{\text{max}}\left( {\sum {\frac{{flux_{{out}} }}{{Volume}}} } \right)}}$$
(7)

\(CFL_{global}\) is the global CFL value desired; the default value is 2 (ANSYS, Inc. 2019), but we reduced it to one for extra measure. Ansys FLUENT then calculates the ratio of the total outgoing fluxes \(flux_{out}\) with respect to cell volume for each cell of the mesh. The maximum ratio is used to determine the timestep. The variable timestep was configured to be limited between 5 ns and 5 \(\upmu\)s, with a default maximum change factor per timestep of 20%. Nonetheless, after initialization, all simulations tended to converge to a stable timestep of around 50 ns.

5.3 Analysis of Time-Dependent Behavior of the Lamella Profile

With the derived model, we compared lamella thickness during 4 ms of operation atomization in experiments and simulations, as shown in Fig. 13. The simulations can mostly capture the unstable nature of the annular flow. However, the artificial dampening of the flow instabilities persists for high viscosity (maltodextrin) at low pressure (0.2 MPa), even if it is not as evident as it was initially during the model selection. For the other evaluated cases, flow instabilities and even complete gas core collapses can be seen on the simulations. In both experiments and simulations, the lamella thickness and the range of its variation increase with viscosity and decrease with pressure.

Fig. 13
figure 13

Simulated and experimental lamella thickness for water (W - \(\upmu\) = 0.001 Pa∙s) and the maltodextrin solution (MD - \(\upmu\) = 0.14 Pa∙s), at different \(p_{gas}\) and \(Q_L=40\) L/h, during 4 ms of atomization. The nozzle radius is represented as a dashed black line; a film thickness of this value means the nozzle outlet is filled completely with liquid

Full size image

However, comparing the profiles in more detail is difficult, because of the difference between the measuring frequency in the experiments (20 kHz) and the “calculation frequency” of the simulations (\(\sim\) 20 MHz), which refers to the inverse of the simulated timestep. This means that 1000 calculated flow conditions are represented by only one photo in the experiments. In fact, at 0.4 MPa, there are gas core collapses that can be observed on simulations but not to this extent in the experiments. The reason for this is not yet determined.

While the under-resolution of the gas turbulence in the simulations certainly plays a role, the relatively low measuring frequency of the experimental setup makes proper validation difficult. Future measurements with an ultrahigh-speed camera are expected to bring more information into how these flow instabilities develop. This will also allow a better comparison of the moment-to-moment profiles from simulation and experiments. In the meantime, a time-averaged analysis provided a clearer comparison between experiments and simulations because it is not affected by the difference in measurement frequencies. This analysis is shown in Sect. 5.5.

From the simulation side, implementing a Large Eddy Simulation (LES) model could help to better capture the moment-to-moment behavior of the lamella. This option was not initially considered because of the mentioned increased computational requirements of LES (Blocken 2018). The algebraic Wall-Modelled LES, originally developed by Shur et al. (2008), would be a promising option. This hybrid LES-RANS approach limits the computational cost of LES while still providing more time accuracy than RANS approaches, and it is already part of FLUENT’s library. Nonetheless, it would still require a reevaluation of the mesh utilized. Adding that to the fact that the time-dependent validation of the simulation is currently limited by the experimental frequency measurement, we decided that the time-averaged approach would still provide enough information about the system, for the purposes of this study.

5.4 Flow Instability Mechanisms

We investigated in more detail the flow instabilities, to reveal the physical mechanisms through which they originate and develop. There are different sources and mechanisms for flow instabilities. When talking about internal-mixing atomization, these instabilities usually refer to either Kelvin–Helmholtz instabilities (which are driven by the slip velocity between two phases) or Rayleigh–Taylor instabilities (driven by a higher-density phase penetrating into a lower density one) (Qin et al. 2018; Kumar and Sahu 2019). These are microscopic instabilities, which occur locally at the interface and then grow exponentially until they cause flow variations. However, these mechanisms do not match the flow behavior observed inside the nozzle. Rayleigh–Taylor instabilities do not apply in this case, because the phases are flowing parallel to each other. Kelvin–Helmholtz instabilities also do not seem to be a relevant factor, because the flow variations are not correlated with the velocity difference between the phases.

Table 6 shows gas (\(v_{gas}\)) and liquid (\(v_{liq}\)) velocities during atomization with the maltodextrin solution at different pressures. It also presents the maximal velocity difference between the phases (\(v_{slip}\)), and the mixture velocity (\(v_{m}\)), which is the combined volumetric flux of air and liquid (Awad 2012). While we already concluded that the flow instabilities diminish with increasing pressure, \(v_{slip}\) first increases with pressure, until 0.4 MPa, and then decreases. If Kelvin–Helmholtz were the instability mechanism, the flow variation should have also increased and then decreased. It should be noted that the average phase velocities are calculated from the mass flows and the lamella thickness measured in the experiments. However, the slip velocity is calculated with the simulations data, by taking the maximum difference between the gas and liquid velocities at the interface region. This maximum difference is typically located near the contraction where the mixing chamber met the outlet channel. This makes sense, since this is the choke point of the gas. As a side note, recalculating the Re and Mach numbers with the phase velocities shown in Table 6 matches the range of our initial assumptions during mesh generation and model selection.

Table 6 Average and maximum velocities at different \(p_{gas}\) for the maltodextrin solution (\(\mu\) = 0.14 Pa∙s, and \(Q_L\) = 40 L/h)
Full size table

Based on these results, we evaluated macroscopic instability mechanisms that may be common in two-phase annular flows. One of these kinds of instabilities is a flow pattern transition in which the flow periodically excurses between flow patterns (Ruspini et al. 2014). These types of instabilities are reflected by an N-shape of one of the characteristic curves of the system, which represent the relation between the pressure drop and the phase velocities, either of air or liquid (Ruspini et al. 2014). One can also calculate a combined characteristic curve taking into account the flux of both phases. This N-shape means that the phase velocity should increase, then decrease, and then increase again with pressure. This possibility matches in principle with the observed behavior inside the atomizer for the air velocity, though a more detailed investigation with more and higher pressure levels would be necessary for a clear correlation with the N-shape of the characteristic curve. It should be noted that the combined flowrate of the phases does not fluctuate. It always increases with pressure. This indicates that the fluctuations come from changes of how air and liquid are spatially distributed, affecting the available area for the air to flow through.

How the phases distribute themselves spatially is directly correlated with the flow pattern inside of the nozzle. If this effect is the source of the instabilities, the flow should oscillate between relatively stable annular flow and a short-lived slug flow. Relatively stable annular flow means that some lamella waviness and thickness variations can occur but there are no complete air-core collapses. In comparison, a short-lived slug flow means that a temporary complete air-core collapse is observed. These two flow patterns can be seen in the simulated and the experimental liquid profiles. Figure 14a shows the relatively stable annular flow. In fact, we can see in both profiles the choke point formed by the liquid in the nozzle contraction, from which waves develop across the lamella. On the other hand, Fig. 14b shows the slug flow with a complete air-core collapse in the nozzle. In this case, both profiles show bubbles trapped by the liquid slug against the wall.

Fig. 14
figure 14

Liquid profile from experiment (left) and simulation (right), for water (\(Q_L\) = 40 L/h and \(p_{gas}\) = 0.2 MPa). In all simulated profiles, the liquid phase is blue, while the air is red. Colors in between represent the interface between the phases or regions with dispersed bubbles. a Annular flow condition with stable air core. The dashed rectangle shows the choke point that forms after the nozzle contraction, where the lamella is at its thickest state. b Air core collapse condition. The dashed rectangle shows air bubbles that become temporally trapped between liquid collapsing from the mixing chamber upstream and the wall. For the simulation, this is seen as the blobs shaded in cyan and green

Full size image

5.5 Analysis of Time-Averaged Lamella Thickness

In order to understand the flow behavior, we calculated the time-averaged statistics of the lamella thickness for experiments and simulations. This time-average analysis is shown in form of box plots in Fig. 15. From these analytics, we observe clearly that increasing pressures and decreasing viscosities reduce flow instabilities and the average lamella thickness. Additionally, the median lamella thickness is predicted by the simulations with a relative error of around 10%, which represents less than 0.02 mm in deviation between experiment and simulation.

Fig. 15
figure 15

Box diagram of experimental lamella thickness for water (W - µ  = 0.001 Pa∙s) and the maltodextrin solution (MD - µ  = 0.14 Pa∙s), at different pressures and \(Q_L=40\) L/h. The box width correlates to a ±15% interval around the median. The whiskers mark the 95% and 5% percentiles. For the simulations (SIM), the corresponding percentiles and median values are indicated as markers

Full size image

It is remarkable that the top and bottom percentiles are also very similar between simulations and experiments, and they have the same tendency with respect to viscosity and pressure. The only exception of the observed tendency is the simulation for maltodextrin at 0.2 MPa. This is the simulation, where the artificial stabilization is at its highest level. It is obvious that range of variation is dampened. Nonetheless, even for this case, the value of the median is still within the 15% interval of the box plot. As a point of reference, this is equivalent to 0.04 ms, which represents around 4 pixels in the experimental recordings.

Further investigation might indeed still be needed to capture the moment-to-moment behavor of the lamella, from the experimental and numerical part. However, the model implemented presents already a significant improvement with respect to the previous model developed by Wittner et al. (2019). On the one hand, the flow pattern and behavior is better modelled, in that complete gas core collapses can now be observed. On the other hand, the prediction of important process parameters such as the median and top percentiles of the lamella thickness, which were identified by Wittner et al. (2019) as relevant parameters to understand the process-function of the nozzle, are significantly better predicted. The errors of up to 33% for the median and 88% for the top percentile were reduced to less than 15% and 30%, respectively, with the new model implemented. The 30% error also refers to the maximum error observed (obtained with the outlier case for maltodextrin at 0.2 MPa). The average error of the top percentile is actually 17%, which is an even more significant increase in accuracy. These improvements are considered to be a direct consequence of introducing gas compressibility into the model.

5.6 Validation of Process Conditions with the ALR

As a secondary validation parameter, we compared the average ALR between the experiments and simulations, for all the cases evaluated. The idea was to validate that the operating conditions of the process were being replicated properly in the results. As mentioned before, Wittner et al. (2018b) identified the ALR as important process parameter for pneumatic nozzles, which is why it was chosen. The results are shown in Table 7. In all cases, the relative error was found to be within ± 10%, including the case of maltodextrin at 0.2 MPa. This aligns with our conclusion that the average behavior of the inner flow that is predicted by the simulation coincides with the results observed in the experiments.

Table 7 Average experimental (EXP) and numerical (SIM) ALR for water (\(\upmu\) = 0.001 Pa∙s) and the maltodextrin solution (\(\upmu\) = 0.14 Pa∙s), at different pressures and \(Q_L=40\) L/h
Full size table

6 Conclusion

A CFD model was implemented to simulate the internal flow conditions of an ACLR nozzle. A mixed unstructured mesh, with both polyhedral and hexahedral cells was created to represent the internal volume of the nozzle. Additionally, the model was evaluated and refined to best capture the flow behavior. It was also successfully validated with experimental results.

The flow inside the nozzle behaves as expected with changes in operating conditions. The liquid film thickness of the annular flow increases with the liquid viscosity and decreases with air pressure. We also found that an increase in film thickness is related with more flow instability, and in consequence more frequent air core collapses. However, this relation seems to be affected by the liquid properties, because it does not occur at the same rate for water as for the higher-viscosity maltodextrin solution.

The numerical model can predict the average lamella thickness and the operating ALR, both with a relative error of around 10%. It can also capture in most cases the variation of the flow, with the exception of the maltodextrin solution at 0.2 MPa, where the artificial stabilization in the simulation persists. However, even for this outlier case, the average thickness was predicted with an error of less than 15%. The model presents and improvement over previous numerical models for this type of application. The inclusion of the gas compressibility is considered to be the main cause, given that it allows the complete gas core collapses to develop in the simulations as they were observed in the experiments.

With respect to the moment-to-moment instabilities, they may be related to periodical transitions in the flow pattern between the more stable wavy annular flow and the temporary slug flow that fills the nozzle outlet with liquid. The relation between phase velocities and pressures, as well as the lamella profiles observed in both experiments and simulations already indicate that this may be the cause of the flow instabilities. However, an in deep analysis of the moment-to-moment instabilities would need experimental investigations at higher recording speeds and with higher and more pressure levels.