1 Introduction

Atomization of liquids is a vital unit operation that is commonly applied in many industrial processes, such as combustion, surface coatings, and spray drying. The purpose of atomizing is to increase the total surface area between the atomized liquid phase and the surrounding gas, which promotes the overall heat and mass transfer flow between the phases (Lee and Abraham 2011). Creating additional surface area requires energy, which must be transferred to the liquid using a suitable atomizer (Lefebvre and McDonell 2017).

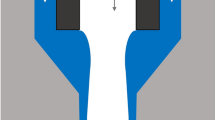
Depending on the application, there is a wide number of different types of atomizers, each with their own advantages and limitations. This particular study focuses on understanding the behavior and performance of the Air-Core-Liquid-Ring (ACLR) nozzle, which is a type of internal-mixing pneumatic nozzle (Stähle et al. 2017). A schematic of the ACLR is shown in Fig. 1. The nozzle forms an internal annular flow, with a liquid lamella (or ring) around the air core. As this two-phase flow exits the outlet channel of the nozzle, the air phase expands, and the liquid film forms a cone that breaks up into droplets (Wittner et al. 2018).

Fig. 1
figure 1

Schematic of the Air-Core-Liquid-Ring (ACLR) nozzle. Adapted from Ballesteros Martínez and Gaukel (2023)

Full size image

The ACLR nozzle is of special importance for spray drying, since it can handle high viscosity fluids while maintaining low Air-to-Liquid Ratios (ALR) (Stähle et al. 2017). Based on a model calculation by Fox et al. (2010), Wittner et al. (2020) showed that the ACLR-nozzle can potentially reduce the total energy consumption in a spray-drying processes up to 29% compared with the utilization of a standard pressure swirl nozzle.

As with most internal-mixing pneumatic nozzles, the free-surface interaction between air and liquid inside the nozzle causes the flow conditions to be unstable. Combined with the highly turbulent flow of the air core, this may lead to fluctuations of the thickness of the liquid film and consequently to a wide droplet size distribution during atomization (Zaremba et al. 2017). However, how the flow conditions mechanistically affect the resulting droplet sizes has so far proven difficult to investigate, since that would involve characterizing the near field of the nozzle, where primary atomization occurs. Gaining this information would be especially useful for the optimization of the nozzle design and the improvement of the obtained droplet size distribution and general spray performance. Unfortunately, the high velocities present near the nozzle outlet limit the amount of information that can be gained from experimental measurements (Ballesteros Martínez and Gaukel 2023), which makes numerical simulations of this primary atomization region a more attractive alternative. Additionally, a numerical model would provide more information on the flow variables (e.g. velocities, pressures) and would allow future evaluation of different nozzle geometries.

Some previous work has already been carried out to model and characterize the flow instabilities inside of the nozzle (Ballesteros Martínez and Gaukel 2023). These internal instabilities have also been shown, through experimental measurements, to be correlated with the time unsteadiness of the droplet size distribution in the far field of the nozzle (Wittner et al. 2019). Nonetheless, simulating primary atomization carries its own set of challenges, mainly because droplets can have a wide variation in sizes (see Fig. 1). While the internal lamella changes at maximum still around the same order of magnitude, the droplets can start as large as the lamella thickness and become as small as one micron. In recent years, different approaches have been developed to tackle this challenge, although none have been investigated specifically for the ACLR nozzle, or in general for internal-mixing pneumatic nozzles. Considering studies for other types of nozzles, Braun et al. (2019) used the Smoothed Particle Hydrodynamics (SPH) method to capture liquid accumulation, ligament flapping and bag breakup in prefilming air-blast atomizers. However, the authors also remarked that SPH presents some limitations in numerical convergence and that interpolation accuracy may compromise the quantitative prediction of flow variables. On the other hand, Eulerian simulations based on the Volume-of-Fluid (VOF) method (Guo et al. 2019; Warncke et al. 2017) report good agreement and accuracy when comparing with experimental observations. However, purely Eulerian simulations require extremely fine resolution in time and space. Consequently, such simulations are related to extremely high numerical costs (Braun et al. 2019). With that in mind, an alternative approach was considered to overcome the aforementioned deficiencies: a coupled Euler-Lagrangian model.

A coupled Lagrangian–Eulerian model has the potential to capture and simulate the flow conditions inside and outside the ACLR atomizer. It works by modelling the continuous phases inside the nozzle using a standard VOF model. Once the liquid exits the nozzle and breaks up into ligaments, the model tracks the liquid structures and converts them to Lagrangian particles once some predefined size and sphericity criteria are fulfilled. The conversion to Lagrangian particles leads to direct computational savings, since they do not require a fine mesh like Eulerian methods. In fact, most drag force correlations for Lagrangian particles are based on the assumption that the surrounding mesh cell is much larger than the particle (Heidarifatasmi et al. 2021). Given that the main liquid breakup is still modelled with VOF, the coupled approach can still benefit from the model accuracy of the Eulerian, i.e. VOF, modelling, while enjoying the computational efficiency of a Lagrangian approach for the droplet tracking. This coupled approach has been recently shown to provide valuable information about primary atomization and droplet sizes in other types of nozzles (Heck and Becker 2023; Lei et al. 2022), although both studies have focused on low viscous jet fuel (2 mPa\(\cdot\)s), and did not simulate the nozzle geometry itself, rather a high-pressure injection jet (Lei et al. 2022) or a spray cone from a pressure swirl nozzle (Heck and Becker 2023). Nevertheless, we expected that the model would also prove itself useful in analyzing the ACLR nozzle. Therefore, the purpose of this study was to implement and validate the coupled approach to represent the flow conditions inside and in the near field of the ACLR nozzle. In doing so, we intended to evaluate the viability and usefulness of this approach for future nozzle optimization.

2 Spray Test Rig

The experimental data used for this work was collected in a spray test rig which is described in detail in our previous study (Ballesteros Martínez and Gaukel 2023). In summary, all trials were performed at room temperature, which was assumed to average 25 \(^\circ\)C for all calculations and simulations. The flow conditions, and more specifically, the thickness of the liquid lamella inside the nozzle outlet channel were measured in a transparent nozzle with a high-speed video at 20 kHz. To characterize the lamella thickness and its range variation, we calculated the bottom 5% percentile, \(h_{5,0}\), the median, \(h_{50,0}\), and the top 95% percentile, \(h_{95,0}\), during 0.5 s of measurement.

Droplet size measurements were performed using a laser diffraction spectroscope (Spraytec, Malvern Instruments, Malvern, UK). It was equipped with a 750 mm focal lens, offering a droplet size measuring range of 2–2000 \(\upmu\)m. The spectrometer was placed 25 cm underneath the exit orifice of the atomizer. Measurements were conducted over a time of 30 s, leading to a time-averaged distribution of the droplet size. To statistically characterize the resulting spray, the bottom 10% volumetric percentile, \(x_{10,3}\), the volumetric median, \(x_{50,3}\), and the volumetric top 90% percentile, \(x_{90,3}\), were calculated for each pressure.

The experiments were carried out with a 47% m/m maltodextrin solution (Cargill C*DryTM MD 01910, Germany). The fluid properties of the model solution and the air are shown in Table 1. These are also the properties used in the simulation. The air properties in the table are averaged, since they change with pressure between measurements and even along the nozzle. The experiments and the simulations were carried at a fixed liquid flowrate (\(Q_L\)) of 40 L/h, and at three different air pressures (\(p_{air}\)): 0.2, 0.4 and 0.6 MPa.

Table 1 Average properties of the simulated phases
Full size table

3 Numerical Model

The numerical model was implemented on STAR-CCM+ v.2206 (Siemens AG, Munich, Germany). The CFD model presented in this study was built up in our previous work (Ballesteros Martínez and Gaukel 2023), which used the Volume Of Fluid (VOF) method to represent the Eulerian multiphase flow as an immiscible mixture of two phases: an incompressible Newtonian liquid, and an ideal gas phase. The details of the governing equations, mesh specifications and numerical schemes of the original model can be found there. In short, with the VOF formulation, the two-phase flow modelled as if it were a single phase. The physical properties are calculated from the volume averages of the properties of the actual phases (Sun and Zhang 2020). This means that only one momentum equation, like the one shown in Eq. 1, and one continuity equation, like the one shown in Eq. 2, are solved to predict the velocity and pressure fields of the mixture.

$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}t} \int _{V} \rho \textbf{u}\textrm{d}V + \int _{A} \rho \textbf{u}\otimes \textbf{u} \cdot \textrm{d}\textbf{A} = - \int _{A} p \varvec{I}\cdot \textrm{d}\textbf{A} + \int _{A} \varvec{\tau } \cdot \textrm{d}\textbf{A} +\int _{V} \mathbf {f_b}\textrm{d}V \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}t} \int _{V} \rho \textrm{d}V + \int _{A} \rho \textbf{u} \cdot \textrm{d}\textbf{A} = \int _{V} S\textrm{d}V \end{aligned}$$
(2)

On the left side of Eq. 1 are the terms for transient accumulation and convective transport. \(\textbf{u}\) is the velocity, while \(\rho\) represents the volume-averaged density. On the right side of the equation are the pressure gradient term, the viscous stress term, and external body force term. Correspondingly, p is the local pressure, \(\varvec{\tau }\) is the stress tensor, and \(\mathbf {f_b}\) is the external body force vector. It should be noted that \(\varvec{I}\) is the identity matrix. As for the integrals, V represents the volume; conversely, \(\textbf{A}\) is the normal vector of the surface area. Finally, t is time. As for Eq. 2, the left side represents as well the transient term and the convective transport. The term on the right side of the equation accounts for any user defined sources or sinks (S).

It should be noted that the model was recreated in STAR-CCM+ from the original model in ANSYS Fluent 2019 R3 (Ansys, Inc., Canonsburg, Pennsylvania, USA). Luckily, the same models and schemes utilized were available in both CFD tools, so the adaptation was relatively straightforward.Nonetheless, in order to capture the primary atomization, three main alteration were introduced to the existing model: a Large Eddy Simulation (LES) turbulence model instead of a Reynolds-Averaged Navier–Stokes (RANS), an Adaptive Mesh Refinement (AMR) scheme instead of the previously used fixed mesh, and a two-way coupling with a Lagrangian Particle Model (LPM) to track the droplets. Additionally, an airbox was introduced at the nozzle exit, to simulate the spray formation.

3.1 Boundary and Simulating Conditions

The boundary and initial conditions were setup following the same procedure from our previous work (Ballesteros Martínez and Gaukel 2023). The way the boundaries were defined can be seen in Fig. 2a. The gas pressure and the liquid mass flow were used as inlet conditions, while the outlet was set as pressure outlet. For the initialization, the nozzle was partially filled with liquid, while keeping a cylindric air core in the center, to approximate the expected liquid profile that is shown in Fig. 1. A more detailed schematic of the initialization is shown in Ballesteros Martínez and Gaukel (2023). Compared to the previous work, however, a half of the nozzle was simulated, instead of just a quarter. The simulated volume was extended to provide more information about the profile of the spray cone. For the same reason, an airbox was added under the nozzle outlet. The dimensions of this airbox is shown in Fig. 2b. Gravity was set in the direction of the outlet (the x-direction in Fig. 2a). For the validation of the LES model, only the internal volume of the nozzle was simulated, without the airbox. Since only half of the nozzle was simulated, the mass flow inlet was set to correspond to 50% of the liquid flow rate used in the experiments. This reduced mass flow amounted to \(6.83\times 10^{-3}\) kg/s.

Fig. 2
figure 2

a Boundary conditions implemented into the nozzle simulation b Airbox dimensions for the primary atomization simulations

Full size image

The adaptive timestep already implemented in the model ensures the stability of the solver (Ballesteros Martínez and Gaukel 2023). The timestep was configured to ensure a maximum Courant–Friedrichs–Lewy (CFL) number of 0.4. The timestep usually stabilized around 0.5 \(\upmu\)s, at least for the base fixed mesh. For the simulations of only internal volume, the simulations were run for 8 ms, of which the last 4 ms were used for data analysis. These times were based on our previous calculations in Ballesteros Martínez and Gaukel (2023). The simulations with the large airbox were run for 12 ms, to allow extra time for the external flow to develop. Again, the data of the last 4 ms of the simulations was used for the droplet size measurements. For every timestep, the convergence criterion was that the absolute residuals reached values below 10\(^{-3}\), which was usually achieved within 20 iterations.

3.2 Turbulence Model

As it is a high-Reynolds-number flow, turbulence has to be accounted for in the simulation. A Reynolds-Averaged Navier–Stokes (RANS) approach has proven to be good for time-averaged prediction of the flow behavior inside of the nozzle (Ballesteros Martínez and Gaukel 2023). However, the time-dependent behavior presented some artificial dampening of the flow variations, especially at lower pressures and higher viscosities. This is expected to be caused by the fact that a RANS approach effectively decomposes the flow variables (e.g. velocity, pressure, or energy) into a time-averaged component, which it solves directly, and a time-dependent component, which it models indirectly through additional equations (Baker et al. 2019). Because of that, the implementation of a LES model was considered.

With LES, the flow variables are not decomposed temporally, like with RANS, but rather spatially into a filtered value and a subgrid component (Baker et al. 2019). By introducing these decomposed variables into the transport equations, the filtered variables can be resolved directly. In contrast, the subgrid stresses are modelled indirectly, estimating them from the filtered values and a turbulent subgrid viscosity. There are different options to determine the turbulent viscosity. From the recommendations of the user guide, the Wall-Adapting Local-Eddy Viscosity (WALE) Subgrid Scale model was selected (Nicoud and Ducros 1999). The WALE model does have the limitation that it includes a user-defined coefficient that is not universal. However, the default value of 0.1 seems to work well for most common applications, so it was not altered (Siemens Industries Digital Software 2020). An all-\(y^+\) wall treatment was also included to improve turbulence modelling in the near-wall region. To ensure that the introduction of the LES model had the intended effect, the model was validated with the experimental data and RANS results from our previous work (Ballesteros Martínez and Gaukel 2023), in which the k-\(\upomega\) SST model was used.

3.3 Mesh Generation

The mesh configuration was based on the mesh independence analysis done on our previous study, which was performed for a quarter of a nozzle (Ballesteros Martínez and Gaukel 2023). More information about the mesh specifics and the results of the mesh sensitivity test can be found there. In short, the regions of interest, i.e. the mixing chamber and the outlet channel, were meshed with a fine polyhedral grid, while the inlet regions upstream, where there is only either gas or liquid, were fitted with a coarser hexahedral grid. To define the optimal mesh density, four meshes were generated in that study, each with a different reference cell size but with the same number of prism layers. The cell size ranged from 33–42 \(\upmu\)m. The thickness of the first prism layer was calculated following good practice recommendations by White (2016, p. 467). The convergence criteria were the lamella average thickness inside the outlet channel and the ALR. The axial velocity profile was also compared between the meshes, to evaluate the spatial resolution of the grids.

After performing the sensitivity test, it was concluded that cell sizes below 39 \(\upmu\)m led to similar results both in the convergence criteria and in the velocity profile. To provide some margin of safety, a cell size of 36 \(\upmu\)m was then selected for the RANS modelling (Ballesteros Martínez and Gaukel 2023). However, LES is known to be more sensitive to mesh fineness than RANS models (Siemens Industries Digital Software 2020), so the same mesh density could not be used for this study. In order to account for this, some reference lengths were derived from the base RANS simulations, so that the appropriate cell sizes for LES could be estimated. These reference lengths, based on the recommendations from Addad et al. (2008), were:

  • The Kolmogorov length scale (KLS): The smallest scale in the turbulent spectrum. A cell size of this magnitude approaches the results of a Direct Numerical Simulation (DNS), so it can be used to limit the local minimum cell size (Tucker 2016).

  • The Taylor micro scale (TMS): Length scales smaller than the TMS are mainly viscous-driven, so it can be used to determine the maximum local cell size (Tucker 2016).

Based on the RANS simulations, the reference scales were calculated for the three investigated pressures. The results are shown in Table 2. As expected, KLS values are always smaller than TMS values. Additionally, both length scales decrease with increasing air pressures, since it also means higher air velocities. Based on that information, a fixed mesh should have a maximum cell size of 33 \(\upmu\)m, since that is the smallest value observed for TMS.

Table 2 Reference length scales used to evaluate mesh size for LES
Full size table

The finest mesh evaluated for RANS, noted as M4 in Ballesteros Martínez and Gaukel (2023), has a reference size of 33 \(\upmu\)m, which means that the cells in the mixing chamber and outlet channel of the nozzle have to be smaller than this set value. Therefore, the M4 mesh already fulfills the KLS and TMS criteria, which is why it was the mesh chosen for the LES validation. For reference, Table 3 summarizes the meshing parameters that correspond to the selected fixed mesh. For simulations of only the internal volume, this amounted to a mesh of around 1.1 million cells. When the external airbox was also included, the cell count increased to 9.4 million.

Table 3 Mesh parameters
Full size table

3.4 Mesh Refinement

While the base fixed mesh might be sufficient to simulate the turbulent flow behavior, it would have to be unfeasibly finer to resolve both the continuous liquid lamella and the atomized droplets. That is why an AMR model was added to locally increase the mesh density where and when it was needed. In this way, the interface between liquid and air could be kept sharp all across the simulated volume, as the lamella disintegrated into ligaments and then further into droplets. The algorithm can also coarsen the refined cells once they are not needed, keeping them always smaller than in the initial mesh.

In order to define where the refinement is needed, STAR-CCM+ has a free surface mesh refinement option available, which was specifically designed for VOF (Siemens Industries Digital Software 2020) simulations. Every couple of timestep, the algorithm identifies the cells where the interface is currently located. A cell is tagged as an interface cell when at least one component i of the volume fraction gradient (\(\nabla \alpha\)) fulfills the following condition:

$$\begin{aligned} |(\nabla \alpha )_i| > \frac{(\nabla \alpha )_{max}}{RCID} \end{aligned}$$
(3)

where \((\nabla \alpha )_{max}\) denotes the maximum gradient value that is achievable on the given cell, and RCID is the Resolution Criterion for Interface Detection. This user-defined value effectively determines the maximum number of cells across which an interphase (i.e., the region where the volume fraction changes from 0 to 1, or vice versa) can be smeared. The default value is five cells. This means that if an interphase between the liquid and the air is equal or less than five cells, the cells are tagged as interface cells, otherwise they are ignored. The set of cells marked as part of interface is denoted as IC\(_0\). Using the IC\(_0\) as an initial condition, the algorithm advects the future downstream position of the interface, based on the current velocity profile, the timestep and a user-defined safety factor. All cells between the initial and the advected interface position are tagged as the set IC\(_{\textrm{f}}\).

With the information from IC\(_0\) and IC\(_{\textrm{f}}\), the algorithm follows then the decision tree shown in Fig. 3 to determine what cells are KEPT, REFINED, or COARSENED. Some additional controls are included into the process. First, the minimum Cell Size (CS\(_{\textrm{min}}\)) that was set as 1 \(\upmu\)m, based both on the KLS shown in Table 2 and the minimum droplet size of 5 \(\upmu\)m. This is the smallest size that can be measured experimentally. Second, the maximum Refinement Level (RL\(_{\textrm{max}}\)) was set to three. It denotes the maximum number of times that a cell from the initial mesh can be split into subdivisions. There is an exception for the first initialization step of the simulation were the AMR algorithm is not run only once, but as many times as the RL\(_{\textrm{max}}\), to ensure that the interface is refined from the start.

Fig. 3
figure 3

Adaptive Mesh Refinement (AMR) algorithm to mark cells for COARSENING, REFINING or KEEPING

Full size image

Cells that are marked for refinement are split using a midpoint subdivision method. This effectively means that every cell is divided into as many child cells as it has vertices, which typically means 12 – 15 new cells (Siemens Industries Digital Software 2020). Each of these new cells is marked with a RL value one larger than the one of the parent cell. Cells tagged for coarsening are attempted to be merged with neighboring cells of the same RL. The model then interpolates the flow solution to the adapted mesh.

The effect of AMR on the flow solution is shown in Fig. 4, where examples of the spray cone profile are plotted. The corresponding meshes are also shown, to make the effect of the refinement clearer. Without the AMR, i.e., with a fixed mesh, the lamella does not disintegrate, but rather smears out inside the air phase. This means that no information on the ligament or droplets formed can be gained. AMR ensures that the two phases remain segregated (see Fig. 4b), so all the liquid structures formed can be correctly observed and tracked.

Fig. 4
figure 4

Simulated liquid profile profiles for the MD solution (\(Q_L\) = 40 L/h) at 0.4 MPa: a with a fixed mesh; and b with AMR. The corresponding grids are also shown: c for the fixed mesh; and d for the AMR. The orange dotted line represents the nozzle exit

Full size image

3.5 Lagrangian Coupling

Using AMR has shown to provide high-fidelity predictions of liquid breakup and spray formation in previous studies. For example, Khan et al. (2018) implemented the model to refine the mesh around the spray plume of a Gasoline Direct Injector (GDI), using the gas velocity magnitude as a refinement criteria. Duronio et al. (2023) also utilized AMR in their study to track the spray cone profile of a flash-boiling GDI spray. Nonetheless, Kuo and Trujillo (2021) have identified that, while AMR can lead to an higher accuracy in spray simulations, it is also extremely computationally expensive. Even with the mesh being only locally refined where it is needed, the liquid ligaments and droplets still require a very fine mesh all around the spray cone region. Furthermore, given that ligaments and droplets tend to break apart further downstream from the nozzle outlet, capturing this in the simulations would mean that the required cell size would be even smaller as one moves away from the nozzle outlet.

This is where a two-way coupling with a Lagrangian modelling of the spray droplets provides an attractive advantage, using the Resolved Eulerian-Lagrangian Transition (RELT) (Siemens Industries Digital Software 2020). This modelling strategy uses the accuracy of the Eulerian phase in areas where needed to track the breakup of the lamella into the ligaments, while employing the computationally more efficient Lagrangian Particle Model (LPM) to only track the already formed droplets as particles. The key to this coupling is the identification of separated and well-resolved Eulerian liquid ligaments, which STAR-CCM+ denominates blobs. The program identifies a blob any separate group of cells, where all the cells have a liquid volume fraction (\(\alpha _{liq}\)) above 0.95. The AMR should ensure that the ligaments maintain a sharp well-resolved interface. Once a blob fulfills some specific user-defined criteria, it is transitioned to a spherical Lagrangian particle. The equivalent diameter (\(D_{eq}\)), the blob sphericity (\(\varphi _{blob}\)) and the volume fraction are the monitored values used to define when the “blob transition criteria” is fulfilled. This is illustrated in Fig. 5, where \(D_{eq}\) is the diameter of an equivalent sphere with the same volume as the blob. \(\varphi _{blob}\) is then the ratio between the surface area of the equivalent sphere and the actual surface area of the blob (Siemens Industries Digital Software 2020).

Fig. 5
figure 5

Schematic of the Resolved Eulerian-Lagrangian Transition (RELT) process. Once the blob transition criteria are fulfilled, the blob is converted to a Lagrangian particle and the mesh can be coarsened

Full size image

When a Eulerian blob is converted to a Lagrangian particle, the \(\alpha _{liq}\) of the corresponding cells is set to zero, and a Lagrangian particle, with the same \(D_{eq}\) and same mass-average velocity as the original cell group, is set at the centroid of the blob. Once the transition occurs, AMR can coarsen the mesh, and the Lagrangian particle becomes sub-grid. In this scenario, the Lagrangian model can be seen as a sub-grid model for the VOF model (Siemens Industries Digital Software 2020). Since the original \(\alpha _{liq}\) is required to be close to one, the mass and momentum of the blob is mostly conserved.

Once the particles are created, it is important to correctly calculate the trajectory and movement of the particles, especially given the turbulent behavior of the multiphase flow. Because the particles are assumed to be spherical and with a fixed sized, the change in their momentum could be calculated every timestep as the sum of the forces acting on them. Five different forces were taken into account in this calculation (Siemens Industries Digital Software 2020). The first one was the gravitational force associated to the particle mass. Second was the drag force of the high-velocity air on the droplets, which was calculated using the Schiller-Naumann correlation (Schiller and Naumann 1933). Third, the shear lift caused by the velocity gradient of the exiting air, which is calculated according to the Sommerfeld method (Sommerfeld 2000). Fourth, the force of the surrounding pressure gradient on the particle volume. Finally, the force that is exerted on the particle as it accelerates the surrounding air phase, which is calculated using a virtual mass model (Auton et al. 1988).

As there is a two-way coupling between the Eulerian and Lagrangian formulations, the effect of the particles on the continuous phases must be also considered. In order to do that, the particles are included as momentum, mass and energy volume source in the transport equations. This approach assumes that the cell volume is large compared to the particle size (Siemens Industries Digital Software 2020), which may not always be the case near the interface, because of the requirements of the AMR. Therefore, to ensure a stable solution, a volume source smoothing method was introduced, namely, the cell cluster method. With it, STAR-CCM+ spreads the effect of each Lagrangian particle over a cluster of cells (Siemens Industries Digital Software 2020). The size of the cluster is relative to the particle size, so no clustering would occur in the cases where the cell volume is already larger enough than the particle.

It should be noted that, while the formation and movement of the particles was simulated, neither collision nor secondary-breakup models were included. Although these secondary models might improve the accuracy of the final particle predictions, we considered that they would increase unnecessarily the complexity of the simulation. Given that this study attempted to evaluate the general viability of the coupled approach, it was also important to simplify the model wherever possible.

4 Results and Discussion

The implementation and evaluation of the Eulerian-Lagrangian approach was carried out incrementally. First, we evaluated the performance of LES for the turbulent modelling of internal flow as an exclusively Eulerian (VOF) simulation. Second, the coupled Eulerian-Lagrangian approach, hereafter referred to as VOF-LPM, was evaluated by comparing the flow conditions, i.e., the lamella thickness and the ALR, with the results from the exclusively Eulerian (VOF) simulation performed with LES. The idea was to verify that the Lagrangian transition was not negatively affecting the mass and momentum conservation in the simulation. Finally, the resulting Droplet Size Distributions (DSD) were validated with experimental results.

4.1 Capturing Time-Dependent Flow Instabilities with LES (VOF Simulation)

Introducing the LES turbulence model was expected to enhance the time-dependent prediction of the internal lamella thickness, as this was identified as one of the weaknesses of using only RANS modelling (Ballesteros Martínez and Gaukel 2023). To assess this improvement, the lamella thickness profiles of the experimental data, LES, and RANS were compared during 4 ms of atomization, for three pressures. These profiles are shown in Fig. 6. For clarification, these simulations were performed exclusively with a Eulerian formulation of the multiphase flow, that is, for a strictly VOF simulation of the flow, without the coupled approach.

Figure 6 shows the results for the simulated and experimental lamella thickness for different air pressures and a constant liquid flow rate. Simulation results are shown for both LES from this study and RANS from our previous study. In general, the simulated and experimental profiles show very similar ranges and even frequencies of variation, at least at 0.4 and 0.6 MPa. The pulsating behavior of the lamella, with intermittent peaks or even full air-core collapses (points where the entire nozzle fills with liquid), has been identified before for the ACLR-nozzle (Wittner et al. 2019). Air-core collapses are seen in Fig. 6 when the lamella thickness reaches the nozzle radius (dashed black line). Comparing the RANS and LES results visually we can state that with LES, the range of values seen in the simulations match better with the range observed in the experiments. One important remark, however, is the evident failure of RANS to capture the lamella variations at 0.2 MPa. In comparison, LES provides a much more equivalent profile compared to the experiments.

Fig. 6
figure 6

Simulated (SIM) and experimental (EXP) lamella thickness for the MD solution, at different \(p_{air}\) and \(Q_L\)=40 L/h, during 4 ms of atomization. The simulation results are shown for both LES and RANS. The black dashed line represents the radius of the nozzle. The RANS and experimental results are taken from Ballesteros Martínez and Gaukel (2023)

Full size image

Nonetheless, it is difficult to visually compare the profiles. In order to get a more quantitative perspective of the performance of LES and RANS, we calculated different percentiles, \(h_{5,0}\), \(h_{50,0}\) and \(h_{95,0}\), of the thickness variation, based on the profiles from Fig. 6. These percentiles are shown in Table 4. For the simulations, the relative error with respect to the experiments is also presented. All profiles show the expected reduction of the median lamella with higher pressures.

Table 4 Percentiles (\(h_{5,0}\), \(h_{50,0}\) and \(h_{95,0}\)) of the simulated (VOF) and experimental (EXP) lamella thickness for the MD solution, at different \(p_{air}\) and \(Q_L\)=40 L/h
Full size table

Looking at the relative errors, LES remarkably improves the predictions for the 0.2 MPa case, in comparison to RANS. The effect of LES at other pressures is not as clear. There is some slight increase in error in the median values, while the top and bottom percentiles show improved predictions. Nonetheless, LES seems to have a general positive effect on the accuracy of the predicted thicknesses. On top of that, it should be considered that the lamella breakup during the primary atomization is driven by Kevin-Helmholtz and Rayleigh-Taylor instabilities (Kumar and Sahu 2019; Lz et al. 2018). RANS modelling, even when modified for unsteady simulations (also known as URANS), is not expected to be able to correctly capture these small-scale stabilities (de Ridder et al. 2019). Adding this to the better time-dependent profiles from Fig. 6, it is fairly clear that LES is the most appropriate option to capture the flow instabilities. Since these flow instabilities lead to the lamella breakup and thus to droplet formation, LES is also the best option for the coupled approach.

However, while there is a clear improvement, there is still some remaining underprediction of the maximum thickness values, \(h_{95,0}\), when comparing to experimental results, especially at 0.2 MPa. Nonetheless, it should be noted that the difference in the “measurement” frequency of the experiments (20 kHz) and simulations (20 MHz) could also play a role here. For every measured point in the experiments, there are a thousand calculated points in the simulations. Looking at Fig. 6 for 0.2 MPa, the effect of the frequency difference can be recognized by the fact that the simulation presents a cloud of points along the range of 0.1–0.3 mm, interspersed by the air-core collapses. In comparison, the experiments present less data points in this medium-thickness region. Experimental measurements with a higher-speed would be required to have a better validation of the simulation data. Regardless, the fact that the behavior is predicted so well for the other pressures speaks for the accuracy of the LES modelling.

4.2 Coupling with Lagrangian Model (VOF-LPM approach)

With the additional introduction of the RELT model, the ligaments and droplets are converted into Lagrangian particles, once the fulfilled the criteria described in Sect. 3.5. Because of this conversion, it was important to verify that the flow conditions of the continuous phases were still correctly modelled, without any loss of accuracy in the momentum or mass conservation. Three criteria were used for this verification: the mass conservation in the simulations, the lamella thickness inside the outlet channel, and the ALR. In the case of the lamella thickness and the ALR, they were compared with the simulation results from only VOF simulations (see Sect. 4.1) and with the experimental results.

Regarding mass conservation, we first calculated the mass conservation error for the liquid Eulerian phase over the entire mesh. This error is determined as the sum of the mass imbalance (difference between incoming and outgoing mass fluxes) across all cells, multiplied by the current time step and divided by the entire liquid mass present in the mesh (Siemens Industries Digital Software 2020). Monitoring these values along time gives a stable mass conservation error of around 0.02%, for all three pressures. Additionally, to evaluate the mass conservation during the Eulerian-Lagrangian transitions across the entire simulated volume, the inlet liquid mass flow was compared with the outlet mass flow of the Eulerian phase plus the outlet mass flow of the Lagrangian particles. In average, the difference between the inlet and outlet flows was 0.3%. This indicates that the liquid phase is correctly conserved when transitioned from the Eulerian to the Lagrangian modelling.

Looking at the outlet mass flow of the Eulerian and Lagrangian phases also reveals that around 60% of the liquid still remains as Eulerian ligaments by the time it exits the airbox. Both Eulerian Blobs and Lagrangian particles can be included in the DSD analysis of the simulations (see Sect. 4.3), so this should not affect the evaluation of the primary breakup. However, it does indicate that further work could be done to optimize the blob transition parameters (see Sect. 3.5) and reduce computational effort.

With respect to the lamella thickness, Fig. 7 illustrates the time-averaged values obtained with the coupled VOF-LPM approach, along with the experimental and purely VOF simulation, both using the LES model. The coupled approach shows very little difference in its lamella thickness predictions compared to the VOF simulations. The most noticeable deviation can be seen at 0.2 MPa for the \(h_{5,0}\) value. The reason for this slight difference is not clear, although the coupled approach shows a value closer to the experimental measurement. In general, the coupled approach shows a good agreement with experimental data for the median thickness values and for most top and bottom percentiles. A particular exception is seen for the \(h_{95,0}\) at 0.2 MPa, though the same deviation is also observed for the purely VOF simulation.

Fig. 7
figure 7

Box diagram of experimental lamella thickness for the MD solution at different \(p_{air}\) and \(Q_L\)=40 L/h. The box width correlates to a ±15% interval around the median. The whiskers mark the 95% and 5% percentiles. For the VOF and VOF-LPM simulations, the corresponding percentiles and median values are indicated as markers

Full size image

In regard to the ALR, Table 5 presents the values obtained for the experiments, Eulerian (VOF), and coupled simulations (VOF-LPM). The relative errors are also shown for the simulations. As a general remark, the ALRs from the simulations follow the experimental trend of increasing with larger pressures. Furthermore, the two simulation approaches seem to match well with each other. Unfortunately, there is some difference to the experimental results, especially at 0.2 MPa. Nonetheless, it should also be considered that the ALR was measured experimentally during the 25 s of the droplet sizes measurements, while the ALR in the simulations refers to 4 ms of flow. This means that small variations in the gas flow may be present in the simulations that simply cannot be observed with the experimental setup. With that in mind, we concluded that the VOF-LPM coupled approach does not affect the flow condition modelling significantly, when compared to the strictly Eulerian (VOF) formulation. In fact, it improved the prediction of the lamella variation when compared to the experimental data.

Table 5 Average experimental (EXP) and numerical (VOF and VOF-LPM models) ALR for the MD solution at different pressures and \(Q_L\) = 40 L/h
Full size table

4.3 Simulating Drop Size Distributions After Primary Atomization

With the flow conditions validated, it is possible to evaluate the droplet formation. Snapshots of the experimental spray profiles as well as the simulated ones for the different pressures are shown in Fig. 8. For reference, the experimental snapshots cover only 2.5 mm below the nozzle exit. In comparison, the airbox in the simulations allowed observing the development of the spray cone up to 8 mm below the nozzle outlet. While comparing two instantaneous snapshots provides only a qualitative appreciation of the accuracy of the simulation. There are two important observations about the experimental and numerical profiles. First, both show the breakup of the continuous lamella into ligaments and droplets, as soon as it leaves the nozzle exit. Second, the spray cone tends to become wider with pressure increase. This is clearer in the simulations, since the simulated airbox is larger than the near field area recorded in the experiments. The widening of the spray angle with higher gas pressure is also consistent with the behavior observed in other internal-mixing nozzles, such as effervescent nozzles (Lefebvre and Chen 1994; Ochowiak et al. 2018). A more in-detail experimental analysis of the spray cone would be required to better confirm this relation between spray angle and pressure (or rather, the ALR) for the ACLR nozzle.

Fig. 8
figure 8

Experimental (top) and simulated (bottom) spray profiles for the MD solution (\(Q_L\) = 40 L/h) at: a 0.2 MPa; b 0.4 MPa; and c 0.6 MPa. The gray area at the top of the simulated profiles represents the nozzle. The size of the Lagrangian particles is not directly correlated to the actual droplet size

Full size image

To analyze the modelled liquid breakup in more detail and compare the droplet size development with the experimental results, we measured the sizes of all Lagrangian particles and Eulerian blobs that crossed the pressure outlet boundary. The volumetric drop size distribution (DSD) of the recorded sizes is compared to the ones obtained from the experiments, all shown in Fig. 9. From the experimental side, the DSD shifts as expected to smaller droplet sizes with higher pressures. From the simulation side, this trend is only evident when raising the pressure from 0.4 MPa to 0.6 MPa. In fact, the size distribution observed for 0.2 and 0.4 MPa are quite similar.

Fig. 9
figure 9

Simulated (SIM) and experimental (EXP) volumetric cumulative distribution for the MD solution, at different \(p_{air}\) and \(Q_L\)=40 L/h

Full size image

To make the comparison between simulations and experiments clearer, we show some volumetric percentiles of the distributions, as well as the Sauter Mean Diameter (SMD) in Table 6. Although the point of the validation was to compare the experimental and simulated DSDs, it should be noted that the distributions were not actually expected to overlap. The experimental distributions were measured 25 cm away from the nozzle, while the airbox in the simulation only covered 0.8 cm below the nozzle. While the large difference between the simulated and experimental breakup lengths might not be ideal, extending the simulated volume further was simply not computationally feasible. Conversely, experimentally measuring the droplet sizes so close to the nozzle outlet was not possible with the existing setup. Because of the larger available breakup length, the experimental distributions were expected to be always smaller than the simulated ones, but they both should follow the same behavior with respect to the pressure. In general, the simulated parameters match this expected behavior, with the \(x_{50,3}\) and SMD being consistently larger than the experimental values. The simulated distributions also follow the same decreasing size trend with pressure as is seen in the experiments. There is an outlier again at 0.2 MPa, especially with regards to the larger droplets, from the simulations.

Table 6 Volumetric percentiles (\(x_{10,3}\), \(x_{50,3}\), and \(x_{90,3}\)) of the simulated (SIM) and experimental (EXP) droplet diameters for the MD solution, at different \(p_{air}\) and \(Q_L\)=40 L/h
Full size table

As it could be noticed both in the distributions from Fig. 9, and the simulated \(x_{90,3}\) in Table 6, there is a consistent underprediction of the droplet sizes at 0.2 MPa. Wittner et al. (2019) showed that the lamella thickness inside the ACLR is directly correlated with the resulting droplet sizes. That means that the underprediction of the droplet sizes, especially the largest droplet sizes, i.e., \(x_{90,3}\), is a direct consequence of the underpredicted \(h_{95,0}\) of the lamella at 0.2 MPa (see Fig. 7). This also explains the overlap between the DSDs from the simulations at 0.2 and 0.4 MPa, since the underprediction at 0.2 MPa leads to a similar range of lamella thicknesses between the two pressures, and thus a similar range of droplet sizes. While this error propagation from the lamella thickness to the droplet size might not be the desired result, it shows that the transition from the continuous lamella to the droplets and, therefore, the Eulerian-Lagrangian coupling are internally consistent. Nonetheless, at higher pressures, the simulated behavior nicely fits the experimental trends. This highlights the possible use of the Eulerian-Lagrangian model to evaluate how geometrical and operational changes in the ACLR atomizer would affect the DSD.

5 Conclusion

A coupled Eulerian–Lagrangian approach was successfully implemented to capture the primary atomization, i.e., the breakup of the liquid lamella as it exists the ACLR nozzle. In order to account for the turbulent flow variations inside of the nozzle, an LES model was implemented, which improved the model predictions of the lamella behavior with respect to previous work that utilized a RANS model. The maximum error in the \(h_{95,0}\) of the lamella thickness was reduced from the 30% observed with RANS to 20% with the LES model. More than that, the moment-to-moment instabilities, measured in the lamella thickness inside the nozzle, match more closely to the experimental observations with LES than with the RANS approach. Given that these internal instabilities are directly correlated with the droplet formation, LES was confirmed to be the best option for the coupled approach.

The complete breakup of the lamella was captured by introducing an AMR method that ensured the resulting ligaments and droplets were well resolved by the simulation. Since refining the mesh indefinitely is unfeasible, the RELT model allowed converting Eulerian ligaments into Lagrangian particles. The mass and momentum conservation of the coupled approach were successfully validated by comparing with experimental data and monitoring the inlet and outlet mass flows. As it stands, around 40% of the liquid phase is converted into Lagrangian particles by the time it exits the airbox. Further tuning of blob transition parameters increase this percentage, which would lead to even higher computational savings.

With respect to the prediction of the primary atomization, the spray cone formation was observed to happen in the simulations in a similar way as in the experiments. The DSDs obtained from the simulations followed the same trend observed in the experiments, with higher pressures leading to smaller droplet sizes. The specific values were not expected to match, since the experimental measurements were taken at a greater distance from the nozzle than in the simulations. There is an outlier case at 0.2 MPa, where the simulated SMD and \(x_{90,3}\) are significantly smaller than in the experiments. The main cause for the deviation is expected to be propagated error from the underpredicted maximum lamella thicknesses (\(h_{95,0}\)) that occurs at this pressure. The relation between the two errors indicates that the modelling of the internal flow and of the droplet formation are internally consistent, which means that the coupling between the Eulerian and Lagrangian phases worked correctly.