LES and PIV Investigation of the Flow Past a Cactus-Shaped Cylinder with Four Ribs

Abstract

The flow past a cactus-shaped cylinder with four ribs is investigated numerically using large eddy simulations (LES) at Reynolds number of 20,000 and experimentally using particle image velocimetry (PIV) at Reynolds number of 50,000. In both approaches, the full range of angle of attack is covered. LES results show a good qualitative and quantitative match of the aerodynamic properties to previous experimental data, although the value of the critical angle of attack is slightly lower. The results confirm that there is no Reynolds number dependency within the investigated range allowing a comparison of the flow fields from the present LES and PIV. Significant variations of the flow patterns with the angle of attack are found and quantified using the recirculation length and wake width. Overall, the observed angle of attack dependence resembles the behaviour of the square cylinder. However, the studied cylinder has a narrower wake at all angular orientations. Proper orthogonal decomposition is used to identify large coherent structures in the flow. At all angles of attack the first two modes remain dominant making it possible to reconstruct the periodic vortex shedding process using a low-order model.

1 Introduction

Understanding the aerodynamics of cylindrical bodies is of importance not only to fundamental fluid dynamics research but also to engineering applications, since many man-made structures exposed to flow, e.g., tall buildings, bridges, risers, and supports, are essentially composed of approximately cylindrical bodies. Consequently, this topic has received considerable attention within the research community (Williamson 1996; Matsumoto 1999). Although most studies focus on cylinders with “classic” cross-section, i.e., circular or square cylinders, real world applications often require modifications to either tackle engineering challenges such as drag reduction or suppression of vortex induced vibrations or to improve aesthetics and practical application of the structure. For example, the current tallest building in the world, the Burj Khalifa, has a modified triangular cross-section, while a number of other skyscrapers are essentially modified square cylinders.

Widely studied configurations derived from the square cylinder are various modifications of its corners, for example, rounding (Cao and Tamura 2017), chamfering (Tamura et al. 1998; Tamura and Miyagi 1999), and corner recesses (He et al. 2014). Other variations such as fins, strakes, and shrouds have also been explored (see, e.g., Naudascher et al. 1981). Several cross-section modifications have been inspired by the natural world. Well-known examples of biomimetic cylinders are helically twisted elliptic cylinders inspired by daffodil stems (Jung and Yoon 2014; Kim et al. 2016) and wavy cylinders inspired by the vibrissae of harbour seals (Hanke et al. 2010; Chu et al. 2021). Another widely studied modification are ribbed circular cylinders that mimic representatives of the Cactaceae plant family known to withstand high wind loading in their natural environment. A number of numerical and experimental investigations have been inspired by the Saguaro cactus (Carnegiea gigantea) (Talley et al. 2001; Babu and Mahesh 2008; Wang et al. 2014).

While the previous biomimetic examples are derived from the circular cylinder cross-section, a number of succulents from the Euphorbiaceae plant family have only four ribs and resemble a square cross-section with concave sides and rounded corners and can thus be viewed from an aerodynamic perspective as biomimetic modifications to the square cylinder. This shape has already been investigated experimentally (Zhdanov et al. 2021) and using 2D unsteady Reynolds-averaged Navier-Stokes (URANS) simulations (Zhdanov and Busse 2019). While the 2D URANS simulations gave useful insight into key features of the flow through qualitative prediction of the trends of aerodynamic properties with the angle of attack, a quantitative mismatch with the experimental data was observed in the values of the aerodynamic coefficients and in the critical angle of attack. This was not unexpected, since it is known that scale resolved methods such as large eddy simulations are required for more accurate numerical prediction of bluff body aerodynamics. In addition, the detailed investigation of the flow field around cactus-shaped cylinder, including wake characteristics and dynamics, and how they change with angular orientation have been out of scope of the past papers on this shape. In the present paper, the aforementioned gaps are addressed by studying the angle of attack dependence of the flow past a cactus-shaped cylinder with four ribs using large eddy simulations and particle image velocimetry.

2 Numerical and Experimental Setup

Fig. 1

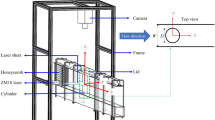
a Cross-section of the studied cactus-shaped cylinder with four ribs with relevant geometrical parameters and angle of attack ($\alpha$) definition. D is the side length of the cylinder, $D^\prime$ is the projected frontal width, A is the diameter of circumscribed circle around the shape. b Schematic diagram of the experimental setup for PIV investigation

Flow past a cactus-shaped cylinder at different angles of attack is studied numerically using large eddy simulations (LES). In addition, quantitative flow visualisations using particle image velocimetry (PIV) are performed in the wind tunnel to complement the numerical investigation.

The studied shape is identical to the shape investigated in our earlier studies using 2D URANS (Zhdanov and Busse 2019) and experimental (Zhdanov et al. 2021) approaches. The cross-section of the cylinder (Fig. 1a) is inspired by a number of succulents with four ribs, e.g., Euphorbia abyssinica, Euphorbia ingens, and resembles a square cylinder with rounded corners and concave sides. Thus, the angle of attack convention used for studies of the flow past square cylinders is adopted for the present investigation. At zero angle of attack the cylinder is facing the flow with a cavity formed by two adjacent ribs, while at the maximum angle of attack, i.e., $\alpha = 45^\circ$, the cylinder is facing the flow with a rib.

2.1 LES Setup

Large eddy simulations are performed using the open source CFD toolbox OpenFOAM, which is based on the finite volume method. The Reynolds number is in all cases set to 20,000 ($Re = \rho U_{\infty } D / \mu$, where $U_{\infty }$ is the free stream velocity, D is the distance between two adjacent ribs (see Fig. 1a), $\rho$ is the fluid density, and $\mu$ is the dynamic viscosity of the fluid). In large eddy simulations large-scale turbulent motions are resolved directly, while smaller scale fluctuations are modelled using a sub-grid scale (SGS) model. In order to separate resolved scales from sub-grid scales a filtering operation is performed. The filtered incompressible Navier-Stokes and continuity equations are given as follows:

$$\begin{aligned} \frac{\partial \overline{u}_i}{\partial t} + \frac{\partial \overline{u}_i \overline{u}_j}{\partial x}= & {} - \frac{1}{\rho }\frac{\partial \overline{p}}{\partial x_i} + \nu \frac{\partial ^2 \overline{u}_i}{\partial x_j \partial x_j} - \frac{\partial \tau _{ij}}{\partial x_j}, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial \overline{u}_i}{\partial x_i}& {}= 0, \end{aligned}$$

(2)

where ${u}_i$ is the $i$th component of the velocity field, the overline indicates a filtered quantity, p is the pressure, and $\tau _{ij}$ is the sub-grid scale stress tensor which is defined as $\tau _{ij} = \overline{u}_i\overline{u}_j - \overline{u_i u_j}$. In the present study, the wall-adapting local eddy-viscosity (WALE) SGS model (Nicoud and Ducros 1999) is employed. This model was designed to give the correct wall asymptotic ($y^3$) eddy-viscosity behaviour for wall bounded flows without damping functions or dynamic procedure (as for example in the dynamic Smagorinsky model). In the WALE SGS model, $\tau _{ij}$ is modelled using the sub-grid scale eddy viscosity ($\nu _{sgs}$) as:

$$\begin{aligned} {} \tau _{ij}-\frac{1}{3}\tau _{kk} \delta _{ij}=2\nu _{sgs}\overline{S}_{ij} = 2C_k\Delta \sqrt{k_{sgs}} \, \overline{S}_{ij}. \end{aligned}$$

(3)

In Eq. (3), $\overline{S}_{ij} = \frac{1}{2} \Big (\frac{\partial \overline{u}_i}{\partial x_j} + \frac{\partial \overline{u}_j}{\partial x_i} \Big )$ is the resolved strain rate tensor, $C_k=0.094$ is a model constant, $\Delta$ is the filter characteristic length defined as the cubic root of the cell volume, and $k_{sgs}$ is the sub-grid scale kinetic energy modelled as:

$$\begin{aligned} {} k_{sgs} = \Bigg (\frac{C^2_w \Delta }{C_k}\Bigg )^2\frac{(\mathscr {S}^d_{ij} \mathscr {S}^d_{ij})^3}{\Big ((\overline{S}_{ij}\overline{S}_{ij})^{5/2} + (\mathscr {S}^d_{ij}\mathscr {S}^d_{ij})^{5/4}\Big )^2}. \end{aligned}$$

(4)

In Eq. (4), $\mathscr {S}^d_{ij}$ is the traceless symmetric part of the square of the velocity gradient tensor:

$$\begin{aligned} \mathscr {S}^d_{ij} = \frac{1}{2}\Bigg (\frac{\partial \overline{u}_k}{\partial x_i} \frac{\partial \overline{u}_j}{\partial x_k} + \frac{\partial \overline{u}_k}{\partial x_j} \frac{\partial \overline{u}_i}{\partial x_k}\Bigg ) - \frac{1}{3}\delta _{ij} \frac{\partial \overline{u}_k}{\partial x_l} \frac{\partial \overline{u}_l}{\partial x_k} , \end{aligned}$$

(5)

where $\delta _{ij}$ is Kronecker delta. $C_w$ in Eq. 4 is the WALE model constant. In the original model formulation (Nicoud and Ducros 1999) the value of $C_w$ was set to 0.5, but in the present study the default OpenFOAM value of $C_w = 0.325$, which showed satisfactory results for a wide range of applications, is used.

The governing equations are solved with the PIMPLE method that represents a combination of the pressure implicit with splitting of operator (PISO) and the semi-implicit method for pressure-linked equations (SIMPLE) algorithms. Second order linear schemes are used for discretisation of the pressure and viscous terms. The convective term is discretised by the second order linear upwind scheme which showed good results for time-averaged and fluctuating quantities in LES of the flow past a square cylinder at $Re = 22{,}000$ (Cao and Tamura 2016).

The linear system of equations for the velocity are solved using the stabilised preconditioned bi-conjugate gradient (PBiCGStab) method (Van der Vorst 1992) with diagonal incomplete-LU (DILU) preconditioner and Gauss-Seidel smoother. The geometric agglomerated algebraic multi grid (GAMG) method with Gauss-Seidel smoother is applied to the pressure equation. An implicit second order backward scheme is used for time integration. The non-dimensional time step ($\Delta t U_{\infty}/D$) is set to approximately $1.00 \times 10^{-3}$. This value ensures the maximum Courant number stays approximately 2 in all simulations consistent with previous LES of the flow past the square cylinder (Cao and Tamura 2016).

Fig. 2

a Computational domain and mesh used for the large eddy simulations. b Close-up view of the computational grid around the cactus-shaped cylinder with four ribs

The computational domain, shown in Fig. 2, has a radial extension of 25D and is discretised with an O-type orthogonal curvilinear grid using the open source 3D mesh generator Gmsh (Geuzaine and Remacle 2009). The cylinder is placed in the centre of the domain. At zero angle of attack, i.e., when a cavity is facing the flow, the spanwise size of the domain is equal to 4D. This value was originally proposed at the LES workshop held in Rottach-Egern, Germany, in 1995 for the flow past a square cylinder (Rodi et al. 1997) and is widely used in numerical studies (Tamura and Kuwahara 1990; Sohankar et al. 2000; Cao and Tamura 2016) for this type of cylinder. For simulations at other angles of attack, the spanwise extent of the domain is increased to 4.5D. The increased spanwise extent is based on the considerations of the projected frontal width ($D^\prime$) of the cactus-shaped cylinder, which increases with angle of attack. Thus, at the maximum angle of attack ($\alpha = 45^\circ$), the spanwise domain size is approximately $\pi D^\prime$, which was successfully used in DNS of turbulent flow around the square cylinder (Trias et al. 2015). In total, 9 simulations at different angles of attack ($\alpha = 0^\circ$, $\alpha = 7.5^\circ$, $\alpha = 10^\circ$, $\alpha = 12.5^\circ$, $\alpha = 15^\circ$, $\alpha = 22.5^\circ$, $\alpha = 30^\circ$, $\alpha = 37.5^\circ$, $\alpha = 45^\circ$) are performed.

The cylinder surface is resolved with 704 cells and 400 uniformly stretched cells are used to discretise domain in the radial direction. To avoid the need for wall functions, the boundary layer around the cylinder is resolved by a grid with sufficiently fine resolution close to the cylinder. Following the approach of Tamura and Ono (2003), the height of the first cell is determined as $\Delta y < 0.1D/Re^{0.5}$. A spanwise grid resolution of 0.05D is set in the present study, matching the spanwise resolution in the LES of the flow past square cylinder by Cao and Tamura (2016). For the $\alpha = 0^\circ$ case, 80 cells are used in the spanwise direction, while for all other cases the cell count in this direction is increased to 90 to maintain a constant resolution in all simulations. In addition, a grid sensitivity study using the present numerical setup has been performed on the square cylinder case. The details of this study can be found in Supplementary Information.

The left boundary of the computational domain is assigned as inlet, while the right boundary is the outlet. Uniform constant flow velocity, that corresponds to the simulation Reynolds number of 20,000 based on the studied cylinder width (D), is prescribed at the inlet together with a zero gradient condition for the pressure. At the outlet, the pressure is set to a fixed value, whereas a zero gradient condition without reverse flow is applied to the velocity field. The cylinder surface is treated as a no-slip wall and periodic boundary conditions are applied in the spanwise direction.

In all simulations the flow statistics are averaged over more than 30 vortex shedding cycles after the initial transition. This value is in line with several previous LES studies of the flow past the square cylinder where 10 to 20 cycles were used (e.g., Rodi 1997; Sohankar et al. 2000; Cao and Tamura 2016; Zeng et al. 2021). Good convergence of the mean and fluctuating lift and mean drag coefficients was established based on the approach of Cao et al. (2020).

2.2 PIV Setup

Two-dimensional quantitative flow visualisation are performed using particle image velocimetry at $Re = 50{,}000$. The Reynolds number is higher compared to the LES; however, similarly to the square cylinder (Bai and Alam 2018), the studied cactus-shaped cylinder is not expected to exhibit significant Reynolds number dependence within this range (Zhdanov et al. 2021).

The PIV experiments are conducted in the same low speed wind tunnel using the same model of the cactus-shaped cylinder as in Zhdanov et al. (2021), where a detailed description of the setup is available. The present experiments focus on the wake behind the cylinder (Fig. 1b). To capture the whole recirculation zone the camera for PIV is equipped with a 50 mm focal length lens at f/1.2 and the field of view is set to 300 mm $\times$ 300 mm. The PIV measurements are taken for six angles of attack, namely $0^\circ$, $10^\circ$, $13^\circ$, $15^\circ$, $30^\circ$, and $45^\circ$. At all angular orientations 144 image pairs are acquired.

A well-established cross-correlation procedure with image shifting is used for the analysis of the PIV images (Green et al. 2005). Initially, the image tile size is selected at $32\times 32$ pixels with 50% overlap and then is reduced to $16\times 16$ pixels for final calculation. The main source of error in the PIV is the digital bias, which is directly related to the field of view, while the errors from spatial calibration and PIV timing are negligible. The overall accuracy in this study is around 2%, based on the field of view (300 mm $\times$ 300 mm) and the wind tunnel speed that corresponds to the required Reynolds number of 50,000 (approximately 8 ms$^{-1}$). Spatial resolution according to vector spacing is around 5 mm $\times$ 5 mm, this is sufficient to capture the gross features of the separated flow field.

3 Results and Discussion

The results of the large eddy simulations and quantitative flow visualisations are presented and discussed in this section. First, the aerodynamic properties of the cactus-shaped cylinder with four ribs and their variation with angle of attack are quantified and compared to previous experimental and URANS results for this shape. This is followed by numerical and experimental results for the flow field around the cylinder and classification of the observed flow patterns at different angular orientations. The cylinder wake is also characterised and discussed. Finally, coherent structures in the flow are identified using proper orthogonal decomposition and vortex shedding is reconstructed using a low-order model.

3.1 Force Coefficients and Strouhal Number

The time-averaged drag ($C_D$) and lift ($C_L$) coefficients, and the fluctuating lift force coefficient ($C^{\prime }_L$) are calculated using the projected frontal area of the cactus-shaped cylinder at the corresponding angle of attack as the reference area. The Strouhal number (St) is determined based on the dominant frequency in the spectra of the lift force coefficient time history taking the projected frontal width $D^{\prime }$ as the characteristic length. The variation of these quantities with angle of attack from the present large eddy simulations are shown in Figs. 3 and 4, where they are also compared to experimental (Zhdanov et al. 2021) and 2D URANS (Zhdanov and Busse 2019) data for the same shape.

Fig. 3

Variation of the mean drag coefficient (a) and mean lift coefficient (b) with angle of attack based on the present LES results. Experimental (Zhdanov et al. 2021) and 2D URANS (Zhdanov and Busse 2019) data for the same cactus-shaped cylinder are also included

Both mean drag and lift force coefficients exhibit strong dependency on the angular orientation of the cactus-shaped cylinder with respect to the incoming flow (Fig. 3). With an increase of the angle of attack from $0^\circ$ to $10^\circ$, $C_D$ drops from 1.78 (at $\alpha = 0^\circ$) to its minimum value of 1.16 (at $\alpha = 10^\circ$). Further increase in $\alpha$ results in a gradual rise of the mean drag coefficient value up to its maximum of 1.97 recorded at $\alpha =45^\circ$ (Fig. 3a). The absolute value of the mean lift coefficient mirrors the behaviour of $C_D$ with angle of attack, i.e., as $\alpha$ is increased from $0^\circ$ to $10^\circ$, $C_L$ reaches its maximum of 1.00 and then drops as angle of attack is increased from $10^\circ$ to $45^\circ$ (Fig. 3b). At both ends of the angle of attack range, i.e., at $\alpha = 0^\circ$ and $\alpha = 45^\circ$, the mean lift force coefficient is zero, as expected, due to the symmetry of the cactus-shaped cylinder with respect to the mean flow direction in these orientations.

The fluctuating lift coefficient drops in the angle of attack range $0^\circ \le \alpha \le 10^\circ$ to its lowest value at $\alpha = 10^\circ$ (Fig. 4a) similar to the behaviour observed for $C_D$ in the same angle of attack range. However, unlike the mean drag coefficient, $C^{\prime }_L$ shows only a slight recovery with further increase of $\alpha$ and remains almost constant for $\alpha \ge 22.5^\circ$. The variation of the Strouhal number with angle of attack partially resembles $C_L$ in the initial increase of the observed values up to a maximum at $\alpha = 10^\circ$ followed by a gradual decrease (Fig. 4b). The minimum value of St in the range $10^\circ \le \alpha \le 45^\circ$ is observed at $\alpha = 37.5^\circ$, followed by a slight increase at $\alpha = 45^\circ$.

Following the convention used for the square cylinder, the angle of attack at which $C_D$, $C_L$, $C^{\prime }_L$, and St reach their extrema are known as the critical angle of attack $\alpha _{cr}$. In case of the square cylinder, $\alpha _{cr}$ is associated with the start of the reattachment of the separated shear layer from the front corners to the lateral surface of the cylinder (Lee 1975). As was shown experimentally (Zhdanov et al. 2021), the same phenomenon is observed at the critical angle of attack for the cactus-shaped cylinder with four ribs. Based on present LES results for the mean and fluctuating force coefficients and Strouhal number, the critical angle of attack for the cactus-shaped cylinder is $10^\circ$, and, as will be confirmed by the flow visualisations in the next subsection, reattachment of the shear layer occurs at this angle of attack. This value is slightly lower compared to the experimental results (Zhdanov et al. 2021), where a critical angle of attack of $13^\circ$ was measured. For the square cylinder it is known that the value of the critical angle of attack depends on a number of factors, such as the level of free stream turbulence, or sharpness of corners due to the manufacturing process (see, e.g., Lee 1975; Cao and Tamura 2020). In addition, as was shown by Cao and Tamura (2016), the spanwise size of the computational domain used for large eddy simulations has influence on the flow around the square cylinder at zero angle of attack due to the phase difference of vortex shedding along the cylinder span. Thus, this parameter could also have an influence on the exact value of the critical angle of attack in numerical simulations. However, to the best of our knowledge this has not been studied for the square cylinder due to the high cost of performing scale resolved simulations with small angle of attack steps and varied spanwise size of the domain. In general, the reported value of $\alpha _{cr}$ for the square cylinder is between $12^\circ$ and $15^\circ$ (Igarashi 1984). Therefore, the difference between experimental and numerical conditions can also be one of the reasons behind the observed mismatch in the value of $\alpha _{cr}$ from the present LES and experimental results. However, compared to the 2D URANS results, where $\alpha _{cr}$ was observed at $5^\circ$, LES gives a significantly better match to the experimental data.

Fig. 4

Variation of the fluctuating lift coefficient (a) and Strouhal number (b) with angle of attack based on the present LES results. Experimental (Zhdanov et al. 2021) and 2D URANS (Zhdanov and Busse 2019) data for the same cactus-shaped cylinder are also included. For symbol key see legend to Fig. 3b

Overall, the present LES results show good agreement with the experimental data (see Figs. 3 and 4). The large eddy simulations capture not only qualitative trends in the variation of the mean and fluctuating force coefficient and Strouhal number with angle of attack, but also give an overall good quantitative match to the experimental data. In addition, the LES give a significantly better prediction of the aerodynamic properties of the cactus-shaped cylinder compared to 2D URANS results. A detailed discussion of the differences between 2D URANS and experimental results is provided in Zhdanov et al. (2021). Moreover, from the present results it can be confirmed that the studied shape does not exhibit Reynolds number dependency in the numerically and experimentally tested range from 20,000 to 150,000. This was expected due to the overall similarity with the square cylinder, where no Reynolds number dependency of aerodynamic properties is observed for $Re \ge 1000$ (Bai and Alam 2018). Based on this, the flow patterns in the wake of the cactus-shaped cylinder will be compared in the next subsection between LES at $Re = 20{,}000$ and PIV experiments at $Re = 50{,}000$.

3.2 Flow Patterns and Wake

Fig. 5

Normalised time and spanwise averaged velocity magnitude ($\overline{U}/U_{\infty }$) contours with mean flow streamlines at all considered angles of attack in LES a $\alpha = 0^\circ$, b $\alpha = 7.5^\circ$, c $\alpha = 10^\circ$, d $\alpha = 12.5^\circ$, e $\alpha = 15^\circ$, f $\alpha = 22.5^\circ$, g $\alpha = 30^\circ$, h $\alpha = 37.5^\circ$, i $\alpha = 45^\circ$. Saddle point in the near wake is marked with ‘S’ in all panels

Normalised contours of the time and spanwise averaged velocity magnitude ($\overline{U}/U_{\infty }$, where $\overline{U} = \sqrt{(\overline{u}^2+\overline{v}^2)}$) with mean flow streamlines from the large eddy simulations are presented in Fig. 5. The corresponding results from the PIV measurements in the cylinder wake are shown in Fig. 6. The recirculation zone length $L_r$ (see Fig. 7a) is determined based on these data as the distance between the centre of the cactus-shaped cylinder and the near wake saddle point, where the mean velocity is zero (Perry and Chong 1987). This approach was also used by Yoon et al. (2010) for measurements of the recirculation region length downstream of a square cylinder at different angles of attack.

Overall, LES and PIV data show good qualitative and quantitative agreement at most angles of attack, except in the vicinity of $\alpha _{cr}$, which is expected, since the value of the critical angle of attack differs by a few degrees between numerical simulations and wind tunnel experiments. At $\alpha = 0^\circ$ (Figs. 5a and 6a) the flow field around the cactus-shaped cylinder and in its wake is symmetric and separation of the shear layer from the upstream ribs can be observed. In addition to the recirculation zone downstream of the cylinder, two more recirculation zones are present in the top and bottom cavities of the cactus-shaped cylinder. Following the classification of flow patterns around the square cylinder introduced by Igarashi (1984), the observed behaviour corresponds to the “perfect separation type, symmetric flow” regime.

Fig. 6

Normalised mean velocity magnitude ($\overline{U}/U_{\infty }$) contours with mean flow streamlines at all considered angles of attack based on the PIV data a $\alpha = 0^\circ$, b $\alpha = 10^\circ$, c $\alpha = 13^\circ$, d $\alpha = 15^\circ$, e $\alpha = 30^\circ$, f $\alpha = 45^\circ$. Saddle point in the near wake is marked with ‘S’ in all panels

As the angle of attack increases, the separation of the shear layer from the front ribs without reattachment is still observed, but the symmetry of the flow field is broken (see Figs. 5b and 6b). The recirculation zones in the top and bottom cavities move deeper inside and an additional recirculation zone starts to develop inside the bottom cavity close to the tip of the front rib. The observed regime can be classified as “perfect separation type, unsymmetric flow". In addition, the recirculation region becomes considerably longer compared to the $\alpha = 0^\circ$ case and the near wake saddle point moves upwards, i.e., in the opposite direction compared to cylinder rotation as the angle of attack increases.

At the critical angle of attack, the reattachment of separated shear layer at the back rib occurs on the lower side (Figs. 5c and 6c) and the recirculation zone is fully enclosed in the cavity on this side of the cactus-shaped cylinder. This is in line with the behaviour observed for this recirculation zone in the earlier experimental study (Zhdanov et al. 2021). The recirculation zone in the wake shortens (Fig. 7a) and the near-wake saddle point is located at the furthest distance from the cylinder centre in cross-stream direction.

With further increase of the angle of attack up to $30^\circ$ (Figs. 5d–f, 6d, e), the flow stays reattached at the bottom side of the cylinder. From $\alpha = 15^\circ$ a recirculation zone starts to develop in the downstream cavity and this zone grows with angle of attack. $L_r$ gradually increases with $\alpha$, while the saddle point in the near wake moves closer to the horizontal axis passing through cylinder centre almost reaching it at $\alpha = 30^\circ$. In addition, at $\alpha = 30^\circ$ one more recirculation zone appears in the top upstream cavity. Similar to the square cylinder, the flow patterns in this angle of attack range can be classified as “reattachment flow type".

As $\alpha$ approaches its maximum value of $45^\circ$, the symmetry of the flow field is gradually restored (Figs. 5h, i and 6f). The recirculation zone length reaches its maximum at $\alpha = 37.5^\circ$ and then slightly drops at the maximum angle of attack (Fig. 7a). At $\alpha = 45^\circ$ one more recirculation zone forms on the upstream rib, restoring the symmetry of the flow. Overall, flow patterns in the high $\alpha$-range correspond to those around the square cylinder in the “wedge flow type" regime, but two additional recirculation zones are present in the downstream cavities of the cactus-shaped cylinder.

Contours of normalised streamwise velocity fluctuations ($u_{rms}/U_{\infty }$) obtained from the LES are shown in Fig. 8. At the initial angle of attack $\alpha = 0^\circ$ (Fig. 8a), the magnitude of $u_{rms}$ is the highest and, in addition to the peak in the wake, a secondary peak close to the trailing rib is observed on both sides of the cactus-shaped cylinder. Similar observations were made for the square cylinder, where a secondary peak over the cylinder surface is present at zero angle of attack for $Re \ge 500$ (Bai and Alam 2018).

Fig. 7

Variation of the recirculation region length (a) and wake width (b) based on the cactus-shaped cylinder width (D) and projected frontal width ($D^{\prime }$) with angle of attack. Experimental data (Huang et al. 2010) for the square cylinder wake width are also included

The $u_{rms}$ contours in the vicinity and in the wake of the cactus-shaped cylinder exhibit strong variation with angle of attack. With the initial increase of the angle of attack up to its critical value (Fig. 8a–c), the magnitude of the streamwise velocity fluctuations in the wake decreases on the side of the cylinder where reattachment occurs, reaching its minimum at $\alpha _{cr}$. In addition, the strength of the secondary peak drops until it disappears at the critical angle of attack (Fig. 8c).

As the angle of attack is increased beyond its critical value, the magnitude of $u_{rms}$ gradually increases on the reattachment side until the symmetry of the flow is restored at $\alpha = 45^\circ$ (Fig. 8d–i). However, it remains substantially lower compared to the other symmetrical orientation of the cylinder at $\alpha = 0^\circ$. On the opposite side of the cylinder, the peak magnitude of $u_{rms}$ drops as the angular orientation is increased from $0^\circ$ to $7.5^\circ$ and remains almost unchanged with further increase in $\alpha$. The area of the flow field affected by the streamwise velocity fluctuations reduces with angle of attack on both sides of the cactus-shaped cylinder and attains is minimum extent at $\alpha _{cr}$. Past the critical angle of attack this area increases with $\alpha$.

Fig. 8

Contours of normalised streamwise velocity fluctuations ($u_{rms}/U_{\infty }$) at all considered angles of attack in LES. a $\alpha = 0^\circ$, b $\alpha = 7.5^\circ$, c $\alpha = 10^\circ$, d $\alpha = 12.5^\circ$, e $\alpha = 15^\circ$, f $\alpha = 22.5^\circ$, g $\alpha = 30^\circ$, h $\alpha = 37.5^\circ$, i $\alpha = 45^\circ$

Based on the contours of the streamwise velocity fluctuations, the wake width (W) of the cactus-shaped cylinder is determined as the cross-stream distance between two peaks in the contours of $u_{rms}$ (Norberg 1986) (see also Fig. 8a) and is presented in Fig. 7b. With the increase of the angle of attack from $0^\circ$ to $\alpha _{cr}$ the wake narrows, and the minimum wake width corresponds to the start of the reattachment of the separated shear layer at one side of the cactus-shaped cylinder. This is consistent with the observations for the square cylinder, where the narrowest wake is also observed at the critical angle of attack (Huang et al. 2010). In contrast, an initial increase in the wake width in the range of $\alpha$ from $0^\circ$ to $10^\circ$ was reported for the square cylinder before a drop at $\alpha _{cr}$(Huang et al. 2010) (see also Fig. 7b). As the angle of attack increases further, the $u_{rms}$ peaks move further apart and the wake downstream of the cactus-shaped cylinder widens. Similarly to $L_r$, the widest wake is observed at $\alpha =37.5^\circ$ followed by a drop at $\alpha = 45^\circ$, where the symmetry of the flow field is restored. For the square cylinder, Huang et al. (2010) observed the maximum wake width at $\alpha = 45^\circ$. However, in their study the preceding angular orientation at which measurements are shown is $\alpha = 29^\circ$ and therefore the possibility of a higher wake width for the square cylinder between $29^\circ$ and $45^\circ$ cannot be excluded. Compared to the data by Huang et al. (2010), the wake of the cactus-shaped cylinder is narrower then for the square cylinder over the entire angle of attack range.

Fig. 9

Contours of normalised fluctuation kinetic energy ($k/U^2_{\infty }$) at all considered angles of attack in LES. a $\alpha = 0^\circ$, b $\alpha = 7.5^\circ$, c $\alpha = 10^\circ$, d $\alpha = 12.5^\circ$, e $\alpha = 15^\circ$, f $\alpha = 22.5^\circ$, g $\alpha = 30^\circ$, h $\alpha = 37.5^\circ$, i $\alpha = 45^\circ$

The fluctuation kinetic energy, $k = 0.5\overline{u^{\prime }_i u^{\prime }_i}$, is presented in normalised form in Fig. 9. The contours of normalised cross-stream ($v_{rms}/U_{\infty }$) and spanwise ($w_{rms}/U_{\infty }$) velocity fluctuations are provided as Supplementary Information (Figs. SI 1 and 2). At all angles of attack the highest levels of k are located in the near wake region of the cylinder but the exact streamwise location varies with $\alpha$. The shortest streamwise extent of k contours is observed at the critical angle of attack (Fig. 9c) revealing that vortices shed from the cactus-shaped cylinder lose their strength at the closest downstream distance compared to the other cases. Consistent with streamwise and cross-stream velocity fluctuations, the k levels drop with an increase of angular orientation up to $\alpha _{cr}$, at which they reach their minima. With the further increase of $\alpha$, levels of fluctuation kinetic energy increase up to the highest values at $\alpha = 45^\circ$. At zero angle of attack (Fig. 9a) additional peaks in the k contours can be observed in the shear layer separated from the front ribs. The magnitude of this peak decreases as $\alpha$ is increased up to $\alpha _{cr}$. Starting from the critical angle of attack no peak in the separated shear layer is present. However, at the maximum angle of attack a new peak at the tip of downstream rib appears (Fig. 9i).

Comparing Figs. 7, 3, and 4 it can be concluded that the minimum drag coefficient of the studied cactus-shaped cylinder is associated with the narrowest wake, which in turn corresponds to the highest vortex shedding frequency and hence Strouhal number. This behaviour is consistent with the square cylinder (see, e.g., Lee 1975). When the wake width is scaled with the projected frontal width at the corresponding angle of attack ($W/D^{\prime }$), it is inversely proportional to St, i.e., as the wake narrows the Strouhal number increases and vice versa. In addition, at $\alpha _{cr}$ the recirculation zone downstream of the cactus-shaped cylinder is the shortest compared to all other angular orientations except for $\alpha = 0^\circ$.

3.3 Proper Orthogonal Decomposition

Fig. 10

Eigenvalue spectrum at all considered angles of attack

To identify dominant coherent flow patterns in the cylinder’s wake, proper orthogonal decomposition (POD) analysis is used. The POD is performed using the snapshot method by Sirovich (1987) based on LES data on instantaneous velocity fields acquired in the midspan section of the computational domain stretching from $-1.5D$ to 10D in the streamwise direction and from $-3.5D$ to 3.5D in the cross-stream direction. More than 500 instantaneous snapshots of the velocity field, interpolated on a uniform rectangular grid, are used for the POD analysis at each angle of attack.

The eigenvalue spectrum showing the contributions of the first 20 eigenvalues to the total kinetic energy of the flow is presented in Fig. 10. The first two modes are largely dominant at all angular orientations and account for between 56% ($\alpha = 37.5^\circ$) to 65% ($\alpha = 0^\circ$) of the kinetic energy.

Variation of the angle of attack has a significant influence on the amount of energy captured by the modes. As angle of attack is increased to $\alpha = 7.5^\circ$ the total energy captured by the first and second modes drops by $7\%$, while the contributions of the higher order modes (modes 3, 4, 5, and 6) is significantly increased. At the critical angle of attack, energy is redistributed back to the first two modes almost reaching the values observed at $\alpha =0^\circ$. As $\alpha$ is increased further, the cumulative amount of energy contained in the modes 1 and 2 gradually decreases, reaching its minimum at $\alpha = 37.5^\circ$, followed by an almost $5\%$ increase as the symmetry of the flow is restored at the maximum angle of attack. The total amount of energy captured by the higher modes, overall, follows an opposite trend. To capture 80% of total kinetic energy, a progressively increasing number of modes from 18 to 32 is required as the symmetry of the flow is broken. This number reduces to 25 as the flow becomes symmetric again at $\alpha =45^\circ$.

Fig. 11

The first four spatial modes of the proper orthogonal decomposition of the velocity field for $\alpha =0^\circ$. The left column shows the modes for the streamwise velocity for the first (a), second (c), third (e), and fourth (g) mode. The right column shows the modes for the cross-stream velocity for the first (b), second (d), third (f), and fourth (h) mode. All spatial modes are normalised by their absolute peak value

Fig. 12

The first four spatial modes of the proper orthogonal decomposition of the velocity field for $\alpha =10^\circ$. The left column shows the modes for the streamwise velocity for the first (a), second (c), third (e), and fourth (g) mode. The right column shows the modes for the cross-stream velocity for the first (b), second (d), third (f), and fourth (h) mode. All spatial modes are normalised by their absolute peak value

Fig. 13

The first four spatial modes of the proper orthogonal decomposition of the velocity field for $\alpha =45^\circ$. The left column shows the modes for the streamwise velocity for the first (a), second (c), third (e), and fourth (g) mode. The right column shows the modes for the cross-stream velocity for the first (b), second (d), third (f), and fourth (h) mode. All spatial modes are normalised by their absolute peak value

The first four spatial modes for the streamwise and cross-stream velocity at $\alpha = 0^\circ$, $\alpha =10^\circ$, and $\alpha =45^\circ$ are shown in Figs. 11, 12, and 13, respectively. All spatial modes are normalised by their absolute maximum value. The spatial modes for other angular orientations can be found in Supplementary Information Figs. SI 3–8. It can be observed that at all angular orientations the first two modes represent alternating patterns behind the cylinder, with anti-symmetric streamwise velocity modes and symmetric cross-stream velocity modes (with respect to the horizontal axis), revealing a typical von Kármán vortex street as formed downstream of a square or circular cylinder (see, e.g., Samani and Bergstrom 2015; Janocha et al. 2022).

Fig. 14

Phase portraits of the first two POD modes of the velocity field for the cactus-shaped cylinder at all considered angles of attack. a $\alpha = 0^\circ$, b $\alpha = 7.5^\circ$, c $\alpha = 10^\circ$, d $\alpha = 12.5^\circ$, e $\alpha = 15^\circ$, f $\alpha = 22.5^\circ$, g $\alpha = 30^\circ$, h $\alpha = 37.5^\circ$, i $\alpha = 45^\circ$

This is also confirmed by the phase portraits of the first and second modes, which represent the correlation between the coefficients of these two modes (Fig. 14). As expected, since the first two modes represent the periodic part of the flow past the cylinder, they form a circle. The observed scatter of data points around the theoretical circle (plotted in red) is the result of the variation between vortex shedding cycles due to small-scale fluctuations.

For some angles of attack (e.g., $\alpha = 0^\circ$), the third and fourth modes also resemble alternating patterns, especially close to the cylinder, that are shifted relative to each other in the downstream direction, representing higher harmonics in the flow. However, from their phase portraits (not shown) no clear correlation between the third and the fourth mode can be observed.

When the cylinder orientation is symmetric with respect to the flow centreline ($\alpha = 0^\circ$ and $\alpha = 45^\circ$), the observed coherent structures in the flow are also symmetric with respect to the flow centreline, although this symmetry is imperfect in the higher modes (Fig. 11 and 13). With the change of angle of attack the observed patterns obviously become asymmetric and shift upwards with respect to the horizontal axis (Fig. 12).

The fact that the first two modes are the most dominant can be used for approximation of the coherent phase-resolved component of the flow using a low-order model based on the mean and the first two POD modes (see, e.g., Van Oudheusden et al. 2005):

$$\begin{aligned} u_{\mathrm {LOM}}(\vec {x}, \varphi ) = U(\vec {x}) + \sqrt{2 \lambda _1} \sin (\varphi ) \cdot \vec {\phi }_1(\vec {x}) + \sqrt{2 \lambda _2} \cos (\varphi ) \cdot \vec {\phi }_2(\vec {x}), \end{aligned}$$

(6)

where $U(\vec {x})$ is the time-averaged velocity field, $\varphi$ is the phase of the vortex shedding, $\vec {\phi }_i$ are the spatial POD modes, and $\lambda _i$ are the eigenvalues of the corresponding POD mode. Random turbulent motions and higher order harmonics that are represented by higher order modes are excluded in this low-order model.

The phase reconstructed shedding cycles using this low-order model for $\alpha = 0^\circ$, $\alpha = 10^\circ$, and $\alpha = 45^\circ$ are presented in Figs. 15, 16, and 17, respectively. Phase reconstruction of the flow for other angles of attack can be found in Supplementary Information Figs. SI 9–14.

As can be observed at phase $\varphi = 0^\circ$ a vortex starts to form at one side of the cylinder. As the phase is increased to $\varphi = 180^\circ$ this vortex grows and sheds, while another vortex on the other side of the cylinder starts to form. At angles of attack $\alpha < \alpha _{cr}$ the vortex shedding occurs from the front ribs, while staring from $\alpha _{cr}$ on the reattachment side the vortex shedding starts at the back rib, due to reattachment of the shear layer at this angular orientation. Thus, the low-order model adequately captures the vortex shedding process from the cactus-shaped cylinder with four ribs at all angles of attack. Overall, the reconstructed vortex shedding resembles the phase-averaged flow fields from the 2D URANS simulations (see Figs. 17 and 18 in Zhdanov and Busse 2019).

Fig. 15

Low-order model reconstruction of the vortex shedding cycle for $\alpha =0^\circ$ with velocity vectors

Fig. 16

Low-order model reconstruction of the vortex shedding cycle for $\alpha =10^\circ$ with velocity vectors

Fig. 17

Low-order model reconstruction of the vortex shedding cycle for $\alpha =45^\circ$ with velocity vectors

4 Conclusions

Scale resolved large eddy simulations of the flow past a cactus-shaped cylinder with four ribs were conducted at Reynolds number of 20,000. Numerical simulations were complemented by quantitative flow visualisations using PIV, which were performed in a wind tunnel at $Re = 50{,}000$. In both, numerical and experimental, parts of this study the angle of attack of the cactus-shaped cylinder was varied from $0^\circ$ to its maximum value of $45^\circ$.

The aerodynamic characteristics of the studied cylinder, such as the mean drag and lift coefficients, the fluctuating lift coefficient, and the Strouhal number show a good quantitative and qualitative agreement with the earlier experimental results obtained for the same shape (Zhdanov et al. 2021). The LES capture the critical angle of attack significantly more accurately compared to 2D URANS simulations, although a difference by a few degrees to the experimental result is still observed. No Reynolds number dependency was observed when comparing LES results at $Re = 20{,}000$ and experimental data, which was acquired in the Re range from 50,000 to 150,000. Thus, a direct comparison of the flow fields between PIV and LES results is possible.

The changes of the recirculation zone length and wake width with angular orientation were quantified based on the LES data; the recirculation length was also measured experimentally. When comparing LES and PIV results for $L_r$, a good agreement is observed over the whole angle of attack range except in the vicinity of $\alpha _{cr}$. As the symmetry of the flow is broken due to an initial increase of the angle of attack, the recirculation zone elongates. At the critical angle of attack $L_r$ substantially drops, followed by a gradual increase as the angle of attack approaches its maximum value. Similarly, the wake width W exhibits significant variation with angle of attack and the narrowest wake is recorded at the critical angle of attack. When scaled with the projected frontal width, W follows an inverse trend to the Strouhal number.

The flow patterns and the wake width of the cactus-shaped cylinder were compared to the square cylinder, which resembles the studied shape. A detailed comparison of the aerodynamic coefficients and Strouhal number between two cylinders is available in Zhdanov et al. (2021). The present LES and PIV data show that the variations of the flow patterns with angle of attack resemble those observed in the square cylinder case. The same classification as proposed by Igarashi (1984) for the square cylinder can be applied to the cactus-shaped cylinder with four ribs. In addition, starting from $\alpha _{cr}$ the same increasing trend in the variation of the wake width with angle of angle was recorded. On the other hand, a number of differences between two cylinders were observed: flow patterns around the cactus-shaped cylinder with four ribs are more complex due to the presence of cavities and hence a larger number of recirculation zones are present. The wake width of the cactus-shaped cylinder is lower over the entire angle of attack range. Furthermore, at low angles of attack the wake behind the cactus-shaped cylinder narrows as the angle of attack is increased from zero, while the opposite behaviour was reported for the square cylinder (Huang et al. 2010).

Coherent structures and their contributions to the total kinetic energy were analysed using proper orthogonal decomposition. At all angular orientations the first two modes are the most dominant and contain from 56% to 65% of the kinetic energy. These two modes represent periodic vortex shedding from the cylinder. A low-order model based on the mean and the first two POD modes can adequately capture the vortex shedding cycle of the cactus-shaped cylinder.

Although the studied shape considerably differs from the square cylinder due to presence of deep cavities, as already mentioned, strong similarities between the two cylinders are observed in many aerodynamic aspects, such as variation of aerodynamic properties and wake dynamics with angle of attack, dominance of the first two POD modes, etc. Thus, it can be conjectured that any cylinder with a cross-section that resembles a square at least qualitatively will have the same behaviour. This brings us back to the importance of the studies focussed on the square cylinder. While this is the second most studied cylindrical body after the circular cylinder, most numerical studies have been conducted at zero angle of attack, i.e., when the flow is normal to the cylinder side (see, e.g., Trias et al. 2015; Bai and Alam 2018), whereas only few studies have considered angle of attack dependency (e.g., Oka and Ishihara 2009; Dong et al. 2022). From experimental studies it is well known that the square cylinder exhibits strong dependence of its aerodynamic properties on the angular orientation. Therefore, detailed angle of attack studies for the square cylinder with high angular resolution around the critical angle using scale resolved simulations such as LES or DNS would be of strong interest but also of considerable computational expense due to the high number of simulations this would incur. With the rapid development of high performance computing, however, this type of simulation becomes more accessible and would significantly contribute not only to a better understanding of the flow past the square cylinder but also to other bluff bodies that resemble this shape.