Multiple Mapping Conditioning Mixing Time Scales for Turbulent Premixed Flames

Abstract

A novel multiple mapping conditioning (MMC) mixing time scale model for turbulent premixed combustion has been developed. It combines time scales for the flamelet and distributed flame regimes with the aid of a blending function. The blending function serves two purposes. Firstly, it helps to identify zones where the premixed flame resides and where the time scale associated with the premixed flame shall be used. Secondly, it uses the Karlovitz number to identify the turbulent premixed combustion regime and to reduce the weighting of the premixed flame time scale if Karlovitz numbers are high and deviations from the flamelet regime are expected. A series of three-dimensional direct numerical simulations (DNS) of statistically one dimensional, freely propagating turbulent methane-air flames provides a wide range of turbulent combustion regimes for the mixing model validation. The new mixing time scale provides correct predictions of the flame speed of freely propagating turbulent flames which could not be matched by most recognized mixing models. The turbulent flame structure predicted by the new model is in good agreement with DNS for all combustion regimes from flamelet to the thickened reaction zone.

1 Introduction

Minimising the production and emission of air pollutants is one of the most important design criteria for modern combustion devices. Lean and ultra-lean premixed combustion is considered to be the most promising strategy to meet any future emission standards for NO$_x$ and soot, but suitable numerical tools that faithfully predict all chemical and physical processes in these, at times metastable, regimes are elusive. This is due to the strongly non-linear dependence of the chemical source term on the composition space and the wide range of length and time scales associated with turbulent combustion processes. Direct Numerical Simulation (DNS) can resolve all interactions but inclusion of detailed chemistry typically results in high computational costs and the computational domain must remain rather small and cannot cover the entire combustion chamber. For practical systems the solution of the Reynolds-averaged Navier-Stokes (RANS) equations or Large Eddy Simulation (LES) are more suitable as some sort of averaging is imposed which allows for the computation of more realistic (larger and more complex) geometries (Bilger et al. 2005; Peters 2009).

In LES, only the large energy-containing turbulent eddies are fully resolved. Spatial variations of the displacement speed created by thermochemical effects and small scale turbulence are likely to wrinkle the premixed flame front at the sub-grid scale. As LES cannot resolve the small scale geometric features at the flame front, one of the key challenges is the modelling of the flame’s response to sub-grid scale structures as the flame’s surface area is expected to determine the kinetics of the flame and thus the entire combustion process. Some commonly used approaches include the flame surface density (FSD) concept (Knikker et al. 2004) and flamelet generated manifolds (FGM) (van Oijen and de Goey 2000) to provide expressions for flame surface area or the averaged chemical source term for closure. Most algebraic chemical source term closures show satisfactory predictive performance for premixed flame cases with moderate values of the Reynolds number (Ma et al. 2013, 2014; Butz et al. 2015). The lack of resolution of the premixed flame front in a typical LES cell can also be addressed using the artificial thickening of the flame (ATF) where modifications of the reaction progress variable conservation equation result in a well resolved reaction progress field on a coarse LES mesh (Colin et al. 2000). A major shortcoming of the conventional closures is, however, the fact that they are based on the assumption of a thin flame front. Thus, strong deviations from a flamelet-like structure cannot be predicted but knowledge of the exact thermochemical state of the flame is needed for accurate pollutant predictions.

The probability density function (PDF) approach (Pope 1985) does not require any assumptions for the closure of the chemical source term. A stochastic particle represents an instantaneous representation of the composition space, and localness of the nonlinear chemical source term and its independence on time and space derivatives allow for a treatment of the reaction in a closed form. Thus, the chemical source term can be computed directly and its computation is independent of the combustion regime. The PDF method can be coupled with LES (Colucci et al. 1998) where it then provides closure for the filtered reaction rate. For the sake of computational efficiency, the PDF transport equations are replaced by an equivalent stochastic system and its solution involves an ensemble of Lagrangian particles (Pope 1994). Diffusive and turbulent mixing on the stochastic particles are represented by a mixing term that is unclosed and needs to be modelled. Well-known particle mixing models include interaction by exchange with the mean (IEM) (Dopazo and O’Brien 1974), the modified Curl’s model (Janicka et al. 1979), and the Euclidean minimum spanning tree (EMST) (Subramaniam and Pope 1998). Computations employing these conventional models show reasonable agreement with experimental data and also indicate that different closures perform better in different cases (Kuron et al. 2017; Zhou et al. 2017; Rowinski and Pope 2013). It needs to be noted, however, that PDF methods do not automatically ensure the correct flame propagation speed. Another shortcoming is that in standard (referred to as “dense” in the following) PDF methods on average 10 to 20 particles are mixed randomly within each CFD cell resulting in high computational costs for PDF-LES, especially when chemical kinetics need to be approximated by large chemical mechanisms. This issue is addressed by the multiple mapping conditioning (MMC) (Klimenko and Pope 2003; Cleary and Klimenko 2009; Galindo-Lopez et al. 2018) approach where the mixing particles are chosen to be close in composition space. This is ensured by conditioning the mixing on a reference field that characterizes the composition space. This allows for mixing over larger spatial distances and a reduction of the number of particles to a number comparable to or less than the number of LES cells (“sparse” method). MMC requires, however, a specific mixing model, the definition of a suitable reference variable, an algorithm for the selection of mixing pairs and an appropriate mixing time scale calculation (Galindo-Lopez et al. 2018).

For premixed combustion the reaction progress variable can be used as a reference field in MMC-LES, however, under-resolution of the progress variable field on a typical LES mesh should be taken into account. Straub et al. (2018, 2019, 2021) proposed an ATF-thickened progress variable as a reference field while the mixing time scale was based on an analogy with models developed by  Cleary and Klimenko (2011) and  Vo et al. (2017). These models have shown accurate MMC-LES predictions of the flame structure and composition for non-premixed and partially premixed flames  (Ge et al. 2013; Vo et al. 2018; Neuber et al. 2019; Huo et al. 2019; Huang et al. 2020). Combining these time scales using blending functions demonstrated decent results for turbulent stratified flames. Nevertheless, purely premixed flames are distinctly different from non-premixed and partially premixed flames with respect to flame dynamics, and mixing time scale models based on an analogy with turbulent time scales used for non-premixed combustion are somewhat ad hoc and are not necessarily applicable to a wide range of premixed combustion regimes. For cases where the premixed flame structure is strongly affected by turbulence, e.g. thickened flames or flames with extinction,  Pope and Anand (1985) and  Kuron et al. (2017) proposed an approach where two different mixing time scales are used in the two asymptotic turbulent premixed combustion limits, namely the flamelet regime and the distributed flame regime. Their models gave satisfactory results, but also notable deviations from reference data. These may originate from some inconsistencies in the model’s implementation for the flamelet regime that (implicitly) omits the convective term from the particle evolution equations in regions close to the flame surface. The random walk model cannot simply be combined with the reactive-diffusive equation for particle composition when the diffusion term cannot be recovered from the Eulerian field. Relating the particle composition to a pre-tabulated flamelet solution that then provides the diffusion term does not respect the change in composition due to particle advection.

A new PDF mixing time scale model which provides a consistent closure for premixed combustion in the laminar flame limit was proposed by Iaroslavtceva et al. (2022). The model demonstrated good predictability of both the laminar flame propagation speed and the laminar flame structure, while models introduced earlier (Tirunagari and Pope 2016; Kuron et al. 2017) were only able to match one of these two characteristics. Iaroslavtceva et al. (2022) introduced a conditioning on a reference field similar to the procedure used in MMC to stabilize the flame predicted by the stochastic particle solution. We expect that this conditioning operation can also be extended to MMC-LES of turbulent premixed flames and should provide a consistent subgrid closure in regions where the premixed flame is in the laminar flame limit. In regions further away from the flame, a conventional turbulent mixing time scale should be used. Blending functions between the time scales were suggested in Straub et al. (2021) or  Kuron et al. (2017) that could provide a suitable transition between mixing in the flame itself and in the preheat and post-flame zones.

In this paper we use MMC-DNS for further model development and validation of the new time scale’s applicability to turbulent combustion. In Sect. 2 the general theory of the MMC approach is described, including the conventional and newly introduced mixing time scale models (Sect. 2.1) and conditioning on the reference variable (Sect. 2.2). Section 3 explains the numerical setup of 3-dimensional (3D) turbulent freely-propagating premixed flames with varying equivalence ratios. Section 4 compares the performance of the new mixing time scale model with existing models and also demonstrates its abilities to predict the turbulent flame speed and structure.

2 The MMC Model

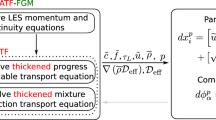
The stochastic part of the MMC model is based on an ensemble of Lagrangian particles, and the evolution equations of the particles are given by (Pope 1985)

$$\begin{aligned} d\mathbf {x}^p= & {} \Big [\widetilde{\mathbf {U}} + \frac{1}{\bar{\rho }}\nabla \big (\bar{\rho } D_{eff}\big )\Big ]^p dt + \Big [\sqrt{2D_{eff}}\Big ]^p d \varvec{\omega }, \end{aligned}$$

(1)

$$\begin{aligned} d\phi _{i}^p= & {} \Big [S_{i}^p + W_{i}^p\Big ]dt, \end{aligned}$$

(2)

where $\mathbf {x}^p$ and $\phi _{i}^p$ denote the position and composition of particle ‘p’, respectively. $\bar{\rho }$ is the filtered density, $\widetilde{\mathbf {U}}$ is the Favre-averaged velocity vector and $d\varvec{\omega }$ is the increment of a stochastic Wiener process. The effective diffusivity is defined as $D_{eff} = D + D_t$, where D is the molecular diffusivity, here assumed to be equal for all scalars, and $D_t$ is the turbulent diffusivity. The chemical source term of scalar i, $W_{i}^p$, appears in closed form, and $S_{i}^p$ is the unclosed mixing term. This set of equations is called the “random walk” model.

The system of Eqs. (1) and (2) is equivalent to the PDF transport equations, but computational requirements for its solution scales linearly with the number of reactive species and is therefore computationally much more efficient than the direct solution of the PDF equation if the composition space exceeds a single scalar. In the random walk model the diffusion is represented by two steps. First, the spatial transport of the particles changes the local mean composition and, second, the particle mixing determines the variance of composition. Properties required in the spatial transport Eq. (1) such as velocity and diffusion coefficient are interpolated from the Eulerian field to the particle position. MMC is intended to serve as an LES subgrid model for closure of the chemical source term, however, in the present work the reference field values required for conditioning of the mixing term are provided by DNS. The use of a fully-resolved DNS combined with a PDF method may seem wasteful but provides - at the current stage of model development - a reliable reference for validation of the particle mixing model and excludes errors related to the underlying velocity and composition fields. Moreover, DNS allows us to consider all turbulent premixed flame regimes, from the flamelet to the distributed regime close to extinction, and avoids the necessity to model any of the subgrid effects on the Eulerian field. In DNS, no modelling is needed since the energy, species and momentum transport equations are solved using computational meshes that are fine enough to resolve a thin premixed flame front as well as all turbulent scales including the Kolmogorov length scale. Therefore $\bar{\rho } = \rho$, $\widetilde{\mathbf {U}} = \mathbf {U}$ in Eq. (1) and the turbulent diffusivity can be set to zero, thus $D_{eff}=D$. It may seem counter-intuitive that even in fully resolved computations (like DNS) a random walk jump appears on the RHS of Eq. (1). However, the use of the interpolated (DNS) velocity accounts for convection only and molecular diffusion continues to require modelling by the two step process involving spatial transport followed by micromixing as described above. The DNS results are used as references to calibrate and assess the mixing term model proposed for the MMC particle solution.

For closure of the mixing term we employ a modified Curl’s mixing model (Janicka et al. 1979) where two particles (‘p’ and ‘q’) are mixed linearly over a time step of $\Delta t$ towards their mass-weighted mean $\overline{\phi }_{i}^{p,q}$. The effect of mixing on the composition of the particles is written as

$$\begin{aligned} \phi _{i}^p(t + \Delta t)= & {} \phi _{i}^p(t) + \gamma (\overline{\phi }_{i}^{p,q}(t)-\phi _{i}^p(t)), \end{aligned}$$

(3a)

$$\begin{aligned} \phi _{i}^q(t + \Delta t)= & {} \phi _{i}^q(t) + \gamma (\overline{\phi }_{i}^{p,q}(t)-\phi _{i}^q(t)), \end{aligned}$$

(3b)

where the mixing extent, $\gamma$, is given by

$$\begin{aligned} \gamma = 1 - \text {exp}\bigg (-\frac{\Delta t}{\tau _L}\bigg ). \end{aligned}$$

(4)

Here $\tau _L$ is the mixing time scale which is discussed in detail in Sect. 2.1. We note that in the random walk model a unity Lewis number assumption is made. The assumption’s validity is likely to be compromised in cases where differential diffusion effects become important. Modifications of the mixing model that account for differential diffusion effects exist (Yang et al. 2020; Zhou et al. 2021; Turkeri et al. 2021) with the model by Sundaram and Klimenko (2017) being specifically developed for MMC. None of the models is, however, well-established so far, and developing a mixing time scale for differentially diffusing scalars is beyond the scope of this paper. Therefore, we proceed here assuming unity Lewis numbers in the MMC solution and the DNS to ensure unbiased comparability of the different solutions. A further assumption is that the mixing time scales of all species are equal to the mixing time scale of the reaction progress variable. This assumption is valid in cases when the reaction progress accurately characterizes the local flame composition (Iaroslavtceva et al. 2022). However, different driving forces for diffusion processes expressed by $(\overline{\phi }_{i}^{p,q}(t)-\phi _{i}^p(t))$ in Eq. (3a) still induce different diffusive velocities for the different species.

2.1 Mixing Time Scale Models

The mixing time scale model developed by Vo et al. (2017) is given by

$$\begin{aligned} \tau _{a-iso}^f = \frac{C_f(d_{x}^{p,q})^2}{2(D + \frac{d_x^{p,q}}{\Delta _{E}}D_t)}, \end{aligned}$$

(5)

where $C_f = 0.1$ and $d_{x}^{p,q}$ is the distance in physical space between the mixing particles. The subscript ‘a-iso’ indicates the notion of “anisotropic” scalar slivers that were assumed for the derivation of the mixing time scale in  Vo et al. (2017). As MMC shall be used as LES subgrid model and particle distances are much larger than DNS cell sizes, we introduce an auxiliary LES mesh with the characteristic filter size $\Delta _E$. The mixing time scale model given by Eq. (5) accounts for the larger distances by scaling $D_t$ with the latter being computed here on the auxiliary LES mesh using the Smagorinsky model with the model constant $C_S = 0.17$ and the turbulent Schmidt number $Sc_t = 0.4$. The sub- and superscripts ‘f’ denote the model’s applicability to mixing conditioned on mixture fraction, f, i.e. to non-premixed flames only. The model demonstrated good performance for turbulent non-premixed flames. For regions where premixed combustion dominates,  Straub et al. (2021) introduced a modification of the original model using

$$\begin{aligned} \tau _{a-iso}^c = \frac{C_c(\delta _L)^2}{2(D + \frac{d_x^{p,q}}{\Delta _{E}}D_t)}, \end{aligned}$$

(6)

with $C_c = 0.0025$ and $\delta _L = (T^b - T^u)/max\big( \vert \partial T/\partial x\vert \big)$ being the laminar flame thickness where $T^b$ and $T^u$ are the temperatures of burnt and unburnt mixture, respectively. The sub- and superscripts ‘c’ indicate the model’s applicability to mixing conditioned on the reaction progress variable, c. The modification given by Eq. (6) was suggested by  Wang et al. (2018) who postulated the relevant mixing length in the premixed flame to be $\delta _L$. We note that there is no validation of the suitability of this assumption by comparison with DNS data but it seems clear that neither the LES cell size (as in conventional PDF-LES modelling) nor the particle distance $d_x^{p,q}$ (as used in MMC-LES) provides a useful length scale if the premixed flame is unresolved on the LES grid. Models presented by Eqs. (5) and (6) are two asymptotic limits. Therefore, modelling of mixed regimes, for example of stratified flames, requires a suitable blending function to approximate $\tau _L$ between these limits.  Straub et al. (2021) used a flame sensor defined by $\Omega = 16[c(1-c)]^2$ as an indicator where $c = Y_{\text {CO}_2}/Y_{\text {CO}_2}^{eq}$ denotes the progress variable and $Y_{\text {CO}_2}^{eq}$ is the equilibrium value of the carbon dioxide mass fraction, $Y_{\text {CO}_2}$. The flame sensor $\Omega$ is equal to 1 in the center of the flame ($c = 0.5$) and 0 outside the flame. The combination of the two mixing time scale models provided decent results for the stratified flames, nevertheless, sufficient validation for the limit of pure premixed flames was not provided and it is uncertain how accurately the premixed flame propagation speed could be captured.

The topic of accurate time scale modelling in the laminar premixed flame limit has recently been investigated in  Iaroslavtceva et al. (2022). We introduced a new closure for the mixing time scale that uses the reaction progress variable as a characteristic scalar, viz.

$$\begin{aligned} \tau _{LPF} = C_L \left| \frac{\rho \nabla c \sqrt{2D\Delta t}}{\nabla \cdot (\rho D \nabla c)}\right| , \end{aligned}$$

(7)

where $C_L$ is a modelling constant which can be calibrated to match the fluctuations around the conditional mean. Its value should, however, be in the interval $C_L \in [0.1, 0.5]$ to ensure sufficiently accurate predictions of the laminar flame speed as demonstrated in Iaroslavtceva et al. (2022). It should be noted that the gradients of c are taken from a precomputed premixed laminar flame. Thus, $\tau _{LPF}$ can be tabulated as function of c and values for $\tau _L$ are read in from the table during run time. It has been shown in Iaroslavtceva et al. (2022) that different definitions of the progress variable such as normalized $Y_{CO_2}$, $(Y_{CO_2} + Y_{CO})$ or the temperature could be used as long as they characterize the flame’s local composition. In this paper we proceed to use the common definition based on $Y_{CO_2}$. In a series of tests studying premixed laminar stoichiometric methane-air combustion the new model demonstrated its ability to accurately predict both the laminar flame propagation speed and the laminar flame structure which was not possible with mixing models published in the archival literature. The model is based on a laminar premixed flame structure and cannot directly be applied to turbulent cases, however, it is expected to hold within the flame when the turbulence intensity is low and flame wrinkling does not impact on the inner flame structure, preserving a locally laminar flame. The model will not be accurate outside the flame front and in cases where turbulence is strong enough to enter the flame such that the flame structure can no longer be faithfully approximated by an unstretched laminar flame.

Outside the flame region and in cases where turbulence modifies the laminar flame structure, mixing should be characterized by the turbulent mixing time scale, $\tau _{turb}$. Only if the turbulence levels are low the mixing inside the flame should be characterized by the appropriate time scale for laminar premixed combustion, $\tau _{lam}$. We therefore introduce a blending function, $\eta$, combining the conventional (turbulent) MMC mixing time scale given by Eq. (5) and the mixing time scale for the laminar premixed flame, viz.

$$\begin{aligned} \frac{1}{\tau _L} = \frac{\eta }{\tau _{lam}} + \frac{1 - \eta }{\tau _{turb}}. \end{aligned}$$

(8)

Here, $\tau _{lam}$ is either given by Eq. (6) or Eq. (7) and we note the ‘dual’ purpose of the blending function. Firstly, it should identify regions inside and outside the flame and provide a transition between them. This is similar to the flame sensor introduced earlier. Secondly, the blending function should distinguish between regimes where the flame can be considered locally laminar and regimes where the interaction of the flame front with the turbulence has a strong influence on the flame structure. Classically, the Karlovitz number is used as a reliable indicator for the interaction of a premixed flame with small scale turbulence (Kheirkhah and Ömer 2021). Therefore, it is used here as a parameter in the blending function that determines to which extent the two limiting mixing time scales should be blended to accurately represent the subgrid mixing process. The blending function is set to be

$$\begin{aligned} \eta = \frac{2\sqrt{c(1-c)}}{\text {max}(1, \text {Ka}^{\alpha })}. \end{aligned}$$

(9)

Here, in the numerator we have a somewhat modified definition of the flame sensor. It equals 1 in the centre of the flame and 0 outside the flame, ensuring that $\tau _{lam}$ is used inside the flame front only. In the denominator of the blending function we introduce the Karlovitz number $\text {Ka} = \delta _L/(s_L\tau _k)$, where $\delta _L$ is the laminar thermal flame thickness, $s_L$ is the laminar flame speed and $\tau _k$ is the Kolmogorov time scale. The exponent $\alpha$ is a modelling constant and Fig. 1 shows that it constitutes a key parameter to control the influence of Ka on the mixing time scale. For Ka of the order of $(O(1))$ and smaller, the flame shall be locally laminar and remain undisturbed by turbulence. For large Ka the flame is expected to be in the distributed regime and a laminar flame structure no longer dominates flame propagation. It seems that a linear dependence on Ka is too strong as $\eta$ decays too quickly and equals 0.5 in the center of the flame for Ka as low as 2 despite our expectations of the flame to preserve a laminar structure and be merely wrinkled by the turbulence. The parameter $\alpha$ is therefore varied in order to determine a value that provides optimal agreement between DNS and particle solutions. Note that this rather heuristic model for the blending function is not likely to discriminate unambiguously between regions of high and low Karlovitz numbers as it serves the dual purpose explained above. It is expected to provide a suitable transition between the limits $\tau _{lam}$ and $\tau _{turb}$ with the aid of modelling parameters that would also be available in LES. The implementation of the model implies that the two limits can be met: first, for Ka $< 1$, we assume a fully laminar flame structure (indicated by the maximum function) and, second, turbulence is expected to affect the time scale seen by the flame only if $\tau _{turb}$ smaller than $\tau _{lam}$

Fig. 1

Blending function dependence on the Karlovitz number and constant $\alpha$

.

2.2 Conditioning on a Reference Variable

Conditioning on a reference variable was introduced in the context of the MMC approach as a way to ensure mixing to be local in composition space and to allow for a significant reduction of the number of stochastic particles required for the computations. In our previous work (Iaroslavtceva et al. 2022) we demonstrated that the concept of conditioning on the reference variable can also be used to approximate a correct flame propagation speed. The MMC model along with other PDF methods does not guarantee an accurate prediction of the flame speed by the particles per se but the underlying Eulerian field makes it possible to compare predictions based on the PDF particles with the actual flame speed.

For non-premixed flames conditioning on the mixture fraction is well established (Ge et al. 2013; Vo et al. 2018; Neuber et al. 2019; Huo et al. 2019). For premixed flames the reaction progress variable is the obvious choice for the reference variable, but its use is impeded by the fact that the flame front is often under-resolved on LES meshes. In MMC-LES,  Straub et al. (2018, 2019, 2021) proposed an artificially thickened progress variable field as a well-resolved reference for conditioning. In this paper we use MMC-DNS for model development and therefore do not require artificial thickening since the premixed flame front is fully resolved on the Eulerian mesh. We introduce $c^p$ as the value of the reference field on the particle which is c interpolated from the Eulerian DNS grid to the particle position. In our previous work (Iaroslavtceva et al. 2022) we showed that the stochastic Wiener process can produce large particle jumps (up to a half of the flame thickness in laminar cases) that lead to situations where a stochastic particle is surrounded by particles that have a significantly different composition. In this case micro-mixing will not be local in composition space despite similar $c^p$ values on the stochastic particles. A ‘relaxed’ reference variable $c^p_{rlx}$ is defined as

$$\begin{aligned} c^p_{rlx} (t + \Delta t) = c^p_{rlx} (t) + \lambda (c^p(t + \Delta t) - c^p_{rlx} (t)), \end{aligned}$$

(10)

where $\lambda$ is a relaxation factor chosen between 0 and 1, and for simplicity, it is the same for all particles. A relaxation of the reference field according to Eq. (10) can alleviate the shortcoming of non-localness of mixing since a particle now “remembers” its position within the flame prior to the stochastic jump. The relaxation factor can be varied based on a comparison of the particles’ flame speed with the respective Eulerian value. A small relaxation factor slows down mixing across the flame front (which is occasionally overpredicted by the large random jumps and compromises the correct flame speed) and decelerates the flame. As a result the particle flame “attaches” to the Eulerian flame position and a correlation between the composition field on the particles and the reference scalar is maintained. A description of the relaxation factor and its variation can be found in (Iaroslavtceva et al. 2022) and in Sect. 4.2.

The relaxed progress variable is calculated for each particle and the mixing pairs are selected by a k-d-tree algorithm (Friedman et al. 1977) that minimizes the effective square distance of a particle pair formed by two particles ‘p’ and ‘q’, $\Big (\hat{d}^{p,q}\Big )^2$, equal to

$$\begin{aligned} \Big (\hat{d}^{p,q}\Big )^2 = \sum _{i=1}^{3}\bigg (\frac{d_{x_i}^{p,q}}{r_m/\sqrt{3}}\bigg )^2 + \bigg (\frac{d_{c^p_{rlx}}^{p,q}}{c_m}\bigg )^2 , \end{aligned}$$

(11)

where $r_m$ and $c_m$ are constant characteristic distances in physical and reference space, respectively. The quantities $d_{x_i}^{p,q}$ and $d_{c^p_{rlx}}^{p,q}$ are the actual distances between the mixing particles in the physical and reference spaces. Typically, $c_m = 0.03$ and $r_m$ is computed from an algebraic relationship given in  Cleary and Klimenko (2011). Following  Straub et al. (2021) we do not mix particle pairs with $d_{c^p_{rlx}}^{p,q} > 2c_m$ (which is true for not more than $5\%$ of particles in the flame region) to ensure localness of mixing in the composition space. The mixing extent $\gamma$ for a particle pair (Eq. (4)) is calculated based on a harmonic mean of the particle’s mixing time scales.

The reference scalar, $c^p_{rlx}$, is also used to select the mixing time scale $\tau _{LPF}$ (Eq. (7)) from the tabulated values that were precomputed for a given composition and boundary conditions. Similarly, we set $c = c_{rlx}^p$ for the blending function given by Eq. (9) as $c_{rlx}^p$ now characterizes the particle composition.

3 Case Setup

A series of DNS of statistically stationary, one-dimensional, freely propagating turbulent premixed methane-air flames is conducted and covers a wide range of premixed combustion regimes, from flamelet and corrugated flames to the thickened and (almost) distributed flame regimes. We employ a four-step chemical mechanism (Jones and Lindstedt 1988) which includes the intermediates H$_2$ and CO. The domain size is $32\times 16\times 16$ mm, the mesh is uniform with $\Delta x = 50$ $\mu$m resulting in about 65 million cells in total. This ensures about 8 grid points across the flame (represented here by the central flame region that covers 80$\%$ of the temperature rise) and provides an adequate resolution of all chemical species but most importantly, a good resolution of the reaction progress (i.e. the reference) variable is ensured. Synthetic turbulence is generated at the inflow and turbulence forcing is applied upstream of the flame front to prevent undue decay of turbulence. The mean inflow velocity is varied with time to match the turbulent flame speed making sure that the flame stays inside the domain. The inflow temperature is $T_{in} = 700$ K, and synthetic turbulence parameters are the average velocity fluctuation $u' = 2.38$ m/s, the integral length scale $l_0 = 3.2$ mm, a Kolmogorov time scale of $\tau _k = 1.3 \cdot 10^{-4}$ s and a Kolmogorov length scale of 100 $\mu$m. These settings provide an integral scale Reynolds number of $Re = 102$. Combustion products are leaving the domain through the outflow boundary and periodic boundary conditions are used at the sides of the domain. In order to resolve particle mixing, the computational time step is set to $\Delta t = 2.5\cdot 10^{-7}$ s. The DNS solver is based on the OpenFOAM libraries and uses temporal and spatial schemes of the second order. More detail on performance and accuracy of the OpenFOAM implementation is given in  Vo et al. (2016).

A wide range of the Karlovitz number values is achieved through variation of the equivalence ratio, $\phi$, while the inlet turbulence stays unaltered. Characteristic values for the different cases are listed in Table 1 with $s_T$ being the turbulent flame speed taken as the mean inflow velocity averaged over time. The laminar characteristics are provided by separate laminar flame computations with respective $\phi$. A classification of the expected turbulent premixed combustion regimes is given by a diagram illustrated in Fig. 2.

Table 1 Characteristic combustion parameters

We note that the definition of premixed regime boundaries differ in literature. Here we use one of the simpler diagrams as proposed by  Peters (1999) for guidance and refer to Figs. 5, 10 and 11 below for a better quantitative assessment of the influence of turbulence on the flame structure. For $\phi = 1.0$ Ka is below 1 indicating that the influence of turbulence on the local flame structure should be very low and the flame is considered to be just at the transition between the wrinkled and corrugated flamelets regimes. For $\phi = 0.6$ (corrugated flamelet) Ka is slightly above 1 and only small (if any) effects of turbulence on the flame structure are expected. For the two other cases with lower equivalence ratios we can expect strong changes in the local flame structure due to turbulence effects. They are both situated in the thin reaction zone regime, where the thermal flame thickness is notably increased and small scale turbulence is likely to disturb the flame structure. We would like to note that for cases with $\phi = 0.2$ and $\phi = 0.15$ we used a somewhat lower DNS resolution with a mesh size of $\Delta x = 100$ $\mu$m as the flame thickness is notably increased and the coarser mesh suffices for resolution of flame and turbulence scales. We further note that the extinction limits predicted by the reduced 4-step chemistry are somewhat artificial ($\phi =0.15$ is beyond the flammability limit of a real methane-air flame). However, as the MMC and DNS simulations use the same chemical mechanism, these simulations provide nonetheless suitable and challenging cases for model development that are needed to cover the full range of premixed flame regimes.

Fig. 2

Turbulent premixed regime diagram

In addition to the DNS solution, Eqs. (1) and (2) are solved to provide an MMC particle solution. The MMC solver is coupled with the Eulerian solver using existing libraries of OpenFOAM (Galindo-Lopez et al. 2018) and described in more detail in e.g.  Vo et al. (2017). The number of stochastic particles is around 128,000 which corresponds to approximately 1 stochastic particle per 512 DNS cells (or 1 stochastic particle per 1 auxiliary LES cell with $\Delta _E = 0.4$ mm) and satisfies all characteristics of a sparse particle method. The new MMC time scale models should be able to capture mixing in each of the premixed combustion regimes accurately to be universal and applicable as a predictive tool.

4 Results

4.1 DNS Solution

Figure 3 shows instantaneous temperature fields for Cases C-1.0 to C-0.15. The figure demonstrates that the different flame regimes can be captured by the DNS. In Case C-1.0 ($\phi = 1.0$) the flame front that separates reactants and products is very thin, its structure can be considered locally laminar and it is located in the flamelet regime despite the flame surface being wrinkled. When moderately lowering the equivalence ratio (Case C-0.6) we observe flame thickening and some island formation but the isocontours of the temperature remain largely parallel and the flame structure is largely undisturbed. However, for C-0.2 and C-0.15 a strongly distributed flame front can be observed. This is corroborated by Fig. 4 presenting isosurfaces of the progress variable with $c = 0.1, 0.4$ and 0.9. The distances between the isosurfaces visibly increase with decreasing $\phi$. We can conclude that in Case C-1.0 the flame is in the flamelet regime, in Case C-0.6 flame front is locally thickened by the turbulence, while in Cases C-0.2 and C-0.15 the turbulent flame is distributed over a large distance in physical space and clear deviations from the laminar flame structure are apparent.

Fig. 3

Planar cut of a 3D-DNS configurations of statistically 1D turbulent premixed flames

Fig. 4

Instantaneous view of reaction progress variable isosurfaces: $c = 0.1$ (blue), $c = 0.4$ (green), $c = 0.9$ (red)

Fig. 5

Progress variable gradient normalized by the maximum gradient from the corresponding laminar case. The red lines present the mean and RMS (indicated by the vertical bars)

Such rather qualitative analysis is accompanied by a more quantitative assessment given in Fig. 5 that allows for the evaluation of the interactions between the premixed flame front and the turbulence in more detail. The gradients of the local progress variable are normalized by the maximum gradient from the corresponding laminar case, $\vert \nabla c_{lam}\vert _{max}$, and plotted as function of c. For $\phi = 1.0$ only a small variation of $\vert \nabla c \vert$ around its mean value is observed. This indicates first, that the turbulent flame is wrinkled but its local structure is not affected by turbulence. It also indicates that the flame resolution provided by the DNS mesh is sufficient to resolve the c-field and its gradients. A reduction of the equivalence ratio to $\phi = 0.6$ leads to a notable increase of the gradient fluctuations around its mean. This indicates considerable stretching and compression of the flame along with other thermochemical effects associated with flame-turbulence interactions but it seems that the local structure is largely preserved. This is different for $\phi = 0.2$ and $\phi = 0.15$ where large variations of the gradients exist. It is apparent that turbulence enters the flame, leads to local variations in the flame structure and the flame can no longer be considered laminar and resemble a flamelet. We therefore conclude that cases C-1.0 to C-0.15 provide a representative and challenging series for validation of the mixing time scale model.

4.2 Predictions of the Correlations Between MMC and the Reference Field

One of the most challenging test cases for a particle mixing model is the accurate prediction of the flame speed of a freely propagating flame. The model introduced by  Iaroslavtceva et al. (2022) demonstrated a reliable prediction of the flame speed in the laminar limit and $\tau _{LPF}$ seemed to approximate the flame dynamics within the flame correctly. It has been pointed out above that its application to turbulent flames requires a blending between this laminar scale and a turbulent scale and this is assessed here. We use C-0.6 as a base case since DNS results discussed above show that for $\phi = 0.6$ the flamelet-like structure is mostly preserved such that the laminar mixing time scale should characterize mixing in the flame, however, flame stretching and compression by the turbulence are notable as well, and accurate modelling of both limiting regimes therefore seems important.

Figure 6 (left) presents two variants of the ‘blended’ time scale function. The blending function is given by Eq. (9) and $\tau _{LPF}$ (Eq. (7)) is used as the appropriate laminar premixed time scale. The second variant uses the time scale given by Eq. (6) and taken in earlier studies (Straub et al. 2021) for comparison. In both cases results are shown for $\alpha = 0$ in Eq. (9) but the exact value of $\alpha$ is of no major concern for this comparison and results obtained with $\alpha = 1$ are almost identical. The model introduced by  Straub et al. (2021) (orange) provides a significantly smaller mixing time scale that is almost constant across the entire flame. In contrast, the new time scale model exhibits a peak at a location within the flame front preventing excessive mixing across the flame. This feature has been discussed in  Iaroslavtceva et al. (2022) as being one of the reasons why the use of $\tau _{LPF}$ achieves the correct laminar flame speed. Here, we need to point out that the determination of the flame speed is not straight-forward for a sparse particle method as it is next to impossible to define a flame front that then propagates. However, if the particle solution correlates well with the Eulerian solution, then the MMC solution must propagate with the same flame speed as the DNS. Figure 6 (right) therefore depicts the correlations between $\phi _c^p$ and $c_{rlx}^p$. A good correlation indicates that the flame predicted by the stochastic particles is aligned with the flame predicted by the DNS on the Eulerian grid. If it is linear the flame positions are exactly the same. The slightly bent profile that can be observed for the new model shows that reaction progress of the particles is somewhat lower than the corresponding value of the reference field (and thus on the Eulerian grid where the particle is located). This indicates that the flame predicted by MMC establishes itself about a quarter to half a flame thickness downstream of the Eulerian flame solution. No correlation can be observed when the reference time scale $\tau _{a-iso}^c$ is used. Stochastic particles representing a burnt mixture can be found at the leading edge of the DNS flame, the flame represented by the particles is much too fast and the reference field no longer serves as a suitable conditioning variable as it no longer guarantees localness of mixing in composition space. These observations are supported by Fig. 7. Here, we compare the (locally averaged and mapped) reaction progress variable of the particles, $\overline{\phi _c^p}$, with the respective Eulerian solution of the reference field. Figure 7 shows $\overline{\phi _c^p}$ as a function of time at the spatial location where the DNS solution equals $c=0.1$. We use the value of 0.1 instead of a perhaps more conventional value of 0.5 as gradients of c are smaller here and uncertainties in determining flame position are reduced. A good correlation exists if $\overline{\phi _c^p}$ continuously equals 0.1. We can see that for the new model $\overline{\phi _c^p}$ is below 0.1 (which is expected after consultation of Fig. 6 (right)) but $\overline{\phi ^p_c}$ stays constant, the correlation persists and the flame predicted by MMC thus propagates with the flame speed being the same as the DNS solution. Using $\tau _{a-iso}^c$ time scale $\overline{\phi _c^p}$ increases fast which is equivalent to too much mixing resulting in an increased flame speed. As discussed above, relaxation of the reference field should reduce mixing across the flame front and has been proven a suitable measure to stabilize PDF predictions of laminar premixed flame propagation. Following  Iaroslavtceva et al. (2022), the relaxation parameter $\lambda$ is reduced by a factor of 10 when $\overline{\phi _c^p}$ surpasses a threshold value of 0.15. It is further decreased to $\lambda =0.01$ when $\overline{\phi _c^p} > 0.2$. Figure 7 shows that even such strong relaxation of the reference variable is unable to prevent the flame acceleration and any variation of the above given critical values does not improve results. We note that the particle flame establishes itself at the leading edge of the flame predicted by the DNS and does not leave the domain. This is because of the relatively slow mixing outside the flame zone where $\tau _{L} = \tau _{a-iso}^f$ such that burnt particles mix with unburnt particles very slowly. This is of course of no major benefit as lack of correlation with the reference scalar will lead to arbitrary mixing pairs and a destruction of the true flame structure. This is demonstrated by Fig. 8 where the predicted intermediate species mass fractions - plotted as function of c - are compared with the DNS data. The new mixing time scale model provides good prediction of the mean values but overpredicts the variance, albeit the correct trends are captured. In contrast, results for $\tau _{lam} = \tau _{a-iso}^c$ demonstrate significant deviations from the correct conditional means and even larger overprediction of the RMS. Overall poor performance of the $\tau _{a-iso}^c$ model is likely related to the fact that the premixed flame thickness does not represent the correct mixing length scale. However, the new model does not match the second moments for the low Ka cases where the flame stays thin. This needs to be accepted as the random walk induces some randomness that cannot entirely be suppressed and has also been observed for the laminar flames investigated in  Iaroslavtceva et al. (2022). The error seems acceptable however, considering the flamelet character of the DNS flame and the very low overall RMS imposed by the conditioning in the corrugated flame regime.

Fig. 6

Mixing time scales (left) and particle progress variable (right) versus the progress variable on the Eulerian field ($\phi = 0.6$)

Fig. 7

Progress variable relaxation performance

Fig. 8

Weighted mean and RMS of the intermediate’s mass fractions versus the progress variable

4.3 Predictions of the Flame Structure

PDF methods have been designed for the modelling of turbulence-chemistry interactions as it shall not depend on the flame regime. They should predict the transition from the flamelet-like to distributed flame regimes that cannot be captured by a standard flamelet method. Figure 9 shows an example for the qualitative change of the mixing time scales with equivalence ratio. Here, $\tau _{lam} = \tau _{LPF}$, $\alpha = 1$ and the constant $C_L$ is set to $C_L = 0.1$. For $\phi = 1.0$ (Ka = 0.7) the mixing time scale in the center of the flame is close to $\tau _{LPF}$ which is expected as the flame is located in the flamelet regime. More scattering is observed for $\phi = 0.6$ (Ka = 1.4) indicating that the turbulence starts to interact with the flame front. In the first two cases, peaks of the mixing time can be observed for positions (progress variable values) close to the flame center. These peaks can be associated with the shape of $\tau _{LPF}$ given by Eq. (7) that implies a maximum at the inflection point of c (where the second derivative approaches zero in the respective laminar case). Such a maximum prevents - or rather slows down - mixing across the flame and thus succeeds in preserving the premixed flame structure in the flamelet regime. This is needed as the random walk model (Eqs. (1) and (2)) allows the particles to jump across the flame front, but conditioning on the reaction progress variable combined with slower mixing prevent micromixing after such jumps that would otherwise lead to subsequent unphysical acceleration of the flame. In cases with $\phi = 0.2$ (Ka = 30) and $\phi = 0.15$ (Ka = 67), turbulence affects the flame structure and the mixing time scale is dominated by $\tau _{a-iso}^f$ as the blending function approximates zero for the entire c-space (cf. Fig. 1).

Fig. 9

Mixing time values calculated using Eq. (8) with $\tau _{lam} = \tau _{LPF}$, $\alpha = 1$ and $C_L = 0.1$

Figures 10 and 11 show predictions of the conditionally averaged mass fractions and RMS of the intermediates CO and H$_2$ for all four cases. The Ka dependence of the blending function and thus of the mixing time scale is tested with $\alpha$ being varied from 0 (no dependence) to 1 (linear dependence). In Case C-1.0 Ka $< 1$ therefore $\alpha$ does not influence the particle mixing (cf. Eq. (9)). The effect of $\alpha$ observed in Case C-0.6 can be considered negligible. For such low Karlovitz numbers variation of $\alpha$ has minor effects since $\tau _{LPF}$ is smaller than $\tau _{a-iso}^f$ and mixing inside the flame is always dominated by the laminar mixing time scale making the influence of $\alpha$ less significant. In cases with $\phi = 1.0$ and $\phi = 0.6$ the mean mass fraction values are predicted well for both intermediate species. The RMS peak predicted by the particles is shifted to higher progress variable values than in the DNS, we also notice a general overprediction of the RMS by the particles. This excessive variance is produced by the random walk jumps and cannot be fully excluded in the flamelet-like regime (Iaroslavtceva et al. 2022).

Fig. 10

Weighted mean (top) and RMS (bottom) of the CO mass fraction versus the progress variable

Fig. 11

Weighted mean (top) and RMS (bottom) of the H$_2$ mass fraction versus the progress variable

The effect of $\alpha$ is more notable on the predictions where the qualitative assessment of the flame indicated a broadened flame zone and where significant disturbances of the flame structure could be observed. Here, the ratio of time scales has to be included with the aid of Ka and variation of $\alpha$ influences the agreement significantly. For $\phi = 0.2$ and $\phi = 0.15$ the mean CO mass fractions are predicted well for all $\alpha$ while the mean H$_2$ mass fractions are notably overpredicted for $\alpha = 0$. This overprediction gets smaller with increasing $\alpha$ and completely disappears for $\alpha = 1$. Inspecting the RMS of the intermediate species mass fractions in Figs. 10 and 11 we notice that values predicted by the stochastic particles are very close to the DNS solution and $\alpha = 1$ provides most accurate predictions for both CO and H$_2$. We can conclude that for wider reaction zones the new mixing time scale model with $\alpha = 1$ provides excellent agreement of both mean and RMS of the intermediate species, indicating that for Ka = 30 and above a purely turbulent mixing time scale should be used. This is also consistent with Figs. 4 and 5 that demonstrate a large influence of turbulence on the flame for the low equivalence ratio cases. Despite this large turbulence effect and the strong variation in species gradients, the means of the species mass fractions conditionally averaged on reaction progress stay close to the corresponding laminar profiles. Conditional RMS are moderate and this observation generally supports the continued existence of flamelet structures in these cases and the regime classification given in Fig. 2.

The maximum RMS are shown in Fig. 12 for different equivalence ratios. The maximum RMS decreases the leaner the flame is and the particle solution predicts this tendency correctly. For $\phi = 1.0$ and $\phi = 0.6$ we again notice the RMS to be overpredicted while for smaller equivalence ratios the maximum RMS is matched well by the particle solution. As pointed out above, this overprediction in the flamelet regime is similar to the behaviour observed in laminar cases (Iaroslavtceva et al. 2022) and cannot be avoided completely with the random walk model.

Fig. 12

Maximum RMS of the intermediate species mass fraction versus the equivalence ratio

Overall we can conclude that when using the new mixing time scale model the flame structure is predicted reasonably well in all the turbulent premixed combustion regimes and $\alpha = 1.0$ provides the best agreement with the DNS data. We acknowledge the existence of two other modelling parameters, namely the relaxation parameter $\lambda$ and the proportionality constant $C_L$ as introduced in Eqs. (10) and (7), respectively. The sensitivity towards these parameters was investigated in Iaroslavtceva et al. (2022), but we note here that relaxation is not likely to be activated in cases where the flame thickness is large. Thus, the exact value of $\lambda$ may not be important in future MMC-LES where we intend to represent the flame by a thickened flame model as introduced in Straub et al. (2021). In contrast, $C_L$ is a true modelling parameter that can be varied to control minor fluctuations around the mean. Previous work established $C_L=0.1$ as a suitable value to sufficiently constrain conditional fluctuations for locally laminar flames (Iaroslavtceva et al. 2022), but this value should be taken as a guideline only and future MMC-LES across a wider range of flow conditions will be needed to demonstrate some universality of this value or to establish new guidelines for the selection of a suitable estimate of $C_L$.

5 Discussion

In the present study, MMC model development and validation are solely based on coupling with a DNS of the flow field. This warrants some discussion as the new mixing time scale model is expected to provide a consistent closure at LES sub-grid level and match the turbulent flame propagation speed in future MMC-LES computations of laboratory turbulent flames. There, the MMC-LES solution shall merely rely on the flame position provided by the Eulerian field, and the accurate prediction of the flame composition including effects like flame extinction and slow pollutant formation will be predicted by the stochastic particles. It can be expected that the mixing time scale model validated here continues to be applicable in MMC-LES without major change. In Sects. 2–4, we have introduced an auxiliary LES mesh and provided LES-filtered input data to the time scale model. Thus, the model should be generally unaffected by the transition from DNS to LES for the flow field solution.

Nevertheless, a transition to stand-alone LES computations is not trivial and therefore not yet attempted here. In LES, the reference field is not resolved and LES models to consider the subgrid contribution to the turbulent premixed flame, e.g. artificial flame thickening, will be needed. It has been demonstrated that - in principle - MMC-LES can be applied to premixed flames (Straub et al. 2021) and this should not change when the new mixing time scale is introduced. However, a rigorous (a posteriori) analysis where turbulent flames speeds are to be predicted, requires the following steps: first, thickening of the DNS field, second, backward-coupling of the density field to the DNS solution and, finally, setting up an LES that is comparable with the DNS for proper model evaluation. Ensuring a direct comparability between LES and DNS will certainly require major work, especially in terms of comparable turbulent inflow conditions, flame corrugation (the DNS domain would need to allow for similarly large scales) and thus flame speed. A large DNS domain using multi-step kinetics may be too costly and extension to LES may follow a different route. Steps one and two described above should ensure that only one scalar field, the reference field, needs to be solved by the DNS. This should then allow for larger DNS domain sizes comparable with the LES. These steps are beyond the scope of one single paper, they are subject to current work and will be addressed in future publications. Independent of these future research directions, coupling of MMC to DNS can be valuable in itself. This is because soon, the available computer power may allow for DNS of applications of engineering interest where the velocity field and one reference scalar can be solved. The inclusion of complex chemistry involving hundreds of chemical species as needed for, e.g., pollutant predictions may, however, be beyond reach for quite some time. Here, MMC as a sparse particle implementation can provide an attractive combustion submodel as it provides closure for the chemical source term including detailed chemistry at a moderate computational cost.

6 Conclusion

An MMC mixing time scale model that has previously been validated for laminar premixed flames (Iaroslavtceva et al. 2022) has been combined with a turbulent mixing time scale with the aid of a modified blending function. The blending function serves a dual purpose: firstly, it acts as a flame indicator that guarantees the turbulent mixing time scale to be used outside the flame front while the laminar premixed time scale is used at positions where the flame is located. Secondly, the inclusion of the Karlovitz number introduces a further dependence of the weighting factor on the flame regime such that higher weighting can be given to the turbulent time scale even within the flame front if turbulence is high and a thin or distributed flame regime is expected. A series of 3D-DNS computations of statistically 1D turbulent premixed methane-air flame with varying equivalence ratio provides combustion regimes from flamelet-like to thickened reaction zone and is used for model validation. Conditioning on the reference variable introduced together with the laminar premixed flame mixing time scale (Iaroslavtceva et al. 2022) provides a smooth transition from a dense-particle approach to a sparse-particle MMC which uses as few as 1 stochastic particle per 512 DNS cells. Computations show that the new mixing time scale model is successful at predicting the turbulent premixed flame propagation speed which cannot be matched by the MMC mixing time scale introduced earlier. The predicted flame structure is evaluated by comparing the intermediates CO and H$_2$ from the DNS and the particle solutions. The mean mass fraction values are predicted well while the variations are slightly overpredicted by the particle solution for regimes close to flamelet, nevertheless, keeping the correct tendencies.