Mixing Time Scale Models for Multiple Mapping Conditioning with Two Reference Variables

Abstract

A novel multiple mapping conditioning (MMC) approach has been developed for the modelling of turbulent premixed flames including mixture inhomogeneities due to mixture stratification or mixing with the cold surroundings. MMC requires conditioning of a mixing operator on characteristic quantities (reference variables) to ensure localness of mixing in composition space. Previous MMC used the LES-filtered reaction progress variable as reference field. Here, the reference variable space is extended by adding the LES-filtered mixture fraction effectively leading to a double conditioning of the mixing operator. The model is used to predict a turbulent stratified flame and is validated by comparison with experimental data. The introduction of the second reference variable also requires modification of the mixing time scale. Two different mixing time scale models are compared in this work. A novel anisotropic model for stratified combustion leads to somewhat higher levels of fluctuations for the passive scalar when compared with the original model but differences remain small within the flame front. The results show that both models predict flame position and flame structure with good accuracy.

1 Introduction

Many premixed flames are not burning in a truly premixed combustion mode due to mixing with the surrounding air and/or stratification of the fuel mixture. The latter is a common design feature as it enhances ignition probability and flame stability in overall lean premixed environments that are favoured due to their relatively benign emission characteristics of pollutants such as $\hbox {NO}_\mathrm {x}$ and soot. However, mixture inhomogeneities require adaption of conventional computational models that were developed and calibrated for the pure premixed case. Here, we use large eddy simulation (LES) as the framework for the investigation of those details, and focus on its coupling with a combustion model that is required to close the turbulence-chemistry interactions that occur at the subfilter scale. Promising combustion models that account for these unclosed terms are—amongst others—(1) the presumed PDF approaches (Peters 1984) which characterize turbulence-chemistry interactions in terms of fluctuations of a low dimensional manifold and (ii) the probability density function (PDF) approaches (Pope 1985). In PDF approaches (or filtered density function (FDF) methods as they are called within the LES framework), a probabilistic treatment is applied to the LES subfilter scales and the FDF transport equation is usually replaced by a system of equivalent stochastic differential equations governing the evolution of Lagrangian stochastic particles. The key advantage of FDF models is the direct treatment of the chemical source term for which no turbulent closure assumptions are needed. Thereby, the FDF methods are not specific to any combustion regime and do not discriminate between non-premixed and premixed combustion. Furthermore, they should be able to predict flamelet-like structures if turbulence levels are low to moderate but they should also be able to predict any deviations thereof if turbulence is strong and the preheat or reaction zones are locally thickened. However, despite the in principle regime independence of FDF models the governing equation contain an unclosed term for the subfilter conditional scalar dissipation which needs to be modelled via a mixing model and some of the common models are not suitable for all regimes due to their violation of the principle that mixing should be local in composition space (Subramaniam and Pope 1998).

Multiple mapping conditioning (MMC) provides a framework that exploits ideas from both the flamelet-like and PDF/FDF approaches. Deterministic and stochastic implementations coupled to Reynolds averaged Navier Stokes (RANS) (Vogiatzaki et al. 2009; Wandel and Klimenko 2005; Vogiatzaki et al. 2011; Straub et al. 2016) or LES (Cleary and Klimenko 2011; Ge et al. 2013; Neuber et al. 2017) flow field solvers have been developed. The key characteristic of MMC is the use of mathematically independent reference variables that help to achieve localness of mixing in composition space. Cleary and Klimenko developed a generalized version of MMC in the LES framework for turbulent non-premixed flames (Cleary and Klimenko 2011). The FDF is represented by a sparse set of stochastic particles where ”sparse” means that the number of stochastic particles, $N_p$, is less than the number of LES cells. The low number of particles is realizable, because mixing is localised in physical space and the reference space. In non-premixed flames, mixture fraction usually characterizes the local species composition well and using the LES filtered mixture fraction as a reference variable has led to good results for a number of applications (Neuber et al. 2017; Huo et al. 2019; Neuber et al. 2019). Specific implementation issues are summarized by Galindo-Lopez et al. (2018). In premixed applications the definition of a suitable reference variable is not that obvious and two different approaches using (1) a reference variable similar to a shadow position with a dense particle distribution (Sundaram and Klimenko 2017; Galindo-Lopez 2018) and (2) a thickened reaction progress variable for a sparse particle distribution (Straub et al. 2018, 2019) have been published so far. At this stage it is unclear whether one of the two approaches is of clear advantage. Both methods require modelling for the prediction of the correct turbulent premixed flame speed as a particle based method for one-point statistics cannot adequately capture flame corrugation at sub-grid level (Tirunagari and Pope 2016). The shadow position method may provide a better resolved reference field as resolution increases with stochastic particle number. It is, however, of computational disadvantage that many particles are needed. For the LES with a thickened reaction progress, the resolution of the reference field depends on the LES grid resolution of the thickened flame, but computational efficiency is preserved as a sparse distribution of stochastic particles can continue to be used for the reactive species fields. The introduction of a thickened reference field does, however, require a new interpretation of the reference variables: We consider the flame real width to be the smallest physical scale and introduce two modelling scales that are larger: the particle mixing distance and the thickened flame width. While conditioning on shadow positions or, in the case of non-premixed flames on mixture fraction, enforces localness in (real) composition space, the interpretation of conditioning on a thickened flame may be different. Here, the conditioning is primarily used for locating the flame position and imposing the correct turbulent flame speed. References Straub et al. (2018, 2019) indicated that this conditioning prevents mixing of fully burnt particles with unburnt particles despite the difference in scales between the ATF solution and the real (physical) flame width.

Here, we choose the thickened reaction progress variable as a reference field. References Straub et al. (2018, 2019) used a single reference variable that is designed to prevent unphysical mixing of burnt and unburnt samples across the premixed flame front. MMC was applied to premixed flames with stratification, but prevention of non-local mixing across variations in the equivalence ratio was not included explicitly in the mixing model formulation. In the present paper, we extend the thickened progress variable MMC model to better control mixing in stratified flames by introducing a second reference variable given by the LES filtered mixture fraction. The idea of increasing the dimension of the manifold is not new and has been applied in the flamelet (Kuenne et al. 2011), conditional moment closure (CMC) (Kronenburg 2004) and conditional source-term estimation (CSE) (Dovizio and Devaud 2016) approaches. Double conditioning on a progress variable and mixture fraction has also been used in the deterministic version of MMC for partially premixed flames in homogeneous, isotropic turbulence (Kronenburg and Cleary 2008). Here, we introduce double conditioning in the context of the sparse, stochastic version of MMC-LES for the first time.

Mixing in the context of sparse MMC-LES requires both the selection of particle mixing pairs that are local in the reference space and modelling of the mixing time scale that scales with the characteristic length scale of relevant distances between the particles so that conditional subfilter variance decays at the physically correct rate. The approaches developed for singly conditioned MMC of non-premixed flames can not be directly transferred to doubly conditioned MMC of stratified flames due to the presence of a relatively thin (unresolved) flame zone and the corresponding locally intense mixing. In earlier work on premixed MMC-LES (Straub et al. 2018, 2019) we formulated time scale models that differ from models validated for non-premixed combustion (Vo et al. 2017). For two-dimensional reference spaces in general (and therefore stratified combustion in particular) the exact choice of the mixing time scale model is not evident. As different models for the time scales exist, its exact modelling warrants some attention and the current work therefore assesses different suitable models and combinations thereof for the mixing frequency. Results for doubly conditioned MMC are compared with the results using one reference variable only. In addition, the computations are compared with experimental data for a turbulent stratified flame (TSF) configuration, namely TSF-A that was experimentally investigated at TU Darmstadt (Seffrin et al. 2010) and at the Combustion Research Facility at Sandia National Laboratories, Livermore (Stahler et al. 2017).

The remainder of the paper is structured as follows: In Sect. 2 we give a brief summary of the coupling between the ATF-FGM approach with the MMC mixing model and present the formulation of MMC with two reference fields including two different mixing time scale models. Section 3 describes the experimental and numerical setups for TSF-A. The results for doubly conditioned MMC with the two different mixing time scale models are presented and compared with singly conditioned MMC and experimental data in Sect. 4. Section 5 provides a summary and an outlook for future work. "Appendix" formulates an approach for the computation on an MMC-specific mixing distance parameter, $r_m$, if two reference variables are used.

2 Doubly Conditioned MMC-LES Approach

2.1 The Transport Equations

We solve the standard Eulerian LES equations for mass, momentum and the two reference fields (namely, reaction progress and mixture fraction). LES resolutions are typically much too coarse to resolve the relatively thin premixed flame fronts, and therefore an artificially thickened flame (ATF) model (Butler and O’Rourke 1977) is introduced for the closure of the filtered reaction progress variable source term. As in previous publications (Kuenne et al. 2011), the $\hbox {CO}_2$ mass fraction is used to represent reaction progress here. The ATF model achieves closure by increasing the molecular diffusion such that the reaction zone is sufficiently broadened and resolved by the LES grid. This is realized by a thickening factor, F, and the filtered transport equations for the reference $\hbox {CO}_2$ mass fraction and reference mixture fraction then read (Kuenne et al. 2011, 2012)

$$\begin{aligned} \frac{\partial {\overline{\rho } {\widetilde{Y}}_{\hbox {CO}_{2}}}}{\partial {t}} + \frac{\partial {\overline{\rho } \widetilde{u}_i {\widetilde{Y}}_{\hbox {CO}_{2}}}}{\partial {x_i}}= \frac{\partial {}}{\partial {x_i}}\left( \left[ FE\overline{\rho }{\mathcal {D}}+(1-{\varOmega })\frac{\mu _t}{\mathrm {Sc}_t}\right] \frac{\partial {{\widetilde{Y}}_{\hbox {CO}_{2}}}}{\partial {x_i}} \right) + \frac{E}{F}{\dot{\omega }}_{\hbox {CO}_{2}}, \end{aligned}$$

(1)

and

$$\begin{aligned} \frac{\partial {\overline{\rho } {\tilde{f}}}}{\partial {t}} + \frac{\partial {\overline{\rho } \widetilde{u}_i {\tilde{f}}}}{\partial {x_i}}= \frac{\partial {}}{\partial {x_i}}\left( \left[ FE\overline{\rho }{\mathcal {D}}+(1-{\varOmega })\frac{\mu _t}{\mathrm {Sc}_t}\right] \frac{\partial {{\tilde{f}}}}{\partial {x_i}} \right) . \end{aligned}$$

(2)

F is computed locally (cell based) and is chosen in such a way that the flame is nominally resolved by 10 LES cells. The efficiency function, E, is introduced to account for the wrinkling that is filtered out by the thickening and is modelled via the formulation proposed by Charlette et al. (2002). The flame sensor is given by

$$\begin{aligned} {\varOmega } = 16[{\widetilde{c}}(1-{\widetilde{c}})]^2 \quad \text{ with } \quad {\widetilde{c}}=\frac{{\widetilde{Y}}_{\hbox {CO}_{2}}}{Y_{\hbox {CO}_{2}}^{\mathrm {eq}}({\tilde{f}})}, \end{aligned}$$

(3)

where, $Y_{\hbox {CO}_{2}}^{\mathrm {eq}}$ is the equilibrium value of ${\widetilde{Y}}_{\hbox {CO}_{2}}$ and is stored in a table as a function of mixture fraction. The flame sensor limits the thickening procedure to the flame front and the method used here is known as the dynamic thickening approach (Durand and Polifke 2007). To include detailed chemistry but preserve low computational cost for the computation of the reference fields, a flamelet generated manifold (FGM) (van Oijen and de Goey 2000) is applied to close the reaction source term of the $\hbox {CO}_2$ mass fraction, ${\dot{\omega }}_{\mathrm {CO}_2}$, in Eq. (1). This chemical source term, the species composition and the density are parameterized by mixture fraction and reaction progress where the former is necessary to account for the stratification. During run-time, these properties are read from a pre-computed two-dimensional chemistry table, which is based on the GRI-Mech 3.0 kinetic scheme (Smith et al. 2019) as indicated on the left hand side in Fig. 1.

Fig. 1

Schematic of the coupling relationship between the submodels LES, ATF, FGM and MMC

It is noted here, that the model described up to now is a well established and stand-alone model. The reader is referred to reference (Kuenne et al. 2011) for complete details on the ATF-FGM model.

Coupling the ATF model for the reference variables with the MMC approach for the reactive subfilter scale fluctuations requires the solution of the joint scalar FDF which models deviations of the flame from the flamelet structure across all premixed flame regimes. Figure 1 gives an overview of the interaction of the Eulerian framework (left) and the Lagrangian approach (right). The reference variables, flow field properties for the particle movement and the mixing time scale are transferred from the Eulerian grid to the Lagrangian particles. The figure also indicates that the FDF transport equation is solved indirectly by an equivalent system of stochastic differential equations (Pope 1985; Cleary and Klimenko 2011) which read as

$$\begin{aligned} dx_i^p= & {} \left[ {\widetilde{u}}_i + \frac{1}{\overline{\rho }} \frac{\partial {}}{\partial {x_i}} \left( \overline{\rho } {\mathcal {D}}_{\mathrm {eff}}\right) \right] ^pdt + \left[ \sqrt{2{\mathcal {D}}_{\mathrm {eff}}} \right] ^pd\omega _i, \end{aligned}$$

(4)

$$\begin{aligned} d{\varPhi }_{\alpha }^p= & {} \left( W_{\alpha }^p + S_{\alpha }^p\right) dt. \end{aligned}$$

(5)

These govern the evolution of an ensemble of stochastic particles, with each particle representing an instantaneous realisation of the composition field. Here, $x^p$ represents the particle position, ${\varPhi }_{\alpha }^p$ the particle composition, where the index $\alpha =1,\ldots ,n_s$ includes the (gaseous) scalar composition, enthalpy and mixture fraction. In Eq. (4) the filtered properties are obtained from the LES and interpolated to the particle position. These are the filtered velocity, ${\widetilde{u}}_i$, density, $\overline{\rho }$, and the effective diffusivity, ${\mathcal {D}}_{\mathrm {eff}}$. The increment of a stochastic Wiener process is given by $d\omega _i$. Eq. (5) accounts for changes of the composition via reaction source term, $W_{\alpha }^p$, and the unclosed mixing operator, $S_{\alpha }^p$. The key feature of MMC is the introduction of reference variables to enforce mixing localness in this reference variable space. As MMC is a high-quality mixing model which by virtue of its design fulfills important principles as localness, linearity and independence, it can be applied in a sparse particle distribution framework. Mixing over larger physical distances, which can occur due to the sparse particle distribution, does not—per se—lead to unphysical solutions provided that the mixing time scale scales with relevant distances to avoid excessive numerical diffusion. However, if mixture compositions of these selected particles differ too much, then a shear layer or flame front may lie inbetween the particles and mixing of these particles leads to unphysical results. This can be alleviated by conditioning on the reference fields. We obtain the reference variables from the LES as $\mathbf {\xi }^p=\{{\tilde{c}},{\tilde{f}}\}(\mathbf {x}^p)$. The conditioning of mixing particles in reaction progress variable space relates the particles to their relative position with respect to the flame and prevents undesired mixing across the flame front. The conditioning on mixture fraction prevents mixing across the stratification and shear layers. The introduction of the latter reference variable is new, and discussion on the influence of a two-dimensional reference space on the mixing model is presented in Sect. 2.3.

It is emphasized here that the ATF-FGM model is a flamelet approach and the flamelet table is needed for closure of the source term for the filtered reaction progress, i.e. there is no imminent need for backward coupling from the stochastic particles to the Eulerian framework if the flame is within the flamelet regime. Only if the flame structure deviated strongly from a flamelet, the flamelet table would provide inaccurate closure of the LES-filtered chemical source term and backward coupling of the (more accurate) stochastic particle solution to the LES-filtered field would be needed. To achieve such backward closure the filtered chemical source term and density could be mapped from the particle solution onto the LES grid but care would need to be taken as the LES-filtered reaction progress variable is artifically thickened while the particle solution represents a thin flame. Backward coupling is beyond the scope of the paper and deferred to future work. For now, this places the model’s application close to the flamelet regime where the conditional density does not deviate too much from the flamelet structure. This certainly limits its application. Flames close to the flamelet regime serve, however, as stringent first test cases as MMC shall be designed to avoid unphysical mixing across the flame front that would be inherent to conventional PDF methods. For the application investigated here, ${\tilde{c}}$ is only used for conditioning of mixing and flame characteristics are extracted from the particle solution, extinction levels are quite low and the ATF-FGM approach should provide a sufficiently accurate approximation of the density, the reference and the flow fields.

2.2 MMC Correlation

The reference variables represent physical quantities and a particle can be associated with specific values of (1) the filtered reaction progress variable, ${\tilde{c}}$, and (2) the filtered mixture fraction, ${\tilde{f}}$. The reference variables are provided by the Eulerian solution and interpolated to the particle position. At the same time there exist the actual (local and instantaneous) stochastic particle solutions obtained by Eq. (5) for the $\hbox {CO}_2$ mass fraction and the mixture fraction, $z^p$, respectively, on the stochastic particles. The $\hbox {CO}_2$ mass fraction can be normalized for each particle in the same manner as ${\tilde{c}}$ (see Eq. (3)) and is denoted in the following by $\theta ^p$. The actual particle values $\theta ^p$ and $z^p$ should not be confused with the interpolated LES-filtered values ${\tilde{c}}$ and ${\tilde{f}}$. Reaction progress and mixture fraction are thus computed twice, once within the Eulerian framework and once for the particles. The reference variables and the corresponding properties are independent, but need to be correlated as otherwise the conditioning of mixing in reference space would not yield localisation in composition space.

2.3 MMC Mixing Model

Within this approach the mixing model is specified by the modified Curl’s mixing model over a finite time step ${\varDelta } t$ using

$$\begin{aligned} {\varPhi }_{\alpha }^{p}(t+{\varDelta } t)= & {} {\varPhi }_{\alpha }^{p}(t) + \mu (\overline{{\varPhi }}_{\alpha }^{p,q}(t) - {\varPhi }_{\alpha }^{p}(t)), \end{aligned}$$

(6)

$$\begin{aligned} {\varPhi }_{\alpha }^{q}(t+{\varDelta } t)= & {} {\varPhi }_{\alpha }^{q}(t) + \mu (\overline{{\varPhi }}_{\alpha }^{p,q}(t) - {\varPhi }_{\alpha }^{q}(t)), \end{aligned}$$

(7)

where particle pairs mix linearly towards their conditional mean, $\overline{{\varPhi }}_{\alpha }^{p,q}$, and $\mu = 1 - \exp (-{\varDelta } t/\tau _L)$ is the extent of mixing defined via a mixing time scale, $\tau _L$, which is discussed in Sect. 2.3.3.

2.3.1 Particle Selection with Two Reference Variables

The key feature of the MMC mixing model is conditioning in reference space that ensures the particle pairs to be mixed are close in composition space. For the particle pair selection the effective square distance

$$\begin{aligned} \left( {\hat{d}}^{p,q}\right) ^2 = \underbrace{\underbrace{\sum _{i=1}^3 \left( \frac{d_{x_i}^{p,q}}{r_m/\sqrt{3}}\right) ^2 + \left( \frac{d_{{\tilde{c}}}^{p,q}}{c_m}\right) ^2}_{\mathrm {single\,conditioning}} + \left( \frac{d_{{\tilde{f}}}^{p,q}}{f_m}\right) ^2}_{\mathrm {double\,conditioning}}, \end{aligned}$$

(8)

is introduced. Here, $d_{\psi }^{\,p,q} = |\psi ^{\,p} - \psi ^{\,q}|$ represents the magnitude of the difference of the corresponding property $\psi$ for a particle pair (p, q), where $\psi \in {\{x_1,x_2,x_3,{\tilde{c}},{\tilde{f}}\}}$. For small enough relative values of the localness parameters $c_m$, $f_m$ and $r_m$ the mixing partners (p, q) are close in reference progress variable space, ${\tilde{c}}$, in reference mixture fraction space, ${\tilde{f}}$, and in physical space, $\mathbf {x}$, respectively. In comparison to our previous singly conditioned MMC mixing model (Straub et al. 2018), Eq. (8) has one additional term that extends the effective square distance to also include mixture fraction. The k-d-tree pair selection algorithm (Friedman et al. 1977) aims to minimize the effective square distance in Eq. (8). Previous work (Vo et al. 2017) shows that while the implemented k-d-tree algorithm minimizes that distance on average, it is an approximate method that does not ensure minimal distance in $({\tilde{f}},{\tilde{c}},\mathbf {x})$-space for all particle pairs. Premixed combustion is more sensitive to the unphysical mixing across large distances in composition space compared to non-premixed combustion (Sundaram and Klimenko 2017). To prevent undesired mixing particle pairs obtained by the k-d-tree algorithm with $d^{p,q}_{{\tilde{c}}}>2c_m$ and $d^{p,q}_{{\tilde{f}}}>2f_m$ are omitted from mixing in the doubly conditioned approach. These events account for no more than 3% of all mixing events. The need for two reference variables is illustrated in Fig. 2 in which the thermo-chemical state is represented by the CO mass fraction as a function of reaction progress and mixture fraction.

Fig. 2

Schematic of particle pair selection in MMC for four exemplary stochastic particles. The solid lines indicate iso-contours of the CO mass fraction as a function of progress variable and mixture fraction extracted from the FGM table

The values are extracted from the FGM table. Additionally, four typical stochastic particles A, B, C and D are plotted and we examine the possible selections of mixing partners for particle A. If we locate the particles within the reaction progress variable space only, as described in the singly conditioned approach (Straub et al. 2018), particle B would be chosen. However, due to the stratification A and B have very different CO mass fractions and pairing based on c alone clearly does not ensure localness in composition space. Alternatively in the sparse particle approach for non-premixed combustion (Cleary and Klimenko 2011), the distance in progress variable space is ignored, and a small $f_m$ value would locate the particle mixing pairs such that they are close in LES mixture fraction space. Then, particle A would mix with particle C. But these two particles have very different reaction progress (vertical distance) such that non-local pairing is also undesirable. In the doubly conditioned model we localise mixing pairs in both reference spaces and particle A will mix with particle D, because they are close in reaction progress variable and mixture fraction spaces. Note, Fig. 2 only demonstrates localisation in the reaction progress and mixture fraction spaces. Additionally, particle pairs are chosen to be as close as possible in physical space, which is not illustrated in Fig. 2.

2.3.2 MMC Localness Parameters

The parameters $c_m$ and $f_m$ are—in principle—free model parameters. They may not be universal and depend on the flame regime. In a perfectly stirred reactor regime, where high Karlovitz numbers prevail, conditioning may not be needed as the flame zone will be distributed and a PDF method should work using any reasonable mixing model. For flamelet-like regimes, low values of $c_m$ are likely to be needed. Standard values of $f_m = c_m = 0.03$ were established in a number of past MMC computations of non-premixed and premixed flames burning close to the flamelet regime with Ka in the range of 1.2–2.1 (Vo et al. 2017; Straub et al. 2018), and these values are also used here. The parameter $r_m$ varies with the particle resolution and is formulated to be dependent on $c_m$ and $f_m$. It is understood that the mixing volume, $V_m$, is defined as the volume represented by a mixing particle pair within a turbulent flow field. The selection of $r_m$ uses the fact that $V_m$ is equal to the nominal fluid volume represented by each particle. This condition reads

$$\begin{aligned} C V_m = {\varDelta }_L^3, \end{aligned}$$

(9)

where ${\varDelta }_L$ is the average particle distance and $C=2$ is introduced for the trivial reason that the fluid domain consist of half as many mixing pairs as there are particles. For singly conditioned, non-premixed MMC, (Cleary and Klimenko 2011) derived a simple expression to relate $r_m$ with $f_m$. A more general derivation relating $r_m$ to the characteristic mixing distance in single dimension reference space is given in “Appendix", Eq. (20). With ${\tilde{c}}$ as reference variable the expression reads

$$\begin{aligned} r_m = C^{-1/D_f} \left[ \frac{|\nabla {\tilde{c}}| {\varDelta }_L^3}{c_m {\varDelta }_E^{2-D_f}} \right] ^{1/D_f}, \end{aligned}$$

(10)

with an equivalent expression for single conditioning in mixture fraction space. Here, the fractal dimension is $D_f=2.36$, and ${\varDelta }_E$ represents the filter size. Equation (10) includes the reference variable gradient, and $r_m$ should change throughout the computational domain. The numerical implementation of a particle pair selection algorithm with varying $r_m$ is not practical, but a previous DNS analysis demonstrated that a global $r_m$ is sufficient (Vo et al. 2017). This is also supported by a number of experimental flame computations where $r_m$ is calculated globally with a characteristic reference variable gradient taken at the position where it is at its maximum. In doubly conditioned MMC, $r_m$ varies with the gradients of ${\tilde{f}}$ and ${\tilde{c}}$ and their relative orientation. It can be computed from

$$\begin{aligned} r_m = C^{-2/D_f} \left[ \frac{|\nabla {\tilde{c}}| |\nabla {\tilde{f}}| \sin (\varphi ) {\varDelta }_L^3}{c_m f_m {\varDelta }_E^{1-D_f/2}} \right] ^{2/D_f}, \end{aligned}$$

(11)

where $\varphi$ is the angle between the reference variable gradients. The reader is again referred to "Appendix" for a detailed (and more generic) derivation. Again, practical aspects of the particle selection numerics mean that spatial variation of $r_m$ is unsuitable for use in Eq. (8) and a global value of $r_m$ is used. The location of determining $r_m$ may be important as the ${\tilde{f}}$ and ${\tilde{c}}$ gradients usually vary within the computational domain and the critical locations differ for different setups. The appropriate locations for the investigated application in this work are discussed in Sect. 3.3 and the corresponding $r_m$ values are presented there.

2.3.3 The Mixing Time Scale Models

Once the particle pairs are selected they mix with a mixing frequency, which is given by the characteristic mixing time scale, $\tau _L$. Here, we introduce two different models that are based on the original formulation derived in Cleary and Klimenko (2011), Straub et al. (2018) and on a modified formulation that was introduced in Vo et al. (2017). The first closure was originally proposed for the mixing time scale in non-premixed combustion and is applied for non-premixed ($\alpha =f$) and premixed ($\alpha =c$) combustion in a generic way by Cleary and Klimenko (2011), Straub et al. (2018)

$$\begin{aligned} \tau ^\alpha _{\mathrm {orig}} = C_\alpha \frac{\beta \left( d_{{\tilde{\alpha }}}^{p,q}\right) ^2}{2{\tilde{N}}_\alpha }. \end{aligned}$$

(12)

The modelling of the scalar dissipation rate ${\tilde{N}}_f$ follows standard procedure (Cleary and Klimenko 2011) while the model for ${\tilde{N}}_c$ as derived by Dunstan et al. (2013) has been adapted to account for the ATF implementation (Straub et al. 2018). $C_f=0.1$ and $C_c=0.5$ are common modelling constants in non-premixed and premixed combustion, respectively. $\beta$ is set to $\beta =3$ as in all existing MMC studies.

Vo et al. (2017) re-assessed MMC time scale models and introduced an alternative model (the anisotropic—or a-iso—model) in non-premixed combustion. The second closure is based on the anisotropic idea and the generic formulation is given by

$$\begin{aligned} \tau ^{\alpha }_{\text {a-iso}} = C^{\prime }_{\alpha } \frac{\left( l_{\alpha }\right) ^2}{2{\mathcal {D}}_{\mathrm {eff}}^*}, \end{aligned}$$

(13)

where again $\alpha =f$ and $\alpha =c$ specify non-premixed and premixed combustion, respectively. ${\mathcal {D}}_{\mathrm {eff}}^* = {\mathcal {D}}^p+\frac{d_x^{p,q}}{{\varDelta }_E^p}{\mathcal {D}}_t^p$ is the modified effective diffusivity and $l_{\alpha }$ is the characteristic length scale of each combustion mode. The length scale in MMC for non-premixed combustion is determined by the distance in physical space of the particle mixing pair $l_f=d_x^{p,q}$ and $C^{\prime }_f\,=\,0.1$ is fixed. Note the similarity of this model with the standard model for the LES sub-grid time scale. For non-premixed flames, this model yielded much improved predictions of the conditional variances (Vo et al. 2017). Note that the use of standard modelling constants is not as intuitive as it seems. The parameters for the mixing time scale relate to the distance between the particles as in previous applications of MMC to non-premixed flames. The parameters for localization in thickened reference space refer, however, to a scale larger than the average particle distance. This is different to conditioning on mixture fraction (or shadow positions) where scales of the reference fields are smaller than the length scale of the particles. As such, conditioning on ${\tilde{c}}$ does not—in a strict sense—ensure localness in the composition space of a real (thin) premixed flame but merely ensures the correct flame position and turbulent flame speed on the LES grid. This imposes a higher sensitivity on the right choice of modelling parameters and their interdependencies (i.e. dependence of the correct mixing time scale on $c_m$), as a “wrong” set of parameters can easily lead to a decorrelation of the particle and the LES solution [cf. ref. Straub et al. (2018) (Fig. 6 therein) and also Fig. 7 of this paper]. Further research is needed to establish a possible correlation between all modelling parameters, but this is beyond the scope of this paper and the standard modelling constants provide a stable solution for the analysis of the double conditioning approach.

In turbulent premixed combustion, however, the conventional time scale models tend to fail once the flame front is thinner than the resolved turbulent scales (Gao et al. 2014). This is because the scalar dissipation rate is substantially underpredicted in zones where the premixed flame is located (Gao et al. 2014). The modelling needs to be based on the correct scales and cannot simply be proportional to the particle distance $d_x^{p,q}$ (Wang et al. 2018). In Wang et al. (2018) the laminar flame thickness is chosen as the characteristic premixed length scale and we set $l_c=\delta _l$. The laminar flame thickness is a function of the local equivalence ratio and is obtained from 1-D laminar freely propagating flame calculations. We apply the thermal flame thickness which is defined via $\hbox {CO}_2$ mass fraction as

$$\begin{aligned} \delta _l = \left( {Y_{\mathrm {CO}_2}^b - Y_{\mathrm {CO}_2}^u}\right) /{\max \left| \frac{\partial {Y_{\mathrm {CO}_2}}}{\partial {x}}\right| }, \end{aligned}$$

(14)

where the subscript b and u refer to the burnt and unburnt state, respectively. The modelling constant in Eq. (13) for premixed combustion is given by $C^{\prime }_c=0.0025$. Differences to the constant chosen in the original publication (Wang et al. 2018) can be explained by the different definitions of the flame thickness $\delta _l$. Wang et al. (2018) use the diffusive thickness ($\delta _l=D_{u}/s_l$) as compared to the thermal thickness that is used here. The model given in Eq. (13) is expected to approximate mixing better in regions away from the premixed flame compared with the model given in Eq. (12). Also note that the definition given by Eq. (13) is independent of the reference variables as opposed to the definition given by Eq. (12).

Some blending between the time scales for premixed and non-premixed combustion is needed. Away from the premixed flame front, the mixing time scale should revert to the expressions given by Eqs. (12) or (13) for $\alpha =f$. This is particularly important in zones where no reaction occurs, but composition varies due to stratification. There, the mixing frequency should not differ from the mixing frequency observed in turbulent non-premixed combustion. To account for the transition between these two regimes, we use the harmonic mean weighted by the flame sensor, ${\varOmega }$, viz.

$$\begin{aligned} \frac{1}{\tau _L} = \frac{{\varOmega }^p}{\tau ^c} + \frac{(1-{\varOmega }^p)}{\tau ^f}, \end{aligned}$$

(15)

where $\tau ^c$ and $\tau ^f$ represent the respective premixed and non-premixed time scale of either approach. For non-premixed combustion and away from the premixed flame zone, (${\varOmega } = 0$), the model reverts to $\tau _L=\tau ^f$ while for ${\varOmega } \rightarrow 1, \tau _L \rightarrow \tau ^c$.

As each stochastic particle within a pair can be associated with a time scale, one further averaging procedure is needed. In previous MMC publications, the maximum mixing time scale ($\tau _L^{p,q} = \mathrm {max}(\tau _L^p,\tau _L^q$)) had been selected to avoid excessive numerical diffusion. Here, we also test the sensitivity of results on this time scale selection and use either the maximum value or the harmonic mean.

3 Case Configuration

3.1 Experimental Setup

We investigate the model performance by comparison with experimental data of a turbulent stratified flame (TSF). The flame is labelled TSF-A and is part of a flame series where detailed species measurements exist and that has been widely used for model validation (Fiorina et al. 2015). The experiments were conducted at TU Darmstadt (Seffrin et al. 2010) and at the Combustion Research Facility at Sandia National Laboratories, Livermore (Stahler et al. 2017). The burner consists of three concentric tubes with inner diameters of 14.8, 37 and $60\,\mathrm {mm}$ (cf. Fig. 3).

Fig. 3

Schematic of the turbulent stratified flame (TSF-A) burner setup with pilot, slot 1 and slot 2. The mean radial positions of the center of the flame brush that is taken as the position of the maximum temperature RMS, $T'_{\mathrm {max}}$, is indicated by dashed lines, and the mean location of the stratification layer, $\phi _m=\frac{\phi _1+\phi _2}{2}$, is represented by the solid lines

The flame is stabilized by the inner pilot of equivalence ratio $\phi {_p}=0.9$, which is identical to the equivalence ratio of the unburnt mixture in the neighbouring slot (slot 1). Slot 2 has a different equivalence ratio of $\phi {_2}=0.6$ and all tubes contain methane/air mixtures. The bulk velocities of the two slots are the same i.e. $U_{\mathrm {slot}1/2}=10\,\mathrm {m/s}$ and result in Reynolds numbers of approximately $Re_{\mathrm {slot}1}=13,800$ and $Re_{\mathrm {slot}2}=13,300$, respectively. The pilot velocity is slightly smaller with $U_{\mathrm {pilot}}=7.7\,\mathrm {m/s}$. These properties place TSF-A within the thin reaction zone regime (Stahler et al. 2017) with only small deviations from the flamelet regime. For more details on this flame series the reader is referred to references Seffrin et al. (2010), Stahler et al. (2017), Straub et al. (2018).

3.2 Numerical Setup

The numerical setup follows the configuration described in Straub et al. (2018). The numerical simulations have been performed with mmcFoam (Straub et al. 2018; Galindo-Lopez et al. 2018), which is based on OpenFOAM. The FGM chemistry model and the ATF-modified transport equations of the filtered reaction progress variable and mixture fraction have been implemented to account for stratified combustion. The computational domain extends $300 \, \mathrm {mm}$ in radial direction and from $-20\,\mathrm {mm}$ to $296 \, \mathrm {mm}$ in the axial $z-$direction. The domain is decomposed into approximately 0.7 million cells and an adequate resolution was verified by a comparison of the results with existing LES-ATF-FGM solutions by Kuenne et al. (2012). Turbulence modelling is based on the Smagorinsky model with $C_s=0.173$. Schmidt numbers are set to $\mathrm {Sc}=0.7$ and $\mathrm {Sc}_t=0.4$. To provide turbulent inlet data for slots 1 and 2 independent pipe flow simulations were conducted prior to the MMC simulation. Zero-gradient pressure boundary conditions are applied at the inlets and fixed pressure at the domain sides and outlets. As in previous publications using single conditioning (Straub et al. 2018), 300,000 stochastic particles are distributed within the computational domain, which corresponds to approximately one Lagrangian particle per 2 LES cells on average. Methane chemistry is governed by the detailed GRI-Mech 3.0 kinetic scheme, which is consistent with the chemistry mechanism applied to create the FGM tables and the flame thickness used for the modelling of the mixing time scale.

3.3 Computation of $r_m$

Three characteristic locations for the computation of $r_m$ are selected as illustrated in Fig. 3 for the target flame TSF-A. (1) “Pos-c” at the upstream location within the flame front between the pilot and unreacted mixture. Here, no stratification exists and MMC (including the computation of $r_m$) should revert to single conditioning with ${\tilde{c}}$ as reference field (use Eq. (10) for computation of $r_m$). (2) “Pos-f” at the upstream location within the stratification layer where mixture fraction gradients are highest and MMC should revert to single conditioning with mixture fraction as a reference variable (use again Eq. (10)). (3) “Pos-cf” where the mean flame brush meets the mean mixing layer. Here, the use of two reference fields is expected to be the most crucial and Eq. (11) should be used.

The value for $r_m$ at “Pos-f” is rather small ($r_m=2.5\,\mathrm {mm}$) compared to the values computed at the other locations. This is due to the relatively small mixture fraction gradient and a larger ${\varDelta }_E$ in this region (cf. Eq. (10)). Using this value throughout the entire domain would enforce strong localization in physical space and prevent localization in reaction progress variable space where needed. The values at the other two characteristic locations provide more reasonable values with $r_m=5.9\,\mathrm {mm}$ (“Pos-c”) and $r_m=8.7\,\mathrm {mm}$ (“Pos-cf”) which is of the order of the inner pilot diameter and about 1 order of magnitude larger than the laminar flame thickness. The larger value for “Pos-cf” is expected as closeness in a two dimensional reference space can only be achieved by relaxing closeness in physical space if the total number of particles (i.e. ${\varDelta }_L$) is kept constant. Sensitivity studies demonstrated that any value between these two limits provides similar results and an intermediate value setting $r_m=6.9\,\mathrm {mm}$ is used here. The values at “Pos-c” and “Pos-cf” represent feasible minimum and maximum values for $r_m$, and it is expected that an intermediate reference length scales provides an overall better condition.

3.4 Investigated Cases

We investigate five different cases for the assessment of the mixing time scale as listed in Table 1. The first case uses the singly conditioned MMC approach and is presented here for comparison. The following two cases are based on the doubly conditioned MMC approach coupled with the original model for the mixing times scale but each uses a different averaging procedure for $\tau _L^{p,q}$. Cases 4 and 5 use doubly conditioned MMC based on the anisotropic approach for the mixing time scale and also differ in the averaging procedure of the two mixing time scales of the particle pair.

Table 1 Overview of conditioning approaches and different mixing time scale combinations for MMC coupled with the ATF-FGM approach

4 Results and Discussion

In doubly conditioned MMC the localness parameters $c_m$, $f_m$ and $r_m$ specify the distances in reference and physical space. Standard values found in the literature are $c_m=0.03$ and $f_m=0.03$ for premixed (Straub et al. 2018) and non-premixed applications (Cleary and Klimenko 2011; Vo et al. 2017), respectively. These values are also used throughout this paper. We first compare results of the doubly conditioned MMC approach with the singly conditioned MMC approach. Then, we present results of the doubly conditioned MMC approach using the different mixing time scale models. The accuracy of the different models is assessed by comparison with experimental data of TSF-A.

4.1 Comparison of Doubly and Singly Conditioned MMC

For the singly conditioned approach $r_m$ is determined from Eq. (10) (cf. Sect. 2.3.2) and we therefore set $r_m=5.9\,\mathrm {mm}$ which is the value calculated at the characteristic location ”Pos-c”. The doubly conditioned MMC approach is represented here by case 3, and we set $r_m=6.9\,\mathrm {mm}$ as discussed in Sect. 3.3.

4.1.1 Flame Brush and Mixing Layer Position

Figure 4 compares the predicted positions of the flame brush (indicated by $T^{\prime }_{\mathrm {max}}$) and the mixing layer (indicated by $\phi _m=0.75$) with the corresponding positions from experiments.

Fig. 4

The mean radial positions of the center of the flame brush that is taken as the position of the maximum temperature RMS, $T'_{\mathrm {max}}$, is indicated by diamonds, the mean location of the stratification layer, $\phi _m=\frac{\phi _1+\phi _2}{2}$, is represented by triangles. The solid lines indicate the experimental data (Straub et al. 2018) and the dashed lines represent the MMC data: black lines (case 1), blue lines (case 3) and orange lines (case 5). The explanation of the case numbers is given in Table 1

The dashed lines indicate MMC predictions while the solid lines show the experimental data. Note that the figure also includes results of the anisotropic mixing time scale model and these results are discussed below in Sect. 4.2. Figure 4 shows that the center of the flame brush is matched quite accurately for the singly conditioned MMC results and only small deviations between singly and doubly conditioned MMC results can be identified. Also, the prediction of the center of the mixing layer is identical for the two approaches up to the axial position $z=45\,\mathrm {mm}$. However, further downstream (between $z=75\,\mathrm {mm}$ and $z=100\,\mathrm {mm}$) the singly conditioned MMC predicts the mixing layer at notably smaller radial positions. This effect is explained with the aid of Fig. 5 that shows radial profiles of mean mixture fraction at two different axial positions for the singly and doubly conditioned approaches.

Fig. 5

Radial profiles of Favre mean mixture fraction at different axial positions. Grey dots represent experimental data. Dotted dashed lines represent the singly conditioned MMC solution, dashed lines represent the doubly conditioned MMC solution and solid lines represent the LES-ATF-FGM solution

At $z=15\,\mathrm {mm}$ only very small differences can be observed for the highest mixture fraction values. Further downstream, however, the mixture fraction profile predicted by the singly conditioned approach is broadened, leading to lower mixture fraction values at $r<55\,\mathrm {mm}$. This overprediction of diffusion is a direct result of the lack of conditioning on mixture fraction space. Particles for mixing are selected independent of their reference mixture fraction values leading to enhanced mixing across the stratification layer which then causes the deviation from the measured profiles. This is even more pronounced further downstream as the smaller mixing time scale within the flame front causes faster mixing. Upstream, the flame front is sufficiently far away from the stratification layer, mixing is slow and omission of conditioning in mixture fraction space has less effect. In contrast, the introduction of two reference fields preserves localness in the combined progress and mixture fraction space throughout the domain and improves results. This fact is strengthened by comparing the MMC data with the ATF-FGM solution, which is also given in Fig. 5. At the upstream position the profiles are quite similar. At the downstream position the doubly conditioned approach is much closer to the ATF-FGM solution when compared to the results of the singly conditioned MMC.

4.2 Comparison of Mixing Time Scale Models

4.2.1 Mean Quantities

As was shown in Fig. 4 the predicted flame positions and the positions of the stratification layer are relatively insensitive to the exact implementation of the mixing time scale, and the results of cases 3 and 5 agree reasonably well with the experimental data. The results of cases 2 and 4 are very similar and not shown in Fig. 4 for clarity of presentation. Comparing the different mixing time scale models, a slight shift to higher radial positions for the anisotropic mixing time scale is observed. This effect will be further investigated below (cf. also Fig. 7).

The mean flame brush and the mean mixing layer positions provide a rather qualitative measure. A more quantitative comparison for the assessment of mixing is provided by the radial profiles of mean mixture fraction and its RMS as depicted in Fig. 6 for the two downstream distances $z=15\,\mathrm {mm}$ and $z=100\,\mathrm {mm}$.

Fig. 6

Radial profiles of Favre mean mixture fraction and RMS at different axial positions. Grey dots represent experimental data and the coloured lines represent the MMC data: red lines (case 2), blue lines (case 3), green lines (case 4) and orange lines (case 5). The explanation of the case numbers is given in Table 1

The mean mixture fraction profiles are accurately predicted by all four cases and differences are very small. However, the original model tends to predict a lower mixture fraction RMS when compared with the anisotropic model. This can be attributed to the different mixing time scale definitions and is—at least for the regions in the flame where non-premixed mixing dominates—expected as $\tau ^f_{\text {a-iso}}>\tau ^f_{\mathrm {orig}}$ in non-premixed flames (Vo et al. 2017). The smaller mixing frequency for the anisotropic model will reduce mixing and allow for larger fluctuations around the mean as observed in the figure. The differences in $\tau _L$ will also be discussed further below. Here, it is also observed that the choice for averaging the time scales of the two particles yields only small changes of the mixture fraction RMS and only at downstream locations. Reducing numerical diffusion, i.e. taking the maximum of the two time scales, results in a slightly increased mixture fraction RMS compared to the harmonic mean. However, the sensitivity of the results to the choice of the mixing time scale of a particle pair is generally very small, indicating overall relatively equal time scales for the two particles when they mix.

4.2.2 Correlation of Reference Variables and Corresponding Stochastic Properties

The similarity of results between the two mixing time scale models can be better understood when analysing the correlation between the stochastic reaction progress $\theta ^p$ and mixture fraction $z^p$ with the corresponding reference fields ${\tilde{c}}$ and ${\tilde{f}}$. Remember that the stochastic reaction progress and mixing evolve independently of the LES-filtered fields, however, a good correlation between the corresponding quantities is required. If the quantities were decorrelated, the LES-filtered field would not characterize the stochastic particles’ species composition and conditioning of mixing on the reference field would become meaningless. Figure 7 presents scatter plots of $\theta ^p$ versus ${\tilde{c}}$ and $z^p$ versus ${\tilde{f}}$. The correlations of cases 3 (original model) and 5 (anisotropic model) are compared here, both employing the harmonic mean.

Fig. 7

Scatter data $\theta ^p$ versus ${\tilde{c}}$ (first column) and $z^p$ versus ${\tilde{f}}$ (second column) of MMC results with the original mixing model (case 3) and the anisotropic mixing model (case 5) at different axial positions

We observe that first and most importantly, the LES and the stochastic solutions do not decorrelate and conditioning on the reference variables ensures localness in composition space even if particles are far away in physical space. As discussed in previous publications (Straub et al. 2018, 2019), the relatively steep and narrow $\theta ^p$-profile indicates that firstly, the stochastic solution correctly predicts a much smaller (and close to realistic) flame thickness than the thickened LES field provides. This can easily be explained with the finite rate chemistry directly integrated on the particles: once a stochastic particle ignites it reaches the fully burnt state within the correct chemical time scale, while the chemical source term for the LES field is artificially reduced by the thickening factor F, leading to a wider flame brush. Secondly, the flame on the particles propagates with the consistent turbulent flame speed of the flame predicted by the LES. If the stochastic solution over-predicted the flame speed, the $\theta ^p$-profile would increase from zero to one at ${\tilde{c}}=0$. If it was under-predicted, the steep increase of $\theta ^p$ would be observed at ${\tilde{c}}=1$. The correlations are somewhat different for each mixing time scale model. However, the exact position of the steep increase of $\theta ^p$ in ${\tilde{c}}$-space is not crucial as long as a clear correlation between $\theta ^p$ and ${\tilde{c}}$ is preserved and conditioning on ${\tilde{c}}$ (localness in reference space) is correlated with localness in particle composition space.

Figure 7 (right) shows the correlation of the stochastic mixture fraction, $z^p$, versus the LES-filtered mixture fraction, ${\tilde{f}}$. In contrast to the correlation of the reaction progress, the scatter plots show an overall linear shape. This is expected as mixture fraction is a conserved scalar and no differences in source terms exist between stochastic and LES solution that could lead to the steepening effects. When comparing the results of the different mixing models it is apparent that the anisotropic approach predicts more scatter which is consistent with the results described in Fig. 6. The increased scatter is expected as Vo et al. (2017) observed higher (and more accurate) conditional fluctuations for the anisotropic model when compared with the original model.

Figure 8 depicts the mixing time scales versus the two reference variables at different axial positions and corroborates above findings.

Fig. 8

Mixing time scale $\tau _L$ versus ${\tilde{c}}$ (first column) and versus ${\tilde{f}}$ (second column) of MMC results with the original mixing model (case 3) and the anisotropic mixing model (case 5) at different axial positions

The mixing time scale given by the original model exhibits more scatter when compared with the anisotropic mixing model. This can be attributed to the square of the particle distance in reference space ($d_{\tilde{c}}$ or $d_{\tilde{f}}$) that appears in the numerator of the model and which is subject to some level of scatter itself. In contrast, $\delta _L$ is a constant and this reduces fluctuations in $\tau _{\text {a-iso}}$. It is also seen that $\tau _{\text {a-iso}}$ tends to be larger than $\tau _{\mathrm {orig}}$, which is in line with the DNS studies by Vo et al. (2017). Larger time scales lead to the increased fluctuations which is also consistent with the above discussion surrounding Figs. 6 and 7.

4.2.3 Flame Structure

While ATF-FGM can predict a flamelet-like flame structure only, the PDF method is able to predict the deviations thereof. These deviations stem from turbulent contributions to (1) the drift term and the Wiener process for particle displacement (i.e. the turbulent contribution to ${\mathcal {D}}_{\mathrm {eff}}$ in Eq. (4)) and (2) the modelling of the mixing operator in Eq. (5) using a turbulent mixing time scale $\tau _L$. Some of these turbulent contributions are implicity modelled by the flamelet method through the presumed subgrid scale distributions of the c and f fields, while in MMC-LES these distributions are solved through the PDF transport equation. Of primary importance is the different treatment of the temporal evolution of the composition space: The flamelet table provides steady state solutions for specific values of the scalar dissipation, while stochastic particle compositions in MMC-LES evolve in time along the Lagrangian trajectories of those particles. This different treatment in MMC preserves the relative importance of the turbulent and chemical time scales of all chemical species (and not of just those species which are closely correlated with either the c or f fields). Lastly, the standard implementation of the flamelet tabulation method omits cross-correlations in reaction progress-mixture fraction space while MMC particles mix across both spaces. Thus, a much wider composition space is accessed by the MMC solution and differences between ATF-FGM and MMC solutions and subsequent comparison with experimental data provide insight on MMC’s capabilities to predict the accurate level of turbulence-chemistry interactions.

Fig. 9

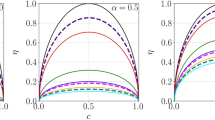
Mass fraction of CO versus temperature for experimental data (grey lines) and MMC results of case 3 (blue lines) and case 5 (orange lines) approach. Left column: conditional mean; center left column: conditional RMS; center right column: conditional mean for specific equivalence ratios and right column: conditional RMS for specific equivalence ratios. The coloured dashed lines within the first and third column are given by the FGM table for different equivalence ratios, namely $\phi =0.9$ and $\phi =0.75$

In Fig. 9, we show the effect of the different mixing time scale models on conditional scalar fluctuations. The flame characteristics are extracted from the particle solution in MMC. In Straub et al. (2019) we showed that singly conditioned MMC can approximate deviations from a flamelet solution quite accurately by analysing the same properties as presented in Fig. 9. In the first and second column the conditional mean mass fraction of CO and its RMS versus temperature are shown. The dashed lines depict the flamelet solution extracted from the FGM table for a specific equivalence ratio. Close to the nozzle (and for $\phi =0.9$) the MMC results and the experimental data approximate the flamelet solution quite well as is evidenced by the similar conditional mean profiles. Reasons for the higher values observed in the measurements were discussed in Straub et al. (2019). Further downstream the deviations from the conditional mean increase and the deviations are slightly underpredicted by the MMC results. The increased deviations around the conditional mean may have two causes: turbulence and stratification, i.e. variation in equivalence ratio. To isolate turbulence-chemistry effects from stratification effects, only data conditioned on a certain equivalence ratio (or mixture fraction) are plotted in the third and fourth column of Fig. 9. The RMS of the doubly conditioned CO mass fraction predicts the deviations from the flamelet solution for a fixed equivalence ratio. The trends for the doubly conditioned mean are correctly captured by MMC. The doubly conditioned RMS are quite similar for the different mixing time scale models, comparable to the experimental data and certainly different from zero as ATF-FGM would predict. The mixing frequency of the original model leads to slightly larger peak values of the doubly conditioned RMS but differences are small overall. Note that the doubly conditioned RMS presented here are similar to predictions using the singly conditioned MMC approach (Straub et al. 2019). This is not surprising as the effect of consistent treatment due to double conditioning is expected to be largest in the outer shear layer where stratification is significant. As all results presented in Fig. 9 are similar, the reader is referred to Straub et al. (2019) for a more detailed analysis of the flamelet structure.

5 Conclusions

A generalized MMC mixing model has been applied to configuration TSF-A of the turbulent stratified flame series. MMC uses reference variables to condition the mixing operator. Previous studies used one reference variable only (the thickened reaction progress), and the present work now extends the reference variable space to two dimensions introducing the LES-filtered mixture fraction as a second conditioning parameter for the MMC mixing term. The introduction of the filtered mixture fraction as an additional reference variable leads to the distinction of fluid elements with different equivalence ratios that originate from the stratification of the flame. At the same time the additional reference variable requires a modification of standard mixing time scale models and we have introduced a blending function that combines the models for premixed and non-premixed combustion. The doubly conditioned MMC results show an improvement of the mean mixing layer position prediction compared to the singly conditioned MMC approach as it prevents unphysical mixing across the shear layer that cannot be captured by the singly conditioned approach. Furthermore, we analysed two different approaches of the mixing time scales and their applicability to stratified flames. While mean properties are quite insensitive to the different mixing time scale models and flame position hardly changes, the anisotropic model predicts—on average—larger mixing time scales leading to larger fluctuations of stochastic mixture fraction ($z^p$) around its corresponding LES-filtered mixture fraction value (${\tilde{f}}$). This does, however, not increase the deviations from the flamelet structure significantly as evidenced by the small changes in doubly conditioned CO mass fractions. The findings of this study for stratified flames are in contrast to the findings for non-premixed flames (Vo et al. 2017; Huo et al. 2019). There, differences in mixing time scale models had significant effects on scalar variances with clearly improved predictions when using an anisotropic time scale model. For stratified flames these differences are much smaller and both models can provide adequate mixing frequencies. The doubly conditioned MMC model with the ”standard” set of MMC parameters predicted accurate results compared to experimental data. The model as presented here does not include backward coupling from the particle solution to the LES flow and reference variable fields. In its current form it is therefore only applicable to flames burning close to the flamelet regime and TSF-A presents a suitable validation case. The application to flame configurations further away from the flamelet regime is subject to future work as it requires backward coupling from MMC to ATF-FGM as the stand-alone ATF-FGM solution will not provide accurate predictions of the flow field and the reference scalars.

Appendix: The Computation of \(r_m\)

We introduce the sliver thicknesses of each generic reference space $l_{\phi _1}=\frac{\phi _{1m}}{|\nabla {\widetilde{\phi }}_1|}$ and $l_{\phi _2}=\frac{\phi _{2m}}{|\nabla {\widetilde{\phi }}_2|}$, respectively. The length scales are visualized in Fig. 10.

Fig. 10

Schematic of the sliver representation with two reference variables of a particle mixing pair (p, q). In this example, particle p lies within the front $x-y$ plane while particle q is located within the extrusion along the z direction and confined to be within the 2 scalar slivers of thicknesses $l_{\phi _1}$ and $l_{\phi _2}$, respectively

The localness parameters are $\phi _{1m}$ and $\phi _{2m}$ and we assume $l_{\phi _1}<l_{\phi _2}$ (if this is not fulfilled the variables can be commuted). The mixing volume is approached via

$$\begin{aligned} V_m = l_{\phi _1} l_{\phi _2}' l_x, \end{aligned}$$

(16)

where $l_{\phi _2}'$ (see Fig. 10) is given by

$$\begin{aligned} l_{\phi _2}' = {\left\{ \begin{array}{ll} \frac{l_{\phi _2}}{\sin \varphi } &{}\text { if } \varphi> 0 \text { and } \frac{l_{\phi _2}}{\sin \varphi }<l_x, \\ l_x &{}\text { if } \varphi = 0 \text { or } \frac{l_{\phi _2}}{\sin \varphi }>l_x \text { or } |\nabla {\tilde{\phi }}_2|=0. \end{array}\right. } \end{aligned}$$

(17)

The case analysis is given by the fact that once the sliver thickness based on $\phi _2$ is bigger than the distance between a particle mixing pair in physical space with fractal properties, $l_x$, particle pairs are chosen close in physical space and $l_x$ defines the mixing volume. The length scale $l_x$ is approximated by

$$\begin{aligned} l_x = \sqrt{A_{\text {surf}}} = {\varDelta }_E^{1-D_f/2} r_m^{D_f/2}, \end{aligned}$$

(18)

where $A_{\text {surf}}$ is the the sliver area modelled in the same manner as in Cleary and Klimenko (2011) with the fractal dimension of $D_f=2.36$. The filter size is given by ${\varDelta }_E$ and defines the fractal inner cutoff scale. The characteristic Lagrangian filter width, $r_m$, is the outer cutoff scale and is the model parameter we want to compute. Inserting Eqs. (17) and (18) in Eq. (16) results in a formula for the particle mixing pair volume. Equating $V_m$ with the volume represented by the particles (see Eq. (9)) and solving for $r_m$ results in the following two cases:

First case $\frac{l_{\phi _2}}{\sin \varphi }<l_x$ and $\varphi > 0$

$$\begin{aligned} r_m = C^{-2/D_f} \left[ \frac{|\nabla {\tilde{\phi }}_1| |\nabla {\tilde{\phi }}_2| \sin (\varphi ) {\varDelta }_L^3}{\phi _{1m}\phi _{2m} {\varDelta }_E^{1-D_f/2}} \right] ^{2/D_f}, \end{aligned}$$

(19)

which corresponds to Eq. (11) with $\phi _1=c$ and $\phi _2=f$.

Second case $\frac{l_{\phi _2}}{\sin \varphi }>l_x$ or $\varphi = 0$ or $|\nabla \phi _2|=0$

$$\begin{aligned} r_m = C^{-1/D_f} \left[ \frac{|\nabla {\tilde{\phi }}_1| {\varDelta }_L^3}{\phi _{1m} {\varDelta }_E^{2-D_f}} \right] ^{1/D_f}, \end{aligned}$$

(20)

which corresponds to Eq. (10) with $\phi _1=c$.

To understand the relationship between the two models for $r_m$, we investigate three different characteristic locations within the stratified flame which are shown in Fig. 3. The different locations and the corresponding $r_m$ values are summarized in Table 2.

Table 2 Overview of different $r_m$ values at different locations within the stratified flame

At “Pos-cf” we take the temporal mean of $\nabla {\tilde{\phi }}_i$ and $\varphi$ at the axial position $z\approx 83\,\mathrm {mm}$ (this is where the mean flame brush meets the mean mixing layer investigated in Sect. 4) and radial position of $\max (|\nabla {\tilde{\phi }}_1||\nabla {\tilde{\phi }}_2|)$. For the other two locations we evaluate $\nabla {\tilde{\phi }}_i$ as the maximum normal gradient. For “Pos-c”, $r_m$ is increased to $r_m=5.9\,\mathrm {mm}$ instead of $r_m=3.47\,\mathrm {mm}$ obtained by Eq. (20), because we applied the former value in previous studies (Straub et al. 2018) and the smaller values lead to too many odd mixing particles with $d_{\tilde{f}}>2f_m$ and $d_{\tilde{c}}>2c_m$, which influenced the flame propagation speed. Generally, the computation of $r_m$ is restricted to a specific grid, because we need $\nabla {\tilde{\phi }}_i$ and ${\varDelta }_E$. Modifying $r_m$ values merely modifies the weighting between the localization parameters for localisation in the composition and physical spaces, but does not introduce errors in the model. For this reason, the influence of $r_m$ variations was also analyzed but differences are small (not shown) as long as $r_m$ is selected in a “reasonable” range (here $5.9\,mm< r_m < 8.7\,mm$ as given by “Pos-c” and “Pos-cf”).

It is noted here, that particle selection based on 5 dimensions seems overrestrictive in a three-dimensional physical space. Seemingly more consistent, alternative methods for a particle selection algorithm may follow from a coordinate transformation: a three-dimensional space could be spanned by

$$\begin{aligned} \mathbf {e}=\left( \frac{\nabla \phi _1}{\mid \nabla \phi _1 \mid }, \frac{\nabla \phi _2}{\mid \nabla \phi _2 \mid }, \frac{\nabla \phi _1}{\mid \nabla \phi _1 \mid } \times \frac{\nabla \phi _2}{\mid \nabla \phi _2 \mid }\right) ^T. \end{aligned}$$

(21)

Then, Eq. (8) may be replaced by

$$\begin{aligned} \left( {\hat{d}}^{p,q}\right) ^2 = { \left( \frac{d_{e_1}^{p,q}}{\phi _{1,m}/\mid \nabla \phi _1 \mid }\right) ^2 + \left( \frac{d_{e_2}^{p,q}}{\phi _{2,m}/\mid \nabla \phi _2 \mid }\right) ^2 + \left( \frac{d_{e_3}^{p,q}}{r_m}\right) ^2} \end{aligned}$$

(22)

with $\mathbf {e}$ being the (non-orthogonal) unit vector. If this strategy was pursued, however, the co-ordinate transformation would need to be effectuated at every particle position at every instant in time which is numerically unfeasible. Also, the k-d-tree algorithm used in this work splits the samples in the direction where the largest (normalized) differences exist. Imagine now that $\nabla \phi _1$ is aligned with the x-axis. If $\phi _{1,m}/\mid \nabla \phi _1\mid$ is smaller than $r_m$, the localness condition in x-direction is ignored. The reverse is true for $\phi _{1,m}/\mid \nabla \phi _1\mid >r_m$. The k-d-tree algorithm thus ensures that conditioning is executed in any suitable three-dimensional space independent of the number of conditioning variables.