A Cartesian Immersed Boundary Method Based on 1D Flow Reconstructions for High-Fidelity Simulations of Incompressible Turbulent Flows Around Moving Objects

Abstract

The aim of the present numerical study is to show that the recently developed Alternating Direction Reconstruction Immersed Boundary Method (ADR-IBM) (Giannenas and Laizet in Appl Math Model 99:606–627, 2021) can be used for Fluid–Structure Interaction (FSI) problems and can be combined with an Actuator Line Model (ALM) and a Computer-Aided Design (CAD) interface for high-fidelity simulations of fluid flow problems with rotors and geometrically complex immersed objects. The method relies on 1D cubic spline interpolations to reconstruct an artificial flow field inside the immersed object while imposing the appropriate boundary conditions on the boundaries of the object. The new capabilities of the method are demonstrated with the following flow configurations: a turbulent channel flow with the wall modelled as an immersed boundary, Vortex Induced Vibrations (VIVs) of one-degree-of-freedom (2D) and two-degree-of-freedom (3D) cylinders, a helicopter rotor and a multi-rotor unmanned aerial vehicle in hover and forward motion. These simulations are performed with the high-order fluid flow solver Incompact3d which is based on a 2D domain decomposition in order to exploit modern CPU-based supercomputers. It is shown that the ADR-IBM can be used for the study of FSI problems and for high-fidelity simulations of incompressible turbulent flows around moving complex objects with rotors.

1 Introduction

The development of accurate, efficient and scalable numerical methods capable of simulating arbitrarily complex moving geometries in turbulent flows remains a considerable challenge for the field of Computational Fluid Dynamics (CFD). Furthermore, Fluid–Structure Interaction (FSI) problems where one or more complex solid structures interact and modify the behaviour of the surrounding fluid pose an even greater challenge to the CFD community as the fluid solvers need to also be coupled with structural ones. FSIs are commonly encountered both in nature and in many engineering fields such as aerospace [aircraft wings (Kamakoti and Shyy 2004), engine blades (Im and Zha 2012)], energy [fixed (Hsu and Bazilevs 2012) and floating wind turbines (Yan et al. 2016), Wave Energy Converters (WECs) (Li and Yu 2012)] and biomedical [heart valves (Meschini et al. 2020)] among others.

While conforming mesh methods (where the mesh conforms to the solid geometry) have been widely used in the past to simulate turbulent flows with complex geometries with (Gee et al. (2011)) or without FSI (Hartmann et al. 2021), the scientific community has recently relied more heavily on non-conforming methods (where the mesh is fixed independently of the solid geometry) (Hou et al. 2012). Even though the implementation of boundary conditions is straightforward for body conforming methods, the requirement of re-meshing at every time-step or employing overset meshing strategies (Sherer and Scott 2005) introduces a huge computational complexity and overhead (Johnson and Tezduyar 1999). Meshing issues involving highly skewed and distorted mesh elements (Sherwin and Peiró 2002; Zheng et al. 2016) often require the accuracy to be reduced near the boundaries and introduces a bottleneck which hinders the performance of these methods at scale (on large numbers of processors). Contrarily, non-conforming methods have recently gained considerable traction within the CFD community due to their ability to avoid meshing issues while also eliminating the need of re-meshing.

A popular non-conforming method is the Immersed Boundary Method (IBM), which was first introduced by Peskin (1972, 2002) for simulations of blood flow in a heart. IBMs rely on a fixed mesh and introduce an extra forcing term in the governing equations in order to simulate the presence of the solid object(s) within the computational domain. IBMs allow the use of both Eulerian and Lagrangian coordinates for the solution of the fluid flow and structural response, respectively. Hence, the coupling of the fluid flow and structural solvers becomes fairly straightforward due to the simplicity, flexibility and robustness of IBMs. As a result, IBMs have been extensively used for the study of FSI problems as evidenced by the review papers by Hou et al. (2012), Kim and Choi (2019).

Following the pioneer work of Peskin (1972, 2002), numerous scientists have proposed improvements and new IBMs (such as cut-cell methods (Ye et al. 1999; Udaykumar et al. 2001), ghost cell methods (Fadlun et al. 2000; Tseng and Ferziger 2003) and volume penalisation methods (Schneider 2015; Truong et al. 2021) to name a few) in order to improve their accuracy and efficiency. According to the classification of Mittal and Iaccarino (2005), when the forcing term of an IBM is added to the governing equations before or after their discretisation, the method is classified as a continuous or a discrete forcing approach, respectively. Continuous forcing approaches employ simplified models of the required forcing which would ideally be derived analytically by integrating the Navier–Stokes equations. Instead, discrete forcing approaches which were first introduced by Mohd-Yusof (1997), extract the required forcing directly from the numerical solution. IBMs can also be classified as diffuse and sharp interface approaches based on the treatment of the immersed boundary interface. Diffuse interface IBMs spread the forcing in a small area surrounding the immersed boundary interface (Yang et al. 2009; Kasbaoui et al. 2021) while sharp interface IBMs avoid the smoothing of the interface entirely in order to increase the local accuracy of the boundary representation which is of particular importance for turbulent flows at high Reynolds numbers. The need for an increased accuracy of the localisation of the immersed boundary interface has led to the development of various sharp-interface IBMs with high-order of accuracy and their combinations with high-order schemes (Seo and Mittal 2011; Brehm and Fasel 2013; Khalili et al. 2018; Tyliszczak and Ksiezyk 2018; Khalili et al. 2019; Brady and Livescu 2021). The interested reader is referred to Mittal and Iaccarino (2005); Kim and Choi (2019) for comprehensive reviews of IBMs and their applications.

In recent years, the complexity of IBMs has increased considerably in order to meet demands for higher accuracy and convergence, multi-phase flow (Stavropoulos Vasilakis et al. 2021) and FSI capabilities (Kim et al. 2018; Tschisgale and Fröhlich 2020), and combination with high-order schemes (Khalili et al. 2018; Tyliszczak and Ksiezyk 2018) and turbulence models (Cheylan et al. 2021). The increased complexity hinders the compatibility of the methods with parallelisation strategies and as a result the majority of published works on the subject is based on 2D or 3D simulations with a small number of mesh nodes or cells (typically few millions).

Recently, Giannenas and Laizet (2021) introduced a simple and scalable sharp interface Alternating Direction Reconstruction Immersed Boundary Method (ADR-IBM) capable of performing high-fidelity simulations of turbulent flows with high-order finite-difference schemes on modern High Performance Computing (HPC) platforms, for relatively complex fixed and moving objects with prescribed motions. It is now well-established that the use of high-order methods is highly beneficial when simulating turbulent flows due to their ability to capture a wider range of spatial length scales when compared to low-order methods (Lele 1992). However, the solution generated by high-order methods when combined with IBMs can be contaminated by Gibbs oscillations (Fornberg 1998) which appear during the calculation of the derivatives (Fang et al. 2011; Li et al. 2016). Giannenas and Laizet (2021) demonstrated that an appropriate reconstruction of the flow field inside the immersed body can be highly beneficial for the quality and accuracy of the solution while also suppressing potential spurious Gibbs oscillations. The reconstructions of the flow inside the solid geometry remove discontinuities from the velocity field, and allow the accurate location of the immersed boundary interface. In turn, this avoids the stair-case immersed body representation which would otherwise appear at marginal spatial resolutions (Stavropoulos Vasilakis et al. 2021; Giannenas and Laizet 2021).

The ADR-IBM relies on 1D cubic spline interpolations to reconstruct an artificial flow field inside the immersed object while imposing the appropriate boundary conditions on the boundaries of the object. It has been demonstrated by Giannenas and Laizet (2021) that the ADR-IBM provides a good computational efficiency and better accuracy compared to conventional IBMs. The excellent strong scaling of the ADR-IBM has been demonstrated by Giannenas and Laizet (2021) with the flow solver Incompact3d for simulations performed with more than 68 billion mesh nodes using up to 65536 computational cores for the flow over fixed and moving spheres at a Reynolds number of 3700 (based on the sphere diameter and free-stream velocity). It has also been demonstrated in Giannenas and Laizet (2021) that the cost of the reconstruction by cubic spline interpolations is negligible when compared to an IBM with no reconstruction.

The present study demonstrates, for the first time, that the recently developed ADR-IBM (Giannenas and Laizet 2021) can be used for high-fidelity simulations of a wide range of flow configurations involving fluid–structure interactions (FSIs) and turbulent multi-rotor simulations by combining the ADR-IBM with an Actuator Line Model (ALM). Further, a new Computer-Aided Design (CAD) interface is introduced in order to allow the inclusion of geometrically complex immersed objects within the computational domain.

The paper is organised as follows: after the introduction in Sect. 1, the numerical methods employed in this work, including the details of the flow solver, governing equations and the Actuator Line Model to simulate rotors/blades, are presented in Sect. 2. The ADR-IBM, with a detailed description of the structural and fluid solver coupling related to FSI simulations, is presented in Sect. 3. The results are presented in Sect. 4. In more detail, a comparison between 2nd- and 6th-order finite-difference schemes combined with the ADR-IBM is presented in Sect. 4.1 for the flow around a 3D cylinder. The capability of the ADR-IBM to accurately simulate wall-bounded flows is demonstrated in Sect. 4.2. The FSI capabilities of the ADR-IBM are demonstrated in Sect. 4.3 and Sect. 4.4 with the study of the Vortex Induced Vibrations (VIVs) of 2D and 3D cylinders. The Actuator Line Model (ALM) is validated for the case of a helicopter rotor in hover in Sect. 4.5, while the study of a multi-rotor unmanned aerial vehicle in hover and forward flight is presented in Sect. 4.6. Finally, Sect. 5 summarizes the key findings of this work and provides a description of the future outlook.

2 Numerical Methods

2.1 Flow Solver

The high-fidelity open-source flow solver Incompact3d is used for the present simulations. It is one of the high-order finite-difference solvers of the framework Xcompact3d (Bartholomew et al. 2020), which is dedicated to the study of turbulent flows on a Cartesian mesh. Sixth-order accurate compact finite-difference schemes are employed for the spatial discretisation and Adams–Bashforth or Runge–Kutta explicit schemes can be used for the time-advancement of the governing equations, depending on the flow configuration. In the present study, all simulations are performed with a third-order Adams–Bashforth method. The ability of high-order finite-difference schemes to provide accurate results using a moderate number of degrees of freedom when compared to low-order schemes makes them desirable for high-fidelity simulations (Direct and Large Eddy Simulations DNS/LES) of turbulent flows. The main originality of Incompact3d is that the Poisson equation for the incompressibility of the velocity field is fully solved in spectral space via the use of relevant 3D Fast Fourier transforms (FFTs). With the help of the concept of modified wavenumber, the divergence-free condition is ensured up to machine accuracy. The pressure mesh is staggered from the velocity one by half a mesh to avoid spurious pressure oscillations observed in a fully collocated approach (Laizet and Lamballais 2009). The simplicity of the mesh allows an easy implementation of a 2D domain decomposition based on pencils (Laizet and Li 2011). The computational domain is split into a number of sub-domains (pencils) which are each assigned to an MPI-process. The derivatives and interpolations in the x-direction (y-direction, z-direction) are performed in X-pencils (Y-pencils, Z-pencils), respectively. The 3D FFTs required by the Poisson solver are also broken down as series of 1D FFTs computed in one direction at a time. Global transpositions to switch from one pencil to another are performed with the MPI command MPI_ALLTOALL(V). Incompact3d can scale well with up to hundreds of thousands MPI-processes for simulations with several billion mesh nodes (Bartholomew et al. 2020; Laizet and Li 2011).

2.2 Governing Equations

The governing equations (1), (2) are the forced incompressible Navier–Stokes equations where u is the velocity, p the pressure, $\rho$ the density of the fluid, $\nu$ the kinematic viscosity and f an extra forcing term related to the ADR-IBM and the ALM (more details will be provided in the following paragraphs). The governing equations are written in their skew-symmetric form in order to reduce aliasing errors (Kravchenko and Moin 1997):

$$\begin{aligned} \frac{\partial u_{i}}{\partial t} +\frac{1}{2} \left[ \frac{\partial }{\partial x_{i}}(\epsilon _{i j k} u_{j} u_{k}) + u_i \frac{\partial u_i}{\partial x_{i}} \right] +\frac{1}{\rho } \frac{\partial p}{\partial x_{i}} - \nu \frac{\partial ^2 u_{i}}{\partial x_j \partial x_j} = f_i, \end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial u_{i}}{\partial x_{i}}=0. \end{aligned}$$

(2)

A three-step fractional step method (Kim and Moin 1985) (see Eqs. 3–5) is employed for the time-integration of the momentum Eq. (1)

$$\begin{aligned} \frac{u_i^{*}-u_i^{k}}{\Delta t}&= a_{k} H_i^{k}+b_{k} H_i^{k-1}- c_{k} \frac{\partial {\tilde{p}}^{k}}{\partial x_{i}} +c_{k} \tilde{f_i}^{k+1}, \end{aligned}$$

(3)

$$\begin{aligned} \frac{u_i^{* *}-u_i^{*}}{\Delta t}& = c_{k} \frac{\partial {\tilde{p}}^{k}}{\partial x_{i}}, \end{aligned}$$

(4)

$$\begin{aligned} \frac{u_i^{k+1}-u_i^{* *}}{\Delta t}& = -c_{k} \frac{\partial {\tilde{p}}^{k+1}}{\partial x_{i}}, \end{aligned}$$

(5)

with

$$\begin{aligned} H_i^{k}&= -\frac{1}{2} \left[ \frac{\partial }{\partial x_{i}}(\epsilon _{i j k} u_{j} u_{k}) + u_i \frac{\partial u_i}{\partial x_{i}} \right] + \nu \frac{\partial ^2 u_{i}}{\partial x_j \partial x_j}, \end{aligned}$$

(6)

$$\begin{aligned} {\tilde{p}}^{k+1}&= \frac{1}{c_{k} \Delta t} \int _{t_{k}}^{t_{k+1}} p d t, \quad \tilde{f_i}^{k+1}=\frac{1}{c_{k} \Delta t} \int _{t_{k}}^{t_{k+1}} f_i dt, \end{aligned}$$

(7)

where $u^{*}$ is the predicted and $u^{**}$ the intermediate velocity field. Since the intermediate velocity (Eq. 4) is not divergence-free, it is corrected by the pressure at the new time-step (Eq. 5) in order to obtain the divergence-free velocity $u^{k+1}$. $\epsilon _{i j k}$ represents the permutation tensor. The constants $a_k, b_k$ and $c_k$ correspond to the coefficients of the time-advancement schemes (see (Laizet and Lamballais 2009) for their values). The time-step is defined as $\Delta t = t_{n+1}-t_n$ and the tilde ~ indicates a time averaged value on a sub-time-step $c_k \Delta t$. The pressure at the new time-step is obtained via a modified Poisson’s equation which is presented in a subsequent paragraph.

2.3 Actuator Line Model

The actuator line method (ALM), originally introduced by Sorensen and Shen (2002), is an actuator-type method (others being the actuator disk and actuator surface methods) that is widely used in numerical simulations of the flow around rotors by both the wind energy (Martínez-Tossas et al. 2015; Sørensen et al. 2015) and helicopter communities (Delorme et al. 2021; Merabet and Laurendeau 2022b). Actuator-type methods attempt to model the presence of rotating blades through representations — of varying fidelity — of their aerodynamic effects on the flow. They are a useful alternative for rotor flow simulations (Merabet and Laurendeau 2022a), as they provide considerable savings in cost and complexity by relaxing the large near-blade resolution requirements of conventional blade-resolved simulations (Delorme et al. 2017, 2018; Brehm et al. 2019).

The ALM represents the blades as lines spanning the blade and following the quarter-chord. The lines are discretised by points into elements, the aerodynamic forces of which are computed through the use of tabulated airfoil polars, after having computed the local flow and blade properties (e.g. pitch angle, angle of attack, Reynolds number etc). The above are illustrated in Fig. 1. The forces computed at the blade elements are subsequently projected to the mesh using a 3D Gaussian kernel, where they act as a source term in the flow governing equations that mimics the effects of the blades on the flow. The details of the implementation of the ALM in Xcompact3d can be found in Deskos et al. (2020), with applications available in Deskos et al. (2019), Bempedelis and Steiros (2022).

Fig. 1

Schematic representation of the actuator line model: (left) representation of blades as discretised actuator lines, (right) calculation of forces at a blade element. Figure adapted from Deskos et al. (2020)

3 Immersed Boundary Method (IBM)

3.1 Modified Equations

The forcing term in the momentum Eq. (1), which consists of the acceleration, inertial, viscous and pressure force components, can be defined as

$$\begin{aligned} c_k \tilde{f_i}^{k+1} = \varepsilon \left( \frac{u_{\scriptscriptstyle IB}-u_i^{k}}{\Delta t} - a_k H_i^k - b_k H_i^{k-1} + c_k \nabla {\tilde{p}}^{k} \right) , \end{aligned}$$

(8)

where $u_{\scriptscriptstyle IB}$ corresponds to the imposed immersed boundary velocity and $\varepsilon$ to a scalar field equal to zero in the fluid and to one in the solid regions. It masks the effect of the forcing in the fluid and is used to ensure that the correct boundary conditions are imposed at the fluid/solid interface. The relation between the predicted velocity $u^{**}$ and the desired immersed boundary velocity $u_{\scriptscriptstyle IB}$ can be described by Eq. (9),

$$\begin{aligned} \frac{u_i^{**}-u_i^{k}}{\Delta t} = \frac{u_{\scriptscriptstyle IB}-u_i^{k}}{\Delta t} \quad \Leftrightarrow \quad u_i^{**} = u_{\scriptscriptstyle IB} . \end{aligned}$$

(9)

Since $u_{\scriptscriptstyle IB}$ does not necessarily satisfy the divergence-free condition, the Poisson equation needs to be modified as follows:

$$\begin{aligned} \nabla \cdot \nabla {\tilde{p}}^{k+1} = \frac{\nabla \cdot [(1-\varepsilon )u_i^{**} + \varepsilon u_{\scriptscriptstyle IB}]}{c_k \Delta t}. \end{aligned}$$

(10)

The conventional Poisson’s equation is recovered in the fluid region (where $\varepsilon = 0$), while the Laplace equation is recovered across the boundary interface and inside the solid region (where $\varepsilon = 1$). Note finally that the ADR-IBM does not impose boundary conditions for the pressure field in the solid region. It will be shown in the results section that even if no forcing is applied on the pressure field (to ensure that the flow remains incompressible), the ADR-IBM is able to capture accurately the correct features of the pressure field in the vicinity of the solid region.

3.2 1D Flow Reconstructions

The recently developed Alternating Direction Reconstruction Immersed Boundary Method (ADR-IBM) (Giannenas and Laizet 2021) is based on third-order 1D flow reconstructions of the velocity field in order to accurately impose the correct boundary condition on the immersed boundary interface of the solid object(s). The 1D reconstructions are performed in the direction of the decomposed pencils with no need for any extra communication. A significant advantage of this IBM is its ability to ensure that the reconstructed velocity field remains smooth in each spatial direction. For a 3D simulation, each of the three components of the velocity field is reconstructed three times, once per spatial direction. By simply performing these 1D reconstructions before the calculation of a spatial derivative or an interpolation, the solution does not become contaminated by spurious oscillations [which are present if the flow is not reconstructed inside the immersed object (Gautier 2013)]. The elimination of these oscillations is of particular significance in the context of high-order schemes in order to avoid the degradation of the solution. Furthermore, the method does not require any special treatment of the spatial discretisation schemes such as reducing the order of accuracy close to the immersed boundaries (Tyliszczak and Ksiezyk 2018).

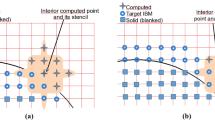
The reconstructions are performed via third-order accurate cubic spline interpolations. The spline interpolations are able to accurately impose the correct boundary conditions on the exact location of the immersed boundary interface via the reconstruction of an artificial flow field within the immersed object(s). It should be noted that even though the velocity is not reconstructed in the wall normal direction, the desired boundary conditions can nonetheless be accurately imposed in the wall normal direction indirectly by imposing the equivalent three components in the x-, y- and z-direction via successive 1D interpolations. The spline interpolations use the velocity values of up to three fluid mesh nodes (which are adjacent to the immersed boundary interface point $IB_P$) as inputs for the interpolation as shown in Fig. 2. Occasionally, the first input point can be extremely close to the immersed interface point. As the distance between the two points tends to zero the accuracy of the spline interpolation can be negatively affected and in turn degrade the quality of the reconstruction. To avoid this issue, the first mesh node is always ignored and the second, third and fourth mesh nodes automatically become the input ones (see Fig. 2). This procedure does not produce a checkerboard pattern near the immersed objects and has a positive impact on the quality of solution as demonstrated by Giannenas and Laizet (2021). In the present work, two input mesh nodes are used, following the recommendation of Giannenas and Laizet (2021) where it was demonstrated that this is the optimum set-up in terms of accuracy and performance. It should be highlighted that the cubic interpolations are solely used for the reconstruction of the velocity field while the pressure field is never reconstructed. If both the velocity and pressure fields were to be reconstructed, the divergence-free condition (see Eq. 2) would be violated.

A well documented problem which often arises when an Immersed Boundary Method is used for the simulations of moving bodies is the appearance of spurious numerical oscillations, commonly known as spurious force oscillations (SFOs), in the vicinity of the immersed boundary interface. While a wide range of remedies have been proposed for the suppression of SFOs (Kim et al. 2001; Kim and Choi 2006; Yang et al. 2009; Lee et al. 2011; Kumar and Roy 2016; Martins et al. 2017), their complete elimination remains a considerable challenge. Their severity and impact on the solution is highly dependent on the immersed boundary method and the problem considered. As it has been demonstrated by Giannenas and Laizet (2021), the ADR-IBM can provide accurate velocity and pressure fields around moving objects with no specific SFO treatment. While the SFOs do contaminate the hydrodynamic coefficients, they can simply be filtered in a post-processing step. For further details on the impact of the SFOs when the ADR-IBM is used for the simulation of moving objects and the details of the filtering procedure, the interested reader is referred to Giannenas and Laizet (2021).

Fig. 2

Illustration that highlights the input, immersed boundary interface ($IB_P$), and skipped points for a 1D problem

3.3 Fluid–Structure Interaction (FSI)

One of the novelties of this work is the extension of the ADR-IBM to Fluid–Structure Interaction (FSI) problems. While this subsection is focused on the FSI formulation for a single body, it can be extended to multiple rigid bodies without loss of generality. The motion of a single rigid and wall mounted object is governed by Newton’s second law of motion which can be described as follows:

$$\begin{aligned} m \frac{\partial ^{2} Q_{i}}{\partial t^{2}}+c \frac{\partial Q_{i}}{\partial t}+k Q_{i}=F_{i}, \end{aligned}$$

(11)

where m is the mass of the object, c is the system damping, k is the stiffness of the spring, $Q_i$ is a vector describing the position of the object with components ($i=1,2$) and $F_i$ represents the force exerted by the fluid on the object. It should be noted that external forces (such as gravity) can be also be incorporated in $F_i$.

In this manuscript, the focus is on the Vortex Induced Vibrations (VIVs) of 2D and 3D rigid cylinders. For an elastically mounted cylinder, the natural frequency f and critical damping factor are respectively described by

$$\begin{aligned} \omega= & {} 2 \pi f=\sqrt{\frac{k}{m}}, \end{aligned}$$

(12)

$$\begin{aligned} c_{c r}= & {} 2 \sqrt{m k}=2 k \omega . \end{aligned}$$

(13)

In the context of the VIVs of a rigid cylinder, equation (11) can be non-dimensionalised by the cylinder diameter D and free-stream velocity $U_{\infty }$ as follows:

$$\begin{aligned} \frac{\partial ^{2} Q_{i}}{\partial t^{2}}+\frac{4 \pi \xi }{U_{\text{ red } }} \frac{\partial Q_{i}}{\partial t}+\frac{4 \pi ^{2}}{U_{\text{ red } }^{2}} Q_{i}=\frac{1}{2 M_{\text{ red } }} C_{i}, \end{aligned}$$

(14)

where $Q_i$ now represents the non-dimensional coordinates of the position vector, $\xi$ is the non-dimensional damping coefficient, $U_{red}$ is the reduced velocity, $M_{red}$ is the reduced mass and $C_i$ is the non-dimensional force coefficient. These quantities are defined as follows:

$$\begin{aligned} \xi =\frac{c}{c_{c r}}, \quad U_{\text{ red } }=\frac{U_{\infty }}{f D}, \quad M_{r e d}=\frac{m}{\rho D^{2}}, \quad C_{i}=\frac{F_{i}}{1 / 2 \rho U_{\infty }^{2} D}. \end{aligned}$$

(15)

The second-order ordinary differential equations (14) are solved numerically by first explicitly calculating the acceleration at the next time-step $n+1$ via Eq. (16) and then by solving for the velocity (see Eq. 17) and position (Eq. 18). In essence, the aforementioned equations describe a loose coupling between the structural and fluid dynamics. The symbol $\Delta t$ in Eqs. (17), (18) denotes the time-step.

$$\begin{aligned} \frac{\partial ^{2} Q_{i}^{n+1}}{\partial t^{2}}= & {} \frac{1}{2 M_{\text{ red } }} C_{i}^{n} - \frac{4 \pi \xi }{U_{\text{ red } }} \frac{\partial Q_{i}^{n}}{\partial t} - \frac{4 \pi ^{2}}{U_{\text{ red } }^{2}} Q_{i}^{n} \end{aligned}$$

(16)

$$\begin{aligned} \frac{\partial Q_{i}^{n+1}}{\partial t}= & {} \frac{\partial Q_{i}^{n}}{\partial t} + \Delta t \frac{\partial ^{2} Q_{i}^{n+1}}{\partial t^{2}} \end{aligned}$$

(17)

$$\begin{aligned} Q_{i}^{n+1}= & {} Q_{i}^{n} + \Delta t \Bigg [ \frac{\partial Q_{i}^{n+1}}{\partial t} + \frac{\partial Q_{i}^{n}}{\partial t} \Bigg ] \end{aligned}$$

(18)

Here, the loose coupling is preferred over the strong one due to its considerably lower computational cost. When a strong coupling is employed the governing equations are solved implicitly by introducing sub-time-steps within the physical time-steps until the coupled fluid and solid solutions converge. These sub-iterations are responsible for the increased computational overhead. It should be noted that unlike loosely coupled algorithms, strongly coupled ones do not suffer from numerical instabilities when the fluid and solid densities are comparable (Causin et al. 2005). However, the use of loose coupling is sufficient for the purposes of this study and can provide accurate results as only large reduced mass values have been considered. The robustness of the loose coupling has also been demonstrated for similar problems by Borazjani et al. (2008) and Bao et al. (2012) among others.

3.4 Computer-Aided Design (CAD) Interface

The ADR-IBM has been designed to simulate fluid flow problems with arbitrarily complex 2D and 3D immersed fixed and moving objects. The representation of the boundary surface should be sufficiently flexible in order to avoid limiting the type of geometries that can be simulated. Xcompact3d offers two options depending on the geometrical complexity of the considered object(s). Objects with simple geometries (cylinder, NACA profile, Ahmed body) can be directly immersed in the computational domain using analytical equations. If the objects cannot be represented with equations (analytically describing the objects), a Computer-Aided Design (CAD) interface has been designed to make it possible to import objects generated by CAD software with the Stereolithography (stl) format. This format is a widely used file type in the CAD community. The surface of the object is described by breaking it into a collection of triangles and listing the location of the triangle vertices as well as which side of the triangle faces outwards.

The sole requirement of the ADR-IBM is the correct identification of the mesh nodes which are inside and outside the solid object(s), for the calculation of the $\varepsilon$ scalar field. The CAD interface in Xcompact3d is based on the robust inside-outside segmentation using generalised winding numbers (Jacobson et al. 2013). CAD models are often composed of many connected components with numerous self-intersections, non-manifold pieces, and open boundaries, which can potentially become problematic when trying to import a geometry into a background computational domain. Jacobson et al. (2013) proposed an algorithm handling all of these issues, while only requiring reasonably consistent orientation of the input triangle mesh from the CAD file. Once the mesh nodes inside and outside the immersed object(s) have been identified, $\varepsilon$ can be obtained and the subroutines dealing with the 1D flow reconstructions can be initialised.

4 Results

4.1 Flow over a 3D Circular Cylinder at Re = 300

In order to investigate whether the endeavour of combining high-order schemes with an immersed boundary method is worthwhile, a detailed comparison between explicit 2nd-order and implicit 6th-order accurate finite-difference schemes is performed for the flow over a fixed 3D circular cylinder at Re $=U_\infty D/\nu =300$, where $\nu$ is the kinematic viscosity of the fluid, D the cylinder diameter and $U_\infty$ the free-stream velocity imposed at the inlet.

Two spatial resolutions are considered: $n_x \times n_y \times n_z = 257 \times 129 \times 32$ and $1025 \times 513 \times 128$ for a domain size $L \times H \times W = 20D \times 12D \times 6D$ along with a constant time-step $\Delta t=2.5 \times 10^{-3} D/U_\infty$. The cylinder is placed at $(x_0,y_0)=(5D, 6D)$. A uniform velocity profile is imposed at the inlet and a 1D convection equation at the outlet in the streamwise direction, see Giannenas and Laizet (2021). The velocity field is initialised with random noise which follows a Gaussian distribution with its peak located at the centre of the domain in the vertical and spanwise directions (with maximum intensity of $0.135 U_\infty$). A free-slip condition is applied in the vertical direction while periodic boundary conditions are applied in the spanwise direction.

Figure 3 compares the mean and fluctuating components of the streamwise velocity profiles at different locations downstream of the cylinder with 2nd- and 6th-order compact schemes against the reference data of Mittal and Balachandar (1997). While the implicit 6th-order schemes with the coarse resolution are in good agreement with the reference data, their explicit 2nd-order counterparts fail to accurately predict both the mean and fluctuating profiles. By increasing the spatial resolution of the simulation by four times in each spatial direction while also reducing the time step of the simulation accordingly, the explicit 2nd-order schemes can eventually reach an accuracy similar to the one obtained on the coarse mesh with the implicit 6th-order schemes. Further improvement of the accuracy could be obtained by increasing the spatial resolution even more but at an increased computational cost, of nearly two orders of magnitude. This demonstrates the superiority of the high-order schemes over their low-order counterparts even when they are combined with an IBM which is formally a low-order approach (at least in our flow solver).

Figure 4 shows instantaneous vortical structures visualised with the Q-criterion for the 2nd- and 6th-order schemes for the coarse and fine mesh resolutions. Unlike the 6th-order schemes, the 2nd-order ones at low spatial resolution can only capture the larger spanwise vortical structures and fail to capture the smaller ones. The ability of implicit 6th-order schemes to capture small vortical structures even at marginal resolution is due to their superior spectral accuracy (compared to their low-order counterparts) which allows them to accurately capture the correct result over a broader range of length scales as demonstrated by Lele (1992). It can be seen that by increasing the resolution further, explicit 2nd-order schemes are eventually able to capture the smaller streamwise vortices which connect the large spanwise ones. Hence, it can be concluded that low-order schemes require much finer mesh resolutions (more than four times in our flow solver for the half staggered mesh arrangement) to accurately capture the flow characteristics. This highlights the superiority of implicit high-order schemes in terms of computational cost (even though implicit 6th-order schemes are twice as expensive as explicit 2nd-order schemes) as they can better capture small-scale turbulent features than their low-order counterparts. Overall, combining Immersed Boundary Methods with high-order schemes becomes highly attractive in the context of high performance computing, as a more accurate solution can be obtained in a cost-effective manner.

At this point, it should be stressed that the maximum error introduced by the ADR-IBM solely affects the area in the immediate vicinity of the immersed interface [as demonstrated in Giannenas and Laizet (2021)]. Hence, a reduced 2nd-order convergence is observed locally near the solid object while the beneficial effects of the high-order schemes are maintained further away. A similar observation was noted by Tyliszczak and Ksiezyk (2018) where lower levels of error were obtained for the laminar and steady flow over a cylinder at Re $=40$ with high-order schemes (an order reduction was used near the boundaries) compared with low-order ones. Similarly, Laizet et al. (2010) noted that despite the local loss of accuracy near the immersed objects the use of high-order schemes remained highly beneficial as a more accurate description of the turbulent flow could be obtained. Hence, it can be concluded that the combination of Immersed Boundary Methods with high-order schemes is beneficial not only for turbulent flows (as demonstrated in this section) but also for laminar flows (Tyliszczak and Ksiezyk 2018).

Fig. 3

Time and spanwise averaged streamwise velocity (left) and Reynolds stress (right) profiles for the flow around a cylinder at different locations downstream of the cylinder for $x=1.5D, 2.0D, 2.5D, 3.0D$ with 2nd- and 6th-order compact schemes compared with the reference data reported by Mittal and Balachandar (1997). Both quantities have been normalised by $U_{\infty }$. Profiles have been displaced based on their downstream location x

Fig. 4

Visualisation of vortical structures through Q-criterion = 0.2 iso-contours for the flow around a cylinder, with a $n_x \times n_y \times n_z = 257 \times 129 \times 32$ with 2nd-order schemes, b $n_x \times n_y \times n_z = 1025 \times 513 \times 128$ with 2nd-order schemes and c $n_x \times n_y \times n_z = 257 \times 129 \times 32$ with 6th-order schemes

4.2 Turbulent Channel Flow

The canonical turbulent channel flow test case is selected to demonstrate the ability of the proposed ADR-IBM to accurately predict the flow characteristics (and especially the pressure field) close to the wall of an immersed solid (as no particular forcing is imposed on the pressure field with the ADR-IBM). A high-fidelity simulation of a turbulent channel flow is performed at Re $_{\tau }=180$ which is based on the friction velocity at the wall and the channel half-height h. The boundary conditions at the upper and lower channel walls are imposed via the ADR-IBM. The domain for the fluid region is $L \times H \times W = 8h \times 2h \times 4h$. The computational domain is padded with an IBM region which consists of 8 mesh nodes for each wall, in the wall normal direction (the channel flow is aligned with the computational domain). A resolution of $n_x \times n_y \times n_z = 128 \times 257 \times 128$ is selected, with a stretched mesh in the wall normal direction (with $\Delta y^+_{min} \sim 1$). Periodic boundary conditions are used in the streamwise and spanwise directions. No-slip boundary conditions are imposed in the wall-normal direction via the ADR-IBM. As periodic boundary conditions are used in the streamwise direction, an extra forcing term is introduced in the momentum equation in order to ensure a constant mass flow rate through the channel. For completeness, a more conventional simulation is also performed with no IBM and the data are compared with three different data sets obtained by different research groups using different numerical methods (Moser et al. 1999; Del Alamo and Jiménez 2003; Vreman and Kuerten 2014).

Fig. 5

Mean streamwise velocity (left) and pressure (right) profiles for the channel flow, with a comparison with the reference data from Moser et al. (1999), Del Alamo and Jiménez (2003) and Vreman and Kuerten (2014)

The mean streamwise velocity and pressure profiles obtained with the ADR-IBM and with no IBM are compared in Fig. 5 against the reference data. Both the mean velocity and pressure are in good agreement with the reference data. In particular, the data obtained with the IBM are similar to the one obtained with no IBM, even though the ADR-IBM solely reconstructs the velocity and not the pressure field. The mean pressure is captured accurately both in the near wall and towards the mid-channel regions. Furthermore, the velocity and pressure fluctuations are also compared against the same reference data in Fig. 6. The ADR-IBM provides accurate predictions for the velocity and the pressure fluctuations are in good agreement with the simulation with no IBM and the reference data. It should be noted that small differences can be observed for the pressure fluctuations among the reference data, suggesting that the evaluations of this quantity is quite challenging, as highlighted by Giannenas and Laizet (2021). These differences (which can only be seen for the pressure fluctuations) can be attributed to the use of different spatial resolutions, numerical methods and mesh arrangements.

Fig. 6

Velocity (left) and pressure (right) fluctuations for the channel flow, with a comparison with the reference data from Moser et al. (1999), Del Alamo and Jiménez (2003) and Vreman and Kuerten (2014)

4.3 VIV of a 2D Cylinder

In this subsection, the Vortex Induced Vibrations (VIV) of a one-degree-of-freedom (1-DOF) elastically mounted two-dimensional (2D) cylinder exposed to a uniform flow of velocity $U_{\infty }$ are studied. The VIVs of an elastically mounted cylinder result in different regimes of synchronous response. Depending on the reduced mass, damping ratio and Reynolds number, there can either be two or three branches. The two branches consist of an initial and an upper branch. The initial branch is characterised by smaller oscillation amplitudes compared to those occurring at the upper branch. The third branch is known as the lower branch and has been shown to exhibit oscillation amplitudes which are smaller than those occurring at the upper branch and larger than those of the initial branch. The transition between the branches is associated with hysteretic and/or intermittent behaviour (Navrose and Mittal 2013). For further details on VIVs the interested reader is directed to the review papers by Williamson and Govardhan (2004, 2008), Wu et al. (2012).

In this study, the Reynolds number is Re $=U_{\infty }D/\nu =200$, where $\nu$ is the kinematic viscosity of the fluid and D represents the cylinder diameter. At this Reynolds number, there are only two branches present (initial and upper). The transition between the branches is evident by a jump in the oscillation and lift amplitudes (Leontini et al. 2006). The motion of the cylinder is described by Eq. (14) where $i=1$ and $C_{1} = C_L = \frac{F_{L}}{1 / 2 \rho U_{\infty }^{2} D}$. This test case has been selected as for a certain range of frequencies f the vortex shedding frequency is synchronised with the frequency of the cylinder’s motion which in turn results in large oscillation amplitudes. The range of frequencies in which this synchronisation occurs is commonly known as the ‘lock-in’ or ‘lock-on’ region (Griffin 1985; Sarpkaya 2004). Outside of the aforementioned range of reduced velocities the ‘lock-in’ cannot be achieved and hence small oscillation amplitudes are observed. Here, the ‘lock-in’ phenomenon is investigated in order to validate the Fluid–Structure Interaction (FSI) extension of the Alternating Direction Reconstruction Immersed Boundary Method (ADR-IBM).

The 2D simulations are performed in a square computational domain of dimensions $L \times H = 30D \times 30D$. The cylinder center is placed at $(x_0,y_0) = (10.0D,15.0D)$. A resolution of $n_x \times n_y = 1537 \times 1536$ is selected along with a time-step of $\Delta t = 2.0 \times 10^{-4} D/U_{\infty }$. A uniform velocity profile is imposed at the inlet and a 1D-convection equation is imposed at the outlet in the streamwise direction. Periodic boundary conditions are imposed in the vertical direction. The flow is initialised with random noise which follows a Gaussian distribution with its peak located at the centre of the domain in the vertical direction (with maximum intensity of $0.125 U_{\infty }$).

In total seven simulations are performed for various reduced velocities with a unit increment within the range of $3.0 \le U_{red} \le 9.0$, for a fixed reduced mass $M_{red}=2$ and damping ratio $\xi = 0.0$. Figure 7 (left) compares the maximum amplitude of oscillation (normalised by the cylinder diameter D) against the data provided by Borazjani and Sotiropoulos (2009), Griffith et al. (2017), Narvaez et al. (2020). Large amplitudes, $(A_y/D)_{max} > 0.4$, may be observed within the ‘lock-in’ range $4.0 \le U_{red} \le 7.0$. Outside this range, the amplitudes remain considerably smaller, $(A_y/D)_{max} < 0.2$, as the ‘lock-in’ cannot be achieved. These observations are in good agreement with those reported in the literature and especially with the results reported by Griffith et al. (2017). The drag and lift root mean square (RMS) obtained with the ADR-IBM are compared against the data reported by Borazjani and Sotiropoulos (2009), Griffith et al. (2017) in Fig. 7 (center and right). The data obtained with the proposed method are in good agreement with those reported in literature throughout the entire range of reduced velocities. The drag RMS shows a clear peak with the maximum occurring when the amplitude of the displacement becomes maximum at $U_{red}=4.0$.

Figure 8 shows the phase diagrams (cylinder displacement versus lift coefficient) for a range of reduced velocities $3.0 \le U_{red} \le 8.0$. For small reduced velocities ($U_{red} \le 5.0$), the cylinder displacement is in-phase with the lift coefficient (the phase diagrams are in the first and third quadrants). With the increase of the reduced velocity, the phase diagrams rotate counterclockwise and at $U_{red}=6.0$ the displacement and lift become out-of-phase (the phase diagrams are in the second and fourth quadrants). Similar observations have been reported by Borazjani and Sotiropoulos (2009), Bao et al. (2012).

Fig. 7

Normalised maximum cylinder displacement (left), drag (middle) and lift (right) RMS for a range of reduced velocities for a 2D cylinder, with a comparison with the data provided by Borazjani and Sotiropoulos (2009), Griffith et al. (2017), Narvaez et al. (2020)

Fig. 8

Phase diagrams of displacement versus lift coefficient for a range of reduced velocities $3.0 \le U_{red} \le 8.0$ for a 2D cylinder

4.4 VIV of a 3D Cylinder

In this subsection, the two-degree-of-freedom (2-DOF) Vortex Induced Vibrations (VIVs) of a three-dimensional (3D) circular cylinder are studied for the further validation of the FSI capabilities of the ADR-IBM. The elastically mounted cylinder is exposed to a uniform flow of velocity $U_{\infty }$ and the Reynolds number is set at Re $=U_{\infty }D/\nu =500$. The motion of the cylinder is described by Eq. (14) where $i=1,2$ and $C_{1} = C_L = \frac{F_{L}}{1 / 2 \rho U_{\infty }^{2} D}$, $C_{2} = C_D = \frac{F_{D}}{1 / 2 \rho U_{\infty }^{2} D}$.

The simulations are performed in a rectangular computational domain of dimensions $L \times H \times W = 30D \times 20D \times 12D$. The cylinder center is placed at $(x_0,y_0) = (10.0D,10.0D)$. A resolution of $n_x \times n_y \times n_z = 1025 \times 768 \times 256$ is selected along with a time-step of $\Delta t = 1.5 \times 10^{-3} D/U_{\infty }$. A uniform velocity profile is imposed at the inlet and a 1D-convection equation is imposed at the outlet in the streamwise direction. Periodic boundary conditions are imposed in the vertical and spanwise directions. The flow is initialised with random noise which follows a Gaussian distribution with its peak located at the centre of the domain in the vertical and spanwise directions (with maximum intensity of $0.125 U_{\infty }$).

In total seven simulations are performed for various reduced velocities within the range of $3.0 \le U_{red} \le 12.0$ for a fixed reduced mass $M_{red}=2$ and damping ratio $\xi = 0.0$. The ratio of the in-line to cross-flow natural frequencies is set to unity. Figure 9 shows the maximum in-line and cross-flow amplitudes against the reduced velocity. Similarly, the response of the mean drag and the RMS of the hydrodynamic coefficients are presented in Fig. 10. The data are compared against those provided by Wang et al. (2017). Overall, a good agreement can be observed between the data obtained with the ADR-IBM and the reference data with few small discrepancies. The ADR-IBM can accurately predict the maximum amplitudes as well as the peak location of the mean drag and drag RMS. The most noteworthy but still small discrepancy involves the location of the lift RMS peak which is predicted at $U_{red}=4.0$ by the ADR-IBM and at $U_{red}=3.0$ by Wang et al. (2017). This discrepancy can potentially be attributed to the different time-integration methods of the structural model (and particularly their different stability criteria) which were used by the two studies. The reference study employed a 2nd-order accurate Newmark integration scheme which is unconditionally stable while a conditionally stable explicit time integration is used in the present study. The same argument was made by Wang et al. (2017) in order to explain similar discrepancies in the VIV response of a cylinder.

Fig. 9

Normalised in-line (left) and cross-flow (right) maximum cylinder displacements for a range of reduced velocities for a 3D cylinder, with comparison with the data provided by Wang et al. (2017)

Fig. 10

Mean drag (left), drag RMS (center) and lift RMS (right) for a range of reduced velocities for a 3D cylinder, with comparison with the data provided by Wang et al. (2017)

Figure 11 shows the vortical structures which have been visualised with the Q-criterion for all the reduced velocities considered. For the smallest reduced velocity $U_{red}=3.0$ which sits outside the ‘lock-in’ range, the spanwise (primary) vortices are clearly observed in the near wake. These vortices exhibit small spanwise undulations. As the reduced velocity is increased to $U_{red}=4$ the flow becomes more chaotic with more intense secondary vortices and the spanwise vortices exhibit slightly stronger spanwise undulations. The strongest spanwise undulation of the primary vortices is observed at $U_{red}=5.0$ when the in-line and cross-flow cylinder displacements along with the mean drag and drag RMS all reach a maximum (see Figs. 9, 10).

Fig. 11

Visualisation of vortical structures through Q-criterion=1.5 iso-contours for a range of reduced velocities $U_{red}$ for a 3D cylinder: a $U_{red}=3.0$, b $U_{red}=4.0$, c $U_{red}=5.0$, d $U_{red}=6.0$, e $U_{red}=8.0$, f $U_{red}=10.0$, g $U_{red}=12.0$. The cylinder surface is shown in black colour

4.5 Helicopter Rotor in Hover

In this subsection, the ALM implemented in Incompact3d is validated for the case of helicopter rotor flows. To this end, the aim is to replicate two cases from the series of experiments conducted at Politecnico di Milano (Gibertini et al. 2015), whose goal was to assess the effects of the ground on the hovering flight of a helicopter. The reference out-of-ground condition is considered first in the present work, where the 4-bladed rotor (the details of which are shown in Table 1) hovers in a quiescent environment at a distance equal to $y/R=4$ above the ground. The rotor is placed in a cubic domain of size $L\times H\times W= 10.67 R \times 10.67 R \times 10.67 R$, with periodic conditions in the horizontal directions, a no-slip condition at the ground, and a slip condition at the top. The domain is discretised with $n_x\times n_y\times n_z = 512 \times 513 \times 512$ mesh nodes, corresponding to 48 mesh nodes per rotor radius. Such a resolution has been shown to be sufficient to properly reproduce the rotor flow field (Deskos et al. 2019, 2020; Bempedelis and Steiros 2022). The actuator lines are discretised into 72 elements. The body of the helicopter is omitted, as often done in numerical studies (e.g., Andronikos et al. 2021a, b). The effects of the unresolved fluid motions are accounted for through the implicit LES approach of Dairay et al. (2017), by introducing targeted numerical dissipation at the smaller scales via the discretisation of the derivatives of the viscous terms. The reader is referred to Dairay et al. (2017), Deskos et al. (2019), Mahfoze and Laizet (2021) for more details on this approach and a few relevant applications. It is noted that as discussed in Mahfoze and Laizet (2021), no particular treatment is required near solid boundaries. The parameter $\nu _0 /\nu$, which corresponds to the added dissipation at the cut-off wavenumber and controls the amount of added dissipation, is set to $\nu _0/ \nu =1000$ following recommendations from wind turbine numerical experiments (Deskos et al. 2019) and comparison with explicit LES approaches.

Table 1 Characteristics of the Politecnico di Milano helicopter rotor (Gibertini et al. 2015)

An example view of the flow field after $\sim 5$ and $\sim 10$ rotations is presented in Fig. 12 (visualised through Q-criterion isocontours). The actuator line model is shown to be capable of reproducing the tip and root vortices that are trailed from the blades. An upwards-travelling vortex located at the rotor centre and a vortex ring travelling towards the ground are formed at the beginning of the simulation. After $\sim 10$ rotor rotations, the vortex ring has travelled $\sim 2 R$ downstream, in agreement with observations in the literature (Andronikos et al. 2021a, b). The measured thrust coefficient, averaged over the rotor’s last two rotations, where $C_T=T / ( \rho \omega ^2 \pi R^4)$, was $C_T = 0.0077$. This can be thought to be in agreement with the values measured in the experiments, $C_{T,exp}=0.0073$, and other numerical simulations (see Andronikos et al. 2021a), considering the omission of the helicopter body and the dependence of the loadings predicted by the ALM to the provided airfoil polars. The torque coefficient, defined as $C_Q = Q/( \rho \omega ^2 \pi R^5)= 0.00074$, is also found to be in agreement with the experimentally measured value, $C_{Q,exp}=0.00075$.

Fig. 12

Visualisation of vortical structures through Q-criterion = 4000 iso-contours after (left) $\sim 5$ and (right) $\sim 10$ rotations for a helicopter rotor in hover. The iso-contours are coloured by vertical velocity

The case of the helicopter hovering over an obstacle is considered next. The obstacle is designed following the description in Gibertini et al. (2015), and the helicopter hovers above its center, at a distance $y/R=2$ from the ground [note the difference in the coordinate system compared with Gibertini et al. (2015)]. Figure 13a shows the distribution of the pressure coefficient $C_p$ on the surface of the obstacle, with $C_p = 2 (p-p_\infty )/ (\rho V_{ind}^2)$, and $V_{ind} = {\omega R} \sqrt{(C_{T,ref}/2)}$. Figure 13b shows the in-plane velocity near the obstacle, non-dimensionalised by $V_{ind}$, at a z-cut that crosses the domain center. Data are averaged over ten rotor rotations, following an initialisation period which ensures that the rotor thrust is converged. Both pressure distribution and velocity contours are in good agreement with the experimental data (Gibertini et al. 2015). In particular, Fig. 13b shows that the flow separates at the upper corner of the obstacle, and a recirculation region is formed on its side. With regard to rotor performance, an increase in both thrust and torque coefficients with respect to the reference condition is found, with $C_T=0.0088$ and $C_Q=0.00078$, respectively, in accordance with the experimentally observed trends.

Fig. 13

a Pressure distribution on the obstacle surface. Also shown are the helicopter rotor and its rotation plane (blades not in scale). b Non-dimensional velocity contours and streamlines in the vicinity of the obstacle

4.6 Multi-rotor Unmanned Aerial Vehicle in Flight

In this subsection, a 6-rotor plant protection drone is considered, whose properties are shown in Table 2, and whose adjoining 2-bladed rotors rotate in opposite directions. The domain is discretised with $n_x \times n_y \times n_z = 1024 \times 1025 \times 1024$ mesh nodes, maintaining the resolution of 48 mesh nodes per actuator line, as in Sect. 4.5. The parameter controlling the numerical dissipation is set to $\nu _0 /\nu =100$ [different values compared with Sect. 4.5 were expected due to the differences in tip Reynolds number and mesh resolution (see Mahfoze and Laizet 2021)]. All other simulation and configuration parameters remain as described in Sect. 4.5. Two simulations for the drone in hover are performed; one where the drone is represented solely by its rotors, and one which also includes a simplified representation of the drone body, designed in the free and open-source 3D computer graphics software Blender, and “imported" in Xcompact3d through the CAD interface presented in Sect. 3.4. The body (shown in Fig. 14, along with the actuator line points representing the blades) extends considerably in the vertical direction, mimicking the design of agricultural drones, which carry tanks filled with pesticide or other chemicals, that are to be sprayed on the crops. The drone wake field is known to dictate to a large degree the efficiency of dispersal of the chemicals (Zhang et al. 2020).

Table 2 Unmanned aerial vehicle characteristics

Fig. 14

(Left) top and (right) 3D view of the drone body and actuator lines

Figure 15 shows the flow field after $\sim 40$ rotor rotations, through Q-criterion visualisations, when the drone body and tanks are neglected or accounted for. The starting vortex at the drone centre is not present when the body is considered, while the vortex ring is located higher above the ground. The above can also be observed in Fig. 16, which shows contours of the vertical component of the velocity at a vertical slice through the rotor centre. In the case where the drone body is considered, the wake is seen to be wider both in the near vicinity of the ground, but also at a higher distance above it, indicating that the drone body acts beneficially in terms of spray dispersal.

Fig. 15

Visualisation of vortical structures through Q-criterion = 6500 iso-contours after $\sim 40$ rotor rotations for a multi-rotor unmanned aerial vehicle in hover. (Left) rotors only, (right) rotors with body. The iso-contours are coloured by vertical velocity

Fig. 16

Instantaneous vertical velocity contours at a vertical slice through the drone centre. (Left) rotors only, (right) rotors with body

The last test case to be considered is the drone, with its body accounted for, in forward flight ($U_\infty =2$ ms$^{-1}$). The domain and mesh nodes are doubled along the streamwise direction to accommodate the streamwise-developing wake. The flow field after $\sim 40$ rotor rotations is shown in Fig. 17. As the wake is convected downstream by the incoming flow, the tip vortices on the external side of the side rotors roll-up, while those trailed from the central rotors and at the inner side of the side rotors are the first to reach the ground. The tip vortices of the central downstream rotor are initially “shielded" from interactions and are convected downstream with limited/late breakdown.

Fig. 17

Visualisation of vortical structures through Q-criterion = 6500 (a, c, d) and 19000 (b) iso-contours after $\sim$ 40 rotor rotations for a multi-rotor unmanned aerial vehicle in forward flight. The iso-contours are coloured by vertical velocity

Figure 18 shows the vertical component of the velocity, normalised by $U_\infty$, at a plane through the rotor centre. The body of the drone disturbs the wake of the upstream rotor, which partially impinges on it and partially flows around it, before interacting with the upstream side of the vortices trailed from the downstream central rotor. The drone wake reaches the ground at a distance of about eight rotor radii downstream of the drone centre, but is shortly after deflected upwards. Together with the direction of the wake in two out-of-centerline streams (see Fig. 17d), it may be concluded that such high flight velocities are not ideal for the purposes of chemicals dispersal.

Fig. 18

Instantaneous normalised vertical velocity at a vertical slice through the drone centre

5 Conclusions

In this manuscript, the simple and scalable Alternating Direction Reconstruction Immersed Boundary Method (ADR-IBM) which was developed by Giannenas and Laizet (2021) has been used for high-fidelity simulations of incompressible turbulent flows with fixed and moving objects. In particular, it was shown that the ADR-IBM can deal with Fluid–Structure Interaction (FSI) problems, and can be combined with an Actuator Line Model (ALM) and a Computer-Aided Design (CAD) interface to study fluid flow problems with multiple rotors and complex geometries. The simulations were performed on the UK supercomputing facility ARCHER2 on up to 8192 computational cores with the high-order finite-difference solver Incompact3d which is part of the Xcompact3d framework (Bartholomew et al. 2020).

The ADR-IBM employs a cubic spline interpolation in order to perform successive 1D reconstructions (in each spatial direction) of the velocity field and to accurately impose the correct boundary conditions on the immersed boundary interface. It was used for the simulations of the flow over a 3D circular cylinder at Re $=300$ with 2nd- and 6th-order finite-difference schemes. It was demonstrated that the combination of 6th-order schemes with the ADR-IBM is beneficial at marginal spatial resolution to reproduce the main turbulent features of the flow, with an excellent prediction of the mean velocity and Reynolds stresses profiles downstream of the cylinder. At marginal resolution, the 2nd-order schemes are not able to capture properly the small streamwise (secondary) vortices in the flow which connect the (primary) spanwise ones, resulting in poor predictions of the first and second order moments. In order to check that the pressure field is properly captured with the ADR-IBM, despite no particular treatments or reconstructions, a channel flow simulation was performed with the walls modelled with the ADR-IBM. The pressure field (and velocity) statistics were in good agreement with published data obtained without IBMs, confirming that the approach is robust enough to capture wall-bounded flow features close to the immersed solid geometry.

The performance of the ADR-IBM in FSI problems was assessed for a rigid and wall mounted cylinder. The structural dynamics of the cylinder were coupled with the fluid dynamics via a robust and computationally inexpensive loose coupling. Firstly, the Vortex Induced Vibrations (VIVs) of a one-degree-of-freedom (1-DOF) elastically mounted 2D cylinder exposed to a uniform flow at Re $=200$ were studied. The ADR-IBM accurately captured the ‘lock-in’ range in which the vortex shedding frequency synchronises with frequency of the cylinder’s motion as well as the drag and lift coefficient RMS. Secondly, the VIVs of a two-degree-of-freedom (2-DOF) elastically mounted 3D cylinder exposed to a uniform flow at Re $=500$ were studied. A good agreement was obtained with the reference data regarding the prediction of the in-line and cross-flow cylinder displacement, mean drag and the RMS of the lift and drag coefficients. Overall, the produced data were in good agreement with published references confirming the robustness of the ADR-IBM to study FSI problems.

Finally, the ADR-IBM was combined with an Actuator Line Model (ALM) and a newly developed CAD interface, to predict the wake of a helicopter and a unmanned aerial vehicle in flight. The aim of these simulations was to demonstrate the ease of use of the CAD interface, and to show that the ADR-IBM can be combined with an ALM to numerically study moving objects with rotors without the need for blade-resolved approaches. The proposed cost-effective approach was able to accurately capture the wake generated by the rotors and the complex phenomena that take place when the rotor wakes interact or impinge on the ground, the fuselage, or obstacles. The main advantage of the proposed methodology is that it can conveniently handle complex geometries for multiple drones at an affordable computational cost.

The next step is to extend this work further by introducing a more complex structural solver in order to perform turbulent flow simulations with multiple flexible structures. This will allow the study of many more relevant engineering applications involving aeroelastic effects, canopy flows and risers among others. Furthermore, the current work will be extended in order to study the flow dynamics and interactions of multiple drones in realistic operating conditions. The CAD interface will also be extended to step files, where each surface is described by continuous equations for a more accurate description of the boundary surface.