1 Introduction

The interaction of water droplets with a premixed flame has relevance in internal combustion engines [e.g., BMW M4 GTS engine (Durst et al. 2017), WaterBoost system by Bosch (Brooke, 2015)], gas turbines (Lellek 2017), and also in the context of fire suppression (Fan et al. 2021) and explosion mitigation (Thomas et al. 1991). For instance, water injection provides increased power in the BMW M4 GTS engine while reducing the burned gas temperature as a result of cooling and dilution effects induced by the water evaporation process. Moreover, the presence of water droplets affects the turbulence level within the flame brush and thereby influences the turbulent burning velocity (Van Wingerden and Wilkins 1995). A recent analysis (Hasslberger et al. 2021) by the present authors utilised three-dimensional carrier phase simple chemistry Direct Numerical Simulation (DNS) of water droplet interaction with n-heptane-air turbulent premixed flames to demonstrate the influence of water droplet loading, droplet diameter and turbulence intensity on flame surface area and overall burning rate. Hasslberger et al. (2021) demonstrated that the large latent heat of water induces a significant cooling effect due to the evaporation of water droplets, which dominates over the changes in the concentration of reactants in the gaseous phase due to evaporation. A reduced order model was developed by Hasslberger et al. (2021), which accounts for the effects of cooling and dilution induced by water droplets on the laminar burning velocity by considering the time scales of droplet evaporation and residence time within the flame. The flame propagation statistics in terms of flame displacement speed and consumption speed in the case of the interaction of water droplets with premixed turbulent flames have received limited attention in comparison to the vast body of literature on flame propagation in both fuel droplet-laden (e.g. (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020 and references therein), and purely gaseous (e.g. Chakraborty et al. 2011; Dave and Chaudhuri 2020; Ozel-Erol et al. 2021; Yu et al. 2021 and references therein) mixtures. It was previously demonstrated that the distribution of water droplets, spacing between droplets and the droplet size have significant influences on the overall burning rate (Hasslberger et al. 2021; Zhang et al. 2014). Xia and Luo (2009) conducted 3D DNS of diluted combustion in a temporal mixing layer configuration for different water droplet sizes and mass loading ratios. Evaporation of smaller water droplets was found more effective in enhancing micro-mixing and combustion performance. To the best of the knowledge of the present authors, to date, there is no DNS based investigation that analysed the physical processes governing the reaction-diffusion (im)balance and the reactive scalar gradient magnitude, which influence the displacement speed statistics in the case of water droplet interaction with premixed turbulent flames. The current analysis addresses this gap in the existing literature by carrying out three-dimensional carrier phase DNS of the interaction of initially mono-sized water droplets with statistically planar stoichiometric n-heptane-air turbulent premixed flames for different turbulence intensities and water droplet diameters. In this respect, the main objectives of the current analysis are: (a) to demonstrate the effects of water droplet size on the density-weighted displacement speed and consumption speed for different turbulence intensities, and (b) to provide physical explanations for the observed trends.

2 Mathematical and numerical background

In the interest of a detailed parametric analysis in terms of water droplet diameter and turbulence intensity, the present analysis adopts a modified single-step irreversible Arrhenius type chemical reaction (Fernández-Tarrazo et al. 2006) for which the activation energy and the heat of combustion are taken to be functions of the equivalence ratio. It has been shown elsewhere (Hasslberger et al. 2021; Ozel-Erol et al. 2020) that this chemical representation accurately captures the variation of laminar burning velocity \(S_{b(\phi _g)}\) with the equivalence ratio \(\phi _g\) obtained from detailed chemistry simulations. Moreover, it was demonstrated previously (Hasslberger et al. 2021) that the chemical representation used in this analysis accurately predicts the influence of water loading in the unburned gas on the laminar burning velocity obtained from a detailed chemical mechanism (Jerzembeck et al. 2009) for the investigated parameter range. Using a detailed chemical mechanism in the context of three-dimensional DNS would be prohibitively expensive for the kind of parametric analysis conducted in this study. It was demonstrated by Hasslberger et al. (2021) that the mass fraction of water vapor arising from droplet evaporation within the flame remains much smaller than the overall mass fraction of water and thus the thermochemical processes within the flame are not significantly affected by the presence of water vapor. Post-flame evaporation of water droplet might create higher values of water vapour concentration in the burned gas region than in a purely gaseous flame, but this does not affect the chemical reaction within the flame. Moreover, it was shown elsewhere (Hasslberger et al. 2021) that a good agreement between the adopted chemical mechanism and the detailed chemical mechanism (Jerzembeck et al. 2009) has been obtained for the steam-diluted unstretched laminar burning velocity normalised by the undiluted unstretched laminar burning velocity. It is also worth noting that the conditions examined in this paper are far from extinction where the accurate representation of chemistry plays an important role (Hasslberger et al. 2021). For the present analysis, the Lewis numbers of all species are assumed to be unity and all species in the gaseous phase are assumed to be perfect gases for the sake of simplicity. The unity Lewis number assumption for all species allows for isolation of the effects of droplet-flame interaction without the additional influence arising from differential diffusion of heat and mass (i.e. non-unity Lewis number). Moreover, the mass transfer modelling for the Lagrangian droplet phase often uses the unity Lewis number assumption and this practice was followed in several previous studies (Reveillon and Vervisch 2000; Schroll et al. 2009; Wandel et al. 2009; Neophytou et al. 2010; Wang and Rutland 2005). Although the Lewis number of n-heptane is significantly larger than unity, it readily breaks down to smaller hydrocarbon molecules which have Lewis numbers close to unity and thus, the unity Lewis number assumption is likely to capture at the least the qualitative nature of water droplet interaction with n-heptane premixed flames. A stoichiometric (i.e. \(\phi _g=1.0\)) n-heptane-air premixed flame is assumed to interact with different initially mono-sized spherical water droplets. In this analysis, the position, velocity, diameter and temperature (i.e. \(\vec {x}_d\), \(\vec {u}_d\), \(a_d\), \(T_d\) with the subscript d referring to droplet quantities) of individual liquid water droplets are tracked in a Lagrangian sense and interested readers are referred to (Hasslberger et al. 2021; Wacks et al. 2016; Ozel-Erol et al. 2019, 2020; Reveillon and Vervisch 2000; Wandel et al. 2009; Schroll et al. 2009; Neophytou et al. 2010) for evolutions of \(\vec {x}_d\), \(\vec {u}_d\), \(a_d\), and \(T_d\). The governing equations of mass, momentum, energy and species conservation for the carrier phase can be expressed in the following manner subjected to the unity Lewis number assumption for all species (Hasslberger et al. 2021; Wacks et al. 2016; Ozel-Erol et al. 2019, 2020; Reveillon and Vervisch 2000; Wandel et al. 2009; Schroll et al. 2009; Neophytou et al. 2010):

$$\begin{aligned} \frac{\partial (\rho \varphi )}{\partial t}+\frac{\partial (\rho u_j \varphi )}{\partial x_j}=\frac{\partial }{\partial x_j}\left( R_\varphi \frac{\partial \varphi _1}{\partial x_j}\right) +\dot{\omega }_\varphi +\dot{S}_g+\dot{S}_\varphi \end{aligned}$$
(1)

where \(\varphi =\{1,u_i,e,Y_F,Y_O,Y_W^g\}\) and \(\varphi _1=\{1,u_i,\hat{T},Y_F,Y_O,Y_W^g\}\) for the conservation equations of mass, momentum, energy, and mass fractions, respectively, \(R_\varphi =\rho \nu /\sigma _\varphi \) for \(\varphi =\{1,u_i,Y_F,Y_O,Y_W^g\}\) and \(R_\varphi =\lambda \) for \(\varphi =e\), respectively, where \(e=\int _{T_{ref}}^T C_V dT+u_i u_i/2\) is the specific stagnation internal energy with \(Y_F\), \(Y_O\),\(Y_W^g\),\(\hat{T}\),\(T_{ref}\) and \(C_V\) being the fuel mass fraction, oxidiser mass fraction, water vapour mass fraction, dimensional temperature, reference temperature and specific heat at constant volume, respectively. Here, \(\nu \), \(\lambda \), and \(\sigma _\varphi \) are the kinematic viscosity, thermal conductivity and the Schmidt number corresponding to \(\varphi \), respectively. In Eq. (1), \(\dot{\omega }_\varphi \) refers to reaction rate, \(\dot{S}_g\) stands for an appropriate source/sink term in the gaseous phase (e.g. pressure forces in the momentum equation) and \(\dot{S}_\varphi =-(1/V_{cell})\sum _d (d(m_d \varphi _d)/dt)\) is the appropriate term due to droplet evaporation and is responsible for two-way coupling, where \(m_d=\rho _d (1/6)\pi a_d^3\) is the individual droplet mass and \(V_{cell}\) is the volume of the control volume. The reaction rate expression for fuel for the present thermochemistry is presented elsewhere and thus is not repeated here and interested readers are referred to Hasslberger et al. (2021) and Ozel-Erol et al. (2019) for further information. The reaction rate of oxygen is 3.52 times the reaction rate of fuel (i.e. n-heptane) and the production rate of water vapour due to combustion is 1.44 times the consumption rate of n-heptane in the context of single-step chemistry.

A reaction progress variable c, which increases monotonically from 0 in the unburned gas to 1.0 in the fully burned gas, can be defined here based on oxygen mass fraction \(Y_O\) and mixture fraction as (Hasslberger et al. 2021; Wacks et al. 2016; Ozel-Erol et al. 2019, 2020; Reveillon and Vervisch 2000; Wandel et al. 2009; Schroll et al. 2009; Neophytou et al. 2010):

$$\begin{aligned}&\xi =\frac{Y_F-Y_O/s+Y_O^\infty /s}{Y_F^\infty +Y_O^\infty /s} \end{aligned}$$
(2)
$$\begin{aligned}&c=\frac{(1-\xi )Y_O^\infty -Y_O}{(1-\xi )Y_O^\infty -\max \{0,(\xi _{st}-\xi )/\xi _{st}\}Y_O^\infty } \end{aligned}$$
(3)

where \(Y_O^\infty =0.233\) is the oxygen mass fraction in air and \(Y_F^\infty =1.0\) is the fuel mass fraction in the pure fuel stream. For n-heptane, C\(_7\)H\(_{16}\), \(s=3.52\) is the stoichiometric mass ratio of oxidiser to fuel and \(Y_{F_{st}}= 0.0621\) and \(\xi _{st}= 0.0621\) are the corresponding stoichiometric fuel mass fraction and mixture fraction, respectively. It is worth noting that it is possible to define a reaction progress variable based on fuel mass fraction but for a stoichiometric mixture as considered in the current study [it was shown elsewhere (Hasslberger et al. 2021) that \(\xi \approx \xi _{st}\) is approximately maintained within the flame front even for droplet cases due to weak evaporation of water droplets], the reaction progress variable based on fuel mass fraction becomes identical to c. In general, for fuels with Lewis number significantly different from unity (e.g. n-heptane), the usual Burke–Schumann relations may not hold for the fuel mass fraction and fuels like n-heptane break down to smaller hydrocarbons before the oxygen is fully consumed even for the stoichiometric mixture. These issues can make the use of a fuel mass fraction based reaction progress variable potentially misleading and hence the definition of progress variable used in the present work is more general than the fuel mass fraction-based progress variable.

The transport equation of c is given as (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020):

$$\begin{aligned} \rho (Dc/Dt)=\nabla \cdot (\rho D \nabla c)+\dot{\omega }_c+\dot{S}_{liq,c}+\dot{A}_c \end{aligned}$$
(4)

In Eq. (4), D is the molecular diffusivity (which is is equal to the thermal diffusivity under the unity Lewis number assumption) while the reaction rate of reaction progress variable, \(\dot{\omega }_c\); the source/sink term arising due to droplet evaporation, \(\dot{S}_{liq,c}\) and the cross-scalar dissipation term arising due to mixture inhomogeneity, \(\dot{A}_c\) are defined as follows (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020):

$$\begin{aligned}&\dot{\omega }_c = {\left\{ \begin{array}{ll} -\xi _{st}\dot{\omega }_O/[Y_O^\infty \xi (1-\xi _{st})] &{} \xi \le \xi _{st}\\ -\dot{\omega }_O/[Y_O^\infty (1-\xi )] &{} \xi>\xi _{st}\\ \end{array}\right. }\nonumber \\&\dot{S}_{liq,c} = {\left\{ \begin{array}{ll} \frac{-{\xi _{st}}[\xi \dot{S}_O+(Y_O^\infty -Y_O)\dot{S}_\xi ]}{{Y_O^\infty \xi ^2(1-\xi _{st})}} &{} \xi \le \xi _{st}\\ \frac{-{[(1-\xi )\dot{S}_O+Y_O\dot{S}_\xi ]}}{[{Y_O^\infty (1-\xi )^2}]} &{} \xi>\xi _{st} \end{array}\right. } \nonumber \\&\dot{A}_c = {\left\{ \begin{array}{ll} 2\rho D\nabla \xi \cdot \nabla c/{\xi } &{} \xi \le \xi _{st}\\ -2\rho D\nabla \xi \cdot \nabla c/[{1-\xi }] &{} \xi >\xi _{st}\\ \end{array}\right. } \end{aligned}$$
(5)

where \(\dot{\omega }_O\) is the reaction rate of oxidiser, \(\dot{S}_\xi =(\dot{S}_F-\dot{S}_O/s)/(Y_F^\infty +Y_O^\infty /s)\) is the droplet source/sink term in the mixture fraction transport equation, \(\dot{S}_F=-\Gamma _mY_F\) and \(\dot{S}_O=-\Gamma _mY_O\) are the droplet source/sink terms in the mass fraction transport equations for fuel and oxygen, respectively, and \(\Gamma _m\) is the source term in the mass conservation equation due to evaporation. Equation (4) can be rearranged in the kinetic form for a given c isosurface as (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020):

$$\begin{aligned} \partial c/\partial t + u_j \partial c / \partial x_j = S_d \vert \nabla c\vert , \end{aligned}$$
(6)

where \(S_d\) is the displacement speed, which is given as (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020):

$$\begin{aligned} S_d =S_n+S_t+S_r+S_s+S_z \end{aligned}$$
(7)

Here \(S_n=\vec {N}\cdot \nabla (\rho D \vec {N}\cdot \nabla c)/\rho \vert \nabla c\vert \), \(S_t=-2D\kappa _m\), \(S_r=\dot{\omega }_c/\rho \vert \nabla c\vert \) are the normal diffusion, tangential diffusion, reaction components of \(S_d\) (where \(\vec {N}=-\nabla c/\vert \nabla c\vert \) is the local flame normal vector and \(\kappa _m=0.5\nabla \cdot \vec {N}\) is the flame curvature), and \(S_z=\dot{A}_c/(\rho \vert \nabla c\vert )\) and \(S_s=\dot{S}_{liq,c}/(\rho \vert \nabla c \vert )\) are the contributions associated with the cross-scalar dissipation term and droplet evaporation, respectively. Equation (7) indicates that density \(\rho \) variation can affect the displacement speed \(S_d\) and its components (i.e. \(S_n\), \(S_t\), \(S_r\), \(S_z\), \(S_s\)). Thus, it is worthwhile to consider density-weighted displacement speed \(S_d^*=\rho S_d/\rho _0\) and its components: \(S_r^*=\rho S_r/\rho _0\), \(S_n^*=\rho S_n/\rho _0\), \(S_t^*=\rho S_t/\rho _0\), \(S_z^*=\rho S_z/\rho _0\) and \(S_s^*=\rho S_s/\rho _0\), where \(\rho _0\) is the unburned gas density. Moreover, \(S_d^*\) is relevant to the Flame Surface Density (Pope 1988) and level-set (Peters 2000) based modelling methodologies. Another flame speed, known as the consumption speed \(S_c\), is often used in the turbulent combustion literature (Ozel-Erol et al. 2021). The consumption speed determines the speed at which the flame burns the reactants based on the reaction rate of the reaction progress variable \(\dot{w}_c\) and it is defined as (Poinsot and Veynante 2005; Ozel-Erol et al. 2021):

$$\begin{aligned} S_c=\rho _0^{-1}\int _{-\infty }^{+\infty }\dot{\omega }_c dn \end{aligned}$$
(8)

where dn is the elemental distance in the local flame normal direction and the limit of the integral goes from the unburned to the burned gas side without crossing the flame more than once. The statistics of \(S_c\) and \(S_d^*\) will be analysed using DNS data in Sect. 3 of this paper.

A well-known DNS code SENGA+ (Hasslberger et al. 2021; Wacks et al. 2016; Ozel-Erol et al. 2019, 2020; Wandel et al. 2009; Schroll et al. 2009; Neophytou et al. 2010) is used for the simulations. High order finite-difference (10th order central difference for the internal grid points with a gradual decrease in the order of accuracy to a 2nd order at the non-periodic boundaries) and Runge-Kutta (3rd order low-storage) schemes are used. In this analysis, DNS of statistically planar turbulent flames have been carried out for two different initial values of the normalised root-mean-square turbulent velocity of \(u'/S_{b(\phi _g=1)}\) (\(= 4.0\) and 8.0) with a non-dimensional longitudinal integral length-scale of \(L_{11}/\delta _{st} =2.5\), where \(\delta _{st}=(T_{ad(\phi _g=1)}-T_0) / max\vert \nabla \hat{T}\vert _L\) is the thermal flame thickness of the stoichiometric mixture with \(T_{ad(\phi _g=1)}\) and \(T_0\) being the stoichiometric adiabatic flame temperature and unburned gas temperature, respectively. Damköhler number can be defined as \(Da=L_{11} S_{b(\phi _g=1)}/(u'\delta _{st})\) and Karlovitz number is estimated with \(Ka=(u'/S_{b(\phi _g=1)})^{1.5} (L_{11}/\delta _{st})^{-0.5}\). The values of Da and Ka are listed in Table 1 and are representative of the thin reaction zones regime combustion (Peters 2000).

Table 1 Turbulence parameters considered in the analysis
Full size table

A pseudo-spectral method proposed by Orszag (1969) and Rogallo (1981) is employed in the current study for the purpose of the turbulence initialisation. This yields an initially homogeneous isotropic incompressible periodic velocity field following a Batchelor–Townsend energy spectrum (Batchelor and Townsend 1948). This initialisation for the turbulent flow field implies the invariance of all statistics under translations, rotations and reflections of the coordinate system. The homogeneous and isotropic turbulence concept has been widely adopted by the turbulent combustion community due to its practicality and validity over a wide range of applications and has provided a considerable understanding of turbulence-flame interaction (Govindaraju et al. 2019; Zhou et al. 2017; Duret et al. 2012; Sreedhara and Huh 2007; Schroll et al. 2009). It is worth noting that displacement speed statistics are determined by the small-scale physics and small-scale turbulence shares, for sufficiently large Reynolds numbers, the attributes of homogeneous isotropic turbulence irrespective of the nature of large-scale fluid motion (Batchelor and Townsend 1948). Thus, the homogeneous and isotropic turbulent flow assumption serves as a reasonable initialisation tool for the analysis of turbulence-flame interaction.

A single realisation of the turbulent flow field is obtained by assigning the random phase angles. Therefore, employing a different value for a phase angle from the previous analysis provides a turbulence flow field that is statistically identical but locally different from the previous initial flow field. In this study, for the purpose of turbulent flow initialisation, a single value of random seed has been used for evaluation of phase angles for all cases. However, a different realisation of initial turbulent velocity is not expected to cause a significant change in statistics of flame propagation presented in this study, as the initial turbulence flow field remains statistically identical (i.e., the same \(L_{11}\) and \(u'\)). For the analysed configuration, there are at least eight integral eddies along one coordinate of the computational domain, which provides a sufficient number of samples for collecting reliable statistics. It has indirectly been substantiated by comparing the statistics obtained based on a distinct half of the domain with the results presented in this paper and in all cases excellent qualitative and quantitative agreements have been obtained. Moreover, it is not computationally practical to conduct a large parametric analysis as in this paper for more than one turbulent flow realisation using DNS. This approach was adopted in several analyses by several authors (Trivedi et al. 2019; Dunstan et al. 2012; Mastorakos 2017; Haworth and Poinsot 1992) in the past. The flame is initialised by a 1D unstretched laminar premixed flame solution. Water is supplied in the form of liquid droplets at the inlet which is placed on the left-hand side of the domain. Liquid water droplets, distributed randomly but statistically uniform in space at the inlet plane, are introduced with a temperature of \(T_0 = 300\) K. There can be local clustering of the droplets governed by the flow physics during the course of the simulation and interested readers are referred to the detailed discussion in Hasslberger et al. (2021). For the present analysis, fully gaseous phase stoichiometric turbulent premixed n-heptane-air flames are also considered for the sake of comparison with the corresponding cases with water droplets.

Table 2 Simulation parameters considered in the analysis
Full size table

The direction of the mean flame propagation aligns with the long side of the simulation domain (i.e. x-direction in this configuration). The boundaries in x-direction are taken to be partially non-reflecting and are specified using the Navier–Stokes Characteristic Boundary Conditions technique. The transverse boundaries are considered to be periodic. For the present analysis, three different initially mono-sized water droplets (i.e. \(a_d/\delta _{st} =0.02,0.04\) and 0.06, which corresponds to a range of \(10-30\mu m\)), have been considered for each value of \(u'/S_{b(\phi _g=1)}\) for a water loading of \(Y_W=0.1\) where \(Y_W=Y_W^l+Y_W^g=m_W/(m_W+m_0)\) is the mass fraction of water (in both liquid (l)+gaseous (g) phases) in the unburned gas (and thus independent of the chemical reaction) with \(m_W\) being the total amount of water injected in a combined mass of air and fuel given by \(m_0\). The simulation parameters used in the current analysis are summarised in Table 2.

Table 3 Simulation parameters related to liquid phase
Full size table

The Stokes number for the water droplets can be defined based on the turbulent (i.e. \(L_{11}/u'\)) and chemical (i.e. \(\alpha _{T0}/S_{b(\phi _g=1)}^2\)) time scales as \(St=\rho _d a_d^2u'/(18C_u\mu L_{11})\) and \(St'=\rho _d a_d^2 S_{b(\phi _g=1)}^2/(18C_u \mu \alpha _{T0})\), respectively. St and \(St'\) for the cases considered in this study are listed in Table 3 along with the mean normalised inter-droplet distance, \(s_d/\eta \) and initial droplet number density, \((\rho _N )^{1/3}\delta _{st}\). The ratio of the initial droplet volume to the computational cell volume \(V_d/V_{cell}\), justifying the point source assumption, is given in Table 3 and is comparable to several previous analyses (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020; Wandel et al. 2009; Schroll et al. 2009; Neophytou et al. 2010; Fujita et al. 2013; Wang and Rutland 2005). For this analysis, flame-turbulence interaction takes place under spatially decaying turbulence and statistics are taken at \(3.0t_{\mathrm{chem}}=3.0\alpha _{T0}/S_{b(\phi _g=1)}^2\) which amounts to \(2.45L_{11}/u'\) and \(4.89L_{11}/u'\) for initial \(u'/S_{b(\phi _g=1)}=4.0\) and 8.0 cases, respectively. This simulation time is consistent with several previous analyses (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020; Wandel et al. 2009; Schroll et al. 2009; Neophytou et al. 2010) and by this time both the volume-integrated burning rate and flame surface area reached a quasi-stationary state (Hasslberger et al. 2021). Therefore, the statistics were extracted once the quasi-steady state is obtained, and they remain qualitatively similar halfway through the simulation.

3 Results and discussion

3.1 Water droplet-flame interaction

Figure 1 shows the distributions of fuel mass fraction \(Y_F\), non-dimensional temperature \(T=(\hat{T} -T_0)/(T_{ad(\phi _g=1)} -T_0)\) and water vapour mass fraction \(Y_W^g\) arising from the evaporation of water droplets (this excludes the water vapour produced by chemical reaction) in the central mid-plane for initial \(u'/S_{b(\phi _g=1)}=4.0\) and 8.0 cases with initial \(a_d/\delta _{st} =0.04\) water droplets. From a physical/chemical point of view, water vapour contributions from droplet evaporation and combustion are identical, but they are originating from different sources. Accordingly, the added water also affects the reaction rate of the fuel mass fraction via the changes in the reactant concentrations. Evaporation of liquid water locally increases the gas density and therefore reduces the concentrations of fuel and oxidizer in order to conserve mass. Hence, the dilution effect due to water addition is generally included in the simulation but it is small compared to the cooling effect for the current conditions (Hasslberger et al. 2021). It is clear from Fig. 1 that water droplets do not evaporate appreciably in the unburned gas and many droplets pass through the flame and complete their evaporation within the burned gas (examples are shown in the insets of Fig. 1). This behaviour does not change with a modification of the turbulence intensity. The latent heat of evaporation of water, which is considerably greater than that of a hydrocarbon fuel, is responsible for the slow evaporation of water droplets. Although the presence of water droplets does not significantly dilute the concentration of reactants within the flame, the extraction of latent heat leads to a reduction of burned gas temperature for the cases with water droplets.

Fig. 1
figure 1

Distributions of (1st column) fuel mass fraction \(Y_F\), (2nd column) non-dimensional temperature T and (3rd column) water vapour mass fraction \(Y_W^g\) arising from water droplets (this excludes the water vapour produced by chemical reaction) in the central mid-plane for initial \(u^{\prime}/S_{b(\phi _g=1)}=4.0\) (top row) and 8.0 (bottom row) cases with initial \(a_d/\delta _{st} =0.04\). Magenta lines show \(c=0.1,0.3,0.5,0.7,0.9\) contours (left to right). The droplet size is not to the scale

Full size image

The equality between c and T (i.e. \(c\approx T\)) is maintained for low Mach number unity Lewis number globally adiabatic gaseous premixed (GP) flames considered here. However, \(c\approx T\) is not maintained for droplet cases and they show a smaller mean value of T conditional upon c than in the corresponding premixed flame cases for all turbulence intensities considered here. This behaviour is the strongest in the initial \(a_d/\delta _{st} =0.02\) cases because smaller droplets extract greater amount of heat due to their higher evaporation rates. The extraction of latent heat acts to reduce the flame and burned gas temperature in the droplet cases in comparison to that in the premixed flame case without droplets, which can be seen from Fig. 2, where the PDFs of T in the flame region (i.e. \(0.01\le c\le 0.99\)) are presented for an x-range corresponding to \(T \ge 0.8\) because the objective of this figure is to demonstrate the impact of water injection on the maximum burned gas temperature. This temperature affects the burning rate, as demonstrated previously based on the analytical flame theory using high activation energy asymptotics (Hasslberger et al. 2021). Under the unity Lewis number assumption, T becomes equal to 1.0 in the burned gas (i.e., \(c \ge 0.99\)) therefore the PDF of T in the burned gas side for the GP flames shows a peak close to \(T\approx 1.0\). The probability of obtaining \(T \approx 1.0\) decreases significantly for the droplet cases in comparison to the corresponding gaseous premixed cases. The reduction of the temperature is more prominent for \(a_d/\delta _{st} =0.02\) in the initial \(u'/S_{b(\phi _g=1)}=4.0\) case than in the initial \(u'/S_{b(\phi _g=1)}=8.0\) case, while temperature profiles remain comparable at different flow conditions for the cases with initial \(a_d/\delta _{st} =0.04\) and 0.06. An increase in \(u'/S_{b(\phi _g=1)}\) reduces the flame residence time of the droplets, which reduces the rate of evaporation within the flame, but the number of droplets crossing the flame also increases at the same time due to the enhanced mixing. The competition of these two opposing effects ultimately determines the variation of the maximum burned gas temperature in response to the changes in \(u'/S_{b(\phi _g=1)}\). As a result, the cooling effect due to the extraction of latent heat remains less prominent within the flame for the initial \(u'/S_{b(\phi _g=1)}=8.0\) case than in the initial \(u'/S_{b(\phi _g=1)}=4.0\) case. The PDF of T in the burned gas (not explicitly shown here for brevity) for the GP flames without droplets is a delta function at \(T\approx 1.0\). However, the probability of finding \(T<1.0\) increases and the mean value of the maximum burned gas temperature decreases with decreasing droplet diameter.

3.2 Flame propagation

The reduction in temperature within the flame acts to alter the reaction rate \(\dot{\omega }_c\), which in turn, influences the statistics of \(S_d^*\) [see Eq. (7)]. The normalised mean values of reaction rate, molecular dissipation rate, flame normal diffusion rate, two-phase coupling contribution in the reaction progress variable transport and the contribution due to mixture inhomogeneity conditional upon c (i.e. \([\langle \dot{\omega }_c\rangle _c\), \(\langle \nabla \cdot (\rho D \nabla c)\rangle _c\), \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c\), \(\langle \dot{S}_{liq,c}\rangle _c\) and \(\langle \dot{A}_c\rangle _c]\times \delta _{st}/\rho _0 S_{b(\phi _g=1)}\) where \(\langle Q \rangle _c\) is the mean value of a general quantity conditioned upon c and the quantities \(\delta _{st}\) and \(S_{b(\phi _g=1)}\), which are used for normalisation, are identical for all cases) for the cases considered here are shown in Fig. 3. Figure 3 illustrates that \(\langle \dot{\omega }_c\rangle _c\) remains small towards the unburned gas side and assumes a peak value at around \(c\approx 0.8\) before decreasing again towards the burned gas side. As the peak reaction rate takes place at \(c\approx 0.8\), the present analysis considers the \(c=0.8\) isosurface as the flame surface following several previous studies (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020; Peters et al. 1998; Echekki and Chen 1999). Figure 3 shows that \(\langle \dot{\omega }_c\rangle _c\) for the droplet cases remain smaller than the corresponding premixed flame case without droplets, and this trend strengthens with decreasing \(a_d/\delta _{st}\) because of the stronger cooling effect induced by higher rate of evaporation of smaller droplets. However, the differences between the values of \(\langle \dot{\omega }_c\rangle _c\) between premixed and droplet cases are smaller in the \(u'/S_{b(\phi _g=1)}=8.0\) cases than in the initial \(u'/S_{b(\phi _g=1)}=4.0\) cases due to weaker cooling effects within the flame for higher values of \(u'/S_{b(\phi _g=1)}\). The quantities \(\langle \nabla \cdot (\rho D\nabla c)\rangle _c\) and \(\langle \vec {N}\cdot \nabla (\rho D \vec {N}\cdot \nabla c)\rangle _c\) assume positive (negative) values towards the unburned (burned) gas side of the flame front. The values of \(\langle \nabla \cdot (\rho D\nabla c)\rangle _c=\langle \vec {N}\cdot \nabla (\rho D \vec {N}\cdot \nabla c)\rangle _c-2\langle \rho D \kappa _m \vert \nabla c\vert \rangle _c\) and \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c\) remain almost equal throughout the flame for all cases considered here. This suggests that \(\langle (-2\rho D\kappa _m \vert \nabla c\vert )\rangle _c\) remains negligible because the mean value of curvature \(\kappa _m\) is close to zero for statistically planar flames. The quantities \(|\langle \nabla \cdot (\rho D \nabla c)\rangle _c|\) and \(|\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c|\) remain comparable to \(\langle \dot{\omega }_c\rangle _c\) towards the burned gas side of the flame for all cases, whereas the magnitudes of \(\langle \dot{S}_{liq,c}\rangle _c\) and \(\langle \dot{A}_c\rangle _c\) remain negligible in comparison to those of \(\langle \dot{\omega }_c\rangle _c\) and \(\langle \nabla \cdot (\rho D\nabla c)\rangle _c\) for all droplet cases considered here (note that \(\dot{S}_{liq,c}\) and \(\dot{A}_c\) are identically zero for premixed flames). This suggests that the evaporation and cross-scalar dissipation do not significantly alter the mean behaviour of \([\nabla \cdot (\rho D\nabla c)+\dot{\omega }_c+\dot{S}_{liq,c}+\dot{A}_c]=\rho _0 S_d^* \vert \nabla c\vert \) in the droplet cases irrespective of \(u'/S_{b(\phi _g=1)}\) and \(a_d/\delta _{st}\).

Fig. 2
figure 2

PDFs of T within the region given by \(0.01\le c\le 0.99\) for gaseous premixed (black), water droplet cases with initial \(a_d/\delta _{st} =0.02\) (blue), 0.04 (red) and 0.06 (orange) for initial \(u'/S_{b(\phi _g=1)}=\) 4.0 a and 8.0 b

Full size image
Fig. 3
figure 3

Variations of the mean values of \(\dot{\omega }_c\) (solid line with triangle), \(\nabla \cdot (\rho D \nabla c)\) (dotted line), \(\vec {N}\cdot \nabla (\rho D\vec {N}\nabla c)\) (square), \(\dot{A}_c\) (star), \(\dot{S}_{liq,c}\) (circle), \(\rho _0 S_d^* \vert \nabla c\vert \) (dashed line) and \(\rho _0 S_{b(\phi _g=1)} \vert \nabla c\vert \) (plus\(\}\) conditioned upon c (i.e. \(\langle \dot{\omega }_c\rangle _c\),\(\langle \nabla \cdot (\rho D \nabla c)\rangle _c\), \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c\), \(\langle \dot{S}_{liq,c}\rangle _c\) and \(\langle \dot{A}_c\rangle _c\)) for initial \(u'/S_{b(\phi _g=1)}=\) 4.0 a and 8.0 b. All terms are normalised by \(\delta _{st}/\rho _0 S_{b(\phi _g=1)}\) which remains identical for all cases. So we should show them in Fig. 2

Full size image

The values of \(\langle \rho _0 S_{b(\phi _g=1)} \vert \nabla c\vert \rangle _c \times \delta _{st}/\rho _0 S_{b(\phi _g=1)}\) conditional upon c are also shown in Fig. 3, which demonstrates that the peak mean value of \(\langle \vert \nabla c\vert \rangle _c\) for droplet cases is smaller than that in the premixed flame without droplets because \(\delta _{st}\) and \(S_{b(\phi _g=1)}\) are identical for all cases as these are quantities corresponding to the unstretched stoichiometric laminar premixed flame. The inverse of the peak mean value of \(\vert \nabla c\vert \times \delta _{st}\) can be taken to be a measure of the flamelet thickness (i.e. \(\delta \sim 1/max\langle \vert \nabla c\vert \rangle _c\)) (Wacks et al., 2016). This suggests that water injection promotes flame thickening. It was demonstrated by Hasslberger et al. (2021) using a reduced order model that the laminar burning velocity in the presence of water droplets \(S_{b(\phi =1)}(Y_w)\) is smaller than the laminar burning velocity without water loading \(S_{b(\phi =1)} (Y_w=0)\), and this reduction in laminar burning velocity is particularly prevalent for small water droplets. As the flamelet thickness \(\delta \) scales as \(\delta \sim \alpha _{T0}/S_{b(\phi =1)} (Y_w)\), the flame thickens for the droplet cases and this tendency strengthens with decreasing \(a_d\). However, this effect weakens for higher values of \(u'/S_{b(\phi _g=1)}\) because of the weaker cooling effects within the flame for higher turbulence intensities. Figure 3 shows that for initial \(u'/S_{b(\phi _g=1)}=4.0\), the peak value of \(\langle \rho _0 S_{b(\phi _g=1)} \vert \nabla c\vert \rangle _c \times \delta _{st}/(\rho _0 S_{b(\phi _g=1)})=\langle \vert \nabla c\vert \rangle _c\times \delta _{st}\) is the smallest for the droplet case with initial \(a_d/\delta _{st}=0.02\), whereas the evaporation effects are relatively weaker for water droplet cases with initial \(a_d/\delta _{st}=0.04\) and 0.06, and accordingly in these cases the peak values of \(\langle \vert \nabla c\vert \rangle _c\times \delta _{st}\) remain smaller but comparable to the corresponding value in the premixed flame without droplets. However, \(\langle \vert \nabla c\vert \rangle _c\times \delta _{st}\) for the droplet cases remain comparable to that of the gaseous premixed flame for the initial \(u'/S_{b(\phi _g=1)}=8.0\) cases. The peak magnitude of \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c=-\langle \vec {N}\cdot \nabla (\rho D\vert \nabla c\vert )\rangle _c\) can be scaled as \(\max \langle -\vec {N}\cdot \nabla (\rho D\vert \nabla c\vert \rangle _c\sim {\max \langle \rho D\vert \nabla c\vert \rangle _c}/\delta \), which implies that the peak magnitudes of \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c\) in water droplet cases are expected to decrease in comparison to the corresponding premixed flame cases without droplets due to smaller values of \(\max \langle \vert \nabla c\vert \rangle _c\) and greater values of flamelet thickness \(\delta \). This behaviour is most prominent for the water droplet cases with initial \(a_d/\delta _{st}=0.02\) and \(u'/S_{b(\phi _g=1)}=4.0\) which can be substantiated from the reduced magnitudes of \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c\) (and thereby \(\langle \nabla \cdot (\rho D\nabla c)\rangle _c\)) of water droplet cases in comparison to that in premixed flames without droplets. Moreover, in droplet cases, the magnitudes of \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c\) decrease with decreasing \(a_d/\delta _{st}\) for initial \(u'/S_{b(\phi _g=1)}=4.0\). However, the differences in the magnitudes of \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c\) between droplet cases and the corresponding premixed flame without droplets remain small in the case of initial \(u'/S_{b(\phi _g=1)}=8.0\) because of the negligible differences in the flamelet thickness in these cases. Figure 3 further shows that the mean value of \([\nabla \cdot (\rho D\nabla c)+\dot{\omega }_c+\dot{S}_{liq,c}+\dot{A}_c ]=\rho _0 S_d^* \vert \nabla c\vert \) for the droplet cases remains smaller than \(\rho _0 S_{b(\phi _g=1)} \vert \nabla c\vert \), but this difference decreases with increasing \(u'/S_{b(\phi _g=1)}\) in accordance to the behaviours of \(\langle \dot{\omega }_c\rangle _c\) and \(\langle \nabla \cdot (\rho D\nabla c)\rangle _c\) discussed earlier. By contrast, \(\langle \rho _0 S_d^* \vert \nabla c\vert \rangle _c\) and \(\langle \rho _0 S_{b(\phi _g=1)} \vert \nabla c\vert \rangle _c\) remain almost equal for the premixed flame cases without droplets for both values of \(u'/S_{b(\phi _g=1)}\) considered here. This suggests that the surface averaged values of the density-weighted displacement speed (i.e. \(\overline{(S_d^* )}_s=\overline{(S_d^* \vert \nabla c\vert )} /\overline{(\vert \nabla c\vert )}\) with the overbar indicating a Reynolds averaging/LES filtering process, as appropriate) cannot be approximated by \(S_{b(\phi =1)} (Y_w=0)\) (here \(S_{b(\phi _g=1)}\)) for small values of \(u'/S_{b(\phi _g=1)}\). By contrast, \(\overline{(S_d^* )}_s\approx S_{b(\phi _g=1)}\) reasonably holds for the droplet cases for large turbulence intensities (e.g. initial \(u'/S_{b(\phi _g=1)}=8.0\) cases) and also for stoichiometric turbulent premixed flames without droplets for the turbulence intensities considered in this analysis.

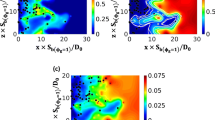
Table 4 The mean values of \(S_d^*/S_{b(\phi _g=1)}\)
Full size table

The PDFs of \(S_d^*/S_{b(\phi _g=1)}\) and its components \(S_r^*/S_{b(\phi _g=1)}\), \(S_n^*/S_{b(\phi _g=1)}\) and \(S_t^*/S_{b(\phi _g=1)}\) for the \(c=0.8\) isosurface in the case of initial \(u'/S_{b(\phi _g=1)}=4.0\) and 8.0 are shown in Fig. 4, which demonstrates that the mean value of \(S_d^*/S_{b(\phi _g=1)}\) remains positive for all cases. The mean values of \(S_d^*/S_{b(\phi _g=1)}\) are also presented in Table 4. Moreover, Fig. 4 shows that the mean values of \(S_d^*/S_{b(\phi _g=1)}\) for water droplet cases are smaller than those in the corresponding premixed flames without droplets, and the behaviour of the droplets approaches to the corresponding premixed flames as droplet diameter increases. In order to explain this behaviour, it is worthwhile to consider the distributions of \(S_r^*/S_{b(\phi _g=1)}\), \(S_n^*/S_{b(\phi _g=1)}\), \(S_t^*/S_{b(\phi _g=1)}\) and \((S_s^*+S_z^*)/S_{b(\phi _g=1)}\).

Fig. 4
figure 4

PDFs of \(S_d^*/S_{b(\phi _g=1)}\) and its components \(S_r^*/S_{b(\phi _g=1)}\), \(S_n^*/S_{b(\phi _g=1)}\) and \(S_t^*/S_{b(\phi _g=1)}\). Vertical lines in the top row show the mean values of \(S_d^*/S_{b(\phi _g=1)}\). See Fig. 2 for colour keys

Full size image

The PDFs of \(S_r^*/S_{b(\phi _g=1)}\) and the normal diffusion component \(S_n^*/S_{b(\phi _g=1)} for \,c=0.8\) show predominantly positive and negative values, respectively, but the probability of obtaining large magnitudes decreases with decreasing \(a_d\) and this trend weakens with increasing \(u'/S_{b(\phi _g=1)}\). This is consistent with the variations of \(\langle \dot{\omega }_c\rangle _c\) and \(\langle \vec {N}\cdot \nabla (\rho D\vec {N}\cdot \nabla c)\rangle _c\) shown in Fig. 3. The PDF of \(S_t^*/S_{b(\phi _g=1)}=-2\rho D\kappa _m/\rho _0 S_{b(\phi _g=1)}\) shows both positive and negative values with a peak value close to zero. This is also consistent with the negligible value of \(\langle -2\rho D\kappa _m \vert \nabla c\vert \rangle _c\) in Fig. 3. However, the PDFs of \(S_t^*/S_{b(\phi _g=1)}\) suggest that \(S_t^*\) can locally play a significant role although its mean value remains close to zero for statistically planar flames.

Fig. 5
figure 5

Variations of the mean values of \(S_d^*/S_{b(\phi _g=1)}\) (red) for \(c=0.8\), \(S_c/S_{b(\phi _g=1)}\) (blue), \(0.5\times S_T/S_{b(\phi _g=1)}\) (black), \(S_T A_p/[A_T S_{b(\phi _g=1)} ]\) (green) for droplet (solid line) and gaseous premixed (dashed line) cases with initial \(u'/S_{b(\phi _g=1)}=\) 4.0 a and 8.0 b

Full size image

It has been found that the PDFs of \((S_s^*+S_z^*)/S_{b(\phi _g=1)}\) resemble delta functions and peak sharply at 0.0 and the magnitude of \((S_s^*+S_z^*)\) remains negligible in comparison to \(S_r^*\) and \(S_n^*\) for all droplet cases and thus are not shown in Fig. 4 for the sake of conciseness. This suggests that the evaporation of water droplets does not directly affect the statistics of \(S_d^*\) through \(S_s^*\) and \(S_z^*\), but through its impact on \(S_r^*\) and \(S_n^*\).

The variations of the mean values of \(S_d^*/S_{b(\phi _g=1)}\) for \(c=0.8\), \(S_c/S_{b(\phi _g=1)}\), \(S_T/S_{b(\phi _g=1)}\), \(S_T A_p/[A_T S_{b(\phi _g=1)} ]\) for initial \(u'/S_{b(\phi _g=1)}=4.0\) and 8.0 cases are shown in Fig. 5. It can be seen from Fig. 5 that \(S_T\) decreases with decreasing \(a_d\). The negligible contribution of \((S_s^*+S_z^* )\) implies that the turbulent flame speed \(S_T=(\rho _0 A_p )^{-1} \int _V\dot{\omega }_c dV\) (where \(A_p\) is the projected flame surface area in the direction of mean flame propagation) can be expressed as (note \(\int _V (S_n^*+S_t^*)\vert \nabla c\vert dV=\rho _0^{-1} \int _V\nabla \cdot (\rho D\nabla c)dV=0\) due to the divergence theorem): \(S_T\approx {(1/ A_p)}\int _V S_d^*\vert \nabla c\vert dV\). The decreasing trends of mean values of \(S_d^*\) and \(\vert \nabla c\vert \) with decreasing droplet diameter \(a_d\) (see Figs. 3, 4) lead to a reduction of \(S_T\) with a decrease in \(a_d\). Moreover, the decrease in the mean value of \(S_d^*\) in the water droplet cases in comparison to the corresponding premixed flame cases without droplets also gives rise to a reduction in turbulent flame speed \(S_T\) in water droplet cases. The normalised \(S_T/S_{b(\phi _g=1)}\) increases with increasing \(u'/S_{b(\phi _g=1)}\), whereas the mean values of \(S_d^*/S_{b(\phi _g=1)}\), \(S_c/S_{b(\phi _g=1)}\) and \(S_T\) \(A_p/[A_T S_{b(\phi _g=1)} ]\) remain comparable for the turbulence intensities considered here. It can further be seen from Fig. 5 that the normalised consumption speed \(S_c/S_{b(\phi _g=1)}\) decreases with decreasing \(a_d\), and a reduction in consumption speed is obtained for water droplet cases, which is qualitatively similar to the variations of \(S_d^*/S_{b(\phi _g=1)}\) and \(S_T/S_{b(\phi _g=1)}\). Figure 5 also shows that the variation of the normalised consumption speed \(S_c/S_{b(\phi _g=1)}\) is qualitatively consistent with the predictions of the reduced order model for \(S_{b(\phi =1)}(Y_w)/S_{b(\phi _g=1)}\) proposed by Hasslberger et al. (2021). The observations made from Fig. 5 suggest that the reduced order model for burning velocity by Hasslberger et al. (2021) can be used for predictions of mean values of \(S_c\) but there are quantitative differences between \(S_c/S_{b(\phi _g=1)}\), \(S_d^*\), \(S_{b(\phi _g=1)}\) and \(S_T/S_{b(\phi _g=1)}\), which is consistent with previous findings (Ozel-Erol et al. 2019, 2020, 2021). Note that \(S_T\) includes the contribution of the augmentation of flame surface area \(\int _V\vert \nabla c\vert dV\) due to turbulence and it can be seen from Fig. 5 that \((\int _V\dot{\omega }_c dV)/([\rho _0 S_{b(\phi _g=1)}] \int _V\vert \nabla c\vert dV)=S_T A_p/[A_T S_{b(\phi _g=1)} ]\) remains comparable to the mean values of \(S_d^*/S_{b(\phi _g=1)}\) for all cases.

Table 5 Correlation coefficients for \(S_d^*-\kappa _m\) and \(S_d^*-a_T\) for \(c=0.8\) and 95% confidence interval limits (CIL) for the corresponding correlation coefficients
Full size table

Figure 5 shows that \(S_T A_p/[A_T S_{b(\phi _g=1)}] =1.0\) is maintained in the premixed flames without droplets for both turbulence intensities. Although \(S_T A_p/[A_T S_{b(\phi _g=1)}]\) values in the droplet cases remain smaller than the premixed flame cases without droplets, \((S_T A_p)/[A_T S_{b(\phi _g=1)}]\) assumes values close to unity for the droplet cases.

It is well-known that the flame curvature \(\kappa _m\) and tangential strain rate \(a_T=(\delta _{ij}-N_i N_j )\partial u_i/\partial x_j\) affect the local behaviour of \(S_d^*\) (Wacks et al. 2016; Ozel-Erol et al. 2019, 2020; Peters et al. 1998; Echekki and Chen 1999; Chakraborty et al. 2011; Ozel-Erol et al. 2021). The correlation coefficients between \(S_d^*\) and \(\kappa _m\), and between \(S_d^*\) and \(a_T\) for \(c=0.8\) isosurface are listed in Table 5 along with 95% confidence interval limits. Table 5 shows that the presence of water droplets does not change the qualitative nature of the correlations, but water droplets alter the strength of these correlations. The physical explanations for the negative correlation between \(S_d^*\) and \(\kappa _m\) and the positive correlation between \(S_d^*\) and \(a_T\) in premixed flames have been explained elsewhere (Peters et al. 1998; Echekki and Chen 1999; Chakraborty et al. 2011; Chakraborty and Cant 2004; Chakraborty 2007; Keil et al. 2021a, b) in detail and thus they are not repeated here. Moreover, the correlations weaken with increasing \(u'/S_{b(\phi _g=1)}\), which is consistent with the weakening of the correlation strengths with increasing Ka (Chakraborty et al. 2011). The consumption speed \(S_c\) does not show any appreciable correlations with \(\kappa _m\) and \(a_T\) for unity Lewis number flames (Ozel-Erol et al. 2021; Poinsot and Veynante 2005), which is valid for both purely gaseous premixed and water droplet cases considered here and thus are not explicitly shown in Table 5. Therefore, the presence of water droplets does not alter the qualitative nature of the local curvature and strain rate dependences of both density-weighted displacement and consumption speeds.

4 Conclusion

The statistics of density-weighted displacement speed \(S_d^*\), consumption speed \(S_c\) and turbulent flame speed \(S_T\) have been investigated for statistically planar stoichiometric n-heptane-air flames interacting with initially mono-sized water droplets using carrier phase DNS. It has been found that most water droplets do not evaporate fully within the flame front and complete their evaporation within the burned gas due to high latent heat of evaporation. As a result, the presence of water droplets does not significantly alter the concentration of the reactants within the flame but acts to reduce the temperatures in the flame and in the burned gas. This acts to decrease the burning rate and thickens the flame in the cases with water droplets in comparison to the corresponding premixed flame cases without droplets. This tendency is particularly strong for small droplets at low turbulence intensities but weakens with an increase in turbulence intensity. The evaporation of water droplets affects \(S_d^*\) by altering the reaction and molecular diffusion components, and the magnitudes of the contributions arising from evaporation and cross-dissipation rate remain negligible in comparison to the reaction and diffusion components. It has been found that the water droplet injection acts to reduce the mean value of \(S_d^*\), \(S_c\) and \(S_T\) for the parameter range considered here, and this reduction is particularly strong for small droplets at low turbulence intensities. Moreover, it has been found that the presence of water droplets does not alter the qualitative nature of the strain rate and curvature dependences of both density-weighted displacement speed and consumption speed for the range of parameters considered here. Although the physics discussed in this paper is unlikely to be affected by the choice of chemical mechanism (see qualitative similarities between simple and detailed chemistry results (Peters et al. 1998; Echekki and Chen 1999; Chakraborty et al. 2011; Ozel-Erol et al. 2021)), further analyses using detailed chemistry and transport will be needed for further validation, and quantitative predictions. Furthermore, this paper mainly focuses on the flame propagation statistics, and it has been shown in the previous studies that the flame speed statistics for turbulent premixed flames obtained from simple chemistry (Chakraborty and Cant 2004; Chakraborty 2007) remain in good agreement with the corresponding results obtained from a detailed chemical mechanism (Peters et al. 1998; Chakraborty et al. 2011). Furthermore, it has been demonstrated by Hasslberger et al. (2021) and Ozel-Erol et al. (2020) that the current chemical mechanism compares favourably with both experiments and detailed chemistry simulations. Recent analyses by Keil et al. (2021a, b) revealed that the displacement speed statistics obtained from simple chemistry DNS remain in good qualitative agreement with the corresponding detailed chemistry results and the quantitative differences are of the order of uncertainties obtained for different definitions of reaction progress variable in detailed chemistry simulations. However, it is necessary to conduct water droplet injected flame simulations using complex chemistry to investigate the effects of water droplets on emissions.