A Priori Direct Numerical Simulation Analysis of the Closure of Cross-Scalar Dissipation Rate of Reaction Progress Variable and Mixture Fraction in Turbulent Stratified Flames

Abstract

The cross-scalar dissipation rate of reaction progress variable and mixture fraction $\widetilde{{\varepsilon_{c\xi } }}$ plays an important role in the modelling of stratified combustion. The evolution and statistical behaviour of $\widetilde{{\varepsilon_{c\xi } }}$ have been analysed using a direct numerical simulation (DNS) database of statistically planar turbulent stratified flames with a globally stochiometric mixture. A parametric analysis has been conducted by considering a number of DNS cases with a varying initial root-mean-square velocity fluctuation $u^{\prime }$ and initial scalar integral length scale $\ell_{\phi }$. The explicitly Reynolds averaged DNS data suggests that the linear relaxation model for $\widetilde{{\varepsilon_{c\xi } }}$ is inadequate for most cases, but its performance appears to improve with increasing initial $\ell_{\phi }$ and $u^{\prime }$ values. An exact transport equation for $\widetilde{{\varepsilon_{c\xi } }}$ has been derived from the first principle, and the budget of the unclosed terms of the $\widetilde{{\varepsilon_{c\xi } }}$ transport equation has been analysed in detail. It has been found that the terms arising from the density variation, scalar-turbulence interaction, chemical reaction rate and molecular dissipation rate play leading order roles in the $\widetilde{{\varepsilon_{c\xi } }}$ transport. These observations have been justified by a scaling analysis, which has been utilised to identify the dominant components of the leading order terms to aid model development for the unclosed terms of the $\widetilde{{\varepsilon_{c\xi } }}$ transport equation. The performances of newly proposed models for the unclosed terms have been assessed with respect to the corresponding terms extracted from DNS data, and the newly proposed closures yield satisfactory predictions of the unclosed terms in the $\widetilde{{\varepsilon_{c\xi } }}$ transport equation.

1 Introduction

Stratified mixture combustion occurs when there is a limited mixing time between the unburned reactants such that some premixing takes place but not to the extent of homogeneity. This type of combustion is often encountered in industrial combustors since it offers benefits in terms of improved energy efficiency and reduced pollutant emissions (Lipatnikov, 2017). Stratified combustion may also occur unintentionally by not allowing a sufficient mixing time in premixed combustors. Therefore, it is necessary to have reliable models for numerical simulations which will be pivotal to the design of future generation combustors that exploit the advantages offered by turbulent stratified mixture combustion.

A complete thermo-chemical description of stratified combustion requires a passive scalar (e.g. mixture fraction $\xi$) to describe the local mixture composition and an active scalar (e.g. reaction progress variable $c$) to determine the progress of the chemical reaction. The normalised mixture fraction assumes a value of zero in the pure air stream and unity in the pure fuel stream, and is defined as (Bilger, 1988):

$$ \xi = \frac{{Y_{F} - Y_{O} /s + Y_{O\infty } /s}}{{Y_{F\infty } + Y_{O\infty } /s}} $$

(1)

where $Y_{F}$ and $Y_{O}$ are the fuel and oxidiser mass fractions respectively, $s = (Y_{O} /Y_{F} )_{st}$ is the mass stoichiometric ratio, and a subscript $F\infty$ ($O\infty$) indicates the mass fraction value of fuel (oxygen) in a pure fuel (air) stream. Likewise, the reaction progress variable $c$ quantifies the extent of completion of the chemical reaction by rising from zero in the unburned reactants to a value of unity in the fully burned products, and can be defined as (Hélie and Trouvé, 1998):

$$ c = \frac{{\xi Y_{F\infty } - Y_{F} }}{{\xi Y_{F\infty } - \max \left( {0, \frac{{\xi - \xi_{st} }}{{1 - \xi_{st} }}} \right)Y_{F\infty } }} $$

(2)

where $\xi_{st} = Y_{O\infty } /(sY_{F\infty } + Y_{O\infty } )$ is the stoichiometric mixture fraction.

Presumed probability density function (PPDF) (Libby and Williams, 2000; Ribert et al., 2005; Robin et al., 2006), flamelet based tabulated chemistry (Darbyshire et al., 2010) and Flamelet Generated Manifold (Nguyen et al., 2010; Fiorina et al., 2015; Marincola et al., 2013) based modelling approaches require solving the transport equations of the Favre averaged active and passive scalar variances, as well as their covariance, which in turn need closures of their respective dissipation rates. Several previous analyses (Mura et al., 2007; Malkeson and Chakraborty, 2010a, 2011a; Chakraborty et al., 2011) focussed on modelling the scalar dissipation rates of mixture fraction and reaction progress variable in turbulent stratified mixture combustion, but relatively limited effort has been directed to the closure of cross-scalar dissipation rate. Mura et al. (2007) and Nguyen et al. (2010) proposed algebraic closures of the cross-scalar dissipation rates of fuel mass fraction and mixture fraction fluctuations $\widetilde{{\varepsilon_{Y\xi } }} = \overline{{\rho D\nabla Y_{F}^{\prime \prime } \cdot \nabla \xi^{\prime \prime } }} /\overline{\rho }$ (where $D$ is the molecular diffusivity, and $\overline{q}$, $\tilde{q} = \overline{\rho q} /\overline{\rho }$ and $q^{\prime \prime } = q - \tilde{q}$ are the Reynolds averaged, Favre-averaged and Favre fluctuation of a general quantity $q$ respectively, with $\rho$ being the gas density) which plays a key role in the context of Libby-Williams (L-W) model (Libby and Williams, 2000). Following this, Malkeson and Chakraborty (2011b) derived the exact transport equation of $\widetilde{{\varepsilon_{Y\xi } }}$ and proposed closures for the unclosed terms based on a-priori DNS analysis. Flame Generated Manifold (Nguyen et al., 2010; Marincola et al., 2013; Fiorina et al., 2015) closures of stratified mixture combustion utilise reaction progress variable $c$ rather than $Y_{F}$ as the active scalar, and therefore it is important to understand the behaviour of $\widetilde{{\varepsilon_{c\xi } }}$ in the flame brush of turbulent stratified flames. However, to date, the closure of the reaction progress variable and mixture fraction cross scalar dissipation rate $\widetilde{{\varepsilon_{c\xi } }} = \overline{{\rho D\nabla c^{\prime \prime } \cdot \nabla \xi^{\prime \prime } }} /\overline{\rho }$ has not been addressed in detail in the existing literature (Malkeson and Chakraborty, 2010a, b) despite its importance in the closure of the transport equation of the Favre averaged reaction progress variable $\tilde{c}$, the covariance $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and flame displacement speed $S_{d}$ in turbulent stratified mixture combustion (Malkeson and Chakraborty, 2013). Although $Y_{F}$ and $c$ are both active scalars, their gradients and correlations with $\nabla \xi$ can vary significantly depending on the extent of mixture stratification. Thus, it is important to analyse $\widetilde{{\varepsilon_{c\xi } }}$ independently since closures of $\widetilde{{\varepsilon_{Y\xi } }}$ do not automatically apply to $\widetilde{{\varepsilon_{c\xi } }}$. Thus, the main objectives of this paper are to:

• (1) analyse the statistical behaviour of $\widetilde{{\varepsilon_{c\xi } }}$ within the flame brush in turbulent stratified flames.

• (2) evaluate the effectiveness of the linear relaxation algebraic model at predicting the variation of $\widetilde{{\varepsilon_{c\xi } }}$ within the flame brush.

• (3) identify the leading order contributors in the transport equation of $\widetilde{{\varepsilon_{c\xi } }}$ for turbulent stratified mixture combustion for different turbulence intensities and mixture stratification conditions.

• (4) provide adequate model expressions for the unclosed terms of the $\widetilde{{\varepsilon_{c\xi } }}$ transport equation.

To meet the objectives, a three-dimensional Direct Numerical Simulation (DNS) database of six statistically planar turbulent stratified flames has been considered (Brearley et al., 2020). This database consists of cases with a globally stochiometric mixture and an initially bimodal distribution of equivalence ratio in the unburned gas. The cases vary by initial values of root-mean-square velocity fluctuation normalised by the laminar burning velocity of the stoichiometric mixture $u^{\prime } /S_{{b\left( {\phi = 1} \right)}}$ and the initial scalar integral length scale normalised by the velocity integral length scale $\ell_{\phi } /\ell$.

The rest of the paper will be organised in the following manner. The mathematical background and numerical frameworks pertaining to this analysis are presented in the next two sections. This will be followed by the discussion of the results before the summary of the main finding, and conclusions are drawn.

2 Mathematical Background

The cross-scalar dissipation rate $\widetilde{{\varepsilon_{c\xi } }}$ can be modelled using an algebraic expression in the context of the linear relaxation (LR) methodology (Mura et al., 2007; Malkeson and Chakraborty, 2010a), where the cross-scalar dissipation rate is modelled as:

$$ \widetilde{{\varepsilon_{c\xi } }} \approx C\left( {\tilde{\varepsilon }/\tilde{k}} \right)\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }} $$

(3)

where $C$ is a model constant of the order of unity, $\tilde{\varepsilon } = \overline{{\rho \nu \left( {\partial u_{j}^{^{\prime\prime}} /\partial x_{k} } \right)\left( {\partial u_{j}^{^{\prime\prime}} /\partial x_{k} } \right)}} /\overline{\rho }$ is the Favre-averaged turbulent kinetic energy dissipation rate, $\tilde{k} = \overline{{\rho u_{j}^{\prime \prime } u_{j}^{\prime \prime } }} /2\overline{\rho }$ is the Favre averaged turbulent kinetic energy and $\nu$ is the kinematic viscosity. Alternatively, an additional modelled transport equation for $\widetilde{{\varepsilon_{c\xi } }}$ can be solved. The transport equation for $\widetilde{{\varepsilon_{c\xi } }}$ can be derived by considering the individual transport equations for the reaction progress variable and the mixture fraction:

$$ \rho \left( {Dc/Dt} \right) = \dot{\omega }_{c} + \nabla \cdot \left( {\rho D\nabla c} \right) + A_{\xi } $$

(4)

$$ \rho \left( {D\xi /Dt} \right) = \nabla \cdot \left( {\rho D\nabla \xi } \right) $$

(5)

where $\dot{\omega }_{c}$ is the reaction rate of reaction progress variable $c$, which takes the following form when $c$ is defined using Eq. 2 (Bray et al., 2005; Malkeson and Chakraborty, 2010b):

$$ \dot{\omega }_{c} = - \dot{\omega }_{F} /\left[ {\xi Y_{F\infty } } \right]\;{\text{for}}\;\xi \le \xi_{st} ,\;\dot{\omega }_{c} = - \dot{\omega }_{F} \left( {1 - \xi_{st} } \right)/\left[ {\xi_{st} \left( {1 - \xi } \right)Y_{F\infty } } \right]\;{\text{for}}\;\xi > \xi_{st} $$

(6)

with $\dot{\omega }_{F}$ being the reaction rate of the fuel. The term $A_{\xi }$ is the cross-scalar dissipation contribution, which is defined as (Bray et al., 2005; Malkeson and Chakraborty, 2010b):

$$ A_{\xi } = 2\rho D\left( {\nabla c \cdot \nabla \xi } \right)/\xi \;{\text{for}}\;\xi \le \xi_{st} \;{\text{and}}\;A_{\xi } = - 2\rho D\left( {\nabla c \cdot \nabla \xi } \right)/\left( {1 - \xi } \right)\;{\text{for}}\;\xi > \xi_{st} $$

(7)

It is worth noting that the statistical behaviour of $N_{c\xi } = D\left( {\nabla c \cdot \nabla \xi } \right)$ determines the behaviour of $A_{\xi }$. The cross-scalar dissipation rate values are often smaller than the values of scalar dissipation rate of the reaction progress variable (Malkeson and Chakraborty, 2010a; Inanc et al., 2022). However, the cross-scalar dissipation rate appears explicitly in the expression of displacement speed $S_{d} = \left| {\nabla c} \right|^{ - 1} \left( {Dc/Dt} \right)$ in stratified flames (Bray et al., 2005; Malkeson and Chakraborty, 2010b) and this quantity accounts for the effects of relative orientations of $\nabla c$ and $\nabla \xi$ on flame propagation (i.e. back-supported or front-supported flame propagation) which may not be negligible for stratified flames (e.g. Marincola et al., 2013; Inanc et al., 2020). Moreover, scalar dissipation rates $N_{\xi } = D\nabla \xi \cdot \nabla \xi$, $N_{c} = D\nabla c \cdot \nabla c$ and cross-scalar dissipation rate $N_{c\xi } = D\nabla c \cdot \nabla \xi$ affect the value of $\dot{\omega }_{c} = [\dot{\omega }_{F} + N_{\xi } \partial^{2} Y_{F} /\partial \xi^{2} + N_{c} \partial^{2} Y_{F} /\partial c^{2} + 2N_{c\xi } \partial^{2} Y_{F} /\partial \xi \partial c]$ in stratified flames (Malkeson et al., 2013).

Differentiating Eqs. 4 and 5 with respect to $x_{i}$ one obtains transport equations for $\partial c/\partial x_{i}$ and $\partial \xi /\partial x_{i}$, respectively. Multiplying the $\partial c/\partial x_{i}$ transport equation by $\partial \xi /\partial x_{i}$, and multiplying the $\partial \xi /\partial x_{i}$ transport equation by $\partial c/\partial x_{i}$, then summing the resulting equations leads to a transport equation for the instantaneous cross-scalar dissipation rate $N_{c\xi } = D\nabla c \cdot \nabla \xi$. The transport equation for the cross-scalar dissipation rate of the Favre averaged scalars can be derived in a similar fashion. The transport equation of the Favre-averaged reaction progress variable $\tilde{c}$ is used to obtain the transport equation of $\partial \tilde{c}/\partial x_{i}$, and the transport equation of the Favre-averaged mixture fraction $\tilde{\xi }$ is used to obtain the transport equation of $\partial \tilde{\xi }/\partial x_{i}$. Multiplying the $\partial \tilde{c}/\partial x_{i}$ transport equation by $\partial \tilde{\xi }/\partial x_{i}$, and multiplying the $\partial \tilde{\xi }/\partial x_{i}$ transport equation by $\partial \tilde{c}/\partial x_{i}$, then summing the resulting transport equations together yields the transport equation for $\tilde{D}\nabla \tilde{c} \cdot \nabla \tilde{\xi }$. The final step of the derivation is to subtract the two derived equations to yield $\widetilde{{\varepsilon_{c\xi } }} = \widetilde{{N}_{c\xi} } - \tilde{D}\nabla \tilde{c} \cdot \nabla \tilde{\xi }$. For further information, interested readers are referred to Malkeson and Chakraborty (2011b) where a full mathematical description of the derivation of the transport equation of $\widetilde{{\varepsilon_{Y\xi } }}$ is presented, which is identical to the derivation of the transport equation of $\widetilde{{\varepsilon_{c\xi } }}$. The $\widetilde{{\varepsilon_{c\xi } }}$ transport equation is shown below after ignoring the terms arising due to diffusivity variations:

$$ \frac{{\partial \left( {\overline{\rho }\widetilde{{\varepsilon_{c\xi } }}} \right)}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\widetilde{{u_{j} }}\widetilde{{\varepsilon_{c\xi } }}} \right)}}{{\partial x_{j} }} = \underbrace {{\frac{\partial }{{\partial x_{j} }}\left( {\overline{\rho }\tilde{D}\frac{{\partial \widetilde{{\varepsilon_{c\xi } }}}}{{\partial x_{j} }}} \right)}}_{{D_{1} }} + T_{1} + T_{2} + T_{3} + T_{4} - D_{2} $$

(8)

The first term on the left-hand side represents the temporal change of ${{\widetilde{{\varepsilon }_{c\xi }}}}$, while the second term represents the effects of mean advection. On the right-hand side, ${D}_{1}$ is the contribution of molecular diffusion, ${-D}_{2}$ is the contribution of molecular dissipation, ${T}_{1}$ is the contribution of turbulent transport, ${T}_{2}$ arises due to density variation, ${T}_{3}$ is the contribution of scalar gradient alignment with fluid dynamic strain rates, and ${T}_{4}$ is the combined contribution of chemical reaction rate and mixture inhomogeneity. The terms ${T}_{1}$, ${T}_{2}$, ${T}_{3}$, ${T}_{4}$ and $-{D}_{2}$ are unclosed and require modelling. The mathematical definitions of these terms are given as:

$$ T_{1} = \underbrace {{ - \frac{\partial }{{\partial x_{j} }}\overline{{\left( {\rho u_{j}^{\prime \prime } \varepsilon_{c\xi } } \right)}} }}_{{T_{11} }} + \underbrace {{\tilde{D}\frac{{\partial \tilde{\xi }}}{{\partial x_{i} }}\frac{{\partial^{2} }}{{\partial x_{i} \partial x_{j} }}\overline{{\left( {\rho u_{j}^{\prime \prime } c^{\prime \prime } } \right)}} }}_{{T_{12} }} + \underbrace {{\tilde{D}\frac{{\partial \tilde{c}}}{{\partial x_{i} }}\frac{{\partial^{2} }}{{\partial x_{i} \partial x_{j} }}\overline{{\left( {\rho u_{j}^{\prime \prime } \xi^{\prime \prime } } \right)}} }}_{{T_{13} }} $$

(9(i))

$$ \begin{aligned} T_{2} = & \underbrace {{ - \overline{{\frac{D}{\rho }\frac{\partial \rho }{{\partial x_{i} }}\left[ {\left( {\dot{\omega }_{c} + A_{\xi } } \right)\frac{\partial \xi }{{\partial x_{i} }} + \frac{\partial \xi }{{\partial x_{i} }}\frac{\partial }{{\partial x_{j} }}\left( {\rho D\frac{\partial c}{{\partial x_{j} }}} \right) + \frac{\partial c}{{\partial x_{i} }}\frac{\partial }{{\partial x_{j} }}\left( {\rho D\frac{\partial \xi }{{\partial x_{j} }}} \right)} \right]}} }}_{{T_{21} }} + \\ \underbrace {{\frac{{\tilde{D}}}{{\overline{\rho }}}\frac{{\partial \overline{\rho }}}{{\partial x_{i} }}\left[ {\begin{array}{*{20}c} {\left( {\overline{{\dot{\omega }_{c} + A_{\xi } }} } \right)\frac{{\partial \tilde{\xi }}}{{\partial x_{i} }} - \frac{\partial }{{\partial x_{j} }}\left( {\overline{{\rho u_{j}^{\prime \prime } c^{\prime \prime } }} } \right)\frac{{\partial \tilde{\xi }}}{{\partial x_{i} }} - \frac{\partial }{{\partial x_{j} }}\left( {\overline{{\rho u_{j}^{\prime \prime } \xi^{\prime \prime } }} } \right)\frac{{\partial \tilde{c}}}{{\partial x_{i} }}} \\ { + \frac{{\partial \tilde{\xi }}}{{\partial x_{i} }}\frac{\partial }{{\partial x_{j} }}\left( {\overline{\rho }\tilde{D}\frac{{\partial \tilde{c}}}{{\partial x_{j} }}} \right) + \frac{{\partial \tilde{c}}}{{\partial x_{i} }}\frac{\partial }{{\partial x_{j} }}\left( {\overline{\rho }\tilde{D}\frac{{\partial \tilde{\xi }}}{{\partial x_{j} }}} \right)} \\ \end{array} } \right]}}_{{T_{22} }} \\ \end{aligned} $$

(9(ii))

$$ \begin{aligned} T_{3} = & \underbrace {{\overline{{\rho D\frac{{\partial c^{\prime \prime } }}{{\partial x_{i} }}\frac{{\partial u_{j}^{\prime \prime } }}{{\partial x_{i} }}}} \frac{{\partial \tilde{\xi }}}{{\partial x_{j} }} - \overline{{\rho D\frac{{\partial c^{\prime \prime } }}{{\partial x_{j} }}\frac{{\partial u_{j}^{\prime \prime } }}{{\partial x_{i} }}}} \frac{{\partial \tilde{\xi }}}{{\partial x_{i} }}}}_{{T_{31}^{\left( i \right)} }}\underbrace {{ - \overline{{\rho D\frac{{\partial \xi^{\prime \prime } }}{{\partial x_{j} }}\frac{{\partial u_{j}^{\prime \prime } }}{{\partial x_{i} }}}} \frac{{\partial \tilde{c}}}{{\partial x_{i} }} - \overline{{\rho D\frac{{\partial \xi^{\prime \prime } }}{{\partial x_{i} }}\frac{{\partial u_{j}^{\prime \prime } }}{{\partial x_{i} }}}} \frac{{\partial \tilde{c}}}{{\partial x_{j} }}}}_{{T_{31}^{{\left( {ii} \right)}} }} \\ \underbrace {{ - \overline{{\rho D\frac{{\partial c^{\prime \prime } }}{{\partial x_{i} }}\frac{{\partial \xi^{\prime \prime } }}{{\partial x_{j} }}\frac{{\partial u_{j}^{\prime \prime } }}{{\partial x_{i} }}}} - \overline{{\rho D\frac{{\partial c^{\prime \prime } }}{{\partial x_{j} }}\frac{{\partial \xi^{\prime \prime } }}{{\partial x_{i} }}\frac{{\partial u_{j}^{\prime \prime } }}{{\partial x_{i} }}}} }}_{{T_{32} }}\underbrace {{ - \overline{{\rho D\frac{{\partial c^{\prime \prime } }}{{\partial x_{j} }}\frac{{\partial \xi^{\prime \prime } }}{{\partial x_{i} }}}} \frac{{\partial \widetilde{{u_{j} }}}}{{\partial x_{i} }} - \overline{{\rho D\frac{{\partial c^{\prime \prime } }}{{\partial x_{i} }}\frac{{\partial \xi^{\prime \prime } }}{{\partial x_{j} }}}} \frac{{\partial \widetilde{{u_{j} }}}}{{\partial x_{i} }}}}_{{T_{33} }} \\ \end{aligned} $$

(9(iii))

$$ T_{4} = \overline {{\underbrace {{ {D}\frac{{\partial ({{\dot{\omega }_{c} + A_{\xi } )}} }}{{\partial x_{i} }}\frac{{\partial {\xi }}}{{\partial x_{i} }}}}_{{T_{41} }}}} \underbrace {{ - \tilde{D}\frac{{\partial (\overline{{\dot{\omega }_{c} + A_{\xi } )}} }}{{\partial x_{i} }}\frac{{\partial \tilde{\xi }}}{{\partial x_{i} }}}}_{{T_{42} }}$$

(9(iv))

$$ D_{2} = \underbrace {{2\overline{{\rho D^{2} \frac{{\partial^{2} c}}{{\partial x_{i} \partial x_{j} }}\frac{{\partial^{2} \xi }}{{\partial x_{i} \partial x_{j} }}}} }}_{{D_{21} }}\underbrace {{ - 2\overline{\rho }\tilde{D}^{2} \frac{{\partial^{2} \tilde{c}}}{{\partial x_{i} \partial x_{j} }}\frac{{\partial^{2} \tilde{\xi }}}{{\partial x_{i} \partial x_{j} }}}}_{{D_{22} }} $$

(9(v))

The statistical behaviours of $T_{1} ,T_{2} ,T_{3} ,T_{4}$ and $\left( { - D_{2} } \right)$ will be extracted from the explicitly averaged DNS data and will be discussed in Sect. 4 of this paper.

3 Numerical Implementation

The simulations of turbulent stratified flames were simulated using the DNS code SENGA + (Jenkins and Cant, 1999). The simulations deal with statistically planar turbulent stratified flames propagating into an inhomogeneous methane-air mixture. A modified single-step chemistry proposed by Tarrazo et al. (2006) representative of methane-air combustion has been considered for the current analysis where the activation temperature and heat of combustion are taken to be functions of equivalence ratio. It has been shown elsewhere (Malkeson and Chakraborty, 2010a, b, 2011a) that the laminar burning velocity variation with equivalence ratio $\phi$ is accurately captured using this thermo-chemistry. This simplification of chemical representation allows for a detailed parametric analysis in terms of $u^{\prime } /S_{{b\left( {\phi = 1} \right)}}$ and $\ell_{\phi } /\ell$ (which was reported in detail by Brearley et al. (2020)) with a reasonable amount of computational cost. The relative costs between simple and detailed chemistry DNS were discussed in detail by Keil et al. (2021a). It has been demonstrated recently by Keil et al. (2021a, b) that the flame propagation statistics obtained from simple chemistry DNS are found to be qualitatively similar to the results obtained from detailed chemistry DNS. Moreover, the quantitative differences between displacement speed statistics between the simple and detailed chemistry results are comparable to the uncertainty involved with the different possible definitions of reaction progress variable. As most of the heat release takes place in premixed mode in stratified mixture combustion, it is expected that the findings of Keil et al. (2021a, b) are likely to be also valid for stratified mixture combustion. It was indeed demonstrated by Malkeson et al. (2013) that the statistics of scalar gradients obtained from the thermochemistry used in this paper remain in good qualitative agreement with detailed chemistry DNS. Finally, several previous simple chemistry based analyses including DNS studies (Hélie and Trouvé, 1998; Ribert et al., 2005; Robin et al., 2006; Mura et al., 2007; Malkeson and Chakraborty, 2010a, b, 2013) gave rise to significant advancements in the fundamental understanding and modelling of stratified mixture combustion and the same approach has been adopted in this paper.

In all cases, a grid size of $800 \times 400 \times 400$ grid points uniformly distributed in a computational domain of size $70.2\delta_{st} \times \left( {30.1\delta_{st} } \right)^{2}$ has been considered, where $\delta_{st} = \left( {T_{{ad\left( {\phi = 1} \right)}} - T_{0} } \right)/\max \left| {\nabla \hat{T}} \right|_{L}$ is the thermal flame thickness of the stoichiometric mixture with $T_{{ad\left( {\phi = 1} \right)}}$, $T_{0}$ and $\hat{T}$ being the adiabatic flame temperature of the stoichiometric mixture, unburned gas temperature, and the instantaneous dimensional temperature, respectively. The subscript $L$ refers to the values in the 1D unstretched laminar premixed stoichiometric methane-air flame. The aforementioned grid spacing satisfies the requirement of having at least ten grid points within $\delta_{st}$. The mean direction of flame propagation runs parallel to the $x$ direction (long side) of the computational domain, with opposite-facing boundaries on the unburned and burned side of the computational domain being taken to be partially non-reflecting and specified in accordance with the Navier–Stokes Characteristic Boundary Conditions technique (Poinsot and Lele, 1992). The transverse boundaries are taken to be periodic. All the spatial differentiations for the internal grid points are carried out using a tenth-order central difference scheme for the internal grid points but the order of accuracy gradually reduces to a one-sided second-order scheme at the two non-periodic boundaries. The time advancement has been conducted using an explicit low storage third-order Runge–Kutta scheme (Wray, 1990). The initial velocity fluctuations were specified using a pseudo-spectral method (Rogallo, 1981) for a prescribed integral length scale $\ell$ and rms of velocity fluctuations $u^{\prime }$ that follows the Batchelor-Townsend spectrum (Batchelor and Townsend, 1948). The mixture inhomogeneity in the unburned gas is initialised by a bi-modal distribution of equivalence ratio $\phi = \left[ {\xi \left( {1 - \xi_{st} } \right)} \right]/\left[ {\xi_{st} \left( {1 - \xi } \right)} \right]$ following the methodology proposed by Eswaran and Pope (1988) for the prescribed values of mean equivalence ratio $\phi$, root-mean-square (rms) equivalence ratio fluctuation $\phi^{\prime }$, and integral length scale $\ell_{\phi }$ of equivalence ratio fluctuations. All species are assumed to be perfect gases with a Lewis number of unity. The heat release parameter $\tau = \left( {T_{{ad\left( {\phi = 1} \right)}} - T_{0} } \right)/T_{0}$ is taken to be 4.5 for all cases considered here, which represents unburned reactants preheated to 415 K for stoichiometric methane-air mixtures. Standard values are considered for Prandtl number $Pr = 0.7$ and the ratio of specific heats $\gamma = 1.4$. The turbulence length scale to stoichiometric flame thickness ratio is taken to be $\ell /\delta_{st} = 3.0$ for all cases. The initial mean equivalence ratio is taken to be unity (i.e., $\phi = 1.0$) and the initial rms equivalence ratio is taken to be $\phi^{\prime} = 0.35.$ The stratified mixture combustion is expected to remain within the flammability limit and thus the range of equivalence ratio $\phi$ encountered in this analysis remains within the flammability range (i.e. $0.6 < \phi < 1.5$) for methane-air combustion for the choices of $\phi = 1.0$ and $\phi^{\prime } = 0.35$.

The reacting scalar and temperature fields within the flame are initialized by 1D unstretched laminar premixed flame solution corresponding to $\phi = 1.0$ and $\tau = 4.5$. Table 1 shows the initial values of the simulation parameters $u^{\prime } /S_{{b\left( {\phi = 1} \right)}} , \ell /\delta_{st}$, $\ell_{\phi } /\ell$, along with Damköhler number $Da = \ell S_{{b\left( {\phi = 1} \right)}} /u^{\prime } \delta_{st}$ and Karlovitz number $Ka = \left( {u^{\prime } /S_{{b\left( {\phi = 1} \right)}} } \right)^{1.5} \left( {\ell /\delta_{st} } \right)^{ - 0.5}$. The Reynolds number $Re_{t} = \rho_{0} \sqrt k \ell /\mu_{0}$ (where $\rho_{0}$ and $\mu_{0}$ are the unburned gas density and viscosity, respectively and $k$ is the turbulent kinetic energy evaluated over the whole domain) is calculated based on the integral length scale and ranges from 42.0 to 84.0 for initial $u^{\prime } /S_{{b\left( {\phi = 1.0} \right)}} = 4.0 \, {\text{to}} \, 8.0$, respectively. All the cases considered here nominally belong to the thin reaction zones regime combustion (Peters, 2000). For these initial conditions, 2.41 and 1.44 grid points reside within the Kolmogorov length scale $\eta$ for initial $u^{\prime } /S_{L} = 4.0$ and 8.0 respectively, with this number increasing as the simulation progresses due to the decay of the turbulence. Under decaying turbulence, the simulations should be run for $t_{{{\text{sim}}}} \ge {\text{max}}\left( {T_{{{\text{turb}}}} ,T_{{{\text{chem}}}} } \right)$, where the eddy turnover time $T_{{{\text{turb}}}} = \ell /u^{\prime }$, and the chemical time scale $t_{{{\text{chem}}}} = \delta_{st} /S_{{b\left( {\phi = 1} \right)}}$. In all the cases, $T_{{{\text{chem}}}}$ remains greater than $T_{{{\text{turb}}}}$, and all cases considered here have been run for $t_{{{\text{sim}}}} = 2.0T_{{{\text{chem}}}}$, which is about $2.67T_{{{\text{turb}}}}$ and $5.33T_{{{\text{turb}}}}$ for initial $u^{\prime } /S_{L} = 4.0$ and 8.0 respectively. This simulation duration remains either comparable to or greater than several previous analyses (Hélie and Trouvé, 1998; Haworth et al., 2000; Jimenez et al., 2002; Malkeson and Chakraborty, 2010a,b, 2011a,b). It is important to note that the cross-scalar dissipation statistics are extracted in this paper at the end of the simulation time when the quasi-stationary state has been obtained in terms of temporal evolutions of flame surface area and turbulent burning velocity, as previously shown by Brearley et al. (2020) for this database. The cross-scalar dissipation rate statistics and model performances reported in this paper remain qualitatively similar at different time instants since the quasi-stationary state is obtained (e.g. roughly halfway through the simulation).

Table 1 Initial values of the simulation parameters

To obtain the Reynolds/Favre-averaged values of a general quantity (i.e. $\overline{Q}$ and $\tilde{Q}$), the quantities of interest are arithmetically averaged over the statistically homogeneous transverse planes (i.e. $y - z$ directions) normal to the direction of mean flame propagation (i.e. the $x$ direction) following previous analyses (Hélie and Trouvé, 1998; Swaminathan and Bray, 2005; Malkeson and Chakraborty, 2010a,b, 2011a,b; Chakraborty et al., 2011). For statistically planar flames, $\tilde{c}$ is a unique function of the coordinate in the direction of the mean flame propagation (i.e. the $x$ direction in this case) and thus all the results in Sect. 4 will be represented as a function of $\tilde{c}$. It has been assessed that halving the sample size in the transverse direction does not significantly alter the results.

Three additional simulation cases where initial $u^{\prime}/S_{{{\varvec{b}}\left( {\phi = 1} \right)}} = 10$ from the database reported by Brearley et al. (2020) were used to assist in the statistical analysis of $\widetilde{{\varepsilon_{c\xi } }}$ and the model development. These results have been omitted for conciseness and because they do not enhance the discussion due to their similarity with the results for initial $u^{\prime } /S_{{b\left( {\phi = 1} \right)}} = 8.0$.

4 Results and Discussion

4.1 Flame-Turbulence Interaction

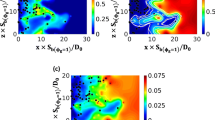
The distributions of normalised mixture fraction $\xi /\xi_{st}$ and reaction progress variable $c$ in the central $x - y$ plane when the statistics are extracted are shown in Fig. 1 for the cases considered here. All the cases considered here are representative of combustion in the thin reaction zones regime (Peters, 2000) and accordingly, local occurrences of flame thickening can be observed from the reaction progress variable contours due to penetration of energetic, turbulent eddies within the preheat zone. However, the reaction zone thickness remains smaller than the Kolmogorov length scale and thus this zone remains unperturbed by the small-scale turbulence but gets wrinkled by the large-scale turbulent motion. It can further be seen from Fig. 1 that the mixture inhomogeneity is predominantly obtained on the unburned gas side of the flame and the effects of stratification decay towards the burned gas side of the flame due to the increase in mass diffusivity with temperature. This behaviour has implications on the distribution of co-variance $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and cross-scalar dissipation rate $\widetilde{{\varepsilon_{c\xi } }}$, which will be discussed in the following sub-section.

Fig. 1

Distributions of mixture fraction normalised by the stoichiometric mixture fraction $\xi /\xi_{st}$ in the central $x - y$ mid-plane with the contours of $c = 0.05$ (dashed black line), 0.5 (solid black line) and 0.95 (dotted black line) superimposed when the statistics are extracted for different initial values of $\ell_{\phi } /\ell$ and $u^{\prime } /S_{{b\left( {\phi = 1} \right)}}$

5 Statistical Behaviours of Co-Variance and Cross-Scalar Dissipation Rate

The variations of the variances $\widetilde{{c^{\prime \prime 2} }}$, $\widetilde{{Y_{F}^{\prime \prime 2} }}$ and $\widetilde{{\xi^{\prime \prime 2} }}$ and co-variances of $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ with $\tilde{c}$ across the flame brush are shown in Fig. 2 for all cases. It can be seen from Fig. 2 that the magnitudes of $\widetilde{{\xi^{\prime \prime 2} }}$, $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ increase with increasing initial $\ell_{\phi } /\ell$ value. The mean scalar dissipation rate of mixture fraction in the volume of inhomogeneous mixture can be taken to scale as $\langle{N_{\xi}\rangle } \sim D\langle{\xi^{\prime 2}\rangle} /\lambda_{\xi }^{2}$ (Hélie and Trouvé, 1998; Malkeson and Chakraborty, 2011a; Brearley et al., 2020) with $\lambda_{\xi }$ being the Taylor micro-scale of mixture fraction distribution. For moderate values of turbulent Reynolds number, $\lambda_{\xi }$ remains of the same order as $\ell_{\phi }$, and thus $\langle{N_{\xi }\rangle}$ assumes high values for small values of $\ell_{\phi }$. This leads to a more rapid mixing rate for smaller values of $\ell_{\phi }$ and that is why the mixture fraction fluctuations and $\widetilde{{\xi^{\prime \prime 2} }}$ remain small for the cases with small initial values of $\ell_{\phi }$. This is reflected in the small magnitudes of $\widetilde{{\xi^{\prime \prime 2} }}$ for small initial values of $\ell_{\phi }$ and accordingly small magnitudes of $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ are obtained for small values of $\ell_{\phi }$. This behaviour is particularly strong for large values of $u^{\prime }$ (e.g. initial $u^{\prime } /S_{{b\left( {\phi = 1} \right)}} = 8.0$ case) because of enhanced mixing, which leads to decreases in magnitudes of $\widetilde{{\xi^{\prime \prime 2} }}$, $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ with increasing $u^{\prime } /S_{{b\left( {\phi = 1} \right)}}$. Figure 2 shows that the variations of $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ within the flame brush can be significantly different from each other. In the unburned gas $Y_{F}^{\prime \prime } = Y_{F\infty } \xi^{\prime \prime }$ and thus at the leading edge $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime 2} }}$ take a value of $\widetilde{{\xi^{\prime \prime 2} }}$ for $Y_{F\infty } = 1.0$, whereas $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ vanishes on the unburned gas side of the flame because $c^{\prime \prime } = 0$ in the unburned gas. Similarly, $c^{\prime \prime } = 0$ in the burned gas and therefore $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ vanishes on the burned gas side of the flame brush but $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ can assume non-zero values in the burned gas. The maximum value of $\widetilde{{Y_{F}^{\prime \prime 2} }}$ is obtained at the middle of the flame brush for all cases. However, it is evident from Fig. 2 that the distributions of $\widetilde{{c^{\prime \prime 2} }}$ and $\widetilde{{Y_{F}^{\prime \prime 2} }}$ are markedly different. The reaction progress variable variance $\widetilde{{c^{\prime \prime 2} }}$ attains the maximum value close to the middle of the flame brush (i.e., $\tilde{c} \approx 0.5$) for all cases but its maximum value remains smaller than 0.25 (i.e., $\max \left\{ {0.02 \times \widetilde{{c^{\prime \prime 2} }}} \right\} < 5 \times 10^{ - 3}$). In the limit of infinitely fast chemistry (i.e., $Da \gg 1$), the PDF of $c$ can be considered to be bimodal with impulses at $c = 0.0$ and $c = 1.0$ (Bray et al., 1985), which yields $\widetilde{{c^{\prime \prime 2} }} = \tilde{c}\left( {1 - \tilde{c}} \right)$ and $\max \left\{ {\widetilde{{c^{\prime \prime 2} }}} \right\} = 0.25$ (i.e. $\max \left\{ {0.02 \times \widetilde{{c^{\prime \prime 2} }}} \right\} = 5 \times 10^{ - 3}$). This further suggests that $\widetilde{{c^{\prime \prime 2} }} = \tilde{c}\left( {1 - \tilde{c}} \right)$ cannot be used for the low Damköhler number (i.e., $Da < 1$) stratified mixture combustion considered here where $\widetilde{{c^{\prime \prime 2} }} < \tilde{c}\left( {1 - \tilde{c}} \right)$ and the PDF of $c$ cannot be approximated by a bimodal distribution with impulses at $c = 0.0$ and $c = 1.0$. Although the distributions of $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ are markedly different within the flame brush, it can be seen from Fig. 2 that both $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ can assume locally negative values (e.g. $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ assumes locally negative values for initial $\ell_{\phi } /\ell = 1.0$ cases and negative values of $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ are obtained for initial $u^{\prime } /S_{{b\left( {\phi = 1} \right)}} = 8.0$ case with $\ell_{\phi } /\ell = 1.0$ and 3.0) and therefore the closures given by $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }} = \sqrt {\widetilde{{c^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }} = \sqrt {\widetilde{{Y_{F}^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}}$ (Ribert et al., 2005; Robin et al., 2006; Nguyen et al., 2010) cannot be used for these cases to model $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$, respectively. Moreover, the variations of $\sqrt {\widetilde{{c^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}}$ and $\sqrt {\widetilde{{Y_{F}^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}}$ across the flame brush are qualitatively different from $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ extracted from DNS data, respectively. Thus, it may be needed to solve a modelled transport equation in order to predict the covariances $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$. The exact transport equation of $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ for turbulent stratified mixtures was presented elsewhere (Malkeson and Chakraborty, 2013) and the transport equation of $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ can be obtained by replacing $Y_{F}$ with $c$ in the transport equation of $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ (Malkeson and Chakraborty, 2013), which yields:

$$ \frac{{\partial \left( {\overline{\rho }\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}} \right)}}{\partial t} + \frac{{\partial \left( {\overline{\rho }\tilde{u}_{j} \widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}} \right)}}{{\partial x_{j} }} = \frac{\partial }{{\partial x_{j} }}\left[ {\rho D\frac{{\partial \widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}}}{{\partial x_{j} }}} \right] - \frac{{\partial \left( {\overline{{\rho u_{j}^{\prime \prime } c^{\prime \prime } \xi^{\prime \prime } }} } \right)}}{{\partial x_{j} }} - \overline{\rho }\widetilde{{u_{j}^{^{\prime\prime}} \xi^{\prime \prime } }}\frac{{\partial \tilde{c}}}{{\partial x_{j} }} - \overline{\rho }\widetilde{{u_{j}^{\prime \prime } c^{\prime \prime } }}\frac{{\partial \tilde{\xi }}}{{\partial x_{j} }} + \left( {\overline{{\dot{\omega }_{c} \xi }} - \overline{{\dot{\omega }_{c} }} \tilde{\xi }} \right) - 2\overline{\rho }\widetilde{{\varepsilon_{c\xi } }} $$

(10)

Fig. 2

Variations of $\widetilde{{c^{\prime \prime 2} }}$, $\widetilde{{Y_{F}^{^{\prime\prime}2} }}$, $\widetilde{{\xi^{\prime \prime 2} }}$, $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{Y_{F}^{{{\prime \prime }}} \xi^{{{\prime \prime }}} }}$ along with the predictions of $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }} = \sqrt {\widetilde{{c^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}}$ and $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }} = \sqrt {\widetilde{{Y_{F}^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}}$ with $\tilde{c}$ across the flame brush for (a–f) cases A-F

It can be seen from Eq. 10 that the closure of $\widetilde{{\varepsilon_{c\xi } }}$ is needed to solve this equation. The variations of $\widetilde{{\varepsilon_{c\xi } }}$ and $\widetilde{{\varepsilon_{Y\xi } }}$ with $\tilde{c}$ for all cases considered here are shown in Fig. 3. The predictions of the linear relaxation model $\widetilde{{\varepsilon_{c\xi } }} \approx C_{c\xi } \left( {\tilde{\varepsilon }/\tilde{k}} \right)\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ and $\widetilde{{\varepsilon_{Y\xi } }} \approx C_{Y\xi } \left( {\tilde{\varepsilon }/\tilde{k}} \right)\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ are also shown for $C_{c\xi } = 3.0$ and $C_{Y\xi } = 3.0$ which provides a reasonable order of magnitude agreement with DNS data for most cases. The results do not reveal any significant relation between $C$ and the parameters tested in this study ($u^{\prime } /S_{{b\left( {\phi = 1} \right)}}$, and $\ell_{\phi } /\ell$). The model performs relatively better for cases with high initial $u^{\prime } /S_{{b\left( {\phi = 1} \right)}}$. The linear relaxation model only considers the turbulent time scale and ignores the contribution of the chemical timescale. Thus, this model performs relatively better for low Damköhler number cases where the effects of chemistry have a reduced influence. The linear relaxation model also performs better for large values of $\ell_{\phi } /\ell$, indicating that the existence of considerable mixture inhomogeneity is a requirement for the model to perform well. Moreover, this model also fails to capture the qualitative behaviour and the correct sign of $\widetilde{{\varepsilon_{c\xi } }}$ for small and moderate values of $\ell_{\phi }$ (see cases A–D in Fig. 3). The findings from Fig. 3 suggest that the linear relaxation model cannot be a sufficiently general model for the closure of $\widetilde{{\varepsilon_{c\xi } }}$ in turbulent stratified mixture combustion. Figure 3 also shows the variation $\widetilde{{\varepsilon_{Y\xi } }}$ and its equivalent linear relaxation model for the sake of comparison. Due to the fact that $Y_{F}$ and $\xi$ are closely related (i.e. $Y_{F} = Y_{F\infty } \xi$) in the unburned gas, $\widetilde{{\varepsilon_{Y\xi } }}$ assumes non-zero value in the unburned gas and decays within the flame brush for all cases. Furthermore, $\nabla Y_{F}^{\prime \prime }$ and $\nabla \xi^{\prime \prime }$ remain significantly correlated inside the flame which is evident from the mostly positive values of $\widetilde{{\varepsilon_{Y\xi } }}$. The quantities $\nabla c^{\prime \prime }$ and $\nabla \xi^{\prime \prime }$ also remain somewhat correlated inside the flame, which yields non-zero values of $\widetilde{{\varepsilon_{c\xi } }}$ within the flame brush. However, the variations of $\widetilde{{\varepsilon_{c\xi } }}$ and $\widetilde{{\varepsilon_{Y\xi } }}$ are qualitatively different which indicates that the correlation between $\nabla c^{\prime \prime }$ and $\nabla \xi^{\prime \prime }$ is fundamentally different to that between $\nabla Y_{F}^{\prime \prime }$ and $\nabla \xi^{\prime \prime }$. The behaviour of $\widetilde{{\varepsilon_{Y\xi } }}$ is found to be consistent with previous findings by Malkeson & Chakraborty (2010a, 2011b). The findings of Fig. 3 indicate that it might be necessary to solve a modelled transport equation for the closures of $\widetilde{{\varepsilon_{c\xi } }}$ and $\widetilde{{\varepsilon_{Y\xi } }}$. The closures of the unclosed terms of the transport equation of $\widetilde{{\varepsilon_{Y\xi } }}$ have been discussed elsewhere (Malkeson and Chakraborty, 2011b) and this analysis will henceforth focus on the closures of the unclosed terms of the $\widetilde{{\varepsilon_{c\xi } }}$ transport equation.

Fig. 3

Variations of $\{ \widetilde{{\varepsilon_{c\xi } }}$ and $\widetilde{{\varepsilon_{Y\xi } }}\} \times \delta_{st} /S_{{b\left( {\phi = 1} \right)}} \xi_{st}^{2}$ (solid lines) along with the predictions of the linear relaxation model for $C_{c\xi } = 3.0$ and $C_{Y\xi } = 3.0$ (dash-dot lines) with $\tilde{c}$ across the flame brush for (a–f) cases A-F

Statistical Behaviours of the Unclosed Terms of the $\varvec{\widetilde{{\varepsilon_{c\xi } }}}$ Transport Equation.

The variations of the terms appearing on the right-hand side of the $\widetilde{{\varepsilon_{c\xi } }}$ transport equation (see Eq. 8), across the flame brush for all cases are shown in Fig. 4. It is evident from Fig. 4 that the magnitude of molecular diffusion $D_{1}$ remains negligible in all cases. The contribution of turbulent transport $T_{1}$ plays a significant role only for the small $u^{\prime } /S_{{b\left( {\phi = 1} \right)}}$ cases but its importance diminishes as the turbulence intensity increases. The remaining terms (i.e. $T_{2}$, $T_{3}$, $T_{4}$, $- D_{2}$) play leading order roles in the evolution of $\widetilde{{\varepsilon_{c\xi } }}$ and have similar orders of magnitude for all cases considered here. The contribution of density variation $T_{2}$ assumes mostly positive values for a major part of the flame brush. The term representing the scalar turbulence interaction $T_{3}$ takes a predominantly negative value throughout the flame brush in these cases with a similar magnitude to that of $T_{2}$. The combined contribution of chemical reaction rate and mixture inhomogeneity $T_{4}$ assumes predominantly positive values towards the unburned gas side of the flame brush before becoming weakly negative towards the burned gas side of the flame brush. The molecular dissipation term $- D_{2}$ exhibits predominantly negative values but local positive values can be discerned on the burned gas side of the flame brush for case B and on the unburned gas side of the flame brush for case E. In cases (A–D) the terms $T_{3} ,T_{4} - D_{2}$ play leading order roles but in these cases $T_{4}$ predominantly assumes negative values for a major part of the flame brush.

Fig. 4

Variations of $\left\{ {T_{1} ,T_{2} ,T_{3} ,T_{4} ,D_{1} , - D_{2} } \right\} \times D_{0}^{2} /\rho_{0} S_{{b\left( {\phi = 1} \right)}}^{4} \xi_{st}^{2}$ with $\tilde{c}$ across the flame brush for the $\widetilde{{\varepsilon_{c\xi } }}$ transport equation in cases (a–f) A-F

Replacing $c$ by $Y_{F}$ ($\dot{\omega }_{c}$ by $\dot{\omega }_{F}$) and setting $A_{\xi } = 0$ in Eqs. 8 and 9 yields the transport equation of $\widetilde{{\varepsilon_{Y\xi } }}$ (see Malkeson and Chakraborty (2011b) for the full equation). The variations of the terms appearing on the right-hand side of the $\widetilde{{\varepsilon_{Y\xi } }}$ transport equation across the flame brush for all cases are shown in Fig. 5. A comparison between Figs. 4 and 5 reveals that the evolution of $\widetilde{{\varepsilon_{Y\xi } }}$ is fundamentally different to that of $\widetilde{{\varepsilon_{c\xi } }}$. Most notably, $T_{3}$ acts as a source term and $- D_{2}$ acts as a sink term in the unburned gas for the $\widetilde{{\varepsilon_{Y\xi } }}$ transport with approximately similar magnitudes. However, the magnitude of the sink term exceeds that of the source term in all cases due to the nature of decaying turbulence. The behaviours of the terms of the $\widetilde{{\varepsilon_{Y\xi } }}$ transport equation were discussed in detail in Malkeson and Chakraborty (2011b) and thus will be not be elaborated further in this analysis. The closures of the unclosed terms of the $\widetilde{{Y_{F}^{\prime \prime } \xi^{\prime \prime } }}$ transport equation were previously proposed by Malkeson and Chakraborty (2011b) but the observations made from Figs. 4 and 5 indicate that those closures cannot be used for the closures of the unclosed terms of the $\widetilde{{c^{\prime \prime } \xi^{\prime \prime } }}$ transport equation.

Fig. 5

Variations of $\left\{ {D_{1} ,T_{1} ,T_{2} ,T_{3} ,T_{4} , - D_{2} } \right\} \times D_{0}^{2} /\rho_{0} S_{{b\left( {\phi = 1} \right)}}^{4} \xi_{st}^{2}$ with $\tilde{c}$ across the flame brush for the $\widetilde{{\varepsilon_{Y\xi } }}$ transport equation in cases (a–f) A-F

The observations made from Fig. 4 can further be substantiated using a scaling analysis where the density is scaled by the unburned gas density $\rho_{0}$, the mean velocity is scaled using a reference mean velocity scale $U_{ref}$, the fluctuating velocity components are scaled by $S_{b}$, spatial derivatives of the mean quantities are scaled by $\ell$, whereas spatial derivatives of fluctuating quantities are scaled by $\delta_{st}$ following Swaminathan and Bray (2005). The assumptions yield the following scaling estimates for the terms shown in Fig. 4:

$$ T_{11} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{{ - \frac{1}{2}}} Da^{{ - \frac{1}{2}}} } \right)\;T_{12} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{ - 1} Da^{ - 1} } \right);\;T_{13} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{ - 1} Da^{ - 1} } \right) $$

$$ T_{21} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}} \right), T_{22} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{ - 1} Da^{ - 1} } \right) $$

$$ T_{31}^{\left( i \right)} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{{ - \frac{1}{2}}} Da^{{ - \frac{1}{2}}} } \right),T_{31}^{{\left( {ii} \right)}} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{{ - \frac{1}{2}}} Da^{{ - \frac{1}{2}}} } \right), T_{32} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}} \right) $$

$$ T_{33} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}\frac{{U_{ref} }}{{S_{b} }}Re^{{ - \frac{1}{2}}} Da^{{ - \frac{1}{2}}} } \right), T_{41} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}} \right);\;T_{42} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{{ - \frac{1}{2}}} Da^{{ - \frac{1}{2}}} } \right) $$

$$ D_{1} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{ - 1} Da^{ - 1} } \right), D_{21} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}} \right);\;D_{22} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{ - 2} Da^{ - 2} } \right) $$

(11(i))

Alternatively, following Tennekes and Lumley (1972) and Mantel and Borghi (1994), if the turbulent velocity fluctuations are scaled using $u^{\prime }$, the mean gradients are scaled using the integral length scale $\ell$, the length scale associated with the gradient of fluctuating velocity and mass fractions are scaled using the Taylor micro-scale $\lambda_{T}$, and the fluctuations of density gradient and reaction rate gradient are scaled with respect to $\delta_{st}$, it is possible to obtain:

$$ T_{11} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}} \right)\;T_{12} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{ - 1/2} } \right);\;T_{13} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{ - 1/2} } \right) $$

$$ T_{21} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\lambda_{T} \delta_{st} }}} \right)\sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{3/4} Ka^{ - 3/2} } \right), \;T_{22} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{ - 1/2} Ka^{ - 1} } \right) $$

$$ T_{31}^{\left( i \right)} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}} \right), T_{31}^{\left( i \right)} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}} \right),\;T_{32} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{1/2} } \right) $$

$$ T_{33} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}\frac{{U_{ref} }}{{u^{\prime}}}} \right), T_{41} \sim \sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\lambda_{T} \delta_{st} }}} \right)\sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{3/4} Ka^{ - 3/2} } \right);\;T_{42} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{{\prime}{2}} }}{{\ell^{2} }}{\text{Re}}^{ - 1/2} Ka^{ - 1} } \right) $$

$$ D_{1} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{ - 1} } \right) $$

(11(ii))

Malkeson and Chakraborty (2011b) argued that the second derivatives of the mass fraction and mixture fraction fluctuations are scaled with respect to the dissipation cut-off scale $\eta_{D}$, which can be taken to be equal to the Obukhov-Corrsin scale $\left( {D^{3} /\tilde{\varepsilon }} \right)^{3/4}$ in the thin reaction zones regime (Peters, 2000). As the Schmidt number $Sc$ remains of the order of unity (i.e. $Sc = 0.7$), it is possible to scale $D_{21}$ and $D_{22}$ as:

$$ D_{21} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{1/2} } \right);D_{22} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{\ell^{2} }}{\text{Re}}^{ - 2} } \right) $$

(11(iii))

In order to demonstrate the applicability of the scaling relations given by Eqs. 11i-iii, the variations of different components of $T_{1}$, $T_{2}$, $T_{3}$, $T_{4}$, $( - D_{2}$) with $\tilde{c}$ are exemplarily shown in Fig. 6 for cases E and F. The same qualitative behaviour has been observed for the other cases, so they are not explicitly shown here for the sake of conciseness. It can be seen from Fig. 6 that all three components $T_{11} , T_{12}$ and $T_{13}$ contribute comparably to $T_{1}$ for the moderate values of $Re_{t}$ simulated here. Equation 11 indicates that the contributions of $T_{12}$ and $T_{13}$ diminish with increasing $Re_{t}$, and $T_{11}$ becomes the dominant contributor to $T_{1}$ for high values of $Re_{t}$ because of $T_{11} /T_{12} \sim O\left( {Re_{t}^{1/2} } \right)$ and $T_{11} /T_{13} \sim O\left( {Re_{t}^{1/2} } \right)$. Moreover, Eqs. 11i and ii reveal that the magnitudes of $D_{1}$ and $T_{1}$ become increasingly insignificant in comparison to $T_{2} ,T_{3} ,T_{4}$ and $\left( { - D_{2} } \right)$ with increasing $Re_{t}$, and the leading order contributions arise from the terms $T_{2} ,T_{3} ,T_{4}$ and $( - D_{2}$). This conclusion is consistent with the observations made from Fig. 4. Figure 6 further shows that $T_{2} \approx T_{21}$, and this is supported by Eqs. 11i and 11ii indicating the weakening of $T_{22}$ with increasing $Re$ and/or $Da$. Equation 11 indicates that $T_{32}$ acts as a leading order term, and the contributions $T_{31}$ and $T_{33}$ weaken with increasing $Re$ and/or $Da$. It can be seen from Fig. 6 that that $T_{32}$ is the dominant contributor to $T_{3}$ but in this case $T_{31}$ and $T_{33}$ play non-negligible roles due to small values of $Da$ (i.e. $Da < 1$). Equation 5 suggests that $T_{41}$ is expected to dominate over $T_{42}$, which is consistent with the results shown in Fig. 6. Finally, Eqs. 11i and 11iii show that $D_{21}$ is the dominant term in $D_{2}$, with the contribution of $D_{22}$ weakening with increasing $Re$ and/or $Da$, which is consistent with the variations shown in Fig. 6. The scaling estimates based on Eq. 11 and their validation based on simulation results will play a key role for the purpose of model development for $T_{1} ,T_{2} ,T_{3} ,T_{4}$ and $( - D_{2}$) for the $\widetilde{{\varepsilon_{c\xi } }}$ transport equation.

Fig. 6

Variations of the different components of {$T_{1}$, $T_{2}$, $T_{3}$, $T_{4}$, $- D_{2} \}$ with $\tilde{c}$ across the flame brush for cases E (1st column) and F (2nd column)

Modelling of the Turbulent Transport Term $\varvec{T_{1}}$.

It can be seen from Eq. 9i that the modelling of $T_{1}$ depends on the closure of $T_{11}$ because $T_{12}$ and $T_{13}$ are closed in the context of second-moment closure as the scalar fluxes $\overline{{\left( {\rho u_{j}^{\prime \prime } c^{\prime \prime } } \right)}}$ and $\overline{{\left( {\rho u_{j}^{\prime \prime } \xi^{\prime \prime } } \right)}}$ are needed for the purpose of solving the transport equations of $\tilde{c}$ and $\tilde{\xi }$, respectively. Furthermore, it can be seen from Eq. 11 that the magnitudes of $T_{12}$ and $T_{13}$ are expected to be smaller than that of $T_{11}$ for high values of $Re_{t}$. Thus, the modelling of $T_{11}$ is the key to the closure of $T_{1}$ and therefore, the modelling of $T_{11}$ will be discussed in this sub-section. Equation 9i further indicates that $T_{11}$ closure depends on the modelling of $\overline{{\rho u_{j}^{\prime \prime } \varepsilon_{c\xi } }}$. The simplest closure that can be used for $\overline{{\rho u_{j}^{\prime \prime } \varepsilon_{c\xi } }}$ is the usual gradient hypothesis which can be expressed as:

$$ \overline{{\rho u_{j}^{^{\prime\prime}} \varepsilon_{c\xi } }} = - \frac{{\mu_{{\text{t}}} }}{{\sigma_{c\xi } }}\frac{{\partial \tilde{\varepsilon }_{c\xi } }}{{\partial x_{j} }} $$

(12)

where $\mu_{{\text{t}}} = \overline{\rho }C_{\mu } \tilde{k}^{2} /\tilde{\varepsilon }$ is the eddy viscosity and $\sigma_{c\xi }$ is the appropriate turbulent Schmidt number. The predictions of Eq. 12 with $\sigma_{c\xi } = 1.0$ are compared to $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$ (i.e. the only non-zero component of $\overline{{\rho u_{j}^{\prime \prime } \varepsilon_{c\xi } }}$) extracted from DNS data in Fig. 7 for the cases considered here. It can be seen from Fig. 7 that Eq. 12 does not adequately capture both qualitative and quantitative behaviours for a major part of the flame brush especially for small values of $u^{\prime } /S_{{b\left( {\phi = 1} \right)}}$ towards the burned gas side of the flame brush. The different sign of the prediction of Eq. 12 in comparison to $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$ extracted from DNS data is indicative of the counter-gradient transport. The effects of counter-gradient transport become strong within the flame brush at the locations where the effects of thermal expansion are strong (Veynante et al., 1997) and therefore the discrepancy between $\overline{{\rho u_{j}^{\prime \prime } \varepsilon_{c\xi } }}$ obtained from DNS data and the prediction of Eq. 12 are particularly prominent from the middle to the burned gas side of the flame brush. Therefore, Eq. 12 cannot be considered as a general model for $\overline{{\rho u_{j}^{\prime \prime } \varepsilon_{c\xi } }}$, and an ideal model for $\overline{{\rho u_{j}^{\prime \prime } \varepsilon_{c\xi } }}$ should be able to capture both gradient and counter-gradient transport. In order to meet this objective, a new for $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$ has been proposed in the following manner:

$$ \overline{{\rho u_{1}^{\prime \prime} \varepsilon_{c\xi} }} = - g\frac{{\mu_{t}}}{{\sigma_{c\xi} }}\frac{{\partial {\widetilde{\varepsilon_{c\xi}}}}}{{\partial x_{1}}} - \left( {1 - g} \right)\frac{{\overline{{(\rho u_{1}^{\prime \prime } c^{\prime \prime} }} ) \left( {\overline{{\rho u_{1}^{\prime \prime} \xi^{\prime \prime} }} } \right) }}{{\overline{\rho }\sqrt {\tilde{k}} \sqrt {\widetilde{{c^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}} }}\widetilde{\varepsilon }_{\xi } \frac{{\widetilde{\varepsilon_{c\xi} }}}{{\sqrt {|{\widetilde{\varepsilon_{c\xi } |} }}}} $$

(13(i))

where

$$ g = {\text{exp}}\left( { - C\left[ {\left( {\frac{{\rho_{0} }}{{\overline{\rho }_{b} }} - 1} \right)\frac{{\overline{S}_{b} }}{{\sqrt {\tilde{k}} }}} \right]^{2} } \right)\;{\text{with}}\;C = 0.5 $$

(13(ii))

Fig. 7

Variations of $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }} \times D_{0} /\rho_{0} S_{{b\left( {\phi = 1} \right)}}^{3}$ with $\tilde{c}$ along with the predictions of Eqs. 12 and 13 for cases A-F (a–f)

The mean burned gas density and the mean laminar burning velocity are evaluated as (Domingo et al., 2002):

$$ \overline{\rho }_{b} = \mathop \smallint \limits_{{\xi_{l} }}^{{\xi_{u} }} \rho_{b} \left( \xi \right)P\left( \xi \right)d\xi \;\text{and}\;\overline{S}_{b} = \mathop \smallint \limits_{{\xi_{l} }}^{{\xi_{u} }} S_{b} \left( \xi \right)P\left( \xi \right)d\xi $$

(13(iii))

Here, $S_{b} \left( \xi \right)$ and $\rho_{b} \left( \xi \right)$ are the laminar burning velocity and burned gas density expressed as a function of mixture fraction $\xi$, respectively, $P\left( \xi \right)$ is the probability density function (PDF) of $\xi$, and the lower and upper limits of mixture fraction are given by $\xi_{l}$ and $\xi_{u}$, respectively. The PDF of $\xi$ can be modelled using a $\beta$-function, which was discussed elsewhere (Poinsot and Veynante, 2001; Malkeson et al., 2013) and thus will not be repeated here. The term $- \overline{{(\rho u_{1}^{\prime \prime } c^{\prime \prime } }} ) \left( {\overline{{\rho u_{1}^{\prime \prime } \xi^{\prime \prime } }} } \right) \tilde{\varepsilon }_{\xi } \tilde{\varepsilon }_{c\xi } /[\overline{\rho }\sqrt {\tilde{k}} \sqrt {|\tilde{\varepsilon }_{c\xi } |} \sqrt {\widetilde{{c^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}} ]$ is dimensionally consistent with $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$ and the inclusion of $- \overline{{(\rho u_{1}^{\prime \prime } c^{\prime \prime } }} ) \left( {\overline{{\rho u_{1}^{\prime \prime } \xi^{\prime \prime } }} } \right)/\left[ {\overline{\rho }\sqrt {\widetilde{{c^{\prime \prime 2} }}} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}} } \right]$ ensures that $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$ assumes the sign depending on the nature of the transport (i.e. whether counter-gradient or gradient) behaviour of $\overline{{(\rho u_{1}^{\prime \prime } c^{\prime \prime } }} )$ because $\left( {\overline{{\rho u_{1}^{\prime \prime } \xi^{\prime \prime } }} } \right)$ predominantly exhibits gradient type transport (i.e. $- \left( {\overline{{\rho u_{1}^{\prime \prime } \xi^{\prime \prime } }} } \right) = (\mu_{t} /\sigma_{\xi } )\partial \tilde{\xi }/\partial x_{1}$ with $\sigma_{\xi }$ being the turbulent Schmidt number), as $\xi$ is a passive scalar. The term $\left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)\overline{S}_{b} /\sqrt {\tilde{k}}$ is representative of the Bray number (Veynante et al., 1997) for turbulent stratified combustion. It was discussed elsewhere (Veynante et al., 1997; Chakraborty and Cant, 2009a, b) that counter-gradient (gradient) type transport is obtained when the Bray number (i.e. $\propto \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)\overline{S}_{b} /\sqrt {\tilde{k}}$) is greater (smaller) than unity (Veynante et al., 1997). A value of $\left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)\overline{S}_{b} /\sqrt {\tilde{k}} \gg 1$ suggests a situation where the flame normal acceleration due to thermal expansion overcomes the effects of turbulent fluctuations, which lead to counter-gradient transport (Veynante et al., 1997). By contrast, turbulent velocity fluctuations overwhelm the effects of thermal expansion effects for $\left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)\overline{S}_{b} /\sqrt {\tilde{k}} \ll 1$ (Veynante et al., 1997). The involvement of $g$ in Eq. 13i ensures that the first term on the right-hand side of Eq. 13i signifying gradient type transport does not play a major role for $\left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)\overline{S}_{b} /\sqrt {\tilde{k}} \gg 1$ and the behaviour of $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$ is governed by the second term on the right-hand side of Eq. 13i. By contrast, the first term on the right-hand side plays the dominant role for small values of $\left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)\overline{S}_{b} /\sqrt {\tilde{k}}$ and ensures gradient type transport of $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$. The predictions of Eq. 13 are also shown in Fig. 7, which shows that Eq. 13 mostly captures the correct sign of $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$ extracted from DNS data more successfully than the gradient hypothesis model (i.e. Equation 12). This also suggests that Eq. 13 allows for the prediction of counter-gradient transport, which Eq. 12, by design, is not able to capture. Although there is a scope for improvement of the performance of Eq. 13 for cases with small initial values of $\ell_{\phi } /\ell$ (e.g. $\ell_{\phi } /\ell = 1.0$ cases A and B) irrespective of turbulence intensities, this model performs reasonably well for high initial values of $\ell_{\phi } /\ell$ (e.g. $\ell_{\phi } /\ell = 2.0$ and 3.0 cases). It is important to note that the mixing rate increases with decreasing $\ell_{\phi } /\ell$ (Hélie and Trouvé, 1998; Brearley et al., 2020) and thus one obtains an almost homogeneous mixture as a result of mixing for small values of $\ell_{\phi } /\ell$ (e.g. cases A and B). Therefore, the inaccurate predictions of Eq. 13 for cases A and B may not have a major implication on the modelling of turbulent stratified mixture combustion. Moreover, Eq. 11 suggests that $T_{1}$ is not the leading order contributor in the $\tilde{\varepsilon }_{c\xi }$ transport equation and this can be substantiated from Fig. 4. Thus, the local discrepancy between Eq. 13 predictions of $\overline{{\rho u_{1}^{\prime \prime } \varepsilon_{c\xi } }}$ may not have a major implication on the transport equation-based closure of $\tilde{\varepsilon }_{c\xi }$. It is important to note that the success of the model given by Eq. 13 depends on the closure of $\overline{{(\rho u_{1}^{\prime \prime } c^{\prime \prime } }} )$. The modelling of $\overline{{(\rho u_{1}^{\prime \prime } c^{\prime \prime } }} )$ was discussed elsewhere (Veynante et al., 1997; Chakraborty and Cant, 2009a,b, 2015; Malkeson and Chakraborty, 2012) in detail and thus is not discussed in this paper.

Modelling of the Density Variation Term $\varvec{T_{2}}$.

The variations of $T_{2}$ with $\tilde{c}$ for cases A-F are shown in Fig. 8a–f, respectively. The density variation term $T_{2}$ predominantly shows positive values for all cases considered here. The order of magnitude of $T_{2}$ can be estimated using $T_{2} \sim \overline{\rho }\tilde{\varepsilon }_{c\xi } \tilde{\varepsilon }_{c} \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)$ upon scaling $\dot{\omega }_{c}$ as $\dot{\omega }_{c} \sim \rho \varepsilon_{c}$ and $- \left( {D/\rho } \right)\left( {\partial p/\partial x_{i} } \right)\left( {\partial \xi /\partial x_{i} } \right)$ can be scaled as: $- \left( {D/\rho } \right)\left( {\partial p/\partial x_{i} } \right)\left( {\partial \xi /\partial x_{i} } \right)\sim \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)D\left( {\partial c/\partial x_{i} } \right)\left( {\partial \xi /\partial x_{i} } \right)\sim \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)\tilde{\varepsilon }_{c\xi }$. It is important to note that the qualitative behaviour of $T_{2}$ was found to be captured by $\overline{\rho }\tilde{\varepsilon }_{c\xi } \tilde{\varepsilon }_{c} \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)$ as dictated by the scaling analysis and a proportionality parameter $K$ is needed for the quantitative prediction. This yields the following model for $T_{2}$:

$$ T_{2} = K\overline{\rho }\tilde{\varepsilon }_{c\xi } \tilde{\varepsilon }_{c} \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right) $$

(14(i))

Fig. 8

Variations of $T_{2} \times D_{0}^{2} /\rho_{0} S_{{b\left( {\phi = 1} \right)}}^{4} \xi_{st}^{2}$ with $\tilde{c}$ along with the predictions of Eq. 14 for cases A-F (a–f)

It has been found that the proportionality parameter $K$ is not sensitive to the $\ell_{\phi } /\ell$ value, but it is a function of the turbulence intensity (or local turbulent Reynolds number). This is empirically expressed as:

$$ K = 0.1 + \frac{0.15}{{1 + {\text{exp}}\left( { - 0.5\left[ {Re_{L} - 15} \right]} \right)}} $$

(14(ii))

where $Re_{L} = \rho_{0} \tilde{k}^{2} /\mu_{0} \tilde{\varepsilon }$ is a measure of the turbulent local Reynolds number. The expression given by Eq. 14ii is one of the possibilities out of several possible ones but this functional form (i.e., $K = a_{1} + a_{2} /\left[ {1 + \exp \left( { - \left[ {a_{3} Re_{L} - a_{4} } \right]} \right)} \right]$) was chosen because it ensures that $K$ increases from 0.1 to an asymptotic value (i.e., $K = 0.25$) for $Re_{L} \to \infty$. The exact values of $a_{1} ,a_{2} ,a_{3}$ and $a_{4}$ are chosen based on a regression analysis based on $T_{2}$ and $\overline{\rho }\tilde{\varepsilon }_{c\xi } \tilde{\varepsilon }_{c} \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)$ extracted from DNS data. The practical applicability of the model is not expected to be sensitive to $a_{3}$ and $a_{4}$ because $Re_{L} \gg 15.0$ is obtained for most practical applications. The predictions of Eq. 14 are compared with $T_{2}$ extracted from DNS data in Fig. 8, which reveals that the density variation term $T_{2}$ can be reasonably predicted by the expression given by Eq. 14.

Modelling of the Scalar-Turbulence Interaction Term $\varvec{T_{3}}$.

In order to model the scalar-turbulence interaction term $T_{3}$, all the components of this term (i.e. $T_{31}$, $T_{32}$ and $T_{33}$) need to be closed. Therefore, modelling of each of the components of $T_{3}$ for the $\tilde{\varepsilon }_{c\xi }$ transport equation will be addressed in turn. The term $T_{31}$ is made up of two sub-terms $T_{31}^{\left( i \right)}$ and $T_{31}^{{\left( {ii} \right)}}$ as shown in Eq. 9iii. The statistical behaviours of $T_{31}^{\left( i \right)}$ and $T_{31}^{{\left( {ii} \right)}}$ are governed by the alignment of local strain rate eigendirections with reaction progress variable gradient and mixture fraction gradient respectively. It has been observed that the mixture fraction gradient aligns preferentially with the most compressive principal strain rate eigendirection. By contrast, reaction progress variable alignment with local strain rate eigendirection is dependent on the relative strengths of turbulent straining and the strain rate induced by heat release (Chakraborty and Swaminathan, 2007a; Chakraborty et al., 2009; Malkeson and Chakraborty, 2011c). The reaction progress variable gradient is shown to align with the most extensive principal strain rate when the strain rate induced by heat release overwhelms the effects of turbulent straining and vice versa (Chakraborty and Swaminathan, 2007a; Chakraborty et al., 2009; Malkeson and Chakraborty, 2011c). The terms $\overline{{\rho D\left( {\partial \xi^{\prime \prime } /\partial x_{i} } \right)\left( {\partial u_{i}^{\prime \prime } /\partial x_{j} } \right)}}$ and $\overline{{\rho D\left( {\partial c^{\prime \prime } /\partial x_{i} } \right)\left( {\partial u_{i}^{\prime \prime } /\partial x_{j} } \right)}}$ can be taken to scale with $\left( {\overline{{\rho u_{j}^{\prime \prime } \xi^{\prime \prime } }} } \right)\left( {\tilde{\varepsilon }/\tilde{k}} \right)$ and $\left( {\overline{{\rho u_{j}^{\prime \prime } c^{\prime \prime } }} } \right)\left( {\tilde{\varepsilon }/\tilde{k}} \right)$ based on previous modelling strategies adopted by Mantel and Borghi (1994) and Chakraborty et al. (2008), which yield the following model expression for $T_{31}$:

$$ T_{31} = T_{31}^{\left( i \right)} + T_{31}^{{\left( {ii} \right)}} = - C_{1} \left( {\overline{{\rho u_{j}^{\prime \prime } c^{\prime \prime } }} } \right)\frac{{\tilde{\varepsilon }}}{{\tilde{k}}}\frac{{\partial \tilde{\xi }}}{{\partial x_{j} }} - C_{2} \left( {\overline{{\rho u_{j}^{\prime \prime } \xi^{\prime \prime } }} } \right)\frac{{\tilde{\varepsilon }}}{{\tilde{k}}}\frac{{\partial \tilde{c}}}{{\partial x_{j} }} $$

(15)

where $C_{1}$ and $C_{2}$ are the model parameters. According to Swaminathan and Bray (2005) the order of magnitudes of $T_{31}^{\left( i \right)}$ and $T_{31}^{{\left( {ii} \right)}}$ are given by:

$$ - C_{1} \left( {\overline{{\rho u_{j}^{^{\prime\prime}} c^{\prime\prime}}} } \right)\frac{{\tilde{\varepsilon }}}{{\tilde{k}}}\frac{{\partial \tilde{\xi }}}{{\partial x_{j} }}\sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{{ - \frac{1}{2}}} Da^{{ - \frac{1}{2}}} } \right) $$

(16(i))

$$ - C_{2} \left( {\overline{{\rho u_{j}^{^{\prime\prime}} \xi^{\prime\prime}}} } \right)\frac{{\tilde{\varepsilon }}}{{\tilde{k}}}\frac{{\partial \tilde{c}}}{{\partial x_{j} }}{ }\sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}Re^{{ - \frac{1}{2}}} Da^{{ - \frac{1}{2}}} } \right) $$

(16(ii))

It is evident from Eqs. 16i and ii that the order of magnitudes of the model expressions are consistent with the order of magnitude estimates of $T_{31}^{\left( i \right)}$ and $T_{31}^{{\left( {ii} \right)}}$ presented in Eq. 11i. Moreover, the model expression given in Eq. 15 is also consistent with the order of magnitude estimates presented in Eq. 11ii when the scaling arguments of Tennekes and Lumley (1972) and Mantel and Borghi (1994) are adopted:

$$ - C_{1} \left( {\overline{{\rho u_{j}^{\prime \prime } c^{\prime \prime } }} } \right)\frac{{\tilde{\varepsilon }}}{{\tilde{k}}}\frac{{\partial \tilde{\xi }}}{{\partial x_{j} }}\sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{l^{2} }}} \right) $$

(16(i))

$$ - C_{2} \left( {\overline{{\rho u_{j}^{\prime \prime } \xi^{\prime \prime } }} } \right)\frac{{\tilde{\varepsilon }}}{{\tilde{k}}}\frac{{\partial \tilde{c}}}{{\partial x_{j} }} \sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{\prime 2} }}{{l^{2} }}} \right) $$

(16(ii))

The predictions of the model given by Eq. 15 are compared to $T_{31}$ obtained from DNS data in Figs. 9a–f for cases A-F, respectively, and it can be seen that Eq. 15 satisfactorily models $T_{31}$ when $C_{1} = 1.0$ and $C_{2} = 0.15$ are considered.

Fig. 9

Variations of $T_{31} \times D_{0}^{2} /\rho_{0} S_{{b\left( {\phi = 1} \right)}}^{4} \xi_{st}^{2}$ with $\tilde{c}$ along with the predictions of Eq. 15 with $C_{1} = 1.0$ and $C_{2} = 0.15$ for cases A-F (a–f)

The term $T_{32}$ is the dominant component of the scalar-turbulence interaction term $T_{3}$ (see Fig. 6 and scaling estimates given by Eq. 11ii) and thus its modelling is crucial to the modelling of the $\tilde{\varepsilon }_{c\xi }$ transport equation. The variations of $T_{32}$ with $\tilde{c}$ across the flame brush for cases A-F are shown in Figs. 10a-f, respectively, which shows that $T_{32}$ assumes both positive and negative values within the flame brush. The relative alignments of $\nabla c$ and $\nabla \xi$ with local principal strain rates effectively determine the behaviour and sign of $T_{32}$. It is well-known (Batchelor, 1959; Gibson, 1968; Kerr, 1985; Ashurst et al., 1987; Ruetsch and Maxey, 1991; Leonard and Hill, 1991; Nomura and Elgobashi, 1992) that the passive scalar gradient (e.g. $\nabla \xi$) preferentially aligns with the most compressive principal strain rate eigendirection. However, the reactive scalar gradient (e.g. $\nabla c$) exhibits preferential collinear alignment with the most compressive principal strain rate eigendirection when turbulent straining dominates over the strain rate arising from the flame normal acceleration, whereas a preferential alignment between the reactive scalar gradient and the most extensive principal strain rate eigendirection is obtained when the strain rate originating from flame normal acceleration overcomes turbulent straining (Chakraborty and Swaminathan, 2007a; Chakraborty et al., 2009; Malkeson and Chakraborty, 2011c). It was demonstrated earlier by Malkeson and Chakraborty (2011c) that $\nabla \xi$ continues to align with the most compressive principal strain rate eigendirection even when $\nabla c$ aligns with the most extensive principal strain rate eigendirection. Thus, the values and signs of $T_{32}$ are determined by the relative competition of the strain rates due to turbulence and flame normal acceleration. This also needs to be reflected in the model expression of $T_{32}$ and accordingly the following model expression is proposed here:

$$ T_{32} = \overline{\rho }\frac{{\tilde{\varepsilon }}}{{\tilde{k}}}\frac{{\tilde{\varepsilon }_{c\xi } }}{{\sqrt {|\tilde{\varepsilon }_{c\xi } |} }}\sqrt {\tilde{\varepsilon }_{c} } \left[ {C_{3} - C_{4} \left( {\frac{{\rho_{0} }}{{\overline{\rho }_{b} }} - 1} \right)Da_{L} } \right] $$

(17)

where $C_{3}$ and $C_{4}$ are the model parameters and $Da_{L} = \tilde{k}\overline{S}_{b} /\tilde{\varepsilon }\delta_{b}$ is the local Damköhler number with $\delta_{b} = 2D_{0} /\overline{S}_{b}$ being a measure of the thermal flame thickness. The first term on the right-hand side (i.e. $\overline{\rho }C_{3} \left( {\tilde{\varepsilon }/\tilde{k}} \right)\tilde{\varepsilon }_{c\xi } \sqrt {\tilde{\varepsilon }_{c} } /\sqrt {|\tilde{\varepsilon }_{c\xi } |}$) accounts for the alignment of scalar gradients with the most compressive principal strain rate eigendirection under the action of turbulent straining (~ $\tilde{\varepsilon }/\tilde{k}\sim u^{\prime } /\ell$). The second term on the right-hand side of Eq. 17 (i.e. $- \overline{\rho }C_{4} \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)Da_{L} (\tilde{\varepsilon }/\tilde{k})\tilde{\varepsilon }_{c\xi } \sqrt {\tilde{\varepsilon }_{c} } /\sqrt {|\tilde{\varepsilon }_{c\xi } |} = - \overline{\rho }C_{4} \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)(\overline{S}_{b} /\delta_{b} )\tilde{\varepsilon }_{c\xi } \sqrt {\tilde{\varepsilon }_{c} } /\sqrt {|\tilde{\varepsilon }_{c\xi } |}$) represents the effects of preferential collinear alignment of $\nabla c$ with the most extensive principal strain rate eigendirection under the action of strain rate induced by flame normal acceleration, which scales with $\left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)(\overline{S}_{b} /\delta_{b} )$ (Chakraborty and Swaminathan, 2007a; Chakraborty et al., 2009). The term $- \overline{\rho }C_{4} \left( {\rho_{0} /\overline{\rho }_{b} - 1} \right)Da_{L} \left( {\tilde{\varepsilon }/\tilde{k}} \right)\tilde{\varepsilon }_{c\xi } \sqrt {\tilde{\varepsilon }_{c} } /\sqrt {|\tilde{\varepsilon }_{c\xi } |}$ scales as $\left( {\rho_{0} S_{b}^{2} /\delta_{b}^{2} } \right)$ according to Swaminathan and Bray (2005). The effects of the strain rate are expected to decrease with increasing Karlovitz number (Chakraborty and Swaminathan, 2007b; Chakraborty et al., 2008, 2011), and thus the model parameter $C_{4}$ may have some dependence on the local Karlovitz number $Ka_{L} = \left( {\tilde{\varepsilon }\delta_{b} } \right)^{1/2} S_{b}^{ - 3/2}$. The predictions of Eq. 17 are shown in Figs. 10a–f where $C_{3} = 0.028$ and $C_{4} = 0.01/\left( {1 + Ka_{L} } \right)^{0.5}$ are used. For these choices of $C_{3}$ and $C_{4}$, the model given by Eq. 17 reasonably captures the behaviour of $T_{32}$ extracted from DNS data for most cases considered here, but there are local discrepancies between the model predictions and DNS data. However, it is worthwhile to recognise that Eq. 17 is the first attempt to model the term $T_{32}$ in the $\tilde{\varepsilon }_{c\xi }$ transport equation and there is a scope for further improvement of the modelling of $T_{32}$. It is also important to note that $C_{4}$ decreases with increasing $Ka_{L}$ and thus the second term on the right-hand side of Eq. 17 tends to weaken as the combustion regime approaches the broken reaction zone with the increase in the value of Karlovitz number.

Fig. 10

Variations of $T_{32} \times D_{0}^{2} /\rho_{0} S_{{b\left( {\phi = 1} \right)}}^{4} \xi_{st}^{2}$ with $\tilde{c}$ along with the predictions of Eq. 17 with $C_{3} = 0.028$ and $C_{4} = 0.01/\left( {1 + Ka_{L} } \right)^{0.5}$ for cases A-F (a–f)

The variations of $T_{33}$ with $\tilde{c}$ across the flame brush for cases A-F are shown in Fig. 11a–f respectively. Figure 11 indicates that $T_{33}$ assumes predominantly negative values for a major part of the flame brush, except for a small region on the burned and unburned gas sides of the flame brush in cases B and C, respectively (see Fig. 11b and c). For the statistically planar flames, $T_{33}$ takes the following form:

$$ T_{33} = - \overline{{\rho D\frac{{\partial c^{\prime \prime } }}{{\partial x_{1} }}\frac{{\partial \xi^{\prime \prime } }}{{\partial x_{1} }}}} \frac{{\partial \widetilde{{u_{1} }}}}{{\partial x_{1} }} - \overline{{\rho D\frac{{\partial c^{\prime \prime } }}{{\partial x_{1} }}\frac{{\partial \xi^{\prime \prime } }}{{\partial x_{1} }}}} \frac{{\partial \widetilde{{u_{1} }}}}{{\partial x_{1} }} $$

(18)

Fig. 11

Variations of $T_{33} \times D_{0}^{2} /\rho_{0} S_{{b\left( {\phi = 1} \right)}}^{4} \xi_{st}^{2}$ with $\tilde{c}$ along with the predictions of Eq. 18 with $C_{{T_{3} }} = 0.03$ for cases A-F (a–f)

Thus, the behaviour of $T_{33}$ is expected to be affected by $\overline{\rho }\tilde{\varepsilon }_{c\xi } \sim \overline{{\rho D(\partial c^{\prime \prime } /\partial x_{1} )(\partial \xi^{\prime \prime } /\partial x_{1} )}}$ and $\partial \widetilde{{u_{1} }}/\partial x_{1}$, and therefore $T_{33}$ is modelled as:

$$ T_{33} = - C_{{T_{3} }} \overline{\rho }\tilde{\varepsilon }_{c\xi } \frac{{\partial \widetilde{{u_{1} }}}}{{\partial x_{1} }} $$

(19)

where $C_{{T_{3} }}$ is a model parameter. The order of magnitude of Eq. 19 takes the following form according to Swaminathan and Bray (2005):

$$ - C_{{T_{3} }} \overline{\rho }\tilde{\varepsilon }_{c\xi } \frac{{\partial \widetilde{{u_{1} }}}}{{\partial x_{1} }}\sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}\frac{{U_{ref} }}{{S_{b} }}Re^{{ - \frac{1}{2}}} Da^{{ - \frac{1}{2}}} } \right) $$

(20)

A comparison between Eqs. 11i and 20 reveals that the model expression given by Eq. 19 is consistent with the order of magnitude of $T_{33}$. Moreover, the modelled expression given by Eq. 19 is also consistent with the order of magnitude estimate predicted by Eq. 11ii, as shown below:

$$ - C_{{T_{3} }} \overline{\rho }\tilde{\varepsilon }_{c\xi } \frac{{\partial \widetilde{{u_{1} }}}}{{\partial x_{1} }}\sim {\mathcal{O}}\left( {\frac{{\rho_{0} u^{{\prime}{2}} }}{{\ell^{2} }}\frac{{U_{ref} }}{{u^{\prime}}}} \right) $$

(21)

The predictions of Eq. 19 are compared to $T_{33}$ extracted from DNS data in Figs. 11a–f for cases A-F, respectively when $C_{{T_{3} }} = 0.03$. It can be seen from Fig. 11a–f that $C_{{T_{3} }} = 0.03$ yields satisfactory agreement with DNS data for all the cases considered here although Eq. 19 locally overpredicts the magnitude of the negative value at the middle of the flame brush in case A. It is worthwhile to note that Eq. 19 provides a simple expression as a first attempt towards the modelling of the $\tilde{\varepsilon }_{c\xi }$ transport equation, and therefore there will be further scope for improvement in the future.

Modelling of the Combined Reaction and Dissipation Contribution $\varvec{\left( {T_{4} - D_{2} } \right)}$.

The reaction rate and the molecular dissipation contributions of the $\tilde{\varepsilon }_{c}$ transport are often modelled by their combined contribution (Mantel and Borghi, 1994; Chakraborty et al., 2008, 2011). A similar approach has been adopted here following Malkeson and Chakraborty (2011b) for the $\tilde{\varepsilon }_{Y\xi }$ transport equation because $T_{4}$ and $\left( { - D_{2} } \right)$ may have larger magnitudes than that of $\left( {T_{4} - D_{2} } \right)$. This is particularly important because an imbalance created by the modelling inaccuracies of individual models for $T_{4}$ and $\left( { - D_{2} } \right)$ may not capture the qualitative behaviours of $\left( {T_{4} - D_{2} } \right)$. The variation of $\left( {T_{4} - D_{2} } \right)$ with $\tilde{c}$ has been found to be best qualitatively captured by the variation of the quantity $\overline{\rho }\tilde{\varepsilon }_{c\xi }$ throughout the flame brush in all cases. Moreover, $\left( {T_{4} - D_{2} } \right)$ is dimensionally inconsistent with $\overline{\rho }\tilde{\varepsilon }_{c\xi }$ and a relevant time scale must be considered, which is estimated to be $\tilde{\varepsilon }_{\xi } /\widetilde{{\xi^{\prime \prime 2} }}$, which yields the following model of $\left( {T_{4} - D_{2} } \right)$:

$$ T_{4} - D_{2} = \overline{\rho }\frac{{\tilde{\varepsilon }_{c\xi } \tilde{\varepsilon }_{\xi } }}{{\widetilde{{\xi^{\prime \prime 2} }}}}\left[ {1 + \left( {\frac{{\tilde{c}}}{{1 + \tilde{c}}}} \right)^{2} } \right]\left[ {C_{D1} \left( {0.2m - \tilde{c}} \right) - C_{D2} m} \right]\;\text{with}\;m = \frac{{\overline{S}_{b} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}/D_{0} \tilde{\varepsilon }_{\xi } } }}{{1 + \overline{S}_{b} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}/D_{0} \tilde{\varepsilon }_{\xi } } }} $$

(22)

Here, $C_{D1}$ and $C_{D2}$ are the model parameters. The parameter $\left[ {1 + \left( {\tilde{c}/\{ 1 + \widetilde{c\}}} \right)^{2} } \right]\left[ {C_{D1} \left( {0.2m - \tilde{c}} \right) - C_{D2} m} \right]$ allows for the correct prediction of the qualitative trend of $\left( {T_{4} - D_{2} } \right)$ across the flame brush. The parameter $\overline{S}_{b} \sqrt {\widetilde{{\xi^{\prime \prime 2} }}/D_{0} \tilde{\varepsilon }_{\xi } }$ accounts for the length scale of mixture inhomogeneity normalised by a characteristic flame thickness $(\sim D_{0} /\overline{S}_{b}$).

The order of magnitude of the model expression given by Eq. 22 can be estimated in the following manner according to the scaling arguments proposed by Swaminathan and Bray (2005):

$$ (T_{4} - D_{2} ) = \overline{\rho }\frac{{\tilde{\varepsilon }_{c\xi } \tilde{\varepsilon }_{\xi } }}{{\widetilde{{\xi^{\prime \prime 2} }}}}\left[ {1 + \left( {\frac{{\tilde{c}}}{{1 + \tilde{c}}}} \right)^{2} } \right]\left[ {C_{D1} \left( {0.2m - \tilde{c}} \right) - C_{D2} m} \right]\sim {\mathcal{O}}\left( {\frac{{\rho_{0} S_{b}^{2} }}{{\delta_{st}^{2} }}} \right) $$

(23)

It can be seen from Eqs. 22 and 11i the order of magnitude of the modelled expression is consistent with the order of magnitudes of $T_{4}$ and $\left( { - D_{2} } \right)$. On scaling $\tilde{\varepsilon }_{\xi }$ as: $\tilde{\varepsilon }_{\xi } \sim 1/t_{D}$, where $t_{D}$ can be expressed as: $t_{D} \sim \eta_{D}^{2} /D$, the right-hand side of Eq. 23 yields an order of magnitude estimate of $\left( {u^{^{\prime}2} /l^{2} } \right)Re_{t}^{1/2}$, which is consistent with the leading order scaling estimate of the combined contribution of $(T_{4} - D_{2} )$ as predicted by Eqs. 11ii.

The performance of the model given by Eq. 22 for all cases considered here is shown in Fig. 12a–f for cases A-F, respectively. It demonstrates that the model satisfactorily captures the behaviour and order of magnitude of $(T_{4} - D_{2} )$ for all cases when $C_{D1} = 0.35$ and $C_{D2} = 0.4$ are taken although this model (i.e. Equation 22) does not adequately capture positive values of $\left( {T_{4} - D_{2} } \right)$. Moreover, $0.35\overline{\rho }\left( {\tilde{\varepsilon }_{c\xi } \tilde{\varepsilon }_{\xi } /\widetilde{{\xi^{\prime \prime 2} }}} \right)\left[ {1 + \left( {\tilde{c}/\{ 1 + \tilde{c}\} } \right)^{2} } \right]\left( {0.2m - \tilde{c}} \right)\;\text{and}\; - 0.40\overline{\rho }\left( {\tilde{\varepsilon }_{c\xi } \tilde{\varepsilon }_{\xi } /\widetilde{{\xi^{\prime \prime 2} }}} \right)\left[ {1 + \left( {\tilde{c}/\{ 1 + \tilde{c}\} } \right)^{2} } \right]m$ can be considered to be the modelled expressions of $T_{4}$ and $\left( { - D_{2} } \right)$, respectively, which is not explicitly shown here for the sake of brevity.

Fig. 12

Variations of $\left( {T_{4} - D_{2} } \right) \times D_{0}^{2} /\rho_{0} S_{{b\left( {\phi = 1} \right)}}^{4} \xi_{st}^{2}$ with $\tilde{c}$ along with the predictions of Eq. 22 with $C_{D1} = 0.35$ and $C_{D2} = 0.4$ for cases A-F (a–f)

6 Conclusions

A Direct Numerical Simulations (DNS) database of freely propagating statistically planar turbulent flames propagating into stratified mixture has been utilised in order to analyse the statistical behaviour of the cross-scalar dissipation rate $\tilde{\varepsilon }_{c\xi }$ transport. The statistical behaviours of the different terms of the $\tilde{\varepsilon }_{c\xi }$ transport equation have been explained based on physical arguments and the relative contributions of these terms to the overall $\tilde{\varepsilon }_{c\xi }$ transport have been explained based on detailed scaling arguments. The modelling of the unclosed terms of the $\tilde{\varepsilon }_{c\xi }$ transport equation has been considered in the context of Reynolds Averaged Navier–Stokes (RANS) simulations. It has been found that the density variation term $T_{2}$, scalar-turbulence interaction term $T_{3}$, reaction rate contribution $T_{4}$ and the molecular dissipation term $\left( { - D_{2} } \right)$ remain the leading order contributors for all cases considered here. It has been observed in all cases that the magnitude of the turbulent transport term $T_{1}$ remains small in comparison to the leading order contributors. Suitable model expressions have been identified for the contributions of the unclosed terms (i.e. $T_{1} ,T_{2} ,T_{3} ,T_{4}$ and $- D_{2}$) of the $\tilde{\varepsilon }_{c\xi }$ transport equation based on a priori analysis of DNS data. These model expressions are proposed in such a manner that the underlying physics and the order of magnitude of the unclosed term in question are adequately addressed. The predictions of the proposed models have been assessed with respect to the corresponding quantities extracted from DNS data. The new models are found to predict the unclosed terms of the $\tilde{\varepsilon }_{c\xi }$ transport equation satisfactorily for all the cases considered here.

It is worthwhile to consider that this analysis is one of the first attempts to model the unclosed terms of the $\tilde{\varepsilon }_{c\xi }$ transport equation and thus there is some scope for improvement in the future for some of the model expressions. Admittedly, the closure of the unclosed terms of the $\tilde{\varepsilon }_{c\xi }$ transport equation involves a number of model parameters but the number of parameters used for the closures of the unclosed terms of the $\tilde{\varepsilon }_{c\xi }$ transport equation is comparable to those used for the closure of the $\tilde{\varepsilon }_{c}$ (Mantel and Borghi, 1994; Chakraborty et al., 2008, 2011) and $\tilde{\varepsilon }_{Y\xi }$ (Malkeson and Chakraborty, 2013) transport equations. Moreover, the effects of the differential diffusion rate of heat and mass and detailed chemical kinetics are not addressed in the current analysis. In order to attain a more comprehensive understanding of the cross-scalar dissipation rate transport, the effects of detailed chemistry and differential diffusion will need to be studied in detail in the future for higher values of turbulent Reynolds numbers. Undoubtedly, the models proposed here need to be implemented in RANS simulations. However, the performance of the $\tilde{\varepsilon }_{c\xi }$ modelling cannot be assessed in isolation because the modelling inaccuracies involved with $\tilde{k},\tilde{\varepsilon },$ $\tilde{\varepsilon }_{c}$ and $\tilde{\varepsilon }_{\xi }$ could potentially affect the predictions of RANS simulations in a complex manner and it is possible that some modelling inaccuracies will either augment each other or cancel with other. In a-priori analysis, such as the one carried out in this study, the true capability of the models is demonstrated but the interaction between the modelling error and numerical error (one of which originates due to discretisation error using a coarser RANS grid) warrants a-posteriori assessment of the models. It is important to note that only the model expressions for $T_{1} ,T_{31}$ and $T_{33}$ (i.e. Equations 12, 13, 15, 16) involve gradients of Favre-mean quantities which need to be evaluated on RANS grids. It is not possible to estimate the numerical error aspect due to discretisation error involving a coarser RANS grid in this type of a-priori analysis because the flame brush thickness scales with the integral length scale of turbulence and therefore the RANS grid size becomes comparable to the size of the simulation domain. Furthermore, the modelling and numerical errors interact not in a straightforward manner in RANS simulations. All of these aspects need to be accounted for a posteriori assessment of the cross-scalar dissipation rate closure based on RANS simulations for configurations in which experimental data is available for comparison with simulation results. This will also form the basis of future analyses on turbulent stratified mixture combustion.