Large-Eddy Simulation Study of Ultra-High Fuel Injection Pressure on Gasoline Sprays

Abstract

The development of gasoline spray at ultra-high injection pressures was analyzed using Large-Eddy simulation (LES). Two different nozzle hole geometries, divergent and convergent shape, were considered to inject the fuel at injection pressures ranging from 200 to 1500 bar inside a constant volume spray chamber maintained at atmospheric conditions. The discrete droplet phase was treated using a Lagrangian formulation together with the standard spray sub-models. The numerical results were calibrated by reproducing experimentally observed liquid penetration length and efforts were made to understand the influence of ultra-high injection pressures on the spray development. The calibrated model was then used to investigate the impact of ultra-high injection pressures on mean droplet size and droplet size distribution. In addition, the spray-induced large-scale eddies and entrainment rate were evaluated at different ultra-high injection pressures. Overall, simulation results showed a good agreement with available measurement data. At ultra-high injection pressures mean droplet sizes were significantly reduced and comprised very high velocities. Integral length scales of spray-induced turbulence and air entrainment rate into the spray were larger at higher injection pressure compared to lower ones.

Graphic abstract

Introduction

Gasoline direct injection (GDI) seems to have great potential to meet future legislation on fuel consumption and exhaust emissions. The main challenge for engine developers is to provide an ignitable fuel-air mixture prior to an ignition process leading to a stable, clean and efficient combustion process. Different concepts were suggested to achieve this goal such as spray-guided direct injection, turbo-charging, nozzle design optimization and high injection pressure. Among these concepts, later seems to be most promising as fuel-air mixture formation is substantially influenced by fuel injection pressure and nozzle geometry. High injection pressure is beneficial not only for mixing but also for enhancing turbulence (Rao et al. 2019) and reducing soot formation (Pickett and Siebers 2004). Hence, it is important to understand the influence of injection pressure and nozzle geometry on the fuel atomization.

The mixture preparation strategy in a GDI engine is highly depend on the turbulence level inside the combustion chamber. Inside the combustion cylinder, the turbulence is mostly generated from a large-scale gas motion which breaks down into small-scale vortices. However, there is another potential source of turbulence which often neglected known as spray-induced turbulence. This turbulence is produced when a fuel spray with a high injection pressure imposes locally high velocities and large velocity gradients, which can be used to promote a better fuel-air mixing. An effective way to enhance the so-called spray-induced turbulence is through reducing the nozzle orifice diameter and/or increasing the fuel injection pressure. A reduced orifice diameter leads to smaller droplets (large surface area) and subsequently faster evaporation (Vuorinen et al. 2011). However, the reduced orifice diameter delivers other important characteristics such as short spray penetration which may adversely influences the spatial distribution of fuel (Jacobsson and Chomiak 1997). Whereas, increasing fuel injection pressure can significantly improve spray characteristics (atomization, spatial fuel distribution) and promote air-entrainment in the spray.

Because of such benefits, fuel injection pressure in injection system has been increased since the introduction of GDI technique. In the beginning, fuel injection systems were operated in the range of 50-100 bar injection pressure. However, the sprays generated from these injectors were very sensitive to the thermodynamic and operating conditions (Jones 2010). Afterwards, the increment of fuel injection pressure was due to the requirement of better fuel atomization (Waltner et al. 2006). Over the last decade maximum fuel injection pressure has been increased up to 250–300 bar. Considering the potential of high-pressure injection, it is expected that fuel injection pressure will increase to 400 bar by 2020 and 600 bar by 2025.

Based on the past trend, it can be concluded that there is an interest in the spray formed at high and ultra-high injection pressure, but detailed investigations on the influence of ultra-high injection pressure on spray formation are rare. Some experimental studies in the context of gasoline spray at ultra-high injection pressure can be found in Kim et al. (2013), Payri et al. (2012). Matousek et al. (2013) investigated the influence of injection pressure on particulate number (PN) and concluded that the PN could reduce by 50% at 300 bar compared to 200 bar injection pressure. Medina et al. (2018) studied gasoline fuel sprays at injection pressures between 300 to 1500 as a function of chamber pressure using high-speed imaging technique and concluded the spray characteristics. Buri et al. (2010) demonstrated the influence of high-pressure fuel injection on mixture preparation and subsequent soot formation. The results show that the injection duration and vaporization time were significantly reduced at 1000 bar compared to 200 bar injection pressure. At 200 bar injection pressure, fuel-mass is not completely prepared at the start of combustion and therefore responsible for high soot levels.

Efforts to analyze the characteristics of spray structure at high injection pressure by experimental techniques are valuable, however, detailed information of atomization characteristics, turbulence and air entrainment is still needed. Previous studies have been mainly focused on macroscopic spray characteristics (spray tip penetration, spray cone-angle and spray area) and relatively limited research relevant to fuel atomization, droplet size distribution, influence of nozzle geometry and spray-induced turbulence at high injection pressure was carried out. Moreover, diagnostic methods are generally restricted by limitations of optical accessibility and non-repeatable boundary conditions.

Due to the limitations of current diagnostic methods, 3D computational fluid dynamics (CFD) simulations are considered to be a reliable and effective tool for a detailed study of spray injection. In CFD, three well-known techniques to consider turbulence are available, each having their own strengths and weaknesses. First, direct numerical simulation (DNS) is the best approach for predictive simulations but is computationally not feasible for most engineering applications, e.g. full cycle engine simulations. Second, Reynolds averaged Navier–Stokes (RANS) technique is an extensively used method in academia and industry but provides ensemble or time-averaged information only and hence is unsuitable for the study of certain transient behavior such as cycle-to-cycle variations in engines. The third approach, large-Eddy simulation (LES), can potentially provide more detailed information by directly resolving large turbulent scales and modeling the small (universal) turbulent scales with reasonable computational cost. In the present work, LES is employed in combinations with a Lagrangian particle approach: the gas phase is solved using the continuum assumption and individual liquid fuel droplets are tracked by solving their Newton’s law of motion.

The present study focuses on the influence of ultra-high injection pressure and nozzle shape on spray-induced turbulence and air-entrainment with the following objectives: (1) Validation of the numerical model using experimental data for two different nozzle geometries, (2) analyzing the impact of ultra-high injection pressures on droplet size and distribution, (3) characterizing the spray-induced large-scale turbulent motion, (4) evaluation of air entrainment in the near nozzle region.

The paper is structured in 6 different sections. This introductory section is followed by Sect. 2, which describes the experimental set-up. The numerical models and simulation set-up are described in Sects. 3 and 4, respectively. In Sect. 5, numerical and experimental results are compared to validate the numerical model, and the impact of the injection pressure on mean droplet size, spray-induced turbulence and entrainment is presented. Some conclusions are summarized in Sect. 6.

Experimental Configuration

Particle Image Velocimetry Set-Up

Particle Image Velocimetry (PIV) was used to study a spray-induced air motion. An experimental setup of PIV used to measure a two-dimensional flow field is shown in Fig. 1. The set-up consisted of a double-pulse Nd-YAG laser, CCD camera, synchronizer, PC, and particle seeder. The laser’s second harmonic (532 nm) was used to illuminate areas of the flow field containing seeded particles, and a laser sheet ($\approx$ 1 mm thick) was formed using lenses. The relationship between the laser sheet and the captured range is shown in Fig. 2. The laser sheet was positioned in such a way that the center of one spray plume laid within it, and images of the air motion were captured from the side window of the constant volume chamber. The image resolution of the CCD camera was 2660$\times$1776 pixels. The synchronizer controlled the timing of the laser, the camera, and the injection. The delay between the 1st and 2nd laser pulses was adjusted based on the velocity of the target flow, and was set to 200 µs during feasibility tests. Spray images were captured at different time steps after the start of injection. A Laskin-type aerosol generator was used to create small seeding particles, which were transferred into the constant volume chamber via the air intake pipe. Olive oil was used to form the seeding particles. The ability to track the seeded particles is essential for PIV measurement; the particle seeder generated particles whose diameters were predominantly around 1 µm. Seeding particles of this size are suitable for tracking typical turbulent or high-speed gas flows (Melling 1997). The number density of the seeded particles in the surrounding air was considerably lower than the number density of the liquid droplets in the spray, so the optical signals from the seeded particles in the surrounding air were significantly weaker than those from the spray. A physical mask was therefore placed between the constant volume chamber and the camera to block light scattered by the spray. Despite this, there were still strong signals from the spray that made it impossible to detect signals from the seeded particles in the spray’s vicinity. Therefore, only the vectors of the air flow at some distance from the spray edge were examined. Interrogation areas were introduced to determine the displacement of the particles in the captured images; the grids of these areas were small enough to reasonably assume the flow to be uniform within individual grid cells. Recursive analysis was used to increase the accuracy of the measured velocities: velocity calculations were initially performed for large interrogation areas (128$\times$128 pixels), and then for smaller ones (64$\times$64 pixels). The experimental conditions used in the PIV measurements are specified in Table 1.

Fig. 1

Schematic depiction of the PIV setup

In addition, injection rate measurements and the phase doppler interferometry measurements were performed to obtain fuel mass flow rates and droplet size distributions at individual injection pressures, respectively. More details about the measurement configuration can be found in Yamaguchi et al. (2019), Wadekar et al. (2019).

Fig. 2

Schematic depiction of the spray image capturing setup: (a) top view, (b) side view

Table 1 Operating conditions considered in the simulations

Postprocessing of PIV Data

The vector fields obtained from the PIV measurements were post-processed to determine the air entrainment rate. The air entrainment is the air flow entrained into the spray, which contributes to atomization and mixture formation. To facilitate the calculation of the air entrainment, a 40 mm long control line was defined. The line was placed 20 mm from the injector axes (see Fig. 3) to minimize the influence of light scattered by the spray droplets. This placement made it possible to reliably capture differences in air motion when using different injection pressures.

Fig. 3

The control line for air entrainment rate calculation

For the air entrainment calculation, the vectors lying on the control line were selected and their orthogonal components to the control line were computed. The air entrainment rate at different time steps was then estimated based on the mean of these orthogonal components over the control line. The air entrainment rate over the whole time period was calculated as:

$$\begin{aligned} U_{entrainment} = \int _{0}^{T} max (~0, \overline{ |\vec {U}_{\perp }|} ~) ~ dt, \end{aligned}$$

(1)

where $\vec {U}$ and $\vec {U}_{\perp }$ is the air flow velocity vector and its orthogonal vector to the control line, respectively. T is the final time of the calculation (5 ms). The total mass of air entrained into the liquid spray was calculted as:

$$\begin{aligned} m_{entrained} = \int _{0}^{T} \rho _{air} ~ U_{entrainment} ~ dt. \end{aligned}$$

(2)

Numerical Modeling

Fluid Motion

The modeling of spray atomization involves modeling of both liquid and gaseous phases. Here, the gas phase was modelled using an Eulerian approach, while the liquid phase was handled using the Lagrangian particle tracking (LPT) method. The interaction between both phases were accounted for by source terms in the Eulerian gas phase equations. The numerical simulations presented here were conducted using the Large-Eddy simulation (LES) approach, in which the flow was described using the following filtered equations for mass (3), momentum (4) and energy (5):

$$\begin{aligned}&\frac{\partial \bar{\rho }}{\partial t} + \frac{\partial (\bar{\rho } \tilde{u}_j)}{\partial {x}_j} = S_{\rho }, \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial (\bar{\rho } \tilde{u}_i)}{\partial t} + \frac{ \partial (\bar{\rho } {\tilde{u}_i \tilde{u}_j})}{\partial {x}_j} = \frac{ \partial \bar{\tau }_{ij} }{\partial x_j} + \frac{ \partial {\tau }_{ij}^{sgs} }{\partial x_j} - \frac{\partial \bar{p}}{\partial x_{i} } + S_{u,i}, \end{aligned}$$

(4)

$$\begin{aligned}&{ \frac{\partial (\bar{\rho } \tilde{h_t})}{\partial t} + \frac{ \partial (\bar{\rho } {\tilde{h_t} \tilde{u}_j)}}{\partial {x}_j} = \frac{\partial }{\partial x_j} \left( \alpha \frac{\partial \tilde{h}}{ \partial x_j} \right) + \frac{ \partial \bar{p} }{ \partial t } +{ {\bar{\tau }}}_{ij} \frac{ \partial \tilde{u_i} }{ \partial x_j} + S_{h}. } \end{aligned}$$

(5)

Here, an overline denotes conventional and a tilde Favre filtered quantities, with relation ${\tilde{\phi }=\overline{\rho \phi } / \bar{\rho }}$. Within the governing equations, $\rho$ is the density, $u_j$ the flow velocity vector, p the pressure, $\tau _{ij}$ the viscous shear stress tensor, $\alpha$ the thermal diffusivity, and $h_t$ the total enthalpy $h_t = h + \frac{u_j u_j}{2}$ with h denoting sensible enthalpy. Moreover, $S_{\rho }$, $S_{u,i}$ and $S_{h}$ are respectively the mass, momentum and energy source terms from the dispersed phase accounting for the coupling between liquid and gas phase. In this study, no heat and no mass transfer between the phases are considered, therefore, the mass and energy source terms are neglected ($S_{\rho }$ = $S_{h}$ = 0). When the liquid is injected at very high pressure in quiescent ambient gas, a sudden high momentum exchange takes place between the two phases. The momentum exchange produces strong shears between both phases, is accounted by the momentum source term $S_{u,i}$. The pressure was calculated using pressure-velocity-density coupling for flows at arbitrary Mach-number (Demirdžić et al. 1993). The molecular viscosity was calculated by the Sutherland law (Sutherland 2009). The unresolved sub-grid stress tensor $\tau ^{sgs}$ arises from residual motions was modelled using the standard Smagorinsky model (Smagorinsky 1963), expressed as:

$$\begin{aligned}&\tau _{ij}^{sgs} = \bar{\rho }~ (\widetilde{u_{i}u_{j}} - \tilde{u_i} \tilde{u_j} ) = -2 \mu _t \tilde{S}_{ij}, \end{aligned}$$

(6)

$$\begin{aligned}&\tilde{S}_{ij} = \frac{1}{2} \left( \frac{\partial \tilde{u}_i}{\partial x_j} + \frac{\partial \tilde{u}_j}{\partial x_i} \right) , \end{aligned}$$

(7)

$$\begin{aligned}&\mu _t = \bar{\rho } C_s \Delta ^2 (2 \tilde{S}_{ij} \tilde{S}_{ij})^2 . \end{aligned}$$

(8)

Here, $\mu _t$ is the turbulent dynamic viscosity, ${S}_{ij}$ is strain rate tensor, and the Smagorinsky constant $C_s$ is set equal to 0.2. The filter size $\Delta$ is calculated using cubic root of the cell volume.

Droplet Motion

A real spray contains a huge number of droplets and solving the equations of motion for each droplet is computationally not feasible for a realistic spray. Therefore, multiple droplets assumed to have identical properties are grouped together into a single parcel, i.e. each parcel represents a certain (large) number of individual droplets which allows to represent and simulate sprays with arbitrary many droplets at reasonable cost.

During the simulation liquid fuel parcels are injected at very high velocities into a quiescent gas followed by strong momentum exchange between gas phase and droplets. This momentum exchanged is assumed to be governed by relative velocities, i.e. drag force, leading to the following form of the momentum equation for each parcel:

$$\begin{aligned} m_p \frac{d \mathbf{u} _p}{d t} = \frac{1}{6} \rho _p \pi d^3 \frac{d \mathbf{u} _p}{d t} = \frac{1}{2} (\mathbf{u} _g-\mathbf{u} _p) |\mathbf{u} _g - \mathbf{u} _p| \rho _g C_D \frac{ \pi d^2}{4}. \end{aligned}$$

(9)

After simplification, the momentum equation for each parcel leading to the following form:

$$\begin{aligned} { \frac{\mathrm {d} \mathbf{u} _p}{\mathrm {d} t} = (\mathbf{u} _g-\mathbf{u} _p) |\mathbf{u} _g - \mathbf{u} _p| \frac{\rho _g}{\rho _p} C_D \frac{3}{4 d}. } \end{aligned}$$

(10)

Where, d, $\rho _p$, $\mathbf{u _p}$ denote the droplet diameter, density and velocity vector, respectively, $\rho _g$ is the gas phase density, and $\mathbf{u _g}$ the gas phase velocity which are interpolated to the droplet position from the adjacent cells. The drag force coefficient $C_D$ is defined as:

$$\begin{aligned} C_D= \frac{24}{Re_p} \left( 1 + \frac{1}{6} Re_{p}^{2/3} \right) \mathrm {for} ~~ Re_p < 1000, \end{aligned}$$

(11)

$$\begin{aligned} C_D&= 0.424 \quad \mathrm {for} \quad Re_p > 1000. \end{aligned}$$

(12)

The position of parcels $x_p$ with respective to time t is updated according to $\mathrm {d}x_p/\mathrm {d}t=\mathbf{u} _p$, and the particle’s Reynolds number is calculated using the viscosity of gas $\nu _g$, as:

$$\begin{aligned} Re_p = \frac{|\mathbf{u} _g - \mathbf{u} _p|d}{\nu _g}. \end{aligned}$$

(13)

Turbulent dispersion of droplets is considered by a stochastic approach suggested by Gosman and Ioannides (1983). The model samples a (non-resolved) sub-grid scale velocity $\mathbf{u} ^\prime$ from a Gaussian distribution with zero mean and standard deviation $\sqrt{2k_{sgs}/3}$ which is added to the interpolated resolved/filtered gas phase velocity at the droplets location to get the instantaneous gas phase velocity in (9):

$$\begin{aligned} \mathbf{u} _g = \tilde{\mathbf{u }} + \mathbf{u} ^\prime . \end{aligned}$$

The interaction time $t_{int}$ of the droplet with this instantaneous velocity is defined as the minimum of a characteristic eddy turn-over time $t_e = l_e / |\mathbf{u} ^\prime |$ and the transit time $t_{tr}$ needed by the droplet to cross the eddy:

$$\begin{aligned} t_{int} = \min (t_e, t_{tr}). \end{aligned}$$

Here, $t_e$ is calculated from the subgrid scale kinetic energy $k_{sgs}$ and the subgrid scale dissipation rate $\epsilon _{sgs}$ via $t_e = C (k_{sgs}^{3/2}/\epsilon _{sgs})$ with constant $C = 0.1643$. The subgrid scale kinetic energy is calculated as $k_{sgs} = ( \widetilde{\mathbf{u}_{i} \mathbf{u }_j} - {\tilde{\mathbf{u }}}_i {\tilde{\mathbf{u }}}_j )$ and the subgrid scale dissipation rate is evaluated from $\epsilon _{sgs} = ~k_{sgs}^{3/2} / \Delta$, where $\Delta$ denotes the filter size. The eddy transit time is estimated from a linearised form of the equation of motion of the droplet, for further details we refer to Gosman and Ioannides (1983).

Blob Injection and Parcel/Droplet Break-Up

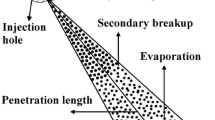
In this work, a blob injection model was used in combination with Kelvin-Helmholtz Rayleigh-Taylor (KH-RT) breakup model, as represented in Fig. 4. In the blob injection method (Perini and Reitz 2016), a set of parcels, representing blobs or portions of injected liquid column, is injected into the computational domain within a prescribed spray-cone angle. Each blob is characterized by an initial diameter $d_{inj}$, which is equal to or less than the effective nozzle orifice diameter $d_{noz}$. The initial diameter and velocity of each injected blob is calculated as:

$$\begin{aligned} d_{inj}&= \sqrt{c_d} ~ d_{noz}, \end{aligned}$$

(14)

$$\begin{aligned} u_{inj}&= \frac{\dot{m}}{\rho _p A c_d}. \end{aligned}$$

(15)

Here, $c_d$ denotes the nozzle discharge coefficient, A is the nozzle orifice cross-section area and $\dot{m}$ is mass flow rate. In this way, a detailed simulation of near nozzle phenomena is replaced by the injection of big spherical droplets which further break-up into smaller droplets. In this work, the number of droplets injected per unit time was calculated based on the measured mass flow rate profile (see “Appendix”).

Fig. 4

Atomization mechanism via the Kelvin–Helmholtz/Rayleigh–Taylor (KH–RT) instability model

Break-up of droplets is modelled via the well-known Kelvin-Helmholtz Rayleigh-Taylor (KH-RT) model which is a standard model for high Weber number jets (Li and Soteriou 2016). The model combines both Kelvin-Helmholtz (KH) and Rayleigh-Taylor (RT) instabilities. The KH instability is the dominant mechanism close to the nozzle where the instability of the fastest growing surface wave due to shear leads to primary breakup of the liquid jet. Compared to the KH break-up mechanism, Rayleigh-Taylor instabilities originate from an acceleration normal to a density gradient, here the droplet-gas interface. When liquid ligaments are decelerated by drag, an RT instability can grow on the trailing edge of the droplet. The RT instability is mainly responsible for secondary breakup of liquid droplets. In the simulation, break-up of the droplets occurs with the mechanism (either KH or RT) predicting the shortest breakup time. The model is described in more detail elsewhere (Beale and Reitz 1999).

Numerical Setup

Nozzle Type

In this work, two axisymmetric nozzle configurations are investigated: divergent and convergent, with orifice hole diameters of 380 µm and 148 µm, respectively. Despite their different geometries and orifice diameters, both nozzles are designed for the same mass flow rate (15 mg/ms at 200 bar). Details of the internal nozzle flow are not simulated here, however, the effect of different nozzle geometries was accounted for by prescribing different spray-jet angles and different coefficients of discharge. Details of the nozzle geometries are summarized in Table 2.

Table 2 Specifications of the injector nozzles used in the study

Computational Mesh and Sensitively Analysis

The computational domain in this study consists of a cylinder with dimensions $h{\times }b$ = $120{\times }180$ mm discretized with almost equidistant hexahedral cells. In the Lagrangian spray simulations within the present modeling framework, a fine-tuning is needed to inject parcels in such a way that an injection process is mimicked as closely as possible to real spray. In previous studies (Senecal et al. 2014a, b), a change in liquid penetration length is observed when the mesh is refined or number of parcels injected is change. Therefore, we have investigated three different grids with the different cell resolutions (shown in Table 3) and the influence of the number of injected parcels for a case with injection pressure of 1000 bar. The results of the liquid penetration length as a function of time on the three different grids are shown in Fig. 5. The finest grid A shows an acceptable conformity between simulation results and experimental data whereas grid B and C under-predicted the penetration length. A similar impact of grid resolution on spray development was reported by Alessandro et al. (2019). Hence, grid A was utilized for all simulations including spray tuning. The total number of cells for grid A was 24 million which did not permit further grid refinements with the available compute resources.

Table 3 Specification of numerical grids used for grid-resolution study

The impact of the number of parcels injected was investigated considering $2{\times }10^7$, $4{\times }10^7$ and $8{\times }10^7$ parcels per second. No significant impact was noticed for the penetration length, see Fig. 5, however, the qualitative description of the spray was substantially improved with increasing number of parcels per second at the cost of increased computational cost. A compromise between the qualitative spray description and the computation time was made by considering $4{\times }10^7$ parcels per second for all simulation cases discussed below.

Fig. 5

Left: Influence of grid-resolution, right: Influence of number of injected parcels per second (pps) on liquid penetration length evolution for the divergent nozzle at 1000 bar injection pressure case

It is relevant to note that the spray model was tuned for one case of each nozzle only (1000 bar injection pressure) by varying/adjusting the discharge coefficient of the nozzle $c_d$ to match the experimental spray penetration length. After tuning for the same setup was used for all simulations with that nozzle. Although slightly better agreement with experimental results would have been possible with individual tuning for each case, the proposed strategy of keeping the model parameters constant for each nozzle type allows for a better evaluation of the predictive capabilities of the modeling strategy.

Simulation Set-Up

Simulations were performed using OpenFOAM-2.2.x (Weller et al. 1998). An implicit, second-order backward scheme was applied for the time discretization. The convective scalar fluxes of momentum were treated with a second-order accurate central differencing scheme. All boundaries of the chamber were treated as walls (zero velocity) except the bottom of the chamber where the spray was allowed to leave the domain at an open boundary. Zero-gradient boundary condition was applied for all scalar quantities at walls. Liquid n-heptane fuel is considered as a reference fuel to investigate gasoline sprays (Gasoline fuel injector spray measurement and characterization 2007) and was injected into the chamber maintained at atmospheric conditions (T = 293 K, p = 1 bar). Initially, the gas-phase (air) inside the chamber was at rest. The total mass of fuel (54 mg) was injected using experimentally determined mass flow rate profile (shown in “Appendix”) in the form of parcels. The experimental condition of a constant fuel mass at different injection pressures results in different injection duration as reported in Table 1. The investigated injector nozzles are design prototype nozzles with an L/D ratio much lower than in a typical diesel injector nozzles. The spray-jet angle significantly differs for both nozzle types. The spray-jet angle extracted from experimental spray images is shown in Fig. 6. The divergent nozzle features a constant spray-jet angle except during an initial transient period. However, the spray-jet angle for the convergent nozzle was quite wide in the beginning and then decreased until half of the injection time. Therefore, the spray-jet angle was set constant to 10$^{\circ }$ and variable from 24$^{\circ }$ to 5$^{\circ }$ for the divergent and the convergent nozzle, respectively.

Fig. 6

Variation of spray-jet angle for the divergent and the convergent nozzle at 1000 bar injection pressure

Monodispersed droplets (blobs) with an initial diameter calculated by Eq. 14 were injected continuously during the injection duration to match the prescribed mass flow rate. It is known that the assumed initial drop size distribution has a significant impact on spray formation (Yoon 2005; Domingo-Alvarez et al. 2019). Since the real drop size distribution is unknown, the simplest case of a uniform droplet size distribution is chosen here.

Results and Discussion

Liquid Penetration Length

Figure 7 compares measured and calculated liquid penetration length for the divergent and the convergent nozzle as a function of time after start of injection (aSOI) for different injection pressure values. The liquid penetration length was defined here as a distance between the nozzle tip and the farthest droplet of the spray tip along the injector axis (vertical axis of spray chamber). Each measured data point shown in Fig. 7 corresponds to an average of 20 injection shots; the shaded band shows the standard deviation of the experimental data.

The calculated spray penetration lengths at all investigated injection pressures for both nozzles show overall good agreement with the experiments (objective 1). When fuel is injected into the spray chamber a gas-phase recirculation zone and turbulence are created through momentum transfer from the liquid jet to the gas-phase. In the simulation results the correct exchange of momentum between the liquid and gas phases and the correct aerodynamic forces acting on the droplets that strongly influence the atomization process is ensured by fine-tuning the penetration length to match experimental data. However, some deviation in penetration length is also observed at lower injection pressure. One of the possible reasons behind such a deviation for low injection pressure values could be the inaccurate values of the arithmetic mean diameter shown in Fig. 9. In general, at all injection pressures the convergent nozzle shows faster penetration rate suggesting a faster disintegration of the spray via secondary breakup than the divergent nozzle.

Fig. 7

Experimental data (point data) and simulation results (line data) of spray liquid penetration length for the divergent and the convergent nozzle at 200, 600, 1000 and 1500 bar injection pressures

Overall, the spray-tip penetration results clearly show increasing penetration length with increasing injection pressure and decreasing injection duration. A short injection duration provides more possibilities to adjust the injection timings, for instance in stratified operation mode and for multiple injections strategies. Also, in the case of early injection a high injection pressure helps by creating more turbulence to create a homogeneous fuel-air mixture. However, the increasing liquid penetration might also lead to issues of wall wetting or liquid fuel film formation at very high injection pressures and therefore fuel injection timing needs to be proper specified. The Authors will discuss this issue in detailed in forthcoming publication.

Mean Droplet Sizes

Figure 8 shows measured and calculated droplet sizes in terms of the arithmetic mean droplet diameter (D10) and the Sauter mean diameter (SMD or D32) for both nozzles at different injection pressures. The results exhibit the impact of injection pressure on the droplet sizes (objective 2). The measured data are time-averaged droplet diameters at probe location 80 mm downstream of the injector tip. In general, the numerical model accurately captures the mean diameter for both nozzles at all injection pressures except for lower injection pressures. The possible reason behind such disagreement is a considerably high contribution of normal (RT) instabilities (refer Fig. 5) at lower injection pressure compared to those at high injection pressures which are associated to higher shear (KH) instabilities. The results confirm the well-known result that droplet sizes decrease with increasing injection pressure, irrespective of nozzle shape. Moreover, the droplet mean diameters (D10 and D32) for the divergent nozzle exceed those for the convergent nozzle, irrespective of injection pressure. However, the arithmetic mean droplet diameter (D10) varies less than the SMD. At high injection pressures droplets quickly reach their stable diameter below which no secondary breakup occurs. Due to its definition, the SMD is quite sensitive to the presence of large droplets. This leads to a decreasing decay of SMD values with increasing injection pressure. A small SMD values (or small droplet size) means a large contact surface area of the droplets, which is beneficial for faster evaporation under real engine conditions.

Fig. 8

Comparison between measured and calculated mean diameter of droplets for the divergent and the convergent nozzle at different injection pressures. Right: Arithmetic mean diameter (D10), left: Sauter mean diameter (D32)

Droplet size distributions provide a more detailed picture of the spray than D10 and D32. Here, the local droplet size distributions were measured experimentally using Phase Doppler Interferometry (PDI). The sampling location was 80 mm downstream of the injector tip and the sampling time window was at full needle open condition, so the contribution of the large initial droplets was not taken into account. More details about the droplets sampling time window can be found in the “Appendix”. In the simulations a corresponding sampling point with a radius of 2 mm was used to determine the droplet size distributions. Figure 9 presents a quantitative comparison between experimental and simulated droplet size distributions at different injection pressures for both the convergent and the divergent nozzle. Reasonable agreement between experimental and simulated size distributions can be observed for all injection pressures. The results indicate that the droplet-size distribution becomes narrower with increasing injection pressure.

Fig. 9

Comparison between measured and calculated droplet size distribution for the divergent and the convergent nozzle at 200, 600, 1000 and 1500 bar injection pressure

For both nozzles, the droplet size distributions at 1500 bar show the highest probability of small droplets. The distribution profiles confirm the above discussed (Fig. 8) finding that the droplet sizes decrease as the fuel injection pressure increases, irrespective of nozzle shape. Accordingly, the ratio of smaller droplets at 1000 bar is lower than at 1500 bar but higher than in the 600 and 200 bar case. Furthermore, the droplet size distributions at pressures 200 bar show comparatively higher probabilities of large droplets. The droplet sizes are more widely distributed and are shifted towards larger droplet sizes (right side).

The droplet size distributions for the divergent nozzle show larger droplet diameters compared to the convergent nozzle. However, it should be noted that the orifice diameter of the nozzles is different. Moreover, the droplet size distributions at injection pressures of 1000 and 1500 bar are quite similar, indicating that raising the injection pressure above 1000 bar may not result in further improvements of spray atomization with respect to creating smaller droplets. It might be possible that droplets reach a limiting low value at 1000 bar here, and all the energy gained from injection pressures above 1000 bar would be converted mainly into kinetic energy. This will be investigated in detail in a forthcoming publication.

In summary, increasing injection pressure has a substantial influence on droplet sizes. The mean droplet sizes are strongly reduced compared to the lowest pressure shown. The droplet size distributions also show a higher probability of finding smaller droplets at high injection pressures.

Spray-Induced Turbulence

The origin and transfer of a turbulent kinetic energy within the spray jet is investigated here with the aim to characterize the impact of nozzle design and injection pressure on turbulence generation (objective 3). Figure 10 shows the turbulent kinetic energy spectra for the divergent and the convergent nozzle. The spectra are calculated by sampling the velocity field data at a point 30 mm downstream the nozzle. The velocity data is collected at every time step after the fuel jet reaches the sampling location. Then, the spectra are constructed by postprocessing the velocity signal using the Fast Fourier Transformation (FFT). Note that the LES results shown are consistent with the traditional view of an equilibrium turbulence energy cascade (Pope 2000).

Fig. 10

Simulated turbulent kinetic energy spectra 30 mm downstream of both nozzles at 200, 600, 1000 and 1500 bar injection pressure

The spectra do not allow any specific conclusions here, but it can be observed that the divergent nozzle spray creates higher turbulent kinetic energy levels than the convergent nozzle spray at almost all frequencies.

Fig. 11

A sample position of spray generated big vortex. The velocity vectors u and v shown for the illustration of the definition of the two-point correlation functions

Fig. 12

Integral length scale as a function of time calculated on the spray axis (top left and right) and on a vertical line with 10 mm of set parallel to the spray-axis (bottom left and right) for the divergent and the convergent nozzles at 200, 600, 1000 and 1500 bar injection pressures

Similar turbulence kinetic energy spectra were calculated for a point outside the spray core region (not shown). The purpose of such calculation was to identify the capability of the spray to generate turbulence outsize the spray-jet region. Similar results as shows in Fig. 10 were observed for both nozzles. The results indicate that the divergent nozzle spray has more potential to develop turbulence kinetic energy compared to the convergent nozzle spray not only in the spray core region but in the whole domain.

When the liquid fuel is injected into ambient gas at high velocities the gas flow quickly becomes turbulent due to strong momentum exchange between the liquid spray and the gas phase. A turbulent flow is comprised of eddies of different scales. One of the potential benefits of ultra-high fuel injection pressures is to enhance the spray-induced turbulence which can be used to promote efficient fuel-air mixing. The large scales of turbulence are characterized by the integral length scale. Therefore, in this work, the integral length scale of spray-induced eddies is calculated at different locations inside the spray chamber by means of the velocity correlation, as:

$$\begin{aligned} L_\delta = \int _{0}^{q} \frac{{u_\alpha ^{'}}(z)~{u_\alpha ^{'}}(z+r)}{ {u}_\alpha ^{'} (z)^2 } dr. \end{aligned}$$

(16)

Here, ${u_\alpha ^{'}}$ is the velocity fluctuation in $\alpha$ direction, r is the distance between the two velocity vectors, and q is the length of the probe line. This two-point correlation function relates the velocity fluctuations of two velocity vector components to each other as a function of their distance r (Pope 2000). However, this classical two-point correlation is reasonable for homogeneous, isotropic turbulence with sufficient statistical data (e.g. via time or ensemble averaging) which is often not available when investigating highly transient sprays. Therefore, we use an alternative definition (Janas et al. 2017) that includes vortex and subsequent coherent structures:

$$\begin{aligned} L_\delta = \int _{0}^{q} \frac{{u_\alpha ^\delta }(z)~{u_\alpha ^\delta }(z+r)}{ {u}_\alpha ^{\delta } (z)^2 } dr, \end{aligned}$$

(17)

where, $u^\delta$ is the deviation of the instantaneous (filtered) velocity $\tilde{u}$ from the spatial mean value $\bar{\tilde{u}}$ along a probe line. The modified function to calculate the integral length scale (Eqn. 17) is evaluated at 3 different vertical locations: x* = 0 mm, x* = 10 mm and x* = 30 mm (illustrated in Fig. 11). Figure 12 shows the integral length scale at different injection pressures for both nozzles at three probe locations. As a general trend it can be observed that higher fuel injection pressures tend to generate larger turbulence structures quicker than lower injection pressures. This is particularly obvious for the divergent nozzle. The final scale of the integral length scale does not depend much on the fuel injection pressure for a given nozzle type particularly along the spray axis (x* = 0 mm). However, the integral length scales at radial locations (x* = 10 mm and x* = 30 mm) clearly show the impact of higher injection pressures such as substantially larger length scale at the highest pressure compared to the lowest pressure. Similar trends can be observed for the convergent nozzle with steeper gradients during the creation of large turbulent eddies by the spray. The spray from the divergent nozzle creates slightly larger turbulence length scales which might have the potential to survive longer.

In summary, the divergent nozzle sprays create more turbulent kinetic energy than the convergent nozzle sprays. Sprays at higher injection pressure quickly generate larger turbulent structures compared to sprays at lower injection pressures. The final integral length scales along the spray axis is almost identical at all injection pressures, however, the impact of higher pressure on length scales is more pronounced at off-axis probe lines.

Air Entrainment

An efficient fuel-air mixing in any direct fuel injection system strongly depends on the entrainment of air into the spray region. Here, the air entrainment is quantified as the mass fluxes across a control line of length 40 mm (see Fig. 3) at different injection pressures (objective 4). The control line was parallel to the spray-axis with an offset of 20 mm. The velocity component on the probe line pointing towards and perpendicular to the spray-axis was considered as air entrainment. The entrainment rate was calculated at the time-step when the liquid penetration reached the bottom of the chamber.

Fig. 13

Normalized flux of entrained air as a function of distance from nozzle-tip for the divergent and the convergent nozzles at 200, 600, 1000 and 1500 bar injection pressure

Fig. 14

The rate of normalized flux over the control line for the divergent and the convergent nozzle at 200, 600, 1000 and 1500 injection pressure

Fig. 15

Total air entrained over the control line for the divergent and the convergent nozzle at 200, 600, 1000 and 1500 bar injection pressures

Figure 13 shows simulation results of the spatially resolved normalized air entrainment flux along the control line for the convergent and the divergent nozzle at different fuel injection pressures. Because of different injection pressures, it was not possible to compare the entrainment flux directly, therefore, the comparison was made on normalized (by the maximum value for each nozzles) entrainment flux scale. In previous studies (Tomita et al. 1995) it was observed that air entrainment is higher close to the nozzle than further downstream.

Overall, the results in Fig. 13 confirm the previous study (Tomita et al. 1995). In particular, the spray from the divergent nozzle features the highest entrainment for all injection pressures except 1500 bar close to the nozzle and a continuous decrease further downstream. In comparison, the convergent nozzle starts with relatively low entrainment in the vicinity of the nozzle and reached a maximum value at 20 to 25 mm downstream for all expect the lowest injection pressure. The qualitative differences in the entrainment profiles along the control line for the different nozzles suggest an important impact of the nozzle shape on the large-scale flow structure.

The development of the normalized air entrainment rate during the complete injection process is summarized in Fig. 14. Here, the entrainment rate corresponds to the mean value along the control line. The figure shows both experimental data and simulation results for the convergent and the divergent nozzle at different injection pressures. Note that, the experimental air entrainment values are based on 2D data, however, 3D flow field data has been used to calculate the air entrainment rate in the simulation. The results indicate that the entrainment rate is significantly influenced by the injection pressure, i.e. entrainment rate was increased by injecting the fuel at high pressure. Similar result can be observed for both nozzles types. However, entrainment for the convergent nozzle dies out quickly while it remains persist longer for the divergent nozzle at the respective pressure. This result suggests that the divergent nozzle is more effective in keeping the flow motion. Simulation results also indicate the presence of a small recirculation zone in the beginning indicated by negative flux values. However, no such effect was observed in the measurement data, though, this could be due to resolution in time and space.

Figure 15 shows the total amount of air entrained over the control line (see Fig. 3) during the complete injection process. Interestingly, the divergent nozzle shows overall a higher amount of entrained air at all injection pressures compared to the convergent nozzle. This suggests that the divergent shape of the injector nozzle helps to generate large turbulent structures and subsequently support to entrain more air in the spray-jet. The total entrained air is larger at higher injection pressures irrespective of nozzle shapes. For the divergent nozzle, the entrained air at 1000 bar injection pressure is similar to 1500 bar injection pressure. This important result indicates that an injection pressure above a certain level (here 1000 bar) might not beneficial for overall air entrainment. This will be investigated in detail in subsequent simulation studies.

Conclusion

In the present study n-heptane fuel sprays were investigated using large-eddy simulation to provide insights into the spray development at ultra-high injection pressures for the divergent and the convergent nozzle shape injector. The main conclusions are as follows:

• The numerical model is able to reproduce experimentally observed liquid penetration length after fine-tuning of an arbitrarily chosen case (i.e. 1000 bar case). However, some deviations in liquid penetration length is observed at lower injection pressure.

  At constant injected fuel mass, the injection duration was significantly reduced with increasing injection pressure. Shorter injection duration might allow more flexibility for advanced injection strategies.

• Simulated mean droplet diameters (D10 and D32) and droplet size distributions agree well with experimental data. The results revealed that the atomization was very sensitive to the injection pressure. Droplet sizes were significantly reduced with by increasing the injection pressure from 200 to 800 bar, increasing the injection pressure even further showed only a marginal impact on droplet sizes.

• Turbulent kinetic energy spectra looks almost identical for different injection pressures. Estimated integral length scales of the spray-induced turbulence turned out to be larger at high injection pressures compared to lower ones.

• Air entrainment rate increases with increasing injection pressure but decline quicker due to the shorter injection duration. The entrainment of air for the convergent nozzle spray at high injection pressure is high in the beginning but dies-out quicker compared to the divergent nozzle at the same injection pressures.

• The total amount of entrained air is higher at higher injection pressure. The divergent nozzle shows higher air entrainment at the same injection pressure and suggest that the divergent shape of the nozzle helps creating and maintaining spray-induced vertexes.

Appendix

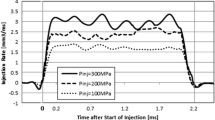
Figure 16 shows the injected fuel mass flow rate for a constant fuel mass (54 mg) at different injection pressures. The fuel injection duration for 1500 bar injection pressure was almost 60 % shorter than the 200 bar injection pressure. This mass flow rate profile is used as an input for the numerical calculations.

Fig. 16

The fuel mass flow rate for a constant fuel mass at different injection pressures

Fig. 17

The time window for the droplets mean size measurement in divergent nozzle at 1000 bar injection pressure

Figure 17 shows the time window used for the measurement of droplets mean sizes (D10 and D32). The time $t_1$ is signal delay time and $t_2$ is the needle opening time. In the post-processing of droplets sampling data, only the the data of highlighted window is considered.