Abstract
Identifying combustion regimes in terms of premixed and non-premixed characteristics is an important task for understanding combustion phenomena and the structure of flames. A quasi-DNS database of the compositionally inhomogeneous partially premixed Sydney/Sandia flame in configuration FJ-5GP-Lr75-57 is used to directly compare different types of flame regime markers from literature. In the simulation of the flame, detailed chemistry and diffusion models are utilized and no turbulence and combustion models are used as the flame front and flow are fully resolved near the nozzle. This allows evaluating the regime markers as a post-processing step without modeling assumptions and directly comparing regime markers based on gradient alignment, drift term analysis and gradient free regime identification. The goal is not to find the correct regime marker, which might be impossible due to the different set of assumptions of every marker and the generally vague definition of the partially premixed regime itself, but to compare their behavior when applied to a resolved turbulent flame with partially premixed characteristics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In many technically relevant combustion devices, flames develop in conditions where fuel and oxidizer are not perfectly mixed. These partially premixed or mixed-mode flames are challenging for numerical simulations due to the co-existence of premixed and non-premixed combustion characteristics. They have, however, the potential to increase stability and reduce pollutant formation. Over the last decades, different approaches have been developed to define markers which can identify different combustion regimes, either from simulation data or measurements.
Historically, the first flame regime marker was developed by Yamashita et al. (1996) and is based on the alignment of gradients of the fuel and oxidizer mass fractions. In the last few years alone, a large number of works has used the concept of the Takeno flame index to study flames and improve their prediction: it was used to understand the structure of blue swirling flames (Chung et al. 2019), identify flame regimes in thickened flame simulations of spray flames (Hu and Kurose 2019b; Dressler et al. 2020) and study the influence of evaporation (Wei et al. 2018) as well as devolatilization (Zhang et al. 2017). Premixed and non-premixed regions in swirl spray flames were analyzed with the flame index concept (Eckel et al. 2019; Paulhiac et al. 2020) and the influence of swirl number on the combustion regime (Fredrich et al. 2019) was evaluated. It was used to study different coal flames (Tufano et al. 2018; Wan et al. 2019; Rieth et al. 2019; Akaotsu et al. 2020), assess the stabilization mechanism of supersonic lifted flames (Bouheraoua et al. 2017) and lifted hydrogen flames (Benim et al. 2019), classify regions of industrial burners by the combustion regime (Zhang et al. 2020), study auto-ignition of supercritical hydrothermal flames (Song et al. 2019), analyze extinction and re-ignition events (Sripakagorn et al. 2004) and gain insight into partially premixed DME flames (Hartl et al. 2019). It was further applied to scram jets (Shen et al. 2020; Zhao et al. 2019), Moderate or Intense Low oxygen Dilution (MILD) combustion (Amaduzzi et al. 2020), compression ignition engines (An et al. 2018), double-cone burners (Zhao et al. 2019), coaxial diffusion flames (Akaotsu et al. 2020), edge flames (Duboc et al. 2019) and jet-in-hot-coflow flames in conjunction with tangential stretching rate analysis (Li et al. 2019). In order to evaluate the flame index experimentally, Rosenberg et al. (2013, 2015) introduced tracer gases. This large number of works in just the last couple of years shows that the flame index and its variations (Fiorina et al. 2005; Lock et al. 2005) based on the alignment of species gradients are actively used to study many different types of flames (Masri 2015). It is therefore important to understand the behavior of this marker when applied to partially premixed flames.
Although the flame index is the most commonly used flame regime marker due to its simplicity, other markers have been developed as well. Based on flamelet analysis, the gradient alignment of mixture fraction and reaction progress variable has been discussed to determine the combustion regime (Favier and Vervisch 2001; Domingo et al. 2002; Nguyen et al. 2010; Lamouroux et al. 2014; Hu and Kurose 2019a). A similar approach can be used to define Damköhler numbers for the premixed, non-premixed and partially premixed regime Domingo et al. (2008) or compare source terms for premixed and non-premixed flamelets (Knudsen and Pitsch 2009, 2012). Another approach uses the chemical explosive mode analysis (CEMA) to differentiate between premixed propagation and diffusion flame characteristics. For example, Lu et al. (2008) compared the flame index to the chemical modes in a turbulent hydrogen flame and Doan and Swaminathan (2019) compared the regime prediction of the flame index with the chemical mode in MILD combustion and concluded that the CEMA based approach identified large parts of the flame as premixed whereas the flame index identified a non-premixed regime. Nordin-Bates et al. (2017) applied a similar concept to a scram jet flame. Hartl et al. (2018, 2019, 2019) and Butz et al. (2019) developed a flame regime marker known as Gradient Free Regime Identification (GFRI) which uses the chemical mode and allows to compute the marker from experiential Raman/Rayleigh spectroscopy results. It has been successfully used to train convolutional neural networks (Wan et al. 2020) for regime identification. Another approach was taken by Wu and Ihme (2015). They developed a marker (Wu and Ihme 2016) that evaluates a drift term. The drift term measures how good the prediction of a set of manifold-based combustion models fits to the current flow field conditions for a set of quantities of interest (QoI). A detailed description of the definition of these flame regime markers and their development is given in the “Appendix”.
All aforementioned regime markers have been derived from different assumptions and have their limitations. For example, the flame index based on fuel and oxidizer gradients is not applicable in regions of the flame where the fuel is completely consumed. Because of this, different multi-species extensions have been used in the past (Lignell et al. 2011; Jangi et al. 2015; Minamoto et al. 2015; Ma et al. 2016; Pei et al. 2016; Wei et al. 2018; Pang et al. 2018; Tufano et al. 2018; Hu and Kurose 2019b; Wan et al. 2019; Wen et al. 2019; Akaotsu et al. 2020). Fiorina et al. (2005) found that even in laminar diffusion flames, the flame index concept can make wrong predictions. They therefore introduced the oxygen gradient of a premixed model flame as an additional parameter. The regime markers based on flamelet analysis have their limitations when used in direct numerical simulation of turbulent flames because instantaneous flame fronts are subjected to unsteady effects, curvature, flame stretch and the direct interaction of different combustion regimes. Different approaches are available to overcome this by incorporating two-dimensional composition space equations (Scholtissek et al. 2020), accounting for curvature effects (Scholtissek et al. 2017) and analyzing the effect of tangential and preferential diffusion (Dietzsch et al. 2018; Han et al. 2019). The drift term approach by Wu and Ihme is not necessarily a marker for premixed and non-premixed regions. Instead, it shows how close the trajectory of a quantity of interest, e.g. a species mass fraction, on the manifold of a combustion model is to the local flow field conditions. It therefore depends on the choice of QoI and the selected combustion models. While partially premixed flames are generally characterized by a mix of premixed and non-premixed characteristics in a compositionally inhomogeneous flow field (Peters 2001), there is no universally accepted formal definition of the partially premixed combustion regime, especially in turbulent flames due to the complexity of the underlying physics (Wu and Ihme 2016; Hartl et al. 2019). Effects like back-supported flame fronts, time history effects of equivalence ratio fluctuations and diffusion of intermediate species in adjacent flame fronts make partially premixed flames fundamentally different from the simple premixed and non-premixed model flames (Lipatnikov 2012). A simple differentiation into premixed and non-premixed can therefore lead to misleading results (Wu and Ihme 2016). Because of this, it cannot be expected that any flame regime marker is able to identify combustion regimes unambiguously in every situation (Wu and Ihme 2016). Nonetheless, using regime markers is important for advancing the understanding of flames and phenomena like flame stabilization as described above. Some combustion models also use regime markers to blend between premixed and non-premixed combustion submodels in the case of partially premixed combustion situations (Domingo et al. 2002; Knudsen and Pitsch 2012; Yadav et al. 2017; Hu and Kurose 2019b, a; Hu et al. 2020).
Because of this, the goal of this work is to provide a side-by-side comparison of different flame regime markers in terms of their ability to classify the combustion regime in a simulation of a turbulent partially premixed flame, where the flame is fully resolved. To the best knowledge of the authors, a direct comparison of all different regime marker concepts in a compositionally inhomogeneous partially premixed flame has not been done before. The flame setup is the Sydney/Sandia flame with inhomogeneous inlets (Meares and Masri 2014; Meares et al. 2015; Barlow et al. 2015) in configuration FJ-5GP-Lr75-57. It is a well documented and experimentally investigated partially premixed turbulent flame of laboratory scale. A retractable central fuel pipe allows adjusting the degree of premixing of fuel and air, thus creating inhomogeneous conditions. An early simulation of this configuration was performed by Wu and Ihme (2016). They performed two LES, one with a reduced-manifold combustion model based on premixed flames (premixed filtered tabulated chemistry LES, FTACLES) and one based on non-premixed flames (flamelet/progress-variable, FPV). Since these models are derived assuming perfectly premixed or non-premixed flames, they cannot describe flames where no single combustion regime dominates. By introducing a drift term, which measures how well a given manifold-based combustion model can represent the flame based on the current flow field, they defined a new regime marker. This marker compares the drift term from the premixed manifold combustion model to that of the non-premixed model. The authors observed that regime markers based solely on major species are insufficient to describe the complex processes in multi-regime combustion and therefore are not suited to blend the two combustion models for improving profiles of intermediate species. In contrast to other regime markers, their drift-term based marker is therefore species-specific and marks regions where a particular species mass fraction is highly sensitive to the manifold representation. They also found that major species can be largely insensitive to the combustion model, while minor species like CO are highly sensitive. Kleinheinz et al. (2017) performed LES with a multi-regime combustion model, which computes the contributions from premixed and non-premixed flamelets and uses this information to blend two combustion models, in order to study the stabilization mechanism of the flame. They found that the high stability of the Lr75 case is due to the high heat release rate in the premixed domain directly at the nozzle. Maio et al. (2017) conducted LES with tabulated chemistry and thickened flame models, and were able to capture radial species profiles from the experiment near the nozzle, but observed large deviations further downstream. Perry et al. (2017) conducted LES with a flamelet model that utilizes two mixture fractions. This approach significantly increased the accuracy of the results compared to using only one mixture fraction for the cases with inhomogeneous inlets and showed that the combustion near the nozzle is predominantly premixed. They also assessed the influence of subgrid filter probability density functions (Perry and Mueller 2019) for this flame. Ji et al. (2018) used a RANS-based multi-environment probability density function (MEPDF) approach, which was able to yield good agreement with the measurements but had some shortcomings in predicting local extinction events downstream. By using a joint composition-enthalpy transported PDF method, Tian and Lindstedt (2019) confirmed that the mixture fraction and reaction progress variable are strongly correlated and that the flame in the inhomogeneous case is predominantly premixed and becomes more diffusion controlled due to the entrainment of the pilot downstream. Chen et al. (2020) showed that an LES model based on unstrained premixed flamelets is able to qualitatively predict the correct trend of local extinction with inflow velocity for the Sydney flame further downstream. Luo et al. (2020) applied a dynamic second-order moment closure model to LES and found that the premixed flame is dominant upstream, causing 70 % of the heat release, which then decreases to about 40 % downstream, with an overall good agreement with measurements. Hansinger et al. (2020) performed LES with the Eulerian Stochastic Fields Method and assessed the influence of the number of stochastic fields on the quality of the simulation results. Shrotriya et al. (2020) conducted LES with reaction diffusion manifolds (REDIM) because it is mostly independent of the combustion regime. They used the flame index to confirm the aforementioned structure of the flame. Due to the high Reynolds number of this setup, it is not possible to simulate the whole flame with a direct numerical simulation. Instead, in this work, data from a quasi-DNS (Zirwes et al. 2020) is used which fully resolves the instantaneous flame fronts and the flow down to the Kolmogorov length in the upstream region (\(x/D<20\)).
The paper is structured as follows: Sect. 2 gives a brief overview of the simulation setup and summarizes the different regime markers used in this work. Section 3 presents the flame structure in terms of averaged heat release rates conditioned to the flame index and statistics of the scalar dissipation rate, mixture fraction and progress variable. A direct comparison of the different regime markers is performed in Sect. 4 on instantaneous cutting planes and radial lines through the flame. In the “Appendix”, different regime markers from the literature are discussed in detail.
2 Numerical Setup
2.1 Simulation Setup
In a previous work (Zirwes et al. 2020), a quasi-Direct Numerical Simulation (quasi-DNS or qDNS) of the Sydney/Sandia flame in configuration FJ-5GP-Lr75-57 has been conducted. The term quasi-DNS has been proposed in the literature (Enger et al. 2000; Nikitin et al. 2000; Touil et al. 2002; Kimura et al. 2002; Sukegawa et al. 2003; Jung and Yoo 2004; Tafti 2005; Raufeisen et al. 2008; Shams et al. 2012; Komen et al. 2014; Mayrhofer et al. 2015; Addad et al. 2015; Chu et al. 2016; Lecrivain et al. 2016; Forooghi et al. 2017; Komen et al. 2017; Zhao et al. 2018; Saeedipour et al. 2019; Wan et al. 2019) to describe a model-free simulation which does not fulfill all of the strict requirements of a DNS, e.g. for complex geometries which do not allow the use of higher order discretization schemes, but is accurate enough so that the results of a full DNS are expected to be similar. In the context of this work, the quasi-DNS resolves the flow field down to the Kolmogorov length and fully resolves the instantaneous flame fronts with at least 20 points while utilizing finite rate chemistry and detailed molecular diffusion. Therefore, no turbulence or combustion models are required. However, because of the large dimensions of this flame, this resolution is only achieved upstream near the nozzle for \(x/D<20\), D = 7.5 mm. Here, x is the direction of the mean flow. Fourth order interpolation schemes for flux reconstruction of the spatial discretization schemes and second order time discretization schemes are employed. Because of this, the term quasi-DNS is chosen to describe this simulation. The accuracy of the employed discretization schemes has been justified by comparing canonical test cases with spectral DNS codes in Zirwes et al. (2020). Running the simulation on a coarser mesh would mean that the flame front cannot be fully resolved anymore, so that the regime markers would have to be evaluated on filtered quantities. Also, additional sub-grid models would be required to recover the correct flame structure, which would interfere with the evaluation of the different types of regime markers in a model-free way.
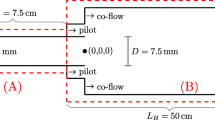
The full description of the simulation setup is given in Zirwes et al. (2020). Here, the simulation setup is described briefly. In configuration FJ-5GP-Lr75-57 (Barlow et al. 2015) of the Sydney/Sandia flame, the central fuel pipe is retracted by 7.5 cm, thus creating compositionally inhomogeneous conditions. Methane/air mixture enters the domain with a bulk velocity of 57 m/s. The simulation consists of three consecutive parts: At first, the fully developed pipe flow of the central methane pipe and annular air flow is simulated using highly resolved LES. The second simulation is a quasi-DNS of the non-reactive mixing of methane and air; and lastly the reactive quasi-DNS of the flame is performed. The simulations have been conducted with an in-house solver (Zhang et al. 2015, 2016; Zirwes et al. 2018, 2019, 2020) that has been validated with and applied to different flame setups (Zhang et al. 2017, 2017; Zirwes et al. 2019; Zhang et al. 2019; Zirwes et al. 2020; Zhang et al. 2020; Zirwes et al. 2020). It uses OpenFOAM (Weller et al. 2017) to solve the conservation equations for mass, momentum, energy and chemical species in compressible formulation with the finite volume method. Cantera (Goodwin et al. 2017) is used for computing detailed transport properties with the mixture-averaged transport model (Kee et al. 2005). A reaction mechanism by Lu and Law (2008) is used for the oxidation of methane, which contains 19 species, 11 quasi steady-state species and about 200 chemical reactions. The computational meshes for both qDNS (non-reactive mixing and the flame) consist of 150 million hexahedral cells each, with a smallest resolution of 5 μm for the non-reactive mixing and 10 μm for the reactive simulation, which is sufficient to resolve the flame front and the flow down to the Kolmogorov scale in the near-nozzle region. Comparison of the qDNS results with experimental data in Zirwes et al. (2020) shows a quantitatively good agreement in terms of time mean and root-mean square values of temperature and species concentrations as well as instantaneous scatter plots. For more detailed information on the grid resolution validation, detailed comparison to experimental data and general numerical setup, see Zirwes et al. (2020).
2.2 Regime Markers
Objective of this work is to utilize the quasi-DNS database of the compositionally inhomogeneous partially premixed Sydney/Sandia flame to evaluate different types of flame regime markers from literature as a post-processing step and to provide a side-by-side comparison of their behavior. In the literature, a direct comparison of all these markers applied to a partially premixed turbulent flame is not available. Because of the qDNS nature of the results and because the reaction zones are fully resolved, the regime markers can be evaluated without modeling assumptions.
In total, three different kinds of flame regime markers are evaluated in this work from the quasi-DNS database and summarized in Table 1.
-
The first type of regime markers uses the alignment of gradients. We evaluate the classical Takeno flame index \(\xi _{{\mathrm {Takeno}}}\) from the mass fractions Y of CH\(_4\) and O\(_2\) as well as its modifications: \(\xi ({{\mathrm {CH}}}_4,{\mathrm {O}}_2)\), which is the normalized Takeno flame index, \(\xi ({\mathrm {CO}},\mathrm{O}_{\mathrm {2}})\) the normalized flame index using CO instead of CH\(_4\) and \(\xi ({{\mathrm {Multi}}},{\mathrm {O}}_2)\) where the fuel species is replaced by the sum \(Y_F=Y_{{{\mathrm {CH}}}_4}+Y_{{\mathrm {CO}}}+Y_{{\mathrm {C}}_2{\mathrm {H}}_2}+Y_{{\mathrm {H}}_2}\). The flame index by Fiorina et al. \(\xi _{{\mathrm {Fiorina}}}\) additionally considers the magnitude of the oxygen gradient and compares it to that in an unstretched premixed flame \(D_O\).
-
The second type of flame regime marker \(\xi _{{\mathrm {GFRI}}}\) uses the gradient free regime identification (GFRI) method based on chemical explosive mode analysis (CEMA) and compares the largest heat release rate in the premixed part of the flame front \(\dot{Q}^{{\mathrm {PF}}}\) to the largest heat release rate peak in the non-premixed part of the flame \(\dot{Q}^{{\mathrm {DF}}}\) along a line.
-
The third marker \(\xi _{{\mathrm {Drift}}}\) computes drift terms which describe how well a given manifold-based combustion model can represent the local flow and flame conditions. The drift term in this work is evaluated in terms of \(D^m={\mathrm {D}}Y_{{\mathrm {CO}}}/{\mathrm {D}}t - {\mathrm {D}}Y_{{\mathrm {CO}}}^m/{\mathrm {D}}t\), which is the value of the substantial derivative of the CO mass fraction in the simulation minus the substantial derivative on the manifold given by combustion model m. The smaller this term, the better can the given model m represent the local conditions. We compare two manifolds: one constructed from steady premixed flames (\(m={\mathrm {PF}}\)) and one constructed from steady diffusion flames (\(m={\mathrm {DF}}\)). As the authors of the drift term analysis note, mass fractions of major species might not be sensitive to the type of manifold, but minor species are. Therefore, we use CO in this study to evaluate the drift terms.
All markers are summarized in Table 1 and defined so that 0 represents the non-premixed regime and 1 the premixed regime (except for the original \(\xi _{{\mathrm {Takeno}}}\) definition). More details about the markers are given in “Appendix A”.
As shown in the introduction, combustion regime markers are widely used to analyze the structure of flames, study phenomena like flame stabilization or flashback, and can aid combustion model selection to improve the accuracy of simulations. Although they have become an important tool for examining flames, different types of flame regime markers can disagree when assigning premixed or non-premixed characteristics to different parts of a flame because they have been derived with varying assumptions and goals. Applying the regime markers to partially premixed turbulent flames for identifying premixed, non-premixed and partially premixed characteristics constitutes an additional problem: Turbulent flames are subject to three-dimensional flame stretch and transient effects like (re-)ignition, which further distorts a clear identification of combustion characteristics in terms of model flames. In addition, since there is no universal formal definition of the partially premixed combustion regime, identifying this regime is mostly done qualitatively. Because of this and due to the complex nature of the physical processes governing partially premixed flames, it cannot be expected that a single regime marker can identify combustion regimes consistently in every situation. It is therefore all the more important to understand the behavior of different regime markers when applied to turbulent partially premixed flames.
Some of the markers from Table 1 require the evaluation of mixture fraction Z and reaction progress c. In this work, the mixture fraction Z is evaluated in terms of the Bilger mixture fraction (Bilger 1979) from the instantaneous species mass fractions:
Here \({\mathrm {C}}\), \({\mathrm {H}}\) and \({\mathrm {O}}\) denote the elements, \(M_i\) is the atomic weight of element i and the subscripts \({\mathrm {F}}\) and \({{\mathrm {Ox}}}\) denote the fuel and oxidizer stream composition.
For the reaction progress variable \(Y_c\), two common definitions are used in this work (Pierce and Moin 2004) and computed in a post-processing step from the simulation data:
Because \(Y_{c_1}\) and \(Y_{c_2}\) are the sum of species mass fractions, they are not normalized. Therefore, a normalized reaction progress variable (Bray et al. 2005) is introduced as
where \(Y_c\) is either \(Y_{c_1}\) or \(Y_{c_2}\). \(Y_c^{{\mathrm {Eq}}}(Z)\) is the value of \(Y_c\) of a mixture with mixture fraction Z at chemical equilibrium, computed from the fresh gas composition at Z, \(T=300\) K, \(p=1\) atm and assuming constant pressure and enthalpy. In this work, \(Y_c^{{\mathrm {Eq}}}(Z)\) has been tabulated for a total number of \(5\cdot 10^4\) mixture fraction values linearly spaced between \(0<Z<1\) for both \(c_1\) and \(c_2\) and interpolated for all cells in the computational domain.
3 Overview of the Flame Structure
Before applying the different regime markers from Table 1, the general flame structure of the Sydney/Sandia flame from the qDNS is discussed in this section. In order to classify the flame, the simulation domain is subdivided into slices with an axial width of \(\varDelta X=10\) mm. The instantaneous volume integrated heat release rate \(\dot{Q}_V\) in each slice is computed by
which is then averaged over ten uncorrelated time steps. The notation \(\langle \dot{Q},\xi ({{\mathrm {CH}}}_4,{\mathrm {O}}_2)>0.5\rangle\) means that only values of the total heat release rate \(\dot{Q}\) are considered, where the flame shows premixed characteristics. In this integration, all values of \(\dot{Q}\) are considered without conditioning to high heat release rates. \(\dot{Q}_{V}^{{\mathrm {PF}}}\) represents the contribution to total heat release rate from regions with premixed combustion mode. The total heat release rate itself is computed from
where \(\dot{\omega }_i\) is the reaction rate of the i-th species and \(\varDelta h^\circ _i\) its enthalpy of formation. The results are depicted in Fig. 1. Black lines show how much heat in total is released depending on the axial position x/D, where D is the diameter of the nozzle, and flame regime (solid line for premixed and dashed for non-premixed). Up to \(10\,D\) near the nozzle, heat is mainly released by premixed regions. Up to \(x/D=2\), heat is released predominantly from lean regions and in the range of \(2<x/D<10\) predominantly from rich regions. Further downstream, total heat release per cross section increases because the reaction zones become generally broader downstream as the flame transitions from a predominantly premixed toward the partially premixed combustion mode. Contributions from both premixed and non-premixed combustion become approximately equal, indicating that both combustion modes are equally important in this mixed-mode flame. Similar results have been found by (Kleinheinz et al. 2017; Perry et al. 2017; Tian and Lindstedt 2019). Luo et al. (2020) found in their LES, that about 70 % of the heat release rate originates from premixed-dominated regions in the upstream part of the flame and further downstream this reduces to 40 %. The quasi-DNS results show that the relative importance of the premixed regions reaches up to 90 % at \(x/D\approx 5\) and stays dominant in the whole range of \(0<x/D<10\). After that, the relative importance of both regions as measured by the heat release rate is about 50 %.
Additionally, the qDNS dataset allows to inspect the heat released from the reaction of each species \(\dot{Q}_i=-\dot{\omega }_i\varDelta h^\circ _i\). Here, the highest contribution to the heat release rate comes from \(\hbox {H}_2\hbox {O}\), \(\hbox {CO}_2\) and H. In the upstream region \(x/D<10\), the product species \(\hbox {H}_2\hbox {O}\) and \(\hbox {CO}_2\) are only produced in premixed regions. H radicals are mainly formed endothermically in non-premixed regions and react exothermically in premixed regions.
The scalar dissipation rate \(\chi _{Z}\) (see Eq. (23) in the “Appendix”) is evaluated using Bilger’s mixture fraction. Its effect on the flame can be seen from Fig. 2. The scatter plot of instantaneous temperature over Bilger mixture fraction at the axial position \(x/D=15\) is colored by the scalar dissipation rate in the range of \(0<\chi _Z<1\,\hbox {s}^{-1}\). The diffusion coefficient for the scalar dissipation rate is assumed to be approximately equal the molecular thermal diffusivity of the mixture. As the scalar dissipation rate increases, the peak temperature decreases, which is consistent with the flamelet assumptions.
Joint probability density function (JPDF) at the position \(x/D=15\), \(r/D=0.75\) of reaction progress variable \(Y_c\) from Eq. (2) and (3) as well as their normalized versions from Eq. (4) and Bilger mixture fraction Z. All JPDFs are conditioned to \(\dot{Q}>10^7\) \(\hbox {W/m}^3\). The center and right column are additionally conditioned to \(\xi ({{\mathrm {CH}}}_4,\,{\mathrm {O}}_2)=1\) (premixed) and 0 (non-premixed)
The structure of the flame at \(x/D>10\) can be understood better by looking at the joint probability density function (JPDF) of mixture fraction and reaction progress. Figure 3 shows the JPDF of the reaction progress \(Y_c\) and normalized reaction progress c at the position \(x/D=15\), \(r/D=0.75\). Additionally, the data is conditioned to only show data points where \(\dot{Q}>10^7\) \(\hbox {W/m}^3\). The first column shows a strong correlation between mixture fraction and reaction progress. This correlation is qualitatively the same for \(c_1\) and \(c_2\). The strong correlation has also been noted by Barlow et al. (2017) and Tian and Lindstedt (2019). Therefore, the commonly made assumption of statistical independence of Z and c does not hold in this partially premixed flame. By conditioning the data to the flame index based on the gradient of fuel and oxidizer species \(\xi ({{\mathrm {CH}}}_4,{\mathrm {O}}_2)\) (see Table 1) in the second and third column, the flame structure can be seen to generate its heat from rich premixed (\(\xi ({{\mathrm {CH}}}_4,{\mathrm {O}}_2)=1\), \(Z>0.055\)) and stoichiometric non-premixed regions.
It is interesting to note that the alignment of mixture fraction and reaction progress variable gradients are mostly parallel or anti-parallel. Figure 4 shows histograms of the cosine of the angle between gradients of Z and c sampled at \(x/D=15\) for regions with \(\dot{Q}>10^7\) \(\hbox {W/m}^3\). This bimodal distribution is true for all different axial positions \(0<x/D<30\). As suggested by Domingo et al. (2002), Favier and Vervisch (2001) and Nguyen et al. (2010), a value of \(\xi (Z,c)\) between 0 and 1 suggests a partially premixed flame. Although the flame shows clear characteristics of partially premixed combustion (see the next section for more details) for \(x/D\ge 10\), the distribution of \(\xi (Z,c)\) is bimodal at 0 and 1. Wu and Ihme (2016) found similar results and concluded that the flame regime marker based on the alignment of Z and c is not able to correctly predict the partially premixed characteristic of this flame. It should be noted, however, that the mixture fraction Z in this work is computed as a post-processing step from the simulation results. Because the simulation considers preferential diffusion, Z is not a conserved scalar here. Nonetheless, the results are consistent to the findings in Wu and Ihme (2016).
4 Direct Comparison of Flame Regime Markers
4.1 Visualization of the Flame Structure
Instantaneous axial cutting planes of: a temperature; b fuel mass fraction gradient; c chemical mode \({{ CM }}\); d non-normalized Takeno flame index; e normalized Takeno flame index; f flame index by Fiorina using \(c_1\) as progress variable; g flame index based on CO and oxidizer. Cutting planes e–g only show regions where \(\dot{Q}>10^7\,\hbox {W/m}_{3}\)
In order to get a better overview of the flame, Fig. 5 presents axial cutting planes \(0<x/D<30\) of different quantities for one instantaneous time step, see Table 1. At the top (Fig. 5a), the temperature field is depicted. On the left, the cold, unburnt and partially premixed methane/air enters the domain from the central nozzle. It is surrounded by a hot pilot flow with the composition of methane/air at an equivalence ratio of unity at chemical equilibrium.
In Fig. 5b, the magnitude of the gradient of fuel mass fraction \(Y_{{{\mathrm {CH}}}_4}\) is shown for the same time step as Fig. 5a. The flow enters the domain in a partially premixed state and creates stratified conditions throughout the whole domain. Figure 5c shows the chemical mode \({{ CM }}\) (see Eq. (30)). Figure 5d depicts the non-normalized Takeno flame index from Eq. (9). Positive values mark premixed regions of the flame and negative ones non-premixed regions. In this picture, the Takeno flame index is shown at every location, e.g. also within the central nozzle, where only inert mixing occurs. In contrast to this, the Fig. 5e–g are conditioned to the heat release rate. The gray areas indicate regions where \(\dot{Q}<10^7\) \(\hbox {W/m}^3\), so that the flame index is only shown where an actual flame front is present. Figure 5e shows the normalized Takeno flame index based on the mass fraction of the fuel species and \(\hbox {O}_2\). Upstream near the nozzle in Fig. 5e, the reaction zone is thin and in the premixed regime, as indicated by \(\xi ({{\mathrm {CH}}}_4,{\mathrm {O}}_2)\) being close to unity (red color). On the outside, two additional reaction zones appear which are a consequence of the hot pilot mixing with the surrounding cold air co-flow, resulting in dissociation reactions. Further downstream, the inner part of the flame front is predicted to be premixed with an outer, non-premixed layer. In the last third of the domain, a triple flame structure is visible, with two premixed reaction zones surrounding a non-premixed one. This structure is discussed in more detail further below.
The regime marker by Fiorina et al. from Eq. (16) in Fig. 5f shows similar results to 5e. Here, \(c_1\) from Eq. (2) is used to lookup the magnitude of the oxygen gradient from premixed flamelet tables. In total, \(10^4\) freely propagating flames were computed between \(0<Z<0.5\) to create the look-up tables for computing \(D_O\) (see Table 1). The largest difference between \(\xi _{{\mathrm {Fiorina}}}(c_1)\) and \(\xi ({{\mathrm {CH}}}_4,{\mathrm {O}}_2)\) occurs downstream, where \(\xi _{{\mathrm {Fiorina}}}(c_1)\) predicts a larger portion of the flame to be non-premixed.
Figure 5g shows the regime marker based on the mass fraction of CO instead of \(\hbox {CH}_4\), as proposed by Som and Aggarwal (2010) (see Table 1 and the discussion in Sect. 1 about using CO instead of \(\hbox {CH}_4\)). According to this marker, the part of the flame near the nozzle, where the reaction zone is thin, consists of an inner non-premixed zone and an outer premixed zone, in contrast to \(\xi ({{\mathrm {CH}}}_4,{\mathrm {O}}_2)\), which predicts a purely premixed zone. Also, the premixed regions downstream predicted by \(\xi ({\mathrm {CO}},{\mathrm {O}}_2)\) are much thinner than those predicted by \(\xi ({{\mathrm {CH}}}_4,{\mathrm {O}}_2)\).
Instantaneous cutting planes at axial positions \(x/D=5\) (top) and \(x/D=20\) (bottom). In the left column, the chemical mode is depicted and on the right the normalized flame index in regions where \(\dot{Q}>10^7\) \(\hbox {W/m}^3\). The yellow line shows the iso-contour of \(Z=Z_{{\mathrm {st}}}\) and the green line the iso-contour of \(\dot{Q}=10^8\) \(\hbox {W/m}^3\). F denotes the fuel species, here \(\hbox {CH}_4\)
In Fig. 1 in Sect. 3, it was already pointed out that the flame shows mostly premixed characteristics near the nozzle and both premixed and non-premixed characteristics further downstream. Also, the reaction zones become broader with increasing axial position. This is illustrated in Fig. 6: In the top row, two instantaneous slices at \(x/D=5\) depicting the chemical mode (left) and flame index \(\xi (F,{\mathrm {O}}_2)\), where the fuel species F is \(\hbox {CH}_4\) (right), illustrate the flame. The right column is additionally conditioned to the heat release rate, showing only regions where \(\dot{Q}>10^7\) \(\hbox {W/m}^3\). The yellow line is the iso-contour of \(Z=Z_{{\mathrm {st}}}\), which shows that the reaction zone lies fully in the rich part of the flame. The green line is the iso-contour of \(\dot{Q}=10^8\) \(\hbox {W/m}^3\). This region of high heat release rate is located exactly where the \({{ CM }}\) has its zero-crossing, jumping from the explosive mode (positive values, red area) to negative values (blue area). High heat release rate near a zero-crossing of \({ CM }\) signifies a premixed reaction zone (Sect. 1) or auto-ignition. Likewise, the flame index on the right shows that the whole region of high heat release rate encompassed by the green iso-contour is premixed (red). Further downstream at \(x/D=20\) (bottom row of Fig. 6), the region of high heat release rate lies directly at \(Z=Z_{{\mathrm {st}}}\) with negative values of \({ CM }\), marking a non-premixed reaction zone. The region with moderate heat release rates \(\dot{Q}>10^7\) \(\hbox {W/m}^3\) is much broader (bottom right of Fig. 6, non-gray area) and contains both premixed and non-premixed parts as identified by the flame index.
4.2 Premixed-Dominated Regime
In this and the following subsections, a direct comparison of the different flame regime markers from Table 1 along instantaneous flame fronts will be given and different aspects of their applicability and behavior highlighted. As shown in Sect. 3, the flame is predominantly premixed at \(x/D<10\). Figure 7 shows the different flame markers along an instantaneous radial line at \(x/D=1\). All gradients and quantities are evaluated in the full 3D space and then plotted along that line. In Fig. 7a, a single heat release rate peak is visible, which lies at the location of the zero-crossing of CM (red line). This heat release rate peak is identified by the GFRI approach as premixed, because it lies within 100 \(\mu \hbox {m}\) of the zero-crossing. Using larger radii can lead to a wrong characterization, because the flame fronts are thin upstream and zero-crossings far away from the heat release rate peaks have to be excluded (see also the “Appendix” for a discussion on this). Further downstream, however, the flame becomes broader and this value has to be increased to 175 \(\mu \hbox {m}\) in order to correctly identify the flame regimes. These values were chosen empirically, so that zero-crossings are assigned to the correct heat release rate peaks. Premixed heat release rate peaks as classified by GFRI are marked by a red dot (from here on, red meaning premixed and blue non-premixed), leading to a value of \(\xi _{{\mathrm {GFRI}}}=1\) (or 100 %).
Figure 7b evaluates the other flame markers from Table 1 along that line. The profile of the heat release rate is overlaid to give a reference where a position is relative to the reaction zone. The percentage numbers on the right show the relative importance of combustion regimes in terms of heat release rate, computed from:
Therefore, a value of 1 or 100 % means a fully premixed flame.
All regime markers classify this flame as mostly premixed. The only two exceptions are the flame index based on the gradient alignment of CO and \(\hbox {O}_2\), which classifies the inner part of the flame as non-premixed, and \(\xi _{{\mathrm {Drift}}}({\mathrm {CO}})\), which predicts a flame that has premixed character on the rich, inner side and mixed-mode character on the lean side. This result is consistent with findings of Wu and Ihme (2016) and shows that even though this flame is predominantly premixed, the evolution of the CO mass fraction is best described by a blending of premixed and non-premixed manifolds due to the flame being stretched and subjected to transient effects.
Direct comparison of flame regime markers along an instantaneous radial line at \(x/D=1\) (left) and \(x/D=3\) (right). Subfigures show: a and c: profiles of \({ CM }\), \(\dot{Q}\) and Z. b and d values of different regime markers from Table 1 along the line
In Fig. 8 on the left, the evaluation of the markers is done for a different time instance at the same radial line as Fig. 7 at \(x/D=1\). Although the flame is predominantly premixed at this position, other combustion modes appear as well. The heat release rate has two distinct peaks (Fig. 8a), where the highest heat release rate is directly located at the zero-crossing of \({ CM }\) and is therefore designated \(\dot{Q}^{{\mathrm {PF}}}\) by GFRI. The second heat release rate peak occurs at a position where \({ CM }\) is negative. However, since \(Z< Z_{{\mathrm {st}}}\), it is identified as part of a premixed flame. \(\dot{Q}^{{\mathrm {DF}}}\) in this case is zero, because within the region of interest (RoI), which is set in this work to \(\pm 0.5\) mm around the zero-crossing due to the broadening of the reaction zone, no heat is released in regions with \({ CM }<0\) and \(0.055>Z> 0.07\) (see the “Appendix” for more information). The flame is therefore classified as premixed by GFRI, which is consistent with most other markers in Fig. 8b. The only marker that identifies the outer part of the flame as non-premixed is \(\xi _{{\mathrm {Drift}}}\) in the last row of Fig. 8b. It is interesting to note that this second heat release rate peak is accompanied by a jump in \({ CM }\) entirely in the negative range.
Another situation where the different flame regime markers disagree is depicted in Fig. 8 on the right at the axial position \(x/D=3\). The maximum heat release rate value is located near the CM zero-crossing and is therefore identified as \(\dot{Q}^{{\mathrm {PF}}}\) by GFRI. Due to the broadening of the reacting zone, \(\dot{Q}^{{\mathrm {DF}}}\) is located on the outer side of the reaction zone, leading to the classification of a predominantly premixed flame. Similarly, the flame index based on \(\hbox {CH}_4\) and \(\hbox {O}_2\) gradients as well as its multi-component extension (second row from the bottom in Fig. 8d) characterize the flame as predominantly premixed. The flame index by Fiorina et al. and the marker based on drift term analysis predict a partially premixed flame, where the heat is released approximately equally in both combustion regimes.
4.3 Partially Premixed Regime
Direct comparison of flame regime markers along an instantaneous radial line at \(x/D=15\). Subfigures show: a profiles of \({ CM }\), \(\dot{Q}\) and Z. b Values of different regime markers from Table 1 along the line
For \(x/D>10\), the statistical average from Fig. 6 shows that heat is generated in equal parts from premixed and non-premixed regions. An instantaneous flame front in this region is depicted in Fig. 9. The heat release rate profile has three distinct peaks, where the global maximum heat release rate at \(r=5\) mm is identified as \(\max (\dot{Q}^{{\mathrm {PF}}})\) (red circle) and the middle peak is the maximum heat release rate \(\max (\dot{Q}^{{\mathrm {DF}}})\) (blue circle) outside the zero-crossing and within the RoI with \({ CM }<0\) and \(Z>Z_{{\mathrm {st}}}\), yielding \(\xi _{{\mathrm {GFRI}}}=0.21\). Most flame markers from subfigure b identify the inner part of the flame as non-premixed as well. The exceptions are the one by Fiorina et al., especially when using \(Y_{c_2}\) from Eq. (3) to retrieve the oxygen mass fraction gradient from the premixed tables, the flame index based on CO and the regime marker based on drift term analysis. The outer part of the flame (\(r>8\) mm) is identified by all regime markers as non-premixed. The flame index based on \(\hbox {CH}_4\) and \(\hbox {O}_2\) as well as the ones by Fiorina et al. (first three rows) identify a section of the flame at \(r=10\) mm as premixed. However, this is only an artifact of the numerical evaluation. The gradient of \(\hbox {CH}_4\) at that position is close to zero, so that the flame index becomes meaningless. Using instead the multi-species marker (second row from the bottom) extends the range of applicability of this marker and consistently identifies the outer part of the flame as non-premixed.
5 Summary and Conclusion
In this work, three types of fundamentally different flame regime markers from the literature have been applied to a simulation database of the compositionally inhomogeneous, partially premixed turbulent Sydney/Sandia flame in configuration FJ-5GP-Lr75-57, where the flame is fully resolved. The simulation has been performed using finite rate chemistry as well as detailed molecular diffusion. This allows computing the markers without the influence of combustion models as a post-processing step. When evaluating the combustion regime as a statistical average in terms of the heat generation, the upstream region of the flame (\(x/D<10\)) is predominantly premixed (lean premixed for \(x/D<2\) and rich premixed for \(2<x/D<10\)), with up to 90 % of heat being generated in regions with premixed characteristics. Downstream of that, heat generated from both the premixed and non-premixed regime becomes approximately equal.
The partially premixed character of this flame at \(x/D>10\) is not only created by having alternating premixed and non-premixed flamelets appear at the same location at different times, but also through direct interaction of premixed and non-premixed flame fronts as identified by all different regime markers. Even at \(x/D<10\), where the heat is generated in predominantly premixed regions, instantaneous flame fronts can show mixed characteristics. Even though direct comparison of the different types of regime markers shows discrepancies and further research for consistent regime identification is required, the following results can be summarized:
-
1.
The flame index based on the alignment of methane and oxygen mass fraction gradients gives wrong results in parts of the reaction zone, where methane is fully depleted. Likewise, using CO instead of CH\(_4\) can only be used in the outer part of the flame to give consistent results. Therefore, a multi-species approach developed in the past (Lignell et al. 2011; Jangi et al. 2015; Minamoto et al. 2015; Ma et al. 2016; Pei et al. 2016; Wei et al. 2018; Pang et al. 2018; Tufano et al. 2018; Hu and Kurose 2019b; Wan et al. 2019; Wen et al. 2019; Akaotsu et al. 2020), where the fuel species is the combination of e.g. \(\hbox {CH}_4\), CO, \(\hbox {H}_2\) and \(\hbox {C}_2\hbox {H}_2\), is able to extend the range of applicability to the whole flame front in all investigated cases.
-
2.
In almost all cases, results of the GFRI method \(\xi _{{\mathrm {GFRI}}}\) are consistent with the flame index based on a combination of fuel and intermediate species \(\xi ({{\mathrm {Multi}}},{\mathrm {O}}_2)\). The regime marker by Fiorina et al. in its original formulation has the same limitations as the classical Takeno flame index, i.e. the depletion of the fuel within the flame front, and is the only marker that predicts non-premixed characteristics at the inner part of the flame for \(x/D<10\) in some cases. Also, the exact way of tabulation for the premixed flamelets for comparing the oxygen gradient, e.g. the choice of progress variable, can have a strong impact on the prediction of \(\xi _{{\mathrm {Fiorina}}}\).
-
3.
The Bilger mixture fraction Z and progress variable c are statistically strongly correlated. Although instantaneous flame fronts have mixed mode characteristics, the alignment of Z and c gradients are mostly parallel and anti-parallel.
-
4.
The GFRI approach yields consistent results with the flame indices based on gradient alignment. For this, the radius around the CM zero-crossing used to find \(\dot{Q}^{{\mathrm {PF}}}\) has to be increased from 100 \(\mu \hbox {m}\) to 175 \(\mu \hbox {m}\) downstream where the flame becomes generally thicker.
-
5.
The regime marker based on drift term analysis is species specific. As intermediate species have higher sensitivity to the choice of combustion model than main species, the drift terms for CO are evaluated. Even for instantaneous flame fronts, where all other regime markers predict a dominant regime in terms of premixed or non-premixed, \(\xi _{{\mathrm {Drift}}}({\mathrm {CO}})\) tends to predict a mixed mode. The reason is that \(\xi _{{\mathrm {Drift}}}({\mathrm {CO}})\) does not specifically determine the combustion regime but finds the optimal blending of two combustion models to represent the profile of the chosen species. In the presence of flame stretch, a blending of the premixed and non-premixed model improves the accuracy of the CO profile even though the flame shows otherwise dominantly premixed characteristics. It is also the only marker that identifies outer heat release rate peaks (in case of instantaneous flame fronts with two heat release rate peaks) near the nozzle as non-premixed. These peaks lie in the negative \({ CM }\) range.
References
Addad, Y., Zaidi, I., Laurence, D.: Quasi-DNS of natural convection flow in a cylindrical annuli with an optimal polyhedral mesh refinement. Comput. Fluids 118, 44–52 (2015)
Akaotsu, S., Matsushita, Y., Aoki, H., Malalasekera, W.: Analysis of flame structure using detailed chemistry and applicability of flamelet/progress variable model in the laminar counter-flow diffusion flames of pulverized coals. Advanced Powder Technology (2020)
Akaotsu, S., Ozawa, R., Matsushita, Y., Aoki, H., Malalasekera, W.: Effects of infinitely fast chemistry on combustion behavior of coaxial diffusion flame predicted by large eddy simulation. Fuel Process. Technol. 199, 106226 (2020)
Amaduzzi, R., Ceriello, G., Ferrarotti, M., Sorrentino, G., Parente, A.: Evaluation of modelling approaches for mild combustion systems with internal recirculation. Front. Mech. Eng. 6, 20 (2020)
An, Y., Jaasim, M., Raman, V., Pérez, F.E.H., Sim, J., Chang, J., Im, H.G., Johansson, B.: Homogeneous charge compression ignition (HCCI) and partially premixed combustion (ppc) in compression ignition engine with low octane gasoline. Energy 158, 181–191 (2018)
Barlow, R., Meares, S., Magnotti, G., Cutcher, H., Masri, A.: Local extinction and near-field structure in piloted turbulent CH4/air jet flames with inhomogeneous inlets. Combust. Flame 162(10), 3516–3540 (2015)
Barlow, R.S., Magnotti, G., Cutcher, H.C., Masri, A.R.: On defining progress variable for Raman/Rayleigh experiments in partially-premixed methane flames. Combust. Flame 179, 117–129 (2017)
Benim, A.C., Pfeiffelmann, B., Ocłoń, P., Taler, J.: Computational investigation of a lifted hydrogen flame with LES and FGM. Energy 173, 1172–1181 (2019)
Bilger, R.: Turbulent jet diffusion flames. In: Energy and Combustion Science, pp. 109–131. Elsevier (1979)
Bouheraoua, L., Domingo, P., Ribert, G.: Large-eddy simulation of a supersonic lifted jet flame: analysis of the turbulent flame base. Combust. Flame 179, 199–218 (2017)
Bray, K., Domingo, P., Vervisch, L.: Role of the progress variable in models for partially premixed turbulent combustion. Combust. Flame 141(4), 431–437 (2005)
Briones, A.M., Aggarwal, S.K., Katta, V.R.: A numerical investigation of flame liftoff, stabilization, and blowout. Phys. Fluids 18(4), 043603 (2006)
Butz, D., Hartl, S., Popp, S., Walther, S., Barlow, R.S., Hasse, C., Dreizler, A., Geyer, D.: Local flame structure analysis in turbulent CH4/air flames with multi-regime characteristics. Combust. Flame 210, 426–438 (2019)
Chen, Z.X., Langella, I., Barlow, R.S., Swaminathan, N.: Prediction of local extinctions in piloted jet flames with inhomogeneous inlets using unstrained flamelets. Combust. Flame 212, 415–432 (2020)
Chu, X., Laurien, E., McEligot, D.M.: Direct numerical simulation of strongly heated air flow in a vertical pipe. Int. J. Heat Mass Transf. 101, 1163–1176 (2016)
Chung, J.D., Zhang, X., Kaplan, C.R., Oran, E.S.: The structure of the blue whirl revealed. arXiv preprint arXiv:1909.12347 (2019)
Dietzsch, F., Scholtissek, A., Hunger, F., Hasse, C.: The impact of thermal diffusion on the structure of non-premixed flames. Combust. Flame 194, 352–362 (2018)
Doan, N.A.K., Swaminathan, N.: Analysis of markers for combustion mode and heat release in MILD combustion using DNS data. Combust. Sci. Technol. 191(5–6), 1059–1078 (2019)
Domingo, P., Vervisch, L., Bray, K.: Partially premixed flamelets in LES of nonpremixed turbulent combustion. Combust. Theor. Model. 6(4), 529–551 (2002)
Domingo, P., Vervisch, L., Réveillon, J.: DNS analysis of partially premixed combustion in spray and gaseous turbulent flame-bases stabilized in hot air. Combust. Flame 140(3), 172–195 (2005)
Domingo, P., Vervisch, L., Veynante, D.: Large-eddy simulation of a lifted methane jet flame in a vitiated coflow. Combust. Flame 152(3), 415–432 (2008)
Dressler, L., Filho, F.S., Sadiki, A., Janicka, J.: Influence of thickening factor treatment on predictions of spray flame properties using the atf model and tabulated chemistry. Flow Turbulence and Combustion (2020)
Duboc, B., Ribert, G., Domingo, P.: Hybrid transported-tabulated chemistry for partially premixed combustion. Comput. Fluids 179, 206–227 (2019)
Eckel, G., Grohmann, J., Cantu, L., Slavinskaya, N., Kathrotia, T., Rachner, M., Le Clercq, P., Meier, W., Aigner, M.: LES of a swirl-stabilized kerosene spray flame with a multi-component vaporization model and detailed chemistry. Combust. Flame 207, 134–152 (2019)
Enger, S., Basu, B., Breuer, M., Durst, F.: Numerical study of three-dimensional mixed convection due to buoyancy and centrifugal force in an oxide melt for Czochralski growth. J. Cryst. Growth 219(1–2), 144–164 (2000)
Favier, V., Vervisch, L.: Edge flames and partially premixed combustion in diffusion flame quenching. Combust. Flame 125(1–2), 788–803 (2001)
Fiorina, B., Gicquel, O., Vervisch, L., Carpentier, S., Darabiha, N.: Approximating the chemical structure of partially premixed and diffusion counterflow flames using FPI flamelet tabulation. Combust. Flame 140(3), 147–160 (2005)
Forooghi, P., Flory, M., Bertsche, D., Wetzel, T., Frohnapfel, B.: Heat transfer enhancement on the liquid side of an industrially designed flat-tube heat exchanger with passive inserts-numerical investigation. Appl. Therm. Eng. 123, 573–583 (2017)
Fredrich, D., Jones, W., Marquis, A.J.: The stochastic fields method applied to a partially premixed swirl flame with wall heat transfer. Combust. Flame 205, 446–456 (2019)
Goodwin, D., Moffat, H., Speth, R.: Cantera: An object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes. version 2.3.0b (2017). Software available at http://www.cantera.org
Gordon, R.L., Masri, A.R., Pope, S.B., Goldin, G.M.: Transport budgets in turbulent lifted flames of methane autoigniting in a vitiated co-flow. Combust. Flame 151(3), 495–511 (2007)
Han, W., Scholtissek, A., Hasse, C.: The role of tangential diffusion in evaluating the performance of flamelet models. Proc. Combust. Inst. 37(2), 1767–1774 (2019)
Hansinger, M., Zirwes, T., Zips, J., Pfitzner, M., Zhang, F., Habisreuther, P., Bockhorn, H.: The Eulerian stochastic fields method applied to large eddy simulations of a piloted flame with inhomogeneous inlet. Flame Turbulence and Combustion (2020)
Hartl, S., Geyer, D., Dreizler, A., Magnotti, G., Barlow, R.S., Hasse, C.: Regime identification from Raman/Rayleigh line measurements in partially premixed flames. Combust. Flame 189, 126–141 (2018)
Hartl, S., Geyer, D., Hasse, C., Zhao, X., Wang, H., Barlow, R.S.: Assessing an experimental approach for chemical explosive mode and heat release rate using DNS data. Combust. Flame 209, 214–224 (2019)
Hartl, S., Messig, D., Fuest, F., Hasse, C.: Flame structure analysis and flamelet/progress variable modelling of DME/air flames with different degrees of premixing. Flow Turbul. Combust. 102(3), 757–773 (2019)
Hartl, S., Van Winkle, R., Geyer, D., Dreizler, A., Magnotti, G., Hasse, C., Barlow, R.: Assessing the relative importance of flame regimes in Raman/Rayleigh line measurements of turbulent lifted flames. Proc. Combust. Inst. 37(2), 2297–2305 (2019)
Hindmarsh, A.C., Brown, P.N., Grant, K.E., Lee, S.L., Serban, R., Shumaker, D.E., Woodward, C.S.: SUNDIALS: Suite of nonlinear and differential/algebraic equation solvers. ACM Trans. Math. Softw. 31(3), 363–396 (2005)
Hu, Y., Kai, R., Kurose, R., Gutheil, E., Olguin, H.: Large eddy simulation of a partially pre-vaporized ethanol reacting spray using the multiphase DTF/flamelet model. Int. J. Multiph. Flow 125, 103216 (2020)
Hu, Y., Kurose, R.: Large-eddy simulation of turbulent autoigniting hydrogen lifted jet flame with a multi-regime flamelet approach. Int. J. Hydrogen Energy 44(12), 6313–6324 (2019)
Hu, Y., Kurose, R.: Partially premixed flamelet in LES of acetone spray flames. Proc. Combust. Inst. 37(3), 3327–3334 (2019)
Huang, Z.W., He, G.Q., Qin, F., Cao, D.Q., Wei, X.Q., Shi, L.: Large eddy simulation of combustion characteristics in a kerosene fueled rocket-based combined-cycle engine combustor. Acta Astronaut. 127, 326–334 (2016)
Jangi, M., Lucchini, T., Gong, C., Bai, X.S.: Effects of fuel cetane number on the structure of diesel spray combustion: An accelerated Eulerian stochastic fields method. Combust. Theor. Model. 19(5), 549–567 (2015)
Ji, H., Kwon, M., Kim, S., Kim, Y.: Numerical modeling for multiple combustion modes in turbulent partially premixed jet flames. J. Mech. Sci. Technol. 32(11), 5511–5519 (2018)
Jung, J.H., Yoo, G.J.: Analysis of unsteady turbulent triple jet flow with temperature difference. J. Nucl. Sci. Technol. 41(9), 931–942 (2004)
Kee, R., Coltrin, M., Glarborg, P.: Chemically Reacting Flow: Theory and Practice. Wiley, London (2005)
Kimura, N., Igarashi, M., Kamide, H.: Investigation on convective mixing of triple-jet-evaluation of turbulent quantities using particle image velocimetry and direct numerical simulation. In: Advances In Fluid Modeling And Turbulence Measurements, pp. 651–658. World Scientific (2002)
Kleinheinz, K., Kubis, T., Trisjono, P., Bode, M., Pitsch, H.: Computational study of flame characteristics of a turbulent piloted jet burner with inhomogeneous inlets. Proc. Combust. Inst. 36(2), 1747–1757 (2017)
Knudsen, E., Pitsch, H.: A general flamelet transformation useful for distinguishing between premixed and non-premixed modes of combustion. Combust. Flame 156(3), 678–696 (2009)
Knudsen, E., Pitsch, H.: Capabilities and limitations of multi-regime flamelet combustion models. Combust. Flame 159(1), 242–264 (2012)
Komen, E., Camilo, L., Shams, A., Geurts, B.J., Koren, B.: A quantification method for numerical dissipation in quasi-DNS and under-resolved DNS, and effects of numerical dissipation in quasi-DNS and under-resolved DNS of turbulent channel flows. J. Comput. Phys. 345, 565–595 (2017)
Komen, E., Shams, A., Camilo, L., Koren, B.: Quasi-DNS capabilities of OpenFOAM for different mesh types. Comput. Fluids 96, 87–104 (2014)
Krisman, A., Hawkes, E.R., Talei, M., Bhagatwala, A., Chen, J.H.: Polybrachial structures in dimethyl ether edge-flames at negative temperature coefficient conditions. Proc. Combust. Inst. 35(1), 999–1006 (2015)
Lamouroux, J., Ihme, M., Fiorina, B., Gicquel, O.: Tabulated chemistry approach for diluted combustion regimes with internal recirculation and heat losses. Combust. Flame 161(8), 2120–2136 (2014)
Lecrivain, G., Rayan, R., Hurtado, A., Hampel, U.: Using quasi-DNS to investigate the deposition of elongated aerosol particles in a wavy channel flow. Comput. Fluids 124, 78–85 (2016)
Li, Z., Galassi, R.M., Ciottoli, P.P., Parente, A., Valorani, M.: Characterization of jet-in-hot-coflow flames using tangential stretching rate. Combust. Flame 208, 281–298 (2019)
Lignell, D.O., Chen, J.H., Schmutz, H.A.: Effects of Damköhler number on flame extinction and reignition in turbulent non-premixed flames using DNS. Combust. Flame 158(5), 949–963 (2011)
Lipatnikov, A.: Fundamentals of Premixed Turbulent Combustion. CRC Press, London (2012)
Lock, A.J., Briones, A.M., Qin, X., Aggarwal, S.K., Puri, I.K., Hegde, U.: Liftoff characteristics of partially premixed flames under normal and microgravity conditions. Combust. Flame 143(3), 159–173 (2005)
Lu, S., Fan, J., Luo, K.: High-fidelity resolution of the characteristic structures of a supersonic hydrogen jet flame with heated co-flow air. Int. J. Hydrogen Energy 37(4), 3528–3539 (2012)
Lu, T., Law, C.: A criterion based on computational singular perturbation for the identification of quasi steady state species: a reduced mechanism for methane oxidation with no chemistry. Combust. Flame 154(4), 761–774 (2008)
Lu, T., Yoo, C., Chen, J., Law, C.: Analysis of a turbulent lifted hydrogen/air jet flame from direct numerical simulation with computational singular perturbation. In: 46th AIAA Aerospace Sciences Meeting and Exhibit, p. 1013 (2008)
Lu, T., Yoo, C.S., Chen, J., Law, C.K.: Three-dimensional direct numerical simulation of a turbulent lifted hydrogen jet flame in heated coflow: a chemical explosive mode analysis. J. Fluid Mech. 652, 45–64 (2010)
Luo, K., Liu, R., Bai, Y., Bi, W., Fan, J.: Large eddy simulation of turbulent partially premixed flames with inhomogeneous inlets using the dynamic second-order moment closure model. Combustion Theory and Modelling, pp. 1–20 (2020)
Luo, Z., Yoo, C.S., Richardson, E.S., Chen, J.H., Law, C.K., Lu, T.: Chemical explosive mode analysis for a turbulent lifted ethylene jet flame in highly-heated coflow. Combust. Flame 159(1), 265–274 (2012)
Ma, L., Naud, B., Roekaerts, D.: Transported PDF modeling of ethanol spray in hot-diluted coflow flame. Flow Turbul. Combust. 96(2), 469–502 (2016)
Maio, G., Cailler, M., Fiorina, B., Mercier, R., Moureau, V.: LES modeling of piloted jet flames with inhomogeneous inlets using tabulated chemistry methods. In: 55th AIAA Aerospace Sciences Meeting, p. 1471 (2017)
Masri, A.: Partial premixing and stratification in turbulent flames. Proc. Combust. Inst. 35(2), 1115–1136 (2015)
Mayrhofer, A., Laurence, D., Rogers, B., Violeau, D.: DNS and LES of 3-D wall-bounded turbulence using smoothed particle hydrodynamics. Comput. Fluids 115, 86–97 (2015)
Meares, S., Masri, A.: A modified piloted burner for stabilizing turbulent flames of inhomogeneous mixtures. Combust. Flame 161(2), 484–495 (2014)
Meares, S., Prasad, V., Magnotti, G., Barlow, R., Masri, A.: Stabilization of piloted turbulent flames with inhomogeneous inlets. Proc. Combust. Inst. 35(2), 1477–1484 (2015)
Minamoto, Y., Kolla, H., Grout, R.W., Gruber, A., Chen, J.H.: Effect of fuel composition and differential diffusion on flame stabilization in reacting syngas jets in turbulent cross-flow. Combust. Flame 162(10), 3569–3579 (2015)
Minamoto, Y., Swaminathan, N., Cant, S.R., Leung, T.: Morphological and statistical features of reaction zones in mild and premixed combustion. Combust. Flame 161(11), 2801–2814 (2014)
Nguyen, P.D., Vervisch, L., Subramanian, V., Domingo, P.: Multidimensional flamelet-generated manifolds for partially premixed combustion. Combust. Flame 157(1), 43–61 (2010)
Nikitin, N., Nicoud, F., Wasistho, B., Squires, K., Spalart, P.R.: An approach to wall modeling in large-eddy simulations. Phys. Fluids 12(7), 1629–1632 (2000)
Nordin-Bates, K., Fureby, C., Karl, S., Hannemann, K.: Understanding scramjet combustion using LES of the HyShot II combustor. Proc. Combust. Inst. 36(2), 2893–2900 (2017)
Pang, K.M., Jangi, M., Bai, X.S., Schramm, J., Walther, J.H.: Modelling of diesel spray flames under engine-like conditions using an accelerated Eulerian stochastic field method. Combust. Flame 193, 363–383 (2018)
Paulhiac, D., Cuenot, B., Riber, E., Esclapez, L., Richard, S.: Analysis of the spray flame structure in a lab-scale burner using large eddy simulation and discrete particle simulation. Combust. Flame 212, 25–38 (2020)
Pei, Y., Hawkes, E.R., Bolla, M., Kook, S., Goldin, G.M., Yang, Y., Pope, S.B., Som, S.: An analysis of the structure of an n-dodecane spray flame using TPDF modelling. Combust. Flame 168, 420–435 (2016)
Perry, B.A., Mueller, M.E.: Effect of multiscalar subfilter PDF models in LES of turbulent flames with inhomogeneous inlets. Proc. Combust. Inst. 37(2), 2287–2295 (2019)
Perry, B.A., Mueller, M.E., Masri, A.R.: A two mixture fraction flamelet model for large eddy simulation of turbulent flames with inhomogeneous inlets. Proc. Combust. Inst. 36(2), 1767–1775 (2017)
Peters, N.: Turbulent combustion (2001)
Pierce, C.D., Moin, P.: Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 504, 73–97 (2004)
Pouransari, Z., Vervisch, L., Fuchs, L., Johansson, A.V.: DNS analysis of wall heat transfer and combustion regimes in a turbulent non-premixed wall-jet flame. Flow Turbul. Combust. 97(3), 951–969 (2016)
Raufeisen, A., Breuer, M., Botsch, T., Delgado, A.: DNS of rotating buoyancy-and surface tension-driven flow. Int. J. Heat Mass Transf. 51(25–26), 6219–6234 (2008)
Rieth, M., Kempf, A.M., Stein, O.T., Kronenburg, A., Hasse, C., Vascellari, M.: Evaluation of a flamelet/progress variable approach for pulverized coal combustion in a turbulent mixing layer. Proc. Combust. Inst. 37(3), 2927–2934 (2019)
Rosenberg, D.A., Allison, P.M., Driscoll, J.F.: Flame index measurements to assess partially-premixed flame models. In: 8th US National Combustion Meeting, Park City, UT (2013)
Rosenberg, D.A., Allison, P.M., Driscoll, J.F.: Flame index and its statistical properties measured to understand partially premixed turbulent combustion. Combust. Flame 162(7), 2808–2822 (2015)
Saeedipour, M., Vincent, S., Pirker, S.: Large eddy simulation of turbulent interfacial flows using approximate deconvolution model. Int. J. Multiph. Flow 112, 286–299 (2019)
Scholtissek, A., Pitz, R., Hasse, C.: Flamelet budget and regime analysis for non-premixed tubular flames. Proc. Combust. Inst. 36(1), 1349–1356 (2017)
Scholtissek, A., Popp, S., Hartl, S., Olguin, H., Domingo, P., Vervisch, L., Hasse, C.: Derivation and analysis of two-dimensional composition space equations for multi-regime combustion using orthogonal coordinates. Combust. Flame 218, 205–217 (2020)
Shams, A., Roelofs, F., Komen, E., Baglietto, E.: Optimization of a pebble bed configuration for quasi-direct numerical simulation. Nucl. Eng. Des. 242, 331–340 (2012)
Shan, R., Yoo, C.S., Chen, J.H., Lu, T.: Computational diagnostics for n-heptane flames with chemical explosive mode analysis. Combust. Flame 159(10), 3119–3127 (2012)
Shen, W., Huang, Y., You, Y., Yi, L.: Characteristics of reaction zone in a dual-mode scramjet combustor during mode transitions. Aerosp. Sci. Technol. 99, 105779 (2020)
Shrotriya, P., Wang, P., Jiang, L., Murugesan, M.: REDIM-PFDF sub-grid scale combustion modeling for turbulent partially-premixed flame: Assessment of combustion modes. Combustion Science and Technology, pp. 1–23 (2020)
Som, S., Aggarwal, S.: Effects of primary breakup modeling on spray and combustion characteristics of compression ignition engines. Combust. Flame 157(6), 1179–1193 (2010)
Song, C., Luo, K., Jin, T., Wang, H., Fan, J.: Direct numerical simulation on auto-ignition characteristics of turbulent supercritical hydrothermal flames. Combust. Flame 200, 354–364 (2019)
Srinivasan, S., Ranjan, R., Menon, S.: Flame dynamics during combustion instability in a high-pressure, shear-coaxial injector combustor. Flow Turbul. Combust. 94(1), 237–262 (2015)
Sripakagorn, P., Mitarai, S., Kosaly, G., Pitsch, H.: Extinction and reignition in a diffusion flame: a direct numerical simulation study. J. Fluid Mech. 518, 231–259 (2004)
Sukegawa, Y., Nogi, T., Kihara, Y.: In-cylinder airflow of automotive engine by quasi-direct numerical simulation. JSAE Rev. 24(2), 123–126 (2003)
Tafti, D.: Evaluating the role of subgrid stress modeling in a ribbed duct for the internal cooling of turbine blades. Int. J. Heat Fluid Flow 26(1), 92–104 (2005)
Tian, L., Lindstedt, R.: Evaluation of reaction progress variable-mixture fraction statistics in partially premixed flames. Proc. Combust. Inst. 37(2), 2241–2248 (2019)
Touil, H., Bertoglio, J.P., Shao, L.: The decay of turbulence in a bounded domain. J. Turbul. 3(1), 49 (2002)
Tufano, G., Stein, O., Wang, B., Kronenburg, A., Rieth, M., Kempf, A.: Coal particle volatile combustion and flame interaction. Part II: effects of particle Reynolds number and turbulence. Fuel 234, 723–731 (2018)
Valorani, M., Ciottoli, P.P., Galassi, R.M.: Tangential stretching rate (TSR) analysis of non premixed reactive flows. Proc. Combust. Inst. 36(1), 1357–1367 (2017)
Wan, K., Hartl, S., Vervisch, L., Domingo, P., Barlow, R.S., Hasse, C.: Combustion regime identification from machine learning trained by Raman/Rayleigh line measurements. Combust. Flame 219, 268–274 (2020)
Wan, K., Vervisch, L., Xia, J., Domingo, P., Wang, Z., Liu, Y., Cen, K.: Alkali metal emissions in an early-stage pulverized-coal flame: DNS analysis of reacting layers and chemistry tabulation. Proc. Combust. Inst. 37(3), 2791–2799 (2019)
Wei, H., Zhao, W., Zhou, L., Chen, C., Shu, G.: Large eddy simulation of the low temperature ignition and combustion processes on spray flame with the linear eddy model. Combust. Theor. Model. 22(2), 237–263 (2018)
Weller, H., Tabor, G., Jasak, H., Fureby, C.: OpenFOAM, openCFD ltd. (2017). Software available at https://openfoam.org
Wen, X., Debiagi, P., Stein, O.T., Kronenburg, A., Kempf, A.M., Hasse, C.: Flamelet tabulation methods for solid fuel combustion with fuel-bound nitrogen. Combust. Flame 209, 155–166 (2019)
Wu, H., Ihme, M.: Compliance of combustion models for turbulent reacting flow simulations. Fuel 186, 853–863 (2016)
Wu, H., See, Y.C., Wang, Q., Ihme, M.: A pareto-efficient combustion framework with submodel assignment for predicting complex flame configurations. Combust. Flame 162(11), 4208–4230 (2015)
Yadav, R., De, A., Jain, S.: A hybrid flamelet generated manifold model for modeling partially premixed turbulent combustion flames. In: Turbo Expo: Power for Land, Sea, and Air, vol. 50855, p. V04BT04A065. American Society of Mechanical Engineers (2017)
Yamashita, H., Shimada, M., Takeno, T.: A numerical study on flame stability at the transition point of jet diffusion flames. In: Symposium (International) on Combustion, vol. 26, pp. 27–34. Elsevier (1996)
Yin, Y., Gong, X., Zhou, H., Ren, Z.: The correlation of species concentration with heat release rate in an auto-igniting turbulent n-heptane spray flame. Fuel 262, 116510 (2020)
Zhang, F., Bonart, H., Zirwes, T., Habisreuther, P., Bockhorn, H., Zarzalis, N.: Direct numerical simulation of chemically reacting flows with the public domain code OpenFOAM. In: Nagel, W., Kröner, D., Resch, M. (eds.) High Performance Computing in Science and Engineering' 14, pp. 221–236. Springer, Berlin (2015). https://doi.org/10.1007/978-3-319-10810-0_16
Zhang, F., Zirwes, T., Häber, T., Bockhorn, H., Trimis, D., Suntz, R.: Near wall dynamics of premixed flames. In: Proceedings of the Combustion Institute (2020). https://doi.org/10.1016/j.proci.2020.06.058
Zhang, F., Zirwes, T., Habisreuther, P., Bockhorn, H.: A DNS analysis of the correlation of heat release rate with chemiluminescence emissions in turbulent combustion. In: Nagel, W.E., Kröner, D.H., Resch, M.M. (eds.) High Performance Computing in Science and Engineering ’16, pp. 229–243. Springer, Berlin (2016). https://doi.org/10.1007/978-3-319-47066-5_16
Zhang, F., Zirwes, T., Habisreuther, P., Bockhorn, H.: Effect of unsteady stretching on the flame local dynamics. Combust. Flame 175, 170–179 (2017). https://doi.org/10.1016/j.combustflame.2016.05.028
Zhang, F., Zirwes, T., Habisreuther, P., Bockhorn, H., Trimis, D., Nawroth, H., Paschereit, C.O.: Impact of combustion modeling on the spectral response of heat release in LES. Combust. Sci. Technol. 191(9), 1520–1540 (2019). https://doi.org/10.1080/00102202.2018.1558218
Zhang, F., Zirwes, T., Nawroth, H., Habisreuther, P., Bockhorn, H., Paschereit, C.O.: Combustion-generated noise: an environment-related issue for future combustion systems. Energy Technol. 5(7), 1045–1054 (2017). https://doi.org/10.1002/ente.201600526
Zhang, W., Watanabe, H., Kitagawa, T.: Direct numerical simulation of ignition of a single particle freely moving in a uniform flow. Adv. Powder Technol. 28(11), 2893–2902 (2017)
Zhang, Z., Liu, X., Gong, Y., Li, Z., Yang, J., Zheng, H.: Investigation on flame characteristics of industrial gas turbine combustor with different mixing uniformities. Fuel 259, 116297 (2020)
Zhao, G., Sun, M., Wu, J., Cui, X., Wang, H.: Investigation of flame flashback phenomenon in a supersonic crossflow with ethylene injection upstream of cavity flameholder. Aerosp. Sci. Technol. 87, 190–206 (2019)
Zhao, P., Ge, Z., Zhu, J., Liu, J., Ye, M.: Quasi-direct numerical simulation of forced convection over a backward-facing step: effect of Prandtl number. Nucl. Eng. Des. 335, 374–388 (2018)
Zhao, T., Liu, X., Yang, J., Zheng, H.: Investigation on effect of mixing distance on mixing process and combustion characteristics of double-cone burner. Fuel 253, 540–551 (2019)
Zirwes, T., Häber, T., Zhang, F., Kosaka, H., Dreizler, A., Steinhausen, M., Hasse, C., Stagni, A., Trimis, D., Suntz, R., et al.: Numerical study of quenching distances for side-wall quenching using detailed diffusion and chemistry. Flow, Turbulence and Combustion pp. 1–31 (2020). https://doi.org/10.1007/s10494-020-00215-0
Zirwes, T., Zhang, F., Denev, J., Habisreuther, P., Bockhorn, H.: Automated code generation for maximizing performance of detailed chemistry calculations in OpenFOAM. In: Nagel, W., Kröner, D., Resch, M. (eds.) High Performance Computing in Science and Engineering ’ 17, pp. 189–204. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-68394-2_11
Zirwes, T., Zhang, F., Denev, J.A., Habisreuther, P., Bockhorn, H., Trimis, D.: Improved vectorization for efficient chemistry computations in OpenFOAM for large scale combustion simulations. In: Nagel, W.E., Kröner, D.H., Resch, M.M. (eds.) High Performance Computing in Science and Engineering ’ 18, pp. 209–224. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-13325-2_13
Zirwes, T., Zhang, F., Häber, T., Bockhorn, H.: Ignition of combustible mixtures by hot particles at varying relative speeds. Combust. Sci. Technol. 191(1), 178–195 (2019). https://doi.org/10.1080/00102202.2018.1435530
Zirwes, T., Zhang, F., Habisreuther, P., Hansinger, M., Bockhorn, H., Pfitzner, M., Trimis, D.: Quasi-DNS dataset of a piloted flame with inhomogeneous inlet conditions. Flow Turbul. Combust. 104, 997–1027 (2020). https://doi.org/10.1007/s10494-020-00159-5
Zirwes, T., Zhang, F., Wang, Y., Habisreuther, P., Denev, J.A., Chen, Z., Bockhorn, H., Trimis, D.: In-situ flame particle tracking based on barycentric coordinates for studying local flame dynamics in pulsating bunsen flames. In: Proceedings of the Combustion Institute (2020). https://doi.org/10.1016/j.proci.2020.07.033
Acknowledgements
We thank Assaad Masri for providing valuable information about the burner setup and access to the experimental results, as well as for helpful discussions. This work utilizes resources from the national supercomputer Cray XC40 Hazel Hen at the High Performance Computing Center Stuttgart (HLRS) and the computational resource ForHLR II at KIT funded by the Ministry of Science, Research and the Arts Baden-Württemberg and DFG (“Deutsche Forschungsgemeinschaft”). The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time on the GCS Supercomputer JUWELS at Jülich Supercomputing Centre (JSC) and on the GCS Supercomputer HAZEL HEN at Höchstleistungsrechenzentrum Stuttgart (www.hlrs.de).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Appendix A: Overview of Flame Regime Markers
Appendix A: Overview of Flame Regime Markers
Over the last decades, different flame regimes markers have been developed. This appendix gives an overview of different flame regime markers developed over the last decades. In the literature, flame regime markers can be divided into five broad categories:
-
Gradient alignment
-
Damköhler numbers
-
Flamelet analysis
-
Gradient free regime identification (GFRI)
-
Drift term analysis.
They are described in detail in the following subsections. It should be noted, that the regime markers discussed in this work are meant to identify flame regimes in terms of premixed, non-premixed or partially premixed regimes. There are other markers from the literature which are concerned with identifying propagation, ignition and quenching regimes, e.g. flux balance analysis (Gordon et al. 2007; Minamoto et al. 2014; Krisman et al. 2015), time scale analysis (Luo et al. 2012; Yin et al. 2020) or tangential stretching rate analysis Valorani et al. (2017), which are not in the scope of the present work.
1.1 Gradient Alignment
The first principle of flame regime markers is based on the alignment of gradients of two scalars. These regime markers have the advantage that they can be evaluated from the numerical solution with little computational or programming effort. The earliest regime marker was proposed by Yamashita et al. (1996) and is commonly referred to as the Takeno flame index:
It compares the alignment of the gradients of the mass fraction of the fuel species and oxygen and has been developed originally for simulations with finite rate chemistry where species profiles are resolved. For \(\xi _{{\mathrm {Takeno}}}>0\), both gradients point in the same direction, indicating a premixed flame. For \(\xi _{{\mathrm {Takeno}}}<0\), the gradients are anti-parallel and signify a non-premixed flame. For \(\xi _{{\mathrm {Takeno}}}\rightarrow 0\), the gradients are either orthogonal, indicating a partially premixed flame, or one of the two gradients becomes zero. This can happen for example, when the fuel species is depleted in the lean part of the flame. The Takeno flame index can also be related to the cross-scalar dissipation rate \(\chi _{{\mathrm {F}},{\mathrm {O}}_2}=D\nabla Y_{{\mathrm {F}}}\cdot \nabla Y_{{\mathrm {O}}_2}\), where D is the diffusion coefficient for the cross-scalar dissipation:
The Takeno flame index is often used in a normalized form:
In this formulation, the flame index can only take two values: \(+1\) for premixed flames and \(-1\) for non-premixed flames. Usually, the denominator is expressed as \(\max (|\nabla Y_{{\mathrm {F}}} \cdot \nabla Y_{{\mathrm {O}}_2}|,\epsilon )\), where \(\epsilon\) is a small number (here \(10^{-30}\)) to avoid division by zero. Therefore, the index can also have a value of zero, if the gradients are at an angle of exactly 90° or one of the gradients becomes zero. Another possible normalization is given by:
In this formulation, the flame index takes continuous values between − 1 and + 1. It is directly related to the cosine of the angle between the two gradients because \(\nabla Y_{{\mathrm {F}}} \cdot \nabla Y_{{\mathrm {O}}_2}/(|\nabla Y_{{\mathrm {F}}} |\,|\nabla Y_{{\mathrm {O}}_2}|)=\cos \theta (\nabla Y_{{\mathrm {F}}},\,\nabla Y_{{\mathrm {O}}_2})\), where \(\theta\) is the angle between two vectors. Although the two normalized versions of the Takeno flame index make interpretation of the flame regimes easier, they do not account for one of the two gradients becoming zero. Therefore, in order to have meaningful results, the normalized flame indices should only be evaluated in regions where \(|\nabla Y_{{\mathrm {F}}} |\) and \(|\nabla Y_{{\mathrm {O}}_2}|\) are sufficiently large. For an example of this, see Sect. 4.
Based on the normalized version of the Takeno flame index, other variants have been developed in the literature. Domingo et al. (2005) introduced a different normalization, which reduces the flame index to a value range of 0 for non-premixed to \(+1\) for premixed flames:
Lock et al. (2005) and Briones et al. (2006) extended the aforementioned flame index by taking the mixture fraction Z into account:
In addition to identifying the flame regime, the sign of the flame index also shows the local equivalence ratio of the premixed branch: When Z is below the stoichiometric mixture fraction \(Z_{{\mathrm {st}}}\), the flame index becomes negative. Therefore, \(-1\) shows a lean premixed flame, \(+1\) a rich premixed flame and 0 a non-premixed flame. Values of |0.5| show a partially premixed flame or a part of the flame where either oxidizer or fuel species are depleted, when \(\epsilon\) is used in the denominator to avoid division by zero. In the flames investigated by the authors (Lock et al. 2005; Briones et al. 2006), values of |0.5| corresponded to non-premixed parts of the flame, because the fuel species was consumed in the premixed parts and therefore \(|\nabla Y_{{\mathrm {F}}}|\) was close to zero.
A different normalization approach was taken by Lu et al. (2012), who defined the flame index as
Fiorina et al. (2005) noticed that there can be parts of the flame which are diffusion controlled, but where the gradients of fuel and oxidizer point in the same direction. Therefore, they modified the normalized Takeno flame index as follows:
If the gradients of fuel and oxidizer are opposed, both Takeno’s and Fiorina’s flame index predict a non-premixed flame. However, if the gradients point in the same direction, Takeno’s flame index always predicts a premixed flame. Fiorina’s index uses additional information from the flame thickness in terms of the oxygen gradient in \(D_O\) to decide if the flame is locally premixed or non-premixed:
If the gradient of the oxygen mass fraction within the flame front is greater or equal than the gradient of the oxygen mass fraction in a freely propagating premixed flame with the same mixture fraction Z at the position corresponding to the reaction progress variable c in the flame (\(D_O\le 1\)), \(\xi _{{\mathrm {Fiorina}}}\) signifies a premixed flame just like \(\xi _{{\mathrm {Takeno}}}\). Otherwise, \(\xi _{{\mathrm {Fiorina}}}\) represents a non-premixed flame whereas \(\xi _{{\mathrm {Takeno}}}\) would indicate a premixed flame.
Instead of using the mass fraction of the fuel and oxidizer species as the two scalars, different authors have proposed alternatives: Som and Aggarwal (2010) investigated n-heptane flames. Because n-heptane, as a long hydro-carbon chain, is broken down quickly before significant heat is generated, the mass fraction of n-heptane goes to zero for large parts of the flame front. Therefore, they used CO as an intermediate fuel mainly produced in rich premixed zones instead of n-heptane in the definition of the flame index, so that the flame index is defined in larger parts of the flame front. Rosenberg et al. (2013, 2015) doted their fuel with acetone and the oxidizer with \(\hbox {NO}_2\). By evaluating the alignment of measured acetone and \(\hbox {NO}_2\) gradients, they found good agreement with the classical Takeno flame index.
Instead of using gradients of species mass fractions, Favier and Vervisch (2001), Domingo et al. (2002), Nguyen et al. (2010) and Lamouroux et al. (2014), Pouransari et al. (2016) and Scholtissek et al. (2020) discussed the alignment of mixture fraction Z and reaction progress variable c gradients. Applying this to the \(\xi _{{\mathrm {Takeno}}}^{{\mathrm {angle}}}\) definition results in:
Although this has the same form as the other gradient alignment markers based on species mass fractions, this marker based on Z and c has to be interpreted differently. The authors make the argument that if c and Z gradients are aligned parallel or anti-parallel (\(\xi _{{\mathrm {Takeno}}}^{{\mathrm {angle}}}=-1\) or \(+1\)), and the flame is only moderately curved, the flame is non-premixed. Mostly premixed flames in a moderately stratified regime will yield values close to zero. Other values signify a partially premixed flame.
Hu and Kurose (2019a) defined a similar indicator, which is not based on the alignment of gradients directly but their magnitude instead:
Z is the mixture fraction and c the reaction progress variable. In a non-stratified premixed flame, \(|\nabla Z|\rightarrow 0\) so that \(\xi _{{\mathrm {mag}}}\rightarrow 1\). For a non-premixed flame, the gradient of Z is the determining factor so that \(\xi _{{\mathrm {mag}}}\rightarrow 0\).
Finally, it should be noted that all regime markers discussed in this section and the following sections are, by definition, defined at every location. For example, if inert mixing takes place, gradients of the fuel and oxidizer mass fractions are present without any chemical reactions. Therefore, flame indices can be conditioned to locations where the flame is present, e.g. due to the presence of sufficient heat release rates or source term of the progress variable. Because of this, different authors have defined the flame index as the product of the normalized Takeno flame index multiplied by the heat release rate, chemical reaction rate or source term of the progress variable (Srinivasan et al. 2015; Huang et al. 2016; Eckel et al. 2019):
where \(\dot{S}\) is the heat release rate, reaction rate of the fuel or reaction progress source term. Another approach of extending the definition range of the flame index is by using not a single species for the fuel, but the sum of selected species mass fractions:
Different authors have proposed different sets of species depending on the flame setup (Lignell et al. 2011; Jangi et al. 2015; Minamoto et al. 2015; Ma et al. 2016; Pei et al. 2016; Wei et al. 2018; Pang et al. 2018; Tufano et al. 2018; Hu and Kurose 2019b; Wan et al. 2019; Wen et al. 2019; Akaotsu et al. 2020).
1.2 Damköhler Numbers
Another method of determining the flame regime is by comparing chemical and mixing time scales in terms of Damköhler numbers Da. Domingo et al. (2008) showed that the flame regime can be expressed from three Damköhler numbers based on flamelet assumptions to be used in conjunction with tabulated chemistry and unity Lewis number:
where \(\rho\) is the density, \(\dot{\omega }_c\) is the source term of the reaction progress variable and \(\chi\) is the scalar dissipation rate
with D being assumed to be the thermal diffusivity of the mixture. For flames that are purely chemically controlled in a homogeneous mixture (e.g. homogeneous auto-ignition), all three Damköhler numbers go to infinity. In premixed (PF) non-stratified propagation (constant mixture fraction Z), \(Da^{{\mathrm {DF}}}\) and \(Da^{{\mathrm {PPF}}}\) go to infinity while \(Da^{{\mathrm {PF}}}\) stays finite. Similarly, for a diffusion flame (DF), \(Da^{{\mathrm {DF}}}\) will be sufficiently small. Lastly, partially premixed flames (PPF) are controlled by the value of \(Da^{{\mathrm {PPF}}}\).
1.3 Flamelet Analysis
A third method of regime identification stems from budget term analysis of the flamelet equations developed for use in LES, comparing the relative magnitude of budget terms from premixed and non-premixed flamelets. The method was developed by Knudsen and Pitsch (2009). In their original formulation, a second reaction progress variable \(\varLambda\) was introduced, which is defined to be statistically independent of the mixture fraction Z, in addition to the classical reaction progress variable c. In practice, however, the precise definition and computation of this second progress variable \(\varLambda\) proved to be difficult (Knudsen and Pitsch 2009, 2012), so that a different formulation was proposed Knudsen and Pitsch (2012) and later applied to a turbulent flame Kleinheinz et al. (2017):
Here, \(\varTheta ^{{\mathrm {DF}}}\) is the budget that balances the source term from the non-premixed flamelet equations and \(\varTheta ^{{\mathrm {PF}}}\) the one that balances the source term from premixed flamelet equations. \(\rho ^0\) is the density of the unburnt mixture at Z and \(c=0\), \(s_{L}^0\) is the flame speed of a freely propagating flame at Z and D is the diffusion coefficient of c and Z. These budget terms are then further constrained by
Finally, a flame regime indicator is defined from these terms as:
As \(\xi _{{\mathrm {KP}}}\) approaches zero, the flame is fully non-premixed. A value of unity indicates a premixed flame. A value of \(0<\xi _{{\mathrm {KP}}}<1\) indicates a partially premixed flame. Again, care has to be taken to avoid division by zero.
Although this regime marker has a strong fundamental basis, some difficulties arise applying it to highly turbulent flames. Firstly, the aforementioned budget terms are derived from steady flamelet equations, so that highly unsteady regions might not be accounted for correctly. Secondly, if the flame violates the flamelet assumptions due to high curvature or stretch rates, the assumptions for \(\xi _{{\mathrm {KP}}}\) are violated as well. Apart from this, the evaluation of partial derivatives involving c and Z is not trivial (Knudsen and Pitsch 2009; Hartl et al. 2018).
1.4 Gradient Free Regime Identification
The gradient free regime identification (GFRI) methodology was recently developed by Hartl et al. (2018, 2019) and applied to turbulent flames by Butz et al. (2019) and Hartl et al. (2019). The motivation of this regime index was to define a marker which can be evaluated from experimental data, where the full 3D information is not available to evaluate gradients of scalars but Raman/Rayleigh data along a line are accessible. The method is based on the chemical explosive mode analysis (CEMA) by Lu et al. (2010) and utilizes the chemical mode profile along lines. As noted in previous works (Lu et al. 2010; Shan et al. 2012), the chemical mode \({ CM }\) can be used to identify premixed reaction zones. Based on this idea, the GFRI distinguishes combustion regimes with the following procedure: First, the chemical mode \({ CM }\) is computed from the chemical Jacobian J:
Here, \({\mathbf {y}}\) is the vector containing the species mass fractions Y and temperature T as \({\mathbf {y}}=(Y_1,\,Y_2,\,\ldots ,\,Y_{N-1},\,T)^T\). \(\dot{{\mathbf {y}}}\) is the vector containing the rate of change of \({\mathbf {y}}\) with respect to the species mass fractions and temperature. The chemical Jacobian can be computed at any location knowing the mixture composition in terms of mass fractions, temperature and density. In this work, J is computed assuming constant volume from a numerical finite difference Jacobian provided by the numerical library Sundials (Hindmarsh et al. 2005). The eigenvalues of J are called \(\lambda _i\). The non-conservative eigenvalue with the largest real part is called explosive mode \(\lambda _e\). Note that some of the eigenvalues correspond to conservative modes (conservation of elements and energy), so that a total of \(N_{{\mathrm {elements}}}+1\) eigenvalues are zero and excluded from the analysis. The chemical mode \({ CM }\) is then defined as:
\({{\mathrm {Re}}}\) is the real part of a number and \({{\mathrm {sign}}}\) is the signum function. Positive values of \({ CM }\) indicate that the chemical system is unstable, which corresponds for example to a fresh gas mixture being hot enough to ignite, thereby moving quickly away from the initial fresh gas condition to a burnt gas condition. A negative value of \({ CM }\) shows a stable mixture composition, e.g. a gas at chemical equilibrium. Values close to zero show that the chemical system behaves inert, e.g. fresh gas at temperatures way below the auto-ignition temperature. Because the GFRI method is the most recent one among the reviewed flame regime markers, it is discussed in more details here.
Figure 10 shows an examples of how \({ CM }\) can be used to detect a premixed flame front. Profiles of chemical mode \({ CM }\), heat release rate \(\dot{Q}\), temperature T, and mass fraction Y of methane CH\(_4\) and oxygen O\(_2\) are depicted along a freely propagating methane/air flame at an equivalence ratio \(\phi =1\), with an initial temperature of 300 K and pressure of 1 bar, using the GRI 3.0 reaction mechanism, computed with Cantera. The \({ CM }\) value is initially close to zero because the fresh gas temperature is below the auto-ignition temperature and therefore behaves inert. In the burnt gas, \({ CM }\) becomes negative as the gas approaches chemical equilibrium. In the flame front, there is a jump from positive to negative CM (zero-crossing) roughly at the position where the heat release rate reaches its maximum. Therefore, a premixed reaction front can be detected by a zero-crossing of \({ CM }\) at the position where the heat release rate has its maximum.
Figure 11 shows the profiles of the previously discussed quantities together with the Bilger (1979) mixture fraction Z for a counterflow diffusion flame setup simulated with Cantera. The left nozzle injects pure methane with a velocity of \(u_{{\mathrm {F}}}=0.05\) m/s and the right nozzle injects air with \(u_{{{\mathrm {Ox}}}}=0.05\) m/s. The distance between the nozzles is \(L=1.25\) cm, leading to a stretch rate of \(a=(u_{{\mathrm {F}}}+u_{{{\mathrm {Ox}}}})/L=8\,\hbox {s}^{-1}\) (case taken from Hartl et al. (2018)). Both streams have a temperature of 300 K and the pressure is 1 bar. The GRI 3.0 reaction mechanism is used and the diffusion model assumes a unity Lewis number \(Le\). In contrast to Fig. 10, the \({ CM }\) value stays negative throughout the whole flame front. By definition, \({ CM }\) only gets the chemical Jacobian as input and therefore does not detect the non-premixed flame front in terms of a \({ CM }\) zero crossing (Lu et al. 2008; Huang et al. 2016), because the flame is diffusion limited. The lack of zero-crossing and a peak of the heat release rate roughly in the region, where Z approaches the stoichiometric mixture fraction \(Z_{{\mathrm {st}}}\), therefore identifies the non-premixed flame front. Even perfectly non-premixed flames can have a zero-crossing of \({ CM }\), which in this case can be achieved e.g. by increasing the stretch rate or changing the diffusion model to the mixture-averaged model. This \({ CM }\) peak is however far away from the heat release rate peak, so that it can be ignored. Butz et al. (2019) recommend to use a region of \(100\,\mu \hbox {m}\) around the zero-crossing in which the highest heat release rate is designated as \(\dot{Q}^{{\mathrm {PF}}}\). As discussed in Sect. 4, this value can change along the axial coordinate of the Sydney/Sandia flame investigated in this work as the flame fronts become generally broader downstream, so that an automated approach for identifying non-premixed heat release rate peaks becomes more difficult.
In summary, the following rules can be established for the GFRI: the maximum value of \(\dot{Q}\) within \(100\,\mu \hbox {m}\) of the \({ CM }\) zero-crossing is designated as \(\dot{Q}^{{\mathrm {PF}}}\). Outside this region but within 0.5 mm of the zero crossing, the highest heat release rate value with \(Z> Z_{{\mathrm {st}}}\) (in the case of methane \(0.055<Z<0.07\)) and a negative value of \({ CM }\) identifies \(\dot{Q}^{{\mathrm {DF}}}\). If no zero-crossing is present, \(\dot{Q}^{{\mathrm {PF}}}\) is zero. Based on these rules, a regime marker can be defined (Butz et al. 2019):
1.5 Drift Term Analysis
A different kind of flame regime marker was developed by Wu et al. (2015); Wu and Ihme (2016). Their goal was to create a marker which can guide combustion model selection to improve the accuracy of blending manifold-based combustion models in partially premixed flames. Although major species profiles in partially premixed flames can be insensitive to the combustion manifold (e.g. from non-premixed or premixed flames), the profiles of minor species can be very sensitive (Wu and Ihme 2016). Therefore, their regime marker was designed to be species-specific.
The basis of this marker is the drift term \(D_{\varPhi }\), which is defined as
\(\varPhi\) is the quantity of interest (QoI) that can be retrieved from the manifold combustion model m, e.g. a species mass fraction. \({\mathrm {D}}/{\mathrm {D}}t=\partial /\partial t+{\mathbf {u}}\cdot \nabla\) is the substantial derivative. The drift term \(D_{\varPhi }\) compares the trajectory of the change of \(\varPhi\) evaluated in the current flow conditions minus its trajectory evaluated on the manifold of the chosen combustion model. This difference represents how fast the evolution of \(\varPhi\) deviates from the current flow conditions if evaluated on its manifold model. By evaluating the drift term with a manifold combustion model based on premixed flames (PF) and on diffusion flames (DF), a regime marker can be defined:
If \(|D_{\varPhi }^{{\mathrm {PF}}}|\gg |D_{\varPhi }^{{\mathrm {DF}}}|\), \(\varPhi\) is described better by the diffusion flame based model and \(\xi _{{\mathrm {Drift}}}=0\). Likewise, \(\xi _{{\mathrm {Drift}}}=1\) indicates a premixed region. However, this region identification is species specific. At any given point, different species can be assigned different combustion regimes. Although this has a practical application in model selection and is well defined from a mathematical point of view, its physical meaning is hard to assess.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zirwes, T., Zhang, F., Habisreuther, P. et al. Identification of Flame Regimes in Partially Premixed Combustion from a Quasi-DNS Dataset. Flow Turbulence Combust 106, 373–404 (2021). https://doi.org/10.1007/s10494-020-00228-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10494-020-00228-9