A Stochastic Backscatter Model for Grey-Area Mitigation in Detached Eddy Simulations

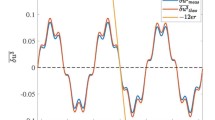
Abstract

A new stochastic backscatter model is proposed for detached eddy simulations that accelerates the development of resolved turbulence in free shear layers. As a result, the model significantly reduces so-called grey areas in which resolved turbulence is lacking after the computation has switched from a Reynolds-averaged Navier–Stokes simulation to a large eddy simulation. The new stochastic model adds stochastic forcing to the momentum equations with a rate of backscatter from the subgrid to the resolved scales that is consistent with theory. The effectiveness of the stochastic model is enhanced by including spatial and temporal correlations of the stochastic forcing for scales smaller than the cut-off scale. The grey-area mitigation is demonstrated for two canonical test cases: the plane free shear layer and the round jet.

Appendices

Appendix A: Rate of Backscatter

The new stochastic backscatter model includes spatial correlation in the stochastic variables, contrary to the models of Leith and Schumann. In this section, it is shown that this spatial correlation does not alter the scaling of the rate of backscatter as κ ⁴ for wave numbers κ → 0.

Consider a homogeneous stochastic forcing term f _i (x,t) added to the right-hand side of the momentum equation:

$$\frac{\partial u_{i}}{\partial t} + {\ldots} = f_{i}(\boldsymbol{x},t) , $$

with its spatial Fourier transform $\hat {f}_{i}(\boldsymbol {\kappa },t)$ given by

$$\hat{f}_{i}(\boldsymbol{\kappa},t) = {\int}_{\mathbb{R}^{3}} f_{i}(\boldsymbol{x},t) \mathrm{e}^{-\mathrm{i}\boldsymbol{\kappa}\cdot\boldsymbol{x}} \mathrm{d}\boldsymbol{x} . $$

Let C _{i j} (r,t) be the two-point correlation of f _i ,

$$C_{ij}(\boldsymbol{r},t) = \left\langle f_{i}(\boldsymbol{x},t) f_{j}(\boldsymbol{x}+\boldsymbol{r},t) \right\rangle , $$

which is independent of x due to homogeneity, and let $\hat {R}_{ij}(\boldsymbol {\kappa },t)$ be the covariance of $\hat {f}_{i}$,

$$\hat{R}_{ij}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) = \left\langle \overline{\hat{f}_{i}(\boldsymbol{\kappa},t)} \hat{f}_{j}(\boldsymbol{\kappa}^{\prime},t) \right\rangle . $$

The two-point correlation and the covariance are related by

$$ \begin{array}{llllllll} \hat{R}_{ij}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) &= {\int}_{\mathbb{R}^{3}} {\int}_{\mathbb{R}^{3}} \left\langle f_{i}(\boldsymbol{x},t) f_{j}(\boldsymbol{x}+\boldsymbol{r},t) \right\rangle \mathrm{e}^{\mathrm{i}\boldsymbol{\kappa}\cdot\boldsymbol{x}} \mathrm{e}^{-\mathrm{i}\boldsymbol{\kappa}^{\prime}\cdot(\boldsymbol{x}+\boldsymbol{r})} \mathrm{d}\boldsymbol{x} \, \mathrm{d}(\boldsymbol{x}+\boldsymbol{r}) \\ &= {\int}_{\mathbb{R}^{3}} \mathrm{e}^{\mathrm{i}(\boldsymbol{\kappa}-\boldsymbol{\kappa}^{\prime})\cdot\boldsymbol{x}} \mathrm{d}\boldsymbol{x} {\int}_{\mathbb{R}^{3}} \mathrm{e}^{-\mathrm{i}\boldsymbol{\kappa}^{\prime}\cdot\boldsymbol{r}} C_{ij}(\boldsymbol{r},t) \mathrm{d}\boldsymbol{r} \\ &= 2\pi\delta(\boldsymbol{\kappa}-\boldsymbol{\kappa}^{\prime}) \hat{C}_{ij}(\boldsymbol{\kappa}^{\prime},t) \end{array} $$

(10)

so that

$$ \hat{C}_{ij}(\boldsymbol{\kappa},t) = \frac{1}{2\pi} {\int}_{\mathbb{R}^{3}} \hat{R}_{ij}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) \mathrm{d}\boldsymbol{\kappa}^{\prime} . $$

(11)

The rate of backscatter at a wave number κ is determined by the spectrum function $\hat {F}(\kappa ,t)$ of f _i [44]. Here, $\hat {F}$ is defined analogous to the energy spectrum function E(κ) of the velocity field as defined in Pope, section 6.5 [45]:

$$\hat{F}(\kappa,t) = \oint_{S_{\kappa}} \hat{C}_{ii}(\boldsymbol{\kappa},t) \mathrm{d} S_{\kappa} $$

with S _κ the sphere around the origin with radius κ. The spectrum function $\hat {F}$ should scale as κ ⁴ for wave numbers smaller than the cut-off wave number κ _c ≈ π/Δ.

If f _i is directly defined as a spatially uncorrelated stochastic variable, then C _{i j} = C δ _{i j} Δ³ δ(r) (with C constant in case of homogeneity), implying $\hat {C}_{ij} = C{\Delta }^{3}\delta _{ij}$ and $\hat {F} = 12\pi C{\Delta }^{3}\kappa ^{2}$ (as δ _{i i} = 3 and the surface of a sphere equals 4π κ ²). Thus, such an approach would give the wrong scaling of the power spectrum.

The correct scaling is obtained if f _i is defined as the gradient of a spatially uncorrelated stochastic variable ξ _i , formulated in case of the Leith model as

$$f_{i}(\boldsymbol{x},t) = \varepsilon_{ijk}\frac{\partial \xi_{k}}{\partial x_{j}} , $$

with ε _{i j k} the alternating symbol. In this case, the Fourier transform of the two-point correlation D _{i j} of ξ _i is given by $\hat {D}_{ij} = D{\Delta }^{3}\delta _{ij} = \tfrac {1}{3} \hat {D}_{kk} \delta _{ij}$ and its covariance by $\hat {S}_{ij} = \tfrac {2}{3} \pi \hat {D}_{kk} \delta _{ij}\delta (\boldsymbol {\kappa }-\boldsymbol {\kappa }^{\prime })$, according to Eq. 10. One then finds that

$$\begin{array}{llllllll} \hat{R}_{ii}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) &= \varepsilon_{ijk}\varepsilon_{ilm}(-\mathrm{i}\kappa_{j})(\mathrm{i}\kappa^{\prime}_{l}) \hat{S}_{km}(\boldsymbol{\kappa},\boldsymbol{\kappa}^{\prime},t) \\ &= (\delta_{jl}\delta_{km} - \delta_{jm}\delta_{kl})\kappa_{j}\kappa^{\prime}_{l} \tfrac{2}{3}\pi\hat{D}_{ii} \delta_{km} \delta(\boldsymbol{\kappa}-\boldsymbol{\kappa}^{\prime}) = \tfrac{4}{3}\pi\hat{D}_{ii} \kappa^{2} \delta(\boldsymbol{\kappa}-\boldsymbol{\kappa}^{\prime}) , \end{array} $$

which implies upon substitution in Eq. 11 that

$$\hat{C}_{ii} = \tfrac{2}{3} \hat{D}_{ii} \kappa^{2} = 2D {\Delta}^{3} \kappa^{2} . $$

It follows that the power spectrum $\hat {F} = 8\pi D{\Delta }^{3}\kappa ^{4}$ has the correct scaling.

Finally, consider the case that ξ _i is spatially correlated according to

$$D_{ij} = \left\langle \xi_{i}(\boldsymbol{x},t) \xi_{j}(\boldsymbol{x}+\boldsymbol{r},t) \right\rangle = D \delta_{ij}\mathrm{e}^{-d^{2}/2} , $$

with d = |r|/b and $b = \sqrt {C_{\Delta }} {\Delta } \approx \sqrt {C_{\Delta }} \pi / \kappa _{c}$. Taking the Fourier transform of D _{i j} gives

$$\hat{D}_{ij} = D \delta_{ij} (2\pi)^{3/2} b^{3} \mathrm{e}^{-(b\kappa)^{2}/2} , $$

so that

$$\hat{C}_{ii} = \tfrac{2}{3} \hat{D}_{ii} \kappa^{2} = 2D \kappa^{2} (2\pi)^{3/2} b^{3} \mathrm{e}^{-(b\kappa)^{2}/2} , $$

following the same derivation as above, and finally

$$\hat{F} = 8\pi D\kappa^{4} (2\pi)^{3/2} b^{3} \mathrm{e}^{-(b\kappa)^{2}/2} , $$

which again scales as κ ⁴ for κ ≪ κ _c .

Appendix B: Correlations of Solutions of the Stochastic Differential Equations

Consider the Langevin-type equation (4) and the spatial stochastic differential equation (6). In this appendix, it is shown that the solution of these equations has the desired spatial and temporal correlation of Eq. 3, interpreted in Lagrangian sense, in case of a uniform flow.

Let G(x,t) be the Green’s function satisfying the equation

$$G + \tau \left( \frac{\partial G}{\partial t} + \boldsymbol{u}\cdot\nabla G \right) = \delta(\boldsymbol{x}) \delta(t) , $$

for a constant velocity u. Applying Fourier transformations of this equation both in space and time results in the following expression for the Fourier transform $\hat {G}$ of G:

$$\hat{G}(\boldsymbol{\kappa},\omega) = \frac{1}{(2\pi)^{2}} \frac{1}{1 + \mathrm{i}\tau\omega + \mathrm{i}\tau\boldsymbol{u}\cdot\boldsymbol{\kappa}} \, , $$

with κ the spatial wave number vector and ω the angular frequency. Applying inverse Fourier transforms, first in time and then in space, gives

$$G(\boldsymbol{x},t) = \frac{1}{\tau} H(t) \mathrm{e}^{-t/\tau} \delta(\boldsymbol{x}-\boldsymbol{u}t) . $$

Using the Green’s function, a general solution of Eq. 4 for arbitrary dW _i can be written as

$$\begin{array}{llllllll} \xi_{i}(\boldsymbol{x},t) &= {\int}_{\mathbb{R}^{3}} {\int}_{-\infty}^{\infty} G(\boldsymbol{x}-\boldsymbol{x}^{\prime},t-t^{\prime}) \sqrt{2\tau} \, \mathrm{d}\boldsymbol{x}^{\prime} \, \mathrm{d} W_{i}(\boldsymbol{x}^{\prime},t^{\prime}) \\ &= {\int}_{-\infty}^{\infty} \sqrt{\tfrac{2}{\tau}} H(t-t^{\prime}) \mathrm{e}^{(t^{\prime}-t)/\tau} \, \mathrm{d} W_{i}(\boldsymbol{x}-\boldsymbol{u}(t-t^{\prime}),t^{\prime}) . \end{array} $$

Given the spatio-temporal correlation of dW _i defined by Eq. 5, the following spatio-temporal correlation is found for ξ _i :

$$\begin{array}{llllllll} \left\langle \xi_{i}(\boldsymbol{x},t) \xi_{j}(\boldsymbol{y},s) \right\rangle &= {\int}_{-\infty}^{\infty} {\int}_{-\infty}^{\infty} \tfrac{2}{\tau} H(t-t^{\prime}) H(s-s^{\prime}) \mathrm{e}^{(t^{\prime}-t)/\tau} \mathrm{e}^{(s^{\prime}-s)/\tau} \\ &\qquad \left\langle \mathrm{d} W_{i}(\boldsymbol{x}-\boldsymbol{u}(t-t^{\prime}),t^{\prime}) \, \mathrm{d} W_{j}(\boldsymbol{y}-\boldsymbol{u}(s-s^{\prime}),s^{\prime}) \right\rangle \\ &= {\int}_{-\infty}^{\infty} {\int}_{-\infty}^{\infty} \delta_{ij} \tfrac{2}{\tau} H(t-t^{\prime}) H(s-s^{\prime}) \mathrm{e}^{(t^{\prime}-t)/\tau} \mathrm{e}^{(s^{\prime}-s)/\tau} \delta(t^{\prime}-s^{\prime}) \\ &\qquad \exp\left( -\tfrac{1}{2b^{2}} \left|\boldsymbol{x}-\boldsymbol{y}-\boldsymbol{u}(t-s-t^{\prime}+s^{\prime})\right|^{2} \right) \mathrm{d} t^{\prime} \, \mathrm{d} s^{\prime} \\ &= \delta_{ij} \exp\left( -\tfrac{1}{2b^{2}} \left|\boldsymbol{x}-\boldsymbol{y}-\boldsymbol{u}(t-s)\right|^{2} \right) {\int}_{-\infty}^{\min(t,s)} \tfrac{2}{\tau} \mathrm{e}^{(2t^{\prime}-t-s)/\tau} \mathrm{d} t^{\prime} \\ &= \delta_{ij} \exp\left( -\tfrac{1}{2b^{2}} \left|\boldsymbol{x}-\boldsymbol{y}-\boldsymbol{u}(t-s)\right|^{2} \right) \mathrm{e}^{-|t-s|/\tau} , \end{array} $$

which is indeed equivalent with Eq. 3 with x and y replaced by the Lagrangian coordinates x −u t and y −u s.

Next, let G(x) be the 1D Green’s function satisfying the equation

$$\left( 1 - b^{2} \frac{\mathrm{d}^{2}}{\mathrm{d} x^{2}} \right) G = \delta(x) , $$

which is given by

$$G(x) = \frac{1}{2b} \mathrm{e}^{-\left|x\right|/b} . $$

A general solution of Eq. 6 for arbitrary dV _i can then be written as

$$\mathrm{d} W_{i}(\boldsymbol{x},t) = {\int}_{\mathbb{R}^{3}} G_{3}(\boldsymbol{x}-\boldsymbol{x}^{\prime}) 8 b^{3/2} \, \mathrm{d} V_{i}(\boldsymbol{x}^{\prime},t) , $$

with $G_{3}(\boldsymbol {x}-\boldsymbol {x}^{\prime }) = G(x_{1}-x^{\prime }_{1}) G(x_{2}-x^{\prime }_{2}) G(x_{3}-x^{\prime }_{3})$. If dV _i is completely uncorrelated both in space and time, as defined by Eq. 7, then it follows that

$$\begin{array}{llllllll} \left\langle \mathrm{d} W_{i}(\boldsymbol{x},t) \mathrm{d} W_{j}(\boldsymbol{y},s) \right\rangle &= 64 b^{3} {\int}_{\mathbb{R}^{3}} {\int}_{\mathbb{R}^{3}} G_{3}(\boldsymbol{x}-\boldsymbol{x}^{\prime}) G_{3}(\boldsymbol{y}-\boldsymbol{y}^{\prime}) \left\langle \mathrm{d} V_{i}(\boldsymbol{x}^{\prime},t) \mathrm{d} V_{j}(\boldsymbol{y}^{\prime},s) \right\rangle \\ &= 64 b^{3} \delta_{ij} \delta(t-s) {\int}_{\mathbb{R}^{3}} G_{3}(\boldsymbol{x}-\boldsymbol{x}^{\prime}) G_{3}(\boldsymbol{y}-\boldsymbol{x}^{\prime}) \mathrm{d} \boldsymbol{x}^{\prime} \\ &= b^{-3} \delta_{ij} \delta(t-s) {\prod}_{m=1}^{3} {\int}_{\mathbb{R}} \mathrm{e}^{-\left|x_{m}-x^{\prime}_{m}\right|/b} \mathrm{e}^{-\left|y_{m}-x^{\prime}_{m}\right|/b} \mathrm{d} x^{\prime}_{m} \\ &= \delta_{ij} \delta(t-s) {\prod}_{m=1}^{3} \left( 1 + \tfrac{1}{b}\left|x_{m}-y_{m}\right| \right) \mathrm{e}^{-\left|x_{m}-y_{m}\right|/b} \\ &= \delta_{ij} \delta(t-s) \left( \mathrm{e}^{-\left|\boldsymbol{x}-\boldsymbol{y}\right|^{2}/(2b^{2})} + \mathcal{O}(\left|\boldsymbol{x}-\boldsymbol{y}\right|^{3}) \right) . \end{array} $$

For small distances, this is the spatio-temporal correlation of dW _i as defined by Eq. 5 up to third order in the distance. For large distances, this correlation rapidly decays, ensuring the correct scaling of the rate of backscatter.

Appendix C: Preservation of the Variance in the Discretized Spatial Stochastic Differential Equation

Consider the 1D stochastic differential equation

$$(1-{\beta\delta_{i}^{2}}) \eta^{\prime}_{i} = \zeta_{i} , $$

with i the grid-cell index, β the smoothing coefficient, and ${\delta _{i}^{2}}$ the second-order difference operator. The stochastic variable ζ _i = N(0, 1) is spatially uncorrelated,

$$\left\langle\zeta_{i} \zeta_{j}\right\rangle = \delta_{ij} . $$

We wish to determine the variance of the smoothed variable η ^′.

Let G _i be the discrete Green’s function satisfying the equation

$$(1-{\beta\delta_{i}^{2}}) G_{i} = \delta_{i0} . $$

Then, the general solution of the 1D stochastic differential equation (assuming periodicity) is given by

$$\eta^{\prime}_{i} = {\sum}_{j} G_{i-j} \zeta_{j} , $$

so that the variance of $\eta ^{\prime }_{i}$ is given by

$$\left\langle(\eta^{\prime}_{i})^{2}\right\rangle = {\sum}_{j} {\sum}_{k} G_{i-j} G_{i-k} \left\langle\zeta_{j} \zeta_{k}\right\rangle = {\sum}_{j} G_{i-j}^{2} = N \left|G\right|^{2} , $$

with N the number of grid cells and |G| the L ² norm of G.

Consider the discrete Fourier transform $\hat {G}_{k}$ of the Green’s function

$$\hat{G}_{k} = \frac{1}{N} {\sum}_{i} G_{i} \mathrm{e}^{-\mathrm{i} \theta_{k} i} $$

with 𝜃 _k = 2π k/N. Applying the Fourier transform to the equation for the Green’s function, one finds

$$\hat{G}_{k} = \frac{1}{N} (1 + 2\beta(1-\cos\theta_{k}) )^{-1} . $$

Thus, the variance of $\eta ^{\prime }_{i}$ is given by

$$\left\langle(\eta^{\prime}_{i})^{2}\right\rangle = N {\sum}_{k} \left|\hat{G}_{k}\right|^{2} = \frac{1}{N} {\sum}_{k} (1 + 2\beta(1-\cos\theta_{k}) )^{-2} . $$

In the limit for zero mesh size (i.e., δ 𝜃 = 2π/N → 0), this summation becomes an integral over the wave number 𝜃, so that

$$\begin{array}{llllllll} \left\langle(\eta^{\prime}_{i})^{2}\right\rangle &= \frac{1}{2\pi} {\int}_{0}^{2\pi} (1 + 2\beta(1-\cos\theta) )^{-2} \mathrm{d}\theta = \frac{1}{\pi} {\int}_{0}^{\pi} (1 + 2\beta(1-\cos\theta) )^{-2} \mathrm{d}\theta \\ &= \frac{1}{\pi} \frac{2}{1+4\beta} \left[ \frac{ \beta \sin\theta }{ 1 + 2\beta (1+\cos\theta) } + \frac{ 1 + 2\beta }{ \sqrt{1+4\beta} } \arctan\left( \sqrt{1+4\beta} \tan\left( \tfrac{1}{2}\theta\right) \right) \right]_{0}^{\pi} \\ &= \frac{ 1 + 2\beta }{ (1+4\beta)^{3/2} } \end{array} $$

Finally, it follows that to obtain a stochastic variable with unit variance, $\eta ^{\prime }_{i}$ should be scaled as

$$\eta_{i} = \frac{ (1+4\beta)^{3/4} }{ (1 + 2\beta)^{1/2} } \eta^{\prime}_{i} . $$

In 3D, this scaling should be applied for each computational direction.

Appendix D: Preservation of the Variance in the Discretized Langevin-Type Equation

Consider the Langevin-type equation in primitive form, discretized as

$$\xi^{n} + \frac{\tau}{\delta t} \left( \xi^{n+1/2} - \xi^{n-1/2} \right) + \tau \boldsymbol{u}^{n} \cdot \nabla\xi^{n} = \sqrt{\frac{2\tau}{\delta t}} \eta^{n} , $$

with $\xi ^{n} = \tfrac {1}{2} (\xi ^{n+1/2} + \xi ^{n-1/2})$.

First, no flow (u = 0) is considered, in which case

$$\left( 1 + \frac{\delta t}{2\tau} \right) \xi^{n+1/2} = \left( 1 - \frac{\delta t}{2\tau} \right) \xi^{n-1/2} + \sqrt{\frac{2\delta t}{\tau}} \eta^{n} . $$

Given that 〈(η ⁿ)²〉 = 1 and 〈η ⁿ ξ ^n−1/2〉 = 0, and assuming that 〈(ξ ^n−1/2)²〉 = 1, it follows that

$$\left( 1 + \frac{\delta t}{2\tau} \right)^{2} \left\langle(\xi^{n+1/2})^{2}\right\rangle = \left( 1 - \frac{\delta t}{2\tau} \right)^{2} + \frac{2\delta t}{\tau} , $$

so that

$$\left\langle(\xi^{n+1/2})^{2}\right\rangle = 1 . $$

Thus, if the initial variance of ξ equals one, then this variance is locally conserved by the central time discretization.

Including the convective term, local conservation of the variance cannot be easily proven. However, one can show global conservation up to third order in the time step. Let ξ be the vector with the values of ξ at all grid points as its components. The Langevin-type equation, discretized both in space and time, can then be written as

$$\boldsymbol{\xi}^{n} + \frac{\tau}{\delta t} \left( \boldsymbol{\xi}^{n+1/2} - \boldsymbol{\xi}^{n-1/2} \right) + \tau \boldsymbol{C}(\boldsymbol{u}^{n}) \boldsymbol{\xi}^{n} = \sqrt{\frac{2\tau}{\delta t}} \boldsymbol{\eta}^{n} , $$

with C the discretized convection operator. For a symmetry-preserving discretization, this operator is skew-symmetric, that is, ξ ^T C ξ = 0 for any ξ. Rewriting the equation as

$$\left( \boldsymbol{I} + \frac{\delta t}{2\tau}\boldsymbol{I} + \tfrac{1}{2}\delta t\boldsymbol{C} \right) \boldsymbol{\xi}^{n+1/2} = \left( \boldsymbol{I} - \frac{\delta t}{2\tau}\boldsymbol{I} - \tfrac{1}{2}\delta t\boldsymbol{C} \right) \boldsymbol{\xi}^{n-1/2} + \sqrt{\frac{2\delta t}{\tau}} \boldsymbol{\eta}^{n} , $$

and taking the square of the L ²-norm of the left-hand and right-hand sides, one finds

$$\begin{array}{@{}rcl@{}} &&\left( 1 + \frac{\delta t}{2\tau} \right)^{2} \left|\boldsymbol{\xi}^{n+1/2}\right|^{2} + \tfrac{1}{4}(\delta t)^{2} \left|\boldsymbol{C}\boldsymbol{\xi}^{n+1/2}\right|^{2} = \left( 1 - \frac{\delta t}{2\tau} \right)^{2} \left|\boldsymbol{\xi}^{n-1/2}\right|^{2} \\ &&+ \tfrac{1}{4}(\delta t)^{2} \left|\boldsymbol{C}\boldsymbol{\xi}^{n-1/2}\right|^{2} + \frac{2\delta t}{\tau} \left|\boldsymbol{\eta}^{n}\right|^{2} + (\ldots) \boldsymbol{\xi}^{n-1/2} \cdot \boldsymbol{\eta}^{n} , \end{array} $$

if C is skew-symmetric. This time, given that 〈|(η ⁿ)²|〉 = N and assuming that 〈|(ξ ^n−1/2)²|〉 = N, with N the total number of grid points, it follows that

$$\begin{array}{@{}rcl@{}} \left( 1 + \frac{\delta t}{2\tau} \right)^{2} \left( \left\langle\left|\boldsymbol{\xi}^{n+1/2}\right|^{2}\right\rangle - N \right) = \tfrac{1}{4}(\delta t)^{2} \left( \left\langle\left|\boldsymbol{C}\boldsymbol{\xi}^{n-1/2}\right|^{2}\right\rangle - \left\langle\left|\boldsymbol{C}\boldsymbol{\xi}^{n+1/2}\right|^{2}\right\rangle \right) . \end{array} $$

This equation allows for the global conservation of the variance of ξ, that is, 〈|(ξ ^n+1/2)²|〉 = N, if either conservation of the variance of C ξ is also assumed or the right-hand side, which is of $\mathcal {O}((\delta t)^{3})$, is neglected. Note that if the discretization is not symmetry-preserving, then a right-hand side of $\mathcal {O}(\delta t)$ is found that leads to considerable dissipation of the total variance of ξ.