Abstract
Many constructs in management studies, such as perceptions, personalities, attitudes, and behavioral intentions, are not directly observable. Typically, empirical studies measure such constructs using established scales with multiple indicators. When the scales are used in a different population, the items are translated into other languages or revised to adapt to other populations, it is essential for researchers to report the quality of measurement scales before using them to test hypotheses. Researchers commonly report the quality of these measurement scales based on Cronbach’s alpha and confirmatory factor analysis results. However, these results are usually inadequate and sometimes inappropriate. Moreover, researchers rarely consider sampling errors for these psychometric quality measures. In this best practice paper, we first critically review the most frequently-used approaches in empirical studies to evaluate the quality of measurement scales when using structural equation modeling. Next, we recommend best practices in assessing reliability, convergent and discriminant validity based on multiple criteria and taking sampling errors into consideration. Then, we illustrate with numerical examples the application of a specifically-developed R package, measureQ, that provides a one-stop solution for implementing the recommended best practices and a template for reporting the results. measureQ is easy to implement, even for those new to R. Our overall aim is to provide a best-practice reference for future authors, reviewers, and editors in reporting and reviewing the quality of measurement scales in empirical management studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Many constructs in management research are latent constructs that cannot be directly observed; therefore, researchers typically measure such constructs using established scales with multiple indicators. However, established scales do not perform equally well in different populations and samples. Moreover, many researchers translate the original scales into different languages or revise the original scales to adapt to the population under study, which are likely for many empirical studies in the Asia–Pacific region. Hence, it is critically important to evaluate and report the reliability, convergent and discriminant validity of multiple-indicator scales before examining relationships among constructs or testing hypotheses (Heggestad et al., 2019). While many researchers report Cronbach’s alpha and confirmatory factor analysis (CFA) results as evidence of the quality of measurement scales in their empirical studies, these are typically inadequate (Fornell & Larcker, 1981). Another problem is that most studies ignore sampling errors when comparing quality measures with specific thresholds (e.g., Cronbach’s alpha > 0.8).
Returning to the foundations of these important psychometric concepts, Campbell and Fiske (1959, p. 83) first defined convergent validity as “the agreement between two attempts to measure the same trait through maximally different methods” and discriminant validity as a trait that “can be meaningfully differentiated from other traits” (Campbell & Fiske, 1959, p. 100) under the multitrait-multimethod (MTMM) context, in which two or more traits are each assessed using two or more methods. They proposed assessing convergent and discriminant validity by referring to the magnitudes of correlation coefficients in the MTMM matrix, which reveal the correlations among multiple constructs (i.e., multitrait) measured from multiple methods (i.e., multimethod). Among the problems associated with employing the MTMM matrix to evaluate convergent and discriminant validity, the most significant drawback is the cumbersome requirement for researchers to collect data on every construct using more than one method (Bollen, 1989).
In practice, unlike scale development research that uses multiple methods to measure constructs, most empirical research measures multiple constructs with a single method. In this multitrait-monomethod context, where each construct is measured using a single method and multiple indicators, Bagozzi (1981, p. 375) defined convergence in measurement, whereby convergent validity constitutes a special case, as “measures of the same construct should be highly intercorrelated among themselves and uniform in the pattern of intercorrelations.” Likewise, Bagozzi (1981, p. 375) defined differentiation in constructs, which is more generalized than discriminant validity, as “cross-construct correlations among measures of empirically associated variables should correlate at a lower level than the within-construct correlations.” Following the common practices of empirical studies, this best practice paper focuses on the multitrait-monomethod context, and we use the terms convergent validity and discriminant validity rather than convergence in measurement and differentiation of constructs.
Through this best practices paper, we aim to achieve four objectives. Our first objective is to critically review the most frequently-adopted approaches to evaluate reliability, convergent and discriminant validity in empirical research. Our second objective, which draws on our review, is to recommend best practices for assessing reliability, convergent and discriminant validity in empirical studies. Although some of these approaches are not widely adopted in management studies, they have been extensively applied in other fields, such as consumer behavior and marketing research. In line with other methodological best-practice papers (Christofi et al., 2022; Ren et al., 2018), we emphasize the utility of these guidelines for future authors, reviewers, and editors. Our third objective is to demonstrate how to implement our recommendations with a specifically developed R package, measureQ. We use five examples to show how one simple step in measureQ, of defining the measurement model, generates all the test results required for evaluating reliability, convergent and discriminant validity. Finally, our last objective is to motivate and enable standardized reporting of results and, relatedly, evaluate measurement scales’ quality in empirical management studies. To this end, we provide a report template covering reliability, convergent and discriminant validity. We emphasize that our recommendations apply to reflective measures only and not formative measures. This aligns with Edwards’ (2011) excellent comparison of reflective and formative measures, in which he argues that reflective measures are more suitable for management studies. We also emphasize that our best practice recommendations apply to empirical studies that utilize established scales only and not scale development research that typically adopts the multitrait-multimethod approach. For best-practice recommendations for scale development research, readers are referred to Cortina et al. (2020), Hinkin (1998), and Lambert and Newman (2022).
Methods for assessing reliability
Cronbach’s alpha greater than 0.7 or 0.8
Cronbach’s alpha is not structural equation modeling (SEM) based, yet it is the most commonly-reported reliability coefficient in studies using SEM (Cho, 2016). This practice continues despite numerous notes of its misuse (Cortina, 1993; Flora, 2020; Schmitt, 1996; Sijtsma, 2009). Although Cronbach’s alpha greater than 0.7 has been widely used as the standard for adequate reliability, Lance et al. (2006) pointed out that Nunnally (1978) and Carmines and Zeller (1979) recommended a reliability standard of 0.8 for the majority of studies, and reliability of 0.7 indicates the scale has only modest reliability. Moreover, Cronbach’s alpha’s assumption of equal factor loadings across indicators (i.e., tau-equivalence) is typically not justified for latent constructs. Of particular concern is that Cronbach’s alpha typically underestimates the reliability of a latent construct when the underlying indicators demonstrate unequal factor loadings (Gerbing & Anderson, 1988). The frequent misuse of Cronbach’s alpha may be attributable to several factors: (a) unawareness of the problems of Cronbach’s alpha (Dunn et al., 2014), (b) easy estimation of Cronbach’s alpha using commonly-available statistical software packages, (c) widely-accepted standards for evaluating the adequacy of Cronbach’s alpha, and (d) requests from reviewers and/or editors for Cronbach’s alpha, resulting in its inclusion in manuscripts.
Construct reliability/composite reliability values greater than 0.7 or 0.8
A more appropriate reliability measure for SEM-based studies is construct reliability (CR; Fornell & Larcker, 1981; Jöreskog, 1971), also known as McDonald’s omega (McDonald, 1999), composite reliability (Raykov, 1997), or congeneric reliability (Graham, 2006). CR is based on the congeneric model that does not require equivalent factor loadings across items, which is defined as:
where λi is the completely standardized factor loading (for which both indicators and latent constructs are standardized) of item i. When the measurement model is tau-equivalent, CR is equivalent to Cronbach’s alpha. Hair et al. (2009, p. 619) noted that CR values of 0.7 or higher denote good reliability. In other words, the total error variance should consist of less than 30% of the variance of the latent variable. It might be thought that unreliable scales are of minimal concern in SEM because measurement errors are accounted for when estimating relationships between constructs. As a result, estimated parameters for these relationships are not biased by measurement errors. However, low reliability in the underlying scales increases the standard errors of estimated parameters, resulting in less powerful testing (Grewal et al., 2004).
Construct reliability for second-order factors
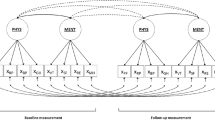
Many measurement scales used in management studies are multidimensional, reflecting the construct’s complexity. Commonly-used multidimensional scales include the Utrecht Work Engagement Scale (Schaufeli et al., 2002, 2006) that measures engagement on three dimensions: vigor, dedication, and absorption; Meyer and Allen’s (1991) commitment scale for measuring affective, continuance, and normative commitment; and Posner and Kouzes’ (1988) Leadership Practices Inventory (LPI) which measures five dimensions of leadership, namely challenging the process, inspiring a shared vision, enabling others to act, modeling the way, and encouraging the heart. These and other measures with second-order factors violate the assumption of unidimensionality of measures (i.e., each indicator assesses a single underlying construct; Clark & Watson, 1995), and therefore Cronbach’s alpha and CR are not appropriate reliability measures because they ignore the second-order factor structure (Raykov et al., 2018). Following Raykov and Marcoulides (2012, p. 496), a second-order factor can be expressed as:
where Λ is the factor loading matrix of the first-order factors ξ on the indicators X, γ is the factor loading matrix of the second-order factor η on ξ, ε is the residual variance of X, and ω is the residual variance of ξ. Substituting (3) into (2) gets (Raykov & Marcoulides, 2012, p. 498):
Suppose there is a p number of indicators measuring m number of first-order factors, and the number of indicators measuring the jth first-order factor is kj. The observed score variance \({\sigma }_{X}^{2}\) equals the sum of all elements of the variance–covariance matrix of all indicators S, which can be decomposed into three terms (Cho, 2016, p. 28; Raykov & Marcoulides, 2012, p. 498):
The last term on the right-hand side is the sum of the indicator variance not explained by the factors, usually referred to as residual variance or error variance (Cortina, 1993). The first two terms together represent the total indicator variance–covariance explained by the first-order factors. The first term represents the total indicator variance–covariance explained by the second-order factor, that is, the variance of X due to the second-order factor (Cho, 2016; Cortina, 1993). Hence, the second term is the total indicator variance–covariance explained by the first-order factors but not the second-order factor. Gerbing and Anderson (1984, p. 576) referred to the second term as the group-specific error that is irrelevant in estimating the second-order factor, and Credé and Harms (2015, p. 854) referred to it as the idiosyncratic influence of the first-order factors. Since under the Classical Test Theory, reliability \(=1- \frac{{\sigma }_{\epsilon }^{2}}{{\sigma }_{X}^{2}}\), McDonald (1999) defined two reliability measures: omegatotal (\({\omega }_{T}\)) and omegahierarchical (\({\omega }_{h}\)):
While some scholars (e.g., Cho, 2016; Raykov & Marcoulides, 2012; Raykov et al., 2018) refer to \({\omega }_{T}\) as second-order factor reliability because they treat \({\sigma }_{\epsilon }^{2}\) as the only error term, we agree with those viewing \({\omega }_{h}\) as being a more appropriate measure of second-order reliability (Kelley & Pornprasertmanit, 2016; Zinbarg et al., 2005) because it considers both \({\sigma }_{\epsilon }^{2}\) and group-specific error as comprising the error term. In other words, \({\omega }_{h}\) accurately shows the proportion of total indicator variance–covariance explained by the second-order factor to the total variance, whereas \({\omega }_{T}\) is more appropriate to represent the reliability of the combined first-order factors.
Methods for assessing convergent validity
Bagozzi’s (1981) definition of convergent validity emphasizes the internal consistency of the indicators measuring the same construct; therefore, four decades ago, researchers used reliability measures as one of the requirements to evaluate convergent validity (Fornell & Larcker, 1981). Yet, researchers also suggest that merely examining reliability is inadequate in assessing convergent validity. To examine convergent validity using SEM, one should first conduct a CFA by estimating a measurement model in which all indicators are related to the constructs they are meant to measure and are not related directly to constructs they are not intended to measure (Fornell & Larcker, 1981; Hair et al., 2009). When the hypothesized measurement model fits the data adequately, this establishes the fundamental requirement for convergent validity: all indicators converge well on their own construct.Footnote 1 However, many researchers have suggested that adequate model fit is insufficient to support convergent validity because model fit does not guarantee measurement quality (Fornell & Larcker, 1981); hence, additional criteria have been proposed.
Standardized factor loadings greater than 0.4, 0.5 or 0.7
Many researchers (e.g., Anderson & Gerbing, 1988; Dunn et al., 1994) have suggested evaluating convergent validity by examining the statistical significance of standardized factor loadings. Nevertheless, as CFA may involve using relatively large samples (typically 200 or more cases) to ensure convergence and reliable results, even a small standardized factor loading may be statistically significant. Hence, simply assessing the significance of a factor loading may not suffice. Steenkamp and van Trijp (1991, p. 289) also noted that “A weak condition for convergent validity is that the factor regression coefficient on a particular item is statistically significant. A stronger condition is that the factor regression coefficient is substantial.” For instance, Wei and Nguyen (2020) conducted a CFA of a five-factor (local responsiveness, Local R-assets, market-seeking FDI, strategic asset-seeking FDI, and host country institutional development) measurement model. They reported support for convergent validity with an acceptable overall model fit, and all the standardized factor loadings in the model were statistically significant and higher than 0.5. Researchers have proposed other rules for evaluating the magnitude of the standardized factor loading. For example, Stevens (2002) suggested that the value of a factor loading should be greater than 0.4 for interpretation purposes, whereas Hair et al. (2009) argued that all standardized factor loadings should be at least 0.5 and, ideally, at least 0.7. In other words, the construct explains at least 25% or, ideally, at least 49% of the variance of each indicator.
Average variance extracted (AVE) value greater than 0.5
In addition to examining the standardized factor loadings, many studies have employed the Fornell and Larcker (1981) criterion for assessing convergent validity (for example, Yu et al., 2021; Zahoor et al., 2022). Fornell and Larcker (1981) suggested that convergent validity is established when a latent construct accounts for no less than half of the variance in its associated indicators. They proposed using the average variance extracted (AVE) to represent the average amount of variance that a construct explains in its indicators relative to the overall variance of its indicators. For construct X, AVE is defined as follows:
where p is the number of indicators of construct X, and \({\lambda }_{i}\) is the completely standardized factor loading of the \({i}^{\mathrm{th}}\) indicator (both indicators and the construct are standardized). Thus, for construct X, the value of AVE is equivalent to the average of the square of completely standardized factor loadings across all its indicators. The AVE should not be lower than 0.5 to demonstrate an acceptable level of convergent validity, meaning that the latent construct explains no less than 50% of the indicator variance (Fornell & Larcker, 1981, p. 46). For example, Yu et al. (2021), in their study of corporate philanthropy, benevolent attributions, and job performance, reported the AVE ranged between 0.50 and 0.62, thus exceeding the 0.5 threshold and supporting the convergent validity of their latent constructs. Nonetheless, using AVE to assess convergent validity relies on a rule of thumb rather than statistical testing procedures; this means that sampling errors are disregarded, and conclusions cannot be generalized to larger populations (Shiu et al., 2011).
Average variance extracted for second-order factors
While Eq. (8) shows the AVE of a first-order factor, the AVE of a second-order factor (AVEsecond-order) measured with p number of indicators and m number of first-order factors is (Credé & Harms, 2015):
where \(({\lambda }_{ij}{\gamma }_{j})^{2}\) is the variance of the ith indicator extracted by the second-order factor. Based on a minimum factor loading of 0.7 for both λ and γ, Credé and Harms (2015, p. 854) suggested a general guideline that the AVE of first-order factors (AVEfirst-order, AVE in Eq. 8) be at least 49% and the AVEsecond-order (in Eq. 9) be at least 24% as evidence of convergent validity for a second-order factor. However, this suggestion applies to Fornell and Larcker’s (1981) recommendation of AVE not less than 0.5 by including the group-specific error in the variance explained by the second-order factor. Instead, we suggest excluding group-specific error when evaluating a second-order factor’s convergent validity; hence, AVEsecond-order should not be less than 0.5. If this criterion is fulfilled, the AVEfirst-order will not be less than 0.5 because the group-specific error will not be negative.
Methods for assessing discriminant validity
The first condition for discriminant validity is establishing convergent validity (Bagozzi & Phillips, 1982). Stated alternatively, unless a construct is well-represented by its indicators, it is pointless to examine whether the construct can be distinguished from others. Many recommendations exist for evaluating discriminant validity, and Rönkkö and Cho (2022) have recently provided a comprehensive summary. Hence, we briefly review these approaches and highlight and explain the issues in a few places with varied opinions.
No cross-loaded indicators (Unidimensionality)
In addition to establishing convergent validity, discriminant validity requires that each indicator loads uniquely on only one construct. If the same indicator is used to measure two constructs, it is difficult to argue that the constructs are distinct. Unidimensionality requires no cross-loaded indicator, a condition for assigning meaning to a latent construct (Anderson & Gerbing, 1988). This criterion was implied in Fornell and Larcker’s (1981) model, wherein they hypothesized no cross-loaded indicators. Further, this criterion was made explicit in Henseler et al. (2015) and Voorhees et al. (2016) when they proposed the Heterotrait-Monotrait (HTMT) approach to examine discriminant validity.
Correlations between two constructs are significantly less than unity
Statistical tests have been developed that assess discriminant validity by evaluating whether a correlation between two constructs is statistically significantly less than unity. First proposed by Jöreskog (1971), with subsequent recommendations by Bagozzi and Phillips (1982, p. 476) and by Anderson and Gerbing (1988, p. 416), this is the most widely-used approach to evaluate discriminant validity. The procedure involves conducting a chi-square difference test between an unconstrained CFA model and a constrained CFA model in which the correlation between the targeted pair of constructs is constrained to 1.0. A statistically significant chi-square difference between the two models (with one degree of freedom) implies the unconstrained model fits the data better; that is, the correlation is statistically significantly less than 1.0. Therefore, discriminant validity is supported between the targeted pair of constructs. For example, Wang et al. (2021b) conducted chi-square difference tests for all paired constructs. In all cases, the constrained model with correlation fixed at 1 fits the data significantly worse than the unconstrained model with freely estimated correlation. Thus, they concluded discriminant validity was supported.
However, many researchers have executed the test inappropriately. Specifically, Anderson and Gerbing (1988, p. 416) stated that “This test should be performed for one pair of constructs at a time, rather than as a simultaneous test of all pairs of interest. The reason for this is that a non-significant value for one pair of constructs can be obfuscated by being tested with several pairs that have significant values.” Further, in the constrained model in which the correlation between two targeted constructs is fixed to unity, researchers must also set equality constraints on the correlations between the two constructs and other constructs of the model. For example, when rxy is fixed to unity, rxz should be fixed as equal to ryz. However, in practice, many researchers fail to adhere to this requirement. The same issue happens when the correlation is fixed at a value other than 1.0. Although Rönkkö and Cho (2022) realized this issue when testing the correlation against 1.0, they recommended comparing the model fit of two nested models by constraining only the correlation between the two constructs at a cutoff value without adding other constraints for the correlations between the two constructs and other constructs.Footnote 2 Because the constraints for other correlations will be more challenging to define, their recommended approach is inappropriate for other cutoff values different from 1.0. In addition, some researchers (e.g., Anderson & Gerbing, 1988; Voorhees et al., 2016) suggest that the Type I error rate for each discriminant validity test should be adjusted by the number of tests conducted to control for overall Type I errors in a study. Against this, we agree with Rönkkö and Cho (2022) and common practice that such adjustment is unnecessary because each discriminant validity test for a pair of constructs is independent of the discriminant validity tests applied to other pairs of constructs.
An alternative approach is to create a constrained model in which all indicators of the two constructs are specified as loading on a single construct. Researchers frequently adopt such an approach by comparing two nested models. In addition to the other constructs in the models, the first model specifies the two targeted constructs remain distinct, and the second model combines the two targeted constructs into one. As an example of this approach, to test the discriminant validity of work-leisure conflict and work engagement, Wang and Shi (2022) compared the hypothesized five-factor measurement model with a four-factor model in which all the indicators of work-leisure conflict and work engagement loaded on one factor. They then conducted a chi-square difference test between the five-factor model and the four-factor model, which was statistically significant (\({\chi }^{2}\left(3\right)=662.09, p<.01)\). This result suggested the five-factor unconstrained model fit the data better, supporting discriminant validity between work-leisure conflict and work engagement.
Instead of determining whether the correlation between two latent variables is significantly less than unity, and rather than using nested models, Anderson and Gerbing (1988) proposed a complementary method based on assessing the confidence interval (CI) for the estimated correlation between the targeted pair of constructs. When the 95% CI for the correlation between two constructs does not include 1.0, this provides evidence of discriminant validity for the two constructs involved. For example, Li and Li (2009) reported that none of the CIs of the correlations of latent constructs included 1.0, supporting discriminant validity for all constructs in their study.
However, Shaffer et al. (2016) summarized two shortcomings of comparing the correlation against 1.0 as a test of discriminant validity. First, the possible outcomes are whether two constructs are perfectly correlated or not, but it is rare for them to be perfectly correlated in the population. Second, with a large enough sample size (e.g., 1,000), even a correlation at 0.95 is statistically significantly different from 1.0. We identify a third shortcoming: assessing whether the correlation is significantly less than 1.0 is a one-tailed test. Hence, it is more appropriate to use a 90% CI such that Type I error is maintained at 5% and higher power can be achieved.
Correlation between two constructs less than 0.9, 0.85, 0.8, or 0.75
Other than testing discriminant validity based on the correlation between two constructs being significantly less than 1.0, the most commonly used criterion is to compare the correlation between two constructs against a fixed value involves determining whether rxy is less than 0.85 (Garson, 2002, p. 195; Kenny, 2016), although researchers have proposed other threshold values. For example, John and Benet-Martínez (2000) suggested a threshold of 0.9. Other researchers implicitly define the threshold values for discriminant validity in their simulation studies. For example, in their simulation study, Rönkkö and Cho (2022, Table 9) define a correlation at 0.8 or higher as having discriminant validity issues. Similarly, Voorhees et al. (2016, Table 4) conducted a simulation study in which they defined a correlation of 0.75 as having no discriminant validity issues and 0.9 as having discriminant validity issues.
Average variance extracted is greater than the shared variance (AVE-SV approach)
The Fornell and Larcker (1981) criterion for assessing discriminant validity is also commonly employed (Voorhees et al., 2016). Specifically, Fornell and Larcker (1981, p. 46) suggested that for construct X and construct Y, discriminant validity is established when AVEs associated with both constructs are greater than the shared variance (i.e., squared correlation; SV) between X and Y. In other words, the latent variable explains more variance of the indicators than another latent variable. Based on their simulation results, Grewal et al. (2004, p. 528) recommended the AVE-SV approach for assessing discriminant validity because the resulting constructs that possess discriminant validity substantially reduced the Type II error resulting from multicollinearity such that “an inference error is unlikely.” An example of this AVE-SV approach is Wang et al. (2021a) demonstration of the discriminant validity of feedback-seeking from team members, creativity, thriving at work, and mindfulness in their study of feedback-seeking.
Despite the increasing popularity of the AVE-SV approach, it has been criticized for relying on rules of thumb rather than statistical test procedures, thus disregarding sampling errors (Shiu et al., 2011). Additionally, the AVE-SV approach tolerates strong correlations when the AVE value is high (Shiu et al., 2011; Voorhees et al., 2016). While several simulation studies (e.g., Henseler et al., 2015; Rönkkö & Cho, 2022) have shown the high false-negative and high false-positive rates for this approach, those simulations defined discriminant validity solely based on the correlation between the two constructs but, importantly, failed to consider the AVE of the two constructs in the population. For example, Rönkkö and Cho (2022, Table 8) defined the correlation between two constructs at 0.7, 0.8, and 0.9 as evidence of discriminant validity while using AVE at 0.64 and 0.42 for the population parameters. Hence, applying the AVE-SV approach, they rejected discriminant validity in the population but considered it false-positive in their simulation.
Heterotrait-monotrait (HTMT) ratio of correlations less than 0.85
Recently, Shaffer et al. (2016) suggested examining the correlation disattenuated for measurement errors to evaluate discriminant validity. Likewise, Henseler et al. (2015) recommended comparing the heterotrait-monotrait (HTMT) ratio of correlations with a threshold value of 0.85 to examine discriminant validity in variance-based SEM (i.e., partial least squares). The HTMT ratio is a ratio of average heterotrait-heteromethod inter-item correlations to the geometric mean of monotrait-heteromethod inter-item correlations, in which each item is treated as a method. Using a simulation study, Voorhees et al. (2016) extended the HTMT method to covariance-based SEM and provided initial supporting evidence. However, there are several shortfalls with the HTMT approach.
First, intending to estimate the disattenuated construct score correlation, Henseler et al.’s (2015, Eq. 6) HTMT equation is incorrect. While Henseler et al.’s (2015) HTMT equation uses inter-item correlations instead of inter-item covariances, that becomes the disattenuated correlation between two composite scores formed by averaging the standardized item scores.Footnote 3 Hence, unless the construct scores are calculated by averaging the standardized item scores, Henseler et al.’s HTMT equation provides a biased estimate of the disattenuated correlation between two composites. As shown in the supplementary file, the corrected HTMT equation should be:
where the numerator is the average heterotrait-heteromethod covariance among the items of the two constructs, and the denominator is the geometric mean of the average monotrait-heteromethod covariance among the items of the two constructs. The corrected HTMT computed with Eq. (10) is equivalent to the correlation between two composite scores formed by simple item averages, disattenuated with Cronbach’s alpha of the two composite scores.
Second, both Henseler et al.’s (2015) HTMT equation and the corrected HTMT equation in Eq. (10) do not allow single-item factors because the denominator will be undefined if one or both constructs are single-item measures. In such cases, the average monotrait-heteromethod covariance of the single-item factor should be replaced by the estimated reliability times the factor variance. The estimated reliability can be fixed at one or a value estimated from previous studies or other methods (Anderson & Gerbing, 1988).
Third, the recommended HTMT threshold of 0.85 was based on the power of detecting a population correlation at 1.0 in a simulation study (Henseler et al., 2015). If a researcher considers a population correlation at a lower value (for example, 0.9) as evidence of insufficient discriminant validity between two constructs, the HTMT criterion of 0.85 fails. Finally, comparing the disattenuated correlation or HTMT ratio with a threshold value of 0.85 disregards sampling error (Shaffer et al., 2016). Hence, the HTMT ratio only describes sample characteristics and cannot infer results to the population of interest. Notably, Henseler et al. (2015) reviewed the effectiveness of a statistical test for HTMT (HTMTinference) by examining the 90% CI of HTMT in their simulation. Ultimately, they did not recommend HTMTinference, given it failed to detect discriminant validity violations even when inter-construct correlations were as high as 0.95.
Recently Roemer et al. (2021) suggested an HTMT2 index as an improvement over the HTMT index since HTMT assumes tau-equivalent measures, whereas HTMT2 allows congeneric measures. Yet, the HTMT2 is still based on inter-item correlations instead of covariances, so it is inappropriate if the composites are not formed with standardized item scores.
Best-practice recommendations
We summarize our preceding review of current practices for testing reliability, convergent and discriminant validity, and their associated concerns in Table 1. Leveraging this review, we present best practices for evaluating the reliability, convergent and discriminant validity of latent constructs for empirical management studies. The recommended best practices incorporate multiple criteria for examining reliability, convergent and discriminant validity, and account for sampling errors by using bootstrapped CIs to resolve the issues identified in Table 1. Our recommendations are summarized in Table 2, in which we also provide normative definitions and operational definitions of the criteria for reliability, convergent and discriminant validity.
The first step is establishing a measurement model in which all indicators are related to the constructs they are intended to measure and unrelated to the other constructs in the model. Moreover, no cross-loading is allowed, that is, each indicator should be related directly to only one construct. Additionally, residuals of indicators should not be correlated unless the same item is used at multiple time points (Anderson & Gerbing, 1988) or from multiple sources (Cheung, 1999). Apart from these noted exceptions, correlated residuals of indicators imply an unknown common source of the indicators, such that the meaning of the constructs becomes unclear (Bagozzi, 1983; Gerbing & Anderson, 1984). When the overall model fit indices indicate that the hypothesized measurement model fits the data adequately (refer to Hu & Bentler, 1999; Kline, 2016), this establishes the essential requirement for evaluating reliability, convergent and discriminant validity. If the overall model fit indices imply that the hypothesized measurement model does not fit the data well, the estimated parameters should not be interpreted. In the latter instance, researchers should not proceed to estimate the construct reliability nor test for convergent and discriminant validity. Researchers may revise the measurement model by examining the modification indices, but a revised model will be sample-specific and should be cross-validated with another sample.
Confidence intervals and testing against a threshold
While most empirical studies consider sampling errors in testing hypotheses, surprisingly few consider the sampling errors of the reliability, convergent and discriminant validity measures. Following Raykov and Shrout (2002), we recommend conducting statistical tests of the criteria with the estimated parameters’ 90% percentile CIs (PCIs) generated by bootstrapping to account for sampling errors of the quality measures. Similar to other researchers (e.g., Dunn et al., 2014; Kelley & Cheng, 2012; Kelley & Pornprasertmanit, 2016; Raykov, 2002), we recommend generating CIs by bootstrapping because the estimated quality measures may not be normally distributed. We prefer PCIs over bias-corrected and accelerated CIs (BCa CI) because PCIs have better coverage for both normal and nonnormal item distributions (Kelley & Pornprasertmanit, 2016). As our criteria imply using one-tailed tests, a 90% PCI is more appropriate than a 95% PCI.
Reliability
We suggest that when latent constructs are used in subsequent analyses, one should report CR as a measure of reliability because it does not assume equal factor loadings across indicators. Following common practice, reliability should not be significantly lower than 0.7 and, ideally, should not be significantly lower than 0.8. When the upper limit of the 90% CI of CR is greater than 0.8, one may conclude that the construct demonstrates an adequate level of reliability. Similarly, a second-order factor’s reliability can be considered adequate if the upper limit of the 90% CI of ωh is greater than 0.8. On the other hand, when summated scales (simple average scores) are used in subsequent path analyses to estimate relationships among constructs and test hypotheses, one should report reliability using Cronbach’s alpha. This is because summated scales are consistent with the tau-equivalent assumption of Cronbach’s alpha.
Convergent validity
Incorporating the Fornell-Larcker AVE criterion for convergent validity along with construct reliability, Hair et al. (2009) suggested that there is evidence for convergent validity when all three of the following conditions are fulfilled: (a) CR values are 0.7 or greater, (b) all standardized factor loadings λ are 0.5 or greater, and (c) AVE values are 0.5 or greater. We support Hair et al.’s (2009) multiple criteria when examining convergent validity, but extend their suggestions to recommend the following operational definitions of the three criteria that account for sampling errors. First, conduct the statistical test for CR against 0.7 and 0.8, as described above. Second, we recommend conducting statistical tests for standardized factor loadings by examining the 90% CI for all indicators of the construct. A one-tailed test and hence the 90% CI is appropriate here because our concern is whether the standardized factor loading of an indicator is significantly less than 0.5 (or 0.7). If the upper limit of the 90% CI of the standardized factor loading for any indicator is lower than 0.5 (or 0.7), we conclude that the construct does not exhibit convergent validity. Third, we recommend conducting a statistical test on the value of AVE relative to the criterion of 0.5 by estimating the 90% CI of the AVE for each construct. As the concern is whether AVE is significantly less than 0.5, if the upper limit of the 90% CI is lower than 0.5, we conclude that the construct does not exhibit convergent validity.
Discriminant validity
While discriminant validity is commonly defined as “two distinct constructs” and measured by the correlation between the two constructs, there is no generally accepted level of “distinctiveness” regarding the level of cross-construct correlation that establishes discriminant validity. As noted above, one commonly used criterion is correlation significantly less than 1.0. Yet, high correlations (e.g., 0.9) that are statistically significantly less than 1.0 are difficult to defend as indicating two distinct constructs.
Building on Bagozzi's (1981) and Fornell and Larcker’s (1981) definitions of discriminant validity, we recommend examining discriminant validity using multiple criteria with sampling errors considered. The four criteria include: (i) evidence of convergent validity is established; (ii) no indicator cross-loads on other constructs; (iii) the level of indicator variance explained by each construct is greater than the shared variance between two constructs (i.e., AVE-SV; both AVEX and AVEY are greater than \({r}_{xy}^{2}\)); and (iv) the correlation between the two constructs is assessed at three levels: 0.85, 0.8, and 0.7. Since the AVE-SV criterion tolerates a high correlation between constructs when the AVEs of both constructs are high, we suggest examining the correlation between constructs in addition to the AVE-SV criterion. This criterion builds on Bagozzi et al.’s (1991, p. 436) suggestion that, in addition to comparing the CI of correlation against unity, when the 95% CI for the correlation between the two constructs includes zero, these two constructs are “totally distinct or nearly so.” Hence, discriminant validity should be considered as a degree of distinctness instead of a dichotomous decision. We recommend examining if the correlation between two constructs is not higher than 0.7 (shared variance of not more than 49%) as evidence of no concern for discriminant validity. That is, the shared variance between the two constructs is less than 50%. In other words, the shared variance between two constructs (< 50%) is less than the unshared variance of each construct (> 50%). At correlations above 0.8 (Rönkkö & Cho, 2022) and 0.85 (Garson, 2002; Kenny, 2016), researchers have increasing cause for concern.
For criteria (iii) and (iv) stated above, we recommend estimating a 90% CI for each of the parameters for the statistical tests so that sampling errors are considered in evaluating discriminant validity. For example, when examining criterion (iv), whether the correlation coefficient is significantly higher than 0.7, 0.8, or 0.85, one should see if the lower limit of the CI is higher than these thresholds. If yes, then the correlation coefficient is significantly higher than the thresholds. An alternative proposed by Rönkkö and Cho (2022) is that the upper limit of the [95%] CI should be below the threshold. Applying their recommendation assumes there is a discriminant validity issue (null hypothesis), and finding an upper limit below the threshold (cutoff value of 0.9) supports the conclusion that there is no discriminant validity issue (alternative hypothesis). However, that approach has lower power to detect discriminant validity issues, and a larger sample size lowers the power further. Consequently, we suggest the more appropriate strategy is to compare the lower limit of the 90% CI with the threshold. If the lower limit of the 90% CI is higher than the threshold, one rejects the null hypothesis of no discriminant validity issues and concludes with the alternative hypothesis that there is a discriminant validity issue.
Implementing the recommended psychometric criteria using the measureQ package
Thus far, we have outlined criteria for establishing reliability, convergent and discriminant validity. Applying these criteria consistently will improve research rigor (Grand et al., 2018). Currently, researchers need to obtain the necessary quality measures using multiple software packages. To this end, we have developed a software package, measureQ, based on the freely-available R software program. measureQ examines the measurement quality of reflective scales against our recommended criteria using the bootstrapping method. When data are nested, measureQ uses parametric bootstrapping (Efron & Tibshirani, 1993) instead of non-parametric bootstrapping. Additionally, measureQ adopts the Maximum Likelihood with Robust Standard Errors (MLR) estimator because it is more robust to nonnormality and can adjust the standard errors and fit indices for nested data. When there are missing values (noting that missing values are often coded as NA in the data file in R), full information maximum likelihood (FIML) computes the likelihood case by case using all available data from that case. For ease of interpretation, deviations from our recommendations (as summarized in Table 2) are indicated in the measureQ output with symbols, allowing the user to quickly identify issues of concern. We next detail the implementation and interpretation of measureQ, noting that all necessary files are in the supplementary materials.
To install measureQ, one should first download the package (measureQ_1.4.1.tar.gz) from the supplementary materials to a folder on the local computer. Then, from the R console, select “Packages”, then “Install package(s) from local files”, and then from the “Select files” pop-up window, select the measureQ package. In addition to measureQ, conducting CFA requires the R package lavaan (Rosseel, 2012), so both measureQ and lavaan should be installed once on the computer. Please note that R functions are case-sensitive. Definitions and examples for the arguments (options) are provided in the measureQ documentation in the supplementary file, and can be accessed directly by typing “? measureQ()” in the R console. Before using measureQ, this package needs to be loaded once each time the R console is launched using the library command:
To start using measureQ, the working directory is first set by using setwd() function. In our example, we have saved the relevant files on the C: drive as per the command below:
In the measure Q documentation, we provide five examples, Examples A through E, to illustrate the use of measureQ across various scenarios that researchers may experience when evaluating reliability, convergent and discriminant validity. Examples A and B are simpler, demonstrating the implementation of criteria using a basic latent measurement model (Example A) and the inclusion of a single-indicator factor (Example B). Example C and Example D demonstrate measureQ in assessing reliability, convergent and discriminant validity with a second-order factor. Example E illustrates the use of measureQ in an empirical study with nested data, multiple first-order factors, a second-order factor, and two single-item factors. We specify our resulting evaluations indicating no concern, minor concern, or major concern for reliability, convergent and discriminant validity. We encourage readers to follow our descriptions and implement measureQ as per our instructions to work through these examples.
Illustrating measureQ – basic model (example A)
For Example A, we simulated a dataset based on the parameters reported in Yu et al. (2020) that examined the moderating effect of institutional voids (IV) on the relationships between entrepreneurial bricolage (EB) and new venture growth (NVG) and adaptiveness (NVA). The original dataset included responses from 354 founders of new ventures in China. The authors adopted Senyard et al.’s (2014) 8-item scale for EB and Anderson and Eshima’s (2013) 3-item scale for NVG, and translated them into Chinese. They also developed 5 items for IV, and 4 items for NVA. All items were measured on a 7-point Likert scale; we refer interested readers to the original article for further details. The simulated dataset (Example_A.csv) is available in the supplementary files.
The first step is to load the data file (Example_A.csv) as a data frame; in this demonstration, we name this Data_A, noting this name can be modified to suit:
Next, we name the measurement model Model.A and define the relevant latent constructs (again noting all these can be modified to suit):
The final step is to command R to use measureQ to examine the specified measurement model (Model.A) using the specified data frame (Data_A). The minimum arguments must include the model’s name and the data frame’s name.
The above function uses several default settings in measureQ, including the number of bootstrapped samples at 1,000 and PCIs. Note that the number of completed bootstrapped samples may be smaller than the number of requested bootstrapped samples because bootstrapped samples with non-converged solutions, negative factor loadings, and improper solutions (such as negative residual variance and correlation greater than 1) are removed in the estimation of CIs. If the number of completed bootstrapped samples is lower than 800, we recommend rerunning measureQ with a larger number of requested bootstrapped samples by changing the b.no argument (e.g., by adding b.no = 2000 in the above command) to get a more stable CI. The lower number of completed bootstrapped samples does not imply the model is wrong, but only that there may be parameters in the original model close to the limits (e.g., variance close to zero and correlation close to one).
While we encourage readers to try measureQ for themselves, for convenience, we have included the outputs for all five examples in the supplementary files, including CIs and p-values for CR, AVE, standardized factor loadings, correlation coefficients, comparisons between AVE and squared correlations, fit indices for overall model fit, unstandardized factor loadings, and other estimated parameters. Since measureQ generates CIs and tests hypotheses based on the bootstrapping procedure, the results from two different trials may be slightly different. However, when 1,000 or more bootstrapped samples are used, it will be rare for researchers to arrive at different conclusions about measurement quality.
The measureQ outputs also include four summary tables. The first table provides the statistical tests of the standardized factor loadings against three thresholds, namely 0.4, 0.5, and 0.7. The second table reports the descriptive statistics of the latent variables, AVE, CR, latent correlation coefficients, and convergent and discriminant validity test results. This table should be reported if subsequent hypothesis tests are based on latent variables. Observed variable means are reported in this table because latent means are undefined in a single-group environment. By default, many SEM software programs (e.g., Mplus, lavaan) fix the latent means to zero. Bollen (1989) suggested that one can define the latent mean by setting the intercept of the referent indicator to zero (noting that the factor loading of the referent indicator is set to unity to provide identification and scale of the latent variable, which by default is the first item in Mplus, lavaan, and LISREL). This approach, in effect, defines the latent mean as the observed mean of the referent indicator. A critical drawback of this approach is that the latent mean will differ when a different indicator is used as the referent indicator. Hence, we suggest defining the latent mean as the observed mean, the same as using effect coding (Little et al., 2006). The third table reports the descriptive statistics of the observed scores, AVE, Cronbach’s alpha, and correlation coefficients among the observed variables. This table should be reported if observed variables are used in subsequent hypothesis testing, such as path analysis. If the corrected HTMT is requested (by including the argument HTMT = "TRUE" in the final argument for measureQ; see the measureQ documentation), the outputs will produce the fourth table with disattenuated correlation coefficients.
Overall model fit
The results for Example A provided in the supplementary file include the fit indices of the hypothesized model, which show that \({\chi }^{2}\) with 164 degrees of freedom = 181.00, RMSEA = 0.017, CFI = 0.994, and SRMR = 0.033, indicating that our measurement model fits the data well.
Construct reliability
The second table of the measureQ outputs for Example A is reproduced here as Table 3. We recommend all empirical studies report this table in their manuscripts. The CRs of the four constructs are displayed on the diagonal of Table 3, ranging from 0.8206 (IV) to 0.8944 (EB). Hence, we conclude that all four constructs in our simulated empirical study demonstrated adequate CR.
Convergent validity
We follow our recommended criteria summarized in Table 2 to evaluate the convergent validity of the measures. Besides assessing the CR, we examine the standardized factor loadings and AVE. The standardized factor loadings of the 20 items on the four constructs, shown in the supplementary file, ranged from 0.5300 to 0.8817. In the measureQ output, standardized factor loadings are indicated with a letter a, b, or c if they are significantly less than 0.4, 0.5, or 0.7 (p < 0.05), respectively. The supplementary file shows three of the 20 items have standardized factor loadings significantly lower than 0.7, though none are significantly lower than 0.5. These results indicate a minor concern for convergent validity. Table 3 shows that although the AVE of IV (0.4819) was lower than 0.5, it is not significantly lower than 0.5 (p < 0.05).Footnote 4 We conclude that convergent validity was achieved for our simulated sample’s scales.
Discriminant validity
We continue to evaluate discriminant validity for the four constructs that met the criteria for convergent validity. First, the fit indices indicate that our measurement model fits the data well. Second, Table 3 shows that none of the AVE is significantly lower than the square of the correlation coefficient, as this would be indicated with the # symbol if present. In addition, none of the correlation coefficients among the four constructs is significantly higher than 0.7 (noting that there is no symbol next to any correlation coefficient). Hence, our final set of analyses raises no concerns, and we conclude that discriminant validity has been achieved for the four constructs.
Illustrating measureQ – model with a single-item factor (example B)
We present a second example (Example B in the measureQ documentation) to demonstrate how measureQ deals with a single-item factor in an empirical study. In this example, we simulated a dataset based on Zahoor et al. (2022). The original study examined the effect of domestic market environment uncertainty on Pakistani small and medium-sized enterprises’ regional expansion through international alliance partner diversity (IAPD). The measures were adapted from previous studies, including 5 items for market dynamism (MD), 4 items for technological dynamism (TD), 4 items for competitive intensity (CI), 4 items for cross-cultural knowledge absorption (CCKA), 4 items for regional expansion within Asia–Pacific markets (RE), and 3 items for domestic performance (DP). All items were measured on a 7-point Likert scale. IAPD was measured by a single item: the square of the proportion of different types of partners maintained by the firm to all possible types. The original dataset included 232 complete responses. The simulated dataset (Example_B.csv) is available in the supplementary files. While the authors did not incorporate the measurement error of the single-item factor IAPD in testing the hypotheses, we demonstrate this in Example B by assuming 20% of the variance of IAPD is due to measurement errors (equivalent to a reliability of 0.8). We name the measurement model Model.B and define the relevant latent constructs:
Since IAPD is a single-item factor, the factor loading was fixed at 1, and the residual variances at (1 – reliability) times the variance of IAPD1 = (1 – 0.8)*0.0487 = 0.0097. We include all the measureQ outputs in the supplementary files.
Results
Results from measureQ in the supplementary file show the fit indices for the overall model fit of Model.B are \({\chi }^{2}\) with 255 degrees of freedom = 283.03, RMSEA = 0.022, CFI = 0.991, and SRMR = 0.034, indicating that our measurement model fits the data well. The second table of the measureQ outputs for Example B is reproduced here as Table 4. The diagonal of Table 4 displays the CR of all constructs. The single-item factor IAPD has a CR of 0.80 since the residual variance has been fixed at 0.20 times the variance of IAPD1. The CR of other factors ranges from 0.8434 to 0.9057, with all CR not significantly lower than 0.8 (p < 0.05). Overall, we conclude that all constructs demonstrated adequate CR in our simulated study.
As shown in the supplementary file (Table 1 of the supplementary file) for the measureQ outputs for Example B, no item has standardized factor loading significantly lower than 0.7. Table 4 shows that the AVE of all factors are not significantly lower than 0.5 (p < 0.05) as there is no asterisk, raising no concerns. Table 4 also shows that the AVE of IAPD is 0.8 because we fixed the measurement error to 0.2 and factor loading to 1. In summary, all the measures demonstrate evidence of convergent validity. Next, we evaluate discriminant validity. Table 4 shows that none of the square correlations is significantly higher than the corresponding AVEs (no # beside these), and none of the correlations is significantly higher than 0.7 (no symbols by these), indicating the simulated scales achieve discriminant validity.
Illustrating measureQ – model with higher-order factors (example C)
For Example C, we simulated a dataset based on the study by Lythreatis et al. (2022). The original study examined the moderating effect of managerial discretion on the indirect effect of participative leadership (PL) on perceptions of responsible innovation (RI) through ethical climate (ETH). This example includes only PL, RI, and ETH because there is not enough information to simulate data for managerial discretion. The original dataset included responses from 487 employees in Seoul, South Korea, and the questionnaire was translated from English into Korean. The scale uses 11 items to measure the three dimensions of ETH: 6 items for caring (CRNG), 3 items for rules (RULES), and 2 items for law and codes (LC). Twelve items were used to measure the four dimensions of RI: 3 items for anticipation (ANTC), 3 items for reflexivity (RFLX), 3 items for inclusion (INCL), and 3 items for responsiveness (RSPN). Six items were used to measure PL. All items were measured on a 7-point Likert scale. The simulated dataset (Example_C.csv) is available in the supplementary files.
After loading the data file (Example_C.csv), we name the measurement model Model.C and define the relevant latent constructs:
When defining a model with a second-order factor, all first-order factors should be defined before any second-order factor. The final step is to command R to use measureQ to examine the specified measurement model (Model.C) using the specified data frame (Data_C).
The above function uses the default settings in measureQ that produces omegaH (\({\omega }_{h}\)) for the reliability of any second-order factor. If the corrected HTMT is requested (by including the argument HTMT = "TRUE" in the final argument for measureQ; see the measureQ documentation), the outputs will produce the fourth table with disattenuated correlation coefficients.
Results
The results for Example C provided in the supplementary file include the fit indices of the hypothesized second-order factor model, which show that \({\chi }^{2}\) with 367 degrees of freedom = 399.40, RMSEA = 0.013, CFI = 0.997, and SRMR = 0.013, indicating that our measurement model fits the data well. The second table of the measureQ outputs for Example C is reproduced here as Table 5. The CRs of the first-order factors are displayed on the diagonal of Table 5, ranging from 0.8393 (LC) to 0.9235 (PL). We conclude that all first-order factors in our simulated empirical study demonstrated adequate CR. The second-order reliability ωh of ETH is 0.8393, and of RI is 0.8868; both are not significantly lower than 0.8 (since there is no symbol to indicate a deviation), raising no reliability concerns.
Besides assessing the CR, we examine the standardized factor loadings and AVE to evaluate convergent validity. The standardized factor loadings, shown in the supplementary file, ranged from 0.6756 to 0.9013; none is significantly lower than 0.7. These results indicate no concern for convergent validity. Table 5 shows that the AVE of all first-order constructs is not lower than 0.5, indicating all constructs have explained no less than 50% of the variance of their corresponding items. Table 5 also shows that the AVE of ETH is 0.4810, which is not statistically significantly lower than 0.5. We conclude that convergent validity was achieved for our simulated sample.
We continue to evaluate discriminant validity. First, the fit indices indicate that our measurement model without secondary loading fits the data well. Second, Table 5 shows that none of the AVE is significantly lower than the square of the correlation coefficient, as this would be indicated with the # symbol if present. Some of the correlation coefficients among the first-order factors of ETH and among those of RI are significantly higher than 0.7, though not significantly higher than 0.8. Following the psychometric approach that suggests a high correlation between the measures of two conceptually similar constructs is due to a common underlying construct (Newman et al., 2016), we consider the high correlation between two first-order factors should not be a problem if further analyses are based on the second-order factor that includes these two first-order factors; in contrast, further analyses should not be conducted at the first-order factor level. Since the correlation coefficients among PL, ETH, and RI were all lower than 0.7, we conclude that discriminant validity has been achieved for PL, ETH, and RI.
Illustrating of measureQ – model with higher-order factor (example D)
For Example D, we simulated a dataset based on the parameters for Sample 3 reported in Way et al. (2015). The original study examined the convergent validity of a newly created multidimensional scale measuring HR flexibility (HRF). The scale uses a total of 21 items to measure the five dimensions of HRF: 5 items for resource flexibility in HR practices (RFHRP), 4 items for resource flexibility in employee skills and behaviors (RFE), 4 items for coordination flexibility in HR practices (CFHRP), 4 items for coordination flexibility in contingent worker skills and behaviors (CFCW), and 4 items for coordination flexibility in employee skills and behaviors (CFE). All items were measured on a 5-point Likert scale. The original dataset (Sample 3) included responses from 221 HR managers. The simulated dataset (Example_D.csv) is available in the supplementary files.
We name the measurement model Model.D and define the relevant latent constructs:
Results
The results for Example D provided in the supplementary file include the fit indices of the hypothesized second-order factor model, which show that \({\chi }^{2}\) with 184 degrees of freedom = 181.17, RMSEA = 0.000, CFI = 1.000, and SRMR = 0.041, indicating that our measurement model fits the data well. The second table of the measureQ outputs for Example D is reproduced here as Table 6. The CRs of the five first-order factors are displayed on the diagonal of Table 6, ranging from 0.7424 (CFHRP) to 0.8269 (RFHRP). One of the CRs (CFHRP) is significantly lower than 0.8 (p < 0.05), which is indicated by the B alongside, although none is statistically significantly lower than 0.7. Overall, we conclude that all five first-order factors in our simulated empirical study demonstrated adequate CR, except there is a minor concern for the reliability of the first-order factor CFHRP. The second-order reliability ωh of HRF is 0.7884, which is not significantly lower than 0.8 (since there is no symbol to indicate a deviation), raising no reliability concerns.
The standardized factor loadings of the 21 items on the five first-order factors, shown in the measureQ output for Example D in the supplementary file, ranged from 0.4779 to 0.8777. Five of the 21 items have standardized factor loadings significantly lower than 0.7, though none are significantly lower than 0.5. The standardized factor loading of the first-order factor CFCW on the second-order factor HRF (0.4140) is significantly lower than 0.7, though not significantly lower than 0.5. These results indicate a minor concern for convergent validity. Table 6 shows that although the AVE of four out of the five first-order factors were lower than 0.5, only one (AVE of CFHRP = 0.4207) is significantly lower than 0.5 (p < 0.05), as indicated by the asterisk. This result indicates that CFHRP explained less than 50% of the variance of its corresponding items, failing the criterion for convergent validity suggested by Fornell and Larcker (1981). Table 6 also shows that the AVE of HRF is 0.2634, suggesting that the second-order construct HRF explained less than 30% of the variance of the 21 items. This is a major concern since the second-order factor HRF is not explaining the variance of the 21 items well.Footnote 5 We conclude that convergent validity was not achieved for our simulated sample’s second-order HRF scale. We recommend that when researchers obtain results like these, they test their hypotheses with only the four first-order factors (i.e., RFHRP, RFE, CFCW, and CFE) that pass the convergent validity test instead of the second-order factor.
We continue to evaluate discriminant validity for the four first-order factors that met the criteria for convergent validity. First, the fit indices indicate that our measurement model without secondary loading fits the data well. Second, Table 6 shows that none of the AVE is significantly lower than the square of the correlation coefficient, as this would be indicated with the # symbol if present. In addition, none of the correlation coefficients among the four first-order factors is significantly higher than 0.7 (noting that there is no symbol next to any correlation coefficient). Hence, our final set of analyses raises no concerns, and we conclude that discriminant validity has been achieved for the four first-order factors (i.e., RFHRP, RFE, CFCW, and CFE).
Illustrating measureQ – model with higher-order factor and nested data (example E)
We present Example E to demonstrate the use of measureQ in an empirical study with nested data, multiple first-order factors, a second-order factor, and two single-indicator factors. In this example, we simulated a dataset based on Wayne et al. (2017). The original study examined the mediating effect of work-family conflict on promotability, performance, and increase in salary through emotional exhaustion and engagement as a second-order factor consisting of three dimensions: vigor, dedication, and absorption. The mediating effects were hypothesized to be moderated by work scheduling autonomy. The measures include Ezzedeen and Swierez’s (2007) 3-item cognitive work-family conflict scale, Morgeson and Humphrey’s (2006) 3-item work scheduling autonomy scale, 3 items extracted from Maslach and Jackson’s (1981) scale measuring emotional exhaustion, a 9-item short form of Schaufeli et al.’s (2002) engagement scale (3 items for each dimension), Thacker and Wayne’s (1995) 3-item measure of employee promotability, a single-item of supervisor’s rating of performance, and increase in salary between the two surveys across a 9-month interval from company records. The original dataset included responses from 192 employees nested within 160 supervisors. The simulated dataset (Example_E.csv) is available in the supplementary files.
We name the measurement model Model.E and define the relevant latent constructs:
where X = work-family conflict; W = work scheduling autonomy; M = emotional exhaustion; YV = engagement – vigor; YD = engagement – dedication; YA = engagement – absorption; Y = second-order engagement; sprom = supervisor-rated promotability; Salary = Increase in salary; and Perform = performance evaluation. Since Salary and Perform are single-item factors, the factor loadings were fixed at 1 and the residual variances at zero (assuming no measurement error).
The final step is to command R to use measureQ to examine the specified measurement model (Model.E) using the specified data frame (Data_E). The arguments to be included are as follows:
The above function requests the reliability and validity analyses on Model.E with the data defined in Data_E, and specifies one thousand bootstrapped samples. Notably, the data in this example are specified as being nested within the variable “leader”; this means that parametric bootstrapping is used because nonparametric bootstrapping is inappropriate for nested data. By default, measureQ produces PCIs for the analyses and \({\omega }_{h}\) for the reliability of the second-order factor. The outputs from measureQ for Example E are included in the supplementary files.
Results
Results from measureQ in the supplementary file show the fit indices for the overall model fit of Model.E are \({\chi }^{2}\) with 208 degrees of freedom = 394.68, RMSEA = 0.068, CFI = 0.945, and SRMR = 0.057, indicating that our measurement model fits the data well. The second table of the measureQ outputs for Example E is reproduced here as Table 7. The diagonal of Table 7 displays the CR of all the first-order factors and the ωh of the second-order factor. Both single-indicator factors have a CR of 1.00 since the residual variances have been fixed at zero. The CR of other first-order factors ranges from 0.7342 to 0.9680, with the lowest CR value (engagement – absorption) significantly lower than 0.8 (p < 0.05), as indicated by the B alongside the CR, although it is not statistically significantly lower than 0.7. Overall, we conclude that all factors demonstrated adequate CR in our simulated study, except for a minor concern for the dimension engagement – absorption. The second-order reliability \({\omega }_{h}\) of engagement is satisfactory at 0.8859.
As shown in the supplementary file for the measureQ outputs for Example E, one item for engagement – absorption and one item for supervisor-rated promotability have standardized factor loadings significantly lower than 0.7, although none is significantly lower than 0.5 – thus, we classify these as minor concerns. Table 7 shows that although the AVE of engagement – absorption was lower than 0.5 (0.4937), as there is no asterisk, it was not statistically significantly lower than 0.5 (p < 0.05). The AVE of all other constructs was greater than 0.5, raising no concerns. Table 7 also shows that the AVE of the second-order factor engagement is 0.5867, suggesting that engagement explained more than 50% of the variance of the 9 items. In summary, all the measures demonstrate evidence of convergent validity.
Next, we evaluate discriminant validity. Table 7 shows (with the # symbol next to the correlation coefficient) that the AVE of engagement – absorption (0.4937) was significantly lower than the square of the correlation coefficient with engagement – dedication (0.8543 × 0.8543 = 0.7298). This shows that the discriminant validity of engagement’s dedication and absorption dimensions is questionable, raising a concern. In addition, the correlation coefficient between engagement – dedication and engagement – absorption is significantly higher than 0.7, but not significantly higher than 0.8. We consider the high correlation between the two dimensions should not be a problem if further analyses are based on the second-order factor (engagement) that includes these two dimensions; in contrast, further analyses should not be conducted at the first-order factor level. All other variables demonstrate evidence of discriminant validity.
Discussion
While most empirical studies report some evidence of the quality of measurement scales in terms of reliability, convergent and discriminant validity, this evidence is gathered through a variety of approaches. In this paper, we have reviewed many of those approaches and, from this basis, suggest best practices for evaluating the quality of measures in empirical research. Overall, our paper makes a number of contributions that enable researchers to accurately analyze and report the quality of the scales used in their empirical studies.
Our first contribution is reviewing and critiquing the most commonly-adopted approaches for evaluating the quality of measurement scales, as summarized in Table 1. Applying inadequate approaches may cause researchers to retain poor-quality scales and reject scales with adequate quality, undermining the value of research (Grand et al., 2018).
Our second contribution is recommending best practices for assessing reliability, convergent and discriminant validity. Despite the importance of evaluating the quality of measurement scales, and although most empirical studies include some relevant information on measurement quality, there has been little consensus on what criteria demonstrate a reliable measure or adequate convergent and discriminant validity. We evaluate commonly used criteria of latent constructs’ reliability, convergent and discriminant validity, and use these as a foundation to recommend best practices. Specifically, as summarized in Table 2, we recommend reporting CR as a reliability measure for a latent construct and using multiple criteria when evaluating convergent and discriminant validity. This overcomes the limitations of most approaches that only examine specific facets of measurement quality. Moreover, our approach overcomes a common problem of many approaches: they do not account for sampling error; we rectify this, accounting for sampling errors by comparing the CI of sample estimates with threshold values. Moreover, most existing approaches suggest cutoff values on various criteria to make dichotomous decisions on whether reliability, convergent and discriminant validity are acceptable. Instead, we propose that the evaluation criteria lie on a continuum, and we recommend various levels indicating a major concern, minor concern, and no concern based on previous literature.
Third, currently, researchers rely on various software packages and syntaxes to examine reliability, convergent and discriminant validity. To support accurate assessments of these fundamental scale measurement qualities, we provide a one-stop solution for researchers through our development of measureQ. Users of measureQ can generate all the results with one simple step of defining the measurement model, enabling them to examine the quality of their measurement scales. measureQ allows data with missing values, nested data, single-item factors, and second-order factors. measureQ provides not only summary tables of measure quality for reporting purposes in the outputs, but also CIs of estimated parameters that allow for further examination of possible problems in the measurement scales.
Fourth, we provide a recommended template for reporting the quality of measurement scales, which serves as a reference for researchers and reviewers. Currently, empirical researchers use a variety of approaches to examine reliability, convergent and discriminant validity, and report their results differently. measureQ produces a table that summarizes crucial information on reliability, convergent and discriminant validity, and reports any concerns for each quality issue. Using a unified reporting template enables reviewers and authors to accurately and comprehensively review and report the quality of measurement scales in future empirical studies, and facilitates comparisons across studies.
Finally, while developing the measureQ package, we compared our results with those from existing software and identified shortcomings in several frequently-used software packages and syntaxes aimed at evaluating the quality of measurement scales. We summarize the identified issues in the supplementary file. We urge software developers, reviewers, and authors of syntaxes to conduct more stringent testing before making software packages publicly available. This is essential because many empirical researchers rely on these problematic software packages and syntaxes to analyze and report their findings without knowing that some results are incorrect. In turn, others may adopt measures that they falsely believe show reliability, convergent and discriminant validity when this is not the case. This will likely maintain problematic measures in the literature rather than enable their shortcomings to be identified and rectified.
Although we presented criteria for evaluating reliability, convergent and discriminant validity of second-order factors for multidimensional scales, not all multidimensional scales should be studied as a second-order factor at the more abstract level. For example, Breaugh (1985) developed a multidimensional scale to measure the three facets of work autonomy: method autonomy, scheduling autonomy, and criteria autonomy. As the correlations among the three dimensions (0.34 to 0.47) were not high (Breaugh, 1985), researchers should study work autonomy as three correlated factors instead of a second-order factor (work autonomy). Similarly, Meyer et al. (1993) showed that affective, continuance, and normative commitment measured by Meyer and Allen’s (1991) scale should be studied as three independent factors because they have different antecedents and consequences.
Limitations
Researchers should note that our discussions focus on empirical management studies adopting established measures in the multitrait-monomethod context and not scale development studies in the multitrait-multimethod context. For scale development studies, in addition to the criteria suggested in Table 2, researchers should provide evidence of convergent validity across similar measures and criterion-related validity (for example, Wang et al., 2022). Our recommended best practices apply to studies employing covariance-based SEM but not variance-based SEM (PLS-SEM) analyses. Similarly, our recommendations relate to latent constructs with reflective measures. They do not apply to formative measures, as these are typically indices that do not require convergent validity or internal consistency. Because we recommend considering sampling errors with CIs when evaluating the quality of measurement scales, a large sample size can guarantee adequate statistical power in identifying quality issues. While the appropriate sample size depends on the complexity of the model and the estimation method, Kelley and Pornprasertmanit (2016) found, using a simulation, that the coverage rates of CIs are good across reliability levels even at N = 50. However, following Anderson and Gerbing’s (1988) suggestion, we recommend a minimum sample size of 150 to obtain standard errors small enough for practical application. Researchers should check if the CIs have substantially wide intervals for studies with smaller sample sizes.
Conclusions
Researchers using SEM with latent constructs in empirical studies wish to produce accurate results and, as part of this, aim to treat reliability, convergent and discriminant validity seriously. Therefore, we suspect mistakes in how researchers present these issues are due to available resources lacking clear explanations of the critical issues and limitations. Hence, we review the current literature to identify best practices and make these simple to implement using the R package, measureQ, that we have developed. We close by urging all editors and reviewers to support authors in implementing best practices by requesting proper tests of reliability, convergent and discriminant validity in all articles and acknowledging the efforts of authors who provide these.
Change history
25 March 2023
A Correction to this paper has been published: https://doi.org/10.1007/s10490-023-09880-x
Notes
Discussion on model fit evaluation goes beyond the scope of this review. The American Psychological Association’s journal article reporting standards (Appelbaum et al., 2018) refer researchers to Kline (2016, Chapter 18), who suggested researchers report chi-square with its degrees of freedom and p-value; RMSEA (Steiger & Lind, 1980) and its 90% confidence interval (Browne & Cudeck, 1992), CFI (Bentler, 1990), and SRMR (Bentler, 1995). Researchers commonly adopt Hu and Bentler's (1999, p. 1) criteria for evaluating model fit, comprising cutoff values close to 0.06 for RMSEA, 0.95 for CFI, and 0.08 for SRMR as indicating “a relatively good fit between the hypothesized model and the observed data.”.
The problem of the \({\chi }^{2}\left(cut\right)\) approach recommended by Rönkkö and Cho (2022) can be demonstrated by fixing the correlation of the two target constructs at a value close to 1.0 (e.g., 0.99). In such a case, the correlation between the two target constructs and other constructs should be close to equivalent. However, applying Rönkkö and Cho’s (2022) approach may result in very different correlation coefficients between the two target constructs and other constructs.
Rönkkö and Cho (2022: 13) also identified the problem of Henseler et al.’s (2015) HTMT as “disattenuated correlation using parallel reliability (i.e., the standardized alpha),” which is the same as the Cronbach’s alpha of the composite score obtained by averaging the standardized item scores. However, they did not suggest corrections for Henseler et al.’s HTMT equation.
The AVE of EB, IV, NVG, and NVA reported in Yu et al. (2020) were 0.499, 0.493, 0.758, and 0.625, respectively.
The AVE of RFHRP, RFE, CFHRP, CFCW, and CFE reported in Sample 3 of Way et al. (2015) were 0.47, 0.56, 0.41, 0.54, and 0.55, respectively. The AVE of HRF was 0.25.
References
Anderson, B. S., & Eshima, Y. (2013). The influence of firm age and intangible resources on the relationship between entrepreneurial orientation and firm growth among Japanese SMEs. Journal of Business Venturing, 28, 413–429.
Anderson, J. C., & Gerbing, D. W. (1988). Structural equation modeling in practice: A review and recommended two-step approach. Psychological Bulletin, 103, 411–423.
Appelbaum, M., Cooper, H., Kline, R. B., Mayo-Wilson, E., Nezu, A. M., & Rao, S. M. (2018). Journal article reporting standards for quantitative research in psychology: The APA Publications and communications board task force report. American Psychologist, 73, 3–25.
Bagozzi, R. P. (1981). Evaluating structural equation models with unobservable variables and measurement error: A comment. Journal of Marketing Research, 18, 375–381.
Bagozzi, R. P. (1983). Issues in the application of covariance structure analysis: A further comment. Journal of Consumer Research, 9, 449–450.
Bagozzi, R. P., & Phillips, L. W. (1982). Representing and testing organizational theories: A holistic construal. Administrative Science Quarterly, 27, 459–489.
Bagozzi, R. P., Yi, Y., & Phillips, L. W. (1991). Assessing construct validity in organizational research. Administrative Science Quarterly, 36, 421–458.
Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107, 238–246.
Bentler, P. M. (1995). EQS 5 [Computer Program]. Multivariate Software Inc.
Bollen, K. A. (1989). Structural equation models with latent variables. John Wiley & Sons.
Breaugh, J. A. (1985). The measurement of work autonomy. Human Relations, 38, 551–570.
Browne, M. W., & Cudeck, R. (1992). Alternative ways of assessing model fit. Sociological Methods & Research, 21, 230–258.
Campbell, D. T., & Fiske, D. W. (1959). Convergent and discriminant validation by the multitrait-multimethod matrix. Psychological Bulletin, 56, 81–105.
Carmines, E. G., & Zeller, R. A. (1979). Reliability and validity assessment. Sage.
Cheung, G. W. (1999). Multifaceted conceptions of self-other ratings disagreement. Personnel Psychology, 52, 1–36.
Cho, E. (2016). Making reliability reliable: A systematic approach to reliability coefficients. Organizational Research Methods, 19, 651–682.
Christofi, M., Khan, H., & Iaia, L. (2022). Responsible innovation in Asia: A systematic review and an agenda for future research. Asia Pacific Journal of Management. https://doi.org/10.1007/s10490-022-09839-4
Clark, L. A., & Watson, D. (1995). Construct validity: Basic issues in objective scale development. Psychological Assessment, 7, 309–319.
Cortina, J. M. (1993). What is coefficient alpha? An examination of theory and application. Journal of Applied Psychology, 78, 98–104.
Cortina, J. M., Sheng, Z., Keener, S. K., Keeler, K. R., Grubb, L., Schmitt, N., Tonidandel, S., Summerville, K. M., Heggestad, E. D., & Banks, G. (2020). From alpha and omega and beyond! A look at the past, present, and (possible) future of psychometric soundness in the journal of applied psychology. Journal of Applied Psychology, 105, 1351–1381.
Credé, M., & Harms, P. D. (2015). 25 years of higher-order confirmatory factor analysis in the organizational sciences: A critical review and development of reporting recommendations. Journal of Organizational Behavior, 36, 845–872.
Dunn, S. C., Seaker, R. F., & Waller, M. A. (1994). Latent variables in business logistics research: Scale development and validation. Journal of Business Logistics, 15, 145–172.
Dunn, T. J., Baguley, T., & Brunsden, V. (2014). From alpha to omega: A practical solution to the pervasive problem of internal consistency estimation. British Journal of Psychology, 105, 399–412.
Edwards, J. R. (2011). The fallacy of formative measurement. Organizational Research Methods, 14, 370–388.
Efron, B., & Tibshirani, R. J. (1993). An introduction to the bootstrap. New York: Chapman & Hall/CRC.
Ezzedeen, S. R., & Swiercz, P. M. (2007). Development and initial validation of a cognitive-based work-nonwork conflict scale. Psychological Reports, 100, 979–999.
Flora, D. B. (2020). Your coefficient alpha is probably wrong, but which coefficient omega is right? A tutorial on using R to obtain better reliability estimates. Advances in Methods and Practices in Psychological Science, 3, 484–501.
Fornell, C., & Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. Journal of Marketing Research, 18, 39–50.
Garson, G. D. (2002). Guide to writing empirical papers, theses, and dissertations. CRC Press.
Gerbing, D. W., & Anderson, J. C. (1984). On the meaning of within-factor correlated measurement errors. Journal of Consumer Research, 11, 572–580.
Gerbing, D. W., & Anderson, J. C. (1988). An updated paradigm for scale development incorporating unidimensionality and its assessment. Journal of Marketing Research, 25, 186–192.
Graham, J. M. (2006). Congeneric and (essentially) tau-equivalent estimates of score reliability: What they are and how to use them. Educational and Psychological Measurement, 66, 930–944.
Grand, J. A., Rogelberg, S., Allen, T. D., Landis, R. S., Reynolds, D. H., Scott, J. C., Tonifandel, S., & Truxillo, D. M. (2018). A system-based approach to fostering robust science in industrial-organizational psychology. Industrial and Organizational Psychology, 11, 4–42.
Grewal, R., Cote, J. A., & Baumgartner, H. (2004). Multicollinearity and measurement error in structural equation models: Implications for theory testing. Marketing Science, 23, 519–529.
Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2009). Multivariate data analysis (7th ed.). Prentice-Hall.
Heggestad, E. D., Scheaf, D. J., Banks, G. C., Hausfeld, M. M., Tonidandel, S., & Williams, E. B. (2019). Scale adaptation in organizational science research: A review and best-practice recommendations. Journal of Management, 45, 2596–2627.
Henseler, J., Ringle, C. M., & Sarstedt, M. (2015). A new criterion for assessing discriminant validity in variance-based structural equation modeling. Journal of the Academy of Marketing Science, 43, 115–135.
Hinkin, T. R. (1998). A brief tutorial on the development of measures for use in survey questionnaires. Organizational Research Methods, 1, 104–121.
Hu, L., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6, 1–55.
John, O. P., & Benet-Martínez, V. (2000). Measurement: Reliability, construct validation, and scale construction. In H. T. Reis & C. M. Judd (Eds.), Handbook of research methods in social and personality psychology (pp. 339–369). Cambridge University Press.
Jöreskog, K. G. (1971). Simultaneous factor analysis in several populations. Psychometrika, 36, 409–426.
Kelley, K., & Cheng, Y. (2012). Estimation and confidence interval formation for reliability coefficients of homogeneous measurement instruments. Methodology, 8, 39–50.
Kelley, K., & Pornprasertmanit, S. (2016). Confidence intervals for population reliability coefficients: Evaluation of methods, recommendations, and software for composite measures. Psychological Methods, 21, 69–92.
Kenny, D. A. (2016). Multiple latent variable models: Confirmatory factor analysis. Retrieved October 2017 from davidakenny.net/cm/mfactor.htm.
Kline, R. (2016). Principles and practice of structural equation modeling (4th ed.). The Guilford Press.
Lambert, L. S., & Newman, M. A. (2022). Construct development and validation in three practical steps: Recommendations for reviewers, editors, and authors. Organizational Research Methods. https://doi.org/10.1177/10944281221115374
Lance, C. E., Butts, M. M., & Michels, L. C. (2006). The sources of four commonly reported cutoff criteria: What did they really say? Organizational, Research Methods, 9, 202–220.
Li, H., & Li, J. (2009). Top management team conflict and entrepreneurial strategy making in China. Asia Pacific Journal of Management, 26, 263–283.
Little, T. D., Slegers, D. W., & Card, N. A. (2006). A Non-arbitrary method of identifying and scaling latent variables in SEM and MACS models. Structural Equation Modeling, 13, 59–72.
Lythreatis, S., El-Kassar, A., Smart, P., & Ferraris, A. (2022). Participative leadership, ethical climate and responsible innovation perceptions: Evidence from South Korea. Asia-Pacific Journal of Management. https://doi.org/10.1007/s10490-022-09856-3
Maslach, C., & Jackson, S. E. (1981). The measure of experienced burnout. Journal of Occupational Behavior, 2, 99–113.
McDonald, R. P. (1999). Test theory: A unified treatment. Lawrence Erlbaum.
Meyer, J. P., & Allen, N. J. (1991). A three-component conceptualization of organizational commitment. Human Resource Management Review, 1, 61–98.
Meyer, J. P., Allen, N. J., & Smith, C. A. (1993). Commitment to organizations and occupations: Extension and test of a three-component conceptualization. Journal of Applied Psychology, 78, 538–551.
Morgeson, F. P., & Humphrey, S. E. (2006). The work design questionnaire (WDQ): Developing and validating a comprehensive measure for assessing job design and the nature of work. Journal of Applied Psychology, 91, 1321–1339.
Newman, D. A., Harrison, D. A., Carpenter, N. C., & Rariden, S. M. (2016). Construct mixology: Forming new management constructs by combining old ones. Academy of Management Annals, 10, 943–995.
Nunnally, J. C. (1978). Psychometric theory (2nd ed.). McGraw-Hill.
Posner, B. Z., & Kouzes, J. M. (1988). Development and validation of the leadership practices inventory. Educational and Psychological Measurement, 48, 483–496.
Raykov, T. (1997). Estimation of composite reliability for congeneric measures. Applied Psychological Measurement, 21, 173–184.
Raykov, T. (2002). Automated procedure for obtaining standard error and confidence interval for scale reliability. Understanding Statistics, 1, 75–84.
Raykov, T., & Marcoulides, G. A. (2012). Evaluation of validity and reliability for hierarchical scales using latent variable modeling. Structural Equation Modeling: A Multidisciplinary Journal, 19, 495–508.
Raykov, T., & Shrout, P. E. (2002). Reliability of scales with general structure: Point and interval estimation using a structural equation modeling approach. Structural Equation Modeling, 9, 195–212.
Raykov, T., Goldammer, P., Marcoulides, G. A., Li, T., & Menold, N. (2018). Reliability of scales with second-order structure: Evaluation of coefficient alpha’s population slippage using latent variable modeling. Educational and Psychological Measurement, 78, 1123–1135.
Ren, S., Tang, G., & Jackson, S. E. (2018). Green human resource management research in emergence: A review and future directions. Asia Pacific Journal of Management, 35, 769–803.
Roemer, E., Schuberth, F., & Henseler, J. (2021). HTMT2 - an improved criterion for assessing discriminant validity in structural equation modeling. Industrial Management and Data Systems, 121, 2637–2650.
Rönkkö, M., & Cho, E. (2022). An updated guideline for assessing discriminant validity. Organizational Research Methods, 25, 6–14.
Rosseel, Y. (2012). lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software, 48, 1–36. Retrieved from http://www.jstatsoft.org/v48/i02/. Accessed 3 Oct 2021.
Schaufeli, W. B., Salanova, M., González-Romá, V., & Bakker, A. B. (2002). The measurement of engagement and burnout: A two sample confirmatory factor analytic approach. Journal of Happiness Studies, 3, 71–92.
Schaufeli, W. B., Bakker, A. B., & Salanova, M. (2006). The measurement of work engagement with a short questionnaire. A cross-national study. Educational and Psychological Measurement, 66, 701–716.
Schmitt, N. (1996). Uses and abuses of coefficient alpha. Psychological Assessment, 8, 350–353.
Senyard, J., Baker, T., Steffens, P., & Davidsson, P. (2014). Bricolage as a path to innovativeness for resource-constrained new firms. Journal of Product Innovation Management, 31, 211–230.
Shaffer, J.A., DeGreest, D., & Li, A. (2016). Tackling the problem of construct proliferation: A guide to assessing the discriminant validity of conceptually related constructs. Organizational Research Methods, 19, 80–110.
Shiu, E., Pervan, S. J., Bove, L. L., & Beatty, S. E. (2011). Reflections on discriminant validity: Reexamining the Bove et al. (2009) findings. Journal of Business Research, 64, 497–500.
Sijtsma, K. (2009). On the use, the misuse, and the very limited usefulness of Cronbach's Alpha. Psychometrika, 74, 107–120.
Steenkamp, J. B., & van Trijp, H. (1991). The use of LISREL in validating marketing constructs. International Journal of Research in Marketing, 8, 283–299.
Steiger, J. H., & Lind, J. C. (1980). Statistically-based tests for the number of common factors. Paper presented at the annual meeting of the Psychometric Society, Iowa, USA, May.
Stevens, J. P. (2002). Applied multivariate statistics for the social sciences (4th ed.). Erlbaum.
Thacker, R. A., & Wayne, S. J. (1995). An examination of the relationship between upward influence tactics and assessments of promotability. Journal of Management, 21, 739–756.
Voorhees, C. M., Brady, M. K., Calantone, R., & Ramirez, E. (2016). Discriminant validity testing in marketing: An analysis, causes for concern, and proposed remedies. Journal of the Academy of Marketing Science, 44, 119–134.
Wang, F., & Shi, W. (2022). The effect of work-leisure conflict on front-line employees’ work engagement: A cross-level study from the emotional perspective. Asia Pacific Journal of Management, 39, 225–247.
Wang, T., Wang, D., & Liu, Z. (2021a). Feedback-seeking from team members increases employee creativity: The roles of thriving at work and mindfulness. Asia Pacific Journal of Management. https://doi.org/10.1007/s10490-021-09768-8
Wang, T., Zhang, T., & Shou, Z. (2021b). The double-edged sword effect of political ties on performance in emerging markets: The mediation of innovation capability and legitimacy. Asia Pacific Journal of Management, 38, 1003–1030.
Wang, A., Chen, Y., Hsu, M., Lin, Y., & Tsai, C. (2022). Role-based paternalistic exchange: Explaining the joint effect of leader authoritarianism and benevolence on culture-specific follower outcomes. Asia Pacific Journal of Management, 39, 433–455.
Way, S. A., Tracey, J. B., Fay, C. H., Wright, P. M., Snell, S. A., Chang, S., & Gong, Y. (2015). Validation of a multidimensional HR flexibility measure. Journal of Management, 41, 1098–1131.
Wayne, S. J., Lemmon, G., Hoobler, J. M., Cheung, G. W., & Wilson, M. S. (2017). The ripple effect: A spillover model of the detrimental impact of work-family conflict on job success. Journal of Organizational Behavior, 38, 876–894.
Wei, Z., & Nguyen, Q. T. K. (2020). Local responsiveness strategy of foreign subsidiaries of Chinese multinationals: The impacts of relational-assets, market-seeking FDI, and host country institutional environments. Asia Pacific Journal of Management, 37, 661–692.
Yu, X., Li, Y., Su, Z., Tao, Y., Nguyen, B., & Xia, F. (2020). Entrepreneurial bricolage and its effects on new venture growth and adaptiveness in an emerging economy. Asia Pacific Journal of Management, 37, 1141–1163.
Yu, M., Lin, H., Wang, G. G., Liu, Y., & Zheng, X. (2021). Is too much as bad as too little? The S-curve relationship between corporate philanthropy and employee performance. Asia Pacific Journal of Management. https://doi.org/10.1007/s10490-021-09775-9.
Zahoor, N., Khan, H., Khan, Z., & Akhtar, P. (2022). Responsible innovation in emerging markets’ SMEs: The role of alliance learning and absorptive capacity. Asia Pacific Journal of Management. https://doi.org/10.1007/s10490-022-09843-8
Zinbarg, R.E., Revelle, W., Yovel, I., & Li, W. (2005). Cronbach's α, Revelle's β, and McDonald's ω : Their relations with each other and two alternative conceptualizations of reliability. Psychometrika, 70, 123–133.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
The authors confirm that the data of the examples in this manuscript are all explicitly simulated for this study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised to update Table 2 information.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cheung, G.W., Cooper-Thomas, H.D., Lau, R.S. et al. Reporting reliability, convergent and discriminant validity with structural equation modeling: A review and best-practice recommendations. Asia Pac J Manag 41, 745–783 (2024). https://doi.org/10.1007/s10490-023-09871-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10490-023-09871-y