Efficient anomaly identification in temporal and non-temporal industrial data using tree based approaches

Abstract

Anomalies indicate impending failures in expensive industrial devices. Manufacturers of such devices or Plant Managers depend heavily on anomaly detection algorithms to perform monitoring and predictive maintenance activities. Since false alarms directly impact any industrial manufacturer’s revenue, it is crucial to reduce the number of false alarms generated by anomaly detection algorithms. Here in this paper, we have proposed multiple solutions to address this ongoing problem in the industry. The proposed unsupervised solution, Multi-Generations Tree (MGTree) algorithm, not only reduced the false positive alarms but is also equally effective on small and large datasets. MGTree has been applied to multiple industrial datasets such as Yahoo, AWS, GE, and machine sensors for evaluation purposes. Our empirical evaluation shows that MGTree performs favorably to Isolation Forest (iForest), One Class Support Vector Machine (OCSVM), and Elliptic Envelope in terms of correctness of the identification (True-Positive and False-Positive) of the anomalies. We have also proposed a time series prediction algorithm Weighted Time-Window Moving Estimation (WTM), which does not rely on the dataset’s stationary characteristics and is evaluated on multiple time-series datasets. The hybrid combination of WTM and MGTree, Uni-variate Multi-Generations Tree (UVMGTree) worked very well in anomaly identification of the time series datasets and outperformed OCSVM, iForest, SARIMA, and Elliptic Envelope. Our approach can have a profound impact on the predictive maintenance and health monitoring of the industrial systems across the domains where the operations team can save significant time and effort in handling false alarms. .

Appendices

Appendix A: Properties of BAT with proof

These properties are related with the Properties of BAT subsection, page 4 of the main text.

Lemma 1

1 The number of leaf nodes in an BAT is $\mathcal {I}+1$ and the total number of internal nodes in a MGTree is ${\sum }_{t=1}^{g}(\mathcal {I}_{t}+1)$ where g is the number of generations.

Proof

Say, there are $\mathcal {I}$ internal nodes, each having 2 children (As Binary Anomaly Tree is a full binary tree). Therefore total children in the tree are $2*\mathcal {I}$. $\mathcal {I}-1$ internal nodes are children of some other nodes (root excluded as it is not a child of any node). Therefore out of $2\mathcal {I}$ nodes, $\mathcal {I}-1$ are internal nodes, and the rest of the nodes are leaf nodes. Hence

$$ \begin{array}{@{}rcl@{}} & =>&\mathcal{L}=2*\mathcal{I-(I-}1)\\ &=>&2*\mathcal{I-I}+1\\ & =>&\mathcal{I}+1 \end{array} $$

Say MGTree has employed g number of generations to corner the anomalies. Each generation produces an BAT. An BAT has $\mathcal {I}+1$ internal nodes. If the first generation BAT generates $\mathcal {I}_{1}+1$ internal nodes and g th generation produces $\mathcal {I}_{g}+1$ internal nodes. Hence the total number internal nodes are $(\mathcal {I}_{1}+1) + (\mathcal {I}_{2}+1)$...+$(\mathcal {I}_{g}+1)$=${\sum }_{\mathcal {t}=1}^{g}(\mathcal {I}_{t}+1)$□

Lemma 2

If BAT $\mathcal {T}$ has ${\mathscr{L}}$ leaves, the number of internal nodes is $\mathcal {I=L}-1$ and the total number of internal nodes in MGTree is ${\sum }_{t=1}^{g} {\mathscr{L}}_{t}-g$

Proof

In Lemma 1, we have already proved the below equation.

$$ \begin{array}{@{}rcl@{}} =>\mathcal{L=I}+1\\ =>\mathcal{I=L}-1 \end{array} $$

If MGTree employs g generations then the total number of internal nodes are $({\mathscr{L}}_{1}-1)+({\mathscr{L}}_{2}-1)....+({\mathscr{L}}_{g}-1)$=${\sum }_{t=1}^{g} {\mathscr{L}}_{t}-g$□

Lemma 3

If BAT $\mathcal {T}$ has $\mathcal {I}$ internal nodes, the total number of nodes is $\mathcal {N}=2\mathcal {I}+1$ and the total number of nodes in MGTree is $2*{\sum }_{t=1}^{g} {\mathscr{L}}_{t}+g$.

Proof

If I is the total number of internal nodes. As it is a full binary tree, the number of children is possible 2I. The root is not a child of any node; hence the total number of nodes $\mathcal {N}=2\mathcal {I}+1$ Say, MGTree has applied till g_th generations. Then the total number of nodes is =$2\mathcal {I}_{1}+1+2\mathcal {I}_{2}+1....+2\mathcal {I}_{g}+1$=$2{\sum }_{t=1}^{g} \mathcal {I}_{t}+g$ If $\mathcal {I}_{1}=\mathcal {I}_{2}=\mathcal {I}_{g}=\mathcal {I}$, then the total number of nodes is $2g\mathcal {I}+g=g(2\mathcal {I}+1)$□

Lemma 4

The number of nodes $\mathcal {N}$ in an anomaly tree is between 5 and $2^{{\mathscr{H}}+1}-3$, where ${\mathscr{H}}$ is the height of the tree and the total number of nodes of MGTree is between 5g and ${\sum }_{t=1}^{g} 2^{{\mathscr{H}}_{t}+1}-3g$.

Proof

The algorithm allows a minimum of two levels; hence ${\mathscr{H}}=2$, 2^{2 + 1} − 3 = 2^{2 + 1} − 3 = 5. The maximum number of nodes in a tree is possible when it generates a complete binary tree. Therefore, the maximum number of nodes in an anomaly tree can be as follow.

$$ \begin{array}{@{}rcl@{}} &&=>2^{0}+2^{1}+2^{2}......+2^{\mathcal{H}}\\ &&=>2^{\mathcal{H}+1}-1 \end{array} $$

Now for an anomaly tree, it will generate a full binary tree, leaves lying in the h-1 level. Hence an anomaly tree has 2 leaves less than a perfect binary tree of height h. Therefore the maximum number of nodes in an Anomaly tree is

$$ \begin{array}{@{}rcl@{}} &&=>2^{(\mathcal{H}+1)}-1-2 \\ &&=>2^{(\mathcal{H}+1)}-3 \end{array} $$

Say ${\mathscr{H}}_{1},{\mathscr{H}}_{2}...{\mathscr{H}}_{g}$ are the height of the BAT of each generation and g is the number of generation. If each generation always produces 2 levels (${\mathscr{H}}_{1}={\mathscr{H}}_{2}={\mathscr{H}}_{g}=2$) then total number of nodes produced by the MGTree is 5 ∗ g. On the other side, for the first generation the total number of nodes in the BAT is $2^{({\mathscr{H}}_{1}+1)}-3$. Similar way, for the second generation is $2^{({\mathscr{H}}_{2}+1)}-3$. Total number of nodes in the MGTree is $2^{({\mathscr{H}}_{1}+1)}-3+2^{({\mathscr{H}}_{2}+1)}-3+...+2^{({\mathscr{H}}_{g}+1)}-3$=${\sum }_{t=1}^{g} 2^{({\mathscr{H}}_{t}+1)}-3g$□

Lemma 5

For a dataset $\mathcal {D}$ with $\lvert \mathcal {D}\rvert =n$, and a minimum clustering threshold 𝜃, the height of BAT ${\mathscr{H}}$ is bound within

$$ \left[\left( \log{\frac{n}{\theta}}\right),(n-\theta)\right] $$

Proof

Case1: When the ClusteringFunc always partitions the input dataset in such way that the left partition $\lvert \mathcal {D}_{L}\rvert =1$ without any loss of generality. When ClusteringFunc is called with $\mathcal {D}_{R}$ as the input, $\mathcal {D}_{R}$ is split again with a singleton left cluster and this process continues till $\lvert \mathcal {D}_{R}\rvert \leq \theta$..As every level produces a cluster with single datapoint, the number of small cluster single data instance is ${\mathscr{H}}_{max}$. The tree grows till the node where it reaches the minimum clustering threshold (𝜃). Hence total number of data points in a dataset can be written as follow:

$$ \begin{array}{@{}rcl@{}} &&n=\mathcal{H}_{max}+\theta\\ &&\mathcal{H}_{max}=n-\theta \end{array} $$

The number of nodes in an BAT is $2{\mathscr{H}}_{max}+1$ as every level produces 2 nodes and 1 root node.

$$ \begin{array}{@{}rcl@{}} &&n=\mathcal{H}_{max}+\theta\\ &&=>\frac{\theta}{n}=1-\frac{\mathcal{H}_{max}}{n} \end{array} $$

First iteration of clustering implies ${\mathscr{H}}_{max}$ falling below n. MGTree algorithm does not allow the tree to grow without any clustering. Hence ${\mathscr{H}}_{max}<n$ and $\frac {\theta }{n}>0$. Therefore the number of nodes $2{\mathscr{H}}_{max}+1<2n+1$ Case2: The minimum height is possible when $\mathcal {D}_{L}$ and $\mathcal {D}_{R}$ are identical and tree generation continues till the cluster size becomes 𝜃, resulting in a balanced tree. Say, $\mathcal {K}$ is the number of leaf nodes.

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{\mathcal{K}} \theta_{i}=n \end{array} $$

𝜃_i is the number of data points in the i th leaf node. If $\theta _{1}=\theta _{2} \dots \theta _{k}=\theta$ then $\mathcal {K}\theta =n$.

The number of leaf nodes ($\mathcal {K}$) in $\mathcal H_{min}$ level $=2^{\mathcal H_{min}}$. Using this value of $\mathcal {K}$,

$$ \begin{array}{@{}rcl@{}} &&2^{\mathcal{H}_{min}}\theta=n\\ &&=>\mathcal{H}_{min}=\log\left( \frac{n}{\theta}\right) \end{array} $$

We obtain the bounds for the height of the tree: $\log (\frac {n}{\theta }) \leq {\mathscr{H}} \leq (n-\theta )$□

Appendix B: Upper bound of BAT height

Conjecture 1

Let ${\mathscr{H}}$ be the (random) height of BAT with the expected value $\mu _{{\mathscr{H}}}$ and variance σ² (σ≠ 0). Then for any positive real number k > 0, $P(\lvert {\mathscr{H}}-\mu _{{\mathscr{H}}} \rvert \geq k\sigma )\leq \frac {1}{k^{2}}$

Proof

Consider X ∈ℵ to be a random variable over natural numbers. Let $\mathcal {I}$ be an indicator random variable such that $\mathcal {I}=1$ when $\mathcal {X}\geq c$ and 0 otherwise, where c ∈ℵ and c > 0. Since $\mathcal {X}/c$ is always > 0 and $\mathcal {X}/c\geq 1$ when $\mathcal {X}\geq c$ we can say

$$\frac{\mathcal{X}}{c}\geq I$$

Taking expectation on both sides we get $\mathcal {E}[\mathcal {I}]\leq \mathcal {E}[\mathcal {X}/c]$ which can be simplified as: $\mathcal {E}[\mathcal {I}]\leq \frac {1}{c}\mathcal {E}[\mathcal {X}]$ since c is an arbitrary constant. Since $\mathcal {I}$ is an indicator variable, we rewrite $\mathcal {E}(\mathcal {I})$ as

$$ \begin{array}{@{}rcl@{}} (\mathcal{I}=0)\cdot \mathcal{P}(x<c)+(\mathcal{I}=1)\cdot \mathcal{P}(x\geq c) & \leq \mathcal{E}[\frac{x}{c}]\\ =>~ \mathcal{P}(x\geq c) & \leq \mathcal{E}[\frac{x}{c}] \end{array} $$

Setting $\mathcal {X}=({\mathscr{H}}-\mu _{{\mathscr{H}}})^{2}$, where ${\mathscr{H}}$ denotes the height of tree generated by the MGBTAI and c = k²σ².

$$ \begin{array}{@{}rcl@{}} &&\mathcal{P}((\mathcal{H}-\mu_{\mathcal{H}})^{2}\geq k^{2}\sigma^{2})\leq \frac{\mathcal{E}(\mathcal{H}-\mu_{\mathcal{H}})^{2}}{k^{2}\sigma^{2}}\\ && =>\mathcal{P}(\lvert \mathcal{H}-\mu_{\mathcal{H}} \rvert\geq k\sigma)\leq \frac{Var(\mathcal{H})}{k^{2}\sigma^{2}}\\ && =>\mathcal{P}(\lvert \mathcal{H}-\mu_{\mathcal{H}} \rvert\geq k\sigma)\leq \frac{1}{k^{2}} \end{array} $$

□

2.1 B.1 Significance of δ

δ or leaf level threshold decides the leaves that form the next generation tree from the current BAT. Since the probable anomalous nodes should be passed to the next generation, leaves at lower levels are the best candidates. Leaf level threshold is defined as a ratio of leaf level and height of the BAT ($\delta =\frac {{\mathscr{L}}}{{\mathscr{H}}}$). Leaf level must be a positive number i.e. δ > 0 and it can not be more than height of the tree. Thus, 0 < δ < 1. Since the objective is to find the leaf level threshold (${\mathscr{L}}$) of a particular Anomaly Tree (BAT), we define it as ${\mathscr{L}}=\delta *{\mathscr{H}}$. Table 19 shows the δ computation of the AWS datasets. Leaf Level column indicates the leaf level where the corresponding anomaly has been cornered and the Tree Height column indicates the height of the BAT. As the empirical study shows, there is a suitable δ value for the corresponding tree height H, controlled by conjecture 1. By conjecture 1, the admissible height values can be estimated based on the probability bound and the number of generations. As the inequality shows, the probability of tree height growing too far from the mean height becomes less as the number of generations increases. This implies that the likelihood of cornering anomalies beyond 2 generations and a height greater than 8 or 9 is low (See Section 3.4.6). We use this argument to arrive at ’reasonably good’ estimates of δ, since ${\mathscr{L}}=\delta *{\mathscr{H}}$. We further show that a relationship between the tree height and δ can be established from data. This relationship can be used to infer suitable δ values.

$$ \begin{array}{@{}rcl@{}} \delta=1.199-0.124*H \end{array} $$

$\mathcal {R}^{2}$ value is 0.75 which means the 75% of the variability of δ is explained by height. The regression coefficients are found to be at 95% significance. The 95% confidence interval (CI) of the coefficient (slope) is (− 0.0936,− 0.155), which means that the probability of the coefficient value being between − 0.0936 to − 0.155 is 95%. The 95% confidence interval (CI) of the intercept is (1.02, 1.37). The regression model is thus meaningful as the CI does not range from negative to positive values. This equation can be considered to identify the δ value for an anomaly tree. As per Section 3.4.6, the mean tree height of MGTree is 5. If the height (H) is 5 then δ is 0.57 which justifies the δ value(0.5) considered during the experiment. Please note, from the fitted model above, the maximum allowed value of H is 9 since 0 < δ < 1. As we observe from Section 3.4.6, ${P}({{\mathscr{H}}}\geq 9) \leq 0.11$ meaning the probability of tree height growing to more than 9 is less than 0.11. Thus, the choice of δ is validated from the probability bound (0 < H ≤ 9) as well.

Fig. 9

Relationship between δ and H fitted by the linear model at 95% confidence

Table 19 δ computation of the AWS datasets

Appendix C: Characterization of the datasets

The datasets which are considered as part of the paper are uni-variate, which means all the datasets have a single feature (Table 20).

Table 20 Table of dataset characterization

Table 21 Performance comparison of the WTM with other forecasting models in terms of Mean Squared Error

Table 22 Performance comparison of the WTM with other forecasting models in terms of Mean Absolute Error

All the data instances across the datasets are numeric. There are no missing data in the datasets. Most of the datasets are unimodal and follows weibull min distribution.

Appendix D: WTM evaluation

Figure 10 shows the comparison of the WTM with EWMA as well as WMA. WTM could able to identify the spike in the datasets better than the other methodologies. It is palpable from the figures that WTM is equally effective with stationary as well as non-stationary datasets.

Fig. 10

Mean squared error comparison of WTM with WMA and EWMA

Appendix E: Parameters of quality

The evaluation process’s objective is to identify the proposed solution’s efficacy in various quality parameters. It is possible to get four categories from a single experiment (see Table 1 of the additional file). These categories are TP, FP, FN, and TN Sensitivity measures the proportion of the actual positives that are correctly identified. The formula is defined as follow:

$$ Sensitivity=\frac{TP}{TP+FN} $$

(E1)

Specificity (also called the true negative rate) measures the proportion of actual negatives that are correctly identified. The mathematical expression of the specificity is as follow:

$$ Specificity=\frac{TN}{TN+FP} $$

(E2)

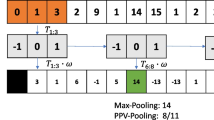
Another essential parameter is the positive predictive value (PPV). PPV decides the probability that a detected outlier is indeed a real one. The mathematical equation is as follow:

$$ PPV=\frac{TP}{TP+FP} $$

(E3)

The negative predictive value (NPV) is defined as the proportion of non-outliers among subjects with a negative test result. Its formula is as follows:

$$ NPV=\frac{TN}{TN+FN} $$

(E4)

Appendix F: Benchmark algorithms on anomaly detection

This section describes various anomaly detection algorithms, which were used for comparison with BAT based algorithms.

6.1 F.1 Isolation Forest

Isolation Forest is an ensemble method that ‘isolates’ data points by randomly selecting a feature and then randomly selecting a split value to divide the data points into two nodes. Recursive partitioning will result in each observation residing in a leaf node. The number of splittings required to isolate a sample is equal to the path length from the root to the leaf of the tree. Suppose this length is averaged over a forest of many such random trees. In that case, it will act as a measure of the outlying behavior, producing a shorter length for anomalies on average.

6.2 F.2 Elliptic Envelope

It is another unsupervised approach that relies on a geometric configuration-ellipse to corner the anomalies. It creates an imaginary elliptic area on the datasets. The datapoints falling outside this elliptical area are considered as an anomaly. The algorithm considers all observations as a whole, not the individual features. We have applied the sklearn package of python with default parameters to implement this algorithm.

6.3 F.3 OCSVM

One-class SVM is a profile-based approach, where the SVM is trained on only one class, which is the normal dataset, and the algorithm tries to capture the normal behavior. OCSVM is based on Support Vector Machines, where the binary classes are separated by a non-linear hyperplane. Any observation that deviates significantly from the normal behavior identified by the OCSVM is declared as an anomaly. We have utilized the sklearn package of python to implement this algorithm.

6.4 F.4 SARIMA

In many scenarios, it is very crucial to conside r the seasonality component in the timeseries forecasting. For example, sales of electronic devices may increase during the time of festivals. For these situations, SARIMA is very effective. SARIMA is a univariate timeseries forecasting model, and it stands for Seasonal Autoregressive Integrated Moving Average. It is an extension of the ARIMA model with a seasonality component. Like many forecasting models, the SARIMA can also be applied as an anomaly detector. If any prediction error violates the threshold, it will be declared as an anomaly.

Appendix G: Various forecasting models

7.1 G.1 WMA

WMA stands for weighted moving average. It is a timeseries forecasting model which is widely used in various fields, including the stock market. WMA puts more weight on the recent data since they are more relevant than data points in the distant past. WMA is computed using the below equation.

$$ \begin{array}{@{}rcl@{}} \frac{T_{n}*n+(n-1)T_{n-1}\cdot+T_{1}}{n+(n-1)+\dots+1} \end{array} $$

Here T_i is the timeseries value.

7.2 G.2 EWMA

The Exponentially Weighted Moving Average (EWMA) is a quantitative or statistical measure used to model univariate timeseries dataset. It is widely used in finance, and its main application is volatility modeling. The model is designed in a fashion that older observations are given lower weights. The weights fall exponentially as the data point gets older – hence the name exponentially weighted. The parameter alpha decides how important the current observation is in the calculation of the EWMA. The higher the value of alpha, the more closely the EWMA tracks the original time series.

Table 23 Assessment of the method

Table 24 Statistical analysis of the MGTree (K-means) on different metrics

7.3 G.3 EWF

An expanding window model calculates a statistic on all available historical data and uses them to forecast a future value. It is called expanding window because it increases in size as more real observations are collected. Two good starting point statistics to calculate are the mean and the median historical observation.

Table 25 Statistical analysis of the MGTree (Agglomerative) on different metrics

Table 26 Statistical analysis of the MGTree (Birch) on different metrics

7.4 G.4 RWF

A rolling window model calculates a statistic on a fixed contiguous block of prior observations and uses it as a forecast. It is similar to the expanding window, but the window size remains fixed and counts backward from the most recent observation. The model is useful for the timeseries dataset where recent lag values are more predictive than older ones.

Table 27 Table of dataset properties

Table 28 The performance comparison of UVMGTree with other standard anomaly identifier algorithms in terms of NPV and Specificity

7.5 G.5 LSTM

LSTM is a well-known deep learning model. It has been widely applied in multiple domains. The same LSTM can be utilized as a forecasting model as well. The LSTM model learns a function that maps a sequence of past observations as input to an output observation. A Vanilla LSTM model has a single hidden layer of LSTM units and an output layer used to forecast future value. In the case of stacked LSTM, Multiple hidden LSTM layers can be stacked one on another.