Bake off redux: a review and experimental evaluation of recent time series classification algorithms

Abstract

In 2017, a research paper (Bagnall et al. Data Mining and Knowledge Discovery 31(3):606-660. 2017) compared 18 Time Series Classification (TSC) algorithms on 85 datasets from the University of California, Riverside (UCR) archive. This study, commonly referred to as a ‘bake off’, identified that only nine algorithms performed significantly better than the Dynamic Time Warping (DTW) and Rotation Forest benchmarks that were used. The study categorised each algorithm by the type of feature they extract from time series data, forming a taxonomy of five main algorithm types. This categorisation of algorithms alongside the provision of code and accessible results for reproducibility has helped fuel an increase in popularity of the TSC field. Over six years have passed since this bake off, the UCR archive has expanded to 112 datasets and there have been a large number of new algorithms proposed. We revisit the bake off, seeing how each of the proposed categories have advanced since the original publication, and evaluate the performance of newer algorithms against the previous best-of-category using an expanded UCR archive. We extend the taxonomy to include three new categories to reflect recent developments. Alongside the originally proposed distance, interval, shapelet, dictionary and hybrid based algorithms, we compare newer convolution and feature based algorithms as well as deep learning approaches. We introduce 30 classification datasets either recently donated to the archive or reformatted to the TSC format, and use these to further evaluate the best performing algorithm from each category. Overall, we find that two recently proposed algorithms, MultiROCKET+Hydra (Dempster et al. 2022) and HIVE-COTEv2 (Middlehurst et al. Mach Learn 110:3211-3243. 2021), perform significantly better than other approaches on both the current and new TSC problems.

1 Introduction

Time series classification (TSC) involves fitting a model from a continuous, ordered sequence of real valued observations (a time series) to a discrete response variable. Time series can be univariate (a single variable observed at each time point) or multivariate (multiple variables observed at each time point). For example, we could treat raw audio signals as a univariate time series in a problem such as classifying whale species from their calls and motion tracking co-ordinate data could be a three-dimensional multivariate time series in a human activity recognition (HAR) task. Where relevant, we distinguish between univariate time series classification (UTSC) and multivariate time series classification (MTSC). The ordering of the series does not have to be in time: we could transform audio into the frequency domain using a discrete Fourier transform or map one dimensional image outlines onto a one dimensional series using radial or linear scanning. Hence, some researchers refer to TSC as data series classification. We retain the term TSC for continuity with past research.

TSC problems arise in a wide variety of domains. Popular TSC archives¹ contain classification problems using: electroencephalograms; electrocardiograms; HAR and other motion data; image outlines; spectrograms; light curves; audio; traffic and pedestrian levels; electricity usage; electrical penetration graph; lightning tracking; hemodynamics; and simulated data. The huge variation in problem domains characterises TSC research. The initial question when comparing algorithms for TSC is whether we can draw any indicative conclusions on performance across a wide range of problems without any prior knowledge as to the underlying common structure of the data. An experimental evaluation of time series classification algorithms, which we henceforth refer to as the bake off, was conducted in 2016 and published in 2017 (Bagnall et al. 2017). This bake off, coupled with a relaunch of time series classification archives (Dau et al. 2019), has helped increase the interest in TSC algorithms and applications. Our aim is to summarise the significant developments since 2017. A new MTSC archive (Ruiz et al. 2021) has helped promote research in this field. A variety of new algorithms using different representations, including deep learners (Fawaz et al. 2019), convolution based algorithms (Dempster et al. 2020) and hierarchical meta ensembles (Lines et al. 2018), have been proposed for TSC. Furthermore, the growth in popularity of TSC open source toolkits such as aeon² and tslearn³ have made comparison and reproduction easier. We extend and encompass recent experimental evaluations (e.g.  Ruiz et al. 2021; Bagnall et al. 2020a; Middlehurst et al. 2021; Fawaz et al. 2019) to provide insights into the current state of the art in the field and highlight future directions. Our target audience is both researchers interested in extending TSC research and practitioners who have TSC problems. Our contributions can be summarised as follows:

• 1. We describe a range of new algorithms for TSC and place them in the context of those described in the bake off.

• 2. We compare performance of the new algorithms on the current UCR archive datasets in a univariate classification bake off redux.

• 3. We release 30 new univariate datasets donated by various researchers through the TSC GitHub repository and compare the best in category on these new datasets.

• 4. We analyse the factors that drive performance and discuss the merits of different approaches.

To select algorithms, we use the same criteria as the bake off. Firstly, the algorithm must have been published post bake off in a high quality conference or journal (or be an extension of such an algorithm). Secondly, it must have been evaluated on one of the UCR/UEA dataset releases, or on a subset thereof, with reasoning provided for any datasets that are missing. Thirdly, source code must be available and easily adaptable to the time series machine learning tools we use (i.e. usable or easily wrappable in a Java or Python environment). Further explanation on our tools and reproducing our experiments is available in Appendix A. We describe many algorithms which inevitably leads to many acronyms and possible naming confusion. We direct the reader to Table 21 for a summary of the algorithms used and the associated reference. Section 2 describes the core terminology relating to TSC. Section 3 summarises how we conduct experimental evaluations of classifiers. We describe the latest TSC algorithms included in this bake off in Section 4. This section also describes the first set of experiments that link to the previous bake off: for each category of algorithms we compare the latest classifiers with the best in class from Bagnall et al. (2017). Section 5 extends the experimental evaluation to include the new datasets. Section 6 investigates variation in performance in more detail. Finally, we conclude and discuss future direction in Section 7.

2 Definitions and terminology

We define the number of time series in a collection as n, the number of channels/dimensions of any observation as d and length of a series as m.

Definition 1

(Time Series (TS)) A time series $A = \left( a_1, a_2,\dots , a_m \right)$ is an ordered sequence of m data points. We denote the i-th value of A by $a_{i}$.

In the above definition, if every point in $a_{i} \in A$ in the time series represents a single value ($a_{i} \in \mathbb {R}$), the series is a univariate time series (UTS). If each point represents the observation of multiple variables at the same time point (e.g., temperature, humidity, pressure, etc.) then each point itself is a vector $a_{i} \in \mathbb {R}^{d}$ of length d, and we call it a multivariate time series (MTS):

Definition 2

(Multivariate Time Series (MTS)) A multivariate time series $A=\left( a_1, \ldots ,a_m \right) \in \mathbb {R}^{(d \times m)}$ is a list of m vectors with each $a_i$ being a vector of d channels (sometimes referred to as dimensions). We denote the i-th observation of the $k-th$ channel by the scalar $a_{k,i}\in \mathbb {R}$.

Note that it is also possible to view a MTS as a set of d time series, since in practice that is often how they are treated. However, the vector model makes it explicit that we assume that the dimensions are aligned, i.e. we assume that all observations in $a_i$ are observed at the same point in time or space. In the context of supervised learning tasks such as classification, a dataset associates each time series with a label from a predefined set of classes.

Definition 3

(Dataset) A dataset $D=(X, Y)=\left( A^{(i)}, y^{(i)}\right) _{i \in [1, \dots , n]}$ is a collection of n time series and a predefined set of discrete class labels C. We denote the size of D by n, and the $i^{th}$ instance by series and its label by $y^{(i)} \in C$.

Many time series classification algorithms make use of subseries of the data.

Definition 4

(Subseries) A subseries $A_{i,l}$ of a time series $A = (a_1, \dots , a_m)$, with $1 \le i < i+l \le m$, is a series of length l, consisting of the l contiguous points from A starting at offset i: $A_{i,l} =(a_i,a_{i+1},\dots ,a_{i+l-1})$, i.e. all indices in the right-open interval $[i,i+l)$.

We may extract subseries from a time series by the use of a sliding window.

Definition 5

(Sliding Window) A time series A of length m has $(m-l+1)$ sliding windows of length l (when increment is 1) given by:

$$sliding\_windows(A)=\{A_{1,l},\dots ,A_{(m-l+1),l}\}$$

A common operation is the convolution operation. A kernel (filter) is convolved with a time series through a sliding dot product.

Definition 6

(Convolution (cross-correlation)) The result of applying a kernel $\omega$ of length l to a given time series A at position i is given by:

$$M_i = (A_{i,l} * \omega ) = \sum _{j=0}^{l-1} A_{i+j} \cdot w_j$$

Fig. 1

The convolution operation as a sliding dot-product. The kernel $\omega =[-1,0,1]$ is convolved with the input series, producing an activation map. Max-pooling extracts the maximum from this activation map

The result of the operation is an activation map M. Figure 1 shows the convolution for an input time series and kernel $\omega =[-1,0,1]$. The first entry of the activation map M is the result of a dot-product between $A_{1:3} * \omega = A_{1:3} \cdot \omega = 0 + 0 + 3 = 3$. Each convolution creates a series to series transform from time series to activation map. Activation maps are used to create summary features.

The dilation technique is a method that enables a filter, such as a sliding window or kernel, to cover a larger portion of the time series data by creating empty spaces between the entries in the filter. These spaces enable the filter to widen its receptive field while maintaining the total number of values constant. To illustrate, a dilation of $d=2$ would introduce a gap of 1 between each pair of values. This effectively doubles the receptive field’s size and enables the filter to analyse the data at various scales, akin to a down-sampling operation.

Definition 7

(Dilated Subseries) A dilated subseries, denoted by $A_{i, l, d}$, is a sequence extracted from a time series $A = (a_1, \dots , a_n)$, with $1 \le i < i + l \times d \le m$. This subseries has length l and dilation factor d, and it includes l non-contiguous points from A starting at offset i and taking every d-th value as follows:

$$A_{i,l,d} =(a_i,a_{i+d \times 1},\dots ,a_{i + d \times (l-1)})$$

The dilation technique is used in convolution-based, shapelet-based and dictionary-based models.

In real-world applications, series of D are often unequal length. This is often treated as a preprocessing task, i.e. by appending tailing zeros, although some algorithms have the capability to internally handle this. We further typically assume that all time series of D have the same sampling frequency, i.e., every $i^{th}$ data point of every series was measured at the same temporal distance from its predecessor.

3 Experimental procedure

The bake off conducted experiments with the 85 UTSC datasets that were in the UCR archive relaunch of 2015. Each dataset was resampled 100 times for training and testing, and test accuracy was averaged over resamples. The evaluation began with 11 standard classifiers (such as Random Forest (Breiman 2001)), then classifiers in each category were compared, including an evaluation of reproducibility. Finally, the best in class were compared to hybrids (combinations of categories).

We adapt this approach for the bake off redux to reflect the progression of the field. First, we take the previously used benchmark of Dynamic Time Warping using a one nearest neighbour classifier (1-NN DTW) and, if appropriate, the best of each category from the bake off and compare them to new algorithms of that type. We do this stage of experimentation with the 112 equal length problems in the 2019 version of the UCR archive (Dau et al. 2019). Performance on these datasets, or some subset thereof, has been used to support every proposed approach, so this allows us to make a fair comparison of algorithms. We have regenerated all results for classifiers described both in the original bake off and this comparison.

Only a subset of the algorithms considered have been adapted for MTSC by their inventors. Furthermore, many algorithms have been proposed solely for MTSC, particularly in the deep learning field. Because of this and the considerable computational cost of including multivariate data, we restrict our attention to univariate classification only in this work.

We resample each pair of train/test data 30 times for the redux, stratifying to retain the same class distribution. We do not adopt the bake off strategy of 100 resamples. We have found 30 resamples is sufficient to mitigate small changes in test accuracy over influencing ranks, and it is more computationally feasible. Resampling is seeded with the resample ID to aid with reproducibility. Resample 0 uses the original train and test split from the UCR archive.

Our primary performance measure is classification accuracy on the test set. We also compare predictive power with the balanced test set accuracy, to identify whether class imbalance is a problem for an algorithm. The quality of the probability estimates is measured with the negative log likelihood (NLL), also known as log loss. The ability to rank predictions is estimated by the area under the receiver operator characteristic curve (AUROC). For problems with two classes, we treat the minority class as a positive outcome. For multiclass problems, we calculate the AUROC for each class and weight it by the class frequency in the train data, as recommended in Provost and Domingos (2003). We present results with diagrams derived from the critical difference plots proposed by Demšar (2006). We average ranks over all datasets and plot them on a line and group classifiers into cliques, within which there is no significant difference in rank. We replace the post-hoc Nemenyi test used to form cliques described in Demšar (2006) with a mechanism built on pairwise tests. We perform pairwise one-sided Wilcoxon signed-rank tests and form cliques using the Holm correction for multiple testing as described in García and Herrera (2008); Benavoli et al. (2016).

Critical difference diagrams can be deceptive: they do not display the effective amount of differences, and the linear nature of clique finding can mask relationships between results. If, for example, three classifiers A, B, C are ordered by rank $A>B>C$, and the test indicates A is significantly better than B, and B is significantly better than C, then we will form no cliques. However, it is entirely possible that A is not significantly different to C, and the diagram cannot display this. Because of this, we expand our results to include pairwise plots, violin plots of accuracy distributions against a base line, tables of test accuracies and heatmap diagrams which include unadjusted p-values (Ismail-Fawaz et al. 2023a).

3.1 New datasets

The 112 equal length TSC problems in the archive constitute a relatively large corpus of problems for comparing classifiers. However, they have been extensively used in algorithm development, and there is always the risk of an implicit overfitting resulting in conclusions that do not generalise well to new problems. Hence, we have gathered new datasets which we use to perform our final comparison of algorithms. These data come from direct donation to the TSC GitHub repository⁴, discretised regression datasets⁵, a project on audio classification (Flynn and Bagnall 2019) and reformatting current datasets with unequal length or missing values. Submissions of new datasets to the associated repository are welcomed.

In total, we have gathered 30 new datasets, summarised in Table 1 and visualised in Fig. 2. Datasets with the suffix _eq are unequal length series made equal length through padding with the series mean perturbed by low level Gaussian noise. 11 of these problems (AllGestureWiimote versions, GestureMidAirD1, GesturePebbleZ, PickupGestureWiimoteZ, PLAID and ShakeGestureWiimoteZ) are already in the archive so need no further explanation.

Table 1 A summary of the 30 new univariate datasets used in our experiments with suffix: _eq, _nmv, _disc

Fig. 2

The 30 new univariate datasets showing one representative series for each class

Four problems with the suffix _nmv (no missing values) are datasets where the original contains missing values. These are also from the current archive. We have used the simplest method for processing the data, and removed any cases which contain missing values for these problems (DodgerLoop variants and MelbournePedestrian). The number of cases removed per dataset amounts to 5-15% of the original size for all four datasets which we deemed acceptable. While there have been imputation methods proposed for time series, the amount of missing values present and their pattern varies. The DodgerLoop datasets have large strings of missing values, while MelbournePedestrian has singular values or small groupings of missing data.

The four datasets ending with _disc are taken from the TSER archive (Tan et al. 2021). The continuous response variable was discretised manually for each dataset, the original continuous labels and new class values for each dataset are shown in Fig. 3. Both Covid3Month and FloodModeling2 had a minimum label value with many cases. For both of these, this minimum label value has been converted into its own class label. For problems where there are no obvious places where the label can be separated into classes by value (including Covid3Month where the value is greater than 0), a split point was manually selected taking into account the average label value and the number of cases in each class for a splitting point.

Fig. 3

The sorted original label values for all discretised regression datasets. Each point is a label for a case, and its colour is the class it is part of for the new classification version

This leaves 11 datasets that are completely new to the archive. The two AconityMINIPrinter data sets are described in Mahato et al. (2020) and donated by the authors of that paper. The data comes from the AconityMINI 3D printer during the manufacturing of stainless steel blocks with a designed cavity. The problem is to predict whether there is a void in the output of the printer. The time series are temperature data that comes from pyrometers that monitor melt pool temperature. The pyrometers track the scan of the laser to provide a time-series sampled at 100 Hz. The data is sampled from the mid-section of these blocks and is organized into two datasets (large and small). The large dataset covers cubes with large pores (0.4 mm, 0.5 mm, and 0.6 mm) and the small dataset covers cubes with small pores (0.05 mm and 0.1 mm).

The three Asphalt datasets were originally described in Souza (2018) and donated by the author of that paper. Accelerometer data was collected on a smartphone installed inside a vehicle using a flexible suction holder near the dashboard. The acceleration forces are given by the accelerometer sensor of the device and are the data used for the classification task. The class values for AsphaltObstacles classes are four common obstacles in the region of data collection: raised cross walk (160 cases); raised markers (187 cases); speed bump (212 cases); and vertical patch (222 cases); flexible pavement (816 cases); cobblestone street (527 cases); and dirt road (768 cases). AsphaltRegularity is a two class problem: Regular (762 cases), where the asphalt is even and the driver’s comfort changes little over time; and Deteriorated (740 cases), where irregularities and unevenness in a damaged road surface are responsible for transmitting vibrations to the interior of the vehicle and affecting the driver’s comfort.

The Colposcopy data is described in Gutiérrez-Fragoso et al. (2017) and was donated to the repository by the authors⁶. The task is to classify the nature of a diagnosis from a colposcopy. The time series represent the change in intensity values of a pixel region through a sequence of digital colposcopic images obtained during the colposcopy test that was performed on each patient included in the study.

The ElectricDeviceDetection data set (Bagnall et al. 2020b) contains formatted image data for the problem of detecting whether a segment of a 3-D X-Ray contains an electric device or not. The data originates from an unsupervised segmentation of 3-D X-Rays. The data are histograms of intensities, not time series.

KeplerLightCurves was described in Barbara et al. (2022) and donated by the authors. Each case is a light curve (brightness of an object sampled over time) from NASA’s Kepler mission (3-month-long series, sampled every 30 min). There are seven classes relating to the nature of the observed star.

The SharePriceIncrease data was formatted by Vladislavs Pazenuks as part of their 2018 undergraduate student project. The problem is to predict whether a share price will show an exceptional rise after quarterly announcement of the Earning Per Share based on the price movement of that share price on the preceding 60 days. Daily price data on NASDAQ 100 companies was extracted from a Kaggle data set⁷. Each data represents the percentage change of the closing price from the day before. Each case is a series of 60 days data. The target class is defined as 0 if the price did not increase after company report release by more than five percent or 1 else-wise.

PhoneHeartbeatSound and Tools are audio datasets. Tools contains the sound of a chainsaw, drill, hammer, horn and sword, with the task being to match which tool the audio belongs to. PhoneHeartbeatSound contains sounds of the heartbeats recorded on a phone using a digital stethoscope gathered for the 2011 PASCAL classifying heart sounds challenge⁸. The time series represent the change in amplitude over time during an examination of patients suffering from common arrhythmias. The classes are Artifact (40 cases), ExtraStole (46 cases), Murmur (129 cases), Normal (351 cases) and ExtraHLS (40 cases).

Figure 4 shows the characteristics of the 30 new datasets when compared to the existing 112 UCR UTSC datasets, across different dimensions including length, train set size, number of classes, and data type. Findings reveal that the new datasets exhibit a broader range of lengths compared to old ones, while showing similar train set size and similar number of classes. It is worth noting that there seems to be a slight bias towards datasets derived from sensor and motion data in the new collection, whereas the majority of older datasets are sourced from the domain of image outlines.

3.2 Reproducibility

The majority of the classifiers described are available in the aeon time series machine learning toolkit (see Footnote 2) and all datasets are available for download (see Footnote 1). Appendix A gives detailed code examples on how to reproduce these experiments, including parameters used, if they differ from the default. All results are available from the TSC website and can be directly loaded from there using aeon. Further guidance on reproducibility, parameterisation of the algorithms used in our experiments and our results files are available in an accompanying webpage⁹. With the exception of three algorithms which only meet our usage criteria with a Java implementation, all the algorithms used in our experiments are runnable using the Python software and guides linked in the webpage.

Fig. 4

Comparison of distribution of the 30 newly acquired to the existing 112 UCR UTSC datasets across dimensions including length, train set size, number of classes, and data type

4 Time series classification algorithms

The bake off introduced a taxonomy of algorithms based on the representation of the data at the heart of the algorithm. TSC algorithms were classified as either whole series, interval based, shapelet based, dictionary based, combinations or model based. We extend and refine this taxonomy to reflect recent developments.

• 1. Distance based: classification is based on some time series specific distance measure between whole series (Section 4.1).

• 2. Feature based: global features are extracted and passed to a standard classifier in a simple pipeline (Section 4.2).

• 3. Interval based: features are derived from selected phase dependent intervals in an ensemble of pipelines (Section 4.3).

• 4. Shapelet based: phase independent discriminatory subseries form the basis for classification (Section 4.4).

• 5. Dictionary based: histograms of counts of repeating patterns are the features for a classifier (Section 4.5).

• 6. Convolution based: convolutions and pooling operations create the feature space for classification (Section 4.6).

• 7. Deep learning based: neural network based classification (Section 4.7).

• 8. Hybrid approaches combine two or more of the above approaches (Section 4.8).

As well as the type of feature extracted, another defining characteristic is the design of the TSC algorithm. The simplest design pattern involves single pipelines where transformation of the series into discriminatory features is followed by the application of a standard machine learning classifier. These algorithms tend to involve an over-production and selection strategy: a large number of features are created, and the classifier determines which features are most useful. The transform can remove time dependency, e.g. by calculating summary features. We call this type series-to-vector transformations. Alternatively, they may be series-to-series, transforming into an alternative time series representation where we hope the task becomes more easily tractable, e.g. transforming to the frequency domain of the series.

The second transformation based design pattern involves ensembles of pipelines, where each base pipeline consists of making repeated, different, transforms and using a homogeneous base classifier. TSC ensembles can also be heterogeneous, collating the classifications from transformation pipelines and ensembles of differing representations of the time series.

The third common pattern involves transformations embedded inside a classifier structure. For example, a decision tree where the data is transformed at each node fits this pattern.

A common theme to all categories of algorithm is ensembling. Another popular method seen in multiple classifiers are transformation pipelines ending with a linear classifier. The most accurate classifiers we find all form homogeneous or heterogeneous ensembles, or extract features prior to a linear ridge classifier.

To try and capture the commonality and differences between algorithms we provide a Table in the Appendix B (Table 22) that groups algorithms by whether they employ the following design characteristics: dilation; discretisation; differences/derivatives; frequency domain; ensemble; and linear classification.

We review each category of algorithms by providing an overview of the approach, review selected classifiers and describe the pattern they use, starting with the best of class from the bake off. We perform a comparison of performance within category on the 112 equal length UTSC problems currently in the UCR archive using 1-NN DTW as a benchmark. More detailed evaluation is delayed until Section 5.

4.1 Distance based

Distance based classifiers use a distance function to measure the similarity between whole time series. Historically, distance functions have been mostly used with nearest neighbour (NN) classifiers. Alternative uses of time series distances are described in Abanda et al. (2019). Prior to the bake off, 1-NN with DTW was considered state of the art for TSC (Rakthanmanon et al. 2013). Figure 5 shows an example of how DTW attempts to align two series, depicted in red and green, to minimise their distance.

Fig. 5

An example of how DTW compensates for phase shift by realigning two series (in red at the bottom and in green at the top)

In addition to DTW, a wide range of alternative elastic distance measures (distance measures that compensate for possible misalignment between series) have been proposed. These use combinations of warping and editing on series and the derivatives of series. See Holder et al. (2022) for an overview of elastic distances. Previous studies (Lines and Bagnall 2014) have shown there is little difference in performance between 1-NN classifiers with different elastic distances.

The flowchart in Fig. 6 visualises the distance based algorithms described in this section and the relation between them. Algorithms following another are not necessarily better than the predecessor, but are either direct extensions or heavily draw inspiration from it.

Fig. 6

An overview of distance based classifiers and the relationship between them. Filled algorithms were released after the 2017 bake off (Bagnall et al. 2017) and algorithms with a thin border are not included in our experiments

4.1.1 Elastic Ensemble (EE)

The first algorithm to significantly outperform 1-NN DTW on the UCR data was the Elastic Ensemble (EE) (Lines and Bagnall 2015). EE is a weighted ensemble of 11 1-NN classifiers with a range of elastic distance measures. It was the best performing distance based classifier in the bake off. Elastic distances can be slow, and EE requires cross validation to find the weights of each classifier in the ensemble. A caching mechanism was proposed to help speed up fitting the classifier (Tan et al. 2020) and alternative speed ups were described in Oastler and Lines (2019). The latter speed up is the version of EE we use in our experiments.

4.1.2 Proximity Forest (PF)

Proximity Forest (PF) (Lucas et al. 2019) is an ensemble of Proximity Tree based classifiers. PF uses the same 11 distance functions used by EE, but is more accurate and more scalable than the original EE algorithm. At every node of a tree, one of the 11 distances is selected to be applied with a fixed hyperparameter value. An exemplar single series is selected randomly for each class label. At every node, r combinations of distance function, parameter value and class exemplars are randomly selected, and the combination with the highest Gini index split measure is selected. Series are passed down the branch with the exemplar that has the lowest distance to it, and the tree grows recursively until a node is pure.

4.1.3 ShapeDTW

Shape based DTW (ShapeDTW) (Zhao and Itti 2019) works by extracting a set of shape descriptors over sliding windows of each series. The descriptors include slope, wavelet transforms and piecewise approximations. Based on the results presented (Zhao and Itti 2019) we use the raw and derivative subsequences. The output data of these series-to-series transformations is then used with a 1-NN classifier with DTW.

4.1.4 Generic RepresentAtIon Learning (GRAIL)

The Generic RepresentAtIon Learning (GRAIL) (Paparrizos and Franklin 2019) paper focuses on efficient learning of time series representations that uphold bespoke distance function constraints. GRAIL harnesses kernel methods, particularly the Nyström method, to learn precise representations within these constraints. The construction of representations involves expressing each time series as a linear combination of expressive landmarks, identified through cluster centroids. This approach gives rise to the Shift-Invariant Kernel (SINK) kernel function, which employs the Fast Fourier Transform to compare time series under shift invariance. GRAIL can be used to multiple time series related tasks, but for classification GRAIL and the SINK kernel are evaluated using a linear SVM.

4.1.5 Comparison of distance based approaches

Figure 7 shows the relative rank test accuracies of the five distance based classifiers we discuss here, and Table 2 summarises four performance measures over these datasets. The results broadly validate previous findings. EE is significantly better than 1-NN DTW and PF is significantly better than EE. GRAIL performs slightly worse than expected. We have used the authors implementation¹⁰ but have made some modifications to prevent the test set from being visible during the initial clustering, as it is incompatible with our experimental procedure. This would introduce bias, and may explain the discrepancy with published results alongside the different datasets and data resampling used.

Table 2 shows PF is over 2.5% better in test accuracy and balanced test accuracy, has higher AUROC and lower NLL. Hence, we take PF as best of the distance based category.

Fig. 7

Ranked test accuracy of four distance based classifiers on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Table 2 Summary performance measures for distance based classifiers on 30 resamples of 112 UTSC problems. Best in bold

4.2 Feature based

Feature based classifiers are a popular recent theme. These extract descriptive statistics as features from time series to be used in classifiers. Typically, these features summarise the whole series, so we characterise these as series-to-vector transforms. Most commonly, these features are used in a simple pipeline of transformation followed by a classifier (see Fig. 8). Several toolkits exist for extracting features.

The flowchart in Fig. 9 displays the feature based algorithms described in this section and related algorithms.

4.2.1 The canonical time series characteristics (Catch22)

The highly comparative time-series analysis (hctsa) (Fulcher and Jones 2017) toolbox can create over 7700 features for exploratory time series analysis. The canonical time series characteristics (Catch22) (Lubba et al. 2019) are 22 hctsa features determined to be the most discriminatory of the full set. The Catch22 features were chosen by an evaluation on the UCR datasets. The hctsa features were initially pruned, removing those which are sensitive to the series mean and variance and those that could not be calculated on over $80\%$ of the UCR datasets. A feature evaluation was then performed based on predictive performance. Any features which performed below a threshold were removed. For the remaining features, a hierarchical clustering was performed on the correlation matrix to remove redundancy. From each of the 22 clusters formed, a single feature was selected, taking into account balanced accuracy, computational efficiency and interpretability. The Catch22 features cover a wide range of concepts such as basic statistics of time series values, linear correlations, and entropy. Reported results for Catch22 are based on training a decision tree classifier after applying the transform to each time series (Lubba et al. 2019), the implementation we use builds a Random Forest classifier.

Fig. 8

Visualisation of a pipeline classifier involving feature extraction followed by classification

Fig. 9

An overview of feature based classifiers and the relationship between them. Filled algorithms were released after the 2017 bake off (Bagnall et al. 2017) and algorithms with a thin border are not included in our experiments

4.2.2 Time Series Feature Extraction based on Scalable Hypothesis Tests (TSFresh)

TSFresh (Christ et al. 2018) is a collection of just under 800 features extracted from time series. While the features can be used on their own, a feature selection method called FRESH is provided to remove irrelevant features. FRESH considered each feature using multiple hypotheses tests, including Fisher’s exact test (Fisher 1922), the Kolmogorov-Smirnov (Massey Jr 1951) test and the Kendal rank test (Kendall 1938. The Benjamini-Yekutieli procedure (Benjamini and Yekutieli 2001) is then used to control the false discovery rate caused by comparing multiple hypotheses and features simultaneously.

Results for the base features and after using the FRESH algorithm are reported using both a Random Forest and AdaBoost (Freund and Schapire 1996) classifier. A comparison of alternative pipelines of feature extractor and classifier found that the most effective approach was the full set of TSFresh features with no feature selection applied, and combined with a Rotation Forest classifier (Rodriguez et al. 2006). This pipeline was called the FreshPRINCE (Middlehurst and Bagnall 2022). We include both TSFresh with feature selection using a Random Forest and the FreshPRINCE classifier in our comparison.

4.2.3 Generalised signatures

Generalised signatures are a set of feature extraction techniques based on rough path theory. The generalised signature method (Morrill et al. 2020) and the accompanying canonical signature pipeline can be used as a transformation for classification. Signatures are collections of ordered cross-moments. The pipeline begins by applying two augmentations. The basepoint augmentation simply adds a zero at the beginning of the time series, making the signature sensitive to translations of the time series. The time augmentation adds the series timestamps as an extra coordinate to guarantee that each signature is unique and obtain information about the parameterisation of the time series. A hierarchical window is run over the two augmented series, with the signature transform being applied to each window. The output for each window is then concatenated into a feature vector. The features are used to build a Random Forest classifier. The transformation was primarily developed for MTSC, but can be applied to univariate series.

4.2.4 Comparison of feature based approaches

Figure 10 shows the relative rank performance, and Table 3 summarises the overall performance statistics. All four pipelines are significantly more accurate than 1-NN DTW. Excluding feature extraction and using Rotation Forest rather than Random Forest with TSFresh increases accuracy by over 0.05. This reinforces the findings that Rotation Forest is the most effective classifier for problems with continuous features (Bagnall et al. 2018).

Fig. 10

Ranked test accuracy of four feature based classifiers and the benchmark 1NN-DTW on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Table 3 Summary performance measures for feature based classifiers on 30 resamples of 112 UTSC problems. Best in bold

4.3 Interval based

Interval based classifiers (Deng et al. 2013) extract phase dependent intervals of fixed offsets and compute (summary) statistics on these intervals. A majority of approaches include some form of random selection for choosing intervals, where the same random interval locations are used across every series. Many of the interval based classifiers combine features from multiple random intervals. The motivation for taking intervals is to mitigate for confounding noise. Figure 11 shows an example problem where taking intervals will be better than using features derived from the whole series.

Fig. 11

An example of a problem where interval based approaches may be superior. Each series is a spectrogram from a bottle of alcohol with a different concentration of ethanol. The discriminatory features are in the near infrared interval (green box to the right). However, the confounding factors such as bottle shape, labelling and colouring cause variation in the visible range (red box to the left). Using intervals containing just the near infrared features is likely to make classification easier. Image taken from Bagnall et al. (2017) with permission

Most recent interval based classifiers adopt a random forest ensemble model, where each base classifier is a pipeline of transformation and a tree classifier (visualised in Fig. 12). Diversity is injected through randomising the intervals for each tree. The relation flowchart for interval based algorithms is shown in Fig. 13.

Fig. 12

Visualisation of an ensemble of pipeline classifiers, as used in interval classifiers

Fig. 13

An overview of interval based classifiers and the relationship between them. Filled algorithms were released after the 2017 bake off (Bagnall et al. 2017) and algorithms with a thin border are not included in our experiments

4.3.1 Time Series Forest (TSF)

The Time Series Forest (TSF) (Deng et al. 2013) is the simplest interval based tree based ensemble. For each tree, $\sqrt{m}$ (following the notation from Chapter 2, where m is the length of the series and d is the number of dimensions) intervals are selected with a random position and length. The same interval offsets are applied to all series. For each interval, three summary statistics (the mean, variance and slope) are extracted and concatenated into a feature vector. This feature vector is used to build the tree, and features extracted from the same intervals are used to make predictions. The ensemble makes the prediction using a majority vote of base classifiers. The TSF base classifier is a modified decision tree classifier referred to as a time series tree, which considers all attributes at each node and uses a metric called margin gain to break ties.

4.3.2 Random Interval Spectral Ensemble (RISE)

First developed for the HIVE-COTE ensemble (described in Section 4.8), the Random Interval Spectral Ensemble (RISE) (Flynn et al. 2019) is an interval based tree ensemble that uses spectral features. Unlike TSF, RISE selects a single random interval for each base classifier. The periodogram and auto-regression function are calculated over each randomly selected interval, and these features are concatenated into a feature vector, from which a tree is built. RISE was primarily designed for use with audio problems, where spectral features are more likely to be discriminatory.

4.3.3 STSF and R-STSF

Supervised Time Series Forest (STSF) (Cabello et al. 2020) is an interval based tree ensemble that includes a supervised method for extracting intervals. Intervals are found and extracted for a periodogram and the first order differences representation as well as the base series. STSF introduces bagging for each tree and extracts seven simple summary statistics from each interval. For each tree, an initial split point for the series is randomly selected. For both of these splits, the remaining subseries is cut in half, and the half with the higher Fisher score is retained as an interval. This process is then run recursively using higher scored intervals until the series is smaller than a threshold. This is repeated for each of the seven summary statistic features, with the extracted statistic being used to calculate the Fisher score.

Randomised STSF (RSTSF) (Cabello et al. 2021) is an extension of STSF, altering its components with more randomised elements. The split points for interval selection are selected randomly instead of splitting each candidate in half after the first. Intervals extracted from an autoregressive representation are included alongside the previous additions. Features are extracted multiple times from each representation into a single pool. Rather than extract different features for each tree in an ensemble, the features are used in a pipeline to build an Extra Trees (Geurts et al. 2006) classifier.

4.3.4 CIF and DrCIF

The Canonical Interval Forest (CIF) (Middlehurst et al. 2020a) is another extension of TSF, that improves accuracy by integrating more informative features and by increasing diversity. Like other interval approaches, CIF is an ensemble of decision tree classifiers built on features extracted from phase dependent intervals. Alongside the mean, standard deviation and slope, CIF also extracts the Catch22 features described in Section 4.2. Intervals remain randomly generated, with each tree selecting $k=\sqrt{m}\sqrt{d}$ intervals. To add additional diversity to the ensemble, a attributes out of the pool of 25 are randomly selected for each tree. The extracted features are concatenated into a $k \cdot a$ length vector for each time series and used to build the tree. For multivariate data, CIF randomly selects the dimension used for each interval.

The Diverse Representation Canonical Interval Forest (DrCIF) (Middlehurst et al. 2021) incorporates two new series representations: the periodograms (also used by RISE and STSF) and first order differences (also used by STSF). For each of the three representations, $(4 + \sqrt{r}\sqrt{d})/3$ phase dependent intervals are randomly selected and concatenated into a feature vector, where r is the length of the series for a representation.

4.3.5 QUANT

QUANT (Dempster et al. 2023) employs a singular feature type, quantiles, to encapsulate the distribution of a given time series. The method combines four distinct representations, namely raw time series, first-order differences, Fourier coefficients, and second-order differences. The extraction process involves fixed, dyadic intervals derived from the time series. These disjoint intervals are constructed through a pyramid structure, where each level successively halves the interval length. At depths greater than one, an identical set of intervals, shifted by half the interval length, is also included. The total count of intervals is calculated as $2^{(d-1)} \times 4 - 2 - d$ for a depth of $d=\min (6, \log _2 n + 1)$. Each representation can have up to 120 intervals, resulting in a total of 480 intervals across all four representations. The concatenated feature vector is used to build an Extra Trees classifier.

4.3.6 Comparison of interval based approaches

Figure 14 shows the relative ranks of seven interval classifiers, with summary performance measures presented in Table 4.

Fig. 14

Ranked test accuracy of seven interval based classifiers on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Table 4 Summary performance measures for interval based classifiers on 30 resamples of 112 UTSC problems. Best in bold

There is no significant difference between QUANT, DrCIF and RSTSF nor between their precursors CIF and STSF. All are significantly better than TSF, the best in class in the bake off. Figure 15(a) shows the scatter plot of QUANT vs DrCIF. QUANT wins on 63, draws 5 and loses 44. Overall, the two algorithms produce very similar results (the test accuracies have a correlation of $98.1\%$).

We choose QUANT as the best in class because it is significantly faster than DrCIF and RSTSF. Figure 15(b) shows QUANT against TSF in order to confirm that QUANT, DrCIF and RSTSF represent genuine improvements to this type of algorithm over the previous best. Table 4 confirms that on average over 112 problems, the accuracy of the top clique is over 0.06 higher than TSF.

Fig. 15

Scatter plot of test accuracies of DrCIF against RSTSF and TSF. TSF is better than DrCIF on just 6 of the 112 datasets

4.4 Shapelet based

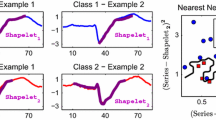
Shapelets are subseries from the training data that are independent of the phase and can be used to discriminate between classes of time series based on their presence or absence. To evaluate a shapelet, the subseries is slid across the time series, and the z-normalised Euclidean distance between the shapelet and the underlying window is calculated. The distance between a shapelet and any series, sDist(), is the minimum distance over all such windows. Figure 16 shows a visualisation of the sDist() process. The shapelet S is shifted along the time series A, and the most similar offset and distance in A are recorded. The distance between a shapelet and the training series is then used as a feature to evaluate the quality of the shapelet.

Fig. 16

Visualisation of the shapelet distance operation sDist() between a shapelet S and a series A, which finds the closest distances to the shapelet from all possible subseries of the same length

Shapelets were first proposed as a primitive in Ye and Keogh (2011), and were embedded in a decision tree classifier. There have been four important themes in shapelet research post bake off: The first has concentrated on finding the best way to use shapelets to maximise classification accuracy. The second has focused on overcoming the shortcomings of the original shapelet discovery which required full enumeration of the search space and has cubic complexity in the time series length; the third theme is the progress toward unifying research with convolutions and shapelets; and the fourth theme is the balance between optimisation, randomisation and interpretability when finding shapelets. The relation flowchart for shapelet based algorithms is shown in Fig. 17.

Fig. 17

An overview of shapelet based classifiers and the relationship between them. Filled algorithms were released after the 2017 bake off (Bagnall et al. 2017) and algorithms with a thin border are not included in our experiments

4.4.1 The Shapelet Transform Classifier (STC)

The Shapelet Transform Classifier (STC) (Hills et al. 2014) is a pipeline classifier which searches the training data for shapelets, transforms series to vectors of sDist() distances to a filtered set of selected shapelets based on information gain, then builds a classifier on the latter. This is in contrast to the decision tree based approaches, which search for the best shapelet at each tree node. The first version of STC performed a full enumeration of all shapelets from all train cases before selecting the top k. The base classifier used was HESCA (later renamed CAWPE,  Large et al. (2019b)) ensemble of classifiers, a weighted heterogeneous ensemble of 8 classifiers including a diverse set of linear, tree based and Bayesian classifiers. Due to its full enumeration and large pool of base classifiers requiring weights, the algorithm does not scale well. We call the original full enumeration version ST-HESCA to differentiate it from the version described below which we simply call STC. It was the best performing shapelet based classifier in the bake off.

The following incremental changes have been made to the STC pipeline, described in Bostrom et al. (2016); Bostrom and Bagnall (2017):

• 1. Search has been randomised, and the number of shapelets sampled is now a parameter, which defaults to 10,000. This does not lead to significantly worse performance on the UCR datasets.

• 2. Shapelets are now binary, in that they represent the class of the origin series and are evaluated against all other classes as a single class using one hot encoding. This facilitates greater use of the early abandon of the order line creation (described in Ye and Keogh 2011), and makes evaluation of split points faster.

• 3. The heterogeneous ensemble of base classifiers in HESCA has been replaced with a single Rotation Forest (Rodriguez et al. 2006) classifier, making STC a simple pipeline classifier.

4.4.2 The Generalised Random Shapelet Forest (RSF)

The Random Shapelet Forest (RSF) (Karlsson et al. 2016) is a bagging based tree ensemble that attempts to improve the computational efficiency and predictive accuracy of the Shapelet Tree through randomisation and ensembling. At each node of each tree r univariate shapelets are selected from the training set at random. Each shapelet has a randomly selected length between predefined upper and lower limits. The quality of a shapelets is measured in the standard way with sDist() and information gain, and the best is selected. The data is split, and a tree is recursively built until a stopping condition is met. New samples are predicted by a majority vote on the tree’s predictions and multiple trees are ensembled.

4.4.3 MrSEQL and MrSQM

The Multiple Representation Sequence Learner (MrSEQL) (Nguyen et al. 2019), is an ensemble classifier that extends previous adaptations of the SEQL classifier (Nguyen et al. 2017). MrSEQL looks for the presence or absence of a pattern (shapelet) in the data. Rather than using a distance based approach to measure the presence or not of a shapelet, MrSEQL discretises subseries into words. Words are generated through two symbolic representations, using SAX (Lin et al. 2007) for time domain and SFA (Schäfer and Högqvist 2012) for frequency domain. A set of discriminative words is selected through Sequence Learner (SEQL) and the output of training is a logistic regression model, which in concept is a vector of relevant subseries and their weights. Diversification is achieved through the two different symbolic representations and varying the window size.

MrSQM (Nguyen and Ifrim 2022) extends MrSEQL. It also combines two symbolic transformations to create words from subseries and trains a logistic regression classifier. What sets it apart is its innovative strategy for selecting features (substrings).

To begin with, MrSQM uses SFA and SAX to discretise time series subseries into words. It then utilizes a trie to store and rank frequent substrings, and applies either (a) a supervised chi-squared test to identify discriminative words or (b) an unsupervised random substring sampling method to prevent overestimating highly correlated substrings that are likely to be redundant. MrSQM establishes the number of learned representations (SFA or SAX) based on the length of the time series and utilizes an exponential scale for the window size parameter.

4.4.4 Random Dilated Shapelet Transform (RDST)

The Random Dilated Shapelet Transform (RDST) (Guillaume et al. 2022) is a shapelet-based algorithm that adopts many of the techniques of convolution approaches described in Section 4.6. While traditional shapelet algorithms search for the best shapelets from the train dataset, RDST takes a different approach by randomly selecting a large number of shapelets from the train data, typically ranging from thousands to tens of thousands, then training a linear Ridge classifier on features derived from these shapelets.

RDST employs dilation with shapelets. Dilation is a form of down sampling, in that it defines spaces between time points. Hence, a shapelet with dilation d is compared to time points d steps apart when calculating the distance. RDST also uses two features in addition to sDist(): it encodes the position of the minimum distance, and records a measure of the frequency of occurrences of the shapelet based on a threshold. Hence the transformed data has 3k features for k shapelets.

4.4.5 Comparison of shapelet based approaches

Table 5 highlights the key differences between the shapelet-based approaches.

Table 5 Key differences in shapelet based TSC algorithms

Fig. 18

Ranked test accuracy of four shapelet based classifiers and the benchmark 1NN-DTW on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Figure 18 shows the relative ranks of the four shapelet classifiers. RDST is the clear winner. Table 6 shows it is, on average more than 1% more accurate than MrSQM, the second-best algorithm. The shapelet based algorithms are more fundamentally different in design than, for example, interval classifiers. This is demonstrated by the spread of test accuracies shown in Fig. 19 of the top three algorithms. The grouping may become redundant: RDST is more similar to convolution based algorithms (Section 4.6) in design than STC, and MrSQM has structure in common with dictionary based classifiers (Section 4.5). However, they still retain the key characteristics that, unlike convolutions, they use the training data to find subseries and, unlike dictionary based algorithms, their features include the presence or absence of a pattern.

4.5 Dictionary based

Similar to shapelet based algorithms, dictionary approaches extract phase-independent subseries. However, instead of measuring the distance to a subseries, each window is converted into a short sequence of discrete symbols, commonly known as a word. Dictionary methods differentiate based on word frequency and are often referred to as bag-of-words approaches. Figure 20 illustrates the process that algorithms following the dictionary model take to create a classifier. This process can be summarized as:

• 1. Extracting subseries, or windows, from a time series;

• 2. Transforming each window of real values into a discrete-valued word (a sequence of symbols over a fixed alphabet);

• 3. Building a sparse feature vector of histograms of word counts, and

• 4. Finally, using a classification method from the machine learning repertoire on these feature vectors.

Table 6 Summary performance measures for shapelet based classifiers on 30 resamples of 112 UTSC problems. Best in bold

Fig. 19

Scatter plot of test accuracies of shapelet based classifiers

Fig. 20

Transformation of a TS into the dictionary-based model (following  Schäfer and Leser 2017) using overlapping windows (second to top), discretisation of windows to words (second from bottom), and word counts (bottom)

Dictionary-based methods differ in the way they transform a window of real-valued measurements into discrete words. For example, the basis of the BOSS model (Schäfer 2015) is a representation called Symbolic Fourier Approximation (SFA) (Schäfer and Högqvist 2012). SFA works as follows:

• 1. Values in each window of length w are normalized to have standard deviation of 1 to obtain amplitude invariance.

• 2. Each normalized window of length w is subjected to dimensionality reduction by the use of the truncated Fourier transform, keeping only the first $l<w$ coefficients for further analysis. This step acts as a low pass filter, as higher order Fourier coefficients typically represent rapid changes like dropouts or noise.

• 3. Discretisation bins are derived through Multiple Coefficient Binning (MCB). It separately records the l distributions of the real and imaginary values of the Fourier transform. These distributions are then subjected to either equi-depth or equi-width binning. The resulting output consists of l sets of bins, corresponding to the target word length of l.

• 4. Each coefficient is discretized to a symbol of an alphabet of fixed size $\alpha$ to achieve further robustness against noise.

Figure 21 exemplifies this process from a window of length 128 to its DFT representation, and finally the word DAAC. The relation flowchart for dictionary based algorithms is shown in Fig. 22.

Fig. 21

The Symbolic Fourier Approximation (SFA) (from  Schäfer and Leser 2017): A time series (top left) is approximated using the Fourier transform (top right) and discretised to the word DAAC (bottom left) using data adaptive bins (bottom right)

Fig. 22

An overview of dictionary based classifiers and the relationship between them. Filled algorithms were released after the 2017 bake off (Bagnall et al. 2017) and algorithms with a thin border are not included in our experiments

4.5.1 Bag-of-SFA-Symbols (BOSS)

Bag-of-SFA-Symbols (BOSS) (Schäfer 2015) was among the top-performing algorithms in the initial bake-off study and led to significant further investigation into dictionary-based classifiers. An individual BOSS classifier undergoes the same process described earlier, whereby each sliding window is transformed into a word using SFA. Subsequently, a feature vector is generated by counting the occurrences of each word over all windows. A non-symmetric distance function is then employed with a 1-NN classifier to categorize new instances. Experiments have shown that when presented with a query and a sample time series, disregarding words that exist solely in the sample time series using, the non-symmetric distance function leads to improved performance compared to using the Euclidean distance metric (Schäfer 2015).

The complete BOSS classifier is an ensemble of individual BOSS classifiers. This ensemble is created by exploring a range of parameters, assessing each base classifier through cross-validation, and keeping all base classifiers with an estimated accuracy within $92\%$ of the best classifier. For new instances, the final prediction is obtained through a majority vote of the base classifiers.

Table 7 Key differences in dictionary based TSC algorithms

4.5.2 Word Extraction for Time Series Classification (WEASEL v1.0)

Word Extraction for Time Series Classification (WEASEL v1.0) (Schäfer and Leser 2017) is a pipeline classifier that revolves around identifying words whose frequency count distinguishes between classes and discarding words that lack discriminatory power. The classifier generates histograms of word counts over a broad spectrum of window sizes and word lengths parameters, including bigram words produced from non-overlapping windows. A Chi-squared test is then applied to determine the discriminatory power of each word, and those that fall below a particular threshold are discarded through feature selection. Finally, a linear Ridge classifier is trained on the remaining feature space. WEASEL utilizes a supervised variation of SFA to create discriminative words, and it leverages an information-gain based methodology for identifying breakpoints that separate the classes.

4.5.3 WEASEL v2.0 (with dilation)

The dictionary-based WEASEL v2.0 (Schäfer and Leser 2023) is a complete overhaul of the WEASEL v1.0 classifier (Schäfer and Leser 2017). It addresses the problem of the extensive memory footprint of WEASEL by controlling the search space using randomly parameterized SFA transformations. It also significantly improves accuracy. Notably, the most prominent modification is the inclusion of dilation to the sliding window approach. Table 7 presents a comprehensive summary of its alterations.

To extract subseries with non-consecutive values from a time series, a dilated sliding window approach is employed, where the dilation parameter maintains a fixed gap between each value. These dilated subseries undergo a Fourier transform, and a word is generated by discretising them using SFA. The unsupervised learning of bins is achieved using equi-depth and equi-width with an alphabet size of 2. To improve performance, a feature selection strategy based on variance is introduced, which retains only the real and imaginary Fourier values with the highest variance.

Each of the 50 to 150 SFA transformations is randomly initialized subject to:

• 1. Window length w: Randomly chosen from interval $[w\_{min}, \dots , w\_{max}]$.

• 2. Dilation d: Randomly chosen from interval $[1,\dots , 2^{\log (\frac{n-1}{w-1})}]$. The formula is inherited from the convolution-based ROCKET group of classifiers (Dempster et al. 2020, 2021; Tan et al. 2022).

• 3. Word length l: Randomly chosen from $\{7,8\}$.

• 4. Binning strategy: Randomly chosen from {“equi-depth”, “equi-width”}.

• 5. First order differences: To extract words from both, the raw time series, and its first order difference, effectively doubling the feature space.

When using an alphabet size of 2 and a length of 8, each SFA transformation creates a dictionary containing only 256 unique words of a fixed size. These dictionaries are then combined to produce a feature vector containing approximately 30k to 70k features. No feature selection is implemented by default. The resulting features serve as input for training a linear Ridge classifier.

4.5.4 Contractable BOSS (cBOSS)

The size of the parameter grid searched by BOSS is data dependent, and BOSS uses a method of retaining ensemble members using a threshold of accuracy estimated from the train data. This makes its time and memory complexity unpredictable. BOSS was one of the slower algorithms tested in the bake off and could not be evaluated on the larger datasets in reasonable time. Contractable BOSS (cBOSS) (Middlehurst et al. 2019) revises the ensemble structure of BOSS to solve these scalability issues, using the same base transformations as the BOSS ensemble. cBOSS randomly selects k parameter sets of hyper-parameters (w, l and $\alpha$) for BOSS base classifiers. It retains the best s classifiers (based on a cross validation estimate of accuracy) are retained for the final ensemble. cBOSS allows the k parameter to be replaced by a train time limit t through contraction, allowing the user to better control the training time of the classifier. A subsample of the train data is randomly selected without replacement for each ensemble member and an exponential weighting scheme used in the CAWPE (Large et al. 2019b) ensemble is introduced. The cBOSS alterations to the BOSS ensemble structure showed an order of magnitude improvement in train times with no reduction in accuracy.

4.5.5 SpatialBOSS

BOSS intentionally ignores the locations of words in series, classifying based on the frequency of patterns rather than their location. Spatial Boss (Large et al. 2019a) introduced location information into the design of a BOSS classifier. Spatial pyramids (Lazebnik et al. 2006) are a technique used in computer vision to retain some temporal information back into the bag-of-words paradigm. The core idea, illustrated in Fig. 23 is to split the series into different resolutions, segmenting the series based on depth and position, then building independent histograms on the splits. The histograms for each level are concatenated into a single feature vector which is used with a 1-NN classifier. While more accurate than BOSS, the increase in parameter search space and bag size makes it very difficult to run in practice.

Fig. 23

An example of using a spatial pyramid to form 7 distinct word count histograms

4.5.6 Temporal Dictionary Ensemble (TDE)

The Temporal Dictionary Ensemble (TDE) (Middlehurst et al. 2020b) combines the best improvements introduced in WEASEL, SpatialBOSS and cBOSS and also includes several novel features. TDE is an ensemble of 1-NN classifiers which transforms each series into a histogram of word counts using SFA (Schäfer and Högqvist 2012). From WEASEL, TDE takes the method for finding supervised breakpoints for discretisation, and captures frequencies of bigrams found from non-overlapping windows. The locality information derived from the spatial pyramids used in SpatialBOSS are incorporated. Word counts are found for each spatial subseries independently, with the resulting histograms being concatenated. Bigrams are only found for the full series. The cBOSS ensemble structure is applied with a modified parameter space sampling algorithm. It first randomly samples a small number of parameter sets, then constructs a Gaussian processes regressor on the historic accuracy for unseen parameter sets. The regressor is used to estimate the parameter set for the next candidate, and the model is then updated before the process is repeated. TDE has two additional parameters for its candidate models: the number of levels for the spatial pyramid and the method of generating breakpoints.

4.5.7 Comparison of dictionary based approaches

Table 7 shows the key design differences between the dictionary based approaches.

Figure 24 shows the ranked test accuracy of five dictionary classifiers we have described, with 1-NN DTW as a benchmark. SpatialBOSS is not included due to its significant runtime and memory requirements which would require the exclusion of multiple datasets. We believe that comparing more recent advances on the full archive is more valuable than its inclusion, and suggest those interested in SpatialBOSS view the results presented in Middlehurst et al. (2020b) which show it is comparable to WEASEL 1.0 in performance. WEASEL 1.0 and TDE are significantly more accurate than BOSS, but WEASEL 2.0 is the most accurate overall. Figure 25(a) illustrates the improvement of WEASEL 2.0 over BOSS, and Fig. 25(b) shows the improvement dilation provides over WEASEL. Table 8 summarises the performance of the four new dictionary algorithms. WEASEL 2.0 is on average $4\%$ more accurate than BOSS and improves balanced accuracy by almost the same amount.

Fig. 24

Ranked test accuracy of five dictionary based classifiers with the benchmark 1-NN DTW on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Fig. 25

Scatter plot of test accuracies of BOSS vs WEASEL 2.0

Table 8 Averaged performance statistics for dictionary based classifiers on 30 resamples of 112 UTSC problems. Best in bold

4.6 Convolution based

Kernel/Convolution classifiers use convolutions with kernels, which can be seen as subseries used to derive discriminatory features. Each kernel is convolved with a time series through a sliding dot product creating an activation map. Technically, each convolution creates a series to series transform from time series to the activation map (see Definition 6). Activation maps are used to create summary features. Convolutions and shapelets share a close methodological relationship. Shapelets can be realised through a convolution operation, followed by a min-pooling operation on the array of windowed Euclidean distances. This was first observed by Grabocka et al. (2014). However, despite this methodological connection, there is significant difference in the results obtained by convolution based and shapelet based approach, as illustrated in the Appendix C, Figure 50. For example, the ROCKET results are negatively correlated with shapelet based approaches such as STC or RDST. The main difference between convolutions and shapelets is that shapelets are subseries from the training data whereas convolutions are found from the entire space of possible real-values.

Convolution based TSC algorithms follow a standard pipeline pattern depicted in Fig. 26. The activation map is formed for each convolution, followed by pooling operations to extract one relevant feature for each operation. The resulting features are then concatenated to form a single feature vector. Finally, a Ridge classifier is trained on the output to classify the data. The relation flowchart for convolution based algorithms is shown in Fig. 27.

Fig. 26

Pipeline of convolution based approaches such as ROCKET, MiniROCKET or MultiROCKET

Fig. 27

An overview of convolution based classifiers and the relationship between them

4.6.1 Random Convolutional Kernel Transform (ROCKET)

The most well known convolutional approach is the Random Convolutional Kernel Transform (ROCKET) (Dempster et al. 2020). ROCKET is a pipeline classifier. It generates a large number of randomly parameterised convolutional kernels (typically in the range of thousands to tens of thousands), then uses these to transform the data through two pooling operations: the max value and the proportion of positive values (PPV). These two features are concatenated into a feature vector for all kernels. For k kernels, the transformed data has 2k features.

In ROCKET, each kernel is randomly initialised with respect to the following parameters:

• 1. the kernel length l, randomly selected from $\{7,9,11\}$;

• 2. the kernel weights w, randomly initialised from a normal distribution;

• 3. a bias term b added to the result of the convolution operation;

• 4. the dilation d to define the spread of the kernel weights over the input instance, which allows for detecting patterns at different frequencies and scales. The dilation is randomly drawn from an exponential function; and

• 5. padding p the input series at the start and the end (typically with zeros), such that the activation map has the same length as the input;

The result of applying a kernel $\omega$ with dilation d to a time series T at offset i is defined by:

$$ T_{i : (i+l)} * \omega = \sum _{j=0}^{l-1} T_{i-(\lfloor m / 2 \rfloor ) \times d)+(j \times d)} \times w_j $$

The feature vectors are then used to train a Ridge classifier using cross-validation to train the $L_2$-regularisation parameter $\alpha$. A Logistic Regression classifier is suggested as a replacement for larger datasets. The combination of ROCKET with Logistic (RIDGE) Regression is conceptually the same as a single-layer Convolutional Neural Network with randomly initialised kernels and softmax loss.

4.6.2 Mini-ROCKET and Multi-ROCKET

ROCKET has two extensions. The first extension is MiniROCKET (Dempster et al. 2021), which speeds up ROCKET by over an order of magnitude with no significant difference in accuracy. MiniROCKET removes many of the random components of ROCKET, making the classifier almost deterministic. The kernel length is fixed to 9, only two weight values are used, and the bias value is drawn from the convolution output. Only the PPV is extracted, discarding the max. These changes alongside general optimisations taking advantage of the new fixed values provide a considerable speed-up to the algorithm. MiniROCKET generates a total of 10k features from 10k kernels and PPV pooling.

MultiROCKET (Tan et al. 2022) further extends the MiniROCKET improvements, extracting features from first order differences and adding three new pooling operations extracted from each kernel: mean of positive values (MPV), mean of indices of positive values (MIPV) and longest stretch of positive values (LSPV). MultiROCKET generates a total of 50k features from 10k kernels and 5 pooling operations.

4.6.3 Hydra and MultiROCKET-Hydra

HYbrid Dictionary-ROCKET Architecture (Hydra) (Dempster et al. 2022) is a model that combines dictionary-based and convolution-based models. It begins by utilizing random convolutional kernels to calculate the activation of time series. These kernels, unlike ROCKET, are arranged into g groups of k kernels each. In each group of k kernels, the activation of a kernel with the input time series is calculated, and we record how frequently this kernel is the best match (counts the highest activation). This results in a k-dimensional count vector for each of the g groups, resulting in a total of $g \times k$ features.

To implement Hydra, the time series is convolved with the kernels, and the resulting activation maps are organized into g groups. Next, an (arg)max operation is performed to count the number of best matches, and the counts for each group’s dictionary are increased. The main hyperparameters to consider are the number of groups and the number of kernels per group, with default values of $g = 64$ and $k = 8$. Hydra is applied to both the time series and its first-order differences. The best results in  Dempster et al. (2022) come from concatenating features from Hydra with features from MultiROCKET to form its pipeline. We call this classifier MultiROCKET-Hydra.

4.6.4 Comparison of convolution based approaches

Table 9 highlights the key differences between the convolution based approaches.

Table 9 Key Differences in approaches from ROCKET to MiniROCKET to MultiROCKET

Figure 28 shows the average ranks of the convolution based classifiers. MultiRO-CKET-Hydra is the top performer, and is significantly better ranked than the next best, Multi-ROCKET. Table 10 and Fig. 29(a) show that the actual difference between the algorithms is small. Progress in the field is demonstrated by Fig. 29(b). MR-Hydra is nearly 2% better on average than ROCKET, which itself was considered state of the art as recently as 2020 (Bagnall et al. 2020a).

Fig. 28

Ranked test accuracy of six convolution based classifiers and the benchmark 1NN-DTW on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Table 10 Summary performance measures for convolution based classifiers on 30 resamples of 112 UTSC problems. Best in bold

Fig. 29

Scatter plot of test accuracies of convolution based classifiers

4.7 Deep learning

Deep learning has been the most active area of TSC research since the bake off in terms of the number of publications. It was thought by many that the impact deep learning had on fields such as vision and speech would be replicated in TSC research. In a paper with “Finding AlexNet for time series classification” in the title, Fawaz et al. (2020) discuss the impact AlexNet had on computer vision and observe that this lesson indicates that “given the similarities in the data, it is easy to suggest that there is much potential improvement for deep learning in TSC.”. A highly cited survey paper (Fawaz et al. 2019) found that up to that point, ResNet (Wang et al. 2017) was the most accurate TSC deep learner. Subsequently, the same group proposed InceptionTime (Fawaz et al. 2020), which was not significantly different to top perfming hybrid algorithms in terms of accuracy (Bagnall et al. 2020a). Since InceptionTime there have been a huge number of deep learning papers proposing TSC algorithms: a recent survey (Foumani et al. 2023) references 246 papers, most of which have been published in the last three years. Table 11 summarises some recently proposed deep learning classification algorithms. Without giving specific examples, there are several concerning trends in the deep learning TSC research thread. Most seriously, there is a tendency to perform model selection on test data, i.e. maximize the test accuracy over multiple epochs. This is obviously biased, yet seems to happen even with publications in highly selective venues. Secondly, many papers do not make their source code available. Given all these algorithms are based on standard tools like TensorFlow and PyTorch, this seem inexcusable. Thirdly, they often evaluate on subsets of the archive without any clear rationale as to why. Most are evaluated only on the multivariate archive. Whilst cherry-picking data is questionable, using just MTSC data is not, since deep learning classifiers are usually proposed specifically for MTSC. However, it puts them beyond the scope of this paper. Fourthly, they frequently only compare against other deep learning classifiers, often set up as weak straw men. Finally, they often do not seem to offer any advance on previous research. We have not seen any algorithm that can realistically claim to outperform InceptionTime (Fawaz et al. 2020), nor its successor H-InceptionTime (Ismail-Fawaz et al. 2022). Because of this, we restrict our attention to five deep learning algorithms. We include a standard Convolutional Neural Network (CNN) implementation as a baseline. We use the same CNN structure as used in the deep learning bake off (Fawaz et al. 2019). We evaluate ResNet since it was best performing in  Fawaz et al. (2019). InceptionTime (Fawaz et al. 2020) is included since it is, to the best our knowledge, best in category for deep learning. We also evaluate two recent extensions of InceptionTime: H-InceptionTime (Ismail-Fawaz et al. 2022) and LiteTime (Ismail-Fawaz et al. 2023b). The relation flowchart for deep learning algorithms is shown in Fig. 30.

Table 11 Overview of recently proposed deep learning classifiers

Fig. 30

An overview of deep learning classifiers and the relationship between them. Filled algorithms were released after the 2017 bake off (Bagnall et al. 2017)

4.7.1 Convolution Neural Networks (CNN)

Convolution Neural Networks (CNN), were first introduced in Fukushima (1980), and have gained widespread use in image recognition. Their popularity has increased significantly since AlexNet won the ImageNet competition in 2012. CNNs comprise three types of layers: convolutional, pooling, and fully connected. The convolutional layer slides a filter over a time series, extracting features that are unique to the input. Convolving a one-dimensional filter with the input produces an activation or feature map.

The result of applying one filter $\omega$ to a time series T at offset t is defined by:

$$ C_t = f\left( \omega * T_{t : (t+l)} + b \right) \forall t \in [1 \dots n-l+1]$$

Where the filter $\omega$ is of length l, the bias parameter is b, and f is a non-linear activation function such as ReLu applied to the result of the convolution. One significant advantage of CNNs is that the filter weights are shared across each convolution, reducing the number of weights that must be learned when compared to fully connected neural networks. But instead of manually setting filter weights, these are learned by the CNN directly from the training data.

As multiple learned filters are applied to the input, each resulting in one activation map of roughly the same size as the input, a pooling layer is used in-between every two convolution layers. A pooling layer, such as Max or Min-pooling, reduces the number of features in each map to i.e. the maximum value, thus providing phase-invariance. After several blocks of convolutional and pooling layers, one or more fully connected layers follow. Finally, a softmax layer with one output neuron per class is used in the final layer.

4.7.2 Residual Network (ResNet)

The Residual Network (ResNet) (Wang et al. 2017), is a deep learning architecture that has been successfully adapted for time series analysis. ResNet is composed of three residual blocks, each comprising two main components: (a) three convolutional layers that extract features from the input data followed by batch normalization and a ReLu non-linear activation function, and (b) a shortcut connection that allows the direct propagation of information from earlier layers to later ones. Figure 31 illustrates the structure.

The shortcut connection is designed to mitigate the vanishing gradients problem for deep neural networks, and the convolutional layers extract features from time series data. At the end of the model, the features are passed through one Global Average Pooling (GAP) and one fully-connected softmax layer is used with the number of neurons equal to the number of classes.

Fig. 31

Overview of the ResNet structure, image taken from Ismail-Fawaz et al. (2022) with permission

4.7.3 InceptionTime

InceptionTime is a deep learning model proposed by Fawaz et al. (2020). It is an ensemble of five deep learning classifiers, each with the same architecture built on cascading Inception modules (Szegedy et al. 2015). Diversity is achieved through randomising initial weight values in each of the five models.

The network, illustrated in Fig. 32, is composed of two consecutive residual blocks. Where each residual block is composed of three inception modules. The input of the residual block is connected via a shortcut connection to the block’s output, to address the vanishing gradient problem. A Global Average Pooling (GAP) layer follows the two residual blocks. Finally, a fully-connected softmax output layer is used with the number of neurons equal to the number of classes. An inception module first applies a bottleneck layer, to transform an input multivariate TS to a lower dimensional TS. It then applies multiple convolutional filters of varying kernel sizes, termed multiplexing convolution, to capture temporal features at different scales.

Key design differences to ResNet are ensembling of models, the use of bottleneck layers, multiplexing convolution using varying kernel sizes, and the use of only two residual blocks, as opposed to three in ResNet.

Fig. 32

Overview of the InceptionTime structure, image taken from Ismail-Fawaz et al. (2022) with permission

4.7.4 H-InceptionTime

Ismail-Fawaz et al. (2022) proposed an extension of InceptionTime that included hand-craft one-dimensional convolution filters to detect very specific patterns in a time series: increasing trends, decreasing trends and peaks. Hybrid Inception (H-Inception) uses the hand-crafted filters in parallel with the first module of the Inception network. Like InceptionTime, H-InceptionTime is an ensemble of five base models. To avoid the need to find the best length of hand-crafted filters, H-InceptionTime chooses different lengths for each hand-crafted filter and used all of them. They found H-InceptionTime provided a small, but significant, improvement over InceptionTime on the 112 UCR datasets.

4.7.5 LITETime

Both ResNet and Inception have approximately 500k trainable parameters and are computationally intensive. In 2023, Ismail-Fawaz et al. (2023b) proposed a smaller model for InceptionTime, called Light Inception with boosTing tEchniques (LITE). LITETime uses the DepthWise Separable Convolutions in order to significantly reduce the number of parameters while using boosting techniques to balance the trade off between complexity and performance. These boosting techniques are multiplexing convolution, dilated convolution and hand-crafted-filters. Multiplexing convolution is the approach of applying multiple convolution layers in parallel of different kernel size, motivated from Inception. The usage of dilated convolution is motivated from the fact of it boosting many TSC models in the literature, such as ROCKET. The LITETime ensemble of five base models is not significantly worse than full InceptionTime, but much faster.

4.7.6 Comparison of deep learning based approaches

Figure 33 shows the relative performance of the five deep learning algorithms and 1NN-DTW. Averaged statistics are shown in Table 12. The results confirm our prior belief: CNN is no better than 1NN-DTW, ResNet is significantly better than CNN, and InceptionTime is significantly better than ResNet. They also confirm recent findings in  Ismail-Fawaz et al. (2022) and Ismail-Fawaz et al. (2023b): H-InceptionTime gives a small, but significant improvement over InceptionTime and LiteTime is as accurate as InceptionTime but takes a fraction of the time. We choose H-InceptionTime as our best in class.

Fig. 33

Ranked test accuracy of five deep learning based classifiers and the benchmark 1NN-DTW on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Table 12 Summary performance measures for deep learning classifiers on 30 resamples of 112 UTSC problems. Best in bold

4.8 Hybrid

The nature of the data and the problem dictate which category of algorithm is most appropriate. The most accurate algorithms on average, with no apriori knowledge of the best approach, combine multiple transformation types in a hybrid algorithm. We define a hybrid algorithm as one which by design encompasses or ensembles multiple of the discriminatory representations we have previously described. Some algorithms will naturally include multiple transformation characteristics, but are not classified as hybrid approaches. For example, many interval approaches extract unsupervised summary statistics from the intervals they select, but as the focus of the algorithm is on generating features from intervals we would not consider it a hybrid.

The overall best performing approach in the bake off by a significant margin was the Collective of Transformation Ensembles (COTE) Bagnall et al. (2015), which at the time was the only algorithm that explicitly ensembles over different representations. It has been subsequently renamed Flat-COTE due to its structure: it is an ensemble of 35 time series classifiers built in the time, auto-correlation, power spectrum and shapelet domains. The components of the ST-HESCA Hills et al. (2014) and EE Lines and Bagnall (2015) ensembles are pooled with classifiers built on autocorrelation (ACF) and power spectrum (PS) representation. All together, this includes the eight classifiers built on the shapelet transform from ST-HESCA, the 11 elastic distance 1-NN classifiers from EE and the eight HESCA classifiers built on ACF and PS transformed series. A weighed vote is used to label new cases, with each classifier being weighted using its train set cross-validation accuracy.

The COTE family of classifiers has evolved since Flat-COTE, and new hybrid algorithms have been produced following the success shown by ensembling multiple representations. The relation flowchart for hybrid based algorithms is shown in Fig. 34

Fig. 34

An overview of feature based classifiers and the relationship between them. Filled algorithms were released after the 2017 bake off (Bagnall et al. 2017) and algorithms with a thin border are not included in our experiments

4.8.1 HIVE-COTE (HC$\alpha$)

The Hierarchical Vote Collective of Transformation Ensembles (HIVE-COTE) (Lines et al. 2018) was proposed to overcome some of the problems with Flat-COTE. This first version of HIVE-COTE, subsequently called HIVE-COTE$_\alpha$ (HC$_\alpha$), is a heterogeneous ensemble containing five modules each from a different representation: EE from the distance based representation; TSF from interval based methods; BOSS from dictionary based approaches and ST-HESCA from shapelet based techniques and the spectral based RISE. The five modules are ensembled using the Cross-validation Accuracy Weighted Probabilistic Ensemble (CAWPE, known at the time as HESCA, Large et al. (2019b)). CAWPE employs a tilted probability distribution using exponential weighing of probabilities estimated for each module found through cross-validation on the train data. The weighted probabilities from each module are summed and standardised to produce the HIVE-COTE probability prediction.

4.8.2 HIVE-COTE version 1 (HC1)

Whilst state-of-the-art in terms of accuracy, HC$_\alpha$ scales poorly. A range of improvements to make HIVE-COTE more usable were introduced in HIVE-COTE v1.0 (HC1) (Bagnall et al., 2020a). HC1 has four modules instead of the five used in HIVE-COTE$_\alpha$: it drops the computationally intensive EE algorithm without loss of accuracy. BOSS is replaced by the more configurable cBOSS (Middlehurst et al. 2019). The improved randomised version of STC (Bostrom and Bagnall 2017) is included with a default limit on the search and the Rotation Forest classifier. TSF and RISE had usability improvements. HC1 is designed to be contractable, in that you can specify a maximum train time.

4.8.3 HIVE-COTE version 2 (HC2)

In 2021, HIVE-COTE was again updated to further address scalability issues and reflect recent innovations to individual TSC representations and HIVE-COTE v2.0 (HC2) (Middlehurst et al. 2021) was proposed. In HC2, RISE, TSF and cBOSS are replaced, with only STC retained. TDE (Middlehurst et al. 2020b) replaces cBOSS as the dictionary classifier. DrCIF replaces both TSF and RISE for the interval and frequency representations. An ensemble of ROCKET classifiers called the Arsenal is introduced as a new convolutional based approach. Estimation of test accuracy via cross-validation is replaced by an adapted form of out-of-bag error, although the final model is still built using all training data. Unlike previous versions, HC2 is capable of classifying multivariate time series. Figure 35 illustrates the structure of HC2, while Fig. 36 visualises the ensemble members of HIVE-COTE over its evolution.

Fig. 35

Overview of the HIVE-COTE version 2 ensemble structure

Fig. 36

A flowchart displaying the progression of the HIVE-COTE meta ensemble

4.8.4 TS-CHIEF

The Time Series Combination of Heterogeneous and Integrated Embedding Forest (TS-CHIEF) (Shifaz et al. 2020) is a homogeneous ensemble where hybrid features are embedded in tree nodes rather than modularised through separate classifiers. The TS-CHIEF comprises an ensemble of trees that embed distance, dictionary, and spectral base features. At each node, a number of splitting criteria from each of these representations are considered. These splits use randomly initialised parameters to help maintain diversity in the ensemble. The dictionary based splits are based on BOSS, distance splits based on EE and interval splits based on RISE. The goal of TS-CHIEF was to obtain the benefits of multiple representations without the massive processing requirement of the original HIVE-COTE.

4.8.5 Randomised Interval-Shapelet Transformation (RIST)

The Randomised Interval-Shapelet Transformation (RIST) pipeline is a simpler approach than the previously described hybrids. Rather than constructing an ensemble, RIST concatenates the output of multiple transformations to form a pipeline classifier. RIST uses the transformation portions from the interval based DrCIF (Middlehurst et al. 2021) and the shapelet based RDST (Guillaume et al. 2022) algorithms. For both of these transformations, features are extracted from both the base series and multiple series representations. These representations are the first order differences, the periodogram of the series and the series autoregression coefficients. After concatenating the output, these features are then used to build an Extra Trees (Geurts et al. 2006) classifier. The aim of RIST is to provide a simple and relatively efficient hybrid algorithm which can be applied to both classification and extrinsic regression tasks.

4.8.6 Comparison of hybrid approaches

Figure 37 shows that HC2 is significantly more accurate than the other three classifiers in terms of accuracy. This is true of all five metrics shown in Table 13. The scatter plots in Fig. 38 shows it is consistently better than HC1 and RIST.

Fig. 37

Ranked test accuracy of hybrid classifiers and the benchmark 1NN-DTW on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Table 13 Summary performance measures for hybrid classifiers on 30 resamples of 112 UTSC problems. Best in bold

5 Results

To keep the analysis tractable, we restrict further analysis of performance to the best classifier in each of the eight categories. Further results tables and figures are available in Appendix C, with all results files available on the accompanying website and can be accessed directly accessible in code withg aeon. Figure 39 shows the ranking of these classifiers on the 112 UCR data for 30 resamples of train/tests splits. HC2 and MR-Hydra are the top performing algorithms in terms of accuracy. There is no significant difference between QUANT, H-IT, RDST and WEASEL 2.0 in terms of test accuracy. HC2 is best performing with AUROC and NLL measures. H-IT performs better with balanced accuracy and NLL.

The AUROC and NLL need to be interpreted in context: Weasel 2.0, RDST and MR-Hydra use classifiers that only produce 0/1 predictions. This means they will inevitably perform poorly on AUROC and NLL.

Fig. 38

Scatter plot of test accuracies of hybrid classifiers

Fig. 39

Averaged ranked performance statistics for eight best of category algorithms on 112 UCR UTSC problems. Statistics are averaged over 30 resamples of train and test splits. Names shortened for clarity: FP is FreshPrince, W 2.0 is Weasel 2.0, MR-H is MR-Hydra and H-IT is H-InceptionTime

For context, Figure 40 shows the scatter plot of HC2 against the next best (MR-Hydra) and the worst performing (PF). It is worth reiterating that PF is significantly better than both EE and 1-NN DTW, both of which were considered state of the art until recently.

Fig. 40

Scatter plot of test accuracies of state of the art classifiers

Table 14 Summary performance measures for best in category classifiers on 30 resamples of 112 UTSC problems. Best in bold

Fig. 41

Averaged ranked performance statistics for eight best of category algorithms on 30 new UTSC problems. Statistics are averaged over 30 resamples of train and test splits

For convenience, Table 14 summarises the summary statistics presented in Section 4. HC2 is on average about 0.5% more accurate than MR-Hydra, over 6% more accurate than PF and over 12% more accurate than 1NN-DTW.

5.1 Performance on new TSC datasets

HC2 performs the best on the 112 datasets. However, HIVE-COTE has been in development for over five years, and all advances were judged by evaluation on these datasets. As acknowledged in Middlehurst et al. (2021), there is always the risk of the introduction of subconscious bias in the design decisions that lead to the new algorithms. To counter this, we have assembled 30 new datasets, as described in Section 3.1. Figure 41 shows the ranks for the eight best of category on these data sets. The top clique for accuracy contains MR-Hydra, HC2, RDST, QUANT and FreshPRINCE. The results for balanced accuracy are similar. Figure 42 shows the results for the combined 142 datasets. The performance of HC2 and MR-Hydra is very similar, and they are in a clique that is significantly better than the other six classifiers.

Fig. 42

Averaged ranked performance statistics for eight best of category algorithms on 142 TSC problems. Statistics are averaged over 30 resamples of train and test splits

Ismail-Fawaz et al. (2023a) noted that critical difference diagrams (CD) can be deceptive and lack stability, with the relative ordering being highly sensitive to the selection of comparates included in the comparisons. This sensitivity renders them susceptible to inadvertent manipulation. To circumvent this problem, they propose a bespoke pairwise comparison tool, called multiple comparative matrix (MCM)¹¹. It shows pairwise comparisons between all comparates, and includes difference in average scores, wins/draws/losses, and Wilcoxon p-values. Colors of the heat map represent mean differences in scores. Red indicates that the comparate in the row wins by more on average than the comparate in the column. Bold text indicates that the difference in significant. Figure 43 summarises the performance of the eight classifiers on 112 datasets using the MCM, with comparisons to the 30 new datasets and 142 datasets available in Appendix C. A notable observation arises when comparing the CD on accuracy in Fig. 39 to this MCM on the 112 UCR UTSC. The rankings of WEASEL 2.0, QUANT, H-IT and RDST are deceptive. Despite WEASEL 2.0 demonstrating more pairwise wins compared to RDST or QUANT in the MCM, its ranking appears higher (worse) than both in the CD when all 8 comparates are taken into account. In addition, H-IT has less pairwise wins than RDST in the MCM, yet shows the lower (better) rank in the CD.

Fig. 43

Summary performance statistics for eight classifiers on 112 datasets, generated using the multiple comparison matrix (MCM). The MCM shows pairwise comparisons. Each cell shows the mean difference in accuracy, wins/draws/losses, and Wilcoxon p-value for two comparates

Table 15 Average accuracy rank of classifiers on 30 resamples of 142 TSC problems split by series length

6 Analysis

Relative performance on test suites is important when evaluating classifiers, but it does not necessarily generalise to new problems. There will be problem domains and specific applications where different classifiers will be the most effective. Furthermore, characteristics such as the variability in performance and the run time complexity of algorithms are also of great interest to the practitioner.

We model the approach used in Bagnall et al. (2017) by comparing performance by data characteristics using all 142 datasets. Tables 15,  16 and 17 break performance down by series length, train set size and number of classes. HC2 and MR-Hydra are first or second on average in each category. HC2 seems to do better with longer series. MR-Hydra performs better with larger train set sizes. Table 18 breaks down performance by problem type. HC2 and MR-Hydra are the top two ranked in all categories except MOTION. MR-Hydra does particularly well on image outlines, whereas HC2 excels at electric devices and spectrograms.

Table 16 Average accuracy rank of classifiers on 30 resamples of 142 TSC problems split by train set size

Run time is clearly an important consideration. The speed of QUANT and the ROCKET family of classifiers is a significant feature. It was stated in the bake off that “[a]n algorithm that is faster than [the current state of the art] but not significantly less accurate would be a genuine advance in the field“. ROCKET and the subsequent refinements fulfil this criteria and represent an important advance. Table 19 shows the total train time for classifiers on the 142 problems and Fig. 44 shows the plot of rank against train time (on a logarithmic scale). We do not include H-IT in these measurements because it was run on two different types of GPU, whereas the other algorithms were all trained on the same CPU (Intel Xeon Gold 5220R 2.2GHz). HC2 is clearly much slower than MR-Hydra. This is at least in parts the result of the configuration and implementation of HC2. For example, TDE, a component of HC2, is not optimised using numba¹². Nevertheless, there is no doubt that MR-Hydra offers a good accuracy/train time trade off: it is on average as accurate as HC2 but orders of magnitude faster. If results are required very quickly or train set sizes are large, MR-Hydra would seem to be the better option. However, for smaller train set sizes (see Table 16), or if probabilities or orderings are required (see Table 14), the results indicate that HC2 is the better option. A special mention must be given to QUANT. It achieves high accuracy remarkably fast: it is an order of magnitude faster. We would recommend QUANT for very large problems, assuming it scales accordingly.

Figure 45 shows the violin plot of the deviation of each classifier from the median performing algorithm. It shows that both HC2 and MR-Hydra have tightly grouped distributions, with HC2 having a wider spread of positive values. H-InceptionTime (H-IT) has a very wide spread, both positive and negative, reflecting the wide variation in performance we have previously observed. FreshPrince (FP), QUANT and Proximity Forest (PF) also have wide distributions. PF performs relatively poorly more often than it does well.

Table 17 Average accuracy rank of classifiers on 30 resamples of 142 TSC problems split by number of classes

Table 18 Average accuracy rank of classifiers on 30 resamples of 142 TSC problems split by problem type

Table 19 Train time statistics on 142 TSC problems. H-InceptionTime is omitted because the times are not comparable. Best in bold

We explored the effect on performance of the design decisions described in Table 22. If we group average accuracy ranks by each design factor of use of dilation, differences, ensemble, frequency domain and discretisation and perform a one factor ANOVA on each factor, we find a significant difference in rank distribution between those using dilation and those that do not, and those that use differences and those that do not. There was no significant difference in distribution when grouped by frequency, ensemble or discretisation. Care must be taken when interpreting these results since the assumptions behind the tests are not satisfied. However, there is at least some support for the utility of using dilation and differenced series. Finally, we have included a comprehensive correlation matrix on average accuracy ranks (Fig. 49 in the appendix). These demonstrate the diversity in performance of these classifiers and show the difference in performance between shapelet based and convolution based algorithms (Fig. 50).

Fig. 44

Averaged rank on accuracy against train time on 142 UTSC problems

Fig. 45

Distributions of the deviation of test accuracies from the median value of eight classifiers

7 Conclusions

Research into algorithms for TSC has seen genuine progress in the last ten years, and the volume of research has dramatically increased. We have provided a particular view of this research landscape by grouping algorithms into eight categories defined by the core representation/transformation. We have compared the best in each category on 112 TSC problem and introduced 30 new datasets to counter any possible bias from over fitting. We evidence progress by benchmarking against algorithms previously considered the best performing, and show that two classifiers, MR-Hydra and HC2, generally perform the best. HC2 performs significantly better on the current UCR archive, but there is less observable difference when we compare them on 30 new problems we have introduced. This could be due to the smaller sample size, the nature of the data sets or reflect some embedded bias in algorithm design. We note that HC2 does worse than MR-Hydra on imbalanced data and with larger train set sizes, but is better with more class balance, smaller train set sizes and with long series.

We are not claiming that these results should be taken to mean practitioners should always use MR-Hydra and/or HC2. There are strengths and weakness to all the algorithms we have described. Indeed, there is a case to be made for using QUANT by default, at least for exploratory analysis, because it is so fast. Understanding when it is appropriate to use which algorithm for a specific problem is an active research area. However, we suggest that, in the absence of any prior information these two algorithms make a sensible starting point for a new TSC problem. Despite significant research effort, there has not been an Alexnet for TSC, i.e. a deep learning approach that has dominated all others. It may be because the problems in the archives are relatively small compared to other archives used for deep learning evaluation: Table 16 shows that H-Inception time improves relative to other algorithms as the number of training cases increases.

However, we think the core reason deep learning has not provided the gains many expected is that, unlike specific applications such as image classification or natural language processing, there is not one common underlying structure for the neural networks to exploit. Nevertheless, there is no doubt scope for improvements in deep learning algorithms for TSC. H-InceptionTime performs well overall, but Fig. 45 demonstrates its limitations: it often performs terribly, and this makes its overall performance worse. If this tendency could be corrected, possibly by some automated structural optimisation, it seems likely that H-InceptionTime could match HC2 and MR-Hydra.

Since the original bake off a number of trends have developed in research, and some prior observations remain true. On average, hybrid algorithms still perform better than single domain approaches on the UCR archive. The ROCKET and HIVE-COTE family of classifiers work well because they combine convolution/shapelet approaches with dictionary based ones, i.e. they look for the presence of or the frequency of subseries. A key component of ROCKET based classifiers is dilation. We have shown that using dilation has significantly improved the single representation classifiers RDST and WEASEL 2.0. Incorporation of dilation could well benefit other algorithms, such as interval based classifiers. Ensemble algorithms are still effective and popular, but pipeline algorithms combining a transformation with a linear classifier such as ridge regression have shown to be just as competitive. The algorithms using linear classifiers such as ROCKET, WEASEL 2.0 and RDST have shown to be more scalable than ensembles generally, but cannot produce good probability estimates. More algorithms now incorporate transformed series such as first-order differences and periodograms into their feature extraction. This has been shown to increase accuracy in the majority of the algorithm types we have presented.

We believe there is great scope for improving time series specific classifiers: None except QUANT scale particularly well for large data, particularly in terms of memory: we are constructing a set of larger problems but none of the classifiers could be built in them in reasonable time and/or memory; there is a lack of principled work flows for using these classifiers to help understand the mechanisms for forming classifiers; multivariate TSC is less understood and many of the classifiers described have not been designed to be used in this way; and there has been little research into how best to handle unequal length series. We believe there are many unanswered questions in the field of TSC and predict it will remain as active and productive for the next 10 years.

Appendices

Appendix A: Reproducibility

The majority of the algorithms we have evaluated in this work are available in the aeon toolkit (see Footnote 2), and those that are not we plan to include over time. aeon is a Python based toolbox for time series analysis which contains a developed classification module. The aeon toolkit is compatible with scikit-learn¹³, and aims to follow its interface and enable usage of its tools where possible.

The version of aeon classifiers used in this work is aeon v0.6.0, with this version and later releases available on PyPi¹⁴. In Listing 1 we show a usage example for a time series classifier in aeon. While we use ROCKET in the example as it is fast, the same interface applied to other aeon classifiers¹⁵.

To run our experiments, we primarily use the tsml-eval¹⁶ package to produce results files for aeon and scikit-learn estimators. The version used for our experiments is tsml-eval v0.2.1, which contains additional estimators not currently available in aeon. Listing 2 gives an example for running an experiment using an aeon classifier loading from .ts files. Alternatively, you can input already loaded data as shown in Listing 3. For more guidance on producing our results using tsml-eval, visit our accompanying webpage hosted on the repository (see Footnote 9).

The experiment functions will output a results file. The format for this file can be found in the results_format.ipynb example Jupyter notebook¹⁷. The utilities used to evaluate algorithms over multiple datasets and resamples can be found in the evaluation.ipynb notebook.

All results files from our experiments and a table of parameters can be found on the accompanying website and the publication directory¹⁸.

Appendix B: Algorithms

Table 20 shows the algorithms used in the original classification bake off (Bagnall et al. 2017). Table 21 shows the algorithms used in our experiments. Table 22 shows the different characteristics for each algorithm.

Table 20 Algorithms used in the 2017 bake off

Table 21 Algorithms used in the Redux bake off

Table 22 Characteristics of the 40 approaches included in our experiments. Columns are dilation (dil), discretisation (disc), differences/derivatives (diff), frequency domain (freq), ensemble (ens) and linear classifier (lin)

Appendix C: Results

Table 23 shows the accuracy results of the best performing algorithms on the 30 new classification datasets. Figure 46 shows a critical difference diagram for all algorithms included in our experiments on the 112 UCR datasets. Figures 47 and  48 contain additional MCM diagrams for the 30 new datasets and original 142 datasets respectively on the best in class algorithms. Figures 49 and  50 show correlation diagrams for the algorithms.

Table 23 Accuracy of classifiers on the 30 new datasets (averaged over 30 resamples)

Fig. 46

Ranked test accuracy of all 40 classifiers in the bake-off on 112 UCR UTSC problems. Accuracies are averaged over 30 resamples of train and test splits

Fig. 47

Summary performance statistics for eight classifiers on 30 datasets, generated using the multiple comparison matrix (MCM)

Fig. 48

Summary performance statistics for eight classifiers on 142 datasets, generated using the multiple comparison matrix (MCM)

Fig. 49

Correlation on Average Accuracy Ranks for all competitors

Fig. 50

Correlation on Average Accuracy Ranks between Shapelet-based and Convolution-based approaches