1 Introduction

Capability of the human brain to process data in a parallel and energy-efficient architecture is driven by its huge network of \(\sim {10^{11}}\) neurons and \(\sim {10^{15}}\) synapses. The biological neuron is the fundamental processing unit inside the brain. A neuron consists of a cell body which is called as the soma to which the axons and dendrites are attached (Fig. 1a). The neuron receives information through the dendrites from the pre-synaptic neuron and the information is passed on to the post-synaptic neuron through the axon using action potentials. These signals arrive at the junction between two adjacent neurons which are referred to as the synaptic cleft. These synapses are capable of processing and memorizing the information signal. The connection strength between the two adjacent neurons is determined by the synaptic weight. Analogous to the biological neural network, researchers have tried to develop hardware neuromorphic systems [1, 2] which emulate the working of the human brain. These are purely electrical circuits composed of neuron circuitry [3,4,5] and the associated synaptic array elements. Such a bio-inspired approach can overcome several of the shortcomings of current computer architectures which require large amount of data transfer between the processing and memory units leading to an increased energy expenditure and computational times. Currently, software-based neural network designs are also in much demand due to their capability to solve data-intensive computational tasks like face recognition, self-driving cars, and big data analytics. A feedforward neural network (Fig. 1b) is an artificial neural network (ANN) which is capable of solving several tasks like pattern recognition, prediction, and function approximation. These artificial neural networks are modelled on the biological neural circuitry and are primarily composed of neurons and synapses. While the synapses are responsible for the storage of information called as the ‘weights’, the neurons implement the processing capabilities of the network using vector matrix multiplication (VMM) [6] followed by input summation and threshold firing. Non-linear mathematical functions called ‘activation functions’ are used for determining the output of the neurons from the integrated input signals. The rectified linear unit (ReLU) [7] function is a popular choice for the neuron activation function because of its similarity to biological neurons in zeroing the negative weight values. In an ANN, these series processes of summing the inputs and computing the VMM followed by the non-linear activation of the neurons are carried forward from the input to the next hidden layer and finally to the output neurons. This process is referred to as the “feedforward” process, and hence, the name of the network is usually called as “feed-forward neural network”. Once the output values are obtained from the final layer neurons, they are compared with the actual values and the difference between the two values is computed using a loss function. The mean cross-entropy loss (MCEL) function is a commonly-used loss function in classification tasks which compare the predicted and actual probabilities of the output. The gradient of the loss function is then computed (referred to as “stochastic gradient descent”) with respect to the weights of each layer and the weights are updated based on the direction of steepest decrease of the gradients. This backward propagation of the errors from the final output layer to the initial layers is called the “back-propagation” method. The “learning rate” determines the magnitude by which the weights are updated at every back-propagation step. A complete cycle of feedforward and backpropagation is computed over a batch of input images called the batch size. For a typical pattern recognition task, the whole dataset is divided into several smaller batches of images with equal batch sizes for the ANN training. Once the training process is carried out over an entire dataset, it is referred to as one “epoch” of training. The same procedure is followed several times through multiple epochs until the mean accuracy and MCEL function converges to a satisfactory value. An ANN network can have multiple layers of neurons between its input and output neurons, depending on the complexity of the problem at hand. A single-layer feedforward neural network (SLFN) is an ANN with a single hidden layer of neurons and is the most commonly used ANN for pattern recognition tasks. Such a neural network can easily be adopted into a hardware synaptic array along with neuron circuits for the realization of hardware neuromorphic system. Hence, optimizing the structural complexity of feedforward neural networks is highly important from a hardware perspective.

Fig. 1
figure 1

Schematics of (a) biological neuron and (b) single-layer feed forward neural network (SLFN)

Full size image

1.1 Motivation

There has been a consistent effort from engineers to realise neuromorphic architecture in hardware sense. Neuromorphic hardware design pursues an in-memory computing with highly energy-efficient parallel processing capability in the end. Realizing the artificial neural network through complementary metal-oxide-semiconductor (CMOS) integrated circuits is the first step in this direction. IBM’s TrueNorth chip has been one of the first major breakthroughs in this respect [8]. This chip encompasses 256 million synapses and 1 million integrate-and-fire (IF) neurons fabricated using the 40-nm-node CMOS technology. Similarly, Intel’s Loihi chip was fabricated with 130 million synapses and 131,072 neurons utilizing 14-nm-node CMOS technology. Both chips support the high capacity and accelerated learning in the specifically designed neuromorphic semiconductor chip. Several other neuromorphic chips have been reported: Neurogrid [9], Braindrop [10], BrainScales [11], SpiNNaker [12], ROLLS [13], Darwin [14], Dynap-SEL [15] etc. Synaptic transistors construct the core of these neuromorphic chips wherein the weight information is stored. Unlike software-based weight initialization, the synaptic devices can only have limited number of conductance values (weights). More recently, the synaptic devices are realized by a single memory device including charge-trap flash (CTF) memory [16], resistive-switching random-access memory (RRAM) [6, 17,18,19,20], phase-change random-access memory (PRAM) [21], ferroelectric random-access memory (FRAM) [22], and magnetic random-access memory (MRAM) [23] for increasing the synapse array density and minimizing the power consumption, departing from the conventional synapses made up of circuits or several electron devices. Also, many of today’s state-of-the-art deep learning models such as Inception v1, VGG-19, ResNet, and others contain huge number of neurons with millions of parameters [24,25,26,27]. These are extremely hard to implement in the hardware due to the limitations with array size constraints (chip compactness) and manufacturing cost. For the widespread adoption of these models in the neuromorphic hardware, their model size needs to be reduced and optimized with the hardware constraints (see Fig. 2). It is in this context that we have verified our current methodology for the optimized SLFN design using the weights extracted from a synaptic transistor device [28]. To the best of our knowledge, this is the first work focusing on the optimization of SLFN for implementation of the specifically designed artificial intelligence chip.

Fig. 2
figure 2

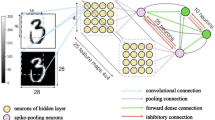
Schematic showing the optimization of an SLFN using SVD method. In the hardware sense, the synaptic weights can be obtained from a single memory component, for example, a 4-terminal synaptic transistor [28, 61, 62] whereas the neurons in the hidden layer are to be realized by relatively bulky CMOS circuits which consume large area and energy [40]. The inset shows a neuron circuit consisting of two n-type metal-oxide-semiconductor field-effect transistors (NMOSFETs) and passive devices (Cmem: membrane capacitor, Vmem: membrane potential). Adapted from [41] with permission from Wiley Books. The SVD approach is highly practical in optimizing the hardware neural network from the design level determining the number of neuron circuits and the size of synapse array

Full size image

1.2 Literature review

A major reason for the structural complexity of a neural network is the number of neurons in the hidden layer used for training the data. Several research groups have attempted to reduce the structural complexity of neural networks. The seminal work by Arai resulted in a hyperplane-based algorithm for estimating the hidden neuron number and found that I − 1 hidden units are sufficient for I learning patterns [29]. Later, Tamura and Tateishi proposed a method to determine the number of hidden neurons using information criteria [30]. Similarly, Fujita et al., statistically estimated the hidden neuron number with the advantage of fast learning [31]. The required neuron number is given by \({N_{h}}=K\log ||{P_{c}}Z||/{\log }S\), where S is defined as the number of candidates which are arbitrarily searched for optimised hidden neurons and c is the acceptable error limit. E. J. Teoh et al. used an SVD-based approach to estimate the number of hidden neurons in a feed-forward network [32]. But the method was empirical in nature with results shown on small datasets only. Pruning is another well-known method for reducing neural network size by removing structural parameters based on the relevance scores. Recently, F.E Fernandes et al. used a filter-pruning strategy followed by fine tuning to reduce the size of some popular models like ResNets, DenseNets etc [33]. There have also been several other strategies adapted for pruning and is the most widely used method for model compression [34, 35]. However, the method often requires several iterations and fine-tuning making it hard to adapt to hardware implementations. There have also been several advanced techniques like quantization [36], Huffman encoding [37], and neural architecture search (NAS) for determining the optimal neural network size [38]. However, most of these algorithms are developed for efficient implementation on software using the conventional von Neumann hardware architecture. They require high computing power using advanced hardware such as GPU or cloud-based computational units. A major limitation of such methods is encountered in their implementation for neuromorphic hardware where these algorithms have never been tested with realistic physical constraints.

1.3 Contribution

The main goal of this work is to optimise the structural complexity of a SLFN for hardware realisation. We propose the use of SVD method for determining the optimized number of neurons in the hidden layer for a SLFN. SVD is a comparably simpler method and require much less iterations to identify the lowest possible model size within an acceptable error limit. Unlike other reported algorithms, we have verified our methodology by incorporating physically reliable weight values from a core-shell dual-gate (CSDG) nanowire transistor [28] device for identifying the convergence criterion. Such a device-based verification is important from a hardware perspective. Through the device-based weights and weight level variations, we have taken into account the hardware limitations like limited range of device conductance values and device non-linearity considerations while defining the convergence criterion for determining the reduced number of neurons. To the best of our knowledge, this is the first work focusing on the optimization of SLFN for hardware implementation. We believe that this is a very important step in realizing compact neural networks for hardware realization.

2 Mathematical preliminaries

We consider a general SLFN consisting of J input neurons, n neurons in the hidden layer, and O output neurons. The SLFN is trained using a set of T training images X ∈{X1,X2,...,XT}. The activation function used is the rectified linear unit (ReLU) function. The trained model is then used to recognize a set of M test images. The activation matrix is given by the matrix K such that \(K\in \mathbb {R}^{M\times n}\).The rows of K can be considered as M data points in an n dimensional space since K is an M × n matrix. From a hardware perspective, realization of such an SLFN would require synaptic devices like resistive-switching random-access memory [17], charge-trap flash memory [16], field-effect transistor [39], phase-change memory [21] for the storage of weight values cooperating with CMOS neuron circuits [40, 41]. Essentially, the synaptic devices utilize their electrical conductance states as the equivalent weight values and the neuron circuits are operated based on the behavior of the activation function. Although the majority of area and power efficiencies are determined by the high-density synaptic device array in the hardware neural network, while a synaptic device can be realized by a single electron device with very high scalability reaching down to nanometer dimension, a neuron is implemented in the form of complementary metal-oxide-semiconductor (CMOS) integrated circuit based on plural passive and active components, and thus, requires relatively larger area and power consumption compared with a single synapse. For this reason, the mathematical approach is focused on reducing the number of neurons, which has not been seriously considered in the conventional purely software-oriented artificial intelligence approach. Hence, optimally minimizing the number of neurons in the hidden layer should be one of the major concerns for the neuromorphic hardware implementation. In the current work, we use the SVD method to reduce the size of the activation matrix K without compromising on the prediction capabilities of the network. This is done by determining the best-fitting lower dimensional subspace for the set of M data points. For the activation matrix K; \(\mathbf {s_{L_{1}},s_{L_{2}},s_{L_{3}},....,s_{L_{n}}}\) are the left singular vectors; \(\mathbf {s_{R_{1}},s_{R_{2}},s_{R_{3}},.., s_{R_{n}}}\) are the right singular vectors and σ1,σ2,σ3,…,σn are the singular values. The left singular vectors:

$$ \mathbf{s_{L_{i}}=\frac{1}{\sigma_{i}}K\mathbf{s_{R_{i}}}} $$
(1)

where the coordinates of \(\sigma _{i}\mathbf {s_{L_{i}}}\) are the projections of rows of K onto \(\mathbf {s_{R_{i}}}\). Essentially, the singular vectors are the orthonormal basis for the lower-dimensional subspaces and the singular values are the projections of the M data points onto these subspaces.

The SVD of the matrix K is the factorization of the matrix into the product of three separate matrices \(S_{L}\in \mathbb {R}^{M\times M},\beta \in \mathbb {R}^{M\times n},\) and \(S_{R}\in \mathbb {R}^{n\times n}\) such that:

$$ K=S_{L}\beta{S_{R}}^{T} $$
(2)

where \(S_{L}={\begin {bmatrix} s_{L_{11}}& .& .& .& s_{L_{1M}}&\\ .& .& & & .&\\ .& & .& & .&\\ .& & & .& .&\\ s_{L_{M1}}& .& .& .& s_{L_{MM}}& \end {bmatrix}}_{M\times M}\), \(S_{R}\! =\! {\begin {bmatrix} s_{R_{11}}& .& .& .& s_{R_{1n}}&\\ .& .& & & .&\\ .& & .& & .&\\ .& & & .& .&\\ s_{R_{n1}}& .& .& .& s_{R_{nn}}& \end {bmatrix}}_{n\times n}\) and \(\beta \! =\! {\begin {bmatrix} \sigma _{1}& 0& .& .& 0&\\ 0& .& & & .&\\ .& & \sigma _{n}& & .&\\ .& & & .& .&\\ 0& .& .& .& \sigma _{M}\!\! \end {bmatrix}}_{M\times n}\)

The columns of SL and SR are the left and right singular vectors of the K matrix, respectively, and are orthonormal to each other. β is a diagonal matrix with n non-zero diagonal elements arranged such that σ1 ≥ σ2 ≥ σ3,… ≥ σn ≥ 0. Further, σn+ 1 = σn+ 2 = ..... = σM = 0. Here, the matrix K can be expressed as \(K={\sum }_{i=1}^{n}\sigma _{i}\mathbf {s_{L_{i}}{s_{R_{i}}}^{T}}\) which can be proved by the following theorem [42]:

Theorem 1

For an M × n matrix K, with right singular vectors \(\mathbf {s_{R_{1}},s_{R_{2}},s_{R_{3}},.., s_{R_{n}}}\); left singular vectors \(\mathbf {s_{L_{1}},s_{L_{2}},s_{L_{3}},....,s_{L_{n}}}\) and corresponding singular values σ1,σ2,σ3,…,σn:

$$ K=\sum\limits_{i=1}^{n}\sigma_{i}\mathbf{s_{L_{i}}{s_{R_{i}}}^{T}} $$
(3)

Proof

We see that multiplying the left-hand side of (3), i.e, matrix K with \(\mathbf {s_{R_{j}}}\) yields \(\sigma _{j}\mathbf {s_{L_{j}}}\) (from (1)). Similarly, multiplying the right-hand side of (3), i.e, \({\sum }_{i=1}^{n}\sigma _{i}\mathbf {s_{L_{i}}{s_{R_{i}}}^{T}}\) with \(\mathbf {s_{R_{j}}}\) yields \(\sigma _{j}\mathbf {s_{L_{j}}}\) since \(\mathbf {s_{R_{i}}}\) are orthogonal to each other and \(\mathbf {{s_{R_{i}}}^{T}}\times \mathbf {s_{R_{i}}}=I\) where I is the identity matrix.

$$ K\mathbf{s_{R_{j}}}=\sigma_{j}\mathbf{s_{L_{j}}}=\sum\limits_{i=1}^{n}\sigma_{i}\mathbf{s_{L_{i}}{s_{R_{i}}}^{T}}\mathbf{s_{R_{j}}} $$
(4)

Any two matrices A and B are equal if Ax = Bx for all vectors x. Hence, from (4),

$$K=\sum\limits_{i=1}^{n}\sigma_{i}\mathbf{s_{L_{i}}{s_{R_{i}}}^{T}}$$

□

3 Reducing the over-estimated rank n

Most often, the number of neurons in the hidden layer taken into account for the SLFN training is highly over-estimated. Such an over-estimation leads to additional neuronal circuitry in physical cross-bar array implementations, which can be avoided by determining the reduced rank. Hence, the reduction of the over-estimated rank n is highly significant from a CMOS manufacturing perspective. In the mathematical sense, the over-estimation of neurons in the hidden layer of SLFN leads to the creation of additional hyperplanes in the hidden layer activation space. Such hyperplanes are essentially parallel planes to the linearly independent basis vectors of the space. An intuitive way of dealing with this problem was put forward by G.W. Stewart, where the excess neurons are considered as “contaminations” to the original matrix [43]. Now, the problem reduces to the determination of the reduced rank g of the hidden-layer activation matrix from the over-estimated matrix with n neurons. The sum of squares of all the entries in a matrix is given by the Frobenius norm of the matrix.

$$ ||K||_{F}=\sqrt{\sum\limits_{j,i}{k^{2}_{j,i}}} $$
(5)

For any row, kj of matrix K, we can show that \({\sum }_{j=1}^{M}{\left | {k_{j}} \right |}^{2}={\sum }_{i=1}^{n}{\sigma _{i}}^{2}\) [42]. Hence from (5), we have:

$$ {||K||_{F}}^{2}=\sum\limits_{i=1}^{n}{\sigma_{i}}^{2} $$
(6)

Thus, the square of the norm of the activation matrix is equal to the sum of the squares of the singular values of K. If we assume E as the “contamination matrix” which accounts for the excess neurons in the K matrix, then from (6),

$$ \sigma^{2}_{g+1}+\sigma^{2}_{g+2}+\ldots+{\sigma^{2}_{n}}\leq||E||_{F}^{2} $$
(7)

Therefore, if σg is sufficiently large in comparison to E, then SVD can provide a reasonable approximation of the subspace spanned by the hidden-layer activation matrix.

3.1 Determination of g

Several different criteria have been previously suggested for the determination of g [44]. within a threshold value γ such that the “spectral energy” of K matrix is retained. We use the convergence criterion for g based on the spectral energy approximation as shown below:

$$ \sum\limits_{i=1}^{g}{\sigma^{2}_{i}}/\sum\limits_{i=1}^{n}{\sigma^{2}_{i}}\geq\gamma $$
(8)

γ has been mostly determined by visual inspection based on the problem in previous works. Although γ originates from the spectral energy equation in (8), it has actual physical significance when dealing with real hardware-based systems. γ has a direct dependence on the final accuracy of the trained model and hence the determination of γ should take into account the device considerations like the number of stable weights attainable by the synaptic device. Unlike the near-continuous weights available for a software based artificial neural network, realistic hardware implementations can only have a finite number of stable conductance levels [45] which can be utilized for the synaptic array fabrication. Such practical considerations are extremely important in the determination of γ since the activation matrix output might alter significantly with a finite-weight network and so does the convergence criterion for the SVD method. Hence, we have taken into consideration the various practical weight levels ranging from 2, 4, 8, 16, and 32 levels for the application of the SVD method in optimizing the number of neurons in the hidden layer.

4 Results & discussion

The proposed method was applied to the Modified National Institute of Standards and Technology database (MNIST) dataset using two types of weight initializations. In the first case, weights were randomly initialised using a purely software-based randomization technique. In the second case, we have utilised discrete synaptic weights extracted from a core-shell dual-gate nanowire synaptic transistor [28].

4.1 Software-based weight initialization

The MNIST dataset consists of hand-written digits of 60,000 training images and 10,000 test images [46]. The images correspond to digits from “0” to “9” with nearly uniform distribution among all the 10-digit classes. Every image is in grayscale format with a resolution of 28 × 28 pixels. Before training, the input data was normalized to a range of [0, 1], and then, reshaped to form a column matrix of 784 rows. The normalized data is then fed to a SLFN with 784 input neurons, 100 neurons in the hidden layer, and 10 output neurons. All the simulations were performed using PyTorch open source package [47]. The input data are trained for 100 epochs within which the mean classification error was reduced to a stable value. The detailed flowchart and algorithm used for optimization of the SLFN are shown in Fig. 3 and Algorithm 1, respectively. Briefly, the training of the SLFN for the input data is initialized using a large estimate for the neurons in the hidden layer, say 100. The model is then trained for all the images in the training dataset using the rectified linear unit (ReLU) as the non-linear activation function for the SLFN. The back-propagation algorithm is implemented using the stochastic gradient descent algorithm. From the trained model, the accuracy is determined using the test dataset. The SVD of the hidden layer activation output is then computed and the β matrix is found. Using a γ value of 0.97, a reduced rank value of 42 is determined for g such that the singular value σg satisfies the threshold criterion in (8). The SLFN training procedure is then repeated for 42 neurons in the hidden layer. Figure 4a shows the variation of digit recognition accuracy with the number of epochs for the network with both 100 and 42 neurons in the hidden layer. We obtained a maximum test accuracy of 97.65% for 100 neurons in the hidden layer and 97.15% for 42 neurons in the hidden layer. From this, it is evident that the test accuracy does not increase appreciably with the addition of neurons beyond 42 in the hidden layer. Similarly, the decrease of MCEL function also follows a similar trend for both 100 and 42 neurons in the hidden layer. The accuracy and the loss function do not vary significantly beyond 42 neurons in the hidden layer since this is the reduced rank representation of the activation matrix space. Further addition of neurons results in the creation of redundant neurons which adversely affects the network since it adds only to the structural complexity of the network leading to increased computational time.

Fig. 3
figure 3

Flowchart describing the execution of the proposed SVD algorithm

Full size image
Fig. 4
figure 4

MNIST digit recognition accuracy (%) and mean cross-entropy loss as a function of (a) number of training epochs for 100 and 42 neurons in the hidden layer. (b) Test accuracy (%) and MCEL variation with neurons. (c) Accuracy and (d) mean cross-entropy loss variation with gamma

Full size image

The variation of test accuracy and MCEL function as a function of the number of neurons in the hidden layer is shown in Fig. 4b. It is observed from the figure that the accuracy does not increase considerably beyond 42 neurons in the hidden layer. As discussed before, the determination of a lower bound for γ is crucial for practical implementation of the SVD method for rank reduction. Figure 4c and d show the dependences of accuracy and MCEL function on the value of γ. We can infer that a value of 0.9 is a safe choice for the lower bound on γ since the percentage loss in accuracy between γ = 1 and γ = 0.9 is below 2.3%. Similarly, the MCEL function also does not increase significantly until about γ = 0.9.

Apart from the recognition accuracy, an important performance metric of a neural network model is its capability to predict all the output classes with a similar level of confidence. The confusion matrix (see Fig. 5) can be used to measure the overall prediction capabilities of a model. It is a square matrix which compares the true output values with that predicted by the model. The diagonal elements represent the cases where the predicted output is same as the true output. All the off-diagonal elements represent the faulty predictions made by the model. From Fig. 5a and b we see that our trained model is showing a high degree of predictability for all the classes even with a reduced number of neurons. This indicates that the SVD method has reduced the effective ranks of the activation matrix without compromising the class separability in model prediction. In order to evaluate the performance of our SVD method on other datasets, we have applied our proposed method on two more datasets – fashion MNIST and Street View House Numbers (SVHN) Datasets [48, 49]. fashion MNIST dataset is similar to the MNIST dataset except for the type of images being classified. The dataset contains greyscale images (28 × 28) of fashion articles which are to be classified into 10 output classes. However, the SVHN dataset consists of RGB images of 32 × 32 resolution consisting of real word images of house numbers from Google Street View images. The dataset is to be classified into 10 output classes corresponding to the images of the digits at the center of the house number. Figure 6a shows the application of the proposed method in reducing the number of neurons in the hidden layer from 100 down to 30 neurons for fashion MNIST pattern recognition tasks. It is observed that, as the number of neurons decreases from 100 down to 30, there is only a marginal drop in test accuracy from 88.67% to 86.73%. Similarly, the MCEL shows only a small drop by the scheme with reduced models. Here, it is evident that the SVD method succeeds in removing redundant neurons from the hidden layer without an appreciable drop in network performances. Also, the variation in test accuracy (%) with the number of neurons in the hidden layer depicted in Fig. 6b reveals that the model performance is not improved with further decrease in neuron number below a cut-off value of 30. The confusion matrices shown in Fig. 6c and d correspond to the SLFNs with 100 and 30 neurons in the hidden layer, respectively. It is shown that the lowering of model complexity depending on application of the SVD method has not affected the capability of the model to make distinctions among the various output classes. Figure 7a shows the SVHN digit recognition accuracy and MCEL as a function of number of training epochs with 100 and 48 neurons in the hidden layer. As compared with the test results from MNIST and fashion MNIST datasets, one from the SVHN dataset show large fluctuations in both accuracy and MCEL over the training process. The saturated accuracy value is lower than those obtained from the previous MNIST and fashion MNIST tests while the saturated MCEL is larger than them. This is largely due to the increased complexity in the SVHN dataset which considers the RGB compositions in an image. However, it is noticeable that the SVD method has not considerably affected the SLFN performance while reducing the number of neurons in the hidden layer. Test accuracy is depicted as a function of number of neurons in Fig. 7b, which validates that the system accuracy is maintained with the reduced number of neurons. However, there is a significant degradation in performance with less than 48 neurons. The confusion matrices with the original 100 neurons and those in a reduced number, 48, are depicted in Fig. 7c and d, respectively, in which a noticeable off-diagonal contribution is not observed. It is revealed that the optimally minimized SLFN architecture is capable of separating the output classes with confidence.

Fig. 5
figure 5

Confusion matrix for the MNIST test data for (a) 100 and (b) 42 neurons in the hidden layer

Full size image
Fig. 6
figure 6

Application of the proposed method to fashion MNIST pattern recognition. (a) Recognition accuracy (solid) and mean cross-entropy loss (MCEL) (dotted) as a function of number of training epochs with 100 and 30 neurons in the hidden layers. (b) Recognition accuracy (red) and MCEL (blue) as a function of neurons in the hidden layer. Confusion matrices for (c) 100 and (d) 30 neurones in the hidden layer

Full size image
Fig. 7
figure 7

Application of the proposed method to SVHN digit recognition. (a) Recognition accuracy (solid) and mean cross-entropy loss (MCEL) (dotted) as a function of number of training epochs with 100 and 48 neurons in the hidden layer. (b) Recognition accuracy (red) and MCEL (blue) as a function of neurons in the hidden layer. Confusion matrices for (c) 100 and (d) 48 neurons in the hidden layer

Full size image

4.2 Performance comparison with previous studies

In order to make the distinction of the main purpose and performances of the methodology in this work, we have made comparisons between recent works and ours. Although several different algorithms have been reported in the literature related with optimization of neural network architectures, most of them have not focused on energy and area efficiency, but rather on expressive power with possibly complicated approximation function that can be obtained by the algorithm, toward a higher accuracy [50]. This is different from the main purpose of this work, the reduction of complexity in physical interconnection inside a hardware neural network architecture. Relatively similar topic was dealt in another literature [51], for a study on effects of neural network depth (number of hidden layers, not that of neurons in the single hidden layer as in this work) on the expressive power of the network. The focus is mainly made on the result of exponential increase in width, number of neurons in a hidden layer, in sacrifice of the reduction in depth, which does not provide any guideline or algorithmic approach for energy and area efficient hardware design of a neural network architecture. As compared with those reported without considerations in the hardware aspects, our methodology attempts to provide a practical algorithm for width reduction of an SLFN from a hardware application perspective. We have specifically chosen SLFN for our simulations due to the current research interest in these neural network architectures towards neuromorphic computing applications [52, 53]. In literature, the most widely used method for network optimization is the pruning technique in which the parameters of an existing network are systematically removed [54]. In general, the pruning technique starts with a pre-trained network, and then, removes the redundant parameters and repeats the training while maintaining a similar model performance as the original unpruned model. A major drawback of some of the pruning techniques reported in literature is the nature of sparse neural network generated due to the removal of parameters. These pruned networks slow down the computation due to the uneven nature of memory access. The more structured pruning models also suffer from issues of pruning convergence, scheduling, and fine tuning. Recently, F. E. Fernandes Jr. et al., proposed the evolution strategy for the elimination of redundant filters from convolutional layers to reduce the computational complexity of the model [33]. Although the deep pruning with evolution strategy demonstrates plausible capabilities in terms of model compression and network performances, the algorithm introduces a major limitation as the method requires a population of individual CNN models of the same size to initiate the pruning process. Similarly, S. K. Yeom et al. proposed a layer-wise relevance propagation (LRP) method to compute the relevance scores for pruning the network. The authors identify a major drawback in their algorithm that the reduced network may not always be the smallest possible network and is strongly dependent on the chosen LRP variant [34]. H. Zhou et al. adopted a hierarchical pruning scheme using a self-organizing fuzzy neural network for nonlinear system modelling in industrial applications. Although the method is successful for non-linear system modelling, its applications is limited to fuzzy neural networks [55]. From a practical viewpoint, pruning adopted in these cases can effectively remove the neurons without considerable loss in accuracy in a given network fixed in the hardware sense but cannot contribute to the minimizing of network size from the initial design level for hardware realization. In comparison, a major achievement of our methodology is the reduction of the network model to the possible smallest representation for hardware realization. Another method for network optimization is the low-rank factorization technique [56]. Our approach is essentially based on this strategy but the optimization procedures are based on realistic hardware-oriented constraints in determining the reduced rank, unlike the existing one that is rather purely mathematical and can be suitable for software neural network, without deep considerations on synaptic device characteristics and number of neuron circuits. An existing technique is the network quantization approach where the number of bits needed to represent individual network parameters is reduced or quantized [36, 57]. Quantization is also applied to activations which saves additional memory allotments. A combination of low-rank compression and post-processing pruning strategy was recently reported [58]. However, the adapted algorithm is highly complex and optimised mainly for software-based implementation. In Table 1, network architecture, methodology, highlights, and comparisons are summarized in comparison between the methodology in this work and the previously reported approaches for reducing the complexity of neural networks. Although the existing methods demonstrate plausible performances for network compression and high test accuracy, most of them are not free from the concerns about computational costs and additional overheads for hardware implementation: all these methodologies have been developed from software perspectives and have no realistic hardware-sense constraints. Hence, their hardware implementation would require additional neuron circuitry and very-large-scale crossbar array fabrication, both of which require time, cost, area, and energy in realization and operation. In comparison, in short, our proposed methodology has been developed specifically from a hardware point of view with requirements of minimal number of synaptic devices and neuron circuits. The reduced rank approximation is simple and effective from the neuromorphic hardware realization perspective.

Table 1 Comparison between methods in the existing reports and in this work
Full size table

4.3 Synaptic transistor-based weight initialization

In order to evaluate the performance of our proposed method on hardware neuromorphic systems, we used a core-shell dual gate nanowire transistor as a synaptic device. Further details regarding the device and its synaptic capabilities has been summarised in our recent publication [28]. We have extracted the synaptic weights from the potentiation/depression characteristics of the device to initialise the neural network weights. The synaptic weights from the device have been chosen to form 2, 4, 8, 16, and 32 weight levels from the device. As discussed before in Section 3.1, these weight levels have been chosen based on practical hardware considerations. The neural network corresponding to each of these weight levels has been trained and optimised in a similar manner as explained in Algorithm 1. The initial network was trained using 100 neurons in the hidden layer whereas the optimised network (γ = 0.99) after the application of the proposed method yielded 15 neurons in the hidden layer. Figure 8a shows the variation of classification accuracy and MCEL function as a function of the training epochs using 32-level device weights. It is evident from the figure that with the reduction in neurons there is no observable drop in the accuracy of the model. The reduction in number of neurons in the hidden layer is extremely significant from a hardware perspective since the CMOS implementation of neuronal circuits [3,4,5, 59, 60] require large capacitors for spike integration and pulse generation circuits which make these circuits bulky and consume more power. Due to the reduction in number of neurons in the hidden layer, the total number of synapses has also decreased from 79,400 to 11,910; which is highly advantageous for device fabrication. From a hardware perspective, such a reduction in the total number of synapses has a major advantage in terms of the synapse array space requirements and circuit integration density. The variation of test accuracy with the number of neurons in the hidden layer for various device weight levels is shown in Fig. 8b. We can observe that for all the weight levels, the test accuracy does not increase significantly beyond 15 neurons in the hidden layer. Additional neurons in the hidden layer are redundant in practice and do not contribute to the improvement of the model in terms of accuracy and generalization. The dependence of the accuracy on both the weight levels and neurons is shown in Fig. 8c, from which it is clear that the accuracy surface is a plane almost parallel to the space spanned by weight levels and neurons in the hidden layer beyond a threshold number of 15. The class separability of the reduced model based on 32 weight levels has been compared with the initial model using the confusion matrix. The matrices for 100 and 15 neurons in the hidden layer are quite similar and there are no major off-diagonal elements which indicate the model capability to distinguish the output classes even with a reduced number of neurons in the hidden layer as demonstrated in Fig. 9a and b. We have also evaluated the performance of the SVD method on fashion MNIST and SVHN datasets similar to the evaluation done in Section 4.1. Figure 10a & b show the accuracies in fashion MNIST image recognition as a function of number of training epochs and that of neurons in the hidden layer. It is explicitly shown in Fig. 10a that the application of SVD has reduced the number of neurons in the hidden layer down to 25 from the original value of 100 without a significant accuracy drop for training with fashion MNIST images. In Fig. 10b, the number of weights realized in a synaptic device is varied from binary to 32 levels and it is observed that it might be desirable to adopt multi-level synaptic device with no less than 4 levels for coping with SVD application. Figure 10c and d depict the accuracies in SVHN image recognition as a function of number of training epochs and that of neurons in the hidden layer. The application of SVD has an effect of reducing the number of neurons in the hidden layer down to 40 from the original value of 100 without experiencing a notable accuracy drop as shown in Fig. 10c. Also, it is revealed from Fig. 10d that multi-level synaptic device with 4 or more weights should be prepared for obtaining a high enough system accuracy. Reduction of the number of neurons is an advantage in terms of hardware implementation of a SLFN for saving area in realizing the neuromorphic chip. It is essential to figure out the optimally minimum number of neuron circuits maintaining the system accuracy, and thus, the proposed SVD method would be effective in reducing the model complexity and realizing area and power-efficient SLFN hardware. Table 2 summarises the reduction in computational parameters (number of synaptic weights) of the proposed model in comparison to the conventional (uncompressed) model. It is notable in Table 2 that both number of neurons in the hidden layer and number of synaptic devices are considerably reduced across different datasets for both software and hardware synaptic weight based implementations. Hence, the proposed SVD method is quite effective in reducing the model complexity and hence the resultant electrical circuitry for hardware realisation of the SLFN can be simplified considerably for practical neuromorphic chip realisation.

Fig. 8
figure 8

Training with MNIST images. (a) Training accuracy (%) and mean cross-entropy loss as a function of the number of training epochs for 100 & 15 neurons in the hidden layer with 32 weight levels from a synaptic transistor device. (b) Test accuracy (%) variation with neurons for various device weight levels. (c) 3D surface plot of the accuracy variation as a function of number of neurons in the hidden layer at different number of synaptic weight levels

Full size image
Fig. 9
figure 9

Confusion matrix for the MNIST test data using 32 device weight levels for (a) 100 and (b) 15 neurons in the hidden layer

Full size image
Fig. 10
figure 10

Training with fashion MNIST and SVHN images. (a) Training accuracy and MCEL as a function of number of training epochs with 100 and 25 neurons in the hidden layer for fashion MNIST training. (b) Training accuracy as a function of number of neurons at different numbers of synaptic weights for fashion MNIST training. (c) Training accuracy and MCEL as a function of number of training epochs with 100 and 40 neurons in the hidden layer for SVHN training. (d) Training accuracy as a function of number of neurons at different numbers of synaptic weights for SVHN training

Full size image
Table 2 Computational complexity comparison
Full size table

5 Conclusion

We have proposed a hardware realistic approach for determining the optimized number of neurons in the hidden layer in a SLFN. The methodology was applied to SLFN based on software (near-continuous) and hardware (discrete) synaptic weights. The application of the proposed method to MNIST dataset with hardware synaptic weights resulted in the reduction of neurons in the hidden layer to 15 from an initial value of 100. We have further verified the class separability of the reduced neuron models to be consistent with the initial model. The proposed method was further extended to fashion MNIST and SVHN datasets where the method was found effective in reducing the model complexity. The method also shines light on the mathematics of the hidden layer activation space. The simple and intuitive nature of the methodology makes it easily extendable for dealing with complicated networks with a large number of hidden layers and neurons.

figure d