Skip to main content
SpringerLink
Log in

Towards continuous consistency axiom

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

It is shown for the first time in this paper, that Kleinberg’s (2002) (self-contradictory) axiomatic system for distance-based clustering fails (that is one of the data transforming axioms, consistency axiom, turns out to be identity transformation) in fixed-dimensional Euclidean space due to the consistency axiom limitations and that its replacement with inner-consistency or outer consistency does not help if continuous data transformations are required. Therefore we formulate a new, sound axiomatic framework for cluster analysis in the fixed dimensional Euclidean space, suitable for k-means like algorithms. The system incorporates centric consistency axiom and motion consistency axiom which induce clustering preserving transformations useful e.g. for deriving new labelled sets for testing clustering procedures. It is suitable for continuous data transformations so that labelled data with small perturbations can be derived. Unlike Kleinberg’s consistency, the new axioms do not lead the data outside of Euclidean space nor cause increase in data dimensionality. Our cluster preserving transformations have linear complexity in data transformation and checking. They are in practice less restrictive, less rigid than Kleinberg’s consistency as they do not enforce inter-cluster distance increase and inner cluster distance decrease when performing clustering preserving transformation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

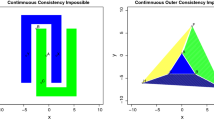
  1. See e.g. https://ifcs.boku.ac.at/repository/, https://archive.ics.uci.edu/ml/datasets.php

  2. This impossibility does not mean that there is an inner-contradiction when executing the inner-Γ-transform. Rather it means that considering inner-consistency is pointless because inner-Γ-transform is in general impossible except for isometric transformation.

  3. This property holds clearly for k-means, if quality is measured by inverted Q function, but also we can measure cluster quality of k-single-link with the inverted longest link in any cluster and then the property holds.

  4. k-means quality function is known to exhibit local minima at which the k-means algorithm may get stuck at. This claim means that after the centric Γ-transformation a partition will still be a local optimum. If the quality function has a unique local optimum then of course it is a global optimum and after the transform the partition yielding this global optimum will remain the global optimum.

  5. A clustering function clustering into k clusters has the locality property, if whenever a set S for a given k is clustered by it into the partition Γ, and we take a subset \({\Gamma }^{\prime }\subset {\Gamma }\) with \(|{\Gamma }^{\prime }|=k^{\prime }<k\), then clustering of \(\cup _{C\in {\Gamma }^{\prime }}\) into \(k^{\prime }\) clusters will yield exactly \({\Gamma }^{\prime }\).

References

  1. Ackerman M (2012) Towards theoretical foundations of clustering, university of Waterloo. PhD Thesis

  2. Ackerman M, Ben-david S, Loker D (2010) Characterization of linkage-based clustering. In: COLT. pp 270–281

  3. Ackerman M, Ben-David S, Loker D (2010) Towards property-based classification of clustering paradigms. In: Adv neural information proc Sys. 23. pp 10–18, Curran Associates, Inc.

  4. Ackerman M, Ben-David S, Brânzei S, Loker D (2021) Weighted clustering: towards solving the user’s dilemma. Pattern Recogn 120:108152. https://doi.org/10.1016/j.patcog.2021.108152

    Article  Google Scholar 

  5. Awasthi P, Blum A, Sheffet O (2012) Center-based clustering under perturbation stability. Inf Process Lett 112(1-2):49–54

    Article  MathSciNet  MATH  Google Scholar 

  6. Balcan M, Liang Y (2016) Clustering under perturbation resilience. SIAM J Comput 45 (1):102–155

    Article  MathSciNet  MATH  Google Scholar 

  7. Ben-David S, Ackerman M (2009) Measures of clustering quality: a working set of axioms for clustering. In: Koller D, Schuurmans D, Bengio Y, Bottou L (eds) Advances in neural information processing systems 21. Curran Associates, Inc., pp 121–128

  8. Campagner A, Ciucci D (2020) A formal learning theory for three-way clustering. In: Davis J, Tabia K (eds) Scalable uncertainty management - 14th international conference, SUM 2020, Bozen-Bolzano, Italy, 23-25 September 2020, proceedings. lecture notes in computer science. Springer, vol 12322, pp 128–140, DOI https://doi.org/10.1007/978-3-030-58449-8_9

  9. Carlsson G, Mémoli F (2008) Persistent clustering and a theorem of j. kleinberg. arXiv:0808.2241

  10. Carlsson G, Mémoli F (2010) Characterization, stability and convergence of hierarchical clustering methods. J Mach Learn Res 11:1425–1470

    MathSciNet  MATH  Google Scholar 

  11. Chang J C, Amershi S, Kamar E (2017) Revolt: collaborative crowdsourcing for labeling machine learning datasets. In: Mark G, Fussell SR, Lampe C, schraefel MC, Hourcade JP, Appert C, Wigdor D (eds) Proceedings of the 2017 CHI conference on human factors in computing systems, Denver, CO, USA, 06-11 May 2017, pp 2334–2346. ACM, DOI https://doi.org/10.1145/3025453.3026044

  12. Lin C-R, chen M-S (2005) Combining partitional and hierarchical algorithms for robust and efficient data clustering with cohesion self-merging. IEEE Trans Knowl Data Eng 17(2):145– 159

    Article  Google Scholar 

  13. Cohen-Addad V, Kanade V, Mallmann-Trenn F (2018) Clustering redemption beyond the impossibility of kleinberg’s axioms. In: Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, Garnett R (eds) Advances in neural information processing systems. Curran Associates, Inc., vol 31

  14. Cui X, Yao J, Yao Y (2020) Modeling use-oriented attribute importance with the three-way decision theory. Rough Sets 12179:122–136. https://doi.org/10.1007/978-3-030-52705-1_9

    Article  Google Scholar 

  15. Duda R, Hart P, Stork G (2000) Pattern Classification. Wiley, New York 2nd edn

  16. Gower JC (1990) Clustering axioms. Classification society of North America newsletter. pp 2–3

  17. Hennig C (2015) What are the true clusters? Pattern Recogn Lett 64(15):53–62

    Article  MATH  Google Scholar 

  18. Hopcroft J, Kannan R (2012) Computer science theory for the information age. chapter 8.13.2. a satisfiable set of axioms, p 272ff

  19. Iglesias F, Zseby T, Ferreira D (2019) Mdcgen: multidimensional dataset generator for clustering. J Classif 36:599–618. https://doi.org/10.1007/s00357-019-9312-3

    Article  MathSciNet  MATH  Google Scholar 

  20. Ke Z, Wang D, Yan Q, Ren J, Lau RW (2019) Dual student: breaking the limits of the teacher in semi-supervised learning. In: Proc. IEEE CVF international conference on computer vision. pp 6728–6736

  21. Kleinberg J (2002) An impossibility theorem for clustering. In: Proc. NIPS 2002. pp 446–453. http://books.nips.cc/papers/files/nips15/LT17.pdf

  22. Kłopotek M (2017) On the existence of kernel function for kernel-trick of k-means. In: Kryszkiewicz M, Appice A, §lȩżak D, Rybiński H, Skowron A, Raś Z (eds) Foundations of intelligent systems. ISMIS, Lecture notes in computer science, Springer, Cham. vol 10352

  23. Klopotek MA (2020) On the consistency of k-means++ algorithm. Fundam Inform 172(4):361–377

    Article  MathSciNet  MATH  Google Scholar 

  24. Kłopotek MA (2022) A clustering preserving transformation for k-means algorithm output

  25. Kłopotek R, Kłopotek M, Wierzchoń S (2020) A feasible k-means kernel trick under non-euclidean feature space. Int J Appl Math Comput Sci 30(4):703–715. https://doi.org/10.34768/amcs-2020-0052

    Article  MathSciNet  MATH  Google Scholar 

  26. Kłopotek MA, Kłopotek R (2020) In-the-limit clustering axioms. In: To appear in proc. ICAISC2020

  27. Kłopotek MA, Wierzchoń ST, Kłopotek R (2020) k-means cluster shape implications. In: To appear in proc. AIAI

  28. van Laarhoven T, Marchiori E (2014) Axioms for graph clustering quality functions. J Mach Learn Res 15:193–215

    MathSciNet  MATH  Google Scholar 

  29. Larsen KG, Nelson J, Nguyundefinedn HL, Thorup M (2019) Heavy hitters via cluster-preserving clustering. Commun ACM 62(8):95–100. https://doi.org/10.1145/3339185

    Article  Google Scholar 

  30. Li W, Hannig J, Mukherjee S (2021) Subspace clustering through sub-clusters. J Mach Learn Res 22:1–37

    MathSciNet  MATH  Google Scholar 

  31. Liu M, Jiang X, Kot AC (2009) A multi-prototype clustering algorithm. Pattern Recognition 42(5):689–698. https://doi.org/10.1016/j.patcog.2008.09.015. http://www.sciencedirect.com/science/article/pii/S0031320308003798

    Article  MATH  Google Scholar 

  32. MacQueen J (1967) Some methods for classification and analysis of multivariate observations. In: Proc. Fifth berkeley symp. on math. statist. and prob. vol 1, pp 281–297, Univ. of calif. Press

  33. Moore J, Ackerman M (2016) Foundations of perturbation robust clustering. In: IEEE ICDM. pp 1089–1094, DOI https://doi.org/10.1109/ICDM.2016.0141

  34. Mount DM (2005) Kmlocal: A testbed for k-means clustering algorithms. https://www.cs.umd.edu/mount/Projects/KMeans/kmlocal-doc.pdf

  35. Nie F, Wang CL, Li X (2019) K-multiple-means: A multiple-means clustering method with specified k clusters. In: Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery and data mining. pp 959–967, KDD ’19, association for computing machinery, New York, NY, USA. https://doi.org/10.1145/3292500.3330846

  36. Pollard D (1981) Strong consistency of k–means clustering. Ann Statist 9(1):135–140

    Article  MathSciNet  MATH  Google Scholar 

  37. Puzicha J, Hofmann T, Buhmann J (2000) A theory of proximity based clustering: structure detection by optimization. Pattern Recogn 33(4):617–634

    Article  Google Scholar 

  38. Qin Y, Ding S, Wang L (2019) Research progress on semi-supervised clustering. Cogn Comput 11:599–612. https://doi.org/10.1007/s12559-019-09664-w

    Article  Google Scholar 

  39. Shekar B (1988) A knowledge-based approach to pattern clustering. Ph.D. thesis Indian Institute of Science

  40. Steinbach M, Karypis G, Kumar V (2000) A comparison of document clustering techniques. In: Proceedings of KDD workshop on text mining, proceedings of the 6th international confer1193 ence on knowledge discovery and data mining, Boston,MA

  41. Strazzeri F, Sánchez-García RJ (2021) Possibility results for graph clustering: a novel consistency axiom. arXiv:1806.06142

  42. Thomann P, Steinwart I, Schmid N (2015) Towards an axiomatic approach to hierarchical clustering of measures

  43. Vidal A, Esteva F, Godo L (2020) Axiomatizing logics of fuzzy preferences using graded modalities. Fuzzy Sets and Systems 401:163–188. https://doi.org/10.1016/j.fss.2020.01.002. https://www.sciencedirect.com/science/article/pii/S0165011419303203,. fuzzy Measures, Integrals and Quantification in Artificial Intelligence Problems – An Homage to Prof. Miguel Delgado

    Article  MathSciNet  MATH  Google Scholar 

  44. Wang P, Yang X (2021) Three-way clustering method based on stability theory. IEEE Access 9:33944–33953. https://doi.org/10.1109/ACCESS.2021.3057405

    Article  Google Scholar 

  45. Wang X, Kihara D, Luo J, Qi GJ (2021) Enaet: a self-trained framework for semi-supervised and supervised learning with ensemble transformations. IEEE Trans Image Process 30:1639–1647

    Article  Google Scholar 

  46. Wierzchoń S, Kłopotek M (2018) Modern Clustering Algorithms. Studies in Big Data 34. Springer

  47. Wright W (1973) A formalization of cluster analysis. Pattern Rec 5(3):273–282

    Article  MathSciNet  Google Scholar 

  48. Zadeh RB, Ben-David S (2009) A uniqueness theorem for clustering. In: Proceedings of the twenty-fifth conference on uncertainty in artificial intelligence. pp 639–646, UAI ’09, AUAI Press, Arlington, Virginia, United States

  49. Zeng G, Wang Y, Pu J, Liu X, Sun X, Zhang J (2016) Communities in preference networks: refined axioms and beyond. In: ICDM. pp 599–608

  50. Zhao Y, Tarus SK, Yang LT, Sun J, Ge Y, Wang J (2020) Privacy-preserving clustering for big data in cyber-physical-social systems: survey and perspectives. Information Sciences 515:132–155. https://doi.org/10.1016/j.ins.2019.10.019. https://www.sciencedirect.com/science/article/pii/S0020025519309764

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Computer Science, Jana Kazimierza 5, 01-248, Warszawa, Poland

    Mieczysław A. Kłopotek

  2. Faculty of Mathematics and Natural Sciences, School of Exact Sciences, Cardinal Stefan Wyszyński University, Dewajtis 5, 01-815, Warszawa, Poland

    Robert A. Kłopotek

Authors
  1. Mieczysław A. Kłopotek
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Robert A. Kłopotek
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mieczysław A. Kłopotek.

Additional information

Publisher’s note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kłopotek, M.A., Kłopotek, R.A. Towards continuous consistency axiom. Appl Intell 53, 5635–5663 (2023). https://doi.org/10.1007/s10489-022-03710-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-022-03710-1

Keywords

Search

Navigation