An integrated fuzzy-grey relational analysis approach to portfolio optimization

Abstract

This paper combines two approaches (Fuzzy set theory and Grey Relational Analysis) for modelling an investor’s imprecise linguistic expectations and the uncertain returns of assets. We propose a novel maximization-type risk measure capable of incorporating the investor’s individual preferences. The investor provides the expectations of what is considered the “ideal” return from the portfolio. We use Credibility theory to capture the investors’ subjective and imprecise expectations in a precise mathematical form. We construct a portfolio return sequence using the assets’ actual return data and an ideal sequence based on investors’ preferences. Subsequently, we calculate the Grey similitude and the closeness incidence degree between the two sequences. The closer the portfolio return is to the ideal return, the better. In this manner, we develop a new risk measure that can quantify an investor’s perception of risk. This measure is intuitive and easy to calculate. It does not involve estimating many parameters, something which would increase the estimation risk. We use a genetic algorithm to solve the resulting portfolio optimization model. We illustrate this method with two case studies: (i) a case study of 100 assets of the U.S. stock market’s NASDAQ-100 index and (ii) a case study of 50 assets of the Indian stock market’s NIFTY-50 index. We comprehensively analyze the model’s out-of-sample performance and discuss its implications. The portfolios obtained using the proposed approach exhibit healthy growth outside the in-sample period. We also compare the out-of-sample performance of the proposed model with several approaches in the literature to establish its superiority.

1 Introduction

A stock market is an elaborate organization that facilitates firms to raise capital through the issuance of stocks. A stock generally represents fractional ownership of a business. The stock market also enables the trading of stocks. A typical investor in any stock market endeavours to create a portfolio of assets with a maximum possible investment return with little variability. However, the prices of assets are hard to predict, with many random and human factors affecting them, including company-specific factors, like the imminent outlook of a company’s business plan, general factors like the supply and demand of stocks, the social and economic laws of the country, etc. Common wisdom dictates that investors diversify their capital over many assets so that losses in some assets can be offset by profits in others. Thus, there are various aspects of portfolio optimization, viz., the investor’s individual preferences and the volatilities of the stock market, which one must consider before deciding on the allocation of capital over different assets. Mathematically, this problem, with its various conflicting objectives, is called multi-objective portfolio optimization. Initially, Markowitz [1] formulated a mathematical model of portfolio optimization. Numerous authors have improved the original mean-variance portfolio optimization model (proposed by Markowitz) to make it more relevant to stock markets’ real-world scenarios. Speranza [2] employed mean absolute semi-deviation (MASD), and Konno and Yamazaki [3] used mean absolute deviation (MAD) to measure the risk and transformed the quadratic mean-variance model into a linear programming problem.

Different investors have diverse perceptions of the current scenarios prevalent in the stock market. This is vital to the facilitation of asset trading in the stock market. The contrasting investor attitudes are the prominent reason for asset transactions. Therefore, any portfolio optimization model must incorporate investor attitudes. Various authors have explored the inclusion of investor attitude into the portfolio optimization model. Li and Yi [4] have proposed coherent fuzzy numbers in a possibilistic environment to model the asset returns. An adaptive index, l, distinguishes between optimistic, pessimistic, and neutral investors. Interested readers can refer to [5,6,7], where a portfolio optimization model that incorporates investor attitude is proposed.

This paper proposes a novel maximization-type risk measure for selecting the optimal portfolio for an investor. The investor provides inputs about the expectations of the returns from the portfolio (which can be understood as a target return). These expectations are generally imprecise and linguistic. Therefore, we use Fuzzy set theory to capture these subjective expectations in a precise mathematical form. The target return is expressed as a fuzzy number and is called the ideal portfolio return. We use fuzzy simulation to generate a sequence of returns based on the investor’s fuzzy ideal returns. This sequence is the “ideal” sequence, which the portfolio sequence should emulate. We calculate the portfolio sequence using the asset weights and the historical return data. We then calculate the Grey similitude and closeness incidence degree between the ideal sequence and the portfolio sequence. The closer the portfolio sequence is to the ideal, the less risky the portfolio is for that investor. Therefore, the objective is to maximize the weighted average of the closeness and the similitude degree. Our method of modelling the risk takes care of only the downside deviations because no rational investor would suggest losses (i.e., negative returns) as ideal portfolio behaviour.

Numerous approaches in the literature have tackled the portfolio optimization problem. A natural question is: what is the need for combining Fuzzy set theory and Grey Systems theory to obtain an optimal portfolio? The success of a portfolio optimization model depends heavily on the accuracy of the prediction of the asset returns. Asset prices are affected by a plethora of factors. Therefore, any endeavour to completely describe such a system is not easy. It may even render the entire exercise meaningless [8]. In such a scenario, the portfolio optimization model can benefit from the experience and intuition of the experts. The model should provide ways to integrate the advice and knowledge of experts in the optimization process. In our previous work [5, 6], we have used the mean absolute semi-deviation (MASD) to estimate the portfolio risk. Although MASD works well, we feel that the investor attitude should play a role in the estimation of the risk. The proposed approach aims to achieve this objective. The investor or the expert provides inputs on the ideal portfolio return in any given scenario. It is a problem of cognitive uncertainty since most investors don’t know the optimal course of action. Therefore, we use fuzzy set theory to model the ideal portfolio return (i.e., the level of return that the investor aims to achieve from the portfolio). The next task is to calculate the risks involved in securing the ideal return. We cannot use the existing risk measures such as the variance or MASD in our model (since we only have a fuzzy estimate of the target return). One could argue that we can use the fuzzy ideal return’s expected value to calculate the variance or MASD, but we would again be using crisp values for estimating the risk. This would defeat the purpose of incorporating the subjective preferences of the investors in assessing the risk of the portfolio. As explained above, asset returns are affected by several factors. A complete enumeration of all these factors is not possible. However, the returns themselves reflect the total effect of these factors. For instance, if an asset’s returns are positive, for whatever reasons, this must imply that the demand for the asset exceeds its supply, i.e., its prospects must be bullish, and vice versa. Therefore, modelling the risk of a portfolio can be simplified if we focus our attention on asset returns. On account of this objective, we propose a risk measure that estimates the closeness and similarity of the portfolio returns with the ideal returns. Grey Systems theory [9] effectively deals with problems of “small sets and poor information” [8]. It focuses on excavating partially known information using the possibility function and sequence operators. It uncovers the hidden patterns in any system for its accurate understanding and description. One advantage of Grey Systems theory is that it constructs models with small amounts of data. Grey Incidence Analysis uses the degree of similarity of geometric curves of the available data sequences (in this case, the asset returns). Therefore, we propose a way of using fuzzy simulation and Grey Incidence Analysis to define a risk measure that quantifies the similarity and the closeness between the ideal returns and those of the portfolio. The proposed risk measure is intuitive and easy to understand. It simply gives a measure of the point-to-point closeness and similarity between the ideal returns and the returns of the portfolio. It does not require the estimation of many parameters, something which would compound errors [10]. The next step is to integrate the investor attitude in the portfolio optimization model. We provide two different methods to accomplish this task using fuzzy set theory. The final step is to determine the optimal asset allocations (i.e., the optimal portfolio weights). We apply a genetic algorithm (a machine learning technique) for this purpose. To summarize, the proposed approach combines human intelligence and artificial intelligence to determine the optimal portfolio that works for the investor. We believe that no model in the literature quantifies the investor’s perception of risk. Consequently, the investor or the expert makes, in the proposed method, an increased contribution in selecting the best portfolio.

We summarize the paper’s novelty and key highlights as follows: (i) We propose a novel maximization-type risk measure based on the Grey similitude and closeness incidence degree between the portfolio returns and the ideal returns (as preferred by the investor). This is a novel contribution to the portfolio optimization problem, to the best of our knowledge. (ii) An aspect of portfolio optimization is that risk is a perception-based, individual-specific concept. The same asset may be considered risky by one investor, while it may be considered less risky by another. From the above discussion, we can conclude that the proposed risk measure can incorporate investor risk perceptions. The optimistic, pessimistic, and neutral investors can specify the ideal portfolio behaviour, modelled using the appropriate fuzzy numbers. (iii) Two separate approaches to integrate investor attitude in the portfolio optimization model using Fuzzy set theory have been discussed. (iv) We provide a method to simulate coherent fuzzy numbers using probability theory. In particular, we modify the triangular probability distribution to generate sequences based on coherent triangular fuzzy numbers. (v) We add several constraints, namely bound and cardinality constraints, in the model to make it more relevant to the practical requirements of investors. We apply the proposed model to a case study involving the 100 assets of the U.S. stock market’s NASDAQ-100 index. We use a genetic algorithm to solve the proposed model. We also perform another case study of the 50 assets listed in the Indian stock market’s NIFTY-50 index to further establish the validity of the proposed model. (vi) We demonstrate the out-of-sample performance of the optimal portfolios and discuss its implications. (vii) Škrinjarić [11] used Grey Incidence Analysis to rank the assets based on the first four moments, viz. expected return, variance, skewness, and kurtosis. These rankings were subsequently used to construct the portfolios using 22 predefined investment strategies. Our model calculates the optimal asset allocations based on historical data using the techniques of multi-criteria decision-making. Thus, our model relies on optimization techniques rather than predefined investment strategies. Our approach combines Fuzzy set theory, Grey Systems theory, and multi-criteria decision-making to provide optimal portfolios based on investors’ preferences.

The rest of this paper is organized as follows: Section 2 provides a brief literature review of the recent studies in portfolio optimization. Section 3 introduces the basic concepts used throughout the paper. In Section 4, we formulate the mathematical model for portfolio optimization, which employs the proposed risk measure. We also develop a genetic algorithm to solve the proposed model. Section 5 provides two case studies: one involving the 100 assets of the U.S. stock market’s NASDAQ-100 index, and the second involving the 50 assets of the Indian stock market’s NIFTY-50 index. We also conduct a comprehensive analysis of the out-of-sample performance of the obtained optimal portfolios and discuss their implications. Finally, Section 6 is the conclusion section with remarks on the possible extensions of this paper.

2 Literature review

An essential ingredient in the success of any mathematical model for obtaining optimal portfolios is an accurate representation of the stock market’s real-life scenarios. As discussed above, asset prices are highly volatile and subject to various human-made and random factors. Thus, the mathematical model for portfolio optimization must be flexible enough to capture the uncertainty inherent in the stock market. One method is to model the asset returns as random variables. There are many studies where the asset returns have been modelled as random variables. Markowitz used a normal distribution to model the asset returns. However, various authors have challenged this assumption [16, 17]. Asset returns exhibit extreme values more frequently than predicted by the normal distribution [18]. This prompted the authors to explore other methods of modelling asset returns. Kamali et al. [19] employed various probability distributions to model asset returns and select the best-fitting distribution for the return data. They employ the MATLAB solver to solve the optimization model. They discover that the kernel distribution is the most appropriate for modelling the asset returns. However, their study is not exhaustive, and there could be other distributions that are a better fit for the return data. Akbay et al. [20] proposed a parallel variable neighbourhood search algorithm for cardinality constrained portfolio optimization problems. They propose a Variable Neighbourhood Search (VNS) algorithm to find the best combination of assets. The asset proportions are determined using Quadratic programming. The algorithm’s computational complexity is O(K² (poolsize_L − K)), where K is the number of assets held in the portfolio, and poolsize_L is the number of solutions in the local search phase. The proposed algorithm provides superior results on five datasets (Hang Seng, DAX100, FTSE100, S&P100, and Nikkei) over various competing algorithms. However, their algorithm is based on the Mean-variance (M-V) framework. We have already discussed the disadvantages of the M-V model. Yu et al. [21] used Autoregressive Integrated Moving Average (ARIMA) to forecast the asset returns. They study the importance of incorporating return forecasting in the portfolio optimization process. Through various models (Mean-variance, Mean-absolute deviation, and so on), they establish that portfolio models with return forecasting outperform their corresponding counterparts (without return forecasting) by 54%–61%. However, the success of their model is heavily dependent on the accuracy of the forecast. Other works include [12, 22,23,24,25,26]. Modelling asset returns as random variables, although popular, requires a significant amount of data for fitting probability distributions with the requisite accuracy in the estimation. It may not always be practical, especially for newly-listed assets. The variations in asset returns are also affected by various human-made factors, which are not random. In such a scenario, it is more prudent to use the judgments of stock market experts. However, these opinions and judgments are usually qualitative rather than quantitative, hence incorporating them into mathematical models is difficult. Fuzzy set theory [27, 28] is an effective method to formulate imprecise judgments in a mathematical form. It is a popular method for modelling the uncertainty in portfolio optimization problems [13, 14, 29,30,31,32,33]. Credibility theory [34, 35], which employs a credibility measure to determine the chance of an event’s occurrence, has the axiomatic properties of self-duality and normality. It is a consistent method for modelling investors’ imprecise and linguistic judgments. Many researchers have used credibility theory to model volatile asset returns [36,37,38,39,40,41,42].

Multi-objective programming determines the optimal tradeoff between return and risk in portfolio optimization. It is an essential branch of Operations Research that transcends disciplines in its application. It has applications in finance, accounting, marketing, supply chain management, and various other fields. Tirkolaee et al. [43] use multi-objective optimization for a reliable pollution routing with cross-dock selection. They propose a bi-objective mixed-integer linear programming problem with cost and supply reliability as the objectives. Two multi-objective metaheuristic algorithms are used to solve the model: Non-dominating Sorting Genetic algorithm-II (NSGA-II) and Multi-Objective Simulated Annealing (MOSA). The computational complexity of NSGA-II is O(mN²), where N is the size of the population, and m is the number of objectives. They discovered that the objective functions are heavily dependent on the demand; thus, the management can evaluate the required resources by analyzing the demand fluctuations. In [44], the authors study the problem of allocation and scheduling rescue units during a natural disaster. They formulate a bi-objective mixed-integer linear programming model to simultaneously minimize the total time to complete all the rescue operations and the total delay time. Multi-choice goal programming was used to solve the model. The model was validated using several comparative studies. Reference [45] is a study of medical waste management during the COVID-19 pandemic. The authors develop a multi-objective mixed linear programming model for a multi-trip location routing problem with time windows. They use fuzzy chance-constrained programming to study the uncertainty of the demand parameter. Based on their case study, the total trip time is reported to be 19.733 hours using three vehicles. The runtime of the solution algorithm is 1029.739 seconds. Thus, we can conclude from the above discussion that multi-objective programming has a wide variety of applications in various branches of Operations Research.

Julong Deng developed Grey Systems theory [9] for dealing with uncertain systems with partially known information. It deals with insufficient information by “generating and extracting useful information from what is available” [8]. In this manner, the operational behaviour of an uncertain system can be effectively monitored and described. There are many instances of small samples and poor information in the real world. Therefore, Grey Systems theory can be applied to a wide variety of problems. Various authors have used the Grey Systems theory to model the uncertainty of asset returns [11, 46,47,48]. As discussed above, asset returns are affected by different kinds of factors. The mutual interaction of these factors determines the behaviour of the asset’s returns. Statistical methods are usually employed for analyzing asset returns. However, these methods suffer from various weaknesses [8]: (i) Large data samples are needed for reliable results. (ii) The available data is assumed to follow a probability distribution, and factors are assumed to have linear relationships. These requirements are hard to satisfy. When historical data is limited, applying the traditional statistical methods is challenging, as a small amount of data is not usually compatible with a conventional probability distribution. Grey Incidence Analysis is a credible alternative to analyze a system when statistical methods are impractical. It applies to large and small samples and involves simple computations. The idea is “to use the degree of similarity of geometric curves formed by the available data sequences” [8]. The higher the degree, the more similarity between the curves and vice-versa [8]. It may seem that Grey Systems theory is similar to Fuzzy set theory; however, as Liu et al. [8] mentioned, “Fuzzy mathematics emphasizes the investigation of problems with cognitive uncertainty, where research objects possess the characteristic of clear intension and unclear extension.” For instance, ”tall man” is a fuzzy concept because everybody vaguely understands a ”tall man”. However, suppose we want to evaluate the particular range within which every person is tall, and those outside it are not tall. In that case, we will have many difficulties because ”tall man” has an unclear extension. This is a problem of cognitive uncertainty, which is resolved using individual judgment (i.e., using the membership function).

The method to measure the risk involved in an investment is another important characteristic of the portfolio optimization model. A quantitative estimate of a portfolio’s prospective losses helps the investor assess its suitability (vis-á-vis returns). The variance was used to measure the portfolio’s risk in the original mean-variance model (Markowitz [1]). However, the variance is known to be a two-sided measure of risk, i.e., it penalizes both upside and downside deviations from the expected return. Only the downside deviations are of concern for the investor; most investors would, in fact, like the upside deviations. Nevertheless, the variance is a prevalent risk measure among researchers [4, 15, 23, 49]. Downside risk measures, which penalize only the negative deviations from the expected return, are more realistic for the portfolio optimization problem. Mean absolute semi-deviation (MASD), Value-at-Risk (VaR), and Conditional Value-at-Risk (CVaR) are some examples of downside risk measures. Each has its advantages and disadvantages. Refer to [50] for an explanation of these. Downside risk measures have also been popular amongst authors [5,6,7, 42, 51, 52]. We have compared the existing literature approaches in Table 1 based on the above discussion.

Table 1 Comparison with existing methodologies

3 Preliminaries

This section provides a primer on the basic concepts used in the paper. The basic theory of each concept is presented in the appendix.

3.1 A brief introduction to coherent Fuzzy Numbers

Definition 1 (Mehlawat et al. 6)

“The credibility function of a coherent triangular fuzzy number ξ_l = (d − δ,d,d + η)_l, $v_{l}(z):\mathbb {R}\rightarrow [0,1]$, is given by

$$ \begin{array}{@{}rcl@{}} v_{l}(z) &=& \begin{cases} \frac{1}{2}\left( \frac{z-d+\delta}{\delta}\right)^{\frac{1}{l}}, & \text{if } d-\delta\leq z \leq d, \\ \frac{1}{2}\left( \frac{d+\eta-z}{\eta}\right)^{l}, & \text{if } d\leq z\leq d+\eta, \\ 0, & \text{otherwise}, \end{cases} \end{array} $$

(1)

where l ∈ℝ, l > 0 (See Fig. 1).”

Fig. 1

Coherent fuzzy numbers’ credibility distribution for different values of l

Remark 1

The adaptive index l specifies the stock market perception of an investor (see Fig. 1). When $1<l<\infty$, the credibility is higher for the left spread (d − δ ≤ z ≤ d), while it is lower for the right spread (d ≤ z ≤ d + η) in comparison to a standard triangular fuzzy number (since 0 ≤ v_l(z) ≤ 1). Thus, if the investors assess the current stock market prospects to be pessimistic, they can assign l in $[1,\infty ]$. When 0 < l < 1, the credibility is lower for the left spread (d − δ ≤ z ≤ d), while it is higher for the right spread (d ≤ z ≤ d + η) in comparison to a standard triangular fuzzy number (since 0 ≤ v_l(z) ≤ 1). Thus, if the investors assess the current stock market prospects to be optimistic, they can assign l in (0,1). For l = 1, the coherent fuzzy number reduces to a standard triangular fuzzy number with similar credibilities assigned to both the spreads. Therefore, a neutral investor can assign l = 1. See Fig. 2 for visual explanation of this concept.

Fig. 2

Change in investor attitude with l

Proposition 1

“Suppose that ξ_1,l = (d₁ − δ₁,d₁,d₁ + η₁)_l, ξ_2,l = (d₂ − δ₂,d₂,d₂ + η₂)_l are two coherent triangular fuzzy numbers. Then, for κ > 0, we have

$$ \begin{array}{@{}rcl@{}} \xi_{1,l}+\xi_{2,l} &=& \left( (d_{1}+d_{2})-(\delta_{1}+\delta_{2}),d_{1}+d_{2},(d_{1}+d_{2})\right.\\&&\left.+(\eta_{1}+\eta_{2})\right)_{l}, (\text{Addition}) \\ \kappa\xi_{1,l} &=& \left( \kappa d_{1}-\kappa \delta_{1},\kappa d_{1},\kappa d_{1}+\kappa \eta_{1}\right)_{l}. \\&&(\text{Scalar multiplication})" \end{array} $$

Proposition 2 (Credibilistic expectation 6)

“Let ξ_l = (d − δ,d,d + η)_l be a coherent fuzzy number. Then, its expected value is given by

$$ \begin{array}{@{}rcl@{}} E[\xi_{l}] &=& d+\frac{1}{2(l+1)}(\eta-l\delta)." \end{array} $$

(2)

3.2 Grey incidence analysis

Proposition 3

“Let Z_i = (z_i(1),z_i(2),…,z_i(n)) be the data sequence of a system’s behaviour, Z_i − z_i(1) denote the zigzag line (z_i(1) − z_i(1),z_i(2) − z_i(1),…,z_i(n) − z_i(1)), and

$$ s_{i}={{\int}_{1}^{n}}\left( Z_{i}-z_{i}(1)\right)dt, $$

when Z_i increases, s_i ≥ 0, when Z_i decreases, s_i ≤ 0, and when Z_i vibrates, the sign of s_i varies.”

Proposition 4

“Assume that the images of the zero-starting point of two behavioural sequences Z_i and Z_j are respectively, ${Z_{i}}^{0}=({z_{i}}^{0}(1),{z_{i}}^{0}(2),\ldots ,{z_{i}}^{0}(n))$ and ${Z_{j}}^{0}=({z_{j}}^{0}(1),{z_{j}}^{0}(2),\ldots ,{z_{j}}^{0}(n))$. Let,

$$ \begin{array}{@{}rcl@{}} s_{i}-s_{j} &=& {{\int}_{1}^{n}}\left( {Z_{i}}^{0}-{Z_{j}}^{0}\right)dt, \\ S_{i}-S_{j} &=& {{\int}_{1}^{n}}\left( Z_{i}-Z_{j}\right)dt, \end{array} $$

when ${Z_{i}}^{0}$ is entirely above ${Z_{j}}^{0}$, s_i − s_j ≥ 0, when ${Z_{i}}^{0}$ is entirely below ${Z_{j}}^{0}$, s_i − s_j ≤ 0, and when ${Z_{i}}^{0}$ and ${Z_{j}}^{0}$ alternate their positions, the sign of s_i − s_j is not fixed. Similarly, the sign of S_i − S_j can be discussed.”

Proposition 5 (Liu 53)

“Assume that Z_i and Z_j are 1-time interval sequences (i.e., the time difference between each observation is 1) of the same length, and the following are the zero-starting point images of Z_i and Z_j,

$$ \begin{array}{@{}rcl@{}} {Z_{i}}^{0} &=& ({z_{i}}^{0}(1), {z_{i}}^{0}(2),\ldots,{z_{i}}^{0}(n)). \\ {Z_{j}}^{0} &=& ({z_{j}}^{0}(1), {z_{j}}^{0}(2),\ldots,{z_{j}}^{0}(n)), \end{array} $$

then,

$$ \begin{array}{@{}rcl@{}} |s_{i}| &=& \left|\sum\limits_{k=2}^{n-1}{z_{i}}^{0}(k)+\frac{1}{2}{z_{i}}^{0}(n)\right|. \end{array} $$

$$ \begin{array}{@{}rcl@{}} |s_{j}| &=& \left|\sum\limits_{k=2}^{n-1}{z_{j}}^{0}(k)+\frac{1}{2}{z_{j}}^{0}(n)\right|. \\ |s_{i} - s_{j}| &=& \left|\sum\limits_{k=2}^{n-1}\left( {z_{i}}^{0}(k) - {z_{j}}^{0}(k)\right) + \frac{1}{2}\left( {z_{i}}^{0}(n) - {z_{j}}^{0}(n)\right)\right|.\\ |S_{i}| &=& \left|\frac{1}{2}z_{i}(1)+\sum\limits_{k=2}^{n-1}{z_{i}}(k)+\frac{1}{2}{z_{i}}(n)\right|. \\ |S_{j}| &=& \left|\frac{1}{2}z_{j}(1)+\sum\limits_{k=2}^{n-1}{z_{j}}(k)+\frac{1}{2}{z_{j}}(n)\right|. \\ \left|S_{i} - S_{j}\right|&=&\left|\frac{1}{2}(z_{i}(1)-z_{j}(1))+\sum\limits_{k=2}^{n-1}\left( z_{i}(k)-z_{j}(k)\right)\right.\\&&\left.\vphantom{{\sum}_{k=2}^{n-1}}+\frac{1}{2}\left( z_{i}(n)-z_{j}(n)\right)\right|." \end{array} $$

Definition 2 (Liu and Xie 54)

“Let Z_i and Z_j be sequences of identical length, and s_i − s_j be as defined in Proposition 5. Then the Grey similitude incidence degree is given by,

$$ \varepsilon_{ij}=\frac{1}{1+\left|s_{i}-s_{j}\right|}." $$

(3)

The similitude degree of Grey incidence measures the geometric similarity of the shapes of the sequences Z_i and Z_j. A greater value of ε_ij indicates a higher similarity of the geometric shapes of Z_i and Z_j and vice-versa

Remark 2

Some properties of the similitude degree are as follows,

• 1. 0 ≤ ε_ij ≤ 1.

• 2. ε_ij is determined by the geometric shape of the sequences Z_i and Z_j and is independent of the relative spatial positions of the sequences. Therefore, any translation of sequences Z_i and Z_j does not affect ε_ij.

• 3. ε_ii = ε_jj = 1, and ε_ij = ε_ji.

Definition 3 (Liu and Xie 54)

“Let Z_i and Z_j be sequences of identical length, and S_i − S_j be as defined in Proposition 5. Then the Grey closeness incidence degree is given by,

$$ \rho_{ij}=\frac{1}{1+\left|S_{i}-S_{j}\right|}." $$

(4)

Closeness degree of Grey incidence measures the spatial closeness of sequences Z_i and Z_j. A greater the value of ρ_ij indicates that the sequences Z_i and Z_j are spatially closer and vice versa.

Remark 3

Some properties of the closeness degree are as follows,

• 1. 0 ≤ ρ_ij ≤ 1.

• 2. The value of ρ_ij depends on both the geometric shapes of the sequences X_i and X_j and their relative spatial positions. Thus, any translation of the sequences will change the value of ρ_ij.

• 3. ρ_ii = ρ_jj = 1, and ρ_ij = ρ_ji.

3.3 Fuzzy simulation

In the proposed approach, the investor provides the expectations on the “ideal” portfolio behaviour. Since the investor expectations will most likely be imprecise and linguistic, we use a credibilistic triangular fuzzy number to capture the expectations in a mathematical form. To apply Grey Incidence Analysis, we need two sequences to calculate the closeness and the similitude degree. The portfolio sequence can be readily constructed using the assets’ historical data and the portfolio’s asset weights. Next, we need the “ideal” sequence, i.e., the sequence that follows the credibility distribution of the triangular fuzzy number given by the investor. The portfolio sequence should emulate the ideal sequence as closely as possible.

3.3.1 Generating sequences of credibilistic triangular fuzzy numbers

Our task is to generate a random sequence of numbers distributed according to a given credibility function (i.e., the given ideal triangular fuzzy number). However, this is not a straightforward process as credibility functions do not obey the laws of probability. Therefore, we use a triangular probability distribution to generate the ideal sequence. In this manner, the shape of the generated sequence will be similar to that of a triangular credibility function (See Fig. 3).

Fig. 3

Comparison of triangular credibility and probability functions

Definition 4

A random variable Y ∈ [a,c] follows triangular distribution if it has the following probability density (P(.)) and cumulative distribution function (F(.)),

$$ \begin{array}{@{}rcl@{}} P(Y=y)&=&\begin{cases} 0, & \text{if } y\leq a, \\ \frac{2(y-a)}{(c-a)(b-a)}, & \text{if } a< y\leq b, \\ \frac{2(c-y)}{(c-a)(c-b)}, & \text{if } b<y\leq c, \\ 0, & y>c. \end{cases},\\ F(Y\leq y)&=&\begin{cases} 0, & \text{if } y\leq a, \\ \frac{(y-a)^{2}}{(c-a)(b-a)}, & \text{if } a< y\leq b, \\ 1-\frac{(c-y)^{2}}{(c-a)(c-b)}, & \text{if } b<y\leq c, \\ 1, & \text{otherwise}, \end{cases} \end{array} $$

(5)

where b is the mode of the distribution.

We summarize the procedure for generating the ideal sequence < I_s >= (i_s(1),i_s(2),…,i_s(L)) for a triangular fuzzy number (a,b,c) in the following steps (L is the historical data length),

• Step 1: For t = 1 to L, do;

• Step 2: Generate r ∈ [0,1] randomly.

• Step 3: If $0\!\leq \! r\!\leq \! \frac {b-a}{c-a}$, then $i_{s}(t) = a+\sqrt {r(c - a)(b - a)}$.

• Step 4: If $\frac {b-a}{c-a}\!\leq \! r\!\leq \! 1$, then $i_{s}(t) = c - \sqrt {(1\! - r)(c\! - a)(c - b)}$.

The basic idea here is to calculate F^− 1(r). The above process is repeated until the sequence’s requisite length has been achieved (i.e., the historical data length).

3.3.2 Generating sequences of credibilistic coherent triangular fuzzy numbers

We need to modify the probability density function of the triangular distribution (see Definition 4) such that it retains the properties of a probability function and has a similar shape, as shown in Fig. 1. The probability density function can be modified as follows,

$$ P_{l}(Y=y)=\begin{cases} 0, & \text{if } y\leq a, \\ \frac{(l+1)(y-a)^{\frac{1}{l}}}{(c+b(l-1)-al)(b-a)^{\frac{1}{l}}}, & \text{if } a\leq y\leq b, \\ \frac{(l+1)(c-y)^{l}}{(c+b(l-1)-al)(c-b)^{l}}, & \text{if } b\leq y\leq c, \\ 0, & y>c. \end{cases} $$

(6)

Proposition 6

The function defined in (6) is a probability density function for all l > 0.

Proof

It is a straightforward exercise to show that ${\int \limits }_{-\infty }^{\infty }P_{l}$ (y)dy = 1∀l > 0. Therefore, we only need to show that c + b(l − 1) − al > 0∀l. Since c > b ⇒ c + b(l − 1) > b + b(l − 1) ⇒ c + b(l − 1) > bl ⇒ c + b(l − 1) > al (since b > a)⇒ c + b(l − 1) − al > 0, and the proof is complete. □

Thus, P_l is a probability density function. The cumulative distribution function of P_l is given by,

$$ F_{l}(Y\!\leq\! y) = \begin{cases} 0, & \text{if } y\leq a, \\ \frac{l(y-a)^{\frac{l+1}{l}}}{(c+b(l-1)-al)(b-a)^{\frac{1}{l}}}, & \text{if } a\leq y\leq b, \\ 1-\frac{(c-y)^{l+1}}{(c+b(l-1)-al)(c-b)^{l}}, & \text{if } b\leq y\leq c, \\ 1, & \text{otherwise}. \end{cases} $$

(7)

Thus, the ideal sequence < I_s,l >= (i_s,l(1),i_s,l(2),…, i_s,l(L)) for the coherent triangular fuzzy number (a,b,c)_l can be generated using the following steps (L is the historical data length),

• Step 1: For t = 1 to L, do;

• Step 2: Generate r ∈ [0,1] randomly.

• Step 3: If $0\leq r\leq \frac {l(b-a)}{c+b(l-1)-al}$, then $i_{s,l}(t)=a+\left (\frac {r(c+b(l-1)-al)(b-a)^{\frac {1}{l}}}{l}\right )^{\frac {l}{l+1}}$.

• Step 4: If $\frac {l(b-a)}{c+b(l-1)-al}\leq r\leq 1$, then i_s,l(t) = c − $((1-r)(c+b(l-1)-al)(c-b)^{l})^{\frac {1}{l+1}}$.

As a check, we plot the frequency distribution of the generated sequence for the triangular fuzzy number (1,2,5), for l = 0.3,2 using the proposed method to verify if the generated sequences are indeed following the required distribution. We have kept the length of the generated sequence sufficiently high to ensure convergence. Figure 4 establishes the validity of the proposed method (see Fig. 1 for a comparison).

Fig. 4

Frequency distribution of the sequences obtained using the proposed method

4 Methodology

4.1 A mathematical formulation of the portfolio optimization model

Suppose that the asset universe comprises N assets (i = 1, 2,…,N). The investor aims to invest the available capital in these assets optimally. Asset returns are modelled using credibilistic triangular fuzzy numbers. We discuss two methodologies for incorporating investor attitude into the model.

• Using standard triangular fuzzy numbers In this method, the pessimistic, optimistic, and neutral investors provide different fuzzy numbers for ideal return, each based on their market assessment. The asset returns are also modelled using standard triangular fuzzy numbers. Suppose that ξ_i = (d_i − δ_i,d_i,d_i + η_i) is the triangular fuzzy number that represents the i^th asset’s return. Let x_i be the proportion of allocation of capital in the i^th asset. The portfolio return is modelled as, ${\sum }_{i=1}^{N}x_{i}\xi _{i}=\left ({\sum }_{i=1}^{N}x_{i}d_{i}-x_{i}\delta _{i},{\sum }_{i=1}^{N}x_{i}d_{i},{\sum }_{i=1}^{N}x_{i}d_{i}+x_{i}\eta _{i}\right )$.

• Using coherent triangular fuzzy numbers If it is not possible to provide different fuzzy numbers for ideal return due to the nature of the historical data (i.e., past performance of the assets), then the coherent triangular fuzzy numbers can be used to provide the ideal return for the optimistic, pessimistic, and the neutral investors. The coherent fuzzy numbers’ adaptive index, l, can be used to incorporate the investor attitude (as explained in Section 3.1). Suppose that $\xi _{i,l}=\left (d_{i}-\delta _{i},d_{i},d_{i}+\eta _{i}\right )_{l}$ is the coherent triangular fuzzy number that represents the return of the i^th asset. By Proposition 1, the portfolio return is modelled as, ${\sum }_{i=1}^{N}x_{i}\xi _{i,l}=\left ({\sum }_{i=1}^{N}x_{i}d_{i}-x_{i}\delta _{i},{\sum }_{i=1}^{N}x_{i}d_{i},{\sum }_{i=1}^{N}x_{i}d_{i}+x_{i}\eta _{i}\right )_{l}$.

Remark 4

We can integrate the investor attitude into the ideal portfolio return by setting appropriate fuzzy numbers. When using coherent fuzzy numbers for ideal return, the adaptive index l is used for investor attitude (an optimistic investor sets 0 < l < 1, a pessimistic investor sets $1<l<\infty$, and a neutral investor sets l = 1). When using standard triangular fuzzy numbers, a typical optimistic investor focused on return maximization will choose a higher fuzzy number with a larger variance. Thus, the generated ideal sequence will also exhibit a larger variance. Therefore, the resulting portfolio will be riskier. On the other hand, a pessimistic investor focused on risk minimization will choose a lower fuzzy number with a smaller variance.

After we get the fuzzy numbers for the ideal return, we use the method described in Section 3.3 to generate the ideal sequence $<I_{s,l}>=\left (i_{s,l}(1),i_{s,l}(2),\ldots ,i_{s,l}(L)\right )$, where L is the length of the available historical data. When using standard triangular fuzzy numbers for modelling, the case of l = 1 will suffice. Therefore, in the sequel, asset returns are modelled using coherent fuzzy numbers. We now formulate the model’s objectives and constraints.

4.1.1 Model objectives

• Portfolio’s expected return This objective maximizes the portfolio’s expected return. It is modelled as follows:

  $$ \begin{array}{@{}rcl@{}} &&\text{Maximize} E\left[\sum\limits_{i=1}^{N}x_{i}\xi_{i,l}\right]\\&&=\sum\limits_{i=1}^{N}x_{i}d_{i}+\frac{1}{2(l+1)}\left( \sum\limits_{i=1}^{N}x_{i}\eta_{i}-l\sum\limits_{i=1}^{N}x_{i}\delta_{i}\right). \end{array} $$

• Weighted Grey closeness and similitude incidence degree This objective minimizes the portfolio’s risk. We use a weighted sum of grey closeness and similitude incidence degree to measure the risk. Suppose that $<I_{s,l}>=\left (i_{s,l}(1),i_{s,l}(2),\ldots ,i_{s,l}(L)\right )$ is the sequence generated from the fuzzy number representing the ideal return, and that $<P_{s}>=\left (p_{s}(1),p_{s}(2),\ldots ,p_{s}(L)\right )$ is the sequence of the portfolio return. As discussed above, the portfolio return is calculated from the historical data of assets and the asset allocations, x_i,i = 1,2,…,N. The Grey closeness incidence degree is calculated from (4) as,

  $$ \rho_{IP}=\frac{1}{1+\left|S_{I}-S_{P}\right|}=\frac{1}{1+\left|\frac{1}{2}(i_{s,l}(1)-p_{s}(1))+{\sum}_{t=2}^{L-1}\left( i_{s,l}(t)-p_{s}(t)\right)+\frac{1}{2}\left( i_{s,l}(L)-p_{s}(L)\right)\right|}, $$

  (8)

  where L is the length of the historical data available. The Grey similitude incidence degree is calculated from (3) as,

  $$ \varepsilon_{IP}=\frac{1}{1+\left|s_{I}-s_{P}\right|}=\frac{1}{1+\left|{\sum}_{t=2}^{L-1}\left( {i_{s,l}}^{0}(t)-{p_{s}}^{0}(t)\right)+\frac{1}{2}\left( {i_{s,l}}^{0}(L)-{p_{s}}^{0}(L)\right)\right|}, $$

  (9)

  where ${i_{s,l}}^{0}(t)=i_{s,l}(t)-i_{s,l}(1)$, ${p_{s}}^{0}(t)=p_{s}(t)-p_{s}(1)$. As discussed before, the portfolio sequence should emulate the ideal sequence as closely as possible. Therefore, the portfolio with a low closeness and similitude incidence degree with the ideal sequence is considered more risky from the investor’s perspective. Thus, the objective to minimize the risk of the portfolio is formulated as

  $$ \text{Maximize} CLSIM=w_{1}\rho_{IP}+w_{2}\varepsilon_{IP}, $$

  where CLSIM is the weighted average of the Grey similitude and closeness incidence degree, and w₁,w₂ are weights representing the relative importance of Grey closeness and similitude incidence degree, respectively.

Remark 5

The concept of maximizing the risk measure may alarm the investors. It is important to note that the proposed risk measure (CLSIM) is different from standard risk measures. Since most risk measures either estimate the volatility of returns or the expected losses, the endeavour to minimize such risk measures is easy to understand. On the other hand, the proposed risk measure estimates the closeness and similarity of the portfolio return and ideal return (i.e., the investor’s target return). A high value of CLSIM indicates that the portfolio return is closer to the ideal return, and thus, is less risky from the investor’s perspective. Therefore, the objective to minimize the risk of the portfolio is to maximize CLSIM in our method.

4.1.2 Model constraints

• Cardinality constraint The investor may require a certain level of diversification in the portfolio. We define a binary variable, y_i,i = 1,2,…,N as

  $$ y_{i}=\begin{cases} 1, & \text{if the $i^{th}$ asset is included in the portfolio,} \\ 0, & \text{otherwise}. \end{cases} $$

  Then the cardinality constraint to ensure at least K assets in the portfolio, is formulated as

  $$ \sum\limits_{i=1}^{N}y_{i}\geq K. $$

  (10)

• Total investment constraint The constraint requires the investment of the entire available capital. Thus, this constraint is formulated as

  $$ \sum\limits_{i=1}^{N}x_{i}=1. $$

  (11)

• Upper bound on investment constraint This constraint places an upper bound, u_i, on the i^th asset’s capital allocation. Then

  $$ x_{i}< y_{i} u_{i} \forall i=1,2,\ldots,N, $$

  (12)

  where y_i is as defined above.

• Lower bound on investment constraint This constraint places a lower bound, l_i, on the i^th asset’s capital allocation. Then

  $$ x_{i}> l_{i}y_{i} \forall i=1,2,\ldots,N, $$

  (13)

  where y_i is as defined above.

• Binary variable constraint y_i can only take values 0 or 1. Thus,

  $$ y_{i}\in \{0,1\} \forall i=1,2,\ldots,N. $$

  (14)

The portfolio optimization model is subsequently formulated as

$$ \begin{array}{@{}rcl@{}} \text{Max} Z_{1}&=&E\left[\sum\limits_{i=1}^{N}x_{i}\xi_{i,l}\right]\\ \text{Max} Z_{2}&=&CLSIM=w_{1}\rho+w_{2}\varepsilon\\ \text{subject to (10)--(14).} \end{array} $$

(M1)

Model (M1) is a multi-objective optimization problem. The next logical step is to devise a method to solve the multi-objective optimization problem. A typical multi-objective optimization problem involves a trade-off between its objectives. Thus, the endeavour to improve one objective’s value may lead to a degradation in other objectives’ values. The primary objective in such a scenario is to find non-dominated solutions.

Definition 5

Suppose that F is the set of all the feasible solutions to a multi-objective programming problem. Let f_j,j = 1,2,…,M, be the objectives. Without loss of generality, assume that f_j is a maximization-type objective for each j = 1,2,…,M. A solution x^∗∈ F is said to be a non-dominated solution to the multi-objective problem if and only if there does not exist any x ∈ F such that,

$$ \begin{array}{@{}rcl@{}} f_{j}(x)&\geq&f_{j}(x^{*}) \forall j=1,2,\ldots,M. j\neq b,\text{ and,} \\ f_{b}(x) &>&f_{b}(x^{*}),\text{ for at least one \textit{b}, }1\leq b\leq M. \end{array} $$

Several literature approaches convert the multi-objective problem to single-objective problem, such as weighted sum and 𝜖-constraint methods. These methodologies guarantee non-dominated solutions to the multi-objective optimization problem under suitable assumptions. We use the 𝜖-constraint method in this paper.

Consider the multi-objective programming problem (MOPP),

$$ \begin{array}{@{}rcl@{}} \text{Minimize } & f_{1}(x) \\ \text{Minimize } & f_{2}(x) \\ {\vdots} & \\ \text{Minimize }& f_{k}(x)\\ \text{subject to }&x\in S, \end{array} $$

where S is the set of feasible solutions of the problem and x ∈ℝⁿ is an n-dimensional vector of decision variables. In the 𝜖-constraint method, a single-objective problem is constructed from the multi-objective problem by treating all but one of the objectives in the constraints. A maximization-type objective is converted to a ≥-type constraint, while the minimization-type objective is converted to a ≤-type constraint. We discuss only the minimization case here, as the maximization-type objective can be converted to a minimization-type by multiplying it with − 1. Typically, the essential objectives are treated in the constraints to control their optimization. Thus the 𝜖-constraint formulation of the MOPP is given by,

$$ \begin{array}{@{}rcl@{}} \text{Minimize } & f_{1}(x) \\ \text{subject to } & f_{2}(x)\leq\epsilon_{2} \\ {\vdots} & \\ & f_{k}(x)\leq\epsilon_{k} \\ & x\in S. \end{array} $$

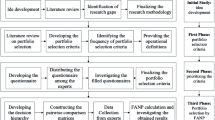
The threshold values for the objectives (i.e., 𝜖_i, i = 2,3, …,k) in the constraints can be calculated by solving the single-objective problem while ignoring the remaining objectives. For our situation, the investor can provide the threshold values for the objectives in the constraints. A flow chart of the proposed method is shown in Fig. 5.

Fig. 5

Flow chart of the proposed solution method

An investor usually has several targets associated with the investments. These targets can easily be expressed in a numerical form (for instance, return expectation, risk tolerance, etc.). The 𝜖-constraint method has the advantage that it can directly incorporate the investor’s goals. Other methods like the weighted sum approach require that the investor specify the relative preferences of the objectives in a numerical form. However, it may not always be possible for the investor to numerically specify the extent to which one objective is preferred over others. No-preference methods are another class of methods for solving a multi-objective optimization problem that do not consider the decision-maker’s preferences. Such methods aim to minimize the distance of the objective function vector from an appropriate reference point. However, it does not fill the bill here as investor preferences play an important role in portfolio optimization. Interactive methods are the most advanced class of methods for solving a multi-objective optimization problem. In such a method, the analyst or an interactive computer program tries to determine the exact preferences of the decision-maker iteratively. First, an initial feasible solution is calculated and presented to the decision-maker. If the decision-maker is satisfied with the solution, the procedure is stopped; otherwise, the process continues until a solution is found that satisfies the decision-maker’s preferences. If we observe Fig. 5, we can immediately deduce that we have used a hybrid of interactive and the 𝜖-constraint method for our problem.

4.2 Solution methodology

We begin this section by illustrating the calculation of CLSIM using an example.

Example 1

Suppose the fuzzy ideal return of an investor is given by, (0.0005,0.0015,0.0035). Suppose the length of the available historical data is 10 (L = 10). Using the method described in Section 3.3, we generate 10 observations based on the credibility distribution of (0.0005, 0.0015,0.0035). Let us assume l = 2.5. Table 2 summarizes the calculations. We have, a = 0.0005,b = 0.0015,c = 0.0035. Thus

$$ \frac{l(b-a)}{c+b(l-1)-al}=0.55556. $$

Consider the first random number in Table 2 (r = 0.56056). Since $r>\frac {l(b-a)}{c+b(l-1)-al}$, we have

$$ \begin{array}{@{}rcl@{}} i_{s,l}(1)&=&c-\left( (1-r)(c+b(l-1)-al)(c-b)^{l}\right)^{\frac{1}{l+1}}\\&=&0.001507. \end{array} $$

The second random number in Table 2 is 0.041383. Since $r<\frac {l(b-a)}{c+b(l-1)-al}$, we have

$$ \begin{array}{@{}rcl@{}} i_{s,l}(2)&=&a+\left( \frac{r(c+b(l-1)-al)(b-a)^{\frac{1}{l}}}{l}\right)^{\frac{l}{l+1}}\\&=&0.000656. \end{array} $$

The rest of the ideal sequence can be generated in an similar manner. Now, let us assume that there are only two assets (A₁ and A₂). We compare the values of CLSIM for three different portfolios, namely, x_A = {0.5,0.5}, x_B = {0.3,0.7}, x_C = {0.8,0.2}. The 10-period historical return data and the return sequence generated by the three portfolios (i.e., the portfolio sequences) have been shown in Table 3. Now that we have the ideal and the portfolio sequences, we can use (8) and (9) to calculate the Grey similitude and closeness incidence degrees. Finally, using w₁ = 0.8, w₂ = 0.2, CLSIM for the three portfolios can be calculated as follows,

$$ \begin{array}{@{}rcl@{}} &&\rho_{IP}(A)=0.972, \varepsilon_{IP}(A)=0.8902,\\&& CLSIM(A) = 0.8*0.972013+0.2*0.890188 = 0.9557, \\ &&\rho_{IP}(B)=0.9749, \varepsilon_{IP}(B)=0.9004,\\&& CLSIM(B)=0.8*0.974921+0.2*0.900437=0.96,\\ &&\rho_{IP}(C)=0.9677, \varepsilon_{IP}(C)=0.8753,\\&& CLSIM(C) = 0.8*0.967683+0.2*0.875245 = 0.9492. \end{array} $$

Therefore, based on CLSIM, we get that x_B > x_A > x_C.

Table 2 Generation of the fuzzy ideal sequence

Table 3 Calculation of the portfolio return sequences

We now describe the method to solve Model (M1) using a genetic algorithm. There are several complexities involved in the proposed approach that render impractical traditional solvers as a solution method. For instance, each iteration requires calculating the Grey closeness and similitude incidence degree between the portfolio and the ideal sequence. The presence of cardinality constraint further exacerbates the complexity of the problem (since the cardinality constraint is an integer valued function). For a problem of higher dimensions (i.e., a large asset universe), obtaining a globally optimal solution becomes a challenge. Therefore, we must forgo the unrealistic expectation of a globally optimal solution and look for alternate solution methodologies to provide an acceptable solution in a reasonable run time.

Genetic algorithms

[55] are a class of metaheuristics for solving optimization problems when traditional methods are impractical. Unlike conventional methods, they simultaneously optimize a population of solutions. Genetic algorithms employ selection, crossover, and mutation operators to explore and exploit the search space for optimal or near-optimal solutions. Genetic algorithms are stochastic, i.e., the rules of transition in the algorithm are dependent upon probabilistic conditions. Observant readers would have guessed by now that the natural process of evolution has inspired the operators and the transition rules of genetic algorithms. The “Survival of the fittest” principle is implemented in genetic algorithms to improve the solutions and weed out unfit solutions iteratively. The fitness of a solution is characterized by its objective function value. In the natural process of evolution, both parents’ fitness characteristics are passed to their offspring, creating even fitter individuals in the process. The selection operator creates a mating pool of solutions, i.e., the set of solutions (parents) that produce the subsequent generation’s solutions (i.e., the solutions for the next iteration). The offspring solutions are created by applying the crossover operator to the parent solutions. The mutation operator involves a random alteration of solutions. The mutation itself is a random walk in the solution space. When occasionally used with crossover and selection, it provides an alternative path to the algorithm if it gets stuck in a locally optimal solution (introducing new solutions in the population). As explained above, the transition rules are probabilistic; thus, a probability condition is associated with each algorithm operator. As with any machine-learning algorithm, we can improve the genetic algorithm’s performance by tuning its parameters (in this case, the crossover and mutation probabilities). Selection and crossover direct the search towards optimal solutions, i.e., these operators exploit the feasible space. However, relying heavily on these operators can lead to a premature convergence (i.e., local optimal solutions). As explained above, mutation aids in exploring the search space, i.e., it provides an alternate route to the algorithm. The trade-off is that the mutation operator slows down convergence. Therefore, one needs to strike a delicate balance between exploitation and exploration operators. This is done by controlling the crossover and mutation probabilities. The size of the population also plays an important role. A large population ensures a sufficient diversity of solutions in the population; however, it increases the algorithm’s runtime. A small population quickens the algorithm’s convergence, but it also risks a locally optimal solution. A trade-off of convergence versus runtime is also involved with the maximum number of generations (iterations). Now, we discuss the operators of a genetic algorithm in detail.

Remark 6

Typically, the solutions are encoded as bit strings in the genetic algorithm. The selection, crossover, and the mutation operator work with an encoding of solutions. It works well for discrete search spaces with countable solutions. In the case of continuous search spaces with uncountable solutions, a lot of bits are required to maintain the requisite precision in the solutions. It hampers the algorithm’s performance. We avoid encoding the solutions and use them directly to overcome this disadvantage (i.e., a real-coded genetic algorithm). The operators described in the sequel apply to a real-coded genetic algorithm only.

• Selection As explained above, the selection operator is used to create a mating pool of solutions (the set of solutions (parents) used to develop the next generation’s solutions). To emulate natural selection, we introduce a bias towards fitter parent solutions. We employ the roulette wheel selection. Each parent receives a slot on the roulette wheel relative to its fitness. Thus, the selection becomes biased towards parents with a higher fitness value. In this manner, the parent solutions are selected to produce the subsequent generation’s solutions (i.e., offspring). The procedure is implemented in the following steps

  • Step 1: Make the fitness value of each solution in the population positive. To achieve this, determine the population’s minimum fitness value. Deduct this value from every solution’s fitness value.

  • Step 2: Evaluate the population’s average fitness, f_av $=\frac {{\sum }_{i}fitness_i}{POP}$. Here fitness_i is the objective value (fitness value) of the i^th solution and POP is the size of the population.

  • Step 3: Calculate the expected copies, $ex\_cpy_i = \frac {fitness_i}{f\_av}$, of each solution.

  • Step 4: Round ex_cpy to the nearest integer. It is the number of copies of the i^th solution in the mating pool.

• Crossover Various literature implementations of the crossover operators are available, viz. flat crossover, BLX-α crossover, Fuzzy connectives-based crossover (FCB), simple crossover. The crossover operator is applied to the selected solutions in the mating pool to produce the subsequent generation’s solutions. In this paper, the simulated binary crossover (SBX) [56, 57] is used. It works well for multi-modal problems. We first determine a spread factor as follows

  $$ \begin{array}{@{}rcl@{}} \zeta &=& \left|\frac{ch_{1}-ch_{2}}{pr_{1}-pr_{2}}\right|, \end{array} $$

  where pr₁,pr₂ are the solutions of the previous generation (parents), and ch₁,ch₂ are the offspring solutions of the current generation. Then, the probability of producing offspring solutions with a particular ζ is evaluated. It obtained as follows

  $$ \begin{array}{@{}rcl@{}} P(\zeta) &=& \begin{cases} 0.5(r+1)\zeta^{m}, & \text{if } \zeta\leq 1 ,\\ 0.5(r+1)\frac{1}{\zeta^{m+2}}, & \text{otherwise}, \end{cases} \end{array} $$

  where m ≥ 0, m ∈ℝ. If the magnitude of m is small, the obtained offspring solutions are far away from the parents. If the magnitude of m is large, it leads to the offspring solutions that are closer to the parent solutions. The implementation of creating offspring solutions in a particular range, say, ch_L ≤ ch ≤ ch_U, is as follows:

  • Step 1: Obtain the following:

    $$ \begin{array}{cc} \zeta_{L} = \frac{pr_{1}+pr_{2}-2ch_{L}}{\left|pr_{2}-pr_{1}\right|},& \zeta_{U} = \frac{2ch_{U}-pr_{1}-pr_{2}}{\left|pr_{2}-pr_{1}\right|}. \end{array} $$

  • Step 2: Evaluate the following probabilities,

    $$ \begin{array}{cc} P_{1}^{\prime} = {\int}_{0}^{\zeta_{L}}P(\zeta) d\zeta, &P_{2}^{\prime} = {\int}_{0}^{\zeta_{U}}P(\zeta)d\zeta. \end{array} $$

  • Step 3: Obtain u ∈ [0,1], where u is a random number.

  • Step 4: Obtain $\zeta _1^{\prime }$ and $\zeta _2^{\prime }$ for which,

    $$ \begin{array}{cc} \frac{{\int}_{0}^{\zeta_{1}^{\prime}}P(\zeta) d\zeta}{P_{1}^{\prime}}=u,&\frac{{\int}_{0}^{\zeta_{2}^{\prime}}P(\zeta) d\zeta}{P_{2}^{\prime}}=u. \end{array} $$

  • Step 5: Finally, the offspring solutions are obtained as follows,

    $$ \begin{array}{@{}rcl@{}} ch_{1} &=& 0.5\left[\left( pr_{1}+pr_{2}\right)-\zeta_{1}^{\prime}\left|pr_{2}-pr_{1}\right|\right], \\ ch_{2} &=& 0.5\left[\left( pr_{1}+pr_{2}\right)+\zeta_{2}^{\prime}\left|pr_{2}-pr_{1}\right|\right]. \end{array} $$

• Mutation There are various mutation operator implementations, viz. non-uniform mutation, Mühlenbein’s mutation, real number creep, etc. If only the crossover operator is present in the algorithm, the solutions will become identical after a specific number of iterations (generations). Thus, the algorithm may get stuck in a locally optimal solution. Mutation provides an alternate path to the algorithm by randomly introducing new solutions in the population. The paper uses the non-uniform mutation operator (Michalewicz [58]). Let y ∈ [lb,ub] be a solution, CG be the current generation, and mut_y be the mutated solution. Then

  $$ mut\_y = \begin{cases} y+g(CG,ub-y), & \text{if } RAND=0, \\ y-g(CG,y-lb), & \text{if }RAND=1, \end{cases} $$

  where RAND is chosen at random from the set {0,1}, and

  $$ g(z,r) = r\left( 1-b^{\left( 1-\frac{z}{MG}\right)^{F} }\right), $$

  where b ∈ℝ,0 ≤ b ≤ 1, is chosen at random, MG is the maximum number of generations, and F is a user-specified parameter, which sets the level of dependency on the number of generations. The function is defined such mut_y is distant from y in the initial generations to encourage exploration, while in the later generations, mut_y comes closer to y for convergence.

• Elitism Elitism operator stores the solutions with the best objective value so that they are preserved during the search

• Constraint handling To dissuade the search from exploring an infeasible region, the objective function is penalized for any constraint violations. The penalty is usually levied in proportion to the extent of the constraint violation. A static penalty function, which remains constant during the entire search process, is used in this paper.

Before closing this section, let us discuss the computational complexity of the proposed genetic algorithm. The computations can be broadly classified into three categories,

• 1. Evaluation of the objective function along with the penalties.

• 2. Applying the roulette wheel selection, SBX crossover, and the non-uniform mutation operator.

• 3. Sorting the solutions according to objective function values for the elitism operator.

The above computations are performed in each generation. Thus, if N is the number of assets (i.e., problem dimension), POP is the population size, MG is the maximum number of generations, and L is the length of the historical data, then the worst case time complexity of each step is given by

• 1. $O\left (MG\times N\times POP\right )$ (for evaluating the return)+O (MG × N × POP × L) (for evaluating the risk)= O(MG × N × POP × L).

• 2. O(MG × N × POP) + O(MG × N × POP) + O(MG × N × POP) = O(MG × N × POP) (for selection, mutation, and crossover).

• 3. O(MG × POPlog(POP)).

Thus, the worst case time complexity of the algorithm is given by O(MG × N × POP × L) + O(MG × POPlog (POP)) < O(MG × N × POP × L) + O(MG × POP²) = O(MG × POP(N × L + POP)) = O(MG × POP × X), where X = N × L + POP. Therefore, the worst-case time complexity of the algorithm is bounded by a polynomial.

5 Numerical experiments

We illustrate the proposed method on a case study of 100-asset of the U.S. stock market’s NASDAQ-100 index. The portfolio sequence is constructed using each asset’s daily return data from 1^st January 2016 to 31^st December 2019 (1004 observations). The asset returns have been modelled as coherent fuzzy numbers. See Appendix C for a method on fuzzy number construction. We demonstrate both methods discussed in Section 4.1. Standard fuzzy numbers can be handled by using the coherent fuzzy numbers with l = 1. The fuzzy return data for each asset is shown in Table 4.

Table 4 Fuzzy return data of the assets (all figures in percentages)

5.1 Solving the model

5.1.1 Using standard fuzzy numbers for the ideal return

As discussed in Section 4.1, the optimistic, pessimistic, and neutral investors provide different fuzzy numbers, conveying their respective perceptions of the ideal return. The ideal sequence is generated based on these fuzzy numbers (Table 5). The investor preferences for the ideal return, bounds, cardinality constraint, and the remaining model parameters have been summarized in Tables 6 and 7. The fuzzy numbers and the ideal return in Tables 4 and 6 are in terms of percentages. The optimistic investor considers higher returns ideal and does not bother about the extra risks (increased variance of the subsequent ideal return sequence). On the contrary, the primary objective of the pessimistic investor is risk minimization. Thus, the pessimistic investor settles for a low positive return. We have kept the remaining model parameters identical for each investor. Since we have chosen w₁,w₂ so that w₁ + w₂ = 1, by definition of CLSIM, we have 0 ≤ CLSIM ≤ 1. Thus, the investors want at least a 75% resemblance to the ideal return (Table 7). It is reasonable to place relatively more importance on the closeness degree (i.e., w₁ > w₂) because the spatial closeness of the portfolio return to the ideal return is more important to the investor than the shape similarity. We generate the ideal sequences based on the fuzzy numbers and solve different portfolio optimization problems (Section 4.2). Example 1 illustrates the procedure to calculate the ideal and the portfolio return sequences. We solve an 𝜖-constraint formulation of Model (M1) with the expected return from the portfolio as the objective and treat CLSIM as a constraint in the single-objective problem. We chose the genetic algorithm parameters shown in Table 5 after extensive experimentation (parameter tuning). As discussed in Section 4.2, the metaheuristic algorithms like genetic algorithms cannot find globally optimum solutions. They optimize a population of solutions simultaneously and use operators to arrive at good solutions in a reasonable run time. The performance of a genetic algorithm is influenced by the parameter setting of the algorithm (probabilities of crossover and mutation, population size, etc.). Theoretically, a universal combination of parameters that works for each problem does not exist, just as there is no single genetic algorithm for every problem (although some general guidelines are available for a good parameter setting). After testing several combinations of parameters for stability and consistency of solutions, it is usually obtained by trial and error. It is beyond the scope of this text to present the results of all the experiments. The optimal allocations for each type of investor have been shown in Table 8. Since the threshold value for CLSIM is the same for each investor, optimistic investors expect the highest return. However, it also entails larger risks as the portfolio sequence of the optimistic investor is similar to the portfolio sequence of a higher variance (i.e., the sequence generated by the fuzzy number (0.1,0.2,0.5)). How this strategy pans out in the real world is another matter entirely. We will take up this discussion during the out-of-sample analysis.

Table 5 Ideal return for different types of investors

Table 6 Parameters for the 𝜖-constraint formulation of Model M1 (Section 5.1.1)

Table 7 Parameter setting of the genetic algorithm

Table 8 Optimal asset allocations (Section 5.1.1)

Remark 7

As explained in Section 1, the ideal return is the target return that the investor aims to achieve with the portfolio (expressed as a fuzzy number). Careful consideration must be given in selecting the ideal return. The investors can consult experts or set the ideal return based on the assets’ historical performance. Setting an unrealistically high ideal return will only result in infeasible solutions. The bound constraints have been added to avoid unrealistic asset allocations in the final solution (10^− 3 or lesser). The cardinality constraint ensures the investors’ desired level of diversification. A pessimistic or conservative investor may want investments in many assets so that profits could offset losses in other assets. An optimistic investor focused on return maximization may not bother about too much diversification. Here, the experience of the investor or expert plays an important role. The threshold value of CLSIM indicates the level of similarity between the ideal return and the investors’ desired portfolio return. A pessimistic or conservative investor may want a very high level of similarity, but this may result in infeasible solutions. In such a scenario, the investor can adjust the preferences (see Fig. 5) until a suitable solution is found.

5.1.2 Using coherent fuzzy numbers for the ideal return

Suppose the evidence from the historical asset data is such that using different fuzzy numbers for the ideal return is not practical. In that case, the same fuzzy number can be used as the ideal return for each investor type. We introduce the investor attitude in the model using the adaptive index, l, of the coherent fuzzy numbers (Section 3.1). For a fair comparison, the remaining model parameters (Table 9) have been kept identical as in Section 5.1.1. The genetic algorithm parameters are also the same as in Table 5. The optimal asset allocations are shown in Table 10. The expected return is highest for the optimistic investor in this case as well. The difference in the expected return from Section 5.1.1 is due to the modelling of investor attitude. We have chosen l = 0.5 for an optimistic investor; any value of l < 1 would suffice for an optimistic investor. The same is the case for a pessimistic investor. Any value of l > 1 can be used for a pessimistic investor. The magnitude of l only indicates the extent of pessimism or optimism (although, for an optimistic investor, the value l works in an opposite sense, i.e., as $l\rightarrow 0$, the optimism increases). We have demonstrated this concept visually in Fig. 2 for a better understanding.

Remark 8

Observing Tables 7 and 9, it may seem unusual that we have chosen identical model parameters for each type of investor (optimistic, pessimistic, and neutral). This has been done deliberately to demonstrate the accuracy of the proposed method of modelling investor attitude using CLSIM and the fuzzy ideal return.

Table 9 Parameters for the 𝜖-constraint formulation of Model M1 (Section 5.1.2)

Table 10 Optimal asset allocations (Section 5.1.2)

5.2 Out-of-sample analysis

This section is dedicated to the optimal portfolios’ out-of-sample performance (Sections 5.1.1 and 5.1.2). We assume that $1 is allocated to the obtained portfolios on January 1^st, 2020, and track the accumulated wealth till December 31^st, 2020. No additional investment is made during this period. Figures 6 and 7 illustrate the accumulated wealth of the obtained portfolios of Sections 5.1.1 and 5.1.2. We have also compared the out-of-sample performance with Markowitz’s [1] mean-variance (M-V) model and Speranza’s [2] mean-MASD model. For a fair comparison, we have imposed the cardinality and the bound constraints in both models. It can be observed that the COVID-19 pandemic significantly affected the portfolios’ performance during the period March-April 2020. Post that, the portfolios make a significant recovery even when no changes were made in the asset allocations. It can be observed from both Figs. 6 and 7 that the pessimistic portfolio can minimize extreme losses during crisis periods. This behaviour is compatible with the pessimistic investor, whose primary objective is risk minimization. In contrast, the optimistic portfolio suffers from severe losses and lags behind the other portfolios during this period. The M-V model and the Mean-MASD model also exhibit poor performance during this period. During the period of the recovery of the stock market (July 2020 onwards), the optimistic portfolio shows a dramatic surge and overtakes all the other portfolios. This illustrates the importance of recognizing the bull and bear stock market trends. Adopting an aggressive trading strategy during periods of stock market crisis can lead to significant losses. When the stock market is on an upward trend, the pessimistic portfolio lags behind the other portfolios because of the pessimistic investors’ conservative attitude. Adopting a conservative attitude when the stock market is in a bullish trend leads to lost opportunities. This also illustrates the criticality of an accurate stock market assessment. From Figs. 6 and 7, we can observe that the pessimistic portfolio performs worse than even the M-V and Mean-MASD portfolios, while the neutral portfolio exhibits near-similar performance. This demonstrates that both of the proposed methods to model the investor attitude are effective and accurate.

Fig. 6

Wealth accumulated by the obtained portfolios (Section 5.1.1)

Fig. 7

Wealth accumulated by the obtained portfolios (Section 5.1.2)

The sample statistics of the optimal portfolios’ out-of-sample performance (Sections 5.1.1 and 5.1.2) are shown in Tables 11 and 12. Apart from the usual statistics, we have also shown two performance indicators: the Sharpe ratio and the Sortino ratio. Sharpe ratio [59], also known as a reward to variability is defined as

$$ \text{Sharpe ratio}=\frac{r_{p}-r_{F}}{\sigma_{p}}, $$

where r_p is the portfolio return, r_F is the risk-free return, and σ_p is the standard deviation of the portfolio return. Sortino ratio [60], a natural extension of the Sharpe ratio, is defined as

$$ \text{Sortino ratio}=\frac{r_{p}-r_{T}}{\sigma_{D}}, $$

where r_p is the portfolio return, r_T is the target return of the investor, and σ_D is defined as

$$ \sigma_{D}=\sqrt{\sum\limits_{i=1}^{T}\frac{\left( \min\{r_{i}-r_{T},0\}\right)^{2}}{T}}, $$

where T is the number of observations, r_i is the realized return of the i^th day. This paper uses U.S. treasury bond futures as a risk-free asset. Each investor’s target return is the expected value of the fuzzy ideal return (Tables 11 and 12). The optimistic portfolio has the best overall performance during the out-of-sample period. Out of the three different kinds of investor attitudes, the pessimistic portfolio exhibits the least standard deviation during the out-of-sample period. In Table 11, the pessimistic portfolio’s standard deviation is less than even the naïve portfolio, with the maximum systematic risk diversification. This is in line with the pessimistic investors’ focus on risk minimization. The optimistic portfolio has the best overall reward to variability, as indicated by the Sharpe ratio. Since the Sortino ratio is dependent on the target return, the optimistic portfolio has a lesser value of the Sortino ratio (Table 11). The optimistic portfolio’s target return is very high, while the target return for the pessimistic portfolio is low. All the portfolios exhibit a slight negative skewness. This could be due to the significant losses incurred during the slowdown during the March-April period (effects of COVID-19). The kurtosis for the optimistic portfolio is only slightly higher than 3. This indicates that the out-of-sample returns were relatively stable around the expected return. This is in contrast with other portfolios, which exhibit a large kurtosis. This shows that these portfolios were more volatile during the out-of-sample period. Thus, the optimistic portfolio outperforms the rest of the portfolios in this aspect as well.

Table 11 Sample statistics of the optimal portfolios’ daily out-of-sample return(Section 5.1.1)

Table 12 Sample statistics of the optimal portfolios’ daily out-of-sample return (Section 5.1.2)

5.3 A case study of the Indian stock market

This section applies the proposed method to a case study involving 50 assets listed in the Indian stock market’s NIFTY-50 index. This section uses a 4-year historical return data of assets beginning from 1^st January 2016 to 31^st December 2019. Table 13 provides the fuzzy data of the assets. We will use the adaptive index, l, to incorporate the investor attitude into the model. Table 14 provides the model parameters. In this study, let us focus on achieving closeness to the ideal return. Therefore, we have chosen w₁ = 1,w₂ = 0, and CLSIM ≥ 0.95. Next, we solve the model to obtain the optimal asset allocations for each investor. Table 15 provides the optimal asset allocations. We can observe that the optimistic investor expects the highest return, while the pessimistic investor expects the lowest return. Now, let us focus on the out-of-sample performance. As in Section 5.2, we assume that the capital of INR 1 (Indian National Rupee) is invested on 1^st January 2020. We track the out-of-sample performance for one year (till 31^st December 2020). Figure 8 traces the movements of all the portfolios during the out-of-sample period. One can immediately observe the impact of COVID-19 on all the portfolios. The risk-seeking optimistic investor faces heavy losses during this period. However, the pessimistic portfolio minimizes the losses and grows steadily throughout the year. The standard deviation of returns for the pessimistic portfolio is also the lowest except for the naïve and NIFTY-50 portfolios. This is consistent with the risk-averse attitude of the pessimistic investor. At the latter end of 2020, when the stock market undergoes a recovery (post-COVID-19), we observe that the optimistic portfolio shows a dramatic surge and overtakes all the other portfolios. This shows that the proposed method consistently captures the investor attitude. The optimistic and the pessimistic portfolios significantly outperform the M-V and the Mean-MASD portfolios as well. Table 16 records the sample statistics of each portfolio during the out-of-sample period. Each portfolio exhibits a negative skewness due to the extreme losses during the crisis period of COVID-19. All the portfolios are highly leptokurtic, which is again the consequence of a higher frequency of extreme returns. This also establishes that each portfolio exhibited a non-normal return during the out-of-sample period. The optimistic and the pessimistic portfolios have the lowest kurtosis, demonstrating that the returns were relatively more stable around the mean than the rest of the portfolios.

Table 13 Fuzzy returns of the assets (Section 5.3)

Table 14 Parameters for the 𝜖-constraint formulation of Model M1 (Section 5.3)

Table 15 Optimal asset allocations (Section 5.3)

Fig. 8

Wealth accumulated by the obtained portfolios (Section 5.3)

Table 16 Sample statistics of the optimal portfolios’ daily out-of-sample return (Section 5.3)

5.4 Managerial implication

We demonstrated the effectiveness and accuracy of the proposed approach by the case studies of Section 5. It is the reason most of the model parameters were kept identical so that impact of modelling the risk and the investor attitude using CLSIM and fuzzy ideal return could be studied (see Remark 8). This section discusses implementing results and conclusions derived in the previous sections in real-life scenarios. The construction of fuzzy asset returns using expert opinion or historical data is straightforward. The method of constructing fuzzy numbers for asset return is described in Appendix C. The next step is to set the ideal return. There is no specific procedure for establishing the ideal return. It depends on the assessment of the investor (whether optimistic, pessimistic, or neutral) based on the historical performance of the assets and the current situation prevailing in the stock market. Using experts’ help is also a good option. We have provided only some general guidelines on setting the investor attitude (using either of the two methodologies described in Section 4.1). The extent of optimism or pessimism depends on the subjective assessment of the investor. In practice, the investor needs to adjust the attitude in response to changing market conditions (either by changing the ideal return or the adaptive index, l). The portfolio also needs to be rebalanced accordingly as new asset information and return data become available. Incorrect assessment of the overall stock market prospects can lead to losses (as illustrated in Figs. 6 and 7). Asset returns are volatile and subject to various random and non-random factors. A universal parameter setting optimal for all problems and time frames does not exist. We cannot provide a theoretical justification for the chosen parameter setting. No study in portfolio optimization can claim that it has developed a model that provides optimal results in all scenarios. It all depends on the skill and experience of the investor. The investor needs to readjust and recalibrate the portfolios in the wake of changing market conditions. Our model provides a mathematical framework for an investor’s subjective and linguistic assessments. Using a numerical study, we have established the model’s accuracy in capturing diverse investor attitudes. The next step is to determine the optimal portfolio weights. Since our method is based on optimization techniques, a discussion of the advantages of optimizing the portfolio is warranted here. Many authors have commented on this subject. Michaud [10] showed that optimizing the portfolio weights multiplies the estimation error of the model parameters. However, Jagannathan and Ma [61] showed that imposing certain constraints (such as the bound constraints) alleviates this problem. Optimizing the portfolio provides an excellent initial recommendation to the investor on the capital allocation based on the natural assumption that assets that have performed well in the past will continue to do so in the future. Some critics also claim that risky assets become less risky if the investments are held for a long time. While this is true in general, it requires a lot of patience and discipline from the investor. Interim losses can trigger irrational or impulsive decisions. Another criticism is that the naïve portfolio performs just as well, if not better than the optimized portfolio. This claim has been proven false in our case study. Each portfolio performs significantly better than the naïve portfolio and the NASDAQ-100 index (the portfolio based on market capitalization). This was observed when there is no rebalancing of the portfolios in response to market conditions. Even the mean-variance (M-V) and the Mean-MASD portfolio outperform the naïve portfolio. Thus, we can conclude that optimization is crucial in the portfolio selection process.

6 Conclusion

Various authors have studied numerous approaches to portfolio optimization, each with its unique perspective. This paper attempts to integrate two techniques of modelling the stock market’s uncertainty and the investor’s imprecise preferences (namely, Fuzzy set theory and Grey Relational Analysis). We use Grey Relational Analysis to model a new measure of risk based on the investor’s subjective requirements. We also incorporate the investor attitude in the model using Fuzzy set theory. We provide a method to simulate coherent triangular fuzzy numbers by modifying the triangular probability distribution. A genetic algorithm is used to solve the resulting optimization model. Numerical examples have been provided to illustrate the proposed method. We tested the real-world performance of the model by conducting an out-of-sample analysis. The obtained results prove the validity of the proposed approach. The proposed method accurately captures the optimistic and pessimistic behaviour of the investors (See Sections 5.2 and 5.3). We can observe from Figs. 6, 7, and 8 that the pessimistic portfolio can minimize heavy losses during periods of recession (i.e., COVID-19). We can also observe that the optimistic portfolio makes above-average gains when the stock market is bullish. The proposed approach also outperforms several competing portfolios such as the naïve, the NIFTY-50, the M-V, and the Mean-MASD portfolios. The conclusion drawn is that the proposed approach effectively captures different investor behaviours observed in the stock market. The main limitation of the study is the heavy dependence on human input. It requires an accurate assessment of the prevailing stock market conditions. As observed in Sections 5.2 and 5.3, an incorrect stock market assessment can lead to underperformance. Therefore, our model cannot be used by novice investors. Our study also does not consider other realistic aspects of the stock market, such as dividends and transaction costs. The accrued wealth shown in Sections 5.2 and 5.3 assumes that all the assets held in the portfolio are liquid and can be quickly sold or bought. Sometimes, it is not easy to sell a particular asset. Therefore, we should consider the liquidity of assets in the portfolio optimization model. The proposed model is difficult to solve using traditional approaches. In non-traditional approaches such as genetic algorithms, the parameter setting influences the performance. Therefore, we need to test the algorithm for several parameter settings before arriving at a stable and consistent solution.

For further research, there can be various extensions of this paper. A multi-period problem with transaction costs can be considered, which would further add another dimension of reality. We can modify the Grey closeness incidence degree to consider only the downside deviations from the ideal return. We can also consider investor attitudes regarding each asset rather than the stock market as a whole.

Appendices

Appendix A: Credibility theory

Refer [62] for a detailed explanation of Credibility theory. To summarize, credibility theory is defined as “the study of fuzzy events in which a credibility measure determines the chances of a fuzzy event occurrence”. Let Θ be a set with at least one element, and U be the set containing all the subsets of Θ. A set function from U to [0,1] is called a credibility measure. Each member of U is called an event. The chance of occurrence of an event E in U is indicated by its credibility. A credibility measure satisfies the following four axioms (See Li and Liu [34]),

• Normality

• Monotonicity

• Duality

• Maximality

Definition 6

“Let Θ be a non-empty set, U be its power set, and Cr is a credibility measure. Then the triplet (Θ,U,Cr) is called a credibility space.”

Definition 7

[62] “A fuzzy variable ξ is a function from a credibility space (Θ,U,Cr) to the set of real numbers ℝ.”

Definition 8

“Let ξ be a fuzzy variable defined on the credibility space (Θ,U,Cr). Then, its credibility function v is given by: v(x) = Cr{ξ = x}, ∀x ∈ℝ.”

Definition 9

“The following credibility function defines a triangular fuzzy number, ξ = (d − δ,d,d + η),

$$ \begin{array}{@{}rcl@{}} v(x) &=& \begin{cases} \frac{x-d+\delta}{2\delta}, & \text{if } d-\delta \leq x \leq d, \\ \frac{d+\eta-x}{2\eta}, & \text{if } d\leq x \leq d+\eta, \\ 0, & \text{otherwise}, \end{cases} \end{array} $$

where d is the core value of the fuzzy number and δ > 0, η > 0 are the left and right spreads, respectively (See Fig. 9).”

Fig. 9

Triangular fuzzy number’s credibility distribution

Definition 10

“Fuzzy variables ξ₁,ξ₂,...,ξ_n are said to be independent if and only if $v(x_1,x_2,...,x_n) = \underset {1\leq i \leq n}{min} v(x_i)$ for all (x₁,x₂,...,x_n) ∈ℝⁿ.”

Proposition 7

[62] “Let ξ₁ = (d₁ − δ₁,d₁,a₁ + η₁) and ξ₂ = (d₂ − δ₂,d₂,d₂ + η₂) be two independent triangular fuzzy numbers with credibility functions v₁ and v₂, respectively. Then, for any λ₁ > 0, λ₂ > 0, we have

$$ \begin{array}{@{}rcl@{}} \lambda_{1}\xi_{1}+\lambda_{2}\xi_{2} &=& ((\lambda_{1}d_{1}+\lambda_{2}d_{2})-(\lambda_{1}\delta_{1}+\lambda_{2}\delta_{2}),\\&&(\lambda_{1}d_{1}+\lambda_{2}d_{2}),(\lambda_{1}d_{1}+\lambda_{2}d_{2})\\&&+(\lambda_{1}\eta_{1}+\lambda_{2}\eta_{2}))." \end{array} $$

Definition 11

“(Credibilistic expectation of a fuzzy variable) Let ξ be a fuzzy variable on a credibility space (Θ,U,Cr). Then its expected value is defined by (Liu and Liu [35])

$$ \begin{array}{@{}rcl@{}} E[\xi] &=& {\int}_{0}^{+\infty}Cr\{\xi\geq r\}dr - {\int}_{-\infty}^{0}Cr\{\xi\leq r\}dr, \end{array} $$

provided that at least one of the two integrals is finite.”

Appendix B: Grey Incidence Analysis

A brief introduction to Grey Incidence Analysis has already been provided in Section 2. Refer to [8] for a detailed explanation of this topic.

Definition 12 (8)

“Assume that X_i is a system factor and its observation value at the ordinal position k is x_i(k), k = 1,2,…,n, then X_i = (x_i(1),x_i(2),…,x_i(n)) is referred as the behavioural sequence of the factor X_i.”

Remark 9

If k stands for the time order, then x_i(k) is referred to as the observational value of factor X_i at time moment k, and X_i = (x_i(1),x_i(2),…,x_i(n)) is the behavioural time sequence of X_i.

Definition 13 (8)

“Assume that X is a data sequence of a system’s behaviour, D is an operator to work on X, and after being applied by the operator D, X becomes the following sequence:

$$ XD=(x(1)d, x(2)d, \ldots, x(n)d), $$

then D is referred as the sequence operator.”

Definition 14 (8)

“Let X_i = (x_i(1),x_i(2),…,x_i(n)) be a data sequence of a system’s behaviour, and D be the sequence operator which satisfies X_iD = (x_i(1)d,x_i(2)d,…,x_i(n)d), and x_i(k)d = x_i(k) − x_i(1),k = 1,2,…,n. Then, D is referred to as the zero-starting point operator, and X_iD is the image of X_i. X_iD is often written as X_iD = X_i⁰ = (x_i⁰(1),x_i⁰(2),…,x_i⁰(n)).”

Appendix C: Construction of fuzzy numbers for asset returns using historical data

In this section, we illustrate the method to construct the fuzzy numbers for the asset return. We determine the fuzzy number that represents AAPL’s returns (Table 4). We create frequency distribution of the return as shown in Table 17. The least return class observed during the estimation period was (− 10%) − (− 9%). Therefore, the average return of this class (− 9.9607) becomes the left endpoint (i.e., d − δ = − 9.9607). Similarly, the highest return class observed during the estimation period was (7%) − (8%). Therefore, the average return of this class (7.0422) becomes the right endpoint (i.e., d + η = 7.0422). For constructing the core of the triangular fuzzy number, we have used a weighted average of the average return of the four classes with the highest frequency. This is worked out to be 0.1412. Thus, (− 9.9607,0.1412,7.0422) represents the return of AAPL. The fuzzy numbers of the returns of the remaining assets can be constructed in a similar manner.

Table 17 Frequency distribution of AAPL’s returns