1 Introduction

In today’s highly competitive manufacturing environment, product demand forecasting plays a critical role in the effective management of inventories. Companies that can accurately forecast market demand can take action to ensure that they hold the correct stocks to maximise sales and profit. Demand forecasting refers to the process of making estimations about future customer demand over a defined period using historical demand data and other external factors [1]. Efficient and accurate forecasting of demand enables supply chain managers to make intelligent decisions about various aspects of their business. It helps them judge their business potential in the current scenario, optimise inventory, improve inventory turnover rates and decrease holding costs. Estimating future demand beforehand helps to identify possible upcoming difficulties and take steps to correct them such as increasing the number of workers during high sales periods. It allows companies to plan their future goals in a better way [2]. Hence, finding efficient and effective product demand forecasting methods is highly important right now. With better data acquisition and storage tools, a huge amount of historical sales data is available in all fields. Data mining approaches are needed to model and make sense of this data to make accurate future predictions about product demand.

Neural network models have been effectively used to capture and model non-linearity in product demand forecasting in the past. However, traditional backpropagated neural networks suffer from several drawbacks like slow computational speed, over-fitting, etc. ELMs have been shown to be more advantageous in efficiency and generalization performance over traditional FNN algorithms on a wide range of benchmark problems from different fields [3, 4]. Moreover, ELMs have also been shown to have universal approximation capabilities [5]. In this work, a novel approach to product demand forecasting - a hybrid extreme learning machine (ELM) model with Harris Hawks optimisation (HHO) algorithm is proposed. The proposed methodology retains the fast computational speed of ELMs while enhancing their ability to correctly predict product demands. The prediction capabilities of ELM are enhanced by auto-tuning its hyper-parameters (number of hidden nodes, number of lags in input data, weights and biases of the hidden layer and the type of activation function) by the HHO algorithm. The superiority of the ELM-HHO approach was tested in comparison with traditional ELM and ELM-Bayesian Optimisation (ELM-BO) approaches. The ELM-HHO algorithm was also compared with GRU, LSTM and ARIMA models commonly used in industry to forecast product demand. Different performance metrics, i.e., Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE) and Mean Percentage Error (MPE) were used for model comparison. Moreover, horizon forecasting at 3 days ahead and 7 days ahead was performed to test how the ELM-HHO approach can be applied in real-time to predict future demand from the previous week’s sales data. The findings indicated that the suggested model outperformed the traditional product demand prediction models in terms of prediction accuracy, making it a strong candidate for real-time product demand forecasting applications. To our knowledge, this is the first time extreme learning machine models optimised by Harris Hawks optimiser have been applied to product demand forecasting contexts. The novelty lies in the way the ELM and HHO approaches have been combined to ensure highly accurate product demand forecasting. Also, an increased number of hyperparameters are being optimised compared to traditional approaches to improve accuracy.

To reiterate, the main contributions of this paper involve :

  1. 1.

    Proposing a novel hybrid ELM optimised by HHO algorithm to perform product demand forecasting.

  2. 2.

    Optimising an increased number of hyperparameters in ELM to improve accuracy.

  3. 3.

    Combining the fast computational speed of ELMs with the accuracy gained by optimisation using HHO.

  4. 4.

    Showing that the ELM-HHO model has superior performance to state-of-the-art models used in the industry like ELM, ELM-BO, LSTM, GRU and ARIMA models considering RMSE of forecasting.

  5. 5.

    Performing horizon forecasting at 3 days ahead and 7 days ahead with good accuracy which confirms that our approach is useful for the industry.

Future avenues of research lie in trying to improve the optimisation part by exploring multi-objective optimisation or trying out newer optimization algorithms like that mentioned in [6]. Multi-variate demand forecasting can also be performed in cases where inputs other than historical sales data are available. Auto-encoders for automatic relevant feature extraction from input time series can be investigated.

The rest of the paper is organised as follows. Section 2 discusses the research background, related works and research gaps in the product demand forecasting area. Section 3 provides a brief introduction to some preliminaries required to understand the proposed model. Section 4 presents the proposed ELM-HHO approach. Section 5 describes the historical dataset used, the experimental setup, experimental results of the proposed model and comparison with the ARIMA, GRU, LSTM, ELM and ELM-BO approaches. Finally, in Section 6, the paper is concluded and future work is outlined.

2 Literature review

Supply chain management is the management of the flow of goods and services and includes all processes that transform raw materials into final products [7]. It involves the active streamlining of a business’s supply-side activities to maximise customer value and gain a competitive advantage in the marketplace [8]. Demand forecasting forms an essential component of the supply chain process. The role of demand forecasting in supply chain management involves strategic business planning. Demand forecasting also sets in motion the push processes of supply chain management such as raw material planning, purchasing and logistics. It steers the pull processes including order management and distribution. While demand forecasting is undeniably important, it is also one of the most difficult aspects of supply chain planning. Demand is often volatile which makes demand forecasting both an art and a science. More than 74\(\%\) of the respondents in a research survey indicated poor forecasting accuracy and demand volatility as the major challenges to supply chain flexibility [9]. Supply chain managers who learn from past experience can utilise demand forecasting to set better business goals and optimise returns [10].

An extensive literature survey has revealed that there are two main types of methodologies that are applied in the domain of product demand forecasting problems [11]. These are: i) stand-alone forecasting models and ii) hybrid forecasting models combining multiple models together. The standalone models can be statistical models or machine learning models. The most commonly used statistical models are simple moving average models [12], autoregressive integrated moving average (ARIMA) and autoregressive integrated moving average with explanatory variables models (ARIMAX). ARIMA models are used to forecast demand data from historical time series data, as in [13]. While ARIMA is a univariate method, ARIMAX uses multiple variables to incorporate external data (e.g., environmental factors) in addition to historical demand data to forecast demand [14]. A lot of regression models have also been used to predict demand, such as: Bayesian Linear Regression [15], Boosted Decision Tree Regression [15], Decision Forest Regression [15], Multiple Regression [12] and Symbolic Regression with Genetic Programming [12]. Recently, quite a few research projects using Artificial Neural Network (ANN) models were carried out to forecast product demand. ANN models are especially effective in forecasting demand when the time series data is non-linear. The properties of ANNs, such as self-learning ability, ability to perform problems with loss of data and ability to operate on multi-task problems, have made them especially useful in demand forecasting. An Integrated Case-Based Reasoning and ANN model was successfully implemented to predict product unit cost for mobile phone companies in Taiwan [16]. A similar study proposed by Islek et al. [11] successfully merged various models, i.e., multi-layer perceptrons with Bayesian networks, linear regression and support vector machines to predict product demands in a real data set derived from a dried fruits and nuts company from Turkey.

Despite the growing applications and usefulness of neural network models in forecasting demand, the forecasts produced by these methods still suffer from several drawbacks such as over-fitting [17], slow learning speed [18], getting stuck at local minima etc. An emerging algorithm for Single Hidden Layer Feed-forward Networks (SLFNs) - the ELM model was proposed in 2004[19]. It overcomes many of the disadvantages of traditional neural network models. ELM models are being used for the past couple of years to forecast a variety of things. A modified teaching-learning based optimised ELM model was used to forecast solar power generation of Chattisgarh state, India [20]. An ELM model was used to forecast monthly stream-flow discharge rates in Tigris river, Iraq [21]. A hybrid model was developed for probabilistic forecasting of wind power generation using ELM and the pairs bootstrap method [22]. In a similar work, forecasting of photovoltaic power was performed using ELM [23]. Various optimisation algorithms have also been employed with ELM to improve its prediction accuracy, though not in a product demand forecasting context. A genetic algorithm optimised ELM model was proposed to optimise gear-blank preforms [24]. In another work, the gravity field of irregular small bodies was modelled using ELM and BO [25]. A number of variants of ELM have also come out, each with its own unique set of advantages. The Optimally Pruned ELM [26], for example, ranks the best-hidden neurons by multi-response sparse regression and then selects the optimal number of neurons using a leave-one-out validation method. The online sequential ELM or OS-ELM [27] can learn data one-by-one or chunk-by-chunk (a block of data) with fixed or varying chunk size, which makes it faster than other sequential algorithms. In voting based extreme learning machine [28], multiple independent ELM trainings are performed instead of a single ELM training and then the final decision is made based on the majority voting method. A detailed review of trends and variants of ELM can be found in [29].

The major issue with time-series approaches to demand forecasting is that a large number of observations is required to determine the best fit model for a time series [13]. Historical data is needed for such methods. In the beginning, there is no information about the past and estimation has to be made based on similar cases. This results in a large amount of uncertainty which can be avoided with time [13]. ARIMA models can only be applied to stationary time series, it fails to capture seasonality. Seasonal factors affecting demand like holidays, festivals, weather conditions and other environmental exogenous factors often influence demand and are not adequately represented in forecasting models. While neural networks help in capturing the non-linearity in data due to external factors, they suffer from certain problems like over-fitting, slow learning speed etc. ELMs help to overcome these difficulties as they have extremely fast learning speed, good generalisation performance and least human intervention [29].

3 Preliminaries

This section outlines some background knowledge required to understand the hybrid ELM-HHO approach proposed in this paper, namely the basics of extreme learning machines and the Harris Hawks optimisation algorithm. In addition, some other common state-of-the-art demand forecasting models are introduced whose results are compared with our proposed model’s results later in the paper.

3.1 Extreme learning machine (ELM)

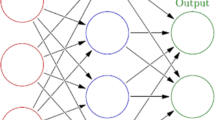
A single hidden-layer feed-forward neural network (ELM) with fast learning speed was put forward by Huang et al. [19] in 2004. The method does not require iterative tuning to reach a global minima [4]. It has been shown to have good generalisation performance, universal approximation capabilities [5], high learning accuracy and least human intervention [29]. The weights and biases of the hidden layer nodes are set randomly, thus saving time required in hyper-tuning by back-propagation. The weights of the output layer can be determined analytically by a Moore Penrose inverse operation. A generic ELM model is given in Fig. 1.

Fig. 1
figure 1

The architecture of the single hidden layer ELM model

Full size image

The output function of the ELM (a SLFN with L hidden nodes) can be represented as follows:

$$\begin{aligned} f_{L}(x) = \sum \limits _{i=1}^{L}\beta _{i}h_{i}(x) = \sum \limits _{i=1}^{L}\beta _{i}h(w_{i} \times x_{j}+b_{i}), j= 1,..,N \end{aligned}$$
(1)

where N is the number of training samples, \(w_{i}\) and \(b_{i}\) are the weight and the bias of the \(i^{th}\) hidden node respectively, \(x_{j}\) is an input vector, h is an activation function (e.g., Relu, sigmoid, Gaussian etc.) and \(\beta _{i}\) is the weight vector between the \(i^{th}\) hidden node and the output. Equation (1) can be written as:

$$\begin{aligned} T = H\beta \end{aligned}$$
(2)

where,

$$\begin{aligned} H = \left[ \begin{array}{ccc} g(w_{1} \times x_{1}+b_{1}) &{} ... &{} g(w_{L} \times x_{1}+b_{L})\\ : &{} ... &{} :\\ g(w_{1} \times x_{N}+b_{1}) &{} ... &{} g(w_{L} \times x_{N}+b_{L}) \end{array}\right] \end{aligned}$$
(3)
$$\begin{aligned} \beta = \left[ \begin{array}{c} \beta _{1}^{T}\\ : \\ \beta _{L}^{T} \end{array}\right] \end{aligned}$$
(4)
$$\begin{aligned} T = \left[ \begin{array}{c} T_{1}^{T}\\ : \\ T_{N}^{T} \end{array}\right] \end{aligned}$$
(5)

H is called the hidden layer output matrix and T is the training data matrix. To minimise the cost function ||H\(\beta\) - T||, the ELM theory claims that the parameters of the hidden nodes \(w_{i}\) and \(b_{i}\) can be assigned randomly without considering the input data. Since H is invertible, the output weights \(\beta\) can be calculated as follows.

$$\begin{aligned} \hat{\beta } = H^{\dagger }T \end{aligned}$$
(6)

where \(H^{\dagger }\) is the Moore-Penrose generalised inverse of H.

The main steps of the ELM algorithm are as follows: i) weights and biases of the hidden layer (\(w_{i}\) and \(b_{i}\)) are randomly assigned, i = 1,...,L, ii) the hidden layer output matrix H is calculated according to (3), iii) The output weight matrix \(\hat{\beta }\) is calculated by \(\hat{\beta } = H^{\dagger }T\), iv) \(\hat{\beta }\) is used to make predictions on new test data \(F= H\hat{\beta }\).

3.2 Harris hawks optimisation (HHO) algorithm

In 2019, Heidari et al. [30] proposed a novel nature-inspired metaheuristic optimisation algorithm - the Harris Hawks Optimiser. It is based on the cooperative predatory strategy of Harris hawks, one of the most intelligent birds in nature. A group of hawks living in the same family or the same stable group collaboratively attack a prey (usually a small rabbit) from different directions in a technique called “surprise pounce” or “seven kills”. The way of pursuing may differ depending on the dynamically changing circumstances and the escape strategy of the prey. The HHO algorithm models this behaviour in two broad phases - an exploration and an exploitation phase. It is a population-based algorithm similar to algorithms such as Particle Swarm Optimisation (PSO) and Ant Colony Optimisation (ACO). Since its development, the HHO algorithm has been used in a variety of fields ranging from design and manufacturing [31], feature selection for data mining [32] and even for optimising deep learning models [33].

In the HHO algorithm, the Harris hawks are considered as candidate solutions, and in each iteration, the fitness value is computed for each solution based on the intended prey. The steps of the HHO algorithm are given in (Fig. 2) and explained as follows:

Fig. 2
figure 2

The steps of the HHO algorithm (adopted from [30])

Full size image

3.2.1 Exploration phase

In this phase, the initial iteration scheme for the solution is decided based on two perching strategies of Harris hawks :

$$\begin{aligned} X(t+1) = {\left\{ \begin{array}{ll} X_{rand}(t) - r_{1} |X_{rand}(t) - 2r_{2}X(t)|&{} q\ge 0.5\\ (X_{rabbit}(t) - X_{m}(t)) - C &{} q<0.5 \end{array}\right. } \end{aligned}$$
(7)
$$\begin{aligned} C = r_{3}(LB + r_{4}(UB - LB)) \end{aligned}$$
(8)

where \(X_{rabbit}(t)\) is the current position of the rabbit, X(t) is the current position vector of the hawks and \(X(t+1)\) is their position vector in the next iteration, \(X_{rand}(t)\) is a randomly selected hawk’s position from the current population, \(X_{m}(t)\) is the average position of the current population of hawks, \(r_{1}\), \(r_{2}\), \(r_{3}\), \(r_{4}\) and q are random numbers inside (0,1) which are updated in every iteration and LB and UB are the lower and upper bounds of variables respectively. \(X_{m}(t)\) is obtained as follows:

$$\begin{aligned} X_{m}(t) = \frac{1}{N}\sum \limits _{i=1}^{N}X_{i}(t) \end{aligned}$$
(9)

where \(X_{i}(t)\) is the location of the \(i^{th}\) hawk in the current iteration and N is the total number of hawks in the population.

3.2.2 Transition from exploration to exploitation

The energy of the prey or rabbit is modeled in this step :

$$\begin{aligned} E = 2E_{0}\left( 1-\frac{t}{T}\right) \end{aligned}$$
(10)

where E indicates the escaping energy of the prey, \(E_{0}\) is its initial energy and T is the maximum number of iterations.

3.2.3 Exploitation phase

Exploitation phase of the HHO algorithm includes the following steps :

  • Soft besiege: This is the phase when the prey/rabbit still has enough energy and tries to escape by some random misleading jumps but finally fails (\(r \ge 0.5\) and \(|E| \ge 0.5\)). The hawks encircle the rabbit softly to make it more exhausted before performing the surprise pounce. This behaviour is modelled by :

    $$\begin{aligned} X(t+1) = \Delta X(t) - E |J X_{rabbit} (t) - X(t)|\end{aligned}$$
    (11)
    $$\begin{aligned} \Delta X(t) = X_{rabbit}(t)-X(t) \end{aligned}$$
    (12)
    $$\begin{aligned} J=2(1-r_{5}) \end{aligned}$$
    (13)

    where \(r_{5}\) is a random number from (0,1), \(\Delta X(t)\) is the difference between the positions of the rabbit and the hawks in the \(t^th\) iteration and J indicates the rabbit’s strength of jumping while it is trying to escape.

  • Hard besiege This is the phase when the prey is very exhausted and has a low escaping energy.(\(r \ge 0.5\) and \(|E| < 0.5\))

    $$\begin{aligned} X(t+1) = X_{rabbit}(t) - E\Vert \Delta X(t)\Vert \end{aligned}$$
    (14)

  • Soft besiege with progressive rapid dives When \(r < 0.5\) but \(|E| \ge 0.5\), a soft besiege is carried out before the surprise pounce although the rabbit still has sufficient energy to escape.

    $$\begin{aligned} Y = X_{rabbit}(t) - E |J X_{rabbit}(t)-X(t)|\end{aligned}$$
    (15)

    The hawks dive based on Levy flight-based patterns according to the following rule :

    $$\begin{aligned} Z = Y + S \times LF(D) \end{aligned}$$
    (16)

    where D is the dimension of the problem, S is a random vector of size 1 \(\times\) D and LF(D) is the Levy flight function which is calculated using:

    $$\begin{aligned} LF(x) = 0.01 \times \frac{u \times \sigma }{|\nu ^{\frac{1}{\beta }}|} \end{aligned}$$
    (17)
    $$\begin{aligned} \sigma = \left( \frac{\Gamma (1+\beta ) \times sin\left( \frac{\pi \beta }{2}\right) }{\Gamma \left( \frac{1+\beta }{2}\right) \times \beta \times 2^{\left( \frac{\beta - 1}{2}\right) }}\right) ^{\frac{1}{\beta }} \end{aligned}$$
    (18)

    where u, \(\nu\) are random variables inside (0,1), \(\beta\) is a constant = 1.5. So the final rule for updating the position of the hawks in this phase is :

    $$\begin{aligned} X(t+1) = {\left\{ \begin{array}{ll} Y &{} \text {if } LF(Y)< LF(X(t)) \\ Z &{} \text {if } LF(Z) < LF(X(t)) \end{array}\right. } \end{aligned}$$
    (19)

    where Y and Z are as calculated earlier in (15) and (16).

  • Hard besiege with progressive rapid dives When \(r < 0.5\) and \(|E| < 0.5\), a hard besiege is performed before the surprise pounce as the rabbit does not have sufficient energy left to escape.

    $$\begin{aligned} X(t+1) = {\left\{ \begin{array}{ll} Y &{} \text {if } LF(Y)< LF(X(t)) \\ Z &{} \text {if } LF(Z) < LF(X(t)) \end{array}\right. } \end{aligned}$$
    (20)

    where Y and Z are calculated using new rules :

    $$\begin{aligned} Y = X_{rabbit}(t) - E |J X_{rabbit}(t)-X_{m}(t) |\end{aligned}$$
    (21)
    $$\begin{aligned} Z = Y + S \times LF(D) \end{aligned}$$
    (22)

3.3 Other methods utilised in the comparison study

There are many state-of-the-art-models which are utilised for product demand forecasting applications in the industry. We have used some of them in this paper to compare the results of our ELM-HHO approach with esixting approaches. This subsection provides an introduction to some of these comparative models we have used in our study.

3.3.1 ELM-BO

ELM-BO is a variant of ELM where the hyperparameters are optimised by Bayesian Optimisation (BO). BO uses Bayes Theorem to direct an efficient and effective search of a global optimisation problem. It constructs a surrogate function to represent the objective function probabilistically. The surrogate function is then explored with an acquisition function to choose potential solutions which are judged on the original objective function. BO is a popular choice of optimisation algorithm to tune hyperparameters in machine learning [34]. The same methodology is followed for building the ELM-BO model as has been described in Section 4 for the ELM-HHO forecasting model. ELM optimised by BO has been used in the past to model the gravity field of irregular small bodies [25].

3.3.2 Autoregressive integrated moving average (ARIMA)

An ARIMA model is a statistical model which is used frequently in the industry for time series forecasting. It is a generalisation of the simpler Autoregressive moving average or ARMA model and adds to it the notion of integration. The main features of an ARIMA (p,d,q) model are:

  • Autoregression (AR): It uses the dependent relation between an observation and p number of lagged observations.

  • Integrated (I): It differences (subtracts an observation from an observation at the previous time step) the raw time series data d times to make it stationary.

  • Moving Average (MA): It uses the dependency between an observation and a residual error from a moving average model applied to q number of lagged observations.

ARIMA models are perhaps the most common models used in industry for time series forecasting [13, 14].

3.3.3 Long short term memory (LSTM)

Recurrent neural networks (RNNs) are a form of Artificial Neural Networks that can memorise arbitrary-length sequences of input patterns by capturing connections between sequential data types. However, owing to the failure of stochastic gradients, RNNs are unable to detect long-term dependencies in lengthy sequences [35]. To address this issue, a number of novel RNN models, notably LSTM, have been suggested. LSTM networks are RNN extensions designed to learn sequential (temporal) data and their long-term connections more precisely than standard RNNs. LSTM models are commonly used in deep learning applications such as stock forecasting, speech recognition, natural language processing and so forth. Some examples of LSTM in time-series forecasting can be found in [36, 37]

3.3.4 Gated recurrent unit (GRU)

A GRU is a RNN architectural variation that employs gating algorithms to regulate information flow among neural network cells. GRUs were initially developed in [38]. They enable the collection of relationships from massive data sequences in a flexible manner without losing information from previous portions of the sequence. This is accomplished through its gating units. These units govern whether or not information should be preserved or deleted at each time step. Some examples of GRU in time-series forecasting applications can be found in [36, 37]

4 Proposed ELM-HHO forecasting model

The main aim of this study is to obtain an accurate model for demand forecasting in an e-commerce company. The proposed methodology focuses on the optimisation of hyperparameters of ELM network using a single-objective Harris hawks optimisation (HHO) algorithm. The model combines the fast computational speed of ELMs with the accuracy gained by optimising hyperparameters using HHO. HHO, being a population-based metaheuristic optimisation algorithm, finds optimum hyperparameters with much higher accuracy compared to solo-search algorithms like Bayesian optimisation [39] or stochastic algorithms like simulated annealing. Also, in most of the optimised ELM approaches mentioned in the literature review, only input weights and biases are optimised. In our method, we have optimised additional hyperparameters like the type of activation function, number of input lags and the number of hidden nodes which contribute greatly to the improved accuracy. To explore any instability arising due to stochasticity of the HHO algorithm, the ELM-HHO model was run a couple of times for each case and it was found that the optimization algorithm converges well in each case such that the standard deviation and the mean of the forecasts do not differ significantly between successive runs.

The proposed methodology for product demand forecasting is illustrated in Fig. 3. The methodological development of the proposed model can be described as follows: i) data cleansing and preparation, ii) selection of hyper-parameters to be optimised (refer to Table 1); iii) random generation of learning parameters within a specified range; iv) implementation of the HHO algorithm; v) iterative generation of model parameters using the HHO algorithm; vi) training ELM using the generated model parameters and calculating RMSE of forecasts with the test dataset; vii) checking fitness (i.e., RMSE of test dataset) at each iteration; viii) generation of optimised values of model parameters based on iterative performance; and ix) finally, validation of the ELM-HHO model using optimised model parameters for the best fitness (i.e., the least Test RMSE). The main steps of the methodology are described in more detail below.

Fig. 3
figure 3

Flowchart of the ELM-HHO approach

Full size image
Table 1 Lower and upper bounds of the ELM-HHO model parameters
Full size table

4.1 Preparing data

Data cleansing and normalisation are the essential initial steps to be taken in any forecasting task. In our methodology, first the noisy values were smoothed and the missing values were replaced through linear interpolation. Then the time series data was normalised according to the following equation before being fed into the model:

$$\begin{aligned} x_{normalised} = \frac{x_{i}-\mu }{\sigma } \end{aligned}$$
(23)

where \(x_{i}\) is \(i^{th}\) data, \(\mu\) is the mean of all training data and \(\sigma\) is the standard deviation of all training data. Note that the predictions were transformed back to the original scale using the following denormalisation equation before making final predictions:

$$\begin{aligned} x_{denormalised} = (x_{normalised} \times \sigma ) + {\mu } \end{aligned}$$
(24)

4.2 Generating hyperparameters for ELM network

ELM models have achieved acceptable forecasting performance when applied on time-series data [26]. However, obtaining good performance with ELM is a tedious task as it involves the optimisation of various hyperparameters. In this study, the following hyperparameters were optimised.

  1. 1.

    Lag size: The number of input lags decides how many previous time steps data should be used to predict data at the next time step. The lag size has a significant influence on the performance of time series forecasting [40]. Hence, it is vital to select the optimal lag size in forecasting applications.

  2. 2.

    Number of hidden nodes: Similar to other artificial neural network methods, the number of hidden neurons in ELM has a significant effect on its performance [41].

  3. 3.

    Input weights and biases: The weights and the biases of the hidden layer of ELM are drawn from a truncated normal distribution [23]. This may lead to non-optimal performance and may result in ill-condition [42]. Random weights and biases may also result in over-fitting due to the ELM’s excessive learning abilities [43]. In this study, due to these limitations, input weights and biases of the ELM network were optimally selected to achieve better generalisation performance and improved forecasting accuracy of the ELM model.

  4. 4.

    Type of activation function: The performance of the network varies according to the type of activation functions used in the ELM structure. The selection of the activation function generally depends on the problem, and this selection might have a significant impact on the performance of ELM networks [44]. In this research, (1) binary step function, (2) sigmoid, (3) hyperbolic tangent (TanH) and (4) rectified linear unit (ReLU) were considered.

4.3 Initialisation of the HHO algorithm

Single-objective Harris hawks optimisation was used to find optimal hyperparameter values. In the proposed model, each individual depicts a potential solution as a real vector I, where I consists of multiple variables to be optimised.

$$\begin{aligned} I = [x_1, x_2, x^{1}_3, x^{2}_3,..., x^{K}_3, x^{1}_4, x^{2}_4,..., x^{x_2}_4, x_5] \end{aligned}$$
(25)

Here, K is the total number of weights (Table 1). The root mean squared error (RMSE) was used as the fitness function since it is the most widely utilised cost function in evolutionary ELMs. RMSE represents the square root of the mean squared differences between predicted values and actual values. The fitness function is given as follows.

$$\begin{aligned} Fitness = \sqrt{\frac{\sum _{i=1}^{N}(Y_{i}-\hat{Y_{i}})^{2}}{N}} \end{aligned}$$
(26)

where \(Y_{i}\) is the actual sales data,\(\hat{Y_{i}}\) is the predicted sales data and N is the total number of days for which forecasting is done. It is a scale-dependent measure used to determine how far the absolute values of the forecasts are from the actual sales data.

4.4 Initialisation of the ELM algorithm

The HHO algorithm was used to find the optimal hyperparameters which gave the least RMSE of forecasting on the test dataset. The final chosen hyperparameters were then used to train ELM to obtain optimal forecasts. An ELM architecture with the optimum number of hidden nodes was used. If the optimum no. of input lags came out to be t, sales data at \((n-1), (n-2), (n-3) ... (n-t)\) days were used as inputs to predict the target sales data at the \(n^{th}\) day. The optimised weights and biases of the hidden layer with the optimised activation function were used to compute the hidden layer output matrix H. The output weight matrix was then calculated by \(\hat{\beta } = H^{\dagger }T\) using the training data T. Finally \(\hat{\beta }\) was used to make predictions on new test data using \(F= H\hat{\beta }\).

5 Experimental results and discussion

5.1 Dataset

In this study, product demand forecasting was performed using historical sales data from the gaming industry. The global video game market has grown a lot in the past few years. Demand volatility is a particular characteristic of this market. Hence predicting future demand in advance can help gaming companies secure and retain new customers and get an edge over others in the market. Demand forecasting can enable these businesses to maintain an appropriate balance between their suppliers and their buyers. It can also help them ensure improved customer satisfaction at less cost to the supply chain. In this context, our article aims mainly to study the historical sales data of multiple products to provide reasonably accurate forecasts within a permissible error range. The dataset was attained from an e-commerce company based in Western Europe. It had daily sales data of 45 different products from multiple stores from January 2013 to December 2017. The original dataset had 4 columns in tabular form corresponding to date, store, item number and number of sales respectively. Data was present from 10 different stores and the daily sales number for each of the 45 products of a particular store was an integer roughly varying between 5 and 150. Data for each product and store showed a similar trend with some variations. Hence results for only Store 1 have been shown in our paper. We also summed over the daily sales data of all 45 products from Store 1 to consider the cumulative sales trend of video games from Store 1. When broken down into trend, seasonality and residual components (Fig. 4), the time series data showed an almost monotonically increasing trend and pronounced seasonality effects, with peaks in sales appearing at regular annual intervals. This showed that the time-series was not random, and hence could be forecasted. Results of Dickey-Fuller test revealed that the series was not stationary, but it became stationary on performing a first-order differencing operation. The statistical description of the utilised dataset (for Store 1) is given in Table 2.

Fig. 4
figure 4

Data visualisation : a) Daily sales data from January 2013 to December 2017, b) Trend component of data, c) Seasonal component of data, d) The residual values, excluding trend and seasonal components

Full size image
Table 2 Descriptive statistics for product sales between Jan. 2013 and Dec. 2017
Full size table

5.2 Experimental setup

Data from January 2013 to September 2017 was used for training and October 2017 to December 2017 data was used for testing. For the ELM-BO and ELM-HHO approaches, an optimum number of lags or previous time steps data was chosen using the optimisation algorithm to be fed as input features into the ELM. The number of hidden nodes, values for hidden weights and biases in the ELM and the type of activation function were also optimally selected. Daily sales data for the last three months (October 2017 to December 2017) of the dataset was predicted. All computer operations were performed in Python environment, where the computer was configured with Intel(R) Core (TM) i7- 10750H CPU @2.60 GHz and 16 GB RAM.

5.3 Performance metrics

Along with RMSE, two additional performance metrics were used to evaluate the accuracy of forecasts by our approach. These metrics are:

  • Mean Absolute Percentage Error (MAPE) : MAPE is calculated as the average absolute percentage error between the observed values and the predictions.

    $$\begin{aligned} MAPE = 100 \times \frac{1}{N}\sum \limits _{i=1}^{N} |\frac{(Y_{i}-\hat{Y_{i}})}{Y_{i}} |\end{aligned}$$
    (27)

    Percentage errors have the advantage of being unit-free and are useful for comparing results among the different stores.

  • Mean Percentage Error (MPE) : MPE is the same as MAPE, but instead of taking the absolute errors in forecasting, we consider the actual errors with sign.

    $$\begin{aligned} MPE = 100 \times \frac{1}{N}\sum \limits _{i=1}^{N}\frac{(Y_{i}-\hat{Y_{i}})}{Y_{i}} \end{aligned}$$
    (28)

5.4 Parameter settings

The number of search agents and the maximum number of iterations are the two primary parameters of the HHO algorithm. The number of search agents has a direct relationship with the search stage’s efficiency. The number of search agents or population size was taken as 15 in Harris hawks optimisation technique. Preliminary testing was performed to choose this number which presented an optimal balance between accuracy and computational costs. The optimisation algorithms for ELM (i.e., BO and HHO) were run for 200 iterations each. Both the algorithms converged well within this number of iterations for our dataset. Bayesian optimisation was performed with the open-source Python library HyperOpt using a Tree of Parzen Estimator (TPE) algorithm to construct the surrogate function. Although the same methodology was followed by both ELM-BO and ELM-HHO, the optimised hyperparameters came out different for both (Table 3). In the traditional ELM approach, none of the hyperparameters were optimised. ELM models with 50 hidden nodes, 100 hidden nodes and 500 hidden nodes respectively with randomly assigned hidden weights and biases and 14 lags as input features were used for the forecasting. 14 lags was chosen as the standard in unoptimised ELM, LSTM and GRU models because the dataset showed a sharp autocorrelation peak at this lag.

Table 3 Optimised hyperparameters for ELM chosen by BO and HHO algorithms
Full size table

ARIMA models commonly used in time series forecasting were also applied to our dataset. Autocorrelation and partial autocorrelation plots of the daily sales data were used to choose the parameters of the ARIMA model. The auto-regressive order was chosen as 7 (from the ACF and PACF plots) and the integrated order as 1 (Dickey-Fuller’s test revealed that the first-order differenced time series was stationary). The predictions of ARIMA (7,1,0) model were compared with our ELM approaches. For fair comparison, a few other ARIMA models: ARIMA(5,1,0), ARIMA(10,1,0), ARIMA(7,1,1) and SARIMAX[(7, 1, 0) x (1, 1, 0, 12)] models were also used to perform forecasting.

A LSTM model was also used for the forecasting. It was a sequential model with the following layers: i) Input layer, ii) LSTM layer of 128 units, iii) LSTM layer of 64 units, iv) Dropout layer with a dropout rate of 0.5, v) LSTM layer of 32 units, vi) Dropout layer with a dropout rate of 0.25, vii) Fully connected layer, viii) Regression layer. A lag of 14 days was used as input features at each time step. The mini batch size was taken as 64 with an initial learning rate of 0.00202 and learn drop factor of 0.25. The L2 regularisation metric was 1e-3 and the optimiser was Adam. The model was trained over 200 epochs with shuffling after every epoch. A GRU model was also used for the forecasting. It was a sequential model with the following layers: i) Input layer, ii) GRU layer of 128 units, iii) GRU layer of 64 units, iv) Dropout layer with a dropout rate of 0.5, v) GRU layer of 32 units, vi) Dropout layer with a dropout rate of 0.25, vii) Fully connected layer, viii) Regression layer. A lag of 14 days was used as input features at each time step. The mini batch size was taken as 64 with an initial learning rate of 0.00202 and learn drop factor of 0.25. The L2 regularisation metric was 1e-3 and the optimiser was Adam. The model was trained over 200 epochs with shuffling after every epoch.

5.5 Comparison of ELM-HHO results with ELM, ELM-BO, LSTM, GRU and ARIMA models

Figure 5 plots the forecasting results for all the models with the error values given in Table 4.

Table 4 Comparison of performance of different models in forecasting sales data for the last 3 months
Full size table
Fig. 5
figure 5

Forecasting sales data for the last 3 months with a) GRU, b) LSTM, c) ARIMA(7,1,0), d) ELM with 100 hidden nodes, e) ELM-BO, f) ELM-HHO

Full size image

RMSE values of the test dataset were used for the comparison. Among the ARIMA models, ARIMA (7,1,0) gave the best results since the order was chosen from the trends observed in the auto-correlation and partial auto-correlation plots of the dataset. The ACF plot was found to be strong to a lag of 7, the inertia of that relationship carried on to subsequent lag values and then trailed off. So 7 was a good choice for the auto-regressive order. The integrated order of 1 was justified by a Dickey-Fuller’s test which showed that the first-order differenced time series was stationary. ARIMA(7,1,0) performed 135.62% better than ARIMA(5,1,0), 1.57% better than ARIMA(10,1,0), 23.38% better than SARIMAX [(7,1,0) \(\times\) (1,1,0,12)] and 1.46% better than ARIMA(7,1,1) in terms of test RMSE of forecasting.

The ELM models, ELM, ELM-BO and ELM-HHO performed better than the ARIMA models in making future demand predictions. ELM-BO showed an improvement in forecasting accuracy of 45.78% over ARIMA(7,1,0) while our proposed approach ELM-HHO was better than ARIMA(7,1,0) by 62.73%. The ELM models performed better than the ARIMA models because ELM, being a neural network model, can capture the non-linearity in sales data better than a statistical model like ARIMA. ARIMA models need to convert the time series to a stationary one, so first order differencing was performed on our dataset. However the underlying process used in ARIMA is linear, so it fails to capture nonlinear models from the time series. Historical sales data like our dataset is often highly non-linear and chaotic because a lot of external environmental factors affect it. ELM models are hence better forecasting models for such datasets.

The LSTM and GRU models also performed better than the statistical ARIMA models since they are also neural network models like ELM. While the performance of LSTM and GRU models was comparable to that of the traditional ELM models without any optimisation, they did not perform as well as the optimised ELM models - ELM-BO and ELM-HHO. The ELM-BO model was 26.07% better than GRU and 20.08% better than the LSTM model while the ELM-HHO model showed an improvement in forecasting accuracy of 40.73% over GRU and 34.05% over the LSTM model. This might be attributed to the fact that the GRU and LSTM architectures were not tuned to achieve optimal performance.

Test RMSE values of ELM with 100, 500 and 1000 hidden nodes respectively confirmed that the performance of ELM depends on the number of hidden nodes. Hence, the ELMs in which no. of hidden nodes and other parameters were optimised - ELM-BO and ELM-HHO performed better forecasting than traditional ELM models in which all parameters were chosen randomly. HHO is a meta-heuristic population based optimisation technique and has been shown to have excellent performance on benchmark problems compared to other well-regarded optimisers [30]. For our problem, ELM-HHO performed better than ELM-BO in forecasting last three months sales data by 11.63%. The superior performance of ELM-HHO to ELM-BO can be explained by the fact that BO learns about the underlying objective function through a trial and error approach which might not always result in finding the exact optimum. The problem may also lie in our choice of algorithm to construct the surrogate function, TPE was used in our case instead of Gaussian process or random forest. There are also a number of mechanisms which benefit population-based algorithms like HHO over solo-search ones like BO [39], such as putting together blocks from different solutions (search agents/ hawks), a population’s ability to search different parts of the fitness landscape to avoid getting stuck in a local optima due to bad initialisation etc.

5.6 Horizon forecasting results

Operation managers need long-range as well as short-range demand forecasts to make strategic decisions about products, processes and facilities. Time horizon of forecasts is an integral part of making efficient supply chain decisions and hence needs to be clearly established. Short range forecasts help to decide how much raw material should be ordered for delivery for the next week, how much of each product should be scheduled for production for the next week, how many workers should be scheduled to work next week etc. In this context, forecasting was performed using a 3 day ahead and a 7 day ahead horizon with ELM-HHO to predict the daily sales data for the last 3 months of the dataset. Figure 6 shows horizon forecasting results for the last 3 months, with error values given in Table 5. As expected, forecasting error increases with the increase in horizon length. Even then, ELM-HHO approach resulted in good horizon forecasting accuracy at 3 days and 7 days ahead, thus making it a promising approach to be applied in real time in companies to predict future demand from last week’s sales data.

Fig. 6
figure 6

Horizon forecasting for last 3 months with ELM-HHO at a) 3 days ahead, b) 7 days ahead

Full size image
Table 5 Performance assessment of horizon forecasting for last 3 months with ELM-HHO
Full size table

5.7 Discussion

Detailed comparisons with traditional forecasting models revealed that the proposed approach ELM-HHO is a highly accurate model for demand forecasting problems. Although the population-based HHO algorithm is computationally costlier than the solo-search Bayesian Optimisation, the rise in computational cost is offset by the huge improvement in accuracy. To summarise, the proposed ELM-HHO model performed 62.73% better than the statistical ARIMA(7,1,0) model, 40.73% better than the neural network based GRU model, 34.05% better than the neural network based LSTM model, 27.16% better than the traditional non-optimised ELM model with 100 hidden nodes and 11.63% better than the ELM-BO model in forecasting demand for last 3 months. Most importantly, our approach is practical and industrially useful as it can predict sales data accurately over a time horizon. The key strength of the proposed approach lies in combining the fast computational speed of ELMs with the accuracy gained by optimising hyperparameters using HHO. Optimising the number of input lags using HHO yields more accurate results than choosing them by seeing ACF and PACF plots, which is prone to human error. Usually, only input weights and biases are optimised in optimised ELM algorithms. In our approach, more hyperparameters like the type of activation function, number of input lags and number of hidden nodes were optimised which contributed to the highly improved forecasting accuracy.

6 Conclusion and future work

There are numerous challenges involved in performing accurate and timely product demand forecasting [45,46,47]. Traditional time series forecasting models like ARIMA can only be applied on stationary time series, and fail to capture non-linearity introduced in sales data due to market volatility, seasonal factors etc. In this context, we introduced a hybrid neural network based demand forecasting model - ELM tuned by Harris hawks optimiser which is able to accurately forecast non-linear sales data of products belonging to an e-commerce store. ELM, being a single layer feed forward neural network, has been shown to be very effective in forecasting non-linear time series data at fast computational speed. We improved the accuracy of ELM further by tuning its hyperparameters with Harris hawks optimisation technique. The ELM-HHO model had better forecasting accuracy than ELM, ELM-BO, GRU, LSTM and ARIMA models, thus making it a great choice for product demand forecasting. The ELM-HHO model also performed good horizon forecasting at 3 days and 7 days ahead, which makes it a good model to be applied by companies in predicting sales data over a horizon. This work can be extended in future by adding auto-encoders for time series feature extraction which might improve accuracy further. CNN or LSTM auto-encoders which can choose the most important time series features to be passed as inputs to the ELM layer, can be analysed. This will help in better identification of the most important input lags and reduce the computational complexity incurred in optimising the number of input lags using an optimisation algorithm. The optimisation part in our approach can be tuned further and multi-objective optimisation can be investigated. The population-based HHO algorithm suffers from certain drawbacks like immature convergence and getting stuck in local optima. Hence, improved versions of HHO, like that mentioned in [48], which uses the Salp Swarm Algorithm (SSA) to enhance the robustness of the HHO algorithm can be explored in future work. The HHO algorithm can even be hybridized with simulated annealing to accelerate its global convergence performance, as shown in [49] and [50]. Newer optimization algorithms like that mentioned in [6] can also be explored. Multivariate demand forecasting which uses inputs other than just the historical sales data can also be explored. For instance, the effect of external factors like seasonal holidays, market volatility etc. can be introduced in our approach to improve robustness.