1 Introduction

Currently, the problem of Multiclass classification with decision making processes is a fundamental problem in supervised learning which is an important problem in classify results by multiple label-classes [1,2,3]. For example, the works [4,5,6] applied to real-life situations such as text categorization, entity recognition, and disease diagnose respectively. Therefore, finding an appropriate method or strategy to solve the multi-class classification problem is important. However, it is difficult to solve multi-class classification problems in order to the scope of a decision for a problem is the decision-making process probably be more complex than the problems of binary classifications [7]. The decision-making process [4, 8,9,10] is another problem that has been studied in this research. Part of the decision to classify the result class of the data set. There is often a problem with multi-class dataset data due to improper classification of results due to the large collection and distribution of class results. From the increasing number of multi-class data sets Therefore, new machine learning algorithms [11,12,13] need to be developed to improve the efficiency of the results class prediction and find that there are multiple learning models that can be used to solve the same problem [14,15,16]. Ensemble learning is a machine learning process to improve the efficiency of predictions [17,18,19]., [20] using a strategy to combine multiple learning predictions and helps to reduce the problem of inappropriate model selection by combining all models. This method is popular and widely used to improve performance than individual models [13, 21, 22]. According to the effectiveness of the ensemble learning method, it is necessary to create Creating a new ensemble model to improve the model’s accuracy and stability [16, 20, 23]. The main challenges of creating a new ensemble model are how to combine strategy and methods. Determine the assigning weight probability, which is the method preceding the final class result classification process for multi-class data. In aspect of designing an efficient new ensemble model method [24,25,26], there are 4 key points to be considered: dataset, based model, combination strategy and method of assigning probability weight. According to previous studies [16, 27, 28] the researcher tends to not pay much attention to multi-class data sets due to the multi-class classification. There is a complex decision-making class classification results that are difficult to manage [29]. To deal with this important problem, there are 2 main methods that are used to create classification methods for multi-class data: The traditional base model method and the ensemble model method. At the traditional base model method [30,31,32,33,34,35,36,37,38,39,40], the model used to classify the resultant class, such as classifying the resultant class The nature of the decision tree, which is the decision tree method [41], is used to predict the pattern recognition class of the individual base model. [5, 42,43,44] Accuracy depends on the factors of the prediction of the result of class [45]. Although the traditional base model method can classify the result class in the case of multi-class data sets, it has difficulty in the decision of classifying the correct results class without information bias is greater than the ensemble model. Therefore, the ensemble learning model [46], is considered to be more appropriate for managing Multi-class classification, complex results in which they can improve the classification performance by using the combination method (multiple classifier) in machine learning [47,48,49]. Decision-making, the method of assigning weight (assigning weight probability to class result) is one of the challenges for classifying new result classes in multi-class data. [50,51,52] Therefore, ensemble learning methodology has been considered for reducing class bias occurrence from classification results [4, 53]. Maintaining good classification performance comes from combining result classes. By determining the appropriate probability weight and obtaining a higher classification accuracy for multi-class data [54, 55]. The latest techniques for the combination method are selection base model and assigning method. Many studies [40, 56,57,58] attempt to optimize the probability weight obtained from the prediction of the class results from the ensemble model. It focuses on the combination strategy process, which is a combination of weighted voting methods, which is a method for assigning appropriate weight values to classifications that do not affect the effectiveness of the model and the accuracy of the classification is derived from the improvement of assigning weight. In this step, the true positive value of the prediction of the resulting class increases and decreases. The misclassified data sets of multi-class data are compared to the base classification model and traditional ensemble model [42, 50, 59]. Another important problem is the lack of complete training samples in the data set, which causes training data insufficient data and the difficulty of using a combination strategy to combine models to create good classification methods for multi-class data. Therefore, recent work focuses on supervised machine learning methods, including cost-sensitive methods. Approach [57] in order to overcome the decision problem of classifying the appropriate outcomes. Most jobs that provide high accuracy (Measure the efficiency of the model by confusion matrix methods including Precision, Recall, F-measure, G-mean, and Accuracy). Only for multi-class data classification that has more than 2 result classes, the accuracy resulting from each the range of the number of classes. The result shows that even if the dataset has more classes, which should not be decrease the accuracy. While evaluating performance using the confusion matrix method of the base classification model and traditional ensemble model, the performance evaluation is lower than the new ensemble model. This is possible because of the information bias. The selection of the result class from a single pattern without randomization appropriate randomization results in incorrect results class predictions due to incorrect probability weight assignments. [5, 60, 61] Current work is trying to improve the efficiency of the method combination by setting cost new cost-sensitive weight (new assigning weight) for more accurate probability weight of class result.

In our research, we present a novel supervised cost-sensitive weighted based on Ensemble learning classification. For process resolution decision-making of multi-class classification. The framework that we have proposed is cost-sensitive probability weighted based on ensemble learning, which differs from the initial classification work [42, 62] that focuses on the pattern recognition of The classification of an individual base model that does not take into account the predisposition of the class result data obtained from predictions from the model may lead to information bias. Complex multi-class data without parameter adjustment prior to testing data, making cost-sensitive probability weighted methods stable in the process [63] while achieving accuracy It must be assessed by the efficiency of good classifying multi-class data. In addition, the cost-sensitive methods weighted based on ensemble learning that are presented are different from the traditional ones that are usually simple votes. [5, 20, 42, 64]. Who use the weight voting method in the assigning probability weight method because cost-sensitive weighted based on ensemble learning. The key principle is to determine the new weight of the final class result. It is used before the result class classification procedure to help reduce the risk of bias data management at the test samples from the base model integration, the proposed cost-sensitive weighted methods have been tested on multi-class benchmark datasets and have been implemented. The comparison of other state-of-the-art methods demonstrates the effectiveness of the framework presented in the areas of Precision, Recall, F-measure, G-mean and Accuracy.

To conclude, our main contributions are four folds:

  1. 1.

    Our proposed method offers cost-sensitive weighted-based on ensemble learning, which is a novel supervised combination model based on Ensemble learning classification Based on machine learning methods to improve the classification of data from individual models to ensemble models for problem solving processes. The costed-weighted approach is to learn multi-class samples without adjusting the parameters of the base model, providing a good evaluation of the model. Than the base model method and the traditional ensemble model.

  2. 2.

    Our proposed method presents the novel supervised learning of the cost-sensitive probability weighting ensemble learning method, where the combination strategy eliminates information bias from the decision to classify wrong outcomes, which is a good way of consolidating when that strategy gives value misclassified by decreasing.

  3. 3.

    The methods is used TPrate-weight, which is a novel combination strategy from the improvement of the probability weight to combine the base model to provides a better classification performance compared to the many existing methods that are tested using benchmarks dataset.

  4. 4.

    In this research, our proposed method present efforts to improve the process decision-making for multi-class data sets by suggesting the combination methods in the constructing ensemble model of the framework

2 Literature review

2.1 Ensemble model

The ensemble learning approach employs diverse classification models to enhance the prediction efficiency on various datasets. Although the individual models provide satisfactory prediction accuracy and precision on the dataset, they are sometimes confronted with the problem of bias when specifying the dataset that is obtained from the prediction or specifying the parameter. One of the approaches to resolving the bias is the joint decision approach, which is called ensemble learning with one additional base classification model. The decision is later combined via voting [64]. In this study, weighted voting was deployed to enhance the efficiency in predicting the classification model. Ensemble learning was utilized in various research studies to enhance the prediction efficiency. Reference [42] applied ensemble learning to multi-class ensemble classification and proposed the Kalman-filter-based heuristic ensemble (KFHE). Based on this approach, ensemble learning was conducted during the final procedure. The data were deployed with Kalman filters to combine various individual models with multi-class classification. The experiment compared the KFHE and the original ensemble model and calculated the efficiency of KFHE for testing data without noise and data with noisy class labels. The KFHE realized a significantly better value.

Ensemble learning has also been used to enhance the efficiency of classifiers. In reference [5], natural language processing (NLP) was conducted via ensemble learning, which employed the voting technique to combine classifiers for named-entity recognition. This approach was crucial for NLP. This study recommended two solutions for generating the ensemble model, which differ in terms of their effects in enhancing the efficiency. It was hypothesized that the reliability of predicting each classifier differed among the output classes. Therefore, the ensemble system must search for each class that was most suitable for the classifier through voting, such as binary voting. Additionally, it must determine the number of votes for each class for the single classifiers, such as the real votes. The applied model classified and selected without domain knowledge or language-specific resources. The results for each language demonstrated that multi-objective optimization (MOO) with real voting could yield higher efficiency than the individual classifiers in the ensemble. For selecting a suitable weight, all the parameters should be set to the most suitable values at the same time. To realize this objective, multi-objective optimization was implemented to enhance the efficiency in evaluating the quality of one additional classification.

In addition to improving the efficiency of machine learning via ensemble learning, reference [20] deployed extreme learning machines to improve the efficiency of the classification model via an advanced ensemble with various models. Extreme learning was efficient in its general operation. However, overfitting of the training data could be likely. To resolve the problem of low efficiency, a heterogeneous ensemble was implemented. This study proposed the advanced ELM ensemble (AELME) for classification. This approach was comprised of the regularized ELM, the 2-norm-optimized ELM (ELML2), and the kernel ELM. The ensemble was generated by training the ELM classifier, which was randomly selected on a subset of the training data with resampling. The resampling subset was selected for the classification of the training data. Each classifier was learned for selecting the data subset randomly via the ELM algorithm. The AELM-Ensemble was developed using the objective function to increase the diversity and accuracy in the group of the final ensemble. The class labels of the unseen data were predicted via majority voting, which were combined with the predictions from ensembles in AELME. The results of the study demonstrate that AELME yielded higher accuracy than the other models on benchmark datasets. Classifying the training data of the subset and combining heterogeneous ELM classifiers yielded high accuracy in the overall operation.

Moreover, in multi-objective optimization, ensemble learning is typically used to increase the efficiency of the classifier. Reference [4] conducted a sentiment analysis. An ensemble was generated via the weighted voting of multi-objective methods that are based on the differential evolution algorithm for text sentiment classification with supervised machine learning. Most approaches that employ ensemble learning for sentiment analysis manage the features to enhance the prediction efficiency. The study attempted to develop a multi-objective method by increase the efficiency via a weighted voting scheme to fix the suitable weights for each classifier and output class to increase the prediction efficiency for all the algorithms and the sentiment classification. Thus, a multi-objective differential evolution algorithm (MODE) was implemented in this study. Several mutation operators were applied to enhance the efficiency of the differential evolution algorithm. The weight of each classifier for each output class was prescribed by the MODE algorithm, whereas the weight of each classifier for each output class was combined by the ensemble to yield the final prediction for each output class.

Ensemble learning is one of the learning algorithms that has the highest efficiency in supervised learning with groups of models. The prediction strategy is to combine the predictions that are derived from multiple learning algorithms to generate the final result [65] and to increase the prediction efficiency [17]. The ensemble learning model utilized the advantages of each base model when combining the models. Then, the resulting model was utilized to generate the final result by combining the subdivisions from the prediction [66]. The model that combines the learning models was regarded as an efficient approach for improving the classification performance, and it realized outclassed management with a small sample size, high dimensionality, and data with complicated structures, such as the individual models [67]. Furthermore, ensemble learning was one of the machine learning approaches that was deployed to combine models to improve the result of each individual model. This approach relies on the combination of the output of sets of learning models according to specified rules to obtain a better model than an individual learner [68]. Ensemble learning is regarded as an efficient machine learning technique, which is comprised of diverse components for a single task instead of various subtasks. Later, the base learning machines were combined to form ensemble learning machines. Compared to the individual algorithms, it was found that the ensemble techniques could reduce the error in determining the mean and combine the multiple classification models to reduce overfitting of the training data. Many research studies have demonstrated the efficiency of ensemble learning, which is an easy technique. In addition, they indicated that ensemble learning realizes higher efficiency than the individual algorithms with the same complexity [27]. Ensemble learning is the combination of the outputs of sets of learning models according to specified rules to obtain a better model than single learners. Ensemble learning has been widely implemented in applications such as image recognition, speech recognition, and industrial process monitoring. Ensemble learning consists of two main procedures: The first procedure involves training. The ensemble model is derived from the base learning algorithms. The second procedure involves prediction. The output of the model is combined to generate the decision. The selection of the ensemble model can be divided into two stages:: The first stage fixes the functions or criteria for evaluating and ranking the model. The second stage deploys a search algorithm to search the group for the best model. The performances of ensemble methods depend on the training data. A severe problem of the ensemble learning algorithm during the stage of learning is maintaining the performance without duplicating the base model. In generating a different model from the feature space, the base models did not reduce the accuracy compared to the individual model, whereas the efficiency of all the ensemble models was enhanced [69]. Regarding ensemble learning, six vital techniques have been employed for analysis. However, the homogenous model is used as a technique for ensemble learning by voting from the separation data. The traditional homogenous model is described as follows.

2.1.1 AdaBoost (adaptive boosting)

AdaBoost [31, 70, 71] is a machine learning algorithm and one of the approaches that has been derived from ensemble learning. The approach combines weak models from various classification models. The main strategy of the AdaBoost algorithm concerns the generation of the model weights and sample weights. Once in the process of repeated training, the model weights and sample weights were trained by the weak model. The weights of the samples, which were inaccurately predicted, would increase to focus on the next training step. The model weights were calculated based on the error rate of each weak model.

2.1.2 Bagging (bootstrap aggregating)

Bootstrap aggregating (bagging) [72,73,74,75] is one of the primary ensemble methods that uses bootstrap sampling. With bagging, the ensemble, as a homogeneous ensemble, was combined to generate the prediction model with data resampling. Bagging was used to generate a subset for resampling, and aggregating was used to generate a subset for bootstrapping. The main objective of bagging was to reduce the error from the variance of the unstable base classifier.

2.1.3 Stacking

Stacking [16, 76, 77] is an approach that combines models. Stacking was deployed to reduce the error rate by reducing the bias in the data. The main strategy of stacking is to combine the outputs of various prediction models.

2.1.4 Random forest

A random forest [29, 78,79,80] or a random decision forest is an ensemble learning method for classification and regression. Moreover, random forest was one of the most powerful and successful machine learning algorithms and combined the diversity of randomized decision trees and prediction via averaging.

2.1.5 Random subspace

Random subspace [28] was proposed in a decision forest. Random subspace consists of multiple decision trees that are generated in multiple random subspaces, which are combined to form a classifier. Random subspace was the approach of the classifier ensemble, which was deployed to resolve the problems of noise and more redundant data than the single classifier. The random subspace of the training dataset was improved similarly to bagging. This improvement was conducted in the feature space, especially in the instance space. This approach was derived from the random subspace for generating the base classifier when the dataset had complicated or irrelevant properties.

2.1.6 Voting

Voting [62] is regarded as the easiest approach for combining individual classification algorithms. To select the rules for combining the classifier ensemble, voting is the decision rule for selecting a single class out of several alternatives. Voting predicts the class via majority voting. Voting is the approach that is most frequently implemented in ensemble learning. The pattern of voting includes unweighted and weighted voting. Unweighted voting involves simple voting or majority voting, while weighted voting involves simple weighted voting.

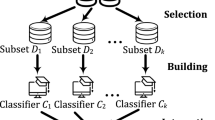
A literature review summary is presented in Table 1. The base learner model depends on the experimental data. For model combination, a strategy of combining the predictions of the classifications that are made is applied to the ensemble. There are two main types of ensembles: homogeneous ensembles and heterogeneous ensembles (Fig. 1).

Table 1 Literature classification according to the base learner and the use of homogeneous and heterogeneous ensembles
Full size table
Fig. 1
figure 1

Categories of Ensemble classifier models. (a) Homogeneous ensemble. (b) Hetorogeneous ensemble

Full size image

Homogeneous ensembles used the same learning algorithm, whereas, heterogeneous ensembles use various learning algorithms, such as the classifier combination model. As an example of the research of Zhibin Wu et al. [73] in which the heterogeneous ensembles ensembles are constructed from two basic methods in comparing the model’s performance. Thus, creating models using the principles of a traditional ensemble model is the bagging method. By creating the ANN model as the 1st ensemble model and the SVM model as the 2nd ensemble model, these methods will be combined. A sample voting technique to create a new ensemble model, then compare to find the best method.

3 Proposed framework

Our proposed framework is a type of heterogeneous ensemble. This study focused on enhancing the efficiency of the data classification. Several classification models are typically employed for the test, such as the naive Bayes, multilayer perceptron, and decision tree models. These approaches were employed to evaluate the efficiency to identify the best approach. The model that was tested by those methods was called the base classifier model. The efficiency of the base classifier model was evaluated to identify the best approach. It was posited that best approach for the dataset depended on the attributes of the input dataset. Therefore, the strategy of testing the base models resulted in testing of the ensemble model, which is a combination of various models, to obtain a model with higher efficiency in testing the datasets and with higher accuracy. This study used a dataset with multiple data types to evaluate the efficiency and probability of the most suitable class and could encourage the dataset to realize the best accuracy. To combine the models, the base model was used to generate an ensemble model for obtaining the predicted class and the weights for calculating and combining the models. The weights from the probability of the class occurrence were calculated with the true positive (TP) rate, which measures the reliability of the class that was predicted by the model in comparison with the actual class. In addition, our purposed model uses the reliability rate as a parameter of the probability weight model to select a class. Before generating the model, the dataset was pre-processed. This procedure prepared the dataset before model testing. In this research study, the test for model efficiency was divided into three parts, namely, testing of the base model, the original ensemble model, and the proposed new ensemble model or the TPweight-voting ensemble model that consists of 3TP-Ensemble, 4TP-Ensemble, 5TP-Ensemble and 6TP-Ensemble. All the models, starting with the base model, consist of six models: the decision tree, k-nearest neighbours, support vector machine, multilayer perceptron, naive Bayes, and Bayesian network approaches. The base model was regarded as the beginning model for generating each new ensemble model. Next, the original ensemble model, which was comprised of another six approaches, namely, AdaBoost, bagging, random forest, random subspace, stacking, and voting, is presented. The models were combined via the traditional approach. Finally, the new ensemble model, namely, the TPweight-voting ensemble model, is presented. This model consists of four approaches: the 3TP-Ensemble model, the 4TP-Ensemble model, the 5TP-Ensemble model and the 6TP-Ensemble model. The TPweight-voting ensemble model consists of the base model and realizes improved prediction performance by combining various datasets into a new model to increase the prediction efficiency. This study aims at developing a more efficient model for multi-class classification datasets than the original individual models. In this study, the original ensemble models were compared.

Before the data are input for the test, they are pre-processed. The procedure for preparing the data before testing is as follows: First, various datasets that were derived from the UCI dataset (Center for Machine Learning and Intelligent Systems) were input for testing. Before testing the model with the datasets, the datasets were handled in two steps. The first step involved preparing the data. This step started with data cleaning, which involved cleaning the data and deleting the instances with large amounts of missing data. The second step replaced the missing values via imputation to make the data smoother. The final data preparation stage was data transformation. This stage transformed the data type according to the testing input pattern of the classification model. Part of the input data described the input attributes. Each dataset contains two or more classes to facilitate learning in multi-class classification problems. After adapting the datasets, the classification models were tested, and the obtained accuracy values were compared to identify the best approach for testing on the multiple datasets after the input data were suitably managed for testing with the classification model as the basis for generating the new ensemble model.

Figure 2 illustrates that the overall generation of the new ensemble model, which is comprised of two main parts: base model classification and ensemble model classification. The first part involves selecting a suitable model for combining and generating the new ensemble model. The second part generates the new ensemble model and is divided into two procedures. The notations that are used in this paper are presented in Table 2. The framework imported of multi-class dataset which has the data set divided into 2 sets, Training dataset and Testing dataset, then import and test with the based model. The reason why the proposed model used train and independent splitting in order to the training set is a set in which the model uses the imported dataset train to verify and assess the accuracy of the model. However, to measure error using data set is independent of all the data for choosing the best model which is simulation to real case study. The split independent train-test data has advantage with case of many attributes to be consider many classes in the experiment. The independent data splitting method will be not bias and overfitting when is considered and applied to real situation that shown the robustness of this methodology. In addition, it will be in the selection process based model. When preparation of testing data into the model, at this stage, the accuracy and predicted result will be obtained in Fig. 3.

Fig. 2
figure 2

Overview of the Newweight-voting ensemble model

Full size image
Table 2 Description of notations for generating the heterogenous ensemble model
Full size table
Fig. 3
figure 3

Instance of corerectness TP rate

Full size image

After obtaining the correctness, the next step will select the based model to create a new ensemble model and also will combine strategy with the base model that work together. Each model from the testing dataset have predicted class result of each model. The Classn value from this process is in the process of generating the heterogenous ensemble model, in which each classes are assigned a new Weight value for each class result. The equation is ProbCn*Combine strategyCn. This results in the Probability weight of the class result multiplied by the method or strategy used to combine the models. Combine strategyCn is divided into four methods: Combine strategyCn with TP rate, Recall, Precision, and Fmeasure. For example, the method presented by the research is Combine strategyCn with TP rate-weight, which details the creation of the heterogenous ensemble model and the calculation example as shown in Fig. 4.

Fig. 4
figure 4

Process of TP-rate weight ensemble model

Full size image

Figure 4 shows the TP weight class calculation process, which contains a combination strategy by using TP rate, calculated with the probability of class result (probability weight). This method is caused by a combination of a variety of base models to achieve a new weight Class N. For example, the probability value of class N generated by a model M and multiplies with the TP rate of class N from model M.

The principle of TP-rate calculation is to calculate the value of the model that the class is actually accurately predicted value from 0 to 1. The true positive calculation of the class is divided by the total number of that class, where True positive is the relative value of the predicted class result and actual class result when the predicted class only meets the actual value. The result of class from the calculation was example that shown how to calculate the new weight of class as Fig. 5: Christian was calculated, the TP rate of 0.667 is derived from the predicted value of model1. In addition, model1 as bayse model was given the probability value that were from 0 to 1 which was 0.211. The new weight of model1 of class 1 as probability weigh of m1 mulplies with TP rate fo class1 as 0.141 approximatly.

Fig. 5
figure 5

Example of prediction with TP-rate weight ensemble model

Full size image

After that the processes find the new weight class of all classes in that datasets when calculating to find all new weight classes that have occurred, therefore, The further calculated for the TP weight ensemble model method will be created a ensemble model, if the number of model N is 3 the new weight class of m1 to m3 shown 3 TP-weight Ensemble model in Fig. 6. The TP weight ensemble model is an example of a combination of 3 based models, which called the 3TP-weight ensemble model method. The 3TP-weight were composed of mlp, svm and bayes methods. The Christian class was calculated as new weight class of Christian from mlp model are combined with new weight class from Christian of svm model and new weight class of Christian from bayes model. For example, the 3TP-weight ensemble model is 0.287 by the 9th instances of classes: Christian with the 3TP-weight ensemble model was maximum value. Therefore, the TP weight is calculated of each class, which will be calculated as the WeightCn value of each class result from each model, the WeightCn value is the new probability weight for each class result and then use the weight averaging method to combine the WeightCn of each class from each model to get a NewWeight_Cn and select the class that has the maximum NewWeight_Cn to be the final class result of new ensemble model.

Fig. 6
figure 6

Process of the TP weight voting ensemble model

Full size image

The process of creating a new ensemble model can be described in 4 steps as follows: Firstly, the models are combined by assigning weights to the predicted class. Secondly, a suitable class for generating another new ensemble model is identified in the voting stage. The overall procedure is described in Algorithm 1.

figure a

Algorithm 1 provides an overview of all the processes in the construction of the Newweight-voting ensemble learning model. First, the dataset was input. The dataset was divided into two parts: the training dataset, which is denoted by Tn, and the testing dataset, which is denoted by Ts. The process of generating the Newweight-voting ensemble learning model was divided into two main procedures: generating the base model and generating the Newweight model. Building the new ensemble model begins with the generation of the base model. The model set M = (m1, m2,…, mb), where b is the number of base models for testing, is generated. Another process involves selecting the model based on the accuracy on the testing dataset (Ts). Algorithm 2 presents the procedure for selecting the model for generating the new ensemble model, which results in the base model that is used in the process of combining the models. In the second procedure, the Newweight model was generated by generating a set of weights from the Newweight set W. In addition, a set of probabilities was generated, where the probability value set is P = (P1, P2,…, Pw) and w refers to the total number of instances in the testing dataset (Ts). Moreover, the set for the Newweight model (w1, w2,…, wd) was generated, and d refers to the number of generated New ensemble models. In Algorithm 3, the calculation function for the Newweight ensemble mode is implemented. The class with the largest Newweight was selected as the classification result of the Newweight-voting ensemble model, as presented in Algorithm 4. Then, the model obtains Newweight, which is the probability weight that is selected as the suitable weight of the new class for the New ensemble result in every sample set (Ts). The final result that is obtained from all the processes is the Newweight-voting ensemble learning model.

figure b

Algorithm 2 describes the selection of the base model for the process of combining the models. In this step, the training dataset was input, where the training sample set is N = (n1, n2,…, nu) and u is the total number of instances in the training dataset. The testing dataset contains the sample set S = (s1, s2,…, sw), where w is the total number of instances in the testing dataset from the class set C = (c1, c2,…, cm), in which m in the number of classes in each dataset that is generated from the testing samples (S) and the accepted accuracy value. In the step of selecting the model, the generated base model accepted the probability set P = (P1, P2,…, Pw) and the predicted result set D = (d1, d2,…, dw) that was derived from the probability of classifying the testing sample set (Ts). For generating the base model, the actual class and the predicted class from the samples in Ts were considered. The accuracy value is equal to the number true positives in the dataset multiplied by one hundred. Then, the obtained result is divided by the number of observations in the testing set (S). Having calculated the accuracy value of the base model, the model use to generate a new ensemble model, which was selected by sorting all the models in descending order of their accuracy values. The step of selecting the model for the combination involves deleting the base model that has the lowest accuracy. The base models were repeatedly deleted until three models remained; these models were combined. Thus, the model combination was the 3new-Ensemble, 4new-Ensemble, 5new-Ensemble and 6new-Ensemble model. After generating the base model and obtaining the accuracy value for selecting the base models, the final result was the various models for generating the Newweight-voting ensemble model.

figure c

Algorithm 3 presents a process for calculating weight in the new ensemble model. The traditional weight is replaced by the new weight from the combination strategy that consists of 4 methods for determining the new weight. Traditional base model combined with TP-weight method, Precision-weight, Recall-weight and Fmeasure-weight method.The input data in this process were the testing sample set S = (s1, s2,…, sw), which was calculated for generating the ensemble model with the class set (C) and probability set (P) that were derived from the testing sample set (Ts). Next, the base model set M = (m1, m2,…, mb) is accepted, where b is the number of tested base models. Algorithm 3 begins by calculating the probability values (P) of the sample set (S) via the measure for each model, and the values were between 0 and 1. The collection of probabilities is expressed in Eq. 1. The class result is predicted with the base model (M), and the prediction result set D = (d1, d2,…, dw) of the testing sample (Ts) is generated. This process results in the actual class and the predicted class.

$$ \left[\left( Prob\ {C}_1^{m_1}\right),\left( Prob\ {C}_2^{m_2}\right),\dots, \left( Prob\ {C}_N^{m_N}\right)\right] $$
(1)

True Positive rate-weight ensemble learning is a method in which various factors Comes from the rate that the class predicted correctly. The TP rate was calculated and used to determine the new weight of the new ensemble model, namely, TP-weight. The procedure for calculating the TPweight values by considering the probability of the class result from the prediction model multiplied by the weight, which was derived from the calculated TP rate (Trw) of each testing sample (Ts). The TP rate was calculated from the number of predicted classes that corresponded to the actual class in each sample set divided by the total number for all classes, as expressed in Eq. 2, from the confusion matrix in Table 3.

$$ T{r}_{c_i}^{m_i}=\left[\left(\frac{TPClass\ {C}_1^{m_1}}{N_{m_1}}\right),\left(\frac{TPClass\ {C}_2^{m_2}}{N_{m_2}}\right),\dots, \left(\frac{TPClass\ {C}_N^{m_N}}{N_{m_N}}\right)\right] $$
(2)
Table 3 Confusion matrix table for each model
Full size table

To combine the models, the TP-weight values of each class were combined through the average weight, which combined the TP-weight from each model to determine the suitable class with the largest TPweight. The class became the TP-weight class ensemble result. The TP-weight class can be calculated via Eq. 3.

$$ TPweight\ {C}_i^{m_i}:\left\{\begin{array}{c}\begin{array}{c}\max \\ {}1\le n< Ci\end{array}\ TPweight\ {C}_i^{m_i}>\alpha, \kern0.75em f(x)=f\left(\hat{x}\right)\\ {}\frac{1}{m_i}\ast {\sum}_{i=1}^{m_i}\left({Prob}_{C_i}^{m_i}\ast {Tr}_{C_i}^m\right)\end{array}\right. $$
(3)

For every class (C) in the TP-weight class ensemble result, an equation for the probability set P = (P1, P2,…, Pw) was obtained, where P was a set of probabilities of the class that were derived from the base model. The probability was multiplied by the weight from calculating the TP-weight values (Tr). The weight from the result that the model could correctly predict (D) was compared to the actual results of the testing samples (Ts), where w is the number of instances in the testing dataset (Ts) divided by the number in the base model set M = (m1, m2,…, mb), in which b is the number of base models that are used in the test to generate the ensemble model.

Precision-weight ensemble learning is a method in which various factors Comes from measuring the accuracy of the model by considering class by class. The Precision was calculated and used to determine the new weight of the new ensemble model, namely, Precision-weight. The procedure for calculating the Precision-weight values by considering the probability of the class result from the prediction model multiplied by the weight, which was derived from the calculated Precision (Pr) of each testing sample (Ts). Precision can be calculated from the ratio of the rows that the class predicted correctly based on the actual class. As for the total number of rows from the class result that is predicted correctly and incorrect prediction of the class being considered. Which will look for every class, the results in the import data set as in Eq. 4.

$$ {Prec}_{C_i}^{m_i}=\left[\left(\frac{ TP Cl ass\ {C}_1^{m_1}}{TP_{m_1}+{FP}_{m_1}}\right),\left(\frac{ TP Cl\mathrm{a} ss\ {C}_2^{m_2}}{TP_{m_2}+{FP}_{m_2}}\right),\dots, \left(\frac{ TP Cl ass\ {C}_N^{m_N}}{TP_{m_N}+{FP}_{m_N}}\right)\right] $$
(4)

To combine the models, the Precision-weight values of each class were combined through the average weight, which combined the Prec-weight from each model to determine the suitable class with the largest Prec-weight. The class became the Prec-weight class ensemble result. The Prec-weight class can be calculated via Eq. 5.

$$ Precweight\ {C}_i^{m_i}:\left\{\begin{array}{c}\begin{array}{c}\max \\ {}1\le n< Ci\end{array}\ Precweight\ {C}_i^{m_i}>\alpha, \kern0.75em f(x)=f\left(\hat{x}\right)\\ {}\frac{1}{m_i}\ast \sum \limits_{i=1}^{m_i}\left({Prob}_{C_i}^{m_i}\ast {Prec}_{C_i}^m\right)\end{array}\right. $$
(5)

For every class (C) in the Prec-weight class ensemble result, an equation for the probability set P = (P1, P2,…, Pw) was obtained, where P was a set of probabilities of the class that were derived from the base model. The probability was multiplied by the weight from calculating the Prec-weight values (Prr). The weight from the result that the model could correctly predict (D) was compared to the actual results of the testing samples (Ts), where w is the number of instances in the testing dataset (Ts) divided by the number in the base model set M = (m1, m2,…, mb), in which b is the number of base models that are used in the test to generate the ensemble model.

Recall-weight ensemble learning is a method in which various factors Comes from measuring the accuracy of the model by considering class by class. The Recall was calculated and used to determine the new weight of the new ensemble model, namely, Recall-weight. The procedure for calculating the Recall-weight values by considering the probability of the class result from the prediction model multiplied by the weight, which was derived from the calculated Recall (Rr) of each testing sample (Ts). The Recall value can be calculated from the ratio that the class predicts correctly to the actual class values. The total number of rows that the class predicts is incorrect and is not considered combined with all the correctly predicted rows, which will be finding the resulting class in the imported data set, as in Eq. 6.

$$ {Rec}_{C_i}^{m_i}=\left[\left(\frac{ TP Class\ {C}_1^{m_1}}{TP_{m_1}+{FN}_{m_1}}\right),\left(\frac{ TP Class\ {C}_2^{m_2}}{TP_{m_2}+{FN}_{m_2}}\right),\dots, \left(\frac{ TP Class\ {C}_N^{m_N}}{TP_{m_N}+{FN}_{m_N}}\right)\right] $$
(6)

To combine the models, the Recall-weight values of each class were combined through the average weight, which combined the Rec-weight from each model to determine the suitable class with the largest Rec-weight. The class became the Rec-weight class ensemble result. The Rec-weight class can be calculated via Eq. 7.

$$ Recweight\ {C}_i^{m_i}:\left\{\begin{array}{c}\begin{array}{c}\max \\ {}1\le n< Ci\end{array}\ Recweight\ {C}_i^{m_i}>\alpha, \kern0.75em f(x)=f\left(\hat{x}\right)\\ {}\frac{1}{m_i}\ast \sum \limits_{i=1}^{m_i}\left({Prob}_{C_i}^{m_i}\ast {Rec}_{C_i}^m\right)\end{array}\right. $$
(7)

For every class (C) in the Rec-weight class ensemble result, an equation for the probability set P = (P1, P2,…, Pw) was obtained, where P was a set of probabilities of the class that were derived from the base model. The probability was multiplied by the weight from calculating the Rec-weight values (Rr). The weight from the result that the model could correctly predict (D) was compared to the actual results of the testing samples (Ts), where w is the number of instances in the testing dataset (Ts) divided by the number in the base model set M = (m1, m2,…, mb), in which b is the number of base models that are used in the test to generate the ensemble model.

Fmeasure-weight ensemble learning is a method in which various factors is derived from the weights of the probability of occurrence of the resulting class. The F-measure was calculated and used to determine the new weight of the new ensemble model, namely, Fm-weight. The procedure for calculating the Fm-weight values by considering the probability of the class result from the prediction model multiplied by the weight, which was derived from the calculated F-measure (Fr) of each testing sample (Ts). The F-measure can be calculated from the combination of the performance indicators of the two class result classification: precision and recall. The F-measure shows the average measurement of the accuracy and accuracy of that class can be calculated. Can be obtained from the following equation, where the F-measure is equal to the precision multiplied by the recall value multiplied by 2 times the precision combined with the recall value as in the 8th equation

$$ F- Measure=\frac{2\times precision\times recall}{precision+ recall} $$
(8)

To combine the models, the Fm-weight values of each class were combined through the average weight, which combined the Fm-weight from each model to determine the suitable class with the largest Fm-weight. The class became the Fm-weight class ensemble result. The Fm-weight class can be calculated via Eq. 9.

$$ Fmweight\ {C}_i^{m_i}:\left\{\begin{array}{c}\begin{array}{c}\max \\ {}1\le n< Ci\end{array}\ Fmweight\ {C}_i^{m_i}>\alpha, \kern0.75em f(x)=f\left(\hat{x}\right)\\ {}\frac{1}{m_i}\ast \sum \limits_{i=1}^{m_i}\left({Prob}_{C_i}^{m_i}\ast {Fm}_{C_i}^m\right)\end{array}\right. $$
(9)

For every class (C) in the Fm-weight class ensemble result, an equation for the probability set P = (P1, P2,…, Pw) was obtained, where P was a set of probabilities of the class that were derived from the base model. The probability was multiplied by the weight from calculating the Fm-weight values (Fr). The weight from the result that the model could correctly predict (D) was compared to the actual results of the testing samples (Ts), where w is the number of instances in the testing dataset (Ts) divided by the number in the base model set M = (m1, m2,…, mb), in which b is the number of base models that are used in the test to generate the ensemble model. According to the equation, the number of classes with class n starts with n = 3, where n is the number of the class that was tested in the dataset, with at least three classes for the test with the objective of determining the multi-class classification results. Then, the class for which the combination strategy weight including the TP-weight, Prec-weight, the Rec-weight and the Fm-weight that exceeds α, which a threshold parameter that is set to 0.8 to yield the maximum accuracy rate in this study, was voted as the Newweight class of the Newweight -voting ensemble learning model.

After the calculation in Algorithm 3, the new weight was obtained. The combination strategy set T, was generated, and every sample set (Ts) in each model was calculated. Then, the models were combined by the new-weight ensemble model set T = (t1, t2,…,tj), where j refers to the total number of strategies. In the final process, The new weight ensemble was calculated continuously until the number of new weight ensemble values in the testing sample set S = (s1, s2,…, sw) was equal to the number in the testing dataset (Ts). The obtained Newweight ensemble was deployed to determine the Newweight ensemble class by the Newweight ensemble-voting maximum class. The results of this process were the Newweight ensemble values of each class, namely, each class of every model had a new weight that was derived from the new ensemble model.

figure d

Algorithm 4 describes the process of selecting the Newweight class that has the largest weight as the classification result of the Newweight -voting ensemble learning model. The input data consist of the testing samples (S) and the class (C) of the testing dataset (Ts). Moreover, the sets of the base model (M) and Newweight (W) were input. The procedure of selecting the weight started with the selection of the largest Newweight values that were calculated from every class compared to all the classes in the dataset and from every sample set (S). Next, the Newweight class set G = (g1, g2,…, gw) was generated. This procedure generates a new class ensemble result set (G), where g is the new class that is obtained by calculating the Newweight values and w is the number of instances in the testing dataset (Ts). This procedure results in new classes of ensemble models. Afterwards, a new ensemble model, namely, the Newweight-voting ensemble model, was generated, and the accuracy value was calculated from the testing samples (S) through the obtained Newweight class. Eventually, the results that were obtained by selecting the largest weight for the Newweight class were the sample classes in Ts or all classes in the testing dataset (Ts) from the new ensemble model.

4 Experimental results

This section describes the results of testing the model classifications. Ten datasets were considered in the test, which were derived from the UCI dataset (Center for Machine Learning and Intelligent Systems). Each dataset is detailed in Table 4. The table describes the attributes of the datasets. Moreover, for each of the ten datasets, it specifies the numbers of attributes, instances, and classes. The data were collected as integers and text files for the tests of the model. The largest dataset contained 8124 instances, and the smallest dataset contained 129 instances. The largest number of attributes was 148, and the smallest number was 5 attributes; hence, the test considers the model and the dataset that collected most and fewest attributes. Finally, the attributes of the classes were collected. It was a test of the multi-class classification performance, where the testing dataset with the most classes had 8 classes and that with the fewest classes had 3 classes. For testing of the model and the data, various datasets were considered. The datasets with the largest amount and the smallest amount of data generated the classifiers or predictors efficiently if there were many data instances to be considered in the test. Then, three types of classification models (the base model, the original ensemble model, and the TPweight-voting ensemble model) were tested. In this study, a test was administered to compare two ensemble models, namely, the original ensemble model and the new ensemble model. The obtained accuracy indicates that the Newweight ensemble model realized higher efficiency of the prediction class than the evaluation of the weight of the classification result using the combination strategy, which encouraged the probability of the class to have higher efficiency (Table 5).

Table 4 Description of the datasets
Full size table
Table 5 Parameter settings for each algorithm
Full size table

5 Disscussion

The weight of cost-sensitive have divided into 4 weight measure as true-positive rate. True Positive rate-weight ensemble learning, Precision-weight ensemble learning, Recall-weight ensemble learning and Fmeasure-weight ensemble learning as Table 7. Each combination strategy is assessed by the overall performance measurements based on cost-sensitive learnings. The TP-rate cost-sensitive probability method was given the best performance measurement methods compared to other methods. The advantage of True positive rate-weight ensemble learning concept as expertise of models is used to able to predict only correct a class that is also high accuracy only each classes. Therefore, the experiment of TP weight will be better than other weighting measure. Our propose model focused on different weight measures is used for value combination from N ensemble methods. The overall performance as Precision, Recall, F-Measure, G-mean and Accuracy are measure repeatly that shown robustness of models definitely.

The overall performances of the classification models with between 3 and 7 classes are compared in Tables 6 and 7. This table compares the precision, recall, F-measure, G-measure and accuracy values of the base model classifications of all six models and six homogenous models. The proposed model with the best performance value was 3TP-ensemble model, as the values on nine datasets indicate that the 3TP-ensemble model yields the best results. On another dataset, the best results are obtained by the 6TP-ensemble, which is of the same type as the proposed model. The homogenous ensemble model that performed the best was the random forest model, whereas the approaches of stacking and voting yielded lower accuracy rates. The Bayes classification models realized satisfactory performance. Therefore, our proposed model was recently improved to enhance the efficiency in predicting the base classification results and to yield high precision, recall, F-measure and G-mean values in classifying the datasets, as shown in Fig. 7.

Table 6 TP-weight cost-sensitive probability of ensemble model
Full size table
Table 7 comparision of all measure of cost-sensitive probability for ensemble model
Full size table
Fig. 7
figure 7

Evaluation measure (Precision, Recall, F-Measure, and G-Mean) performances of each data set and model

Full size image

The multi-classes datasets in Fig. 8 were divided into three groups: First, the datasets with between 3 and 4 classes were grouped, which are balance scale, lymphographic, vehicle, grass grab, car evaluation, and user knowledge modelling. The best model is 3TP-ensemble, whereas the percentage accuracy rate is the same as those of classification models MLP and Bayes. Second, the datasets with 5 and 6 classes were grouped, which are eucalyptus soil and urban land cover. The highest accuracy rates are realized by 3TP and 6TP, respectively. This type of proposed model yields the best results. Finally, the datasets with 7 and 8 classes were grouped.

Fig. 8
figure 8

Accuracy performance versus the number of classes for multi-class classification

Full size image

In addition, the F-measure performance of 3TP-ensemble is compared with those of other homogenous models in Reference [14], which proposed KFHE-e (noise 5%) and KFHE-1 (noise 5%), which were also based on the limitations of current multi-class classification ensemble algorithms. Our proposed model, namely, 3TP-ensemble, yields F-measure values of 0.909, 0.75, and 0.463 on the balance scale (3 classes), lymphography (4 classes) and flags (8 classes) datasets, as shown in Fig. 9. The percentage accuracy of 3TP-ensemble is the highest, namely, 85.74%, on the Lymphography dataset (4 classes) compared with mlp:NS ECOC V1, mlp:NS ECOC V2, svm: NS ECOC V1 and svm: NS ECOC V2 in reference [4] and NP-AVG and NP-MAX in reference [37], as shown in Fig. 10. The experimental results demonstrate the robustness and high performance measure values of the 3TP-Ensemble model.

Fig. 9
figure 9

F-measure performance comparison with other works

Full size image
Fig. 10
figure 10

Accuracy performance comparison with other works (Lymphography dataset)

Full size image

The TPweight ensemble could yield the most suitable predicted class among the new multi-classes of the classification result with increased accuracy. According to our approach, the model that provided the highest average accuracy value was the TPweight-voting ensemble model. Comparing the best accuracy values on each dataset between the homogenous ensemble model and the newly proposed ensemble model, the TPweight ensemble realized higher efficiency for predicting the result than the ten datasets and the original ensemble model. The TPweight-voting ensemble model was proposed for increasing the efficiency of predicting the classes in various datasets with multi-class labels in practice. The model encouraged the prediction in each sample set Ts to obtain the most suitable class, which was deriven by parameter α, which reflected the reliability of probability weight for each model, in combination with the TP rate. According to the experimental results for this approach, it could increase the accuracy value of the prediction to a higher value than those that were realized by other models of the original ensemble model.

6 Conclusions

In this research, we present a novel supervised cost-sensitive weighted based on Ensemble learning classification. By the framework of the method cost-sensitive probability weighted based on ensemble learning is introduced with the machine learning concept of cost-sensitive weighted ensemble learning which takes advantage of combining results to improve predictive performance -sensitive weighted is designed to reduce class bias occurring as a result of classification The focus is on the combination strategy that combines weighting with the method of weight voting, which is a method for determining the appropriate weight value. The method presented is based on instructional learning. That is, to learn the model first by dividing test data sets into training data and testing data in order to design a class result. For a multi-class dataset test data set, we demonstrate comprehensive results when compared to methods and apply it to 10 multi-class data sets. We clearly show that the method cost-sensitive probability. Our weighted based probability on ensemble learning has superior methods other state-of-the-art features in Accuracy, Recall, F-measure, G-mean and Accuracy, and reduce misclassified performance. And achieve accuracy values ​​based on good evaluation of classifying multi-class data. Our methods are efficient and stable for problem sets in decision making processes. The multi-class dataset for future work will explore the management of selection base model for creating a new ensemble model to enhance the classification of data sets resulting from the combined prediction.