Plan merging by reuse for multi-agent planning

Abstract

Multi-Agent Planning deals with the task of generating a plan for/by a set of agents that jointly solve a planning problem. One of the biggest challenges is how to handle interactions arising from agents’ actions. The first contribution of the paper is Plan Merging by Reuse, pmr, an algorithm that automatically adjusts its behaviour to the level of interaction. Given a multi-agent planning task, pmr assigns goals to specific agents. The chosen agents solve their individual planning tasks and the resulting plans are merged. Since merged plans are not always valid, pmr performs planning by reuse to generate a valid plan. The second contribution of the paper is rrpt-plan, a stochastic plan-reuse planner that combines plan reuse, standard search and sampling. We have performed extensive sets of experiments in order to analyze the performance of pmr in relation to state of the art multi-agent planning techniques.

1 Introduction

Consider a warehouse where everyday hundreds of orders are received and have to be delivered into the shortest period of time. First, the warehouse workers need to get the corresponding products to complete each order. In order to speed up the process, some robots are available to fetch the products for them. Workers will only focus on receiving the products and checking that the order has been completed. After that, orders need to be delivered to the clients’ addresses using trucks. When reasoning about this scenario, some coordination systems are needed: (1) a system should divide up the work into the workers; (2) also robots should move autonomously and individually through the warehouse avoiding collisions; and (3) each driver needs to be assigned a set of deliveries based on the deliveries’ location or some other minimization cost feature to improve efficiency. Automated Planning is the subarea of Artificial Intelligence that reasons on how to synthesize sequences of actions for solving tasks within this kind of scenarios. When multiple agents are involved (e.g robots, workers, drivers) or some coordination is needed, we talk about Multi-Agent Planning (MAP).

MAP aims at solving planning tasks for/by a set of agents. Usually, it is assumed that these agents collaborate to reach common goals. Two main approaches have been commonly used: centralized and distributed. The former builds a common plan for all agents by merely considering the agents as another planning resource. This was the usual way of dealing with MAP tasks in the Automated Planning community until recently. When MAP complexity was studied in [10], Brafman and Domshlak showed that MAP’s complexity depends on the number of agents, the difficulty of their individual planning tasks and the number of interactions between agents (points where some coordination is needed). Thus, centralized planning is usually more efficient when computing a plan with a reduced number of agents and goals. On the other hand, in distributed planning, agents generate their plans either synchronously with the rest of agents as in fmap [45] or ma-fs [40], or independently [36]. When planning synchronously, agents need to share information during planning. Thus, these approaches incur in a high communication cost. Also, they require to modify the code of an existing planner in order to accommodate the communication among agents. In the case of planning independently, agents do not employ any communication among agents while planning. Therefore, they have to later merge their plans. In that case, some merging function is applied to the set of plans to generate a joint plan [17, 35]. Planning domains can vary from loosely-coupled, where there is almost no interference among the agents’ plans to tightly-coupled, with higher interaction [10]. Plan merging has been shown to work best in loosely-coupled domains.

Regarding MAP in real world scenarios, in most domains the solution should be executed in the shortest possible time. Hence, concurrent execution of agents’ actions is needed. One way to deal with the task of finding the plan that minimizes the number of concurrent execution steps (makespan) consists of planning explicitly taking into account that minimization criteria. Another alternative consists of generating a sequential plan and convert it into a parallel one. The parallel plan is partially-ordered, which means that a set of actions that do not have dependencies among them can be executed at the same time step. By doing so, we can use any standard total-order planner in the state-of-the-art to generate the set of sequential MAP plans, and then apply some parallelization algorithm to improve the makespan.

This paper focuses on classical deterministic planning tasks, where a set of agents should find a common plan. We describe a new MAP approach, whose objectives are to: efficiently solve MAP tasks by combining distributed and centralized MAP techniques; directly reuse existing planning techniques without further code modification; effectively apply factorization to divide the main task into subtasks regarding some minimization criteria such as plan length or makespan; and automatically adjust to the interaction level among agents and goals. In order to satisfy those objectives, we employ three off-the-shelf planners inside our first contribution: a MAP algorithm called Plan Merger by Reuse (pmr). Experimental results show that our approach is competitive with state-of-the-art techniques and planners, as the ones that participated in the first Competition of Distributed and Multi-agent Planners (CoDMAP).¹

We also propose a novel use of planning by reuse as plan repair for plan merging. Planning by reuse has been widely employed in areas such as Case-Based Planning [7], or replanning when plan execution fails [19]. A planning-by-reuse planner works best when the invalid plan and the final plan are similar, as only a small set of actions need to be changed or added to the invalid plan for it to become valid. This situation is usually given on easy-to-solve interactions e.g grabbing the same resource or passing through the same door at the same time step. As a result, the planner will be able to efficiently generate a valid solution without generating an entire valid plan from scratch.

However, depending on the features of the given problem, interactions might be harder to fix regarding plan immutability e.g. when an agent drives to pick up a package but another agent has already picked it up or when a resource has been consumed and is not available anymore. As a result, new actions are applied to fix the current state of the problem, as agents’ original plans have been forcedly changed. Usually, an alternative path has to be found for those agents that still need to achieve some goals. Thus, the final valid plan turns out to be completely different from the invalid plan. Plan-reuse planners’ performance noticeably decreases on this second scenario. They cannot reuse most of the actions so they look up for new actions on the search space closer to the invalid plan, but at the same time, they are still reusing the old actions whenever possible.

In order for pmr to perform better on both scenarios, we have also developed a new algorithm called rrpt-plan, which is our second contribution. rrpt-plan is a stochastic plan-reuse planner that combines search, sampling and plan reuse, performing one of the three stochastically on each iteration depending on the values of two parameters that represent the probability of executing each one of the three techniques. This contribution is inspired on two previous works, errt-plan [6] and rpt [1]. Experiments not only show how rrpt-plan can adapt itself to both scenarios but also how it can be included inside pmr as its plan-reuse planner, obtaining similar results as the other state-of-the-art plan-reuse planners and adapting better to a wide variety of scenarios.

A version of pmr was published in a workshop [33] in 2014, when the work was still into a very preliminary stage. We also participated in CoDMAP (June 2015) using that version. The main differences regarding the algorithm are that in the workshop paper:

• rrpt-plan had not been yet designed; instead, we were using lpg-adapt as plan-reuse planner.

• There was not a centralized phase in case the individual planning phase failed.

• The individual planning phase was using lama with Greedy-Best First Search (GBFS) and unitary costs (lama-unit-cost), instead of using GBFS with costs (lama-first). Hence, the quality of individual plans was worse in general, as lama-unit-cost cannot minimize the cost metric.

• The input invalid plan sent to the plan-reuse planner (lpg-adapt) was the joined parallel plan instead of the joined sequential plan. The input plan is read sequentially in lpg-adapt and rrpt-plan. Thus, altering the actions’ order before running a plan-reuse phase did not benefit the success of plan-reuse. Sending as input a parallel plan did not have any advantage.

The main contributions of this paper are:

• A new MAP system, pmr, whose main focus is on improving the work load among the agents, resulting in an improvement of the makespan.

• Development of a new plan-reuse planner, rrpt-plan, that interleaves search, sampling and plan-reuse to solve replanning tasks. It can be included as the plan-reuse planner of pmr.

We have also contributed by modelling three domains to test concrete features of pmr and rrpt-plan:

• Definition of a new domain, Hammers, as a proof-of-concept to exemplify and analyze the impact of different plan-reuse approaches to solve MAP tasks. This domain is explained in Section 5.2.

• A variation of the classical IPC Rovers domain called Rover-graph which changes the usual waypoints’ topology. This domain is explained in Section 5.6.

• New version of the Depots-Robots [5], inspired in the Kiva-Amazon robots, which now contains the pods organized in vertical columns. This domain is explained in Section 5.6.

Finally, we contribute with an analysis on the performance of pmr and rrpt-plan. We have identified domains’ features that characterize when these two techniques work well. This analysis has been performed from the results obtained of an extensive experimental evaluation:

• A CoDMAP rerun using the new pmr version jointly with rrpt-plan. We compared our contribution against the CoDMAP winners.

• Evaluation of rrpt-plan parameters to choose the best configuration. We created a benchmark of problems where the number of goals was increased to analyze the impact on rrpt-plan performance.

• Comparison of performance between rrpt-plan and lpg-adapt.

• Evaluation of pmr jointly with rrpt-plan in loosely-coupled and tightly-coupled domains.

This paper is organized as follows: Section 2 presents a formal definition of the MAP task and its preprocessing. Section 3 describes the pmr algorithm and its different phases and properties. Section 4 presents our second contribution, the rrpt-plan algorithm. Then, Section 5 shows the experiments and results of comparing both pmr and rrpt-plan with other similar approaches. Section 6 presents related work. And, finally, in Section 7 we present some conclusions and directions for future work.

2 Multi-agent planning formalization

In this section, we first formalize the MAP task and briefly mention some MAP languages that are being used to define those tasks. Then, we also describe the way we handle the agentification and factorization of the problem.

2.1 Multi-agent planning task

Here we first define the standard planning task, using a propositional description. We also describe each of its elements and its lifted representation, which is known as the domain and problem representation in the planning community. After that, we define the MAP task and its components. In Automated Planning, the planning task is defined as follows:

Definition 1

Planning Task (Single Agent). A single-agent strips planning task [16] is a tuple π = 〈F,A,I,G〉, where F is a set of propositions, A is a set of instantiated actions, I ⊆ F is an initial state, and G ⊆ F is a set of goals.

Each action a ∈ A is described by (1) a set of preconditions (pre(a)) that represent literals that must be true in a state to execute the action; (2) and a set of effects (eff(a)), which are literals that are expected to be added (add(a) effects) or removed (del(a) effects) from the state after the execution of the action. The definition of each action might also include a cost c(a) (the default cost is one).

A state s ⊆ F describes the current situation of the environment. In order to transit to a different state s’, an action a must be applicable to s. The application of an action a in a state s is defined by the function γ(s,a) = (s∖del(a))∪ add(a) if pre(a)⊆ s. Otherwise a cannot be applied in s.

The solution of a planning task is a plan, which is a sequence of actions π = (a₁,…,a_n) that, if executed in order from the initial state, reaches another state s_G where all the goals in G are satisfied, G ⊆ s_G. Thus, the execution of a plan π from a state s can be defined as:

$$ {\Gamma}(s, \pi) = \left\{ \begin{array}{ll} {\Gamma}(\gamma(s, a_{1}),(a_{2},...a_{n})) &\ \ if \ \pi \neq \emptyset \\ s & \ \ if\ \pi = \emptyset \end{array}\right. $$

(1)

Our planning task is encoded in the propositional fragment of the standard Planning Domain Description Language (PDDL) [18]. It is automatically generated from the PDDL description of a domain D and a problem P. The domain in PDDL contains a hierarchy of types to characterize the problem objects; a set of predicates and a set of functions, respectively, whose instantiations generate the facts in F; and a set of generalized actions, defined using variables—parameters, par(a). The instantiations of those actions with problem objects generate the actions in A. A planning problem in PDDL contains a set of objects (instances of types in the domain); the initial state I; the set of goals G; and an optional metric to define the optimization criteria.

In order to work with multiple agents in Automated Planning, we have to define the Multi-Agent Planning Task.

Definition 2

Multi Agent Planning Task. We consider a multi-agent setting where a set of m agents, Φ = {ϕ₁,…,ϕ_m}, has to solve the task π. We define the MAP task M as a set of planning subtasks, π_i, one for each agent. Thus, M = {π₁,…,π_m} being i = {1...m}. For representation convenience, an alternative equivalent lifted representation of each single-agent planning task in PDDL would be a pair (domain, problem): π_i = 〈D_i,P_i〉.

Since there does not exist yet a standard to represent MAP tasks, as PDDL for planning tasks, there have been several proposals. MAP usually considers that agents can have private information. Therefore, these proposals also include a way of describing agents’ private information. MA-STRIPS [9] takes as input a standard PDDL description, as well as a list of agents, and automatically extracts the public and private components.

MA-PDDL [29], which was used in CoDMAP [43], is an extension of PDDL where agents and their private knowledge are explicitly defined in the input files.

Therefore, when working on MAP, it is common to find information that either belongs to the agents or belongs to the elements of the environment. When maintaining agents’ privacy, the former is the one that should be hidden (total or partially) to other agents. We prefer to attach the property of privacy to the information available to agents (states, goals and objects) as in [5].

In that work, the information is parameterized by the user indicating the agent’s type and by setting the types and predicates as private or public. We followed the same procedure in our approach but omitting privacy issues. In order to prevent confusions, we will refer to agent’s information and public information. Thus, we have considered the agent’s predicates as the elements that, when instantiated, will generate the propositions that belong to each agent. This process is applied during factorization to transform the original planning task π into the MAP task M.

Once the MAP task has been defined and agents’ and public information described, this is our definition of the individual planning task:

Definition 3

Individual agent task (π_i). For each agent ϕ_i ∈Φ^′ a specific task π_i is generated, which is described as a tuple π_i = 〈F_i,A_i,I_i,G_i〉 where:

• $F_{i} = (F_{\phi _{i}} \cup F_{pub} )\subseteq F \mid$$F_{\phi _{i}}$ and F_pub are disjoint sets, $F_{\phi _{i}} \cap F_{pub} = \emptyset$.

• $A_{i} = (A_{\phi _{i}} \cup A_{pub} )\subseteq A \mid A_{\phi _{i}}$ and A_pub are disjoint sets, $A_{\phi _{i}} \cap A_{pub} = \emptyset$.

• $I_{i} = (I_{\phi _{i}} \cup I_{pub} ) \subseteq I$ is the initial state of agent ϕ_i, where $I_{\phi _{i}} \subseteq F_{\phi _{i}}$ and I_pub ⊆ F_pub.

• G_i ⊆ G is the set of ϕ_i’s assigned goals.

In Definition 3, the set of agent’s propositions is identified as $F_{\phi _{i}}$ and the set of agent’s actions as $A_{\phi _{i}}$.

$F_{\phi _{i}}$ includes ϕ_i’s propositions that have been instantiated through the generic agent’s predicates, i.e. the predicates parameterized as private and the predicates that include as argument either the agent or one of the object types parameterized as private that belongs to the agent. For example, agent’s location, agent’s features, agent’s instrument, or agent’s instrument’s features.

$A_{\phi _{i}}$ represents ϕ_i’s instantiated actions. They were generated from the generic actions that included the agent itself and/or the agent’s objects as argument. For instance, in the Rovers domain, they could include actions as “take a picture” that requires the rover, or “camera calibration” that only mentions the camera of a given rover.

The set of public propositions is identified as F_pub and the set of public actions as A_pub. We assume that both the complete initial state, $I=\cup _{i=1}^{m} I_{i}$, and the set of goals, $G=\cup _{i=1}^{m} G_{i}$ are consistent; that is, they are conflict-free (there are no mutexes). In Automated Planning, a set of propositions M ∈ F is mutually exclusive (mutex) if there is no state s that may be reached from the initial state by application of any sequence of actions in A, such that M ⊆ s.

MAP planners need some preprocessing to generate the set of planning tasks for each agent, π_i. The process to obtain the MAP task from the planning task as well as the individual planning tasks is explained in the following subsection.

2.2 Agentification and factorization

In order to work on MAP environments, agentification and factorization are two methods to simplify the planning task. Agentification consists on identifying which are the agents of the given problem. This identification can be done in many different ways. If the planning task is defined using MA-STRIPS, the agents are given as input to the planner along with the domain and problem. Inside MA-STRIPS there is no information that explicitly indicates which type of agent can execute which action. Alternatively, if the planning task is defined using MA-PDDL, the agents are explicitly included on the domain and problem files. Each action has a keyword :agent in order to know which type of agents can execute the action.

Our approach works with both language definitions, either by explicitly receiving the list of potential agents or by getting the information through the :agent keyword of MA-PDDL to create the agents’ list afterwards. It is important to choose as agents the elements of the domain that suit best the division of tasks. An advantage of dealing with MAP domains is that, in most of them, agentification comes naturally and the agents-to-be are immediately identified.

Factorization is the ability to divide a planning problem into subproblems using some criteria. For instance, it is common to apply factorization dividing the problem regarding goals [3, 15]. In our approach, the problem is first factorized from the agents’ point of view. The aim is to transform the planning task into easier tasks so that each agent can solve its factorized problem individually. Definition 2 describes the factorization of the Planning Task in terms of agents, which gives as a result the Multi-Agent Planning Task.

Regarding goals, current MAP techniques in the Automated Planning community consider the MAP task M where goals are considered achievable by the collaboration of all agents [40, 45]. So goals are pursued by all agents and no further factorization is applied. In other areas, as in Multi-Agent Systems or robotics, some approaches first perform task allocation (assignment of each public goal to a single agent) to improve the efficiency of problem solving [13, 21]. Inspired by that, our approach has a second factorization step, which consists on dividing the goals among the agents by following some strategy. Specifically, some of the goal assignment (GA) strategies defined in a previous work [3] are included in pmr. In particular, we use:

• All, that assigns all goals to all agents;

• Best-cost (BC), where each goal g ∈ G is assigned to the agent ϕ_i ∈Φ that could achieve it with the least cost; and

• Load-balance (LB) that first calculates $k=\left \lceil {\frac {|G|}{|{\Phi }|}}\right \rceil$, which will be the average number of goals per agent. Then it assigns each goal g ∈ G to the best agent ϕ_i ∈Φ as in BC. This strategy avoids, if possible, assigning more goals than k to each agent.

As in [3], in order to assign a goal g ∈ G to an agent ϕ_i ∈Φ, a relaxed plan is computed using the ff heuristic [24]. Depending on the strategy selected, GA might leave some agents without any assigned goal. Hence, the output of goal allocation is a new MAP task, M^′, with goals assigned to a set of n agents Φ^′⊆Φ [5]. If the agent’s cost of a goal is infinite (it cannot be reached), the goal is not assigned to that agent ϕ_i ∈Φ but if there is some goal that cannot be reached individually by any agent, the previous process assigns that goal to all agents. Then, Φ^′ = Φ since all agents will have at least one goal assigned. Further details on the consequences of this situation will be given on Section 3.

After the second factorization step has been applied, each π_i of the MAP task M^′ is formally described by Definition 3. Also, M^′ can be defined in terms of π_i or using the lifted representation.

Definition 4

Factorized MAP task (M^′). Being π the tuple described in Definition 4 and n = |Φ^′|, the M^′ task is defined as:

$$ \begin{array}{@{}rcl@{}} M^{\prime} = \langle {\Pi}_{1},..,{\Pi}_{n} \rangle = \left\{ \langle F_{1} ,A_{1},I_{1},G_{1} \rangle ,..., \langle F_{n} ,A_{n},I_{n},G_{n} \rangle \right\} \end{array} $$

Definition 5

Lifted representation of the M^′ task. Considering the lifted representation of π_i = 〈D_i,P_i〉 and being n = |Φ^′|, the M^′ task is defined as:

M^′ = 〈π₁,...,π_n〉 = {〈D₁,P₁〉,〈D₂,P₂〉,...,〈D_n,P_n〉}

We now describe through a simple example how agentification and factorization work before generating and delivering to pmr the input M^′.

Example (Logistics domain)

Given a Logistics domain where trucks need to deliver packages to a set of locations, our example contains three trucks and four goals (package-delivery to its destination). Trucks initially located at CityA can traverse any kind of road (lined, dotted). Trucks from other cities can only traverse lined roads. Also, only trucks marked with “F” can deliver fragile “F” packages. The initial state of the problem is shown in Fig. 1. The destination of each package is described inside the square box of the figure. Costs of driving between each pair of cities are shown over the lined/dotted city connections. There is also a cost of 1 for loading and unloading a package. Agentification comes naturally on this example, as trucks are the ones performing the actions. As a result, the first factorization generates the MAP task M, which contains an individual planning task for each truck. Table 1 shows an example of the estimated cost per truck and goal when delivering each package to its destination.

Fig. 1

Example of a simple Logistics problem where trucks (ϕ₁, ϕ₂, ϕ₃) have to deliver some packages to the destinations (g₁,g₂,g₃,g₄) specified on the square box. Trucks marked with “F” (ϕ₁, ϕ₂) are the only ones allowed to transport fragile packages (p₁,p₄). Trucks that start in CityA can traverse any kind of road (lined, dotted). Trucks from other cities can only traverse lined roads

Table 1 Example of an estimated-cost matrix from the problem pictured in Fig. 1

Taking the information presented on Table 1 and the three GA strategies mentioned before, goals would be assigned to each agent as follows:

• All: ϕ₁(g₁,g₂,g₃,g₄), ϕ₂(g₁,g₂,g₃,g₄), ϕ₃(g₁,g₂, g₃,g₄)

• Best-cost: ϕ₁(g₄), ϕ₂(g₁,g₂,g₃), ϕ₃(∅)

• Load-balance: ϕ₁(g₄), ϕ₂(g₁,g₂), ϕ₃(g₃)

The second factorization of the MAP task M varies depending on which GA is chosen. The GA strategy All assigns every goal to every agent even if the goal cannot be reached (represented with ∞ cost). There are three cases where ∞ cost is returned by h_FF: Cost(ϕ₁,g₃) because the truck ϕ₁ cannot traverse dotted roads as it does not start at CityA; Cost(ϕ₃,g₁) and Cost(ϕ₃,g₄) because the truck ϕ₃ cannot transport fragile packages (marked with “F”). The Best-cost (BC) strategy does not assign any goal to ϕ₃ even though it can reach two of the four goals. Instead, they are assigned to ϕ₂, who is the first on the list of agents that can reach (g₂,g₃) with an estimated cost of 2. Finally, Load-balance (LB) returns an average of k = 2. Thus, it assigns two goals per agent. After assigning g₁ and g₂ to ϕ₂, ϕ₂’s goal capacity has been reached. Then, g₃ is assigned to ϕ₃ even though ϕ₂ could achieve it with less cost.

After this process is completed, the M^′ task is generated and our algorithm pmr would receive the following as input: (1) if LB or All were chosen, the MAP task M^′ = {π₁,π₂,π₃} (2) if BC was chosen, M^′ = {π₁,π₂}, as ϕ₃ has no assigned goals.

3 Plan Merging by Reuse (PMR)

In this section, our first contribution, called pmr, is presented in detail. A general description as well as the description of each one of its components is included in the following subsections.

3.1 Algorithm

Plan Merging by Reuse (pmr) receives as input a MAP task (M^′). As shown in the pseudocode in Algorithm 1, M^′ is formed by a number of π_i tasks, each of them containing the information included in Definition 3. In the first step, each agent in ϕ_i ∈Φ^′ builds its plan individually (line 1). Then, we find three different scenarios:

• If all agents failed at generating a plan (lines 2-4), a centralized planner solves the MAP task Mjoined′ from Definition 6.

• Otherwise, the plans are merged. If the merged plan is valid, pmr returns it as the solution to the MAP task (lines 6-7).

• If the merged plan is invalid, pmr calls a plan-repair planner that can perform plan reuse, sending the merged plan and Mjoined′ as input. The plan-repair planner will try to find a solution based on the actions of the input plan (lines 9-10).

Given that we are dealing with MAP tasks, it is expected that agents can execute the actions in their plans in parallel when possible. Thus, the aim of pmr is to minimize the makespan. In non-temporal domains, we refer to the makespan as the length of the parallel plan (number of execution steps, where several actions can be executed at each execution step). Therefore, in any of the three scenarios, if the plan is valid, it is parallelized to improve the makespan of the solution as explained later on Section 3.5.

pmr contains three off-the-shelf planners: one for each agent to plan individually, P (it can be the same or a different planner); another one capable of applying plan repair by reusing an invalid/incomplete plan (R); and the third one, which is employed by pmr when all the individual agents’ planning tasks fail. In this work we use the same planner, P, used by individual agents to run the centralized phase. In order to check the validity of the plans, VAL, the validator from the International Planning Competition, has been used [25]. The following sections explain in detail the main steps and the properties of pmr.

3.2 Planning

In this first step, each agent ϕ_i ∈Φ^′ receives as input the description of its domain and problem. The problem includes the facts, actions and goals assigned to ϕ_i. Each agent invokes a planner P to solve its planning task. As a result, a partial solution π_i to the overall MAP task is obtained per agent. Any state-of-the-art planner can be used for this task and each agent could use a different planner.

When the distributed phase fails

If all agents fail to generate a solution, it could mean that more than one agent might be needed to achieve the goals. In those cases, pmr resorts to a centralized planner. Centralized planners usually receive as input the lifted representation of the planning task (one domain and one problem file). Thus, the elements of the MAP task M^′ should be first joined as follows:

Definition 6

The Mjoined′ task.

$$ \begin{array}{@{}rcl@{}} M'_{\text{\textit{joined}}} &=& \left\langle \bigcup\limits_{i=1}^{n} F_{\phi_{i}} \cup F_{pub},\bigcup\limits_{i=1}^{n}A_{\phi_{i}} \cup A_{pub}, \bigcup\limits_{i=1}^{n}I_{\phi_{i}} \cup I_{pub}, \bigcup\limits_{i=1}^{n}G_{i} \right\rangle \end{array} $$

$$ \begin{array}{@{}rcl@{}} {M^{\prime}}_{joined} &=& \{\bigcup\limits_{i=1}^{n} {\Pi}_{i} \} = \{D_{joined},P_{joined}\}\\ &=& \{\bigcup\limits_{i=1}^{n}D_{i},\bigcup\limits_{i=1}^{n} P_{i}\} \end{array} $$

The centralized planner receives as input Mjoined′ and finds a solution from scratch to the MAP problem (π_cen).

In Algorithm 1, we have used the same planner for the centralized phase as in the individual calls. However, since pmr is planner-independent, we could have used any other planner.

When distributed phase works

If at least one agent generates a solution to its task, pmr merges all the solutions. We have implemented a basic merge strategy, which is a simple concatenation. Other more elaborated techniques could be used to improve the performance of pmr. The output of the merge process is the plan π_seq. pmr checks if that plan is valid. If so, pmr will parallelize it as explained below. Finally, if π_seq was invalid, the plan reuse phase will be executed, providing Mjoined′ and π_seq as input.

Example (Logistics domain)

Following the example explained at the end of Section 2, we want to illustrate what would be the result after pmr’s individual planning phase. The goal strategy chosen is still LB. The assignment of agents and goals was GA = ϕ₁(g₄), ϕ₂(g₁,g₂), ϕ₃(g₃). Agents are ordered by name. ϕ₁ is the first one to start planning.

3.3 Plan Reuse

We assume that often the current invalid plan does include most of the actions that would make it a valid plan. Thus, by using plan repair techniques we are expecting pmr to generate a plan faster than planning from scratch. In the worst case, plan repair is PSPACE-complete [38]. But, in practical terms and under our assumption of closeness between the invalid plan and the valid one, plan repair techniques have shown good results [19].

Usually, planners that perform plan repair receive three inputs: a domain, a problem and a plan. Examples of plan-repair planners are lpg-adapt [19] and our contribution rrpt-plan that will be explained on Section 4. We use such a planner to transform an invalid input plan (π_seq) into a valid plan. In case the plan-repair planner solves the planning task and the plan is valid (π_reuse), pmr parallelizes it to improve the makespan and returns it.

Example (Logistics domain)

For instance, following the example explained at the end of Section 2, two scenarios could trigger pmr’s plan reuse phase. The first scenario is given when solving the problem using the goal strategy All. This implies that each agent has to plan individually to deliver the four packages marked as goals. After concatenation (π_seq), ϕ₂ will not find any of the packages at the original locations, as ϕ₁ has already moved them. The same happens to ϕ₃. Thus, π_seq is invalid and needs to be fixed. pmr will call the plan-reuse phase. The second scenario is given when two agents need the same resource. For instance, suppose that trucks need drivers in order to transport the packages. If there was only one driver per city, trucks would need that driver to move from one city to another. Each agent would need to pick up a driver, and independently of the goal strategy selected, two trucks could pick the same driver during the individual planning phase. When concatenating the plans, ϕ₂ could have picked up the same driver as ϕ₃ (as they are located at the beginning at the same city). Thus, a failure would arise when ϕ₃ needs the driver as she is not at CityA.

3.4 Centralized planning

Centralized planning within pmr is only used when the individual planning phase fails. For instance, a situation where pmr would fail using the same example presented at the end of Section 2 is the following: if the All GA strategy was selected instead of LB or BC, as agents have to achieve every goal from the problem individually, ϕ₁ and ϕ₃ would not be able to make it because they cannot achieve all goals (see Table 1). ϕ₁ has an estimated cost of ∞ for g3 as well as ϕ₃ for g1 and g4. Additionally, if ϕ₂ was not able to transport fragile packages, g1 and g4 could not be delivered either. As a result, π_seq would not be generated and the centralized planner would be called instead.

3.5 Parallelization

Most state-of-the-art planners return sequential plans, since they do not usually consider minimizing the temporal execution window. As said before, in order to benefit from the existence of multiple agents executing in parallel a plan, we parallelize either the sequential plans generated by merging, the centralized plan, or the repaired plan. This function transforms the plan received as input into a parallel one.

It performs two steps: converting the input total-order plan into a partial-order one by a similar algorithm to [47]; and parallelizing this partial-order plan by ordering actions in the first time step that satisfies all ordering constraints in the partial-order plan. The cost of the parallelization is quadratic in the number of actions in the plan.

Due to the parallelization process, more than one action might be executed at each plan step, as long as they are not mutex. In loosely-coupled domains, parallelization usually reduces the makespan of the solution plan proportionally to the number of agents. As actions and predicates of one agent are independent of those of the rest of agents, a considerable amount of actions can be executed in the same time step. However, as the level of interaction increases (e.g tightly-coupled domains), parallelization will not cause such an impact in terms of makespan.

Example (Logistics domain)

Following the example, the plan π_seq described in Section 3.2 is validated by VAL. As this was a simple example with no interaction among agents, the plan is valid and the parallelization phase starts by receiving π_seq as input. The resulting plan, π_PMR, will be:

3.6 Properties

As most work on plan merging, pmr performs suboptimal MAP. Even if we used optimal planners at each planning step of the algorithm, the simple merging of individually generated plans cannot assure optimality. Another reason for being suboptimal is the GA step, but it can be solved by using the All strategy. This GA strategy is the only one that ensures that all agents are included in the process of planning. Thus, an optimal solution could be found. In relation to soundness, each individual (agent) plan is valid, when using sound planners. If the centralized planner is invoked, soundness is ensured by using a sound planner. However, after merging, soundness cannot be ensured because each agent plans separately for a subset of goals and the merged plan might not be valid due to the agents’ interactions within the elements of the domain. Thus, pmr checks for validity, and if the plan is invalid, the soundness depends on the plan repair step. In summary, pmr is sound if the planners used are sound (both P and R).

In relation to completeness, pmr is complete if all goals are assigned to all agents and the off-the-shelf planners (planners and plan repair planner) used are complete too. Under those conditions, the first planning step of each agent (individual planning) is globally incomplete (since there might be a joint plan that is not contained in the space of each agent working separately), but it is locally complete for each agent. Once the plans are generated, pmr calls either a centralized planner or the plan repair strategy, which are both complete if the chosen planners for P and R are as well. The parallelization step does not affect the completeness. Finally, pmr has the same complexity as Automated Planning and MAP, which is PSPACE [9, 12].

4 RRPT-plan

As it was briefly mentioned in Section 1, among the spectrum of different scenarios that can be given in trying to repair a plan, the most frequent one is when the invalid input plan is very similar to the final solution. Plan reuse will be very efficient as most of the final plan’s actions are already on the invalid input plan. Thus, the planner reuses most of the invalid plan actions and has only to include a small set of new actions to transform it into a valid one. However, sometimes, the solution plan should be completely changed, as when trying to solve the Rovers scenario described on Fig. 2. In order to be more efficient, combining search and plan-reuse would help any plan-reuse planner to better solve a wide variety of scenarios: from the ones that are very similar to the ones that look similar but they are not.

Fig. 2

Example of a simple Rovers problem. a depicts the initial state of a Rovers problem where the Rover agent has to take the soil and rock samples to later send them to the lander. b depicts the same problem as on the left, but now the Rover agent can directly traverse 0-10 to reach the samples. As both problems are very similar, any plan-reuse planner would usually choose the solution obtained from problem (a) to solve problem (b). Unfortunately, that would not be efficient, as the plan-reuse planner would ignore the existence of the new path 0-10. Thus, the plan-reuse planner will return as a solution the same one obtained on problem (a)

We have developed a stochastic plan-reuse planner, called rrpt-plan, that combines search, sampling and plan reuse. rrpt-plan means Reuse & Randomly exploring Planning Tree and it is our second contribution on this paper. We were inspired by two previous works that are explained as follows.

The first previous work is errt-plan [6], which already explored the behavior of a plan-reuse planner and proposed a solution to adapt the algorithm to a broader set of plan reuse scenarios. It builds a solution tree inspired on the Rapidly-exploring Random Trees (RRTs) [32]. errt-plan receives as input the domain and problem description, the probabilities for node expansion and the solution (plan) represented as an ordered set of pairs of actions and their weakest preconditions. Given a plan π, the weakest preconditions of any action a_i ∈ π represent the set of propositions that are required to be true before applying a_i in the current state s_i so that the goals can be achieved from a_i when applying the remaining actions of the plan; the weakest preconditions act as subgoals of π. errt-plan has a probability of p to expand the tree towards the goal, a probability of r to expand towards an action of the input plan and a third probability to expand towards one of the weakest preconditions. errt-plan employs a reimplementation of METRIC-FF [23] as the heuristic planner and EHC [24] as the search algorithm.

The second work is rpt [1]. In order to implement rrpt-plan, the rpt algorithm was taken as a basis for developing our contribution. rpt was already able to combine two different types of search: one towards the nearest goal and another one towards a sampled state, which is any mutex-free state of the search space. rpt builds the solution tree inspired on the RRT’s structure.

Our contribution, rrpt-plan, emulates the errt-plan behavior by receiving as input the invalid plan, the domain and problem description and the set of probabilities; the weakest preconditions that errt-plan stored are not considered on our implementation. rrpt-plan combines search, plan reuse and sampling using the state-of-the-art planner Fast Downward [22], which was the base planner used by rpt. Details on rrpt-plan and the main differences regarding rpt and errt-plan are explained later on Section 4.6.

As a result, rrpt-plan has three parameters:

• 𝜖: limits the number of expanded nodes of the local search.

• p: probability of executing local search towards the nearest goal.

• r: probability of executing plan reuse.

Depending on the initial values of the set of parameters (explained later on detail), rrpt-plan performs either search, sampling or plan reuse on each iteration. The result will be a valid plan based on the input plan. rrpt-plan works as outlined in Algorithm 2. The main steps are: preprocessing, search-reuse-sampling and tracing back the solution.

The following subsections explain in detail first the current configuration of rrpt-plan and then each step of the algorithm. Section 4.5 describes the planning properties of rrpt-plan. Finally, Section 4.6 explains the differences between rrpt-plan, errt-plan and rpt.

4.1 Configuration

rrpt-plan follows the same configuration as rpt. Thus, the local planner Fast Downward was configured with greedy best-first search choosing lazy evaluation as its local search algorithm. The heuristic used is the h_FF heuristic [24].

As both rpt and rrpt-plan are inspired on RRTs, a tree structure is built during the planning process. rpt originally had local search and sampling phases. We have added the plan reuse phase. Details on the implementation of the tree are explained in [1].

As it was mentioned before, rrpt-plan has three parameters (p, r, 𝜖). Parameters p and r set the probability of performing search, reuse or sampling on each iteration; except for the first iteration, in which plan reuse will be performed. Parameter 𝜖 sets the maximum number of expanded nodes per iteration.

In order to build the solution tree, we have to describe the node structure that stores the information on each iteration:

• Every node of the tree (we refer to them as q in Algorithm 2), contains: a state (s_i), a pointer to the previous node (parent ρ_i), the sequence of actions that reaches s_i from the parent (subplan τ_i), the number of the last reused action of the input plan (it is zero when none of the input plan’s actions has been reused yet) and the cached best supporters for every proposition q ∈ F.

• We refer to cached best supporters as the implementation previously included in rpt [1] where the actions that first achieve a given proposition in the reachability analysis are stored in order to compute h_FF efficiently.

The following subsections explain in detail the preprocessing, the loop search-reuse-sampling of the rrpt-plan algorithm and some key details.

4.2 Preprocessing

The first step of the preprocessing translates the PDDL domain and problem to the SAS+ language [2] by calling and using Fast Downward’s Translate module [22]. This module also returns a list of operators, which contains every valid combination of actions and parameters that can be generated from the given domain and problem. Our algorithm rrpt-plan uses that list to translate the input plan to the SAS+ language. Thus, for each action of the plan, the algorithm looks for the equivalent SAS+ operator on that list (line 1, Algorithm 2). As a result, the input plan is transformed into a sequence of SAS+ operators instead of instantiated PDDL actions. For simplicity, along the following sections we will use the word action when referring to these SAS+ operators.

4.3 Search-reuse-sampling

After preprocessing is completed, rrpt-plan executes a loop (lines 4-16, Algorithm 2) that launches either the search, reuse or sampling phase until a valid solution is found. The algorithm only returns that no solution was found after all the search space has been explored. At each iteration, a random number (n) is generated. Depending on the value of the random number and the values set on p and r, one of the following scenarios is executed.

4.3.1 Search

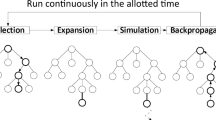
When n < p, rrpt-plan runs the local search scenario (lines 6-7, Algorithm 2). Algorithm 3 describes the local search algorithm and Fig. 3 shows the process inside the tree. The algorithm receives as input the node (identified as q). The local search can only expand a maximum of 𝜖 nodes. In order to differentiate each node on Fig. 3 and Algorithm 3, a brief description of them is given below:

• q_init: first node on the tree. It contains the initial state of the problem.

• q_near: last expanded node of the tree before applying local search towards the goal.

• q_new: last expanded node after applying local search towards the goal.

• q_goal: node that contains the goal state of the problem. When it is reached, it means that a plan has been found.

Before explaining the process, some general remarks and data structures are presented:

• After running local search, rrpt-plan only adds a single node to the final tree structure, which is the last expanded node of the local search.

• A node can be expanded during search only once.

• There is an open list to store the unexpanded nodes for the local search. That list is ordered: nodes closer to the goal first, for efficiency reasons. The algorithm always extracts the first node on the list.

The search function is called (line 7, Algorithm 2), so the local search is performed towards the goal state, q_goal. The algorithm takes the first node of the open list (q_near - Algorithm 3, line 1), which is the closest expanded node found towards the goal state (q_goal). Thus, the initial state of the local search is the one stored on q_near. Local search is then executed until the solution is found or 𝜖 number of nodes are expanded. Finally, the last expanded node from the local search (q_new - Algorithm 3, line 2) is stored on the tree (Fig. 3). As it was previously said, this node contains a pointer to its parent, q_near, and also the subset of actions that were instantiated during the local search to reach the node’s current state from its parent q_near.

Fig. 3

The first step of rrpt-plan search towards the goal is shown on the left. Local search is run from q_near, which is the closest expanded node found to the goal so far. The second step is shown on the right. After expanding 𝜖 number of nodes, q_new is the closest node to q_goal. The node q_new stores the plan to reach q_new’s state from q_near. Finally, q_new is stored into the tree

4.3.2 Reuse

When p ≤ n < (p + r), rrpt-plan runs the plan reuse scenario (lines 8-11, Algorithm 2). During the first iteration, the algorithm always performs plan reuse regardless of the values of p and r. This decision is further justified on Section 5. Algorithm 4 describes the steps to run plan reuse. Figure 4 shows the process inside the tree. In order to differentiate each node on Fig. 4 and Algorithm 4, a brief description of them is given below.

• q_init: first node on the tree. It contains the initial state of the problem.

• q_reuse: first node of the plan reuse open list. Its state is is checked when trying to reuse the first action.

• $q_{reuse^{\prime }}$: node created after the first action is reused. Its state and its plan are being updated during the plan reuse process as long as new actions can be reused. At the end of the process it is added to the tree as child of q_reuse.

• q_goal: node that contains the goal state of the problem. When it is reached, a plan has been found.

Before explaining the process, some general remarks and data structures are presented:

• Plan reuse can be applied to a node as long as the number of the last reused action does not reach the last action of the input plan.

• There is an open list to store and provide the nodes to whom plan reuse is applied. The algorithm always extracts the first node on the list. When local search or sampling add new nodes to the tree, they are also automatically added to the plan-reuse open list.

The algorithm takes the first node of the plan reuse open list (q_reuse, line 1 Algorithm 4) and gets the position of the last action reused (stored on the node; by default 0 when none of the actions has been yet reused). Then, it iterates over the sequence of actions of the input invalid plan. For each one of them it checks if the action can be applied to the current state of the node (Fig. 4a). If this is true, the action (current) is added into the plan and the current state and index i are updated (lines 10-11, Algorithm 4). In addition, when an action is added to the new plan, the algorithm checks if the goal state has been reached as well (line 12, Algorithm 4). The reuse process will be repeated until an action cannot be applied (Fig. 4b). In that case, the position of the last reused action, the current state and the sequence of the reused actions are stored into the node $q_{reuse^{\prime }}$. Also, the previous node q_reuse is set as parent.

Fig. 4

The first step of plan reuse in rrpt-plan is shown on Fig. 4a. The state of q_reuse is evaluated to see if the first action from the input plan can be directly applied. The second step of plan reuse in rrpt-plan is shown on Fig. 4b. As long as there are actions that can be applied to the current state, they will be stored inside a new node $q_{reuse^{prime}}$ which at the end of the process, when no more actions can be reused, will be the child of q_reuse

4.3.3 Sampling

When (p + r) ≤ n < 1, rrpt-plan runs the sampling scenario. Lines 13-15 of Algorithm 2 describe the steps to run the sampling process. Figure 5 shows the process inside the tree. In order to differentiate each node on Fig. 5, a brief description of them is given below.

• q_init: first node on the tree. It contains the initial state of the problem.

• q_rand: node that contains a random valid state from the search space.

• q_sampling: closest node from the tree to the sampled state.

• q_new: last expanded node towards q_rand.

• q_neargoal: last expanded node towards the goal.

• q_goal: node that contains the goal state of the problem. When it is reached, it means that a plan has been found.

Before explaining the process, some general remarks and data structures are presented:

• A new node is added to the tree at every iteration. If the solution is not reached during sampling, the last expanded node is added to the tree.

• After sampling, when the new node is obtained (q_new), a new local search is performed towards the goal until the limit 𝜖 is reached. This is equivalent to the Extend phase of RRTs.

First, the algorithm obtains a random valid state (q_rand) after sampling the search space ($\mathcal {S}$). Then, the closest node to the sampled state is found (q_sampling, Fig. 5a) by computing h_FF. Details about how the random state and the distance are computed can be found in [1]. After q_sampling is identified, a local search is performed from there towards q_rand. However, q_rand might not be reached because of the limit 𝜖. If this happens, the last expanded node is stored on the tree (q_new). The next step is to perform a new local search from q_new towards the goal (q_goal, Fig. 5b). This is the Extend phase, already implemented in rpt[1]. The last expanded node from the Extend local search is then stored into the tree (q_neargoal, Fig. 5c).

Fig. 5

The first step of sampling in rrpt-plan is shown on the left. Once the sampled node q_rand is obtained, a local search is run from q_sampling towards that node. q_sampling represents the closest node from the tree to the sampled node. The second step of sampling in rrpt-plan is shown on the right. After local search is performed, q_new is added into the tree. Now a local search towards the goal (q_goal) is run. The third step of sampling in rrpt-plan is shown below the previous steps. After expanding 𝜖 number of nodes, q_neargoal is the closest node to q_goal so it is stored into the tree

The search-reuse-sampling phase is repeated once per iteration, independently of the strategy (search, reuse, sampling) used. The following subsection explains how the algorithm is capable of tracing back the solution through the tree.

4.4 Tracing back the solution

In order to retrieve the solution plan π, the algorithm has to check if q_goal’s state s_goal satisfies every proposition in G, so that G ⊆ s_goal. If so, rrpt-plan starts tracing back the solution plan from the node q_goal. From q_goal, rrpt-plan obtains the link (ρ_goal) to the parent’s node and repeats the process until the initial node (q_init) has been reached. Figure 6 illustrates the process. Solution nodes are stored into a list called Tree_sol = {q_init,...,q_goal} where q_init’s state s_init = I and q_goal’s state G ⊆ s_goal. Nodes’ subplans are concatenated to obtain π = {τ_init ⊕ τ₂ ⊕ ... ⊕ τ_goal}. Each τ_i contains at least one action of the solution plan. The concatenation gives as a result the solution plan π = {a₁,a₂,...,a_m}.

Fig. 6

Tracing back the solution in rrpt-plan. The algorithm starts on q_goal and goes backwards on the Tree, obtaining on each step a new solution node through the link ρ_i. Black nodes of the Figure represent the solution nodes. They are stored in order on a list called Tree_sol

4.5 Properties

rrpt-plan is an algorithm that performs suboptimal planning. Optimality is out of the scope of this work. Also, rrpt-plan is incomplete, as it cannot assure that a solution will always be found. For instance, extreme cases where p = 1.0 (only search) or r = 1.0 (only plan-reuse) or both have 0.0 values (only sampling); these are some configurations where rrpt-plan could fail to find a solution - specially if there exist some timeout. Regarding only search (p = 1.0 r = 0.0), rrpt-plan can get stuck after exploring and expanding every existing node of the search space and still not being able to obtain a solution. Regarding only plan reuse (p = 0.0 r = 1.0), if no action of the input plan can be reused or every action has been reused but it is not enough to solve the problem, rrpt-plan will constantly enter into the reuse phase and will never obtain a solution to the problem. Regarding only sampling (p = 0.0 r = 0.0), it is the same case as only applying search. Sampling explores the search space randomly, but after exploring and expanding every node of the search space, the solution might still not be found.

Finally, the plans generated by rrpt-plan are sound. First, when performing local search, actions are only applied to valid planning states. Second, when reusing actions, the successors of the current state are generated to obtain the list of applicable operators that reach those successors. Before including the action into the plan, it is verified that the equivalent operator of the action-to-be-reused appears on the list of applicable operators. Third, when performing sampling, the random node will be valid, as rpt included a procedure to only consider valid states. Fourth, we formally demonstrate Γ(s_init,π)⊧s_goal to proof the soundness of rrpt-plan. Given q_init as the first node on the Tree, which contains s_init = I; and q_goal as the last expanded node which contains the goal state G ⊆ s_goal. Given the list Tree_sol, which contains the sequence of nodes starting on q_init that reaches the goal state; and given plan π which contains the sequence of actions to reach s_goal from s_init, where τ_init = ∅ as the initial node does not contain any action of the plan yet.

$$ \begin{array}{@{}rcl@{}} \pi &=& \{\tau_{init} \oplus \tau_{2} \oplus ... \oplus\tau_{goal}\}\\ &=& \{\overbrace{a_{1}, a_{2},..., a_{k}}^{\tau_{2}},\overbrace{a_{k+1},... a_{p}}^{\tau_{3}},...,\overbrace{a_{r+1},...,a_{m}}^{\tau_{goal}}\} \end{array} $$

(2)

From the set of nodes of Tree_sol and the actions from π, using the function γ(s_i,a_i) = s_i+ 1 we can generate every intermediate state (${s_{i}^{j}}$) between the q_i nodes as follows.

$$ S=\left\langle \underbrace{s_{init}}_{q_{init}},\overbrace{(s_{init}^{1},s_{init}^{2}...s_{init}^{k-1}) , \underbrace{s_{2}}_{q_{2}},}^{\tau_{2}}\overbrace{({s_{2}^{1}},{s_{2}^{2}}...s_{2}^{p-1}),s_{3}}^{\tau_{3}},...,\overbrace{({s_{r}^{1}},{s_{r}^{2}}...s_{r}^{m-1}),\underbrace{s_{goal}}_{q_{goal}}}^{\tau_{goal}}\right\rangle $$

(3)

Thus, when the subplan τ₂ is applied to s_init following (1), the resulting state is s₂.

$$ {\Gamma}(s_{init},\tau_{2}) \models s_{2} $$

(4)

Theorem 1

rrpt-plan is sound

Proof By induction:

Base case: s_init = I is reachable from the initial state by q_init construction.

Inductive step: if s_i is reachable from s_init, s_i+ 1 is a reachable state from s_init.

By construction:

$$ {\Gamma}(s_{init},\tau_{2}\oplus\tau_{3}...\oplus\tau_{i})\models s_{i} $$

(5)

$$ {\Gamma}(\underbrace{s_{init},\tau_{2}\oplus\tau_{3}...\oplus\tau_{i}}_{s_{i}}\oplus \tau_{i+1})\models s_{i+1} $$

(6)

Thus, s_goal is reachable from the initial state s_init and G is satisfied.

$$ {\Gamma}(s_{init},\underbrace{\tau_{2} \oplus...\oplus\tau_{goal}}_{\pi})\models s_{goal}, where\ G\subseteq s_{goal} $$

(7)

□

4.6 Differences of rrpt-plan regarding previous works

Apart from the obvious difference in implementation (errt-plan code was based on a reimplementation of Metric-FF in Lisp), rrpt-plan presents some differences with respect to the previous works.

• First, rrpt-plan presents a more clear bias towards search than errt-plan. While errt-plan considered the search step as adding one more node to the tree, rrpt-plan search algorithm works by expanding 𝜖 nodes in the same step, where we have found that 𝜖 should take big values.

• Second, errt-plan sampling of goals was directed by the computation of weakest preconditions from the input plan, while rrpt-plan sampling uses rpt sampling procedure instead. However, rrpt-plan does not use rpt’s computation of h2 mutexes for that task. By avoiding that computation, the aim is to speed up the process.

• Third, errt-plan and rpt considered the goal sampling step as equally relevant. On the contrary, rrpt-plan assigns a very small role to goal sampling by assigning a very low probability of using sampling.

All these differences are due to the diverse uses of errt-plan, rpt and rrpt-plan. In the case of errt-plan, we were studying the effects of different strategies of plan reuse (replanning from scratch vs. eager use of the previous plan) in a wide variety of scenarios. In rrpt-plan we are interested in a very particular kind of plan reuse scenario, where in most cases, the reuse strategy is a mixture between the two extremes. Finally, the obvious difference with respect to rpt is that rrpt-plan can partially reuse a previous plan and that the sampling phase is not considered as important as the other two.

5 Experiments

This section presents some experiments on the performance of our two contributions, pmr and rrpt-plan, and their comparison with other state-of-the-art planners. We have divided the experiments and results in six different sections structured as follows.

First, Section 5.1 describes metrics and configuration environments. Section 5.2 presents some experiments specifically designed to explain the flexible behavior of rrpt-plan in different plan-reuse scenarios. Section 5.3 analyzes rrpt-plan in terms of parameters to select the best configuration. Section 5.4 shows the results of running the CoDMAP competition with different configurations of pmr and other state-of-the-art, multi-agent and centralized, planners. Also, Section 5.5 shows the performance of pmr when scaling the number of agents. Section 5.6 shows the performance of pmr against the same set of planners previously used on Section 5.4. However, the set of problems is harder to solve, containing a reasonable amount of agents and goals to reach. We have also included three new domains specifically designed to evaluate the makespan metric in order to show pmr’s potential. Finally, Section 5.7 describes some general remarks and conclusions extracted from the extensive set of experiments.

5.1 Experimental setup

For each set of experiments described in the following sections, results of coverage (number of solved problems), quality (cost and makespan) and planning time are shown. In order to compute these metrics, we have used the scores of the International Planning Competition (IPC)². Coverage is computed increasing by one each time a planner solves a given problem of a given domain. Makespan refers to the number of execution steps, where several actions can be executed at each execution step. Cost refers to the sum of costs of all the actions contained in the plan. For computing both metrics, makespan and cost, we use Q_best/Q, where Q_best is the cheapest value obtained for a specific problem by the set of planners and Q is the value obtained for the same problem by one of those planners. In order to compute the time score, we use 1/(1 + log10(T/T_best), where T_best is the lowest time in which a specific problem has been solved by any planner and T is the time in which one of those planners has solved the specific problem. The time bound to solve each problem is 1800s. The quality/makespan/time score of a planner is the sum of its scores for all problems. For every domain presented on the tables, 20 problems were run, except for the ones of Section 5.3 where 15 problems per domain were run instead (the reason is explained on that Section). All the experiments were run on an Intel(R) Xeon(R) X3470 2.93GHz with 8 GB RAM.

In order to distinguish among the different configurations of pmr that appear on the experiments, the notation used in the next sections is the following.

• Every configuration of pmr is using lama-first as the planner P of the algorithm. lama-first corresponds to the first search that lama performs, using greedy-best-first with unit costs for actions [41]. We have also used lama-first for the centralized planning step.

• We have used lpg-adapt [19] and rrpt-plan for the plan reuse experiments. When they have been used inside pmr we refer to them as pmr-lpg-adapt or pmr-rrpt-plan. Otherwise it means they were executed outside pmr. lpg-adapt has always been run in the speed mode. Additionally, we have compared rrpt-plan against errt-plan [6] and rpt [1], as our contribution is an evolution of those approaches combined. rpt has been configured with p= 0.3 and errt-plan with p= 0.3 and r= 0.6. The reason is explained on Section 5.3.

• rrpt-plan has three additional parameters set on each configuration. We refer to them as p, r and 𝜖. The way these parameters affect rrpt-plan is explained on Section 4.

• Our configurations of pmr have been evaluated using different goal assignment strategies. We refer to them as BC (Best-cost), LB (Load-balance) and ALL i.e. pmr-lpg-adapt-BC means that pmr was executed using Best-cost as goal assignment and lpg-adapt as plan reuse planner.

• We have tested our pmr configurations against two centralized planners, lama-first and yahsp [48].

• Also, we have compared our configurations with three multi-agent planners (cmap-t [4], adp-l [14] and siw [37]). They will be later explained in Section 5.4. They were chosen because of their remarkable performance on some metrics of CoDMAP.

5.2 Results of pmr-rrpt-plan and pmr-lpg-adapt when solving different plan-reuse scenarios

The aim of this section is to analyze in detail the behavior of rrpt-plan. A simple multi-agent scenario was designed to force pmr to use its plan reuse planner to fix the plan (either rrpt-plan or lpg-adapt on these experiments). The Load-Balance (LB) strategy was chosen for this experiment in order to assign goals using as many agents as possible and balancing the number of assigned goals per agent at the same time.

We are calling this domain Hammers, for which we have generated a set of problems. The aim was to show how interactions are handled when a set of agents has to share a set of resources. Thus, the designed domain contains robots (agents), hammers, nails and paintings. The robot needs first to find and grab a hammer and a nail. It is not allowed for robots to grab more than one hammer and nail at the same time. Once the robot has grabbed the pair hammer-nail it should go to some room that contains a painting and hang it up. Each scenario is completely solved when all paintings are hanged up.

The ideal multi-agent situation (reflected on Fig. 7a) has as many robots, hammers and nails as paintings. Thus, each robot will be in charge on hanging one painting up when goals are divided among the set of agents. However, the bottleneck of the problem is the number of hammers; if the robots need to share the hammer(s), many interactions arise and need to be fixed by a plan reuse planner. As agents (robots) plan individually on pmr’s first step, all of them are forced to use a hammer on their individual plans.

Fig. 7

a presents the first scenario (6 robots, 6 nails, 6 hammers, 6 paintings). This problem is an ideal multi-agent planning scenario. There are as many hammers as robots. Thus, they do not need to share any resource during planning. In the second scenario (b) there is only one hammer for six robots. Paintings and nails are placed as in case (a). Interactions arise when merging the robots’ plans as they all use the hammer in their individual plans. The third scenario (c) not only shows hammer interaction issues, but also interactions caused by nails. Nails are grouped into two rooms. Thus, multiple robots could have used the same nail in their individual plans

Through these experiments we are able to explain the potential of our plan reuse contribution, rrpt-plan, when used inside pmr. We compare pmr-rrpt-plan configuration results with the ones obtained with pmr-lpg-adapt. Also we show a comparison with pmr-lama at the end in order to show how pmr-rrpt-plan performs better in these situations as it is in the middle of two extremes: pmr-lpg-adapt (plan-reuse) and pmr-lama(centralized planning).

The first scenario presents six robots starting in a common room, C, plus a hammer and a nail per room (Fig. 7a). When computing this ideal scenario for MAP with either pmr-rrpt-plan or pmr-lpg-adapt using the LB strategy, the planner will assign to each robot one of the goals. Thus, each robot will move to a different room, pick up the hammer and the nail and hang the painting on the wall. As a result, after the individual planning step, the concatenation and parallelization of the resulting plan will return a valid plan. There is no need for replanning in this first case as there is no interaction among agents.

The second scenario is the same as the previous one but the difference lies in the number of hammers: it has just one hammer in C (Fig. 7b). This reflects a common MAP issue on how agents deal with a shared resource (hammer) and how the planner deals with agents’ interactions.

Each robot will plan individually to take first the hammer from C and then move to some room to grab the nail and hang the painting up. As a result, the concatenation of plans is not entirely valid. Some actions need to be included into the plan such as dropping the hammer so that the next robot can pick it up later, if necessary. This issue is fixed on the plan reuse step of both pmr-lpg-adapt and pmr-rrpt-plan but following different approaches. The lpg-adapt version takes as input plan the non-valid concatenation of plans and adds the following actions between each robot’s set of actions: move robot to C and drop hammer. Thus, from the planning point of view, the actions from the input invalid plan were easily reused, as only some new actions were added to the final plan to share the hammer. On the other hand, rrpt-plan directly reuses the set of robot1’s actions (first agent on the list). Then, when it is time to reuse actions from robot2, the process fails because the hammer is not in C anymore. Thus, rrpt-plan changes to the search phase and decides to finish the plan using only robot1. As a result, pmr-rrpt-plan returns a plan of length 24 while pmr-lpg-adapt returns a plan of length 34. As there is only one hammer available, agents cannot solve their goals in parallel. Therefore, the makespan metric on both configurations has the same value as plan length.

We can see in this example that calling a pure plan-reuse planner to fix a plan might not always be a good choice. It will always either reuse as many actions as possible from the input invalid plan, or, when this is not possible, it generates new ones to be later reused. This issue can generate noise on the plan’s actions, later explained on the third scenario. If the aim is to obtain an efficient valid plan fast, plan reuse needs to be combined with search to solve these specific multi-agent scenarios. Also, when a shared resource is limiting the number of agents that can perform actions, the best solution will probably be to involve a number of agents close to the number of available shared resources.

The third case presents six robots starting in C, six nails and paintings equally divided among two rooms and one hammer at Room 6 (Fig. 7c). After obtaining the concatenated plan and checking that it is not valid, several parts of the plan need to be fixed. Not only the actions related with grabbing and dropping the hammer must be fixed, but also the ones related with looking for nails (Table 2).

Table 2 Besides the three problems previously generated to explain three different cases of plan-reuse, a set of four problems were generated based on Fig. 7c’s distribution to show the impact of increasing the number of paintings and hammers while having the same number of rooms and agents

This time, as nails are grouped into two different rooms that have the same distance to C and robots plan individually, the robots pick up the hammer and the same nail on its individual plan. Thus, to transform these sequences into a valid plan, robots only need to look for the nails that are still available and the hammer. pmr-lpg-adapt reuses as many actions as possible from the invalid plan. It also decides to use the set of six robots to hang up all the paintings (as suggested in the input invalid plan). As a result, the final plan has redundant actions. pmr-lpg-adapt adds redundancy when reusing actions that are always valid regardless of the current state of the problem. They are supposed to help each agent to reach its goal; e.g (1) a robot moves to a room, (2) a robot grabs a nail, and (3) a robot drops a nail. These situations are given quite often while the set of six robots is being forced to look for the same hammer in order to hang up the assigned painting. Some of them even grab and drop several nails until they finally can hang the painting up. For instance, it might happen once a robot grabs a nail, as heuristics consider it is one step closer towards the goal. However, the robot might enter into some room where there is another robot that already grabs the hammer, but it does not grab any nail. Usually, the first robot drops the nail when there are no other available nails in the room. As a consequence, the other robot can grab it and hangs the painting up. From the point of view of planning, even though there were parts of the input plan that could be reused, they only cause pmr-lpg-adapt to return a worse plan (more actions).

On the other hand, when using the pmr-rrpt-plan approach, the set of actions performed by robot1 will be directly reused until it finishes hanging the first painting. When moving robot2 to room6 and realizing that the hammer is not there, the plan-reuse phase ends and the search phase starts, discarding the rest of the actions from the input plan. As a result, again only robot1 is used to hang all the paintings up and redundant actions are avoided except for the one action from robot2 moving to room6. Even though only one robot is used to execute the whole plan, the plan length is 43. That value is still lower than the one from pmr-lpg-adapt, which returns a plan of length 149. Regarding makespan, pmr-lpg-adapt returns 118 and pmr-rrpt-plan, 38.

In Table 2, the first three rows are related to the three cases explained above. The following rows represent new problem-variations generated from the Fig. 7c scenario where paintings and nails are equally divided into two sets of different rooms and hammers’ location vary. The aim is to show the evolution of plan length, makespan and time when increasing number of paintings and hammers. Due to this fact, the complexity of the problem increases depending on where the hammers are initially placed and the number of interactions that have arisen.

Tables 3 and 4 show the plan length, makespan and time obtained for each pmr configuration, other multi-agent and centralized planners on each Hammer problem. As Table 3 shows, pmr-lama and pmr-lpg-adapt are not able to solve most of the problems where all hammers are placed on the same room (version b problems). pmr-lama gets lost on the search space as there is a huge number of possible combinations of movements with the same heuristic estimation (known as plateaux) to solve the problem. On the other hand, pmr-lpg-adapt gets lost when reusing the actions of the invalid plan, as most of them are valid, but they still do not solve the problem. This ends up generating redundancy and causes the planner to search for new actions, while always looking up at the ones on the invalid plan again on each iteration. However, pmr-rrpt-plan performs better than the other two configurations, as it has the opportunity to change between plan reuse, search and sampling to solve the problem and this has an impact on the number of problems solved as well as on the makespan metric. pmr-rrpt-plan is more flexible and in summary obtains the best performance on the three metrics regarding the three pmr configurations. Regarding multi-agent planners cmap-t, adp-l and siw, the best configuration is siw. siw’s serialization of goals allows the planner to use efficiently most of the agents resulting in the improvement of makespan at the same time. adp-l and cmap-t behave very similar to lama, the centralized planner. These planners (except for siw) try to solve the problem with the smallest possible number of agents, as a consequence of minimizing the plan length. adp-l is the only one able to avoid the plateaux of the search space and does not get lost on version b problems. The centralized planner yahsp was run as well, but it was not able to solve any of the problems.

Table 3 This table shows the plan length (L) and makespan (M) obtained for every scenario of the Hammer domain with multi-agent planners pmr-rrpt, pmr-lpg-ad, pmr-lama, cmap-t, adp-l, siw and centralized planners lama, yahsp and rpt

Table 4 Time in seconds that each configuration of pmr, cmap-t, adp-l, siw, lama and rpt took to solve the Hammer domain scenarios

When hammers are distributed among rooms 1, 4 and 6 (version “a” problems) the interactions are easier to solve by all planners. On pmr configurations, when agents plan individually, they choose the hammer that is closer to the set of paintings they have to hang up. Thus, less number of interactions arises and agents are better self-organized. Same effect is given on the rest of the planners.

Regarding times on Table 4, pmr-lpg-adapt is faster when it is capable of solving the problems but pmr-rrpt-plan is more regular on performance.

5.3 Analyzing the impact on performance of rrpt-plan’s parameters

After explaining the difference between the performance of rrpt-plan and a classical plan reuse planner, such as lpg-adapt, we wanted to test both of them outside of pmr. We have compared both plan reuse planners against a centralized planner, lama-first, and the two planners, errt-plan and rpt, in which rrpt-plan was inspired. This experiment is divided into two parts. Firstly, we present an analysis of rrpt-plan’s performance depending on a set of values assigned to its parameters p,r and 𝜖. The aim is to find the best parameter configuration for rrpt-plan. Secondly, after choosing the best configuration for rrpt-plan, we compare the results obtained in coverage, quality and time against the ones obtained by lpg-adapt, lama-first, errt-plan and rpt. In order to compare rrpt-plan’s performance, rpt and errt-plan were run using the same values as rrpt-plan’s best configuration, which will be explained later on this Section. Both parts of the experiment share the same benchmark, which was created as follows: first, a set of hard planning problems was generated (Rovers, Zenotravel, Driverlog, Depots, Elevators and Logistics) per domain. These domains were chosen because they have different levels of interaction and dependency among the different elements of the domain, which is a feature that directly affects the difficulty of reusing a previous plan. Any agent’s decision from Rovers or Zenotravel seldom interfere the decisions taken by the other agents. There are not common resources either. This is the easiest scenario to be solved by a plan reuse planner, as interactions, if any, are easy to solve. However, Driverlog and Depots’ agents share partially the domain resources, as most of them need to be delivered to some concrete places. On Elevators and Logistics the level of interaction is similar but dependency increases, as the problem goals usually need collaboration among two agents besides dealing with the sharing of common resources.

We made three versions of each problem; the first one contains one more goal than the original problem; the second contains five more and to the third, ten more goals were added. For each domain we took three original problems per domain so we created nine new problems based on the originals.

The original problems were first run with lama-first in order to obtain the resulting plans. These plans were later used as input plans for rrpt-plan, errt-plan and lpg-adapt for each one of the modified problems. As the number of added goals gets increased, the resulting plans should be very similar at the beginning but more different as more goals are added to the original version. Also, as lama-first and rpt are not able to reuse, they had to run each modified problem from scratch.

As it was mentioned in Section 4, rrpt-plan has three parameters that change the behaviour of the algorithm. Parameters p and r control the probability of running local search, plan reuse or sampling, e.g. values p = 0.6,r = 0.3 cause rrpt-plan to have a probability of 0.6 to run the local search phase, 0.3 to run plan-reuse and 0.1 to run the sampling one. In addition, the parameter 𝜖 limits the number of expanded nodes per iteration during local search, e.g a value of 𝜖 = 1000 means that 1000 nodes will be expanded at most per local search iteration.

We have tested eight different configurations of rrpt-plan in this experiment explained as follows.

• 1. p = 0.3, r = 0.3; this configuration gives equal probability to search and reuse and 0.4 to sampling.

• 2. p = 0.3, r = 0.6; this configuration benefits plan-reuse over search and leaves a probability of 0.1 to sampling.

• 3. p = 0.3, r = 0.7; same to the previous one but rrpt-plan will not perform the sampling phase.

• 4. p = 0.6, r = 0.3; this configuration benefits local search over plan-reuse and leaves a probability of 0.1 to sampling.

Each of these parameter configurations was tested for 𝜖 = 1000 and 𝜖 = 10000 to analyze the impact on the solution when allowing a smaller or greater number of nodes to be expanded during search. For this experiment, the execution of plan reuse on the first iteration of rrpt-plan is avoided in order to focus on the impact of these probabilities. We also show the comparison against lama-first, lpg-adapt, errt-plan and rpt. Results of errt-plan are not shown on the tables below, as it was not able to solve any of the problems in 1800 seconds. errt-plan uses Enforced Hill Climbing (EHC) as the search method [24]. Since EHC performs a form of hill climbing without backtracking, the heuristic can guide the search towards dead-end states, big plateaux, or very long paths. Therefore, errt-plan could not solve any problem.

Results of this experiment are shown on the following tables. Table 5 shows the number of problems solved per configuration. Table 6 shows the summary of the obtained quality score per configuration. Finally Table 7 shows the summary of the time scores per configuration.

Table 5 Coverage score obtained on each domain

Table 6 Quality score obtained on each domain

Table 7 Time score obtained on each domain

Table 5 shows that coverage is very similar between rrpt-plan and lpg-adapt. lama-first and rpt perform a bit worse, especially on high-interaction domains (e.g. depots, logistics, driverlog). As they do not reuse a previous plan, they had to run each modified problem from scratch and those domains are harder to solve. rrpt-plan (p = 0.6, r = 0.3) is the best configuration followed by rrpt-plan (p = 0.3, r = 0.6).

Quality results show that rrpt-plan and lpg-adapt results are similar. The small difference between them was given on the Depots domain, where lpg-adapt performs slightly better. The best configuration is lpg-adapt followed closely by rrpt-plan (p = 0.6, r = 0.3) and (p = 0.3, r = 0.6).

On the other hand, regarding time, the fastest configuration is lpg-adapt. If we considered only planning time, rrpt-plan results would be similar to those of lpg-adapt. Before starting to plan, our planner, first translates the domain and the problem and computes mutexes and disambiguation (which is useful for search and sampling). Thus, our planner’s performance is worse than lpg-adapt in time (not in quality). lpg-adapt’s preprocessing phase only translates the domain and problem. lama-first applies the same translation process as rrpt-plan but it does not compute mutexes and disambiguation. rpt performs an exhaustive computation of mutexes and disambiguation, which is why its time results are the worst ones. As it can be seen on Table 8, the fastest preprocessing is performed by lpg-adapt. Also, the impact on computing mutexes and disambiguation can be seen by comparing rrpt-plan, rpt and lama-first preprocessing results. On the other hand, even though it is not explicitly reflected on Tables 7 and 8, the harder the problem, the closer the time score gets rrpt-plan to the one of lpg-adapt. The reason is the following: when the number of added goals to the problem increases, plan reuse performance decreases, as the input plan is not similar anymore. On the other hand, search becomes more useful. In Table 7 is shown the poor performance of a centralized planner (lama-first, rpt) in comparison with plan-reuse ones. When the problems are similar, reusing input plans is faster than planning from scratch. Table 8 shows the average time employed on preprocessing by each planner on each domain.

Table 8 Average time (in seconds) spent on preprocessing each problem per planner and domain

In order to choose the best configuration of rrpt-plan to later compare itself against other planners in the following experiments, we decided to choose (p = 0.3, r = 0.6, 𝜖 = 1000). There was a minimal difference regarding the p = 0.6, r = 0.3 configuration. We realized that it was due to the execution of the plan reuse phase on the first iteration on both configurations. The stochasticity of rrpt-plan on this experiment turned out to discover the following: in order to stabilize the performance and commitment of rrpt-plan inside and outside of pmr, it is essential to always first execute plan reuse on the first iteration. This is also why we chose a higher probability on r (0.6 instead of 0.3).

5.4 Results in CoDMAP problems

In this Section the results of the CoDMAP benchmark are shown. CoDMAP was a preliminary version of what could be a multi-agent planning competition in the future, that took place in 2015. Here we have rerun the competition with our contributions to compare ourselves against two centralized planners (lama-first, yahsp) and three of the best multi-agent planners that participated in the competition (adp-l, cmap-t, siw). There are 12 domains with 20 problems each. The time limit to solve each problem was 1800 seconds. We have also used the same agentification as it was explicitly noted on the MA-PDDL files (official language of the competition).

Tables 9 and 10 show the obtained results in coverage (number of problems solved). We have used the three different goal allocation strategies: Best-cost (BC), Load-balance (LB) and All. Since pmr can solve each problem in three different ways, we show the coverage obtained on each one separately: merge (M, when plans are valid after merging), centralized planning (C, when no agent could generate any plan) or plan reuse (R, when the merged plan was invalid). The configuration pmr ALL was added in order to make pmr complete. It shows a similar behavior as a centralized algorithm. Thus, when pmr ALL fails in the M and R steps, it usually solves the problems in the C step. On the other hand, pmr LB and BC solve more problems in the M and R steps than pmr ALL. The aim of pmr is to solve as many problems as it can executing the M and R phases.

Table 9 pmr with lpg-adapt and rrpt-plan configuration in combination with up to three goal assignments: BC (Best-cost); LB (Load-balance) and All

The best configurations of our contributions in coverage are pmr-lpg-adapt-ALL and pmr-rrpt-plan-ALL followed by pmr-rrpt-plan-BC. In general, all our contributions are similar in terms of coverage, they all have passed the barrier of 200 problems solved (over 240). Our contributions had very good coverage in all domains, except for Wireless that was the hardest domain in CoDMAP; none of the planners obtained good results on it.

Analyzing the coverage results of pmr in relation to which phase solved the problems allows us to classify the domains in three groups. This classification reflects in turn the interaction level among agents and goals: low, medium and high.

Low interaction domains

Zenotravel, Rovers and Satellites. pmr often solves problems in these domains by merging the individual agents’ plans, because these plans are mostly independent. However, it depends on the type of goal allocation strategy selected. Take, for instance, the Zenotravel domain. Both BC and LB assign only one agent to each goal. Since the plans generated by agents can solve all their individual goals and do not interfere with other agents’ plans, the merge step solves all problems. But, in the case of the ALL strategy, it will assign each passenger to all airplanes. The first agent will move all passengers, the second agent will also move all of them, and so on. Therefore, the merged plan will be invalid (all airplanes will try to move all passengers). These problems are easily solved then by plan repair.

Medium interaction domains

Driverlog, Blocks and Depots. In these domains, when the goal assignment strategy selects several agents for planning, problems are mostly solved in the plan repair step. So, individual agents are able to solve their problems, but the merged plans are invalid due to interaction among the plans to achieve the goals. Then, the plan repair step can generate a valid plan by solving the negative interactions.

High interaction domains

Elevator, Logistics, Sokoban, Taxi, Wireless and Woodworking. In these domains, a single goal might need the collaboration among two or more agents. For instance, in the Logistics domain, most packages need at least two trucks and one airplane to reach their destination. In those cases, pmr individual plans will fail and the centralized planning solves most problems.

A key related issue is how domains are modeled. For instance, if the only agents considered in the Logistics domain are the airplanes, then BC and LB would solve all problems just by either merging the resulting individual plans or by plan repair. Similarly, in the case of Elevator and Taxi, one could define fast elevators or taxis respectively as the only agents and pmr would solve all problems without the centralized planner.

We have compared our contributions against the winner of CoDMAP in coverage, adp-l [14]. Note that adp-l does not preserve privacy and it uses a different agents’ configuration than the one proposed in the competition. We also compare against cmap-t [4] that obtained the best coverage and time score from the planners that preserved privacy. Finally, we also included siw [37] as it was one of the best planners of the competition. Results of this comparison are shown on Table 10.

Table 10 IPC scores in Coverage per configuration in CoDMAP domains

Regarding Table 10, adp-l obtains the best coverage followed up by siw and pmr-ALL (both with lpg-adapt and rrpt-plan). yahsp coverage is the worst. Related to coverage in the official CoDMAP, after the summer-run³pmr-ALL would share the first position with adp-l, which was 219.

Regarding time scores (Table 13 in the Appendix), the fastest planner is adp-l followed very closely cmap-t. The performance on time of pmr configurations is homogeneous. The time score in pmr was computed using the total amount of time spent by the whole process. Since the individual agents’ planning processes were executed in sequence, the total time is computed as the sum of all these processes. However, considering that the merging phase could be implemented fully distributed, the total time would be less by using the maximum planning time among all agents instead of the sum.

In relation to quality scores, Tables 14 and 15 (in the Appendix) show the results of makespan and cost of plans, respectively. As lama and adp-l did not compute the makespan metric, our parallelization algorithm was applied to their resulting plans to fairly compare the results of makespan. siw makespan results are not shown in the table because our parallelization algorithm could not support the use of constants that they include in the PDDL domain and problem to respect the privacy of objects and fluents after they transform the MA-PDDL files into PDDL [37]. This issue does not happen when the domain and problem are directly given in PDDL.

Regarding pmr configurations, it can be seen how BC is better in cost and LB in makespan. The difference between these numbers lies in the number of agents involved in the planning process. BC often includes the minimum necessary number of agents to plan (the ones that expectedly achieve goals with the minimum cost), so the plans’ cost will usually be low (good score). In the extreme, some problems were solved using only one agent. However, the makespan is penalized given that the same agent is achieving all goals, so many actions cannot be executed in parallel. On the other hand, LB tries to include as many agents as possible, as long as they can solve at least one of the goals of the problem. The makespan will be better than that of BC, because actions can be easily parallelized. But, the cost is penalized when choosing LB, as it uses agents whose plans are worse in terms of cost. Potentially more interactions need to be solved (causing an increase in the number of plans solved by R instead of M).

pmr-rrpt-plan configurations perform better on quality and pmr-lpg-adapt configurations, better on time. Moreover, pmr-lpg-adapt-ALL, which was one of the best configurations in coverage, is the worst of our configurations in quality scores. The All strategy uses all agents in the problem to plan leading to long merged plans. pmr-rrpt-plan-ALL performs better in quality than pmr-lpg-adapt-ALL because it obtains better results mainly in Driverlog and Blocks thanks to the combination of plan-reuse and search. Although adp-l obtains a better value in makespan than all pmr-LB configurations, it is mainly due to the difference in solved problems in Wireless and Sokoban. It is also remarkable the result obtained by lama-first (best configuration in cost and makespan) because it is just a centralized planner. This clearly shows that the CoDMAP problems are not hard to solve even for classical planners, as there is no huge impact during the planning process even when agents try to solve all goals at once because goals are not assigned specifically.

5.5 Results scaling the number of agents

In order to analyze how pmr configurations scale with the number of agents, we generated one medium-sized problem in the Zenotravel domain. It has 63 goals. Then, we increased the number of agents. For each instance of the Zenotravel problem, agents were increased by 10 starting on 10 agents and stopping at 70. The configuration used for this experiment was pmr-rrpt-plan. Zenotravel belongs to the low interaction group identified in Section 5.4. The domains that belong to these groups are the ones where generally pmr performs better, as most problems are solved during merging or plan-reuse phases, avoiding the centralized planning step. Thus, we were interested in exploring in detail the evolution of makespan and plan length when increasing the number of agents. Results are shown in Fig. 8. X axis represents the maximum number of agents that can plan per problem. In Zenotravel, BC uses 10, 16, 18, 21, 21, 22 and 23 agents per problem while LB uses 10, 20, 30, 34, 37, 59 and 62. As Zenotravel belongs to the low interaction level group, the bigger the number of agents is, the better the makespan obtained by LB. The performance decreases drastically using ALL (only 3 problems out of 7 were solved in 1800s), because all goals are assigned to all agents in the problem, which makes the process of solving the interactions harder during plan-reuse.

Fig. 8

Evolution of Cost and Makespan in a Zenotravel problem when increasing the number of agents gradually (x axis). The configuration used was pmr-rrpt-plan with Best-cost (BC), Load-balance (LB) and All

When solving a MAP problem with pmr, our goal is to obtain the makespan effect shown on Zenotravel. This will not be possible in every domain, as it will mainly depend on the number of interactions (coupling), but it is the ideal scenario to follow regarding the potential of our contributions.

5.6 Multi-agent hard problems

One of the key goals when working on multi-agent environments consists on improving the distribution of the work load among agents, which directly improves the makespan of the resulting plans. Also, ideally, one would expect multi-agent planners that maximize the work-load distribution to scale up as the number of agents increases.

In this section we show some experiments on eight domains whose problems are harder to solve than the ones used on previous experiments. Tables 11 and 12 show the IPC scores on coverage and makespan respectively. Table 12 also contains the summary of time scores. For these experiments we have used the same planners and configurations shown on the CoDMAP experimentation (Section 5.4). In order to select the domains on this experimentation, we decided to include some domains from the group of low interaction (Zenotravel, Satellite, Rover), and some from the group of medium interaction (Driverlog, Blocks). We excluded the ones that had higher interaction (Elevator, Logistics) as they were only solved on the centralized phase, so the work-load distribution of pmr would not affect the result.

Table 11 Coverage results in hard and specific problems

Table 12 Makespan score in hard and specific problems

Additionally, we show on the same tables the results obtained on three domains that were specifically chosen to show the strength of pmr on Makespan. Two of those, Rover-graph and the new version of Depots-robots, are contributions of this work. After all the previous experiments, we realized that the MAP problems that fitted pmr best were those where the initial state can be easily divided in regions for the agents to “work” on a specific part of the search space. The lower the number of interactions between them the better.

The Rover-graph domain is an evolution of the usual Rover domain where two huge grids of waypoints are generated independently and then joined by an edge between those grids. This simulates environments where there is a bottleneck in the connection between two areas. The aim was to test how the planners’ performance changes when a different configuration of the environment penalizes the use of a single agent to solve the whole problem. The number of goals in the set of problems oscillates between 150-200. The minimum number of predicates per problem is 5100. Goals are the same as in the classical Rover domain (e.g. communicate soil, image, rock data etc.). The number of agents varies from 2 to 6. The two grids contain around 400 waypoints in total. On this variation of the usual Rover domain, planners (centralized-based ones specially) get lost because of the size of the search space. Instead of applying factorization to alleviate the agents’ individual planning process, those planners employ the smallest possible number of agents to solve the problem. As a result, an agent has to deal with almost all the goals, which makes its planning task harder to solve.

Depots-Robots is the planning version of a warehouse environment inspired on the Kiva Robots[49] where robots have to deliver to humans a list of products from the storage pods to complete a list of delivery orders. This new version works over a grid of waypoints where pod storages follow a classical structure of a warehouse by being stored in columns. There is an empty column between each pair of pod-occupied columns for robots to move. The first and last rows of the grid are empty. The last row is where humans are situated for the reception of products. The original version, where restrictions on the placements of pods and empty rows are not applied, is described in [5]. Robots are spread through the grid. Thus, pmr can indirectly assign a specific zone of the grid to a robot to pick up the nearby packages. As a result, planners that factorize the problem for each robot regarding human goals and pods’ locations will obtain better results.

VPR is the usual Vehicle Routing Problem where trucks need to deliver packages to some cities. The aim is to reduce the cost as much as possible. Here, again the problem can be easily divided as trucks will only care of delivering the packages by themselves. Usually, when goals are well-balanced among the agents, a different portion of the grid of waypoints is assigned to each of them. Thus, the problem is easier to solve for pmr; factorization again is key to simplify the planning tasks.

Coverage results on Table 11 show how a planner like siw that had promising results on CoDMAP now cannot solve more than half of the problems due to their complexity. The rest of the planners, including our configurations, except for yahsp have a similar coverage.

Table 12 shows that our LB configuration outperforms the rest of the planners regarding makespan. These planners were again multi-agent (cmap-t, adp-l, siw) and centralized (lama, yahsp) planners. Hence, even though our configurations might be slower, they are still capable of solving harder problems by involving multiple agents. Dividing the number of goals as much as possible among the agents has a direct impact on makespan. In VRP, Rover-graph and Depots-robots domains, pmr-rrpt-plan-LB increases the makespan score more than the other planners; problems can be easily divided, creating balanced subtasks for each agent. In VRP, pmr-rrpt-plan outperforms the rest of planners, as it is a good example of domain, where multi-agent planning can improve through factorization. This can also be seen on Rover-graph with cmap-t and lama. The main difference between them is factorization. cmap-t is able to solve every problem while lama cannot scale enough to solve a task of 200 goals. Domains such as Zenotravel, Satellite and Rover, that have a low number of interactions, are also good for our LB configuration.

Table 16 in the Appendix shows the time score, where adp-l and lama are the fastest ones. pmr is slower, because of the goal assignment phase, as our algorithm spends some time on identifying which agent solves best each goal. The fastest configurations usually assign all goals to all agents by default. This strategy works well when optimizing for time or coverage. However, we claim that the makespan score should be the main performance criteria if the goal is to generate plans in a real multi-agent environment, where a big number of agents is available to work.

5.7 Discussion on the experiments’ results

After describing the results of six different sets of conducted experiments some specific conclusions and remarks can be extracted from them:

• The performance of pmr and its adaptability cannot be appreciated on easy MAP tasks. For instance, results on CoDMAP (Section 5.4) reflect that the centralized planner lama was able to solve more problems than pmr’s BC, LB and cmap-t; even its coverage results are very close to those of adp-l and siw. This indicates that MAP planners do not usually have a remarkable advantage over centralized approaches on easy MAP tasks.

• Regarding interactions among agents, pmr works best on low and medium interaction domains. Those are generally identified as loosely-coupled domains by the planning community. Some of those domains are: Rovers, Satellite, Zenotravel, Depots, Hammer and VRP.

• pmr biases towards optimizing the makespan metric, independently of the MAP task received as input. Thus, the more the task can be factorized and work equally distributed among agents, the better the makespan obtained will be. Usually, those tasks are the loosely-coupled ones.

• pmr scales well on hard loosely-coupled planning tasks, and also in those that contain a topology that can be factored for the agents to work independently. This can be appreciated on the results from Rovers-graph or VRP.

• The goal assignment strategy Load-Balance works best for loosely-coupled domains, as it balances the amount of goals among the agents. In turn, this has a direct impact on improving the makespan. Best-cost biases towards improving the plan length and works best for tightly-coupled domains. As less agents are used during planning, it will reduce the number of conflicts to solve.

• rrpt-plan behaves very similar to lpg-adapt, which is important regarding that lpg-adapt is considered the state-of-the-art replanner.

  In addition, rrpt-plan covers the full range of reuse scenarios from the best case for reuse (when the input incorrect plan is very similar to the final correct one) and the worst case (when the input and final plans are very different).

• The plan-reuse phase of rrpt-plan is more useful when it is selected first. If we assume that the input plan is similar to the final plan, running plan-reuse first will automatically include most of the input plan actions into the final plan, boosting the performance of rrpt-plan as a result. However, in case the input plan is completely different from the final plan, we expect that the plan-reuse will fail fast and rrpt-plan will switch to the search phase. This issue was tested on the experiments with increasing number of goals in Section 5.3.

Also, some limitations have been identified:

• The main issue that faces pmr with tightly coupled domains is the number of interactions to solve. If the planning task presents many interactions, the plan-reuse phase could be potentially solved better by planning from scratch. Examples of such planning tasks are the ones defined in the IPC for the Driverlog or Sokoban. However, one must take into account that the distribution of problems generated by the IPC organizers for each domain, albeit randomly generated, usually focus on a specific subarea of the set of potential problems that can be generated. Therefore, it is easy to see that even in these two tightly-coupled domains, one can generate problems with lower interaction. For instance, one could have several rooms in Sokoban, each with its own set of robots, or one could have different network subgraphs in Driverlog, each one with its own set of drivers and vehicles. So, the property of being tightly-coupled is connected to the planning task (domain and problem) and not only to the domain.

• There exists a bottleneck on the goal assignment process. When the MAP task contains a considerable amount of goals, the time spent on estimating the cost per goal-agent can be heavily increased if the search space of the problem is big. In real-life environments, this issue can be solved by including external information to boost the cost estimation process.

• Given that our objective was to focus on loosely-coupled tasks, pmr cannot deal with joint actions (actions that require more than one agent to be executed, as moving a table by using two agents).

6 Related work

MAP lies between the automated planning and multi-agent communities, with strong implications in other areas, as robotics. As it was discussed in the introduction, approaches range from centralized to distributed planning. In case of distributed planning, some papers employ a distributed coordinated approach when generating plans [26, 39, 42, 46], while others delay coordination and perform plan merging after generating the individual plans [17].

MAP is an active topic within the planning community as shown by the organization of the CoDMAP competition and the wide range of planners that participated [43]. The planners vary from strong privacy preservation to no privacy preservation, from fully distributed to centralized; there are many ways of classifying MAP algorithms. Different classifications are explained in the survey [44]. pmr automatically changes its behavior from a purely distributed planner to a centralized planner depending on the input planning task. It is also capable of maintaining weak privacy.

In relation to plan merging, Mali devised algorithms for performing plan merging by removing or rearranging actions [35], while pmr can also modify the input merged plan by adding actions. Furthermore, pmr can handle plans where the same action appears in several individual plans. Britanik and Marefat proposed to perform plan merging within HTN planning [11]. Merging appears at different levels of abstraction by decomposing a plan into subplans. Our approach, pmr, does not work on HTN planning and neither has different levels of abstraction. Instead of decomposing a plan into subplans, we focus on decomposing the problem into subtasks. In the field of temporal planning, Mudrova et al. [36] propose an algorithm that merges partial order plans with durative actions for solving robotic tasks. A different approach close to plan merging is conflict solving. Jordan presents one such approach where conflicts are identified while agents generate the solution [27]. The algorithm works at the same time on a joint plan and penalizes the agents that generate a conflict.

Regarding factorization on MAP, some works in MAP deal with plan decomposition. Brafman and Domshlak propose a decomposition method of the planning domain [8]. Crosby et al. present a centralized total ordered planning algorithm that decomposes, with the help of heuristics, a loosely coupled problem into agents and subtasks [15]. In a recent work, Mali and Puthiyattil transform a MAP task into a set of subplans encoded in SAT to be later assigned to the agents [34]. Our approach, pmr, decomposes the problem into subtasks by assigning goals to agents. Then each subtask is given to a different agent. We are also helped by heuristics to proceed with the goal assignment.

Plan Reuse has also been studied in Automated Planning. Gerevini et al. define a new domain-independent planning system in [20]. They use two techniques: the first one divides the actions of the plan to repair in subgroups to later solve the conflicts with a Planning Graph; the second technique uses Action Graphs to reduce the number of inconsistencies reflected in the plan that needs to be adapted. Related with MAP, van der Krogt et al. apply a plan repair system to a MAP problem so that agents can adapt their plans iteratively by exchanging goals in an auction until all plans generated are valid [30]. The main difference with respect to our work is that we use a plan reuse phase after all plans from agents are merged and parallelized and plan reuse is executed only once. Krogt et al. also presented an extension of the VHPOP planner called POPR [31]. Their approach computes a set of partial plans similar to the given input plan. Then, it analyzes the dependencies of predicates and actions of those plans by generating removal trees and uses a heuristic to compute the most promising candidate. Finally, once the candidate plan is selected, plan reuse is applied to it. As it can be seen, the procedure is very different from rrpt-plan, but it is one of the first works that combines search and plan reuse on the same planner. The first plan reuse planner that incorporated heuristic search inside the replanning process was SHERPA [28]. It stores knowledge about both previous plans and previous plan-construction processes. rrpt-plan does not use heuristic search inside the plan reuse phase. We just try to reuse as many actions as possible from the input plan but we do not modify them. If plan reuse is not applicable anymore, classical heuristic search is performed from that point.

7 Conclusions and future work

We have presented pmr, an algorithm capable of solving a MAP task by merging individual plans and applying plan-reuse techniques, if needed. A key feature of pmr is that it automatically adapts to the interaction level among agents and goals, varying its behavior from distributed to centralized. It generates many valid plans in the merge phase (M) with a low computational effort if the domain has a low degree of interaction. Otherwise, it uses plan reuse (R) in domains with more interaction and resorts to centralized planning (C) in case of domains with strong interactions.

Another advantage of pmr is that it only includes off-the-shelf planners in its three phases (M, C and R). Hence, we can trivially improve the performance of pmr by just changing the planners used by better ones once they are developed. Moreover, pmr can easily be configured to target coverage, cost or makespan by just changing its goal allocation strategy.

When testing the set of planners against the last benchmark of hard problems, the results of pmr-rrpt-plan have shown that it easily adapts to any type of MAP problem, independently of the problem’s features (e.g. number of agents, goals, interactions). pmr-rrpt-plan maintains good results on coverage and time and remarkable results on makespan, specially in combination with the Load-balance strategy.

Regarding plan reuse, we have presented another contribution, rrpt-plan, which is an algorithm that combines plan reuse, sampling and local search to solve a planning problem. rrpt-plan receives the domain, the problem and an input plan (usually invalid) from which it will try to reuse actions to include in the final plan. We have shown in the experiments that rrpt-plan adapts to diverse plan reuse scenarios, including the ones that are not usually considered by state-of-the-art plan reuse planners. Also, we have shown experiments of rrpt-plan outside of pmr and the results were very similar to the state-of-the-art planner lpg-adapt.

As future work, we would like to define new techniques for plan repair, improving the way probabilities change the behavior of rrpt-plan and also to work on different plan merging strategies for pmr to merge more efficiently the individual plans obtained from the agents. A third option would be to make more efficient, in terms of time, the goal-assignment process.

Appendices

Appendix

A CoDMAP extra results

The following tables show specific results on Time, Makespan and Cost obtained on the CoDMAP experiments from Section 5.4.

Table 13 IPC scores in Time per configuration in CoDMAP domains

Table 14 IPC scores in Makespan per configuration in CoDMAP domains

Table 15 IPC scores in Cost per configuration in CoDMAP domains

B Hard problems extra results

Table 16 shows results on the time score obtained on the Hard problems experiments from Section 5.6. Time score score in hard and specific problems

Table 16