Abstract
Constraints, although ubiquitous in production and distribution planning, scheduling and control, often lead to inconsistencies in the decision-making process. The constraint-based modeling helps circumvent many organization-impacting issues. To address this, we developed a multi-level approach to the modeling and solving of combinatorial optimization problems. It is versatile and effective owing to the use of multi-level presolving and multiple paradigms, such as constraint programming, logic programming, mathematical programming and fuzzy logic, for their complementary strengths. The capability of this framework and its advantage over mathematical programming alone or over hybrid frameworks is shown in the illustrative example, in which combinatorial optimization is used as a benchmark to prove the effectiveness of the proposed approach. Knowledge of the problem is stored in the form of facts.
Similar content being viewed by others
1 Introduction
Constraints are ubiquitous in various areas of production and distribution. They may correspond to materials, technologies, resources, time, capacity, interoperation transport, etc. (production) or to available storage capacity, selection of distributors, transport duration, number of transport means, their types, etc. (distribution). Proper constraint modeling and solving will have a considerable impact on production-distribution planning and control and will allow decision-makers to detect difficult situations early enough to handle them safely. If the constraints are modeled and solved, fully or partially, at the moment they appear in a given area or for a given problem, but not collectively in subsequent stages, the global decision or optimization model will be simpler and solving it will take less time. We can thus talk about ubiquitous modeling and solving of constraints (UMSC) in these problems.
The concept of UMSC can be the basis for creating decision support systems and process optimization and control at various levels. Planning, scheduling and resource allocation problems are usually modeled using OR (operation research) approaches such as mathematical programming (MP) methods, with linear programming (LP) used at the strategic or tactical level (aggregated level). More detailed planning, scheduling and resource allocation require integer and binary decision variables and to this end, MIP (Mixed Integer Programming), IP (Integer Programming) or MILP (Mixed Integer Linear Programming) Schrijver [17] models have to be employed. The resulting models are very complex. To solve them, substantial computing effort is necessary. Real problems may become NP-hard problems. In the 1990s, constraint programming-based environments appeared Rossi et al. [16]; Benhamou et al. [3]; Tsang [25]; Apt [1] and their implementations to production and distribution problems were reported Liess and Michelon [12]; Rocha and Ramos [15]; Bocewicz and Banaszak [4]. Enormous flexibility, easiness and the range of constraint modeling gave them definite advantage over OR-based environments. But only at the modeling stage – CP-based environments turned out to be less effective at the solving stage, in particular, in solving combinatorial optimization problems. Their effectiveness often depends on the structure of modeled constraints and data, or on decision variable domain range. This issue does not exist in the MP-based environments, where model-solving methods are independent of both constraint structure and data. As for the UMSC concept, the approach that combines multiple paradigms such as CP- constraint programming, LP- logic programming, MP-mathematical programming, FL-fuzzy logic, etc. is the best solution.
The paper is organized as follows. Section 2 describes the constraint-based methods. The multi-level approach to ubiquitous constraints modeling and solving is presented in Section 3. The illustrative example and computational results of the proposed approach are described in Sections 4 and 5. Final remarks and possible future development and applications are shown in Section 6.
2 Constraint-driven programming, mathematical programming and integrated methods – basic principles
For the ubiquitous modeling and solving of different types of constraints, the most effective and most flexible are constraint-driven methods and environments based mostly on constraint satisfaction problems (CSPs) Tsang [25]; Apt [1]. A constraint satisfaction problem (CSP) is defined by a set of decision variables, X 1,X 2,...,X n , and a set of constraints, C 1,C 2,...,C m . Each decision variable X i has a nonempty domain D Xi of possible values. Each constraint C i involves some subset of the decision variables and specifies the feasible combinations of values for that subset. A state of the problem is defined by an assignment of values to some or all of the decision variables, {X i = v i ,X j = v j , ...}. An assignment that does not violate any constraints is called a consistent or legal assignment. A complete assignment is one in which every variable is mentioned, and a solution to a CSP is a complete assignment that satisfies all the constraints. Some CSPs also require a solution that maximizes an objective function than we speak about COP (Constraint Optimization Problem).
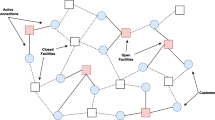
The CSP is typically determined on a constraint network (Fig. 1). A constraint network (CN) comprises a set of decision variables, each associated with a domain of values and a set of constraints. A CN defines the feasible combination of values of decision variables through a constraint subset. Formally, constraints are functions that effectively define the assignment of decision variables to some domain (Figs. 1 and 2).
Several modifications to the classic CSP model have been proposed: Flexible CSPs (relaxation of assumption that each solution must satisfy all constraints, including Fuzzy_CSP and Weighted_CSP), Dynamic_CSPs (a sequence of static CSPs) and Decentralized_CSPs. CSPs are to solve problems by modeling constraints, which represent all properties and requirements of the problem, and by finding solutions that satisfy all these constraints. CSP on finite domains are usually solved using different forms of search such as local search, constraint propagation and many variants of backtracking methods Rossi et al. [16]. A general search algorithm for solving a CSP is shown in Fig. 3. The highest effectiveness of CSPs is reported for binary constraint problems, where each constraint binds only two decision variables (Fig. 2).
For constraints that bind more than two decision variables, constraint propagation effectiveness decreases significantly and the number of backtrackings increases rapidly Sitek and Wikarek [20]. This feature makes the CSP-based environment, such as CP (Constraint Programming) and CLP (Constraint Logic Programming) less effective in solving complex problems, such as planning, scheduling or resource allocation. The structure of the constraints has no effect on the effectiveness of the MP methods, in contrast to a large number of integer decision variables, which, when present, reduce it substantially. Both MP and CLP involve decision variables and constraints. However, the types of the decision variables and constraints that are used and the way the constraints are solved are different in the two approaches Bockmayr and Kasper [5]; Hooker [11]; Barth and Bockmayr [2]. MP methods take into account only linear constraints (equations and inequalities) which include binary, integer and continuous decision variables. In the constraint-driven approach, the programming language is richer in terms of the types of constraints. In addition to linear equations and inequalities, there are various other constraints: nonlinear, disequalities, and symbolic (disjunctive, exclude, cumulative, alldifferent, profile etc.) Rossi et al. [16]. Moreover, CLP is less effective in combinatorial optimization problems Escudero et al. [9] that often occur in planning, scheduling, and control in manufacturing and distribution.
To sum up, in mathematical programming, the sets of constraints (equations) describe the problem but do not indicate how to solve it. In constraint programming, each constraint invokes a procedure that screens out unacceptable solutions. The most important elements that decide the effectiveness of mathematical programming include: relaxation, tools for filtering and duality theory Schrijver [17]. Relaxation methods in MP tend to be more effective when constraints and/or objective functions contain many decision variables. In general, MP relies on numerical calculation, which increases its effectiveness. In contrast, constraint-based environments (CP/CLP) may fail when constraints contain many decision variables. This follows from the fact that these environments (CP/CLP) are based on logic processing and the constraints do not propagate well. Moreover, CP/CLP are often insufficient for finding optimal solutions due to lack of relaxation technology and numerical calculation. However, the CP/CLP environments are a more powerful modeling language with which any type of constraints can be easily modeled and they use the structure within a problem (horizontal structure), thus contrary to MP with real vertical structure (a model is independent from data). Also, the CP/CLP environments have built in methods for removing infeasible values from variable domains (filtering, domain consistency, constraint propagation, etc). It is clear that both approaches (MP and CP/CLP) are complementary in many aspects and areas.
With this in mind, research has been undertaken to attempt integrating these paradigms. Several scenarios of their integration were reported in the literature Hooker [11]:
-
Double modeling - use both CLP and MP models and exchange information while solving.
-
Search-inference duality - view CLP and MP methods as special cases of a search/inference duality.
-
Decomposition - decompose problems into a CLP part and an MP part using a Benders scheme (Benders decomposition integrates two solution methods: one that solves the master problem, and one that solves the subproblem).
Integration and hybridization of CLP and MP environments was also a subject of research conducted by the authors of this paper Sitek and Wikarek [20]; Sitek et al. [23]; Sitek and Wikarek [19]; Sitek and Wikarek [22]. Elimination and replacement of the variable distribution mechanism but retaining the mechanism of constraint propagation has become the key research direction. The introduction of transformation as a critical component of hybrid approach and backtracking from the distribution of variables in the CLP clearly distinguishes our approach from those known from the literature Bockmayr and Kasper [5]; Hooker [11]; Caricato and Grieco [7], Milano and Wallace [14].
In all our previous papers dealing with hybridization Sitek and Wikarek [20,21,22], the problem was modeled as a whole at one level, the model was transformed and on the basis of the post-transformation model, the ultimate problem in the form of MILP was generated. Even though the hybrid approach made it possible to solve larger problems and to reduce optimization time relative to mathematical programming methods, its effectiveness in these two areas was insufficient for SSCM (Sustainable Supply Chain Management) problems. This is how the idea of developing a multi-level approach implementing the UMSC concept appeared. The proposed solution was especially effective in solving discrete optimization problems for SSCM, as shown in the form of comparative analysis with the hybrid and MP methods in Fig. 13a, b and c. The contribution of this study is in the modification of the original hybrid approach and its extension to the multi-level form represented by a modified model transformed for the SSCM problem. This approach is able to use the ubiquitous modeling and solving constrains for combinatorial optimization problems in manufacturing and distribution problems. The proposed approach integrates CP, CLP, MP and Fuzzy Logic (FL). It is an extension of the hybrid approach but differs from it in two aspects. The problem has to be modeled in the form of a set of CSPs and new methodology of constraint solving (e.g. multiple presolving) has to be employed. In addition, the models in this paper, in the form of CSPs and CSPsT before and after transformation, were presented for SSCM problem for the first time. The corresponding constraints have a new, mostly binary, structure.
3 A multi-level approach to ubiquitous modeling and solving constraints for combinatorial optimization
The need for a convenient, efficient and effective way of modeling and solving various types of constraints was conducive to the development of the multi-level approach based on the results of the previous studies on hybridization Sitek and Wikarek [20,21,22] and different, often complementary properties of individual paradigms (Section 2). The multi-level architecture results from the prevalence of constraints at various levels of the modeled problems. Figure 4 shows the conceptual diagram of the proposed approach.
The problem is modeled as a set of sub-problems in the form of CSPs for particular areas of production, distribution, storage, etc. (Level 1).
All CSPs are modeled using the set of CLP predicates. This set includes the predicates dedicated to a given CSP, e.g., predicates implementing individual constraints, general predicates used in each modeled problem, such as those creating lists of data from the sets of facts, and incorporated predicates (disjunctive(), exclude(), cumulative(), alldifferent() etc. ). The modeling process uses the set of facts as an information layer for the problem.
The CSP, standard or variant (DCSP, FCSP etc.) is then presolved (Level 2), using the methods which reduce the decision variable domains and can transform the variables and constraints. Constraint propagation, problem transformation or both methods combined into one are used as presolving methods (Section 3.1). In the next step, the constraints (financial, environmental or transport constraints) that bind the subproblems are modeled (Level 3). They are also presolved (Level 4). Now the additional and auxiliary constraints are modeled. These do not result directly from the structure of the problem but from the data instances, the user’s specific requirements or possibility of increasing the effectiveness of the solution (Level 5). The next step involves presolving the model and generating the ultimate MP model. Finally, the MP model is optimized using the MP-based environment (Level 6). For illustrative example (Section 4) the MP model takes the form of MILP (Mixed Integer Linear Programming) model.
The multi-level architecture allows modeling complex problems through the parallel modeling of sub-problems at a given level and related constraints at subsequent levels. This will result in the multiple use of presolving thus increasing its effectiveness.
3.1 Presolving
Presolving methods used at various levels constitute an important element of the proposed approach (Fig. 4). Presolving eliminates redundant information from the problem formulation while simultaneously trying to simplify and strengthen the formulation. It can be very effective and is often essential for solving instances. Especially for integer programming problems, fast and effective presolving methods are very important. Here, presolving may have a form of standard constraint propagation, problem transformation or a combination of these two methods. Constraint propagation is one of the CSP algorithm methods Rossi et al. [16]; Apt [1] whereas the transformation is the author’s concept introduced, to varying degrees and in varying forms, to CP/MP environments hybridization Sitek and Wikarek [20, 22]; Sitek [18]; Wikarek [26].
In our approach, the transformation is the element that makes it possible to eliminate infeasible points in the decision variable space prior to defining the values of the decision variables. Typically, the transformation precedes the constraint propagation. The transformation method uses the set of data facts for describing the structure of a problem, and variable facts (orders, plans, etc. In this phase, the instances of facts are used in the analysis of relationships between data. The analysis allows determining which connections or allocations are unacceptable/infeasible because no relevant/corresponding/adequate fact instances are available to describe them. As a result, adequate/corresponding decision variables will be removed in the presolving phase. For example, some of decision variables X f,c,t that define the value of transport between factory f and distribution center c by transport means t will be removed from the model if a connection between f,c is impossible and/or a means of transport along the f,c route cannot be used. Therefore, let’s do a simple analysis. Based on the illustrated example (Section 4, Appendix A), we know that f = 1..6, c = 1..3, t = 1..4. Thus the potential number of decision variables X f,c,t is 6x3x4 = 72. On the other hand, the number of instances of the fact fact_f_c_t () is 24 (Appendix A). In this case, the reduction involves 48 decision variables. So in the future it will be possible to define values only for 24 decision variables X f,c,t for illustrative example (Figs. 5 and 6).
Likewise, the analysis of the remaining facts may result in the reduction of other decision variables of the modeled problem. In the transformed model, there will be much less decision variables than the initial one. Due to the multi-level hybrid approach, the reduction information will be transferred to the next level, resulting in further reductions in both decision variables and constraints. The application of presolving in practice is shown in (Section 4).
3.2 Multi-level model
One of the distinguishing features of this multi-level approach is the method of modeling the problem. The model is represented as a set of CSPs with an architecture related to the modeled problem (Table 6 in Appendix D). Figure 7 shows a schematic diagram of the model together with possible architectures, depending on the problem characteristic features for illustrative example. The models can have a form of CSPs occurring in parallel at the same level, in series at different levels or in a mixed form as in the illustrative example (Section 4). Each CSP uses a set of facts as data and a set of questions (objectives) defining the way the constraints will be satisfied.
This way of modeling makes it very easy for a given class/type of problems, where changing sets of fact instances is all that has to be done. Modeling becomes more complicated in the case of a new problem class/type with new constraint types. These new constraints have to be modeled in the form of CLP predicates (Section 4).
For the illustrative example, completely new constraint formalization is proposed, resulting from the application of the new multi-level architecture of the model. As a result, a large part of constraints had a binary form (Fig. 2), which is especially beneficial for the effectiveness of constraints propagation and transformation.
3.3 Innovativeness presented approach
Introducing presolving methods (constraint propagation and transformation) at different levels of problem modeling (Fig. 4) and mathematical programming solving methods is an important innovation of the proposed approach. Extremely time-consuming and generating a lot of backtrackings labeling is eliminated from the general search algorithm for solving CSPs (Fig. 3). Ubiquitous use of presolving methods in various forms and manners contributes substantially to the reduction, aggregation and transformation of decision variables and constraints. Thus the ”lean” CSPs become the basis for generating a noticeably smaller MILP model.
For the solution of the generated model, we use mathematical programming methods and techniques instead of CLP, which is possible to avoid a lot of backtracking labeling techniques (extremely time-consuming). You can also skip other CLP techniques such as variable ordering, forward checking etc.
Another important novelty of the proposed approach is the ability to expand each of the subproblems modeled as CSPs without having to change and implement the whole problem as such Sitek and Wikarek [21, 22] This allows the use of a model with an architecture as presented in (Section 3.2). Knowledge of the problem is stored in the form of facts, which is possible due to the declarative approach – CLP. Facts are also transformed (Fig. 6) and become a data layer for the model (3.2) (Appendix A, B).
4 Illustrative example
To show the practical application of the multi-level approach (Fig. 4), we used the problem of sustainable supply chain management (SSCM) Brandenburg and Rebs [6], with the formal model proposed in Sitek and Wikarek [19]. The problem, studied before, was chosen to compare the effectiveness of the proposed multi-layer approach with other solutions, in particular with our previous results Sitek and Wikarek [19], Sitek [19]. It is the combinatorial optimization problem which consists of the layers corresponding to production, distribution, recycling and retail. These layers are connected by transport (most frequently multimodal), as shown in Fig. 5. Each modeled layer has a specific set of constraints (mode of transport, production and distribution capacity, recycling centers capacity, etc.) presented in the form of interconnected CSPs. Such a method of modeling constraints essentially distinguishes the presented model from those published previously Sitek and Wikarek [21]; Sitek [19] where all constraints and objectives were modeled globally at the same time. The set of constraints that bind the layers (the number and capacity of transport means, environmental constraints, etc.) are also modeled as CSPs. The forms of CSPs for consecutive layers, the connecting, additional and logical constraints are shown in Table 1. The proposed way of problem modeling (Section 3.1) gave many of the constraints (1C1, 1C2, 2C2, 2C3, 2C4, 1C5, 2C5, 3C5, 1C6, 2C6, 3C6, see Appendix C and D) of the model (Table 1 and Appendix D) a binary character. This is another feature that differentiated SSCM problem formalization from other models already presented in Sitek and Wikarek [21], Sitek [19]. The remaining constraints also have different forms. Thus, the proposed formalization (Appendix D) is a completely new concept.
All the experiments and studies were carried out for the same data instances and in the same computational environment. Data instances for CSPs are presented using a set of facts. The structure of the facts describing the illustrative example, the relationship between facts and keys attributes for facts are shown in Fig. 6. The schematic diagram follows that well known from the database design, ERD (Entity Relationship Diagram) Teorey et al. [24] .The same diagram (Fig. 6) shows the transformation of facts for the illustrative example which is a presolving element and refers to the model data layer (Table 1 and Appendix A, Appendix B). Some of the facts after transformation change their structure and some are eliminated (15 facts before and 10 after transformation). It has to be noted that the number of instances of each fact is also greatly reduced.
Appendix A and B list the facts and decision variables for particular CSPs and CSPsT.
The implementation of the approach in Fig. 4, Section 3, which took the form of the framework, Fig. 7, was used to model and solve the illustrative example. Practical implementation of the UMSC concept in the framework form contains ubiquitous CSPs and ubiquitous presolving methods. Both elements are present at many levels (Fig. 7).
In this illustrative example, the presolving methods are represented by constraint propagation (Level 2, Level 4) and transformation with constraint propagation (Level 5). Constraint propagation reduces the domains of decision variables and, in some cases, detects the situations, in which certain decision variables do not satisfy the constraints and removes them. In our example, constraint propagation defined, among others, the minimum number of distribution and recycling centers needed for the processing of an order set and the minimum number of transport means needed for the distribution of products, etc. Transformation in this example included the change of problem representation by the elimination of infeasible routes, that is, the routes left out due to technological constraints or lack of orders for specific products from specific distributors and manufacturers. The additional (CSP9T) and logical (CSP8T) constraints were modeled at the same level (Level 5). Table 2 shows the CSPsT after transformation. The transformation technique for the decision variables and constraints from the illustrative example is included in Appendix D (Tables 8 and 9). The Level 5 CSPs and selected objective functions (examples of objective functions are listed in Appendix A) were used to generate the problem formulated as an MILP model solved in the next step with an MP solver (Level 6). Full forms of CSPs and CSPsT with a description of the constraints are included in Appendix D (Tables 6 and 7).
An alternative approach consists of modeling the whole problem in the form of an MILP model that covers all the areas and all the constraints and solves the problem using the MP solver. This approach is less effective computationally, as only small size problems can be solved within acceptable time (Appendix E), with nonlinear and logical constraints excluded.
The tool of choice for the implementation of the framework (Fig. 7) was ECLi PS e Eclipse [8] which is an open-source software system for the cost-effective development and deployment of constraint programming applications. MP-based environment in the implementation framework was EPLEX built in ECLi PS e MP-solver. ECLi PS e was used to implement the levels of the framework: Level 1, Level 2, Level 3, Level 4 and Level 5. EPLEX was used for implementing Level 6 and for solving.
5 Computational experiments for illustrative example
In order to verify and evaluate the proposed framework, many computational experiments were performed for the illustrative example. All the experiments relate to the supply chain with six manufacturers (f = 1..6), three distributors (c = 1..3), ten customers (r = 1..10), four modes of transportation (t = 1..4), two center_2 (recycling) (y = 1..2), fifteen product items (p = 1..15), and nine sets of orders (Or 1 (5), Or 2 (10), Or 3 (15), Or 4 (20), Or 5 (30), Or 6 (40), Or 7 (60),Or 8 (75), Or 9 (90),-(N)- the number of orders in set Or i ). Two objective functions F1 (total supply chain costs) and F2 (total environmental costs) were used during the generation of the MILP model (Section 4, Fig. 7, Level 5). Both functions are shown in detail in Appendix C. The experiments were carried out in two directions. Firstly, the methods for applying the proposed approach as a framework to the complex illustrative model (Implementation A) and examining the properties for the sample instance of data (Figs. 8a, b, 9a, b and 10a, b) are shown. At this stage, the values of Vx- current use of distributors’ capacity, Dx- current use of transportation units were determined for different numbers of orders. The impact of parameter V- distributors’ capacity on the objective function was defined. The same procedure can be applied to evaluate the values and impacts of other model parameters. The information obtained from the evaluations forms the basis for decision support in SSCM. The key element of the proposed experiments was the consecutive stage in which effectiveness analysis for the proposed approach is performed in terms of computing time and problem size. For the comparative analysis, the same illustrative example was implemented in the MP-based approach and hybrid approach. Over 200 computational experiments were carried out for different model parameters and for nine series of data varied by the number of orders N. Analysis of the results of the second part of experiments clearly shows the benefit of the proposed approach (Implementation A) in relation to classical approaches based on mathematical programming (Implementation B) and hybrid approach (Implementation C). To ensure comparable conditions, all experiments were performed using a PC Intel core (TM2), 2.4 GHz, 2 GB RAM. The same MP solver was used in the same configuration in all three implementations (A,B,C).
a Current use of distributors’ capacity (Vx1,Vx2,Vx3) for particular distributors depending on the numbers of orders (N) (F1-objective function, V1,V2,V3- distributors’ capacity). b Current use of distributors’ capacity (Vx1,Vx2,Vx3) for particular distributors depending on the numbers of orders (N) (F2-objective function, V1,V2,V3- distributors’ capacity)
a Current use of transportation units (Dx1,Dx2, Dx3, Dx4) for different mode of transportation (F1-objective function, D1,D2,D3,D4 - the number of transportation units for different mode of transportation) . b Current use of transportation units (Dx1,Dx2, Dx3, Dx4) for different mode of transportation (F2-objective function, D1,D2,D3,D4 - the number of transportation units for different mode of transportation)
Implementation A offers a 5-fold reduction in the number of variables (Fig. 11a, b), a 35-fold reduction in the number of constraints (Fig. 12a, b) and a 25-fold reduction in the calculation time (Fig. 13a, b) compared with Implementation B. The search time was reduced when the data instances were small (up to 15 orders). In the case of larger size instances, the optimal solution could not be found with less than 600 s and the mathematical programming calculations were stopped (Appendix E). Compared with Implementation C, Implementation A offers a 3-fold reduction in the number of variables (Fig. 11a, b), a 6-fold reduction in the number of constraints (Fig. 12a, b) and a 6-fold reduction in the calculation time (Fig. 13a, b) for the same computational examples. The search time was reduced when the data instances were medium size (up to 60 orders). In the case of larger sizes of the data instances, the optimal solution could not be found with less than 600 s and the calculations were stopped (Appendix E). The results can be explained by analyzing potential solution space for each implementation. The space defined by the Cartesian product of V(variables)xC(Constraints) was determined for all numerical cases Or(N). Figure 13c compares the size of these spaces for each implementation. Due to large differences between the sizes, the logarithmic scale was used. The differences between implementations reach at least an order of magnitude.
a Graph showing the calculation time of the implementation A, implementation B and implementation C for objective function F1 (Time stop= 600s). b Graph showing the calculation time of the implementation A, implementation B and implementation C for objective function F2 (Time stop= 600s). c Graph showing the size (VxC) of the solution space for the implementation A, implementation B and implementation C (V-the number of decision variables, C-the number of constraints)
6 Conclusions
The paper provides a robust modeling and solving method to combinatorial optimization for production and distribution problems. This method, based on the concept of UMSC in multi-level architecture, is an extension to the hybrid approach, discussed in previous studies Sitek and Wikarek [20], Sitek and Wikarek [21], both in the area of modeling (modeling subproblems as separate CSPs, linked CSPs, logical CSPs and ancillary CSPs) and solving (with multiple use of presolving). The efficiency of the proposed method was examined through a set of computational experiments for illustrative example (optimization of SSCM). The experiments were also performed for the hybrid approach and mathematical programming. The outcome of the proposed method includes (a) flexible modeling and introduction of many binary constraints to the model, (b) a significant reduction in solution space, which allows solving larger problems in shorter times compared with hybrid approach and mathematical programming and (c) a possibility of independent modification and extension of the model CSPs.
The multi-level architecture is suitable for problems such as ubiquitous manufacturing, supply chain management, distribution, vehicle routing etc., because it allows the implementation of constraints and presolving of the constraints in all areas and at all levels of the problem. This property is very important as it makes it possible to early detect constraint infeasibility in each subproblem. The use of the paradigms of constraint logic programming and mathematical programming in multi-level architecture takes advantage of the synergy of individual paradigms, which is clear in numerical experiments (Section 5 Fig. 11a and b, Appendix E Tables 10, 11, 12, 13, 14 and 15).
Further studies will focus on the implementation of other production-distribution models with the use of the proposed approach (Nielsen at al. [13]; Grzybowska and Gajšek [10]). The proposed method can be extended to modeling and solving soft and fuzzy constraints and multi-objective optimization. In the further extension of the method MP solvers will be replaced with heuristics and metaheuristics for solving industrial size problems. In future, a comparative analysis between the proposed approach and the pure CLP-based approach will be carried out. Advanced CLP techniques like different variable ordering techniques, GAC (Generalized-Arc-Consistency) for n-constraints will be tested in the context of modeling and solving distribution problems.
References
Apt K (2003) Principles of constraint programming, Cambridge University Press, Cambridge
Barth P, Bockmayr A (1998) Modelling discrete optimisation problems in constraint logic programming. Ann Oper Res 81:467. https://doi.org/10.1023/A:1018981813157
Benhamou F, Jussien N, O’Sullivan BA (2007) Trends in Constraint Programming, ISBN: 978-1-905209-97-Wiley-ISTE
Bocewicz G, Banaszak Z (2013) Declarative approach to cyclic steady states space refinement: periodic processes scheduling. Int J Adv Manuf Technol 67(1-4):137–155. https://doi.org/10.1007/s00170-013-4760-0
Bockmayr A, Kasper T (2004) Branch-and-infer, a framework for combining CP and IP. Constraint Integer Programm Oper Res/Comput Sci Interfaces Ser 27:59–87. https://doi.org/10.1007/978-1-4419-8917-8_3
Brandenburg M, Rebs T (2015) Sustainable supply chain management: a modeling perspective. Ann Oper Res 229:213. https://doi.org/10.1007/s10479-015-1853-1
Caricato P, Grieco A (2009) A DSS for production planning focused on customer service and technological aspects. Robot Comput-Integr Manuf 25:871–878. https://doi.org/10.1016/j.rcim.2009.06.003
Eclipse (2015) Eclipse - The Eclipse Foundation open source community website, Accessed May 4, https://www.eclipse.org
Escudero LF, Martello S, Strusevich V (2013) An overview of computational issues in combinatorial optimization. Ann Oper Res 207:1. https://doi.org/10.1007/s10479-013-1400-x
Grzybowska K, Gajšek B (2016) Regional logistics information platform as a support for coordination of supply chain. In: Bajo J et al (eds) Highlights of Practical Applications of Scalable Multi-Agent Systems, The PAAMS Collection. https://doi.org/10.1007/978-3-319-39387-2_6, pp 61–72
Hooker JN (2002) Logic, optimization, and constraint programming. J Comput 14(4):295–321
Liess O, Michelon P (2008) A constraint programming approach for the resource-constrained project scheduling problem. Ann Oper Res 157(1):25–36. https://doi.org/10.1007/s10479-007-0188-y
Nielsen I, Dang Q, Nielsen P, Pawlewski P (2014) Scheduling of mobile robots with preemptive tasks. Adv Intell Syst Comput 290:19–27. https://doi.org/10.1007/978-3-319-07593-8_3
Milano M, Wallace M (2010) Integrating operation research in constraint programming. Ann Oper Res 175(1):37–76.
Roch J, Ramos C (1994) Task planning for flexible and agile manufacturing systems. IROS ’94 1:105–112. https://doi.org/10.1109/IROS.1994.407403
Rossi F, Van Beek P, Walsh T (2006) Handbook of constraint programming. Elsevier Science Inc, New York
Schrijver A (1998) Theory of linear and integer programming, ISBN 0-471-98232-6. Wiley, NY
Sitek P (2014) A Hybrid Approach to the Two-Echelon Capacitated Vehicle Routing Problem (2E-CVRP). In: Recent Advances In Automation, Robotics And Measuring Techniques, Advances in Intelligent Systems and Computing. https://doi.org/10.1007/978-3-319-05353-0_25, vol 267, pp 251–263
Sitek P (2015) A hybrid approach to sustainable supply chain optimization. In: Progress in Automation, Robotics and Measuring Techniques. https://doi.org/10.1007/978-3-319-15796-2_25 , pp 243–254
Sitek P, Wikarek J (2013) A hybrid approach to modeling and, optimization for supply chain management with multimodal transport. In: IEEE Conference: 18th International Conference on Methods and Models in Automation and Robotics (MMAR). https://doi.org/10.1109/MMAR.2013.6670011, pp 777–782
Sitek P, Wikarek J (2015) A hybrid framework for the modelling and optimisation of decision problems in sustainable supply chain management. In: International Journal of Production Research. https://doi.org/10.1080/00207543.2015.1005762, pp 6611–6628
Sitek P, Wikarek J (2016) A hybrid programming framework for modeling and solving constraint satisfaction and optimization problems. In: Scientific Programming, Volume 2016, Article ID 5102616. https://doi.org/10.1155/2016/5102616
Sitek P, Nielsen IE, Wikarek J (2014) A hybrid multi-agent approach to the solving supply chain problems. Procedia Comput Sci KES 35:1557–1566. https://doi.org/10.1016/j.procs.2014.08.239
Teorey T, Lightstone S, Nadeau T, Jagadish H (2011) Database Modeling and Design: Logical Design, The Morgan Kaufmann Series in Data Management Systems 5th Edition, ISBN-13: 978-0123820204
Tsang E (1993) Foundation of constraint satisfaction. Academic Press, London and San Diego
Wikarek J (2016) An integrated declarative approach to decision support for scheduling groups of jobs. In: Information Systems Architecture And Technology, ISAT 2015, PT I Advances in Intelligent Systems and Computing. https://doi.org/10.1007/978-3-319-28555-9_5, vol 429, pp 53–64
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A
The tables show the fact structure, including key attributes and parameters (Table 3), and decision variables (Table 4). All this information is needed to formalize the CSPs of the modeled problem. In brackets is the number of instances of a given fact, which are used for computational experiments (Section 4).
Appendix B
The tables show the fact structure, including key attributes and parameters (Table 4), and decision variables (Table 5) after transformation. All this information is needed to formalize the CSPTs of the modeled problem. In brackets is the number of instances of a given fact, which are used for computational experiments (Section 4).
Appendix C
F1- total supply chain costs minus the profit from recycling
Appendix D
Table 6 shows the explicit form of CSPs. For each CSP the set of constraints is presented in algebraic form.
Analogously, Table 7 shows the explicit form of CSPsT (after transformation). Comparison of decision variables and constraints before and after transformation are presented in Tables 8 and 9.
Appendix E
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sitek, P., Wikarek, J. A multi-level approach to ubiquitous modeling and solving constraints in combinatorial optimization problems in production and distribution. Appl Intell 48, 1344–1367 (2018). https://doi.org/10.1007/s10489-017-1107-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-017-1107-9