Solving the uncapacitated facility location problem under uncertainty: a hybrid tabu search with path-relinking simheuristic approach

Abstract

The uncapacitated facility location problem (UFLP) is a well-known combinatorial optimization problem that finds practical applications in several fields, such as logistics and telecommunication networks. While the existing literature primarily focuses on the deterministic version of the problem, real-life scenarios often involve uncertainties like fluctuating customer demands or service costs. This paper presents a novel algorithm for addressing the UFLP under uncertainty. Our approach combines a tabu search metaheuristic with path-relinking to obtain near-optimal solutions in short computational times for the determinisitic version of the problem. The algorithm is further enhanced by integrating it with simulation techniques to solve the UFLP with random service costs. A set of computational experiments is run to illustrate the effectiveness of the solving method.

1 Introduction

The facility location problem (FLP) was initially addressed by Stollsteimer [1], Kuehn and Hamburger [2], Manne [3] and Balinski [4] to determine a set of facilities that minimizes the aggregation of two inversely correlated costs: (i) the cost of opening facilities; (ii) the cost related to servicing customers from the opened facilities. In most formulations of the problem, a set of customers and a set of potential facility locations are known in advance. Likewise, the opening costs associated with each facility and the costs of servicing each customer from every potential facility are also known. Hence all inputs are deterministic insofar as they are static inputs that are given from the very beginning. So the FLP is a frequent optimization problem used in very diverse application fields, from logistics and inventory planning (e.g., where to allocate distribution or retailing centers in a supply chain) to telecommunication and computing networks (e.g., where to allocate cloud service servers in a distributed network, cabinets in optical fiber networks, etc.).

Fig. 1

Illustrative example of a solution for the UFLP under uncertainty

As one of the most frequent optimization problems in the logistics and supply chain management area, several versions of the FLP have been analyzed in the scientific literature. The uncapacitated FLP (UFLP) assumes that each facility’s capacity is virtually unlimited or is, at least, far beyond expected customer demands. Despite being known as the simple facility location problem, the simple warehouse location problem, or the simple plant location problem for its apparent simplicity [5], the UFLP has been proved to be NP-hard [6]. Therefore, heuristic and metaheuristic approaches become a natural choice for solving large-scale instances of the UFLP in reasonably short computing times. This is because exact and approximate methods are unable to accurately solve large instances during short periods of time. Another variant is the capacitated FLP (CFLP), where each open facility has a limited servicing capacity; i.e., there is limit to customers’ demand that can be served by any single facility. According to Silva and de la Figuera [7], both Lagrangian-based heuristics and metaheuristics have been demonstrated as effective methods for solving the CFLP. The single-source CFLP (SSCFLP) also requires each customer having to be supplied by exactly one facility. As stated by Klose and Drexl [8], the SSCFLP is generally more difficult to solve than the multiple-source CFLP. In fact the SSCFLP also belongs to the class of NP-hard problems [9]. Therefore, heuristic approaches become a natural choice for solving large-scale instances of the SSCFLP in reasonably short computing times.

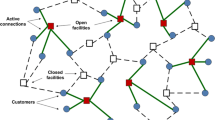
Uncertainty permeates all real-world systems, including supply chain management, logistics and facility locations. The inherent unpredictability of various variables poses a significant challenge in designing efficient and cost-effective solutions. Correia and Saldanha-da Gama [10] reviewed the FLP with stochastic components by exploring different methods proposed in the recent literature to optimize the FLP under uncertainty. These stochastic components arise when inputs, such as customer demands or service costs, are random variables instead of deterministic values. Effectively recognizing and accounting for this uncertainty become crucial in providing optimal solutions for real-life combinatorial optimization problems. Simulation-based optimization approaches have been proposed to tackle such problems [11, 12]. These approaches encompass diverse optimization methods, including mathematical programming, metaheuristics, and even machine learning. In recent decades, the hybridization of metaheuristics with simulation has emerged as a popular and effective approach for solving stochastic optimization problems [12]. Simheuristics, a simulation-optimization method that combines simulation with metaheuristics, has been widely used to address various combinatorial optimization problems with stochastic elements [13, 14]. This work proposes a novel simheuristic algorithm to address the UFLP under uncertainty by specifically considering stochastic components in the form of random service costs. These service costs can be modeled using probability distributions that can be either theoretical or empirical. Figure 1 provides an illustrative example of a solution for the UFLP under uncertainty. The example depicts the locations where facilities have been opened (indicated by red squares) and the closed facilities (represented by white squares). Customers, depicted by blue circles, are served by the open facilities to which they are actively connected. Each facility has a fixed opening cost, and servicing a customer throughout an open facility has an associated service cost, which is uncertain and, therefore, modeled as a random variable.

Accordingly, the main contributions of this paper can be summarized as follows: (i) a tabu search metaheuristic [15] to efficiently solve the UFLP in short computational times; (ii) a path-relinking approach to obtain near-optimal solutions by exploring paths that connect good quality solutions; (iii) a simheuristic algorithm that integrates the tabu search metaheuristic and path-relinking approach with simulation techniques to efficiently solve the aforementioned problem. Note that the tabu search and path-relinking algorithms are shown to be highly effective in practice for finding near-optimal or optimal solutions to large-scale optimization instances in short computational times [16, 17]. However, without the support of simulation-based extensions like that introduced in this paper, these techniques do not account for the inherent unpredictability found in real-life systems when solving the UFLP under uncertainty.

The remainder of this paper is structured as follows: Section 2 formulates the mathematical model for the UFLP with random service costs. Section 3 reviews the literature on the UFLP under uncertainty. Section 4 presents a tabu search metaheuristic with path-relinking as a solving method for the UFLP, and how the algorithm can be extended into a simheuristic one to solve the UFLP under uncertainty. Section 5 describes the computational study performed to test the proposed solving method. Finally, Section 6 discusses the main conclusions of this work and open research lines.

2 Model formulation

By following the mixed-integer linear programming model for the deterministic UFLP proposed by Erlenkotter [18], the stochastic version of the problem can be modeled using the following set of parameters and variables

• I - Set of m alternative facility locations, indexed by i.

• J - Set of n customer zones, indexed by j.

• $f_i$ - Fixed cost of establishing a facility at location i.

• $C_{ij}$ - Random variable that models the cost of servicing customer j

• from facility i.

• $x_{ij}$ - It takes the value 1 if the demand of customer j is supplied from

• facility i, and 0 otherwise.

• $y_{i}$ - It takes the value 1 if facility i is open, and 0 otherwise.

Then the stochastic UFLP considered in this work is formulated as follows:

$$\begin{aligned}{} & {} \text {Minimize} \qquad \qquad E\left[ \sum _{i \in I}\sum _{j \in J} C_{ij}x_{ij}\right] + \sum _{i\in I}f_iy_i \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \text {subject to:}\qquad \qquad \nonumber \\{} & {} \qquad \qquad \sum _{i \in I}x_{ij} = 1 \qquad \qquad \forall ~j \in J\end{aligned}$$

(2)

$$\begin{aligned}{} & {} \qquad \qquad x_{ij}\le y_i \qquad \qquad \forall ~i \in I, \forall ~j \in J\end{aligned}$$

(3)

$$\begin{aligned}{} & {} \qquad \qquad P\left( C_{ij} \le c_{max} \right) > p_0 \qquad \qquad \forall ~i \in I, \forall ~j \in J\end{aligned}$$

(4)

$$\begin{aligned}{} & {} \qquad \qquad y_i\in \{0,1\} \qquad \qquad \forall ~i \in I\end{aligned}$$

(5)

$$\begin{aligned}{} & {} \qquad \qquad x_{ij}\in \{0,1\} \qquad \qquad \forall ~i \in I, \forall ~j \in J \end{aligned}$$

(6)

The objective function (1) represents the minimization of the sum of the expected total cost of servicing customers and the total fixed costs of facility establishment.

Constraint (2) ensures that the demand for each customer zone is met. Constraint (3) makes sures that customer demand can only be produced and shipped where the facility is established. Constraint (4) features probabilistic constraints. These constraints add a probabilistic aspect to the model by ensuring that the cost of serving each customer from each facility falls within a certain threshold $c_{max}$ with a specified level of confidence $p_0$. This allows the model to account for the uncertainty in the cost values and helps more robust decisions to be made that consider the risk associated with the random variable $C_{ij}$. As discussed later, this can be considered a soft constraint, which will generate a penalty cost every time it is violated. Finally, Constraints (5) and (6) define the binary decision variables. The deterministic version of this model (considering constant costs $c_{ij}$ instead of variable ones $C_{ij}$) was implemented using Python and solved with commercial solver Gurobi to calculate the optimal values for different instances of the deterministic UFLP. In this way, the performance of the metaheuristic proposed in this work can be compared to the mathematical approach. Additionally, a simheuristic was developed to solve the stochastic version of the problem at different uncertainty levels, which is a very common situation in real-life problems.

3 Related work on the UFLP under uncertainty

The FLP was initially introduced as the plant location problem by Stollsteimer [1] and Balinski [4]. Traditionally, the FLP has been approached from several perspectives, including worst-case analysis, probabilistic analysis and empirical heuristics. Although exact algorithms for the problem can be found in the existing literature, the NP-hard nature of the FLP makes heuristics a more practical approach for quickly obtaining solutions, especially for larger and more realistic instances. One of the first works on the FLP was carried out by Efroymson and Ray [19], who developed a branch-and-bound algorithm. They utilize a compact formulation of the FLP by leveraging the fact that its linear programming relaxation could be solved through inspection. However, this linear programming relaxation is known to be weak and does not, therefore, provide tight lower bounds. Another early approach was proposed by Spielberg [20], which employs a direct search or implicit enumeration method. The authors present two different algorithms based on the same directed search: one considering the facilities to be initially open and another one contemplating initially closed ones. Later Erlenkotter [18] proposed a dual-based exact approach that differed from previous approaches by considering a dual objective function. An improved version of this work was presented by Körkel [21]. Although exact approaches provide optimal solutions for small or medium instances, they are unsuitable for solving large-scale real-world problems in reasonable computational times. Therefore, employing approximate methods is advisable. One of the earliest approximation methods was that by Hochbaum [22], and it consists of a simple and fast greedy heuristic. More recently, Ghosh [23] put forward a neighborhood search heuristic by incorporating a tabu search as the local search component. This approach yields competitive solutions in significantly shorter computational times compared to exact algorithms. A similar approach with a tabu search was proposed by Michel and Van Hentenryck [24]. This algorithm shows competitive performance compared to previous literature results. The algorithm utilizes a linear neighborhood approach, where a single facility is flipped at each iteration. Resende and Werneck [25] introduced an algorithm based on the GRASP metaheuristic. This algorithm incorporates a greedy construction phase combined with a local search operator and path-relinking. It obtains results that come close to the lower bound values for a wide range of different instances. Recently, Martins et al. [26] introduced an ‘agile optimization’ framework for the UFLP. This framework combines a biased-randomized algorithm with parallel programming techniques to offer real-time solutions. The key feature of this approach is its ability to react and swiftly adapt to rapidly changing customer demands. It achieves this by re-optimizing the system whenever new information is incorporated into the model.

The FLP was initially introduced as the plant location problem by Stollsteimer [1] and Balinski [4]. Traditionally, the FLP has been approached through various perspectives, including worst-case analysis, probabilistic analysis, and empirical heuristics. While exact algorithms for the problem can be found in the existing literature, the NP-hard nature of the FLP makes heuristics a more practical approach for obtaining solutions quickly, especially for larger and more realistic instances. One of the first works on the FLP was carried out by Efroymson and Ray [19] who developed a branch-and-bound algorithm. They utilized a compact formulation of the FLP, leveraging the fact that its linear programming relaxation could be solved through inspection. However, this linear programming relaxation is known to be weak and therefore does not provide tight lower bounds. Another early approach was proposed by Spielberg [20], which employed a direct search or implicit enumeration method. The authors present two different algorithms based on the same directed search, one considering the facilities initially open and another one considering the facilities initially closed. Later, Erlenkotter [18] propose a dual-based exact approach, differing from previous approaches by considering a dual objective function. An improved version of this work was presented by Körke [21]. Although exact approaches provide optimal solutions for small or medium instances, they are unsuitable for solving large-scale real-world problems in reasonable computational time. Therefore, it is advisable to employ approximate methods. One of the earliest approximation methods was proposed by Hochbaum [22], consisting of a simple and fast greedy heuristic. More recently, Ghosh [23] proposed a neighborhood search heuristic, incorporating tabu search as the local search component. This approach yields competitive solutions within significantly reduced computational times compared to exact algorithms. A similar approach using a tabu search was proposed by Michel and Van Hentenryck [24]. This algorithm has shown competitive performance compared to previous literature results. The algorithm utilizes a linear neighborhood approach, where a single facility is flipped at each iteration. Resende and Werneck [25] introduced an algorithm based on the GRASP metaheuristic. This algorithm incorporates a greedy construction phase combined with a local search operator, and a path-relinking. It achieved results close to the lower bound values for a wide range of different instances. Recently, Martins et al. [27] introduced an Agile Optimization framework [26] for the UFLP. This framework combines a biased-randomized algorithm with parallel programming techniques to offer real-time solutions. The key feature of this approach is its ability to react and adapt swiftly to rapidly changing customer demands. It achieves this by re-optimizing the system whenever new information is incorporated

A wide range of variants of the FLP have been extensively addressed in the literature, regardless of the employed solution method. One of the most studied variants is the SSCFLP. Similarly to the original version of the FLP, several exact methods have also been proposed to solve small instances of this problem. For example, Holmberg et al. [28] described a matching algorithm incorporated into a Lagrangian heuristic. In another study, Díaz and Fernández [29] developed an exact algorithm that integrates a column generation procedure for finding upper and lower bounds within a branchand-price framework. Similarly, Yang et al. [9] introduced an exact algorithm based on a cut-and-solve framework designed explicitly for the SSCFLP. Regarding the use of approximate methods, Chen and Ting [30] proposed a hybrid algorithm that combines a Lagrangian-based heuristic with an ant colony method. This approach aims to leverage the strengths of both techniques to solve the problem. Ahuja et al. [31] presented a large-scale neighborhood search algorithm, which focuses on efficiently exploring the solution space of the problem. This approach allows large-scale instances to be effectively handled in a reasonable computational time. Filho and Galvão [32] proposed a tabu search metaheuristic that is also able to handle large instances, while Delmaire et al. [33] put forward a more sophisticated algorithm also based on a tabu search, which combines a reactive GRASP algorithm with a tabu search. This algorithm incorporates elements of both techniques to enhance search capabilities and to find high-quality solutions. Finally, Estrada-Moreno et al. [34] presented a biased-randomized iterated local search metaheuristic to solve the SSCFLP with soft capacity constraints. This variant of the SSCFLP assumes that the maximum capacity at each facility can be potentially exceeded by incurring a penalty cost, which increases with the constraint-violation gap. For a more comprehensive literature review on the FLP and its variants, readers are referred to [8, 35], and the book edited by Eiselt and Marianov [36] covers many relevant works on the FLP.

In real life, the inputs of combinatorial optimization problems are typically nondeterministic. This means that they are subject to random events; i.e.., random failures of some components, stockouts due to random demands, etc. Therefore, Simulation-based optimization approaches are required. These methods aim to find a solution that performs well for any possible realization of the random variables, i.e., a robust solution that can handle variations and fluctuations in the problem parameters that may occur in real-world scenarios s [37]. Although the stochastic FLP has not been paid significant attention in the literature, we can find several works, some of which have been published only a few years after the problem’s definition. For example, Balachandran and Jain [38] presented a stochastic FLP model with piece-wise linear production. This model takes demands to be random and continuous variables. Later Correia and Saldanha-da Gama [10] examined distinct modeling frameworks for facility location under uncertain conditions, which specifically distinguish among robust optimization, stochastic programming and chance-constrained models. Another simulation-optimization approach to address this problem is the simheuristics [39], which is a promising approach based on the combination of simulation with metaheuristics, used for solving efficiency different combinatorial optimization problems with stochastic elements. Indeed simheuristics has been used by different authors to solve the UFLP under uncertainty. De Armas et al. [40] proposed a simheuristic approach to address the UFLP with random service costs. This simheuristics combines an ILS metaheuristic with Monte Carlo simulation to deal with uncertainty by providing flexibility to consider diverse optimization objectives beyond minimizing the expected cost. A similar approach is that proposed in Quintero-Araujo et al. [41], which proposes a SimILS framework, a simheuristic algorithm that combines Monte Carlo simulation with a biased-randomized metaheuristic algorithm to solve the capacitated location routing problem (CLRP) with stochastic demands. Another interesting approach i that reported Bayliss and Panadero [42], where a learnheuristic algorithm [43] is presented to solve the temporary-facility location and queuing problem. It integrates a biased randomization algorithm with simulation and a machine-learning component to tackle not only uncertain components, but also dynamics components of problems.

To further extend the landscape of facility location problems under uncertainty, other methodological approaches have emerged in recent years. Marques and Dias [44] introduced a dynamic UFLP by considering uncertainty in fixed and assignment costs, customer and facility locations. They aimed to minimize the expected total cost, while explicitly considering regret. Regret, as a measure of loss for not choosing an optimal scenario solution, is upper-bounded. Their mixed integer programming model and solution approach demonstrates potential through illustrative examples and computational results. Another exciting approach was that proposed by Zhang et al. [45], which tackles another variant, the squared metric two-stage stochastic FLP by focusing on uncertainty in client sets and facility costs with squared metric connection costs. They proposed a new integer linear programming formulation and evaluated two algorithms’ performance by analyzing approximation ratios and per-scenario bounds. Moreover, Ramshani et al. [46] explored disruptions in two-level UFLPs by including additional facilities between customers and the main facilities, and by acknowledging disruptions’ impact on facility reliability for meeting customer demands. They developed mathematical formulations and algorithms, such as a tabu search and a problem-specific heuristic, to address disruptions in a two-level distribution chain scenario. By extending this research, Koca et al. [47] addressed two-stage stochastic UFLPs by emphasizing system nervousness. They introduced models to consider uncertain location and allocation decisions adaptable to realizations of uncertain parameters. Their proposed models incorporated restricted recourse to control deviations between first-stage and scenario-dependent allocation decisions by showcasing Benders-type decomposition algorithms and computational enhancements.

4 Proposed methodology

Simulation methods are frequently employed by experts to address stochastic uncertainty because they enable several scenarios to be analyzed to support decision-making processes. However, it is important to note that simulation itself is not an optimization tool. Therefore, hybrid simulation-optimization methodologies have been proposed to efficiently cope with large-scale optimization problems under uncertainty. One such simulation-optimization method is simheuristics, which combines metaheuristics with simulation [48]. Its efficiency as a method for solving different combinatorial optimization problems with stochastic elements has been shown in several studies [43]. This success can be attributed to the method’s ability to evaluate solutions using simulation and problem-specific analytical expressions. Simheuristic algorithms are ‘white-box’ approaches designed specifically to solve large-scale and NP-hard combinatorial optimization problems with stochastic elements, which can come in the form of stochastic objective functions or probabilistic constraints [49]. The proposed simheuristic method combines a tabu search metaheuristic with path-relinking, which is then integrated with Monte Carlo simulation (MCS) to solve the UFLP with random service costs. Using the tabu search metaheuristic with path-relinking combination allows us to obtain near-optimal solutions to the deterministic version of the problem in short computational times. This combination is successfully employed to solve NP-hard optimization problems in vehicle routing and scheduling domains [50, 51]. The algorithm is further combined with simulation techniques to guide the algorithm during the search for near-optimal solutions to the stochastic version of the problem.

4.1 Tabu search with path-relinking

The algorithm for a tabu search with path-relinking is now described. We represent a state in the tabu search by vector $y_i$ as defined in the model formulation. It is a natural choice seeing that the facility locations are the only combinatorial component. To solve the UFLP, it is enough to know the set of open facilities because customer zones are connected to the cheapest open facilities.

As shown in Algorithm 1, three sections can be identified. The first section applies the tabu search metaheuristic N times to the same problem instance, but uses different seeds. The best solutions are stored in a pool of elite solutions of size L. Subsequently, the path-relinking technique is applied for each pair of elements in the elite solution pool. The new solutions produced to create the next pool of elite solutions are employed (new generation pool). Only those solutions that improve the two used in the path-relinking process are considered the candidates to be inserted into the new generation pool of size L. Note that the best solution found so far is inserted directly into the new generation of elite solutions (1-elitism). The criterion for inserting a new solution into the elite solutions pool is the lowest total cost. The creation of new pools is repeated as long as new generation pools of at least two solutions are produced. After the path-relinking phase, the algorithm begins a local search process around $sol_{best}$. This procedure consists of applying a well-known 2-opt local search to every possible combination of two facility locations in the solution.

Algorithm 1

Tabu search with path-relinking

Algorithm 2

Tabu search

The tabu search is presented in Algorithm 2. First, a random solution is generated to provide each facility location with an opening probability. The neighborhood consists in flipping the state of a facility from open to closed, or vice versa. After scanning the neighborhood, if there is an improvement is calculated. Then the facility location involved in the improvement is added to the tabu list to prevent it from being chosen for a defined number of iterations (tenure). The tabu list is implemented by associating a simple counter tabu[i] for each facility i. When a facility is inserted on the tabu list, the counter tabu[i] is updated by adding the actual iteration count, plus the tenure ($tabu[i] = iteration+tenure$). This expression states that the facility will remain in the tabu search memory for as many iterations as the value of the tenure parameter. The algorithm can quickly check if a facility is on the tabu list if $tabu[i] > iteration$. If there is no improvement in the solution, the algorithm randomly closes a previously open facility location. If only one site remains to be closed, a new one is randomly opened. Tenure is adjusted during the search process. If the algorithm finds improvements in the neighborhood, it decreases tenure to improve exploitation. On the contrary, if it does not find improvements when changing the state of any of the facility locations of a solution, tenure is increased to improve search diversification (never without exceeding a given maximum value). The process is repeated until the stopping criterion is met, which consists in exceeding a number M of iterations without finding an improvement in the solution. The tabu search algorithm uses three different pieces of information for each customer zone j: the number of open facilities that offer the cheapest connection to j, the cost of that connection, and the cost of the second cheapest connection to an open facility. These details allow the gains from opening and closing a facility to be incrementally updated by eliminating the need to compute the entire objective function for a new solution (line 10). A similar approach is used in Michel and Van Hentenryck [24].

Algorithm 3

Path-relinking

The path-relinking subroutine is comprehensively described in Algorithm 3. Given the origin and reference solutions, we first calculate which one gives the best cost and store it in $sol_{best}$. Then cardinality is calculated as the number of differences between the origin and reference solutions. Next, the algorithm starts from $sol_O$ and gradually transforms into $sol_R$ by flipping the facilities that are different between the two solutions. During this transformation process, intermediate solutions are evaluated to see if they improve the overall result. Finally, the best found solution is returned.

The algorithm’s computational complexity is next reported. For the tabu search component, the complexity per iteration is $O(n \cdot log(m))$, where n represents the number of clients and m denotes the number of facilities. This complexity accounts for the calculation of the cost of flipping each facility in a solution, while tracking the best and second-best facilities to assign clients to. These operations are repeated until a number of failed runs is reached, which contributes to the constant factor of the computational complexity. In other words, as the number of iterations is constant (not dependent on the size of the problem), the overall computational complexity of the tabu search component is expressed as $O(n \cdot log(m))$. The path-relinking component has a similar complexity per iteration of $O(n \cdot log(m))$. This also involves updates to the best and second-best facilities assigned to clients, because intermediate solutions have to be evaluated to see if they improve current solutions. Similar to the tabu search component, the actual number of iterations performed by the path-relinking component depends on the cardinality of solutions along with the number of elite generations, which are not dependent on the size of the instance. Thus, the overall computational complexity of the path-relinking component is $O(n \cdot log(m))$. The local search component, the computational complexity per iteration is associated with the process of exploring the neighborhood of the current solution. This involves flipping each facility in the solution and checking if the new solution is improved, whose computational complexity is $O(n \cdot log(m))$. This process is repeated until no further improvements are found, so the overall computational complexity of the local search is $O(n \cdot log(m))$. Finally, as the three components discussed are executed in a serial manner, we can conclude the proposed algorithm has a worst-case computational complexity of $O(n \cdot log(m))$.

Fig. 2

Flowchart of the simheuristic methodology

4.2 The simheuristic framework

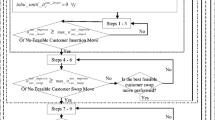
Figure 2 illustrates a flow chart of our simheuristic methodology for dealing with the UFLP under stochastic uncertainty. Every time a new solution is generated by the tabu search, path-relinking or a local search, it is simulated with a few runs to obtain an estimate of the solution’s average stochastic cost. On the one hand, regarding the tabu search, all the N times when the algorithm reaches the stopping criterion and finds the best solution (Algorithm 1), the fast simulation is run. On the other hand, the simulations of the path-relinking solutions are the most important in the proposed simheuristic. Path-relinking as an intensive process done on a set of elite solutions allows a sufficiently large set of potential solutions to be explored that could perform well in a stochastic environment. For this reason, every time a new solution is generated during the gradual transformation of $sol_O$ into $sol_R$, it is simulated regardless of whether it improves the deterministic solution. In addition, whenever the local search procedure reaches a new improved solution, this is also simulated. The solutions with the best-estimated cost are stored in a pool of elite stochastic solutions. Once an overall stopping criterion is met, a limited set of elite stochastic solutions is sent to a more intensive simulation stage to obtain accurate estimates on their behavior in a stochastic scenario. The general stopping criterion consists of satisfying the stopping criteria of each section of the proposed metaheuristic (M failed tabu search runs, a new pool generation with < than 2 solutions during path-relinking and no new improvements during the local search).

Algorithm 4 depicts the main characteristics of our simheuristic algorithm. The code is similar to that shown in Algorithm 1. The solutions obtained by the tabu search are quickly simulated, while those with the lowest expected cost are included in the pool of elite stochastic solutions (lines 13-17). Then when the path-relinking (PR-SIMH) and local search (LS-SIMH) functions are called, the pool is passed as an argument to be updated according to the simulations of the newly generated solutions (as explained above). In lines 34-38, intensive simulation is performed to obtain better estimates of the elite solutions. The best solutions are selected according to the lowest expected cost. However, other estimates, such as risk or reliability, may also be used as discussed in Chica et al. [52].

Algorithm 4

Simheuristic for the UFLP

5 Computational study

Several computational experiments were carried out to evaluate and assess the performance of our solving method. To comprehensively illustrate the experiments conducted in this section, a detailed presentation of the utilized benchmark instances, that outlines their characteristics, is first provided. Next the presented benchmark instances are extended to consider random service costs, which model the uncertainty that is inherent in practical scenarios, and penalty costs, by addressing several real-world situations. Then Section 5.4 identifies the significantly affected parameters and decides the optimal parameter settings for the algorithm through the Design of Experiments (DoE). Last, the obtained results and the discussion are presented in Section 5.5. All the numerical experiments were implemented using the C++ programming language. The code was compiled on a Manjaro Linux machine with the GCC version 12.3 compiler and executed on a computer with an Intel Core i5-9600K 3.7 GHz and 16 GB RAM.

5.1 Description of benchmark instances

In order to evaluate the performance of the proposed simheuristic algorithm for the UFLP with random service costs, we used the classic instances originally proposed for the p-median problem by Ahn et al. [53], later employed in the UFLP context by Barahona and Chudak [54]. This set of large instances is called MED, which is the most used set of instances in the UFLP literature for being the most challenging ones to solve. To the best of our knowledge, the results of these instances have not been improved from 2006 [25]. This makes them the perfect benchmarks to test the quality of our algorithm. Each instance is composed of a set of n points picked uniformly at random in the unit square. A point represents both a user and facility, and the corresponding Euclidean distance determines service costs. Additionally, each instance is characterized by the following nomenclature $x - y$, where x represents the number of facilities and customers, while y refers to the opening cost scheme. The set of instances consists of six different subsets, each with a different number of facilities and customers (500, 1000, 1500, 2000, 2500 and 3000), and three different opening cost schemes per subset ($\sqrt{n}/10$, $\sqrt{n}/100$, and $\sqrt{n}/1000$ corresponding to 10, 100, and 1000 instance suffixes, respectively). The larger instances and those with suffix 1000 are the most difficult to solve. As they have lower opening costs, the number of open facilities in the solution is bigger, which increases the number of possible combinations and, thus, the complexity of finding the optimal solution.

5.2 Extending benchmark to address uncertainty

To the best of our knowledge, there are no stochastic FLP instances that employ random service costs to be used as a benchmark. So instead of assuming constant service costs $c_{ij}$ ($\forall i\in I, \forall j\in J$), we consider a more realistic scenario in which service costs are modeled as random variables $C_{ij}$. The service cost represents the cost required to service a customer zone $j \in J$ throughout a facility location $i \in I$ under perfect conditions. Accordingly, we extend the previously described set of instances called MED to assess both the performance and quality of the proposed simheuristic algorithm. The dataset construction process involves transforming the deterministic service costs into random service costs following a probability distribution function. Specifically, the deterministic service costs are transformed into stochastic ones when solutions are sent to the simulation phase. Hence the service costs $c_{ij}$ found in instances are used as the expected values of the random service costs $C_{ij}$, which are modeled to follow a log-normal probability distribution. The log-normal distribution is a natural choice for describing nonnegative random variables, such as service costs [55]. The log-normal distribution has two parameters: the location parameter, $\mu _{ij}$, and the scale parameter, $\sigma _{ij}$, which relate to the expected value $E[C_{ij}]$ and to variance $Var[C_{ij}]$, respectively. Equations 7-8 define how these parameters have been modeled. We assume service cost $C_{ij} \sim LogNormal(\mu _{ij}, \sigma _{ij})$ with $E[C_{ij}] = c_{ij}$, where $c_{ij}$ is the deterministic service delay found in instances, and variance $Var[C_{ij}] = k \cdot E[C_{ij}]$. Parameter k is a design parameter that allows us to set up the uncertainty level. It determines how much stochastic costs deviate from their expected values ($c_{ij}$ derived from deterministic costs) and, therefore, influences the degree of randomness or uncertainty in the simulated costs. So as k converges to zero, the more the results will move toward the deterministic state, and by increasing the value of k, the results will converge to the stochastic state. The selection of k values depends on the uncertainty level desired in stochastic costs. We consider three different uncertainty levels: low ($k = 5$), medium ($k = 10$) and high ($k = 20$). The main objective of setting different k values is to simulate a range of real-world scenarios for the variability and unpredictability of service costs. By employing multiple k values, the algorithm’s performance can be evaluated under diverse conditions, which allows for a comprehensive assessment of its robustness and adaptability to varying cost uncertainty levels.

$$\begin{aligned} \mu _{ij}&= ln(E[C_{ij}]) - \frac{1}{2} \cdot ln \left( 1 + \frac{Var[C_{ij}]}{E[C_{ij}]^2}\right) \end{aligned}$$

(7)

$$\begin{aligned} \sigma _{ij}&= \left| \sqrt{ln\left( 1 + \frac{Var[C_{ij}]}{E[C_{ij}]^2}\right) } \right| \end{aligned}$$

(8)

This approach enables us to test the effectiveness of our simheuristic algorithm in handling UFLP instances with varying uncertainty levels, and to showcase its adaptability at different degrees of random service costs without having to create brand-new datasets.

5.3 Extend benchmark with penalty costs

In order to address real-world situations where certain facilities’ costs need to be controlled or limited, a nonlinear penalty cost is added. This approach aligns the optimization process with practical considerations and allows decision makers to make more informed choices regarding facility selection and cost management. Note in the basic UFLP under uncertainty with a linear objective function that the solution which minimizes the total expected cost will be the same as the optimal solution for the deterministic UFLP. This property will not hold if, for instance, a nonlinear penalty cost is added in the objective function to account for facilities with a total higher service cost than a threshold, etc. Thus we introduce a non linear penalty cost that is twice the cost of opening a facility if the instance maximum service cost of a deterministic solution is exceeded. This parameter, denoted as $c_{\text {max}} = \max {c_{ij}}$, represents the maximum $c_{ij}$ value between all the facilities opened in the best-found deterministic solution. It is worth noting that when this nonlinear penalty is incorporated into the objective function of the UFLP under uncertainty, the solution that minimizes the total expected cost may no longer be the same as the optimal solution for the deterministic UFLP. This deviation from linearity arises because the penalty cost is included. In other words, the best-known deterministic solution, which will still be optimal in a deterministic scenario for not being affected by the $c_{\text {max}}$ threshold, will perform quite poorly in a stochastic scenario because in many simulation runs there will be service costs that will exceed the $c_{\text {max}}$ threshold, which will result in a severe penalty. Furthermore, the simheuristic algorithm tends to open some more facilities than those in the deterministic solution to avoid the number of times that the threshold is exceeded. Therefore, the simheuristic approach aims to search for solutions that mitigate the impact of penalties associated with exceeding the $c_{\text {max}}$ threshold in multiple simulation runs.

5.4 Parameter analysis by design of experiments

In this section, we use DoE to identify the significantly affected parameters and decide the best combination of each parameter for the TS+PR algorithm. As shown in Table 1, a two-level full factorial design with three replications [56] is adopted to investigate the significant effect of four parameters of the TS+PR algorithm on both the objective value and the calculation time. The following parameters are considered: N (maximum runs of the algorithm with different seeds), M (maximum number of the tabu iterations without improvement), L (elite pool length) and Tenure (number of iterations a move is considered to be tabu, expressed as a percentage of the number of facility locations of the problem). The high and low levels of each parameter are displayed in Fig. 4.

Table 1 Results of the experiment

Table 2 Analysis of variance for AVG GAP (%)

The results are shown in Table 1 for a randomly generated test problem of size ($|I| = |J|=2000$). The problem was created following the same structure as the large instances called MED. The selected opening cost scheme was $\sqrt{n}/1000$ because, as previously mentioned, it is the most challenging. The response variable AVG GAP (%) is the average gap of 30 different independent runs compared to the optimal solution obtained with Gurobi for the generated test problem. The response variable AVG TIME is the average execution time for the 30 independent runs. In all, 3 * $2^{4}$ * 30 = 1440 trials were conducted in this experiment. Table 1 shows the average (best) values for the 30 runs and displays 48 trials.

Fig. 3

Pareto chart for AVG GAP(%)

Fig. 4

Main effect plot for AVG GAP(%)

According to the ANOVA results (Table 2) and the Pareto chart (Fig. 3) for the response AVG GAP (%), only parameters M and L are statistically significant for the proposed problem. The values RSquare = 92.21%, RSquare(Adj) = 88.19%, and Square(Pred) = 81.33% obtained in Statgraphics mean that this model fits the data well and can be used to accordingly determine the suitable parameters (Fig. 4).

For the response AVG TIME (see Fig. 5), all the parameters except Tenure are the algorithm’s most significant and critical parameters at $\alpha = 0.05$. The model fits the data very well (RSquare = 99.25%, RSquare(Adj) = 98.86%, and Square(Pred) = 98.20%).

Fig. 5

Pareto chart for AVG TIME(s)

Fig. 6

Main effect plot for AVG TIME(s)

To find the best parameters for the algorithm, we focus mainly on the response AVG GAP (%). The best parameter settings on N, M, L and Tenure, according to AVG GAP(%), are 64, 500, 10 and 10%, respectively (see Fig. 4). Although M and L prolong the computation time (see Fig. 6), they are statistically significant and their higher values are necessary. Coosing a value of 64 vs. 32 for N negatively affects the execution time (it increases by more than 40%) and is not statistically significant. Furthermore, the best gap for $N=64$ is 0.02% and 0.03% for $N=32$, a minimal difference for the longer computational time required. Finally, Tenure does not statistically affect either AVG GAP or AVG TIME. As explained previously, the reason lies in the algorithm’s capacity to adjust the tenure value as the search progresses. So it does not affect starting with a slightly higher or lower value.

Table 3 Parameter setting

The main objective of this paper is not to obtain the best possible solutions in the deterministic environment. So we explore the possibility of considering $N=64$ and of even analyzing the results of larger values for the most significant factors, such as M and L. This paper focuses on uncertain conditions using a simulation optimization approach, such as the simheuristics concept. For this reason, having a good deterministic search algorithm (i.e. 0.03% gap) with reasonable computation times is sufficient. In this way, the algorithm can be efficiently combined with Monte Carlo simulations to search for the best solutions under uncertainty. For all these reasons, the values chosen for the adjustment of the TS+PR algorithm, used later within the simheuristic framework, are $N = 32, M = 1000, L = 10$ and $Tenure = 10\%$.

Three more parameters are defined by applying the simheuristic approach described in Algorithm 2, which are longSim, shortSim and L2. The first parameter is defined as being large enough to have a full, meaningful simulation of a solution under stochastic uncertainty. The second parameter attempts to quickly evaluate a solution in an uncertain environment to guide the search for better ones. The last parameter consists of a pool of elite solutions (quickly evaluated) to be finally validated in the complete simulation. This pool is ordered from the best to the worst result of the fast simulation. A solution in a lower position may obtain a better result in the long simulation than another in a higher initial position. For this reason, pool size must be large enough to capture the best possible solution in the global simulation. The exploratory studies indicate that the best final solution after the full simulation appears before the first five positions of the elite pool. To ensure that the best solution is obtained in the complete simulation, a value higher than five is finally chosen.

Table 3 summarizes all the parameters and the values selected for the following computational experiments applied to the benchmark instances described in the previous points (Table 4).

5.5 Results and discussion

Table 5 includes the results obtained for four different approaches to solve the UFLP with the MED benchmark instances. The first column displays instances, whose names are combinations of the number of demand points and the opening cost scheme. The next two columns show the solutions obtained using the Gurobi Optimizer solver, along with the corresponding computational time required to reach those solutions. The subsequent three columns present the best-found solutions obtained from our tabu search with the path-relinking approach, along with the computational time needed to obtain them. Each instance is run 30 times using a different seed for the random number generator, and the best and average results are reported. Furthermore, the three columns that follow depict the best-found solutions achieved using the multi-start heuristic proposed by Resende and Werneck [25], along with the computational time required for each solution. The next three columns illustrate the best-found solutions obtained with the ILS-based approach proposed by De Armas et al. [40], along with the computational time taken to achieve those results. Finally, the last three columns display the best-found solutions obtained using the multi-wave algorithm approach by Glover et al. [57], plus the computational time taken to reach these solutions. To deal with the different CPU performance times for each previous method found in the literature, the results can be refactored in time using the performance characteristics of the employed CPUs. We used the tables published on specialized websites; i.e., http://www.techarp.com and https://www.userbenchmark.com, which evaluate CPU performance, to complete the conversion and normalisation for fair results. Based on the PLUS column, in Table 4 we include the number of times that our computer was faster than each computer used in the literature. It should be noted that it was not possible to normalize the times reported in Resende and Werneck [25] due to lack of comparative information and the difficulty of the conversion process when employing a CPU with a different architecture (RISC). However, it is reasonable to assume that the normalized times of their work would be very competitive.

Table 4 Performance measures between different computers used in the literature to evaluate MED instances of the UFLP

Table 5 Comparison of different approaches to solve the UFLP

Table 6 presents the results obtained for the uncertainty levels considered using the MED benchmark instances. Each instance was run 10 times using our simheuristic algorithm with different seeds for the random number generator, and the best results are reported. The first column identifies the instances, while the following three display the results obtained by our approach for the deterministic UFLP. First, the column labeled BKS reports the best-known solutions provided by the Gurobi Optimizer solver, along with our best-found deterministic solutions labeled OBD. We also calculate the percentage gaps of the best-found deterministic solutions compared to the best-known solutions. The remaining columns showcase the results obtained for three different uncertainty levels. In the second section of the table, we report the results obtained for the low uncertainty level. The OBD-S column displays the expected cost obtained when evaluating the best deterministic solution (OBD) in a stochastic scenario with a low uncertainty level. To compute the expected cost, an intensive simulation process is applied to the OBD. This process aims to assess the quality of our best-found deterministic solutions at varying uncertainty levels. The next column (OBS) shows the expected cost obtained using our simheuristic approach for the stochastic version of the problem. This approach considers the random service costs during the solution search. The subsequent section of the table presents the results for the medium uncertainty level. In the OBD-S column, we report the expected cost obtained when evaluating the best deterministic solution (OBD) in a stochastic scenario with medium uncertainty. Similarly, the next column (OBS) displays the expected cost obtained using our simheuristic algorithm. Finally, the last section of the table exhibits the results for the high uncertainty level. The OBD-S column shows the expected cost obtained when evaluating the best deterministic solution (OBD) in a stochastic scenario with high uncertainty. The last column (OBS) displays the expected cost obtained with our simheuristic approach.

Table 6 Computational results of the different uncertainty levels

Table 7 Additional details of the computational results

For the sake of completeness, Table 7 covers the additional details of the computational results omitted in Table 6. The first column identifies the instances, while the following four columns display the facilities open cost, the related nonlinear penalty cost, the threshold defined as the instance maximum service cost and the number of open facilities of the best-found solution, respectively. The remaining columns showcase the percentage gaps obtained for three different uncertainty levels, along with the number of open facilities of the best-found stochastic solutions. In the second section of the table, we report the results obtained for the low uncertainty level. The OBD-S GAP (%) column displays the percentage gap obtained when comparing the best deterministic solutions simulated in a low uncertainty scenario with the best-known solutions (BKS). The next column (OBS GAP (%)) shows the percentage gap obtained when comparing our simheuristic approach. The subsequent column (OPEN) presents the number of open facilities of the best-found stochastic solution. The subsequent section of the table offers the results for the medium uncertainty level. In the OBD-S GAP (%) column, we report the percentage gap obtained when comparing the best deterministic solution at a medium uncertainty level to the best-known solutions (BKS). The next column (OBS (%)) displays the percentage gap obtained using our simheuristic algorithm. Moreover, the subsequent column (OPEN) presents the number of open facilities of the best-found stochastic solution. Finally, the last section of the table exhibits the results for the high uncertainty level. The OBD-S GAP (%) column depicts the percentage gap obtained when comparing the best deterministic solution at a high uncertainty level. The next column (OBS GAP (%)) displays the percentage gap obtained using our simheuristic algorithm. The last column (OPEN) displays the number of open facilities of the best-found stochastic solution.

Fig. 7

Gaps of $\sqrt{n}/10$ opening cost scheme instances w.r.t the BKS

Fig. 8

Gaps of $\sqrt{n}/100$ opening cost scheme instances w.r.t the BKS

Fig. 9

Gaps of $\sqrt{n}/1000$ opening cost scheme instances w.r.t the BKS

Figures 7, 8 and 9 depict an overview of Table 6 by showing our algorithm’s performance for all the considered uncertainty levels. In these box plots, the horizontal and vertical axes represent the three uncertainty levels and the percentage gap obtained in relation to the BKS reported by the Gurobi Optimization solver, respectively. Note for the deterministic version of the UFLP, that our tabu search with the path re-linking approach nearly reaches the BKS for the $\sqrt{n}/10$, $\sqrt{n}/100$, and $\sqrt{n}/1000$ opening cost schemes, with a gap of approximately $0.00\%$, $0.03\%$, and $0.04\%$, respectively. These results highlight the quality of our algorithm because our approach provides highly competitive solutions. Regarding the stochastic version of the UFLP, which is the main contribution of this paper, the obtained results show that the solutions provided by our heuristic approach for the three different uncertainty levels clearly outperform the solutions for the deterministic UFLP when they are simulated at the corresponding uncertainty level. In other words, our best-found solutions for the deterministic version of the problem (OBD) might be suboptimal when uncertainty is considered. Hence the importance of integrating simulation methods when dealing with optimization problems with uncertainty. Note also that the OBD can be seen as a reference lower bound in an ideal scenario with perfect information (i.e., without uncertainty) for the expected cost under uncertainty conditions. Similarly, OBD-S can be seen as an upper bound for the expected cost at the different uncertainty levels. As expected, the gaps for all three opening cost schemes worsen as the uncertainty level of k increases. For the specific case of the $\sqrt{n}/10$ opening cost scheme, gaps increase more than for others. As shown in Table 7, this is because the penalty cost (opening cost) is higher in this case. The penalty amounts to 3-5% of the total costs, but is less than 1.5% for the $\sqrt{n}/100$ opening cost scheme and less than 0.5% for the remaining one. In addition, the number of open facilities is much smaller. These are cases in which a few facilities with high capacity serve many customers. The average number of open facilities for this opening cost scheme is around 18 in the best-found deterministic solutions, but rises to over 430 for the instances with suffix 1000. In this high opening cost scheme, where there are few viable facilities to open and with a high cost penalty, the OBD-S result is that which obtains the worst values on average, with a gap of 8.99%, 15.42% and 30.56% for all three uncertainty levels. In this environment, our simheuristic approach is able to achieve a 3 to 5 times better improvement (1.81%, 3.80%, and 10.71%). For the remaining cases (suffixes 100 and 1000) where the penalty costs are lower and the number of open installations is bigger, and the gaps shown in Table 7 and Figs. 7, 8 and 9 are smaller. It is not surprising that the OBD solutions better perform under uncertainty when the penalty cost is lower. Our OBS solutions improve the deterministic model’s performance for all the different k uncertainty levels, and also for all the opening cost schemes, which demonstrates the validity of the proposed approach.

When taking everything into account, the findings validate the significance of factoring in uncertainty while searching for a solution because it can greatly affect the quality of our best-found solutions. For instance, when our best deterministic solution is simulated in a stochastic scenario, it yields a much higher expected cost. Conversely, our best-found stochastic solution (OBS) provides a lower expected cost. Therefore, incorporating uncertainty aspects during the search process produces better results than when simulating uncertainty elements after finding a solution for the deterministic version of the problem.

6 Conclusions

In this paper, we analyze the UFLP under uncertainty, which occurs in several real-life systems. This uncertainty arises when inputs, such as customer demands or service costs, are random variables instead of deterministic values. To solve this optimization problem, we propose a novel solving methodology that combines a tabu search metaheuristic with path-relinking. The proposed algorithm is tested on the largest instances from the literature because they are the most challenging ones. The results show that our approach is capable of obtaining near-optimal solutions in short computational times. Additionally, the results are compared to the BKS from the literature, along with other competitive approaches, to validate our algorithm’s effectiveness in the deterministic scenario. Then the algorithm is converted into a simheuristic by integrating it with a simulation component to solve the UFLP with random service costs. The log-normal probability distribution is employed to model the random service costs. The obtained results show our simheuristic approach outperforms the simulated deterministic solutions when uncertainty is considered. Thus our simheuristic approach constitutes a general methodology that can be employed to efficiently solve several FLP variants under uncertainty.

One of the limitations of the present work is that it considers only uncertainty of a stochastic nature. Thus extending the simheuristic algorithm to address the UFLP in a more general setting, including stochastic and nonstochastic uncertainty elements like type-2 fuzzy systems [58] and rough sets [59], is a future research line. Another limitation is that simulations are performed on a single CPU core. As a future research line, it would be interesting to consider a parallel version of the simheuristic algorithm to obtain optimal solutions in an even shorter time, which may allow fast decision making in time-sensitive scenarios. Finally, another possible extension for this paper is to develop a similar combination of a tabu search metaheuristic with a path-relinking simheuristic to obtain near-optimal solutions in short computational times for other optimization problems under uncertainty, for example, vehicle routing problems, arc routing problems and scheduling problems.