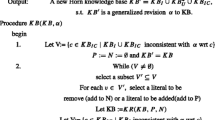Abstract
The dynamics of belief and knowledge is one of the major components of any autonomous system that should be able to incorporate new pieces of information. In order to apply the rationality result of belief dynamics theory to various practical problems, it should be generalized in two respects: first it should allow a certain part of belief to be declared as immutable; and second, the belief state need not be deductively closed. Such a generalization of belief dynamics, referred to as base dynamics, is presented in this paper, along with the concept of a generalized revision algorithm for knowledge bases (Horn or Horn logic with stratified negation). We show that knowledge base dynamics has an interesting connection with kernel change via hitting set and abduction. In this paper, we show how techniques from disjunctive logic programming can be used for efficient (deductive) database updates. The key idea is to transform the given database together with the update request into a disjunctive (datalog) logic program and apply disjunctive techniques (such as minimal model reasoning) to solve the original update problem. The approach extends and integrates standard techniques for efficient query answering and integrity checking. The generation of a hitting set is carried out through a hyper tableaux calculus and magic set that is focused on the goal of minimality.
Similar content being viewed by others
Notes
A ground instantiation of a definite program P is the set of clauses obtained by substituting terms in the Herbrand Universe for variables in P in all possible ways.
References
Alchourron CE et al (1985) On the logic of theory change: partial meet contraction and revision functions. J Symb Log 50:510–530
Aliseda A (2006) Abductive resoning logic investigations into discovery and explanation, vol 330. Springer Book Series
Aravindan C, Dung PM (1994) Belief dynamics, abduction, and database. JELIA:66–85
Aravindan C (1995) Dynamics of belief: epistmology, abduction and database update. Phd Thesis, AIT
Aravindan C, Baumgartner P (1997) A rational and efficient algorithm for view deletion in databases. ILPS:165–179
Baumgartner P et al (1997) Semantically guided theorem proving for diagnosis applications. IJCAI 1:460–465
Behrend A, Manthey R (2008) A transformation-based approach to view updating in stratifiable deductive databases. FoIKS:253–271
Bessant B et al (1998) Combining nonmonotonic reasoning and belief revision: a practical approach. AIMSA:115–128
Biskup J (2012) Inference-usability confinement by maintaining inference-proof views of an information system. IJCSE 7(1):17–37
Caroprese L et al (2012) The view-update problem for indefinite databases. JELIA:134–146
Calvanese D et al (2012) View-based query answering in description logics semantics and complexity. J Comput Syst Sci 78(1):26–46
Chen H, Liao H (2010) A comparative study of view update problem. DSDE:83–89
Christiansen H, Dahl V (2009) Abductive logic grammars. WoLLIC:170–181
Cong G et al (2012) On the complexity of view update analysis and its application to annotation propagation. IEEE Trans Knowl Data Eng 24(3):506–519
Delgrande JP, Peppas P (2011) Revising horn theories. IJCAI:839–844
Delhibabu R, Lakemeyer G (2013) A rational and efficient algorithm for view revision in databases. Appl Math Inf Sci 7:843–856
Delhibabu R (2014) An abductive framework for knowledge base dynamics. Appl Math Inf Sci (accepted)
Delhibabu R (2014) Comparative study of view update algorithms in rational choice theory. Appl Intell. doi:10.1007/s10489-014-0580-7 10.1007/s10489-014-0580-7
Eiter T, Makino K (2007) On computing all abductive explanations from a propositional Horn theory. J ACM 54(5):54
Falappa MA et al (2012) Prioritized and non-prioritized multiple change on belief bases. J Philos Log 41(1):77–113
Ferme EL, Hansson SO (2011) AGM 25 years - twenty-five years of research in belief change. J Philos Log 40(2):295–331
Hansson SO (1991) Belief contraction without recovery. Studia Logic 50(2):251–260
Hansson SO (1997) A textbook of belief dynamics. Kluwer Academic Publishers, Dordrecht
Herzig A, Rifi O (1999) Propositional belief base update and minimal change. Artif Intell 115(1):107–138
Jackson EK, Schulte W (2008) Model generation for Horn logic with stratified negation. FORTE:1–20
Keller A (1985) Updating relational databases through views. Phd Thesis
Kogalovsky MR (2012) Ontology-based data access systems. Programm Comput Softw 38(4):167–182
Konieczny S (2011) Dynamics of beliefs. SUM:61–74
Lakemeyer G (1995) A logical account of relevance. IJCAI 1:853–861
Langlois M et al (2008) Horn complements: towards Horn-to-Horn belief revision. AAAI:466–471
Laurent D et al (1998) Updating intensional predicates in deductive databases. Data Knowl Eng 26(1):37–70
Liberatore P (1997) The complexity of belief update (extended in 2003). IJCAI 1:68–73
Liberatore P, Schaerf M (2004) The compactness of belief revision and update operators. Fundam Inform 62(3–4):377–393
Lobo J, Trajcevski G (1997) Minimal and consistent evolution of knowledge bases. J Appl Non-Class Log 7(1):117–146
Lu W (1999) View updates in disjunctive deductive databases based on SLD-resolution. KRDB:31–35
Makinson D (1997) Screened revision. Theoria 63:14–23
Mayol E, Teniente E (1999) A survey of current methods for integrity constraint maintenance and view updating. ER (Workshops):62–73
Mota-Herranz L et al (2000) Transaction trees for knowledge revision. FQAS:182–191
Nayak A et al (2006) Forgetting and knowledge update. Aust Conf Artif Intell:131–140
Nayak A (2011) Is revision a special kind of update? Aust Conf Artif Intell:432–441
Nebel B (1998) How hard is it to revise a belief base? Handb Defeasible Reas Uncertain Manag Syst:77–145
Papini O (2000) Knowledge-base revision. Knowl Eng Rev 15(4):339–370
Qi G, Yang F (2008) A survey of revision approaches in description logics. Description Logics
Sakama C, Inoue K (2003) An abductive framework for computing knowledge base updates. TPLP 3(6):671–713
Schulte O (1999) Minimal belief change and Pareto-optimality. Aust Joint Conf Artif Intell:144–155
Segerberg K (1998) Irrevocable belief revision in dynamic doxastic logic. Notre Dame J Formal Log 39(3):287–306
Teniente E, Urpí T (2003) On the abductive or deductive nature of database schema validation and update processing problems. TPLP 3(3):287–327
Wrobel S (1995) First order theory refinement. IOS Frontier in AI and Application Series
Acknowledgments
The author acknowledges the support of RWTH Aachen, where he is visiting scholar with an Erasmus Mundus External Cooperation Window India4EU by the European Commission when the paper was written. I would like to thanks Chandrabose Aravindan and Gerhard Lakemeyer both my Indian and Germany PhD supervisor, give encourage to write the paper.
Author information
Authors and Affiliations
Corresponding author
Appendix:
Appendix:
Proof of Theorem 1
Follows from Algorithm 1 and 2. □
Proof of Theorem 2
Follows from the result of [7] □
Proof of Lemma 1
Follows from the result of [5] □
Proof of Lemma 2 and 5
-
1.
Consider a \({\Delta } ({\Delta }\in {\Delta }_{i} \cup {\Delta }_{j})\in S\). We need to show that Δ is generated by algorithm 3 at step 2. It is clear that there exists a A-kernel X of D D B G s.t. \(X \cap EDB = {\Delta }_{j}\) and \(X \cup EDB = {\Delta }_{i}\). Since \(X \vdash A\), there must exist a successful derivation for A using only the elements of X as input clauses and similarly \(X \nvdash A\). Consequently Δ must have been constructed at step 2.
-
2.
Consider a \({\Delta }^{\prime }(({\Delta }^{\prime }\in {\Delta }_{i} \cup {\Delta }_{j})\in S^{\prime }\). Let \({\Delta }^{\prime }\) be constructed from a successful(unsuccessful) branch i via Δ i (Δ j ). Let X be the set of all input clauses used in the refutation i. Clearly \(X\vdash A\)(\(X\nvdash A\)). Further, there exists a minimal (wrt set-inclusion) subset Y of X that derives A (i.e., no proper subset of Y derives A). Let \({\Delta } = Y \cap EDB\) (\(Y \cup EDB\)). Since IDB does not(does) have any unit clauses, Y must contain some EDB facts, and so Δ is not empty (empty) and obviously \({\Delta }\subseteq {\Delta }^{\prime }\). But, Y need not (need) be a A-kernel for I D B G since Y is not ground in general. But it stands for several A-kernels with the same (different) EDB facts Δ in them. Thus, from lemma 1, Δ is a DDB-closed locally minimal abductive explanation for A wrt I D B G and is contained in \({\Delta }^{\prime }\).
□
Proof of Lemma 3 and 6
-
1.
(Only if part) Suppose H is a minimal hitting set for S. Since \(S \subseteq S^{\prime }\), it follows that \(H \subseteq \bigcup S^{\prime }\). Further, H hits every element of \(S^{\prime }\), which is evident from the fact that every element of \(S^{\prime }\) contains an element of S. Hence H is a hitting set for \(S^{\prime }\). By the same arguments, it is not difficult to see that H is minimal for \(S^{\prime }\) too.
(If part) Given that H is a minimal hitting set for \(S^{\prime }\), we have to show that it is a minimal hitting set for S too. Assume that there is an element E ∈ H that is not in \(\bigcup S\). This means that E is selected from some \(Y \in S^{\prime }\backslash S\). But Y contains an element of S, say X. Since X is also a member of \(S^{\prime }\), one member of X must appear in H. This implies that two elements have been selected from Y and hence H is not minimal. This is a contradiction and hence \(H \subseteq \bigcup S\). Since \(S \subseteq S^{\prime }\), it is clear that H hits every element in S, and so H is a hitting set for S. It remains to be shown that H is minimal. Assume the contrary, that a proper subset \(H^{\prime }\) of H is a hitting set for S. Then from the proof of the only if part, it follows that \(H^{\prime }\) is a hitting set for \(S^{\prime }\) too, and contradicts the fact that H is a minimal hitting set for \(S^{\prime }\). Hence, H must be a minimal hitting set for S.
-
2.
(If part) Given that H is a hitting set for \(S^{\prime }\), we have to show that it is a hitting set for S too. First of all, observe that \(\bigcup S = \bigcup S^{\prime }\), and so \(H \subseteq \bigcup S\). Moreover, by definition, for every non-empty member X of \(S^{\prime }\), \(H \cap X\) is not empty. Since \(S \subseteq S^{\prime }\), it follows that H is a hitting set for S too.
(Only if part) Suppose H is a hitting set for S. As observed above, \(H \subseteq \bigcup S^{\prime }\). By definition, for every non-empty member X ∈ S, \(X \cap H\) is not empty. Since every member of \(S^{\prime }\) contains a member of S, it is clear that H hits every member of \(S^{\prime }\), and hence a hitting set for \(S^{\prime }\).
□
Proof of Lemma 4 and 7
Follows from the lemma 2,3 (minimal test) and 5,6 (materialized view) of [7] □
Proof of Theorem 3
Follows from Lemma 4 and Theorem 1. □
Proof of Theorem 4
Follows from Lemma 7 and Theorem 3. □
Rights and permissions
About this article
Cite this article
Delhibabu, R., Behrend, A. A new rational algorithm for view updating in relational databases. Appl Intell 42, 466–480 (2015). https://doi.org/10.1007/s10489-014-0579-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10489-014-0579-0